-
通过共振探测一个系统的内部结构和相互作用是物理学研究的常用手段。作为一个复杂的自束缚体系,原子核的共振激发也吸引了核物理研究的极大兴趣。通过共振态的研究可以探测原子核内部的核结构信息,如壳演化、形变等,还能为天体核合成提供重要的输入量,如16O的低能激发态会影响被称为核天体物理的“圣杯反应”的12C(α, γ)16O的反应截面,原子核的低能矮偶极共振(Pygmy Dipole Resonance)对快中子俘获(r-)过程的中子俘获率有重要影响[1−2],电荷交换的低能共振态决定的β衰变是r-过程中把铁元素推向重元素的重要机制[3−4]。此外,同位旋标量巨单极共振的激发能与无限核物质的不可压缩系数$ K_\infty $紧密关联[5],后者对中子星物理和超新星核心坍缩有重要影响。
在众多的微观核理论模型中,密度泛函理论基于有效核子-核子相互作用能对几乎全核素图的原子核的基态和激发态性质进行描述。狭义的密度泛函理论(即平均场理论)只考虑占据态之间的相互作用,能对原子核的基态性质包括结合能、电荷半径等进行成功描述[6]。但对于原子核的共振态,仅靠平均场理论无法准确计算巨共振的强度和激发能,需要在此基础上对强度分布进行展宽[7]。巨共振的总宽度主要来自三方面的贡献[8],可以写为
$$ \begin{array}{*{20}{l}} \varGamma_{{\mathrm{tot}}}\simeq\varGamma_{{\mathrm{fr}}}+\varGamma^{\uparrow}+\varGamma^{\downarrow}, \end{array} $$ (1) 其中:$ \varGamma_{{\mathrm{fr}}} $来自1粒子1空穴(1p-1h)的碎裂效应,该效应可以使用无规相近似(RPA)模型计算;$ \varGamma^{\uparrow} $是由于1p-1h组态和连续谱的关联,计算该效应需要使用考虑连续谱的连续无规相近似(CRPA)模型[9−10];而贡献最大的$ \varGamma^{\downarrow} $则来源于1p-1h 组态和更高阶组态(2p-2h, 3p-3h, ···)的混合,密度泛函理论中,目前只有自洽考虑2p-2h组态的二阶无规相近似(SRPA)。
早在20世纪80年代初,Bertsch等[11]就用微扰的方式研究了2p-2h组态混合对GT跃迁的显著效应,1988年在文献[12]中实现了包含2p-2h关联的SRPA计算,并将该计算应用于磁跃迁的研究中[13]。但由于SRPA需要巨大的算力,受限于当时的计算条件,这些计算都使用了较小的组态空间,以及不自洽的相互作用。此后,为了考虑2p-2h混合的效应,有一系列近似方法被提出,如考虑粒子振动耦合的RPA模型[14−15],该模型中考虑了1p-1h组态与RPA声子的混合;以及声子-声子耦合模型[16]。21世纪初,出现自洽HF+SRPA模型计算[17−18]。但这些计算对于截断能量不收敛,而且给出的低能激发态的激发能过低。其原因是SRPA模型中存在重复计算[19],解决的方法是在对角化SRPA方程前采用扣除(subtraction)程序[20]。2015年,基于Skyrme密度泛函并考虑了扣除程序的自洽SRPA被发展出来[21],后来该模型被用于一系列闭壳核的GT跃迁和β衰变的研究[22−23] 并获得了巨大成果。但由于这些工作中没有加入张量力,对GT跃迁的巨共振能量和低能部分累积强度求和描述还不够好。
张量力作为原子核中核子-核子相互作用的重要组成部分,其在原子核基态性质[24−26]、丰中子核的幻数演化[27−29]、集体激发态的性质的描述[30−33]以及原子核的β衰变[34−35]等方面都有很重要的作用,但这些研究都是基于平均场或者(Q)RPA模型框架。本文将介绍在基于Skyrme有效相互作用的自洽HF+SRPA模型中加入张量力后对闭壳核0+、2+、3−和电荷交换的伽莫夫-泰勒(GT)跃迁,以及对闭壳核准闭壳核的β衰变的描述。本文将在第1节介绍理论模型,在第2节给出理论结果,在第3节给出总结和展望。
-
SRPA模型基于微观有效核子-核子相互作用,相应哈密顿量为
$$ H=\displaystyle\sum\limits_{k_1,\,k_2}T_{k_1k_2}a_{k_1}^\dagger a_{k_2}+\frac{1}{4}\displaystyle\sum\limits_{k_1,\,k_2,\,k_3,\,k_4}\bar{V}_{k_1k_2,\,k_3k_4}a_{k_1}^\dagger a_{k_2}^\dagger a_{k_3}a_{k_4}, $$ (2) 其中k可以是占据态(空穴态)也可以是非占据态(粒子态),相互作用由此可以划分为4空穴(4h)、1粒子-1空穴(1p-1h)、1粒子-3空穴(1p-3h)、1空穴-3粒子(1h-3p)、4粒子(4p)相互作用。计算原子核的基态性质时,作Hartree-Fock(HF)近似,认为基态是所有占据态构成的Slater行列式:
$$ |HF\rangle=\sum\limits_{i=1}^A a_{i}^\dagger|-\rangle, $$ (3) 其中$ |-\rangle $是HF真空。为方便起见,本文中$i,\;j,\;h$代表HF占据态(空穴态),$m,\;n,\;p$代表非占据态(粒子态)。在此近似下,体系的能量为
$$ E=\sum\limits_i \left\langle i\left|\frac{p^2}{2m}\right|i \right \rangle+\sum\limits_{ij} \left\langle ij\left|\bar{V}\right|ij\right\rangle=\int H(\rho(\boldsymbol{r})){\mathrm{d}}^3r, $$ (4) 从上式可以看出,HF近似只考虑了空穴态之间的4h相互作用,能量密度H是密度的泛函。对密度求变分可以得到HF近似下的单粒子方程,迭代地求解该方程可以得到HF单粒子态波函数和原子核基态的大块性质如结合能、电荷半径等[6]。
基于HF的结果,可以计算空穴态到粒子态之间的跃迁,由于该跃迁的计算涉及粒子态,但HF近似只考虑了空穴态之间的相互作用,导致得到的3−态跃迁强度在中重以上的核中与实验结果相差一个数量级[36]。RPA模型认为实际的激发态是所有1p-1h激发(组态)构成的共振态,并很好地解决了这一问题,即
$$ \begin{array}{*{20}{l}} |\nu\rangle=Q_\nu^\dagger|RPA\rangle, \end{array} $$ (5) $$ Q_\nu^\dagger=\sum\limits_{ph}X_{ph}^\nu a_p^\dagger a_h-\sum\limits_{ph}Y_{ph}^\nu a_h^\dagger a_p, $$ (6) 其中:$ |RPA\rangle $是RPA真空,叠加系数$ X,Y $可以通过RPA方程解出:
$$ \begin{array}{*{20}{l}} \left(\begin{array}{cc} A & B \\ -B^* & -A^* \end{array}\right)\left(\begin{array}{c} X^\nu \\ Y^\nu \end{array}\right)=E_\nu\left(\begin{array}{c} X^\nu \\ Y^\nu \end{array}\right)。 \end{array} $$ (7) 用HF基态代替RPA真空,以及准玻色子近似下,上述RPA方程中的A,B 矩阵元可以计算为
$$ \begin{array}{*{20}{l}} A_{p_1h_1,\,p_2 h_2}=(\epsilon_{p_1}-\epsilon_{h_1})\delta_{p_1p_2}\delta_{h_1h_2}+\bar{v}_{p_1h_2,\,h_1p_2}, \end{array} $$ (8) $$ \begin{array}{*{20}{l}} B_{p_1h_1,\,p_2h_2}=\bar{v}_{p_1p_2,\,h_1h_2}, \end{array} $$ (9) 从上两式可以看出,自洽的RPA模型考虑了核子-核子有效相互作用式(2)中的1p-1h部分。
RPA模型能很好地解释自旋无关的电跃迁强度,但对于自旋相关的磁跃迁和自旋-同位旋跃迁如伽莫夫-泰勒跃迁、电荷交换的自旋-偶极跃迁,理论结果显著地高估了跃迁强度,这导致了著名的强度压低问题(Quenching)[37]。研究表明,考虑高阶的单粒子跃迁组态如2p-2h 组态,使跃迁强度分布到高能区可以有效地解决这个问题[11, 13]。考虑2p-2h组态的SRPA中,激发态为[21, 38]
$$ \begin{split} Q_\nu^\dagger = & \sum\limits_{ph}X_{ph}^\nu a_{p}^\dagger a_{h}^{}-\sum\limits_{ph}Y_{ph}^\nu a_{h}^\dagger a_{p}+ \\ & \sum\limits_{p_1h_1p_2h_2}X_{p_1h_1,\,p_2h_2}^\nu a_{p_1}^\dagger a_{p_1}^\dagger a_{h_1}^{} a_{h_2}^{}- \\ & \sum\limits_{p_1h_1p_2h_2}Y_{p_1h_1,\,p_2h_2}^\nu a_{h_1}^\dagger a_{h_2}^\dagger a_{p_1} a_{p_2}, \end{split} $$ (10) 求解叠加系数的SRPA方程与RPA方程式(7),只是其中增加了使1p-1h组态和2p-2h组态、2p-2h组态之间关联(即混合)的矩阵元,如:
$$ \begin{split} A_{12} & = A_{ph;\,p_1p_2h_1h_2} \\& =<HF\left|\left[a_h^\dagger a_p,\left[H,a_{p_1}^\dagger a_{p_2}^\dagger a_{h_2}a_{h_1}\right]\right]\right|HF > \\ & = U(h_1h_2)\bar{V}_{p_1p_2ph_2}\delta_{hh_1}-U(p_1p_2)\bar{V}_{hp_2h_1h_2}\delta_{pp_1}, \end{split} $$ (11) $$ \begin{split} A_{22}=\; &A_{p_1p_2h_1h_2;\,p_1^\prime p_2^\prime h_1^\prime h_2^\prime}\\ = \; & \left\langle HF|[a_{h_1}^\dagger a_{h_2}^\dagger a_{p_2}a_{p_1},[H,a_{p_1^\prime}^\dagger a_{p_2^\prime}^\dagger a_{h_2^\prime}a_{h_1^\prime}]]|HF \right\rangle \\ =\; &(E_{p_1}+E_{p_2}-E_{h_1}-E_{h_2})U(p_1p_2)U(h_1h_2)\times \\ & \delta_{p_1p_1^\prime}\delta_{p_2p_2^\prime}\delta_{h_1h_1^\prime}\delta_{h_2h_2^\prime}+ \\ &U(h_1h_2)\bar{V}_{p_1p_2p_1^\prime p_2^\prime}\delta_{h_1h_1^\prime}\delta_{h_2h_2^\prime}+ \\ &U(p_1p_2)\bar{V}_{h_1h_2h_1^\prime h_2^\prime}\delta_{p_1p_1^\prime}\delta_{p_2p_2^\prime}- \\ &U(p_1p_2)U(h_1h_2)U(p_1^\prime p_2^\prime)U(h_1^\prime h_2^\prime)\times \\ & \bar{V}_{p_1h_1^\prime p_1^\prime h_1}\delta_{p_2p_2^\prime}\delta_{h_2h_2^\prime},\end{split} $$ (12) 其中$ U(k_1,k_2) $是对$ k_1,k_2 $的反对称算符。从式(11~12)可以看出,1p-1h组态和2p-2h组态之间的关联引入了有效相互作用中的1p-3h和1h-3p部分,而2p-2h组态之间的关联则引入了4p和4h部分,至此,有效相互作用式(2)中的所有可能形式的相互作用都被考虑到了。由于引入了2p-2h的组态可能会引起重复计算的问题以及导致SRPA方程不稳定收敛[19, 39],需要通过一个扣除程序来修复。扣除程序[20−21],即在对角化SRPA方程前,考虑$ A_{12} $和$ A_{22} $对$ A_{11} $矩阵的修正:
$$ \begin{split} A_{11^\prime}^S=A_{11^\prime}+\sum_{2}A_{12}(A_{22})^{-1}A_{2 1^\prime}+\sum_{2}B_{12}(A_{22})^{-1}B_{21^\prime}, \\ B_{11^\prime}^S= B_{11^\prime}+\sum_{2}A_{12}(A_{22})^{-1}B_{21^\prime}+\sum_{2}B_{12}(A_{22})^{-1}A_{2 1^\prime}, \end{split} $$ (13) 本文所使用的SRPA模型也包含了一样的扣除程序。
-
由于16O占据态较少,组态个数也少,此外,虽然RPA模型有许多不足之处,但其考虑了主要的1粒子-1空穴组态的效应,该模型能够较好地描述原子核的巨共振能区的主峰能量,却对16O的0+,2+低能峰描述不好,所以其适合SRPA模型的计算检验。2015年Gambacurta等[21]在工作中用SRPA模型详细研究了16O的0+和2+态的强度分布,该研究验证了扣除程序对SRPA模型的重要效果。此外,对16O激发态研究的主要成果是一方面由于SRPA引入的2p-2h 组态的展宽效应,使得给出的强度大小和实验结果高度一致同时对于巨共振能区也可以给出与RPA类似的主峰位置,另一方面能给出低能16O的0+和2+态的激发能,这是RPA模型无法给出的。但在该工作中没有加入张量相互作用,同时没有考虑$ A_{22} $中的4p部分,该计算给出的这些低能激发态的跃迁强度几乎不可见。
2021年,我们也发展了SRPA模型程序,并在计算中加入了张量相互作用,同时$ A_{22} $中也自洽地加入了4p部分。我们在工作[38]中,研究了16O和40Ca的0+,2+,3−态。对于16O的低能2+态,我们给出了与文献[21]类似的结果,即能较好地重复低能激发态的激发能,但给出的强度依然过低。
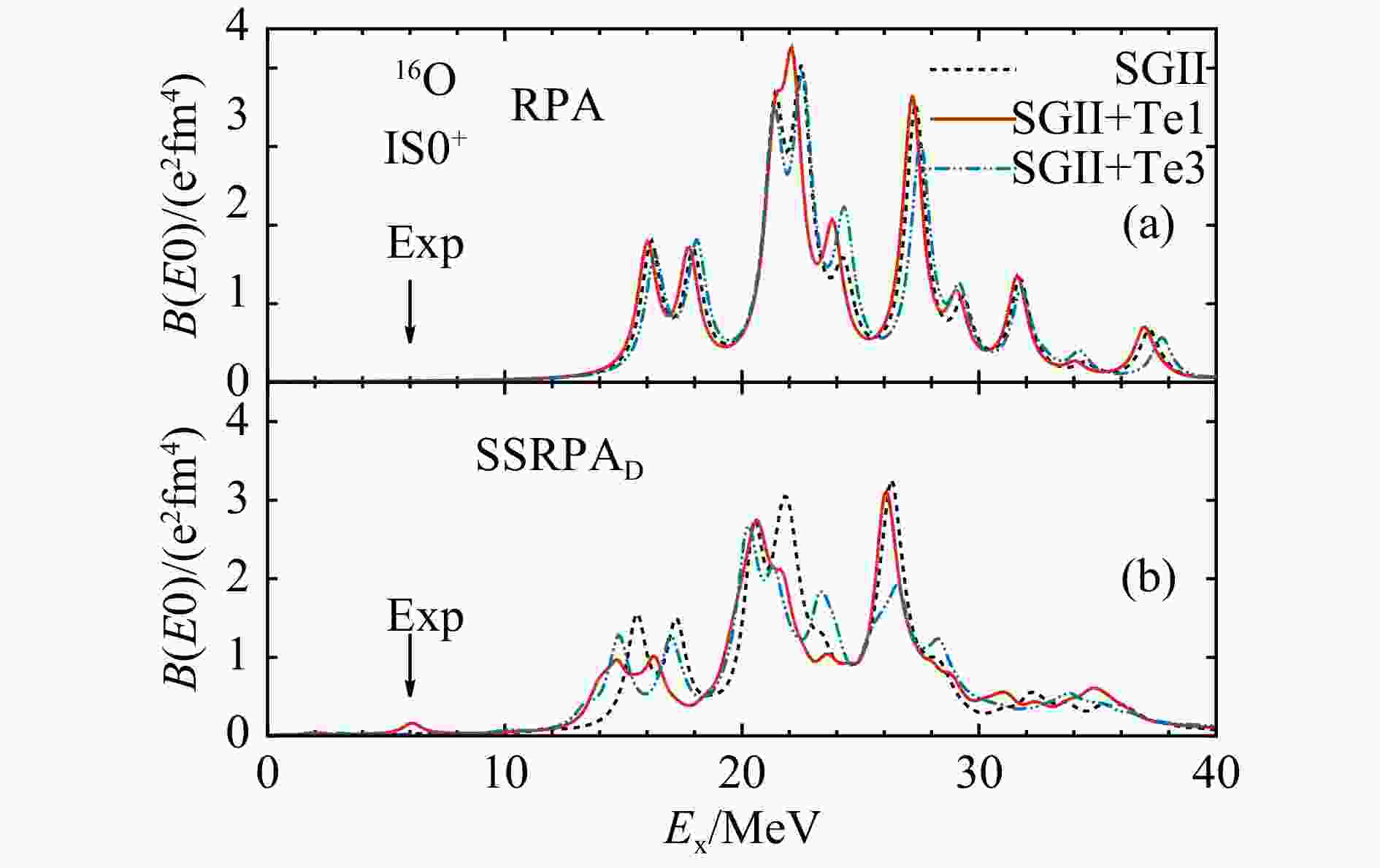
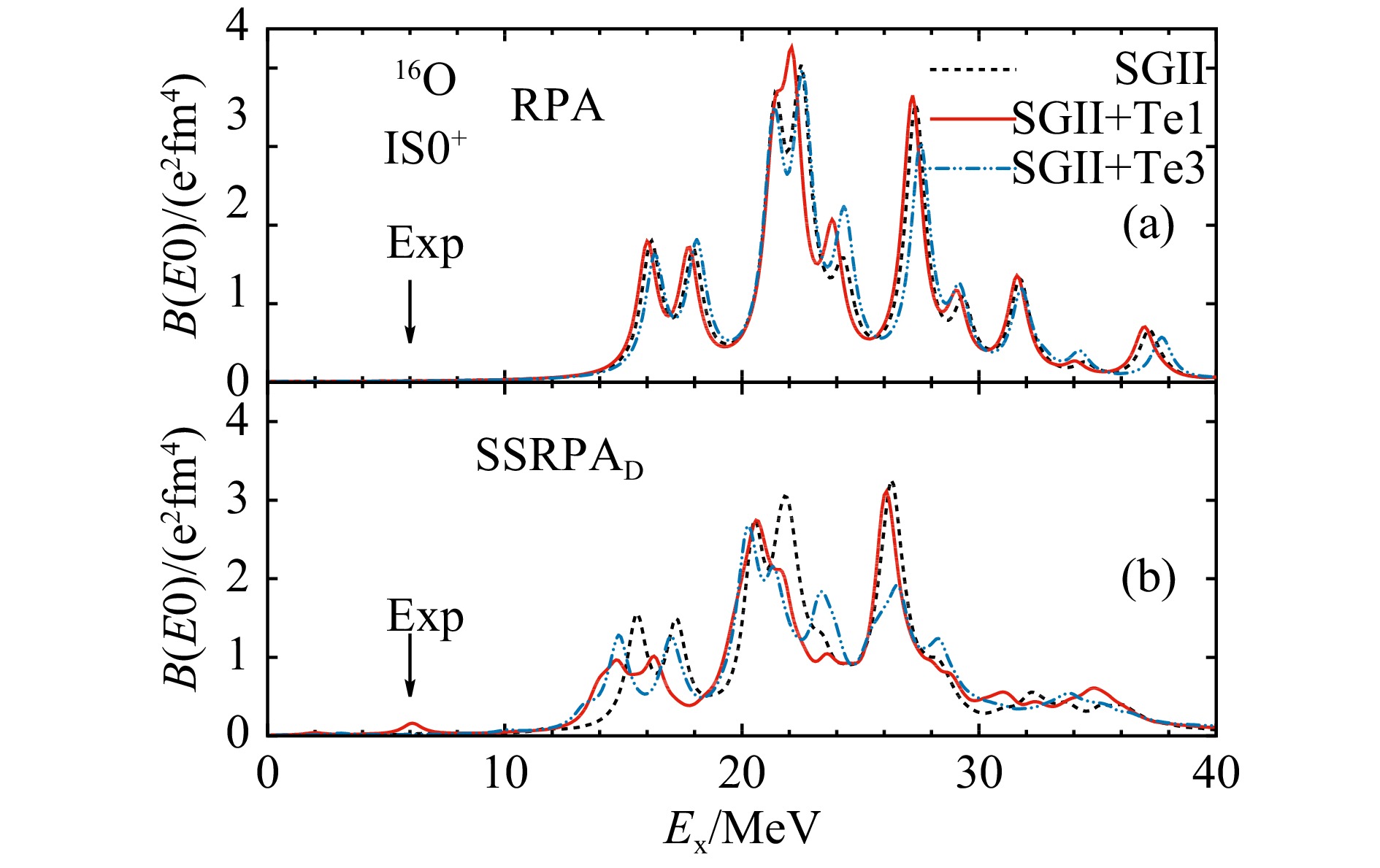
我们用自洽HF+RPA和HF+SRPA模型计算了16O的0+态的同位旋标量强度分布,如图1所示。计算时我们采用了 Skyrme相互作用SGII[40],由于张量力的强度不太确定,我们采用了SGII+Te1和SGII+Te3[41], 其中的中心部分和自旋轨道耦合部分保持不变,但张量力的参数分别取为有很大区别的(T, U) = (500.0, −350.0)和(650.0,+200.0) MeVfm5。对0+态,RPA计算在低能区可能出现伪态,文献[19−21]指出,加入扣除程序后则不会出现伪态,我们在计算中也未出现过伪态。从图中可以看出,SRPA模型给出的强度分布在更宽的能区,不加张量力时,SRPA给出的主峰能量与RPA基本一致,但在16O中,对于0+和2+态,加入张量力后主峰能量会下移约2 MeV。特别地,在低能区域 SGII+Te1能重复实验的激发能,同时给出可见的强度,这是之前不考虑张量相互作用的SRPA模型无法给出的。需要指出的是,加入张量力后SRPA模型也能给出与实验能量一致的低能2+态,但是其强度远低于实验,从集体振动这方面来分析,这种差异很有可能是没有考虑到连续态[9−10]的效应所致。
对于16O的3−态,如图2所示。我们首次给出了SRPA对该激发态同位旋标量强度分布的计算结果。从图中可以发现,采用SGII和SGII+Te3的RPA和SRPA计算都高估了第一个3−态的激发能。与0+态相同,采用SGII+Te1的SRPA计算能给出第一个3−态的激发能,同时采用该相互作用的RPA模型也能重复该激发能,这主要张量力的效应。
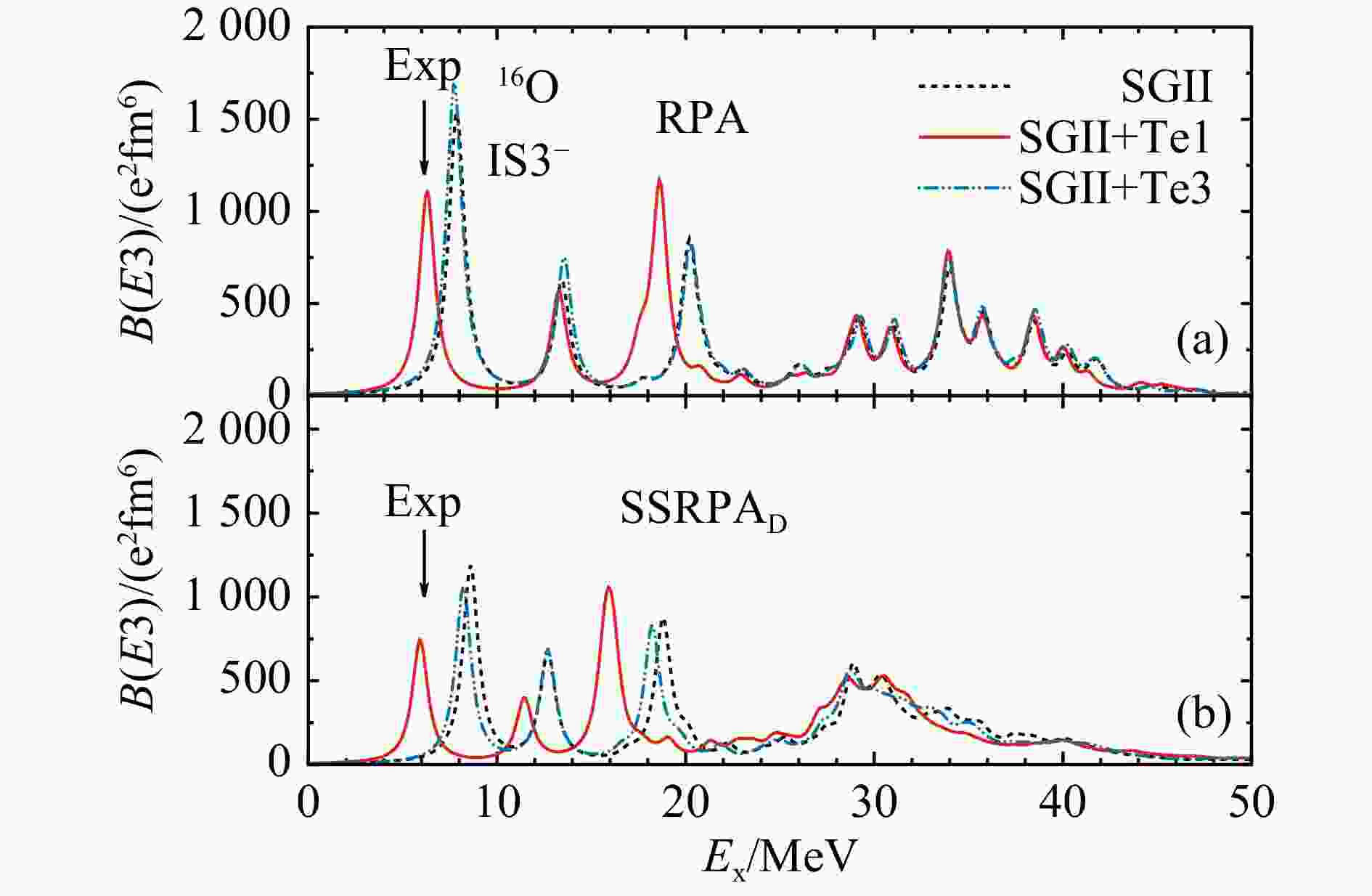
图 2 与图1相同,但是16O的3−态(在线彩图)
本小结的研究表明,取适当的参数即SGII+Te1后,自洽SRPA模型能很好地描述16O的0+,2+,3−低能激发态的激发能,同时对于0+态,加入张量力后能给出可见的低能激发态的同位旋标量激发强度;对于3−低能激发态的描述,必须需要加入该强度的张量力才能实现。
-
GT跃迁是原子核在自旋和同位旋空间的振动,其巨共振部分能给出核子-核子相互作用的自旋-同位旋部分的信息。此外,GT跃迁中存在一个模型无关的求和规则,
$$ \begin{array}{*{20}{l}} S_{-}- S_+=3(N-Z), \end{array} $$ (14) 其中S±分别是t±道强度的总和。对于丰中子核,t+道跃迁被压制,其强度接近0,此时该求和规则给出t−道的强度总和。但实验只能在低能区域测出该强度总和的60%~70%,这就是著名的GT强度压低问题。
对于这一问题,有效的解决方案是在计算中加入2p-2h组态[11]。2021年,Gambacurta等[44]把SRPA模型应用于48Ca的GT跃迁强度分布。该工作得到的GT巨共振强度和能量与实验一致,且在低于20 MeV的能区得到的总强度也与实验一致,这个结果堪称完美。但他们在随后的工作中,又计算了90Zr和132Sn的GT强度分布,在这个工作中得到的GT主峰能量比实验低约2 MeV以上,而且在低于20 MeV的能区得到的强度总和明显高于实验结果,如在132Sn 中,理论比实验值高出约60%。可能原因是计算中未考虑相互作用的4p部分,以及没有加入张量力。
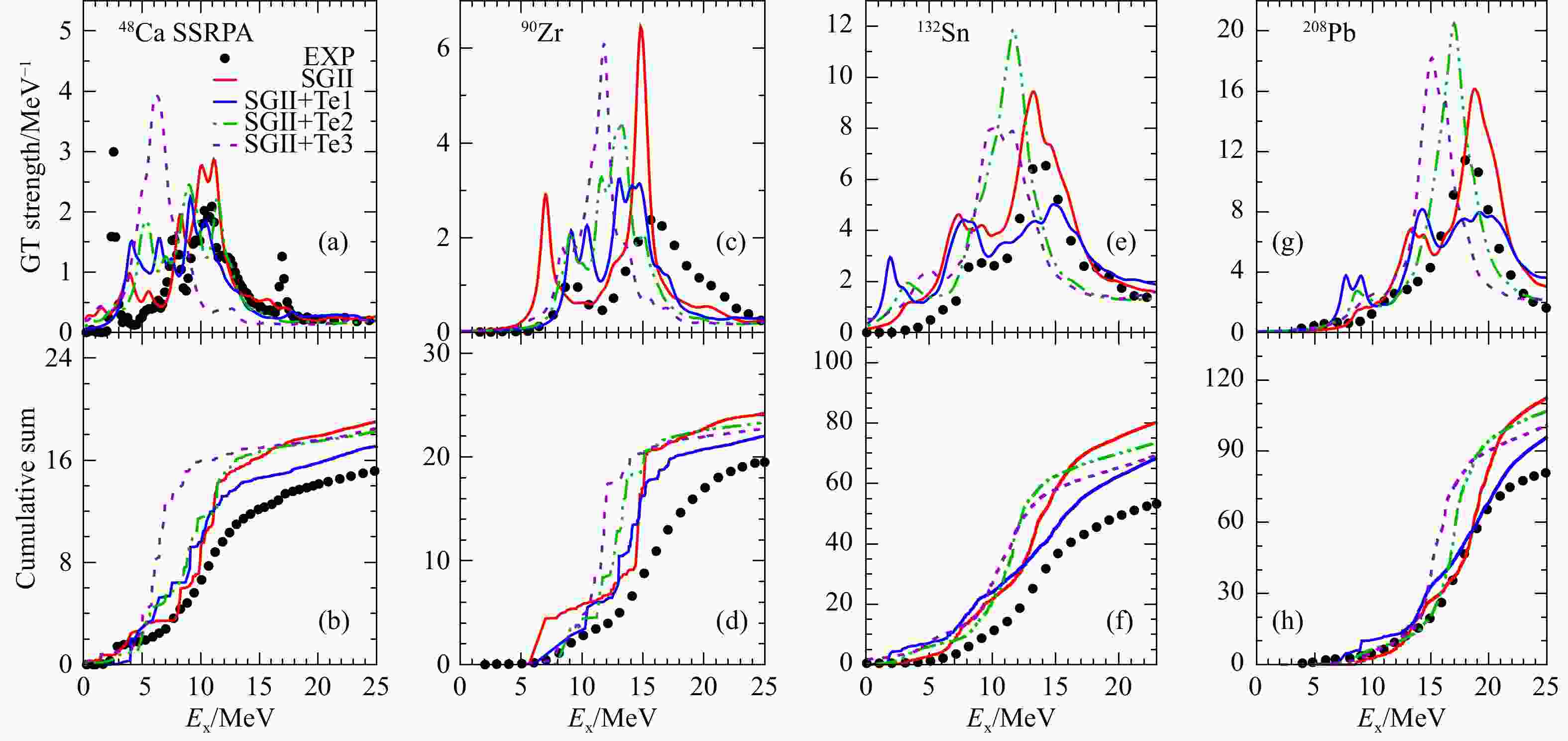
基于上述原因,我们对四个闭壳核48Ca,90Zr,132Sn和208Pb的GT跃迁作了SRPA计算,计算中完整考虑了SRPA的所有矩阵元,并加入了张量力,计算结果如图3所示。SRPA计算时采用相互作用参数 SGII、SGII+Te1、SGII+Te1、SGII+Te3,其中SGII中没有张量力,后面3套参数加入了张量力。从图中可以发现,采用加入张量力的相互作用SGII+Te1时,能对主峰的激发能和强度给出较好的描述。此外,使用该参数时张量力能有效减少25 MeV以下能区的GT强度总和。
为了更明确地标记有多少GT强度被移到高激发能区,我们定义压低因子:
$$ Q=\frac{3(N-Z)-\displaystyle\sum\limits_{0<Ex<E_{\rm max}}B(GT:E_{\mathrm{x}})_{{\mathrm{calc}}}}{3(N-Z)}, $$ (15) 图3所示强度分布的压低因子在表1中列出。从表中可以看出,不加张量力时,理论和实验压低因子的差异为20%左右;加入张量力并使用参数SGII+Te1时,理论和实验压低因子的差距约为10%。
表 1 SRPA计算的闭壳核48Ca,90Zr,132Sn,和208Pb的GT强度压低因子,计算中采用了相互作用参数 SGII,SGII+Te1,SGII+Te2,和SGII+Te3(GT强度的累积求和计算到$ E_{{\mathrm{max}}}=25 \; {\mathrm{MeV}}$)
Force (T,U) 48Ca 90Zr 132Sn 208Pb SGII (0,0) 20.7% 19.2% 16.4% 14.7% SGII+Te1 (500, −350) 28.7% 26.6% 28.7% 27.3% SGII+Te2 (600, 0) 23.8% 22.1% 23.3% 19.0% SGII+Te3 (650, 200) 22.9% 24.1% 27.6% 23.6% Exp. 36.7 % 34.9 % 44.5% 38.6 % -
比铁重的核素的合成中,超过一半的核素由快中子俘获过程产生,在该过程中原子核迅速俘获中子后,由于中子过多会通过β衰变形成更重的元素。但由于非常多的丰中子核素是目前实验条件无法测量的,天体核合成模拟时需要理论计算β衰变半衰期,GT跃迁对β衰变半衰期起重要作用。
对于闭壳和准闭壳核34Si,68, 78Ni和132Sn,GT 跃迁主导β衰变,其半衰期可以计算为
$$ T_{1/2}=\frac{D}{g_A^2 \displaystyle\sum_n ^{\varDelta_{nH}} B_{1^+_n }^{GT^-}f_0(Z,A,\omega_n ) }, $$ (16) 其中常数D = (6163.4±3.8) s, $ f_0 $是相因子函数,$ \Delta_{nH} $ = 0.78 227 MeV是中子和氢原子质量差,$ B_{1^+_n }^{GT^-} $为满足衰变Q值得GT跃迁的强度。轴矢量和矢量耦合常数的初始比值$ g_A=G_A/G_V=1.26 $,为与文献[23]中的GT强度压低因子保持一致,本文中我们取$ g_A=1.0 $。
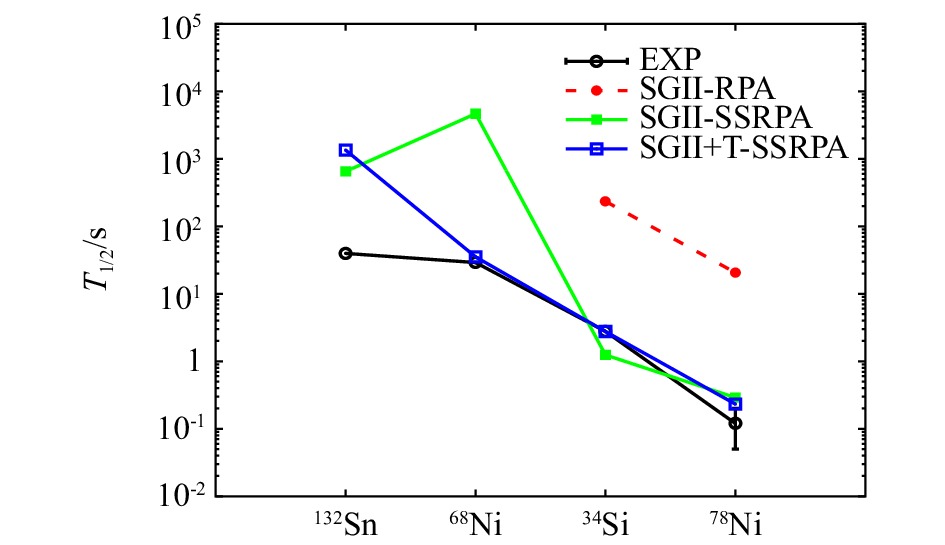
图4给出了上述4个闭壳和准闭壳核34Si,68, 78Ni和132Sn的β衰变半衰期。从式(16)中可以看出,GT激发态的能量和强度对β衰变半衰期都会产生影响,但能量的影响会更大。Otsuka等[27]在文献中提到张量力对不同单粒子能级间核子的吸引或者排斥的单极效应,即对$ j_\gtrless $和$ j_\lessgtr $轨道中的质子或中子是吸引,对$ j_\gtrless $和$ j_\gtrless $轨道中的质子或者中子是排斥。在RPA和SRPA中,张量力对集体激发态的效应与单极效应是一致的,根据集体激发态中占主要贡献的组态类型,张量力可能是吸引或者排斥,因此张量力有可能在不同原子核中增大或者减小β衰变的半衰期。在计算中,我们期望实现对GT主峰和β衰变半衰期的统一和更优化描述。因此,我们经过大量SRPA计算对张量力的参数进行了优化,即(T, U) = (500, −280) MeVfm5,使用该参数能对上一小节中四个闭壳核的GT跃迁巨共振能量和强度给出比SGII+Te1略好的描述。从图中可以看出,除寿命较长的132Sn外,SRPA模型使用SGII+T(500, −280)时,对34Si,68, 78Ni的半衰期给出非常好的描述。对132Sn半衰期的计算偏长的原因是低能 GT态的强度偏低, 实际上我们也可以通过调节张量力参数U符合实验结果,但这样对GT主峰和其它核的β衰变半衰期描述就不一致了。
-
原子核的共振态能有效反映原子核的结构性质和原子核的核子-核子相互作用,低能激发态还能影响天体核合成的一些重要反应的截面。本文介绍了研究这些激发态的SRPA理论,该理论模型包含了相互作用哈密顿量中所有形式的相互作用。此前的RPA模型考虑了1p-1h剩余相互作用,解决自旋无关的正常巨共振的强度问题,但给出的自旋相关的磁跃迁以及自旋-同位旋激发的强度在低能区明显高于实验观测,导致了强度压低问题。SRPA模型加入了2p-2h组态,引入更多剩余相互作用,一方面能对正常巨共振的强度和激发能给出更好的描述;另一方面能显著展宽自旋-同位旋激发的强度分布,能显著改善强度压低问题。我们在SRPA模型中加入张量力并选择合适的SGII+Te1后,能改进对16O的低能0+和3−态的描述,并对一系列闭壳核的GT巨共振能量和强度给出较好的描述,同时能进一步改善强度压低因子约10%左右。至此,SRPA对GT强度压低还差10%左右。进一步,采用更优化的包含张量力的参数SGII+T(500, −280) MeVfm5后,能对闭壳核的GT巨共振能量和强度给出比SGII+Te1更好的描述,同时还能很好地描述闭壳和准闭壳核 34Si,68, 78Ni的β衰变半衰期。但即使加入张量力后,目前的SRPA模型给出的低能激发态的强度依然较低。
除高阶组态能展宽对集体激发态强度分布外,连续态的耦合能显著增强低能激发态的强度,为此,我们将在今后的工作中进一步考虑连续态对强度分布的展宽效应。
Research of Second Random-Phase-Approximation on the Nuclear Collective Excited States
-
摘要: 原子核的集体激发态是原子核在坐标、自旋和同位旋等空间的共振产生。研究这些激发态可以获取原子核结构性质以及内部核子-核子相互作用的信息,此外还能为天体核物理提供重要的输入量。基于Skyrme密度泛函的自洽二阶无规相近似(SRPA)理论被用于研究闭壳原子核的这些集体激发态,包括无电荷交换的正常宇称态0+、2+、3−,以及电荷交换的伽莫夫-泰勒(GT)跃迁。此外,两粒子-两空穴组态下的张量力效应被突出讨论,研究指出它能产生低能正常跃迁或者提高它们的跃迁强度,另外加入张量力后能系统地描述一系列闭壳核的GT巨共振的强度和激发能,并自洽地描述不稳定闭壳或准闭壳核的β衰变半衰期。Abstract: The collective excited states are macroscopically described as the nuclear resonances in coordinate, spin, and isospin spaces. Researching these excited states may acquire the properties of nuclear structure and the information of nucleon-nucleon interaction inside nucleus. In addition, it may also provide important input for nuclear astrophysics. The self-consistent Second Random Approximation (SRPA) theory based on Skyrme density functional was applied to research these collective excited states, including normal parity 0+, 2+, 3− sates, and charge-exchange Gamow-Teller (GT) transition. In addition, the effects of tensor force under the two particle-two hole configurations are discussed primarily. And the research points out that it may produce low-energy normal transition states or enhance their transition strengths. Moreover, the including of tensor force is helpful for the systematical describing of the strength and excitation energy of GT giant resonances of a series of closed-shell nuclei, and the β decay half-lives of closed-shell or quasi closed-shell nuclei.
-
表 1 SRPA计算的闭壳核48Ca,90Zr,132Sn,和208Pb的GT强度压低因子,计算中采用了相互作用参数 SGII,SGII+Te1,SGII+Te2,和SGII+Te3(GT强度的累积求和计算到$ E_{{\mathrm{max}}}=25 \; {\mathrm{MeV}}$)
Force (T,U) 48Ca 90Zr 132Sn 208Pb SGII (0,0) 20.7% 19.2% 16.4% 14.7% SGII+Te1 (500, −350) 28.7% 26.6% 28.7% 27.3% SGII+Te2 (600, 0) 23.8% 22.1% 23.3% 19.0% SGII+Te3 (650, 200) 22.9% 24.1% 27.6% 23.6% Exp. 36.7 % 34.9 % 44.5% 38.6 % -
[1] GORIELY S. Phys Lett B, 1998, 436: 10. doi: 10.1016/S0370-2693(98)00907-1 [2] MEYER B S, MATHEWS G J, HOWARD W M, et al. Astrophys J, 1992, 399: 656. doi: 10.1086/171957 [3] BURBIDGE E M, BURBIDGE G R, FOWLER W A, et al. Rev Mod Phys, 1957, 29: 547. doi: 10.1103/RevModPhys.29.547 [4] COWAN J K, THIELEMANN F K, TRURAN J W. Phys Rep, 1991, 208: 267. doi: 10.1016/0370-1573(91)90070-3 [5] BLAIZOT J P, BERGER J F, DECHARGE J, et al. Nucl Phys A, 1995, 591: 435. doi: 10.1016/0375-9474(95)00294-B [6] VAUTHERIN D, BRINK D M. Phys Rev C, 1972, 5: 626. doi: 10.1103/PhysRevC.5.626 [7] SPETH J, WOUDE A. Rep Prog Phys, 1981, 44: 719. doi: 10.1088/0034-4885/44/7/002 [8] AIT-TAHAR S, BRINK D. Nucl Phys A, 1993, 560: 765. doi: 10.1016/0375-9474(93)90170-3 [9] SHLOMO S, BERTSCH G. Nucl Phys A, 1975, 243: 507. doi: 10.1016/0375-9474(75)90292-4 [10] ZHANG C L, ZHANG H Q, ZHANG X Z, et al. J Phys G, 2006, 32: 2261. doi: 10.1088/0954-3899/32/11/017 [11] BERTSCH G F, HAMAMOTO I. Phys Rev C, 1982, 26: 1323. doi: 10.1103/PhysRevC.26.1323 [12] TAKAYANAGI K, SHIMIZU K, ARIMA A. Nucl Phys A, 1988, 477: 205. doi: 10.1016/0375-9474(88)90319-3 [13] TAKAYANAGI K, SHIMIZ U, ARIMA A. Nucl Phys A, 1988, 481: 313. doi: 10.1016/0375-9474(88)90499-X [14] NIU Y F, COLO G, VIGEZZI E. Phys Rev C, 2014, 90: 054328. doi: 10.1103/PhysRevC.90.054328 [15] ROBIN C, LITVINOVA. Phys Rev Lett, 2019, 123: 202501. doi: 10.1103/PhysRevLett.123.202501 [16] SEVERYUKHIN A P, VORONOV V V, BORZOV I N, et al. Phys Rev C, 2014, 90: 044320. doi: 10.1103/PhysRevC.90.044320 [17] GAMBACURTA D, GRASSO M, CATARA F, et al. Phys Rev C, 2006, 73: 024319. doi: 10.1103/PhysRevC.73.024319 [18] PAPAKONSTANTINOU P, ROTH R. Phys Lett B, 2009, 671: 356. doi: 10.1016/j.physletb.2008.12.037 [19] TSELYAEV V I. Phys Rev C, 2007, 75: 024306. [20] TSELYAEV V I. Phys Rev C, 2013, 88: 054301. [21] GAMBACURTA D, GRASSO M, ENGEL J. Phys Rev C, 2015, 92: 034303. doi: 10.1103/PhysRevC.92.034303 [22] GAMBACURTA D, GRASSO M, ENGEL J. Phys Rev Lett, 2020, 125: 212501. doi: 10.1103/PhysRevLett.125.212501 [23] GAMBACURTA D, GRASSO M. Phys Rev C, 2022, 105: 014321. doi: 10.1103/PhysRevC.105.014321 [24] COLO G, SAGAWA H, BORTIGNON P F. Phys Rev C, 2010, 82: 064307. doi: 10.1103/PhysRevC.82.064307 [25] BROWN B A, DUGET T, OTSUKA T, et al. Phys Rev C, 2006, 74: 061303(R). doi: 10.1103/PhysRevC.74.061303 [26] ZUO W, COLO G, MA Z Y, et al. Phys Rev C, 2008, 77: 014314. doi: 10.1103/PhysRevC.77.014314 [27] OTSUKA T, SUZUKI T, FUJIMOTO R, et al. Phys Rev Lett, 2005, 95: 232502. doi: 10.1103/PhysRevLett.95.232502 [28] COLO G, SAGAWA H, FRACASSO S, et al. Phys Lett B, 2007, 646: 227. doi: 10.1016/j.physletb.2007.01.033 [29] BRINK D M, STANCU F. Phys Rev C, 2007, 75: 064311. doi: 10.1103/PhysRevC.75.064311 [30] BAI C L, SAGAWA H, ZHANG H Q, et al. Phys Lett B, 2009, 675: 28. doi: 10.1016/j.physletb.2009.03.077 [31] CAO L G, COLO G, SAGAWA H, et al. Phys Rev C, 2009, 80: 064304. doi: 10.1103/PhysRevC.80.064304 [32] JIANG L J, YANG S, SUN B Y, et al. Phys Rev C, 2015, 91: 034326. doi: 10.1103/PhysRevC.91.034326 [33] WANG S, TONG H, ZHAO P, et al. Phys Rev C, 2019, 100: 064319. doi: 10.1103/PhysRevC.100.064319 [34] MINATO F, BAI C L. Phys Rev Lett, 2013, 110: 122501. doi: 10.1103/PhysRevLett.110.122501 [35] BAI C L, FANG D L, ZHANG H Q. Chin Phys C, 2022, 46: 114104. doi: 10.1088/1674-1137/ac80ee [36] LANG A M, PENDLEBURY E D. Nucl Phys, 1960, 15: 39. doi: 10.1016/0029-5582(60)90280-7 [37] RAPAPORT J, TADDEUCCI T, WELCH T P, et al. Nucl Phys A, 1983, 410: 371. doi: 10.1016/0375-9474(83)90632-2 [38] YANG M J, BAI C L, SAGAWA H, et al. Phys Rev C, 2021, 103: 054308. doi: 10.1103/PhysRevC.103.054308 [39] PAPAKONSTANTINOU P. Phys Rev C, 2014, 90: 024305. [40] GIAI N VAN, SAGAWA H. Phys Lett B, 1981, 106: 379. doi: 10.1016/0370-2693(81)90646-8 [41] BAI C L, ZHANG H Q, SAGAWA H, et al. Phys Rev C, 2011, 83: 054316. doi: 10.1103/PhysRevC.83.054316 [42] TILLEY D, WELLER H, CHEVES C. Nucl Phys A, 1993, 564: 1. doi: 10.1016/0375-9474(93)90073-7 [43] KIBEDI T, SPEAR R H. At Data Nucl Data Tables, 2020, 80: 35. [44] GAMBACURTA D, GRASSO M, ENGEL J. Phys Rev Lett, 2021, 125: 212501. [45] YANG M J, BAI C L, SAGAWA H, et al. Phys Rev C, 2022, 106: 014319. doi: 10.1103/PhysRevC.106.014319 [46] YAKO K, SASANO M, MIKI K, et al. Phys Rev Lett, 2009, 103: 012503. doi: 10.1103/PhysRevLett.103.012503 [47] WAKASA T, SAKAI H, OKAMURA H, et al. Phys Rev C, 1997, 55: 2909. doi: 10.1103/PhysRevC.55.2909 [48] YASUDA J, SASANO M, ZEGERS P G T, et al. Phys Rev Lett, 2018, 121: 132501. doi: 10.1103/PhysRevLett.121.132501 [49] WAKASA T, OKAMOTO M, DOZONO M. Phys Rev C, 2012, 85: 064606. doi: 10.1103/PhysRevC.85.064606 [50] National Nuclear Data Center[EB/OL].[2023-07-15].http:/www.nndc.bnl.gov. [51] YANG M J, SAGAWA H, BAI C L, et al. Phys Rev C, 2023, 107: 014325. doi: 10.1103/PhysRevC.107.014325 -





 下载:
下载:

 甘公网安备 62010202000723号
甘公网安备 62010202000723号