Nuclear clustering is a universal phenomenon in light nuclei^[1–3]. The $ \alpha $ cluster can be considered one of the most stable subunits in light nuclei^[4]. More than half a century ago, Ikeda and Horiuchi proposed that $ \alpha $-clustering structures can occur near the $ \alpha $ threshold of $ A=4N $ nuclei^[5]. For example, the ground state of $ \rm {}^{8}{\mathrm{Be}} $ exhibits a structure of two $ \alpha $ clusters, while the well-known Hoyle state ($ 0_2^+ $) of $ \rm {}^{12}{\mathrm{C}} $ consists of three $ \alpha $ clusters^[6–8]. Currently, the search for Hoyle-analog states, such as $4\alpha$ and $5\alpha$, has garnered significant attention^[9–12].

More and more research show that there are also rich cluster structures^[13–14] in non-conjugate atomic nuclei. The $ \rm{}^{10}Be $ nucleus can be considered as one typical case with the $ 2\alpha+2{\mathrm{n}} $ clustering structure. Many experiments take much efforts to investigate the clustering structure of $ \rm{}^{10}Be $. In Ref. [15], the characteristics of high-lying excited states of $ \rm{}^{10}Be $ up to 18.80 MeV were explored via the $ \rm{}^{9}Be(\rm{}^{9}Be,\,\rm{}^{10}Be)\rm{}^{8}Be $ reaction, and new resonance states at 15.6 MeV and 18.8 MeV were found from the $ \alpha+\rm {}^{6}He $ and $ {\mathrm{t}}+\rm {}^{7}Li $ decay channels. Moreover, two-proton pick-up reactions^[16–17] $ \rm{ {}^{12}C}({}^{6}He,{}^{8}Be)\rm {}^{10}Be $ and $ \rm{ {}^{12}C}({}^{12}C,\,{}^{14}O)\rm {}^{10}Be $ discussed the structure of the rotational bands. Recent experimental studies^[14] show even the ground state of $ \rm {}^{10}Be $ can be described by a dumbbell-shaped 2$ \alpha $ core (with moderate extension) surrounded by the two valence neutrons occupying the $ \pi $ orbit.

On the other hand, various theoretical models have been used to study the structure of $ \rm{}^{10}Be $, including shell models^[18–21], nuclear cluster models^[22–26] and some $ ab $ $ initio $ methods^[27–29]. In Ref. [30], the shell model calculations with 4$ \hbar \omega $ model space with a microscopic effective nucleon-nucleon interactions, and it did not well reproduce the energy levels of $ \rm{}^{10}Be $. Moreover, the $ 0_2^+ $ state, considered an intruder state, cannot be described by simple shell model methods.

Within microscopic cluster models, the studies indicated that many states of $ \rm Be $ isotopes have 2$ \alpha $ clustering structure. In Refs. [31–34], it was found that the developed 2$ \alpha $ clustering structure in the ground state of $ \rm{}^{8}Be $ weakens in $ \rm{}^{10}Be $ due to the valence neutrons. The antisymmetrized molecular dynamics (AMD) discussed the band structure as $ K^{\pi}=0_1^+,\, 0_2^+,\, 1^- $, and $ 2^+ $. It is found that the molecular-like states with the developed 2$ \alpha $ structure construct the rotational bands $ K^{\pi}=0_2^+ $ and $ 1^- $ with small level spacing, which is supported by the experimental energy level. Recently, the AMD under a constrain on the deformation parameter^[35] analyzed the single particle orbits of the valence neutrons. It was found that the main component of the valence neutrons which are around two $ \alpha $ clusters seems to be the $ \sigma $ orbit for the negative parity of $ \rm{}^{10}Be $. The resonating group method (RGM) described the $ \alpha+\alpha+ {\rm{n}}+ {\rm{n}} $ four-body wave function of $ \rm{}^{10}Be $^[36], and the calculation indicated that the $ 2^- $ state has a polarized $ \rm{}^{9}Be $ core, influenced by molecular-like configurations, but well decouple from the $ s $-wave valence neutron, making it a clear candidate for an excited state neutron halo. Furthermore, in Ref. [37], the wave function of $ \rm{}^{10}Be $ is a superposition of various spatial configurations and deformations, including clustering of $ \rm {}^{5}He+ {}^{5}He $, $ \rm {}^{6}He + \alpha $, $ \rm {}^{7}Li+ {}^{3}H $, $ \rm {}^{8}Be + 2n $, and $ \rm {}^{9}Be + n$. More recently, The Tohsaki-Horiuchi-Schuck-Röpke (THSR) wave function^[38–39] was extended to describe $ \rm{}^{10}Be $^[40] within a new nonlocalized picture. It is found that the $ 0_1^+ $ and $ 0_2^+ $ states calculated by a single THSR wave function are consistent with other models as well as with experimental results.

In the present work, we aim to conduct studies on the clustering structure of the ground and excited states of $ \rm{}^{10}Be $. The $ \alpha+\alpha+ {\rm{n}}+ {\rm{n}} $ configuration is included within generator coordinate method (GCM) framework.

The paper is organized as follows: in Sec. I, we explain the framework of the GCM and the computational details. In Sec. II, we present and discuss the results for the ground and excited states of $ \rm{}^{10}Be $. The key conclusions of this study are summarized in Sec. III.

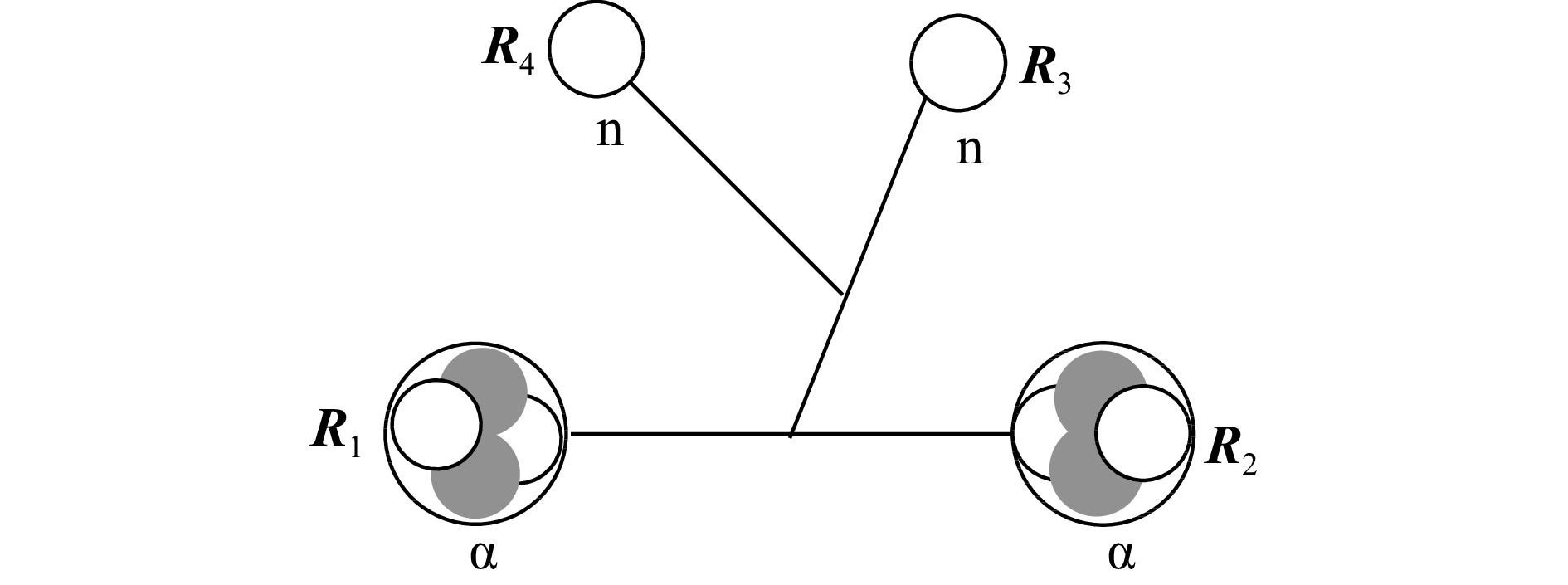
The $ \rm{}^{10}Be $ is described by four-body cluster model, involving two $ \alpha $ particles and two valence neutrons. The $ \alpha+\alpha+ {\rm{n}}+ {\rm{n}} $ configuration is illustrated in Fig. 1.

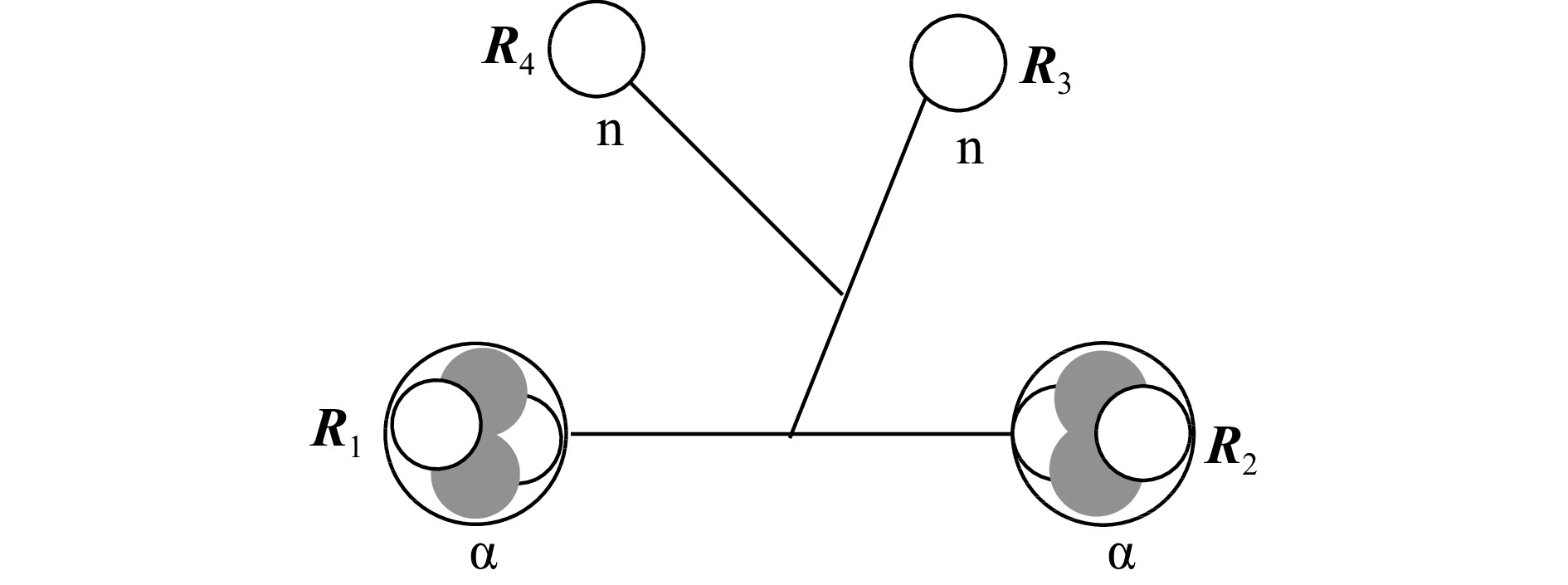
Figure 1.  Schematic diagram of $ \alpha+\alpha+ {\rm{n}}+ {\rm{n}} $ clustering configuration of $ \rm{}^{10}Be $.

The Brink wave function^[41] is used as the basis wave function for $ \alpha+\alpha+ {\rm{n}}+ {\rm{n}} $ configuration as follows,

where $ \varPhi_{\alpha} $ and $ \varPhi_{{\mathrm{n}}} $ are the wave functions of the $ \alpha $ particle and valence neutron, respectively. $ {\boldsymbol{R}}_1 $, $ {\boldsymbol{R}}_2 $, $ {\boldsymbol{R}}_3 $ and $ {\boldsymbol{R}}_4 $ are the generator coordinates of two $ \alpha $ and two valence neutrons, abbreviated as $ \{{\boldsymbol{R}}\}=\{{\boldsymbol{R}}_1, {\boldsymbol{R}}_2, {\boldsymbol{R}}_3, {\boldsymbol{R}}_4 \} $. The condition $ (4{\boldsymbol{R}}_1+4{\boldsymbol{R}}_2+{\boldsymbol{R}}_3+{\boldsymbol{R}}_4)/10=0 $ is applied. $ \phi({\boldsymbol{R}},{\boldsymbol{r}}_i)\chi_i \tau_i $ represents the i-th single-particle wave function, where $ \phi({\boldsymbol{R}},{\boldsymbol{r}}_i) $ is the spatial wave function. $ \chi_i $ and $ \tau_i $ denote the spin and isospin of each nucleon, respectively. The spin of two valence neutrons is set to up and down, respectively. The oscillator width b = 1.46 fm is chosen for all clusters to avoid the spurious center-of-mass problem in this work. Assuming that the two valence neutrons are placed in the same position ($ {\boldsymbol{R}}_3={\boldsymbol{R}}_4 $), Eq. (1) simplifies to the tri-cluster wave function of $ \alpha+\alpha+2{\mathrm{n}} $. Similarly, $ \alpha+\rm {}^{6}He $ configuration can be constructed by positioning one $ \alpha $ closer to the two valence neutrons.

The GCM wave functions of $ \rm {}^{10}Be $ are obtained by superposing over various $ \alpha+\alpha+ {\rm{n}}+ {\rm{n}} $ configuration, which can be written as

where $ \varPhi_{MK}^{J \pi}(\{R\}) $ is the projected wave functions,

$ P_{MK}^J $ and $ P_{\pi} $ denote the parity and angular momentum projector, respectively. The coefficients $ f_{\{R\} K} $ are determined by solving the Hill-Wheeler equation^[42], which is given by

The Hamiltonian employed in this study is as follows,

where $ t_i $ denotes the kinetic energy operator for the $ i $-th nucleon, while $ t_{\rm c.m.} $ corresponds to the kinetic energy operator for the center-of-mass. We adopted the Volkov No.2 interaction^[43] combined with the G3RS potential^[44–45] as the nucleon-nucleon interaction, which is given as

where $ P_{\sigma} $ and $ P_{\tau} $ stand for the spin and isospin exchange operators, respectively. $ V_1 = - 60.65 \; {\mathrm{MeV}} $, $ V_2 = 61.14\; {\mathrm{MeV}}$, $ a_1 $ = 1.80 fm, $ a_2 $ = 1.01 fm, $ W = 1 - M $, $ M $ = 0.60, and $ B=H=0.125 $. For the two-body spin-orbit force, $ P({}^{3}O) $ represents the projection operator to the triplet-odd states, $ b_1 = 5.0 \rm \ fm^{-2} $, $ b_2 = 2.778 \rm \ fm^{-2} $, and $ w_1=-w_2 = 2000 \; {\mathrm{MeV}} $.

To study the two-body clustering structure in $ \rm {}^{10}Be $, we calculate the reduced width amplitudes (RWAs) in the $ \alpha+\rm {}^{6}He $ and $ \rm {}^{9}Be + n$ channels. The RWAs in two-body channel is defined as

where $ \varPhi_{C_1}^{j_1 \pi_1} $ and $ \varPhi_{C_2}^{j_2 \pi_2} $ are the wave functions of cluster $ C_1 $ and $ C_2 $. The spins $ j_1 $ of cluster $ C_1 $ and $ j_2 $ of cluster $ C_2 $ are coupled to $ j_{12} $, then the $ j_{12} $ is coupled to the orbital angular momentum $ l $ of the relative-motion function to yield the total spin-parity $ J^{\pi} $. The parity $ \pi_1 $, $ \pi_2 $ and the orbital angular momentum $ l $ satisfy the relation $ \pi=\pi_1\pi_2(-)^{l} $. More details can be found in Refs. [46–48].

The ISM transition has been regarded as a powerful probe to identify the developed cluster states^[49–52] and is defined by

The isoscalar dipole (ISD) transitions as another probe for studying asymmetric cluster structures^[53–55]. The operator and transition strength are defined as follows,

where $ J_i $ and $ J_f $ are the angular momentums of the initial state $ |J_i M_i\rangle $ and final state $ |J_f M_f\rangle $, respectively. $ {\boldsymbol{r}}_i $ and $ {\boldsymbol{r}}_{\rm{c.m.}} $ denote the coordinate of the $ i $-th nucleon and the center of mass of the system, respectively. The $ Y_{1\mu} $ represents the solid spherical harmonics of degree 1 and order $ \mu $.

The electric dipole and quadrupole transition strengths $ B(E1) $ and $ B(E2) $ are important observational quantities, which can be represented as follows,

where $ \tau_{i{\textit{z}}} $ is the isospin projection of the $ i $-th nucleon.

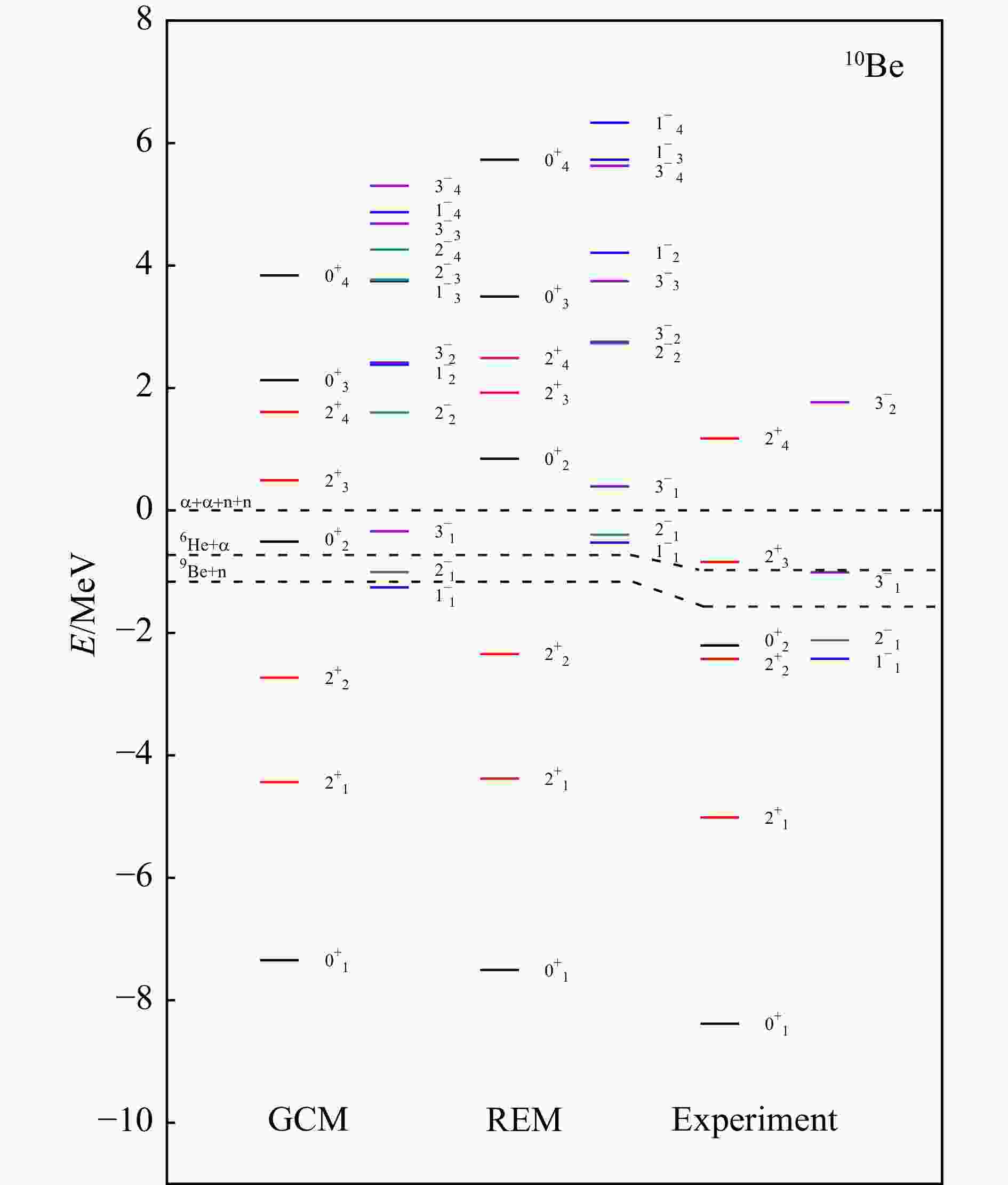
We performed GCM calculations by superposing 1 200 basis wave functions. The calculated energy spectrum is compared with experimental data and real-time evolution method (REM) results from Ref. [56], as shown in Fig. 2.

Figure 2.  The calculated and experimental energy spectra of ¹⁰Be. (color online)

For the low-lying states, the calculated ground state energy is slightly higher than that from REM calculations. However, for the bound $ 2_1^+ $ and $ 2_2^+ $ states, the calculated energies are lower than those of REM. The calculated energies of the $ 1_1^- $, $ 2_2^- $ and $ 3_1^- $ states are below the $ \alpha+\alpha+ {\rm{n}}+ {\rm{n}} $ threshold and basically consistent with the experimental data, whereas the $ 3_1^- $ state energy is slightly higher the threshold for the REM calculation. Notably, both our calculations and REM fail to describe the experimental $ 2_3^+ $ state. For the high-lying states, the calculated energies of $ 2_4^+ $ and $ 3_2^- $ states agree with experimental results. On the whole, our results basically reproduce the current experimental energy spectrum for both positive and negative parity states and is consistent with the REM calculations.

The isoscalar monopole transition is a measure of probing cluster structures. As discussed in the Refs. [51–52], the enhancement of monopole transitions strength reflect the degree of radial excitation from the excited cluster state to the ground state. In Table 1, we list the radii and ISM transition strengths based on present GCM calculations and AMD results. The ground state radius obtained from GCM calculation is 2.5 fm, which is consistent with the radius calculated by AMD. However, the radii of excited states of $ 0_2^+ $ and $ 0_3^+ $ calculated by AMD are larger than those of GCM. It is noted that both GCM and AMD calculations show enhancement in the monopole transition from the $ 0_3^+ $ state to the ground state. This enhancement indicated that the $ 0_3^+ $ state could be the well-developed cluster structure. Actually, in Ref. [57], they consider the $ 0_3^+ $ state would have a gaslike expanded dineutron nature.

The significant low-energy dipole (LED) strengths may suggest the emergence of new excitation modes, typically interpreted as collective oscillations of the entire system. In Ref. [58], three $ 1^- $ states in $ E_{\rm x} < 15 $ MeV were calculated using AMD+GCM with $ \alpha+\rm {}^{6}He $ and $ \alpha+\alpha+2{\mathrm{n}} $ cluster model. They found the $ 1_1^- $ state is dominated by the $ \alpha + \rm {}^{6}He $ configuration, whereas the $ 1_2^- $ and $ 1_3^- $ states can be explained by three-body excitations of the $ \alpha + \alpha + 2{\mathrm{n}} $ clustering.

We calculated the isoscalar dipole transition strengths from the ground state to $ 1^- $ states using superposed $ \alpha+\alpha+ {\rm{n}}+ {\rm{n}} $ wave function for comparison, and the results are listed in Table 2. We found that the $ 1_1^- $, $ 1_2^- $ and $ 1_3^- $ states all exhibit strong ISD transition strengths. However, the $ 1_2^- $ state has a small ISD strength in Ref. [58]. This discrepancy may arise from different configurations, particularly, the present GCM calculation include $ \alpha+\alpha+ {\rm{n}}+ {\rm{n}} $ configuration. In Ref. [58], only 198 $ \alpha+\rm {}^{6}He $ and $ \alpha+\alpha+2{\mathrm{n}} $ basis functions were utilized, whereas we superposed 1200 basis functions with $ \alpha+\alpha+ {\rm{n}}+ {\rm{n}} $ configuration.

The $ E1 $ and $ E2 $ transition strengths can give the deformation to reflect the cluster structure of excited states. The results for GCM, AMD, shell model and experimental data of transition strengths $B(E1,\,0^+_2 \to 1_1^-)$, $B(E2,\,2^+_1 \to 0_1^+)$, and $B(E2,\,0^+_2 \to 2_1^+)$ are presented in Table 3. The calculated $ E1 $ and $ E2 $ transition strengths agree well with the experimental data and close to the AMD calculation. For example, the experimental $ B(E2) $ value is 10.5, while our calculated result is 11.72, and the AMD result is 11. In contrast, the shell model gives a significantly overestimated value of 16.26^[21].

The two-body structure of $ {}^{6}\text{He}+\alpha $ and $ ^9\text{Be}+ {\rm{n}} $ configuration are important channels of ¹⁰Be and have been studied in many works^{[36, 56–57]}. By the use of Eq. (7), the RWAs of $ ^6\text{He}(0^+,2^+)+\alpha $ and $ ^9\text{Be}(3/2^-,1/2^+)+ {\rm{n}} $ configurations are calculated and the results are shown in Figs. 3~7. The RWAs measure the two-body clustering in the nuclei and can further serve as the input data to calculate the cross sections of reactions^[59]. From the results we can see that, in the first two $ 0^+ $ states, the structure of $ ^6\text{He}+\alpha $ is well formed. The RWAs of the ground state is basically consistent with the REM result^[56]. Notably, the $ ^6\text{He}(0^+)+\alpha $ curve, exhibiting two nodes in the ground state, is excited to three-node structure in the $ 0^+_2 $ state. The nodal excitation from the ground state to the $ 0^+_2 $ state has also been obtained by the calculation of Kobayashi et al^[57]. Analogically, the $ ^6\text{He}(2^+)+\alpha $ configuration present a one-node curve in the ground state, but two-node in the excited $ 0^+_2 $ state. In the ground state, the configurations of $ ^9\text{Be}(3/2^-)+ {\rm{n}} $ is comparable with $ ^6\text{He}(0^+)+\alpha $ and $ ^6\text{He}(2^+)+\alpha $, while the $ ^9\text{Be}(1/2^+)+ {\rm{n}} $ amplitude is negligible. In the higher $ 0^+ $ states, the amplitudes of $ ^9\text{Be}+ {\rm{n}} $ are further suppressed. Due to the complexity of angular-momentum coupling, more channels emerge in higher angular-momentum states of ¹⁰Be. Mainly three channels of $ ^6\text{He}+\alpha $ exist in the $ 2^+ $ states, namely $ [^6\text{He}(0^+)+\alpha]_0\otimes2 $, $ [^6\text{He}(2^+)+\alpha]_2\otimes0 $, and $ [^6\text{He}(2^+)+\alpha]_2\otimes2 $. The channels of $ [^6\text{He}(0^+)+\alpha]_0\otimes2 $ and $ [^6\text{He}(2^+)+\alpha]_2\otimes2 $ dominate in the $ 2^+_1 $ state, while in the $ 2^+_2 $ state, the $ [^6\text{He}(2^+)+\alpha]_2\otimes0 $ and $ [^6\text{He}(2^+)+\alpha]_2\otimes2 $ channels are more significant. In the higher $ 2^+_3 $ sate, the node-excitation of the above three channels can be observed. For the $ 2^+_4 $ state, all the three channels are obviously suppressed, as the result of that the state is too high above the $ ^6\text{He}+\alpha $ threshold. Meanwhile, in terms of the $ ^9\text{Be}+ {\rm{n}} $ structure, only the $ [^9\text{Be}(3/2^-)+ {\rm{n}}]_1\otimes1 $ channel is prominent in the $ 2^+_1 $ and $ 2^+_2 $ states. For the $ 2^+_3 $ and $ 2^+_4 $ states, all $ ^9\text{Be}+ {\rm{n}} $ configurations are insignificant.

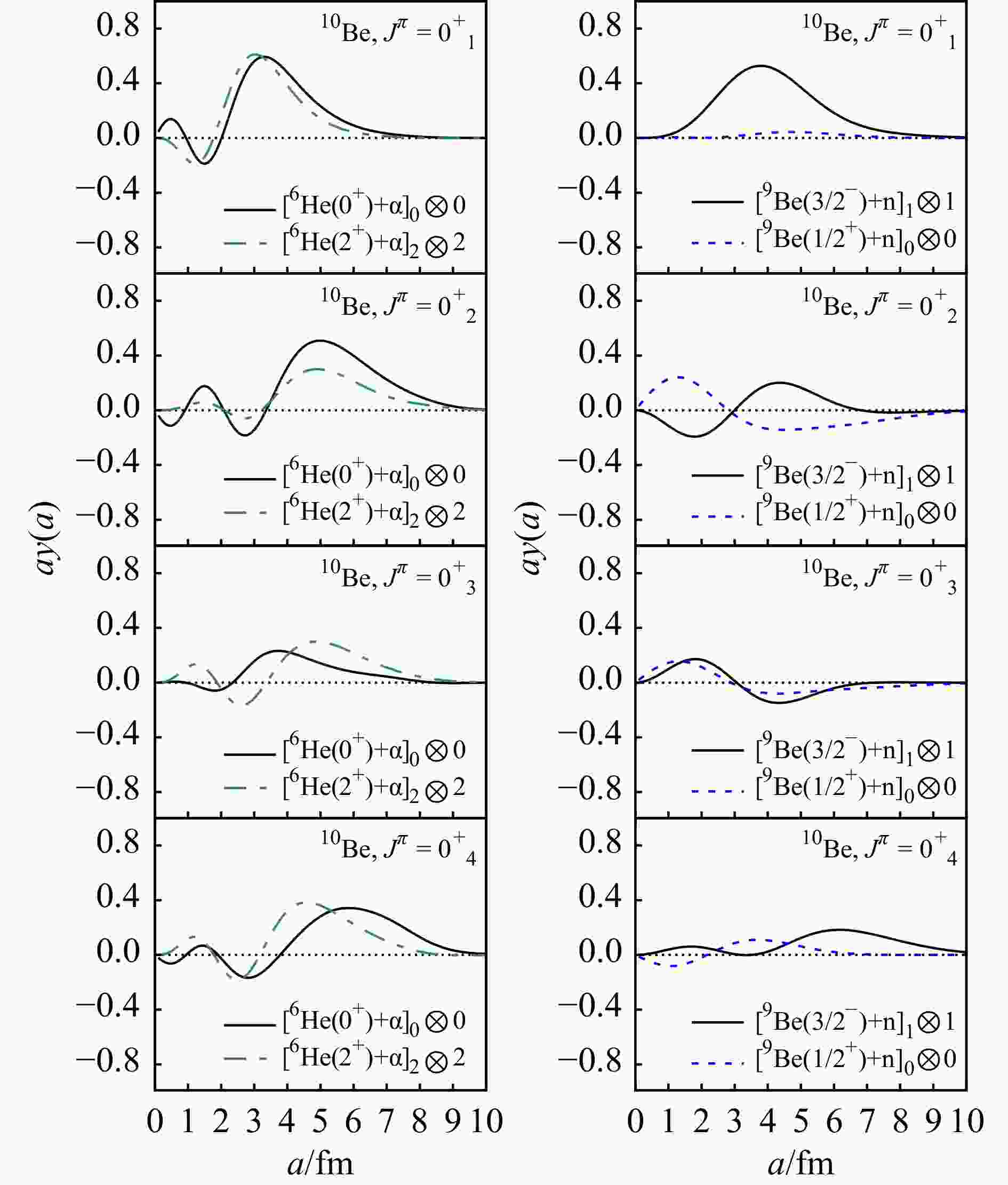
Figure 3.  The calculated RWAs of ¹⁰Be for $ 0^+_1 $, $ 0^+_2 $, $ 0^+_3 $, and $ 0^+_4 $ states. In the left panel are the RWAs of $ [^6\text{He}(0^+)+\alpha]_0\otimes0 $ and $ [^6\text{He}(2^+)+\alpha]_2\otimes2 $ channels. In the right panel are the RWAs of $ [^9\text{Be}(3/2^-)+ {\rm{n}}]_1\otimes1 $ and $ [^9\text{Be}(1/2^+)+ {\rm{n}}]_0\otimes0 $ channels. (color online)

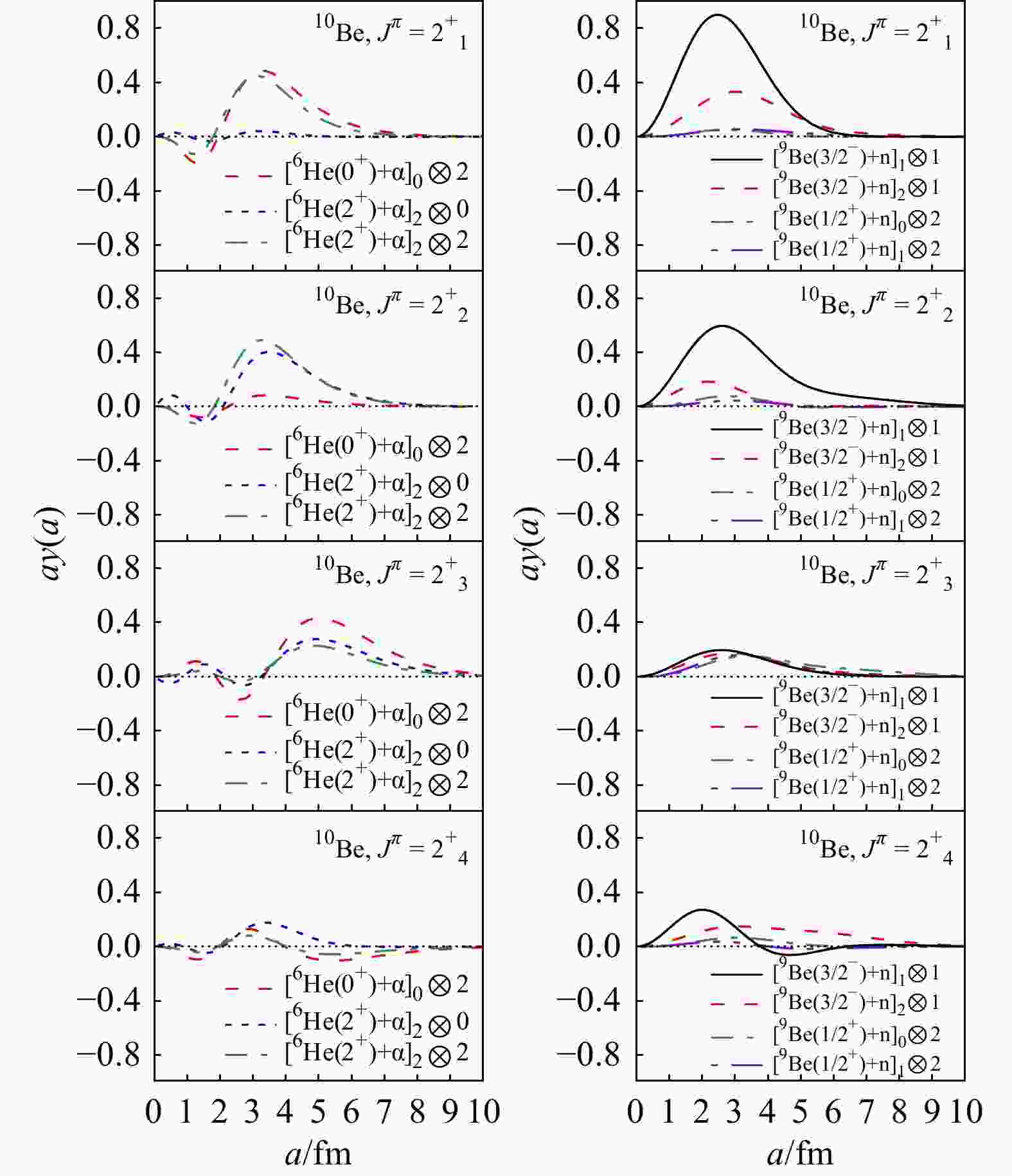
Figure 4.  The calculated RWAs of ¹⁰Be for $ 2^+_1 $, $ 2^+_2 $, $ 2^+_3 $, and $ 2^+_4 $ states. In the left panel are the RWAs of $ [^6\text{He}(0^+)+ $$ \alpha]_0\otimes2 $, $ [^6\text{He}(2^+)+\alpha]_2\otimes0 $, and $ [^6\text{He}(2^+)+ \alpha]_2\otimes2 $ channels. In the right panel are the RWAs of $ [^9\text{Be}(3/2^-)+ $$ {\rm{n}}]_1\otimes1 $, $ [^9\text{Be}(3/2^-)+ {\rm{n}}]_2\otimes1 $, $ [^9\text{Be}(1/2^+)+ {\rm{n}}]_0\otimes 2 $, and $ [^9\text{Be}(1/2^+)+ {\rm{n}}]_1\otimes2 $ channels. (color online)

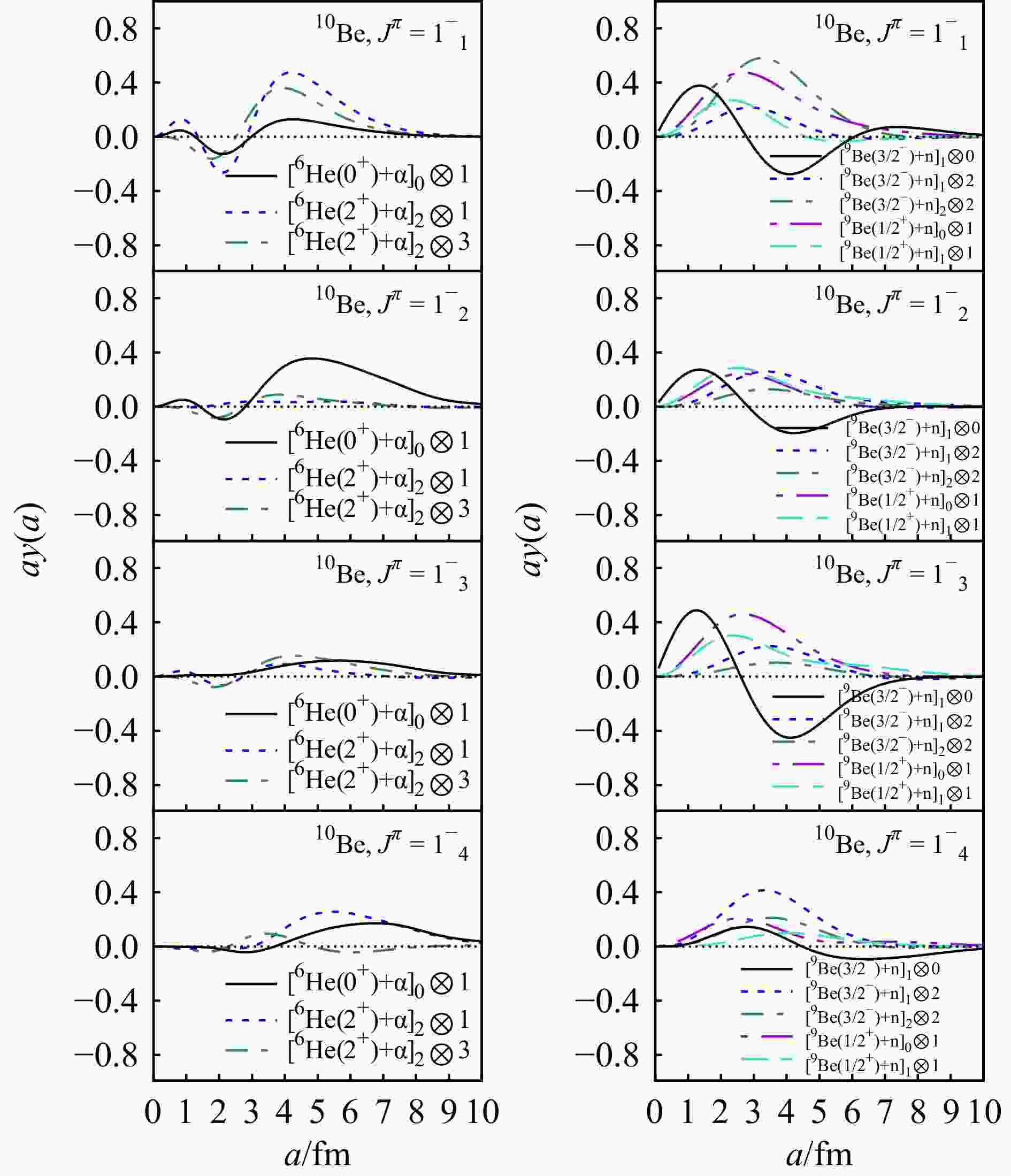
Figure 5.  The calculated RWAs of ¹⁰Be for $ 1^-_1 $, $ 1^-_2 $, $ 1^-_3 $, and $ 1^-_4 $ states. In the left panel are the RWAs of $ [^6\text{He}(0^+)+ $$ \alpha]_0\otimes1 $, $ [^6\text{He}(2^+)+\alpha]_2\otimes1 $, and $ [^6\text{He}(2^+)+\alpha]_2\otimes3 $ channels. In the right panel are the RWAs of $ [^9\text{Be}(3/2^-)+ $$ {\rm{n}}]_1\otimes0 $, $ [^9\text{Be}(3/2^-) + {\rm{n}}]_1\otimes 2 $, $ [^9\text{Be}(3/2^-) + {\rm{n}}]_2 \otimes 2 $, $ [^9\text{Be}(1/2^+)+ $$ {\rm{n}}]_0\otimes1 $, and $ [^9\text{Be}(1/2^+)+ {\rm{n}}]_1\otimes1 $ channels. (color online)

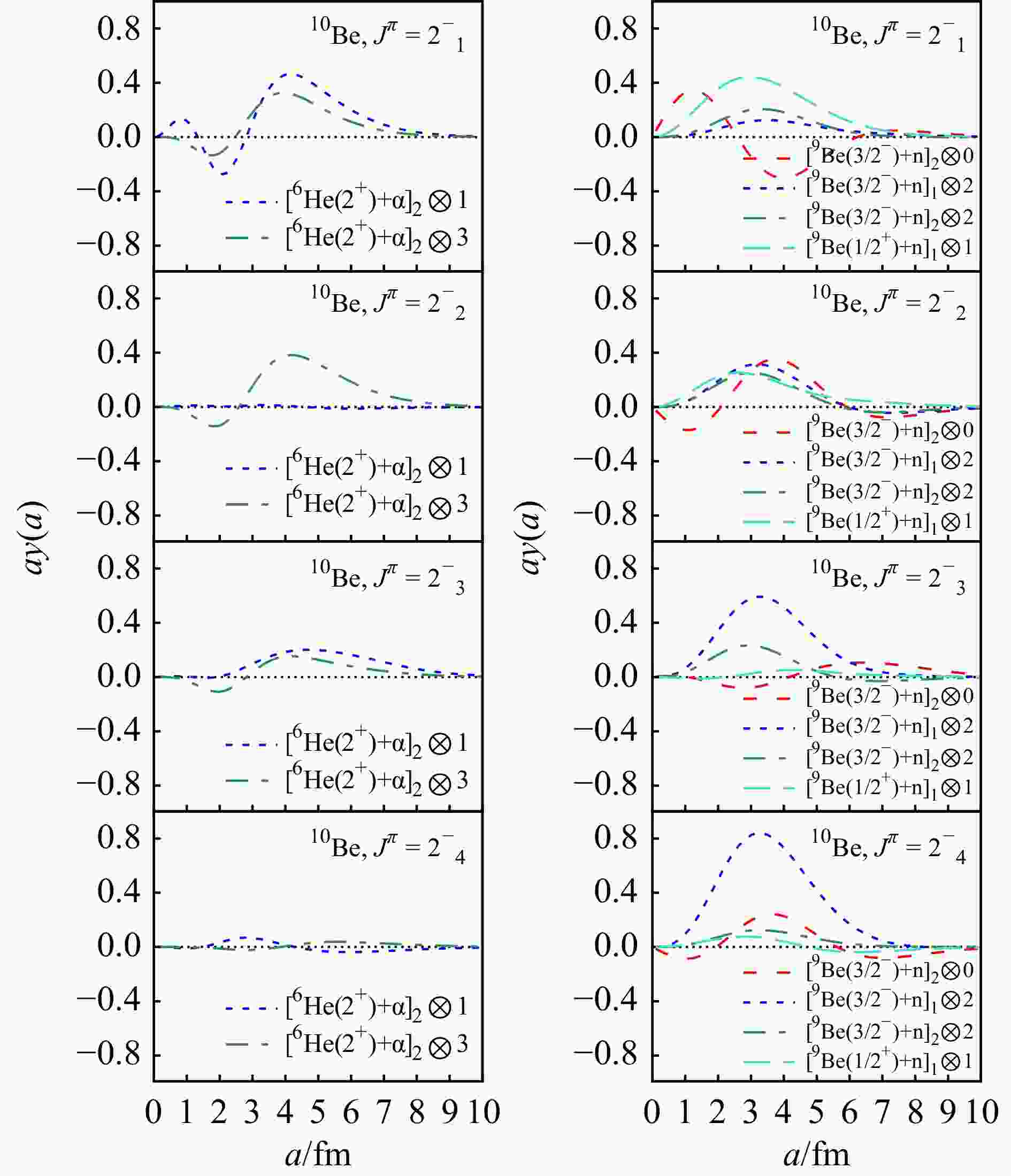
Figure 6.  The calculated RWAs of ¹⁰Be for $ 2^-_1 $, $ 2^-_2 $, $ 2^-_3 $, and $ 2^-_4 $ states. In the left panel are the RWAs of $ [^6\text{He}(2^+)+ $$ \alpha]_2\otimes1 $, and $ [^6\text{He}(2^+)+\alpha]_2\otimes3 $ channels. In the right panel are the RWAs of $ [^9\text{Be}(3/2^-)+ {\rm{n}}]_2\otimes0 $, $ [^9\text{Be}(3/2^-)+ $$ {\rm{n}}]_1\otimes2 $, $ [^9\text{Be}(3/2^-)+ {\rm{n}}]_2\otimes2 $, and $ [^9\text{Be}(1/2^+)+ {\rm{n}}]_1\otimes1 $ channels. (color online)

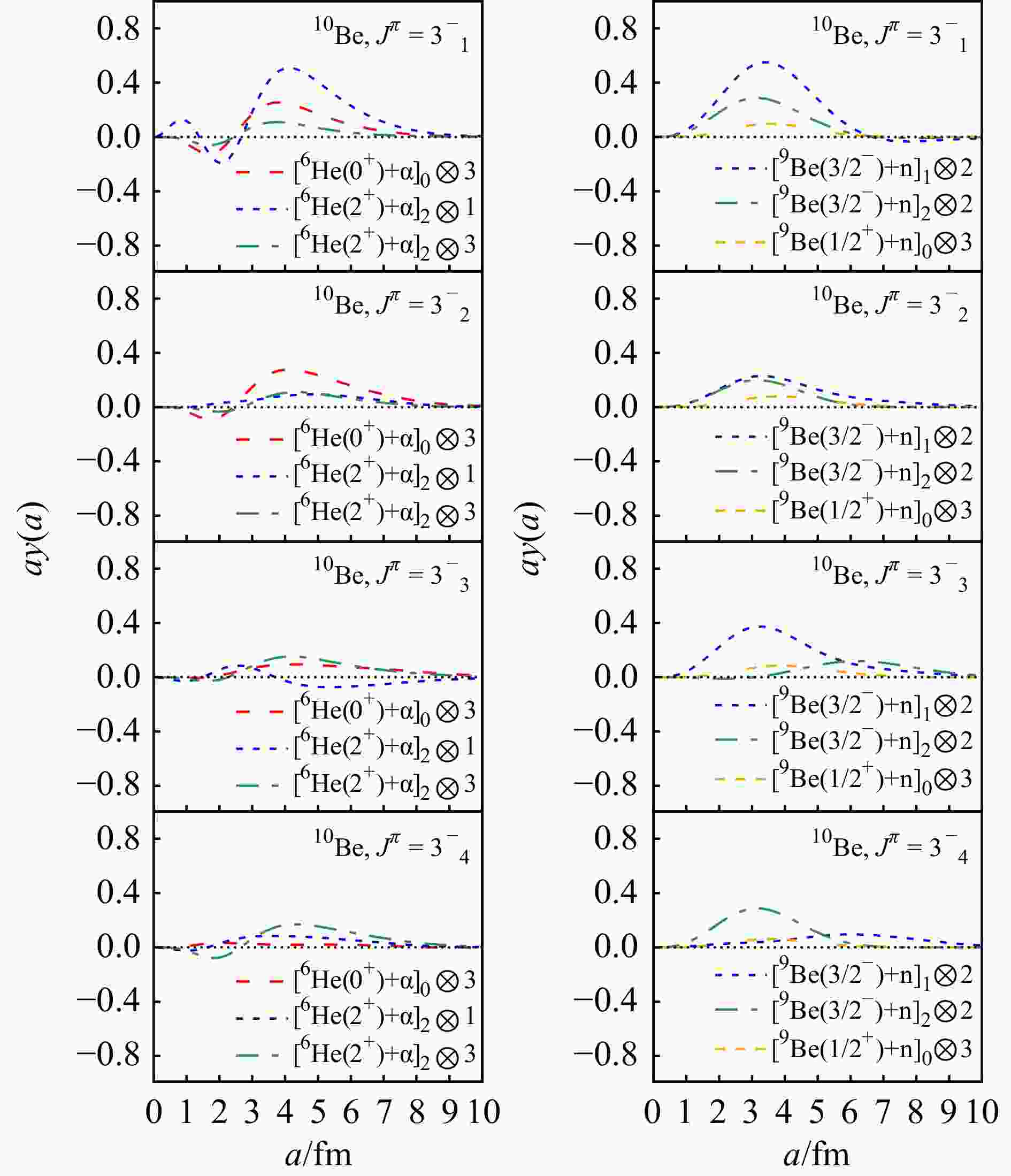
Figure 7.  The calculated RWAs of ¹⁰Be for $ 3^-_1 $, $ 3^-_2 $, $ 3^-_3 $, and $ 3^-_4 $ states. In the left panel are the RWAs of $ [^6\text{He}(0^+)+ $$ \alpha]_0\otimes3 $, $ [^6\text{He}(2^+)+\alpha]_2\otimes1 $, and $ [^6\text{He}(2^+)+\alpha]_2\otimes3 $ channels. In the right panel are the RWAs of $ [^9\text{Be}(3/2^-)+ $$ {\rm{n}}]_1\otimes2 $, $ [^9\text{Be}(3/2^-)+ {\rm{n}}]_2\otimes2 $, and $ [^9\text{Be}(1/2^+)+ {\rm{n}}]_0\otimes3 $ channels. (color online)

In the lowest three negative states near the $ ^6\text{He}+\alpha $ and $ ^9\text{Be}+ {\rm{n}} $ thresholds, namely $ 1^-_1 $, $ 2^-_1 $, and $ 3^-_1 $, the RWAs curves exhibit multi-configuration features, as in the lowest positive states $ 0^+_1 $, $ 2^+_1 $, and $ 2^+_2 $. Notably, the arrangements of $ ^6\text{He}+\alpha $ structure channels are quite similar in the $ 1^-_1 $ and $ 2^-_1 $ states, both containing significant $ [^6\text{He}(2^+)+\alpha]_2\otimes1 $ and $ [^6\text{He}(2^+)+\alpha]_2\otimes3 $ components, which is consistent with the results obtained by Arai^[36]. Additionally, the $ [^6\text{He}(2^+)+\alpha]_2\otimes1 $ channel in the $ 3^-_1 $ state also exhibit the alike curve as in $ 1^-_1 $ and $ 2^-_1 $. However, although still exhibit the one-node feature, the $ [^6\text{He}(2^+)+ \alpha]_2\otimes3 $ curve in $ 3^-_1 $ is obviously reduced, compared with that in the $ 1^-_1 $ and $ 2^-_1 $ states. The $ ^9\text{Be}+ {\rm{n}} $ channels also show some common features in the $ 1^-_1 $ and $ 2^-_1 $ states, but behave differently in $ 3^-_1 $. The $ [^9\text{Be}(3/2^-)+ {\rm{n}}]_1\otimes0 $ in $ 1^-_1 $ and $ [^9\text{Be}(3/2^-)+ {\rm{n}}]_2\otimes0 $ in $ 2^-_1 $, as well as the $ [^9\text{Be}(1/2^+)+ {\rm{n}}]_0\otimes1 $ in $ 1^-_1 $ and $ [^9\text{Be}(1/2^+)+ {\rm{n}}]_1\otimes1 $ in $ 2^-_1 $, exhibit analogical amplitudes, while the pattern of $ 3^-_1 $ is distinct from that of $ 1^-_1 $ and $ 2^-_1 $. Such characteristics, along with the fact that the $ 1^-_1 $ and $ 2^-_1 $ states are very close in the spectra, suggest the similarity between these two states in structure. The other higher negative states do not show significant $ ^6\text{He}+\alpha $ component, since most of the maximum amplitudes are less than $ 0.4 $. In these states, due to the high excited energy, are more likely to be dominated by three-body or four-body configurations. However, regarding the $ ^9\text{Be}+ {\rm{n}} $ structure, some of the high negative states exhibit pronounced $ \text{core}+ {\rm{n}} $ configurations. In the state $ 1^-_3 $, significant $ [^9\text{Be}(3/2^-)+ {\rm{n}}]_1\otimes0 $ and $ [^9\text{Be}(1/2^+)+ {\rm{n}}]_0\otimes1 $ channels exist, exhibiting one-node and zero-node curves, respectively. Besides, the $ [^9\text{Be}(3/2^-)+ {\rm{n}}]_1\otimes2 $ configuration is prominent in both the $ 2^-_3 $ and $ 3^-_3 $ states.

The spectra and electromagnetic transition strengths of ¹⁰Be are analysed using the microscopic four-body cluster model, in which the structure of $ \alpha+\alpha+ {\rm{n}}+ {\rm{n}} $ is employed and several correlations between the clusters are considered. For the low-lying states, the results of our GCM calculation are consistent with that of the REM and experiments. The monopole transition strength indicates the existence of well-developed cluster structures in the $ 0_3^+ $ state, and the $ E1 $ and $ E2 $ transition strengths are consistent with AMD calculations.

The RWAs results show that, in most of the states below or around the two-body thresholds, the structures of $ ^6\text{He}+\alpha $ and $ ^9\text{Be}+ {\rm{n}} $ are both significant. As the energy increasing, the components of two-body structures are suppressed, which may be due to the breakup of $ \rm{}^6{He} $ and $ \rm{}^9{Be} $ at higher excitation energies. However, in a few states high above the $ \alpha+\alpha+ {\rm{n}}+ {\rm{n}} $ threshold, prominent $ ^9\text{Be}+ {\rm{n}} $ channels exist.

Acknowledgments The work was supported by China National Key R&D Program (2022YFA1602402) and Shanghai "Science and Technology Innovation Action Plan" Natural Science Foundation Project (21ZR1409500)