-
从现实核力出发的第一性原理计算(ab initio calculations)已成为当今核理论领域的重要前沿研究方向。它不仅能够提供高精度的计算结果与可靠的理论预言,同时由于没有额外的参数依赖,能够在有效场论的框架下建立起与量子色动力学(QCD)联系的桥梁。因此第一性原理计算对核理论的发展、核实验的解释及预言、核天体环境下元素合成过程的理解以及中子星结构的研究等都非常重要。近些年来随着手征有效核力的逐步完善[1−6]与量子多体方法的不断发展,第一性原理计算取得了许多令人瞩目的成就。较早出现的无芯壳模型(NCSM)[7]与量子蒙特卡罗(QMC)方法[8]能够对较轻的原子核进行严格计算,但由于其计算量随核子数呈指数增加,难以触及更重的原子核体系。现实核力(Realistic Nuclear Forces)壳模型(SM)[9−10]通过多体微扰的方法构建出模型空间哈密顿量, 在保证精度的同时有效地降低了计算量, 拓展了其理论描述的能力。非微扰的Coupled Cluster[11]和介质中相似重整化群IM-SRG[12−13]将满壳或半满壳核作为参考态, 以此能够对中重核进行理论计算与预言。而价空间的IMSRG[14],则能够对开壳原子核进行可靠的描述。通过采用Gamow-Berggren基,现实核力Gamow壳模型[15−25]与Gamow IM-SRG[26]能够将连续谱效应考虑进来对弱束缚区原子核进行有效的理论计算。
原子核格点有效场论(Nuclear Lattice Effective Field Theory, NLEFT)是近些年发展起来的一种第一性原理计算方法[27−37]。它将有效场论与格点蒙特卡罗方法有机地结合在一起。相较于其他第一性原理方法,NLEFT最大的优势是在格点的框架下能够同时构建起核子间相互作用与求解量子多体问题。得益于蒙特卡罗方法的特性,它的计算复杂度随核子数成多项式增长,同时能够提取诸如核集团结构[34, 37]、α-α散射[32]等其它第一性原理方法难以计算的强关联信息。
与其它量子蒙特卡罗方法一样,NLEFT也面临着“符号问题”的困难。在NLEFT中,我们使用辅助场(Auxiliary field)方法将核子间相互作用转变为核子与“背景场”间的相互作用。但核力的排斥部分会使得核子与“背景场”间的相互作用出现振荡的虚部相位,从而降低蒙卡计算中的统计信号,导致计算结果出现很大的统计误差。为此,原子核格点有效场论合作组发展出波函数匹配(Wave Function Matching, WFM)方法[38]与微扰量子蒙特卡罗方法(perturbative Quantum Monte Carlo method, pQMC)[36],其核心是构建出一个幺正变换,它能将高精度的手征哈密顿量H变换到$ H' $,其中$ H' $靠近一个没有符号问题的、容易处理的哈密顿量$H^0$。因此,较小的$ H' - H^0 $部分则可以通过微扰论的方法进行计算。基于以上方法,我们与合作者发展了Rank-one Operator (RO)方法[39]对算符进行微扰计算。
在本文中,我们进一步发展格点上的微扰计算方法,通过引入两点关联函数进行原子核电荷半径的计算。在第1节,我们将对格点有效场论中的微扰计算进行简要介绍;在第2节,给出在格点上、半径算符的计算方法;在第3节,将讨论微扰计算的收敛性与有限体积效应,并给出使用完整N3LO核力的计算结果;最后作出总结与展望。
-
格点有效场论是一种基于时空格点离散化的量子蒙特卡罗方法[27, 31]。它使用虚时投影得到体系的基态波函数$ |\varPsi\rangle=\lim _{L_t \rightarrow \infty} M^{L_t / 2}|\varPsi_T\rangle $,其中$ |\varPsi_T\rangle $为试探波函数,而$ M $是每一个虚时时间隔$ a_t $所对应的转移矩阵$ M=: e^{-a_tH}: $。冒号表示算符正规乘积。在得到基态波函数后,算符的期望通过振幅$ {\cal{M}} $的比值求得,$ \langle {\cal{O}} \rangle = {{\cal{M}}({\cal{O}})}/{{\cal{M}}} $,其中振幅$ {{\cal{M}}({\cal{O}})}=\langle \varPsi \vert {{\cal{O}}} \vert \varPsi \rangle $,代表了包含有算符的关联矩阵行列式(determinant of correlation matrix)。通过辅助场(Auxiliary Field)的引入,我们可以严格地将哈密顿量H中两体和三体相互作用转化为单个粒子与辅助场间的相互作用。但经过辅助场变换后,核力中的排斥部分会造成计算中出现复的相因子。这个相因子会导致在蒙卡统计中出现强烈的正负相消,也就是著名的"符号问题"。迄今为止还没有解决"符号问题"的一般方案。所有解决方法都仅适用于特定系统。
为了克服“符号问题”所带来的计算困难,我们发展了WMF[38]方法和pQMC[36]方法。从高精度的手征哈密顿量$ H_{{\rm{N3LO}}} $出发,WMF方法构建出一组幺正变换将$ H_{{\rm{N3LO}}} $变为$ H'_{{\rm{N3LO}}} $。这组幺正变换使得在两体系统下,$ H'_{{\rm{N3LO}}} $与一个易处理的$ H^S $的波函数在短程部分相匹配。此幺正变换确保了高精度哈密顿量与易处理的哈密顿量之间的差异$ H'_{{\rm{N3LO}}}-H^S $较小,并且能够通过微扰的方法进行计算。通常我们选取近似SU(4)对称性(Leading-order, LO)手征哈密顿量作为$ H^S $。更多相关细节,请查看文献[36, 38−39]。
为了计算格点上的微扰波函数与算符,我们将哈密顿量$ H $拆分成非微扰与微扰两个部分$ H=H_0+H_1 $,与之相对应的转移矩阵为$ M=M_0+M_1 $。对于基态波函数$ |\varPsi\rangle=\lim _{L_t \rightarrow \infty} (M_0+M_1)^{L_t / 2}|\varPsi_T\rangle $,我们有0阶非微扰部分:
$$ \begin{array}{*{20}{l}} |\varPsi^{(0)}\rangle=\lim \limits_{L_t \rightarrow \infty} M_0^{L_t / 2}|\varPsi_0\rangle , \end{array} $$ (1) 与1阶微扰修正:
$$ \begin{array}{*{20}{l}} |\varPsi^{(1)}\rangle=\lim \limits_{L_t \rightarrow \infty} \displaystyle\sum\limits_{k=1}^{L_t / 2} M_0^{L_t / 2-k} M_1 M_0^{k-1}|\varPsi_0\rangle 。 \end{array} $$ (2) 对于能量期望我们有$ E = E^{(0)}+ E^{(1)}+\cdots $,其中
$$ E^{(0)} = \frac{\langle\varPsi^{(0)}|H_0| \varPsi^{(0)}\rangle }{\langle\varPsi^{(0)} \mid \varPsi^{(0)}\rangle} $$ (3) 以及
$$ E^{(1)} = \frac{\langle\varPsi^{(0)}|H_1| \varPsi^{(0)}\rangle }{\langle\varPsi^{(0)} \mid \varPsi^{(0)}\rangle} 。 $$ (4) 而算符期望则相对复杂,包含0阶非微扰部分:
$$ \langle {\cal{O}} \rangle^{(0)} =\frac{\langle\varPsi^{(0)}|{\cal{O}}| \varPsi^{(0)}\rangle }{\langle\varPsi^{(0)} \mid \varPsi^{(0)}\rangle} = \frac{{\cal{M}}^{(0)}_o}{{\cal{M}}^{(0)}} ; $$ (5) 与1阶修正:
$$ \begin{split} \langle{\cal{O}}\rangle^{(1)} =&\frac{\langle\varPsi^{(0)}|{\cal{O}}| \varPsi^{(1)}\rangle +\text { c.c. }}{\langle\varPsi^{(0)} \mid \varPsi^{(0)}\rangle} - \frac{\langle\varPsi^{(0)}|{\cal{O}}| \varPsi^{(0)}\rangle}{\langle\varPsi^{(0)} \mid \varPsi^{(0)}\rangle} \frac{\langle\varPsi^{(1)} \mid \varPsi^{(0)}\rangle+c.c}{\langle\varPsi^{(0)} \mid \varPsi^{(0)}\rangle} \\ =&\frac{ {\cal{M}}_o^{(1)}}{ {\cal{M}}^{(0)}}-\frac{ {\cal{M}}_o^{(0)}}{ {\cal{M}}^{(0)}} \frac{ {\cal{M}}^{(1)}}{ {\cal{M}}^{(0)}},\\[-121pt] \end{split} $$ (6) 其中共有四种不同类型的振幅:$ {\cal{M}}^{(0)} $、$ {\cal{M}}^{(1)} $、$ {\cal{M}}_o^{(0)} $与$ {\cal{M}}_o^{(1)} $。前三种振幅的计算相对容易处理,这里$ {\cal{M}}^{(0)} $为非微扰波函数的关联矩阵行列式$ {\mathcal{M}}^{(0)}=\det {\mathcal{A}}^{(0)} $, 关联矩阵$ {\cal{A}}^{(0)} $的矩阵元由单粒子波函数积分求得$ {\cal{A}}^{(0)}_{ij} = \langle \phi_i \vert \phi_j \rangle $。类似地$ {\cal{M}}^{(1)} $为微扰波函数的关联矩阵行列式。对于包含有算符$ {\cal{O}} $的振幅$ {\cal{M}}_o^{(0)} $,我们可以通过Jacobi方法求得:
$$ \begin{split} \det {\cal{A}}({\cal{O}}) &= \frac{{\rm d} \det {\cal{A}}[e^{t {{\cal{O}}}}] }{{\rm d} t } \Big{|}_{t=0}\\ & = \det {\cal{A}} [e^{t {{\cal{O}}}} ] \, {\rm{tr}} \big{\{} {\cal{A}}^{-1} e^{t {{\cal{O}}}} {\cal{A}}[{{{\cal{O}}}} e^{t {{\cal{O}}}} ] \big{\}} \Big{|}_{t=0}\\ &= \det {\cal{A}} \, {\rm{tr}} \big{[} {\cal{A}}^{-1} {\cal{A}}({{{\cal{O}}}} ) \big{]},\\[-104pt] \end{split} $$ (7) 更多细节请查看文献[27, 31]。真正的困难出现在微扰的转移矩阵$ M_1 $与算符$ {\cal{O}} $同时存在的$ {\cal{M}}_o^{(1)} $。最直接的原因来自于多于三体的算符插入将会使得Jacobi公式变得非常复杂,而微扰转移矩阵$ M_1 $中已经包含了手征两体与三体算符,与此同时我们还需要考虑可观测量的算符插入(例如两点关联函数算符),这将使计算变得异常困难。
为此我们与合作者发展出RO (Rank-one Operator)方法[39]。在这个方法中,单体算符可以被拆分成秩为1的组分,$ {\cal{O}} = \sum_{\alpha\alpha',\, is} F_{\alpha',\, is}^{\dagger}F_{\alpha,\, is} $,其中$ \alpha $为轨道标记,$ F_\alpha= \sum_{{\boldsymbol{n}}} a_{is}({\boldsymbol{n}}) f_{\alpha,\, is}({\boldsymbol{n}}) $,$ F_\alpha^{\dagger}=\sum_{{\boldsymbol{n}}} a_{\alpha, is}^{\dagger}({\boldsymbol{n}}) f_{\alpha, is}^*({\boldsymbol{n}}) $以及代表同位旋与自旋的$i,\; s$。可以看出$ F_{\alpha',\, is}^{\dagger}F_{\alpha,\, is} $的秩为1,任何指数高于1的$ F_{\alpha',\, is}^{\dagger}F_{\alpha,\, is} $组合在normal ordering后作用在单体波函数上将为0。因此我们有关$ F_{\alpha',\, is}^{\dagger}F_{\alpha,\, is} $线性关系式:
$$ \begin{array}{*{20}{l}} F_{\alpha_1^{\prime}}^{\dagger} F_{\alpha_1}=\lim \limits_{c \rightarrow \infty} c^{-1}: \exp \left(c F_{\alpha_1^{\prime}}^{\dagger} F_{\alpha_1}\right):, \end{array} $$ (8) 并可以应用到求解$ {\cal{M}}_o^{(0)} $中:
$$ \begin{array}{*{20}{l}} {\cal{M}}_o^{(0)} = \lim\limits_{c \rightarrow \infty} \displaystyle\sum\limits_{\alpha\alpha',\, is} {\cal{M}}^{(0)}[c F_{\alpha',\, is}^{\dagger}F_{\alpha,\, is}]/ c 。 \end{array} $$ (9) 对于求解$ {\cal{M}}_o^{(1)} $,我们能够通过RO方法与Jacobi方法分别处理算符$ {\cal{O}} $与微扰转移矩阵$ M^{(1)} $的插入,最终对其进行计算。值得一提的是,Rank-one Operator方法拓展到两体或多体算符非常直接,并且原则上能够应用到任何依赖于使用行列式做反对称化的量子多体方法中。更多有关细节请参考文献[39]。
-
原子核电荷半径的理论计算通常包含以下几项的贡献[40]:
$$ \langle r_{\mathrm{ch}}^2\rangle=\langle r_{\mathrm{pp}}^2\rangle+R_{\mathrm{p}}^2+\frac{N}{Z} R_{\mathrm{n}}^2+\frac{3 \hbar^2}{4 m_{\mathrm{p}}^2 c^2} , $$ (10) 质子相对于原子核质心的半径、质子半径、中子半径修正以及相对论修正项。本文中质子半径$ R_{\mathrm{p}} = 0.840^{+0.003+0.002}_{-0.002-0.002}\; \mathrm{fm} $[41],中子半径$ R_{\mathrm{n}}^2= -0.105^{+0.005}_{-0.006}\; \mathrm{fm}^2 $[42], 以及$\frac{3 \hbar^2}{4 m_{\mathrm{p}}^2 c^2} \approx 0.033~172 \;\mathrm{fm}^2$。除此之外,自旋轨道耦合也会带来很小的相对论修正,这部分的贡献将在未来的工作中加入。电荷半径的主要贡献来自于质子相对于原子核质心的半径$ r_{\rm pp} $,这也是计算中的难点。
在NLEFT中目前有两种方案来计算$ r_{\mathrm{pp}} $:Pinhole方法与两体关联函数。Pinhole方法中[34],我们通过引入Pinhole来确定每个核子的位置坐标,进而计算质心位置与半径。但是由于Pinhole方法通常会引入更大的“符号问题”,在本文中我们选择使用两体关联函数来计算质子相对于质心的半径:
$$ \begin{split} \langle r_{\rm pp}^2 \rangle = &\frac{1}{Z A} \int {\mathrm{d}}^3 r {\mathrm{d}}^3 r^{\prime} \langle\rho_p(\boldsymbol{r}) |\boldsymbol{r}-\boldsymbol{r}^{\prime}|^2 \rho (\boldsymbol{r}^{\prime} ) \rangle - \\ &\frac{1}{2 A^2} \int {\mathrm{d}}^3 r {\mathrm{d}}^3 r^{\prime} \langle\rho(\boldsymbol{r}) |\boldsymbol{r}-\boldsymbol{r}^{\prime}|^2 \rho (\boldsymbol{r}^{\prime} ) \rangle, \end{split} $$ (11) 其中:$ \rho(\boldsymbol{r}) $为单体密度算符;$ |\boldsymbol{r}-\boldsymbol{r}^{\prime}| $则代表了两个密度测量点间的距离。
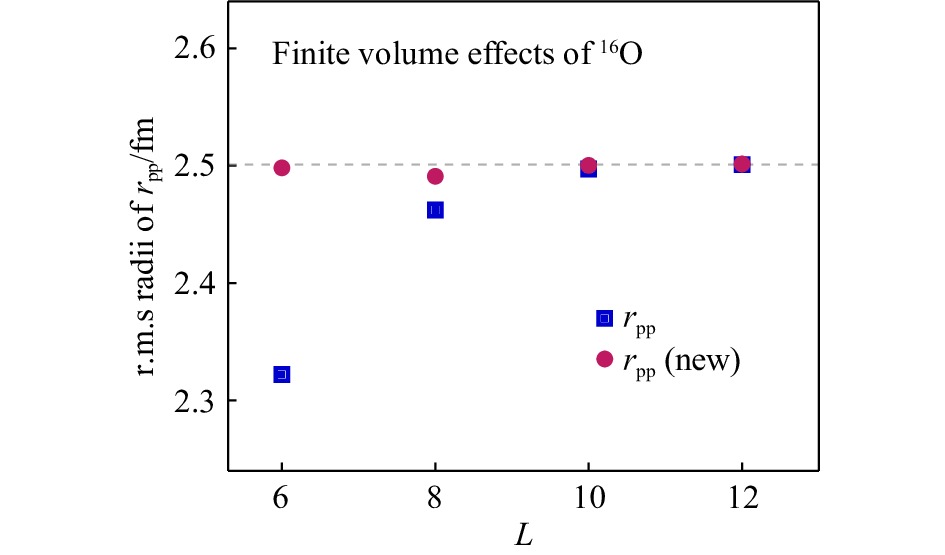
在具有$ L^3 $个格点的立方盒子中,我们采取周期边界条件,并有$ -{L}/{2}< r_x, r_y, r_z \leqslant{L}/{2} $。在格点上计算两点距离时我们也通常要求$ -{L}/{2}< r_x - r'_x \leqslant{L}/{2} $。可以看到,当格点$ L $不足够大时由于$ | r_x - r'_x |\leqslant{L}/{2} $会使测量半径偏小,引入额外的有限体积效应(Finite Volume Effects)。为此,我们发展出一个新的方法来测量两点间距离,包含有两个步骤:1) 通过计算在$ x,\, y,\, z $方向上的单体密度并找到大致的质心位置$ (x_{cm},\, y_{cm},\, z_{cm}) $;2) 两点间的距离由$ | {\rm{Lmod}}(r_x - x_{cm}) - {\rm{Lmod}}(x_{cm} - r'_x) | $给出,其中$ {\rm{Lmod}} $会将数值约化到$ (-{L}/{2},\, {L}/{2}] $区间。在下一个小节中我们将看到,使用新定义的格点上的两点距离将有效地减小有限体积效应。
为了在格点上进行半径计算,我们首先定义点状粒子半径算符:
$$ \hat{{\cal{R}}}^2_i = \sum_{{{\boldsymbol{y}}}} \hat{\rho}_i[{{\boldsymbol{y}}}] \sum_{x} \hat{\rho}[{{\boldsymbol{x}}}+{{\boldsymbol{y}}}] {{\boldsymbol{r}}}^2[{{\boldsymbol{x}}}], $$ (12) 其中:$ {{\boldsymbol{x}}} $和$ {{\boldsymbol{y}}} $代表三维格点坐标;指标i代表同位旋:质子、中子或不加指标代表质子加中子。因此我们可以写出:
$$ \langle r^2 \rangle=\frac{1}{2 A^2} \langle \hat{{\cal{R}}}^2 \rangle, $$ (13) $$ \langle r_{\rm pp}^2 \rangle= \frac{1}{Z A} \langle \hat{{\cal{R}}}_p^2 \rangle - \frac{1}{2 A^2} \langle \hat{{\cal{R}}}^2 \rangle, $$ (14) 与
$$ \langle r_{{\mathrm{nn}}}^2 \rangle= \frac{1}{N A} \langle \hat{{\cal{R}}}_p^2 \rangle - \frac{1}{2 A^2} \langle \hat{{\cal{R}}}^2 \rangle 。 $$ (15) 我们结合RO方法与式(7)第一行中的求导方法,可以得到关于算符$ \hat{{\cal{R}}}^2_i $的振幅计算公式:
$$ \begin{split} {\cal{M}}(\hat{{\cal{R}}}_i^2) =& \lim_{c \to \infty} \frac{d \langle \varPsi_0 \vert \cdots \left(1+c\displaystyle\sum_{{{\boldsymbol{y}}}}\displaystyle\sum_{s}\hat{\rho}_{is}[{{\boldsymbol{y}}}]\right) e^{\epsilon \hat{{\cal{P}}}} \cdots \vert \varPsi_0 \rangle}{c d \epsilon} |_{\epsilon = 0}\\ =& \lim_{\substack{c \to \infty \\ \epsilon \to 0}} \sum_{s} \frac{1}{c \epsilon} \left\{ {\cal{M}}\left[\left(1+c\sum_{{{\boldsymbol{y}}}}\hat{\rho}_{is}[{{\boldsymbol{y}}}]\right)\left(1+\epsilon \hat{{\cal{P}}}\right)\right]-\right. \\ & \left. {\cal{M}}\left[\left(1+c \sum_{{{\boldsymbol{y}}}}\hat{\rho}_{is}[{{\boldsymbol{y}}}]\right)\right] \right\} \\ =& \lim_{\substack{c \to \infty \\ \epsilon \to 0}} \sum_{s} \frac{1}{c \epsilon} ( {\cal{M}}_{c\epsilon} - {\cal{M}}_c ), \\[-1pt] \end{split} $$ (16) 其中$ \hat{\rho}_{is} = a^{\dagger}_{is}a_{is} $是秩为1的算符,为了公式简洁,我们新定义了算符$ \hat{{\cal{P}}} = \sum_{{{\boldsymbol{x}}}} \hat{\rho}[{{\boldsymbol{x}}}+{{\boldsymbol{y}}}] {{\boldsymbol{r}}}^2[{{\boldsymbol{x}}}] $。
本文中我们将首次应用上述方案计算原子核半径,同时结合第1节中所概述的微扰蒙特卡罗方法,使用高精度的手征N3LO核力对原子核半径进行微扰计算。在以下计算中,我们设置格点的间距$ a=1/150 \; {\rm{MeV}}^{-1}\approx 1.32 \; {\mathrm{fm}}$以及虚时间隔$ a_t=1/1000 \;{\rm{MeV}}^{-1} $。
-
为了验证半径微扰计算的可靠性,我们首先使用一个简单模型进行验证。在这个模型中,哈密顿量$ H $包含两部分$ H=T+V $,其中$ T $是动能项,$ V $是两体接触项,耦合强度为$ -4.2\times 10^{-7} $MeV$ ^{-2} $。我们将$ H $拆分成非微扰的$ H_0=T + (1-x)V $与微扰的$ H_1=xV $,同时引入了参数$ x $控制微扰部分的大小。
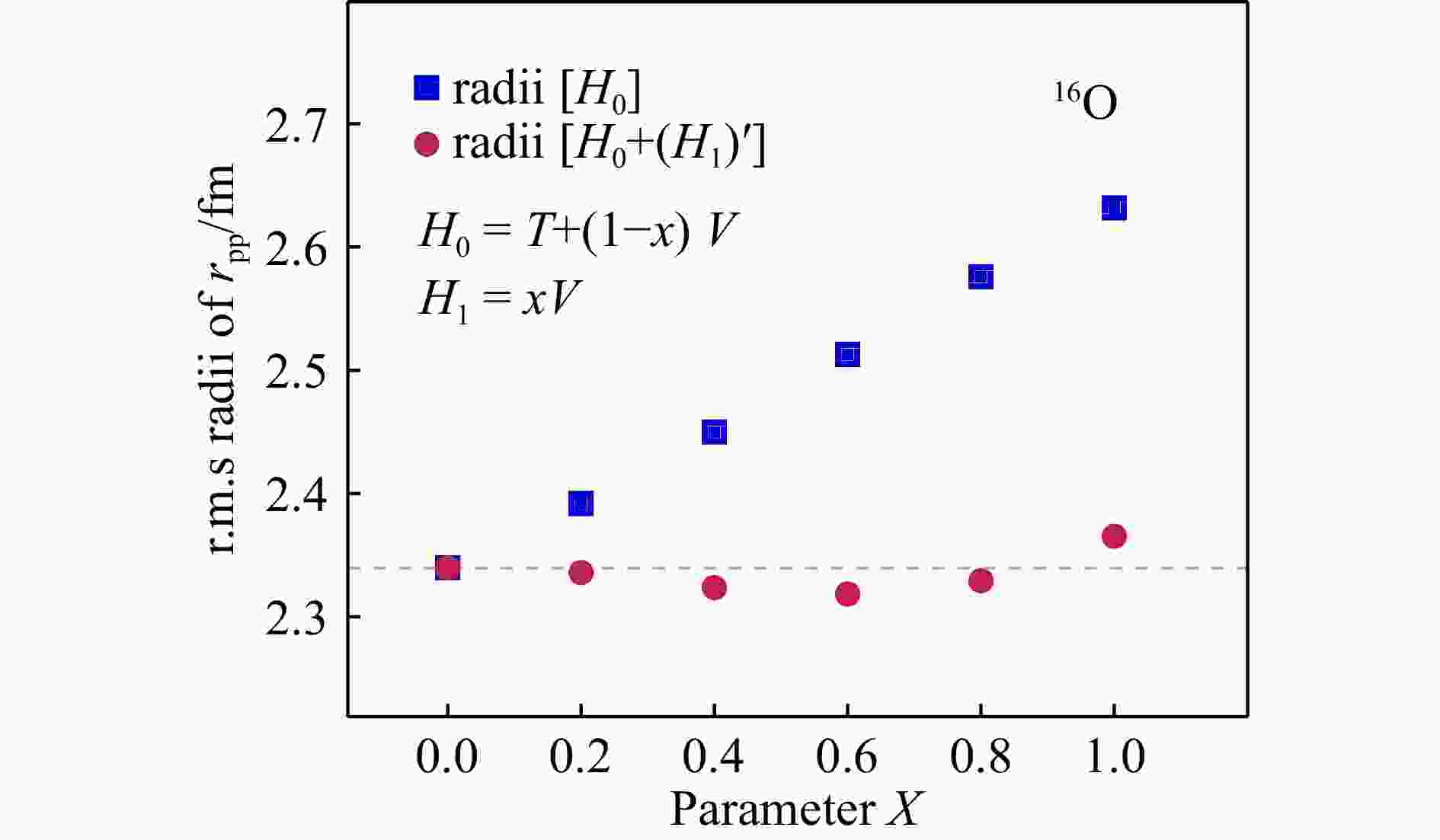
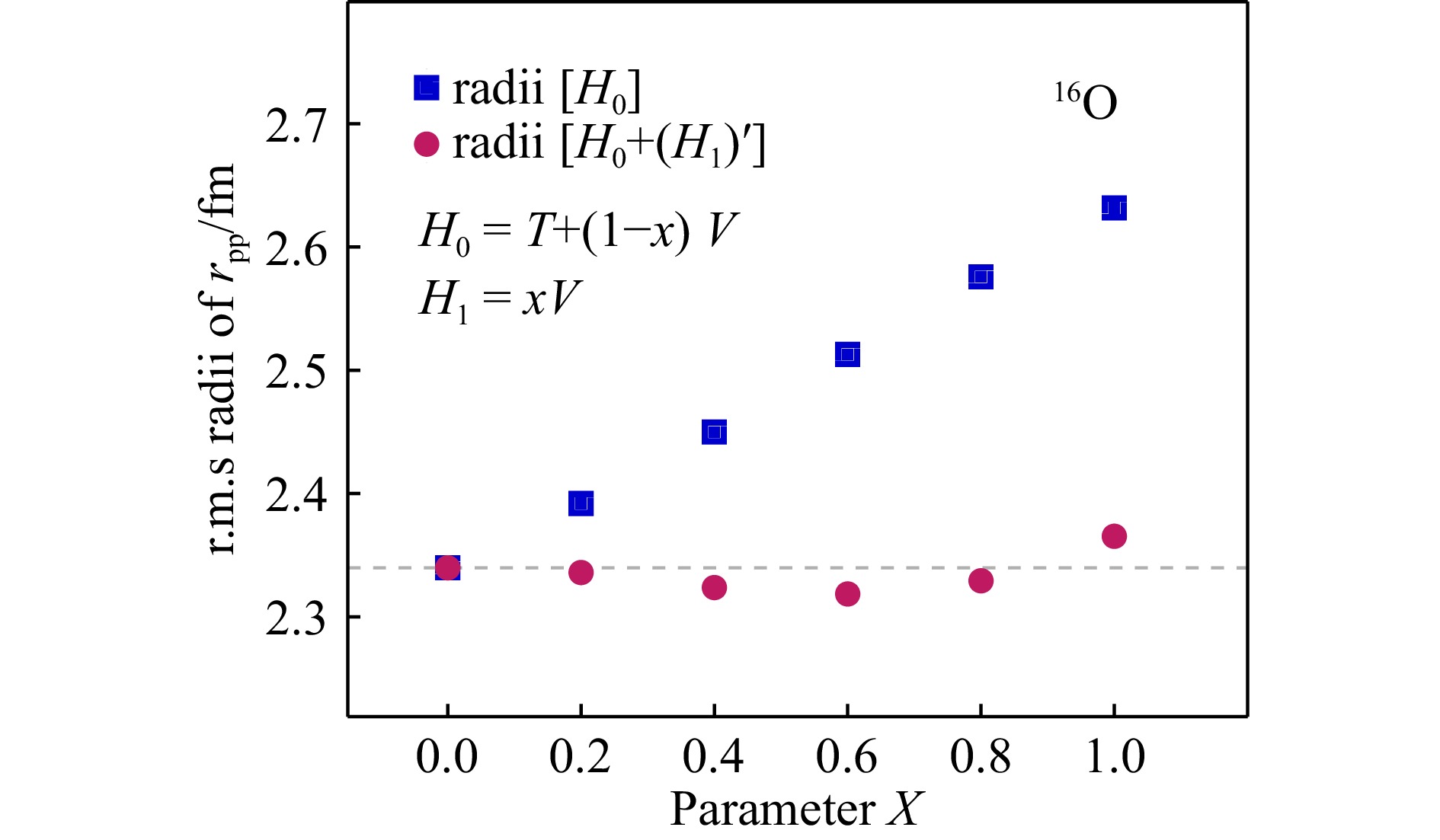
这里我们选取$ L^3=6^3 $的格点以及$ L_t = 100 $对16O进行微扰验证计算。当$ x=0 $时,非微扰计算将给出完整哈密顿量下的$ r_{\rm pp} $,而微扰计算中的微扰贡献为零。当$ x=1 $时,非微扰计算中将只有动能项,相互作用项将全部由微扰修正给出。在表1中,我们列出$ x=0.0,\, 0.2,\, 0.4 $与1.0的能量1阶微扰计算。可以看出当$ x=0.2 $时,一阶微扰已经能给出约40%的能量修正。即使当$ x=0.4 $,微扰修正后的能量与准确值间的差别也仅为4%。
表 1 验证计算I:能量微扰计算E
单位:MeV x 0.0 0.2 0.4 1.0 $ E_0 $ −212.32(30) −118.436(37) −30.04(34) 183.87(28) $ E_1 $ 0.0 −92.20(1) −173.80(6) −322.05(14) $ E_0 $+$ E_1 $ −212.32(30) −210.64(29) −203.84(25) −138.18(22) 在图1中,我们给出与之相对应的半径微扰计算结果。其中当$x=0$时,计算得到的半径为使用完整哈密顿量的"准确值",我们将其作为参考并在图中以灰色虚线表示。可以看出,当$ x=0.2 $时,非微扰计算给出的$ r_{\rm pp} $显著偏离正确值,而微扰计算则能将其很好的修正。随着$ x $增加,非微扰的$ r_{\rm pp} $呈线性增长并逐渐偏离准确值。通过算符的微扰计算,$ r_{\rm pp} $则会被极大地修正到准确值附近。即便当体系中的相互作用项全部为$ H_1 $时,$ E_1 $超过两倍的体系总能量,一阶微扰修正后的$ r_{\rm pp} $与准确值间的差别也不超过2%。可以看出,此方法中,微扰对半径的修正非常准确。
在上一小节中,为了消除有限体积效应,我们引入一个新的计算格点上距离的方法。这里我们采用了领头阶(Leading Order)的手征核力,并设定$ L_t=100 $,对16O进行非微扰的计算验证。在图2中可以看到,使用常规方法计算的质子相对于质心的半径$ r_{\rm pp} $在格点$ L $较小时,明显偏小,直到$ L=10 $才足够接近无穷大空间中的极限值。而使用新方法计算的结果则明显地减少了有限体积效应。
最后,我们使用两体N3LO核力与三体N2LO核力,对4He、12C与16O进行了完整的微扰计算,并将结果列在表2中。这里我们采用$ L=10 $的格点,以及$ L_t=200 $作为参数进行计算。值得一提的是表2中的误差仅为蒙特卡罗采样的统计不确定度,更多关于手征核力的截断误差、$ L_t $外推以及有限体积效应等系统误差将在未来的工作中讨论。
表 2 NLEFT使用手征N3LO核力计算的结合能和电荷半径与实验数据的对比(其中实验数据来源于文献[43])
E/MeV $ R_{{\rm{ch}}} $/fm Exp NLEFT Exp NLEFT 4He 28.30 28.42(3) 1.6755(28) 1.7368(140) 12C 92.16 95.38(36) 2.4702(22) 2.5272(141) 16O 127.62 129.98(63) 2.6991(52) 2.8163(175) 从表2中我们可以看出,我们的NLEFT计算能够给出与实验符合非常好的原子核结合能。其中最大的差别出现在12C,我们计算的结合能比实验大3.5%。同时,通过新发展的电荷半径计算方法,我们能够非常好地复现4He与12C的实验测量结果,给出的16O的计算结果仅稍大于实验值约5%。以上结果均验证了本文中新发展的格点上微扰计算方法的可靠性。
-
本文中,我们发展了在格点上微扰计算原子核半径的新方法。通过使用WMF和pQMC方法,避免了严重的“符号问题”,并结合两点关联函数,能够有效地测量半径算符。为了减小格点的有限体积效应,我们用了新的方法计算格点上的两点距离。验证计算表明了格点上半径微扰计算的可靠性。接着,我们使用完整的N3LO手征核力对4He、12C与16O的结合能与半径进行了计算,结果很好地复现了实验数据。该方法将成为新的第一性原理计算原子核半径的有效工具。未来,我们将使用该方法对更多的原子核体系进行高精度的格点计算。
-
摘要: 原子核格点有效场论(Nuclear Lattice Effective Field Theory)是近些年发展起来的一种高精度原子核第一性原理计算方法。它将手征有效场论与格点量子蒙特卡罗方法有机结合起来,能够在统一的理论框架下构建核力与求解量子多体问题。近年来新发展出来的波函数匹配(wave function matching)方法与微扰量子蒙特卡罗方法(perturbative quantum Monte Carlo method)为解决著名的“符号问题”开辟了全新的路径。本工作在这些方法的基础上,通过计算两点关联函数发展出格点上电荷半径的微扰计算方法,验证计算表明了本工作的可靠性。使用手征N3LO核力的计算能够很好地复现4He、12C与16O的实验测量结果。Abstract: With recent years of development, Nuclear Lattice Effective Field Theory (NLEFT) is becoming a powerful and high-fidelity ab initio method. It takes advantage of the chiral effective field theory and quantum Monte Carlo on lattice and can build nuclear forces and solve quantum many-body problems in the same framework. The newly developed wave function matching method and perturbative quantum Monte Carlo method pave the way to avoid the "sign problem". In this work, we implement all these new techniques along with the two-point correlation function to measure the charge radii on lattice. Benchmark calculations show our method is solid and full N3LO calculation can well reproduce the experiment data of 4He, 12C and 16O.
-
表 1 验证计算I:能量微扰计算E
单位:MeV x 0.0 0.2 0.4 1.0 $ E_0 $ −212.32(30) −118.436(37) −30.04(34) 183.87(28) $ E_1 $ 0.0 −92.20(1) −173.80(6) −322.05(14) $ E_0 $+$ E_1 $ −212.32(30) −210.64(29) −203.84(25) −138.18(22) 表 2 NLEFT使用手征N3LO核力计算的结合能和电荷半径与实验数据的对比(其中实验数据来源于文献[43])
E/MeV $ R_{{\rm{ch}}} $/fm Exp NLEFT Exp NLEFT 4He 28.30 28.42(3) 1.6755(28) 1.7368(140) 12C 92.16 95.38(36) 2.4702(22) 2.5272(141) 16O 127.62 129.98(63) 2.6991(52) 2.8163(175) -
[1] WEINBERG S. Phys Lett B, 1990, 251(2): 288. doi: 10.1016/0370-2693(90)90938-3 [2] VAN KOLCK U. Phys Rev C, 1994, 49: 2932. doi: 10.1103/PhysRevC.49.2932 [3] MACHLEIDT R, ENTEM D. Physics Reports, 2011, 503(1): 1. doi: 10.1016/j.physrep.2011.02.001 [4] EPELBAUM E, HAMMER H W, MEIßNER U G. Rev Mod Phys, 2009, 81: 1773. doi: 10.1103/RevModPhys.81.1773 [5] LONG B, YANG C J. Phys Rev C, 2011, 84: 057001. doi: 10.1103/PhysRevC.84.057001 [6] HAMMER H W, KÖNIG S, VAN KOLCK U. Rev Mod Phys, 2020, 92: 025004. doi: 10.1103/RevModPhys.92.025004 [7] BARRETT B R, NAVRáTIL P, VARY J P. Progress in Particle and Nuclear Physics, 2013, 69: 131. doi: 10.1016/j.ppnp.2012.10.003 [8] CARLSON J, GANDOLFI S, PEDERIVA F, et al. Rev Mod Phys, 2015, 87: 1067. doi: 10.1103/RevModPhys.87.1067 [9] CORAGGIO L, COVELLO A, GARGANO A, et al. Progress in Particle and Nuclear Physics, 2009, 62(1): 135. doi: 10.1016/j.ppnp.2008.06.001 [10] MA Y Z, CORAGGIO L, DE ANGELIS L, et al. Phys Rev C, 2019, 100: 034324. doi: 10.1103/PhysRevC.100.034324 [11] HAGEN G, HJORTH-JENSEN M, JANSEN G R, et al. Physica Scripta, 2016, 91(6): 063006. doi: 10.1088/0031-8949/91/6/063006 [12] HERGERT H, BOGNER S, MORRIS T, et al. Physics Reports, 2016, 621: 165. doi: 10.1016/j.physrep.2015.12.007 [13] YUAN Q, FAN S Q, HU B S, et al. Phys Rev C, 2022, 105: L061303. doi: 10.1103/PhysRevC.105.L061303 [14] STROBERG S R, HOLT J D, SCHWENK A, et al. Phys Rev Lett, 2021, 126: 022501. doi: 10.1103/PhysRevLett.126.022501 [15] SUN Z, WU Q, ZHAO Z, et al. Phys Lett B, 2017, 769: 227. doi: 10.1016/j.physletb.2017.03.054 [16] LI J G, MICHEL N, HU B S, et al. Phys Rev C, 2019, 100: 054313. doi: 10.1103/PhysRevC.100.054313 [17] HU B S, WU Q, YUAN Q, et al. Phys Rev C, 2020, 101: 044309. doi: 10.1103/PhysRevC.101.044309 [18] MA Y, XU F, CORAGGIO L, et al. Phys Lett B, 2020, 802: 135257. doi: 10.1016/j.physletb.2020.135257 [19] HU B, WU Q, LI J, et al. Phys Lett B, 2020, 802: 135206. doi: 10.1016/j.physletb.2020.135206 [20] MA Y, XU F, MICHEL N, et al. Phys Lett B, 2020, 808: 135673. doi: 10.1016/j.physletb.2020.135673 [21] LI J G, HU B S, WU Q, et al. Phys Rev C, 2020, 102: 034302. doi: 10.1103/PhysRevC.102.034302 [22] LI J G, MICHEL N, ZUO W, et al. Phys Rev C, 2021, 104: 024319. doi: 10.1103/PhysRevC.104.024319 [23] ZHANG S, MA Y, LI J, et al. Phys Lett B, 2022, 827: 136958. doi: 10.1016/j.physletb.2022.136958 [24] GENG Y F, LI J G, MA Y Z, et al. Phys Rev C, 2022, 106: 024304. doi: 10.1103/PhysRevC.106.024304 [25] MICHEL N, NAZAREWICZ W, PŁOSZAJCZAK M. Phys Rev Lett, 2023, 131: 242502. doi: 10.1103/PhysRevLett.131.242502 [26] HU B S, WU Q, SUN Z H, et al. Phys Rev C, 2019, 99: 061302. doi: 10.1103/PhysRevC.99.061302 [27] LEE D. Progress in Particle and Nuclear Physics, 2009, 63(1): 117. doi: 10.1016/j.ppnp.2008.12.001 [28] LU B N, LI N, ELHATISARI S, et al. Phys Lett B, 2019, 797: 134863. doi: 10.1016/j.physletb.2019.134863 [29] LU B N, LI N, ELHATISARI S, et al. Phys Rev Lett, 2020, 125: 192502. doi: 10.1103/PhysRevLett.125.192502 [30] LEE D. Phys Rev Lett, 2007, 98: 182501. doi: 10.1103/PhysRevLett.98.182501 [31] LÄHDE T A, MEIßNER U G. Nuclear Lattice Effective Field Theory: An Introduction: volume 957[M]. Switzerland: Springer Cham, 2019. [32] ELHATISARI S, LEE D, RUPAK G, et al. Nature, 2015, 528(7580): 111. doi: 10.1038/nature16067 [33] ELHATISARI S, LI N, ROKASH A, et al. Phys Rev Lett, 2016, 117: 132501. doi: 10.1103/PhysRevLett.117.132501 [34] ELHATISARI S, EPELBAUM E, KREBS H, et al. Phys Rev Lett, 2017, 119: 222505. doi: 10.1103/PhysRevLett.119.222505 [35] LI N, ELHATISARI S, EPELBAUM E, et al. Phys Rev C, 2018, 98(4): 044002. doi: 10.1103/PhysRevC.98.044002 [36] LU B N, LI N, ELHATISARI S, et al. Phys Rev Lett, 2022, 128: 242501. doi: 10.1103/PhysRevLett.128.242501 [37] SHEN S, ELHATISARI S, LÄHDE T A, et al. Nature Commun, 2023, 14(1): 2777. doi: 10.1038/s41467-023-38391-y [38] ELHATISARI S, BOVERMANN L, MA Y Z, et al. arXiv: 2210.17488. [39] MA Y Z, LIN Z, LU B N, et al. arXiv:2306.04500. [40] HU B S, XU F R, SUN Z H, et al. Phys Rev C, 2016, 94: 014303. doi: 10.1103/PhysRevC.94.014303 [41] LIN Y H, HAMMER H W, MEIßNER U G. Phys Rev Lett, 2022, 128: 052002. doi: 10.1103/PhysRevLett.128.052002 [42] FILIN A A, MÖLLER D, BARU V, et al. Phys Rev C, 2021, 103: 024313. doi: 10.1103/PhysRevC.103.024313 [43] WANG M, HUANG W, KONDEV F, et al. Chin Phys C, 2021, 45(3): 030003. doi: 10.1088/1674-1137/abddaf -





 下载:
下载:

 甘公网安备 62010202000723号
甘公网安备 62010202000723号