Since the seminal paper titled “Remarks on the chiral phase transition in chromodynamics” by Pisarski and Wilczek in 1984^[1], tremendous progress has been made in our understanding of the phase structure of strong-interaction matter^[2−3]. One of the milestones in studying the phase structure of strong-interaction matter is that it has been established from lattice-regularized Quantum Chromodynamics (QCD) that strong-interaction matter undergoes a rapid crossover transition from the hadronic phase to the quark-gluon plasma phase^[4]. The transition temperature has been determined at a high precision to be $ T_{{\mathrm{pc}}}=156.5(1.5) $ MeV^[5−6], and the temperature at which the chiral phase transition occurs has also been determined recently to be $ T_{\rm c}=132^{+3}_{-6} $ MeV^[7].

Despite this progress, see e.g. Ref. [8], key questions related to the fate of symmetry breaking patterns under extreme conditions of high temperature and large baryon number density as well as other control parameters, and particularly the influence of the axial anomaly on QCD phase transitions still remain elusive.

In this contribution to CNPC2023 Special Issue we start with our recent findings on the fate of axial U(1) anomaly and its microscopic origin at a temperature high above the chiral phase transition temperature $ T_{\rm c} $^[9], and then review our recent results on how the macroscopic criticality is encoded in the microscopic degrees of freedom^[10].

It has been conjectured that if axial U(1) anomaly is manifested at the chiral phase transition temperature the chiral phase transition will be second order belonging to the O(4) universality class^[1], otherwise the chiral phase transition can even be a first order or a second order belonging to a different universality class^[11−13]. As the relevant physics is highly non-perturbative, the studies using lattice QCD will be important, see recent studies and reviews^[14−21]. However, the fate of the axial U(1) anomaly is still undetermined. This is mainly due to two main issues in lattice QCD studies. One is that considerable computing resources are required. This is because that one has to take the chiral limit of massless quarks and the continuum limit. The simulation of lattice QCD in the chiral limit becomes significantly costly because the fermion matrix becomes more singular with smaller quark masses and consequently the inversion of the fermion matrix, which is the most time consuming part in lattice QCD computations, involves more numerical work. The other one is the unknown microscopic origin of the axial U(1) anomaly in the proximity of the chiral phase transition temperature. Although the microscopic origin can be inferred from the eigenvalue spectrum $ \rho(\lambda) $ of the Dirac fermion matrix there exist difficulties to be elaborated at length. $ \rho(\lambda) $ is connected to the order parameter $ \langle \bar{\psi}\psi\rangle $ of chiral phase transition, and the signature of axial U(1) anomaly $ \chi_\pi-\chi_\delta $ and $ \chi_{{\mathrm{disc}}} $ as follows

The Dirac eigenvalue spectrum $ \rho(\lambda) $ might have the following forms

Here $c_i^{}$ with $ i= $1, 2, 3 and 4 are parameters which are independent of quark mass ($ m $) and eigenvalue $ \lambda $. Note that $c_2^{} m^2 \delta(\lambda)$ is of most interest as in the chiral limit of massless quarks it makes $ \bar{\psi}\psi $ go to zero and $ \chi_\pi-\chi_\delta $ and $ \chi_{\rm disc} $ stay nonzero, i.e. it restores the SU(2)$ \times $ SU(2) symmetry and breaks the axial U(1) symmetry. However, as quark mass $ m\rightarrow 0 $ it is hard to observe the contribution from the term e.g. $c_2^{} m^2 \delta(\lambda)$ since it is $ m^2 $ suppressed. Also it is difficult to disentangle the contribution from $c_3^{} m$ and $c_4^{} m^2$ when $ m $ approaches zero.

Concerning the first issue, we performed lattice QCD simulations at a temperature well above the $ T_{\rm c} $, i.e. at $ T\simeq 205 $ MeV$ \simeq 1.6T_{\rm c} $. At this temperature the simulation is supposed to be cheaper compared to that at temperature in proximity of $ T_{\rm c} $. If one finds the axial U(1) remains manifested at this 1.6 $ T_{\rm c} $, it is natural to deduce that at a lower temperature, i.e. $ T_{\rm c} $, the axial U(1) anomaly also remains manifested with a larger strength. Thus we were able to perform simulations at pion masses much lower compared to the physical one with affordable computing resources. In our lattice QCD simulations we adopted the discretization scheme of highly improved staggered quarks with pion mass ranging from 160 MeV to 55 MeV on $ N_\tau =8, 12 $ and 16 lattices^[9]. This allows us to perform the continuum and chiral extrapolations.

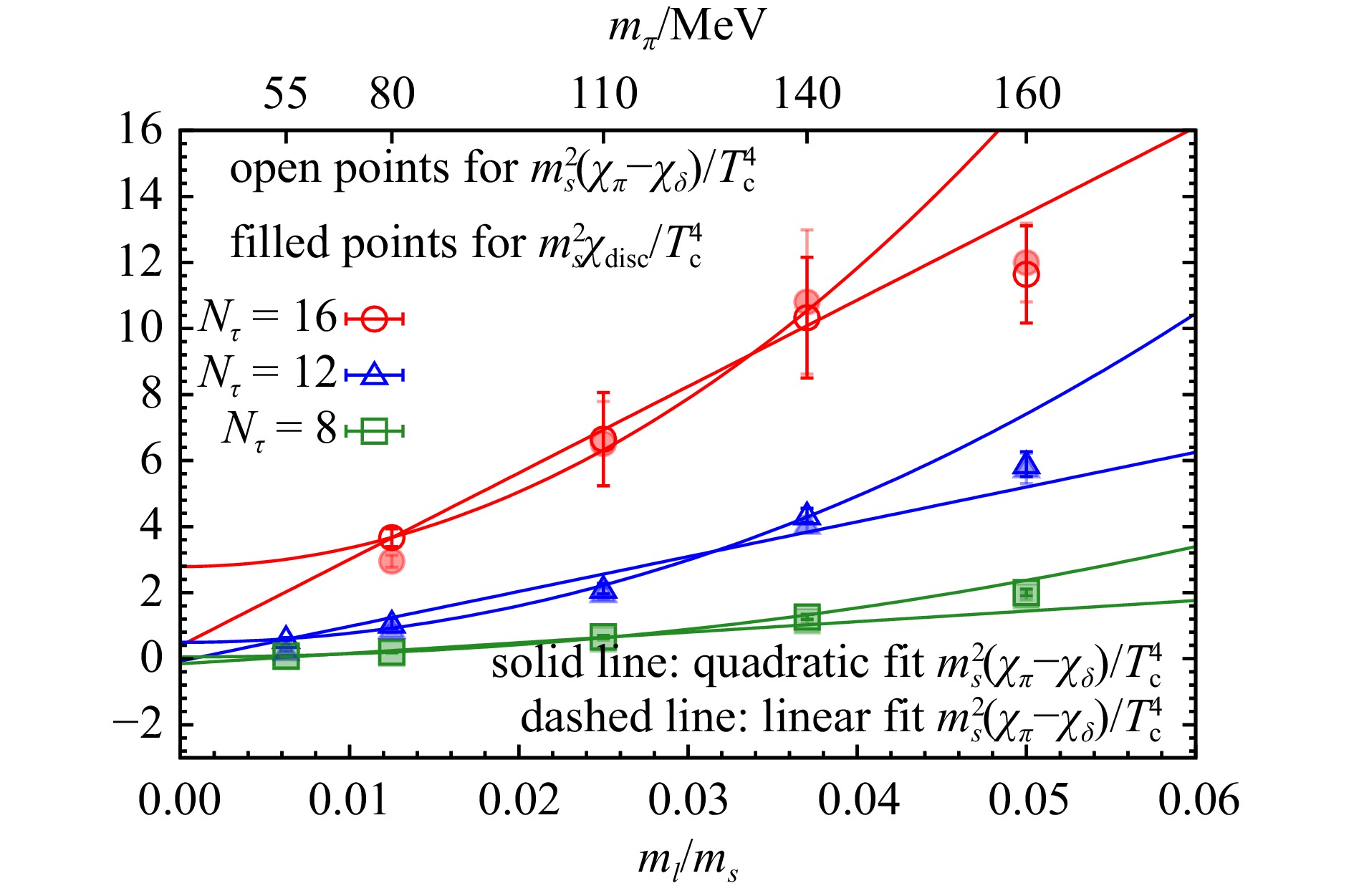
To perform the continuum and chiral extrapolations, we first need to understand the quark mass dependence of $ \chi_\pi - \chi_\delta $ and $ \chi_{\rm disc} $. In Fig. 1, we show $ \chi_\pi - \chi_\delta $ (open points) and $ \chi_{\rm disc} $ (filled points) as a function of the quark mass ratio $ m_l/m_s $ at three different lattice cut-offs. In the high-temperature phase, where chiral symmetry is restored, the QCD partition function should exhibit a Z(2) symmetry and thus be even in quark mass. Consequently, the first-order derivative of the QCD partition function with respect to quark mass, i.e., the chiral condensate, should be odd in quark mass, and the second-order derivative, i.e., $ \chi_{\rm disc} $, should be quadratic in quark mass as the chiral limit is approached.

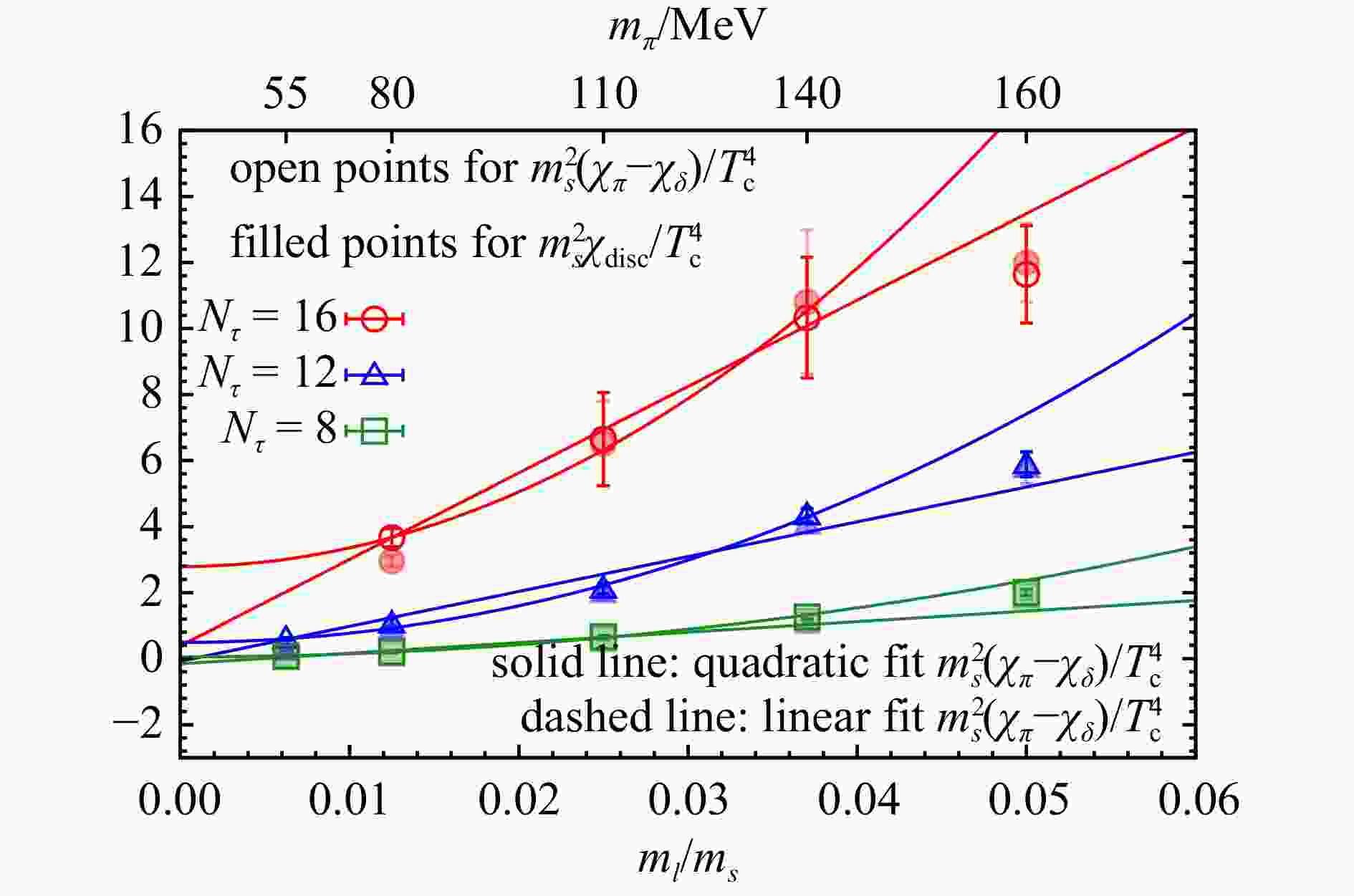
Figure 1.  Quark mass dependence of $ \chi_\pi-\chi_\delta $ (open points) and $ \chi_{\rm disc} $ (filled points) obtained from lattices with $ N_\tau= $8, 12 and 16. (color online)

As seen in Fig. 1, $ \chi_\pi - \chi_\delta $ agrees with $ \chi_{\rm disc} $ within errors, as expected from the restoration of chiral symmetry. Furthermore, we performed fits linear and quadratic in quark mass to $ \chi_\pi - \chi_\delta $. These fits are shown as dashed and solid lines in Fig. 1, respectively. The values of $ \chi^2/{\mathrm{d}}.{\mathrm{o}}.{\mathrm{f}}. $ listed in Table 1 indicate that the quadratic behavior in quark mass of $ \chi_\pi - \chi_\delta $ is favored. It is worth noting that the difference in $ \chi^2/{\mathrm{d}}.{\mathrm{o}}.{\mathrm{f}}. $ between the linear and quadratic fits is more pronounced in the fits to $ \chi_{\rm disc} $ and the light quark chiral condensate^[22].

Based on these findings, we present the continuum and chiral extrapolated results of $ \chi_\pi-\chi_\delta $ (top) and $ \chi_{\rm disc} $ (bottom) in Fig. 2, using a quadratic dependence on quark mass for the chiral extrapolation. It can be seen that in the continuum and chiral limit, $ \chi_\pi-\chi_\delta $ and $ \chi_{\rm disc} $ are nonzero and consistent with each other. This tells us that the SU(2)×SU(2) symmetry is restored while the axial U(1) anomaly still remains manifested at 1.6 $ T_{\rm c} $. Consequently it is suggested that at $ T_{\rm c} $ the axial U(1) anomaly remains manifested and the chiral phase transition should be of second order belonging to the O(4) universality class.

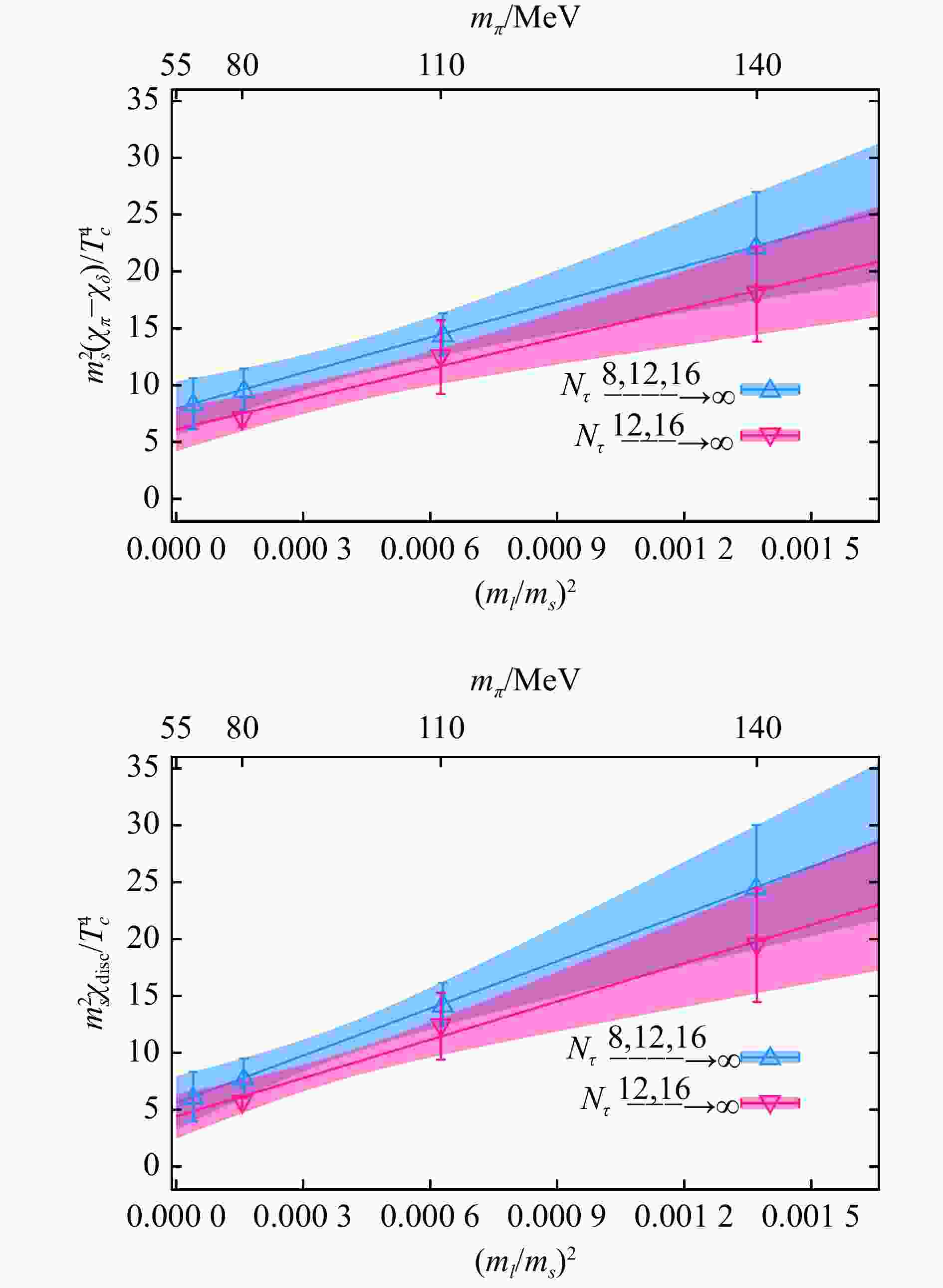
Figure 2.  Continuum and chiral extrapolations for $ \chi_\pi-\chi_\delta $ (top) and $ \chi_{\rm disc} $ (bottom) as function of the quark mass ratio $ (m_l/m_s)^2 $ at $ T\approx 1.6T_{\rm c} $. In the chiral limit of massless quarks, i.e. at $ (m_l/m_s)^2=0 $, $ \chi_\pi-\chi_\delta $ and $ \chi_{\rm disc} $ are shown to be nonzero in the continuum limit. The figure is taken from Ref. [9]. (color online)

The observation from Fig. 2 suggests that a term like $c_2^{} m^2 \delta(\lambda)$ is favored in the Dirac eigenvalue spectrum [Eq. (2)], as it ensures $ \chi_\pi - \chi_\delta = \chi_{\rm disc} \neq 0 $. However, as discussed before it is difficult to disentangle the contribution of $ c_2 m^2 \delta(\lambda) $ from other terms in $ \rho(\lambda) $. One possible way out could be to investigate the $ n $th order derivatives of $ \rho(\lambda) $ with respect to quark mass. In the quark mass derivatives of $ \rho(\lambda) $ the suppression brought by certain powers of $ m $ in the limit of $ m\rightarrow 0 $ will go away, e.g. $ \partial^2 (c_2m^2\delta(\lambda))/ \partial {m^2} = c_2\delta(\lambda) $.

However, the numerical computation of derivatives is highly non-trivial. For instance,

suffers from the discretization error in $ \epsilon $. Furthermore, this requires unwanted two sets of lattice QCD simulations at two different quark masses which should be infinitesimal adjacent.

To avoid the above-mentioned issue in Eq. (3) we proposed a novel method to compute $ n $th order quark mass derivative of $ \rho(\lambda) $ without the needs for computing $ \rho $ at an additional different quark mass^[9]. Although it seems to be counter-intuitive at first sight the method is straightforward by starting with the definition of $ \rho(\lambda) $

where $\rho_U^{}(\lambda)=\sum_{j} \delta(\lambda-\lambda_{j})$, and $ \lambda_{j} $ is the eigenvalue of massless Dirac matrix $ \cancel{D}[{\cal{U}}] $ with a given SU(3) gauge field. Here $ V $ is the volume, $ S_G[{\cal{U}}] $ is the gauge action and the partition function $ Z[{\cal{U}}]=\int {\cal{D}}[{\cal{U}}] \; e^{-S_G[{\cal{U}}]} \det[\cancel{D}[{\cal{U}}]+m_s] (\det[\cancel{D}[{\cal{U}}]+m_l] )^2 $.

Note that in Eq. (4) only $ Z({\cal{U}}) $ and $\det[\cancel{D}[{\cal{U}}]+m_l^{}]$ depends on the quark mass $m_l^{}$ while $\rho_U^{}$ is independent of $m_l^{}$. Furthermore, $\det[\cancel{D}[{\cal{U}}]+m_l^{}]$ can be expressed in terms of Dirac eigenvalues $ \lambda $ as follows

Thus when taking derivatives of Eq. (4) with respect to $ m_l $ with the help of Eq. (5) one can easily obtain the $ n $th order derivative of $ \rho(\lambda) $ with respect to $m_l^{}$. For instance here we list the first and second order derivatives of $ \rho(\lambda) $ as follows^[9]

where $ C_n $ is the first order cumulant of $ n $ variables $\rho_U^{}(\lambda_1), \rho_U^{}(\lambda_2), \cdots, \rho_U^{}(\lambda_n)$. Here $ C_2 $ and $ C_3 $ can be expressed explicitly as follows^{[9, 23]}

Note that the derivation of $ \partial^n \rho/\partial m_{l}^n $ is exact without any assumptions. Once $\rho_{U}^{}(\lambda)$ is computed using a certain numerical method, e.g. Chebyshev filtering method^[24−28], $ \partial^n \rho/\partial m_{l}^n $ can be obtained.

In the top panel of Fig. 3 we show $ m_l^{-1}\partial \rho/\partial m_l $ and $ \partial^2 \rho/\partial m_l^2 $ as a function of $ \lambda $ obtained from lattice QCD simulations with pion mass ranging from 160 MeV to 55 MeV on $ N_\tau=8 $ lattices at $ T\simeq205 $ MeV$ \simeq 1.6T_{\rm c} $. It can be clearly seen that $ m_l^{-1}\partial \rho/\partial m_l \approx \partial^2 \rho/\partial m_l^2 $ and both quantities are almost quark mass independent. A peak structure can also be found in $ m_l^{-1}\partial \rho/\partial m_l $ and $ \partial^2 \rho/\partial m_l^2 $ in the infrared region of $ \lambda $.

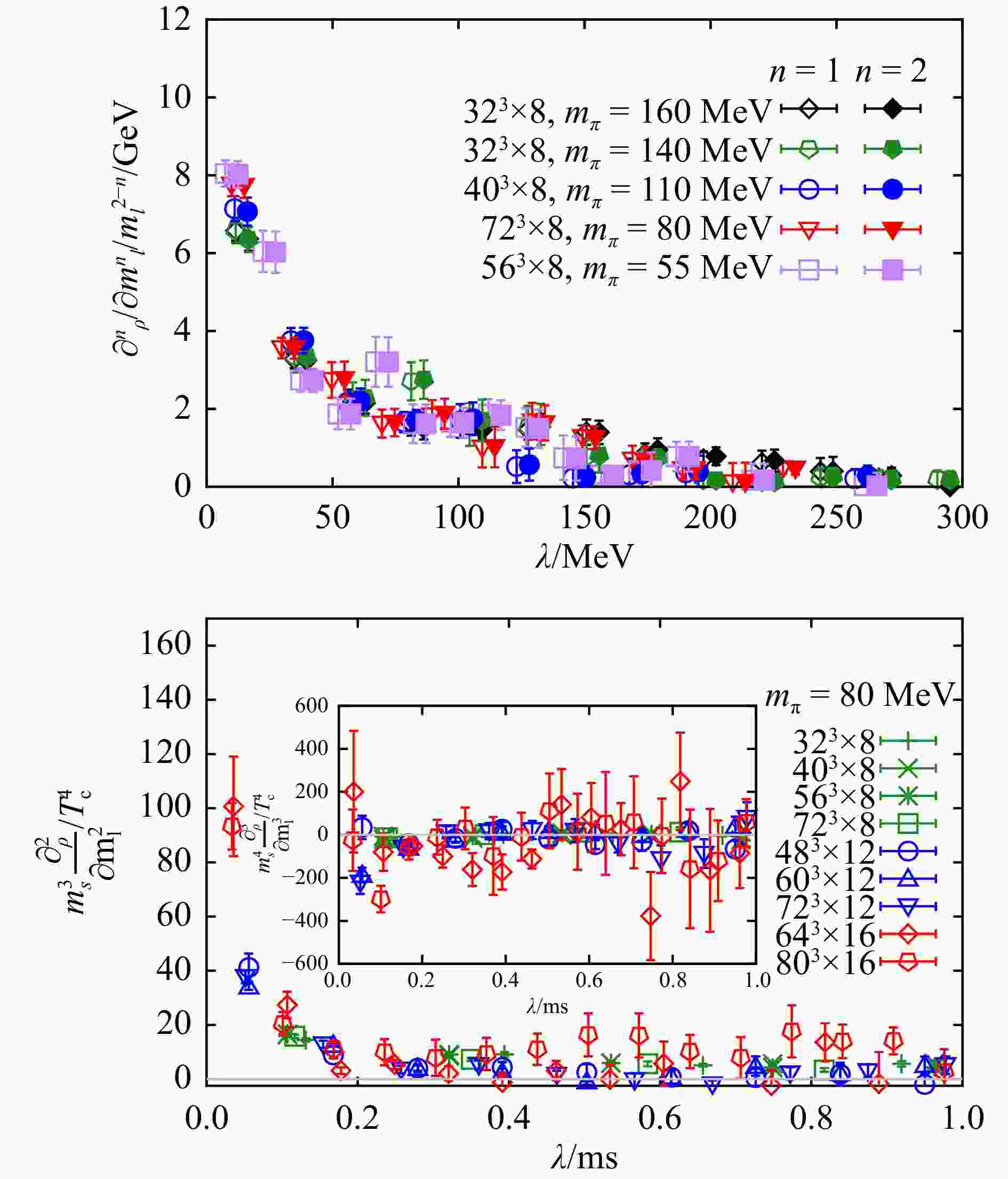
Figure 3.  The derivatives of Dirac eigenvalue spectrum with respect to quark mass. The figure is taken from Ref. [9]. (color online)

In the insert of the bottom panel of Fig. 3 we show $ \partial^3 \rho/\partial m_{l}^3 $ as a function of $ \lambda $. It can be observed that $ \partial^3 \rho/\partial m_{l}^3\approx 0 $. Together with the observation that $ m_l^{-1}\partial \rho/\partial m_l \approx \partial^2 \rho/\partial m_l^2 $ it can be deduced that $ \rho\propto m_l^2 $. As can also be seen that the peak structure in $ \partial^2 \rho/\partial m_{l}^2 $ becomes sharper as one approaches the continuum limit with increasing value of $ N_\tau $ from 8 to 16. This resembles a $ \delta(\lambda) $-like peak structure at the origin. In summary $ \rho\propto m_l^2\delta(\lambda) $ at $ 1.6T_{\rm c} $, which is consistent with the manifestation of axial U(1) anomaly in $ \chi_\pi-\chi_\delta $ and $ \chi_{\rm disc} $ and the dilute instanton gas approximation.

As suggested by the studies of the fate of axial U(1) anomaly in the chiral and continuum limit at $ 1.6 T_{\rm c} $, the chiral phase transition should be of second order belonging to the O(4) universality class^{[9, 22]}. In the proximity of a continuous phase transition, the free energy of the system can be decomposed into two parts,

where $ F_{{\mathrm{sing}}} $ is the singular part of the free energy and overwhelmingly dominates over the regular part $ F_{{\mathrm{reg}}} $. The order parameter $ M $ of the phase transition can be defined as the first order derivative of the free energy with respect to an external field $ H $^[29],

where $ h=H/h_0 $ and $ {\textit{z}}={\textit{z}}_0(T-T_{\rm c})/T_{\rm c} H^{-1/\beta\delta} $. Here $ h_0 $ and $ {\textit{z}}_0 $ are non-universal parameters specific for a certain system while $ \beta $ and $ \delta $ are universal critical exponents. The singular behavior will be more pronounced in higher order derivatives, e.g.

Here $ f_n $ is the scaling function, and in the ordinary convention $ f_1\equiv f_G $ and $ f_2\equiv f_\chi $. In the case of QCD, the order parameter of the chiral phase transition is the chiral condensate while the external field is the quark mass. Unlike the case of spin models, in QCD, $\chi_{M,\, 2}$ or $\chi_{M,\, n}$ also receives the contribution from the connected diagrams, which makes the computation more involved in lattice QCD simulations.

We proposed to investigate the $ n $th order cumulant of chiral condensate^[10],

Here the generating functional $ \mathbb{G}( m_l;\epsilon) $ can be defined as

where $ \langle{{\cdot}}\rangle_{{0}} $ denotes expectation value with respect to the QCD partition function in the chiral limit, $ Z(0)= \int \exp\left(-S[{\cal{U}}, 0]\right) {\cal{D}}[{\cal{U}}] $. Since

with the QCD partition function $Z( m_l^{})=\int \exp \left({-S[{\cal{U}}, m_l^{}]}\right) {\cal{D}}[{\cal{U}}]$ and $Z( m_l)/Z(0)= \langle{{ \exp\{ - m_l^{} \bar{\psi}\psi( m_l^{}) \} }}\rangle_{{0}}$, it is straightforward to find out that $ \mathbb{K}_{{n}} $ are the standard cumulants of $ \bar{\psi}\psi( m_l) $; e.g. $\mathbb{K}_{{1}}\left[ \bar{\psi}\psi \right]=T\langle \bar{\psi}\psi( m_l^{})\rangle/V$, $\mathbb{K}_{{2}}\left[ \bar{\psi}\psi \right]= T\langle[ \bar{\psi}\psi( m_l^{})-\langle \bar{\psi}\psi( m_l^{})\rangle]^2\rangle/V$, $\mathbb{K}_{{3}}\left[ \bar{\psi}\psi \right]=T\langle[ \bar{\psi}\psi( m_l^{})- \langle \bar{\psi}\psi ( m_l^{})\rangle]^3\rangle/ V$ etc.

The connection of $ \mathbb{K}_{{n}} \left[ \bar{\psi}\psi \right] $ to the Dirac eigenvalue $ \lambda $, i.e. energy levels of quarks, is bridged via $ \bar{\psi}\psi(\epsilon) $ which is a probe operator for a valence quark with mass $ \epsilon $ and has a form

By combing Eqs. (13), (14) and (16), one can obtain the expression of $ \mathbb{K}_{{n}} $ in terms of Dirac eigenvalue spectrum as follows^[10]

where $ P_1( \lambda)=K_1[P_U( \lambda_{{}};{{ m_l}})] $ for $ n=1 $, and for $ n\geqslant2 $

Here $ K_1 $ is the first order joint cumulant of $ n $-variables ($ X_i $) defined as

and

Note that in the limit of $ \epsilon\rightarrow 0 $ $P_U^{}(\lambda;\epsilon)$ is proportional to a delta function. Thus in the chiral limit of massless quarks one can arrive at the following generation of the Banks-Casher formula^[10]

Based on the above relation, two important questions can be asked. One is what the scaling behavior of $ \mathbb{K}_{{n}} $ is in the proximity of $ T_{\rm c} $. The other one is how the scaling behavior of $ \mathbb{K}_{{n}} $ is encoded in $ P_n(\lambda) $[Eq. (17)]. Concerning the first question, since $ \mathbb{K}_{{n}} $ is only a part of the $ n $th order susceptibility of the order parameter, a simple conjecture is that $ \mathbb{K}_{{n}} $ is linearly proportional to the critical behavior encoded in $\chi_{M,\, n}$[Eq. (12)], i.e.

Concerning the second question, as seen from the generalized Banks-Casher relation [Eq. (21)], the criticality, if any, must arise from the $ \lambda $-independent region or the deep infrared part of the eigenvalue spectrum. Based on the first conjecture, one may expect

where all the $ \lambda $ relevant information is encoded in $ g(\lambda/m) $.

To check the first conjecture we look in the ratio of cumulant of chiral condensate, i.e. $ \mathbb{K}_{{n}}({\textit{z}})/\mathbb{K}_{{n}}({\textit{z}}=0) $ for $ n=2 $ (top) and 3 (Bottom) as a function of $ {\textit{z}}/{\textit{z}}_0 $. Here $ {\textit{z}}=0 $ means the case at temperature $ T=T_{\rm c} $ since $ {\textit{z}}={\textit{z}}_0\frac{T-T_{\rm c}}{T_{\rm c}}/H^{1/\beta\delta} $. If the conjecture holds one expects $ \mathbb{K}_{{n}}({\textit{z}})/\mathbb{K}_{{n}}({\textit{z}}=0)=f_n({\textit{z}})/f_n(0) $ in terms of $ {\textit{z}} $ or $ {\textit{z}}/{\textit{z}}_0 $ is independent on the quark mass dependent and temperature. This is exactly what is seen in Fig. 4 in the window of $ z/z_0\in (-0.2, 0.2) $. Note that although $ z_0 $ is an undetermined non-universal parameter of QCD in the range of $ z/z_0\in (-0.2, 0.2) $ $ f_n(z)/f_n(0) $ is almost independent on the value of $ z_0 $. While outside the window of $ z/z_0\in (-0.2, 0.2) $ we see the data points at various temperature and pion masses do not overlap each other anymore. We can also see in the inserts of Fig. 4 that $ \mathbb{K}_{{n}}(z) $ rescaled by $ H^{1/\delta-n+1} $ is also quark mass and temperature independent in the same region of $ z/z_0 $. Thus the results shown in Fig. 4 suggests $ \mathbb{K}_{{n}}(z) \propto H^{1/\delta-n+1} f_n(z) $. It is worth mentioning that our approach to investigating these cumulant ratios complements the study of the magnetic equation of state, which is typically conducted using the chiral condensate and its susceptibilities. In the latter case, careful modeling of the regular configurations is important^[30−31]. However, in our approach, we do not need to compute connected susceptibilities; instead, we rely solely on the cumulants of the chiral condensates, where the regular contributions are expected to be mild.

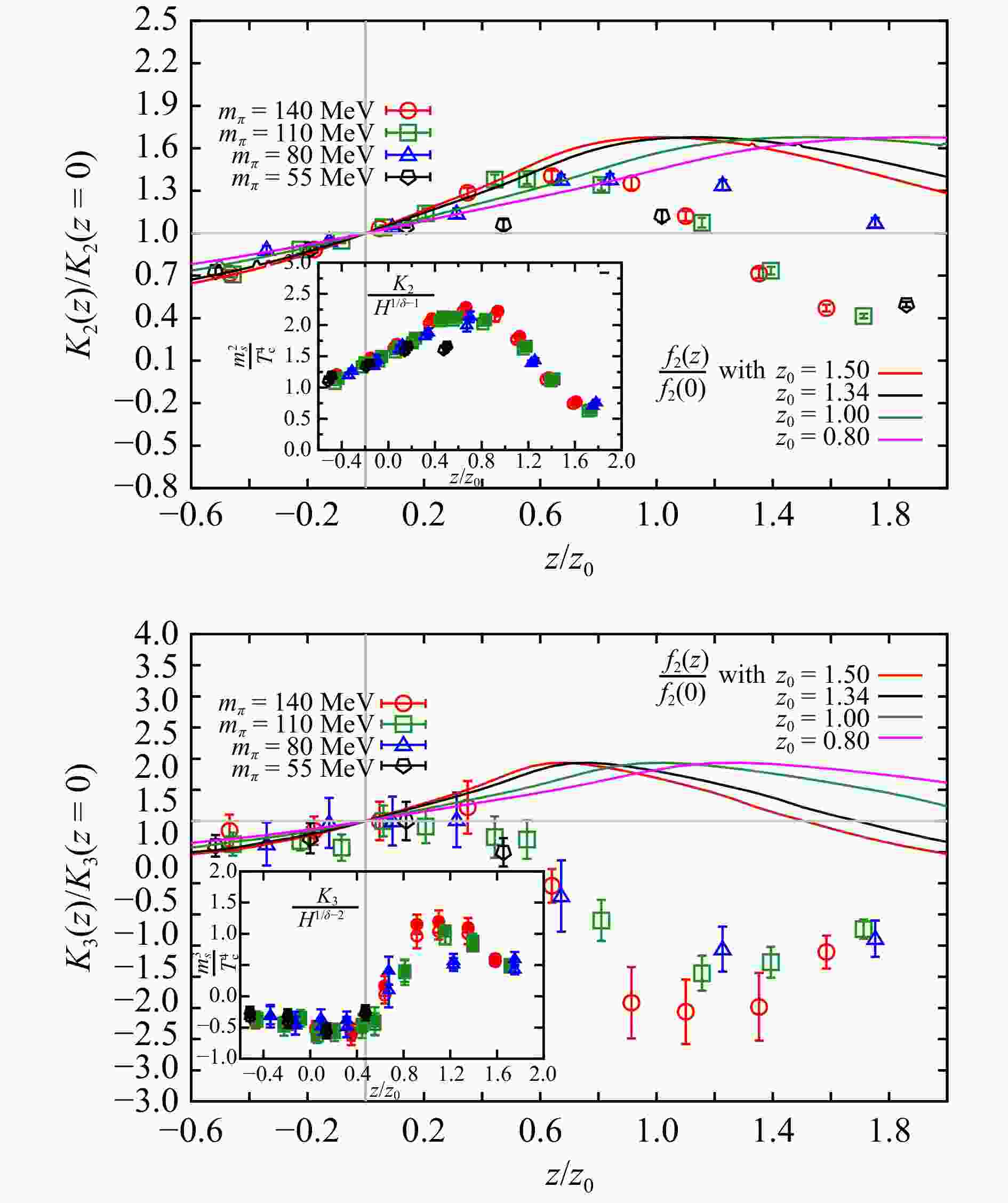
Figure 4.  $ \mathbb{K}_{{n}}(z)/\mathbb{K}_{{n}}(0) $ as a function of $ z/z_0=\frac{T-T_{\rm c}}{T_{\rm c}}/H^{1/\beta/\delta} $ with $ n=2 $ (top) and $ n=3 $ (Bottom) for pion mass ranging from 140 MeV to 55 MeV in the proximity of chiral phase transition temperature. The broken lines show $ f_n(z)/f_n(0) $ with various values of undetermined $ z_0 $. The inserts show ratios of $ \frac{m_s^3}{T_{\rm c}^4}\frac{T}{V}\mathbb{K}_{{n}}(z)/H^{1/\delta-n+1} $ as a function of $ z/z_0 $ where the prefactors of $ \mathbb{K}_{{n}}(z) $ are used to make the quantity renormalization group invariant. (color online)

To check the second conjecture, since the relevant infrared energy scale should be $ \lambda\sim m_l $ for small values of $ m_l $ as expected from the generalized Banks-Casher relation [Eq. (21)] we express all quantities as functions of the dimensionless and renormalization group invariant $ \lambda/ m_l $

where the dimensionless and renormalization group invariant $ \mathbb{\hat K}_{n} [ \bar{\psi}\psi] = m_s^n \mathbb{K}_{{n}} [ \bar{\psi}\psi] / T_{\rm c}^4 $.

In Fig. 5 we show $ \hat{P}_{{n}}( \hat{\lambda}) $ for $ n $=1 (left), 2 (middle) and 3 (right) as a function of $ \hat{\lambda}\equiv\lambda/m $ in the proximity of $ T_{\rm c}=144.2(6) $ MeV on $ N_\tau=8 $ lattices^[32]. These $ \hat{P}_{{n}}( \hat{\lambda}) $ can reproduce $ \mathbb{K}_{{n}} $ as shown in the inserts of Fig. 4. It can be seen that $ \hat{P}_{{n}}( \hat{\lambda}) $ rapidly goes to zero with increasing $ \hat{\lambda} $ at $ \hat{\lambda}\sim 1 $, and the regions where $ \hat{P}_{{n}}( \hat{\lambda}) $ is nonzero get smaller with increasing $ n $. This reinforces that the relevant infrared energy scale turn out to be $ \hat{\lambda}\sim1 $ as indicated from the generalized Banks-Casher relation. In this deep infrared region $ \hat{P}_{{n}}( \hat{\lambda}) $ at a fixed temperature shows clear dependences on $ m_l $. These dependences becomes stronger for increasing $ n $. Meanwhile the form of $ m_l $-dependence of $ \hat{P}_{{n}}( \hat{\lambda}) $ also changes with varying values of temperature. As also seen from Fig. 5 it is expected that our results become increasingly noisy with increasing $ n $ and decreasing $ m_l $.

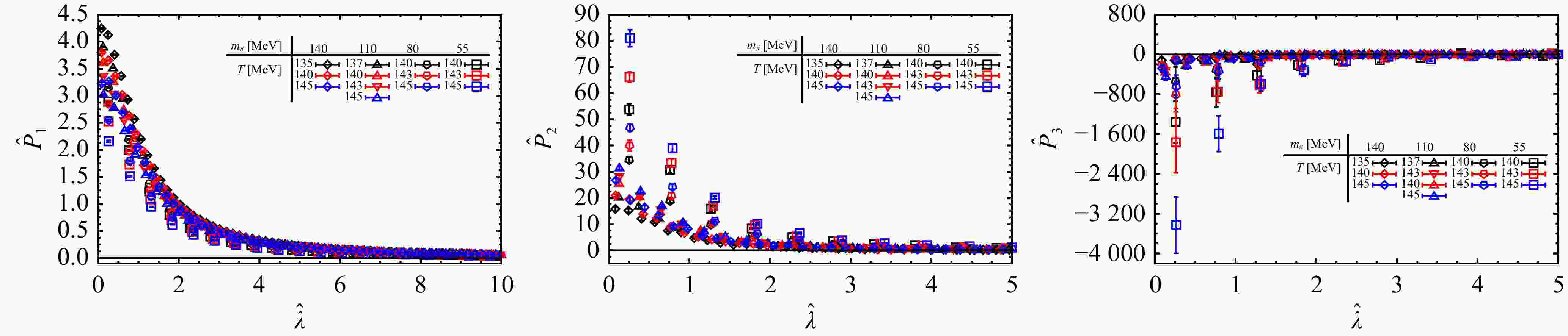
Figure 5.  $ \hat{P}_n $ as function of $ \hat{\lambda}\equiv\lambda/m $ for $ n=1 $ (left), $ n=2 $ (middle) and $ n=3 $ (right) with pion mass ranging from $ 140 $ to 55 MeV in the proximity of $ T_{\rm c} $. The plots are taken from Ref. [10]. (color online)

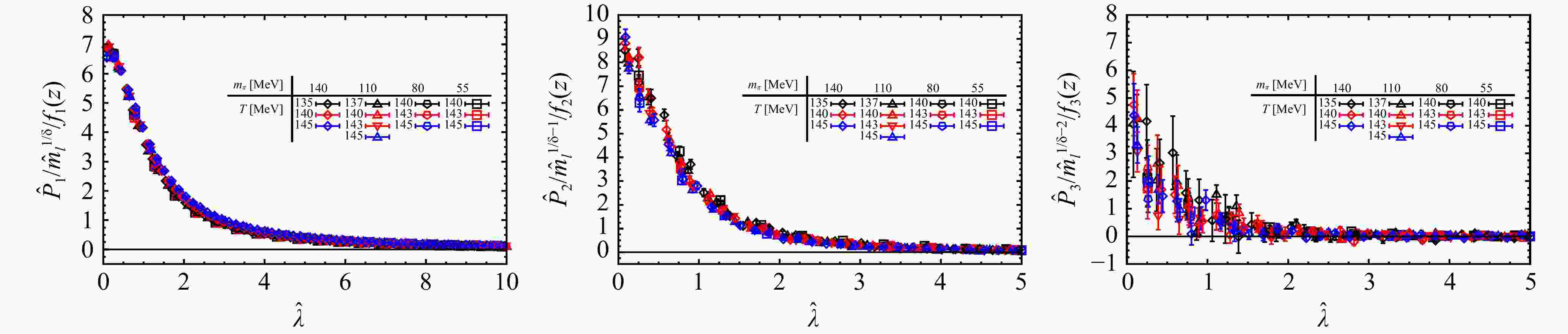
As discussed before, the $ m_l $ and $ T $ dependence of $ \hat{P}_{{n}}( \hat{\lambda}) $ shown in Fig. 5 could be understood in terms of the 3-dimensional $ O(2) $ scaling property, cf. Eq. (24). To obtain $ f_n(z) $ we adopted the system-specific parameters $ T_{\rm c}=144.2(6) $ MeV and $ z_0=1.83(9) $ from Ref. [32], where 3-dimensional $ O(2) $ scaling fits were carried out for the same lattice ensembles but using an entirely different macroscopic observable, namely the $ m_l $ dependence of the static quark free energy. As seen from Fig. 6 once the $ \hat{P}_{{n}}( \hat{\lambda}) $ are rescaled with respective $ \hat{m}_l^{1/\delta+1-n}f_n(z) $ the data points in Fig. 5 collapse onto each other, i.e. $ \hat{P}_{{n}}( \hat{\lambda})/( \hat{m}_l^{1/\delta+1-n}f_n(z)) $ as a function of $ \hat{\lambda} $ is independent of quark mass and temperature for n = 1, 2 and 3.

Figure 6.  Similar as Fig. 5 but for $ \hat{P}_n/\hat{ m_l}^{1/\delta-n+1}/f_n(z) $. The plots are taken from Ref. [10]. (color online)

Thus, according to the observation from Fig. 5 and Fig. 6 the macroscopic criticality of chiral phase transition is encoded microscopically in terms of Dirac eigenvalues and their correlations as follows

where $ \hat{g}_n(\hat{\lambda}) $ characterize the system-specific of the $ n $th order energy-level correlations. As inferred from our generalized Banks-Casher relations of Eq. (21) the $ \hat{g}_n(\hat{\lambda}) $ must also satisfy $ \lim_{V\to\infty} \lim_{a\to0} \lim_{ m_l\to0} \hat{g}_n(\hat{\lambda}) \to \delta( \hat{\lambda}) $, such that $ \mathbb{K}_{{n}}[ \bar{\psi}\psi] $ has the correct scaling behavior in $ (T-T_{\rm c})/T_{\rm c} $.

In this contribution we review our recent work on the microscopic origin of the axial U(1) anomaly at 1.6 $ T_{\rm c} $ as well as the macroscopic criticality of chiral phase transition in the proximity of $ T_{\rm c} $^[9−10]. To access the quarkuaku mass dependence of the Dirac eigenvalue spectrum $ \rho(\lambda) $ a novel method to compute the quark mass derivative of $ \rho(\lambda) $ was proposed [Eqs. (6)~(7)]. By investigating on the first, second and third order derivatives of $ \rho(\lambda) $ with respect to quark mass from lattice QCD simulations with pion mass down to 55 MeV on $ N_\tau=8 $, 12 and 16 lattices it is found that it is $ \rho(\lambda)\propto m^2\delta(\lambda) $ that breaks the axial U(1) symmetry and restores the SU(2)$ \times $SU(2) chiral symmetry at 1.6 $ T_{\rm c} $. This is consistent with the dilute instanton gas approximation and also the observation of $ \chi_\pi-\chi_\delta= \chi_{\rm disc}\neq 0 $ in the chiral and continuum limit at $1.6\;T_{\rm c}$. These findings suggests the axial U(1) anomaly still remains manifested at $ T_{\rm c} $, which is lower than $1.6\;T_{\rm c}$. Thus the chiral phase transition should be of second order belonging to the O(4) universality class.

The relation between $ n $th order cumulant of chiral condensate $ \mathbb{K}_{{n}}[ \bar{\psi}\psi] $ and the correlation between Dirac eigenvalue spectrum $ P_n(\lambda) $ has been established [ Eq. (17)]. Accordingly the Banks-Casher relation is generalized [Eq. (21)]. Based on these relations it is conjectured that $ \mathbb{K}_{{n}}[ \bar{\psi}\psi]\propto h^{1/\delta-n+1}f_n(z) $ and $ P_n(\lambda)=h^{1/\delta-n+1} f_n(z) g(\lambda/m) $. By performing lattice QCD simulations using HISQ fermions with pion mass ranging from 140 MeV to 55 MeV on $ N_\tau=8 $ lattices in the proximity of chiral phase transition the conjecture is confirmed for $ n $ up to 3.

Since the manifestation of the axial U(1) anomaly at a high temperature of 1.6 $ T_{\rm c} $ and the chiral phase transition near $ T_{\rm c} $ have been demonstrated microscopically, it would be interesting to investigate the temperature range between 1.6 $ T_{\rm c} $ and $ T_{\rm c} $ in the near future. Specifically, examining how the dilute instanton gas approximation breaks down and transitions to the scenario of the chiral phase transition could provide valuable insights into the nature of the QCD transition. Additionally, exploring the connection between the Dirac eigenvalue spectrum and other thermodynamic quantities would be highly worthwhile.

Acknowledgments I thank Wei-Ping Huang for his assistance in producing Fig. 1 and Table 1. This material is based upon work supported partly by the National Key Research and Development Program of China under Contract No. 2022YFA1604900; the National Natural Science Foundation of China under the grant numbers 12293064, 12293060 and 12325508.