The typical features for octupole correlations in the ground-state reflection-asymmetric (RA) nuclei are the occurrence of alternating-parity bands in the even-even nuclei and parity-doublet bands in the odd-$ A $ nuclei^[1]. These correlations in nuclei arise from the octupole-octupole interaction between single-particle states with differences in angular momentum $\varDelta l = \varDelta j = 3$. In the light actinide mass region, the proton Fermi surface lies between $ f_{7/2}^{} $ and $ i_{13/2}^{} $ orbitals, while the neutron Fermi surface lies between $ g_{9/2}^{} $ and $ j_{15/2}^{} $ orbitals in nuclei with proton number $Z \approx 88$ and neutron number $N \approx 134$. Since the proximity of these levels, strong octupole coupling lead to intrinsic reflection asymmetric shapes in the ground-state nuclei.

In the actinide mass region, most odd-$ A $ and even-even nuclei behave striking features of octupole correlations in the experiment^[2−6]. The rotational behaviors of the yrast and negative-parity bands in $^{236, \, 237, \, 238} {\rm{U}}$ and those in $^{238, \, 239, \, 240} {\rm{Pu}}$ exhibit significant differences, which is due to variations in octupole correlation strength^[7−11]. In terms of theoretical investigations, many approaches have been developed to describe the octupole correlations in the reflection-asymmetric nuclei. These include reflection-asymmetric mean-field approach^[12], cluster model^[13], vibrational approach^[14], reflection asymmetric shell model^[15], and cranked shell model^[16].

In the present work, the cranked shell model (CSM) with the pairing correlations treated by a particle-number-conserving (PNC) method is developed to investigate the alternating-parity bands in even-even nuclei $^{236, \, 238} {\rm{U}}$ and $^{238, \, 240} {\rm{Pu}}$, as well as the parity-doublet bands in odd-$ A $ nuclei $ ^{237} {\rm{U}}$ and $ ^{239} {\rm{Pu}}$. In the PNC method, the CSM Hamiltonian is diagonalized directly in the truncated Fock space. Thus, the particle number is conserved exactly and the Pauli blocking effect is taken into account spontaneously. The effects of rotation, Pauli blocking, and octupole deformation on the pairing correlations in U and Pu isotopes have been investigated in detail by the PNC-CSM method.

In the framework of the cranked shell model, the Hamiltonian of an axially deformed nucleus is^[17−20]

where $H_{\rm{Nil}}^{} = \sum h_{\rm{Nil}}^{}(\varepsilon_2^{},\,\varepsilon_3^{},\,\varepsilon_4^{})$ is the Nilsson Hamiltonian, in which the quadrupole ($ \varepsilon_2^{} $), octupole ($ \varepsilon_3^{} $) and hexadecapole ($ \varepsilon_4^{} $) deformation parameters are included^{[16, 21]}. $ -\omega J_{x}^{} $ is the Coriolis interaction with the rotational frequency $ \omega $ about the x axis (perpendicular to the symmetry z axis here).

When $ \omega = 0 $, the single-particle Hamiltonian $ h_{\rm{Nil}}^{} $ has nonzero matrix elements of $ Y_{30}^{} $ between different shell $ N $. Since $ p = (-1)^{N} $, the parity is no longer a good quantum number, but $ \Omega $ (the single-particle angular momentum projection on the symmetry axis) is still a good quantum number. However, when $ \omega \neq 0 $, the symmetry with respect to the reflection through plane yoz, $S_{ x}^{}$ operator, still holds. The single-particle orbitals can be labeled with the simplex quantum number s (the eigenvalues of $S_{ x}^{}$ operator, $ s = \pm i $).

The pairing includes the monopole and quadrupole pairing correlations,

where $ \xi $ is the eigenstates of the Nilsson Hamiltonian $ h_{\rm{Nil}}^{} $, and $ \bar{\xi} $ is the time-reversed states, $ q_{2}^{}(\xi) = \sqrt{16 \pi/5}\langle\xi|r^{2}Y_{20}^{}|\xi\rangle $ is the diagonal element of the stretched quadrupole operator, and $ G_{0}^{} $ and $ G_{2}^{} $ are the effective strengths of monopole and quadrupole pairing interactions, respectively.

By diagonalizing the cranked shell model Hamiltonian in a sufficiently large cranked many-particle configuration (CMPC), a sufficiently accurate low-lying excited intrinsic wave function of the reflection-asymmetric nuclei are obtained as

where $ |i\rangle = |\mu_{1}^{}\mu_{2}^{}\cdots\mu_{n}^{}\rangle $ is a CMPC for an $ n $-particle system, and $ \mu_{1}^{}\mu_{2}^{}\cdots\mu_{n}^{} $ are the occupied cranked Nilsson orbitals. Each configuration $ |i\rangle $ is characterized by the simplex $ s_{i}^{} $,

where $ s_{\mu}^{} $ is the simplex of the particle occupying in orbital $ \mu $. The kinematic moment of inertia (MoI) of eigenstate $ |\psi \rangle $ can be written as

Experimentally, the rotational band with simplex quantum number s is characterized by spin states I of alternating parity^[22]

Therefore for reflection-asymmetric systems with even number of nucleons we have

while for systems with odd number of nucleons we have

The moments of inertia for alternating parity bands can be expressed as

where $ |\psi \rangle $ is the parity-independent wave function with the rotational frequency $ \omega $ obtained by the PNC-CSM method. The $ \varDelta J^{(1)}(\omega) $ is the parity splitting of the moments of inertia in the experimental alternating-parity bands, which can be obtained by

in which $ J^{(1)}_{-}(\omega) $ and $ J^{(1)}_{+}(\omega) $ are the experimental MoIs of the negative and positive parity rotational bands corresponding to the rotational frequency $ \omega $.

In this work, the Nilsson parameters ($\kappa,\,\mu$) are taken from Ref. [23]. The deformations $ \varepsilon_2^{} $, $ \varepsilon_3^{} $, and $ \varepsilon_4^{} $ are input parameters in the PNC-CSM method. The values of $ \varepsilon_2^{} $ and $ \varepsilon_4^{} $ are chosen close to the calculated deformations of the ground states in the actinide region^[24]. The $ \varepsilon_3^{} $ values used in this work are chosen by fitting the experimental MoIs and alignments of the ground-state bands in the U and Pu isotopes. The deformation parameters ($ \varepsilon_2^{} $, $ \varepsilon_3^{} $, $ \varepsilon_4^{} $) used in our PNC-CSM calculations are (0.200, 0.110, −0.055), (0.220, 0.130, −0.040), (0.228, 0.025, −0.065), and (0.230, 0.010, −0.045) for even-even nuclei $ ^{236} {\rm{U}}$, $ ^{238} {\rm{U}}$, $ ^{238} {\rm{Pu}}$, and $ ^{240} {\rm{Pu}}$, respectively. The deformation parameters of odd-A nuclei $ ^{237} {\rm{U}}$ and $ ^{239} {\rm{Pu}}$ are taken as the average of the neighboring even-even nuclei.

The effective pairing strengths $ G_0^{} $ and $ G_2^{} $, in principle, can be determined by the odd-even differences in nuclear binding energies. The values are connected with the dimensions of the truncated cranked many-particle configuration space. For even-even nuclei $^{236, \, 238} {\rm{U}}$ and $^{238, \, 240} {\rm{Pu}}$, the effective monopole and quadrupole pairing strengths are $ G_{0{\rm{p}}}^{} = 0.25 $ MeV, $ G_{2{\rm{p}}}^{} = 0.03 $ MeV and $ G_{0{\rm{n}}}^{} = 0.25 $ MeV, $ G_{2{\rm{n}}}^{} = 0.015 \; {\rm{MeV}} $ for protons and neutrons, respectively. For odd-A nuclei $ ^{237} {\rm{U}}$ and $ ^{239} {\rm{Pu}}$, the neutron pairing strengths are little smaller than those in even-even nuclei. For all nuclei studied in this work, the CMPC space is constructed in the proton $N = 5,\,6$ and neutron $N = 6,\,7$ shells. The dimensions of the CMPC space are about 1 000 for both protons and neutrons.

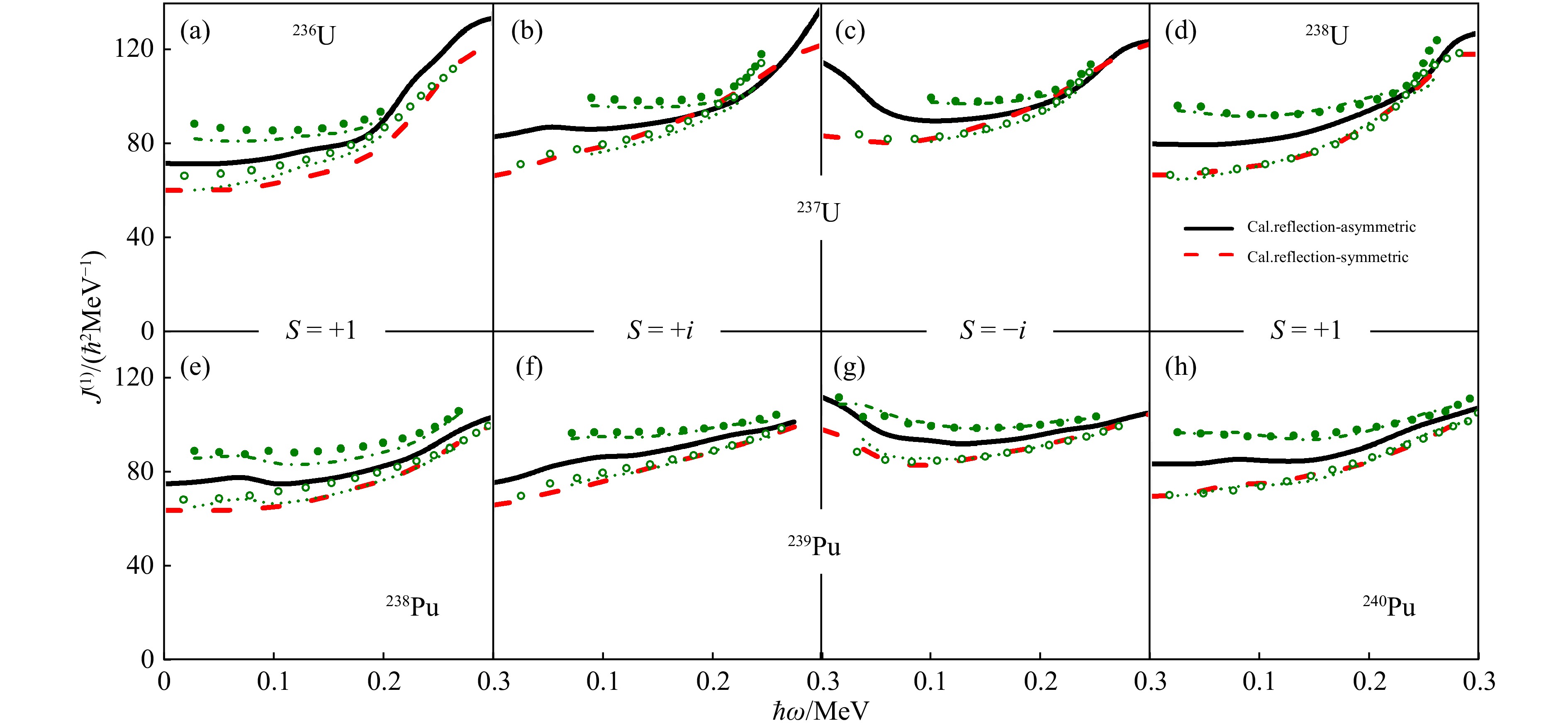
Figure 1 shows the experimental and calculated kinematic moments of inertia $ J^{(1)} $ for the alternating-parity bands ($ s = +1 $) in even-even nuclei $ ^{236, \; 238} {\rm{U}}$ and $ ^{238, \; 240} {\rm{Pu}}$, and parity-doublet bands ($ s = \pm i $) in odd-$ A $ nuclei $ ^{237} {\rm{U}}$ and $ ^{239} {\rm{Pu}}$. The experimental data for the negative (positive) parity bands are denoted by green solid (open) circles. The PNC-CSM calculations in the reflection-asymmetric nuclei are denoted by black solid lines. After considering the parity spitting of Eqs. (12) and (13), the $ J^{(1)} $ of negative and positive parity bands are denoted by dash-dotted and dotted lines, respectively. The PNC-CSM calculations in the reflection-symmetric (RS) nuclei (without $ \varepsilon_3^{} $ deformation) are shown by red dashed lines. It can be seen that the experimental moments of inertia versus the rotational frequency $ \hbar\omega $ are reproduced very well by the PNC-CSM calculations. As shown in Figs. 1(b), 1(c), 1(f), and 1(g), there are simplex splittings between $ s = + i $ and $ s = -i $ partner bands (solid black lines) at $ \hbar\omega < $0.10 MeV in both odd-$ A $ nuclei $ ^{237} {\rm{U}}$ and $ ^{239} {\rm{Pu}}$.

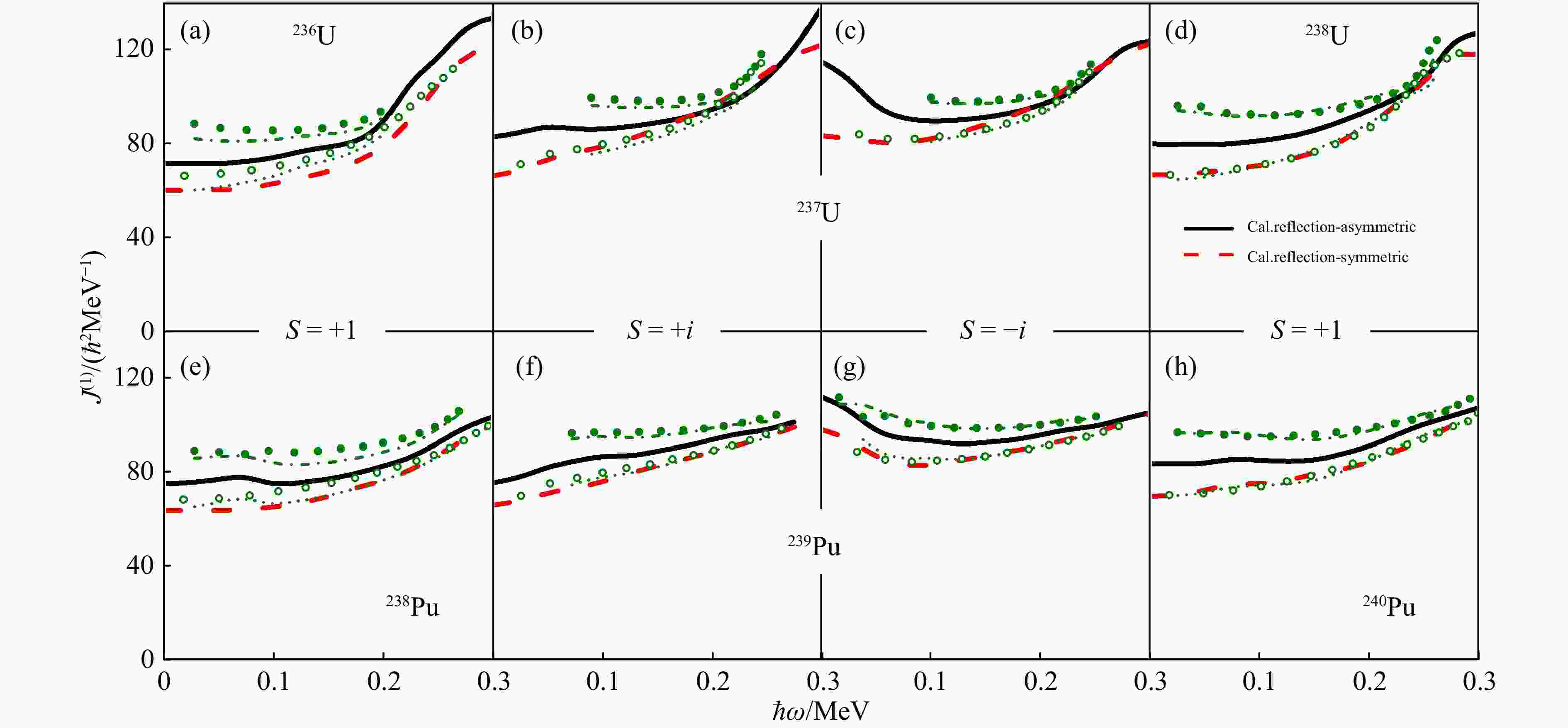
Figure 1.  The experimental and calculated kinematic moments of inertia $ J^{(1)} $ for the alternating-parity bands in even-even nuclei $^{236, \, 238} {\rm{U}}$ and $^{238, \, 240} {\rm{Pu}}$, and parity-doublet bands in odd-$ A $ nuclei $ ^{237} {\rm{U}}$ and $ ^{239} {\rm{Pu}}$. The experimental data for the negative (positive) parity bands are denoted by solid (open) circles. The PNC-CSM calculations in the reflection-asymmetric nuclei are denoted by black solid lines. After considering the parity spitting of Eqs. (12) and (13), the negative and positive parity bands are denoted by dash-dotted and dotted lines, respectively. The PNC-CSM calculations in the reflection-symmetric nuclei (without $ \varepsilon_3^{} $ deformation) are shown by red dashed lines. The $ \varepsilon_3^{} $ deformation parameters for $ ^{236} {\rm{U}}$, $ ^{237} {\rm{U}}$, and $ ^{238} {\rm{U}}$ are 0.110, 0.071, and 0.130, and those for $ ^{238} {\rm{Pu}}$, $ ^{239} {\rm{Pu}}$, and $ ^{240} {\rm{Pu}}$ are 0.025, 0.010, and 0.010. (color online)

From Fig. 1, we can see that the moments of inertia $ J^{(1)} $ gradually increase with rotational frequency in all nuclei. For intrinsic rotational band in $ ^{236} {\rm{U}}$, the calculated difference in MoIs $ \delta J/J $ with increasing $ \omega $ is

It can be seen that the $ J^{(1)} $ of intrinsic rotational band in $ ^{236} {\rm{U}}$ increase about 87% at the frequency $ \hbar\omega = 0.30\; {\rm{MeV}} $ compared with that at the bandhead. For other nuclei, the results are very similar, and will not be shown here.

At the bandhead, the calculated odd-even differences in MoIs $ \delta J/J $ between the intrinsic $ s = -i $ rotational bands in odd-$ A $ nuclei $ ^{237} {\rm{U}}$ and $ ^{239} {\rm{Pu}}$ and those in the neighboring even-even nuclei $ ^{236} {\rm{U}}$ and $ ^{238} {\rm{Pu}}$ are:

Therefore, the higher $ J^{(1)} $ in the odd-A nuclei compared with those in the neighboring even-even nuclei mainly attribute to the blocking of unpaired neutron.

Furthermore, as shown in Fig. 1, the calculated MoIs of the intrinsic rotational bands in the reflection-asymmetric nuclei are obviously higher than those in reflection-symmetric nuclei. At the bandhead, the calculated differences in MoIs $ \delta J/J $ between the RA and RS rotational bands for the U isotopes are:

and the calculated results for the Pu isotopes are:

We can see that the differences in MoIs $ \delta J/J $ in the U isotopes are almost larger than those in the Pu isotopes. In this work, the $ \varepsilon_3^{} $ deformation parameters for $ ^{236} {\rm{U}}$, $ ^{237} {\rm{U}}$, and $ ^{238} {\rm{U}}$ are 0.110, 0.071, and 0.130, while those for $ ^{238} {\rm{Pu}}$, $ ^{239} {\rm{Pu}}$, and $ ^{240} {\rm{Pu}}$ are 0.025, 0.010, and 0.010. Thus, it can be seen clearly that $ \varepsilon_3^{} $ deformation gives a very significant contribution to the variation of $ J^{(1)} $.

In order to have a more clear understanding of the variation of $ J^{(1)} $, we study the effects of rotation, blocking and octupole deformation on the pairing correlations in the U and Pu isotopes in detail.

The nuclear pairing gap is defined as^[25]

Figure 2 shows the calculated proton and neutron pairing gaps $ \tilde{\varDelta} $ versus the rotational frequency $ \hbar\omega $ for the alternating-parity bands in even-even nuclei $^{236, \, 238} {\rm{U}}$ and $^{238, \, 240} {\rm{Pu}}$, and the parity-doublet bands in odd-A nuclei $ ^{237} {\rm{U}}$ and $ ^{239} {\rm{Pu}}$. The effective pairing strengths are the same for the reflection-asymmetric and reflection-symmetric nuclei in the PNC-CSM calculations. As shown in Fig. 2, the pairing gaps $ \tilde{\varDelta} $ in the reflection-asymmetric nuclei are almost smaller than those in the reflection-symmetric nuclei for both protons and neutrons. The pairing gaps decrease with increasing rotation frequency $ \hbar\omega $, and significantly decrease for the neutrons in the odd-A nuclei $ ^{237} {\rm{U}}$ and $ ^{239} {\rm{Pu}}$.

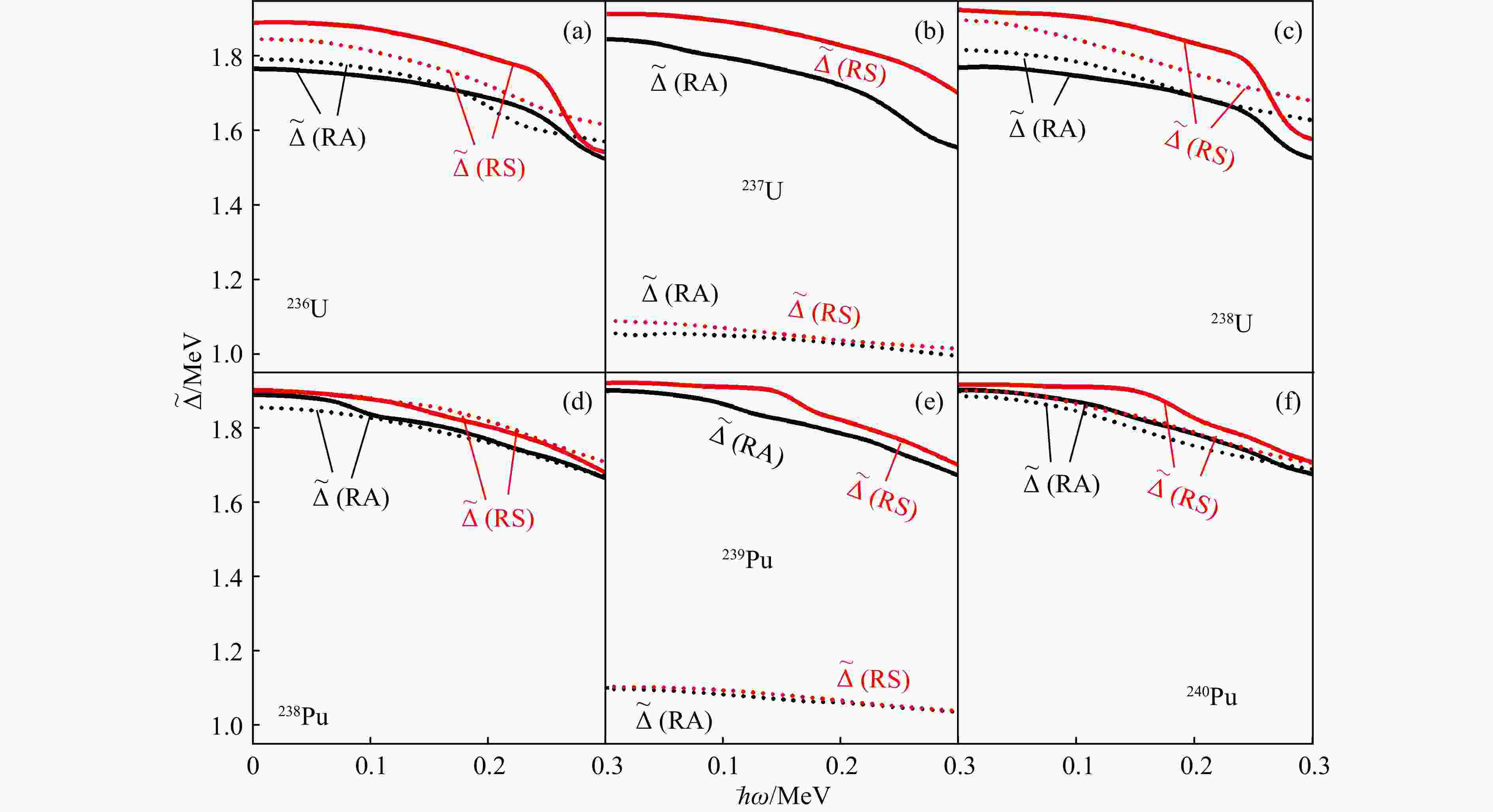
Figure 2.  The calculated proton and neutron pairing gaps $ \tilde{\varDelta} $ versus the rotational frequency $ \hbar\omega $ for the alternating-parity bands in even-even nuclei $^{236, \, 238} {\rm{U}}$ and $^{238, \, 240} {\rm{Pu}}$, and parity-doublet bands in odd-$ A $ nuclei $ ^{237} {\rm{U}}$ and $ ^{239} {\rm{Pu}}$. The PNC-CSM calculations in the reflection-asymmetric nuclei are denoted by black lines, and those in the reflection-symmetric nuclei (without $ \varepsilon_3^{} $ deformation) are denoted by red lines. The solid and dotted lines are for protons and neutrons, respectively. The $ \varepsilon_3^{} $ deformation parameters for $ ^{236} {\rm{U}}$, $ ^{237} {\rm{U}}$, and $ ^{238} {\rm{U}}$ are 0.110, 0.071, and 0.130, and those for $ ^{238} {\rm{Pu}}$, $ ^{239} {\rm{Pu}}$, and $ ^{240} {\rm{Pu}}$ are 0.025, 0.010, and 0.010. (color online)

The calculated pairing gap reductions with increasing rotational frequency in the reflection-asymmetric nuclei $ ^{236} {\rm{U}}$ are:

The results are very similar for other nuclei, which are not shown here. For both protons and neutrons, it can be seen that the pairing gaps decrease by about $ 10 {\text{%}} $ at the frequency $ \hbar\omega = 0.30\; {\rm{MeV}} $ compared with those at the bandhead. These result in the gradual increase of $ J^{(1)} $ versus rotational frequency in all nuclei.

Comparing Figs. 2(a), 2(d) and Figs. 2(b), 2(e), it is seen that the pairing gaps of neutrons decrease in the odd-$ A $ nuclei $ ^{237} {\rm{U}}$ and $ ^{239} {\rm{Pu}}$. At the bandhead, the calculated neutron pairing gap reductions for these nuclei are:

We can see that the pairing gaps decrease about $ 40 {\text{%}} $ in the odd-$ A $ nuclei compared with the neighboring even-even nuclei, which lead to higher $ J^{(1)} $ for the $ s = -i $ bands in these odd-$ A $ nuclei [see Figs. 1(a), 1(c), 1(e) and 1(g)].

At the bandhead, the calculated pairing gap reductions for $ ^{236} {\rm{U}}$ with reflection-asymmetric deformation and reflection-symmetric deformation are:

and the calculated results for $ ^{238} {\rm{Pu}}$ are:

We can see that the pairing gaps decrease in the reflection-asymmetric nuclei compared with the reflection-symmetric nuclei. Furthermore, the pairing gap reduction becomes even more significant with increasing the octupole deformation [see Figs. 2(a) and 2(c)]. Therefore, the octupole correlations give a certain effect on the increase of $ J^{(1)} $ in the reflection-asymmetric nuclei. The results are very similar for other nuclei, which are not shown here.

The reflection-asymmetric nuclei $^{236, \, 237, \,238} {\rm{U}}$ and $^{238, \, 239, \, 240} {\rm{Pu}}$ are investigated by the cranked shell model with pairing correlations treated by the particle-number-conserving method. The experimental moments of inertia of the alternating-parity bands in the even-even nuclei $^{236, \, 238} {\rm{U}}$ and $^{238, \, 240} {\rm{Pu}}$ and the parity-doublet bands in the odd-$ A $ nuclei $ ^{237} {\rm{U}}$ and $ ^{239} {\rm{Pu}}$ are reproduced well by the PNC-CSM calculations. The pairing gaps in these nuclei are significantly influenced by rotation, Pauli blocking, and octupole deformation. The gradual increases of $ J^{(1)} $ versus rotational frequency in these nuclei are mainly due to the pairing gap reductions with increasing $ \omega $. The higher $ J^{(1)} $ for the intrinsic $ s = -i $ bands in the odd-$ A $ nuclei compared with the neighboring even-even nuclei can be attributed to the pairing gap reductions due to Pauli blocking effects. The $ J^{(1)} $ of the intrinsic rotational bands in the RA nuclei are higher than those in the RS nuclei. Furthermore, a larger octupole deformation $ \varepsilon_3^{} $ in the RA nuclei results in more significant pairing gap reduction compared with the RS nuclei.