-
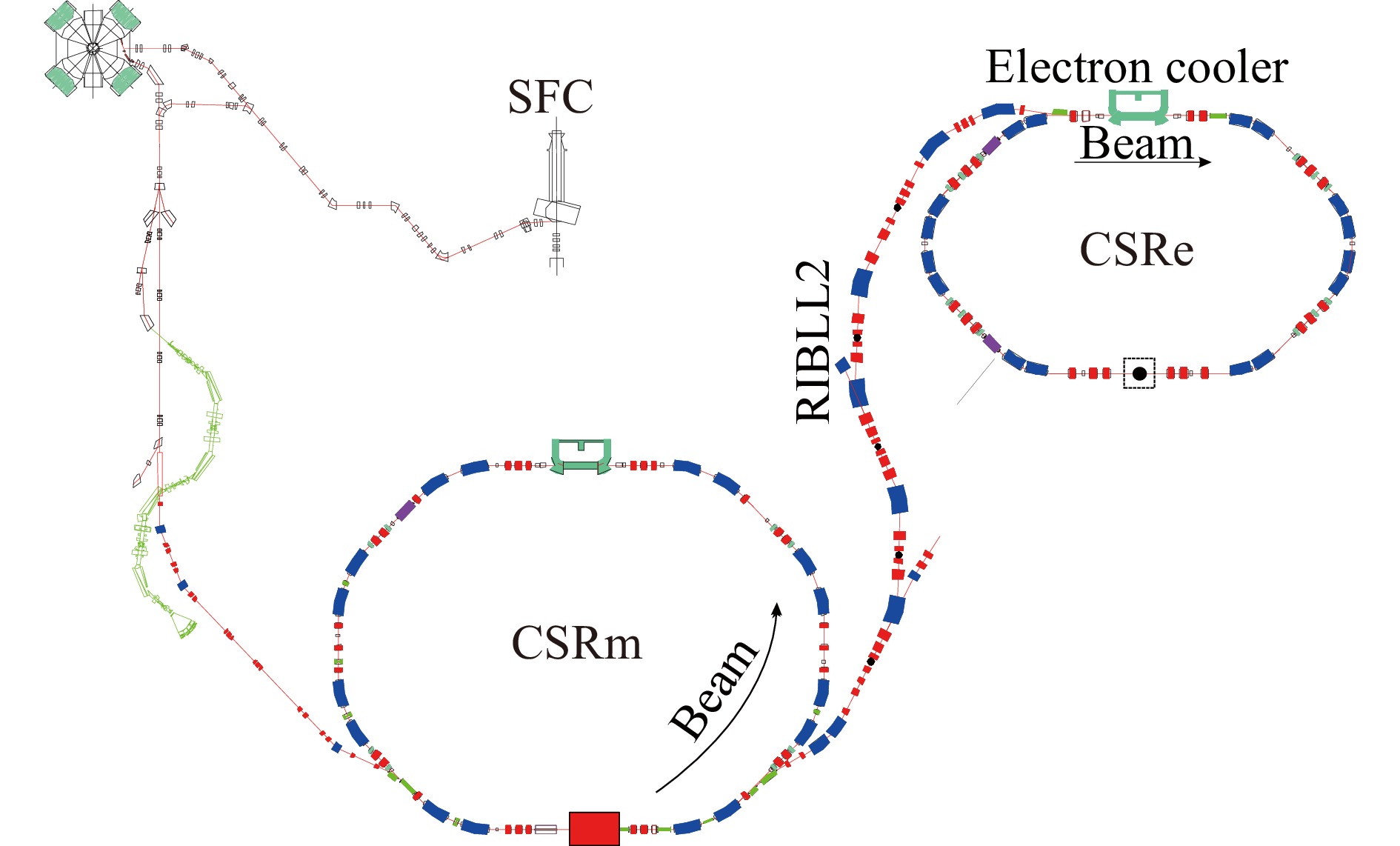
兰州重离子冷却储存环HIRFL-CSR[1]是一个多功能的双冷却储存环同步加速器系统,由主环CSRm(main cooler-storage ring)和实验环CSRe(experimental cooler-storage ring)构成。CSRm和CSRe通过放射性束流线RIBLL2(radioactive ion beam line 2 in Lanzhou)连接,如图1所示。基于HIRFL-CSR的等时性质量谱仪(Isochronous mass spectrometry, IMS)[2]开展短寿命、高电荷态离子的衰变研究是近些年来发展的新技术。在基于IMS高电荷态离子$ ^{94m} {\rm{Ru}} ^{44+} $寿命测量实验中,$ ^{94m} {\rm{Ru}} ^{44+} $通过弹核碎裂反应产生。初级束流$ ^{112} {\rm{Sn}} ^{35+} $在CSRm中强累积到约为150 μA、能量加速到376.42 MeV/u后,快引出在放射性束流线(RIBLL2)入口处轰击厚约为10.0 mm的$ ^{9} {\rm{Be}}$靶发生弹核碎裂反应,产生次级碎片。次级碎片经过RIBLL2的筛选后,注入并储存在实验环CSRe中。安装在CSRe上的飞行时间探测器[3],持续记录并存储离子每次通过飞行时间探测器的时间信号。每次注入记录时间为200 μs,对应离子循环~300圈。如果离子在循环过程中发生衰变,那么其质量就会改变,相应的循环周期就会产生变化,变化的数值大概是11.9 ps。而大部分的离子在储存环中能够循环1 000多圈[4],循环1 000多圈对应的飞行时间的变化大概是20 ps,所以$ ^{94m} {\rm{Ru}} ^{44+} $衰变后的子核$ ^{94} {\rm{Ru}} ^{44+} $依然可以储存在CSRe中不丢失。同时,因为$ ^{94m} {\rm{Ru}} ^{44+} $和$ ^{94} {\rm{Ru}} ^{44+} $都是等时性中心离子,所以$ ^{94} {\rm{Ru}} ^{44+} $的飞行时间在衰变后受能量损失的影响比较小。因此,即使母核$ ^{94m} {\rm{Ru}} ^{44+} $发生了衰变,其子核$ ^{94} {\rm{Ru}} ^{44+} $也依旧可以循环足够久的时间以供我们测量。
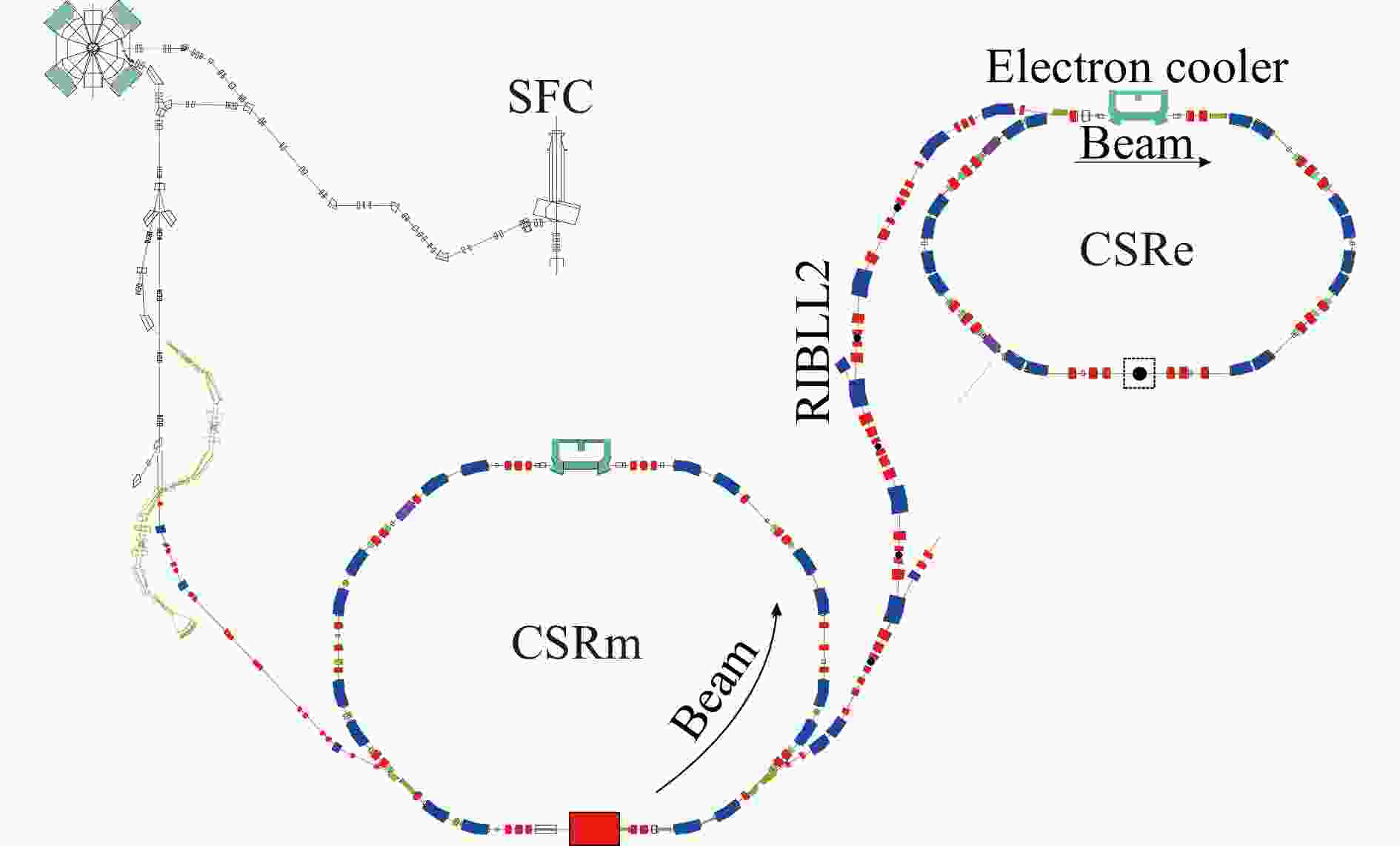
图 1 兰州重离子冷却储存环装置示意图[5]
通过分析模拟结果[4]可知,平均大量圈数的时间数据点可以减小由离子发射度引起的波动对循环周期的影响。通过平均~30圈(~20 μs)的数据点,得到循环周期的不确定性为~2 μs,对应的质量分辨率为~8$\times10^4$[6]。即观测时间窗口为数据采集开始后(20 μs, 180 μs) 内,可以有效鉴别衰变事件。在之前的数据分析方法中,我们通过观测循环周期的变化来鉴别衰变事件。如果$ ^{94m} {\rm{Ru}} ^{44+} $衰变发生在观测时间窗口外,由于衰变事件无法有效地鉴别而忽略对应衰变事件。此外,利用一条直线拟合离子的飞行时间和循环圈数的关系,就可以得到直线拟合残差。当$ ^{94m} {\rm{Ru}} ^{44+} $发生衰变时,衰变前后的循环周期将发生变化,直线拟合残差数据点为一条折线似的扭曲,如果未发生衰变,则无扭曲。以上方法观测衰变事件的有效时间窗口为 (20 μs, 180 μs),鉴别出的衰变事件为49个。为了进一步扩展观测时间窗口,鉴别出更多的衰变事件,本文通过模拟数据研究了直线拟合残差的频谱,通过频谱的幅度与衰变圈数的关系,得到一种新的鉴别方法。
-
本节主要介绍的是非周期性不对称三角波的傅里叶变换公式的推导过程。时域转化成频域的关系式为
$$ F(\omega) = \int_{-\infty }^{+\infty } f(t){\rm{e}}{}^{-{\rm{j}}\omega t} {\rm{d}}t , $$ (1) 其中:$ f(t) $为时域表达式;$ F(\omega $)为频域表达式。
假设非周期性三角波的分段函数的表达式为$ f(t) $,
$$ f(t) = \left\{ {\begin{array}{*{20}{l}} {a(t - t_1^{}),t \in [t_1^{},{\textit{z}})}\\ {b(t_2^{} - t),t \in ({\textit{z}},t_2^{}]}\\ {0,t \in ( - \infty ,t_1^{}) \cup (t_2^{}, + \infty )} \end{array}} \right. , $$ (2) 其中$ a $, $ b $, $ t_1^{} $, $ t_2^{} $均为常数。
$$ \begin{split} F(\omega ) =\; &{\rm{e}}^{-{\rm{j}}\omega {\textit{z}}}\left(\dfrac{at_{1}^{}-a{\textit{z}} }{j\omega }+\dfrac{a}{\omega ^{2} }\right)-\dfrac{a}{\omega ^{2} }{\rm{e}}^{-{\rm{j}}\omega t_{1}^{}}+\\ & {\rm{e}}^{-{\rm{j}}\omega {\textit{z}}}\left(\dfrac{bt_{2}^{}-b{\textit{z}} }{j\omega }+\frac{b}{\omega ^{2}}\right)-\dfrac{b}{\omega ^{2}}{\rm{e}}^{-{\rm{j}}\omega t_{2}^{} } 。 \end{split} $$ (3) 两条直线的交点为z = ($ {a} $·$ t_{1}^{} $+$ b $·$ t_{2}^{} $)/($ {a} $+$ b $) 代入式(3)后,做个简单的移项后可以得到:
$$ F(\omega) = \frac{1}{\omega^{2}} \left[(a+b){\boldsymbol{\cdot}} {\rm{e}}^{-{\rm{j}}\omega {\textit{z}}} -a{\boldsymbol{\cdot}} {\rm{e}}^{-{\rm{j}}\omega t_{1}^{} } -b{\boldsymbol{\cdot}} {\rm{e}}^{-{\rm{j}}\omega t_{2}^{} } \right] 。 $$ (4) 通过欧拉公式$ {\rm{e}}^{-{\rm{j}}x} $= cos($ x $) − sin($ x $)、二倍角公式cos($ x $) = 1 − 2sin2($ x $/2) 以及抽样函数的表达式$ Sa(x $) = sin($ x $)/$ x $。将式(4)写成:
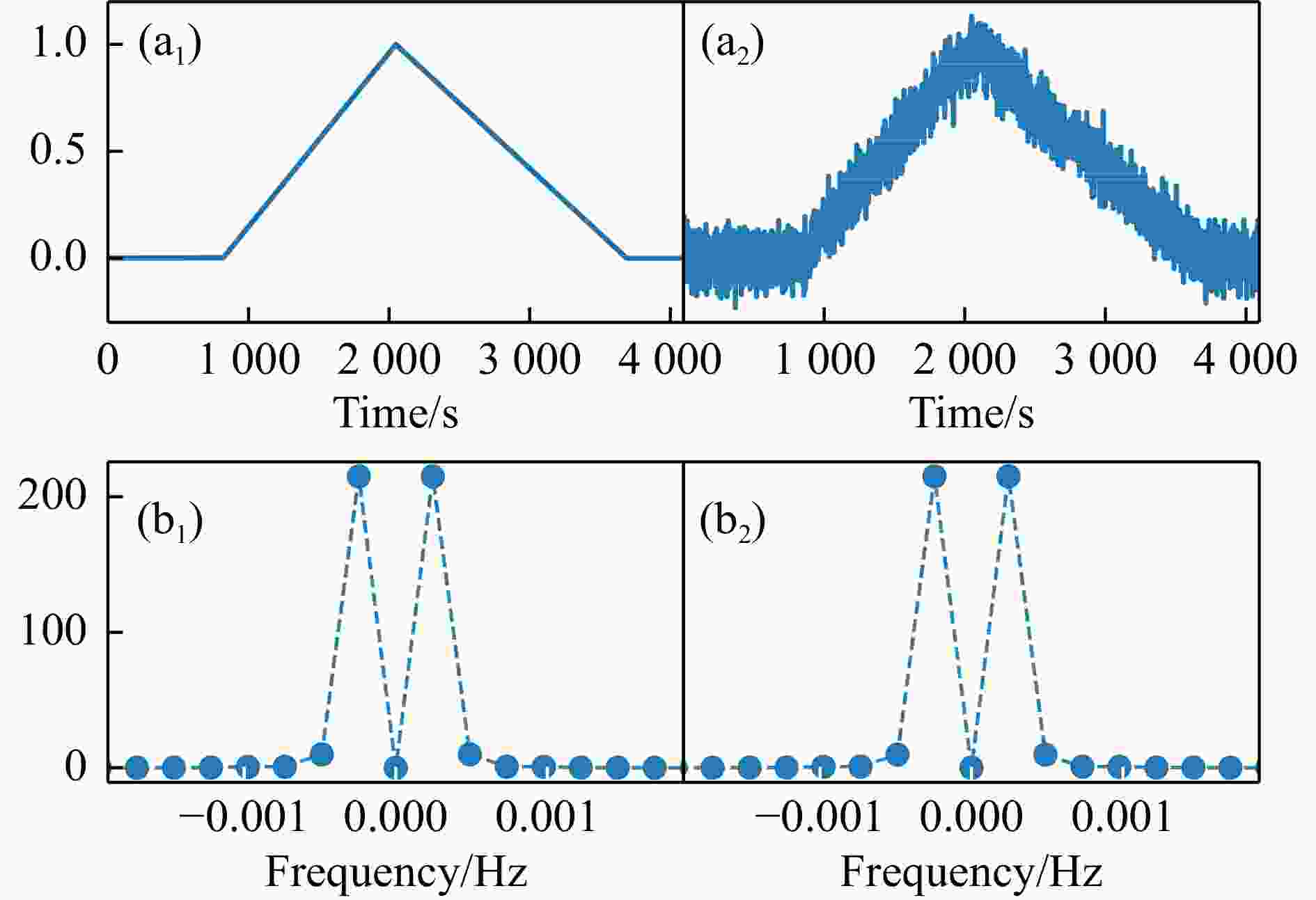
$$ \begin{split} F(\omega) =\;& -\dfrac{{\textit{z}}^{2} (a+b)}{2}{\boldsymbol{\cdot}} Sa^{2} \left(\dfrac{{\textit{z}}\omega }{2} \right) -\dfrac{{\rm{i}}(a+b){\textit{z}}}{\omega }{\boldsymbol{\cdot}} Sa({\textit{z}}\omega )+\\ &\dfrac{a{t_{1}^{2} } }{2} {\boldsymbol{\cdot}} Sa^{2} \left(\dfrac{\omega t_{1}^{} }{2}\right) +\dfrac{{\rm{i}}{\boldsymbol{\cdot}} at_{1}^{}}{\omega }{\boldsymbol{\cdot}} Sa(t_{1}^{}\omega)+\\ & \dfrac{b{\boldsymbol{\cdot}} {t_{2}^{2} } }{2}{\boldsymbol{\cdot}} Sa^{2} \left(\dfrac{\omega t_{2}^{} }{2}\right)+\dfrac{{\rm{i}}{\boldsymbol{\cdot}} bt_{2}^{} }{\omega }{\boldsymbol{\cdot}} Sa(t_{2}^{}\omega ), \end{split} $$ (5) 由式(5)可得$ F(\omega) $的模与频率$ \omega $的关系,通过这两者的关系就可以得到如图2(b1)、图2(b2)的模拟结果。
图2展示了在其他条件相同的情况下,未考虑噪声和考虑噪声两种情况的时域图和频域图。从图2(a1)、图2(b1)可以看出,当时域图出现折线时,对应频谱图会出现一个最大值。图2(a2) 显示,当考虑噪声,即考虑误差条件,时域图出现具有毛刺的折线时,对应频域图2(b2)也出现一个最大值,并且此频谱最大值与未考虑误差的图2(b1) 频谱最大值基本一致,无明显变化。因此,可以通过频谱的最大值来鉴别$ ^{94m} {\rm{Ru}} ^{44+} $的衰变事件。接下来我们基于该方法,通过模拟数据来检验该方法的指认效果。
-
首先需要估计$ ^{94} {\rm{Ru}} ^{44+} $和$ ^{94m} {\rm{Ru}} ^{44+} $在本次实验中的初始循环时间$RevT_{\rm{g,\, 1}}^{}$和$RevT_{\rm{m,\, 1}}^{}$。假设$ ^{94} {\rm{Ru}} ^{44+} $的质量为$ M_{\text{g}}^{} $,$ ^{94m} {\rm{Ru}} ^{44+} $的质量为$ M_{\text{m}}^{} $,则有:
$$ M_{\text{g}}^{} = A{\boldsymbol{\cdot}} M_{\text{u}}^{}-Q{\boldsymbol{\cdot}} M_{\text{e}}^{}+ME_{\text{g}}^{} +Be(Z), $$ (6) $$ M_{\text{m}}^{} = A{\boldsymbol{\cdot}} M_{\text{u}}^{}-Q{\boldsymbol{\cdot}} M_{\text{e}}^{}+ME_{\text{g}}^{} +Be(Z)+E_{\text{X}}^{}, $$ (7) 其中:$ A $ = 94为质量数;$ M_{\text{u}}^{} $为931.494 MeV,是核子质量;$ M_{\text{e}}^{} $为0.511 MeV,是电子质量;$ ME_{\text{g}}^{} $为−82.584 MeV,是$ ^{94} {\rm{Ru}} ^{44+} $的质量过剩;$ Be(Z) $是核外所有电子的结合能;$ E_{\text{X}}^{} $为2.644 MeV,是同核异能态的激发能。
$ ^{94m} {\rm{Ru}} ^{44+} $和$ ^{94} {\rm{Ru}} ^{44+} $的质量$ M_{\text{m}}^{} $、$ M_{\text{g}}^{} $以及$ ^{94} {\rm{Ru}} ^{44+} $的初始磁刚度$ B{\rho}_{\text{g}}^{} $= 5.529 4 Tm,对应的轨道长度$ L_{0}^{} $= 128.8 m。假设两个离子初始的洛伦兹因子为 $ {\gamma}_{0}^{} $、相对论速度为 $ {\beta}_{0}^{} $以及离子刚进入实验环的单核子的能量$ E_{\alpha}^{} $是相同的,那么它们的表达式为
$$ \gamma _{0}^{} = \sqrt{\left ( \frac{B\rho _{\text{g}}^{}}{M_{\text{g}}^{}/(Q{\boldsymbol{\cdot}} c) } \right ) ^{2} }+1, $$ (8) $$ \beta_{0}^{} = \sqrt{1-\frac{1}{\gamma _{0}^{2}}}, $$ (9) $$ E_{\alpha }^{} = \frac{M_{\text{g}}^{}{\boldsymbol{\cdot}} (\gamma _{\text{g}}^{}-1 )}{A} , $$ (10) 其中$ Q $为44,是该全剥离离子的电荷态;$ c $为2.997 9$ \times $108 m/s,是光在真空中传播的速度。由以上式子可以得到$ ^{94m} {\rm{Ru}} ^{44+} $的初始磁刚度$ B{\rho}_{\text{m}}^{} $:
$$ B\rho _{\text{m}}^{} = \frac{M_{\text{m}}^{}{\boldsymbol{\cdot}} \beta _{0}^{}{\boldsymbol{\cdot}} \gamma _{0}^{}}{Q{\boldsymbol{\cdot}} c}, $$ (11) 然后计算出在$ B{\rho}_{\text{m}}^{} $下的轨道长度$ L_{\text{m}}^{} $为
$$ L_{\text{m}}^{} = L_{0}^{}{\boldsymbol{\cdot}} \left(1+\frac{B\rho _{\text{m}}^{} /B\rho _{\text{g}}^{}-1}{\gamma _{\text{t}}^{2}}\right) , $$ (12) 其中$ {\gamma}_{\text{t}}^{} $= 1.302,是实验环的转变能[2]。因此$ ^{94} {\rm{Ru}} ^{44+} $和$ ^{94m} {\rm{Ru}} ^{44+} $初始循环时间$RevT_{\rm{g,\,1}}^{}$和$ RevT_{\text{m,1}}^{} $为
$$ RevT_{\text{g,1}}^{} = \frac{L_{0}^{}}{\beta _{0}^{}{\boldsymbol{\cdot}} c} , $$ (13) $$ RevT_{\text{m,1}}^{} = \frac{L_{\text{m}}^{}}{\beta _{0}^{}{\boldsymbol{\cdot}} c}。 $$ (14) 随后,继续推算出$ ^{94} {\rm{Ru}} ^{44+} $和$ ^{94m} {\rm{Ru}} ^{44+} $在第$ {i} $圈的循环时间$RevT_{\rm {g,\,i}}^{}$和$RevT_{\rm{m},\, i}^{}$。当CSRe中的存储离子经过碳膜时,存储离子会损失能量,估算出离子循环300圈的能量损失$ E_{\text{al}}^{} $为36.695 MeV,平均每圈的能损$ E_{\text{l}}^{} $为36.695/300等于0.122 3 MeV。然后计算出每圈洛伦兹因子的变化量$ {\Delta}{\gamma} $为$ E_{\text{l}}^{} $/$ M_{\text{m}}^{} $等于1.398 6×10−6。以此类推,离子循环$ {i} $圈后,其洛伦茨因子${\gamma}_{{i}}^{}$为
$$ \gamma _{{i}}^{} = \gamma _{0}^{}-({i}-1){\boldsymbol{\cdot}} \bigtriangleup \gamma , $$ (15) 其相对论速度${\beta}_{{i}}^{}$为
$$ \beta _{{i}}^{} = \sqrt{1-\frac{1}{\gamma _{{i}}^{2}}}, $$ (16) 在第i圈时,$ ^{94} {\rm{Ru}} ^{44+} $和$ ^{94m} {\rm{Ru}} ^{44+} $的磁刚度分别为$B{\rho}_{\text{g},\, i}^{}$和$B{\rho}_{\text{m},\, i}^{}$:
$$ B\rho _{\text{g},\,i}^{} = \frac{M_{\text{g}}^{}{\boldsymbol{\cdot}} \beta _{{i}}^{}{\boldsymbol{\cdot}} \gamma _{{i}}^{}}{Q{\boldsymbol{\cdot}} c}, $$ (17) $$ B\rho _{\text{m},\, i}^{} = \frac{M_{\text{m}}^{}{\boldsymbol{\cdot}} \beta _{{i}}^{}{\boldsymbol{\cdot}} \gamma _{{i}}^{}}{Q{\boldsymbol{\cdot}} c} 。 $$ (18) 在第i圈时,$ ^{94} {\rm{Ru}} ^{44+} $和$ ^{94m} {\rm{Ru}} ^{44+} $的轨道长度分别为$L_{\text{g},\,i}^{}$和$L_{\text{m},\,i}^{}$:
$$ L_{\text{g},\,i}^{} = L_{0}^{}{\boldsymbol{\cdot}} \left(1+\frac{B\rho _{\text{g},\,i}^{} /B\rho _{\text{g}}^{}-1}{\gamma _{\text{t}}^{2}}\right), $$ (19) $$ L_{\text{m},\, i}^{} = L_{0}^{}{\boldsymbol{\cdot}} \left(1+\frac{B\rho _{\text{m},\,i}^{} /B\rho _{\text{g}}^{}-1}{\gamma _{\text{t}}^{2}}\right), $$ (20) 从而可以得到$ ^{94} {\rm{Ru}} ^{44+} $和$ ^{94m} {\rm{Ru}} ^{44+} $在第$ {i} $圈的循环时间$RevT_{\text{g},\,i}^{}$和$RevT_{\text{m},\,i}^{}$分别为
$$ RevT_{\text{g},\,i}^{} = \frac{L_{\text{g},\,i}^{}}{\beta _{{i}}^{}{\boldsymbol{\cdot}} c}, $$ (21) $$ RevT_{\text{m},\,i}^{} = \frac{L_{\text{m},\,i}^{}}{\beta _{{i}}^{}{\boldsymbol{\cdot}} c}。 $$ (22) 最终得到$ ^{94} {\rm{Ru}} ^{44+} $和$ ^{94m} {\rm{Ru}} ^{44+} $在$ {n} $圈内的总飞行时间分别为$t_{\text{g},\,n}^{}$和$t_{\text{m},\,n}^{}$:
$$ t_{\text{g},\,{n}}^{} = \sum\limits_{{{i}}^{} = 1}^{{n}}RevT_{\text{g},\,i}^{} , $$ (23) $$ t_{\text{m},\,n}^{} = \sum\limits_{{{i}}^{} = 1}^{{n}}RevT_{\text{m},\,i}^{} 。 $$ (24) 如果$ ^{94m} {\rm{Ru}} ^{44+} $在第$ {s} $圈衰变成$ ^{94} {\rm{Ru}} ^{44+} $,那么可以假设该离子序列在$ {n} $圈内总飞行时间是$t_{\text{d},\,n}^{}$,则$t_{\text{d},\,n}^{}$为
$$ t_{\text{d},\,n}^{} = \sum\limits_{{{i}}^{} = 1}^{{s}}RevT_{\text{m},\,i}^{}+\sum\limits_{{{i}}^{} = {\text{s}}+1}^{{n}}RevT_{\text{g},\,i}^{} 。 $$ (25) 在实验中,飞行时间探测器的时间分辨率为50 ps(标准偏差),为了使模拟数据和实验数据更加接近,在第$ {n} $圈内的总时间$t_{\text{d},\,n}^{}$加上了一个高斯分布式随机数N(0, 502)。所以假设$t_{\text{d},\,n}'$为该离子序列在$ {n} $圈内的总飞行时间,$ X $为产生的随机数($ X $模拟飞行时间探测器的时间分辨),总飞行时间$t_{\text{d},\,n}'$就可以表示为
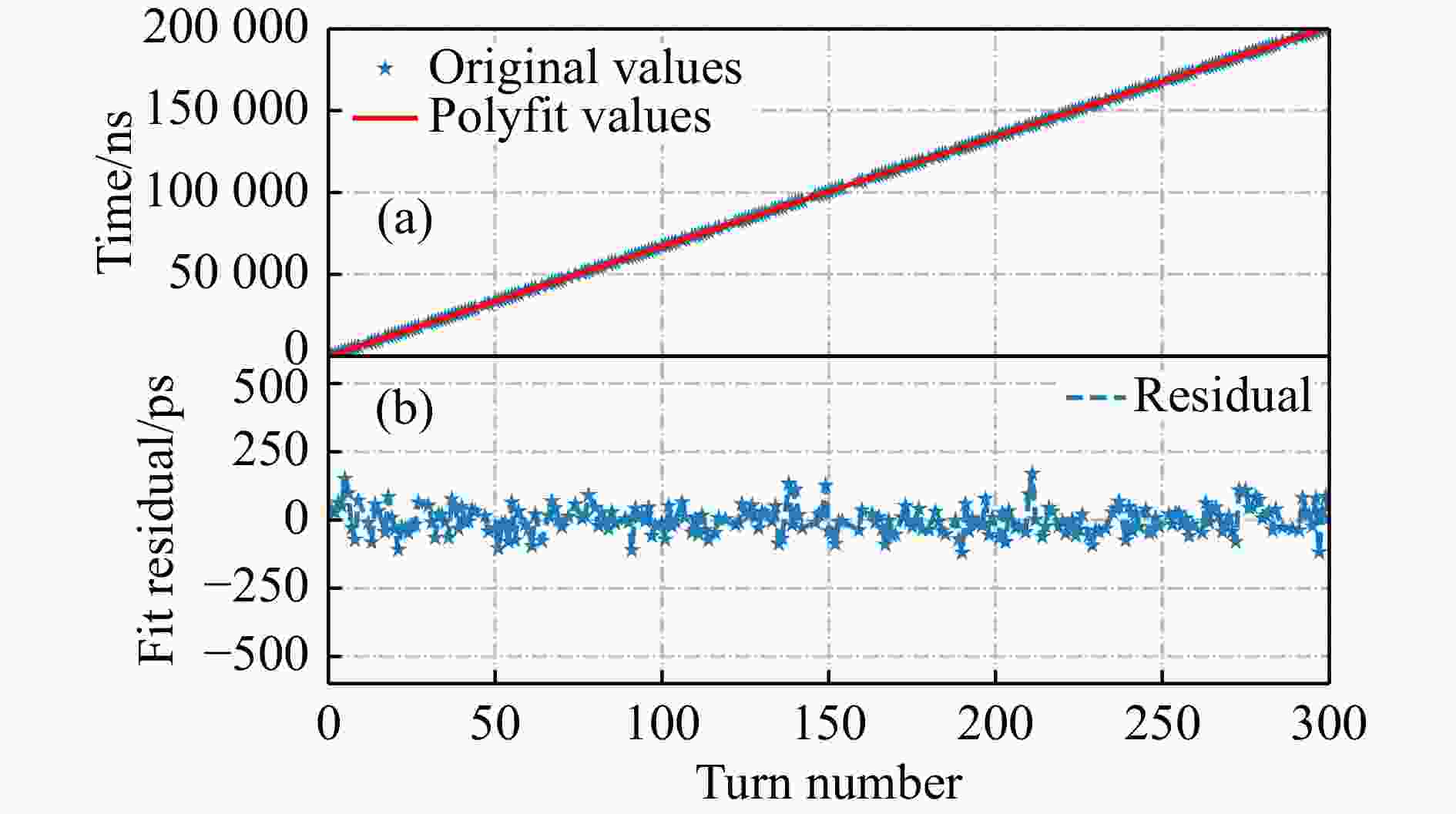
$$ t _{\text{d},\,n}' = t_{\text{d},\,n}^{}+X。 $$ (26) 图3(a)是模拟得到的离子飞行时间随循环圈数的变化图,蓝色点为实验数据点,红线为直线拟合曲线。图3(b)是该离子直线拟合残差图。
-
在观测时间窗口中离子发生衰变时,直线拟合残差将出现一个明显的扭曲。这个扭曲是由于衰变前后,离子的循环周期发生了变化,这也是前面工作中直观指认衰变时间的方法。本文中新的指认方法也是在直线拟合残差的基础上,对数据进行进一步分析。本节的主要方法是通过对直线拟合残差做傅里叶变换,将时域信号变成频域信号,再通过频谱的幅度对衰变事件进行鉴别,随后通过衰变前后的周期差进行进一步鉴别。
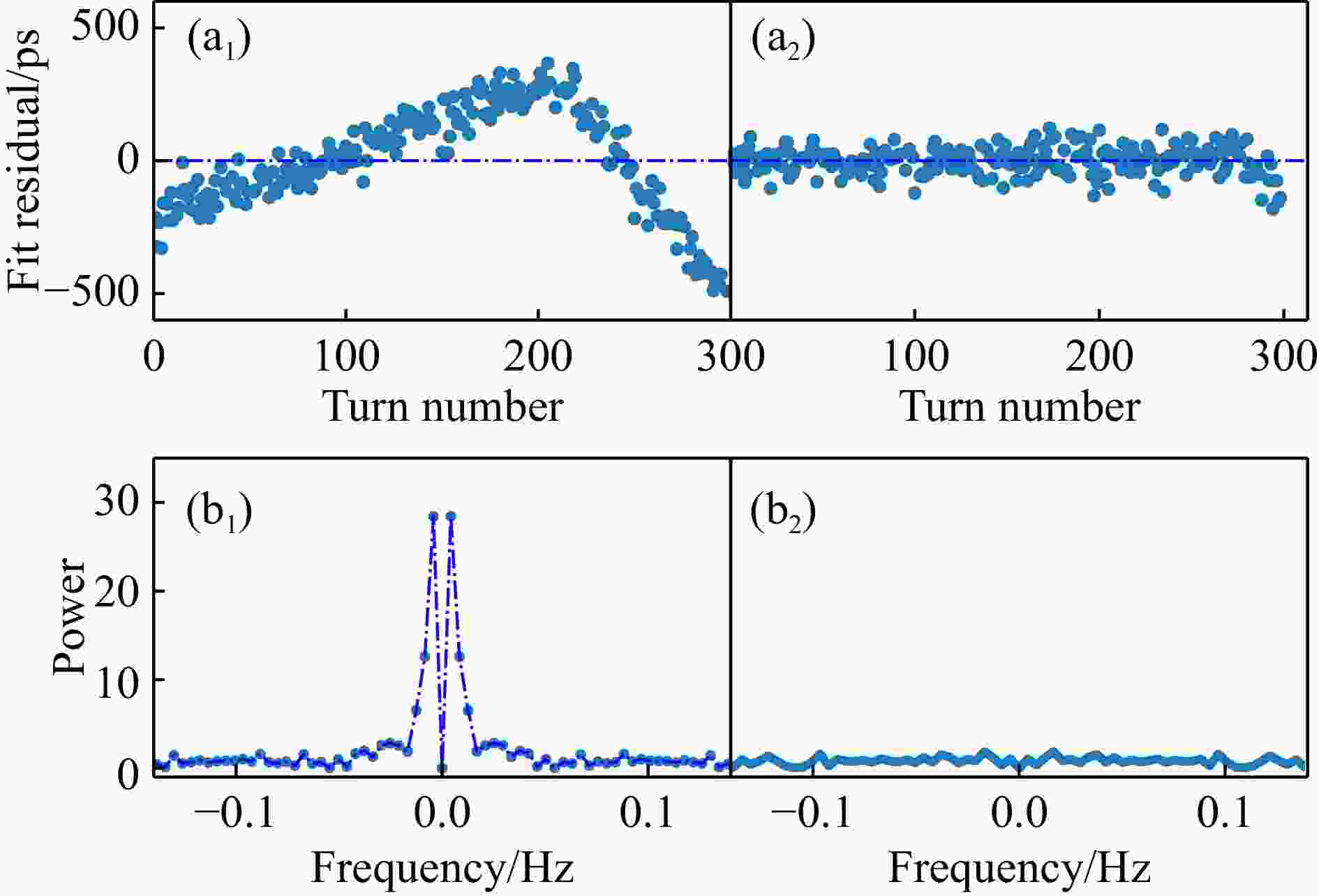
我们模拟了衰变和未衰变事件的飞行时间随循环圈数的变化,用直线拟合这些数据,得到衰变事件和未衰变事件的拟合残差,如图4(a1)和图4(a2) 所示。对衰变事件和未衰变事件的拟合残差做傅里叶变换得到频谱,如图4(b1)和图4(b2)所示。
假设所有的$ ^{94m} {\rm{Ru}} ^{44+} $离子在飞行时间探测器中并没有发生衰变,并且在实验中,每次注入记录的时间是200 μs。在这200 μs内,离子可以在实验环(CSRe)中循环大概300圈。当离子的直线拟合残差的形状类似一个非周期性的不对称三角波,如图4(a1)所示,并且对应频域图4(b1)出现了一个非常明显的峰,就认为$ ^{94m} {\rm{Ru}} ^{44+} $离子衰变成了$ ^{94} {\rm{Ru}} ^{44+} $离子。图4(a2)所示,图中没有出现扭结,并且相应频域图4(b2) 的数值都是在横轴0点处振荡,所以就认为该$ ^{94m} {\rm{Ru}} ^{44+} $没有发生衰变。为了筛选出更多衰变事件,我们模拟了20~280圈内每一圈的衰变事件。对这些衰变事件逐一用直线拟合残差,并进行傅里叶变换得到频谱,最后提取出频谱幅度最大值。
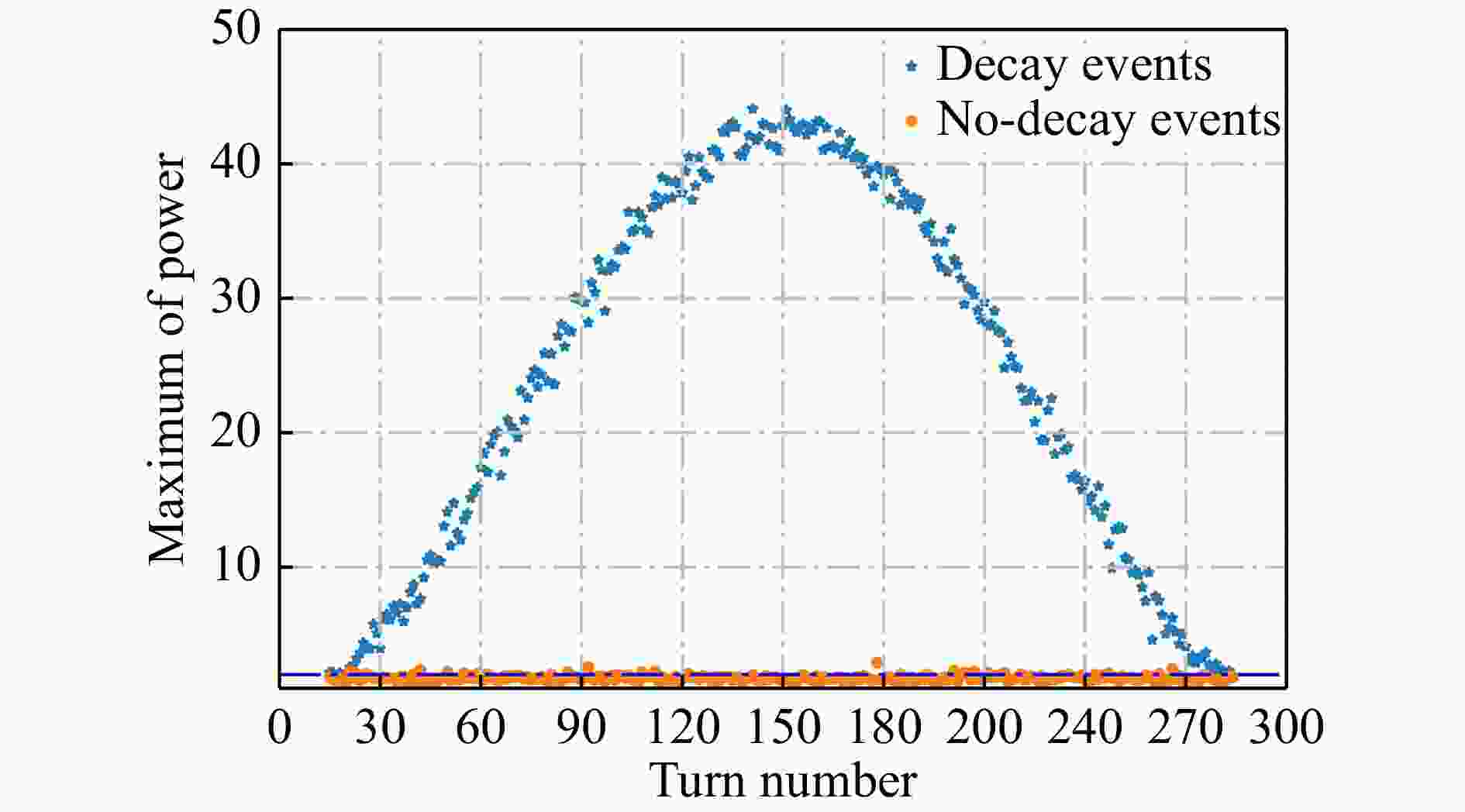
衰变事件和未衰变事件的频谱最大幅度值随圈数的变化如图5所示,衰变事件的最大幅度随着衰变圈数的变化,呈现先增大后减小的趋势,且频谱最大幅度都大于2.0。未衰变事件的频谱最大幅度则大部分小于2.0。因此该值可以作为对衰变事件初步指认的数值。
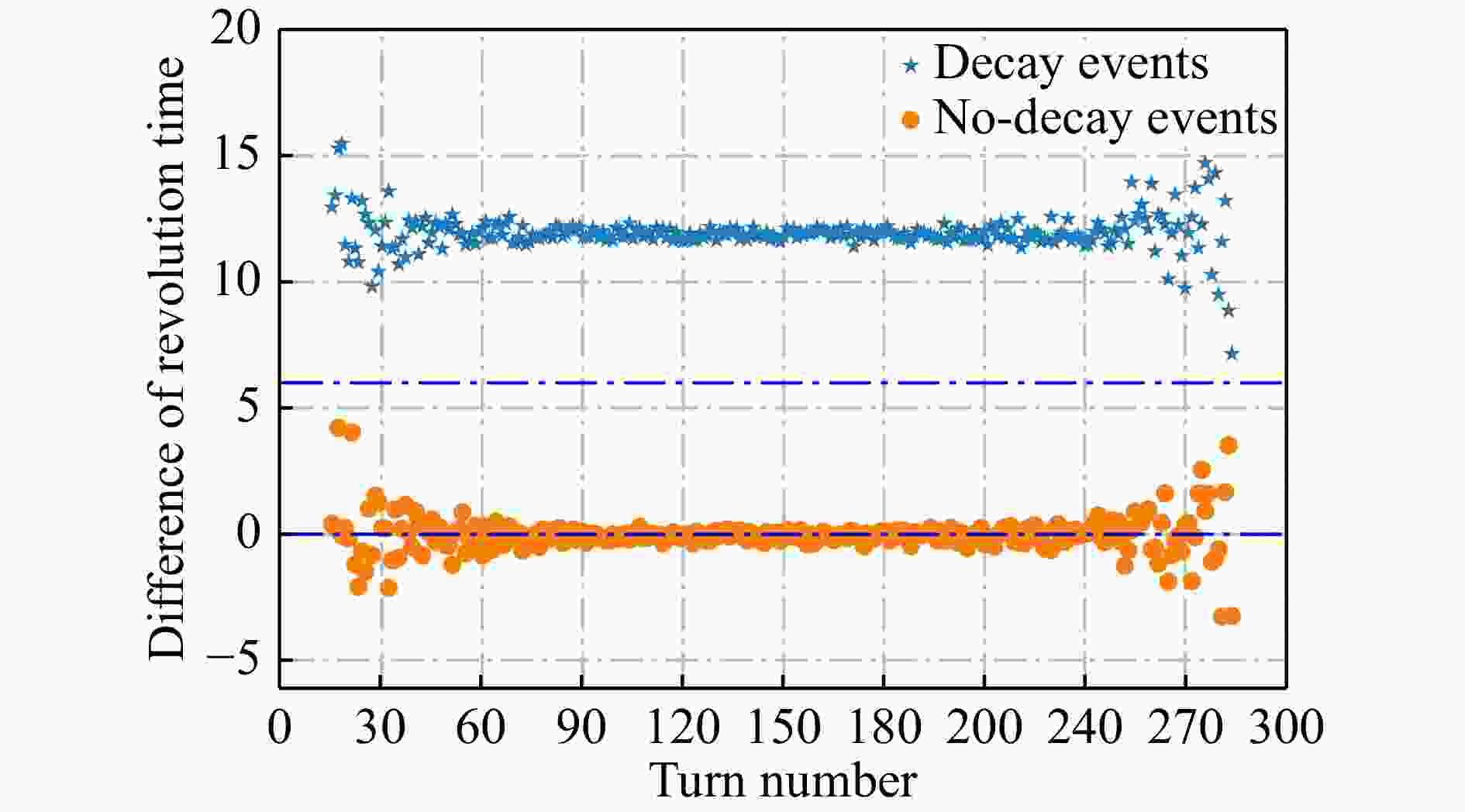
为了进一步准备指认衰变事件,计算了衰变点前后的循环周期差值,衰变事件和未衰变事件的循环周期差值如图6所示。$ ^{94m} {\rm{Ru}} ^{44+} $衰变事件的循环周期差值都在6 ps以上。因此在后续的实验数据分析中,将周期差值的范围确定为6 ps,作为寻找衰变事例的标准。
-
由模拟数据得出结论,当拟合残差经过傅里叶变换的频谱最大幅度大于2、残差衰变圈数拟合曲线周期差大于6 ps时,就可以判断$ ^{94m} {\rm{Ru}} ^{44+} $发生了衰变,具体过程如下。
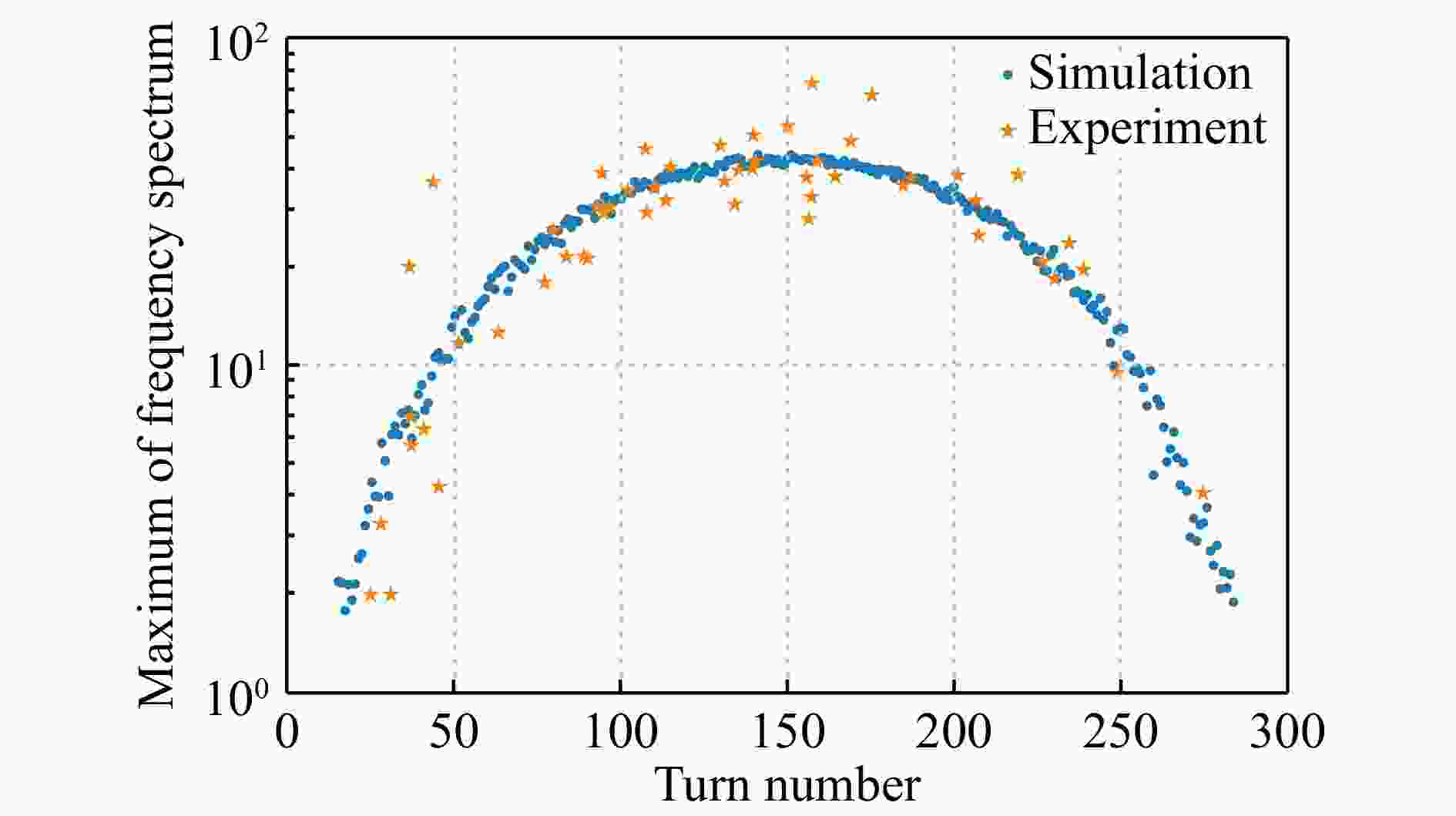
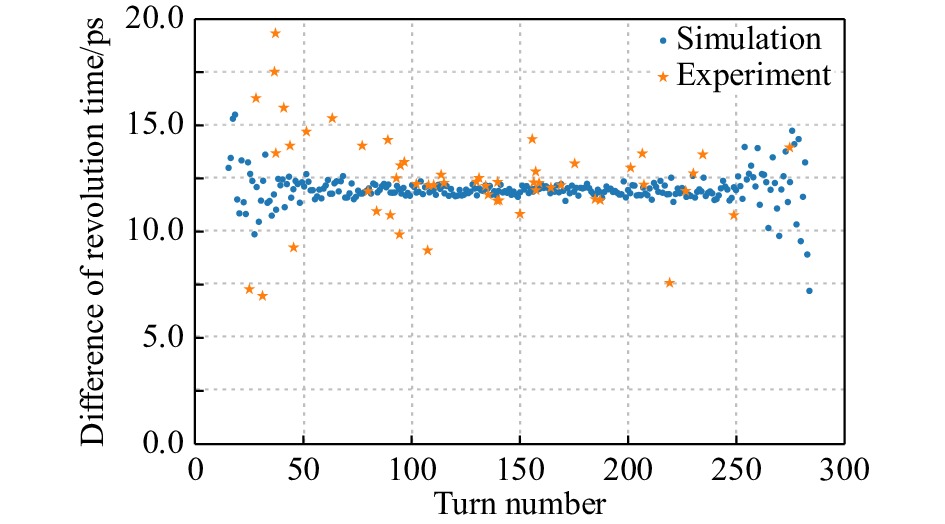
$ ^{94} {\rm{Ru}} ^{44+} $和$ ^{94m} {\rm{Ru}} ^{44+} $的循环周期在670.9~671.0 ns之间。对循环周期在这个周期范围内的所有事例提取直线拟合残差的频谱幅度最大值,初步筛选出了235个衰变候选事例。再提取全部衰变候选事例的衰变时刻,衰变时刻提取方法参考文献[7]。计算衰变前后的循环周期差值,差值大于6 ps的候选事件为54个。最后将实验数据和模拟数据结果对比,如图7和图8所示。从图7可以看到,这54个衰变事件的残差经过傅里叶变换得到的频谱最大幅度,随着衰变圈数的增大有一个先增大后减小的趋势。并且实验数据点按照模拟数据点图形的变化而变化,都围绕着模拟数据点;从图8 可以看到,衰变事件的衰变点前后的周期差值同样也围绕着模拟结果数据点,并且在11.9 ps来回浮动。
为了计算离子的寿命,我们运用了一种基于限定时间范围内的寿命计算方法,详细介绍可参考文献[8]。根据滤波场景的测量条件,我们对寿命进行估计,估计值及其误差的公式分别为
$$ \hat{\tau} = \frac{1}{{n}}\sum\limits_{{{i}}^{} = 1}^{{n}} t_{{i}}^{} +\frac{T}{e^{\tfrac{T}{\hat{\tau}}}-1 } , $$ (27) $$ \sigma( \hat{\tau}) = \frac{\hat{\tau}^{2} }{\sqrt{{n}} \sigma(t_{{i}}^{})}, $$ (28) 其中:$ \hat{\tau} $和$ \sigma( \hat{\tau}) $为寿命的极大似然估计量及其误差;$ {n} $为离子的衰变事件个数;$t_{{i}}^{}$为离子的衰变时间;$ T = T_{2}^{}-T_{1}^{} $为观测时间窗口大小。将这54个衰变事件的平均衰变时间71.7 μs,观测时间窗口大小$ T $= 170 μs,代入式(27)和(28)得到$ ^{94m} {\rm{Ru}} ^{44+} $在相对论坐标系下的寿命为194(121) μs。
因为使用这种方法找到了54个衰变事件,也就是$ {n} $的数目增大了。所以由式(28)可知,极大似然估计量的误差的与衰变事件个数成反比,即当衰变事件的个数变多时,其误差将变小,精确度将提高。
中性原子同核异能态$ ^{94m} {\rm{Ru}}$在静止坐标系下半衰期的理论值为71(4) μs[9]。$ ^{94m} {\rm{Ru}}$通过$ \gamma $级联衰变或内转换过程衰变成基态。当原子外层电子被完全剥离时,通过内转换的衰变通道被关闭,全剥离同核异能态离子只能通过$ \gamma $级联衰变通道衰变[10]。BRICC代码[11]计算得到的$ ^{94m} {\rm{Ru}}$的内转换系数为0.335,理论预测在实验室坐标系下$ ^{94m} {\rm{Ru}} ^{44+} $寿命($ \gamma $= 1.302)延长为178(10) μs。
-
本文介绍了一种新的准确鉴别离子衰变的指认方法,通过测量全剥离离子$ ^{94m} {\rm{Ru}} ^{44+} $和其衰变后的离子$ ^{94} {\rm{Ru}} ^{44+} $在CSRe中的回旋周期和飞行时间后,得到直线拟合残差的频谱。基于频谱幅度的最大值,初步指认衰变事件。然后提取衰变离子相应的衰变时间,得到衰变点前后的周期差,从而有效且快速地鉴别出$ ^{94m} {\rm{Ru}} ^{44+} $离子的衰变事件,并且拓展了离子发生衰变的时间窗口。之前的鉴别方法观测离子发生衰变的时间窗口是(20 μs, 180 μs),通过这个方法将时间窗口拓展为(15 μs, 185 μs)。按照原来的方法只发现了49个衰变事件,运用新的分析方法对实验数据进行重新分析,鉴别出了54个衰变事件,比原来多找到了5个衰变事件。通过对这54个衰变事件的衰变时间重新计算得到$ ^{94m} {\rm{Ru}} ^{44+} $在实验室坐标系下的寿命为194(121) μs,与前期工作的结果218(148) μs[7]在误差范围内一致,且具有更高的精确度。
An Effective Method for Identifying Decay Events in Storage Rings and Its Application in 94mRu44+ Lifetime Measurement
-
摘要: 兰州重离子加速器冷却储存环上的等时性质量谱仪是开展高电荷态、短寿命同核异能态衰变研究的理想装置。在短寿命高电荷态离子$^{94m}{\rm{Ru}}^{44+}$的寿命测量实验中,我们直接观测到了$^{94}{\rm{Ru}}$的$8^+$态isomer衰变到基态的过程。在观测时间窗口(20 μs, 180 μs)范围内,鉴别出了49个衰变事件。为了能够鉴别出更多的衰变事件,研究了一种基于频谱幅度来指认衰变事件的方法。基于模拟结果,该方法可以有效鉴别(15 μs, 185 μs) 内的衰变事件。将新的鉴别方法应用到实验数据处理中,在(15 μs, 185 μs)内,鉴别出了54个衰变事件。基于这54个衰变事件,计算得到$^{94m}{\rm{Ru}}^{44+}$在实验室坐标系下的寿命为194(121) μs。新的寿命结果与之前的结果218(148) μs在误差范围内一致。
-
关键词:
- 兰州重离子加速器冷却储存环 /
- 等时性质量谱仪 /
- 全剥离离子 /
- 94mRu /
- 寿命测量
Abstract: The Lanzhou Heavy Ion Accelerator Cooling Storage Ring(HIRFL-CSR) is an ideal device for studying the decay of highly charged and short-lived isomers. In the lifetime measurement experiment of the short-lived highly charged ion $^{94m}{\rm{Ru}}^{44+}$, we directly observed the decay of $^{94}{\rm{Ru}}$ from 8+ isomer to the ground state, and identified 49 decay events in the observation time window of (20 μs, 180 μs). In order to identify more decay events, a new method based on amplitude of frequency spectrum was studied in this paper. Based on the simulation results, this new method can effectively identify decay events within (15 μs, 185 μs). By applying the new identification method to the experimental data processing, 54 decay events were identified within (15 μs, 185 μs). Based on these 54 decay events, the lifetime of $^{94m}{\rm{Ru}}^{44+}$ in the laboratory frame was calculated to be 194(121) μs. The new lifetime result is within the error range of the previous result 218(148) μs.-
Key words:
- HIRFL-CSR /
- isochronous mass spectrometry /
- fully stripped ions /
- 94mRu /
- lifetime measurements
-
图 1 兰州重离子冷却储存环装置示意图[5]
-
[1] XIA J W, ZHAN W L, WEI B W, et al. Nucl Instr and Meth A, 2002, 488: 11. doi: 10.1016/S0168-9002(02)00475-8 [2] HAUSMANN M, STADLMANN J, ATTALLSH F, et al. Nucl Instrum Meth A, 2000, 446: 569. doi: 10.1016/S0168-9002(99)01192-4 [3] MEI B, TU X L, WANG M, et al. Nucl Instr and Meth A, 2010, 624: 109. doi: 10.1016/j.nima.2010.09.001 [4] CHEN R J, YUAN Y J, WANG M, et al. Phys Scr T, 2015, 166: 014044. doi: 10.1088/0031-8949/2015/T166/014044 [5] 曾奇, 张景涛, 岳珂, 等. 科学通报, 2021, 66: 3395. doi: 10.1360/TB-2021-0215 ZENG Q, ZHANG J T, YUE K, et al. Chinese Science Bulletin, 2021, 66: 3395. (in Chinese) doi: 10.1360/TB-2021-0215 [6] 曾奇, 王猛, 张玉虎, 等. 原子核物理评论, 2017, 34(3): 414. doi: 10.11804/NuclPhysRev.37.2019CNPC26 ZENG Q, WANG M, ZHANG Y H, et al. Nuclear Physics Review, 2017, 34(3): 414. (in Chinese) doi: 10.11804/NuclPhysRev.37.2019CNPC26 [7] ZENG Q, WANG M, ZHOU X H, et al. Phys Rev C, 2017, 96: 031303(R). doi: 10.1103/PhysRevC.96.031303 [8] CHEN X C, ZENG Q, LITVINOV Y A, et al. Phys Rev C, 2017, 96: 034302. doi: 10.1103/PhysRevC.96.034302 [9] AUDI G, KONDEV F G, WANG M, et al. Chin Phys C, 2017, 41: 030001. doi: 10.1088/1674-1137/41/3/030001 [10] ABRIOLA D, SONZOGNI A A. Nucl Data Sheets, 2006, 107: 2423. doi: 10.1016/j.nds.2006.08.001 [11] KIBDI T, BURROWS T W, TRZHASKOVSKAYA M B, et al. Nucl Instr and Meth A, 2008, 589: 202. doi: 10.1016/j.nima.2008.02.051 -





 下载:
下载:

 甘公网安备 62010202000723号
甘公网安备 62010202000723号