-
极端相对论重离子对撞实验的主要目标之一是研究强相互作用物质在极端高温度或高净重子数密度条件下解禁闭态[1-2](也称夸克-胶子等离子体,QGP)的存在与演化性质。QGP被普遍认为产生于大爆炸后几微秒(μs)的早期宇宙或当前宇宙中的致密中子星内部。因此,对QGP的研究不仅能帮助了解早期宇宙的演化历史,还可以研究当前物质世界的基本组成结构。
在高能重离子对撞实验的众多末态观测量当中,各向异性流[3-4]作为反映夸克物质的状态方程特性及其流体动力学演化特征的重要探针,一直是人们研究的热点。受入射核子的初态核环境、逐碰撞事件涨落和由碰撞几何不对称性所导致的压力梯度各向异性的影响,实验中产生的末态粒子具有方位角各向异性。对末态粒子方位角分布做傅立叶展开[5-6]:
$$ \frac{{\rm{d}}N}{{\rm{d}}\varphi} \propto 1 + 2 \sum\limits_{n = 1}^{\infty}\upsilon_{n}^{}\mathrm{cos}\big[n(\varphi-\varPsi_{n}^{})\big], $$ (1) $ \varphi $是末态粒子的方位角;$ \varPsi_{n}^{} $是$ n $阶事件反应平面角[7-8];各阶展开项系数$ \upsilon_{n}^{} $,被称为各向异性流参数。其中第二项系数$ \upsilon_{2}^{} $,被称为椭圆流参数,它表征了在QGP演化过程中,由初始椭球状(也称杏仁状)碰撞区域的空间各向异性传导到末态动量空间中方位角分布的各向异性的大小。椭圆流的大小对QGP火球的基本输运性质十分敏感,如温度依赖的状态方程、夸克物质内部黏滞性等[9-10]。因此,在高能重离子碰撞中观测到末态粒子具有显著的$ \upsilon_{2}^{}>0 $是判定QGP物质形成的重要判据之一。
在过去几十年中,运行在相对论重离子对撞机(RHIC)[11-13]和大型强子对撞机(LHC)[14-17]上重离子碰撞实验对椭圆流进行了一系列的测量,构建了一套完整的研究强耦合QGP的范式。通过提取剪切黏滞系数与熵密度的比值($ \eta/s $)并与流体动力学计算进行比较后发现,QGP表现出近乎完美流体的行为。此外,末态鉴别粒子椭圆流在不同的横动量($ p_{\rm{T}}^{} $)区域内的测量结果[18-19]也反映了不同的物理机制。在低$ p_{\rm{T}}^{} $区间,椭圆流被观测到具有明显的质量排序效应,即在相同$ p_{\rm{T}}^{} $下,较重的粒子(如重子)相比于较轻的粒子(如介子)具有更小的椭圆流。这一效应归因于QGP的径向膨胀,并得到了流体动力学计算的良好解释。在中等横动量区间,粒子的椭圆流会根据强子种类(介子或重子),呈现出不同的分组现象,而这一现象通常被解释为夸克重组或聚合理论的特征。这些理论认为,不同强子的椭圆流$ \upsilon_{2}^{} $,经过组分夸克数(NCQ或$ n_q^{} $)的缩放[20-21],可以表现出近似的统一行为,即
$$ \upsilon_{2}^{B}(p_{\mathrm{T}}^{}/3)/3 = \upsilon_{2}^{M}(p_{\mathrm{T}}^{}/2)/2 $$ (2) 或
$$ \upsilon_{2}^{B}(kE_{\mathrm{T}}^{}/3)/3 = \upsilon_{2}^{M}(kE_{\mathrm{T}}^{}/2)/2 , $$ (3) 其中:上标B(M)表示由3个(2个)成分夸克组成的重子(介子);$ kE_{\mathrm{T}}^{} $为横向动能($ kE_{\mathrm{T}}^{} = m_{\mathrm{T}}^{} − m_{0}^{} $, $ m_{\mathrm{T}}^{} $ 和 $ m_{0}^{} $分别为粒子的横质量和不变质量)。
相较于重离子碰撞,质子-质子与质子-核这类碰撞系统由于其碰撞尺度较小,一般认为没有QGP物质产生。然而近年来,在RHIC与LHC上针对小系统碰撞的测量中,也有类流现象的出现。CMS, ATLAS和ALICE实验组在高多重数质子-质子与质子-铅核碰撞中首次观测到轻味强子与奇异强子的长程双脊结构,并伴随有显著非流的椭圆流$ \upsilon_{2}^{} $[22-25]。在中等横动量区域内,末态鉴别粒子的$ \upsilon_{2}^{} $表现出与重离子碰撞中类似的组分夸克标度性,但其背后的主导机制仍然不清楚。一些基于末态效应的研究将流体动力学计算从大系统拓展到小系统,其结果能够很好地描述末态强子的$ \upsilon_2^{} $[26-28],但这些理论的成立必须基于一个很强的假设,即小系统中成分之间存在足够的散射。另一方面,基于色玻璃凝聚(CGC)模型和IP-Glasma模型[29-30],通过考虑初态动量关联等效应,能够定量描述质子-铅核碰撞中的末态粒子的某些集体行为,但对于碰撞系统和快度的依赖性尚无明确结论。此外,近些年对部分子逃逸机制的研究表明,即使少量散射也足以产生足够的方位各向异性,且该机制在多相输运(AMPT)模型中得到了很好的验证[31-32]。AMPT模型计算能够定量地描述质子-铅核碰撞中轻味强子的$ \upsilon_2^{} $,而其中非平衡态的各向异性粒子逃逸机制有着重要贡献[31]。
本研究利用AMPT模型,首次将$ \sqrt{s_{\mathrm{NN}}^{}} = $5.02 TeV质子-铅核碰撞中末态鉴别粒子($ \pi^{\pm} $,$ {\rm{K}}^{\pm} $,$ {\rm{p}} $($ \bar{{\rm{p}}} $))的$ \upsilon_{2}^{} $的计算拓展到高达8 GeV/$ c $的横动量区域,并系统研究了其组分夸克标度性。同时,本工作还探究了AMPT模型中的关键机制,如夸克级联和强子再散射,对小碰撞系统中末态粒子椭圆流及其组分夸克标度性的影响。此外,非流减除方法对计算结果的影响也在本工作中被讨论。
-
本研究采用了带有弦融化机制的AMPT模型(版本号为v2.26t9b)[32-33] 来计算5.02 TeV质子-铅核碰撞中末态粒子的$ \upsilon_{2}^{} $。AMPT模型包括四个主要过程:初态条件、部分子级联、强子化和强子相互作用。初态条件由重离子喷注相互作用生成器[34-35] (HIJING)产生。HIJING首先产生了微喷注(minijet)和软激发弦,随后这些部分子会通过隆德(Lund)碎裂机制生成初始强子。在弦融化机制的作用下,这些初始强子依据它们的味与自旋结构被“融解”成部分子,并进入随后的部分子级联(Zhang’s parton cascade, ZPC)模型[36]中。目前的部分子级联模型中只考虑了两体弹性散射过程,其散射截面可以被简化表示为
$$ \sigma_{{\rm{gg}}}^{}\approx\frac{9\pi\alpha_{{\rm{s}}}^{2}}{2\mu^{2}}。 $$ (4) 在本工作中,强耦合常数$\alpha_{{\rm{s}}}^{}$被设为0.33,德拜屏蔽质量$ \mu $被设为$2.2~814\; \mathrm{fm}^{-1}$,从而总散射截面$ \sigma $被控制在3 mb左右。随着德拜屏蔽质量$ \mu $的增大,散射截面$ \sigma $将逐渐减少并趋近于0。因此,本工作还尝试将$ \mu $设为一个极大值(如$ 1\times10^{5} $),使得$\sigma \sim 0$,并据此研究部分子散射过程对末态集体流的影响。
当散射过程完成后,部分子会进入到强子化阶段[31],与距离最近的一(或两)个部分子进行组合形成介子(或重子)。强子化形成的这些强子会进入随后的强子再散射阶段,该阶段主要由包含了重子-重子、重子-介子和介子-介子相互作用的相对论输运(a relativistic transport, ART)模型来描述。强子散射时间在默认情况下被设为$ t_{\mathrm{max}}^{} $= 30 $ \mathrm{fm}/c $。此外,本工作也测试了$ t_{\mathrm{max}}^{} $= 0.4 $ \mathrm{fm}/c $情况下末态粒子椭圆流的变化情况,从而研究强子散射过程对粒子集体运动行为的影响。在该配置下,强子之间基本不进行散射,但模型中仍保留了共振态衰变的过程[37]。
-
两粒子关联函数(2PC)作为计算椭圆流信号的常用方法之一,因其具有较好的非流背景减除的效果,已经在小系统碰撞的相关实验测量中被广泛运用[38]。与式(1)类似,末态观测到的两粒子关联函数$ C(\varDelta\varphi) $可以表示为粒子对个数($ N^{\mathrm{pairs}} $)随两粒子(记作粒子$ a $,$ b $)极角差$ \varDelta\varphi = \varphi^{a}-\varphi^{b} $变化的函数形式,并作傅里叶展开:
$$ C(\varDelta\varphi) = \frac{\mathrm{d}N^{\mathrm{pair}}}{\mathrm{d}\varDelta \varphi} \propto 1 + 2 \sum\limits_{n = 1}^{\infty}V_{n\varDelta}^{}\left(p_{\mathrm{T}}^{a}, p_{\mathrm{T}}^{b}\right)\mathrm{cos}(n\varDelta\varphi) , $$ (5) 其中$V_{n\varDelta}^{}\left(\it{p}_{\rm{T}}^{a},\it{p}_{\rm{T}}^{b}\right)$表示两粒子$ n $阶谐波。由于粒子的射出在无非流贡献的情况下是相互独立的,根据因子化法则,$V_{n\varDelta}^{}\left(\it{p}_{\rm{T}}^{a},\it{p}_{\rm{T}}^{b}\right)$可以表示为单粒子流$\upsilon _{n}^{}\left(\it{p}_{\rm{T}}^{a}\right)$和$\upsilon_{n}^{}\left(\it{p}_{\rm{T}}^{b}\right)$的乘积,即
$$ V_{n\varDelta}^{}\left(p_{\mathrm{T}}^{a},p_{\mathrm{T}}^{b}\right) = \upsilon_{n}^{}\left(p_{\mathrm{T}}^{a}\right)\upsilon_{n}^{}\left(p_{\mathrm{T}}^{b}\right)。 $$ (6) 因此,单粒子$ a $的流$ \upsilon_{n}^{} $的计算可以通过近年PHENIX实验组所提出的3$ \times $2PC方法[39]来实现,即构建三组相互关联的粒子(记作$ a $, $ b $, $ c $),并通过对它们进行组合来提取流系数:
$$ \upsilon_{n}^{}(p_{\mathrm{T}}^{a}) = \sqrt{\frac{V_{n\varDelta}^{}\left(p_{\mathrm{T}}^{a},p_{\mathrm{T}}^{b}\right)V_{n\varDelta}^{}\left(p_{\mathrm{T}}^{a},p_{\mathrm{T}}^{c}\right)}{V_{n\varDelta}^{}\left(p_{\mathrm{T}}^{b},p_{\mathrm{T}}^{c}\right)}}。 $$ (7) 在小系统碰撞中,主要的非流来源是喷注关联与共振态衰变。短程喷注关联与共振态衰变可以通过在3×2PC方法中引入足够大的快度间隔被去除,而长程喷注关联的贡献需要利用边缘碰撞事件来估计[40]。在本工作中,我们将采用ATLAS实验组开发的模板拟合[41](Template Fit)方法去除掉非流的贡献。在该方法中,一般认为高多重度事件中获得的关联函数分布$ C^{\mathrm{HM}}(\varDelta\varphi) $,可由低多重度事件中的关联函数经过因子F缩放后与$ {\rm{cos}}(n\varDelta\varphi) $($ n>1 $)的叠加来拟合,即
$$ C(\varDelta\varphi) = FC^{\mathrm{LM}}(\varDelta\varphi) + G\left[1 + 2 \sum\limits_{n = 1}^{3}V_{n\varDelta}^{}\mathrm{cos}(n\varDelta\varphi)\right], $$ (8) 其中$ G $是归一化因子用于保证$ C(\varDelta\varphi) $的积分结果与$ C^{\mathrm{HM}}(\varDelta\varphi) $相等。
为了能和ALICE实验数据直接对比,本工作研究了赝快度($ \eta $)为$ -0.8<\eta<0.8 $的中心区粒子,该赝快度范围与ALICE实验上时间投影室(TPC)所覆盖的范围一致。基于3$ \times $2PC方法,本研究构建了向前区($-4 < \eta < -2.5$),向后区($ 2.5<\eta<4 $)和中心区($ -0.8<\eta<0.8 $)粒子之间的三组长程关联,即中心-向前(Central-Forward,CF)关联,中心-向后(Central-Backward, CB)关联,向前-向后(Forward-Backward, FB)关联,从而计算出$ V_{2\varDelta}^{}(\mathrm{CF}) $,$ V_{2\varDelta}^{}(\mathrm{CB}) $与$ V_{2\varDelta}^{}(\mathrm{FB}) $。因此,在给定的$ p_{\mathrm{T}}^{} $区间内,末态粒子$ \upsilon_{2}^{} $的计算公式即为
$$ \upsilon_{2}^{} = \sqrt{\frac{V_{n\varDelta}^{}(\mathrm{CF})V_{n\varDelta}^{}(\mathrm{CB})}{V_{n\varDelta}^{}(\mathrm{FB})}}。 $$ (9) 此外,本研究中通过计算在ALICE V0A[42]探测器的赝快度接受范围($ 2.8<\eta<5.1 $)内的粒子数目来定义碰撞中心度的大小。
-
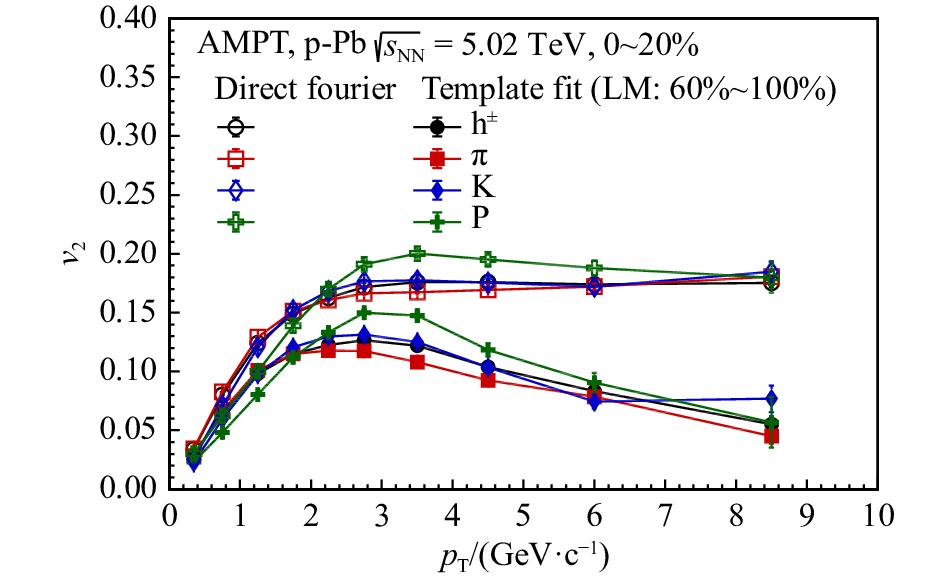
图1为AMPT模型在$ \sqrt{s_{\mathrm{NN}}^{}} = 5.02 $ TeV 高多重数(中心度0~20%)的质子-铅核碰撞中对带电强子$ {\rm{h}}^{\pm} $、$ {\rm{K}}^{\pm} $介子、$ \pi^{\pm} $介子及质子$ {\rm P(\bar{P})} $的$ \upsilon_{2}^{} $随横动量$ p_{\mathrm{T}}^{} $分布的计算结果,同时也比较了作非流减除(即“Template Fit”)和不作非流减除(即“Direct Fourier”)这两种情况下各种粒子的$ \upsilon_{2}^{} $。可以看到,基于Template Fit的非流减除方法能够很好地压低长程喷注等非流信号的贡献,且该部分贡献随横动量增大而增大。在扣除了非流贡献之后,AMPT模型计算仍能够在较大的横动量区域内(0 $ <p_\mathrm{T}^{}<8 $ GeV/$ c $)得到显著非零的$ {\rm{K}}^{\pm} $,$ \pi^{\pm} $和$ {\rm{P}}(\bar{{\rm{P}}}) $的$ \upsilon_{2}^{} $。在较低横动量区间(0 $ <p_\mathrm{T}^{}<2 $ GeV/$ c $)内,AMPT模型计算能够很好地重现质量排序效应[43],即$\upsilon_{2}^{}(K^{\pm})\approx \upsilon_{2}^{}(\pi^{\pm}) > \upsilon_{2}^{}({\rm{P}}(\bar{{\rm{P}}}))$,这表明AMPT模型中非流体力学机制(如部分子逃逸机制)也能够产生类径向流信号。在中等横动量区域内(2 $ <p_\mathrm{T}^{}<5 $ GeV/$ c $),重子与介子的$ \upsilon_{2}^{} $发生了明显的分离,且$ \upsilon_{2}^{}({\rm{P}}(\bar{{\rm{P}}}))>\upsilon_{2}^{}({\rm{K}}^{\pm})\approx \upsilon_{2}^{}(\pi^{\pm}) $,这表明重子-介子分组(baryon-meson grouping)现象在AMPT模型中也能被重现。而在较高横动量区间内($ p_\mathrm{T}^{}> $ 5 GeV/$ c $),各类末态粒子的$ \upsilon_{2}^{} $趋于一致,这暗示着主导小系统高$ p_\mathrm{T}^{} $粒子$ \upsilon_{2}^{} $的物理机制可能不依赖粒子的种类。
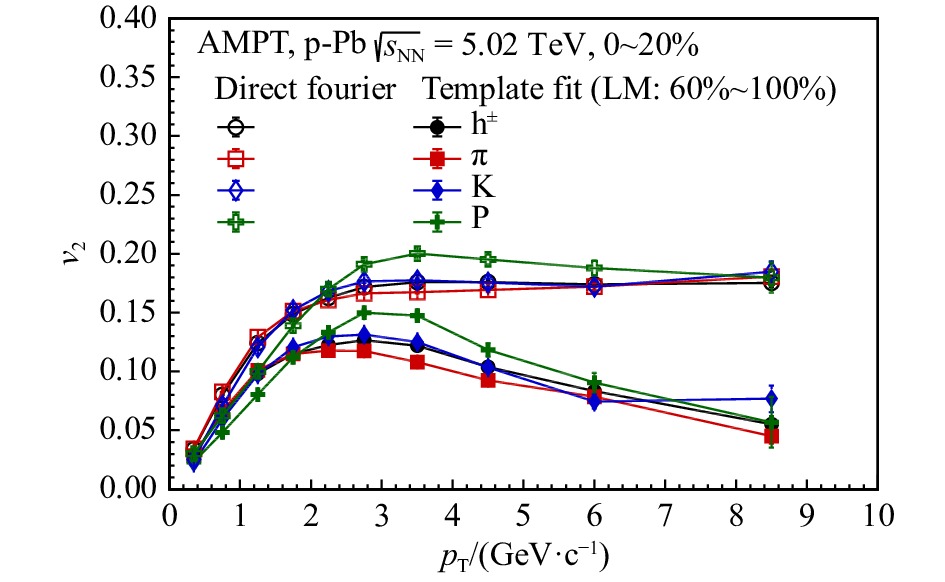
图 1 AMPT模型在$ \sqrt{s_{\mathrm{NN}}} = 5.02 $ TeV 高多重数(中心度0~20%)的质子-铅核碰撞中对带电强子$ {\rm{h}}^{\pm} $、$ {\rm{K}}^{\pm} $介子、$ \pi^{\pm} $介子及质子$ {\rm{P}}(\bar{{\rm{P}}}) $的$ \upsilon_{2} $随横动量$ p_{\mathrm{T}} $分布的计算结果
图2比较了在$ \sqrt{s_{\mathrm{NN}}^{}} = 5.02 $ TeV高多重数(中心度0~20%)的质子-铅核碰撞中AMPT模型对$ {\rm{h}}^{\pm} $,$ {\rm{K}}^{\pm} $,$ \pi^{\pm} $和$ {\rm{P}}(\bar{{\rm{P}}}) $的$ \upsilon_{2}^{} $计算结果与ALICE的实验测量。在减除了非流背景之后,AMPT模型的计算结果能够很好地描述实验上观测到的$ {\rm{h}}^{\pm} $, $ {\rm{K}}^{\pm} $, $ \pi^{\pm} $的$ \upsilon_{2}^{} $。但对于$ {\rm{P}}(\bar{{\rm{P}}}) $的$ \upsilon_{2}^{} $,理论计算结果在$ p_{\mathrm{T}}^{}<2 $ GeV/$ c $区间内比实验结果略高,这可能是由于目前使用的AMPT模型版本中的强子化机制仍需要改进。目前的强子化机制倾向先将临近的两个夸克组合成介子,然后再将剩余的邻近夸克组合成重子,这可能会导致重子的产额与集体流都与实验有偏差。但AMPT模型的计算结果整体趋势与实验测量仍然相符,这表明本工作中使用的AMPT模型以及相关参数配置能够定性地重现实验结果。
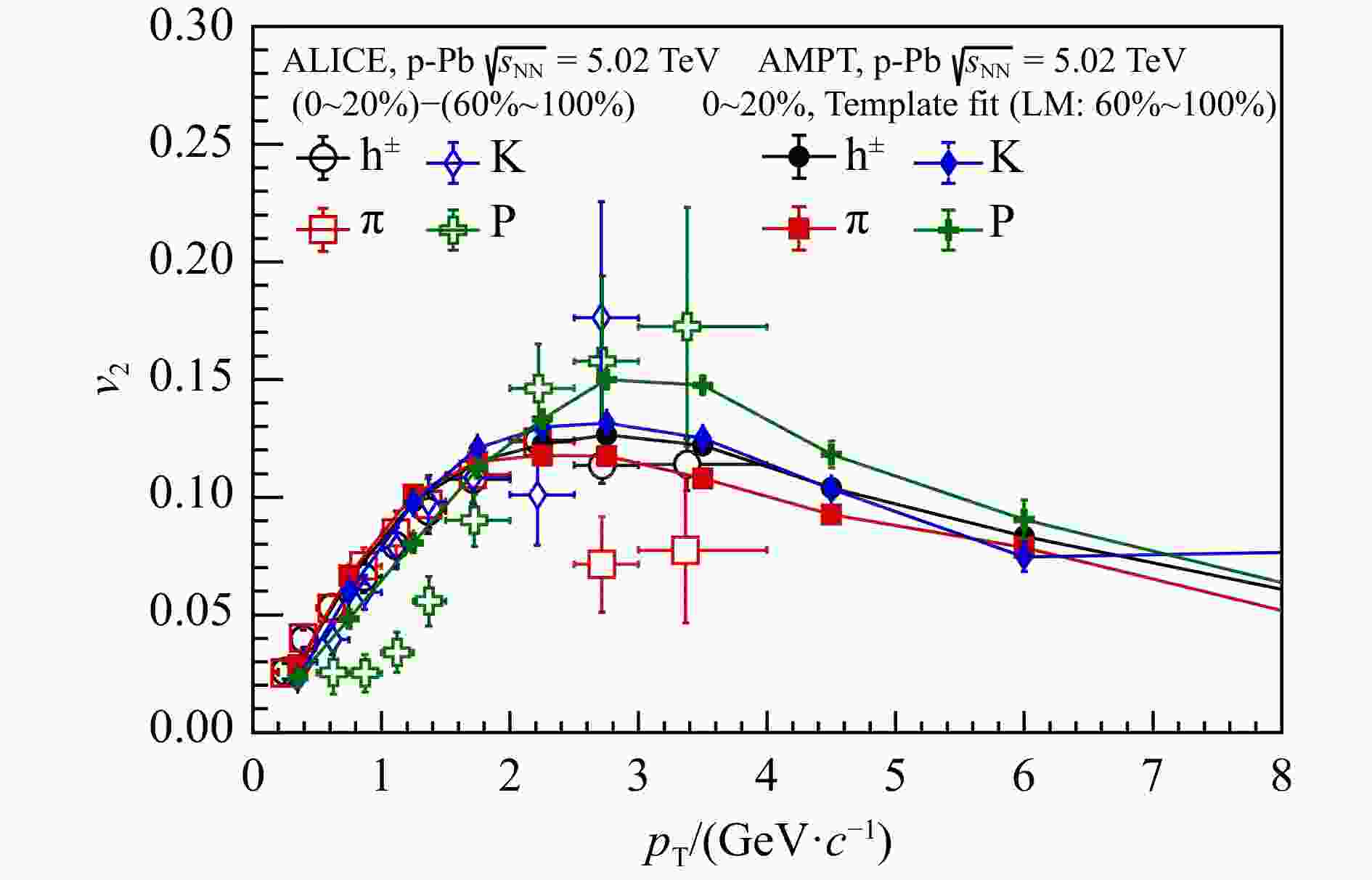
图 2 AMPT模型在$ \sqrt{s_{\mathrm{NN}}} = 5.02 $ TeV高多重数(中心度0~20%)的质子-铅核碰撞中带电强子$ {\rm{h}}^{\pm} $、$ {\rm{K}}^{\pm} $介子、$ \pi^{\pm} $介子及质子$ {\rm{P}}(\bar{{\rm{P}}}) $的$ \upsilon_{2} $ 的计算结果与ALICE的实验观测结果的比较
图3展示了AMPT模型在$ \sqrt{s_{\mathrm{NN}}^{}} = 5.02 $ TeV 高多重数(中心度0~20%)的质子-铅核碰撞中组分夸克($ n_{q}^{} $)标度下对$ {\rm{K}}^{\pm} $介子、$ \pi^{\pm} $介子及质子$ {\rm{P}}(\bar{{\rm{P}}}) $的$ \upsilon_{2}^{} $随$ kE_{\mathrm{T}}^{}/n_{q}^{} $的分布,其中重子的$ n_{q}^{} $取3,介子的$ n_{q}^{} $取2。在经过组分夸克标度过后,所有的粒子在$ kE_{\mathrm{T}}^{}/n_{q}^{}<1 $ GeV的范围内展现出相似大小的$ \upsilon_{2}^{} $,这证实了在输运模型的框架下流体物质中的确存在着夸克自由度。然而当$ kE_{\mathrm{T}}^{}/n_{q}^{}>1 $ GeV,组分夸克标度行为被破坏。这一方面可能是因为现有版本的AMPT模型中形成重子的夸克重组合行为只在介子形成后才发生[44],另一方面可能是因为高横动量粒子的椭圆流产生机制与中低横动量完全不同。未来对升级AMPT模型的诸多研究将有效地解释这个问题。
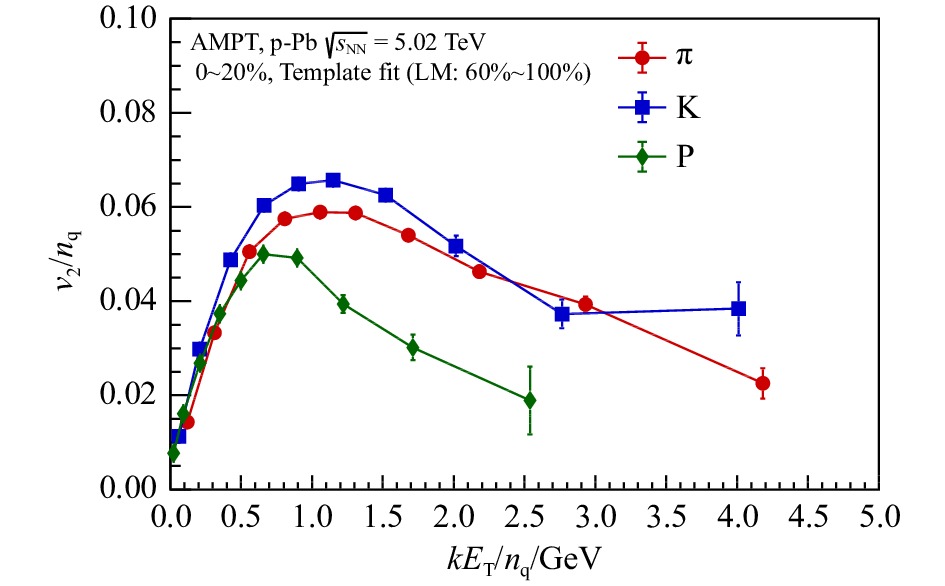
图 3 AMPT模型在$ \sqrt{s_{\mathrm{NN}}} = 5.02 $ TeV 高多重数(中心度0~20%)的质子-铅核碰撞中组分夸克($ n_{q} $)标度下对$ {\rm{K}}^{\pm} $介子、$ \pi^{\pm} $介子及质子$ {\rm{P}}(\bar{{\rm{P}}}) $的$ \upsilon_{2} $随$ kE_{\mathrm{T}}/n_{q} $的分布
为了进一步量化组分夸克标度性的符合程度,并研究影响其行为的潜在机制,本工作参考先前的研究[37],引入了如下计算量:
$$ \chi = \sqrt{\sum\limits_{K,P}^{}\left(\frac{\upsilon_{2}^{K,P}/n_{q}^{K,P}-\upsilon_{2}^{\pi}/n_{q}^{\pi}}{\upsilon_{2}^{\pi}/n_{q}^{\pi}}\right)^{2}} , $$ (10) 其中$ \upsilon_{2}^{} $为0.4 $ <kE_{\mathrm{T}}^{}< $ 1 GeV范围内的积分流。当$ \chi $越小时,说明粒子的$ \upsilon_{2}^{} $越符合组分夸克标度性,反之则说明违背组分夸克标度性越严重。图4展示了打开和关闭强子再散射过程的AMPT模型在5.02 TeV质子-铅核碰撞中对$ \chi $随中心度分布的计算结果。从中心碰撞到边缘碰撞,$ \chi $有逐渐减小的趋势,说明碰撞系统越边缘,组分夸克标度符合得越好,这一点与之前在重离子碰撞系统中得到结果相一致[37]。在扣除了非流效应之后,$ \chi $的值更接近于0,说明非流贡献是破坏组分夸克标度的来源之一。另一方面,当在AMPT模型中考虑了强子再散射效应后,计算得到$ \chi $相比于在不考虑强子再散射的模型中得到的$ \chi $更大。这表明在小系统碰撞中,强子再散射过程也会使组分夸克标度行为的破坏程度变得更大,这也与之前在重离子碰撞系统中的研究发现保持一致[37]。
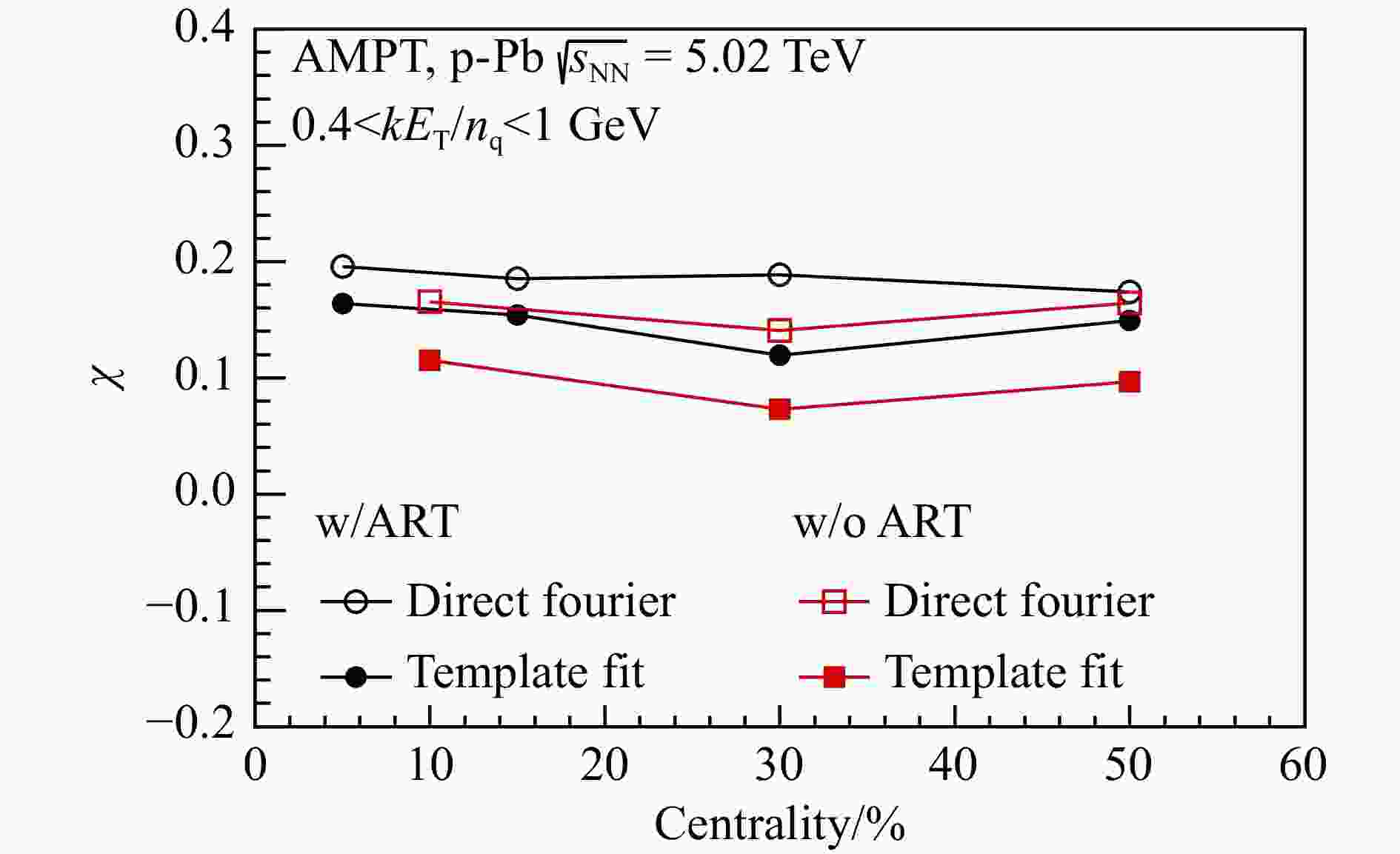
图 4 打开和关闭强子再散射过程的AMPT模型在$ \sqrt{s_{\mathrm{NN}}} = 5.02 $ TeV质子-铅核碰撞中对$ \chi $[$ \chi $定义见式(10)]随中心度分布的计算结果。空心点和实心点分别对应非流效应被减除前与减除后的结果
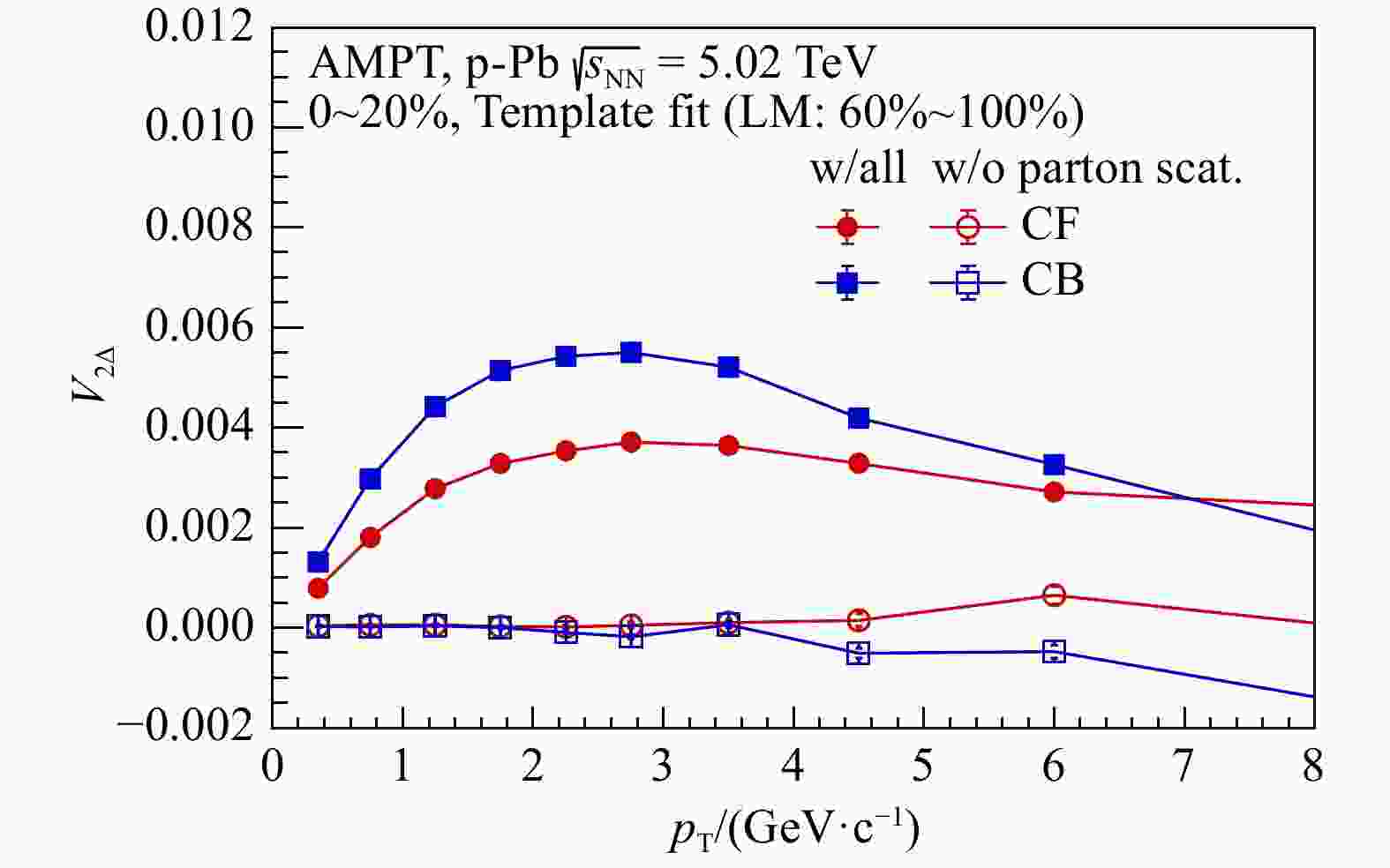
为进一步研究小系统碰撞中主导末态粒子椭圆各向异性的物理机制,我们在AMPT模型中比较了部分子散射过程对$ V_{2\varDelta}^{} $[见式(9)]的影响。图5展示了打开和关闭部分子散射过程的AMPT模型在$ \sqrt{s_{\mathrm{NN}}^{}} = 5.02 $ TeV质子-铅核碰撞中对带电强子$ V_{2\varDelta}^{} $(CF)和$ V_{2\varDelta}^{} $(CB)随$ p_{\mathrm{T}}^{} $分布的计算结果。当部分子散射过程被关闭后(即$ \sigma\sim0 $),带电粒子的$ V_{2\varDelta}^{} $几乎等于0。这表明在高多重数小系统碰撞中,末态粒子的椭圆各向异性主要来自于部分子散射。这些研究表明,在小系统碰撞中,部分子之间即使相互散射次数较少,也能通过逃逸机制产生显著的椭圆各向异性[32]。
-
本文利用AMPT模型系统地研究了$ \sqrt{s_{\mathrm{NN}}^{}} = 5.02 $ TeV质子-铅核碰撞中鉴别粒子($ {\rm{K}}^{\pm} $介子、$ \pi^{\pm} $介子及质子$ {\rm{P}}(\bar{{\rm{P}}}) $)的椭圆流$ \upsilon_{2}^{} $。基于最新的非流减除方法,我们首次在AMPT模型计算中将高多重数质子-铅核碰撞中鉴别粒子$ \upsilon_{2}^{} $推广到高达8 GeV/$ c $的横动量区域内,并较好地重现了组分夸克标度性。研究发现,小系统碰撞中组分夸克标度性同时依赖于非流效应与强子再散射过程的影响,部分子散射过程是末态粒子椭圆各向异性的主要来源。总的来说,本工作将为理解小碰撞系统中部分子集体性的起源提供新的思路与见解。
Study of the NCQ Scaling of Elliptic Flow in p–Pb Collisions with a Multiphase Transport Model
-
摘要: 高能重离子碰撞中末态鉴别粒子的椭圆流组分夸克标度现象被认为是展现部分子各向异性自由度的重要信号之一。本研究利用多相输运(AMPT)模型系统地研究了质心能量为5.02 TeV的质子-铅核碰撞中末态轻味强子的椭圆流$ \upsilon_{2}^{}$及其组分夸克标度行为。基于最新的小系统流分析方法,AMPT模型的计算结果很好地描述了轻味介子的$ \upsilon_{2}^{}$,但与重子的测量结果略有偏离。研究结果显示,耦合了部分子级联与夸克重组合机制的AMPT模型能产生显著的组分夸克标度现象,该现象也同时依赖于非流效应与强子再散射过程。这些研究结果将为小系统碰撞中末态粒子集体行为的起源问题提供进一步的解释。Abstract: The number of constituent quark(NCQ) scaling of elliptic flow in heavy-ion collisions is one of the important signals of parton anisotropic degrees of freedom. In this work, we systematically study the $\upsilon_{2}^{}$ of light flavor hadrons as well as its NCQ scaling in p−Pb collisions at 5.02 TeV, with a multiphase transport(AMPT) model. Based on the advanced flow extraction method, the AMPT model calculations provide a good description of the measured transverse momentum($p_{\mathrm{T}}^{}$)-differential $\upsilon_{2}^{}$ of mesons but exhibit a slight deviation of the baryon $\upsilon_{2}^{}$. We find that the NCQ scaling is mainly driven by the combination of parton cascade and quark recombination, and also affected by the nonflow contribution and hardronic rescattering. This study provides new insights into understanding the origin of collective-like behaviors in small collision system.
-
Key words:
- azimuthal anisotropy /
- small collision systems /
- transport model /
- nonflow effect
-
图 4 打开和关闭强子再散射过程的AMPT模型在$ \sqrt{s_{\mathrm{NN}}} = 5.02 $ TeV质子-铅核碰撞中对$ \chi $[$ \chi $定义见式(10)]随中心度分布的计算结果。空心点和实心点分别对应非流效应被减除前与减除后的结果
-
[1] SHURYAK E V. Phys Lett B, 1978, 78: 150. doi: 10.1016/0370-2693(78)90370-2 [2] SHURYAK E V. Phys Rept, 1980, 61: 71. doi: 10.1016/0370-1573(80)90105-2 [3] OLLITRAULT J Y. Phys Rev D, 1992, 46: 229. doi: 10.1103/PhysRevD.46.229 [4] VOLOSHIN S A. Nucl Phys A, 2009, 827: 377C. doi: 10.1016/j.nuclphysa.2009.05.082 [5] VOLOSHIN S, ZHANG Y. Z Phys C, 1996, 70: 665. doi: 10.1007/s002880050141 [6] POSKANZER A M, VOLOSHIN S A. Phys Rev C, 1998, 58: 1671. doi: 10.1103/PhysRevC.58.1671 [7] ALVER B, ROLAND G. Phys Rev C, 2010, 81: 054905. doi: 10.1103/PhysRevC.82.039903 [8] ALVER B H, GOMBEAUD C, LUZUM M, et al. Phys Rev C, 2010, 82: 034913. doi: 10.1103/PhysRevC.82.034913 [9] QIN G Y, PETERSEN H, BASS S A, et al. Phys Rev C, 2010, 82: 064903. doi: 10.1103/PhysRevC.82.064903 [10] TEANEY D, YAN L. Phys Rev C, 2011, 83: 064904. doi: 10.1103/PhysRevC.83.064904 [11] AFANASIEV S, AIDALA C, AJITANANDET N N, et al. Phys Rev Lett, 2007, 99: 052301. doi: 10.1103/PhysRevLett.99.052301 [12] ADAMS J, ADLER C, AGGARWAL M M, et al. Phys Rev Lett, 2004, 92: 052302. doi: 10.1103/PhysRevLett.92.052302 [13] ADARE A, AFANASIEV S, AIDALA C, et al. Phys Rev Lett, 2007, 98: 162301. doi: 10.1103/PhysRevLett.98.162301 [14] AAMODT K, ABELEV B, QUINTANA A A, et al. Phys Rev Lett, 2011, 107: 032301. doi: 10.1103/PhysRevLett.107.032301 [15] ACHARYA S, ACOSTA F T, ADAMOVÁ D, et al. JHEP, 2018, 07: 103. doi: 10.1007/JHEP07(2018)103 [16] AAD G, ABBOTT B, ABDALLAH J, et al. Phys Rev C, 2012, 86: 014907. doi: 10.1103/PhysRevC.86.014907 [17] CHATRCHYAN S, KHACHATRYAN V, SIRUNYAN A M, et al. Phys Rev C, 2014, 89(4): 044906. doi: 10.1103/PhysRevC.89.044906 [18] ACHARYA S, ADAMOVÁ D, ALEXANDER A, et al. JHEP, 2023, 05: 243. doi: 10.1007/JHEP05(2023)243 [19] ACHARYA S, ADAMOVÁ D, ALEXANDER A, et al. JHEP, 2021, 10: 152. doi: 10.1007/JHEP10(2021)152 [20] MOLNAR D, VOLOSHIN S A. Phys Rev Lett, 2003, 91: 092301. doi: 10.1103/PhysRevLett.91.092301 [21] LIN Z W, MOLNAR D. Phys Rev C, 2003, 68: 044901. doi: 10.1103/PhysRevC.68.044901 [22] CHATRCHYAN S, KHACHATRYAN V, SIRUNYAN A M, et al. Phys Lett B, 2013, 718: 795. doi: 10.1016/j.physletb.2012.11.025 [23] ABELEV B, ADAM J, ADAMOVA D, et al. Phys Lett B, 2013, 719: 29. doi: 10.1016/j.physletb.2013.01.012 [24] AAD G, ABAJYAN T, ABBOTT B, et al. Phys Rev Lett, 2013, 110(18): 182302. doi: 10.1103/PhysRevLett.110.182302 [25] ABELEV B, ADAM J, ADAMOVÁ D, et al. Phys Lett B, 2013, 726: 164. doi: 10.1016/j.physletb.2013.08.024 [26] BOZEK P. Phys Rev C, 2012, 85: 014911. doi: 10.1103/PhysRevC.85.014911 [27] BOZEK P, BRONIOWSKI W. Phys Lett B, 2013, 718: 1557. doi: 10.1016/j.physletb.2012.12.051 [28] NAGLE J L, ZAJC W A. Ann Rev Nucl Part Sci, 2018, 68: 211. doi: 10.1146/annurev-nucl-101916-123209 [29] DUSLING K, VENUGOPALAN R. Phys Rev D, 2013, 87(9): 094034. doi: 10.1103/PhysRevD.87.094034 [30] DUSLING K, VENUGOPALAN R. Phys Rev D, 2013, 87(5): 051502. doi: 10.1103/PhysRevD.87.051502 [31] LIN Z W, KO C M, LI B A, et al. Phys Rev C, 2005, 72: 064901. doi: 10.1103/PhysRevC.72.064901 [32] HE L, EDMONDS T, LIN Z W, et al. Phys Lett B, 2016, 753: 506. doi: 10.1016/j.physletb.2015.12.051 [33] LIN Z W, ZHENG L. Nucl Sci Tech, 2021, 32(10): 113. doi: 10.1007/s41365-021-00944-5 [34] WANG X N, GYULASSY M. Phys Rev D, 1991, 44: 3501. doi: 10.1103/PhysRevD.44.3501 [35] GYULASSY M, WANG X N. Comput Phys Commun, 1994, 83: 307. doi: 10.1016/0010-4655(94)90057-4 [36] ZHANG B. Comput Phys Commun, 1998, 109: 193. doi: 10.1016/S0010-4655(98)00010-1 [37] ZHENG L, LI H, QIN H, et al. Eur Phys J A, 2017, 53(6): 124. doi: 10.1140/epja/i2017-12312-8 [38] KHACHATRYAN V, SIRUNYAN A M, TUMASYAN A, et al. Phys Lett B, 2017, 765: 193. doi: 10.1016/j.physletb.2016.12.009 [39] ABDULAMEER N J, ACHARYA U, ADARE A, et al. Phys Rev C, 2023, 107(2): 024907. doi: 10.1103/PhysRevC.107.024907 [40] LIM S H, HU Q, BELMONT R, et al. Phys Rev C, 2019, 100(2): 024908. doi: 10.1103/PhysRevC.100.024908 [41] AAD G, ABBOTT B, ABDALLAH J, et al. Phys Rev Lett, 2016, 116: 172301. doi: 10.1103/PhysRevLett.116.172301 [42] ABELEV B, ABRAMYAN A, ADAM J, et al. Int J Mod Phys A, 2014, 29: 1430044. doi: 10.1142/S0217751X14300440 [43] LI H, HE L, LIN Z W, et al. Phys Rev C, 2016, 93(5): 051901. doi: 10.1103/PhysRevC.93.051901 [44] HE Y, LIN Z W. Phys Rev C, 2017, 96(1): 014910. doi: 10.1103/PhysRevC.96.014910 -





 下载:
下载:

 甘公网安备 62010202000723号
甘公网安备 62010202000723号