-
核子-核子短程关联(nucleon-nucleon short-range correlation , NN-SRC)效应对于理解原子核的结构和核子的性质至关重要,并且对核反应、核天体物理等领域有着重要影响[1-3] 。NN-SRC会导致有限核的核子动量分布中出现高动量尾[4-5],提供关于核子的少体行为信息,可以用来验证超越平均场的相关效应[6-7]。在核反应领域中,NN-SRC所引起的高动量尾会导致核子的平均动能增加,进而对重离子碰撞过程产生影响[8-11]。此外,在核天体领域的研究中,NN-SRC会引起丰中子核物质的状态方程中同位旋相关项的增强[12]。鉴于NN-SRC的重要性,有必要在实验和理论上深入探究这一领域。
电子-原子核散射是研究NN-SRC的有效实验手段。根据探测到的出射粒子不同,准弹性电子散射实验可以分为两类: 遍举电子散射$({\rm e,\, e{'}p})$实验和单举电子散射${\rm{(e,\, e{'})}}$实验[13]。在遍举准弹性电子散射$({\rm{e,\, e'p}})$实验过程中,被击出的核子与出射电子同时被探测器测量。在单举准弹性电子散射${\rm {(e,\, e')}}$实验中,只对出射电子进行探测,因此${\rm{(e,\, e')}}$截面反映了所有最终核态的综合性质。随着研究NN-SRC等核结构信息的${\rm{(e,\, e')}}$散射实验的发展,对相应的${\rm{(e,\, e')}}$散射理论模型的可靠性的需求也进一步提高。其中,平面波脉冲近似(plane-wave impulse approximation, PWIA)理论是一种被广泛应用的方法[14-16]。在PWIA框架下,${\rm{(e,\, e')}}$散射截面取决于两个关键的物理量:表示原子核结构的谱函数$ S({\boldsymbol{p}},E) $,和描述电子被离壳核子散射的基本截面$ {\sigma _{{\text{eN}}}} $。$ {\sigma _{{\text{eN}}}} $主要取决于核子的电磁结构信息,对于准弹性散射区域,基本截面$ {\sigma _{{\text{eN}}}} $可以很好地定量计算出来。然而,由于Δ共振区域核子形状因子的不确定性,理论与实验数据存在差异,仍需进一步研究[17]。
${\rm{(e,\, e')}}$散射的另一个关键问题是谱函数的精确计算。谱函数$ S({\boldsymbol{p}},E) $的理论研究可以分为平均场(mean-field, MF)部分${S_{{\rm{MF}}}}({\boldsymbol{p}}, E)$和NN-SRC部分${S_{{\rm{corr}}}}({\boldsymbol{p}},E)$[18-20]。MF部分谱函数${S_{{\rm{MF}}}}({\boldsymbol{p}},E)$主要描述受平均中心核势场影响的、费米面以下的、具有低能$ E $和低动量p的核子。相对于${S_{{\rm{MF}}}}({\boldsymbol{p}},E)$,NN-SRC部分谱函数${S_{{\rm{corr}}}}({\boldsymbol{p}},E)$提供了费米面以上的、具有高动量p和高能量$ E $的短程关联核子的描述[21-22]。
本文将${\rm {(e, \,e')}}$散射理论与微观核结构模型联系起来,研究NN-SRC对${\rm {(e,\, e')}}$截面的影响。在计算Δ共振电子散射时,将考虑散射过程中的能量和动量守恒以及Δ(1232)的衰减宽度,并采用合适的形状因子。在理论结果的基础上,我们将分别研究NN-SRC部分和MF部分对${\rm{(e,\, e')}}$截面的影响。在此基础上,分析不同散射条件下${\rm{(e,\, e')}}$散射对NN-SRC的敏感性。最后,将提出了一种从实验截面中提取NN-SRC强度的方法。论文第1节介绍了通过核子动量分布和谱函数来计算${\rm {(e,\, e')}}$截面的理论框架。第2节展示了包含核子-核子短程关联的核子动量分布与谱函数的结果,并计算了${\rm {(e,\, e')}}$截面。然后,探究了MF部分与NN-SRC部分对${\rm{(e,\, e')}}$截面的贡献,并进一步分析了NN-SRC的强度对${\rm{(e,\, e')}}$截面的影响。最后给出研究结论。
-
本文中对谱函数的计算分为两部分:MF部分$ {S_{\rm MF}}({\boldsymbol{p}},E) $和NN-SRC部分$ {S_{\rm corr}}({\boldsymbol{p}},E) $:
$$ S({\boldsymbol{p}},E) = {S_{{\text{MF}}}}({\boldsymbol{p}},E) + {S_{{\text{corr }}}}({\boldsymbol{p}},E), $$ (1) 谱函数归一化到核子数$ \int {} {{\text{d}}^3}p {\text{d}}E S({\boldsymbol{p}},E) $。本文采用轴向变形相对论平均场(relativistic mean field, RMF)模型计算MF部分。在低能$ E $和低动量p下,MF部分$ {S_{\rm MF}}({\boldsymbol{p}},E) $由单粒子性质主导:
$$ {S_{\rm MF}}({\boldsymbol{p}},E) = \sum\limits_i {{C_i}} \left( {{{\left| {{f_i}({\boldsymbol{p}})} \right|}^2} + {{\left| {{g_i}({\boldsymbol{p}})} \right|}^2}} \right){L_i}\left( {E - {E_i}} \right), $$ (2) 式中:$ {f_i}({\boldsymbol{p}}) $和$ {g_i}({\boldsymbol{p}}) $为单粒子态$ i $在动量空间中的二维狄拉克旋量;$ {C_i} $为单粒子态$ i $对应的占有数;核子的能量分布可以用洛伦兹函数$ {L_i} $表示[23]。
在高能和高动量区域,由于NN-SRC效应会将核子激发到费米面以上的状态,因此NN-SRC部分的谱函数$ {S_{\rm corr}}({\boldsymbol{p}},E) $起主导作用。$ {S_{\rm corr}}({\boldsymbol{p}},E) $由NN-SRC对和$ (A - 2) $剩余核子系统的基态构型决定,由下式计算得到[19]:
$$ {S_{{\text{corr}}}}({\boldsymbol{p}},E) = {n_{{\text{corr }}}}({\boldsymbol{p}})\frac{m}{{|{\boldsymbol{p}}|}} \sqrt {\frac{{{\alpha _{\rm P}}}}{\pi }} \times \big[ {\exp \left( { - {\alpha _{\text{P}}}{{\boldsymbol{p}}_{{{\min }^2}}}} \right) - \exp \left( { - {\alpha _{\text{P}}}{{\boldsymbol{p}}_{{{\max }^2}}}} \right)} \big], $$ (3) 其中:$ {{\boldsymbol{p}}_{\min }} $和$ {{\boldsymbol{p}}_{\max }} $分别是质心动量的上限值和下限值;$ {n_{{\text{corr }}}}({\boldsymbol{p}}) $为短程关联部分动量分布;$ m $为核子质量。 ${\alpha _{\rm{P}}} = {{\left[ {3(A - 1)} \right]} \mathord{\left/ {\vphantom {{\left[ {3(A - 1)} \right]} {\left[ {4\left\langle {p_{{\text{MF}}}^2} \right\rangle (A - 1)} \right]}}} \right. } {\left[ {4\left\langle {{\boldsymbol{p}}_{{\text{MF}}}^2} \right\rangle (A - 1)} \right]}}$,其中$ \left\langle {{\boldsymbol{p}}_{{\text{MF}}}^{}} \right\rangle $为平均场部分的平均核子动量[24]。
本文采用light-front dynamics (LFD)方法计算短程关联部分。在LFD方法中,$ {n_{\rm corr}}({\boldsymbol{p}}) $可以通过重新缩放氘核精确动量分布的NN-SRC部分来获得。动量分布可以表示为
$$ n_{{\text{corr }}}^\tau ({\boldsymbol{p}}) = {N_\tau }\tau {C_A}\big[ {{n_2}({\boldsymbol{p}}) + {n_5}({\boldsymbol{p}})} \big], $$ (4) 其中$ {n_2}({\boldsymbol{p}}) $和$ {n_5}({\boldsymbol{p}}) $两个分量反映氘核的短程关联部分,由LFD波函数给出[25]。比例因子$ {C_A} $代表了NN-SRC的强度。$ \tau $代表相应的质子数和中子数,$ {N_\tau } $为归一化因子。
在单举电子散射${\rm{(e,\, e')}}$过程中,入射电子与目标核相互作用,并有初始四动量$k \equiv ({E_{\rm{k}}},\;{\boldsymbol{k}})$和末态四动量$k' \equiv ({E_{\rm{k}}},\;{\boldsymbol{k}}')$。散射电子的四动量转移为$ q \equiv (\omega ,\;{\boldsymbol{q}}) $,其中$ \omega $为电子转移能量,q为电子的转移动量。忽略末态相互作用,双微分截面可表示为[26]
$$ \frac{{{{\text{d}}^2}\sigma }}{{{\text{d}}\varOmega {\text{d}}{E_{{{\mathbf{k}}^\prime }}}}} = \frac{{{\alpha ^2}}}{{{Q^4}}}\frac{{{E_{{{\mathbf{k}}^\prime }}}}}{{{E_{\mathbf{k}}}}}{L_{\mu \nu }}{W^{\mu \nu }}, $$ (5) 其中:$ \alpha $为精细结构常数;$ {Q^2} $为四动量传递的平方,${Q^2} = - {q^2} = {\omega ^2} - {{\boldsymbol{q}}^2}$。在式(5)中,轻子张量$ {L_{\mu \nu }} $包含了电子在散射过程中的所有信息,原子核的强子张量$ {W^{\mu \nu }} $包含了目标核的所有的核结构信息,因此原子核张量可以描述为
$$ {W}^{\mu \nu } = {\displaystyle \sum _{i}{\displaystyle \int {\text{d}}^{3}}p\text{d}ES({\boldsymbol{p}},E){w}_{i}^{\mu \nu }(q)\left(\frac{m}{{E}_{p}}\right)}\text{,} $$ (6) $ w_{}^{\mu \nu } $为核子的强子张量,反映了动量为p的束缚态核子的电磁结构。$ {E_p} $为散射前核子的初始能量。
结合式(5)和(6),${\rm{(e, e')}}$截面可以写成
$$ \begin{split} \frac{{{{\text{d}}^2}\sigma }}{{{\text{d}}\varOmega {\text{d}}{E_{{{\mathbf{k}}^\prime }}}}} =& \int {{{\text{d}}^3}} p {\text{d}}E\left[ {{S_{\text{p}}}({\boldsymbol{p}},E)\frac{{{{\text{d}}^2}{\sigma _{{\text{ep}}}}}}{{{\text{d}}\varOmega {\text{d}}{E_{{{\mathbf{k}}^\prime }}}}}} \right.\left. { + {S_{\text{n}}}({\boldsymbol{p}},E)\frac{{{{\text{d}}^2}{\sigma _{{\text{en}}}}}}{{{\text{d}}\varOmega {\text{d}}{E_{{{\mathbf{k}}^\prime }}}}}} \right]\\ & \delta \left( {\omega - E + m - {E_{\left| {{\boldsymbol{p}} + {\boldsymbol{q}}} \right|}}} \right), \end{split}$$ (7) 其中:基本截面$ {\sigma _{{\text{en}}}} $($ {\sigma _{{\text{ep}}}} $)描述电子与自由中子(质子)之间发生散射时的散射截面[19]。在准弹性电子散射过程和Δ共振电子散射中,$ {\sigma _{{\text{en}}}} $($ {\sigma _{{\text{ep}}}} $)的计算分别使用相应的形状因子,分别反映了核子和Δ(1232)粒子的电磁结构。$ {E_{\left| {p + q} \right|}} $为出射核子的能量。
-
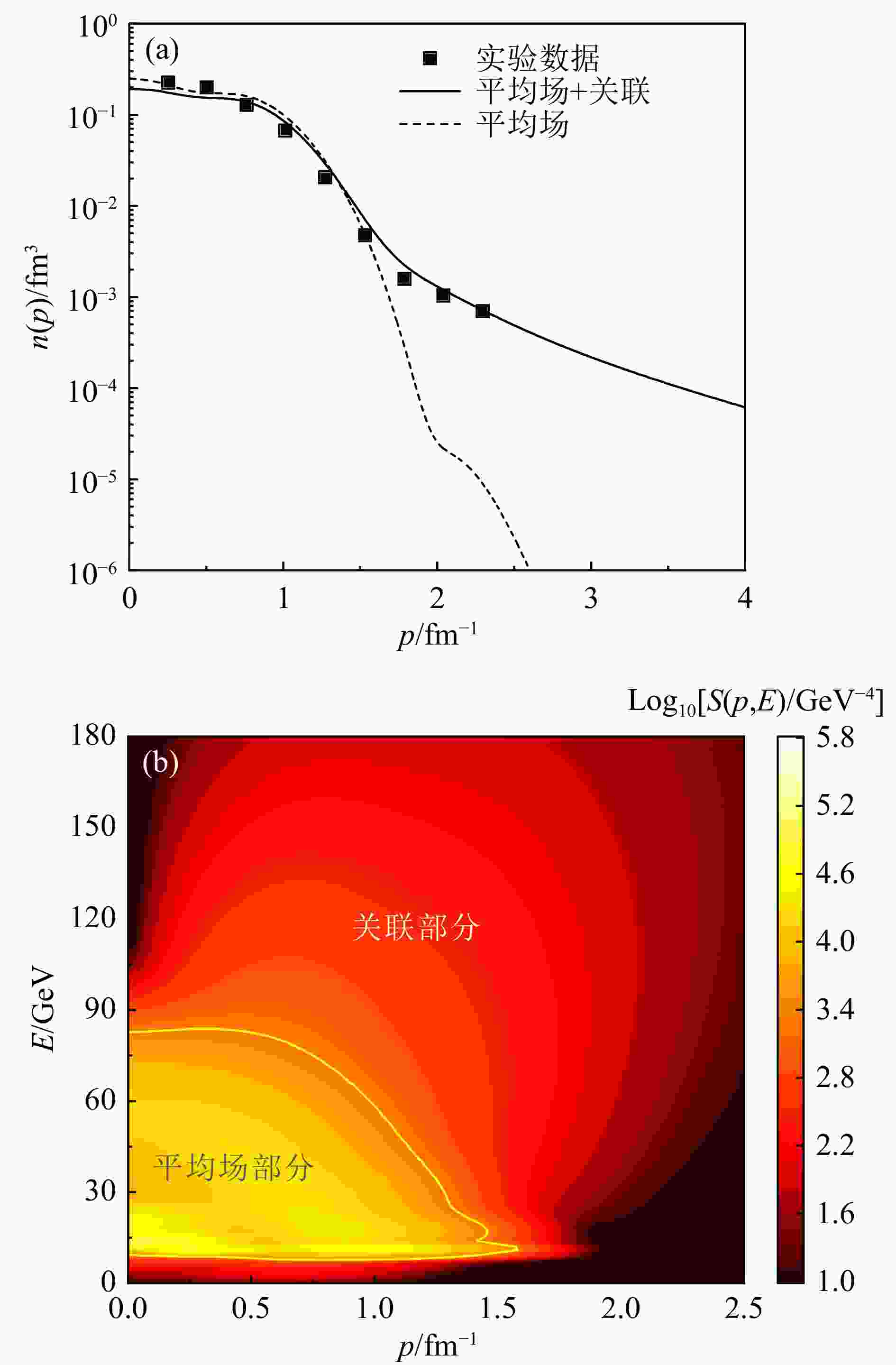
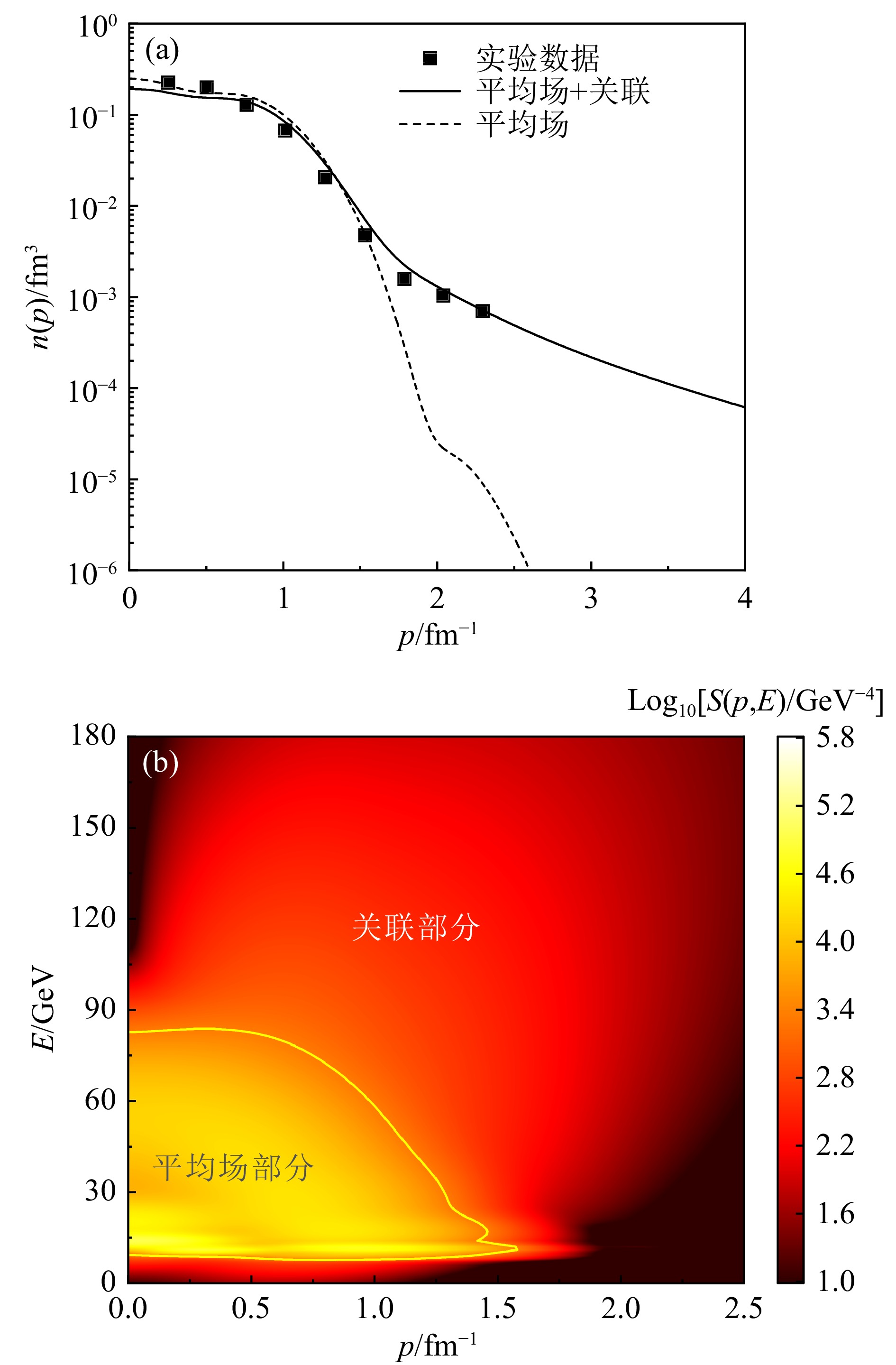
根据式(1)~(4),我们分别计算了核子动量分布n(p)和原子核谱函数$ S({{p}},E) $。平均场部分根据轴向变形RMF模型采用NL3*参数计算。关联部分由LFD方法得到,采用的关联强度为$ {C_A} = 4.5 $。在图1(a)中,给出了56Fe原子核的核子动量分布,对于$ {n_{\rm MF}}(p) $,在核子动量$p < 1.5\;{\rm{f}}{{\rm{m}}^{ - 1}}$处可以很好地描述实验数据。在核子动量$p > 1.5\;{\rm{f}}{{\rm{m}}^{ - 1}}$时,动量分布迅速下降至趋于0,此时$ {n_{\rm MF}}(p) $与实验数据出现了显著偏离。对于含有NN-SRC的核子动量分布$ n(p) $,在核子动量$p < 1.5\;{\rm{f}}{{\rm{m}}^{ - 1}}$时可以很好地描述实验数据。然而在核子动量$p > 1.5\;{\rm{f}}{{\rm{m}}^{ - 1}}$时,NN-SRC使得$ n(p) $出现了高动量尾部,并且可以很好地描述实验数据。图1(b)中给出了添加了NN-SRC的56Fe原子核的总谱函数$ S({{p}},E) $。为了更明显地观察到NN-SRC部分的原子核谱函数,我们采用对数坐标来显示谱函数的大小。在图1(b)中,平均场部分谱函数$ {S_{\rm MF}}({{p}},E) $被黄色实线圈出。从图中可以看出,$ {S_{\rm MF}}({{p}},E) $对总谱函数$ S({{p}},E) $的贡献主要在低能$(E < 90\;{\rm{MeV}})$和低动量$(p < 1.5\;{\rm{f}}{{\rm{m}}^{ - 1}})$的区域,大约占总核子数的80%。而对于高能$(E > 90\;{\rm{MeV}})$和高动量$(p > 1.5\;{\rm{f}}{{\rm{m}}^{ - 1}})$的区域,原子核谱函数主要来源于NN-SRC的贡献。相较于$ {S_{\rm MF}}({{p}},E) $,$ {S_{\rm corr}}({{p}},E) $给出的核子仅占总核子数的大约20%,这一理论结果与遍举电子散射当中提取的原子核谱函数的结果相符合[27]。
-
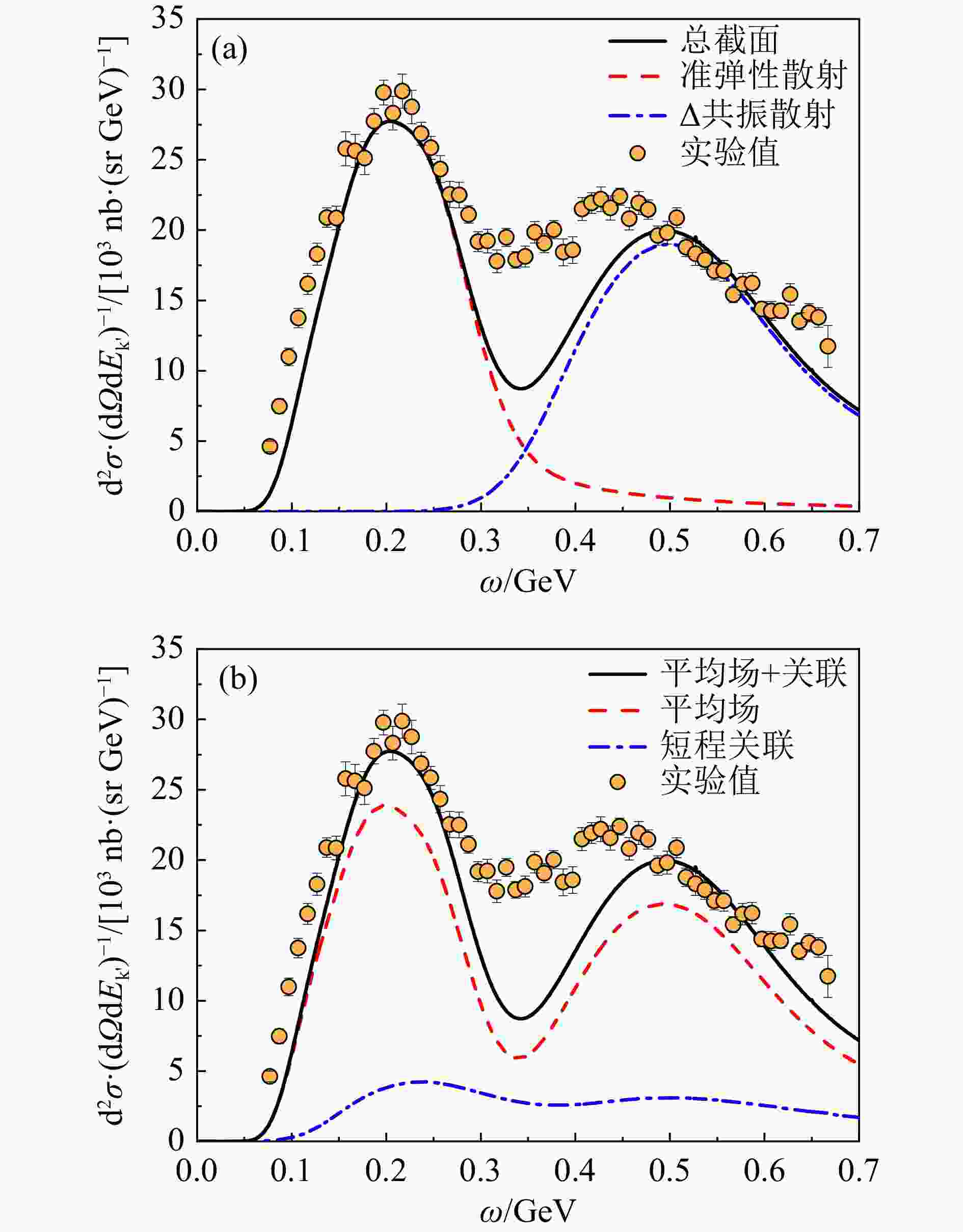
在图2(a)中给出了根据PWIA 理论框架下的谱函数方法计算的56Fe的${\rm{(e,\, e')}}$散射截面。从图中可以看出,总的理论截面与实验数据吻合较好。说明在准弹性散射峰及Δ共振散射峰的位置,我们的理论公式可以很好地再现实验数据。Δ共振截面的计算依赖于Δ共振区域的核子结构函数,其中包括了磁形状因子、电形状因子和库仑激发形状因子。由此可见,Δ共振散射峰包含了核子共振态中Δ(1232)粒子的电磁结构信息,这些信息有助于理解在强相互作用中的夸克禁闭现象[28]。从图2中还可以看到,在转移能量$\omega = 0.35\; {\text{GeV}}$的区域,PWIA给出的理论和实验值有明显的差别,这是介子交换流的影响导致的。在这个区域,介子交换流会激发2p-2h的末态,对散射截面产生较大的贡献[29],在后续的计算中,需要进一步考虑介子交换流的影响。
验证了散射截面计算的准确性后,我们进一步地将${\rm{(e,\, e')}}$总截面分成了MF核子的贡献与关联核子的贡献,并展示在图2(b)中。从图中可以看出,在两个散射峰的峰值位置,MF核子对散射截面的贡献占主导地位,而关联核子对散射截面的贡献较小但不可忽略。同时考虑MF核子和关联核子对散射截面的贡献,可以很好地描述实验散射截面。56Fe的短程关联核子大约占据总核子数的21.8%,而${\rm{(e, \,e')}}$截面峰值处短程关联核子的贡献约为16%,关联核子在散射截面中的权重被削弱;MF核子占总核子数的78.2%,对散射截面的贡献约为84%,MF核子在散射过程中的权重有所提升。从以上两组数据可以看出,相较于短程关联核子,MF场核子对${\rm{(e,\, e')}}$截面峰值处的贡献能力更强。因此,如果在谱函数的计算中过程中选择越大的短程关联强度$ {C_A} $,MF核子占比就会越低,原子核整体上对散射截面峰值处的贡献能力会更弱,散射截面就会越小。根据这一现象,可以利用准弹性散射峰和Δ共振散射峰峰值处的实验截面来约束并提取原子核内的短程关联核子的占比。
-
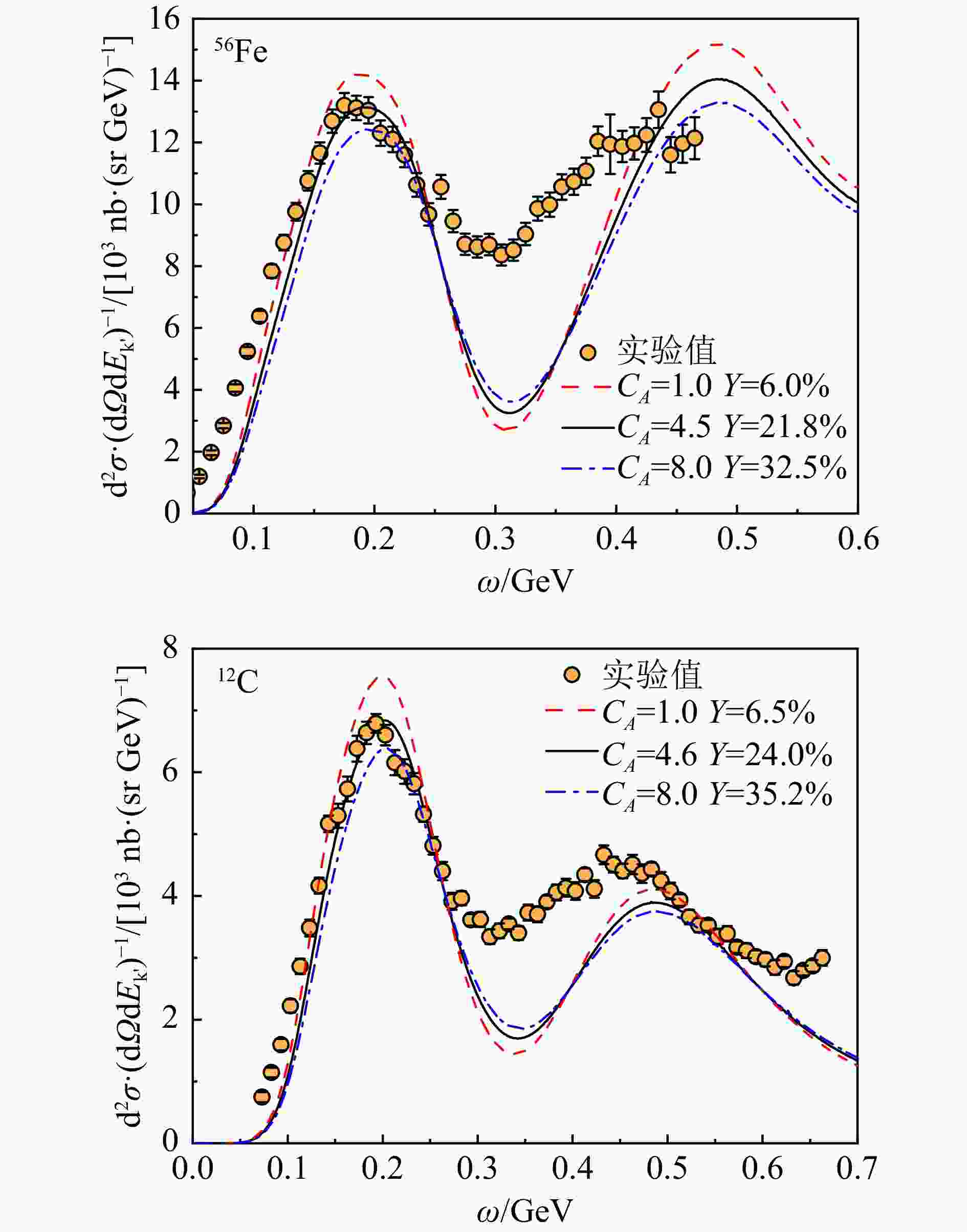
为了提取原子核内短程关联效应的信息,我们分别计算了56Fe和12C原子核在不同关联强度下的散射截面。对于图3(a)中的56Fe原子核,图中的三条线分别对应了短程关联强度$ {C_A} = 1.0 $, $ 4.5 $和$ 8.0 $,短程关联核子数分别占总核子数的6.0%, 21.8%和32.5%。将理论${\rm{(e,\, e')}}$ 散射截面与实验数据进行比较,发现对于56Fe原子核,短程关联强度为$ {C_A} = 4.5 $时,理论计算得到的${\rm{(e,\, e')}}$散射截面与实验截面吻合得最好。这表明在56Fe原子核中,LFD方法中的原子核短程关联强度应当为$ {C_A} = 4.5 $,此时短程关联核子约占核子总数的21.8%。此外对于12C原子核,与实验截面吻合的最好的理论截面所对应的原子核短程关联强度为$ {C_A} = 4.6 $,与之相对应的短程关联核子占比为24.0%。在上述分析中,我们发现原子核中短程关联核子约占总核子数的20%~25%,这验证了从头算法的相关的计算结果[31],并与遍举电子散射的实验结果一致[12, 32]。图3中的结果是基于RMF模型NL3*参数给出的核子动量分布$ n(p) $和原子核谱函数$ S({{p}},E) $得到的,但结果并不依赖于RMF模型参数组的选取,因为不同的模型和参数给出的$ n(p) $接近,不影响后续散射截面的计算[33]。
-
短程关联是验证的重要性质,与核动量分布的高动量分量有关。本文系统地研究了NN-SRC对单举电子散射过程的影响,并结合变形RMF模型和LFD方法获得了核谱函数。通过使用合适的形状因子,我们准确地计算了理论截面。我们进一步将${\rm{(e,\, e')}}$截面分成MF和NN-SRC部分。可以看出,随着NN-SRC强度的增加,准弹性和Δ 共振散射峰附近的截面减小。利用本文提出的方法,在合适的散射条件下从实验数据中提取了56Fe,和12C原子核的短程关联强度分别为$ {C_A} = 4.5 $和$ 4.6 $,对应高动量核子的比例为21.8%和24.0%。本文的研究有助于区分中微子核散射实验中的核效应和超标准模型效应。此外,这些研究对理解核结构和强相互作用有重要意义。
-
摘要: 核子-核子短程关联是核物理的关键问题之一,它会导致核子动量分布出现高动量尾。本工作首先基于轴向形变相对论平均场模型构建了平均场部分原子核的谱函数,并在此基础上引入了短程关联效应的修正。然后利用谱函数在平面波脉冲近似框架内计算了单举电子散射截面,包括准弹性散射部分和Δ共振散射部分。特别是在Δ共振散射区域,通过重新考虑了核子共振态Δ(1232)的电磁结构,有效地改进了理论计算,使理论散射截面与实验数据很好地吻合。本工作进一步将单举散射截面分为短程关联的贡献和平均场的贡献。研究发现,准弹性峰和Δ共振峰不仅反映了平均场结构,而且对短程关联信息敏感。最后,本工作提出了一种从实验截面中提取原子核短程关联强度的方法。Abstract: The nucleon-nucleon short-range correlation(NN-SRC) is one of the key issues in nuclear physics that cause high-momentum tails in the nucleon momentum distributions. In this paper, the nuclear spectral functions are constructed based on the axially deformed relativistic mean-field model, and the correction of the short-range correlation effect is introduced. Then, the inclusive scattering cross sections are calculated using the nuclear spectral function and the framework of the plane wave impulse approximation, including both the quasielastic and Δ resonance parts. In particular, in the Δ resonance region, the electromagnetic structure of the nucleon resonance state Δ(1232) is reconsidered, which effectively improves the theoretical calculations that can be in better agreement with experimental data. The paper further divides the inclusive scattering cross sections into the contributions of NN-SRC and mean-field. It is found that, the quasielastic peak and Δ resonance peak not only reflect the mean-field structure but also are sensitive to NN-SRC information. Finally, we propose a method for extracting the NN-SRC strength of nuclei from experimental cross-section data.
-
图 1 根据形变的RMF模型和LFD方法计算的56Fe 原子核的计算结果(在线彩图)
(a) 平均场核子动量分布与包含关联的总动量分布;(b) 包含关联的原子核谱函数。图中核子动量分布的实验值取自文献[16]。
图 2 56Fe原子核在入射电子能量为Ek = 0.961 GeV,散射角θ = 37.5°时的散射截面(在线彩图)
(a) 准弹性散射截面、Δ共振散射截面与总截面;(b) MF部分的截面、NN-SRC部分的截面的贡献与两部分相加的总截面。实验数据来自参考文献[30]。
图 3 不同原子核在不同关联强度下的散射截面(在线彩图)
(a) 56Fe在入射电子能量为Ek = 0.62 GeV,散射角θ = 60°时的散射截面;(b) 12C在入射电子能量为Ek = 0.961 GeV,散射角θ = 37.5°时的散射截面。实验数据来自参考文献[34]。
-
[1] PATSYUK M, KAHLBOW J, LASKARIS G, et al. Nature Physics, 2021, 17: 693. doi: 10.1038/s41567-021-01193-4 [2] HEN O, LI B A, GUO W J, et al. Phys Rev C, 2015, 91: 025803. doi: 10.1103/PhysRevC.91.025803 [3] PIASETZKY E, SARGSIAN M, FRANKFURT L, et al. Phys Rev Lett, 2006, 97: 162504. doi: 10.1103/PhysRevLett.97.162504 [4] CAI B J, LI B A, CHEN L W. AIP Conference Proceedings, 2018, 2038: 020041. doi: 10.1063/1.5078860 [5] HEN O, MILLER G A, PIASETZKY E, et al. Reviews of Modern Physics, 2017, 89: 045002. doi: 10.1103/RevModPhys.89.045002 [6] DUER M, SCHMIDT A, PYBUS J R, et al. Phys Rev L, 2019, 122: 172502. doi: 10.1103/PhysRevLett.122.172502 [7] COLLABORATION C. Nature, 2018, 560: 617. doi: 10.1038/s41586-018-0400-z [8] QIN Y, NIU Q, GUO D, et al. Phys Lett B, 2024, 850: 138514. doi: 10.48550/arXiv.2307.10717 [9] COLLABORATION C. Nature, 2019, 566: 354. doi: 10.1038/s41586-019-0925-9 [10] YONG G C. Phys Lett B, 2017, 765: 104. doi: 10.1016/j.physletb.2016.12.013 [11] XUE H, XU C, YONG G C, et al. Phys Lett B, 2016, 755: 486. doi: 10.1016/j.physletb.2016.02.044 [12] SUBEDI R, SHNEOR R, MONAGHAN P, et al. Science, 2008, 320: 1476. doi: 10.1126/science.1156675 [13] WAN N, MYO T, XU C, et al. Chin Phys C, 2020, 44: 124104. doi: 10.1088/1674-1137/abb4d1 [14] EGIYAN K S, DASHYAN N B, SARGSIAN M M, et al. Phys Rev Lett, 2006, 96: 082501. doi: 10.1103/PhysRevLett.96.082501 [15] KULAGIN S A, PETTI R. Nucl Phys A, 2006, 765: 126. doi: 10.1016/j.nuclphysa.2005.10.011 [16] ATTI C C D, PACE E, SALME G. Phys Rev C, 1991, 43: 1155. doi: 10.1103/physrevc.43.1155 [17] RING P, SCHUCK P. The Nuclear Many-body Problem[M]. New York: Springer Science & Business Media, 2004. [18] WANG L, NIU Q, ZHANG J, et al. Science China Physics, Mechanics & Astronomy, 2023, 66: 102011. doi: 10.1007/s11433-023-2135-x [19] BENHAR O, DAY D, SICK I. Reviews of Modern Physics, 2008, 80: 189. doi: 10.1103/RevModPhys.80.189 [20] ANKOWSKI A M, SOBCZYK J T. Phys Rev C, 2006, 74: 054316. doi: 10.1103/PhysRevC.74.054316 [21] WANG H, SU Q, XU C, et al. Journal of Physics G: Nuclear and Particle Physics, 2023, 50: 095104. doi: 10.1088/1361-6471/ace6c3 [22] NIU Q, LIU J, GUO Y, et al. Phys Rev C, 2022, 105: L051602. doi: 10.1103/PhysRevC.105.L051602 [23] KOROVER I, MUANGMA N, HEN O, et al. Phys Rev Lett, 2014, 113: 022501. doi: 10.1103/PhysRevLett.113.022501 [24] ANKOWSKI A M, SOBCZYK J T. Phys Rev C, 2008, 77: 044311. doi: 10.1103/PhysRevC.77.044311 [25] CARBONELL J, KARMANOV V A. Nucl Phys A, 1995, 581: 625. doi: 10.1016/0375-9474(94)00430-U [26] FORIS B, PAPANICOLAS C N. Annual Review of Nuclear and Particle Science, 1987, 37: 133. doi: 10.1146/annurev.ns.37.120187.001025 [27] ROHE D, ARMSTRONG C S, ASATURYAN R, et al. Phys Rev Lett, 2004, 93: 182501. doi: 10.1103/PhysRevLett.93.182501 [28] ROBERTS C D. Few-Body Systems, 2018, 59: 72. doi: 10.1007/s00601-018-1385-8 [29] AMARO J E, BARBARO M B, CABALLERO J A, et al. Phys Rev C, 2010, 81: 014606. doi: 10.1103/PhysRevC.81.014606 [30] SEALOCK R M, GIOVANETTI K L, THORNTON S T, et al. Phys Rev L, 1989, 62: 1350. doi: 10.1103/PhysRevLett.62.1350 [31] LYU M, MYO T, TOKI H, et al. Phys Lett B, 2020, 805: 135421. doi: 10.1016/j.physletb.2020.135421 [32] HEN O, SARGSIAN M, WEINSTEIN L, et al. Science, 2014, 346: 614. doi: 10.1126/science.1256785 [33] WANG X, NIU Q, ZHANG J, et al. Science China Physics, Mechanics & Astronomy, 2021, 64: 292011. doi: 10.1007/s11433-021-1729-5 [34] MEZIANI Z E, BARREAU P, BERNHEIM M, et al. Phys Rev Lett, 1984, 52: 2130. doi: 10.1103/PhysRevLett.52.2130 -





 下载:
下载:

 甘公网安备 62010202000723号
甘公网安备 62010202000723号