-
近年来,高温、高密等极端条件下强相互作用物质性质的研究、量子色动力学(Quantum-Chromo-Dynamics, QCD)相图和相结构的确定已成为中高能核物理、核天体物理等领域的热点课题[1-2]。从第一性原理出发的格点QCD计算表明,在零重子化学势(
$ \mu_{\rm{B}} = 0 $ MeV)下强子相与夸克胶子等离子体(Quark-Gluon-Plasma, QGP)相之间的相变是连续过渡,随着重子化学势的升高,格点QCD由于存在符号问题而无法开展计算[3-5]。基于QCD的有效模型计算表明,在较大重子化学势区域,连续过渡相变可能转变为一阶相变,而一阶相变的终点则被称为QCD临界点(Critical End Point, CEP)[3]。然而,不同的理论模型及计算给出的临界点位置仍具有很大的不确定性,存在明显的模型依赖性[6-8]。重离子碰撞(Heavy Ion Collisions, HICs)实验为人们研究极端条件下核物质的性质提供了条件[9-10]。通过改变弹靶核的质量、碰撞能量和碰撞中心度,人们可以通过HICs产生不同密度、温度等条件下的核物质。为了研究QCD相图结构和确定CEP在QCD相图中的位置,在过去的20多年间,世界上众多重离子对撞机上进行了一系列的实验,如美国布鲁克海文国家实验室的相对论重离子对撞机(Relativistic Heavy Ion Collider, RHIC)上进行了束流能量扫描实验(
$ \sqrt{s_{\rm{NN}}} = 3\sim200 $ GeV的Au+Au碰撞,其中7.7 GeV以下为固定靶模式)[11]。通过对多个敏感于关联长度的观测量进行分析,人们将感兴趣的QCD临界点可能出现的能区缩小至了相对较低的能量范围内[6, 11-12]。此外,世界上大批拟建及新建的加速器装置也拟开展质心系能量为几个GeV的重离子碰撞实验以及高密核物质性质的研究工作[13-15]。理论上,输运模型作为抽取核物质属性的重要工具之一,经过多年的不断发展和完善,已经形成了多种基于不同理论假设和处理的用于描述从低能到相对论能区HICs的输运模型[16-18]。为了理解和降低理论系统误差以及模型不确定性从而提高模型的可靠性,多年来国际输运领域专家对不同的输运模型进行了多项比较工作,如评估了约二十余种输运模型对HICs体系和周期性边界的箱体体系中的模拟计算结果,包括核子之间的碰撞率与泡利阻塞、核子的集体流以及介子的产生等,并取得了阶段性的成果[17]。
在抽取核物质属性的过程中,实验测量和理论计算结果的对比需要基于同一观测量,因此构建和选取敏感于核物质状态方程(Equation of State, EoS)的观测量尤为重要。人们构建并提出了多种可观测量用以探索QCD相边界和寻找CEP的位置,如集体流、守恒荷的高阶累积矩、轻核的产额比、间歇分析、强子的Hanbury-Brown-Twiss(HBT) 关联[5-6]。本文将重点关注两π介子的HBT关联[19-23],它可以用于揭示HICs中冻结时刻π介子发射源的时空属性和π介子之间的动量相关性[22]。研究表明,粒子发射源的半径(也被称为HBT半径)敏感于EoS,在临界点附近时由于相变的发生状态方程将会变得非常软,导致系统膨胀放缓效应的出现,而这一效应可以通过π介子发射源的HBT半径之比或者平方差的激发函数的非单调(出现极大值)行为得以体现[24-26]。
基于RHIC束流能量扫描实验数据,STAR实验组对两π介子HBT关联进行了分析。结果表明,在
$ \sqrt{s_{\rm{NN}}}\approx 20 $ GeV时,π介子发射源的HBT半径之比存在极大值[27]。然而通过对比现有的HBT实验数据可以发现,π介子发射源的HBT半径之比在$ \sqrt{s_{\rm{NN}}}\approx 4 $ GeV时也存在着极大值,但具有极大的不确定度[28-29]。理论上,目前基于不同模型的强子HBT关联的研究主要集中在高能重离子碰撞领域[30-33]。此外,对于基于同一实验数据或者输运模型得出的不同观测量的碰撞能量依赖关系,非单调行为出现的能量区间也存在一定的差异。因此,发展一套能够自洽地描述大入射能量范围内的HICs,并可以描述多个观测量并直接与实验数据对比的输运模型显得十分重要。最新升级的极端相对论量子分子动力学(Ultrarelativistic Quantum Molecular Dynamics, UrQMD)模型可以引入任意的密度依赖的状态方程[23, 34-35],这为自洽地研究密度依赖的势相互作用、不同密度条件下的相变对不同观测量的影响提供了可能。文献[35]基于UrQMD模型展示了碰撞能量为$ \sqrt{s_{\rm{NN}}} = 2\sim10 $ GeV的重离子碰撞中不同的密度依赖的势相互作用以及相变对集体流的影响,其结果排除了4倍饱和密度$ \rho_{0} $ 以下发生相变的可能性。因此,我们期待密度依赖的势相互作用也将对重离子碰撞中粒子关联效应带来明显的影响,从而澄清~GeV能区π介子发射源HBT参数的能量依赖谜团并确定该能区核物质状态方程的密度依赖行为。本文框架如下:在第1节中对UrQMD模型和两π介子HBT关联进行简要描述;在第2节中展示核物质状态方程对π介子发射源的HBT半径的影响;最后,在第3节中给出总结与展望。
-
极端相对论量子分子动力学(UrQMD)模型起源于20世纪90年代,经过多个研究组持续不断的更新,现已被广泛地用于模拟从费米能区到LHC能区相对论重离子碰撞[36-37]。在UrQMD模型框架下,具有一定宽度的高斯波包所表示的强子将在平均场和碰撞项的共同作用下进行演化,第
$ i $ 个粒子的坐标$ \dot{\boldsymbol{r}}_{i} $ 和动量$ \dot{\boldsymbol{p}}_{i} $ 的时空演化遵循哈密顿运动方程:$$ \begin{array}{l} \dot{\boldsymbol{r}}_{i} = \dfrac{\partial H}{\partial{\boldsymbol{p}}_{i}},\; \; \; \dot{\boldsymbol{p}}_{i} = -\dfrac{\partial H}{\partial {\boldsymbol{r}}_{\rm{i}}}, \end{array} $$ (1) 其中:
$ H = \sum_{i}H_{i} $ 是系统的总哈密顿量;第$ i $ 个粒子的哈密顿量由动能和势能构成$ H_{i} = E_{i}^{\rm{kin}}+U_{i} $ 。默认版本的UrQMD模型中势能包含两体Skyrme势能、三体Skyrme势能、Yukawa势能、Pauli势能和库仑势能[36-37]。在几个GeV以上能区的重离子碰撞中Yukawa势能、Pauli 势能对整个动力学演化过程影响较小[38],因此在本文的研究中被忽略。密度依赖的Skyrme势能
$ U_{\rm{Skyrme}} $ 可以通过密度依赖的单粒子势得到并表达为$$ \begin{array}{l} U_{\rm{Skyrme}} = \alpha\left(\dfrac{\rho_{{\rm{b}}}}{\rho_{0}}\right)+\beta\left(\dfrac{\rho_{{\rm{b}}}}{\rho_{0}}\right)^{\gamma}, \end{array} $$ (2) 其中:
$ \rho_{0} = 0.16\; \text{fm}^{-3} $ 为核物质饱和密度;$ \,\rho_{{\rm{b}}} $ 为重子密度。通过选取不同的势能参数可以给出不同的状态方程。鉴于目前人们对高密区核物质状态方程的软硬尚未取得统一的认知[12],本文采用不可压缩系数$ K_0 = 200 $ MeV和$ K_0 = 380 $ MeV两种较软和较硬的状态方程,相应的参数如表1中所列。需要指出的是,本文暂时没有在平均场中考虑π介子-核子相互作用势,因为致密核物质中的π介子-核子相互作用势目前为止还没有得到很好的理解,尚存在一定的争议[39-42]。而且,在我们之前的工作中[43-44],通过在UrQMD模型中引入不同强度的πN相互作用势,发现π介子的集体流及其中心度、快度依赖的实验数据支持一个较弱的πN相互作用势。表 1 Skyrme势能参数
参数 Hard EoS Soft EoS $ \alpha $ −124 −356 $ \beta $ 71 303 $ \gamma $ 2.0 1.17 除了上述基于Skyrme模型给出的EoS外,基于考虑不同强相互作用相变模式的手征平均场(Chiral Mean Filed, CMF)模型的EoS也被引入到了UrQMD模型中[23, 34-35, 45],通过基于CMF模型得到的平均每重子能量计算出粒子坐标和动量时空演化所需要的平均场势能[46],通过改变势能极小值点所处的密度区可以引入在不同密度区发生强子相与QGP相的一阶相变[23, 34-35]。
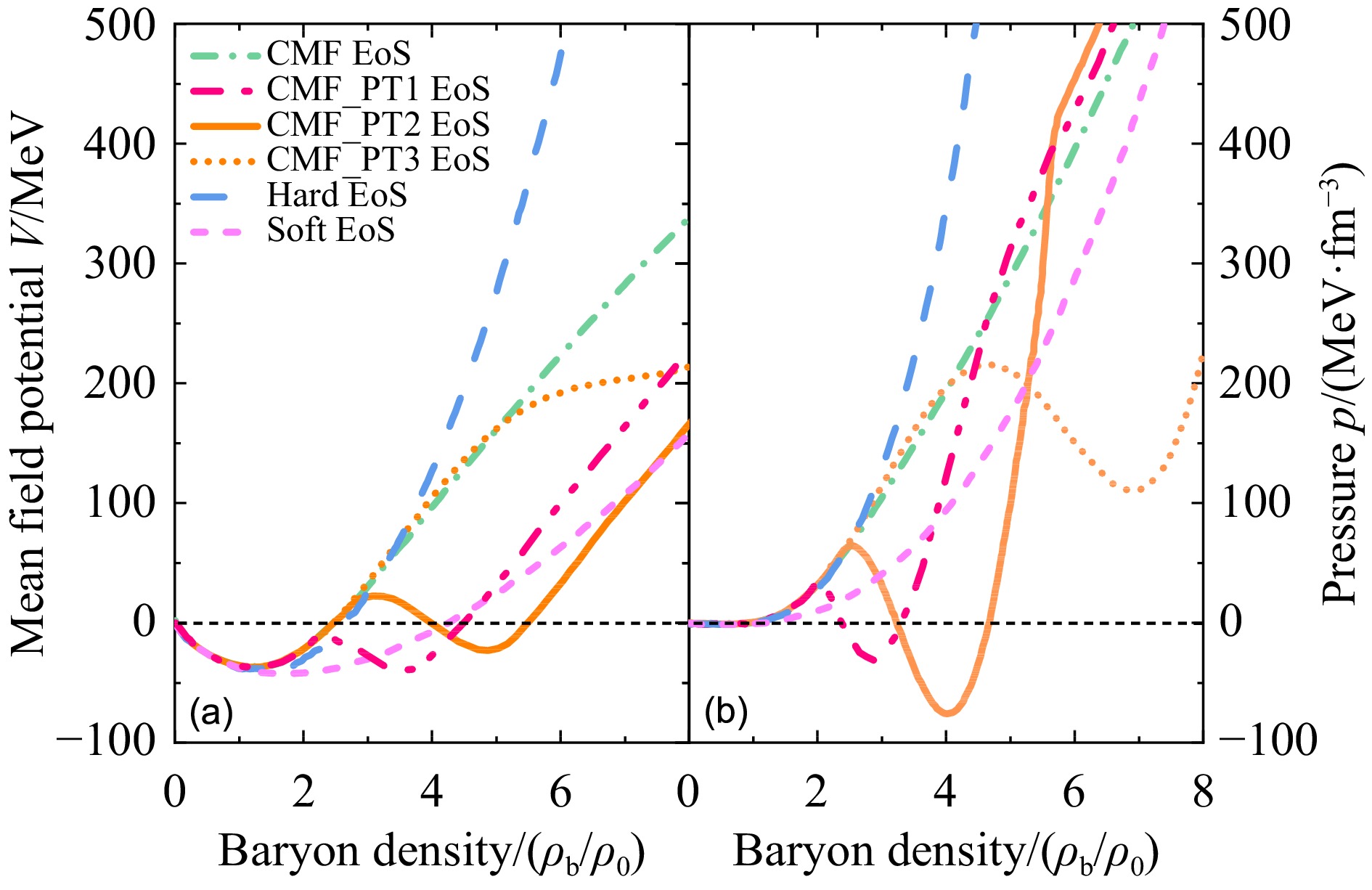
图1(a)展示了不同EoS给出的平均场势随重子密度的变化情况。由于根据压强来讨论核物质状态方程的属性更加具有指导意义且清晰明了,因此图1(b)展示了不同EoS下压强随重子密度的变化,其中压强计算公式为[35]
$$ \begin{array}{l} P(\rho_{\rm{b}},T) = P^{\rm id}(\rho_{\rm{b}},T) + \displaystyle\int\nolimits_0^{\rho_{\rm{b}}} \rho' \dfrac{\partial U(\rho')}{\partial \rho'} {\rm{d}}\rho', \end{array} $$ (3) 这里
$P^{\rm id}(\rho_{\rm{b}},T)$ 是强子的理想费米气体压强;$ U(\rho_{\rm{b}}) $ 是密度依赖的单粒子势能。图1中,标准的CMF EoS含有从强子气到QGP的平滑过渡相变,CMF$ \_ $ PT EoSs 中含有从强子气到QGP的一阶相变,其中CMF$ \_ $ PT1 EoS中的QCD一阶相变发生在低重子密度区,CMF$ \_ $ PT3 EoS中的QCD一阶相变发生在高重子密度区,CMF_PT2 EoS中的QCD一阶相变发生的密度区位于二者之间。在参考文献[35]中,作者探究了不同EoS对集体流的影响,通过与实验数据的比较排除了在$ 4 \rho_{0} $ 以下发生强相互作用相变的可能性,即排除了CMF_PT1 EoS。因此,接下来我们将重点研究CMF、CMF_PT2、CMF_PT3、Hard 和Soft EoSs对两π介子HBT关联的影响。 -
本文将基于UrQMD模型,通过以下三步利用两π介子HBT关联抽取表征粒子发射源时空属性的HBT半径及参数。首先,利用UrQMD模型获得冻结点的π介子相空间信息,这里的冻结点指的是动力学冻结点,即最后一次发生相互作用(碰撞或者衰变)的时空点。然后,将粒子在冻结点的坐标和四动量作为Correlation After-Burner(CRAB)
1 模型的输入量构建关联函数:$$ \begin{array}{l} C({\boldsymbol{k}},{\boldsymbol{q}}) = 1+\dfrac{\displaystyle\int {\rm{d}}^4x_1 {\rm{d}}^4x_2 S(x_1,{\boldsymbol{p}}_1) S(x_2,{\boldsymbol{p}}_2) |\phi({\boldsymbol{q}}, {\boldsymbol{r}})|^2} {{\displaystyle\int {\rm{d}}^4x_1 S(x_1,{\boldsymbol{p}}_1)}{\displaystyle\int {\rm{d}}^4x_2 S(x_2,{\boldsymbol{p}}_2)}}, \end{array} $$ (4) 这里
$ {\boldsymbol{q}} = {\boldsymbol{p}}_1-{\boldsymbol{p}}_2 $ 和$ {\boldsymbol{k}} = ({\boldsymbol{p}}_{1}+{\boldsymbol{p}}_{2})/2 $ 分别是两粒子相对动量和平均动量。$ S(x,{\boldsymbol{p}}) $ 表示从时空点$ x = ({\boldsymbol{r}}, t) $ 处发射动量为$ {\boldsymbol{p}} $ 的粒子的概率,它包含了发射源的时空信息。两粒子的相对波函数$ \phi({\boldsymbol{q}}, {\boldsymbol{r}}) $ 包含粒子间的末态相互作用信息以及量子统计信息。最后,采用三维高斯函数拟合构建的关联函数,提取出粒子发射源的三维半径:
$$ \begin{split} C(q_{\rm{L}},q_{\rm{O}},q_{\rm{S}}) = \;&N\left[1+\lambda \text{exp}\left(-R_{\rm{L}}^2q_{\rm{L}}^2-R_{\rm{O}}^2q_{\rm{O}}^2 \right.\right. - \\ &\left.\left. R_{\rm{S}}^2q_{\rm{S}}^2-2R_{{\rm{OL}}}^2q_{\rm{O}}q_{\rm{L}}\right)\right], \end{split} $$ (5) 其中:
$ N $ 为归一化因子;$ \lambda $ 是相干因子。这里我们采用纵向协变运动坐标系(the longitudinal comoving system, LCMS)进行三维分析。粒子对的相对动量$ q $ 被分解为Out、Side、Long三个方向,其中纵轴Long (L)沿着束流方向,Out(O)轴与粒子对的横向动量方向${\boldsymbol{k}}_T = ({\boldsymbol{p}}_{\rm{T1}}+ {\boldsymbol{p}}_{\rm{T2}})/2$ 平行,Side(S)轴与Long轴及Out轴垂直。当研究对象为带电粒子时,构建关联函数的过程中必须考虑末态相互作用中的库仑相互作用,同时在拟合过程中也应当进一步考虑库仑修正[23, 47-48]。本文主要研究目标为π介子,因此,为了和实验数据进行严格的对比,进而抽取更为可靠的核物质属性信息,在分析过程中我们采用和实验分析[28-29]一样的Bowler-Sinyukov方法来考虑库仑相互作用的修正[49],则式(5)变为
$$ \begin{split} C(q_{\rm{L}},q_{\rm{O}},q_{\rm{S}}) = & N\Big\{(1-\lambda)+\lambda K_{\rm{C}}(q_{\rm{inv}},R_{\rm{inv}})\Big[1+\text{exp}\big(-R_{\rm{L}}^2q_{\rm{L}}^2 -\\ & R_{\rm{O}}^2q_{\rm{O}}^2-R_{\rm{S}}^2q_{\rm{S}}^2-2R_{\rm{OL}}^2q_{\rm{O}}q_{\rm{L}}\big)\Big]\Big\}, \\[-12pt] \end{split} $$ (6) 其中
$ K_{\rm{C}} $ 为$ q_{\rm{inv}} $ 和$ R_{\rm{inv}} $ 依赖的库仑修正因子,不变相对动量$ q_{\rm{inv}} $ 定义为$$ \begin{array}{l} q^{}_{\rm{inv}} = \dfrac{1}{2}\sqrt{({\boldsymbol{p}}_1 - {\boldsymbol{p}}_2)^2-(E_1-E_2)^2}。 \end{array} $$ (7) 通过拟合得到的
$ R_{\rm{L}} $ 、$ R_{\rm{O}} $ 和$ R_{\rm{S}} $ 分别对应三个方向的HBT半径;$ R_{\rm{OL}} $ 为交叉项,通常在分析对称碰撞体系中大快度区间的粒子关联时发挥作用。 -
图2展示了碰撞能量为
$ \sqrt{s_{\rm{NN}}} = 4.5 $ GeV的Au+Au中心(0~10%)碰撞中π−π−的三维HBT关联函数,理论计算均采用Hard EoS模式,红色圆点为STAR的实验数据[29]。图2(a~c)主要展示了粒子冻出前库仑相互作用的影响,即在CRAB分析中不考虑末态相互作用中的库仑修正,而在UrQMD模拟过程中分别考虑(黑色方块)和不考虑(绿色菱形)库仑相互作用。可以看出,冻出前库仑相互作用(即UrQMD模型模拟过程中的库仑相互作用)对π−π−关联函数的影响很弱,这与文献[26, 48]的结论一致。图2(d~f)展示的是在UrQMD模拟过程中考虑库仑相互作用,而在CRAB分析中分别考虑(蓝色三角)和不考虑(黑色方块)末态相互作用中库仑修正的结果。可以看到,在考虑了末态相互作用中的库仑相互作用后,π−π−的HBT关联函数能够更好地描述实验数据。此外,图中给出了一维拟合结果(蓝色实线),拟合得到的Adj. R-Square ($ R^2 $ )值和三维HBT半径分别展示在对应的图中,可以看出关联函数的计算值和实验值均能通过一维高斯形式得到较为完美的拟合。因此,上述关联函数的构建和拟合方法可以用来提取表征粒子发射源时空属性的HBT半径。
图 2 碰撞能量为
$ \sqrt{s_{\rm{NN}}} = 4.5 $ GeV的Au+Au中心(0~10%)碰撞中,π−π−介子对的HBT关联函数(实验数据来自于STAR合作组[29])图3展示了碰撞能量为
$ \sqrt{s_\mathrm{NN}} = 2.4 $ GeV 下Au+Au中心(0~10%)碰撞中横动量$ k_{\rm{T}} $ 依赖的HBT半径。为了阐明势修正及EoS对π介子发射源时空属性的影响,计算过程中分别采用了不含势修正的Cascade 模式和含有势修正的Hard EoS、Soft EoS模式,相应的结果分别由灰色短划线、蓝色实线、红色点线分别表示,HADES实验组的实验数据由红色五角星表示。首先,相较于Cascade模式,考虑势修正后的平均场模式下的结果能够较好地描述实验数据。其次,由于平均场势修正提供了更强的粒子间的时间-空间关联,导致大$ k_{\rm{T}} $ 区间内的$ R_{\rm{O}} $ 被压低,小$ k_{\rm{T}} $ 区间的$ R_{\rm{S}} $ 被抬升。最后,随着EoS硬度的增加(不可压缩系数$ K_{\rm{0}} $ 数值的增大),密度依赖的强子相互作用带来更大的压强并进一步增强粒子之间的时间-空间的关联性,大(小)$ k_{\rm{T}} $ 区间内的$ R_{\rm{O}} $ ($ R_{\rm{S}} $ )被进一步压低(抬升)。基于上述分析,可以看出π介子发射源的HBT半径对EoS比较敏感,因此可以用来约束高密区的EoS。
图 3
$ \sqrt{s_\mathrm{NN}} = 2.4 $ GeV下Au+Au中心(0~10%)碰撞中横动量$ k_{\rm{T}} $ 依赖的HBT半径$ R_{\rm{O}} $ ,$ R_{\rm{S}} $ 和$ R_{\rm{L}} $ 。实验数据来自于HADES合作组[28]此外,通过束流能量扫描还发现密度依赖的势修正的效应随着束流能量的升高而逐渐降低。为了清晰地展示势修正对π介子发射源HBT半径的影响及其随束流能量的变化,图4展示了不同能量下Cascade模式与Hard EoS模式的HBT的半径之比。左图为大横动量(
$ 275\leqslant k_{\rm{T}}\leqslant 375 $ MeV/c)区间$ R_{\rm{O}} $ 的比值随碰撞能量的变化,中间图和右图分别为小横动量($75\leqslant k_{\rm{T}}\leqslant 175$ MeV/$ c $ )区间$ R_{\rm{L}} $ 、$ R_{\rm{S}} $ 的比值随碰撞能量的变化。发现$ R_{\rm{O}} $ 的比值大于1并且随着束流能量的升高而下降,$ R_{\rm{L}} $ 和$ R_{\rm{S}} $ 的比值随着碰撞能量的升高而上升,即考虑势修正后的大$ k_{\rm{T}} $ 区间内的$ R_{\rm{O}} $ 和小$ k_{\rm{T}} $ 区间的$ R_{\rm{L}} $ 、$ R_{\rm{S}} $ 在数值上分别小于或大于Cascade模式的结果;同时随着束流能量的升高,势修正的效应逐渐减弱,两种模式下结果之间的差异也逐渐减小,这与正反粒子椭圆流之间的流差随着束流能量的升高而逐渐降低一致[50]。 -
为了更加清晰地展示势修正对两π介子HBT关联及π介子发射源时空属性的影响及其随碰撞能量的变化,图5比较了不同EoS下π−介子发射源的半径
$ R_{\rm{O}}/R_{\rm{S}} $ 之比随碰撞能量的变化,并且与实验数据进行了对比。首先,通过对比Cascade模式和Hard EoS模式下的结果发现,引入强子相互作用势后,
$ R_{\rm{O}}/R_{\rm{S}} $ 的值降低,并且能够较好地描述现有的实验数据,同时二者之间的差异随着碰撞能量的升高逐渐减小,这意味着π介子的HBT半径参数敏感于核物质状态方程,但随着碰撞能量的升高,强子势的效应逐渐减弱。其次,对比Hard EoS和CMF EoSs的结果,发现在该能区Hard EoS、CMF EoS和CMF
$ \_ $ PT3 EoS给出了非常相似的结果。因为在所研究的碰撞能量范围内,0~10$ \% $ 的Au+Au中心碰撞中的重子密度范围约为$ 2\sim5\rho_{0} $ 。结合图1发现,当$ \rho_{{\rm{b}}}<3\rho_{0} $ 时,CMF、CMF$ \_ $ PT2 和 CMF_PT3 EoSs给出了和Hard EoS几乎相同的压强,因此在$ \sqrt{s_\mathrm{NN}} = 2.4 $ GeV时,除了Cascade模式外,其余含有势修正的模式给出了几乎一样的$ R_{\rm{O}}/R_{\rm{S}} $ ;而在重子密度小于$ 5\rho_{0} $ 区域内,CMF和CMF$ \_ $ PT3 EoSs给出了和Hard EoS几乎相同的压强,因此在所研究的能量范围内三者给出了相似的$ R_{\rm{O}}/R_{\rm{S}} $ 随碰撞能量的变化。最后,对比不同CMF EoSs的结果,发现随着碰撞能量的增大,相比于CMF和CMF
$ \_ $ PT3 EoSs模式的结果,由于CMF$ \_ $ PT2 EoS中强子气到QGP相的一阶相变发生在相对较低的密度区间,CMF$ \_ $ PT2 EoS模式下的结果随碰撞能量的升高逐渐增大并最终靠近Cascade模式的结果。这里需要特别指出的是,Cascade模式可以看做一种非常软的EoS模式,即发生了相变的模式。因此在相对较高的能量下Cascade的结果与CMF$ \_ $ PT2的结果相似。综上所述,可以得出结论:直到4~5
$ \rho_{0} $ 附近,π−介子发射源的HBT半径参数$ R_{\rm{O}}/R_{\rm{S}} $ 对EoS非常敏感;现有的HBT实验数据支持一个在低密度时表现为相对较硬然后在高密区由于相变而逐渐软化的EoS;同时在所研究的能量范围内,CMF$ \_ $ PT3 EoS中强子气到QGP相之间一阶相变发生所需要的高密条件从未真正达到。 -
为了理解不同EoS对两π介子HBT关联及π介子发射源HBT半径的影响,接下来将对不同EoS下π介子的冻出时间进行系统的分析。图6给出了Au+Au中心碰撞(0~10%)中π−介子的平均冻出时间随碰撞能量的变化。首先,可以看到在低碰撞能量(
$ \sqrt{s_\mathrm{NN}} = 2.4 $ GeV)时,考虑势修正后(Hard, CMF, CMF$ \_ $ PT2和CMF$ \_ $ PT3) 的π−介子的平均冻出时间基本一致,并且早于Cascade模式下π−介子的平均冻出时间,这是因为在该能量下CMF、CMF$ \_ $ PT2和CMF$ \_ $ PT3 EoSs 给出了和Hard EoS相似的密度依赖的排斥的势相互作用,而硬的密度依赖的势相互作用将提供较强的压强(排斥)并带来更强的膨胀,因此π−介子被更早地冻出。其次,随着碰撞能量的升高,在CMF$ \_ $ PT2 EoS模式下,由于相变的发生,状态方程逐渐软化,因此其结果逐渐靠近Cascade模式下的结果。此外,在$ \sqrt{s_\mathrm{NN}} = 7.7 $ GeV时,CMF和CMF$ \_ $ PT3 EoSs的结果位于Hard EoS和CMF$ \_ $ PT2 EoS的结果之间,这是因为在该碰撞能量下CMF和CMF$ \_ $ PT3 EoSs比Hard EoS软,但比CMF$ \_ $ PT2 EoS硬,如图1中所示。有意思的是,在图6中无论是否考虑强子势或者相变,π−介子的平均冻出时间
$ \langle t\rangle $ 随能量的变化在$ \sqrt{s_\mathrm{NN}}\approx $ 4 GeV时均出现了极小值点。同时,我们注意到在现有的HBT数据分析中,π介子发射源的体积$ V_{\rm{f}} = (2\pi)^{3/2}R_{\rm{side}}^{2} R_{\rm{long}} $ 的激发函数也在$ \sqrt{s_\mathrm{NN}}\approx4 $ GeV时呈现出了相似结构[27-28]。我们提出以下两种原因来解释这一极小值谜团。第一,粒子产生机制的转变。如图7(a)所示,在UrQMD模型中,当束流能量$ \sqrt{s_\mathrm{NN}}\lesssim4 $ GeV时,π介子的产生机制主要以共振衰变为主,随着能量的升高,通过弦激发和碎裂产生的π介子逐渐增多,并且更多的π介子将在经历过再散射后被冻出,因此平均冻出时间将会增加[36, 51]。这里需要指出,在高能量重离子碰撞,π介子的产生及演化过程非常复杂。一方面,弦激发和碎裂可以直接产生π介子并被直接冻出或者通过MM、MB相互作用重新产生弦并进一步碎裂,同时弦激发和碎裂也可以产生共振态并通过共振衰变产生π介子或者通过BB相互作用重新产生弦并进一步碎裂。另一方面,共振衰变产生的π介子和共振态也可能经历上述过程。第二,自由度的变化。如图7(b)所示,在考虑和不考虑势相互作用的两种模式下,Au+Au中心碰撞(b=0 fm)中重子-介子多重数比值随碰撞能量的变化表现一致,并且在$ \sqrt{s_\mathrm{NN}}\approx4 $ GeV时$ N_{{\rm{baryon}}}\approx N_{{\rm{meson}}} $ 。因此,在π−介子的平均冻出时间和粒子发射源体积的激发函数上所体现出来的最小值可能由不同的粒子产生机制之间的竞争与改变或重子-重子相互作用与介子(重子)-介子相互作用的竞争与转变来解释。 -
基于UrQMD模型,本文讨论了密度依赖的核物质状态方程和相变对两π介子HBT关联和π介子发射源的HBT半径参数的影响。主要结论如下:首先,厘清了π介子冻出前后库仑相互作用对π介子对的HBT关联函数以及HBT半径的影响。发现冻出前的库仑相互作用对π−π−的HBT半径和
$ R_{{\rm{O}}}/R_{{\rm{S}}} $ 之比有着很弱的影响,而末态库仑相互作用却对π−π−的HBT关联函数有着较强的影响。其次,通过对比Cascade、Hard EoS和Soft EoS模式下的结果发现,密度依赖的排斥的势修正会进一步增强粒子之间的时空关联性,导致大$ k_{{\rm{T}}} $ 区间的$ R_{{\rm{O}}} $ 降低,小$ k_{{\rm{T}}} $ 区间的$ R_{{\rm{S}}} $ 上升,从而导致$ R_{{\rm{O}}}/R_{{\rm{S}}} $ 之比降低并且能够较好地描述实验数据。最后,在$ 4\sim5 $ 倍饱和密度以下,HBT半径和$ R_{{\rm{O}}}/R_{{\rm{S}}} $ 之比敏感于核物质状态方程,通过与实验数据的比较,发现现有的HBT实验数据支持一个在相对低密区($ \lesssim4\rho_{0} $ )表现偏硬,然后在高密区由于相变而逐渐软化的核物质状态方程,并且排除了在$ \lesssim4\rho_{0} $ 以下发生一阶相变的可能性。但是,在本文所研究的碰撞能量范围内,实验数据依旧存在很大的不确定性。因此,一方面需要更加精确的实验数据,相信未来德国GSI上FAIR的CBM实验和俄罗斯杜布纳NICA上的MPD实验以及美国RHIC-STAR固定靶项目将提供更加精确的实验数据;另一方面也需要更多的理论研究来探讨模型等不确定性,如初始化结构效应、量子效应、粒子势相互作用及动力学效应对粒子关联效应所带来的影响,其中介子(K、π)-核子势相互作用对两粒子HBT关联的影响的研究正在进行中。
The High-density Equation of State in Heavy-ion Collisions: Constraints from Two-pion HBT Correlation
-
摘要: 高重子密度区核物质状态方程的研究是当前核物理研究的前沿热点问题之一。利用极端相对论量子分子动力学(UrQMD)模型,以两π介子Hanbury-Brown-Twiss(HBT)关联为例讨论了2~5倍饱和密度(
$\rho_{0}$ )区核物质状态方程对两粒子关联效应的影响。通过使用不同的核物质状态方程,展示了密度依赖的势相互作用以及相变对两π介子HBT关联和π介子发射源时空属性的影响。结果显示,在$\sim 5 \rho_{0}$ 以下,π介子发射源的HBT半径及参数敏感于核物质状态方程的软硬,通过与实验数据的比较,现有的HBT半径实验数据排除了$\sim 4\rho_{0}$ 以下发生一阶相变的可能性,并支持一个在低密区($\lesssim4\rho_{0}$ )表现偏硬,且在高密区由于相变而逐渐软化的核物质状态方程。研究结果强调了π介子发射源的HBT半径及参数敏感于核物质状态方程的软硬,可用于理解和约束高重子密度区的核物质状态方程。Abstract: The investigation of the equation of state(EoS) of nuclear matter, especially at high baryon densities is one of the hot topics in the frontier of nuclear physics. The impact of the EoS at 2~5 times saturation density$\rho_{0}$ on the two-particle correlation is discussed with the ultra-relativistic quantum molecular dynamics(UrQMD) model. Focusing on the two π Hanbury-Brown-Twiss(HBT) correlations, by adopting different EoSs, the effects of potential interaction and phase transition on the HBT correlation and the spatiotemporal properties of the emission source of π are investigated. The results show that below$\sim5 \rho_{0}$ , the HBT radius and parameters are sensitive to the stiffness of the EoS. By comparing with the experiment data, first-order phase transition with a significant softening of the equation of state below 4 times nuclear saturation density can be excluded using HBT data, and the available data on the HBT radii in the investigated energy region favor a relatively stiff EoS at low densities, which then turns into a soft EoS at high densities. These results highlight that the pion's HBT radius and parameters are sensitive to the stiffness of the equation of state, and can be used to constrain and understand the equation of state in the high baryon density region.-
Key words:
- heavy-ion collisions /
- equation of state /
- transport model /
- HBT correlation
-
图 2 碰撞能量为
$ \sqrt{s_{\rm{NN}}} = 4.5 $ GeV的Au+Au中心(0~10%)碰撞中,π−π−介子对的HBT关联函数(实验数据来自于STAR合作组[29])图 3
$ \sqrt{s_\mathrm{NN}} = 2.4 $ GeV下Au+Au中心(0~10%)碰撞中横动量$ k_{\rm{T}} $ 依赖的HBT半径$ R_{\rm{O}} $ ,$ R_{\rm{S}} $ 和$ R_{\rm{L}} $ 。实验数据来自于HADES合作组[28]表 1 Skyrme势能参数
参数 Hard EoS Soft EoS $ \alpha $ −124 −356 $ \beta $ 71 303 $ \gamma $ 2.0 1.17 -
[1] 马余刚, 许怒, 刘峰. 中国科学: 物理学 力学 天文学, 2020, 50(11): 112009. doi: 10.1360/SSPMA-2020-0302 MA Y G, XU N, LIU F. Sci Sin-Phys Mech Astron, 2020, 50(11): 112009. (in Chinese) doi: 10.1360/SSPMA-2020-0302 [2] 马余刚. 科技导报, 2023, 41(1): 14. doi: 10.3981/j.issn.1000-7857.2023.01.002 MA Y G. Sci Tech Rev, 2023, 41(1): 14. (in Chinese) doi: 10.3981/j.issn.1000-7857.2023.01.002 [3] HALASZ A M, JACKSON A D, SHROCK R E, et al. Phys Rev D, 1998, 58: 096007. doi: 10.1103/PhysRevD.58.096007 [4] BAZAVOV A, et al. Phys Rev D, 2012, 85: 054503. doi: 10.1103/PhysRevD.85.054503 [5] PANDAV A, MALLICK D, MOHANTY B. Prog Part Nucl Phys, 2022, 125: 103960. doi: 10.1016/j.ppnp.2022.103960 [6] BZDAK A, ESUMI S, KOCH V, et al. Phys Rept, 2020, 853: 1. doi: 10.1016/j.physrep.2020.01.005 [7] GUNKEL P J, FISCHER C S. Phys Rev D, 2021, 104(5): 054022. doi: 10.1103/PhysRevD.104.054022 [8] 尹伊. 核技术, 2023, 46(4): 040010. doi: 10.11889/j.0253-3219.2023.hjs.46.040010 YIN Y. Nucl Tech, 2023, 46(4): 040010. (in Chinese) doi: 10.11889/j.0253-3219.2023.hjs.46.040010 [9] 肖志刚. 物理, 2020, 49(3): 137. doi: 10.7693/wl20200301 XIAO Z G. Physics, 2020, 49(3): 137. (in Chinese) doi: 10.7693/wl20200301 [10] 罗晓峰, 刘峰, 许怒. 物理, 2021, 50(2): 98. doi: 10.7693/wl20210205 LUO X F, LIU F, XU N. Physics, 2021, 50(2): 98. (in Chinese) doi: 10.7693/wl20210205 [11] 张宇, 张定伟, 罗晓峰. 核技术, 2023, 46(4): 040001. doi: 10.11889/j.0253-3219.2023.hjs.46.040001 ZHANG Y, ZHANG D W, LUO X F. Nucl Tech, 2023, 46(4): 040001. (in Chinese) doi: 10.11889/j.0253-3219.2023.hjs.46.040001 [12] SORENSEN A, AGARWA A, BROWNET K W, et al. Prog Part Nucl Phys, 2024, 134: 104080. doi: 10.1016/j.ppnp.2023.104080 [13] ABLYAZIMOV T, ABUHOZA A, ADAKET R P, et al. Eur Phys J A, 2017, 53(3): 60. doi: 10.1140/epja/i2017-12248-y [14] ABGARYAN V, KADO R A, AFANASYEVET S V, et al. Eur Phys J A, 2022, 58(7): 140. doi: 10.1140/epja/s10050-022-00750-6 [15] ZHOU X H. Nucl Phys Rev, 2018, 35(4): 339. doi: 10.11804/NuclPhysRev.35.04.339 [16] 徐骏. 中国科学: 物理学 力学 天文学, 2019, 49(7): 072001. doi: 10.1360/SSPMA-2019-0068 XU J. Sci Sin-Phys Mech Astron, 2019, 49(7): 072001. (in Chinese) doi: 10.1360/SSPMA-2019-0068 [17] WOLTER H, COLONNA M, COZMA D, et al. Prog Part Nucl Phys, 2022, 125: 103962. doi: 10.1016/j.ppnp.2022.103962 [18] BLEICHER M, BRATKOVSKAYA E. Prog Part Nucl Phys, 2022, 122: 103920. doi: 10.1016/j.ppnp.2021.103920 [19] HANBURY B R, TWISS R Q. Nature, 1956, 178: 1046. doi: 10.1038/1781046a0 [20] HANBURY B R, TWISS R Q. Phil Mag Ser 7, 1954, 45: 663. doi: 10.1080/14786440708520475 [21] PRATT S. Phys Rev Lett, 1984, 53: 1219. doi: 10.1103/PhysRevLett.53.1219 [22] LISA M A, PRATT S, SOLTZ R, et al. Ann Rev Nucl Part Sci, 2005, 55: 357. doi: 10.1146/annurev.nucl.55.090704.151533 [23] LI P C, STEINHEIMER J, REICHERT T, et al. Sci China Phys Mech Astron, 2023, 66(3): 232011. doi: 10.1007/s11433-022-2041-8 [24] PRATT S. Phys Rev D, 1986, 33: 1314. doi: 10.1103/PhysRevD.33.1314 [25] BERTSCH G, GONG M, TOHYAMA M. Phys Rev C, 1988, 37: 1896. doi: 10.1103/PhysRevC.37.1896 [26] LI P C, WANG Y J, LI Q F, et al. Sci China Phys Mech Astron, 2023, 66(2): 222011. doi: 10.1007/s11433-022-2026-5 [27] ADAMCZYK L, ADKINS J K, AGAKISHIEV G, et al. Phys Rev C, 2015, 92(1): 014904. doi: 10.1103/PhysRevC.92.014904 [28] ADAMCZEWSKI M J, ARNOLD O, BEHNKEET C. et al. Eur Phys J A, 2020, 56(5): 140. doi: 10.1140/epja/s10050-020-00116-w [29] ABDALLAH M S, ADAM J, ADAMCZYK L, et al. Phys Rev C, 2021, 103(3): 034908. doi: 10.1103/PhysRevC.103.034908 [30] LI Q F, STEINHEIMER J, PETERSEN H, et al. Phys Lett B, 2009, 674: 111. doi: 10.1016/j.physletb.2009.03.012 [31] ZHANG C J, XU J. Phys Rev C, 2017, 96(4): 044907. doi: 10.1103/PhysRevC.96.044907 [32] BATYUK P, KARPENKO I, LEDNICKY R, et al. Phys Rev C, 2017, 96(2): 024911. doi: 10.1103/PhysRevC.96.024911 [33] ALQAHTANI M, STRICKLAND M. Phys Rev C, 2020, 102(6): 064902. doi: 10.1103/PhysRevC.102.064902 [34] OMANA K M, MOTORNENKO A, STEINHEIMER J, et al. Eur Phys J C, 2022, 82(5): 427. doi: 10.1140/epjc/s10052-022-10400-2 [35] STEINHEIMER J, MOTORNENKO A, SORENSEN A, et al. Eur Phys J C, 2022, 82(10): 911. doi: 10.1140/epjc/s10052-022-10894-w [36] BASS S A, BELKACEM M, BLEICHERET M, et al. Prog Part Nucl Phys, 1998, 41: 255. doi: 10.1016/S0146-6410(98)00058-1 [37] BLEICHER M, ZABRODIN E, SPIELES C, et al. J Phys G, 1999, 25: 1859. doi: 10.1088/0954-3899/25/9/308 [38] LI Q F, LI Z X. Mod Phys Lett A, 2012, 27: 1250004. doi: 10.1142/S0217732312500046 [39] XIE W J, SU J, ZHU L, et al. Phys Rev C, 2018, 97(6): 064608. doi: 10.1103/PhysRevC.97.064608 [40] ZHANG Z, KO C M. Phys Rev C, 2017, 95(6): 064604. doi: 10.1103/PhysRevC.95.064604 [41] FENG Z Q. Phys Rev C, 2016, 94: 054617. doi: 10.1103/PhysRevC.94.054617 [42] XU J, KO C M, OH Y. Phys Rev C, 2010, 81: 024910. doi: 10.1103/PhysRevC.81.024910 [43] 邹丽艳, 郭琛琛, 李淼, 等. 中国科学: 物理学 力学 天文学, 2017, 47(12): 122001. doi: 10.1360/SSPMA2016-00446 ZHOU L Y, GUO C C, LI M, et al. Sci Sin-Phys Mech Astron, 2017, 47(12): 122001. (in Chinese) doi: 10.1360/SSPMA2016-00446 [44] LIU Y Y, WANG Y J, LI Q F, et al. Phys Rev C, 2018, 97(3): 034602. doi: 10.1103/PhysRevC.97.034602 [45] REICHERT T, SAVCHUK O, KITTIRATPATTANA A, et al. Phys Lett B, 2023, 841: 137947. doi: 10.1016/j.physletb.2023.137947 [46] MOTORNENKO A, STEINHEIMER J, VOVCHENKO V, et al. Phys Rev C, 2020, 101(3): 034904. doi: 10.1103/PhysRevC.101.034904 [47] LI Q F, BLEICHER M, STOCKER H. Phys Lett B, 2008, 659: 525. doi: 10.1016/j.physletb.2007.11.080 [48] LI Q F, BLEICHER M, STOCKER H. Phys Lett B, 2008, 663: 395. doi: 10.1016/j.physletb.2008.04.024 [49] ADAMCZEWSKI M J, et al. Phys Lett B, 2019, 795: 446. doi: 10.1016/j.physletb.2019.06.047 [50] LI P C, WANG Y J, STEINHEIMER J, et al. Mod Phys Lett A, 2020, 35(35): 2050289. doi: 10.1142/S0217732320502892 [51] LI Q F, SHEN C W, BLEICHER M. Central Eur J Phys, 2012, 10: 1131. doi: 10.2478/s11534-012-0093-0 -












 下载:
下载:











































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号