-
根据现有理论,当物质的密度足够高时,构成质子与中子的夸克会发生退禁闭相变,由此形成的物质我们称之为夸克物质。如果夸克物质只是由u、d两种夸克构成(为满足电中性条件,此时还可能有电子e和缪子μ),我们称其为u-d夸克物质;如果除u、d夸克外,还有s夸克,我们称其为奇异夸克物质。
有研究猜想奇异夸克物质可能是量子色动力学(QCD)的真正基态[1-4],从而可以稳定地存在于宇宙当中。夸克物质是强相互作用占主导的系统,理论上我们可以从强相互作用的基本理论QCD出发对其进行详细的研究。然而,因为夸克在低密度(可能是中子星内部相关的密度)时的非微扰效应,直接用微扰计算并不可靠;另外,由于符号问题,格点QCD在有限化学势下的计算无法进行。所以,目前人们大多采用各种唯象模型对夸克物质进行研究,例如质量密度依赖模型[5-9]、夸克集团模型[10-11]、准粒子模型[12-13]、NJL模型[14]等。
如果采用唯象模型进行研究,其中非常重要的一点是确定模型参数的取值范围。根据夸克物质可以稳定存在的假设,最常用的约束条件为夸克物质的平均重子能量小于930 MeV。另外,如果考虑奇异夸克物质的稳定性,还必须要求在同一理论框架下u-d夸克物质的平均重子能量大于930 MeV。近些年天文观测也取得了若干重要进展,特别是对脉冲星质量的精确测量发现PSR J1614-2230和PSR J0348+0432的质量分别达到了(1.97±0.04)$ {{M}}_\odot $[15](更精确的测量给出的结果是(1.928 ± 0.017)$ {{M}}_\odot $[16])和(2.01 ± 0.04)$ {{M}}_\odot $[17]。另外,对PSR J0740 + 6620的近期测量结果显示其质量达到了$ 2.14^{+0.20}_{-0.18} $$ {{M}}_\odot $[18](最近更新的数据为$ 2.08^{+0.07}_{-0.07} $$ {{M}}_\odot $[19])。总之,它们的质量接近甚至超过了2倍太阳质量。除此之外,随着引力波探测设备和技术的升级,越来越多的引力波事件被发现。特别是在双中子星并合事件GW170817[20]中测量到潮汐形变$ \varLambda_{1.4} = 190^{390}_{-120} $[21],这为进一步限制致密物质的状态方程提供了重要信息。在下面的研究中我们将利用上述天文观测数据来约束夸克物质的状态方程。
就目前而言,对于核物质,虽然对称能在饱和密度以下和其附近的密度行为已经被很好地确定,但在超饱和密度下对称能密度行为的确定仍然是一个很大的挑战。在超饱和密度下,强相互作用物质可能发生相变,并可能出现各种新形式的物质。事实上,由于不同相的对称能项不同,同位旋效应相当显著[22]。与核物质相比,夸克物质的对称能研究相对更少[23-24]。
在本文中,我们将在等效质量模型[25]下考虑夸克间的同位旋效应[26],并结合上述约束条件来研究夸克物质的稳定窗口和对称能。本文的安排如下:在第1节简要介绍含有同位旋效应的等效粒子模型。第2节计算夸克物质的稳定窗口和对称能,并对结果进行讨论。最后,给出一个简单的总结。
-
在等效粒子模型中我们通过引入有效化学势$ \mu_i^* $可以将夸克物质的热力学势密度简单地写为
$$ \varOmega_{0}(\mu_i^*, m_i) = -\sum\limits_{i} \frac{g_{i}m_i^4}{24 \pi^{2}}f\left(\frac{\mu_i^*}{m_i}\right), $$ 其中:$ f(x) = x\sqrt{x^2-1}\left(x^2-\frac{5}{2}\right)+\frac{3}{2}{\rm{arch}}(x) $;$ g_i $是粒子简并度(对夸克有$ g_{\rm q} = 6 $,对电子有$ g_{\rm e} = 2 $);$ m_i $是同位旋依赖的等效粒子质量。另外,我们定义$ \nu_i = \sqrt{\mu_i^{*2}-m_i^2} $作为粒子的费米动量。根据基本的热力学关系$ \,\rho_{i} = -{\rm{d}} \varOmega_{0} / {\rm{d}} \mu_{i}^{*} $,我们可以很容易得到粒子数密度$ \,\rho_i $,
$$ \begin{split} \rho^{}_{i}=&- \frac{{\rm{d}}\varOmega_0}{{\rm{d}}\mu_i^*} =-\frac{\partial \varOmega_0}{\partial \mu_i^*} -\frac{\partial \varOmega_0}{\partial \nu_i}\frac{\partial \nu_i}{\partial \mu_i^*}=\frac{g_{i} \nu_{i}^{3}}{6 \pi^{2}} \\ =&\frac{g_{i}}{6 \pi^{2}}\left(\mu_{i}^{* 2}-m_{i}^{2}\right)^{3 / 2}。 \end{split} $$ (1) 为了考虑夸克之间的强相互作用,人们对等效粒子质量进行了不同形式的参数化[5, 8, 25, 27]。一般而言,在等效质量模型中粒子质量$ m_i $是重子数密度$ \,\rho_{\rm{b}} $的函数。因此,为了将同位旋效应包含在夸克物质的状态方程中,可以将同位旋不对称度参数$ \delta \equiv 3(\rho_{\rm{d}}-\rho_{\rm{u}})/(\rho_{\rm{d}}+\rho_{\rm{u}}) $引入粒子的质量标度中。在之前的文献中[27],$ m_i $被参数化为$m_{i}\left(\rho_{{\rm{b}}}, \delta\right) = m_{i 0}+D \rho_{{\rm{b}}}^{-1 / 3}-\tau_{i} \delta D_{I} \rho_{{\rm{b}}}^{\alpha}{\rm{e}}^{-\beta\rho_{{\rm{b}}}}$,其中$ \tau_i $是夸克在同位旋空间中的第三分量。在当前的研究中,我们采用之前工作中曾使用过的夸克质量标度[26],即
$$ \begin{split} m_i(\rho_{\rm{b}},\delta) = & m_{i0}+m_{{\rm{I}}i}(\rho_{\rm{b}},\delta) \\ = & m_{i0}+D \rho_{{\rm{b}}}^{-1 / 3}+C \rho_{{\rm{b}}}^{1 / 3}+C_{Ii} \delta^{2} \rho_{{\rm{b}}}, \end{split} $$ (2) 其中:$ m_{i0} $是夸克流质量;D是表征线性禁闭效应的禁闭参数;$C < 0$表示夸克间的单胶子交换作用[27];$C > 0$表示领头阶的微扰相互作用[25],$ C_{I{\rm{i}}} $($ C_I \equiv C_{I{\rm{u}}} = C_{I{\rm{d}}},C_{I{\rm{s}}} = 0 $)是同位旋强度依赖参数,其大小表示粒子质量对同位旋不对称度的依赖强度。此外我们注意到,在忽略夸克之间的电磁相互作用后此夸克质量标度满足u、d夸克间的交换对称性。
关于系统的能量密度E和压强P,它们分别由以下计算公式给出:
$$ E = \varOmega_{0}-\sum\limits_{i} \mu_{i}^{*} \frac{\partial \varOmega_{0}}{\partial \mu_{i}^{*}} = \sum\limits_{i} \frac{g_{i}m_i^4}{16 \pi^{2}}g\left(\frac{\mu_i^*}{m_i}\right), $$ (3) 其中:$ g(x) = x\sqrt{x^2-1}(2x^2-1)-{\rm{arch}}(x) $;
$$ P = -\varOmega_0+\rho_{\rm{b}}\sum\limits_j\frac{\partial \varOmega_0}{\partial m_j}\frac{\partial m_{{j}}}{\partial \rho_{\rm{b}}} +\sum\limits_{i,j}\rho_i\frac{\partial \delta}{\partial \rho_i}\frac{\partial \varOmega_0}{\partial m_j} \frac{\partial m_{{j}}}{\partial \delta}。 $$ (4) 根据同位旋不对称度$ \delta $的定义,我们容易得到$ \delta $对u夸克数密度$\,\rho_{\rm{u}}$和d夸克数密度$\,\rho_{\rm{d}}$的导数,
$$ \frac{\partial \delta}{\partial \rho_{\rm{u}}} = -\frac{6 \rho_{\rm{d}}}{(\rho_{\rm{d}}+\rho_{\rm{u}})^2}\ {\text{和}}\ \frac{\partial \delta}{\partial \rho_{\rm{d}}} = \frac{6 \rho_{\rm{u}}}{(\rho_{\rm{d}}+\rho_{\rm{u}})^2}。 $$ (5) 由此可以看出,压强计算式(4)右侧第三项求和后的结果为0。因此,压强计算公式可以化简为
$$ P = -\varOmega_0+\rho_{\rm{b}}\sum\limits_i\frac{\partial \varOmega_0}{\partial m_i}\frac{\partial m_i}{\partial \rho_{\rm{b}}}。 $$ (6) 为得到夸克物质的状态方程,我们可以求解以下方程组:
1) 电中性条件
$$ 2\rho_{\rm{u}}-\rho_{\rm{d}}-\rho_{\rm{s}}-3\rho_{\rm{e}} = 0, $$ (7) 2) 重子数守恒条件
$$ \rho_{\rm{b}} = \frac{1}{3}(\rho_{\rm{u}}+\rho_{\rm{d}}+\rho_{\rm{s}}), $$ (8) 3) $ \beta $-平衡条件
$$ \mu_{\rm{u}}+\mu_{\rm{e}} = \mu_{\rm{d}} = \mu_{\rm{s}}。 $$ (9) 需要强调的是,在以上$ \beta $-平衡条件中的化学势是夸克真实的化学势。如果只研究u-d夸克物质,则以上方程中不需要考虑奇异夸克s的贡献。为了求解以上方程,我们需要给出有效化学势与真实化学势的关系,即
$$ \begin{split} \mu_{i}= &\mu_{i}^{*}+\sum\limits_{j} \frac{\partial \varOmega_{0}}{\partial m_{j}} \frac{\partial m_{j}}{\partial \rho_{i}} \\= &\mu_i^*+\frac{1}{3}\sum\limits_j\frac{\partial \varOmega_0}{\partial m_j}\frac{\partial m_j}{\partial \rho_{\rm{b}}} +\frac{\partial \delta}{\partial \rho_i}\sum\limits_j\frac{\partial \varOmega_0}{\partial m_j}\frac{\partial m_j}{\partial \delta}。 \end{split} $$ (10) 关于对称能,根据定义有
$$ E_{{\rm{sym}}}(\rho_{\rm{b}},\rho_{\rm{s}}) = \frac{1}{2} \frac{\partial^2 E_{{\rm{uds}}}/\rho_{\rm{b}}}{\partial \delta^2}\bigg|_{\delta = 0}, $$ (11) 其中$E_{{\rm{uds}}}$的是
$$ \begin{split} E_{{\rm{uds}}} = \;& \frac{g}{2\pi^2}\int\nolimits_0^{\nu_{\rm{u}}} \sqrt{k^2+m_{\rm{u}}^2} k^2 {\rm d}k +\frac{g}{2\pi^2}\int\nolimits_0^{\nu_{\rm{d}}} \sqrt{k^2+m_{\rm{d}}^2} k^2 {\rm{d}}k + \\ & \frac{g}{2\pi^2}\int\nolimits_0^{\nu_{\rm{s}}} \sqrt{k^2+m_{\rm{s}}^2} k^2 {\rm{d}}k。\\[-10pt] \end{split} $$ (12) 为了计算夸克物质的对称能,我们将u、d夸克的费米动量重新写为
$$ \begin{aligned}& \nu_{{\rm{u}}} = (1-\delta / 3)^{\frac{1}{3}} \nu, \\ & \nu_{{\rm{d}}} = (1+\delta / 3)^{\frac{1}{3}} \nu, \end{aligned} $$ (13) 其中:$ \nu $是对称的u-d夸克物质在夸克数密度$\,\rho = 2\rho_{\rm{u}} = 2\rho_{\rm{d}}$时的夸克费米动量。根据式(11),我们计算得到
$$ \begin{aligned} E_{{\rm{sym}}}(\rho_{\rm{b}},\rho_{\rm{s}}) = \left(\frac{9 C_I \rho_{\rm{b}} m}{2 \nu^3}A+\frac{1}{18}\frac{\nu^2}{\sqrt{\nu^2+m^2}}\right) \frac{3\rho_{\rm{b}}-\rho_{\rm{s}}}{3\rho_{\rm{b}}}, \end{aligned} $$ (14) 其中
$$ A = \nu \sqrt{\nu^2+m^2}-m^2 \rm{arcsh}\left(\frac{\nu}{m}\right), $$ (15) $$ m = m_{0}+D \rho_{\rm{b}}^{-1/3}+C \rho_{\rm{b}}^{1/3}。 $$ (16) 在上面对称能公式的推导过程中,我们假设u夸克与d夸克的流质量相等,即$m_0 \equiv m_{{\rm{u}}0} = m_{{\rm{d}}0}$. 另外,如果我们只考虑u-d夸克物质的对称能,可以分别令式(12)中的$ \nu_{\rm{s}} = 0 $和式(14)的$ \,\rho_{\rm{s}} = 0 $.
在计算得到夸克物质的状态方程后,夸克星的结构可以通过求解TOV方程得到:
$$ \frac{{\rm{d}} P} {{\rm d} {r}} = -\frac{G m_r E}{r^{2}} \frac{(1+P / E) \left(1+4 \pi r^{3} P / m_r\right)}{1-2 G m_r / r}, $$ (17) $$\frac{{\rm{d}} m_r} {{\rm d} r} = 4 \pi r^{2} E, $$ (18) 其中$G = 6.707 \times 10^{-45}\; {\rm{MeV}}^{-2}$是万有引力常数,$ m_r $是半径$ r $的球体内夸克物质的质量。无量纲化的潮汐形变$ \varLambda \equiv \frac{2}{3} k_{2} C^{-5} $可以结合TOV方程求出[28-32],其中$ C \equiv \frac{M}{R} G $是星体的致密度。
-
为了计算夸克物质的状态方程,我们需要指定模型参数的值。在以下的计算过程中,我们令u、d、s夸克的流质量分别为$m_{{\rm{u}}0} = m_{{\rm{d}}0} = 7.5\; \rm{MeV}$,$m_{{\rm{s}}0} = 100 \; \rm{MeV}$。对于模型参数C、D、$ C_I $,我们需要根据其他条件对其进行限制。根据奇异夸克物质可以绝对稳定存在的假设,要求其平均重子能量小于930 MeV;另外,因为在现实世界中暂时没有发现稳定存在的u-d夸克物质,所以我们假设u-d夸克物质的平均重子能量大于930 MeV。除此之外,根据近些年大质量脉冲星的测量,致密星的质量可以达到甚至超过2倍太阳质量,因此我们要求模型参数的选择需要支持2倍太阳质量的观测结果。在天文观测中,除了脉冲星质量对状态方程的限制外,随着引力波天文学的快速发展,引力波的探测也对极端条件下的物质状态方程给出了较为严格的约束。特别是双中子星并和事件GW170817中测量到星体潮汐形变值$ 70 \leqslant \varLambda_{1.4} \leqslant 580 $,这对核物质状态方程的研究意义重大。基于以上叙述,我们首先根据上述约束条件给出夸克物质的稳定窗口。
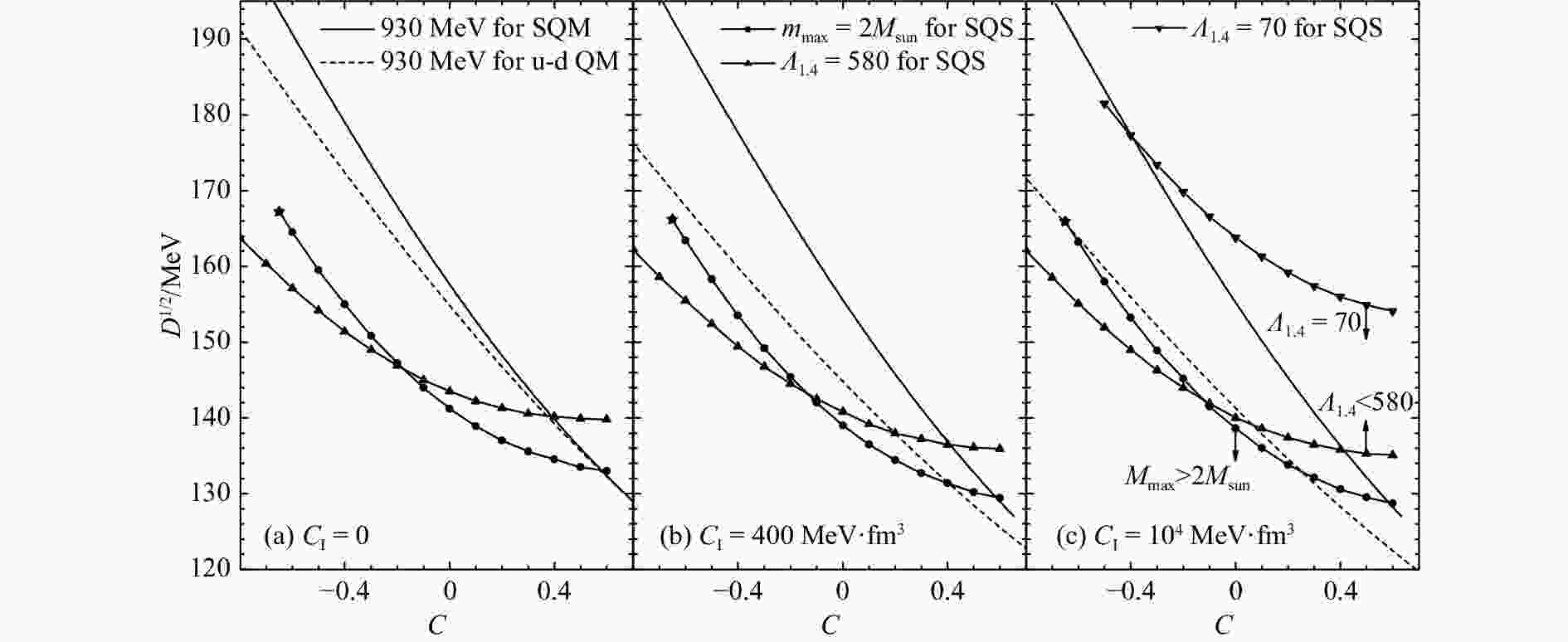
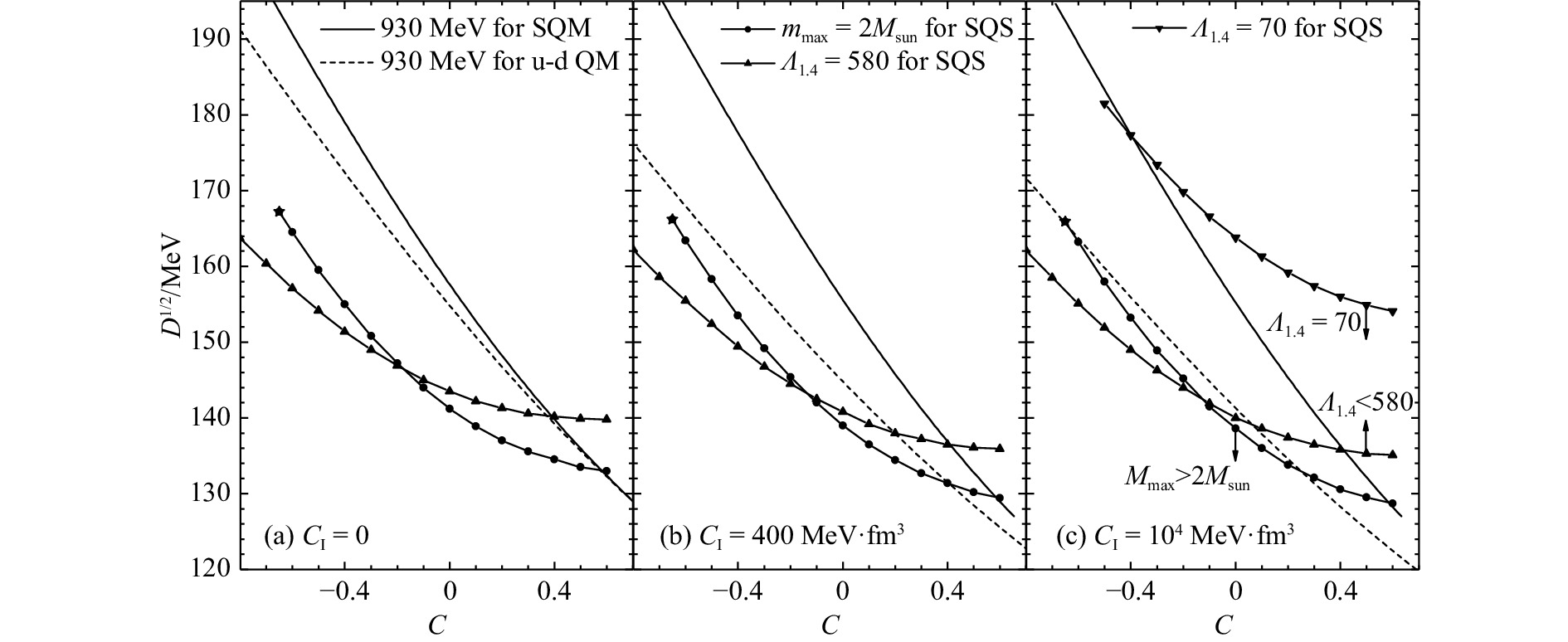
图1给出了奇异夸克物质的稳定窗口,其横轴和纵轴分别是模型参数$ C $和$ \sqrt{D} $。图1(a)~(c)中同位旋强度依赖参数取值依次为0、400 MeV·fm3、104 MeV·fm3,其中黑色实线对应奇异夸克物质平均重子能量930 MeV,黑色虚线对应着u-d夸克物质平均重子能量930 MeV。根据奇异夸克物质可以绝对稳定存在的假设可知,由上述实线与虚线所夹的区域为奇异夸克物质绝对稳定区域。由图1(a)~(c)三分图可以看出,随着同位旋强度依赖参数的增大,奇异夸克物质的绝对稳定区域变大,即夸克间的同位旋效应可以使奇异夸克物质有更大的概率可以绝对稳定存在。
另外,带有实心点的黑线给出了满足奇异星2倍太阳质量的$ C $和$ \sqrt{D} $的关系,其最左端用一五角星符号标出,这是因为超过此点(即$ C $进一步减小),随着奇异星中心密度的继续变大,夸克的等效质量会小于零,从而不能支持2倍太阳质量奇异星的存在。带有上三角的黑线给出了满足$ \varLambda_{1.4} = 580 $的$ C $和$ \sqrt{D} $的关系,而(c)分图中带有下三角的黑线给出了满足$ \varLambda_{1.4} = 70 $的$ C $和$ \sqrt{D} $的关系,即在双中子星并合事件中观测到的$ 70 \leqslant \varLambda_{1.4} \leqslant 580 $位于两条带有三角符号的线之间,而绝对稳定区有很大一部分也在这两条线之间,这说明当前模型中的计算结果支持GW170817事件的并合对象是奇异星的假设。
从图1还可以看出,在不考虑同位旋效应[图1(a)]或同位旋强度依赖参数较小[图1(b)]时,只有很小的参数范围支持2倍太阳质量约束条件。而此时,并不能同时支持$ 70 \leqslant \varLambda_{1.4} \leqslant 580 $的潮汐形变条件。只有在同位旋强度依赖参数足够大[图1(c)]时,才能同时满足2倍太阳质量约束条件与潮汐形约束变条件,即图1(c)分图中2倍太阳质量线最左端的五角星区域。由此得出,为满足奇异夸克物质绝对稳定存在的假设和现有天文观测数据,夸克间的同位旋效应非常重要。
需要指出的是,如果继续增大同位旋强度依赖参数,并不能进一步明显地增大奇异夸克物质绝对稳定区域。因此,在此模型中如果要支持更大质量的奇异星,单靠增大同位旋强度依赖参数并不能达到,这暗示夸克间的其他效应应该需要进一步被考虑。
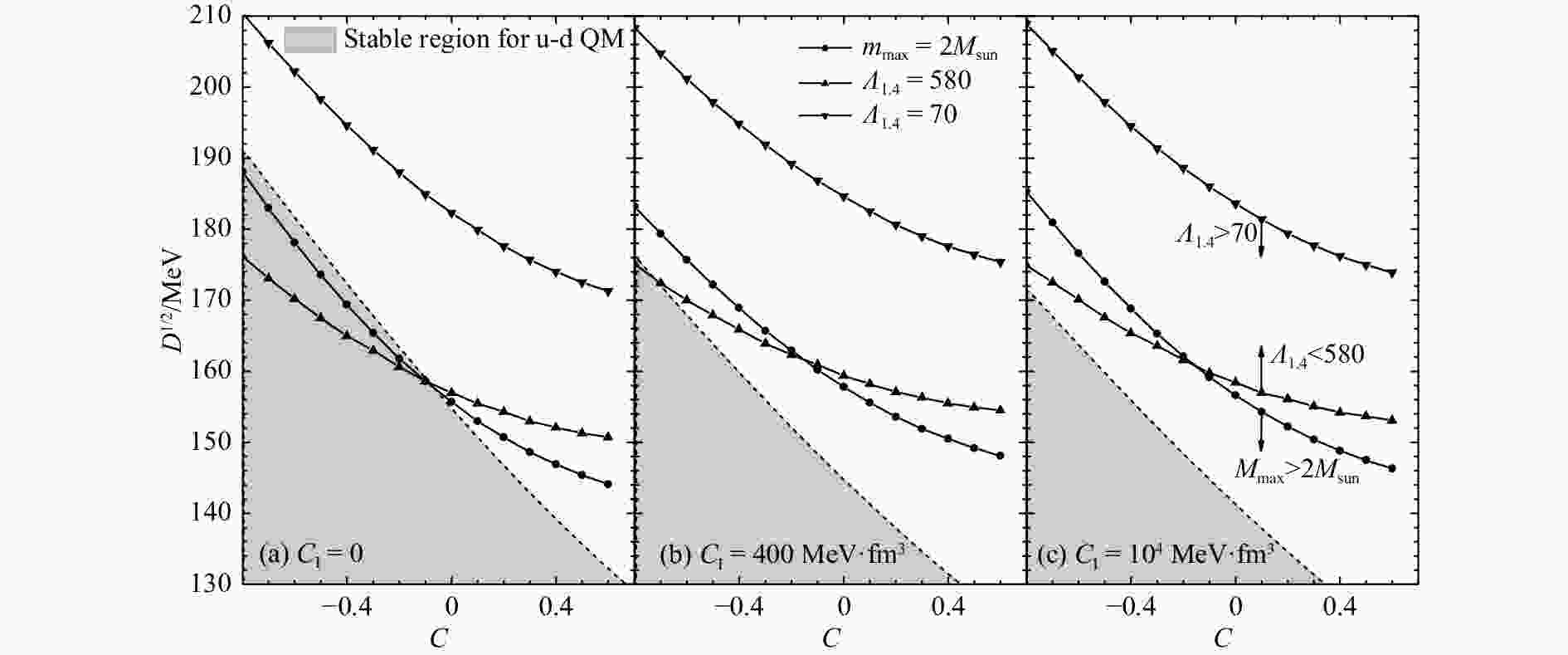
近期有研究指出,QCD的真正基态可能是u-d夸克物质,而不是奇异夸克物质[33]。基于此,u-d夸克物质的平均重子能量应小于930 MeV。下面,我们研究同位旋效应对u-d夸克物质稳定窗口的影响,结果如图2所示,图中各条线的含义与图1相同。从图2可以看出,与奇异夸克物质的情况相反,随着同位旋强度依赖参数的增大,其稳定区域(阴影区域)逐渐减小。在图2(a)中,同位旋强度依赖参数为0,此时有相当一部分参数满足2倍太阳质量约束条件和$ 70 \leqslant \varLambda_{1.4} \leqslant 580 $的潮汐形变条件;而当同位旋强度依赖参数增大到$ 10^4 $ MeV·fm−3[图2(c)]时,已经没有模型参数可以同时满足上述两个条件。因此,u-d夸克物质绝对稳定的假设和现有的天文观测数据(2倍太阳质量致密星与$ 70 \leqslant \varLambda_{1.4} \leqslant 580 $的潮汐形变值)不支持较大的夸克间的同位旋效应。
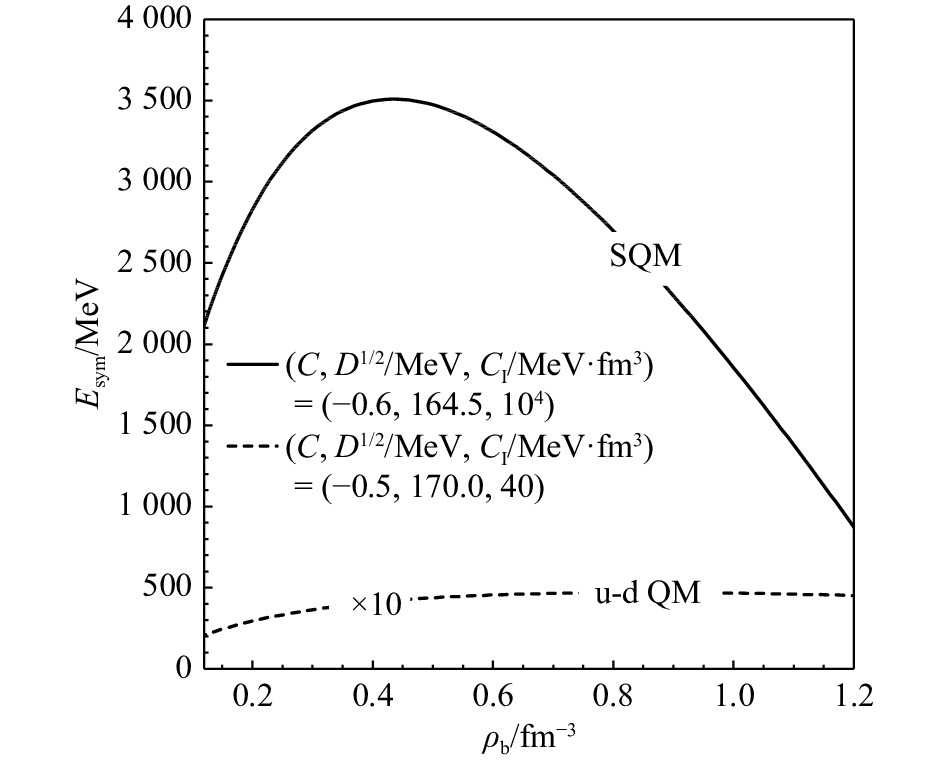
下面我们研究夸克物质的对称能。根据夸克物质的状态方程和式(14),选择两组模型参数。对于奇异夸克物质,我们选择参数组为$(C,\;\sqrt{D}/{\rm{MeV}},\;C_I/{\rm{MeV}}\boldsymbol\cdot{\rm{fm}}^3) = (-0.6,\;164.5,\;10^4)$;对于u-d夸克物质,我们选择模型参数组为$(C,\;\sqrt{D}/{\rm{MeV}},\;C_I/{\rm{MeV}}\boldsymbol\cdot{\rm{fm}}^3) = (-0.5,\;170,\;40)$。我们选择这两组模型参数值的原因是由此得到的状态方程可以满足夸克物质绝对稳定存在的假设和前面提到的天文观测数据的约束条件。我们将这两组典型模型参数得到的奇异夸克物质与u-d夸克物质的平均重子能量最小值$ (E/\rho_{\rm{b}})_{\rm{min}} $、夸克星的最大质量$ M_{\rm{max}} $、潮汐形变$ \varLambda_{1.4} $的值列于表1。通过此表我们可以看到,其平均重子能量都小于930 MeV,夸克星的最大质量在2倍太阳质量附近,潮汐形变$ \varLambda_{1.4} $的值都在70~580之间。
表 1 图3中,典型模型参数下奇异夸克物质与u-d夸克物质的平均重子能量最小值$(E/\rho_{\rm{b}})_{\rm{min}}$、夸克星的最大质量$ M_{\rm{max}} $、潮汐形变$ \varLambda_{1.4} $的对比
夸克物质类型 $(E/\rho_{\rm{b}})_{\rm{min} }$/MeV $ M_{\rm{max}} $/${{M} }_\odot$ $ \varLambda_{1.4} $ 奇异夸克物质 ~ 818 ~ 1.97 ~ 354 u-d夸克物质 ~ 911 ~ 2.06 ~ 503 基于这两组模型参数,我们计算了夸克物质的对称能,结果如图3所示,其中,实线为奇异夸克物质的对称能,虚线为u-d夸克物质的对称能。为了方便比较,我们将u-d夸克物质的对称能$ \times 10 $。从图3可以看出,在密度小于约8倍饱和核密度$ \rho_0 $($\rho_0 \approx 0.16$ fm-3)时,奇异夸克物质的对称能远远大于u-d夸克物质的对称能。这是因为为了满足2倍太阳质量和前面提到的天文观测数据,从图3可以看出,对于奇异夸克物质而言,同位旋依赖参数应该足够大,在这里其值取为$ C_I = 10^{4}\; {\rm{MeV}}\cdot{\rm{fm}}^3 $;对于u-d夸克物质,从图2可以看出情况恰好相反,同位旋依赖参数应该要足够小,在计算图3的过程中,我们使用了$ C_I = 40 \; {\rm{MeV}} \cdot{\rm{fm}}^3 $. 从式(14)可以看出,夸克物质对称能是与$ C_I $成正比的,因此,在图3中我们得到奇异夸克物质和u-d夸克物质的对称能差异巨大。另外,与u-d夸克物质的对称能随着密度增大而增大不同,奇异夸克物质的对称能在密度较大时会随密度的增大而减小。这在之前的研究中我们指出,这是因为夸克间的单胶子交换效应引起的[32],即模型参数$C < 0$时,奇异夸克物质有较软的对称能。
-
在本文中,我们考虑夸克间的同位旋效应,在等效粒子模型下研究了奇异夸克物质和u-d夸克物质的稳定性窗口。结合夸克物质可以绝对稳定存在的假设、2倍太阳质量观测数据的约束和双中子星并合事件GW170817中给出的潮汐形变$ 70 \leqslant \varLambda_{1.4} \leqslant 580 $的约束,发现夸克间的同位旋效应非常重要,它可以显著地增大奇异夸克物质绝对稳定的区域,从而使状态方程可以满足上述三个约束条件;与奇异夸克物质不同的是,同位旋效应对u-d夸克物质的稳定性正好相反,它可以使u-d夸克物质的稳定区域减小,过大的同位旋强度依赖参数会使其状态方程不能同时满足上述的约束条件。最后,我们计算了夸克物质的对称能,发现奇异夸克物质的对称能远大于u-d夸克物质的对称能,并且夸克间的单胶子交换效应会导致奇异夸克物质的对称能变软。
总之,根据目前的理论和天文观测数据,如果想进一步确定夸克间同位旋效应的大小,还需要更加全面和广泛的天文学观测数据和更加成熟可靠的理论计算。
On the Study of Symmetry Energy of Quark Matter and Tidal Deformability of Quark Stars
-
摘要: 近十年的研究表明,夸克物质对称能对夸克物质的状态方程有重要影响。在本研究中,通过采用等效质量模型并在夸克质量标度中引入同位旋依赖项来研究夸克物质的稳定窗口。研究结果表明,足够大的同位旋强度依赖参数$ C_I $可以显著地增大奇异夸克物质的稳定窗口,从而使计算结果可以同时满足天文观测数据PSR J1614-2230具有$ 1.928 \pm 0.017 $倍太阳质量和双中子星并合事件GW170817中得到的潮汐形变$ 70 \leqslant \varLambda_{1.4} \leqslant 580 $的约束。与奇异夸克物质的情况相反,u-d夸克物质的稳定窗口会随着同位旋强度依赖参数的增大而减小,从而使u-d夸克星无法支持相应的天文观测数据。最后,发现奇异夸克物质的对称能远大于u-d夸克物质的对称能,并且夸克间的单胶子交换相互作用会导致奇异夸克物质的对称能变软。Abstract: Research performed during the past decade revealed an important role of symmetry energy in the equation of state of quark matter. By introducing an isospin-dependent term into the quark mass scaling, the stability window of quark matter was studied in the equivparticle model. The results show that a sufficiently strong isospin dependence $ C_I $ can significantly widen the absolute stable region of strange quark matter, yielding results that simultaneously satisfy the constraints of the astrophysical observations of PSR J1614-2230 with (1.928 ± 0.017) $ {{M}}_\odot $ and tidal deformability $ 70 \leqslant \varLambda_{1.4} \leqslant 580 $ measured in the event GW170817. Contrary to the case of strange quark matter, the stable region of u-d quark matter narrows with isospin dependence $ C_I $, leading to inconsistency with astrophysical observations. Finally, we found that the symmetry energy of strange quark matter is much larger than that of u-d quark matter, and one-gluon exchange interaction between quarks causes the symmetry energy of strange quark matter to become softer.
-
Key words:
- symmetry energy /
- quark matter /
- quark star /
- tidal deformability /
- stability window
-
图 2 两味夸克物质的稳定窗口
各线的含义如图1;阴影区域为u-d夸克物质绝对稳定的区域。
表 1 图3中,典型模型参数下奇异夸克物质与u-d夸克物质的平均重子能量最小值$(E/\rho_{\rm{b}})_{\rm{min}}$、夸克星的最大质量$ M_{\rm{max}} $、潮汐形变$ \varLambda_{1.4} $的对比
夸克物质类型 $(E/\rho_{\rm{b}})_{\rm{min} }$/MeV $ M_{\rm{max}} $/${{M} }_\odot$ $ \varLambda_{1.4} $ 奇异夸克物质 ~ 818 ~ 1.97 ~ 354 u-d夸克物质 ~ 911 ~ 2.06 ~ 503 -
[1] BODMER A R. Phys Rev D, 1971, 4: 1601. doi: 10.1103/PhysRevD.4.1601 [2] WITTEN E. Phys Rev D, 1984, 30: 272. doi: 10.1103/PhysRevD.30.272 [3] TERAZAWA H. J Phys Soc Jpn, 1989, 58: 3555. doi: 10.1143/JPSJ.58.3555 [4] FARHI E, JAFFE R L. Phys Rev D, 1984, 30: 2379. doi: 10.1103/PhysRevD.30.2379 [5] FOWLER G, RAHA S, WEINER R. Z Phys C, 1981, 9: 271. doi: 10.1007/BF01410668 [6] CHAKRABARTY S, RAHA S. Phys Lett B, 1989, 229: 112. doi: 10.1016/0370-2693(89)90166-4 [7] BENVENUTO O, LUGONES G. Phys Rev D, 1995, 51: 1989. doi: 10.1103/PhysRevD.51.1989 [8] PENG G X, CHIANG H C, YANG J J, et al. Phys Rev C, 1999, 61: 015201. doi: 10.1103/PhysRevC.61.015201 [9] PENG G X, CHIANG H C, ZOU B S, et al. Phys Rev C, 2000, 62: 025801. doi: 10.1103/PhysRevC.62.025801 [10] XU R X. Astrophys J Lett, 2003, 596: L59. doi: 10.1086/379209 [11] XU R X. Int J Mod Phys D, 2010, 19: 1437. doi: 10.1142/S0218271810017767 [12] GARDIM F G, STEFFENS F M. Nucl Phys A, 2009, 825: 222. doi: 10.1016/j.nuclphysa.2009.05.001 [13] WEN X J, FENG Z Q, LI N, et al. J Phys G, 2009, 36: 025011. doi: 10.1088/0954-3899/36/2/025011 [14] XIA T, HE L, ZHUANG P. Phys Rev D, 2013, 88: 056013. doi: 10.1103/PhysRevD.88.056013 [15] DEMOREST P, PENNUCCI T, RANSOM S, et al. Nature, 2010, 467: 1081. doi: 10.1142/S0217732316502199 [16] FONSECA E, PENNUCCI T T, ELLIS J A, et al. Astrophys J, 2016, 832: 167. doi: 10.3847/0004-637X/832/2/167 [17] ANTONIADIS J, FREIRE P C C, WEX N, et al. Science, 2013, 340: 1233232. doi: 10.1126/science.1233232 [18] CROMARTIE H T, FONSECA E, RANSOM S M, et al. Nat Astron, 2020, 4: 72. doi: 10.1038/s41550-019-0880-2 [19] FONSECA E, CROMARTIE H T, PENNUCCI T T, et al. Astrophys J Lett, 2021, 915: L12. doi: 10.3847/2041-8213/ac03b8 [20] ABBOTT B P, ABBOTT R, ABBOTT T D, et al. Phys Rev Lett, 2017, 119: 161101. doi: 10.1103/PhysRevLett.119.161101 [21] ABBOTT B P, ABBOTT R, ABBOTT T D, et al. Phys Rev Lett, 2018, 121: 161101. doi: 10.1103/PhysRevLett.121.161101 [22] TORO M, LIU B, GRECO V, et al. Phys Rev C, 2011, 83: 014911. doi: 10.1103/PhysRevC.83.014911 [23] CHU P C, CHEN L W. Astrophys J, 2014, 780: 135. doi: 10.1088/0004-637X/780/2/135 [24] CHEN L W. Nucl Phys Rev, 2017, 34: 20. doi: 10.11804/NuclPhysRev.34.01.020 [25] XIA C J, PENG G X, CHEN S W, et al. Phys Rev D, 2014, 89: 105027. doi: 10.1103/PhysRevD.89.105027 [26] WANG L, HU J, XIA C J, et al. Galaxies, 2021, 9: 70. doi: 10.3390/galaxies9040070 [27] CHEN S W, GAO L, PENG G X. Chin Phys C, 2012, 36: 947. doi: 10.1088/1674-1137/36/10/005 [28] DAMOUR T, NAGAR A. Phys Rev D, 2009, 80: 084035. doi: 10.1103/PhysRevD.80.084035 [29] HINDERER T, LACKEY B D, LANG R N, et al. Phys Rev D, 2010, 81: 123016. doi: 10.1103/PhysRevD.81.123016 [30] POSTNIKOV S, PRAKASH M, LATTIMER J M. Phys Rev D, 2010, 82: 024016. doi: 10.1103/PhysRevD.82.024016 [31] ZHOU E P, ZHOU Z, LI A. Phys Rev D, 2018, 97: 083015. doi: 10.1103/PhysRevD.97.083015 [32] XU J F, XIA C J, LU Z Y, et al. Nucl Sci Tech, 2022, 33: 143. doi: 10.1007/s41365-022-01130-x [33] HOLDOM B, REN J, ZHANG C. Phys Rev Lett, 2018, 120: 222001. doi: 10.1103/PhysRevLett.120.222001 -





 下载:
下载:

 甘公网安备 62010202000723号
甘公网安备 62010202000723号