-
The nuclear wobbling mode, which is uniquely related to triaxiality of nuclear shape, has become an hot topic in recent years from both experimental and theoretical sides. It was first proposed by Bohr and Mottelson[1] for a triaxial rotor, i.e., for an even-even nuclei without coupling quasiparticles and the only angular momentum in the system is the total angular momentum. The nucleus rotates around the principal axis having the largest moment of inertia, usually the intermediate axis, which executes harmonic oscillations about the space-fixed angular momentum vector. The expected energy spectra related to this motion are characterized by a series of rotational E2 bands corresponding to the different oscillation quanta ($ n $). The transitions among them are $ \Delta I = 1 $ transitions with dominant E2 character, since the wobbling is generated by the motion of the entire triaxial charge density with respect to the angular momentum vector.
Although Bohr and Mottelson predicted this motion for even-even nuclei where no intrinsic angular momentum is involved, the phenomenon in this simple form has not been experimentally confirmed yet. In contrast, the possible presence of the angular momentum coming from the intrinsic single particle motion can in many ways make the nuclear wobbling mode much richer in its structure and easier to be observed, e.g., in the odd-A mass nuclei. When the triaxial rotor is coupled to a high-j valence particle, Frauendorf and Dönau proposed that there are two kinds of wobbling modes, namely, longitudinal wobbling(LW) and transverse wobbling (TW)[2]. The longitudinal wobbling refers to that the angular momentum of the high-j valence particles is parallel to the principal axis with the largest moment of inertia, while the transverse wobble the angular momentum of the high-j valence particles perpendicular to the principal axis with the largest moment of inertia. Very recently, Chen and Frauendorf further proposed a more comprehensive classification for the wobbling motion based on the topology of the classical orbits visualized by the corresponding spin coherent state (SCS) maps[3]: LW corresponds to a revolution of total angular momentum J around the axis with the largest moment of inertia and TW corresponds to a revolution of J around an axis perpendicular to the axis with the largest moment of inertia. The salient experimental criteria for TW and LW are manifested on the excitation energy and the E2 transition. The excitation energy of the LW (TW) states increases(decreases) with increasing angular momentum. Both TW and LW have enhanced $I \to I - 1$ ${{E}}2$ transitions between adjacent wobbling bands.
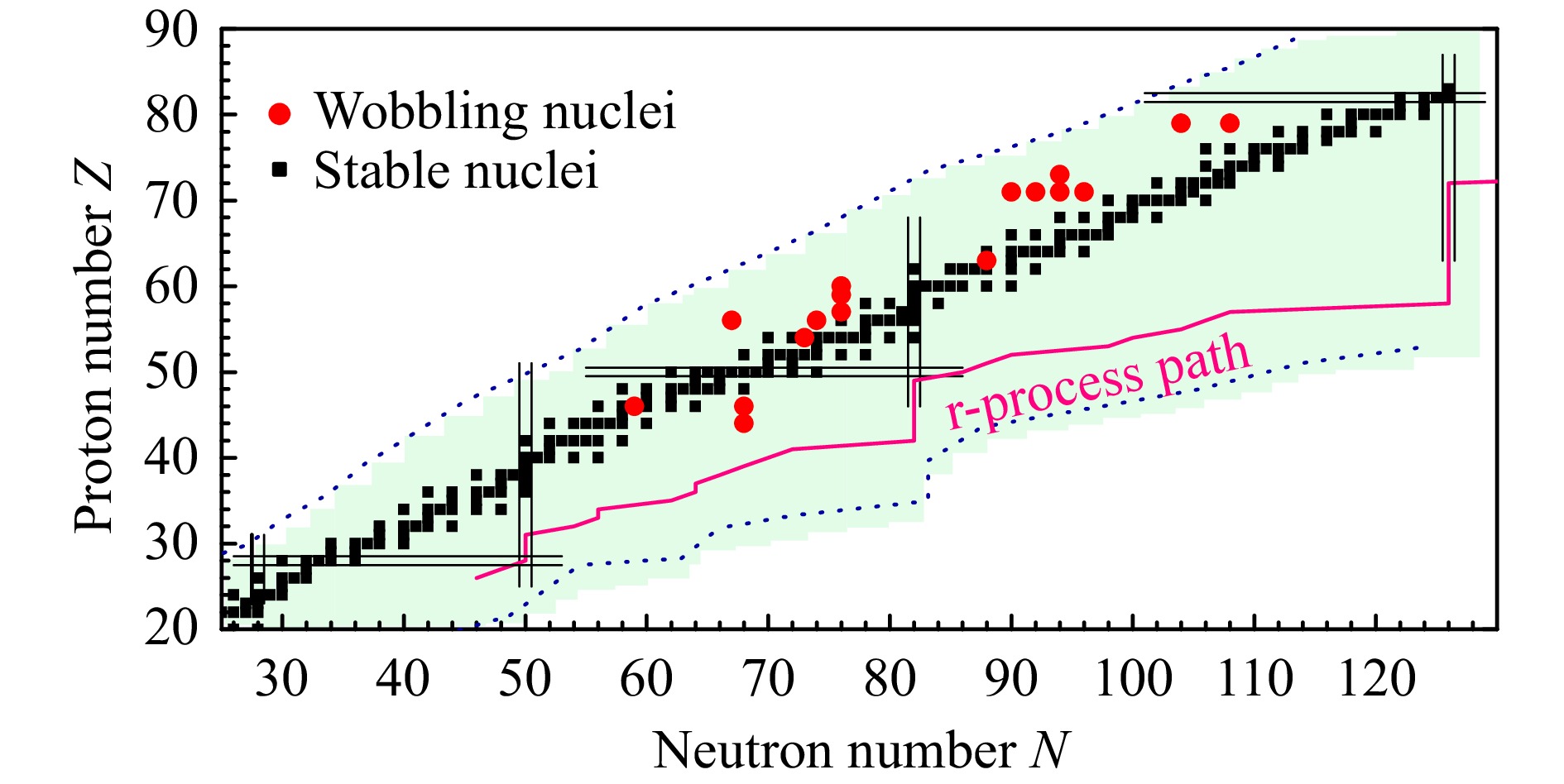
The reported wobbling candidates in the nuclear chart up to now are summarized in Fig. 1. Most of them are in odd-proton nuclei, including 161Lu[4], 163Lu[5-6], 165Lu[7], 167Lu[8], 167Ta[9], and 151Eu[10] in $ A\approx 160 $ mass region, 135Pr[11-12], 133La[13], 130Ba[14-15], 127Xe[16], 133Ba[17], and 136Nd[18] in the $ A\approx 130 $ mass region. Of which the 135Pr is the first observation of transverse wobbling at low deformation[11-12] and the 130Ba is the first example of two-quasiparticle wobbling bands in an even-even nucleus[14-15, 19]. In the heavier $ A\approx 190 $ mass region, the candidates are 187Au[20] and 183Au[21]. In the lighter $ A \approx 100 $ mass region, there is only one candidate 105Pd with odd neutron number $ N = 59 $, which had been suggested as TW and the first nucleus that the wobbling excited state is based on a quasi-neutron configuration[22]. One is aware of that some of these suggested wobblers remain controversial[23-30].
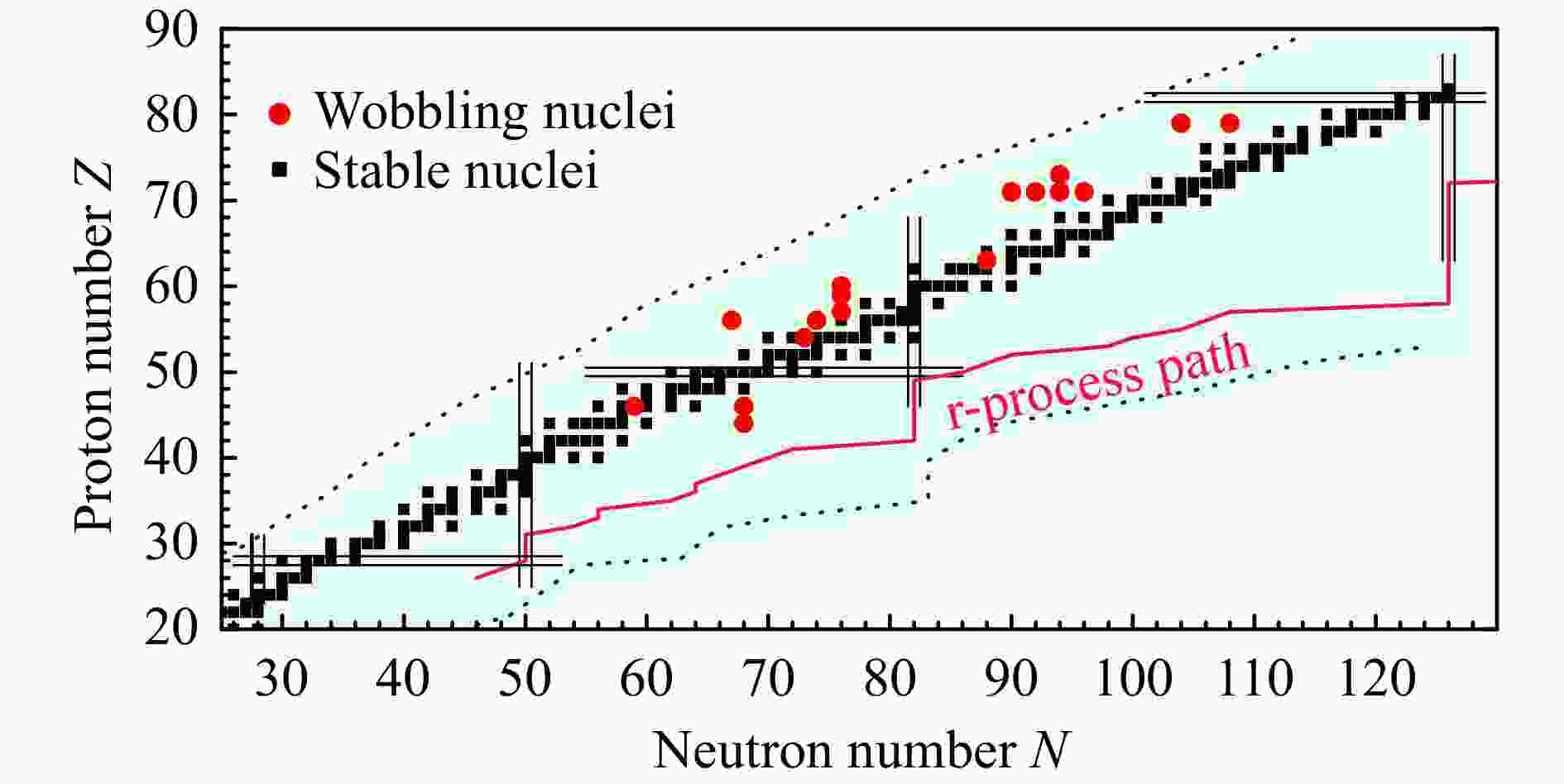
Figure 1. Reported wobbling candidates are spread over the $A\approx100$, 130, 160 and 190 mass regions. (color online)
Theoretically, the triaxial rotor model[1, 31] or particle rotor model (PRM)[2-3, 15, 32-36] and its approximation solutions based on the angular momentum coherent states[37-39], the cranking model plus random phase approximation (RPA)[40-42], the collective Hamiltonian based on titled axis cranking model[43-44], as well as the project shell model[19, 45-46] have been developed to study the wobbling motion. In particular, the combination of quantal PRM and the state-of-art covariant density functional theory (CDFT) (abbreviate as CDFT+PRM)[47-49] have been used to describe the wobbling candidates reported in the 105Pd[22], 130Ba[15], 187Au[20], and 183Au[21]. In this framework, the adiabatic and configuration fixed constraint triaxial CDFT calculations are first carried out to obtain the potential energy surfaces in the $ \beta $-$ \gamma $, the potential energy curves along the $ \beta $ direction, as well as the single-particle energy levels to analyze the possible existence of the configuration and deformation parameters. The obtained configuration and deformation parameters are then input to the PRM to calculate the energy spectra, the electromagnetic transition probabilities, as well as the angular momentum geometries of the wobbling motion. The underlying physics of the observed rotational bands can be eventually revealed.
As mentioned before, the evidence for wobbling in even-even nuclei is fragmentary. In this special issue (CNPC2023) we will present some brief results on the wobbling motion in an even-even nucleus. It contains two parts. One is the wobbling motion in a two-quasiparticle configuration, and the other one is the time-evolution of wobbling motion for a triaxial rotor.
-
In the following, we take the two-quasiparticle wobbling candidate 130Ba as an example to show the calculations within the CDFT+PRM approach.
As mentioned, the 130Ba is the first example of the two-quasiparticle wobbling bands in an even-even nucleus[14-15, 19]. The calculated energy spectra by the PRM in comparison with the experimental has been given in Ref. [15]. Here we show the potential energy curve as a function of deformation $ \beta $ in Fig. 2 obtained by the adiabatic and configuration fixed constraint triaxial CDFT calculations. In the calculations, the effective interaction PC-PK1[50] was used, while the pairing correlations were neglected for simplicity. The Dirac equation was solved employing a spherical harmonic oscillator basis with 12 major shells. The adiabatic constrained CDFT calculation is to solve the Dirac equation by filling the protons and neutrons into the single-particle energy levels according to their energies from the bottom of the well. During the constrained calculations for the given deformation $ \beta $, the triaxial deformation is automatically obtained by minimizing the energy. The configuration fixed constrained calculation requires that the occupied single-particle orbits are fixed during the constrained calculation with $|\langle \phi_j(\beta +\delta \beta)| \phi_i(\beta)\rangle| \approx 1$[47] (in practical calculations the overlap is set as $ \geqslant 0.90 $). One sees clearly from Fig. 2 that the advantages of the configuration fixed constrained calculations is that the continuous and smooth energy curves and the unambiguous local minima for each configuration are yielded in comparison with the irregularities of energy curve in adiabatic constrained calculations.
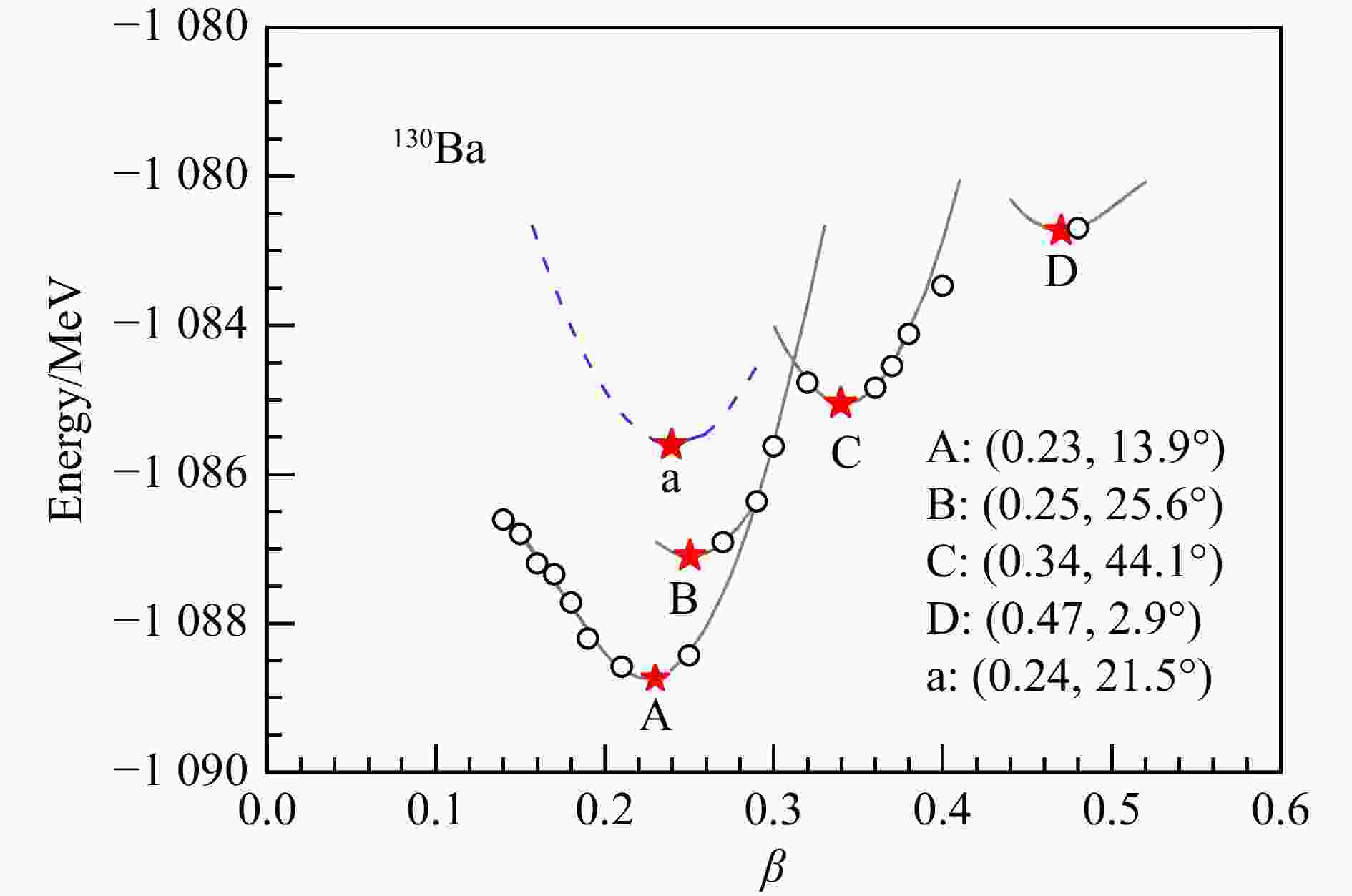
Figure 2. The potential energy as a function of deformation $ \beta $ in adiabatic (open circles) and configuration-fixed(lines) constrained triaxial CDFT calculations with the PC-PK1 effective interaction for 130Ba. The local minima in the energy surfaces for fixed configuration are represented as stars and labeled, respectively, as A-D and a. (color online)
The ground state (labeled as “A” in Fig. 2) deformation of 130Ba is $(\beta,\; \gamma) = (0.23, 13.9^\circ)$. There are several local minima in the potential energy curve, in which the protons and neutrons are also zero-quasiparticle configuration. To find the configuration responsible for establishing the wobbling motion in 130Ba, we excited one paired protons to the $ h_{11/2} $ orbit and do the configuration fixed calculations to obtain the excited configuration $ \pi(1h_{11/2})^2 $ (labeled as “a” in Fig. 2). Definitely other excited configurations can be obtained in a similar way. They are used to describe the other observed rotational bands[14]. The configuration $ \pi(1h_{11/2})^2 $ has the deformation $(\beta,\; \gamma) = (0.24, 21.5^\circ)$ and an excitation energy of 3.13 MeV with respect to the ground state, which is comparable with the experimental excitation energy of 3.79 MeV of the $I = 10\,\hbar$ state of the yrast wobbling band[14]. The obtained deformation parameters and configuration information are then input to the PRM to describe the experimental energy spectra, energy difference between the two bands, as well as the available electromagnetic transition probabilities $B({{M}}1)_{ \rm{out}}/B({{E}}2)_{ \rm{in}}$ and $B({{E}}2)_{ \rm{out}}/B({{E}}2)_{ \rm{in}}$[51]. One finds that in comparison with TW in odd-A nuclei, the mixing ratios $\delta = \langle {{E}}2\rangle_{ \rm{out}}/\langle {{M}}1\rangle_{ \rm{out}}$ in the 130Ba are in fact small. This is attributed to the fact that one more high-$j$ quasiparticle is involved in the two-quasiparticle configuration, which enlarges the $ {\rm{M}}1 $ matrix elements. This is a characteristic for the two-quasiparticle wobbling motion.
In order to delve deeper into the angular momentum geometry associated with the wobbling motion, a more detailed analysis was conducted. Fig. 3 displays the probability density distributions $\mathcal{P}(\theta,\;\varphi)$ for the orientation of the total angular momenta $ {\boldsymbol{J}} $ with respect to the body-fixed frame. Specifically, the distributions are shown for $ I = 14 $ corresponding to states with $ n = 0 $ and $ 2 $, and $ I = 15 $ corresponding to states with $ n = 1 $ and $ 3 $. It is noteworthy that the probability distributions $\mathcal{P}(\theta,\;\varphi)$ exhibit a prominent concentration around the $ \theta = 90^\circ $ plane, which signifies a minimal contribution from the $ l $-component of $ {\boldsymbol{J}} $. Specifically, in the $ n = 0 $ state, there is a maximum probability at $ \varphi = 0^\circ $, indicating the occurrence of maximal alignment between $ {\boldsymbol{J}} $ and the s-axis, as permitted by the principles of quantum mechanics. Conversely, the $ n = 1 $ state exhibits a minimum probability at this particular orientation. The regions of highest probability revolve around this minimum, forming a ring-like structure. This behavior is a direct manifestation of the wobbling motion (precession) of $ {\boldsymbol{J}} $ about the s-axis. These probability distributions align with the anticipated patterns for the $ \varphi $-symmetric states with $ n = 0 $ and $ 2 $, as well as the $ \varphi $-antisymmetric states with $ n = 1 $ and $ 3 $. Importantly, the absence of merging between the probability distributions centered at $ \varphi = 0^\circ $ and $ \varphi = \pm 180^\circ $ when passing through $ \varphi = \pm 90^\circ $ clearly indicates the stability of the TW mode. Comparatively, the TW mode observed in 130Ba demonstrates significantly greater stability compared to its counterparts in odd-A nuclei. This enhanced stability arises from the fact that the two-quasiparticle system in 130Ba can achieve a considerably higher alignment along the s-axis. The detail results can be found in Ref. [51].
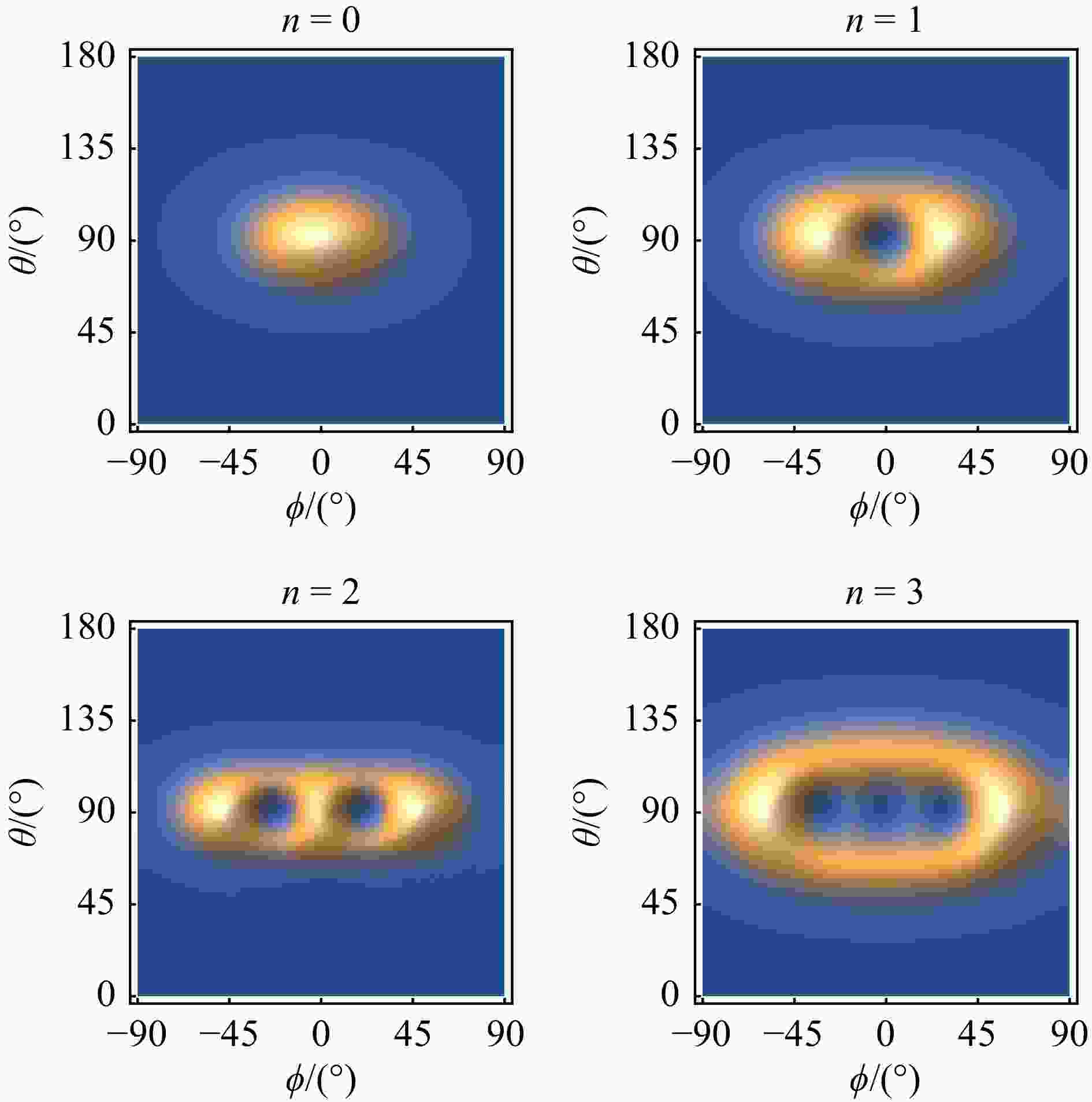
Figure 3. Distributions of the probability $ P(\theta, \phi) $ for the orientation of the angular momentum $ {\boldsymbol{J}} $ with respect to the body-fixed frame at $ I = 14 $ ($ n = 0 $ and $ 2 $) and 15 ($ n = 1 $ and 3). Brown indicates maximal and blue minimal probability. Here, $ \theta $ is the angle between $ {\boldsymbol{J}} $ and the $ l $-axis, and $ \phi $ is the angle between the projection of $ {\boldsymbol{J}} $ onto the $ sm $-plane and the s-axis. The panels are labeled by the wobbling phonon $ n $. (color online)
The success of the CDFT+PRM on the study of the two-quasiparticle wobbling motion in 130Ba[51] has motivated the project shell model to study the wobbling in 130Ba[19] and 136Nd[46], the collective Hamiltonian constructed from a semiclassical treatment to study the wobbling in 130Ba, 134Ce, 136,138Nd[52], as well as the experimental study on the wobbling in 136Nd[18]. More candidates of two-quasiparticle wobbling nuclei are expected on this or other mass regions. The related work along this direction is in progress[53]. It is also worth pointing out that the CDFT+PRM has also been applied successfully on the study of the nuclear chirality[54-65] and the single particle and collective motion in the light nuclei[66-67].
-
The CDFT+PRM provides a microscopic and quantal approach to study the wobbling motion. In the following, a classical view on the wobbling motion is provided by investigating the time evolution of wobbling motion. To study the time evolution of wobbling motion, we start from the triaxial rotor Hamiltonian, which is written as[1]
$$ \begin{aligned} H_{ \rm{TR}} = \sum_{i = 1,2,3}\frac{\hat{J}_i^2}{2\mathcal{J}_i}, \end{aligned} $$ (1) where $ \hat{J}_i $ are the components of the collective angular momentum with respect to the principal axes of the rotor and $ \mathcal{J}_i $ the corresponding moments of inertia. Classically, the angular momentum components are expressed, in the spherical coordinate frame for a given spin value I, by the polar angle $ \theta $ and azimuthal angle $ \phi $ as
$$ \begin{aligned} & J_1 = {\sqrt{I(I+1)}}\sin \theta\cos \phi,\\ & J_2 = {\sqrt{I(I+1)}}\sin \theta\sin \phi,\\ & J_3 = {\sqrt{I(I+1)}}\cos\theta. \end{aligned} $$ (2) Here, $ \theta $ is defined as the angle between J and the long($ l $) axis, and $ \phi $ is the angle between the projection of J onto the short-intermediate ($ sm $) plane and the s-axis.
The orbits of the angular momentum on the unit angular momentum sphere are determined by the implicit equation[3]
$$ \begin{aligned} E& = \frac{J_3^2}{2B(\phi)}+V(\phi),\qquad\quad\; \end{aligned} $$ (3) $$ \begin{aligned} V(\phi)& = I(I+1)\left(\frac{\sin^2\phi}{2\mathcal{J}_2} +\frac{\cos^2\phi}{2\mathcal{J}_1}\right), \end{aligned} $$ (4) $$ \begin{aligned} \frac{1}{2B(\phi)}& = \left(\frac{1}{2\mathcal{J}_3}- \frac{\sin^2\phi}{2\mathcal{J}_2} -\frac{\cos^2\phi}{2\mathcal{J}_1}\right) ,\;\;\;\; \end{aligned} $$ (5) which are obtained by the intersection lines between the sphere of constant angular momentum ${\boldsymbol{J}}^2 = J_1^2+ J_2^2+J_3^2 = I(I+1)$ and the ellipsoid of constant energy given in Eq. (1).
According to the Euler equation for a classical rotor, the angular velocity tangential to the orbit is[3]
$$ \begin{aligned} \omega_\parallel(\phi) = \frac{{\rm{d}}l_\parallel}{{\rm{d}}t} = \sqrt{\left(\frac{{\rm{d}}\phi}{{\rm{d}}t}\right)^2 +\left(\frac{{\rm{d}}\theta}{{\rm{d}}t}\right)^2},\qquad\qquad\qquad\quad\; \end{aligned} $$ (6) $$ \begin{aligned} \frac{{\rm{d}}\phi}{{\rm{d}}t} & = \sqrt{I(I+1)}\cos\theta\left(\frac{\cos^2\phi}{\mathcal{J}_1} +\frac{\sin^2\phi}{\mathcal{J}_2}-\frac{1}{\mathcal{J}_3}\right),\, \end{aligned} $$ (7) $$ \begin{aligned} \frac{{\rm{d}}\theta}{{\rm{d}}t} & = \sqrt{I(I+1)}\sin\theta\left(\frac{1}{\mathcal{J}_1} -\frac{1}{\mathcal{J}_2}\right)\sin\phi\cos\phi, \;\;\; \end{aligned} $$ (8) where $ \theta(\phi) $ can be derived from the Eq. (3) for a given energy value $ E_\nu $, i.e.,
$$ \begin{aligned} \cos^2\theta(\phi) = \frac{2B(\phi)}{I(I+1)}[E_\nu-V(\phi)]. \end{aligned} $$ (9) Therefore, once the moment of inertia and the initial condition of the triaxial rotor are known, the time evolution equation Eqs. (7)~(8) can be solved.
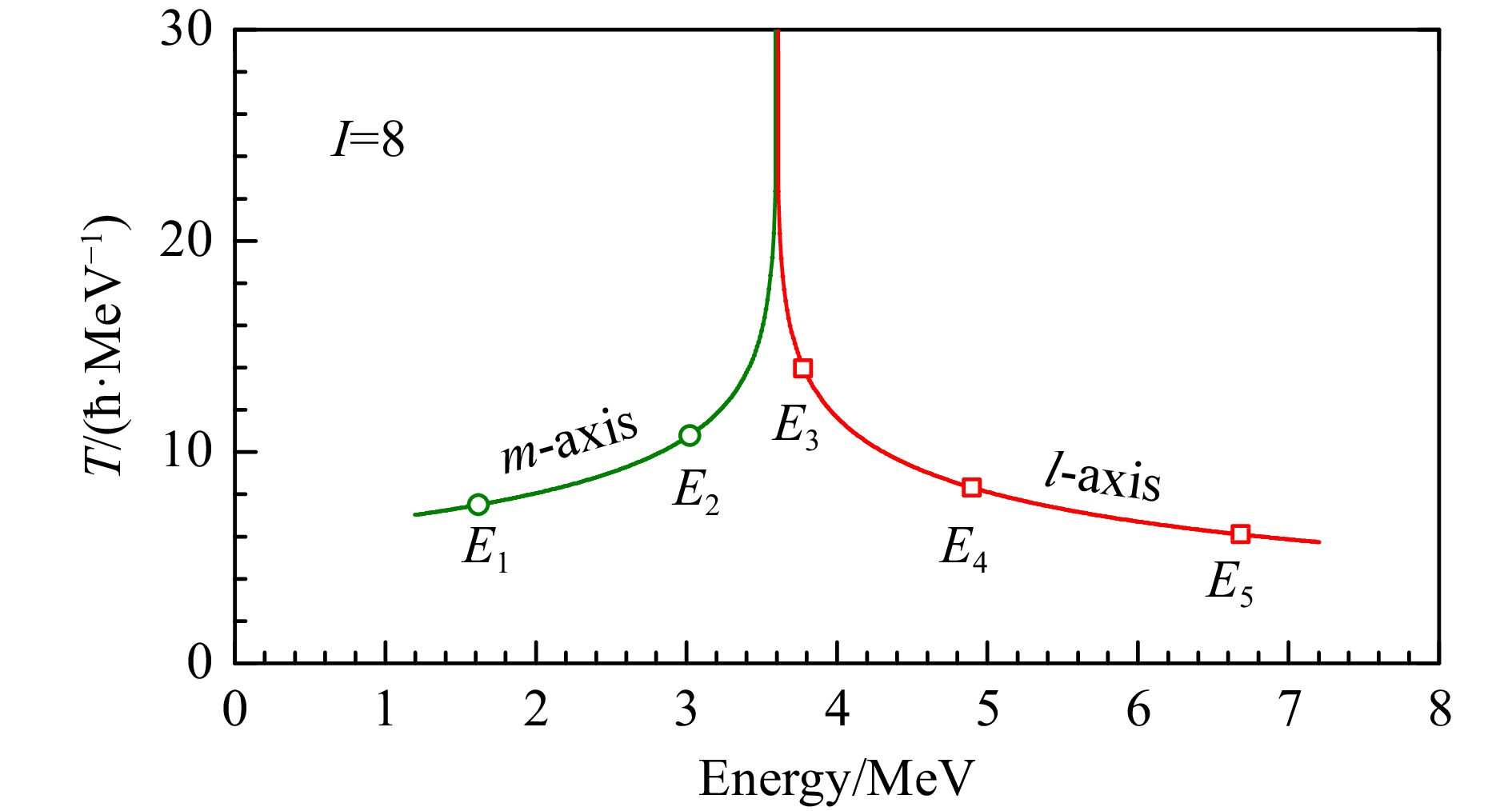
In Fig. 4, an example of the orientation angles $ \theta $ and $ \phi $ as well as the corresponding angular momentum components along the intermediate($ J_m $), short($ J_s $), and long($ J_l $) principal axis of the triaxial rotor are shown as functions of $ t $ for given values of $I = 8\,\hbar$ and $\mathcal{J}_m = 30\, \hbar^2/ \rm{MeV}$, $\mathcal{J}_s = 10\, \hbar^2/ \rm{MeV}$, and $\mathcal{J}_l = 5\, \hbar^2/ \rm{MeV}$. This system has been studied in the framework of triaxial rotor model[3] and has been revealed as a good example to show the wobbling picture. The initial condition is chosen as $(\theta = \pi/2, \; \phi = 2)$, which corresponding to the lowest energy state orbit calculated by Eq. (9) with $ E_1 = 1.616\; \rm{MeV} $. The $ \theta $ and $ \phi $ oscillate with respect to $ \theta = \pi/2 $ and $ \phi = \pi/2 $, respectively. Correspondingly, the angular momentum aligns mainly along the m-axis with $J_m \approx 8\,\hbar$. The $ J_s $ and $ J_l $ are small but not negligible. They drive the rotational axis precess and wobble around the axis with the largest moment of inertia. All of these characteristic present the wobbling motion with respect to the m-axis.
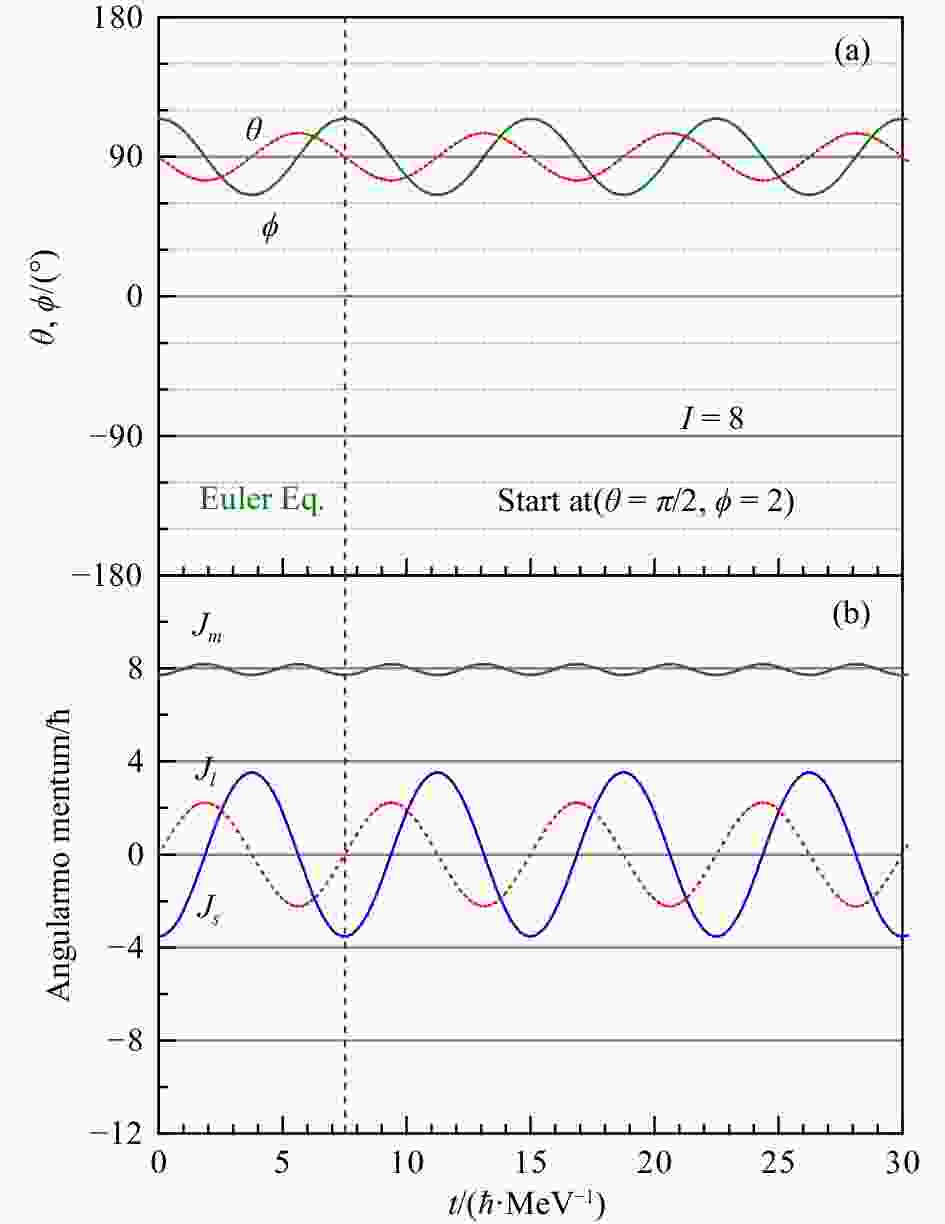
Figure 4. (a) The orientation angles $ \phi $ and $ \theta $ as a function of time t at $I = 8\,\hbar$ obtained by solving the Euler equation Eq. (6). (b) The corresponding angular momentum components along the intermediate($ J_m $), short($ J_s $), and long($ J_l $) principal axis of the triaxial rotor as a function of t . (color online)
Both $ \theta $ and $ \phi $ develop periodically with time under the same period of $T = 7.5\, \hbar/ \rm{MeV}$. The periodic characters are also seen for the angular momentum components. The period $ T $ will vary as the initial condition of $(\theta,\; \phi)$ or say the excitation energy $ E $. In Fig. 5, we delineate the variation of the wobbling motion periods $ T $ as a function of excitation energy, with respect to both the m-axis (the eigen-states of TRM with $n = 0\sim 4$) and the l-axis (the eigen-states of TRM with $n = 5\sim 8$) for $I = 8\,\hbar$. Our analysis reveals a distinctive behavior in these two regimes. Specifically, within the domain corresponding to m-axis wobbling, there is a noticeable increment in the period of wobbling motion as the excitation energy increases. This trend suggests that the dynamical stability associated with rotational motion around the m-axis diminishes progressively with higher excitation energies. Conversely, in the context of l-axis wobbling, an inverse relationship is observed: the period of wobbling motion exhibits a decrement with an increase in excitation energy. Such a trend indicates an enhanced dynamical favorability for rotational motion around the l-axis at higher excitation energies. Moreover, T will become infinite when the initial condition is chosen as $(\theta = \pi/2,\; \phi = 0)$, i.e., starting from the s-axis. Namely, the wobbling motion with respect to the s-axis (intermediate moment of inertia axis) does not exist. The behavior of the period can be also seen for the other spins. The period decreases with spin, indicating the faster rotation. More detailed results will be published elsewhere[68].
-
In summary, the recent progresses on the wobbling motion are briefly introduced. So far 17 wobbling candidates have been reported in odd-A and even-even nuclei that spread over $A \approx 100$, 130, 160 and 190 mass regions. Various kinds of theoretical approach have been developed to study the wobbling motion. Of which the CDFT+PRM is a powerful tool to study the wobbling motion. From the CDFT calculations, the possible existence of the configuration and deformation parameters can be obtained in a microscopic manner. From the PRM calculations, the experimental spectroscopic properties can be well described and the underlying physics can be explored in a fully quantal view. The two-quasiparticle configuration wobbling in 130Ba and the wobbling motion in a triaxial rotor are taken as examples to show the wobbling motion in even-even nuclei. The time evolution of the wobbling motion is an interesting topic, from which the wobbling nature is intuitively revealed. Further experimental and theoretical efforts on the wobbling motion are expected.
Acknowledgments This work was supported by the National Natural Science Foundation of China under Grant No. 12205103 and East China Normal University Undergraduate Innovation and Entrepreneurship Training Program under Grants No. 202310269091X and No. 202410269133S.
-
摘要: 本工作简要介绍了摇摆运动的近期研究进展。目前在质量数为100, 130, 160, 190核区的奇A核与偶偶核中已报导了17个摇摆候选核。以130Ba中的两准粒子组态摇摆及三轴转子的摇摆运动为例说明偶偶核中的摇摆运动。对于130Ba,采用协变密度泛函理论(CDFT)和粒子转子模型(PRM)来进行研究。CDFT为观察到的能带的组态和变形参数提供了关键信息,并为PRM计算提供了输入量。在130Ba中,理论计算再现了实验能谱和电磁跃迁概率。角动量几何的分析揭示了两准粒子组态的横向摇摆相比单准粒子组态的横向摇摆更加稳定。对于三轴转子,利用欧拉方程来研究时间演化问题,给出了方位角($\phi $和$\theta $)以及角动量分量随时间的演化图像。研究表明,三轴转子的低能激发态主要展示围绕中间轴的摇摆运动。随着激发能量的增加,中间轴摇摆运动的周期延长。相反,在长轴摇摆的情况下呈现出一种截然不同的趋势,即激发能量的增加导致摇摆周期减少。Abstract: The recent progresses on the wobbling motion are briefly introduced. So far 17 wobbling candidates have been reported in odd-A and even-even nuclei that spread over A≈100, 130, 160 and 190 mass regions. The two-quasiparticle configuration wobbling in 130Ba and the wobbling motion in a triaxial rotor are taken as examples in this paper to show the wobbling motion in even-even nuclei. For the 130Ba, the wobbling are investigated based on the combination of the covariant density functional theory (CDFT) and the particle rotor model (PRM). The CDFT provides crucial information on the configuration and deformation parameters of observed bands, serving as input for PRM calculations. The corresponding experimental energy spectra and electromagnetic transition probabilities are reproduced. An analysis of the angular momentum geometry reveals the enhanced stability of transverse wobbling of a two-quasiparticle configuration compared to a single-quasiparticle one. For the triaxial rotor, the time evolution of wobbling motion is explored through the solution of Euler equations. This investigation yields valuable insights into the evolution of orientation angles ($\phi $ and $\theta $) and angular momentum components. Notably, the study reveals that low-energy states of a triaxial rotor predominantly exhibit wobbling motion around the intermediate axis. Moreover, an increase in excitation energy corresponds to a prolonged period of intermediate axis wobbling motion. Conversely, a contrasting trend is observed in the case of long axis wobbling, where an increase in excitation energy leads to a decrease in the wobbling period.
-
Key words:
- wobbling motion /
- even-even nucleus /
- two-quasiparticle /
- time evolution
-
Figure 2. The potential energy as a function of deformation $ \beta $ in adiabatic (open circles) and configuration-fixed(lines) constrained triaxial CDFT calculations with the PC-PK1 effective interaction for 130Ba. The local minima in the energy surfaces for fixed configuration are represented as stars and labeled, respectively, as A-D and a. (color online)
Figure 3. Distributions of the probability $ P(\theta, \phi) $ for the orientation of the angular momentum $ {\boldsymbol{J}} $ with respect to the body-fixed frame at $ I = 14 $ ($ n = 0 $ and $ 2 $) and 15 ($ n = 1 $ and 3). Brown indicates maximal and blue minimal probability. Here, $ \theta $ is the angle between $ {\boldsymbol{J}} $ and the $ l $-axis, and $ \phi $ is the angle between the projection of $ {\boldsymbol{J}} $ onto the $ sm $-plane and the s-axis. The panels are labeled by the wobbling phonon $ n $. (color online)
Figure 4. (a) The orientation angles $ \phi $ and $ \theta $ as a function of time t at $I = 8\,\hbar$ obtained by solving the Euler equation Eq. (6). (b) The corresponding angular momentum components along the intermediate($ J_m $), short($ J_s $), and long($ J_l $) principal axis of the triaxial rotor as a function of t . (color online)
-
[1] BOHR A, MOTTELSON B R. Nuclear Structure: Ⅱ[M]. New York: Benjamin, 1975. [2] FRAUENDORF S, DÖNAU F. Phys Rev C, 2014, 89: 014322. doi: 10.1103/PhysRevC.89.014322 [3] CHEN Q B, FRAUENDORF S. Eur Phys J A, 2022, 58: 75. doi: 10.1140/epja/s10050-022-00727-5 [4] BRINGEL P, HAGEMANN G B, HÜBEL H, et al. Eur Phys J A, 2005, 24: 167. doi: 10.1140/epja/i2005-10005-7 [5] ØDEGÅRD S W, HAGEMANN G B, JENSEN D R, et al. Phys Rev Lett, 2001, 86: 5866. doi: 10.1103/PhysRevLett.86.5866 [6] JENSEN D R, HAGEMANN G B, HAMAMOTO I, et al. Phys Rev Lett, 2002, 89: 142503. doi: 10.1103/PhysRevLett.89.142503 [7] SCHÖNWASSER G, HÜBEL H, HAGEMANN G B, et al. Phys Lett B, 2003, 552: 9. doi: 10.1016/S0370-2693(02)03095-2 [8] AMRO H, MA W C, HAGEMANN G B, et al. Phys Lett B, 2003, 553: 197. doi: 10.1016/S0370-2693(02)03199-4 [9] HARTLEY D J, JANSSENS R V F, RIEDINGER L L, et al. Phys Rev C, 2009, 80: 041304. doi: 10.1103/PhysRevC.80.041304 [10] MUKHERJEE A, BHATTACHARYA S, TRIVEDI T, et al. Phys Rev C, 2023, 107: 054310. doi: 10.1103/PhysRevC.107.054310 [11] MATTA J T, GARG U, LI W, et al. Phys Rev Lett, 2015, 114: 082501. doi: 10.1103/PhysRevLett.114.082501 [12] SENSHARMA N, GARG U, ZHU S, et al. Phys Lett B, 2019, 792: 170. doi: 10.1016/j.physletb.2019.03.038 [13] BISWAS S, PALIT R, FRAUENDORF S, et al. Eur Phys J A, 2019, 55: 159. doi: 10.1140/epja/i2019-12856-5 [14] PETRACHE C M, WALKER P M, GUO S, et al. Phys Lett B, 2019, 795: 241. doi: 10.1016/j.physletb.2019.06.040 [15] CHEN Q B, KAISER N, MEISSNER U G, et al. Phys Rev C, 2019, 99: 064326. doi: 10.1103/PhysRevC.99.064326 [16] CHAKRABORTY S, SHARMA H P, TIWARY S S, et al. Phys Lett B, 2020, 811: 135854. doi: 10.1016/j.physletb.2020.135854 [17] ROJEETA D K, KUMAR S, KUMAR N, et al. Phys Lett B, 2021, 823: 136756. doi: 10.1016/j.physletb.2021.136756 [18] LV B F, PETRACHE C M, BUDACA R, et al. Phys Rev C, 2022, 105: 034302. doi: 10.1103/PhysRevC.105.034302 [19] WANG Y K, CHEN F Q, ZHAO P W. Phys Lett B, 2020, 802: 135246. doi: 10.1016/j.physletb.2020.135246 [20] SENSHARMA N, GARG U, CHEN Q B, et al. Phys Rev Lett, 2020, 124: 052501. doi: 10.1103/PhysRevLett.124.052501 [21] NANDI S, MUKHERJEE G, CHEN Q B, et al. Phys Rev Lett, 2020, 125: 132501. doi: 10.1103/PhysRevLett.125.132501 [22] TIMÁR J, CHEN Q B, KRUZSICZ B, et al. Phys Rev Lett, 2019, 122: 062501. doi: 10.1103/PhysRevLett.122.062501 [23] FRAUENDORF S. Phys Rev C, 2018, 97: 069801. doi: 10.1103/PhysRevC.97.069801 [24] TANABE K, SUGAWARA T K. Phys Rev C, 2018, 97: 069802. doi: 10.1103/PhysRevC.97.069802 [25] LAWRIE E A, SHIRINDA O, PETRACHE C M. Phys Rev C, 2020, 101: 034306. doi: 10.1103/PhysRevC.101.034306 [26] LV B F, PETRACHE C M, LAWRIE E A, et al. Phys Rev C, 2021, 103: 044308. doi: 10.1103/PhysRevC.103.044308 [27] TANABE K, SUGAWARA T K. Phys Rev C, 2017, 95: 064315. doi: 10.1103/PhysRevC.95.064315 [28] LV B F, PETRACHE C M, LAWRIE E A, et al. Phys Lett B, 2022, 824: 136840. doi: 10.1016/j.physletb.2021.136840 [29] GUO S, ZHOU X H, PETRACHE C M, et al. Phys Lett B, 2022, 828: 137010. doi: 10.1016/j.physletb.2022.137010 [30] NOMURA K, PETRACHE C M. Phys Rev C, 2022, 105: 024320. doi: 10.1103/PhysRevC.105.024320 [31] SHI W X, CHEN Q B. Chin Phys C, 2015, 39: 054105. doi: 10.1088/1674-1137/39/5/054105 [32] HAMAMOTO I. Phys Rev C, 2002, 65: 044305. doi: 10.1103/PhysRevC.65.044305 [33] STRECK E, CHEN Q B, KAISER N, et al. Phys Rev C, 2018, 98: 044314. doi: 10.1103/PhysRevC.98.044314 [34] CHEN Q B, FRAUENDORF S, KAISER N, et al. Phys Lett B, 2020, 807: 135596. doi: 10.1016/j.physletb.2020.135596 [35] BROOCKS C, CHEN Q B, KAISER N, et al. Eur Phys J A, 2021, 57: 161. doi: 10.1140/epja/s10050-021-00482-z [36] ZHANG H, QI B, WANG X D, et al. Phys Rev C, 2022, 105: 034339. doi: 10.1103/PhysRevC.105.034339 [37] BUDACA R. Phys Rev C, 2018, 97: 024302. doi: 10.1103/PhysRevC.97.024302 [38] BUDACA R. Phys Rev C, 2021, 103: 044312. doi: 10.1103/PhysRevC.103.044312 [39] RADUTA A A, POENARU R, RADUTA A H. J Phys G: Nucl Part Phys, 2018, 45(10): 105104. doi: 10.1088/1361-6471/aadc58 [40] MATSUZAKI M, SHIMIZU Y R, MATSUYANAGI K. Phys Rev C, 2002, 65: 041303. doi: 10.1103/PhysRevC.65.041303 [41] MATSUZAKI M, SHIMIZU Y R, MATSUYANAGI K. Phys Rev C, 2004, 69: 034325. doi: 10.1103/PhysRevC.69.034325 [42] FRAUENDORF S, DÖNAU F. Phys Rev C, 2015, 92: 064306. doi: 10.1103/PhysRevC.92.064306 [43] CHEN Q B, ZHANG S Q, ZHAO P W, et al. Phys Rev C, 2014, 90: 044306. doi: 10.1103/PhysRevC.90.044306 [44] CHEN Q B, ZHANG S Q, MENG J. Phys Rev C, 2016, 94: 054308. doi: 10.1103/PhysRevC.94.054308 [45] SHIMADA M, FUJIOKA Y, TAGAMI S, et al. Phys Rev C, 2018, 97: 024318. doi: 10.1103/PhysRevC.97.024318 [46] CHEN F Q, PETRACHE C M. Phys Rev C, 2021, 103: 064319. doi: 10.1103/PhysRevC.103.064319 [47] MENG J, PENG J, ZHANG S Q, et al. Phys Rev C, 2006, 73: 037303. doi: 10.1103/PhysRevC.73.037303 [48] MENG J, TOKI H, ZHOU S, et al. Prog Part Nucl Phys, 2006, 57: 470. doi: 10.1016/j.ppnp.2005.06.001 [49] MENG J. International Review of Nuclear Physics: Volume 10 Relativistic Density Functional for Nuclear Structure[M]. Singapore: World Scientific, 2016. [50] ZHAO P W, LI Z P, YAO J M, et al. Phys Rev C, 2010, 82: 054319. doi: 10.1103/PhysRevC.82.054319 [51] CHEN Q B, FRAUENDORF S, PETRACHE C M. Phys Rev C, 2019, 100: 061301. doi: 10.1103/PhysRevC.100.061301 [52] BUDACA R, PETRACHE C M. Phys Rev C, 2022, 106: 014313. doi: 10.1103/PhysRevC.106.014313 [53] JI Y Z, CHEN Q B. In Preparation, 2023. [54] AYANGEAKAA A D, GARG U, ANTHONY M D, et al. Phys Rev Lett, 2013, 110: 172504. doi: 10.1103/PhysRevLett.110.172504 [55] LIEDER E O, LIEDER R M, BARK R A, et al. Phys Rev Lett, 2014, 112: 202502. doi: 10.1103/PhysRevLett.112.202502 [56] KUTI I, CHEN Q B, TIMÁR J, et al. Phys Rev Lett, 2014, 113: 032501. doi: 10.1103/PhysRevLett.113.032501 [57] LIU C, WANG S Y, BARK R A, et al. Phys Rev Lett, 2016, 116: 112501. doi: 10.1103/PhysRevLett.116.112501 [58] PETRACHE C M, CHEN Q B, GUO S, et al. Phys Rev C, 2016, 94: 064309. doi: 10.1103/PhysRevC.94.064309 [59] GRODNER E, SREBRNY J, DROSTE C, et al. Phys Rev Lett, 2018, 120: 022502. doi: 10.1103/PhysRevLett.120.022502 [60] LV B F, PETRACHE C M, CHEN Q B, et al. Phys Rev C, 2019, 100: 024314. doi: 10.1103/PhysRevC.100.024314 [61] PETRACHE C M, LV B F, CHEN Q B, et al. Eur Phys J A, 2020, 56(8): 208. doi: 10.1140/epja/s10050-020-00218-5 [62] CHEN Q B, LV B F, PETRACHE C M, et al. Phys Lett B, 2018, 782: 744. doi: 10.1016/j.physletb.2018.06.030 [63] PENG J, CHEN Q B. Phys Lett B, 2019, 793: 303. doi: 10.1016/j.physletb.2019.04.065 [64] PENG J, CHEN Q B. Phys Lett B, 2020, 806: 135489. doi: 10.1016/j.physletb.2020.135489 [65] GRODNER E, KOWALCZYK M, KISIELIńSKI M, et al. Phys Rev C, 2022, 106: 014318. doi: 10.1103/PhysRevC.106.014318 [66] AYANGEAKAA A D, SENSHARMA N, FULGHIERI M, et al. Phys Rev C, 2022, 105: 054315. doi: 10.1103/PhysRevC.105.054315 [67] SENSHARMA N, AYANGEAKAA A D, JANSSENS R V F, et al. Phys Rev C, 2022, 105: 044315. doi: 10.1103/PhysRevC.105.044315 [68] SUN B W, CHEN Q B. in Preparation, 2023. -




 下载:
下载:

 甘公网安备 62010202000723号
甘公网安备 62010202000723号