-
双幻核
$ _{}^{40}{\rm{Ca}} $ 附近原子核的能级信息一直是核结构研究的一个热点。这类原子核核芯外的价核子数目较少时,可以作为单粒子研究的良好对象,其机制也可以通过壳模型进行较好的描述[1-3]。另一方面,该核区的原子核也呈现出集体性甚至表现出形变。通过对这一核区原子核的研究,人们可以更深入地理解核的单粒子自由度和集体自由度之间的竞争与转化。已有的研究表明,质量数在40附近的Ca、Sc、Ti等核的激发态中存在着球形结构与形变结构的共存[4-5]。然而,在解释这些性质上,目前的模型并不是很成功。例如在对
$ _{}^{46}{\rm{Ti}} $ 低激发态的描述中,壳模型的计算值与实验值还存在一定的偏差[6]。因此,深入研究其性质还需要更多的实验信息,一方面可以进一步检验理论模型,另一方面又可以相互检验实验结果的准确性。在这之中,原子核的能级寿命就是一个重要物理观测量。通过对能级寿命的提取,来提取其跃迁概率,进而研究跃迁的初态和末态的波函数等信息。在实验中,根据能级寿命的不同范围,人们常采用不同的测量方法[7]。对于~100 ps以上的能级寿命,通过电子学定时的方法即可得到[8]。这种方法需要分别测量待研究能级上下两条
$\gamma$ 射线的发射时刻,进而通过斜率法、卷积法、中心位移法等来提取能级寿命。对于~1 ps 到~100 ps 区间的能级寿命,通常采用多普勒能移反冲距离法[9](Recoil Distance Doppler Shift)。该方法通过研究$\gamma$ 射线多普勒能移产生的飞行峰和阻停峰的变化关系来得到激发态的能级寿命。对于~100 fs 到~10 ps 区间的能级寿命,人们通常采用多普勒移动衰减法[10](Doppler Shift Attenuation Method, DSAM)。$ _{}^{46}{\rm{Ti}} $ 核激发态能级寿命恰好在该区间,本工作将报道利用多普勒移动衰减法进行测量,并结合壳模型程序进行物理机制的分析。 -
实验在兰州重离子研究装置(HIRFL)[11]完成,采用扇聚焦回旋加速器把
$ _{}^{36}{\rm{Ar}} $ 离子加速到145 MeV的能量,并轰击由聚醚醚酮(PEEK)材料制成的自支撑碳氢靶。靶厚度约9 mg/cm2用于核反应和阻停反应产物。由于靶材料中C的比重占到了75%,所以$ _{}^{12}{\rm{C}} $ ($ _{}^{36}{\rm{Ar}} $ , 2p)$ _{}^{46}{\rm{Ti}} $ 反应为主反应道之一,而其它产物主要由$ _{}^{45}{\rm{Ti}} $ 和$ _{}^{45}{\rm{Sc}} $ 组成。实验采用新组建的大型HPGe探测器阵列进行$\gamma$ 射线的符合测量。该阵列由15台同轴型HPGe探测器和6台Clover型HPGe探测器组成,同轴型探测器分别放置在与束流呈$26 ^{\circ}$ 、$ 52^{\circ} $ 、$ 128^{\circ} $ 、$ 154^{\circ} $ 的位置,Clover型探测器放置在与束流呈$ 90^{\circ} $ 的方向上。其中每台同轴型HPGe 探测器的相对效率[12]为 70%;每台Clover型探测器[13]由4块独立HPGe晶体组成,每块晶体的相对探测效率为40%。为进一步提高$\gamma$ 能谱的峰总比,本次实验为8台同轴型HPGe配备了BGO反康普顿系统,其余探测器的锗晶体部分均采用厚度为2.5 cm的铅来屏蔽外界$\gamma$ 射线,实验中共获取了约$ 8\times10^8 $ 个两重符合事件。实验前后分别利用$ _{}^{60}{\rm{Co}} $ 、$ _{}^{133}{\rm{Ba}} $ 、和$ _{}^{152}{\rm{Eu}} $ 源进行了能量和相对效率刻度。对于$ _{}^{60}{\rm{Co}} $ 源发射的1 332.5 keV的$\gamma$ 射线,单个探测器得到的半高全宽在2.5 keV左右。 -
为了检验能级纲图,利用
$\gamma$ -$\gamma$ 符合事件建立一个对称的符合矩阵。矩阵的两个轴分别放置符合的两个$\gamma$ 射线,在一个轴上选择相应能量进行开窗投影便可以得到与其相符合的$\gamma$ 能谱。本工作中通过符合关系所确立的$ _{}^{46}{\rm{Ti}} $ 能级纲图如图1所示,其中$\gamma$ 射线能量和自旋值取自文献[14]。在能级寿命的提取过程中采用了DSAM方法。该方法被广泛用于ps量级寿命的测量。其原理是核反应中产生的目标核具有一定的运行速度,并在衬底 (在本实验中,靶以自身为衬底)中被慢化以至于停止。由于目标核的早期运动速度比较快(在本实验中,初始速度约为0.07
$ c $ ),发射的$\gamma$ 光子会发生较为明显的多普勒频移,使得前角探测器测得的能量在高能处有拖尾甚至移动,而后角探测器测得的能谱向低能处频移。与目标核运动方向垂直的探测器测到的能谱只有多普勒展宽,而没有拖尾。前后角探测器频移后能谱的形状依赖于原子核的能级寿命,因此可以对感兴趣的$\gamma$ 射线在不同角度探测器产生的能谱进行综合分析得到寿命测量值。在文献[15-17]中,作者也对DSAM方法进行了较为详细的讨论。在数据分析中,利用两重的
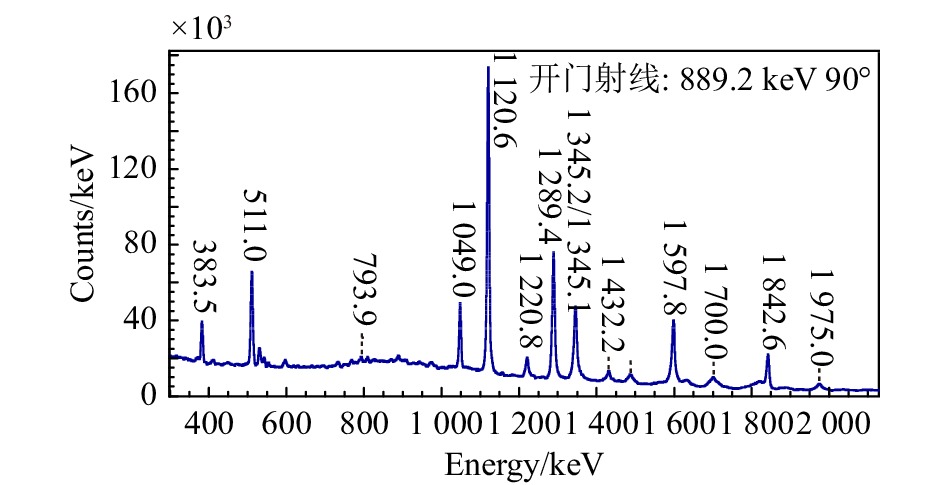
$\gamma$ -$\gamma$ 符合事件分别建立三个不对称的符合矩阵。在矩阵的第一个轴上,分别放置52°、90°、和154°位置探测器测到的$\gamma$ 射线,第二个轴放置除第一轴之外的所有角度探测器测得的$\gamma$ 射线。在三个矩阵的第二轴上选择能量分别进行开窗投影,可以得到对应符合的$\gamma$ 射线在不同角度的能谱。作为例子,图2展示了本次实验中889.2 keV能量开门得到的90°位置探测器测得的能谱。本工作中所研究的1 120.6, 1 220.8和1 842.6 keV三条$\gamma$ 射线在不同角度探测器上产生的符合谱(开窗能量为889.2 keV)如图3所示。在能谱分析过程中采用了LINESHAPE程序[18]。该程序基于核反应统计模型,计算熔合蒸发反应的相应参数,并利用蒙特卡罗方法模拟反冲核在衬底中减速的过程。程序中的参数,如本底的斜率和截距、
$\gamma$ 射线峰的半高宽和污染峰的位置等都会影响LINESHAPE 的拟合值。根据实验能谱设定相应参数,并将理论计算得到的$\gamma$ 射线能谱与实验谱相比较,通过$ \chi^{2} $ 检验可以得到与实验能谱最相吻合的拟合值。图3也给出了LINESHAPE程序对三个$\gamma$ 峰在不同角度的拟合值。从图中可以看出,在考虑沾污峰后的拟合结果与实验结果符合较好。本工作中得到的$ 6^- $ 态和4+ 态的能级寿命与文献[14]评价值较为吻合,但是$ 5^- $ 态的能级寿命与文献值有相对较大的偏差。在对$ 5^- $ 态进行分析时,考虑了实验测量的$5^- $ 态到$ 3^- $ 态的跃迁分支。需要指出的是,对于$ 5^- $ 态的能级寿命,Rammo等[19]也利用DSAM的方法通过$ _{}^{40}{\rm{Ar}} $ ($ _{}^{9}{\rm{Be}} $ , 3n)$ _{}^{46}{\rm{Ti}} $ 和$ _{}^{43}{\rm{Ca}} $ ($ \alpha $ , n)$ _{}^{46}{\rm{Ti}} $ 反应进行了测量,但在该文章的报道中并没有给出多普勒峰形的拟合结果以及其它细节。其实验测量结果与我们的结果出现偏差的具体原因无从得知。我们还根据实验获得的能级寿命提取了与三个能级相对应的电四极约化跃迁概率B(E2)或电偶极跃迁概率B(E1)值。详细的对比列于表1中。表 1 使用LINESHAPE程序拟合实验数据得到的能级寿命值,以及相对应的跃迁概率的实验和理论值
能量/keV 初末态 $ J_i $$ \rightarrow $$ J_f $ 能级寿命$ \tau $/ps B(E1)/W.U. B(E2)/W.U. 理论值/W.U. 数据来源 1 120.6 $ 4^{+} $$ \rightarrow $$ 2^{+} $ 2.14(21)
2.20(43)$ - $ 22.0(20)
23.5(10)16.5
$ - $本工作
文献[14]1 220.8 $ 6^{-} $$ \rightarrow $$ 4^{-} $ 2.07(20)
2.02(57)$ - $ 12.4(11)
12.9(9)13.7
$ - $本工作
文献[14]1 842.6 $ 5^{-} $$ \rightarrow $$ 4^{+} $ 0.98(10)
6.90(12)1.2(1)*$ 10^{-4} $
1.3(5)*$ 10^{-5} $$ - $ 3.6*$ 10^{-4} $
$ - $本工作
文献[14] -
$ _{}^{46}{\rm{Ti}} $ 核位于双幻核$ _{}^{40}{\rm{Ca}} $ 附近。在本研究中,选用大规模组态混合壳模型[20-21]对此原子核的激发态以及电磁跃迁性质进行计算, 并与实验结果进行对比。在计算中,选用较为普适的SDPF-MU有效相互作用[22],选取$ _{}^{16}{\rm{O}} $ 为核芯,价质子与价中子的模型空间均为{$ 0d_{5/2, \, 3/2}, \, 1s_{1/2}, \, 0f_{7/2, \, 5/2}, \, 1p_{3/2, \, 1/2} $ }。对于$_{}^{46}{\rm{Ti}}$ ,由于价质子与价中子数较多,壳模型计算的维数巨大,在实际的大规模壳模型计算中需要对模型空间进行截断。在本工作的计算中采用$ 3\hbar\omega $ 激发的截断,并限制$ d_{5/2} $ 轨道上的价质子与价中子无激发。价质子与价中子的有效电荷,计算中选取为$e_{\rm p}=1.5\;e$ 和$e_{\rm n}=0.5\;e$ 。为了较好地重现46Ti负宇称的激发能,将$0f_{7/2,\, 5/2}, \, 1p_{3/2,\, 1/2}$ 轨道的单粒子能调整$ -3 $ MeV。最终得到的低激发态能级与实验对比如图4。从图中可以看出,大规模组态混合壳模型计算结果与实验符合较好,实验值与理论结果的能级差异最大约为500 keV。在此基础上得到的
$ _{}^{46}{\rm{Ti}} $ 的轨道价核子占有数如图5所示,其中上方带有阴影部分代表中子的单粒子轨道占有数,下方为质子的单粒子轨道占有数。可以观察到,对于正宇称能级而言,随着自旋的上升,中子和质子逐渐收敛到$ 0f_{7/2} $ 并在自旋值为$11\;\hbar$ 达到最大值。因为$ _{}^{46}{\rm{Ti}} $ 极为接近$ _{}^{48}{\rm{Cr}} $ ,而$ _{}^{48}{\rm{Cr}} $ 在$ 0f_{7/2} $ 壳层价核子数最大,因此具有更强的集体特性[23]。由此可以推断出,波函数主要受到来自$ 0f_{7/2} $ 轨道的贡献,$ 1p_{3/2}、0f_{5/2}、1p_{1/2} $ 也在其中有着一定作用。正如文献[24]的计算结果,在自旋大于$8\;\hbar$ 后,$ 1p_{3/2}、0f_{5/2}、1p_{1/2} $ 等轨道的贡献可以忽略,这意味着自旋仅仅通过$ 0f_{7/2} $ 轨道粒子的排列来构建。对于负宇称能级,能级主要是由$ _{}^{40}{\rm{Ca}} $ 中$ \pi 0d_{3/2} $ 轨道上的单个质子激发到$ pf $ 壳导致的。此外,负宇称能级与正宇称能级具有相似的粒子数占据情况,并且负宇称中$ 1p_{3/2} $ 轨道的贡献也比正宇称中大。 -
通过
$ _{}^{12}{\rm{C}} $ ($ _{}^{36}{\rm{Ar}} $ , 2p)$ _{}^{46}{\rm{Ti}} $ 重离子熔合蒸发反应布居了$ _{}^{46}{\rm{Ti}} $ 的高自旋态,采用新组建的大型HPGe探测器阵列进行$ \gamma $ 射线测量。利用DSAM的峰形分析法分析了$ 4^+ $ 、$ 5^- $ 、$ 6^- $ 态的能级寿命,并进而提取了对应的跃迁概率值。实验值在$ 4^+ $ 态和$ 6^- $ 态与文献值符合较好,在$ 5^- $ 态上却有一定偏差。理论上采取壳模型进行计算,选取SDPF-MU相互作用,得到了与实验激发能和跃迁概率值较为符合的结果。此外还计算了各个能级的轨道价核子占有数。研究表明,随着自旋上升$ 0f_{7/2} $ 轨道在波函数中占据主导位置。
Studies on the Lifetimes of 46Ti Excited States via the Doppler Shift Attenuation Method
-
摘要: 原子核的能级寿命直接反映了其内部的结构信息,是核性质研究中一个十分重要的物理参量。本工作报道了依托兰州重离子加速器装置,首次采取多普勒移动衰减法(DSAM)开展的原子核能级寿命测量。采取核反应
$_{}^{12}{\rm{C}}$ ($_{}^{36}{\rm{Ar}}$ , 2p)来布居$_{}^{46}{\rm{Ti}}$ 的高激发态,利用新组建的大型高纯锗(HPGe)探测器阵列进行符合测量。根据$\gamma$ 能谱分别提取了$4^+$ 、$5^-$ 、$6^-$ 态的能级寿命,并得到了这些态的跃迁概率。理论上采取大规模组态混合壳模型进行计算,并得出了能级的组态信息。Abstract: Lifetimes of nuclear excited states are related to its internal structure, and considered as one of most important values in the nuclear property studies. In this paper, we report the first lifetime measurements of nuclear excited states at the HIRFL facility via Doppler Shift Attenuation Method(DSAM). The excited states of$_{}^{46}{\rm{Ti}}$ were populated by the$_{}^{12}{\rm{C}}$ ($_{}^{36}{\rm{Ar}}$ , 2p) reaction, and coincidence measurements were performed by the newly upgraded HPGe detector array. Lifetimes of 4+, 5−, and 6−states were extracted from the gated spectra, and corresponding transition probabilities were deduced. Further theoretical calculations have been performed using the large scale configuration-mixing shell model, and configurations of those states are suggested.-
Key words:
- lifetime /
- DSAM /
- shell model calculation /
- level configuration
-
图 1 本工作确立的
$ _{}^{46}{\rm{Ti}} $ 能级纲图其中能级的自旋值和宇称值取自文献[14]。
表 1 使用LINESHAPE程序拟合实验数据得到的能级寿命值,以及相对应的跃迁概率的实验和理论值
能量/keV 初末态 $ J_i $$ \rightarrow $$ J_f $ 能级寿命$ \tau $/ps B(E1)/W.U. B(E2)/W.U. 理论值/W.U. 数据来源 1 120.6 $ 4^{+} $$ \rightarrow $$ 2^{+} $ 2.14(21)
2.20(43)$ - $ 22.0(20)
23.5(10)16.5
$ - $本工作
文献[14]1 220.8 $ 6^{-} $$ \rightarrow $$ 4^{-} $ 2.07(20)
2.02(57)$ - $ 12.4(11)
12.9(9)13.7
$ - $本工作
文献[14]1 842.6 $ 5^{-} $$ \rightarrow $$ 4^{+} $ 0.98(10)
6.90(12)1.2(1)*$ 10^{-4} $
1.3(5)*$ 10^{-5} $$ - $ 3.6*$ 10^{-4} $
$ - $本工作
文献[14] -
[1] CAURIER E, ZUKER A P, POVES A, et al. Phys Rev C, 1994, 50(1): 225. doi: 10.1103/PhysRevC.50.225 [2] CAURIER E, EGIDO J L, MARTÍNEZ-PINEDO G, et al. Phys Rev Lett, 1995, 75(13): 2466. doi: 10.1103/PhysRevLett.75.2466 [3] ARNSWALD K, BRAUNROTH T, SEIDLITZ M, et al. Phys Lett B, 2017, 772: 599. doi: 10.1016/j.physletb.2017.07.032 [4] BRANDOLINI F, OLIVEIRA J, MEDINA N H, et al. Phys Rev C, 2004, 70(3): 034302. doi: 10.1103/PhysRevC.70.034302 [5] BEDNARCZYK P, STYCZEŃ J, BRODA R, et al. The European Physical Journal A-Hadrons and Nuclei, 1998, 2(2): 157. doi: 10.1007/s100500050105 [6] MEDINA N, OLIVEIRA J, BRANDOLINI F, et al. Phys Rev C, 2011, 84(2): 024315. doi: 10.1103/PhysRevC.84.024315 [7] NOLAN P J, SHARPEY-SCHAFER J F. Reports on Progress in Physics, 1979, 42(1): 1. doi: 10.1088/0034-4885/42/1/001 [8] LI C, WU X, LI X, et al. Phys Rev C, 2012, 86(5): 057303. doi: 10.1103/PhysRevC.86.057303 [9] ZHU B, LI C, WU X, et al. Phys Rev C, 2017, 95(1): 014308. doi: 10.1103/PhysRevC.95.014308 [10] YAO S, MA H, ZHU L, et al. Phys Rev C, 2014, 89(1): 014327. doi: 10.1103/PhysRevC.89.014327 [11] ZHAN W, XIA J, ZHAO H, et al. Nuclear Physics A, 2008, 805(1-4): 533c. doi: 10.1016/j.nuclphysa.2008.02.292 [12] LEE I, DELEPLANQUE M, VETTER K, et al. Reports on Progress in Physics, 2003, 66: 1095. doi: 10.1088/0034-4885/66/7/201 [13] DUCHÊNE G, BECK F, TWIN P, et al. Nucl Instr and Meth A, 1999, 432(1): 90. doi: 10.1016/S0168-9002(99)00277-6 [14] WU S C. Nuclear Data Sheets, 2000, 91(1): 1. doi: 10.1006/ndsh.2000.0014 [15] ALEXANDER T, FORSTER J. Bar anger-Vogt, 1978, 10: 258. doi: 10.1007/978-1-4757-4401-9_3 [16] ROHILLA A, LI G, QIANG Y, et al. Nuclear Physics A, 2021, 1006: 122116. doi: 10.1016/j.nuclphysa.2020.122116 [17] ROHILLA A,李广顺,王建国,等. 原子核物理评论, 2020, 37(3): 542. doi: 10.11804/NuclPhysRev.37.2019CNPC17 ROHILLA A, LI G, WANG J, et al. Nuclear Physics Review, 2020, 37(3): 542. (in Chinese) doi: 10.11804/NuclPhysRev.37.2019CNPC17 [18] WELLS J, JOHNSON N. Report No ORNL-6689[R]. Oak Ridge:Oak Ridge National Laboratory, 1991: 44. [19] NRF R, PJ N, AN J, et al. J Phys G, 1982, 8: 101. [20] CAURIER E, MARTÍNEZ-PINEDO G, NOWACKI F, et al. Reviews of Modern Physics, 2005, 77(2): 427. doi: 10.1080/16258312.2005.11517138 [21] OTSUKA T, GADE A, SORLIN O, et al. Reviews of Modern Physics, 2020, 92(1): 015002. doi: 10.1103/RevModPhys.92.015002 [22] UTSUNO Y, OTSUKA T, BROWN B A, et al. Phys Rev C, 2012, 86(5): 051301. doi: 10.1103/PhysRevC.86.051301 [23] BUCURESCU D, UR C, LENZI S, et al. Phys Rev C, 2003, 67(3): 034306. doi: 10.1103/PhysRevC.67.034306 [24] ZUKER A, RETAMOSA J, POVES A, et al. Phys Rev C, 1995, 52(4): R1741. doi: 10.1103/PhysRevC.52.R1741 -

















 下载:
下载:








































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号