-
强流重离子加速器[1-2](High Intensity heavy-ion Accelerator Facility, HIAF)是国际上在建的最大的质子-重离子加速器之一。它由超导回旋共振离子源SECR、超导离子直线加速器iLinac、增强器BRing、放射性分离束线HFRS、高精度环形谱仪SRing以及众多实验终端组成。增强器BRing是HIAF的核心加速器装置,具有在100 ms内将流强
$ 6.0\ \times 10^{12} $ ppp质子束流从48 MeV加速至9.3 GeV,$ 1.0\ \times 10^{11} $ ppp的$ \rm{^{238}U^{35+}} $ 束流从17 MeV/u加速至835 MeV/u的能力。无论是束流能量或是流强都远超位于我国的兰州重离子研究装置—冷却储存环[3](The heavy ion cooler-storage-ring project, HIRFL-CSR),这对加速器设计和建设提出了很高的挑战。在正常情况下,束流将在环内围绕着参考轨道作betatron运动[4],而一旦出现设备故障,束流将不再按照设计的轨道和包络运行从而最终损失在真空管道上,对加速器造成严重的辐射损伤。形成束流损失的原因众多[5-7],一般可分为两类,第一类是束流动力学原因,如各种束流集体效应、束流-残余气体相互作用以及非线性效应等。另一类则是由于加速器关键设备故障造成的束流损失,如电源、磁铁,高频等关键系统故障,这类故障通常会造成十分严重的后果[8]。举例而言,对于BRing一旦电源系统和高频系统故障,高达10 kJ能量的束流将在毫秒量级的时间轰击在加速器管道和设备上,产生严重的热沉积和核辐射,造成加速器的设备损伤和停机,消耗大量的人力、物力进行机器维护,影响相关科学实验的效率。为阻止或减缓束流损失造成的影响,HIAF正在设计、建造一套机器保护系统[2](Machine Protection System, MPS),该系统会持续监测加速器和束流的运行状态,并在必要时发出“保护”指令,将潜在风险或已经失控的束流安全地传输到事先设计好的束流吸收体内,该过程即所谓的beam dump过程。
为研究设备故障下的束流损失和beam dump过程的束流动力学,为机器保护系统建设提供参考,对其进行详细的数值模拟是非常有必要的。目前国际上各大加速器实验室开发的束流动力学模拟程序有欧洲核子中心的MAD-X[9]、SixTrack[10]、WinAgile[11]以及美国橡树岭国家实验室开发的Orbit等[12],这些软件通常不支持磁场随时间任意变化和设备故障下的束流跟踪。尽管有文献报道利用MAD-X可以实现设备故障下的束流模拟,但其要用到非常复杂的外部脚本,同时整个过程是非常缓慢的[13]。这些软件无法满足我们束流模拟的需求,因此我们开发了一套逐元件多粒子束流跟踪软件,用以模拟各类设备故障下的束流损失分布。该软件基于Python和C++语言混合开发,支持任意可变磁场和任意形状真空孔径,相比其他软件大幅提升了多粒子跟踪速度。此外,该程序设计了灵活的接口,可以方便轻松地嵌入其他第三方程序供其调用。基于本软件,我们对BRing的电源故障造成的束流损失展开了模拟,并与MAD-X软件得到的结果作了校验。
-
本节分别介绍束流生成算法、束流传输模型、电源故障模型以及真空管道孔径模型。
-
生成横向相空间匹配的初始粒子参考了文献[14]中的方法,其中水平方向粒子生成的详细步骤如下。
1) 确定束流初始分布的参数:Twiss参数[4](
$ \alpha_x^{} $ ,$ \beta_x^{} $ ,$ D_x^{} $ ,$ D_x^\prime $ ,$ X_{co.}^{} $ ,$ X_{co.}^\prime $ ),分布类型$ m $ ,粒子个数$ N $ ,束流发射度$ \epsilon $ 及截断倍数$ t $ ,束流动量分散$ \delta $ 等,得到如下参数:$$ \begin{array}{l} \cos\chi = \sqrt{\dfrac{1}{1+\alpha^2}},\\ \sin\chi = -\alpha \cos\chi, \\ X_m^{} = \sqrt{\varepsilon\ \beta}, \\ X_m^\prime = \sqrt{\varepsilon\ \gamma} 。 \end{array} $$ (1) 2) 生成两组[0, 1]之间均匀分布的随机数
$ S_1^{} $ 和$ S_2^{} $ ,应用如下变化:$$ \begin{array}{l} a = \sqrt{\dfrac{m+1}{2}} \boldsymbol\cdot \sqrt{1-S_1^{1/m}},\\ u = a \boldsymbol\cdot \cos (2\pi S_2^{}),\\ v = a \boldsymbol\cdot \sin (2\pi S_2^{}),\\ x = X_m^{} \boldsymbol\cdot u + D_x^{} \boldsymbol\cdot \delta + X_{co.}^{},\\ x^\prime = X_m^\prime \boldsymbol\cdot(u\sin\chi + v\cos\chi)+ D_x^\prime \boldsymbol\cdot \delta + X_{co.}^\prime , \end{array} $$ (2) 得到的
$x,x^\prime$ 即为满足条件的初始粒子分布。对于垂直方向而言,其步骤完全一致。值得注意的是,若生成粒子的位置存在色散或非零的闭合轨道,则需要考虑其影响,否则在进行多粒子跟踪时会造成错误的束流包络和束流中心较大的振荡。参数$ m $ 控制着分布类型,其对应关系如表1所列:表 1 粒子生成算法中参数和对应的分布类型
参数m 束流分布类型 0.0 Hollow shell 0.5 Flat profile 1.0 Uniform 1.5 Elliptical 2.0 Parabolic $\infty$ Gaussian 生成高斯分布粒子分布的算法除可将
$ m $ 设为一个较大的参数外(如$ 1\times10^3 $ ),也可采用著名的“Box-Muller”算法[15],相比其他算法,该算法使用简单,同时具有更好的性能[16]。上述算法也可用以生成一维分布的粒子分布。 -
生成的粒子沿着全环进行逐元件传输,基础元件的传输模型如下所示。
1) 漂移节、四极磁铁和二极磁铁线性元件采用一阶传输矩阵进行束流传输,传输矩阵如下所示:
$$ R = \left( {\begin{array}{*{20}{c}} {c_x^{}}&{s_x^{}}&0&0&0&{\dfrac{h}{{{\beta _s^{}}}}d_x^{}}\\ { - k{{_x^{}}^2}s_x^{}}&{c_x^{}}&0&0&0&{\dfrac{h}{{{\beta _s^{}}}}s_x^{}}\\ 0&0&{{c_y^{}}}&{{s_y^{}}}&0&0\\ 0&0&{ - k_y^2{s_y^{}}}&{{c_y^{}}}&0&0\\ { - \dfrac{h}{{{\beta _s^{}}}}s_x^{}}&{ - \dfrac{h}{{{\beta _s^{}}}}d_x^{}}&0&0&1&{\dfrac{L}{{\beta _s^2\gamma _s^2}} - \dfrac{{{h^2}}}{{\beta _s^2}}J_1^{}}\\ 0&0&0&0&0&1 \end{array}} \right), $$ (3) 其中
$ (c_x^{}\,,s_x^{},\,c_y^{},\,s_y^{}) $ 为对希尔方程求解得到的类余弦、正弦项;$ J_1^{} $ 为$ s_x^{} $ 关于元件长度$ L $ 的积分项;$h = 1/\rho$ 为二极磁铁偏转半径的倒数;$ \beta_s^{}、\gamma_s^{} $ 为洛伦兹因子。二极磁铁边缘角对束的流影响可以等效为长度为0的冲击元件,其传输矩阵如下所示:
$$ \begin{array}{l} {R_{\rm{f}}} = \left( {\begin{array}{*{20}{c}} 1&0&0&0&0&0\\ {h\tan {\phi _i}}&1&0&0&0&0\\ 0&0&1&0&0&0\\ 0&0&{ - h\tan \overline {{\phi _i}} }&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right)\\ {{\bar \phi }_i} = {\phi _i} - hg{I_1}\sec {\phi _i}(1 - {\sin ^2}{\phi _i}), \end{array},$$ (4) 其中
$ \phi_i^{} $ 是二极铁边缘角;$ \overline{\phi}_i^{} $ 是边缘场的垂直方向修正项[17];g是二极磁铁全高宽;$ I_1^{} $ 是一阶边缘场积分常数,在MAD-X软件中它是我们所熟知的“FINT”值,其由二极磁铁的边缘场分布决定,具体模型这里不再赘述。为了考虑色品效应,对于具有动量偏差的粒子,需要对其磁场聚焦强度进行修正:
$$ K_n^{}(\delta) = \frac{K_n^{}}{1+\delta} , $$ (5) 其中
$ K_n^{} $ 为n阶磁场聚焦强度;$ \delta $ 为当前粒子和参考粒子的动量偏差,这种修正方法可以实现对具有非零动量偏差粒子的精确传输,其中MAD-X和Sixtrack均采用这种修正。对于二极磁铁仅对边缘聚焦项进行修正而对磁铁主体并未作修正处理,其粒子传输精度为关于动量分散的一阶精度。2) 场误差采用
$ \frac{1}{2}R + {\rm{Kicker}} + \frac{1}{2}R $ 传输模型,其中$ R $ 是漂移节或对应元件的一阶传输矩阵,位于元件中心的Kicker对束流产生的冲击如下:$$ \begin{array}{l} P = \varDelta K_0^{}L-K_0^{}L\dfrac{p_t^{}}{\beta_s^{}}+\displaystyle\sum\limits_{n = 1}^N{K_n^{}L\dfrac{\left( x+ \mathrm{i} y \right) ^2}{n!}},\\ x_1^\prime = x_0^\prime - {\rm{Re}} P, \\ y_1^\prime = y_0^\prime - {\rm{Im}} P, \end{array}$$ (6) 其中
$ L $ 是元件长度;$K_0^{} = 1/\rho$ ;$ K_n^{} $ 为$ n $ 阶磁场聚焦强度;$ \beta_s^{} $ 是洛伦兹因子;Re和Im为对P取其实部或虚部。 -
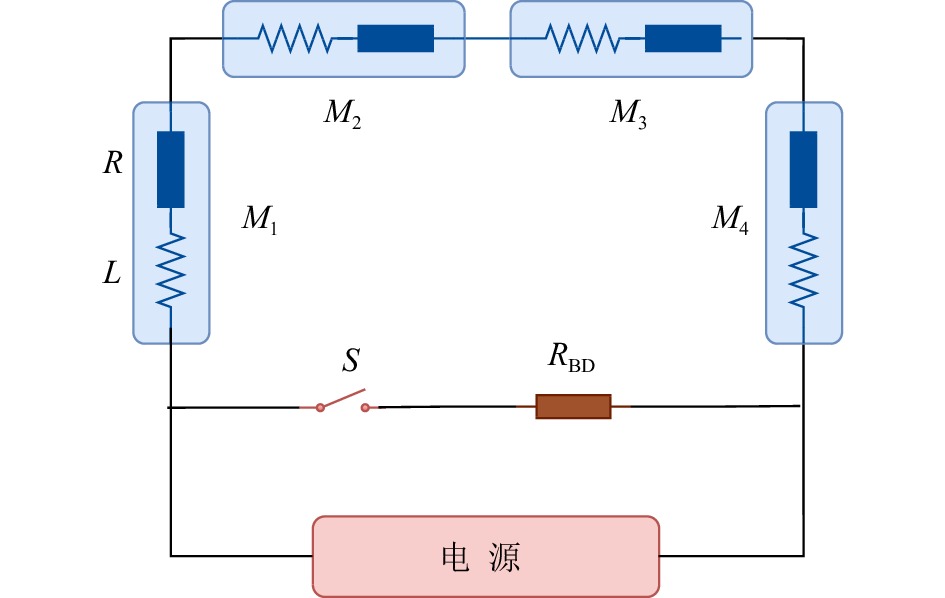
BRing的二极磁铁为常温磁铁,其磁铁-电源的拓扑结构如图1所示。在正常情况下,磁铁由电源驱动,而一旦电源出现故障,保护开关
$ S $ 会立即导通,储存在磁铁线圈中的能量会通过简单的$ R-L $ 回路放电[13, 18]。磁铁线圈中的电流演化如式(7)所示:$$ I\left( t \right) = I_0^{}\exp \left( -\frac{t}{\tau} \right)。 $$ (7) 图中
$ L $ 为磁铁线圈电感,$ R $ 为磁铁线圈电阻,$ R_{\rm{BD}}^{} $ 为电路的剩余电阻和某些特殊二极磁铁的吸能电阻[2, 19],$\tau = 4L/\left(R_{\rm{BD}}^{}+4R\right)$ 为该放电电路的时间常数。对于四极磁铁和其他常温磁铁,放电规律和二极磁铁类似。 -
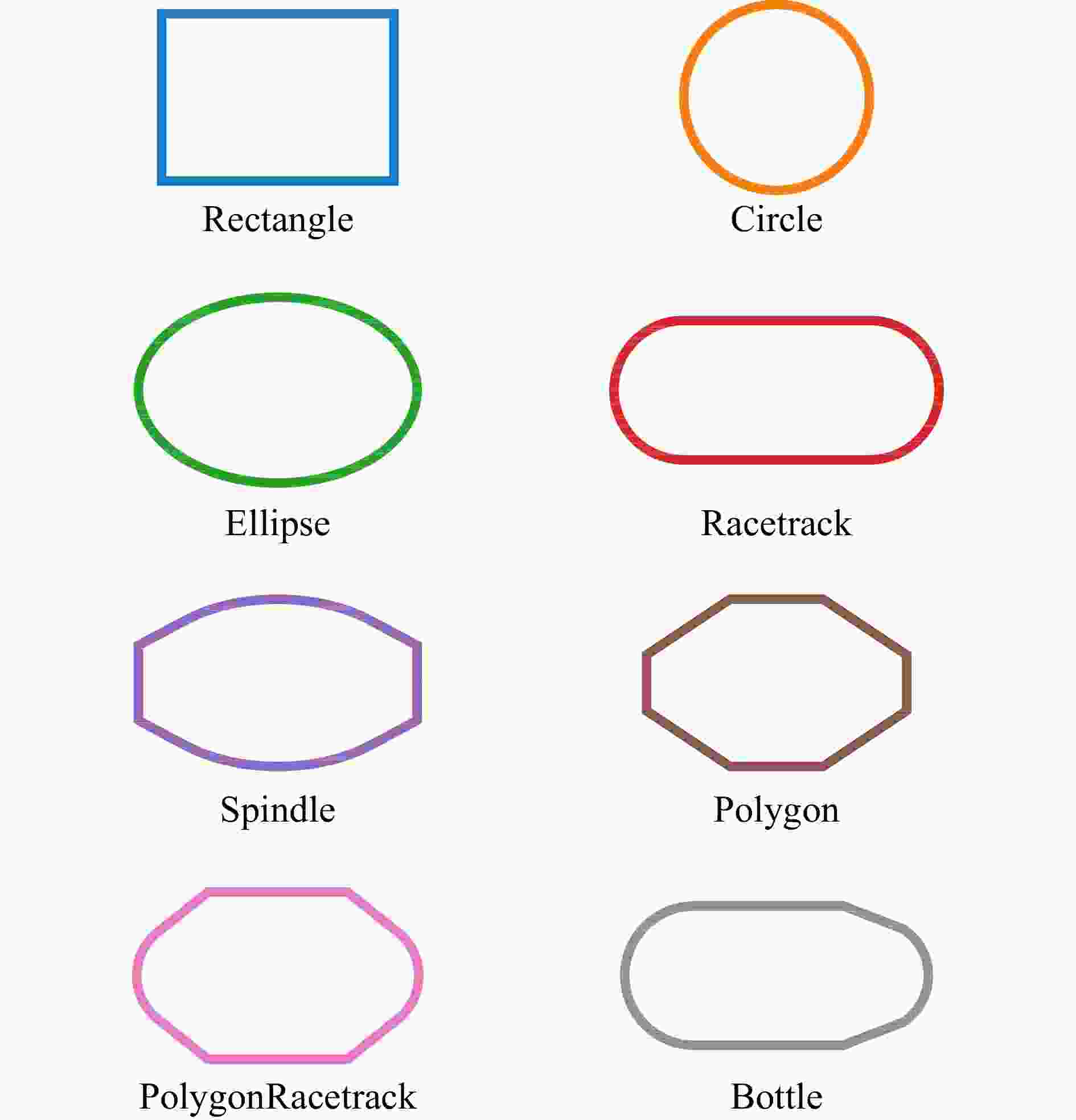
图2列出了几种典型的真空室孔径形状,如常见的圆形、跑道形、椭圆形以及在BRing注入、引出段的异形形状等。在程序中每个加速器元件都有相对应的孔径,当粒子跟踪至元件位置处时,通过比较粒子的坐标和孔径尺寸来判断粒子是否超出损失,一旦粒子坐标超出孔径边界,则该粒子标记为“已损失”而在后续的模拟中跳过该粒子而不再进行传输,同时记录该粒子的信息如损失的位置和时刻以便结果分析。
对于磁铁准直误差的影响以及Twiss函数等其他光学参数的计算方法在文献[20-21]中已有详细描述,由于其形式较为冗长,这里不再赘述。
-
Python[22]是一种面向对象的动态解释型高级编程语言,其诞生于20世纪90年代,历经30余年的发展,目前是世界上最流行的编程语言之一。其语法简单,易于开发,具有众多功能强大的第三方库,非常适合处理对计算性能要求不高但逻辑复杂的任务,经常作为其他语言的“胶水语言”使用。C++[23]是一种发展自C语言的静态类型的、编译式的面向对象编程语言,其结合了低级语言和高级语言的优点,广泛应用于对计算性能要求较高的计算密集型任务。
本程序采用Python和C++混合编程的方式。Python作为程序的主体框架语言,负责程序IO、粒子跟踪预处理以及后续的结果分析。C++语言用以核心粒子跟踪模块,并将其编译为可执行文件供其他模块调用。
-
Json[24]是一种轻量级的数据交换格式,具有清晰和简洁的层次结构,易于阅读、修改和机器的解析和生成,其支持丰富的数据结构,具有和python内置的字典相同的“键-值”属性,另外还具有众多高性能解析库供选择。对于本程序而言,json是非常理想的数据、文件接口格式。此外,对于“表”形式的数据如粒子分布、元件列表和加载的曲线等,采用程序内部数组和外部“csv”文件格式的数据、文件接口。
-
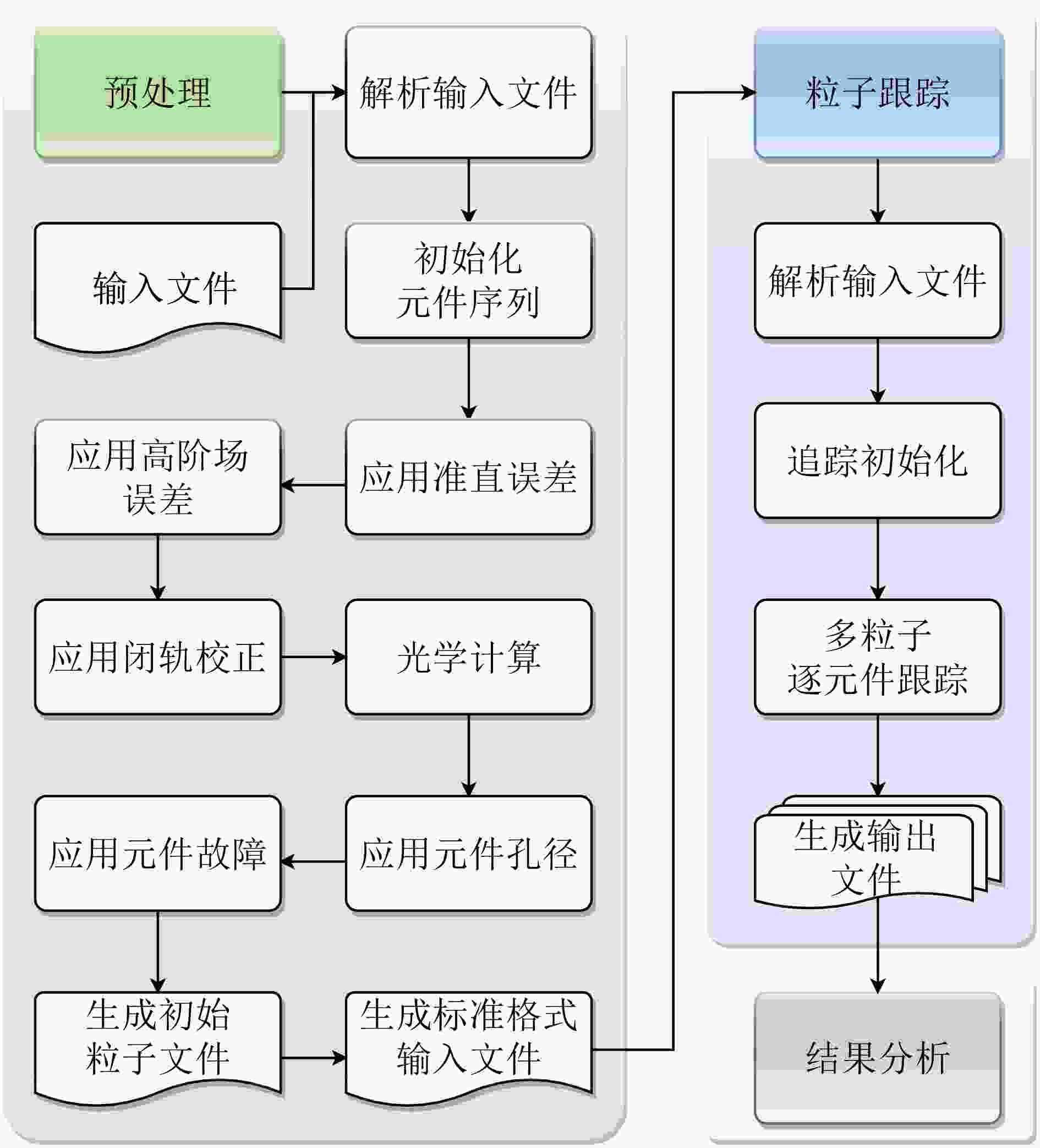
如图3所示,程序采用预处理、粒子跟踪、结果分析三层架构。其中主体框架基于Python编写,粒子跟踪层基于C++开发。每层都由若干模块组成,每个模块之间相互独立,留有标准的IO接口提供数据交换。
预处理层的主要模块功能有:1) 解析输入文件:为了软件的使用方便,可以支持多种格式的输入文件,如“json”自由格式输入文件、“csv”规范格式输入文件,此外还提供了解析MAD-X软件输入文件的功能;2) 初始化元件序列;3) 应用准直、高阶场误差:为每个磁铁元件应用准直误差(
${\rm{d}} x $ ,${\rm{d}} y $ ,${\rm{d}} z $ ,${\rm{d}} \phi $ ,${\rm{d}} \theta $ ,${\rm{d}} \psi $ )和最高20阶的高阶场误差;4) 应用元件孔径:按照输入文件为每个元件定义管道孔径;5) 应用闭轨校正:若有需要,可将轨道矫正至目标值,同时为使用到的校正磁铁定义踢角;6) 粒子生成:生成6D相空间中的粒子;7) 生成标准格式输入文件用以多粒子跟踪层进行读取。粒子跟踪层的主要功能为对初始粒子进行逐元件跟踪,该模块采用C++语言编写,利用OpenMP[25]框架可以充分利用电脑的多个CPU进行并行加速,大大提高计算的速度。
结果分析层主要功能包括束流损失结果统计和分析,在完成跟踪后,可以迅速分析结果并将其可视化表示。
-
在相同的条件下,我们就Twiss参数(包括
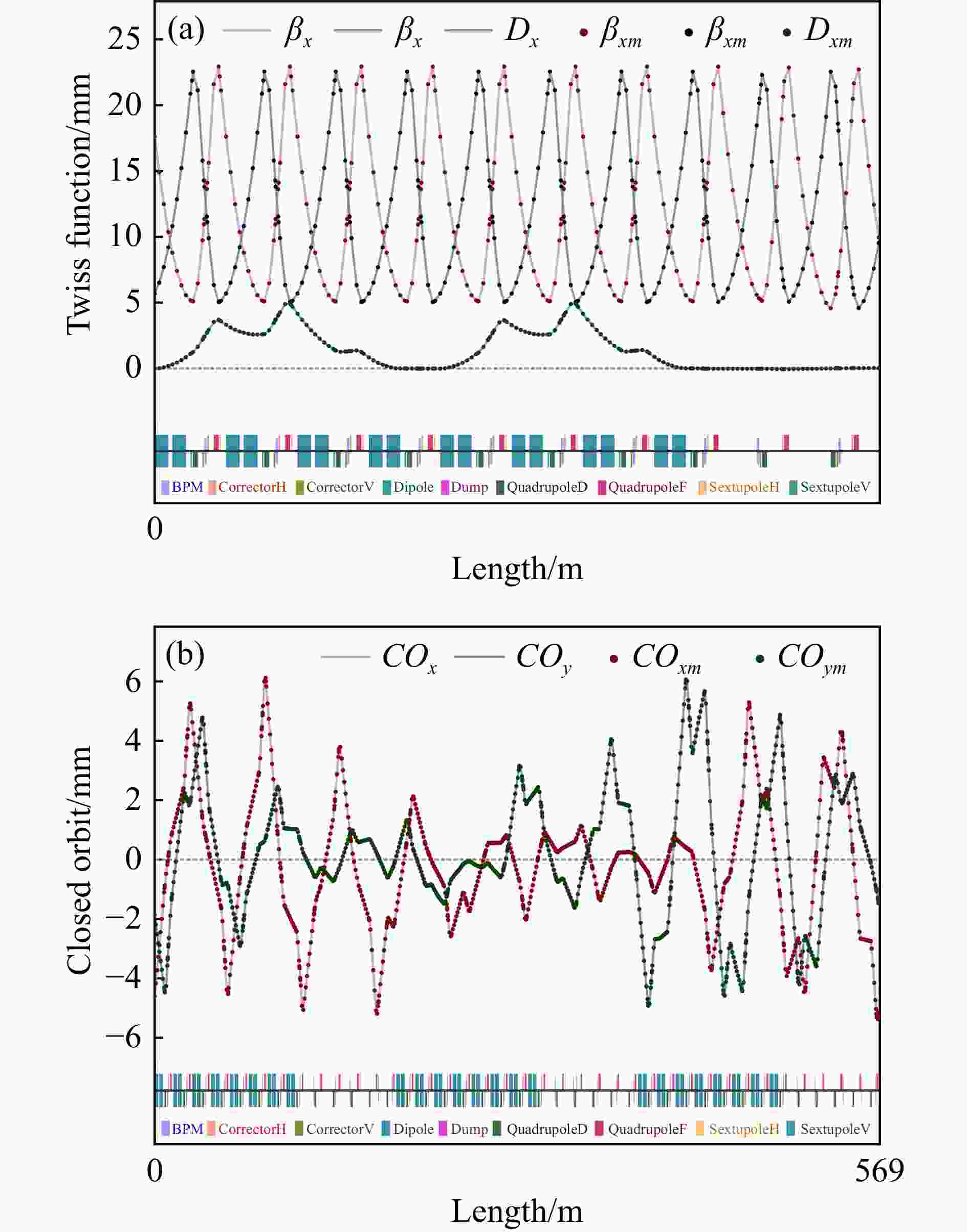
$ \beta $ 函数、色散函数)、误差下的闭合轨道、多粒子跟踪统计的束流发射度稳定性以及betatron工作点和色品这几个方面和MAD-X的模拟结果作了检验。Twiss参数如图4(a)所示,我们选取了BRing三个超周期中的一个,在不考虑各种误差的条件下,本程序计算的
$ \beta_x^{} $ 、$ \beta_y^{} $ 以及色散函数$ D_x^{} $ 均与MAD-X得到的结果完全一致。当考虑了BRing二极磁铁和四极磁铁的安装误差后,我们计算了其中一组误差下的闭合轨道,得到了如图4(b)的结果,其水平方向的闭合轨道$ X_{co}^{} $ 和垂直方向的闭合轨道$ Y_{co}^{} $ 和MAD-X的结果相比亦无区别。我们跟踪10 000个初始宏粒子在环内循环10 000圈的情况,束流的初始分布参数如表2所列,在模拟中我们不考虑安装误差和高阶场误差并逐圈记录所有粒子的坐标。图5统计了束流发射度随圈数变化的情况。结果表明,在10 000圈内,水平和垂直方向的束流发射度均保持稳定,没有增长或收缩情况;而对于更长圈数(
$ 1\times10^7 $ 圈)情况亦是如此。这说明本程序可以用来对束流进行长期稳定跟踪。表 2 多粒子跟踪的束流参数
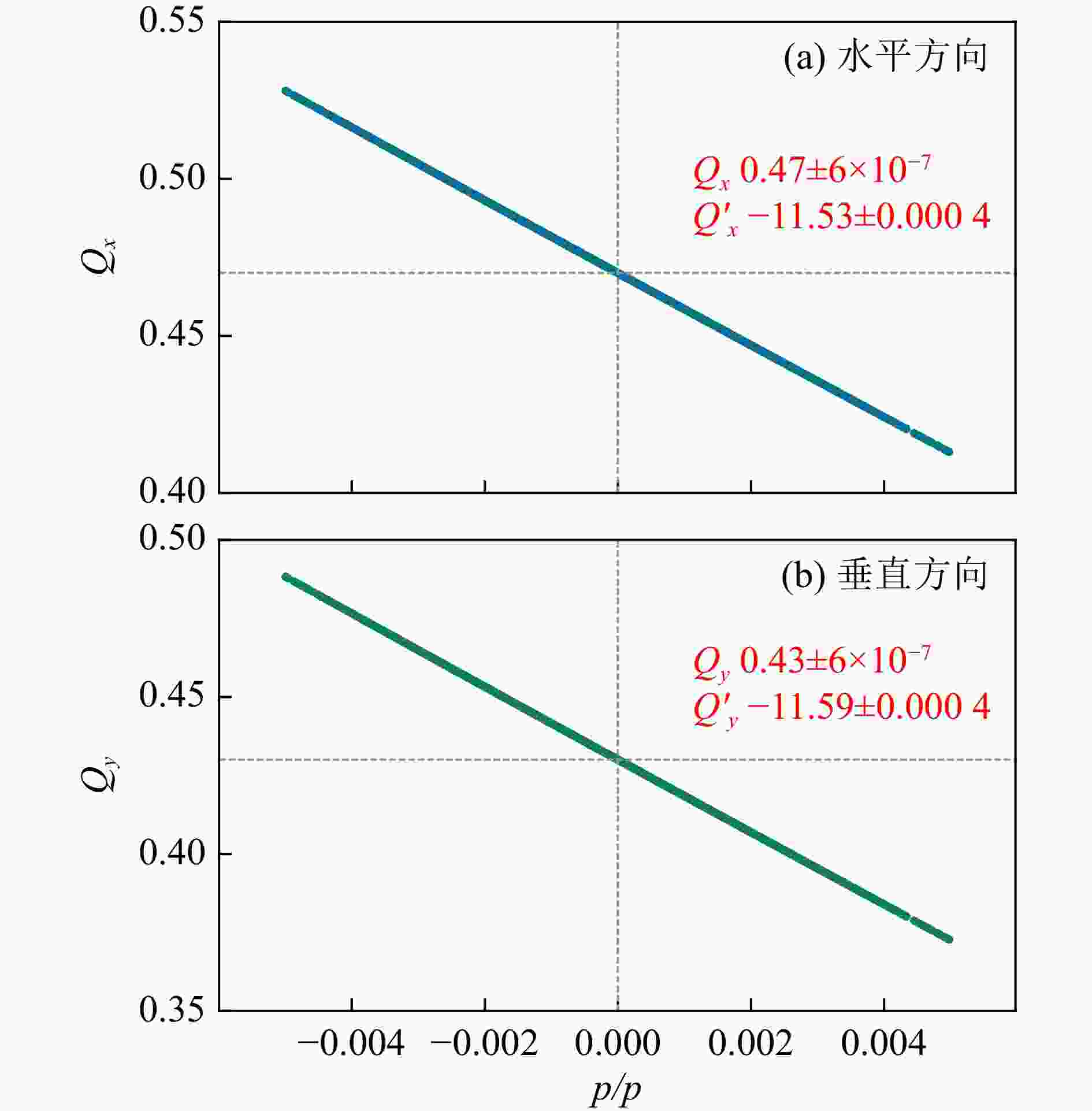
参数 值 束流种类 ${^{238}{\rm{U}}^{35+}}$ 束流能量/(MeV·u−1) 17 束流分布 Gaussian 截断倍数 6 最大发射度/(πmm·mrad) 200/100 统计6倍rms.发射度/(πmm·mrad) 167.2/84.6 基于上述跟踪得到的粒子坐标,我们计算了每个粒子在归一化相空间中的逐圈相移,得到了工作点的小数部分。同时,我们采用多项式拟合的方法得到了统计的工作点和一阶色品,并和MAD-X计算的结果进行了比较(见表3)。如图6所示,除水平方向色品
$ Q_x^\prime $ 外,其余的结果完全一致。$ Q_x^\prime $ 有细微差别的原因是我们跟踪的所用的二极磁铁模型关于动量分散$ \delta p/p $ 是一阶精度的。该差别足够小,对本文要模拟的束流动力学过程几乎没有任何影响。表 3 BRing的betatron工作点、色品与MAD-X计算结果比较
项目 $Q_x^{}$ $Q_y^{}$ $Q_x^\prime$ $Q_y^\prime$ BTracker 0.47 0.43 −11.53 −11.59 MAD-X 9.47 9.43 −11.47 −11.59 -
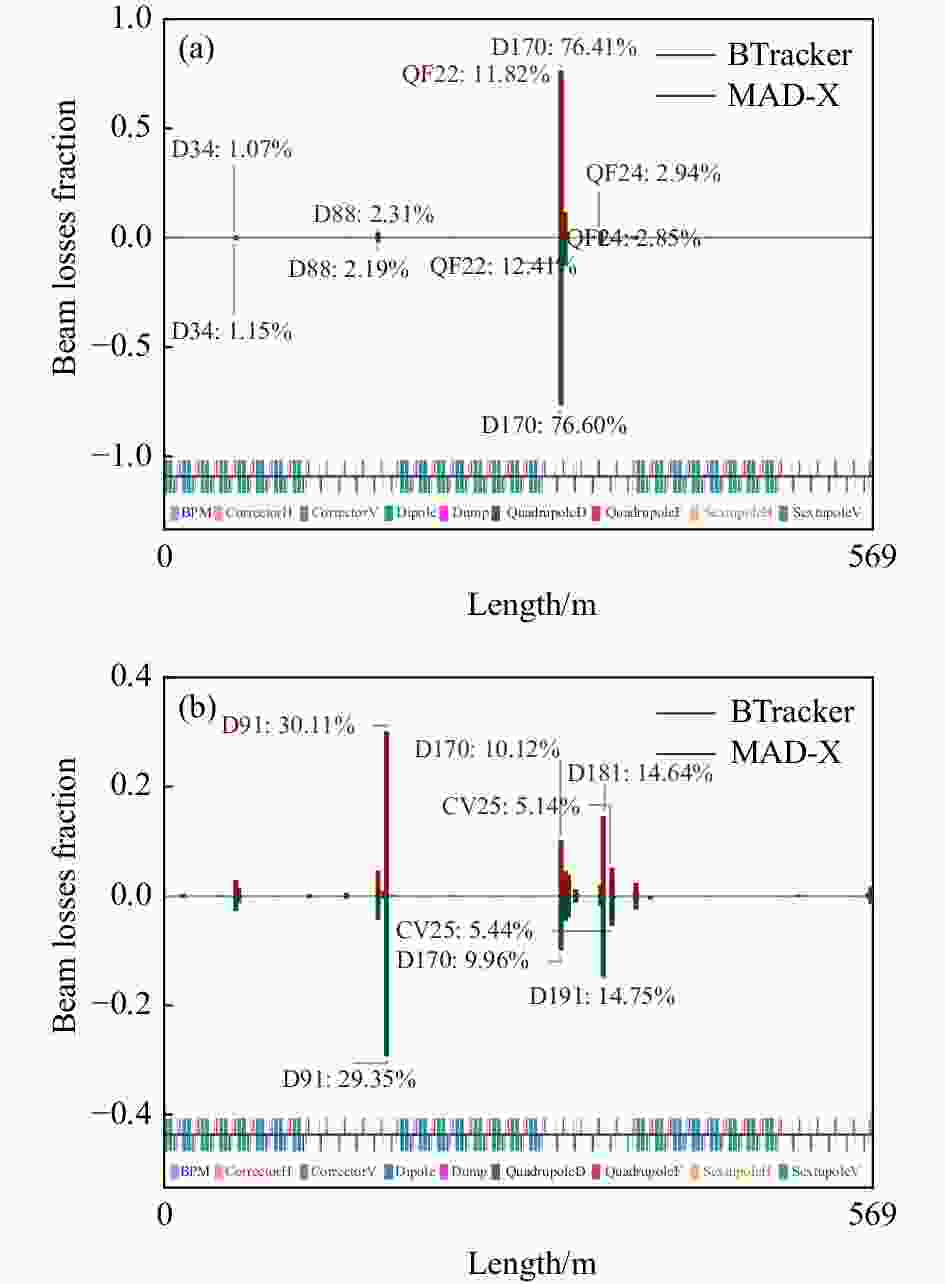
我们模拟BRing中两台典型的二极磁铁和四极磁铁电源故障后的束流损失,并和MAD-X模拟的结果作比较。图7所示为二极磁铁电源PS41D01和四极磁铁电源PS41QD01故障下的束流损失沿全环的分布。可见PS41D01故障后,束流主要损失在D170漂移节和其附近的四极磁铁QF24上,束流损失相对集中,而PS41QD01这台散焦四极磁铁电源故障后,束流损失相对分散,主要损失在D91和D181附近的漂移节上。MAD-X得到的结果和本程序相比,无论是束流损失的主要位置还是每个位置处的束流占比,均有很好的一致性。
图8所示为上述模拟下的束流损失时间分布。结果可见,二极磁铁故障后,束流损失过程较快,束流在250 μs时刻开始损失,在1.5 ms内完全损失掉,而四极磁铁对应的束流损失相对较慢,大约在15 ms的时间内全部损失。以上结果也表明二极磁铁故障相比四极磁铁故障通常会造成更严重的后果。MAD-X软件得到的结果和本程序的模拟结果在时间分布上也是基本符合的。
-
在相同模拟条件下(参数如表4所列)利用Btracker和MAD-X进行了多粒子跟踪,得到了如图9所示的运行时间结果比较,结果表明本程序相较MAD-X在计算性能上有明显的提升。
表 4 多粒子跟踪相关参数
参数 值 CPU Intel Core i9-9900K@3.6 GHz 平台 Windows 10 64 Bit 宏粒子数 10 000 跟踪圈数 10 000 通过外部脚本逐圈修改MAD-X软件的输入文件以改变磁铁的磁场强度,可以实现电源故障下的束流损失模拟,但其存在着使用繁琐和计算速度慢的问题。MAD-X采用Fortran和C++语言编写,由于设计之初并未针对多粒子模拟,相关算法并未做相关优化,并且只能使用单个线程,因此对于多粒子跟踪这种计算密集型任务而言,其速度较慢。对于BTracker,由于其粒子跟踪模块基于C++语言编写,跟踪算法也作了大量的优化以保证基础性能,同时利用CPU缓存和OpenMP并行技术进一步提高运算能力,可以充分、高效地利用计算机资源以实现高性能计算,在速度上较MAD-X有将近80倍的提升。利用该软件我们可以非常迅速地在分钟量级甚至秒量级时间完成模拟,得出结果;而使用MAD-X软件,同样的单次模拟则会需要若干小时的时间。基于BTracker计算性能高的特点,还可以通过多粒子跟踪进行加速器参数优化,这类优化过程通常需要进行非常可观的模拟次数,若使用MAD-X软件,其所需要的耗时将是非常冗长的。在HIAF机器保护模拟研究中本程序已得到应用[19]。
-
在强流机器中,关键设备故障导致的束流损失其影响是非常严重的,为评估该束流损失对HIAF-BRing的影响,为机器保护系统的建设提供参考,进行多粒子跟踪模拟是很有必要的。国际上通用的束流模拟软件如MAD-X存在着使用繁琐、计算速度慢等诸多问题,为此我们自主开发了一套逐元件束流跟踪软件BTracker。基于该软件,我们模拟了BRing的二极磁铁和四极磁铁故障下的束流损失,得到的结果和MAD-X完全一致,并在模拟速度上相比MAD-X有将近80倍的提升。此外,BTracker还保留了灵活的接口、提供了用户友好的使用体验,可以非常方便地和第三方软件集成使用,这为我们在HIAF-BRing研究束流损失和设计机器保护系统提供了良好的条件和有力的通用工具。
The Development of BTracker, a Simulation Code for Beam Losses From Magnet Power Failure
-
摘要: 强流重离子加速器HIAF的增强器BRing具有高流强、高能量的特点,其关键设备如磁铁、高频系统的故障将会造成严重的束流损失和对加速器的损伤。为了研究关键设备故障下的束流损失分布和beam dump过程中的束流动力学,为HIAF机器保护系统建设提供参考,开发了一套通用的逐元件的束流动力学模拟软件BTracker。利用该软件模拟了二极磁铁和四极磁铁电源故障下的束流损失分布并与MAD-X软件作了相互校验,结果符合较好。除此之外,BTracker还具有用户友好、接口灵活以及计算性能优秀的特点,满足HIAF-BRing机器保护研究的需求。Abstract: The booster ring(BRing) of High Intensity heavy-ion Accelerator Facility(HIAF) is characterized by high intensity and high energy. Failures of key equipment such as magnets and RF system will lead to significant beam losses and damage to the accelerator. A beam dynamics simulation code BTracker is developed to study beam losses under equipment failures and beam dynamics during beam dumping for the HIAF machine protrection. With this code, beam loss distribution under power failure of dipole and quadrupole magnets is simulated, and the results are benchmarked with MAD-X code. In addition, BTracker provides user-friendliness, interface flexibility and high performance to meet the requirements of machine protection simulation for HIAF-BRing.
-
表 1 粒子生成算法中参数和对应的分布类型
参数m 束流分布类型 0.0 Hollow shell 0.5 Flat profile 1.0 Uniform 1.5 Elliptical 2.0 Parabolic $\infty$ Gaussian 表 2 多粒子跟踪的束流参数
参数 值 束流种类 ${^{238}{\rm{U}}^{35+}}$ 束流能量/(MeV·u−1) 17 束流分布 Gaussian 截断倍数 6 最大发射度/(πmm·mrad) 200/100 统计6倍rms.发射度/(πmm·mrad) 167.2/84.6 表 3 BRing的betatron工作点、色品与MAD-X计算结果比较
项目 $Q_x^{}$ $Q_y^{}$ $Q_x^\prime$ $Q_y^\prime$ BTracker 0.47 0.43 −11.53 −11.59 MAD-X 9.47 9.43 −11.47 −11.59 表 4 多粒子跟踪相关参数
参数 值 CPU Intel Core i9-9900K@3.6 GHz 平台 Windows 10 64 Bit 宏粒子数 10 000 跟踪圈数 10 000 -
[1] YANG J C, XIA J W, XIAO G Q, et al. Nucl Instr and Meth B, 2013, 317: 263. doi: 10.1016/j.nimb.2013.08.046 [2] HIAF-COLLABORATION. The High Intensity Heavy Ion Accelerator Facility Technical Design Report[R].Lanzhou: IMP Internal, 2018. [3] XIA J W, ZHAN W L, WEI B W, et al. Nucl Instr and Meth A, 2002, 488(1): 11. doi: 10.1016/S0168-9002(02)00475-8 [4] COURANT E D, SNYDER H S. Annals of Physics, 1958, 3(1): 1. doi: 10.1016/0003-4916(58)90012-5 [5] KAIN V. arXiv: 1608.02449. [6] FILIPPINI R, GODDARD B, GYR M, et al. Possible Causes and Consequences of Serious Failures of the lhc Machine Protection System[C]//9th European Particle Accelerator Conference (EPAC 2004). 2004. [7] BRÜNING O S. Mechanisms for Beam Losses and Their Time Constants[Z]. 2001. [8] SCHMIDT R. arXiv: 160802433, 2016. [9] DENIAU L, GROTE H, ROY G, et al.The Mad-x Program User’s Reference Manual[R]. Geneva: CERN, 2017. [10] SCHMIDT F. Sixtrack version 1.2: Single Particle Tracking Code Treating Transverse Motion with Synchrotron Oscillations in a Symplectic Manner; User’s Reference Manual[R]. Geneva: CERN, 1994. [11] BRYANT P. Agile, a tool for Interactive Lattice Design[R]. Geneva: CERN, 2000. [12] GALAMBOS J, DANILOV S, JEON D, et al. Orbit-a Ring Injection Code with Space Charge[C]//Proceedings of the 1999 Particle Accelerator Conference (Cat. No. 99CH36366): volume 5. New York: IEEE, 1999: 3143. [13] GOMEZ A A. Redundancy of the lhc Machine Protection Systems in Case of Magnet Failures[EB/OL].[2022-09-01].http://cds.cern.ch/record/1171279. [14] JOHO W. Representation of Beam Ellipses for Transport Calculations[M]. Villigen: Schweizerisches Institut für Nuklearforschung, 1980. [15] BOX G E P, MULLER M E. Ann Math Statist, 1958, 29(2): 610. doi: 10.1214/aoms/1177706645 [16] ROY R. Journal of East Central Europe, 2002, 545: 5. [17] BROWN K L. First-and Second-order Matrix Theory for the Design of Beam Transport Systems and Charged Particle Spectrometers[R]. California: Stanford Linear Accelerator Center, 1971. [18] KAIN V. Power Converter Failure of the Normal Conducting d1 Magnet at Experiment Insertions ir1 and ir5[R]. Geneva: CERN-LHC-Project-Note-322, 2003. [19] REN H, YANG J CH, SHEN G D, et al. Radiation Detection Technology and Methods, 2022, 6(4): 530. doi: 10.1007/s41605-022-00353-1 [20] ISELIN F C. The Mad Program (Methodical Accelerator Design) Version 8.7 Physical Methods Manual[R]. Geneva: CERN, 1992. [21] DRAGT A J, NERI F, RANGARAJAN G. Annual Review of Nuclear and Particle Science, 1988, 38: 455. doi: 10.1146/annurev.ns.38.120188.002323 [22] VAN ROSSUM G, DRAKE F L. Python 3 Reference Manual[M]. Scotts Valley, CA: CreateSpace, 2009. [23] STROUSTRUP B. The C++ Programming Language[M]. Pearson Education India, 2000. [24] PEZOA F, REUTTER J L, SUAREZ F, et al. Foundations of Json Schema[C]//Proceedings of the 25th International Conference on World Wide Web. International World Wide Web Conferences Steering Committee, 2016: 263. [25] CHANDRA R, DAGUM L, KOHR D, et al. Parallel Programming in Openmp[M]. Massachusetts: Morgan Kaufmann, 2001. -





 下载:
下载:








































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号