-
The charge exchange between partially or fully stripped ions and atomic targets is one of the most important subjects to be studied in ion-atom collisions. One- and two-electron atoms are the fundamental systems employed in experiments and theories to test atomic processes. The knowledge obtained from fundamental theoretical and experimental studies can be applied in different fields, such as plasma and astrophysics. Various theories including quantal and semiclassical approaches[1-3] have been developed to understand the electron-transfer process in ion-atom collisions. In all these approaches, a classical model is being studied, not only because it is simple and timesaving, but because it allows us to get physical insight through the analytical formulas. The first classical description of electron capture in collisions of highly charged ions with atoms was provided by Bohr and Lindhard[4]. The Bohr-Lindhard (B-L) model is expected to be valid at low and intermediate velocities. Instead, for very low velocities
$ v\ll {v}_{\rm e} $ , with ve the orbital velocity of the target electron, calculations may be performed in the framework of the Molecular Orbital(MO) model[5] or Over Barrier Model(OBM)[6].Many extended calculations have been carried out in the frame of the B-L model. Brandt[7] introduced the impact-parameter dependence into the B-L model, incorporating the different times within the capture sphere spent by projectiles with different impact parameters, with an exclusion of the contribution from large impact parameters in his calculation. Thereafter, the impact-parameter dependence of the electron-capture probability was further derived by considering the spatial distribution of target electron[8-11]. However, the multiple numerical integral had to be carried out.
In this work, the impact-parameter dependence of the electron-capture probability is predicted to be an exponentially decaying function. In the framework of the B-L model, the electron-capture processes in collisions of ions with hydrogen and helium atoms are investigated in the velocity range of 0.5~8 a.u.. The reactions are of the form,
$$ {\mathrm{A}}^{q+}+\mathrm{H}\to {\mathrm{A}}^{\left(q-1\right)+}+{\mathrm{H}}^+, $$ (1) $$ {\mathrm{A}}^{q+}+\mathrm{H}\mathrm{e}\to {\mathrm{A}}^{\left(q-2\right)+}+{\mathrm{H}\mathrm{e}}^{2+}, $$ (2) where Aq+ represents the projectile with the charge state q. Except where otherwise stated, atomic units (ћ=me=e=1) will be used throughout.
-
According to the B-L model[4], the electron is released from the target atom at an internuclear separation RR, at which the Coulumb force from the projectile attracting the electron is equal to the binding force by the target nucleus, i.e.,
$\frac{q}{{R}^{2}_{\rm R}}\!=\!\frac{{v}_{\rm e}^{2}}{a}$ , where a and ve are the orbital radius and velocity of target electron, respectively. A released electron may be captured when the potential energy of the projectile is sufficiently strong to the kinetic energy of the released electron in the frame of the projectile. The critical distance for electron capture RC can be determined by$-\frac{q}{{R}_{\rm C}}+\frac{1}{2}{v}^{2}\!=\!0$ , where v is the projectile velocity. The geometrical capture cross section is given by${\sigma }_{\mathrm{C}}\!=\!\pi {R}_{\mathrm{R}}^{2}$ at the condition of RR<RC, suggesting that the capture cross section is independent of the impact velocity in the lower energy region. However, at higher velocities, due to RC<RR a released electron is not always captured. The electron-capture probability within the distance RC is written as$\xi \!=\!\left({R}_{\mathrm{C}}/v\right)\times $ $ \left(1/\tau \right)$ , where τ is given by the order of the electron period. Thus, the electron-capture cross section can be given as${\sigma }_{\mathrm{C}}\!=\!\pi {R}_{\mathrm{C}}^{2}\xi$ .Grozdanov[12], who revised the electron Hamiltonian in terms of prolate spheroidal coordinates and solved the Hamilton–Jacobi equation, has investigated the role of classically allowed, over-barrier transitions in determining the electron capture cross section. For the atomic hydrogen target in its ground state, the release distance is defined by
${R}_{0}\!=\!2\times $ $ {\left(2q-1\right)}^{1/2}$ . In the present calculation, the release distance RR in the B-L model is replaced by R0. The critical velocity${v}_{1}\!=\!{q}^{1/2}{\left(2q-1\right)}^{-1/4}$ is defined by RC=R0. Because only the electron released from the target may be captured, the capture radius can be written as RC≡R0 at velocities below v1. Thus the electron-capture cross section in the whole energy region can be written as$$ {\sigma }_{\mathrm{C}}=\pi {R}_{\mathrm{C}}^{2}\xi . $$ (3) Further, the chance of electron gaining the necessary momentum for capture increases with the electron orbital velocity, thus, we have employed the release rate
$1/\tau\! =\!{v}_{\rm e}$ .In the present work, the impact-parameter dependence for one-electron-capture probability is supposed as an exponentially decaying function[13-14]
$$ {P}_{\mathrm{C}}\left(b\right)={P}_{\mathrm{C}}\left(0\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-b/R\right). $$ (4) It is obvious that b=R corresponds to the impact parameter where the reduced probability bPC(b) is maximum, i.e., largest contribution to the total cross section at impact parameter R. In terms of the above discussion, parameters PC(0) and R may be chosen in the way, PC(0)=ξ and
$ R\!=\!{R}_{\mathrm{C}}/\sqrt{2} $ . In this case, the electron-capture cross section can be calculated by$$ {\sigma }_{\mathrm{C}}=2\pi {\int }_{0}^{\infty }\mathrm{d}b b{P}_{\mathrm{C}}\left(b\right)=\pi {R}_{\mathrm{C}}^{2}\xi. $$ (5) For the helium target, two electrons may be treated independently based on the independent electron approximation (IEA)[15]. The impact-parameter dependence for the one-electron-capture probability can be given by
${P}_{\mathrm{C}i}\left(b\right)\!=\!{P}_{\mathrm{C}i}\left(0\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-b/\left({R}_{\mathrm{C}i}/\sqrt{2}\right)\right)$ , where subscript$i\!=\!1$ or 2 represents the first or the second electron, respectively, and the electron-capture distance${R}_{\mathrm{C}i}\!=\!2{q}_{i}/{v}^{2}$ . According to the Grozdanov’s work[12, 16] the release distance can be expressed as${R}_{0i}\!=\!2{\left(2{q}_{i}/{Z}_{i}^{*3}-1/{Z}_{i}^{*2}\right)}^{1/2}$ , where${Z}_{i}^{*}\!= $ $ {\left(-2{n}^{2}{I}_{i}\right)}^{1/2}$ is the target effective charge, n is the quantum number of the initial orbital and$ {I}_{i} $ is the binding energy. The impact-parameter dependence of the double-electron-capture probability is given by${P}_{\mathrm{D}\mathrm{C}}\left(b\right)\!=\!{P}_{\mathrm{C}1}\left(b\right)\times $ $ {P}_{\mathrm{C}2}\left(b\right)$ . Finally, the double-electron-capture cross section can be obtained by the integral$$ {\sigma }_{\mathrm{D}\mathrm{C}}=2\pi {\int }_{0}^{\infty }\mathrm{d}b b{P}_{\mathrm{D}\mathrm{C}}\left(b\right). $$ (6) It should be noted that, based on the B-L model, the cross section as a function of the incident velocity will be discontinuous at
$v\!=\!{v}_{1}$ if${P}_{\mathrm{C}}\left(0\right)\!\ne\! 1$ . To avoid this problem, the electron-capture probability${P}_{\mathrm{C}}\left(0\right)\!=\!\left({R}_{\mathrm{C}}/v\right)\left(1/\tau \right)$ is applied in the whole velocity range. However, PC(0) may exceed unity at the velocity$ v<{v}_{2} $ , with v2 critical velocity defined by PC(0)=1. To ensure${P}_{\mathrm{C}}\left(0\right)\leqslant 1$ for all velocities we have capped the PC(0) by PC(0)=1 if PC(0)>1. -
In Fig. 1 the calculated cross sections for electron capture by Aq+ (q=2~6) from atomic hydrogen are plotted as functions of the projectile velocity and compared with the existing experimental data. It can be seen that the present calculations are in good agreement with the experimental results. Cross sections for different velocity ranges can be given as
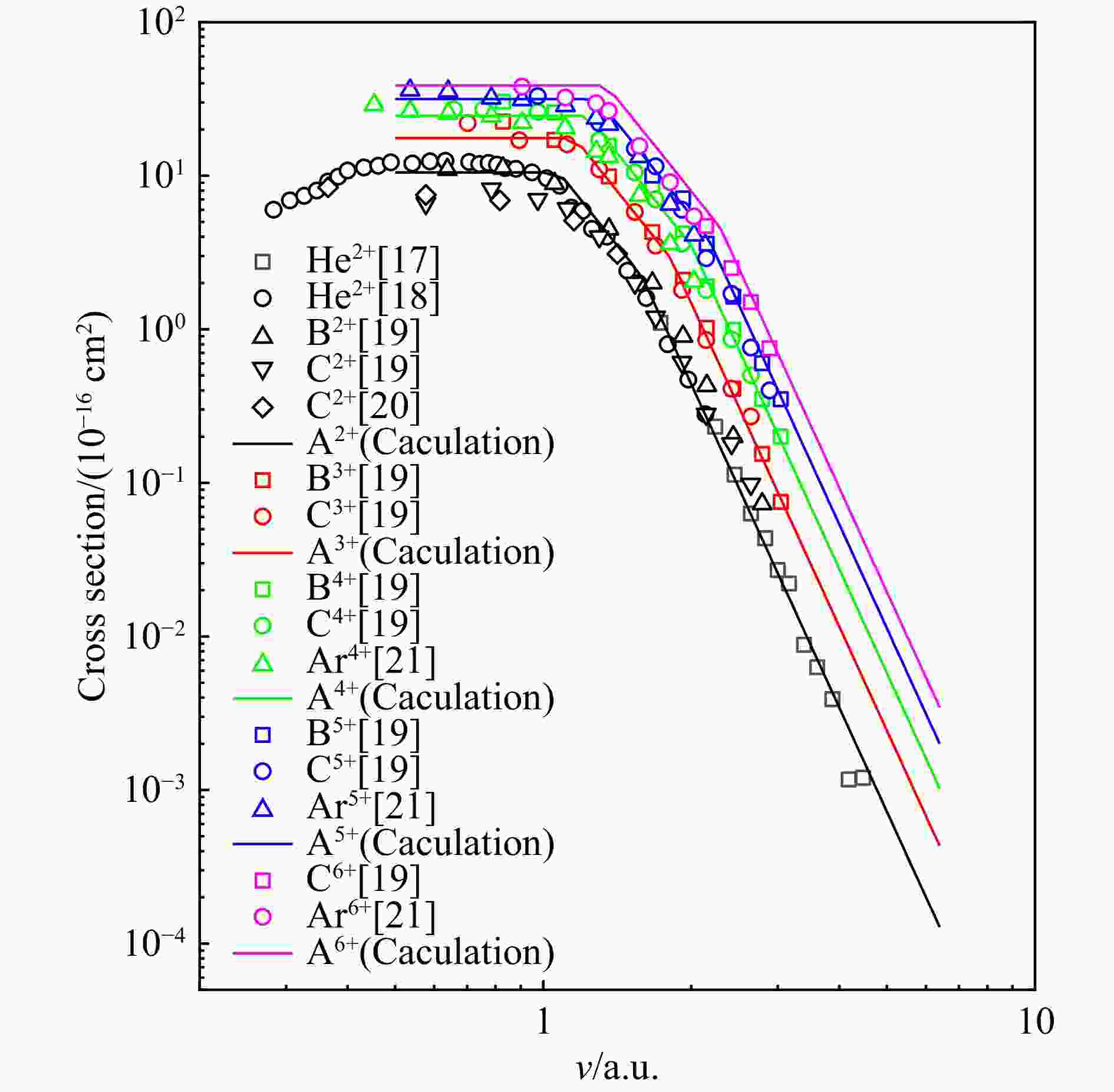
Figure 1. (color online)Cross sections for electron capture of H by the impact of various ions as functions of the incident velocity.
$$ {\sigma }_{\mathrm{C}}=\left\{\begin{array}{ll}\pi {R}_{0}^{2}=4\pi \left(2q-1\right),& v<{v}_{1}\\ \pi {R}_{\mathrm{C}}^{2}=4\pi {q}^{2}{v}^{-4},& {v}_{1}<v<{v}_{2}\\ \pi {R}_{\mathrm{C}}^{2}\left(\dfrac{{R}_{\mathrm{C}}}{v} \cdot \dfrac{1}{\tau }\right)=8\pi {q}^{3}{v}^{-7},& v>{v}_{2}\end{array}\right.. $$ (7) At the impact velocities below v1 the capture cross section is independent of the projectile velocity because RC≡R0 and PC(0)≡1. The cross section is only determined by the critical capture radius RC in the velocity range v1<v<v2 because PC(0) is still equal to 1. As a result, the decay of the cross section behaves as
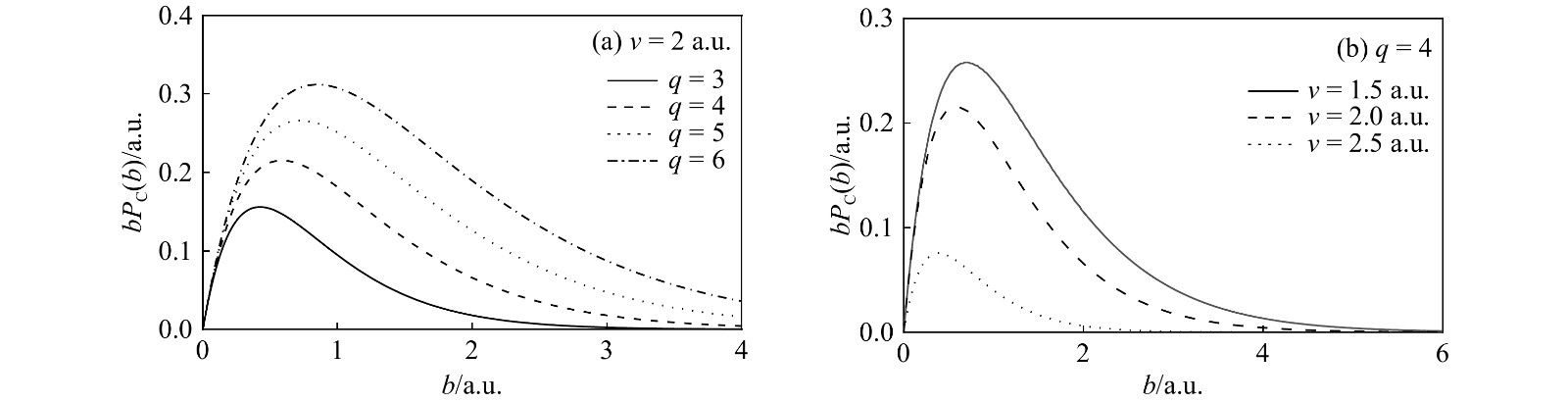
$ {v}^{-4} $ . When the velocity is further increased, the release probability for the target electron decreases due to the lack of the collision time. At the same time, the released electron cannot be effectively accelerated from the target to the projectile. Thus, this leads to the capture cross section to decrease rapidly as$ {v}^{-7} $ in the velocity range$v \! > \! {v}_{2}$ . In velocity ranges$v \! < \! {v}_{1}$ ,${v}_{1} < v < {v}_{2}$ and$ v>{v}_{2} $ , the present results give q, q2 and q3 scaling, respectively. Thus, the behavior of the cross section as a function of the projectile charge q is also of interest in the present study.Figure 2(a) and (b) show the impact-parameter dependences of the electron-capture probability, from which the cross section behavior with dependence on q and v can be studied in more detail. As seen from Fig. 2(a), the peak at
${b}_{\mathrm{m}\mathrm{a}\mathrm{x}}\!=\! {R}_{\mathrm{C}}/\sqrt{2}$ is shifted towards the larger b value with the increasing projectile charge q. This indicates that the electron transfer is more likely to occur at larger impact parameters due to the stronger field of the projectile. On the other hand, the smaller internuclear separation is required for the fast collision because the Coulomb potential energy in the field of Aq+ has to balance the final electronic translational kinetic energy. As, it can be seen in Fig. 2(b), the peak is shifted towards the smaller value of b with the increasing impact velocity, suggesting the increasing importance of closer collisions during capture process in fast collisions.In the double-electron-capture process for the helium target, once one of the target electrons is captured, a stronger coulomb field from the target nucleus will be felt by the remaining electron. Meanwhile, the screening effect of the captured electron results in the reduction of the projectile charge state. Therefore, two electrons of helium can be treated in different ways. The binding energies are conveniently chosen as I1=–0.903 a.u. and I2=–2 a.u., and the projectile charge states as q1=q and q2=q–1. The velocity dependences of the calculated double-electron-capture cross sections in collisions of Aq+ (q=3~6) with helium are compared with the experimental data in Fig. 3. The theoretical results are in good agreement with the experimental data, indicating that our simple treatment within the IEA is valid for this system. This simple method gives the double-electron-capture probability as
${P}_{\mathrm{D}\mathrm{C}}\left(b\right)\!=\!{P}_{\mathrm{D}\mathrm{C}}\left(0\right)\mathrm{exp}\left(-\sqrt{2}b/{R}_{\mathrm{D}\mathrm{C}}\right)$ , where${P}_{\mathrm{D}\mathrm{C}}\left(0\right)\!=\!{\left(\sqrt{{R}_{\mathrm{c}1}{R}_{\mathrm{c}2}}/v\right)}^{2}$ and the double-electron-capture radius$ {R}_{\mathrm{D}\mathrm{C}}={R}_{\mathrm{C}1}{R}_{\mathrm{C}2}/\left({R}_{\mathrm{C}1}+{R}_{\mathrm{C}2}\right) $ . According to Eq. (6) the double-electron-capture cross section is obtained as${\sigma }_{\mathrm{D}\mathrm{C}}\!=\!\pi {R}_{\mathrm{D}\mathrm{C}}^{2}{P}_{\mathrm{D}\mathrm{C}}\left(0\right)$ . The behavior of the double-electron-capture cross section depends on the different collision velocity ranges, which is divided by the critical velocities defined by${R}_{\mathrm{C}i}\!=\!{R}_{0i}~{\rm and}~{P}_{\mathrm{C}i}\left(0\right)= $ $ 1(i\!=\!1,\mathrm{ }2)$ . In the lower velocity range, the cross section can be given as${\sigma }_{\mathrm{D}\mathrm{C}}=\pi {\big[{R}_{01}{R}_{02}/\left({R}_{01}+{R}_{02}\right)\big]}^{2}$ , which is independent of the velocity. In the higher velocity range the cross section is evaluated as${\sigma }_{\mathrm{D}\mathrm{C}}\!=\!16\pi {\big[q(q-1)\big]}^{3}{\left(2q-1\right)}^{-2}{v}^{-10}$ . Hence one can see that the double-electron-capture cross section, which decreases with the increasing velocity as v–10, and is more sensitive to the collision time than single-electron capture.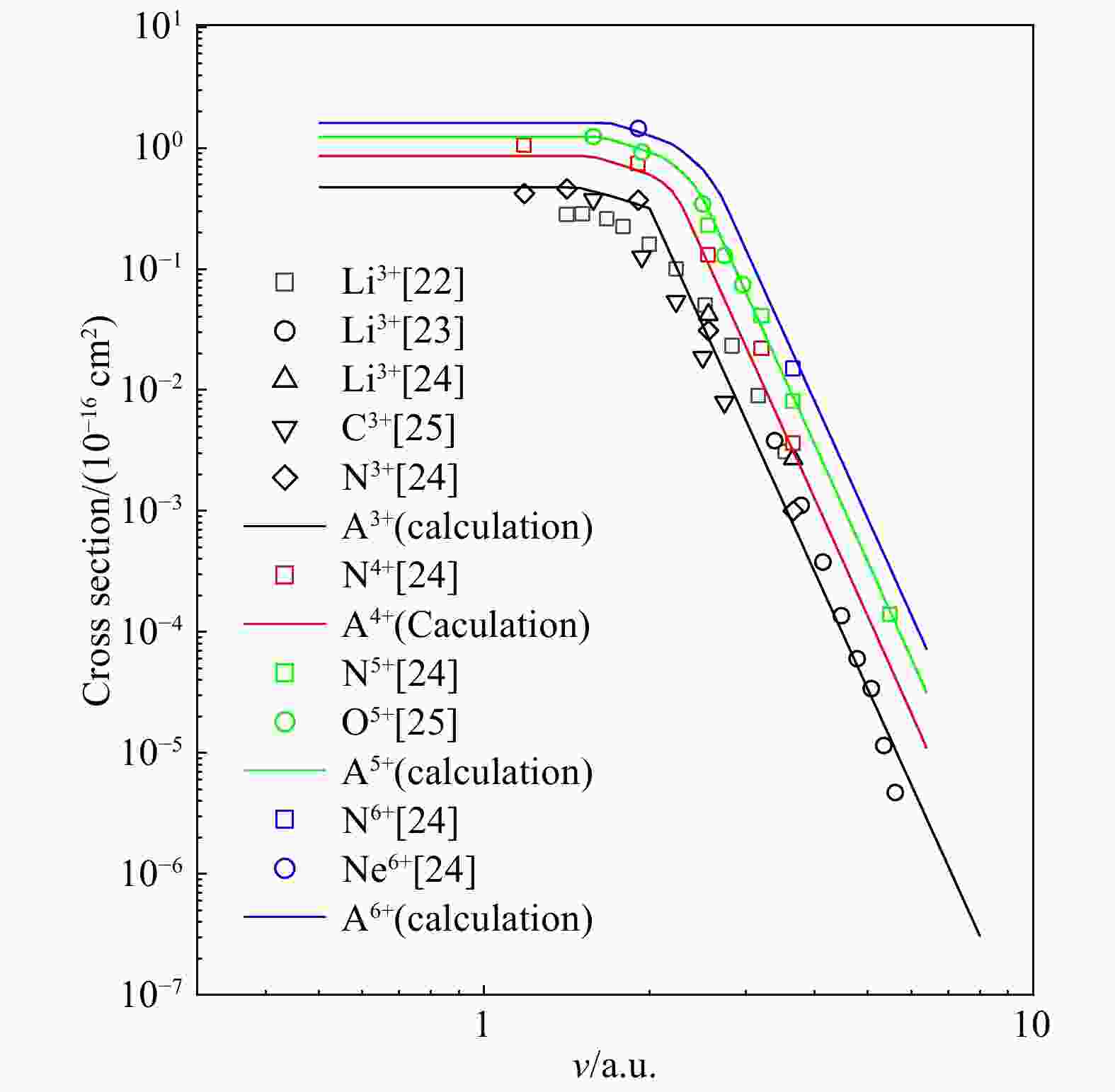
Figure 3. (color online)Cross sections for double-electron capture of He by the impact of various ions as functions of the incident velocity.
Figure 4(a) and (b) show the impact-parameter dependences of the double-electron-capture probability. The impact parameter, with the largest contribution to the double-electron-capture cross section, is at
${b}_{\mathrm{m}\mathrm{a}\mathrm{x}}\!=\!{R}_{\mathrm{D}\mathrm{C}}/\sqrt{2}$ . The bPDC(b) for lower charge states or higher velocities are shifted toward smaller values of b. In addition, it is obvious that the double-electron capture occurs at the distance${R}_{\rm DC}\! < \! \frac{{R}_{\mathrm{C}1}+{R}_{\mathrm{C}2}}{4}$ , a narrower impact-parameter range compared with the one-electron capture. -
Based on the Bohr-Lindhard model, the capture probability is expressed as a simple exponential decay function of the impact parameter. Using this approach, we have calculated the electron-capture cross sections for Aq+(q=2~6)-H collisions, and double-electron-capture cross sections for Aq+(q=3~6)-He collisions in the velocity range from 0.5 to 8 a.u.. Good agreement with the experimental data is obtained. The present method is very convenient, especially for the double-electron capture in Aq+-He collision systems.
Classical Electron Capture in Collisions of Ions with H, He Atoms at Low and Intermediate Velocities
-
摘要: Bohr-Lindhard模型被用来描述中低能速度能区离子—原子碰撞中的经典电子俘获过程。根据离子与原子的作用时间与碰撞参数的关系,建立俘获几率对碰撞参数的依赖性,碰撞参数范围被限定在俘获半径之内。在该模型的框架内,人们试图通过电子的空间分布函数来研究所有碰撞参数的贡献,但存在较为复杂的数值计算。基于Bohr-Lindhard模型,本工作提出通过简单的指数衰减函数来描述电子俘获几率对碰撞参数的依赖性,计算了Aq+(q = 2~6)-H碰撞中的单电子俘获截面和Aq+(q = 3~6)-He碰撞中的双电子俘获截面,计算结果与已有实验数据符合很好,很好地描述了低能和中能区的电子俘获截面随能量和电荷态的变化,该工作还可计算其他不同电荷态离子与He和H靶的电子俘获截面。Abstract: The Bohr-Lindhard (B-L) model is used to describe the classical electron-capture process. The impact-parameter dependence of the capture probability is derived by considering the impact-parameter dependence of the collision time between ion and atom. This model limits the impact parameter to be less than the capture radius. In the framework of the B-L model, although the contribution from all impact parameters may be studied through the spatial distribution function of electrons, the multiple numerical integral has to be carried out. In this work, it is proposed that the impact-parameter dependence of the electron-capture probability can be given by a simple exponential decay function based on the (B-L) model. Electron-capture cross sections for Aq+(q=2~6)-H collisions, and double-electron-capture cross sections for Aq+(q=3~6)-He collisions are calculated at low and intermediate velocities. The calculated results are in good agreement with the existing experimental data. The energy and charge-state dependences of the electron-capture process are well described. This work can also be used to calculate the cross sections of electron capture from He and H targets by other ions with different charge states.
-
-
[1] IGENBERGS K, SCHWEINZER J, VEITER A, et al. J Phys B, 2012, 45: 065203. doi: 10.1088/0953-4075/45/6/065203 [2] ABDURAKHMANOV I B, KADYROV A S, AVAZBAEV S K, et al. J Phys B, 2016, 49: 115203. doi: 10.1088/0953-4075/49/11/115203 [3] ALLADUSTOV S U, ABDURAKHMANOV I B, KADY-ROV A S, et al. Phys Rev A, 2019, 99: 052706. doi: 10.1103/PhysRevA.99.052706 [4] BOHR N, LINDHARD J. Dan Mat Fys Medd, 1954, 28: 1. [5] PANO U, LICHTEN W. Phys Rev Lett, 1965, 14: 627. doi: 10.1103/PhysRevLett.14.627 [6] BÁNÁRY A, ASTNER G, CEDERQUIST H, et al. Nucl Instr and Meth B, 1985, 9: 397. doi: 10.1016/0168-583X(85)90332-5 [7] BRANDT D. Nucl Instr and Meth B, 1983, 214: 93. doi: 10.1016/0167-5087(83)90545-8 [8] BEN-ITZHAK I, JAIN A, WEAVER O L. J Phys B, 1993, 26: 1711. doi: 10.1088/0953-4075/26/11/007 [9] DING B W, WANG B H, HU B T. Phys Lett A, 2009, 373: 3047. doi: 10.1016/j.physleta.2009.06.044 [10] DING B W. Phys Scr, 2012, 85: 015302. doi: 10.1088/0031-8949/85/01/015302 [11] DING B W, LI H CH, ZHANG W J. Int J Mass Spectrom, 2012, 313: 41. doi: 10.1016/j.ijms.2011.12.016 [12] GROZDANOV T P. J Phys B, 1980, 13: 3835. doi: 10.1088/0022-3700/13/19/022 [13] DUBOIS R D. Phys Rev A, 1987, 36: 2585. doi: 10.1103/PhysRevA.36.2585 [14] GALASSI M E, RIVAROLA R D, FAINSTEIN P D. Nucl Instr and Meth B, 2010, 268: 1637. doi: 10.1016/j.nimb.2010.03.003 [15] CROTHERS D S F, MCCARROLL R. J Phys B, 1987, 20: 2835. doi: 10.1088/0022-3700/20/12/027 [16] HUANGY M T, STÖCKLIY M P, FEHRENBACHZ C W, et al. J Phys B, 1997, 30: 2425. doi: 10.1088/0953-4075/30/10/016 [17] HVELPLUND P, ANDERSEN A. Phys Scr, 1982, 26: 375. doi: 10.1088/0031-8949/26/5/005 [18] SHAH M B, GILBODY H B. J Phys B, 1978, 11: 121. doi: 10.1088/0022-3700/11/1/016 [19] GOFFE T V, SHAH M B, GILBODY H B. J Phys B, 1979, 12: 3763. doi: 10.1088/0022-3700/12/22/021 [20] PHANEUF R A, MEYER F W. Phys Rev A, 1978, 17: 534. doi: 10.1103/PhysRevA.17.534 [21] SHAH M B, GILBODY H B. J Phys B, 1983, 16: 4395. doi: 10.1088/0022-3700/16/23/021 [22] SHAH M B, GILBODY H B. J Phys B, 1985, 18: 899. doi: 10.1088/0022-3700/18/5/010 [23] SANT'ANNA M M, SANTOS A C F, COELHO L F S, et al. Phys Rev A, 2009, 80: 042707. doi: 10.1103/PhysRevA.80.042707 [24] DMITRIEV I S, TEPLOVA Y A, BELKOVA Y A, et al. At Data Nucl Data Tables, 2010, 96: 85. doi: 10.1016/j.adt.2009.09.003 [25] MELO W S, SANT'ANNA M M, SANTOS A C F, et al. Phys Rev A, 1999, 60: 1124. doi: 10.1103/PhysRevA.60.1124 -




 下载:
下载:





















































 甘公网安备 62010202000723号
甘公网安备 62010202000723号