-
束流输运线路系统中磁场的性能会极大地影响粒子束的轨道中心、横向调谐等参数[1]。在特殊的应用场合中,这些参数往往有着严苛的要求[2-4]。以离子探针(SIMS)为例,其使用加速的离子束轰击样品表面,并通过分析产生的二次离子荷质比来确定样品表面元素组成[5]。磁场的性能将直接影响离子束轰击的位置以及深度,进而影响同位素分析质量。而直接通过磁铁电源给定恒定励磁电流的开环控制方式,磁场常因为电源性能以及励磁带来的涡流效应等原因而发生偏移[6],难以满足性能要求。因此需要为高稳定性磁场的需求设计闭环控制系统。
当前实现高稳定磁场的方案可以分为两种。其一是在对磁铁进行建模的基础上,使用输入磁铁的励磁电流或电压作为反馈。将电源输出电流/电压与负载参数进行匹配,从而实现高性能的磁铁电源,以达到提升磁场品质的作用[7-9]。但磁铁作为巨大的感性元件,其电感值在不同的电流下可能会发生畸变[10]。该现象将会给控制系统带来扰动,影响磁场的稳态性能。且会对磁铁的建模产生影响,方法,在一定程度上削弱了畸变电感值的影响。但这种基于建模的方法仍有可能受环境影响而导致导致电流与负载参数的失配。其二是使用磁场系统的磁场值作为反馈。根据磁铁的电流-磁场(I/B)关系对电源进行补偿,间接提升电源性能,从而实现磁场反馈控制[11-12]。这种类似查表的反馈控制工作点偏离。
上述两种方案都需要对系统进行建模,且在应对环境中可能出现的随机扰动方面也略有欠缺。因此,本文设计了基于PID算法的磁场闭环控制系统。
-
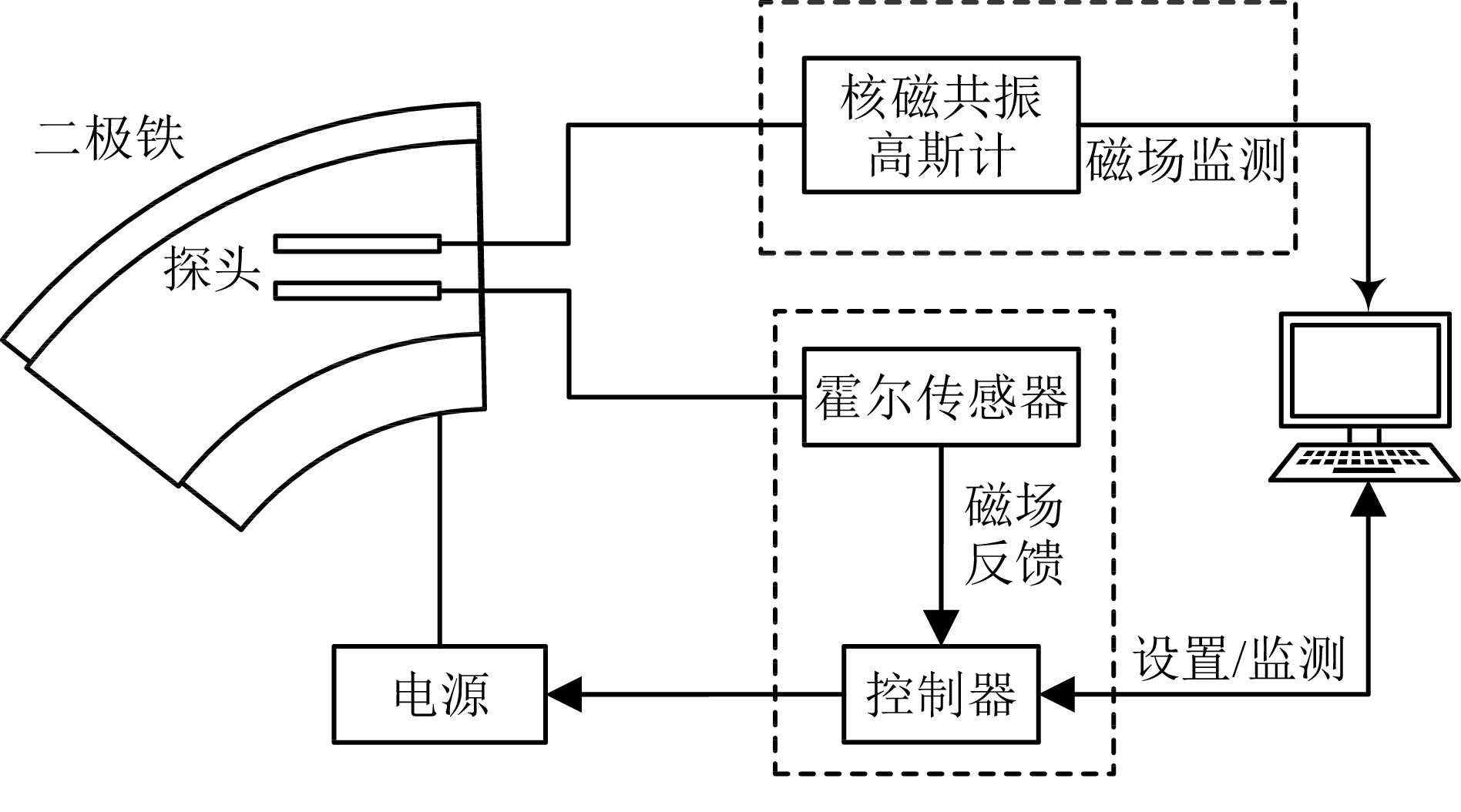
本闭环控制系统由磁场反馈控制系统和磁场监测系统两个子系统构成。系统结构如图1所示。为保证磁场测量与反馈的两个子系统的探头处于同一匀场区,被控对象选择好场区大的用于束流偏转的二极磁铁。
反馈控制子系统负责磁场控制。此部分由霍尔传感器、PID控制器以及电源组成。霍尔传感器为反馈控制回路的测量元件,实时采集磁场数据并返回模拟量。电源为执行机构,接收控制信号并输出相应的电流。控制器内运行PID算法,完成磁场数据的AD转换并进行补偿。计算机为控制器设定预期的磁场值后,控制器接收霍尔传感器所采集到的磁场值,并经PID算法计算后,输出相应控制量对电源输出的励磁电流进行调整,从而保证磁场稳定。
磁场监测子系统负责磁场监测。此部分使用核磁共振高斯计完成对磁场的测量。实现对霍尔传感器模拟量与磁场值的标定。并对磁场稳态性能进行实时监测,且保证霍尔传感器不会因老化而导致工作点漂移。计算机接收高斯计所测量的磁场值,可以通过上位机界面对磁场变化的实时监测,并将磁场数据保存到磁盘中,以便进行后续的分析。
-
PID控制因无需对被控对象进行建模,控制性能好,而在工业中应用广泛。其原始数学表达如式(1)所示[13]:
$$ {u}(t) = {K_{\text{p}}}\left[ {e(t) + \frac{1}{{{T_i}}}e(t){\text{d}t + }}{{{T}}_{\text{d}}}\frac{{{\rm d}e(t)}}{{\rm d} t} \right] , $$ (1) 式中:u(t)为控制系统输出量;e(t)为设定值与反馈值的误差;Kp为控制系统的比例系数;Ti为控制系统的积分时间;Td为控制系统的微分时间。
由于系统使用数字控制器,因此需要对PID算法进行离散化。离散PID控制算法可分为增量式PID和位置式PID两种。其数学表达如式(2)~(3)所示,式(2)为增量式PID算法,式(3)为位置式PID算法[14]:
$$\begin{split} \Delta u(k) =& {K_{\text{p}}}\big[ {e(k) - e(k - 1)} \big] + {K_i}e(k) + \\&{K_{\text{d}}}\big[ {e(k)} -{ 2e(k - 1) + e(k - 2)} \big] ,\end{split} $$ (2) $$ u(k) = {K_{\text{p}}}e(k) + {K_i}\sum\nolimits_{i = 0} {e(i) + {K_{\text{d}}}} \big[ {e(k) - e(k - 1)} \big]{\text{。}}$$ (3) 其中:Ki为控制系统的积分系数;Kd为控制系统的微分系数;k为当前时刻;u(k)为当前时刻输出;Δu(k)为当前时刻输出与上一次输出的差值;
$ \sum\nolimits_{i = 0} {e(i)} $ 为累加时刻k以前的所有误差。由式(2)~(3)可知,增量式PID是一种递推式的算法,其输出的Δu(k)是本次输出的控制量的增量,该增量只于最近的几次采样偏差有关。而位置式PID则是非递推式的算法,其直接计算出当前所需要的控制量,过去每一时刻的状态都会影响当前的输出。
增量式PID输出的控制量是由多个增量合成,有可能会出现截断效应,该效应会使得控制量出现尖峰。在磁场控制中,电源输出的尖峰会在磁体中形成谐振而使得磁场发生震荡。同时,磁铁以及电源属于不带积分元件的被控对象,位置式PID算法对不带积分元件的被控对象有较好的控制效果[15]。因此本控制系统中选择位置式PID作为控制算法。
-
PID参数整定是该磁场控制系统极为重要的一环。PID参数采取不同的设定策略,将会对磁场控制性能产生不同的影响。
二极磁铁这一被控对象可以简化为含有滞后环节的阻感元件。整个系统的控制过程可以使用一阶惯性环节加纯滞后模型来近似描述。基于此可为被控对象建立如式(4)的传递函数:
$$ G(s)=\frac{K{\text{e}}^{-\tau \text{s}}}{Ts+1} , $$ (4) 其中:K、
$ \tau $ 、T分别为磁场控制系统模型的开环增益、纯滞后时间常数和惯性时间常数。在使用如式(1)的经典PID控制器的情况下,可以得到整定PID控制器参数的Ziegler-Nichols经验公式[16],如式(5)所示:
$$ \left\{ \begin{array}{l} {K_{\rm{p}}} = \dfrac{{1.2T}}{{K\tau }}\\ {T_i} = 2\tau \\ {T_{\rm{d}}} = 0.5\tau \end{array} \right. {\text{。}} $$ (5) 将控制系统中所使用二极磁铁测定的各项常数代入到经验公式,即可求得该控制系统的PID整定参数。
-
受现场复杂环境的影响,往往需要根据模型所计算的整定参数附近进行重新调整,才能取得最好的控制性能。而PID参数的调整,将直接影响磁场稳态时的表现。下面针对部分整定参数对磁场稳定度产生的影响进行讨论。
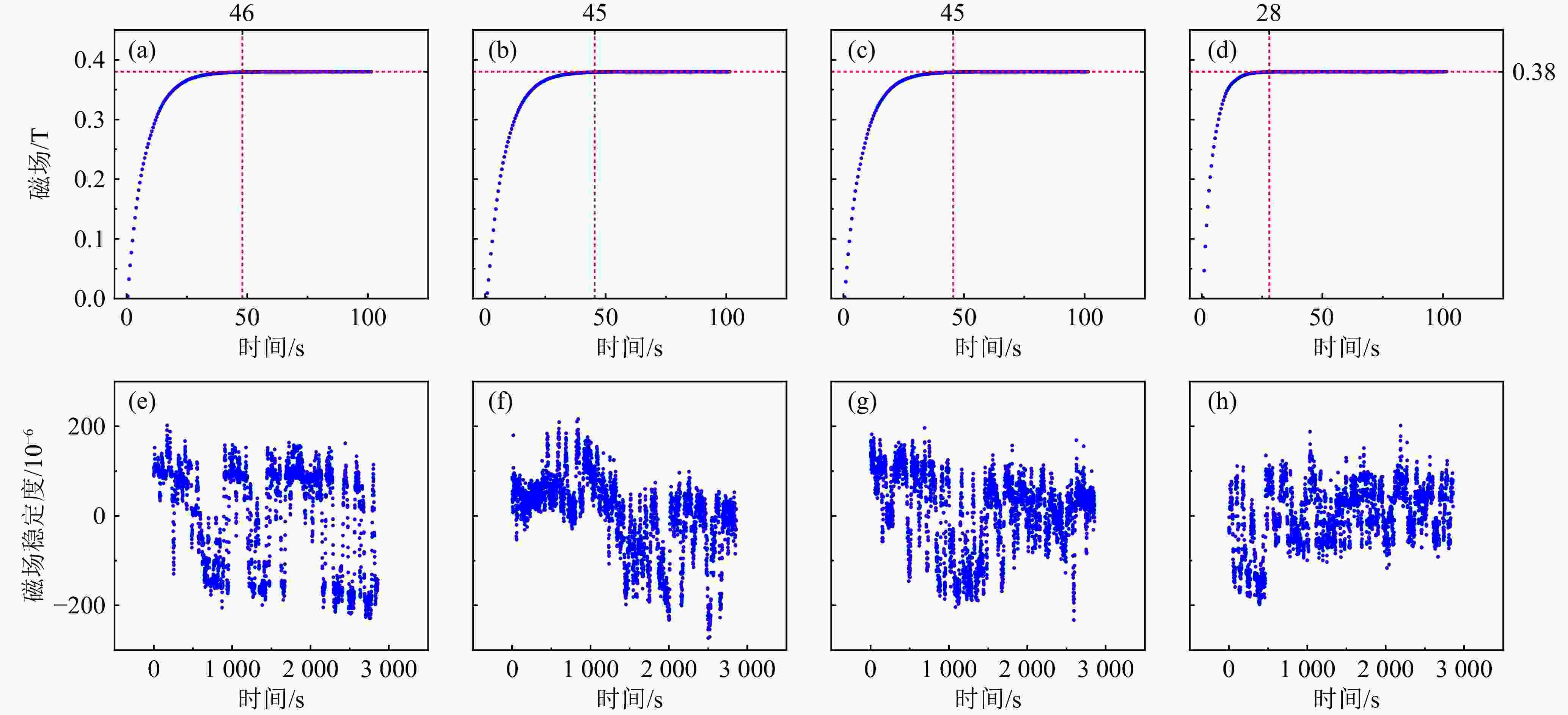
设定P=0.081, I=0.012 3, D=0.005 18,其磁场以及稳定度变化分别如图2(a)与(e)所示。系统在46 s后达到稳态。其磁场在10–6附近呈现约±200×10–6较为均匀的小幅度震荡。
适当增大P值,设定P=0.15, I=0.012 3, D=0.005 18,其磁场以及稳定度变化如图2(b)与(f)所示。可以发现,小幅增大P值后,磁场进入稳态的时间得到了加快,在45 s时达到稳态。进入稳态后磁场震荡幅度相对减少,震荡频率有所加快。但由于I值较小,使得系统出现了稳态误差,如图2(f),磁场在500~1 000 s出现持续地偏差,磁场的稳态工作点发生变化,磁场最终在–50×10–6的位置上下波动。
适当增大D值,设定P=0.081, I=0.012 3, D=0.010 18,其磁场以及稳定度变化如图2(c)以及图2(g)所示。磁场进入稳态的时间减小,磁场振幅降低,但磁场的振荡频率增加。
适当增加I值,设定PID值为P=0.081, I=0.022 3, D=0.005 18,其磁场以及稳定度变化如图2(d)以及图2(h)所示。可以发现,其磁场达到稳态的时间明显加快,在28 s即可达到稳态。且在稳态后,磁场的振荡幅度也有所下降。但由于在磁场上升初期所产生的误差累积,磁场达到稳态初期,会出现较大地振幅。因此I参数的设置应相对谨慎,其值若偏大,将会导致磁场性能地急剧恶化,甚至导致磁场无法稳定。
-
当磁场控制系统处于开环状态时,反馈回路断开。根据磁铁I/B曲线,将电源输出的励磁电流设定为恒定值。对开环状态下的磁场值进行采集,所得的磁场稳定度如图3所示。在此状态下,由于电源性能以及环境噪声等因素,磁场发生偏移,在经过较长时间才能重新达到稳定状态。由图可看出,磁场经过大约2 500 s后进入稳定状态,总体漂移的误差为150×10–6,稳定后磁场纹波保持在50×10–6以内。
-
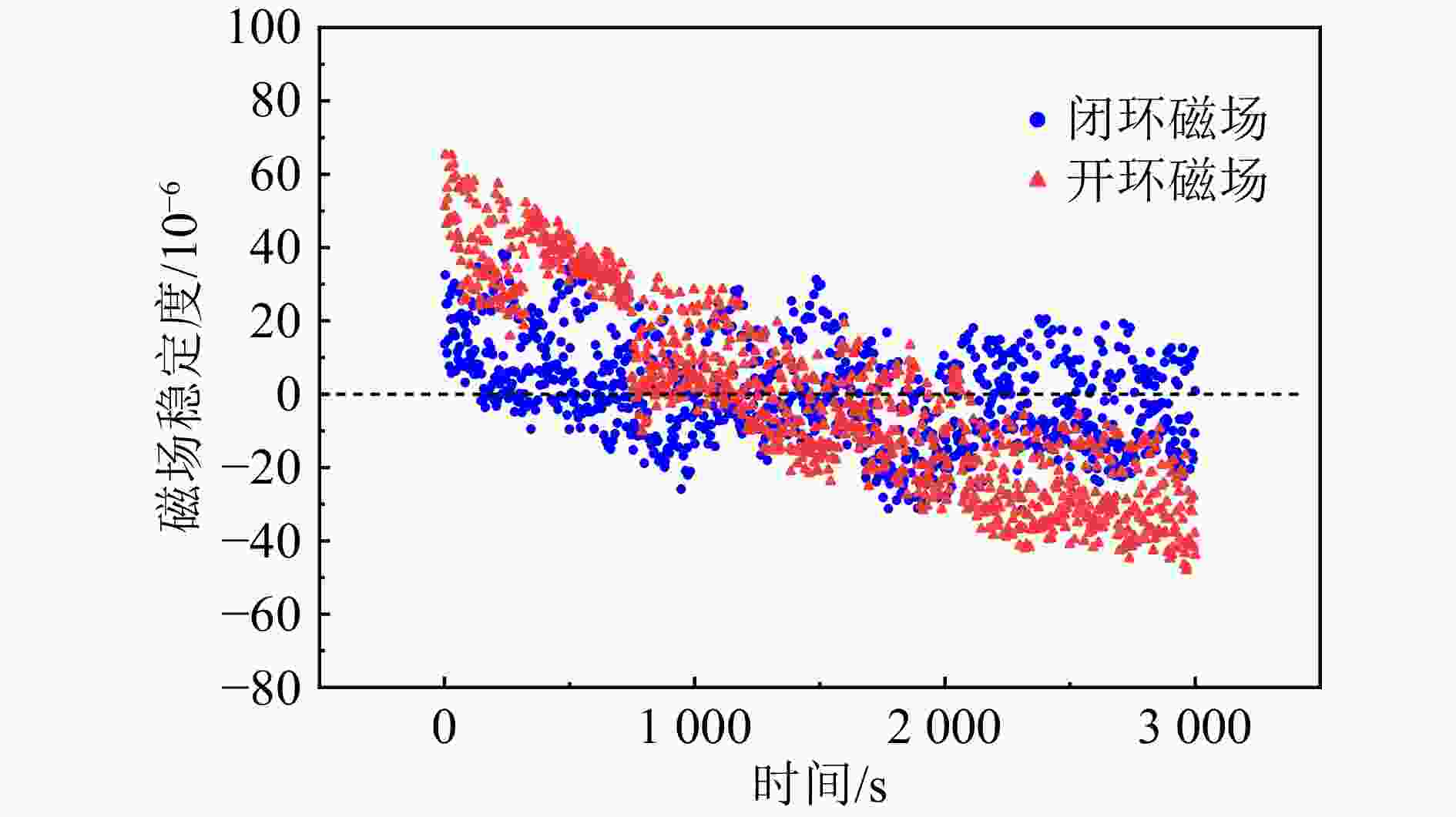
当磁场控制系统处于闭环状态时,控制器接收霍尔传感器反馈的模拟量,并自动调整电源输出。优化系统PID参数后,闭环磁场稳态与开环磁场表现如图4所示。与开环系统相比,开环系统会出现磁场工作点偏移的问题,且需要经过较长时间才能达到稳态。而闭环磁场则能快速稳定下来,有效地将磁场偏移降低到了100×10–6以内,同时稳定后磁场纹波保持在50×10–6以内。
-
本系统直接将磁场值作为控制系统的反馈,通过位置式PID算法实现了对磁场的闭环控制。同时还利用高精度的核磁共振高斯计对磁场进行测量,研究了PID参数设定对磁场反馈控制系统的影响。与开环控制相比,该方案有效地减小了磁场偏差,使得磁场稳定度保持在100×10–6以内。由于该方法避免了对磁铁进行建模。因而极大地增加了控制系统的鲁棒性,也使得该系统具有较强的泛化能力。该系统也存在一定问题,针对磁铁这种非线性的被控对象,PID算法虽然能在一定程度上削弱磁场偏移,但难以同时保证较高的控制精度和较快的稳态时间。引入非线性控制算法,可能能够进一步改善控制性能。
Research on Closed Loop Control Technology of Magnetic Field Based on PID Algorithm
-
摘要: 已有的束流磁场控制方法大多采用开环的方式,即根据磁场需求直接设置磁铁电源输出的电流或电压值。但开环状态的磁场在现场噪声以及磁铁自身涡流效应的影响下,极容易发生偏移。针对此问题,设计了基于PID算法的磁场闭环控制系统。该系统以偏转磁铁为控制对象,使用霍尔传感器获取磁场值作为反馈,磁铁电源励磁电流的输出作为控制系统的输入量。控制器使用PID算法对磁铁电源输出进行自动调整,从而实现对磁场的闭环控制。最终结果表明,在PID参数调试得当的情况下,使用磁场在线测量值作为反馈信号,去实时调节磁铁电源的励磁电流大小的闭环控制方法,可以有效地降低磁场偏移。Abstract: Most of the existing methods for beam control using magnet field use the open-loop mode, which is to directly set the value of current and voltage of the magnet power supply output based on the demand of magnetic field intensity. However, magnetic fields in the open-loop state are easy to be deflected due to the field noise and the eddy current effect of the magnet. To solve this problem, the closed-loop control system of the magnetic field based on the PID algorithm is developed in this article. This system takes the deflection magnet as the control object, uses the Hall sensor to obtain the magnetic field intensity as the feedback, and utilizes the output of the excitation current of the magnet power supply as the input of the control system. The controller uses the PID algorithm to automatically tune the output of the magnet power supply to achieve the closed-loop control of the magnetic field. The result shows that when the PID parameters are properly set, the magnetic field offset can be significantly reduced by the closed-loop control method which takes the online measured value of the magnetic field as the feedback signal to simultaneously tune the excitation current value of the magnet power supply.
-
Key words:
- PID algorithm /
- magnetic control /
- deflecting magnet
-
[1] 冯哲. 强流ECR质子源及束流引出和传输特性的研究[D]. 北京: 清华大学, 2011. FENG Zhe. Study on the High Intensity ECR Proton Source with Beam Extraction and Transmission Characteristics[D]. Beijing: Tsinghua University, 2011. (in Chinese) [2] 张灿哲, 侯德义, 张桂莲, 等. 核技术, 1997, 37(05): 7. doi: 10.7538/yzk.1997.31.05.0007 ZHANG Canzhe, HOU Deyi, ZHANG Guilian, et al. Atomic Energy Science and Technology, 1997, 37(05): 7. (in Chinese) doi: 10.7538/yzk.1997.31.05.0007 [3] 李泉凤, 邹昀, 刘耀红, 等. 清华大学学报(自然科学版), 1996, 36(06): 31. LI Quanfeng, ZHOU Yun, LIU Yaohong, et al. Journal of Tsinghua University(Science and Technology), 1996, 36(06): 31. (in Chinese) [4] 彭月梅. 原子能科学技术, 2019, 53(09): 1702. doi: 10.7538/yzk.2019.53.09.1702 PENG Yuemei. Atomic Energy Science and Technology, 2019, 53(09): 1702. (in Chinese) doi: 10.7538/yzk.2019.53.09.1702 [5] 刘晓旭, 齐国臣, 包泽民, 等. 中国测试, 2016, 42(01): 130. doi: 10.11857/j.issn.1674-5124.2016.01.028 LIU Xiaoxu, QI Guochen, BAO Zemin et al. China Measurement & Test, 2016, 42(01): 130. (in Chinese) doi: 10.11857/j.issn.1674-5124.2016.01.028 [6] WILSON E J N. The Motivation for Magnet Measurements [R]//TURNER S. CAS: Measurement and Alignment of Accelerator and Detector Magnets. Geneva: CERN, 1998: 27. [7] KURIMOTO Y, MORITA Y, NAKAMURA S, et al. IEEE Transactions on Nuclear science, 2014, 61(1): 546. doi: 10.1109/TNS.2013.2293024 [8] 刘鹏, 龙锋利, 李洋, 等. 原子能科学技术, 2020, 54(11): 2252. doi: 10.7538/yzk.2019.youxian.0843 LIU Peng, LONG Fengli, LI Yang, et al. Atomic Energy Science and Technology, 2020, 54(11): 2252. (in Chinese) doi: 10.7538/yzk.2019.youxian.0843 [9] 王有云, 高大庆, 丁军怀, 等. 原子能科学技术, 2010, 44(01): 499. doi: 10.7538/yzk.2010.44.04.0499 WANG Youyun, GAO Daqing, DING Junhuai, et al. Atomic Energy Science and Technology, 2010, 44(01): 499. (in Chinese) doi: 10.7538/yzk.2010.44.04.0499 [10] 孔晓民, 杨旭, 叶海忠. 电力电子技术, 2010, 44(12): 38. doi: 10.3969/j.issn.1000-100X.2010.12.006 KONG Xiaomin, YANG Xu, YE Haizhong. Power Electronics, 2010, 44(12): 38. (in Chinese) doi: 10.3969/j.issn.1000-100X.2010.12.006 [11] GRECH C, BUZIO M, SAMMUT N. IEEE Transactions on Instrumentation and Measurement, 2019(99): 1. doi: 10.1109/TIM.2019.2904073 [12] PEZZETTA M, BAZZANO G. B-train Performances at CNAO[C]//Proceedings of IPAC2011, San Sebastián, Spain, 2011. [13] ANG K H, CHONG G, LI Y. IEEE Transactions on Control Systems Technology, 2005, 13(4): 559. doi: 10.1109/TCST.2005.847331 [14] CLARKE D W. Transactions of the Institute of Measurement and Control, 1984, 6(6): 305. doi: 10.1177/014233128400600605 [15] 王祎晨. 工业控制计算机, 2018, 31(05): 123. WANG Yichen. Industrial Control Computer 2018, 31(05): 123. (in Chinese) [16] ZIEGLER J G, NICHOLS N B. Asme Trans, 1993, 64(2B): 759. doi: 10.1115/1.2899060 -






 下载:
下载:









 甘公网安备 62010202000723号
甘公网安备 62010202000723号