-
回旋加速器具有造价低、可加速粒子种类多以及平均流强大等特点,从发明之初就得到了广泛的应用。目前,回旋加速器除应用于原子核物理基础研究之外,在同位素生产、粒子束治疗等诸多应用领域也得到了广泛的应用[1-3]。很多大学和研究机构都配备有不同种类的回旋加速器,使其成为应用最广泛的加速器类型之一[4-5]。回旋加速器引出束流能量是固定的,在实际应用中,不同的实验和应用对束流能量的要求并不尽相同。为了满足具体实验和应用对束流能量要求,往往需要对加速器引出束流的能量进行调节[6-8]。从原理上说,改变束流能量的方式有两种,一种是采用与加速器类似电磁场对带电粒子进行减速;另一种是采用薄膜降能器[9-11]。电磁减速器对束流流强没有大的限制,减速后束流的品质基本没有降低,是最好的能量降低方式,这种降能方式的缺点是成本高。当需要降低的能量较大时,其成本和加速同样能量的加速器是一样的,因此并不适用于大范围的能量降低。薄膜降能器利用带电粒子在通过由特定材料构成的薄膜时,通过带电粒子与靶原子中的核外电子或原子核之间弹性、非弹性碰撞,将能量转移给靶原子,从而使带电粒子的动能降低[12]。薄膜降能器常用于低功率束流,其最大优势是造价低。常用作降能器的材料主要是一些轻元素及其化合物。自2000年以来,基于回旋加速器的质子治疗装置的商用供应商如比利时IBA、日本住友和美国Varian都拥有石墨制成的降能器系统。当初始束流能量较低,要求的降能器厚度比较薄时,一般采用金属薄膜,如土耳其(TAEA PAF)采用的是毫米量级的铝薄膜材料[6]。此外,铍或石墨碳化硼混合材料也常应用于降能器,能有效提高束流传输效率[1-2]。降能器材料的选择,与待降能束流种类、束流功率、应用方式等因素有关,应综合考虑上述诸因素决定。
四川大学拟建造的α辐照装置,要求将回旋加速器引出的流强20 μA、能量30 MeV的α束流降低到9 MeV,降能器上沉积的束流功率将近200 W。同时为了保证实验终端维持较低的辐射剂量,以便于实验人员随时进行操作,在降能器之后,还需要进行约10 m的传输才能到达靶室并对束流能散进行限制。由于带电粒子与靶原子中的核外电子碰撞的随机性,其引入的束流附加能散也较大,束流发射度会发生明显的增长[13]。因此有必要对束流经过薄膜降能器后的性能改变进行系统的研究。本文将用SRIM[14]与G4Beamline[15]程序,系统研究30 MeV α束流穿过不同厚度、不同材料的靶(金刚石、铝、铜)之后,在最终能量相同的情况下束流特性的变化,分析不同材料对α束流的能量、能散及发射度等束流参数的影响。
-
当荷能重带电粒子入射到靶物质时,与靶原子发生相互作用而损失能量。能量损失可分成两部分:与靶原子核外电子的非弹性碰撞损失和与靶原子核的弹性碰撞损失,即电子阻止和核阻止。对于快速、高能重带电粒子,电子阻止是能量损失的主要过程,且远远大于核阻止[12, 16-17]。重带电粒子的平均能量损失率(电子阻止本领)可用Bethe-Bloch公式表示:
$$\begin{split} \left(-\frac{\mathrm{d}E}{\mathrm{d}x}\right)=&4\pi {N}_{\rm A}{{r}_{\rm e}}^{2}{m}_{\rm e}{c}^{2}{{Z}_{1}}^{2}\frac{{Z}_{2}}{A}\frac{1}{{\beta }^{2}}\times\\&\left[\mathrm{ln}\left(\frac{2{m}_{\rm e}{c}^{2}{\gamma }^{2}{\beta }^{2}}{I}\right)-{\beta }^{2}-\frac{C}{{Z}_{2}}-\frac{\delta }{2}\right], \end{split}$$ (1) 式中: x=ρs为粒子经过靶物质的质量厚度;ρ为靶物质密度;s为靶物质的厚度;NA为阿伏伽德罗(Avogadro)常量;re为经典电子半径;me为电子的静止质量;c为真空中的光速;Z1为入射粒子的原子序数;Z2/A为靶原子的荷质比;
$ \beta =v/c $ 为入射粒子的相对速度;$\gamma $ 为相对论因子;I为靶原子的平均激发电离能;C/Z2是壳修正项;δ/2为密度修正项,在能量低于1 GeV时可忽略密度修正项;$ \mathrm{d}E/\mathrm{d}x $ 单位为$ \mathrm{M}\mathrm{e}\mathrm{V}{\mathrm{c}\mathrm{m}}^{2}/\mathrm{g} $ 。靶物质平均激发能I通常由经验公式(2)计算[18-19]。$$ I\cong \left\{\begin{array}{l}19.0\,{\rm{eV}},~~{Z}_{2}=1,\\ \left(11.2+11.72{Z}_{2}\right){\rm{eV}},~~{2\leqslant Z}_{2}\leqslant 13,\\ \left(52.8+8.71{Z}_{2}\right){\rm{eV}},~~{Z}_{2}>13\text{。}\end{array}\right. $$ (2) Bethe-Bloch公式表明,电子阻止本领与入射重带电粒子速度的平方(v2)成反比,与入射重带电粒子电荷数的平方(
$Z_1^2 $ )成正比,与靶物质密度ρ成正比。靶物质密度越高,降能越快,即降低到相同能量所需靶物质的厚度越小[12, 20]。表1列出了典型薄膜材料的一些物理性能参数,平均激发能根据参考文献[18-19]中经验公式计算所得。表 1 不同薄膜材料的物理参数
材料 密度/(g·$ {\mathrm{c}\mathrm{m}}^{-3} $) 平均激发能/eV 铝 2.70 163.6 金刚石 3.52 81.5 铜 8.92 305.4 对于一束具有相同能量的入射粒子,由于它们与靶原子碰撞过程的随机性,每个粒子的能量在穿过靶物质后并不完全相同,能量损失是对所有入射粒子求平均得到的平均能量损失,而每一个粒子的能量损失是在这平均值附近涨落。这种能量损失的统计分布称为能量分散[16, 21-22]。能散分布一般服从高斯分布[21]。根据Bohr理论,对于厚度为t的靶,能量分散的均方偏差(Bohr值)可表示为
$$ {\sigma }_{\rm B}=2z{e}^{2}{\left(\pi NZt\right)}^{1/2}, $$ (3) 式中:z为入射粒子的原子序数;Z为靶原子的原子序数;N为靶原子单位体积的原子数,该公式采用的是静电单位制。Bohr理论表明,能量分散与入射粒子的能量无关,与靶原子序数和靶厚平方根成正比。
重带电粒子(如α粒子)与靶原子核外电子发生非弹性碰撞导致能量损失的同时,还由于原子核多重库仑散射,从而造成穿过薄膜材料的带电粒子散角增大,使得束流几何发射度增大。多重散射角
$ \theta $ 的经验公式表示为[2, 23]:$$ \theta =\frac{13.6\,\mathrm{M}\mathrm{e}\mathrm{V}}{\beta cp}z\sqrt{\frac{x}{{X}_{0}}}\cdot \left[1+0.038\mathrm{ln}\left(\frac{x}{{X}_{0}}\right)\right], $$ (4) 式中:βc、p、z分别为入射粒子的速度、动量和电荷数;x、X0分别为薄膜材料的厚度和辐射长度,辐射长度由材料原子序数Z决定,辐射长度可用下列公式计算[23]:
$$ {X}_{0}=\frac{A}{Z}\frac{716.4}{\left(Z+1\right)\mathrm{ln}\left(287/\sqrt{Z}\right)}\text{。} $$ (5) 式(4)、(5)表明,低原子序数的薄膜材料辐射长度更大,重带电粒子穿过后散角较小。结合电子阻止本领,α粒子束穿过低原子序数、高密度材料的薄膜可使得散射角增长更小。
束流与薄膜相互作用过程采用G4Beamline程序进行模拟,物理模块采用程序自带的适用于低能量带电粒子与物质相互作用的QGSP_BERT模块[15]。初始束流采用与加速器引出的实际束流相近的高斯分布[24],束流能量30 MeV,发射度10 πmm·mrad,横向均方根大小σx=1.67 mm,横向散角均方根大小σx'=0.75 mrad,粒子总数为
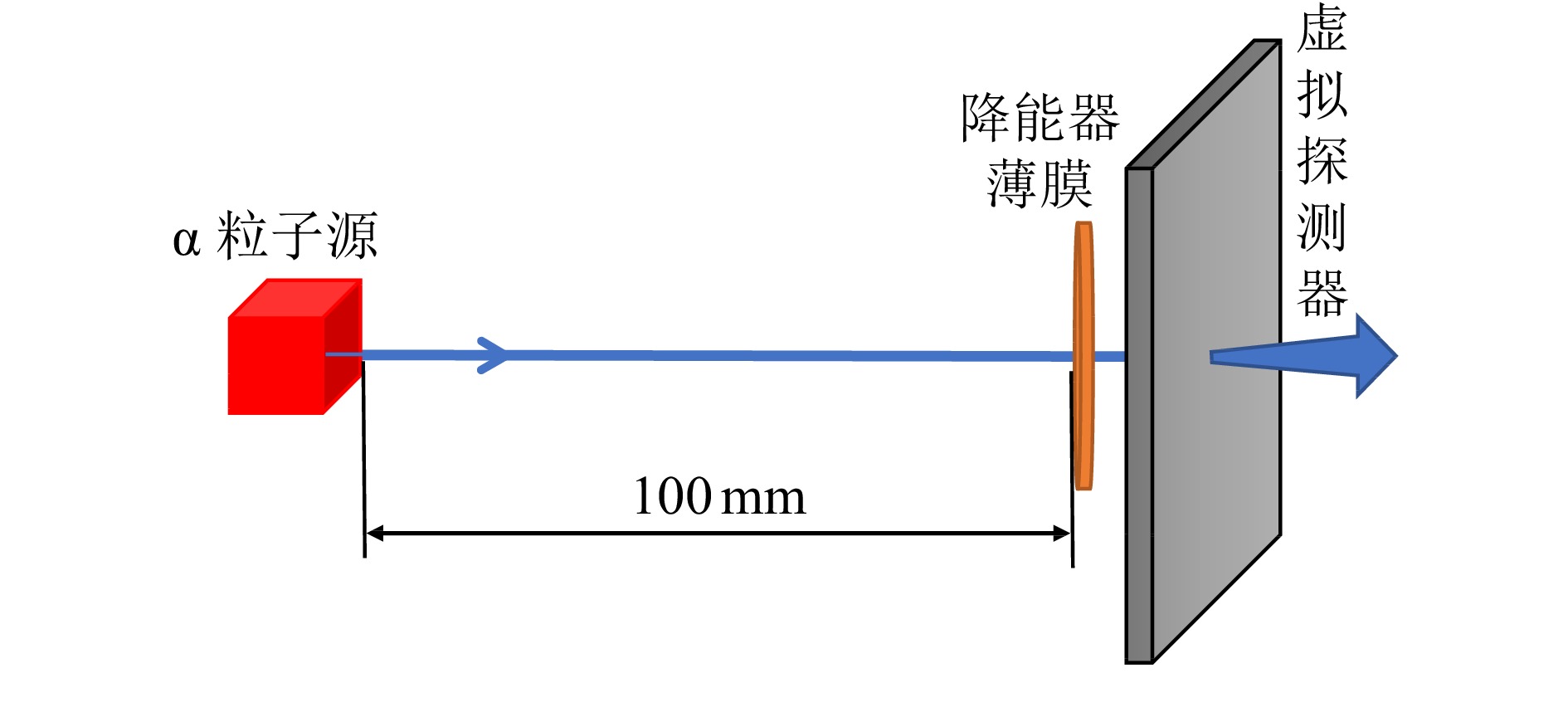
$ 1\times {10}^{6} $ 。薄膜在离初始位置100 mm处,虚拟探测器紧靠在薄膜之后5 mm处,整个模拟模型示意图如图1所示。 -
采用G4Beamline程序模拟计算了30 MeV 的α束流穿过不同厚度薄膜后的能散分布,通过高斯拟合发现,其满足高斯分布。图3给出了α束流经过不同厚度金刚石薄膜的能谱图。
从图3的能谱分布可见,在薄膜厚度很小时,能量分布很窄,随着薄膜厚度的增加,能量分布越来越宽,且图中标注的数据也能说明,降低的能量越低,所需薄膜的厚度越大。还分别计算了α束流通过铜和铝之后的能量分散,结果如图4所示。由式(3)计算的能量分散σB随粒子能量的变化也用线条画在图4中。对比G4Beamline程序的计算结果和式(3)的计算结果,可以发现:在中心能量大于18 MeV时,两者符合得较好;但是当中心能量小于18 MeV时,G4Beamline模拟得到的能量分散要远远大于式(3)的计算结果。这主要是由于当中心能量小于18 MeV时,α粒子速度小于靶原子内层电子轨道速度,靶原子的内层电子无法被电离,此时需要引进壳修正项,而其对不同薄膜材料的能量损失贡献有所差异,导致了式(3)失效,显然式(3)仅适用于能量降低范围较小的情况。
当束流能量被降低到9 MeV时,三种材料的半高宽能散大约在1 MeV左右,约为中心能量的10%,具体数值如表2所列。从表2中的数据可以发现,金刚石和铝的半高宽能散相差不大,铜的半高宽能散较铝和金刚石的要大。
表 2 中心能量降低到9 MeV时的束流能散
薄膜材料 FWHM/MeV 金刚石 1.168 铝 1.026 铜 1.613 -
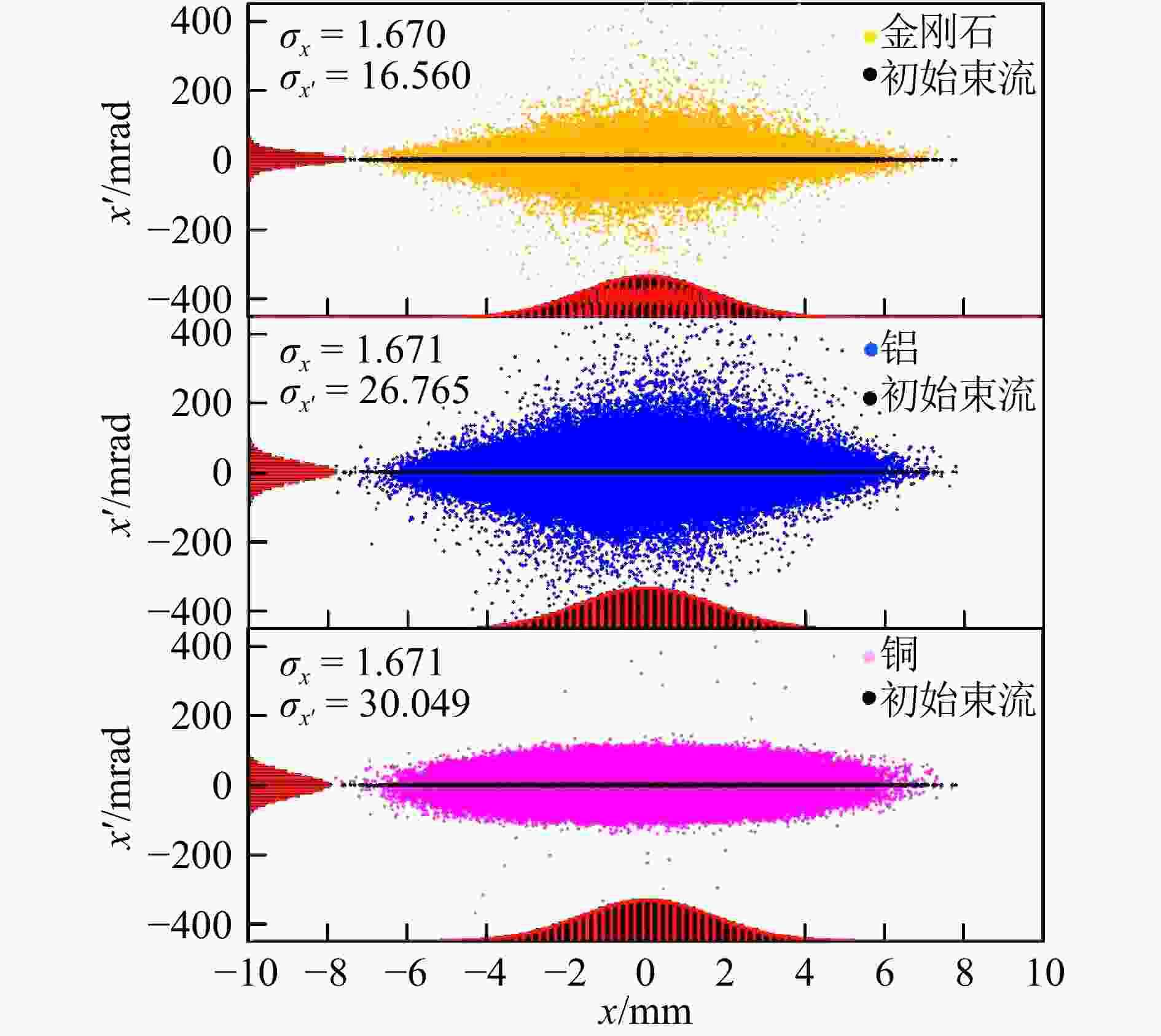
基于模拟计算得到的相空间信息,统计绘制了30 MeV 的α束流分别与129 μm 铜、209 μm 金刚石、334 μm 铝薄膜材料相互作用后,束流的横向相空间分布图,结果如图5中所示。从图5可以看出,对于高斯分布的初始束流,在与薄膜材料相互作用后,其分布仍然为高斯分布,其中束流横向大小几乎与原束流相同,但是横向散角显著增加。对粒子横向位置分布与横向散射角分布分别作高斯拟合,拟合得到的均方差值如表3所列。可以发现,与初始束流相比,σx基本没有变化,说明束流横向尺寸几乎没有改变;σx'变化较大,对于金刚石薄膜,横向散射角增长最小,为16.6 mrad,对应的三倍RMS束流发射度相对于初始束流发射度增长了约25倍。铜的横向散角增长最大,其三倍RMS发射度增长为原来的45倍。这与式(4)、(5)结论一致,即薄膜材料原子序数越大,束流的横向散角增长得越大。所以,从降低束流横向散角来考虑,金刚石这种低原子序数、高密度材料比铜和铝的效果更好。
表 3 中心能量降低到9 MeV时束流的横向参数
薄膜材料 σx/mm σx'/mrad 209 μm 金刚石 1.670 16.560 334 μm 铝 1.671 26.765 129 μm 铜 1.670 30.049 -
表4给出了α束流从30 MeV降低到9 MeV时,与三种不同薄膜相互作用后次级粒子产额的统计数据。从表4可以看出,
$\gamma $ 产额较高,中子和次级α粒子产额相对较少,而其中铝薄膜的次级粒子产额最高,其次是铜薄膜,金刚石薄膜的次级粒子产额最低。次级粒子的平均能量均较低,其中$\gamma $ 产额最高的铝薄膜平均能量也仅为2.2 MeV。次级粒子产生的原因是α粒子束在与薄膜材料相互作用时会与薄膜材料中的原子发生核反应。为了降低这些次级粒子对实验结果产生的干扰,降能装置应与实验靶室之间保持足够的距离[25-26]。表 4 束流经过薄膜后次级粒子产额
参数 金刚石 铝 铜 中子产额/% 0.037 0.16 0.10 中子平均能量/MeV 3.040 3.42 2.61 γ产额/% 0.128 0.42 0.38 γ平均能量/MeV 3.890 2.21 1.27 次级α产额/% 0.012 5 0.013 4 0.003 1 次级α平均能量/MeV 4.670 3.90 3.12 -
本文使用G4Beamline程序模拟了30 MeV 的α束流与铜、铝和金刚石三种薄膜材料的相互作用过程,计算了α束流穿过薄膜后束流能量分散,得到束流降低到指定平均能量时各薄膜的厚度,同时分析了不同薄膜材料对束流发射度的影响以及散射角变化情况,统计计算了α束流与不同材料薄膜作用后次级粒子产额。通过对比发现,材料的密度越大,对α束的阻止本领越强,降低到相同能量时相比于金刚石和铝,铜所需的厚度更小。三种薄膜材料对束流的能量发散效果相当,随着α能量的降低,束流能量高斯分布的σ值越大,能量分散越严重,其中金刚石和铝对束流的能散增长相比于铜较小。α束流穿过薄膜后的相空间信息统计结果显示,铜导致束流发射度增长最大、铝次之、金刚石的发射度增长最小。α粒子与薄膜材料相互作用后产生的次级粒子主要有
$\gamma $ 、中子和次级α粒子,其中铜、铝产额较大,金刚石产额最小。综合考虑后得出研究结论,30 MeV的α束流降能到9 MeV时薄膜材料的最优选择为209 μm的金刚石薄膜。
Simulation Study about the Effects of Different Film Materials on α Beam Properties
-
摘要: 由于回旋加速器引出的束流能量固定,为了满足不同实验对束流能量的不同需求,需要对束流的能量进行调节。为此,研究了利用薄膜材料对束流能量进行改变的可行性。用SRIM程序分析计算了30 MeV α束流(回旋加速器引出能量)穿过金刚石、铝和铜材料后的射程,确定了材料厚度与所需能量之间的关系。利用G4Beamline程序计算了束流经过薄膜后的相空间分布,分析了束流经过不同材料、降低到相同能量(9 MeV)后的横向、纵向发射度的变化,结果显示:束流在经过薄膜材料后,束斑大小几乎不发生改变,束流横向发射度的增长主要由散角的增加引起,其中金刚石薄膜引起的束流发射度增长最小,散角的均方根值约为16 mrad左右,且与初始束流的散角大小没有明显的依赖关系(初始散角均方根值小于1 mrad);不同材料引起的纵向能散均约为1 MeV(半高宽),与材料无关,只与束流的最终能量有关,降能越多,能散越大。此外,对于30 MeV的初始α束流,与金刚石、铜、铝等材料作用后,均会产生约109/μA的中子及γ粒子,在实际应用中应考虑相关的辐射防护问题。Abstract: The beam energy extracted from cyclotron is fixed, it is necessary to adjust it to meet different demands of different experiments. This study focuses on the feasibility of using thin film materials to change the beam energy. The ranges of 30 MeV α beams (extracted from cyclotron) in materials include diamond, aluminum and copper are calculated by the SRIM program, and the relationship between material thickness and the required beam energy is determined. The horizontal and vertical emittances of α beams, after being reduced to 9 MeV by interacting with different materials, are calculated by G4Beamline program. The following results are obtained: After penetrating the thin film materials, the size of beam spot approximately remained the same. The growth of beam transverse emittances is mainly caused by the increase of the divergence angles, among which the diamond film causes the least increase of beam emittance, and the root mean square value of the divergence angle is about 16 mrad. There is no significant dependency on the value of initial beam divergence angle (the root mean square value of initial divergence angle is less than 1 mrad). Vertical energy spread caused by different materials is about 1 MeV (FWHM) that is only determined by the final beam energy and has no connection with the kind of material. The more energy has lost, the greater the energy spread would be. Besides, the 30 MeV initial α beams interacting with thin film materials (diamond, copper, aluminum etc.) could produce about 109/μA neutrons and γ particles, so radiation protection must be considered in practical applications.
-
Key words:
- cyclotron /
- energy spread /
- emittance growth /
- angular scattering
-
表 1 不同薄膜材料的物理参数
材料 密度/(g·$ {\mathrm{c}\mathrm{m}}^{-3} $) 平均激发能/eV 铝 2.70 163.6 金刚石 3.52 81.5 铜 8.92 305.4 表 2 中心能量降低到9 MeV时的束流能散
薄膜材料 FWHM/MeV 金刚石 1.168 铝 1.026 铜 1.613 表 3 中心能量降低到9 MeV时束流的横向参数
薄膜材料 σx/mm σx'/mrad 209 μm 金刚石 1.670 16.560 334 μm 铝 1.671 26.765 129 μm 铜 1.670 30.049 表 4 束流经过薄膜后次级粒子产额
参数 金刚石 铝 铜 中子产额/% 0.037 0.16 0.10 中子平均能量/MeV 3.040 3.42 2.61 γ产额/% 0.128 0.42 0.38 γ平均能量/MeV 3.890 2.21 1.27 次级α产额/% 0.012 5 0.013 4 0.003 1 次级α平均能量/MeV 4.670 3.90 3.12 -
[1] 刘红冬, 阳露, 裴曦, 等. 原子核物理评论, 2018, 35(001): 78. doi: 10.11804/NuclPhysRev.35.01.078 LIU Hongdong, YANG Lu, PEI Xi, et al. Nuclear Physics Review, 2018, 35(001): 78. (in Chinese) doi: 10.11804/NuclPhysRev.35.01.078 [2] LIANG Zhikai, LIU Kaifeng, QIN Bin, et al. Nucl Instr and Meth A, 2018, 890: 112. doi: 10.1016/j.nima.2018.01.073 [3] ALEXANCDER G, BAUMGARTEN C, KISELEV D, et al. Phys Med Biol, 2016, 61: N337. doi: 10.1088/0031-9155/61/14/N337 [4] JONGEN Y. Proceedings of Cyclotrons, 2010, 3(2): 58. [5] Medical Cyclotron Market by Product and Geography [EB/OL]. [2020-9-15]. https://www.technavio.com. [6] YÜKSEL A, TÜREMEN G, BULUT S, et al. Nucl Instr and Meth A, 2020, 977: 164290. doi: 10.1016/j.nima.2020.164290 [7] FRÉDÉRIC S, JONGEN Y. Progress in Nuclear ence and Technology, 2014, 4: 272. doi: 10.15669/pnst.4.272 [8] GAGNON K, JENSEN M, THISGAARD H, et al. Applied Radiation & Isotopes, 2011, 69(1): 247. doi: 10.1016/j.apradiso.2010.09.012 [9] AMATO C, MARTISIKOVA M, GEHRKE T. Medical Physics, 2020, 47(5): 2212. doi: 10.1002/mp.14051 [10] VALVE A, KULMALA A, FOLLOWILL D, et al. Physics and Imaging in Radiation Oncology, 2019, 10(C): 25. doi: 10.1016/j.phro.2019.04.003 [11] PAGANETTI H. Proton Therapy Physics[M]. Boca Raton: CRC Press, 2010: 20. [12] 吴治华. 原子核物理实验方法[M]. 3版. 北京: 原子能出版社, 1997: 22. WU Zhihua. Nuclear Physics Experimental Methods[M]. 3rd ed. Beijing: Atomic Energy Press, 1985: 22. (in Chinese) [13] ANFEROV V. Nucl Instr and Meth, 2003, 496(1): 222. doi: 10.1016/S0168-9002(02)01625-X [14] ZIEGLER F, BIERSACK P, ZIEGLER D. SRIM, The Stopping and Range of Ions in Matter[M]. Maryland: SRIM Company, 2008: 256. [15] TOM Roberts. G4Beamline User’s Guide 3.06[EB/OL]. [2019-07-15]. https://g4beamline.muonsinc.com. [16] MARMIER P, SHELDON E. Physics of Nuclei and Particles [M]. New York: Academic Press Inc, 1969: 23. [17] EVENS D. The Atomic Nucleus[M]. New York: McGraw-Hill Inc, 1955: 18. [18] BETHE H. Annalen Der Physik, 1930, 397(3): 325. doi: 10.1002/andp.19303970303 [19] TURNER E. Atoms, Radiation, and Radiation Protection [M]. New Jersey: John Wiley and Sons, 2008: 189. [20] WILLIAM L. American Journal of Physics, 1987, 58(12): 1216. [21] CHU K. Backscattering Spectrometry[M]. New York: Academic Press Inc, 1978: 35. [22] DECONNINCK G. Introduction to Radioanalytical Physics [M]. Amsterdam: Elsevier Scientific Publishing Company, 1978: 267. [23] GROOM E. KLEIN R. European Physical Journal Plus, 2000, 15(C): 1. [24] INGO Hofmann. Space Charge Physics for Particle Accelerators[M]. Berlin: Springer, 2017: 27. [25] 刘世耀. 质子和重离子治疗及其装置[M]. 北京: 科学出版社, 2012: 546. LIU Shiyao. Proton and Heavy Ion Therapy and the De-vices[M]. Beijing: Science Press, 2012: 546. (in Chinese). [26] URBAN T, KLUSON J. Radioprotection, 2012, 47(4): 583. doi: 10.1051/radiopro/2012029 -






 下载:
下载:



















 甘公网安备 62010202000723号
甘公网安备 62010202000723号