-
最大似然期望最大化(Maximum Likelihood-Expectation Maximization, MLEM)迭代算法能重建出高质量的可视化图像,常用于
$\gamma $ 射线图像重建中[1-3]。放射性物质活度较高时,仅需要较少的迭代次数就能重建出质量较高的放射源图像,而在内污染成像中,探测器接收到的光子数较少,获得的投影数据会伴随较高的统计噪声,需要大量的迭代次数才能重建出图像,但MLEM算法迭代次数过多,会在迭代过程产生非收敛性,出现局部噪声放大、尖锐离散的斑点以及图像失真等情况,从而导致重建图像的质量会下降。2008年,Wang等[4]通过小波变换对投影数据进行处理,显著提高了重建图像的质量;2013年,Zhang等[5]提出一种基于各项异性扩散加权先验的方法,对贝叶斯统计的正弦图进行平滑,保持了图像的边缘。本文将基于差分曲率的各项异性扩散小波图像降噪(Anisotropic Diffusion Wavelet Image Denoising based on Differential Curvature,ADWIDDC)算法与MLEM重建算法相结合,即MLEM-ADWIDDC,先对探测器上获得编码图像进行MLEM图像重建,并利用互补运算消减近场伪影,得到初步的重建图像;再对重建图像进行小波分解,对低频信号进行基于差分曲率的各项异性扩散算法降低噪声,对高频信号进行硬阈值降噪;最后用小波反变换得到最终的重建图像。通过比较不同算法得到的点源、圆环源、“CDUT”字符源的重建图像,分析讨论重建图像的算法运行时间、重建图像信噪比及探测效率。
本文安排如下:在第2节介绍修正均匀冗余阵列(Modified Uniformly Redundant Array, MURA);第3节阐述肺部内污染模型、周期嵌套反对称修正冗余阵列(Mosaicked Pattern-centered and Anti-symmetric MURA, MPA-MURA)编码孔准直器模型及探测器模型;第4节着重介绍MLEM图像重建算法;第5节简述互补编码成像;第6节概述基于差分曲率的各项异性扩散算法和小波变换;第7节分析131I放射源不同分布的活度;第8节将从算法运行时间、信噪比、探测效率三方面讨论不同算法的重建图像效果;在最后一节给出结论。
-
MURA是在均匀冗余阵列(Uniformly Redundant Array, URA)的基础上发展而来的,MURA可以看做是行列数相等的URA,在MURA阵列中每一个元素都可以按照URA的定义方式来定义。令
$ {B}_{p\times q} $ 为修正均匀冗余阵列,其中p=q,两者都为质数,$ {B}_{ij} $ 为阵列中的i行j列一个元素。则对于MURA编码孔径准直器,由式(1)可得元素$ {B}_{ij} $ 的值[6]:$$ {{B}_{ij}\left\{\begin{array}{l}0\;\;\;\left(i=0\right)\\ 1\;\;\;\left(i\ne 0,j=0\right)\\ 1\;\;\;\left({C}_{p}\left(i\right){C}_{q}\left(j\right)=1\right)\\ 0\;\;\;\left({\text{其他}}\right)\end{array}\right.}, $$ (1) 其中:p为行数,q为列数,且有
$0 \leqslant i < p,~0\leqslant j < q$ 。$ {C}_{p}\left(i\right) $ 和$ {C}_{q}\left(j\right) $ 为一个求余判定操作,可由式(2)求得$ {C}_{p}\left(i\right) $ 值:$$ {C}_{p}\left(i\right)=\left\{\begin{array}{l}1\quad\left({\text{存在整数}}x,1\leqslant x < p,i={\mathrm{M}\mathrm{o}\mathrm{d}}_{p}{x}^{2}\right)\\ -1\quad\left({\text{其他}}\right)\end{array}\right. {\text{。}} $$ (2) 其中:
$1\leqslant x < p$ ,$ {\mathrm{M}\mathrm{o}\mathrm{d}}_{p}{x}^{2} $ 为p除以x2所得到的余数。同理可以计算得出$ {C}_{\mathrm{q}}\left(j\right) $ ,最终可得到$ {B}_{ij} $ 的值,即可判断每个小孔是否开孔,其中1表示不开孔,0表示开孔,开孔率一般在50%左右,这样可以在保证集光率的同时,又能减少探测效率的损失。 -
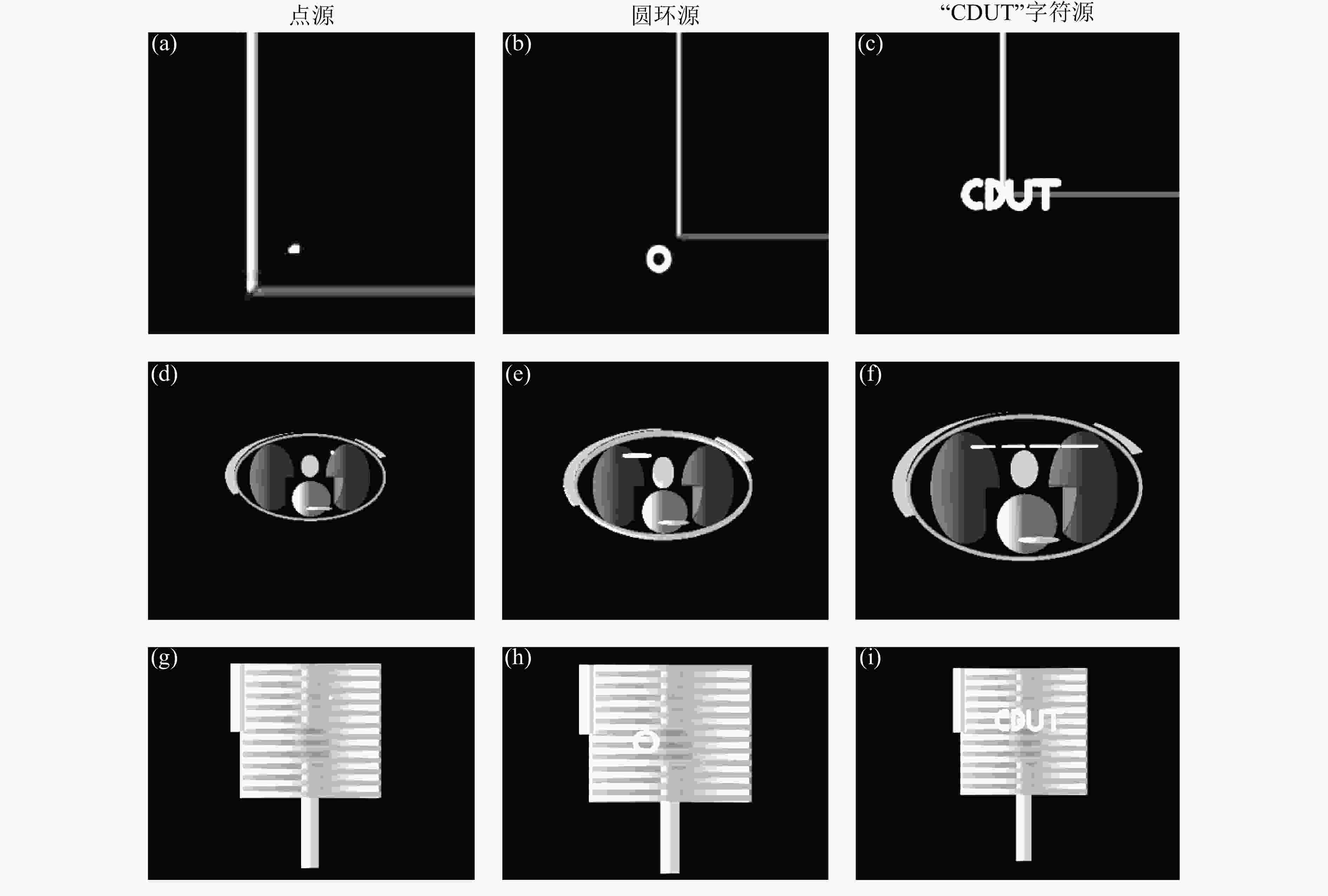
1969年,Snyder等[7]发表了第一个不均匀体模 (MIRD-5体模),该体模被美国核医学内照射剂量委员会 (MIRD,Medical Internal Radiation Dosimetry Committee) 所接受。本文使用的是Geant4自带的MIRD体模,并建立了MIRD体模胸腔模型,如图1所示。其中图1(a)为MIRD成年男性的左右肺,高×宽为240 mm×290 mm;图1(b)中蓝色部分为左右双肺,密度为0.295 8 g/cm3,绿色部分为胸腺体,密度为0.986 9 g/cm3,红色部分为人体心脏,密度为0.986 9 g/cm3,黄色块状部分为肩胛骨,密度为1.936 2 g/cm3,中间黄色部分为脊柱,密度为1.936 2 g/cm3;图1(c)中黄色条状部分为12根肋骨组织,透明红色部分是肋骨周围加入肌肉等软组织,密度为0.986 9 g/cm3。本文模拟了X-Y轴位置坐标(50 mm, 50 mm)的点源;外径为25 mm,内径为20 mm,圆心为(–50 mm, –50 mm)的圆环源;整体大小长宽为167.5 mm×50 mm的字符源“CDUT”,如图2所示,其中(a)、(b)、(c)为放射源分布图,(d)、(e)、(f)为胸腔肺部内放射源分布(俯视图),(g)、(h)、(i)为胸腔肺部内放射源分布(正视图)。
-
本文中的编码孔准直器采用MPA-MURA,大小为
$ 301\,\mathrm{m}\mathrm{m}\times 301\,\mathrm{m}\mathrm{m} $ ,编码孔开孔$ 1\,\mathrm{m}\mathrm{m}\times 1\,\mathrm{m}\mathrm{m} $ ,编码区域规格取为301×301,黑色为不开孔部分,白色为开孔部分,如图3所示[8]。
图 3 (在线彩图)301×301周期嵌套反对称修正冗余阵列编码板[8]
-
本文选择CsI(Tl)闪烁体构建位置敏感探测器,采样数
$ \alpha $ 取1,探测器矩阵为301×301。CsI位置敏感探测器像素边长$ {H}_{\mathrm{d}} $ 取$ 1\,\mathrm{m}\mathrm{m}\times 1\,\mathrm{m}\mathrm{m} $ [3],CsI晶体厚度取38.1 mm,如图4所示。 -
文中模拟计算131I点源在等比例成像条件下,源-探测器距离(Z)和编码厚度(t)对131I点源成像质量的影响,如图5和图6所示。根据图5和图6[8],随着Z距离的增加,图像质量逐渐变好,探测效率逐渐降低。为了兼顾探测效率和成像质量,本文选取的源-探测器距离Z为
$ 160\;\mathrm{m}\mathrm{m} $ ,物距a为80 mm,焦距b为80 mm。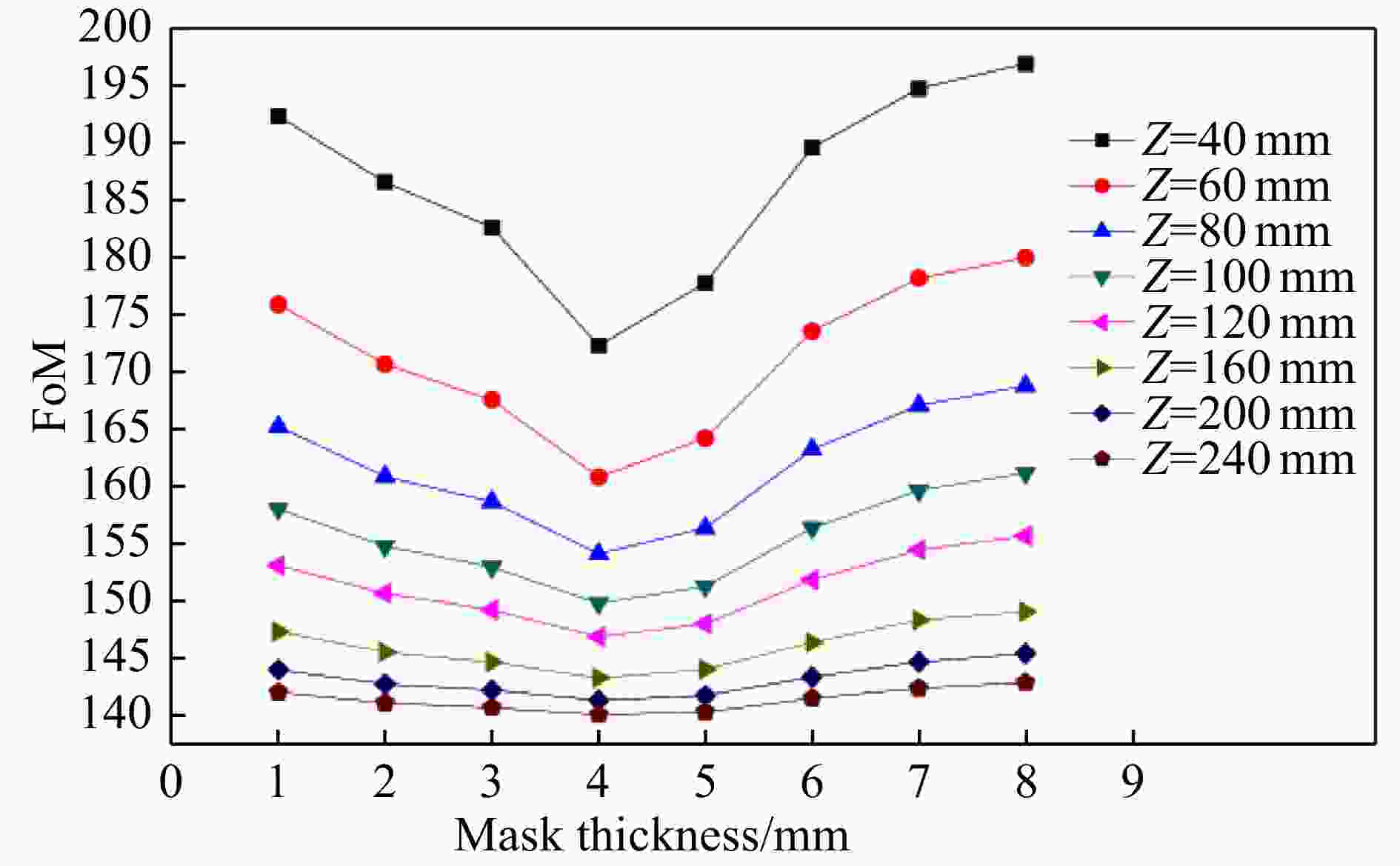
图 5 (在线彩图)不同放射源到探测器距离下由编码孔准直器厚度引起的点源重建图像的质量变化[8]
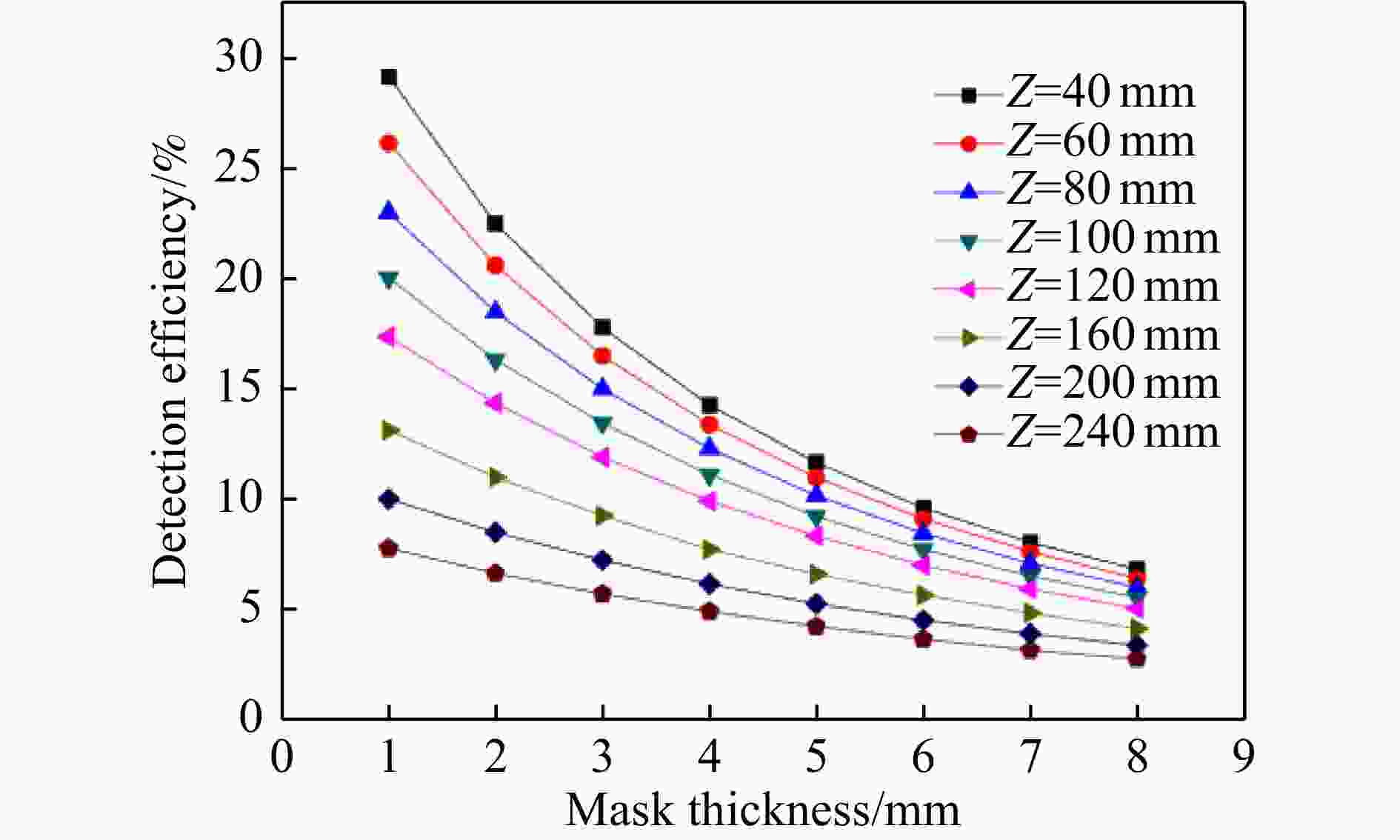
图 6 (在线彩图)不同放射源到探测器距离下由编码孔准直器厚度引起的探测效率变化[8]
-
MLEM迭代算法先给定图像的初始估计值,令初始值
$ {X}^{0}\left(x,y\right)\equiv 1 $ 。对当前估计图像进行一个投影运算,然后将其与探测器获得编码图像做对比,再将比值反投影到估计值图像空间,获得修正因子,对估计值图像进行修正。重复投影和反投影的过程,直至满足迭代停止条件——${\mathrm{M}\mathrm{a}\mathrm{x}}_{\left(x,y\right)}\left(\right|\frac{{X}^{k+1}\left(x,y\right)}{{X}^{k}\left(x,y\right)}-1\left|\right)\leqslant 0.005$ 时,停止迭代,从而得到逼近源分布图像的估计值。MLEM算法可表示为[1]
$$ {X}^{k+1}\left(x,y\right)={X}^{k}\left(x,y\right)\times \left[\frac{Y\left(x,y\right)}{{X}^{k}\left(x,y\right)*h\left(x,y\right)}\otimes h(x,y)\right] , $$ (3) 式中:
$ {X}^{k}\left(x,y\right) $ 为第k次迭代后放射源强度分布图像估计值;$ Y\left(x,y\right) $ 为探测器获取的编码图像;$ h\left(x,y\right) $ 为采样放大后的编码矩阵函数,由采样数$ \alpha $ 和编码矩阵$ {A}_{{i}{j}} $ 决定;$ \otimes $ 为周期相关运算。 -
传统的高斯低通滤波图像降噪方法是各向同性扩散的,它在降噪同时模糊边界[15]。为此而Perona等[16]提出了一种基于偏微分方程模型的非线性扩散滤波方法,即PM方法,也就是各项异性扩散算法,如式(4)所示[17]:
$$ \frac{\partial {f}_{x,y}^{t}}{\partial t}=\mathrm{d}\mathrm{i}\mathrm{v}\left[{C}_{t}\boldsymbol\cdot \nabla {f}_{x,y}^{t}\right] {\text{。}} $$ (4) 其中
$ {C}_{t} $ 为扩散系数函数:$$ {C}_{t}=g\left(\nabla f\right)=\frac{1}{1+{\left(\left|\nabla f\right|/k\right)}^{2}} , $$ (5) 式中k为常数。
差分曲率的表达式为[17]
$$ D=\Big|\left|{f}_{\mathrm{\eta }\mathrm{\eta }}\right|-\left|{f}_{\mathrm{\xi }\mathrm{\xi }}\right|\Big| , $$ (6) 式中:
$ \eta $ 为梯度方向;$ \xi $ 为水平方向;$ {f}_{\mathrm{\eta }\mathrm{\eta }} $ 和$ {f}_{\mathrm{\xi }\mathrm{\xi }} $ 分别表示图像在梯度方向和水平方向的二阶导数,其表达式为$$ {f}_{\mathrm{\eta }\mathrm{\eta }}=\frac{{f}_{x}^{2}{f}_{xx}+2{f}_{x}{f}_{y}{f}_{xy}+{f}_{y}^{2}{f}_{yy}}{{f}_{x}^{2}+{f}_{y}^{2}} , $$ (7) $$ {f}_{\mathrm{\xi }\mathrm{\xi }}=\frac{{f}_{y}^{2}{f}_{xx}-2{f}_{x}{f}_{y}{f}_{xy}+{f}_{x}^{2}{f}_{yy}}{{f}_{x}^{2}+{f}_{y}^{2}} {\text{。}} $$ (8) 将差分曲率引入后的各项异性扩散系数函数为
$$\begin{split}& g\left[\nabla {f}_{t}^{i}\left(x,y\right)\boldsymbol\cdot {d}_{t,N}\left(x,y\right)\right]=\\&1\Big/\left[1+{\left(\frac{\nabla {f}_{t}^{i}\left(x,y\right)\boldsymbol\cdot {d}_{t,N}\left(x,y\right)}{k}\right)}^{2}\right] , \end{split}$$ (9) 其中
${d}_{t,N}\left(x,y\right)=\frac{D\left(x,y\right)}{D_{\mathrm{m}\mathrm{a}\mathrm{x}}}$ ,为归一化的差分曲率。小波变换是图像去噪中的一种非常重要的方法,图像经过小波变换后,分为高频和低频两部分。图像的主要信息集中在低频部分,噪声和边缘信号主要集中在高频部分,而且图像边缘对应的小波系数幅值较大,噪声对应的小波系数幅值较小,因此可以采用小波变换的方法达到去除噪声的目的。
因此,本文利用以上方法的优势,提出了ADWIDDC算法,并与MLEM算法相结合进行图像处理,即MLEM-ADWIDDC算法。该算法首先使用MLEM进行图像重建,然后对重建后的图像进行小波变换,对包含噪声少的低频系数进行基于差分曲率的各项异性扩散处理,对高频系数进行硬阈值处理[17]。在Matlab中,使用db3小波对原始信号进行三层分解,再使用硬阈值函数,对小波系数进行阈值处理,就可以达到去除噪声而保留有用信号的目的。
-
本文对365 keV 131I的3种分布(点源、圆环源、“CDUT”源)进行模拟成像。其中点源模拟
$ 1\times {10}^{5} $ 个光子(1988年9月4日测量切尔诺贝利核事故受污染人员全身的核素活度最高是$1.88\times {10}^{5}\, $ Bq),另外两种分布模拟$ 5\times {10}^{7} $ 个光子。在Geant4模拟中,抽样的次数为50万,131I的
$\gamma $ 射线分支比为81.8%,由式(10)可将模拟的光子数转换为放射源活度:$$ A=\frac{{N}_{\mathrm{b}\mathrm{e}\mathrm{a}\mathrm{m}}}{\varphi }=\frac{1\times {10}^{5}}{81.8\%}=1.22\times {10}^{5}\,\mathrm{B}\mathrm{q} {\text{。}} $$ (10) 式中:
$ {N}_{\mathrm{b}\mathrm{e}\mathrm{a}\mathrm{m}} $ 为点源模拟的光子数;$ \varphi $ 为131I的γ射线分支比;A为放射源活度。 -
本文对不同算法在信噪比、探测效率和算法运行时间三个方面的性能表现进行了对比,由于信噪比和探测效率不能同时兼顾,且本文重点是获得更高的重建图像质量,因此牺牲了一定的探测效率。图像信噪比(Signal-to-noise Ratio,SNR)的公式:
$$ \mathrm{SNR} = {10} \times {\log _{10}}(k/b) , $$ (11) 式中:k为图像矩阵的平均值;b为图像矩阵的均方差。本文的探测效率为成像的粒子数与粒子枪发射粒子数的比值。
-
由图7可见,图7(a)、(b)中圆环源周围存在较多的背景噪声和伪影。将(a)和(b)相减得到(c),噪声和伪影基本被消除,圆环源的重建图像清晰。由表1可知(c)较(a)而言,信噪比增加了226.83%。本文为了得到质量更高的图像,所以牺牲掉了一定的探测效率,图7(a)、(b)中,噪声和伪影也有一定的粒子数,因此互补成像(c)中的圆环源所占的粒子数会减少,探测效率比正编码图像低了两个数量级。由此可见,互补成像可有效地减少放射源重建图像的近场伪影,提高重建图像的质量。
表 1 正编码圆环图像与互补圆环图像的参数比较
图像 信噪比/dB 探测效率/% 正编码图像 1.64 3.72 互补图像 5.36 5.32×10–2 -
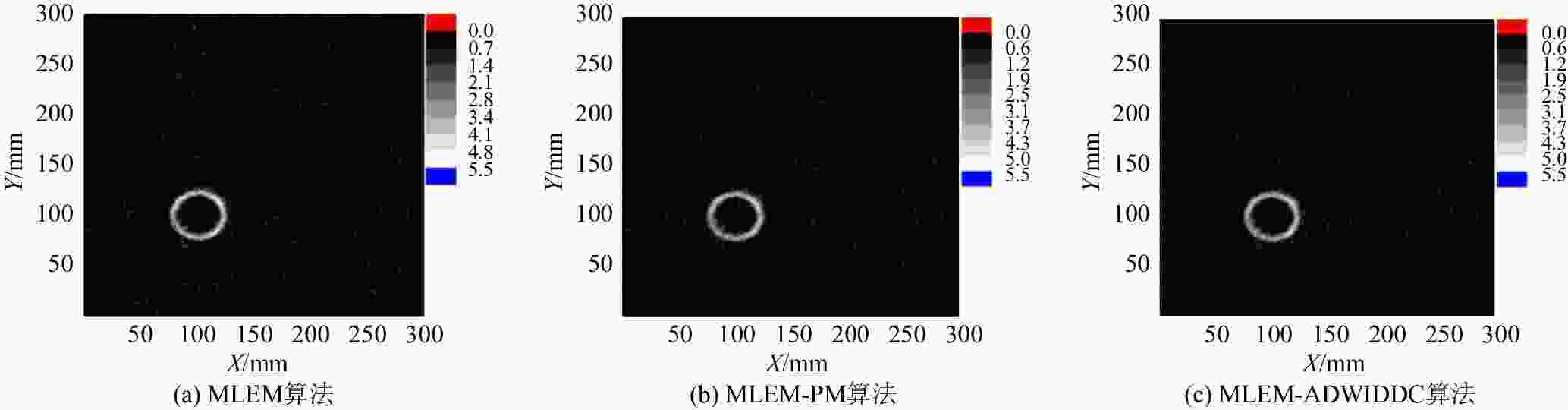
本文使用Geant4模拟发射
$ 5\times {10}^{7} $ 个光子,得到131I圆环放射源编码图像,并用不同的算法重建图像,其图像重建结果如图8所示。将图8(c)和图8(a)、(b)做比较,可以明显地看出,图8(c)包含的伪影更少,图像清晰、质量高,即MLEM-ADWIDDC算法处理后的图像优于MLEM算法和MLEM-PM算法处理后的图像,本文的算法可以在去噪的同时保持图像的纹理和边缘信息。
表2从算法运行时间、信噪比、探测效率三个方面对成像结果进行了评价。在三种算法运行时间相差不大的情况下,对于131I圆环放射源,本文MLEM-ADWIDDC算法重建图像的信噪比高出MLEM重建算法31.72%。因此结合图8和表2可知,本文提出的MLEM-ADWIDDC算法应用于低活度内污染图像重建是有效的。
表 2 不同重建算法获得的圆环图像参数比较
算法 算法运行时间/s 信噪比/dB 探测效率/% MLEM算法 195.23 5.36 5.32×10–2 MLEM-PM算法 195.94 5.59 4.55×10–2 MLEM-ADWIDDC算法 196.12 7.06 2.83×10–2 -
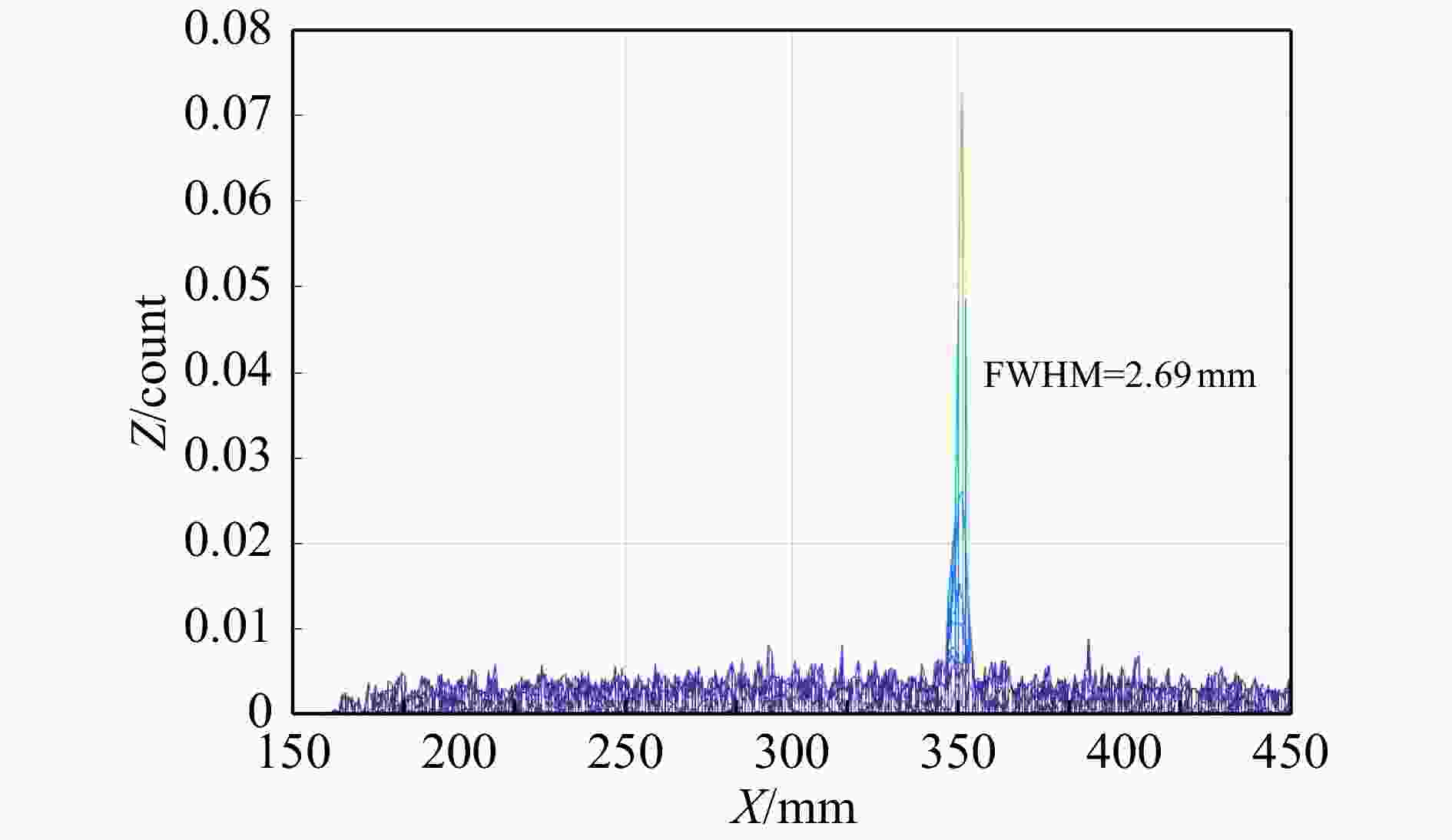
空间几何分辨率为成像系统点扩散函数半高宽(Full Width at Half Maximum, FWHM)。点扩散函数(Point Spread Funtion, PSF)也称为点源响应,它表示处于物平面位置的点被成像系统扩展到成像面上的一个区域的二维函数[18]:
$$ \mathrm{P}\mathrm{S}\mathrm{F}=h(x,y)\times G , $$ (12) 其中:h(x,y)为采样放大后的编码矩阵;
$ G $ 为解码矩阵。$ G $ 函数矩阵与h(x,y)函数矩阵相对应,当h(x,y)矩阵上的数为$ 0 $ 时,$ G $ 矩阵对应位置的数为–1;当矩h(x,y)阵上的数为$ 1 $ 时,$ G $ 矩阵对应位置的数为1[18]。文中设定的空间几何分辨率为$ 2\,\mathrm{m}\mathrm{m} $ ,实际的点源响应受射线能量大小的影响。根据第7节设定的点源活度,模拟$ {10}^{5} $ 个光子,得到的X-Z平面点源重建图像如图9所示。模拟中得到点源的空间分辨率FWHM为2.69 mm,本文中设定的空间几何分辨率FWHM为2.00 mm,因此该系统达到了设计要求。本文参考了核事故下吸入人体内核素的活度,设定了低活度点源成像,如图10所示。当重建图像信噪比达到6.184 8 Bq时,其图像重建时间仅为15.73 s,探测效率为0.05%,因此系统可对低活度的核素进行快速成像。
-
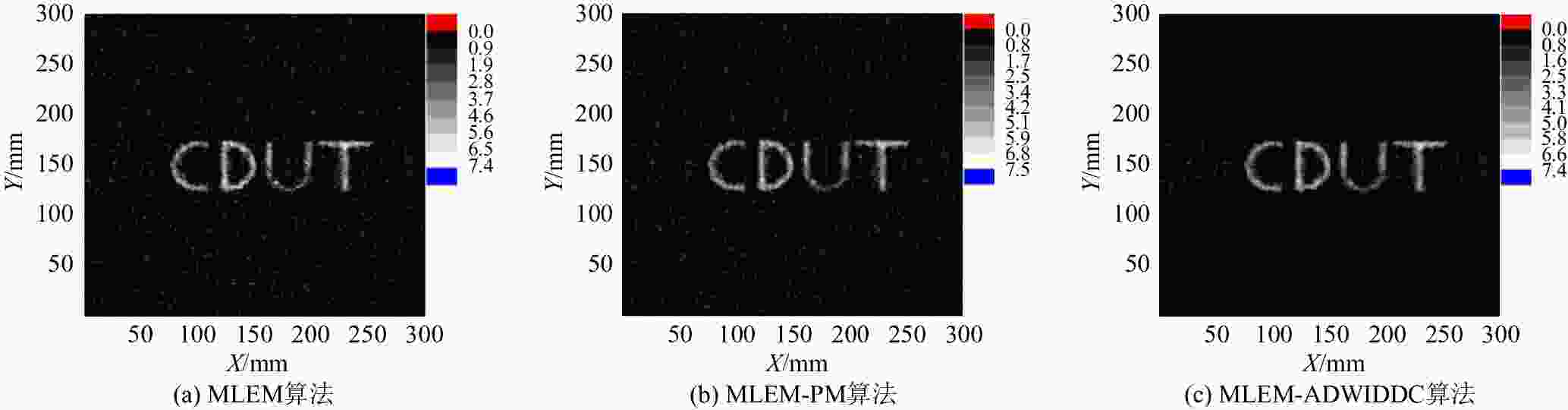
本文使用Geant4模拟发射
$ 5\times {10}^{7} $ 个光子,得到“CDUT”字符131I放射源的编码图像,并用不同的算法重建图像。从图11和表3可知,对于“CDUT”字符131I放射源,在重建算法运行时间相同的情况下,本文的算法依旧可以更清晰地重建出放射源图像,再次验证了本算法在低活度内污染图像重建中的可行性。表 3 不同重建算法获得的"CDUT"图像参数比较
算法 算法运行时间/s 信噪比/dB 探测效率/% MLEM算法 193.34 5.11 9.83×10–2 MLEM-PM算法 194.12 5.27 8.58×10–2 MLEM-ADWIDDC算法 194.36 8.39 3.31×10–2 由表4可知,对呈“CDUT”分布131I放射源的编码图像进行重建,以重建图像信噪比达到5.10 dB为截止条件,本文采用的MLEM-ADWIDDC算法运行的时间为98.36 s,比仅采用MLEM算法消耗的时间缩短了49%,提高了重建图像的速度。
表 4 在信噪比相同的情况下,不同重建算法的运行时间比较
“CUDT” 信噪比/dB 算法运行时间/s MLEM算法 5.10 193.34 MLEM-ADWIDDC算法 5.10 98.36 -
本文使用Geant4模拟了核事故中131I放射源成像系统;利用MLEM解码算法对放射源图像进行重建;采用双模成像的方法降低伪影对成像的干扰,增加了图像的清晰度;后续图像采用ADWIDDC算法,进一步减小重建图像的伪影和噪声。同时本文研究了分布于胸腔模型中的点源、环形源、“CDUT”源的成像,实现了在肺部模型中3种放射源的图像重建。模拟实验结果表明,本文提出的MLEM-ADWIDDC算法可以更好地减少MLEM算法产生的重建图像伪影,并能够提高重建的效率。
Research on Anisotropic Diffusion Wavelet Image Denoising Algorithm Based on Differential Curvature
-
摘要: 在
$\gamma $ 放射性内污染修正均匀冗余阵列编码成像中,为了进一步减少使用最大似然估计(Maximum Likelihood Expectation Maximisation,MLEM)算法进行编码图像重建的伪影,并且提高重建的效率,本文提出了基于差分曲率的各项异性扩散小波图像降噪(Anisotropic Diffusion Wavelet Image Denoising based on Differential Curvature, 简称ADWIDDC)算法, 结合MLEM算法得到了改进的应用于编码成像的MLEM-ADWIDDC算法。该算法首先采用MLEM算法对探测器得到的投影数据进行图像重建,再利用互补成像方法消减近场伪影,最后采用ADWIDDC算法进一步降低图像伪影。模拟结果表明,对于131I源呈圆环分布的编码图像,以重建算法运行时间为195 s为截止条件,MLEM-ADWIDDC算法能够更好地去除伪影,重建的$\gamma $ 放射源图像纹理也更加清晰;对于131I源呈“CDUT”分布的编码图像,以重建图像信噪比达到5.10 dB为截止条件,本文的MLEM-ADWIDDC算法运行时间为98.36 s,比仅采用MLEM算法消耗的时间缩短了49%。Abstract: In modified uniformly redundant arrays code imaging of gamma radiation internal contamination, in order to further decrease reconstruction artifacts with Maximum Likelihood Expectation Maximisation(MLEM) algorithm and to improve the efficiency of reconstruction, this paper proposed an anisotropic diffusion wavelet image denoising algorithm based on differential curvature (ADWIDDC algorithm), and combining with MLEM algorithm, a modified code imaging MLEM-ADWIDDC algorithm was obtained. Firstly, the reconstruction of the projection data obtained from the detector was conducted with MLEM algorithm. Secondly, the near-field artifacts were decreased with complementary imaging method. Finally, the image artifacts were further reduced by ADWIDDC algorithm. The simulation results show that the MLEM-ADWIDDC algorithm can better remove the artifacts and the texture of the reconstructed gamma source image is clearer when 131I source is designed as circular distribution, with the cut-off time of 195 s for the reconstruction algorithm to run. When 131I source is designed as “CDUT” distribution and the signal-to-noise ratio is set 5.10 dB as cut-off condition of code imaging reconstruction, the real reconstruction time of the MLEM-ADWIDDC algorithm is 98.36 s, which is 49% shorter than that of MLEM algorithm alone. -
图 3 (在线彩图)301×301周期嵌套反对称修正冗余阵列编码板[8]
图 5 (在线彩图)不同放射源到探测器距离下由编码孔准直器厚度引起的点源重建图像的质量变化[8]
图 6 (在线彩图)不同放射源到探测器距离下由编码孔准直器厚度引起的探测效率变化[8]
表 1 正编码圆环图像与互补圆环图像的参数比较
图像 信噪比/dB 探测效率/% 正编码图像 1.64 3.72 互补图像 5.36 5.32×10–2 表 2 不同重建算法获得的圆环图像参数比较
算法 算法运行时间/s 信噪比/dB 探测效率/% MLEM算法 195.23 5.36 5.32×10–2 MLEM-PM算法 195.94 5.59 4.55×10–2 MLEM-ADWIDDC算法 196.12 7.06 2.83×10–2 表 3 不同重建算法获得的"CDUT"图像参数比较
算法 算法运行时间/s 信噪比/dB 探测效率/% MLEM算法 193.34 5.11 9.83×10–2 MLEM-PM算法 194.12 5.27 8.58×10–2 MLEM-ADWIDDC算法 194.36 8.39 3.31×10–2 表 4 在信噪比相同的情况下,不同重建算法的运行时间比较
“CUDT” 信噪比/dB 算法运行时间/s MLEM算法 5.10 193.34 MLEM-ADWIDDC算法 5.10 98.36 -
[1] 洪俊杰. γ相机中编码孔径准直器设计及数字图像重建[D]. 武汉: 华中科技大学, 2006. HONG Junjie. Design of Coded Aperture Collimator in Camera and Digital Image Reconstruction [D]. Wuhan: Huazhong University of Science and Technology, 2006. (in Chinese) [2] 高艳. 单光子成像理论与实现[D]. 杭州: 浙江大学, 2002. GAO Yan. Theory and Realization of Single Photon Imaging [D]. Hangzhou: Zhejiang University, 2002. (in Chinese). [3] 卢位. 肺部内污染成像模拟研究[D]. 成都: 成都理工大学, 2018. LU Wei. Imaging Simulation of Pulmonary Contamination [D]. Chengdu: Chengdu University of Technology, 2018. (in Chinese). [4] WANG Jing, LU Hongbing, WEN Junhai, et al. IEEE Transactions on Biomedical Engineering, 2008, 55(3): 1022. doi: 10.1109/TBME.2007.909531 [5] ZHANG Quan, GUI Zhiguo, CHEN Yang, et al. Optik-International Journal for Light and Electron Optics, 2013, 124(17): 2811. doi: 10.1016/j.ijleo.2012.08.045 [6] 冷逢庆. γ放射性内污染成像中MURA编码准直器设计[D]. 成都: 成都理工大学, 2017. LENG Pengqing. Coded Aperture Imaging with MURA for γ Internal Contamination[D]. Chengdu: Chengdu University of Technology, 2017. (in Chinese). [7] SNYDER W S, FORD MR, WARNER G G. Estimates of Specific Absorbed Fractions for Photon Sources Uniformly Distributed in Various Organs of a Heterogeneous Phantom[M]. Pamphlet: Health Physics Division(Oak Ridge National Laboratory), 1978. [8] ZHANG Ting, WANG Lei, NING Jing, et al. Nuclear Science and Techniques, 2021, 32: 17. doi: 10.1007/S41365-021-00849-3 [9] 陈立宏, 李勇平, 赵翠兰, 等. 核技术, 2013, 36(8): 080402. doi: 10.11889/j.0253-3219.2013.hjs.36.080402 CHEN Lihong, LI Yongping, ZHAO Cuilan, et al. Nuclear Techniques, 2013, 36(8): 080402. (in Chinese) doi: 10.11889/j.0253-3219.2013.hjs.36.080402 [10] 肖洒, 兰明聪, 党晓军, 等. 核技术, 2013(08): 913. doi: 10.11889/j.0253-3219.2017.hjs.40.050202 XIAO Sa, LAN Mingcong, DANG Xiaojun, et al. Nuclear Techniques, 2013(08): 913. (in Chinese) doi: 10.11889/j.0253-3219.2017.hjs.40.050202 [11] MCCONNELL M L, FORREST D J, CHUPP E L, et al. IEEE Transactions on Nuclear Science, 1982, 29(1): 155. doi: 10.1109/TNS.1982.4335818 [12] DUNPHY P P, MCCONNELL M L, OWENS A, et al. Nucl Instr and Meth A, 1989, 274(1): 362. doi: 10.1016/0168-9002(89)90403-8 [13] JAYANTHI U B, BRAGA J. Nucl Instr and Meth A, 1991, 310(3): 685. doi: 10.1016/0168-9002(91)91118-F [14] BARRETT H H, SWINDELL W. Radiation Imaging[M]. Beijing: Science Press, 1988. [15] 张权, 付学敬, 桂志国, 等. 计算机应用与软件, 2013, 30(11): 50. doi: 10.3969/j.issn.1000-386x.2013.11.014 ZHANG Quan, FU Xuejing, GUI Zhiguo, et al. Computer Applications and Software, 2013, 30(11): 50. (in Chinese) doi: 10.3969/j.issn.1000-386x.2013.11.014 [16] PERONA P, MALIK J. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 12(7): 629. doi: 10.1109/34.56205 [17] 董婵婵, 张权, 郝慧艳, 等. 中北大学学报, 2015, 36(04): 488. doi: 10.3969/j.issn.1673-3193.2015.04.017 DONG Chanchan, ZHANG Quan, HAO Huiyan, et al. Journal of North Central University, 2015, 36(04): 488. (in Chinese) doi: 10.3969/j.issn.1673-3193.2015.04.017 [18] 赵翠兰, 陈立宏, 李勇平, 等. 核技术, 2014, 037(008): 30. ZHAO Cuilan, CHEN Lihong, LI Yongping, et al. Nuclear Techniques, 2014, 037(008): 30. (in Chinese) -







 下载:
下载:

































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号