-
1937年,一篇题目为“Molecular View points in Nuclear Structure” 的文章,首次提出原子核可能像分子一样由团簇构成[1]。1938年,Hafstad等[2]通过分析8Be,12C,16O,20Ne等n
$ \alpha $ 原子核(质量数是4 的倍数的原子核)的结合能,发现它们有很好的线性关系,暗示这些核中可能存在$ \alpha $ 团簇。直到1968年日本科学家Ikeda提出Ikeda图,原子核中团簇的研究才逐渐被重视起来[3-8]。近年来随着原子核中团簇结构的研究成为了热点,越来越多的实验上的间接证据被提出。如,12C的第二个$ 0^+ $ 态(即Hoyle态,它在星体核合成的过程中扮演重要角色)被认为是由3个$ \alpha $ 团簇组成。Fred Hoyle在1954年提出,如果没有Hoyle态,那么就不会有稳定的12C 存在。Hoyle态的存在确保了具有足够的12C、使得碳基生命(比如人类)得以出现。相关的实验在1957年证明了Fred Hoyle的猜想是正确的[9]。2011年Epelbaum等[10]基于第一性原理方法计算了12C基态及其激发态的能量,提出Holye态中的3 个$ \alpha $ 团簇很接近链状(直线)的形式存在。后来他们的研究中指出,12C的基态及其第一个2+态是一个正三角形构型,而对于Hoyle态和第二个2+态中的3个$ \alpha $ 团簇构成一个钝角三角形[11]。2014年,Marin-Labarri等[12]在一项研究中测量了激发能为22.4(+2) MeV的12C的$ J\! =\! 5^- $ 态,结果明确指出了12C的基态具有D3对称性(正三角形),Hoyle态是这种等边三角形呼吸激发产生。此外,费米子分子动力学模型[13]、反对称化的分子动力学模型[14]、协变密度泛函理论等[15]也对12C的团簇结构进行了研究,关于16O中$ \alpha $ 团簇的构型的研究也有差异,Ichikawa等[16]的研究指出快速自旋的16O的原子核中的$ \alpha $ 团簇可以呈直线的链状。Epelbaum等[17]利用从头算方法指出16O的基态是一个四面体结构,这与Bijker等[18]的研究结果一致。He等[19-20]提出,利用原子核的巨偶极共振谱来提取团簇结构的信息,利用扩展的量子分子动力学模型对8Be,12C,16O不同$ \alpha $ 团簇构型的巨偶极共振谱进行计算,通过与巨偶极共振谱实验数据的比较可以提取出团簇构型的信息。Yang等[21]通过测量12Be的反常增强的单极跃迁强度,清楚标识了近阈激发态的分子团簇结构。Broniowski等[22]提出,利用相对论的重离子碰撞研究轻原子核中的团簇结构,他们指出,初始时不同的团簇构型会导致形成的高温高密火球的形状不同,最终导致出射粒子方位角分布的差异,即不同的集体流。欧洲核子研究中心(CERN)的实验学家已经在计划开展此类实验进行轻核中团簇结构的探测。我们团队在过去几年里做了大量工作探究团簇结构对集体流的影响[23-27]。另外Huang等[28-29]通过光核反应来探究团簇核的结构效应也是一些探索。总之,轻核中存在团簇结构已被广泛证实,但团簇的几何构型仍然有较大争议,相关的实验探测也十分困难,是亟需解决的课题。本文基于我国兰州重离子加速器设施,通过费米能区的重离子碰撞来研究轻16O的
$ \alpha $ 团簇结构。通过在EQMD模型中构建初始化时不同的团簇构型,模拟费米能区的重离子碰撞16O+16O产额分布,寻找敏感观测量,探究团簇结构对观察量影响的原因,为相关的实验研究提供有益的参考。 -
QMD模型是一个多体的半经典的微观动力学输运模型,核子被看作是有限宽度的高斯波包,同时考虑了平均场和两体碰撞两部分效应,被应用于从低能熔合反应到高能的核反应[30-31]。拓展的QMD模型被Maruyama等[32]提出,称为Extension of Quantum Molecular Dynamics (EQMD)模型。EQMD模型通过采用复数形式的高斯波包形式,引入泡利势,引入摩擦冷却过程,使模型具有比标准QMD更多的优势。EQMD 模型能够部分描述核子的费米子属性,在一定程度上唯象地实现费米系统的反对称性质描述,可以很好地描述原子核基态性质,尤其是原子核的团簇结构。另外EQMD模型沿袭了QMD两体碰撞部分,能够较好地描述碎裂反应。近年来EQMD模型在原子核团簇结构、巨共振、中低能核核碰撞、光核反应等研究中得到了应用和扩展,比如基于EQMD模型揭示了GDR能谱结构与12C、16O等原子核的
$ \alpha $ 团簇构型存在密切关系[19-20],在EQMD 模型框架加入($ {\rm{\gamma }}$ , np)反应道后使得EQMD模型可以研究准氘核能区的光核反应[28-29],加入费米能区的直接光子产生道后,使得EQMD模型可以研究此能区的光子发射谱[33]。 -
EQMD模型中对核子的描述仍然用高斯波包,只是波包宽度用了相对复杂的复数形式:
$${\phi _i}\left( {{{{r}}_i}} \right) = {\left( {\frac{{{\nu _i} + \nu _i^*}}{{2\pi }}} \right)^{3/4}}\exp \left[ { - \frac{{{\nu _i}}}{2}{{\left( {{{{r}}_i} - {{{R}}_i}} \right)}^2} + \frac{\rm i}{\hbar }{{{P}}_i} \cdot {{{r}}_i}} \right],$$ (1) 这里的
$ {{{R}}}_i $ 和$ {{{P}}}_i $ 分别表示波包的位置中心和动量中心。其中对于波包宽度$ \nu_i $ 的描述采用了如下复数的形式:$$ {\nu_i} = \frac{1}{{{\lambda _i}}} + {\rm i}{\delta _i} , $$ (2) 这里的
$ \lambda_i $ 和$ \delta _i $ 分别表示实数部分和复数部分。对波包函数形式做复共轭内积可得单核子对应的密度分布函数形式,其中坐标空间的密度形式为$$\begin{split}\rho \left( {{{{r}}_i}} \right) =& {\varphi _i}{\left( {{{{r}}_i}} \right)^ * } {\varphi _i}\left( {{{{r}}_i}} \right) \\=& {\left( {\frac{1}{{\pi {\lambda _i}}}} \right)^{\frac{3}{2}}}\exp \left[ { - \frac{1}{{{\lambda _i}}}{{\left( {{{{r}}_i} - {{{R}}_i}} \right)}^2}} \right]{\text{。}} \end{split}$$ (3) -
系统的哈密顿量如下:
$$ \begin{split} H =& \Big\langle {\varPsi \Big| {\sum\limits_i { - \frac{{{\hbar ^2}}}{{2{m}}}\nabla _i^2 - {{\hat T}_{\rm c.m.}} + {{\hat H}_{\rm int }}} } \Big|\varPsi } \Big\rangle \\ =& \sum\limits_i {\left[ {\frac{{{{p}}_i(t)^2}}{{2m}} + \frac{{3{\hbar ^2}\left( {1 + \lambda _i^2\delta _i^2} \right)}}{{4m{\lambda _i}}}} \right]} - {T_{\rm c.m.}} + {H_{\rm int}}, \end{split} $$ (4) 这里
$ H_{\rm int} $ 表示相互作用势能;$ {T_{\rm c.m.}} $ 代表零点质心动能,是由结团的总波函数决定的。它是由对于核子波函数的描述中,波包的宽度是动态的,系统演化过程中$ {T_{\rm c.m.}} $ 不再是常数,从而对于哈密顿量的变分计算须将零点质心动能项显示扣除。为了能够更好地描述碎裂过程,必须合理地扣除零点质心动能,Antisymmetrized Molecular Dynamics(AMD)模型等也做了类似处理[34]。每个碎片都有自己的零点质心动能,如果不扣除这个零点能,会导致系统衰变位垒升高。EQMD模型中零点质心动能是按照下面的方式扣除的。单高斯波包的零点质心动能可以表示为$$ t_i^{\rm c.m.} = \frac{{\left\langle {{\phi _i}} \right|\hbar {\nabla ^2}\left| {{\phi _i}} \right\rangle }}{{2m}} - \frac{{\left\langle {{\phi _i}} \right|\hbar \nabla {{\left| {{\phi _i}} \right\rangle }^2}}}{{2m}}{\text{。}} $$ (5) 碎片的整体的零点质心动能形式为
$$ {T_{\rm c.m.}} = \sum\limits_i {\frac{{t_i^{\rm c.m.}}}{{{M_i}}}}, $$ (6) 其中
$ M_i $ 表示第i个核子(波包)所在的碎片质量数。这样扣除的零点质心动能包含了所有碎片的零点能。这里既包含发射的碎片,也包含了原子核的不同团簇结构。这对团簇结构的判断很关键,决定了$ M_i $ 值的大小。EQMD选取的团簇判断机制如下:$$ {M_i} = \sum\limits_j {{F_{ij}}}, $$ (7) $$ {F_{ij}} = \left\{ {\begin{array}{*{20}{c}} 1&{\left( {\left| {{{{R}}_i} - {{{R}}_j}} \right| < a} \right)} \\ {{{\rm e}^{ - {{\left( {\left| {{{{R}}_i} - {{{R}}_j}} \right| - a} \right)}^2}/b}}}&{\left( {\left| {{{{R}}_i} - {{{R}}_j}} \right| \geqslant a} \right)}, \end{array}} \right., $$ (8) 上述是判断i,j的核子是否在一个团簇内的公式,类似于标准QMD模型中的coalescence方法,这里的参数取值分别为a=1.7 fm和b=4 fm2。确定系统哈密顿量后就可以通过如下变分公式得到系统的运动方程,系统波函数为单核子波包的直积:
$$ \delta \int_{{t_1}}^{{\;t_2}} \ell {\rm d}t = 0, $$ (9) $$ \ell \left( {{R_i},{P_i},{\lambda _i},{\delta _i}, {{\dot R}_i},{{\dot P}_i},{{\dot \lambda }_i}, {{\dot \delta }_i}} \right) = \Big\langle \varPsi \Big|{\rm i}\hbar \frac{{\rm d}}{{{\rm d}t}} - \widehat H\Big| \varPsi \Big\rangle{\text{。}} $$ (10) 通过对系统拉格朗日量的时间变分得到了一个8A维度的经典的运动方程。可以分解为如下4个运动方程:
$$ \begin{split}& {{\dot { R}}_i} = \frac{{\partial H}}{{\partial {{ P}_i}}},\quad {{\dot { P}}_i} = - \frac{{\partial H}}{{\partial {{ R}_i}}},\\ & \frac{{3\hbar }}{4}{{\dot \lambda }_i} = - \frac{{\partial H}}{{\partial {\delta _i}}}, \quad \frac{{3\hbar }}{4}{{\dot \delta }_i} = \frac{{\partial H}}{{\partial {\lambda _i}}}{\text{。}} \end{split} $$ (11) -
在原子核相空间初始化过程中,为了准确地描述系统的基态,需要对由随机抽样得到的相空间数据进行摩擦冷却的计算,以得到最低能量的相空间状态,也就是系统的基态。这种初始化冷却过程是通过对正则演化方程加入阻尼项来实现的。加入阻尼项的演化方程形式如下:
$$ \begin{split}& {{{\mathop {{R}}\limits^. }_i} = \frac{{\partial H}}{{\partial {{{P}}_i}}} + {\mu _{ R}}\frac{{\partial H}}{{\partial {{ R}_i}}}}, \quad {{{\mathop {{P}}\limits^. }_i} = - \frac{{\partial H}}{{\partial {{{R}}_i}}} + {\mu _{ P}}\frac{{\partial H}} {{\partial {{ P}_i}}}},\\ & {\frac{{3\hbar }}{4}{{\dot \lambda }_i} = - \frac{{\partial H}}{{\partial {\delta _i}}} + {\mu _\lambda }\frac{{\partial H}}{{\partial {\lambda _i}}}}, \quad {\frac{{3\hbar }}{4}{{\dot \delta }_i} = \frac{{\partial H}}{{\partial {\lambda _i}}} + {\mu _\delta }\frac{{\partial H}}{{\partial {\delta _i}}}}, \end{split} $$ (12) 这里的
$ \mu _{{{R}}} $ ,$ \mu _{{{P}}} $ ,$ \mu _{{\lambda }} $ ,和$ \mu _{{\delta }} $ 是阻尼系数,取小于0的值,阻尼系数的大小决定每一个时间步长内冷却的能量大小。计算这个演化方程可以使系统冷却到更低的能量状态。计算的最终结果会是所有核子静止在使系统处在最低能量的位置,这时有:$$ \begin{array}{l} {\mathop {{{R}}}\limits^. _i} = 0,\quad {\mathop {{{P}}}\limits^. _i} = 0,\\ {{\dot \lambda }_i} = 0,\quad {{\dot \delta }_i} = 0{\text{。}} \end{array} $$ (13) EQMD模型的费米动量主要是包含在可变的复数形式的波包展宽内。
-
$ H_{\rm int} $ 是核子相互作用势,包含Skyrme势($ H_{\rm{Skyrme}} $ ),库仑势($ H_{\rm{Coulomb}} $ ),对称能($ H_{\rm{Symmetry}} $ )和泡利势($ H_{\rm{Pauli}} $ )[32]:$$ H_{\rm int} = H_{\rm Skyrme}+H_{\rm Coulomb}+H_{\rm Symmetry}+H_{\rm Pauli}, $$ (14) Skyrme 势包括两体相互作用和三体相互作用,形式如下:
$$ \begin{split} {H_{\rm Skyrme}} =& \frac{\alpha }{{2{\rho _0}}} \sum\limits_{i,j \ne i} {\int {\delta \left( {{r_i} - {r_j}} \right){\rho _i}\left( {{r_i}} \right){\rho _j}\left( {{r_j}} \right){{\rm d}^3}{r_i}{{\rm d}^3}{r_j}} }+ \\ & \frac{\beta }{{\left( {\gamma + 1} \right)\rho _0^\gamma }}\sum\limits_{i,j \ne i} {\int {\delta \left( {{r_i} - {r_j}} \right){\rho _i}{{\left( {{r_i}} \right)}^{\gamma - 1}}} }\times \\ & {\rho _i}\left( {{r_i}} \right){\rho _j}\left( {{r_j}} \right){{\rm d}^3}{r_i}{{\rm d}^3}{r_j}\equiv {H_2} + {H_{\gamma + 1}}{\text{。}}\\[-12pt] \end{split} $$ (15) 参数取值分别为:
$ \alpha \!=\! -124.3 $ MeV,$ \beta \!=\! 70.5 $ MeV,$ \gamma \!=\! 2 $ ,$ \rho_0 \!=\! 0.16 $ fm–3。不考虑核子的自相互作用。这里的密度依赖项$ H_{\gamma+1} $ 在实际的数值计算中,必须采用$ \gamma \!=\! 2 $ 的三层嵌套循环来求解。这是导致EQMD计算机时间远大于标准QMD模型的关键所在。密度项为所有核子密度函数的叠加:$$ {\rho}\left( {{r}} \right) = \sum\limits_i^A {{\rho _i}\left( r \right)} = \sum\limits_i^A\frac{1}{{{{\left( {\pi {\lambda _i}} \right)}^{{3/2}}}}}\exp \left[ {\frac{{ - {{\left( {{{r}} - {{r}}_i} \right)}^2}}}{{{\lambda _i}}}} \right]{\text{。}} $$ (16) 库仑势,形式如下:
$$ H_{\rm{Coulomb}} = \frac{1}{2}\int \rho _p({{r}})\frac{e^{2}}{|{{r-r}} ^{\prime }|}\rho _p({{r}}^{\prime }){\rm d}^3 r {\rm d}^3 r^{\prime}, $$ (17) 对称势,形式如下:
$$ {H_{\rm symmetry}} = \frac{{{c_{\rm s}}}}{{2{\rho _0}}}\sum\limits_{i,j \ne i} {\int {\big[ {2\delta \left( {{T_i},{T_j}} \right) - 1} \big]{\rho _i}\left( r \right){\rho _j}\left( r \right){{\rm d}^3}r} }, $$ (18) $ T_i $ 表示第i个核子的同位旋量子数。对于原子核物质可以简化为$$ {H_{\rm symmetry}} = \int {\frac{{{c_{\rm s}}}}{2}\frac{{{{\left( {{\rho _{\rm p}} - {\rho _{\rm n}}} \right)}^2}}} {{{\rho _0}}}{{\rm d}^3}r},$$ (19) 参数
$ C_{\rm s} \!=\! 25 $ MeV是对称能密度依赖系数。$ \rho_{\rm p} $ 和$ \rho_{\rm n} $ 分别表示质子和中子的密度。除了泡利势,EQMD模型中没有使用其它动量相关势。因为泡利势低于费米能,所以高于几十MeV的能区对动量依赖的描述不好。对于更高能量的核反应需要引入更合理的相互作用势。泡利势用的是一个唯象的排斥势,能够阻止相同同位旋、相同自旋的核子相空间距离太近。泡利势来补偿波函数的反对称化部分,形式如下:$$ \begin{split} H_{\rm{Pauli}} =& \frac{c_{\rm p}}{2}\sum_i(f_i-f_0)^\mu\theta(f_i-f_0), \\ f_i\equiv& \sum_j\delta(S_i,S_j)\delta(T_i,T_j)|\langle\phi_i|\phi_j\rangle|^2, \end{split} $$ (20) 这里
$ f_i $ 代表第$ i $ 个核子与其它核子的波包重叠函数。强度系数$ c_{\rm p} $ 、位垒参数$ f_0 $ 、指数项$ \mu $ 分别设置为15 MeV,1.0,1.3。通过无限大核物质的统计性性质,我们可以验证泡利势的有效性。在无限大核子系统极限下,使波包具有平面波的形式,这样使得坐标空间具有均匀的密度分布。这是区别于标准QMD模型的,固定的波包宽度在无限大核子系统极限下仍然没有均匀的物质密度分布。在只有泡利势的情况下,参数取为$ c_{\rm p} \!= $ $ 15 $ MeV,$ f_0\! =\! 1.05 $ ,$ \mu \!=\! 2.0 $ 。模拟结果显示,在低温区和费米气体相似,在高温区和玻尔兹曼气体符合。 -
在EQMD模型中,弹核和靶核的初始化不同于其它QMD类模型。EQMD初始化核中心的波包是随机分布的。初始化随机给定核子坐标和动量后,得到的原子核并不是处于基态(能量最低的状态),为了使初始化的核处于基态,在正则演化方程中加入了阻尼项,使其演化到能量最低的状态。大部分抽样的弹核和靶核不是很稳定,经过了摩擦冷却过程后,可以保持稳定。同时在保证结合能、均方根半径等物理量与实验数据相接近的基础上筛选出反应所需的不同构型的原子核。EQMD给出的初始化相空间中,
$ \alpha $ 团簇的构型类似于晶格结构的构型,比如16O存在4种可能的几何构型,分别为长链型、风筝型(3个$ \alpha $ 构成正三角形结构,第4个$ \alpha $ 出现在三角形结构的顶点外侧)、正方型、正四面体型。这4种构型可以通过判断不同$ \alpha $ 之间的距离进行区分,判选结果可以通过坐标空间的可视化程序进行验证。对于比较轻的原子核,由于核子数目少,需要大量的抽样次数才能找出想要的结构。得到弹靶核的相空间之后,在程序中根据碰撞参数,入射能等计算系统的正则演化方程,得到一个完整的反应事件。 -
首先为了检验EQMD模型描述费米能区核反应的能力,我们在图1中显示了EQMD产生的碎片的电荷分布与相关实验数据的比较情况。图1(a)为入射能量
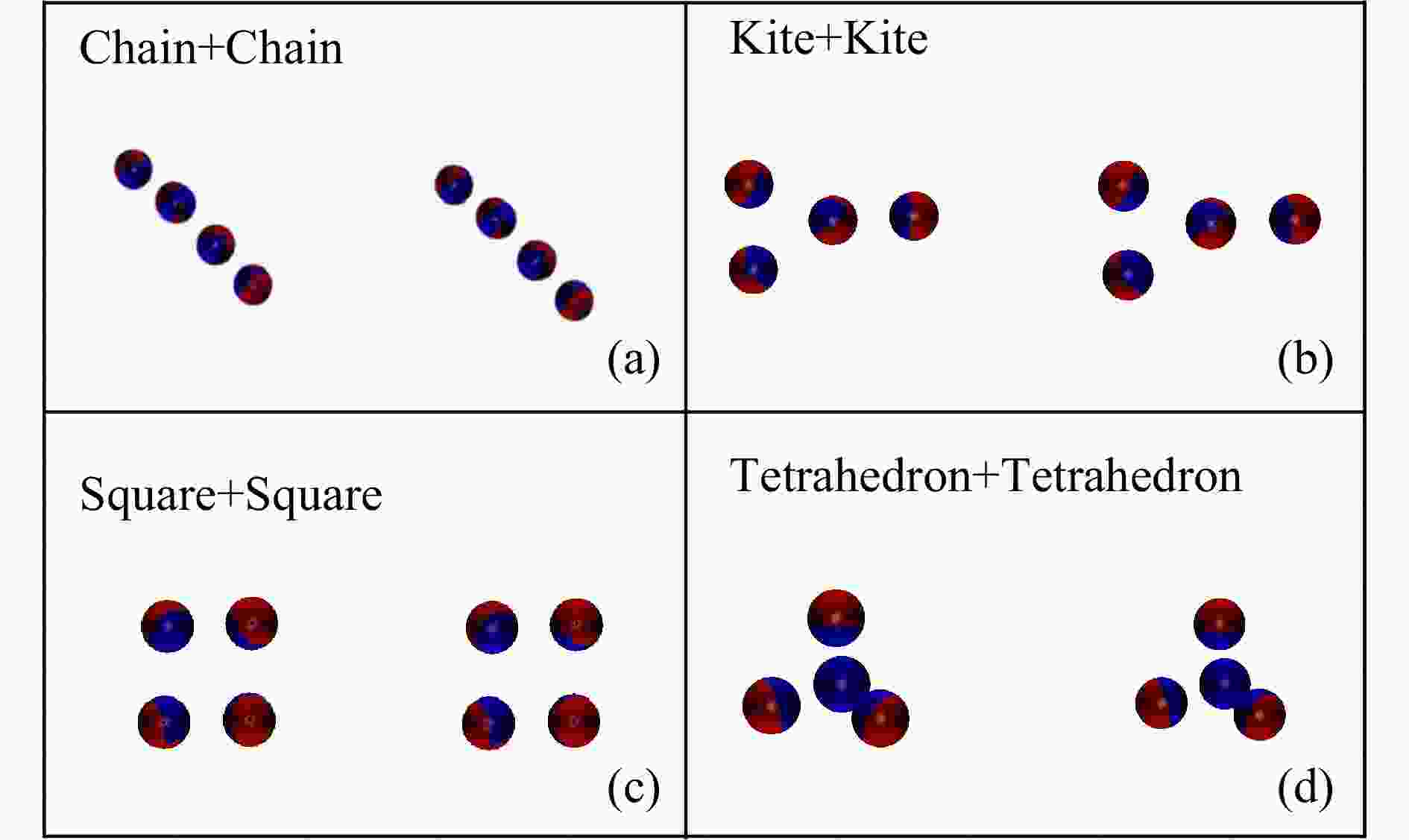
$ E_{\rm lab} $ =30 MeV/nucleon、碰撞参数b = 0~4 fm,选取的角度范围$ 50 $ °$ <\theta<120 $ °的12C+197Au的碎片电荷数分布,实验数据取自文献[35]。图1(b)为入射能量$ E_{\rm lab} $ =40 MeV/nucleon、碰撞参数b=0~4 fm,选取的角度范围是$ 20 $ °$ <\theta<160 $ °的14N+197Au的碎片电荷数分布,实验数据取自文献[36]。图1(c)为入射能量$ E_{\rm lab} $ =35 MeV/nucleon、碰撞参数b=4.4 fm,选取的角度范围16°$ <\theta<120 $ °的36Ar+197Au产生的碎片的电荷分布,相关的实验数据取自文献[37]。图1(d)为入射能量$ E_{\rm lab} $ =35 MeV/nucleon、碰撞参数b=4 fm时,40Ca+40Ca产生的碎片的电荷分布,相关的实验数据取自文献[38]。图中的黑方块实线为EQMD所计算结果,红星为相同条件下对应的实验数据。将图1中EQMD给出的Z=3的产额与实验值约化对比后,可以看出,理论模型能够给出与实验基本一致的图像,证明选取参数的合理性。整体上能够再现相关的实验数据,进一步表明选取参数的合理性和显示EQMD模型描述费米能区重离子碰撞过程的能力。图2显示了EQMD初始化好的16O中4种不同
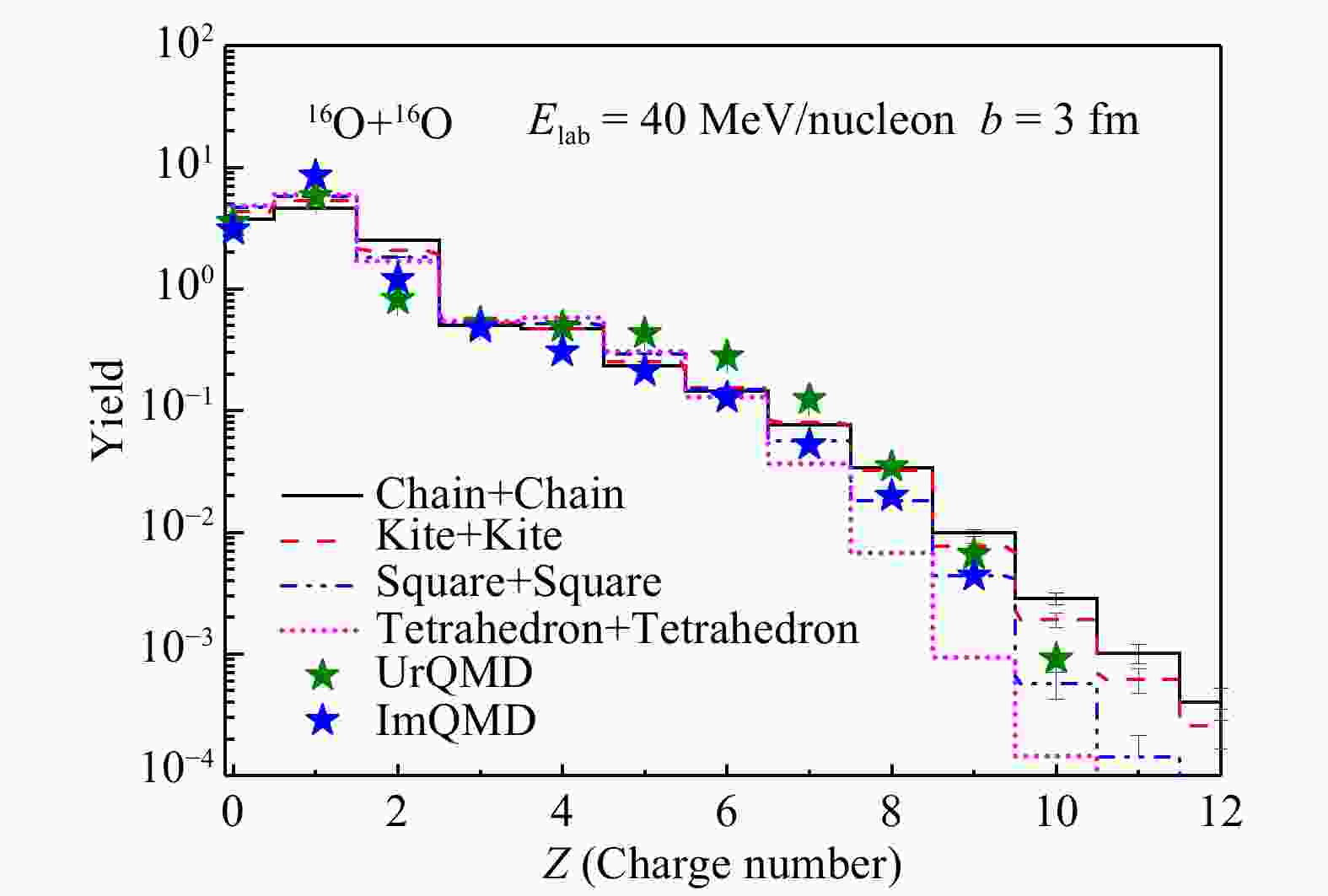
$ \alpha $ 团簇构型(a) 长链型、(b) 风筝型、(c) 四方型、(d) 正四面体型所对应的16O+16O的示意图。不同的16O构型被挑选出来以后,初始化好的核在演化过程基本可以保持原有构型。16O每核子结合能对于长链型、风筝型、四方型、正四面体型分别为7.781, 7.556, 7.501, 7.831 MeV,很接近实验值7.98 MeV。4种不同团簇构型的16O核被筛选出来后,采用相同构型进行碰撞,且构型的方向是随机的,每次碰撞都有一个随机转动的角度。初始弹核和靶核的距离被设定为10 fm,每种构型用3万个事件进行模拟。在反应末期,判断碎片的方法为同位旋依赖的Minimum Span Tree(MST)方法。即当两个核子的相对动量$ \Delta p<0.2 $ GeV/c,质子中子(pn)以及中子中子(nn)的相对距离$ \Delta r<1.5 $ fm,就被认为它们在一个碎片中。这个判断的依据是通过之前的工作建立起的方法,具体判断方法参照文献[39-40]。图3显示的是16O+16O碰撞系统在
$ E_{\rm lab} $ =40 MeV/nucleon碰撞参数b = 3 fm时的电荷分布。我们对不同的构型的电荷分布进行比较,因为目前为止还没有相关实验数据,所以相同条件下UrQMD[41]和IQMD模型[42]结果也显示在图中。首先可以看出,不同模型给出的结果基本一致。随着电荷数的增加,产额逐渐降低。我们发现EQMD给出的4He的产额会比其他模型更高一些,因为EQMD初始化16O是以4个$ \alpha $ 团簇存在,一些$ \alpha $ 团簇在碰撞中被保留了下来。不同构型对应的Z=10附近的多重度有较大的差别,我们认为对于$ Z\leqslant6 $ 的碎片,由16O原子核直接碎裂产生的碎片占主要部分,此时不同构型的区别较小。而对于$ Z>6 $ 的碎片来自于两个16O先融合再碎裂,此时的几何构型对于融合过程以及碎片产生都会带来显著影响。当然选择的判断碎片的方法对多重数也有一些影响。另外如果我们仔细观察EQMD计算的不同$ \alpha $ 构型的结果,可以发现,紧凑构型(比如16O的正四面体构型)比松散构型(比如16O的长链型构型)产生的大块少,碎化程度较高。这是因为紧凑构型碰撞的几率更大,减少了大碎片产额,自由核子的产额较多。为了探究团簇构型对产额多重数分布影响的原因,图4给出了16O+16O的长链构型、风筝型、四边形和正四面体型对应的自由质子的产额和4He产额分布随时间的演化情况(a)(b),以及在100 fm/
$ c $ 对应的产额纵向快度分布(c)(d)。纵向快度的表达式为$ y_z \!=\! \frac{1}{2}\ln\frac{E+p_z}{E-p_z} $ 这里$ p_z $ 是$ z $ -方向的动量,$ E $ 是质心系下总能量。通常情况下,x-轴是碰撞参数的方向,y-轴是垂直于反应平面的方向,z-轴是沿着束流的方向。由图4(a)(b)可以看到,大部分的质子在20到60 fm/$ c $ 之间产生的,之后自由质子产额增长变缓。EQMD模型把初始化核16O看成4个$ \alpha $ 粒子,随着碰撞时间演化,4个$ \alpha $ 粒子被打碎,4He的产额逐渐下降,系统在100 fm/$ c $ 时达到稳定。不同构型对自由质子和4He产额影响明显,随着构型紧凑程度不同,自由质子和4He的产额会有规律的变化。紧凑构型(正四面体型、四方型)给出的自由质子的产额更高,而松散构型(长链型、风筝型)给出的4He的产额更高。这是因为紧凑构型比非紧凑构型碰撞更为剧烈,在团簇中的核子更容易被打碎,产生更多的自由质子,而碰撞相对不剧烈的松散构型更容易把初始时候的$ \alpha $ 团簇保留下来,导致4He产额较高。另外从图4(c)(d)快度分布来看,自由质子产额快度分布是类似于高斯分布,自由质子的产额峰值出现在中心快度区域,说明自由质子产生于高温高密区,是由碰撞产生的。而4He产额快度分布有明显的双峰结构,4He的产额峰值在碰撞的弹靶区域,可以看到,排列最为紧凑的正四面体型产生$ \alpha $ 粒子最少,相应的排列最为松散的长链型$ \alpha $ 粒子最多,4He大多产生于快度为$ -0.1 $ 及+0.1左右区域,说明一部分是碰撞后的碎片形成的,还有一部分是未参与碰撞的旁观者保留下来的。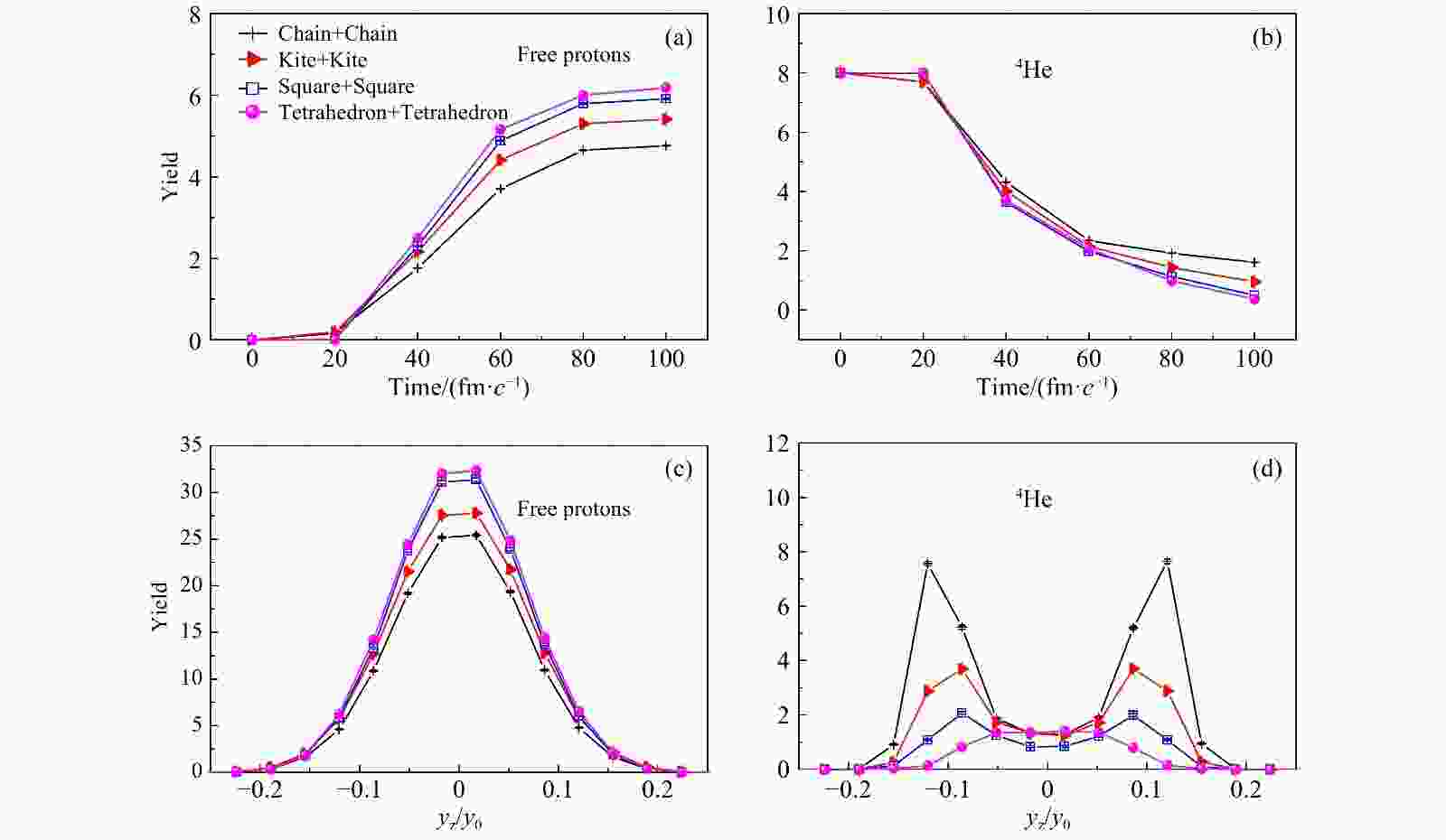
图 4 (在线彩图)入射能量为
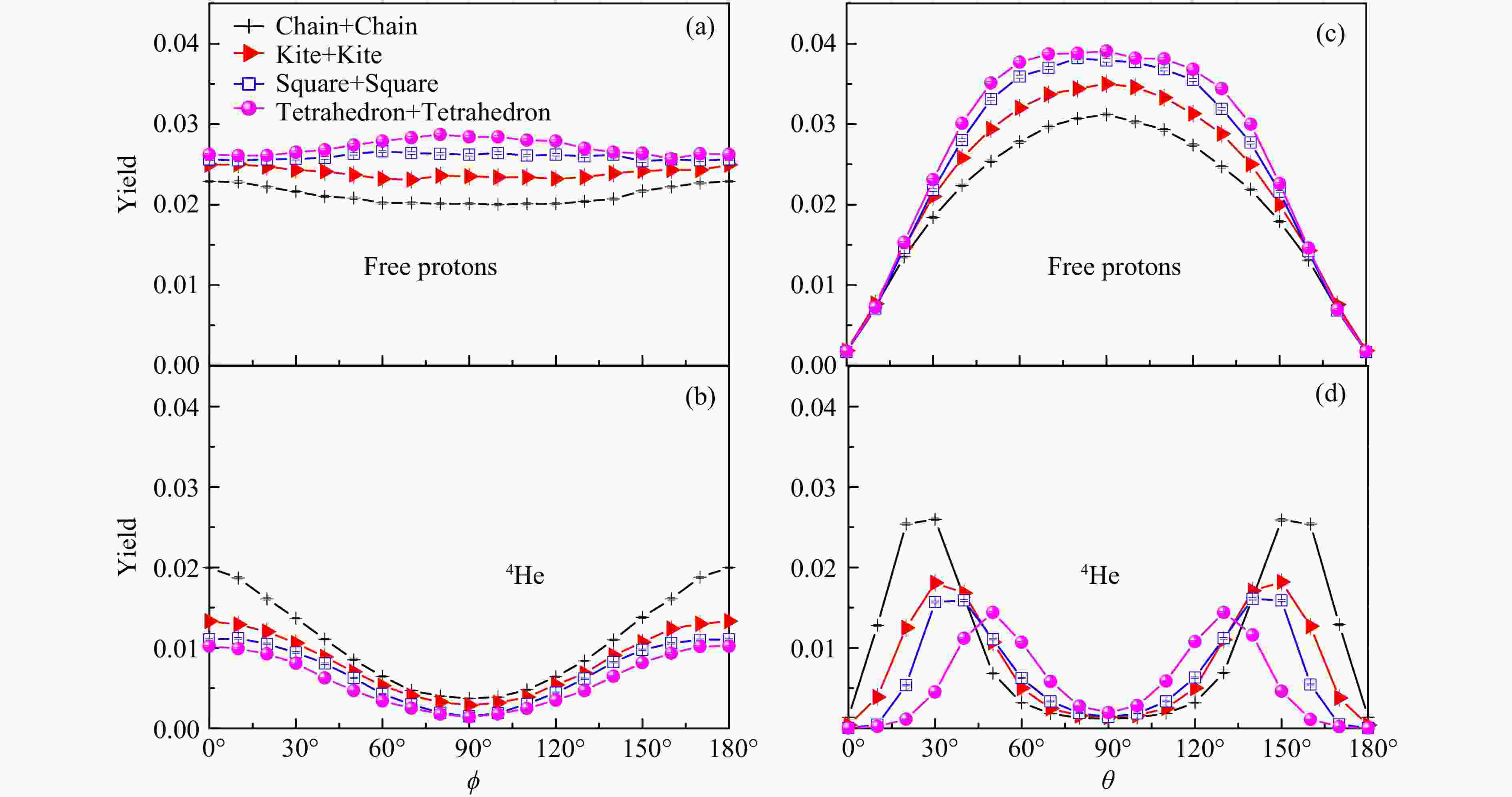
$E_{\rm lab}$ = 40 MeV/nucleon的16O+16O碰撞系统给出的不同构型对应的自由质子(a)和4He(b)的产额随反应时间的演化图及末态自由质子(c)和4He(d)的产额快度分布图为了寻找实验上探究团簇结构的敏感窗口。图5 给出了16O+16O的长链构型、风筝型、四边型和正四面体型对应的自由质子的产额 和4He产额的
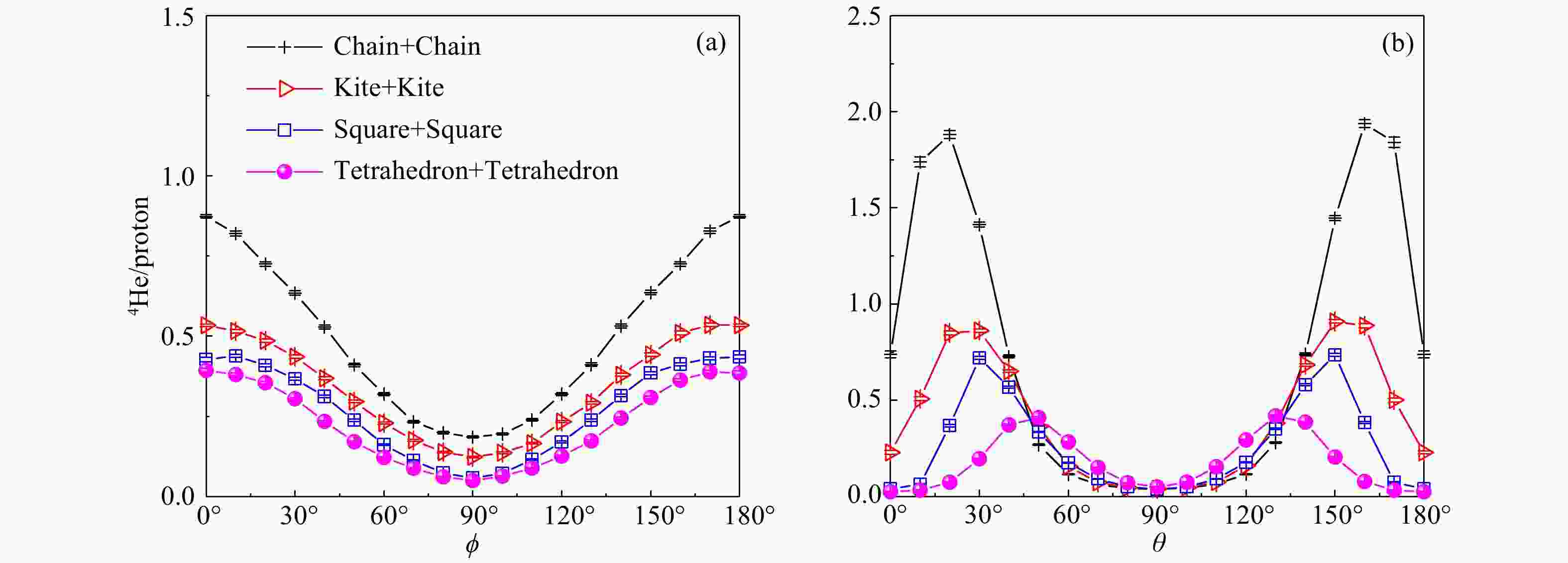
$ \phi $ 角分布(a)(c)和$ \theta $ 角分布(b)(d)。$ \theta $ 角、$ \phi $ 角表示出射粒子的发射方向。$ \theta $ 角为反应平面内出射粒子和束流z方向的夹角,$ \phi $ 是相对于反应平面的方位角。从图5(a)(c)可以看出,自由质子在$ \phi $ = 90°时产额最多,说明自由质子更趋于出平面发射,进一步说明了自由质子是由碰撞产生,挤出效应明显。可以发现不同构型产生的自由质子 在$ \phi $ =90°,$ \theta $ =90°时(y方向)产额差别最为明显,这表明我们可以根据y方向产生自由质子的产额多少来探究结构的差异。从图5(b)(d)我们发现4He在$ \phi $ =0°时产额最多,说明4He更趋于反应平面发射。同时发现不同构型4He出射$ \phi $ 角有明显差别。随着紧凑程度变化出射角也会有规律变化,排列松散的构型更倾向于小$ \phi $ 角出射,而排列最为紧凑的正四面体构型出射$ \phi $ 角最大。说明我们可以根据4He的出射$ \theta $ 和$ \phi $ 角来进一步判断16O的$ \alpha $ 团簇结构信息。为了便于实验探测,除探测器接收度的影响。图6给出4He/质子产额比值随着
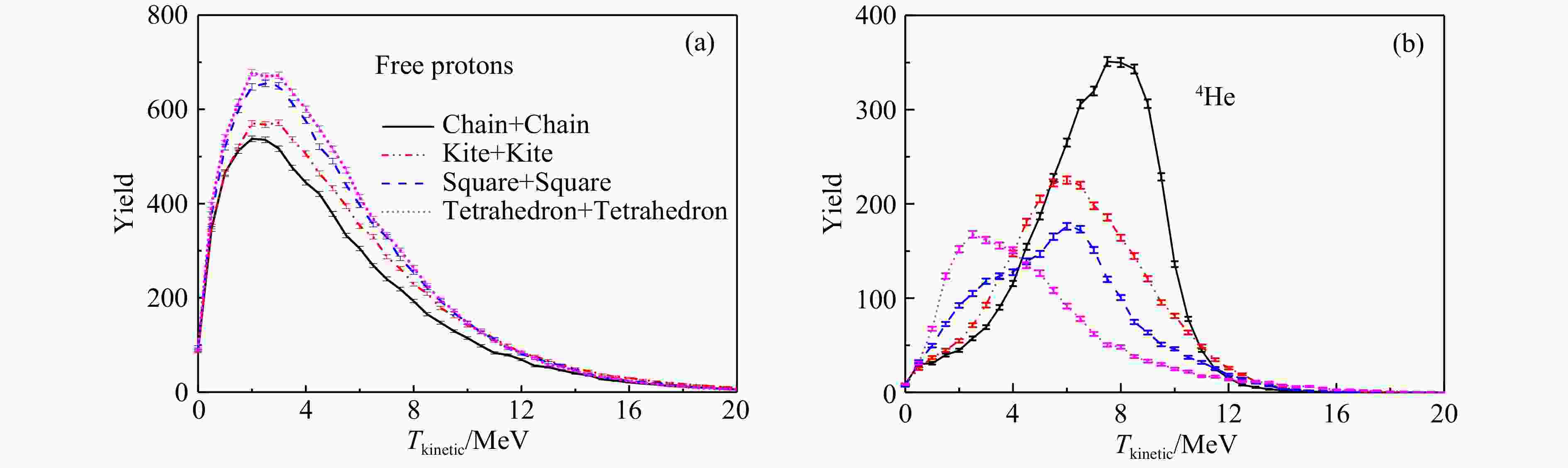
$ \theta $ 和$ \phi $ 的分布的变化情况。我们发现4He/proton产额比显示的构型差异比质子和4He产额显示构型差异更加明显,所以我们认为4He/proton可以作为团簇结构的另一个表征量。为了探究不同结构信息对能量的影响,图7给出了16O+16O的长链构型、风筝型、四边型和正四面体型所对应的自由质子及4He 产额随动能的变化情况。其中
$ T_{\rm kinetic} = \sum_{i}\left(E_{i}-m_{i}\right) = \sum_{i}\left(\sqrt{m_{i}^{2}+ {{p}}_{i}^{2}}-m_{i}\right) $ 。从图7可以清晰地看到,对于自由质子产额,不同构型的产额都在动能2.5 MeV时出现峰值。对于4He的产额,不同构型的的峰值不同。排列最为紧凑的正四面体4He的产额峰值出现在2.5 MeV,随着构型紧凑程度变化,峰值对应的动能逐渐增大,排列最为松散的长链型4He所对应的动能在8 MeV左右。这是因为高动能的核子主要产生于反应的早期,只经过1~2次的碰撞就快速飞离弹靶的重叠区域,受到相对较弱的核作用势的影响,所以这些核子的运动更容易保留初始化的信息。而自由质子及排列紧凑构型4He的产生是多次碰撞后形成的。多次碰撞会消耗部分动能,导致这些核子的动能比较低。我们发现,4He产额的动能能谱可以用来鉴别16O的团簇构型信息,排列越紧凑的构型所产生的4He的动能越低。 -
我们利用EQMD模型研究了不同
$ \alpha $ 团簇结构对重离子碰撞中16O+16O系统产额的影响。通过对重离子碰撞中的碎片产额分布的系统研究,我们发现:(1) 费米能区的重离子碰撞产生的自由质子和4He的产额对原子核的初始构型非常敏感,随着构型紧凑程度不同,自由质子和4He的产额会有规律的变化,紧凑构型(正四面体型、四方型)给出的自由质子的产额更高,而松散构型(长链型、风筝型)给出的4He的产额更高。这是因为排列紧凑构型碰撞最为激烈,挤出效应更加明显,而排列松散的构型因为碰撞较弱更容易保留初始化的信息;(2) 不同构型产生4He出射$ \phi $ 角有明显差别,排列最为紧凑的正四面体构型出射$ \phi $ 角最大。4He/proton可以作为团簇结构的一个表征量;(3) 4He产额的动能能谱可以用来鉴别16O的团簇构型信息,排列越紧凑的构型所产生的4He的动能越低。根据上述的结果,我们认为alpha团簇结构对于费米能区重离子碰撞产额分布有着可观测的影响。随着新技术的发展与革新,一些新的技术和手段(譬如:深度学习)结合对alpha团簇结构敏感的末态观测量将有助于我们进一步理解轻核的团簇信息。
Probing Clustering Configurations of 16O by the Yield Distribution in Heavy Ion Collisions at Fermi Energy
-
摘要: 近几年来,原子核核内的
$\alpha$ 团簇结构引起了人们的广泛关注。本工作的目的是讨论在费米能区下重离子碰撞的碎片产额分布是否可以作为研究轻核中$\alpha$ 团簇结构的工具。本文基于扩展的量子分子动力学输运模型(EMQD)模拟了16O具有4种不同的初始化$\alpha$ 构型(长链型、风筝型、四方型以及正四面体型)的16O+16O反应,通过观察碎片产额多重数分布情况研究了具有不同结构的团簇核的核反应。计算结果表明,碰撞后产生的自由质子及4He的产额受不同构型的影响明显,表明4He/proton可以作为团簇结构的一个表征量。此外,自由质子及4He的出射$\theta$ 和$\phi$ 角及动能能谱可以用来提取16O的$\alpha$ 团簇构型信息。-
关键词:
- $\alpha$团簇结构 /
- 产额分布 /
- 重离子核反应 /
- EQMD模型
Abstract: In recent years, the cluster structure in nuclei has attracted a lot of attention. The goal of this work is to investigate the yield distribution of heavy ion collisions at Fermi energy and evaluate the$\alpha$ cluster configurations in light nuclei. The 16O+16O reactions with four different initialization$\alpha$ configurations (long chain, kite, square, tetrahedron)are simulated based on the Extended Quantum Molecular Dynamics (EQMD) transport model. The nuclei with different structures are investigated by observation of the multiplicity distribution of yields in nuclear reactions. It is found that the yields of free protons and 4He were affected by different cluster configurations, which indicates that 4He/proton can be used as a characterization of cluster structure. In addition, the$\alpha$ cluster configuration information of 16O can be extracted from the outgoing$\theta$ and$\phi$ and the kinetic energy spectrum of of free protons and 4He. -
-
[1] WHEELER J A. Phys Rev, 1937, 52: 1083. doi: 10.1103/PhysRev.52.1083 [2] HAFSTAD L R, TELLER E. Phys Rev, 1938, 54: 681. doi: 10.1103/PhysRev.54.681 [3] FESHBACH H, IACHELLO F. Phys Lett B, 1973, 45: 7. doi: 10.1016/0370-2693(73)90239-6 [4] DENNISON D M. Phys Rev, 1954, 96: 378. doi: 10.1103/PhysRev.96.378 [5] ROBSON D. Phys Rev Lett, 1979, 42: 876. doi: 10.1103/PhysRevLett.42.876 [6] BAUHOFF W, SCHULTHEIS H, SCHULTHEIS R. Phys Rev C, 1984, 29: 1046. doi: 10.1103/PhysRevC.29.1046 [7] TOHSAKI A, HORIUCHI H, SCHUCK, et al. Phys Rev Lett, 2001, 87: 192501. doi: 10.1103/PhysRevLett.87.192501 [8] EBRAN J P, KHAN E, NIKSIC T, et al. Nature, 2012, 487: 341. doi: 10.1038/nature11246 [9] COOK C W, FOWLER W A, LAURITSEN C C, et al. Phys Rev, 1957, 107: 508. doi: 10.1103/PhysRev.107.508 [10] EPELBAUM E, KREBS H, LEE D, et al. Phys Rev Lett, 2011, 106: 192501. doi: 10.1103/PhysRevLett.106.192501 [11] EPELBAUM E, KREBS H, LAHDE T A, et al. Phys Rev Lett, 2012, 109: 252501. doi: 10.1103/PhysRevLett.109.252501 [12] MARIN-LAMBARRI D J, BIJKER R, FREER M, et al. Phys Rev Lett, 2014, 113: 012502. doi: 10.1103/PhysRevLett.113.012502 [13] CHERNYKH M, FELDMEIER H, NEFF T, et al. Phys Rev Lett, 2007, 98: 032501. doi: 10.1103/PhysRevLett.98.032501 [14] KANADA-EN'YO Y, KIMURA M, ONO A. PTEP, 2012, 2012: 01A. doi: 10.1093/ptep/pts001 [15] LIU L, ZHANG Z H, ZHAO P W. Phys Rev C, 2015, 92: 044304. doi: 10.1103/PhysRevC.92.044304 [16] ICHIKAWA T, MARUHN J A, ITAGAKI N, et al. Phys Rev Lett, 2011, 107: 112501. doi: 10.1103/PhysRevLett.107.112501 [17] EPELBAUM E, KREBS H, LÄHDE T A, et al. Phys Rev Lett, 2014, 112: 102501. doi: 10.1103/PhysRevLett.112.102501 [18] BIJKER R, IACHELLO F. Phys Rev Lett, 2014, 112: 152501. doi: 10.1103/PhysRevLett.112.152501 [19] HE W B, MA Y G, CAO X G, et al. Phys Rev Lett, 2014, 113: 032506. doi: 10.1103/PhysRevLett.113.032506 [20] HE W B, MA Y G, CAO X G, et al. Phys Rev C, 2014, 94: 014301. doi: 10.1103/PhysRevC.94.014301 [21] YANG Z H, YE Y L, LI Z H, et al. Phys Rev Lett, 2014, 112: 162501. doi: 10.1103/PhysRevLett.112.162501 [22] BRONIOWSKI W, RUIZ ARRIOLA E. Phys Rev Lett, 2014, 112: 112501. doi: 10.1103/PhysRevLett.112.112501 [23] GUO C C, MA Y G, AN Z D, et al. Phys Rev C, 2019, 99: 044607. doi: 10.1103/PhysRevC.99.044607, [24] GUO C C, HE W B, MA Y G. Chin Rev Lett, 2017, 34: 092101. doi: 10.1088/0256-307x/34/9/092101 [25] ZHANG S, MA Y G, CHEN J H, et al. Phys Rev C, 2017, 95: 064904. doi: 10.1103/PhysRevC.95.064904 [26] ZHANG S, MA Y G, CHEN J H, et al. Eur Phys J A, 2018, 54: 161. doi: 10.1140/epja/i2018-12597-y [27] XU Z W, ZHANG S, MA Y G, et al. Nucl Sci Tech, 2018, 29: 186. doi: 10.1007/s41365-018-0523-9 [28] HUANG B S, MA Y G, HE W B. Eur Phys J A, 2017, 53: 119. doi: 10.1140/epja/i2017-12300-0 [29] HUANG B S, MA Y G, HE W B. Phys Rev C, 2017, 95: 034606. doi: 10.1103/PhysRevC.95.034606 [30] AICHELIN J, STOECKER H. Phys Lett B, 1986, 176: 14. doi: 10.1016/0370-2693(86)90916-0 [31] AICHELIN J. Phys Rept, 1991, 202: 233. doi: 10.1016/0370-1573(91)90094-3 [32] MARUYAMA T, NIITA K, IWAMOTO A. Phys Rev C, 1996, 53: 297. doi: 10.1103/PhysRevC.53.297 [33] SHI C Z, MA Y G, CAO X G, et al. Phys Rev C, 2020, 102: 014601. doi: 10.1103/PhysRevC.102.014601 [34] ONO A, HORIUCHI H. Prog Part Nucl Phys, 2004, 53: 501. doi: 10.1016/j.ppnp.2004.05.002 [35] FIELDS D J, LYNCH W G, CHITWOOD C B, et al. Phys Rev C, 1984, 30: 1912. doi: 10.1103/PhysRevC.30.1912 [36] WILE J L, FIELDS D E, KWIATKOWSKI K, et al. Phys Rev C, 1992, 45: 2300. doi: 10.1103/PhysRevC.45.2300 [37] KIM Y D, DE SOUZA R T, BOWMAN D R, et al. Phy Rev C, 1992, 45: 338. doi: 10.1103/PhysRevC.45.338 [38] HAGEL K, GONIN M, WADA R, et al. Phys Rev C, 1994, 50: 2017. doi: 10.1103/PhysRevC.50.2017 [39] LI Q F, WANG Y J, WANG X B, et al. Sci China Phys Mech Astron, 2016, 59: 622001. doi: 10.1007/s11433-015-5768-2 [40] LI Q F, WANG Y J, WANG X B, et al. Sci China Phys Mech Astron, 2016, 59: 632002. doi: 10.1007/s11433-015-5775-3 [41] GUO C C, WANG Y J, LI Q F, et al. Sci China Phys Mech Astron, 2012, 55: 252-259. doi: 10.1007/s11433-011-4616-2 [42] LI C, TIAN J L, ZHANG F S. Phys Lett B, 2020, 809: 135697. doi: 10.1016/j.physletb.2020.135697 -












 下载:
下载:








































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号