-
高能电子成像(High Energy Electron Radiography, HEER)[1]技术由美国洛斯阿拉莫斯国家实验室首次提出,并开展了相关研究。他们利用30 MeV的电子束对薄的静态和动态进行了成像实验,获得100 μm空间分辨,证明了电子成像对具有薄面密度的物体具有极高的灵敏度。高能电子成像作为射线成像的一种,相比于X射线成像,对高Z和低Z混合材料的分辨率高,同时可以获得更高的空间分辨率。在2013年底,国内由中国科学院近代物理研究所和清华大学工程物理系合作首次展开高能电子成像研究,提出将高能电子成像技术作为高能量密度物质诊断工具[2-3],应用于高能量密度物理研究和惯性约束聚变物理过程中的ICF靶丸压缩过程的实时诊断及信息反馈。随后开展了一系列研究工作,实验验证了HEER的空间分辨优于10 μm[4],可作为高能量密度物理诊断方法,并搭建了兰州高能电子成像实验平台以进一步开展相关实验研究。高能电子二维成像主要是用加速器产生的高能电子束直接穿过样品靶xy平面(假定束流方向沿z),再经过磁透镜系统对透射电子聚焦,实现对点成像,最后获得xy平面成像。二维成像的缺陷是不能精确确定样品三维结构。当样品在xy平面的投影具有相同的图像,但是内部缺陷位于不同的z位置的时候,二维成像不能准确判断缺陷z的位置。中国科学院近代物理研究所于国内首次提出将3D tomography算法引用到高能电子成像中,通过在多个成像视角下采集二维成像数据,利用三维图像重建算法实现高能电子三维成像,进一步实现了样品内部结构位置的确定,拓宽高能电子成像技术的应用领域[5]。
基于投影数据的图像重建算法中常用的有解析重建算法和迭代重建算法,在传统的X射线CT成像[6-7]中已广泛应用和发展。在同样的投影数据采集频率情况下或在投影数据不足时,迭代算法如代数重建技术(Algebraic Reconstruction Technique,ART)成像精度高于非迭代算法。目前高能电子成像领域普遍采用滤波反投影(Filtered Back Projection,FBP)算法,重构模拟靶标的三维结构,验证了高能电子三维成像的可行性[5]。为进一步提高图像重建精度,本文将ART算法应用于高能电子三维成像。通过蒙卡模拟仿真,分别用FBP和ART算法进行了高能电子三维成像模拟图像重建,并对两种算法的图像质量进行了定量对比分析,再进行实际实验验证其结果与仿真结果是否一致,进一步验证高能电子三维成像的可行性。
-
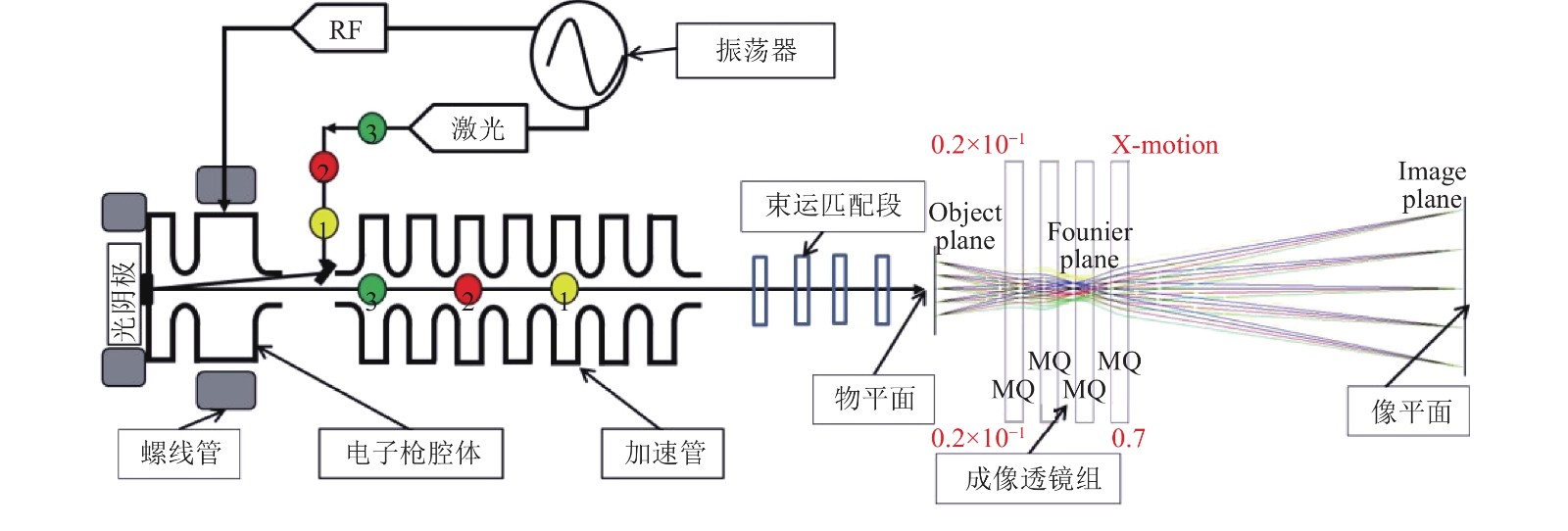
HEER的基本成像原理如图1[8]所示:以一台热阴极电子枪为注入器,再利用α磁铁结合四极磁铁组完成低能线相空间匹配、束流纵向压缩以及刮束选能,最后被注入行波加速管进行加速,并在加速管出口处获得能量为50 MeV的高能电子束。电子束照射靶物质并与靶物质相互作用后,利用点对点磁透镜成像系统和傅里叶平面,将通过靶物质后并携带靶物质信息的电子束在荧光屏上成像。电子束与靶物质的相互作用包括弹性散射及非弹性散射(包括电离和激发等)。高能电子三维成像与电子断层扫描相似,主要区别在于,由于磁透镜系统的存在高能电子三维成像呈现相反的图像[5]。在原理上,所有穿透照相中粒子在物质中的穿透过程都遵循lambert-beer定律[9-10]。电子束成像是穿透射线束成像,因此,射线经过物体后强度会衰减,且服从lambert-beer定律。高能电子三维成像实验中,靶物质将固定在可旋转物平面上,连续旋转物平面,并用CCD相机采集在荧光屏上的图像,CCD的采集时间与电子束的脉冲同步。在本研究中,旋转间隔角度为1度,共计旋转179次,获得180幅图像,然后通过三维重建算法重构出靶物质三维图像,获得靶物质结构的内部信息。
高能电子成像与X射线成像在原理上主要有以下区别,与靶物质的相互作用以及相互作用后对出射电子角度的筛选。高能电子成像过程中,激发作用、电离作用以及韧致辐射作用会造成出射电子的能量损失;多库仑散射导致电子的角度发散。高能电子成像的空间分辨率与透射电子角度成正比,透射电子的散角与入射电子能量成反比,提高入射电子能量可以有效降低透射电子的角度发散,进而提高空间分辨率[11]。X射线在穿过物体后会发生光电效应、康普顿散射和电子对效应等,X射线的能量区间不同,与物体作用的反应不同,与物体相互作用还需考虑X射线的软硬。高能电子束带电,在与靶物质作用后经过磁透镜系统及傅里叶平面,通过将散射角度较大的出射电子滤除,提高成像的空间分辨率,最后由CCD相机采集图像。光子不带电,无法加磁场将散射角度大的粒子滤除,X射线与物体相互作用后,直接由探测器探测。此过程会对最终的成像分辨率有影响。
-
FBP算法以傅里叶中心切片定理[12]为基础。针对重建图像,能够直接从投影数据进行反投影获得原图像,但由于反投影过程中数据是均匀分摊,会导致图像模糊,因此在反投影操作之前需先进行滤波。滤波反投影算法在获得投影的一维傅里叶变化后,在通过傅里叶反变换之前先进行滤波处理,进而改善重建后函数的模糊程度,使得重建后的图像质量更好。
FBP算法的具体步骤为:
步骤1 对投影数据
${P_\phi }\left( {{x_r}} \right)$ 作一维傅里叶变换,得到$F\left( {\rho ,\phi } \right)$ ;步骤2 选择合适的滤波器
$H\left( \omega \right)$ 与$F\left( {\rho ,\phi } \right)$ 相乘,即计算$F\left( {\rho ,\phi } \right) \times H\left( \omega \right)$ ,再将滤波后的结果傅里叶反变换得到滤波后的投影数据$P_\phi '\left( {{x_r}} \right)$ ;步骤3 将步骤2中的
$P_\phi '\left( {{x_r}} \right)$ 进行反投影并将所有反投影进行叠加,得到重建图像$f\left( {x,y} \right)$ 。 -
ART算法将连续的图像离散化,把待重建的断层图像
$f\left( {x,y} \right)$ 分成N个离散的像素方格,并把像素方格内的像素值$f\left( {x,y} \right)$ 看成常数,记作${f_j}$ 。用线性方程组$\sum\limits_{j = 1}^N {{\omega _{ij}}{f_j} = {p_i}} ,i = 1,2, \cdots ,M$ [13]来描述重建图像和投影数据之间的关系,具体公式如式(1)所示。$$\begin{gathered} {\omega _{11}}{f_1} + {\omega _{12}}{f_2} + \cdots + {\omega _{1N}}{f_N} = {p_1} \\ {\omega _{21}}{f_1} + {\omega _{22}}{f_2} + \cdots + {\omega _{2N}}{f_N} = {p_2} \\ \vdots \\ {\omega _{M1}}{f_1} + {\omega _{M2}}{f_2} + \cdots + {\omega _{{\rm{M}}N}}{f_N} = {p_M} \\ \end{gathered} ,$$ (1) 式中:
${\omega _{ij}}$ 是权重因子,表示第j个像素对第i条射线投影值的贡献,在数值上等于第i条射线与第j个像素相交的长度;${f_j}$ 表示第j个像素值,N是像素的总个数;${p_i}$ 代表第i条射线的投影值,M为投影总数,等于射线条数与投影角度数的乘积。在本文中,${p_i}$ 是由高能电子成像获得的图片,${f_i}$ 是待重建图片的像素单元灰度值。ART算法的具体步骤为:
步骤1 设定图像初始值,初始值的设定会直接影响图像迭代的次数,一般情况下设初始值为0,本文采用0值;
步骤2 根据估算的投影数据与实际获得的投影数据相比较,获得图像的修正值,具体公式如式(2)所示:
$$f_j^{\left( {k + 1} \right)} = f_j^{\left( k \right)} + \lambda \frac{{{p_i} - \sum\limits_{n = 1}^N {{\omega _{in}}f_n^{\left( k \right)}} }}{{\sum\limits_{n = 1}^N {\omega _{in}^2} }}{\omega _{ij}},$$ (2) 式中:λ为松弛因子(0<λ<2),k为迭代次数;1≤i≤M;1≤j≤N。为了抑制伪影,将像素值小于零的值变为0。当全部射线完成修正后,完成一次迭代;
步骤3 判断迭代终止条件是否成立,若成立迭代终止,不成立则将上轮迭代结果作为初始值,继续步骤2直至迭代终止条件成立。
-
为定量评价不同种算法的重建质量,采用均方根误差(RMSE)[14],结构相似性(SSIM)[15]作为评价标准。均方根误差衡量重建值与真实值之间的偏差,值越小,重建图片越接近原图,具体公式如式(3)。结构相似性是一种衡量两幅图像相似度的指标,其取值范围为[0,1],值越大,则表示重建后图像失真越小,具体公式如式(4)。
$$RMSE = \sqrt {\frac{1}{N}{{\sum\limits_{j = 1}^N {\left( {{f_j} - f_j'} \right)} }^2}} ,$$ (3) $$SSIM\left( {x,y} \right) = \frac{{\left( {2{\mu _x}{\mu _y} + {c_1}} \right)\left( {2{\sigma _{xy}} + {c_2}} \right)}}{{\left( {\mu _x^2 + \mu _y^2 + {c_1}} \right)\left( {\sigma _x^2 + \sigma _y^2 + {c_2}} \right)}},$$ (4) 式中:
${f_j}$ 是重建后图像的第j个像素值,$f_j'$ 是原图的第j个像素值。x, y分别是原图和重建后图像,${\mu _x}$ ,${\mu _y}$ 分别是原图x和重建后图像y的像素平均值,${\sigma _x}$ 是x的方差,${\sigma _y}$ 是y的方差,${\sigma _{xy}}$ 是x, y的协方差,${c_1} = {\left( {k1 \times L} \right)^2}, $ $ {c_2} = {\left( {k2 \times L} \right)^2}$ 是用来维持稳定的常数,L是像素值的动态范围,$k1 = 0.01,\;k2 = 0.03$ 。 -
高能电子成像仿真采用了EGS[16]、PARMELA[17]等程序。EGS是一个通用程序包,用蒙特卡罗方法模拟电子和光子在任意几何形状下的靶物质的耦合传输,PARMELA是一款束流动力学模拟软件,用来模拟电子束的传输及分布。为了探究高能电子三维成像的性能,模拟的靶物质是半径为0.01 cm的实心铝球并且在内部留有一个偏置的半径为0.003 cm的空心小球,靶物质的模型参数如表1所列。利用EGS模拟平行电子束与靶物质相互作用,PARMELA模拟透过靶后的电子的成像。高能电子成像过程中,加速器运行过程中产生的γ射线辐射以及CCD相机采集时带来的噪声给投影图片带来干扰,这些噪声多以椒盐噪声为主。为了模拟结果可靠,在模拟过程中,将获得的投影图像加入椒盐噪声。编写基于FBP算法和ART算法的三维重建程序,完成高能电子三维重建。其中ART重建算法的参数设置为:固定松弛因子λ=0.5,迭代次数5次。
表 1 模拟靶物质的参数
靶物质 X/cm Y/cm Z/cm R/cm 铝球 0 0 0 0.010 空心球 –0.004 0.005 0 0.003 -
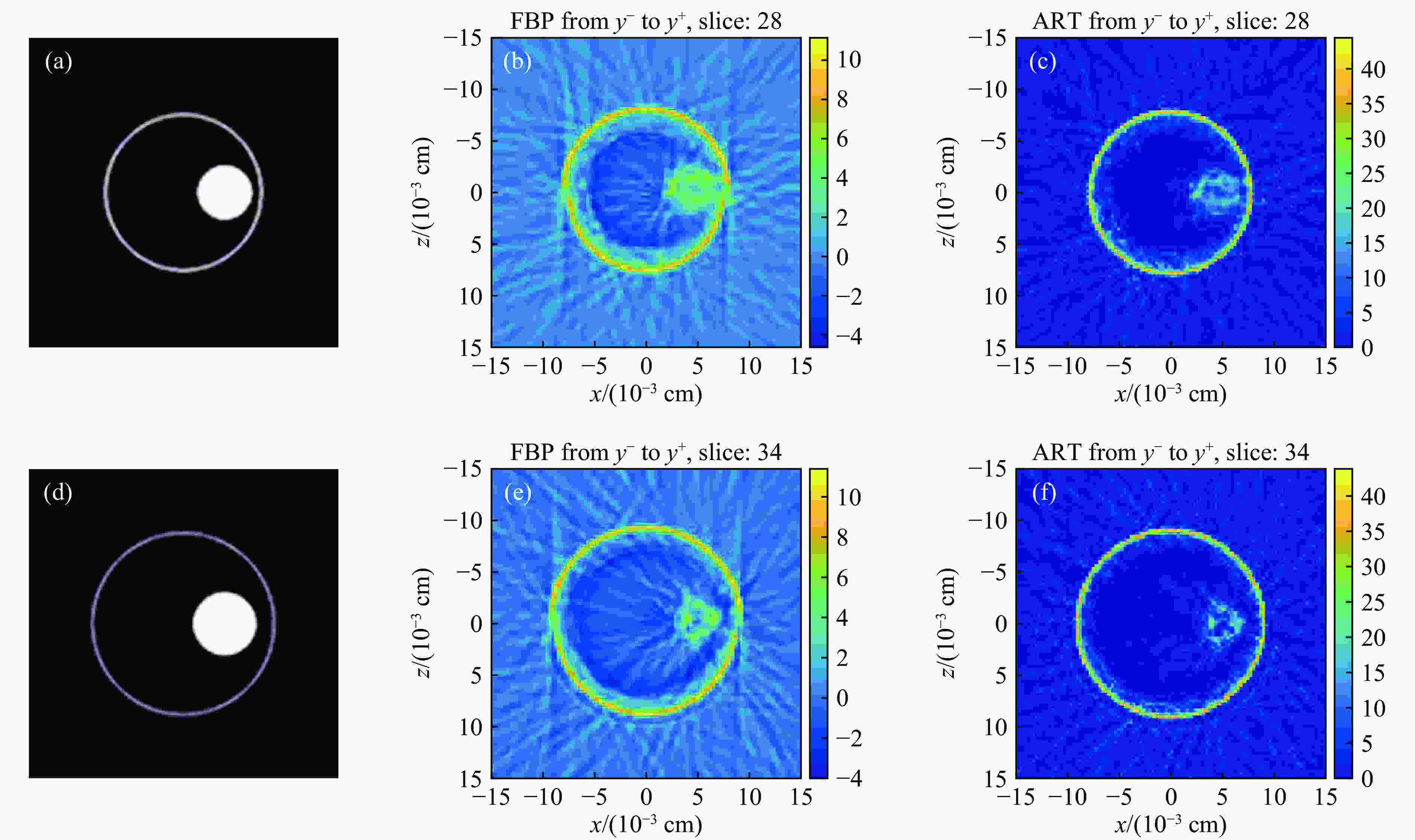
在HEER过程中,模拟的电子束团能量使用真实实验所能达到的最高值50 MeV,模拟的靶物质从0度旋转到179度(限于靶安装及实际实验情况,最多旋转180度),每旋转一度采集一个成像矩阵,共计获得180个成像矩阵,每个成像矩阵大小为100×100,同时加入椒盐噪声,再经过中值滤波器滤波来削弱噪声影响,再分别采用FBP算法和ART算法重建,并用重建评价指标评价重建性能。重建结果分为x, y, z三个方向,每个方向上共计100个重建切片,切片大小为0.03 cm×0.03 cm。为能清楚地观测模拟靶物质的内部,每个方向上选择重建能观察到内部空心球的切片。x方向上,重建结果如图2所示,显示了从x-到x+的第60层和第72层切片;y方向上,重建结果如图3示,显示了从y-到y+的第28层和第34层切片;z方向上,重建结果如图4示,显示了从z-到z+的第47层和第50层切片。
通过重建评价指标对比分析了三维方向上的对应切片的重建图像质量评估结果,如表2所列。通过比较结构相似性发现,基于ART算法重建的数值大于基于FBP算法重建的数值,即ART重建后的图像失真更小。通过比较均方根误差,基于ART算法的重建误差要比基于FBP算法的重建误差小,即基于ART算法重建后的结果更接近原图。
表 2 重建结果质量评估
切片位置 结构相似性(SSIM) 均方根误差(RMSE) FBP ART FBP ART x=60 0.187 4 0.352 8 62.866 2 47.046 5 x =72 0.156 6 0.390 5 66.268 1 33.269 0 y=28 0.104 6 0.519 5 75.781 6 36.533 2 y=34 0.089 3 0.429 9 73.187 5 44.502 2 z=47 0.131 1 0.325 6 88.138 2 52.202 7 z=50 0.118 4 0.362 0 89.879 0 47.093 3 结合各方向上的重建图像,基于两种算法重建的图片的内部小圆位置区别较小。在y方向上的重建图片中,基于ART算法重建图像外围大圆的轮廓更清晰,大圆内部无其他明显的伪影,能够明显区别出小圆。相对于FBP算法,基于ART算法重建结果的边缘信息保真度高,伪影减少。
-
实验中,给样品赋予三维坐标,高能电子束沿z轴方向直接通过样品的x-y面,经过磁透镜系统实现点对点成像。样品放置在可旋转平台上,该平台可以绕y轴(±90度)旋转,每间隔1度旋转一次并获得样本的一张2D HEER图像,通过CCD相机收集0~179度的共180张图像,最后利用算法重建。实验样品是手表的一小部分,图片显示在图5中,该样品的尺寸:宽度×厚度×高度为1.12 mm×0.15 mm×2.06 mm。图5(a, b)分别是样品的主视图和左视图,以厚度为x轴,宽度为y轴,高度为z轴建立3D坐标系如图5(c)所示。该实验是在中国科学院近代物理研究所的高能电子照相实验平台上进行的,实验中使用的电子束参数如下:束流能量为50 MeV,能散为0.1%,归一化发射度约为8.0 mm·mrad,束团电荷量约为100 pC,束团长度约为1.5 ps。
图6显示的是获得2D HEER图像,图6(a)是0度投影图,图6(b)是90度投影图, 图6(c)是180度投影图。将这180幅HEER图像分别用FBP和SART算法进行重建,样品x方向上重建的断层切片结果如图7所示,挑选的切片位置是沿x-到x+方向上的第94和100层切片。
对比分析图7的重建结果,两种算法都存在伪影,样品右边轮廓被模糊显示。但ART的结果相对比与FBP而言伪影较少,样品左侧轮廓更加清晰,实验重建的结果基本与模拟实验的结果一致,表明在180个投影数据下,ART的结果伪影更少,边缘信息保真度高。
-
为了提高高能电子三维成像的性能,本文研究将ART算法三维重建应用于HEER三维成像。论文通过蒙特卡罗模拟进行了高能电子束成像仿真实验,并进行了实际实验,验证了ART算法对靶物质内部结构实现三维重建的可行性。相对于FBP算法,基于ART算法的重建结果抑制伪影效果好,边缘信息保真度高。两种算法重建时使用的投影数据都是180个角度的投影数据,就重建时间来说,ART算法重建使用的时间比FBP算法长。但ART算法为高能电子成像三维成像不同的应用需求提供了更多选择,同时ART算法结合TV(Total Variation)正则化适用于稀疏采样投影重建[18],即增大采样间隔,减少投影数据采集的总数,既可以减少数据采集的时间,同时加快重建速度。Li[19]等提出将ART算法与FBP算法结合,可在少量投影时提高图像锐度。本文对ART算法在高能电子三维成像的应用研究为解决投影数据不足情况下的成像应用提供了思路和方法。
致谢 感谢兰州大学的李公平教授、张催博士对本论文提供的帮助。
Study on Three-dimensional High Energy Electron Radiography Based on Algebraic Reconstruction Algorithm
-
摘要: 本工作将代数重建算法应用于新兴发展的高能电子成像技术开展三维成像研究,实现对样品靶物质内部结构信息的精确诊断。通过蒙特卡罗程序及粒子追踪程序模拟高能电子成像过程,包括电子束与靶物质相互作用过程,获得样品靶物质成像角度下的高能电子二维成像结果。利用代数迭代重建ART(Algebraic Reconstruction Technique)算法和滤波反投影算法分别进行了高能电子三维成像仿真测试,重建出靶物质的三维图像,并将两种算法重建的断层图像用图像评价指标进行了定量对比分析。结果表明:在投影角度数为180个的条件下,ART的重建结果更接近靶物质原图,能有效抑制伪影,图像保真度较高。为进一步验证模拟结果,展开了实际实验,得到的结论与模拟结果相同。本研究结果为后续高能电子三维成像重建算法的优化提供了依据。Abstract: In this paper, the algebraic reconstruction algorithm is applied to the newly developed High Energy Electron Radiography(HEER) technology to carry out three-dimensional imaging research, which realizes the accurate diagnosis of the internal structure information of the sample material. The Monte Carlo program and the particle tracking program are used to simulate the high-energy electron imaging process, including the interaction process between the electron beam and the target substance, and obtain the high-energy electron two-dimensional imaging results under the imaging angle of the sample. The ART(Algebraic Reconstruction Technique) algorithm and the Filtered Back Projection (Filtered Back Projection) algorithm were used to simulate experiment of Three-Dimensional High Energy Electron Radiography(TDHEER) respectively, and the three-dimensional images of the sample were reconstructed. These images have been quantitatively compared and analyzed through evaluation indexes. The results show that under the condition that the angle number of projection is 180, the reconstruction results of ART are closer to the original image of the sample, which have higher fidelity and fewer image artifacts. In order to further verify the simulation results, actual experiments were carried out, and the conclusions are the same as the simulation. The results of this study provide a basis for the optimization of the subsequent TDHEER.
-
表 1 模拟靶物质的参数
靶物质 X/cm Y/cm Z/cm R/cm 铝球 0 0 0 0.010 空心球 –0.004 0.005 0 0.003 表 2 重建结果质量评估
切片位置 结构相似性(SSIM) 均方根误差(RMSE) FBP ART FBP ART x=60 0.187 4 0.352 8 62.866 2 47.046 5 x =72 0.156 6 0.390 5 66.268 1 33.269 0 y=28 0.104 6 0.519 5 75.781 6 36.533 2 y=34 0.089 3 0.429 9 73.187 5 44.502 2 z=47 0.131 1 0.325 6 88.138 2 52.202 7 z=50 0.118 4 0.362 0 89.879 0 47.093 3 -
[1] ZHAO Y T, ZHANG Z M, XU H S, et al. A High Resolution Spatial-temporal Imaging Diagnostic for High Energy Density Physics Experiments[C]//Proceedings of IPAC2014, Dresden, Germany. 2014: 2819. [2] ZHAO Quantang, CAO S C, LIU M, et al. Nucl Instr and Meth A, 2016, 832: 144. doi: 10.1016/j.nima.2016.06.103 [3] 赵全堂, 张子民, 曹树春, 等. 原子能科学技术, 2019, 53(9): 1651. doi: 10.7538/yzk.2019.youxian.0160 ZHAO Quantang, ZHANG Zimin, CAO Shuchun, et al. Atomic Energy Science and Technology, 2019, 53(9): 1651. (in Chinese) doi: 10.7538/yzk.2019.youxian.0160 [4] ZHAO Quantang, CAO Shuchun, CHENG Rui, et al. High Energy Electron Radiography Experiment Research Based on Picosencond Pulse Width Bunch[C]//Proceedings of Linac. [S. 1.]: [s. n.], 2014. [5] ZHAO Quantang, MA Yuanyuan, XIAO Jiahao, et al. Applied Sciences, 2019, 9(18): 3764. doi: 10.3390/app9183764 [6] 窦少彬. CT图像优化重建算法研究[D]. 合肥: 中国科学技术大学, 2019. DOU Shaobin. Study on Optimal Reconstruction Algorithm of CT Image[D]. Hefei: University of Science and Technology of China, 2019. (in Chinese) [7] 毛小渊. 二维CT图像重建算法研究[D]. 南昌: 南昌航空大学, 2016. MAO Xiaoyuan. Study on the Reconstruction Algorithm of Two-dimensional CT Image[D]. Nanchang: Nanchang Hangkong University, 2016. (in Chinese) [8] GAI Wei, QIU Jiaqi, JING Chunguang. Electron Imaging System for Ultrafast Diagnostics of HEDLPSPIE[C]//Target Diagnostics Physics & Engineering for Inertial Confinement Fusion II. Bellingham WA: SPIE, 2014: 921104. [9] 严岩. 高能质子照相束线的模拟设计与成像特性的初步研究[D]. 兰州: 兰州大学, 2015. YAN Yan. Preliminary Study on Simulation Design and Imaging Characteristics of High-energy Proton Radiography Beam Line[D]. Lanzhou: Lanzhou University, 2015. (in Chinese) [10] BEER. Ann Phys Chem, 1852, 86: 78. doi: 10.1002/andp.18521620505 [11] 肖家浩. 高能电子成像技术在高能量密度物质诊断中的应用[D]. 兰州: 中国科学院大学(中国科学院近代物理研究所), 2019. XIAO Jiahao. Application of High Energy Electronic Imaging Technology in the Diagnosis of High Energy Density Materials[D]. Lanzhou: University of Chinese Academy of Sciences(Institute of Modern Physics, Chinese Academy of Sciences), 2019. (in Chinese) [12] LIU Botao, LV Boying, TIAN Yishuai. American Journal of Computer Engineering, 2020, 3: 10. doi: 10.28933/ajce-2020-04-1105 [13] AGARWAL C, MHATRE A, PATRA S, et al. SN Applied Sciences, 2019, 1: 1157. doi: 10.1007/s42452-019-1201-1 [14] 贾俊平. 统计学基础[M]. 北京: 中国人民大学出版社, 2010. JIA Junping. Basis of statistics[M]. Beijing: China Renmin University Press, 2010. (in Chinese) [15] WANG Zhou, BOVIK A C, SHEIKH H R, et al. IEEE Transactions on Image Processing, 2004, 13 (4): 600. [16] EGS (Electron Gamma Shower)[EB/OL]. [2020-05-26]. http://rcwww.kek.jp/research/egs/. [17] PARMELA[EB/OL]. [2020-05-26]. http://laacg.lanl.gov/laacg/services/serv-codes.phtml. [18] 熊军. 代数迭代CT图像重建算法研究[D]. 成都: 成都理工大学, 2015. XIONG Jun. Study on Algebraic Iterative CT Image Reconstruction Algorithm[D]. Chengdu: Chengdu University of Technology, 2015. (in Chinese) [19] LI Sangang, DONG Zhengyun, GAN Quan, et al. Annals of Nuclear Energy, 2020, 145: 107515. doi: 10.1016/j.anucene.2020.107515 -






 下载:
下载:





































 甘公网安备 62010202000723号
甘公网安备 62010202000723号