-
随着科学技术的迅速发展,我国在核工业,核技术及射线装置方面取得了许多突出的成就。全国从事生产、销售、使用放射性同位素和射线装置的单位共73 070家,但随之而来的放射源污染带来的环境污染和社会问题也不可小觑[1-2]。以三哩岛核事故、切尔诺贝利核事故、福岛核事故为首的三大震惊世界的核危机造成了极大的社会恐慌[3-5]。同时,某些行业由于管理不善造成放射源丢失,被盗而失去控制,给人们的生命健康问题带来了严重的安全隐患[6]。因此,快速、准确地搜寻放射源已成为核辐射应急处置面临的重要问题。
近年来,专家和学者们在源搜寻方面取得了一定的成就。源搜寻主要分为人工协助寻源和机器协助寻源两类。人工协助寻源依靠人工协助移动放射性探测仪器采集数据,进而调整策略来实现对放射性目标的搜寻,但操作人员面核辐照的风险。相关研究成果有:刘新华等[7]采用平行线搜索法,通过携带仪器探测地图剂量,进而绘制等剂量率图搜寻放射源,但其方法工作量大、精度较差。左国平等[8]自主设计了一种三角圆筒铅屏蔽的NaI探测器,人工协助移动到多个点测量放射源的方位角进而定位放射源。王明生等[9]提出自适应M-H采样来对放射源进行定位,需要人工携带个人剂量仪采集数据。相对而言,机器协助寻源较为安全。相关研究成果有:Hmam[10]采用雷达扫描辐射源的方法来对放射源进行定位,但需要得到辐射源扫描速率的先验信息。何友等人[11]提出一种最大似然定位算法,解决了文献[10]需要扫描速率的先验信息的问题,但二者都需要建立一定数量的观测站。倪诗翔等[12]针对一个无线信号源,提出一种高斯回归方法并完成源搜寻的模拟实验,其源定位精度受到栅格边长的影响。
针对放射源搜寻过程中难度大、定位精度低等问题,本文拟开展对移动机器人的放射源搜寻研究工作。该工作融合粒子滤波算法和人工势场法,实现未知放射源的渐进式搜索。同时,讨论自适应更新对放射源定位算法稳定性及精度的影响。寻源步骤大致分为:首先,建立放射性物质在环境中的辐射环境模型,在环境地图区域均匀生成描述放射源参数(位置和剂量计数值)的粒子集;其次,记录下机器人自定位的坐标值和探测器采集的剂量计数值;然后,基于该辐射模型结合粒子滤波算法来对粒子进行筛选,缩小粒子的范围,并将筛选出来的粒子的期望值作为未知放射源的估计位置;最后,建立人工势场的路径规划模型,将来自障碍物和估计位置的虚拟力进行矢量合成,合力方向即为机器人前进的方向。另外,为保证粒子的多样性,利用高斯函数对重采样后的粒子进行自适应更新。通过不断地重复放射源参数估计和机器人移动观测过程,直到机器人的当前位置和放射源的估计位置的欧式距离差小于阈值。
-
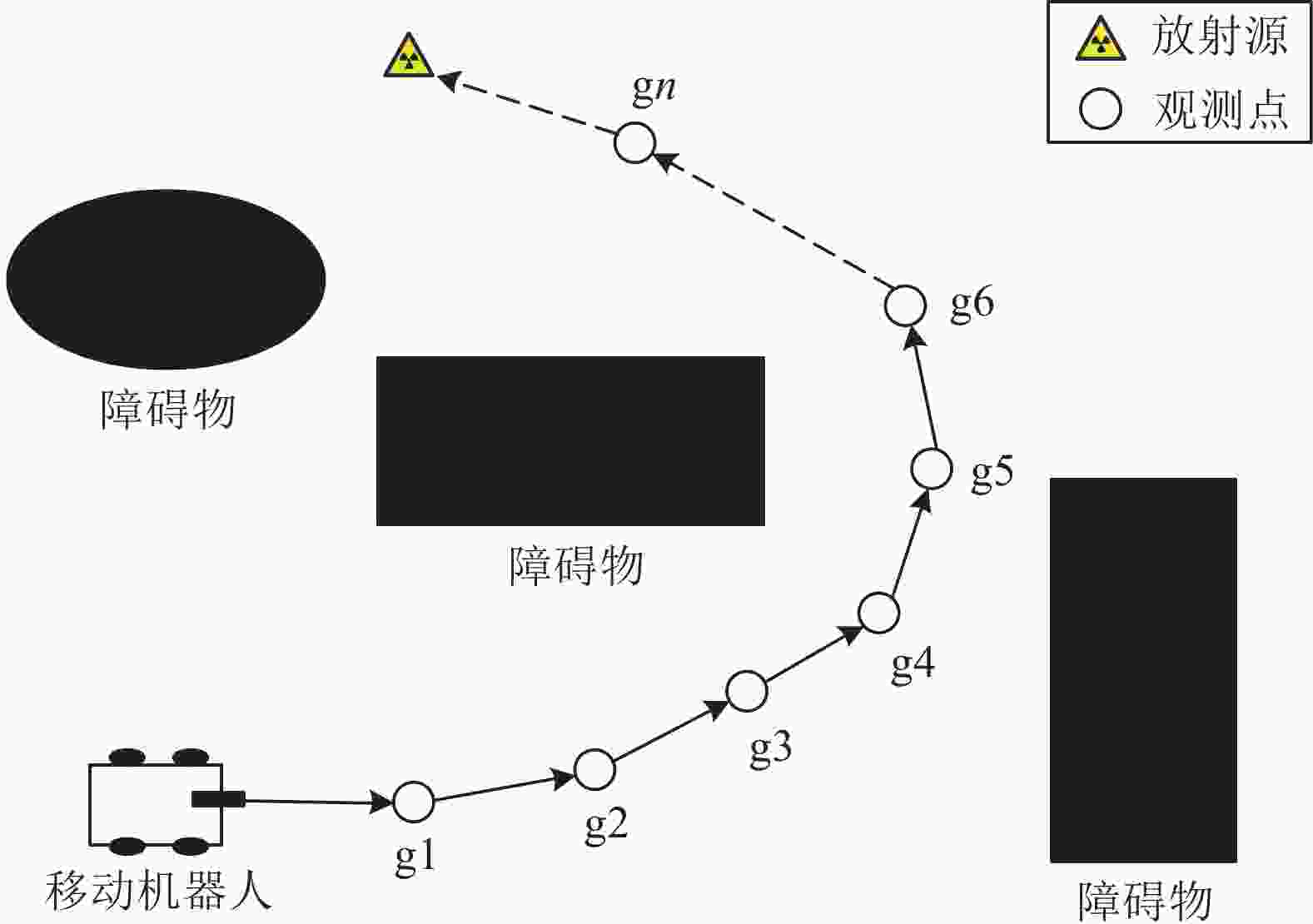
${\rm{\gamma }}$ 射线具有穿透能力强、辐射范围广的特点,可对人体、电子设备等造成严重的损伤,因此常将${\rm{\gamma }}$ 射线作为放射性物质剂量检测的目标。假设二维区域内存在一个位置和剂量均未知的放射源,处于该区域的移动机器人在前进过程中不断通过探测器获取观测值,进而进行位置估计,并逐步朝着估计位置前进。放射源参数估计示意图如图1所示。辐射剂量计数器能探测单位时间内的
${\rm{\gamma }}$ 射线粒子数,该计数存在涨落现象,并服从于泊松分布[13-14]。若放射源单位时间发射$\mu $ 个粒子,辐射探测器在$\tau $ 秒内对粒子计数为z的概率为$$P(z;\lambda ) = \frac{{{\lambda ^z}}}{{z!}}{{\rm{e}}^{ - \lambda }},$$ (1) 其中:
$\lambda = \mu \times \tau $ ;$z \in {N^ + }$ 为实际计数值(cps);$\lambda $ 为探测器的期望计数值(cps)。放射源相对于地图来说较小,因此可将放射源视为点源。假设点源
${\rm{s}}$ 的参数满足于${R_{\rm{s}}}{\rm{ = [}}{x_{\rm{s}}}{\rm{ }}{y_{\rm{s}}}{\rm{ }}{\phi _{\rm{s}}}{{\rm{]}}^T}$ ,其中$({x_{\rm{s}}},{y_{\rm{s}}})$ 为源s的坐标值,${\phi _{\rm{s}}}$ 为距离放射源1 m处的剂量计数值。放射性物质的辐射衰减主要与距离和障碍物自身属性有关,可表示为$${\lambda _k} = \Big[{\mu _{\rm{b}}} + \frac{{{\phi _{\rm{s}}}}}{{{{({\xi _k} - {x_{\rm{s}}})}^2} + {{({\zeta _k} - {y_{\rm{s}}})}^2}}}{e^{ - {\beta _{ks}}d_k^{is}}}\Big]{\tau _k},$$ (2) 其中:
${\mu _{\rm{b}}}$ 为本底剂量计数值;$({\xi _k},{\zeta _k})$ 为第k个观测点的坐标;$d_k^{is}$ 为放射源与第k个观测点的欧氏距离;${\beta _{ks}}$ 为障碍物的衰减因子;${\tau _k}$ 为探测器的辐射暴露时间。 -
未知放射源的搜寻采用渐进式。首先,将探测器采集剂量值作为粒子滤波的观测值,得到源的估计位置;其次,利用路径规划使得机器人向估计位置前进多个步长;最后,重复上述过程,直到找到放射源。本寻源算法仅适用于单点放射源搜寻,当地图中出现多个放射源时,观测点处的剂量计数值将会相互叠加,可能造成放射源位置存在多种可能,进而造成本文算法失效。
放射源搜寻环境地图如图2所示,其中,图2(a)为真实辐射环境,图2(b)为基于该环境的仿真地图。由于湖泊对于机器人来说是不可通过区域,因此在路径规划中当做障碍物处理。
-
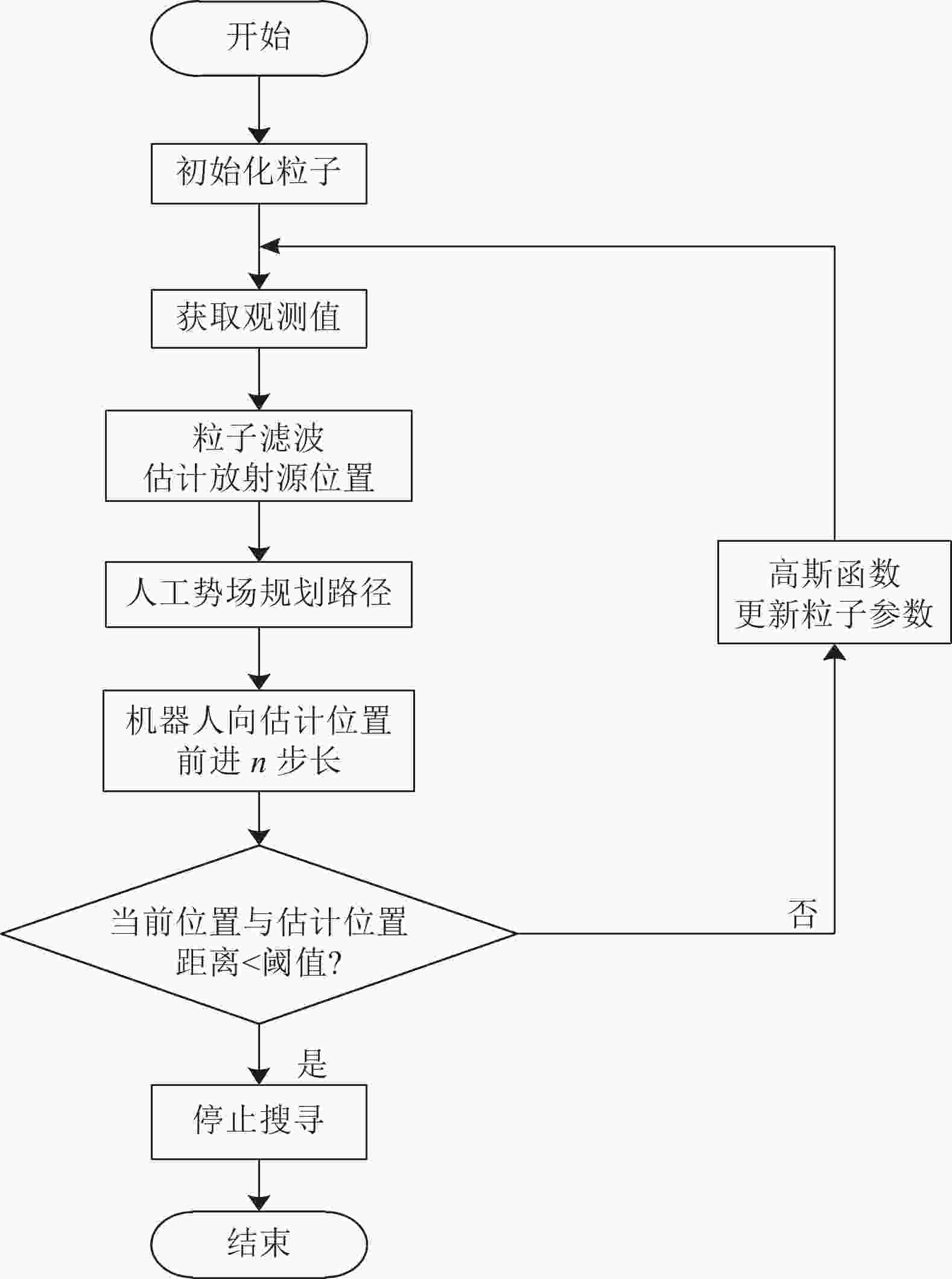
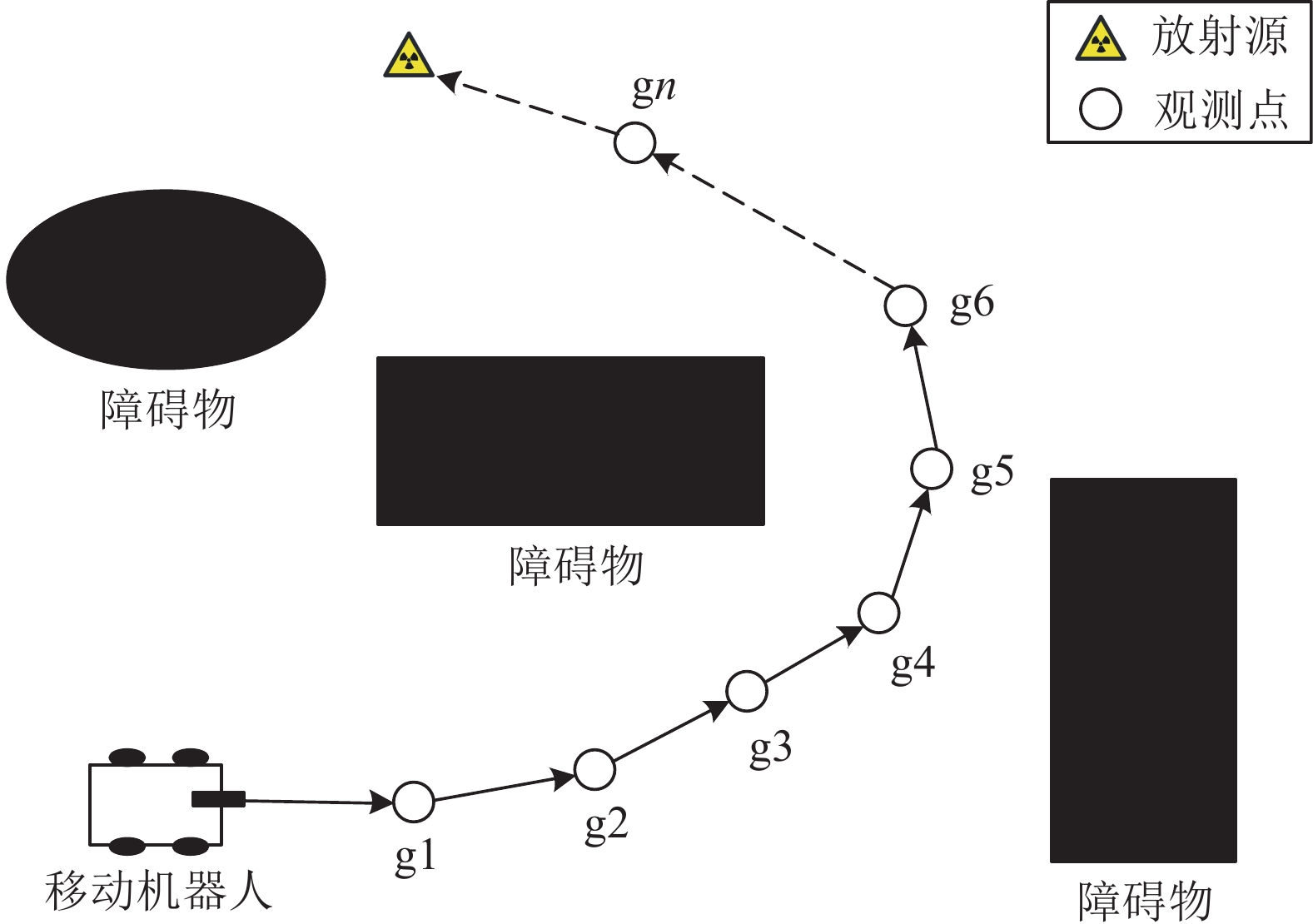
移动机器人的放射源搜寻流程图如图3所示,先对粒子集进行初始化,获取机器人当前位置的观测参数。再进行滤波得到放射源估计位置,并将其位置作为人工势场的目标,且前进n个步长。最后判断当前位置和估计位置之间的距离是否小于距离阈值D,如果小于距离阈值D,则停止放射源搜寻,否则继续上述操作。为保证粒子的多样性,利用高斯分布函数将重采样后的粒子进行自适应更新。机器人通过多次移动和位置估计,粒子的范围将会逐步缩小,机器人将逐步靠近源,直到找到源。
-
粒子滤波最早是由Moral[15]提出,通过不断的发展,也适用于移动机器人渐进式寻源。它对权重大的粒子进行筛选,缩小粒子范围,进而对放射源位置进行估计。粒子滤波算法的关键在于解决粒子多样性缺失的问题,主要通过以下两种方法来解决:(1)通过增加粒子数目的方法来保证粒子多样性,但会使得计算量成倍增加,导致机器人等待时间过长;(2)通过改进重采样方法解决多样性问题,可适用于机器人的寻源策略。本文基于辐射环境,采用高斯分布函数将重采样后的粒子进行自适应更新,以解决上述问题。源位置估计具体步骤如下。
(1)粒子集初始化。利用均匀分布在机器人搜索区域内随机生成N个粒子,其参数为
${R_i}{\rm{ = [}}{x_i}{\rm{ }}{y_i}{\rm{ }}{\phi _i}{{\rm{]}}^T}$ ,其中,${x_i},{y_i},{\phi _i}$ 分别表示粒子二维坐标及剂量计数值。同时,将粒子集表示为$\{ R_0^{{i}},w_k^i\} _{i = 1}^N$ ,$w$ 表示k次观测时第i个粒子的权重,初始化的粒子具有相同的权重,即$\{ R_0^{{i}},\frac{1}{N}\} _{i = 1}^N$ 。粒子的参数向量$R_0^i = {[x_0^i{\rm{ }}y_0^i{\rm{ }}\phi _0^i]^{\rm{T}}}$ 通过均匀分布产生:$$\begin{split}& x_0^i\sim U({x_{\min }},{x_{\max }}), \;\; y_0^i\sim U({y_{\min }},{y_{\max }}),\\& \phi _0^i\sim U({\phi _{\min }},{\phi _{\max }}) {\text{。}} \end{split} $$ (3) (2)粒子权重更新。设观测参数为
$G{}_k{\rm{ = [}}{\xi _k}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\zeta _k}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {I_k}{]^{{T}}}$ ,则源的后验概率密度$p(R|G)$ 可用粒子集$\{ R_{0:k}^i,w_k^i\} _{i = 1}^N$ 表示。由于难以从$p(R_{0:k}^i|{G_{1:k}})$ 中进行抽样,因此引入重要性分布函数$q(R_{0:k}^i|{G_{1:k}})$ ,可通过贝叶斯重要性采样和序贯重要性采样抽取样本。贝叶斯采样在获取新观测值时需要重新从分布函数中抽取独立同分布粒子集,将耗费大量资源。而序贯重要性采样将贝叶斯重要性采样写成观测序列,通过递归更新获得权重可获得较好的效果[16]。序贯重要性采样将分布函数分解为$$q(R_{0:k}^i|{G_{1:k}}) = q(R_k^i|R_{0:k - 1}^i,{G_{1:k}})q(R_{0:k - 1}^i|{G_{1:k{\rm{ - }}1}}),$$ (4) 即新的采样集与新样本、旧样本有关。又粒子权重可表示为
$$W_k^i(R_{0:k}^i) = \frac{{p(G_{1:k}^i|R_{0:k}^i)p(R_{0:k}^i)}}{{q(R_{0:k}^i|G_{1:k}^i)}}{\text{。}}$$ (5) 将式(4)带入式(5)有
$$W_k^i(R_{0:k}^i) = \frac{{p({G_{1:k}}|R_{0:k}^i)p(R_{0:k}^i)}}{{q(R_k^i|R_{0:k - 1}^i,{G_{1:k}})q(R_{0:k - 1}^i|{G_{1:k{\rm{ - }}1}})}}{\text{。}}$$ (6) 又由式(5)可得
$$W_{k - 1}^i(R_{0:k - 1}^i) = \frac{{p({G_{1:k - 1}}|R_{0:k - 1}^i)p(R_{0:k - 1}^i)}}{{q(R_{0:k - 1}^i|{G_{1:k{\rm{ - }}1}})}},$$ (7) 联立式(6)和式(7),则
$$W_k^i(R_{0:k}^i) = W_{k - 1}^i(R_{0:k - 1}^i)\frac{{p({G_k}|R_k^i)p(R_k^i|R_{0:k - 1}^i)}}{{q(R_k^i|R_{0:k - 1}^i,{G_{1:k}})}}{\text{。}}$$ (8) $p(R_k^i|R_{0:k - 1}^i)$ 表示源参数的状态转移过程,假设在整个放射源搜寻过程中源的参数恒定不变,则可取$$q(R_k^i|R_{0:k}^i,{G_{1:k}}) = p(R_k^i|R_{0:k - 1}^i),$$ (9) 权重可近似为
$$W_k^i(R_{0:k}^i) \approx W_{k - 1}^i(R_{0:k - 1}^i)p({G_k}|R_k^i),$$ (10) 其中
$$p({G_k}|R_k^i) = P({z_k};\lambda _k^i){\text{。}}$$ (11) 由式(10)和式(11)可得
$$W_k^i(R_{0:k}^i) \approx W_{k - 1}^i(R_{0:k - 1}^i){\rm{P}}({z_k};\lambda _k^i),$$ (12) 将权重进行归一化处理,则
$$w_k^i(R_{0:k}^i) = \frac{{W_k^i(R_{0:k}^i)}}{{\sum\limits_{i = 1}^N {W_k^i(R_{0:k}^i)} }}{\text{。}}$$ (13) 故放射源参数后验概率估计可表示为
$$p(R|G) = p({R_{0:k}}|{G_{1:k}}) \approx \sum\limits_{i = 1}^N {{w_k}(R_{0:k}^i)} \delta ({R_{0:k}} - R_{1:k}^i),$$ (14) 其中
$\delta $ 为狄拉克(Dirac)函数。序贯重要性采样虽然能够获得放射源参数估计,但其存在粒子退化问题。在进行若干次迭代之后,粒子会集中于少数粒子上,继续迭代将浪费大量计算资源,同时可能造成估计误差较大,为了抑制粒子退化,引入粒子重采样。(3)粒子重采样。粒子滤波重采样方法遵循优胜劣汰的原则,通过多次复制权值大的粒子、舍弃小权值粒子来抑制粒子退化问题。常见的重采样方法有简单重采样、分层重采样、系统重采样和残差重采样四种,从采样质量和时间复杂度考虑,系统重采样(SR)更优[17]。系统重采样流程如下:
第一步:将区间
$\left( {0,1} \right]$ 均匀划分成M个互补区间,即$\left( {0,1} \right] = \left( {0,\frac{1}{M}} \right] \cup \ldots \cup \left( {\frac{{M{\rm{ - }}1}}{M},\;1} \right]$ ;第二步:对每个独立的子区间同分布采样可得
${\mathop U\limits^{\rm{\sim }} _i}$ ,其中${\mathop U\limits^\sim _i} = \frac{{i - 1}}{M} + U(0,\frac{1}{M}]$ ,其中$U(x,y]$ 表示区间$(x,y]$ 上的均匀分布;第三步:令累积分布函数为
$cdf$ ,满足${I^i} = cdf({u_i})$ 。若将权值集合表示为$\{ {w^i}\} _{i = 1}^N$ ,则${u_i} \in \left(\sum\limits_{j = 0}^{i - 1} {{w^j},} \sum\limits_{j = 0}^i {{w^j}} \right)$ ;第四步:通过循环比较
${I^i}$ 与${\mathop U\limits^\sim _j}$ 的值复制权值大的粒子,得到新的粒子集。(4)放射源参数的估计。在经过重采样之后,权值大的粒子获得了多次复制,粒子将会更多地集中于权值高的区域。源参数的估计值为重采样后粒子参数的期望值,表示为
$$\begin{split} & E({x_k}) = \sum\limits_{i = 1}^N {x_k^iw_k^i} {\text{ ,}} \\ & E({y_k}) = \sum\limits_{i = 1}^N {y_k^iw_k^i} {\text{ ,}} \\ & E({\phi _k}) = \sum\limits_{i = 1}^N {\phi _k^iw_k^i} {\text{ 。}} \end{split} $$ (15) (5)粒子自适应更新。重采样使得粒子延缓了集中于少数粒子的速度,但其仅复制权值高的粒子,并未进行本质上的粒子更新。因此,粒子在进行多次迭代后依旧会集中于初始权值高的粒子,因此源位置估计精度受到粒子初始化值的影响较大。为了解决这一问题,从而提高粒子滤波的精度和稳定性,引入自适应系统重采样。高斯分布函数具有对称性,易调整其均值和方差,因此将高斯函数作为粒子更新函数。重采样初期与后期粒子参数调整范围不同,随着重采样次数的增加粒子范围将逐步减小,因此需要自适应调整偏差参数。将重采样后权值不为0的粒子作为有效粒子,其最大、最小权值粒子参数用于自适应更新粒子,则新的粒子参数可表示为:
$\begin{split} &x_k^i\sim N\left(x_k^i,\frac{{\sqrt {{{\left( {{{\{ x_k^{0:{N_{{\rm{eff}}}}}\} }_{\max }} - {{\{ x_k^{0:{N_{{\rm{eff}}}}}\} }_{\min }}} \right)}^2} + {{\left( {{{\{ y_k^{0:{N_{{\rm{eff}}}}}\} }_{\max }} - {{\{ y_k^{0:{N_{{\rm{eff}}}}}\} }_{\min }}} \right)}^2}} }}{2}\right)\\[1mm] & y_k^i\sim N\left(y_k^i,\frac{{\sqrt {{{\left( {{{\{ x_k^{0:{N_{{\rm{eff}}}}}\} }_{\max }} - {{\{ x_k^{0:{N_{{\rm{eff}}}}}\} }_{\min }}} \right)}^2} + {{\left( {{{\{ y_k^{0:{N_{{\rm{eff}}}}}\} }_{\max }} - {{\{ y_k^{0:{N_{{\rm{eff}}}}}\} }_{\min }}} \right)}^2}} }}{2}\right)\\[1mm] &\phi _k^i\sim N\left(\phi _k^i,\frac{{\sqrt {{{\left( {{{\{ \phi _k^{0:{N_{{\rm{ef}}f}}}\} }_{\max }} - {{\{ \phi _k^{0:{N_{{\rm{eff}}}}}\} }_{\min }}} \right)}^2} + {{\left( {{{\{ \phi _k^{0:{N_{{\rm{eff}}}}}\} }_{\max }} - {{\{ \phi _k^{0:{N_{{\rm{eff}}}}}\} }_{\min }}} \right)}^2}} }}{2}\right) \end{split},$ (16) 其中:
${N_{{\rm{eff}}}}$ 为重采样中有效粒子的个数(即权值不为0的粒子);$[{\{ x_k^{0:{N_{{\rm{eff}}}}}\} _{\min }},{\{ x_k^{0:{N_{{\rm{eff}}}}}\} _{\max }}]$ ,$[{\{ y_k^{0:{N_{{\rm{eff}}}}}\} _{\min }}, $ $ {\{ y_k^{0:{N_{{\rm{eff}}}}}\} _{\max }}]$ ,$[{\{ \phi _k^{0:{N_{{\rm{eff}}}}}\} _{\min }},{\{ \phi _k^{0:{N_{{\rm{eff}}}}}\} _{\max }}]$ 分别表示第k次重采样后粒子的横纵坐标及剂量值范围。(6)重复步骤(2)至(5),直到机器人的位置与放射源的估计位置小于阈值D (D为常数)时停止搜寻。
-
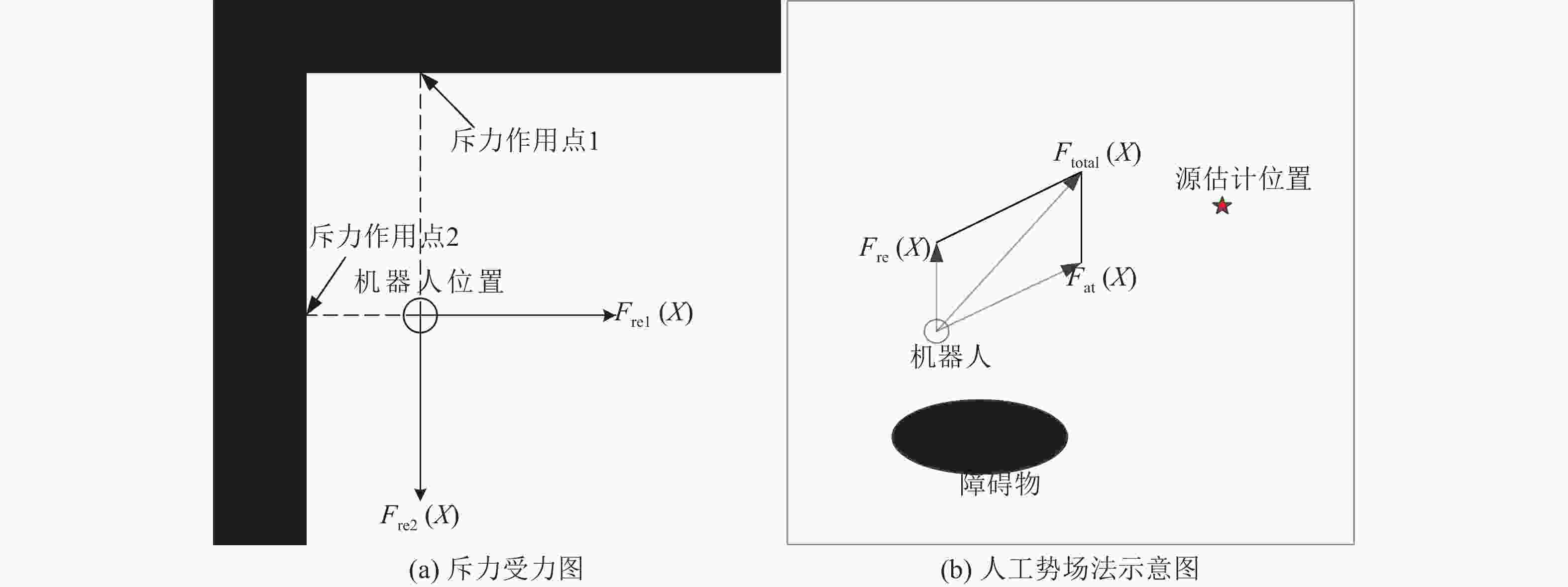
KHATIB[18]在有障碍物的环境中使用了人工势场法,利用虚拟力的方法规划机器人路径。机器人分别将目标和障碍物作为引力极和斥力极,在矢量合力作用下向前运动。假设机器人的斥力只受其前后左右四个方向的影响,斥力作用点处于障碍物上且为单方向上距离机器人最近的点(同一障碍物可能存在多个斥力作用点),如图4(a)所示。人工势场法的示意图如图4(b)所示。其中:
${F_{{\rm{re}}}}(X)$ 定义为障碍物形成的斥力;${F_{{\rm{at}}}}(X)$ 定义为放射源的估计位置处形成的引力,${F_{{\rm{total}}}}{\rm{(}}X)$ 为排斥力与吸引力的矢量合力。假设机器人在环境中的起始位置为$X{\rm{ = [}}{x_0},{y_0}]$ ,则基于放射源环境下构建引力场可定义为$${U_{{\rm{at}}}}(X) = {K_{{\rm{at}}}}\ln \rho (X - {X_{{\rm{goal}}}}),$$ (17) 其中:
${K_{{\rm{at}}}}$ 为引力增益系数;${X_{{\rm{goal}}}}$ 为源估计位置;$\rho (X - {X_{{\rm{goal}}}})$ 为机器人与源估计位置的欧氏距离。引力为引力场函数的负梯度,可表示成$$\begin{split}{F_{{\rm{at}}}}(X) =& - \operatorname{grad} [{U_{{\rm{at}}}}(X)] \\=&- \operatorname{grad} [{K_{{\rm{at}}}}\ln \rho (X - {X_{{\rm{goal}}}})] \\=& - \frac{{{K_{{\rm{at}}}}}}{{\rho (X - {X_{{\rm{goal}}}})}}{\text{。}}\end{split}$$ (18) 障碍物给移动机器人施加的斥力场函数可定义为
${U_{{\rm{re}}}}(X) = \left\{ \begin{split} &- {K_{{\rm{re}}}}{\rm{[}}\ln \rho \left( {{\rm{X}} - {X_{{\rm{obs}}}}} \right) -\frac{1}{{{\rho _0}}}\rho \left( {{\rm{X}} - {X_{{\rm{obs}}}}} \right){\rm{] ,}}\quad\rho \left( {{\rm{X}} - {X_{{\rm{obs}}}}} \right) \leqslant {\rho _0}\\ &~0,\;\;\qquad\rho \left( {{\rm{X}} - {X_{{\rm{obs}}}}} \right) \geqslant {\rho _0} \end{split} \right\},$ (19) 其中:
${K_{{\rm{re}}}}$ 表示斥力增益系数;$\rho \left( {X - {X_{{\rm{obs}}}}} \right)$ 代表机器人与障碍物斥力点之间的欧氏距离,${\rho _0}$ 表示受到障碍物影响的最大欧氏距离。斥力可定义为$$\begin{split} {{{F}}_{{\rm{re}}}}(X) =& - {\mathop{\rm grad}\nolimits} [{U_{{\rm{re}}}}(X)]= - {\mathop{\rm grad}\nolimits} [ - {K_{{\rm{re}}}}{\rm{[}}\ln \rho \left( {{\rm{X}} - {X_{{\rm{obs}}}}} \right) - \frac{1}{{{\rho _0}}}\rho \left( {{\rm{X}} - {X_{{\rm{obs}}}}} \right){\rm{]}}]\\=& \left\{ \begin{array}{l} {K_{{\rm{re}}}}\left(\dfrac{1}{{\rho \left( {{\rm{X}} - {X_{{\rm{obs}}}}} \right)}} - \dfrac{1}{{{\rho _0}}}\right){\rm{ ,}}\quad\rho \left( {{\rm{X}} - {X_{{\rm{obs}}}}} \right) \leqslant {\rho _0}\\ 0,\;\;\quad\quad\rho \left( {{\rm{X}} - {X_{{\rm{obs}}}}} \right) > {\rho _0} \end{array} \right\}{\text{。}}\\[-34pt] \end{split}$ $ (20) 假设机器人受到
$N{}_{{\rm{re}}}$ 个斥力点的影响,则机器人受到的合力可表示为$${F_{{\rm{total}}}}(X) = {F_{{\rm{at}}}}(X) + \sum\limits_{n = 1}^{{N_{{\rm{re}}}}} {{F_{{\rm{re}}}}(X)} {\text{。}}$$ (21) 人工势场法效果的好坏主要受到引力增益系数和斥力增益系数的影响。引力增益系数过大导致引力远大于来自障碍物的斥力,可能使机器人撞向障碍物;斥力增益系数过大导致斥力远大于引力时,如果放射源与障碍物位置过近,机器人在斥力的影响下将无法靠近放射源。在该辐射环境下进行多次实验,最终参数设定如表1所列。
表 1 参数设定
仿真参数 值/单位 引力增益系数Kat 300 000 斥力增益系数Kre 260 000 斥力影响最大距离ρ0 500 m 障碍物最小安全距离da 1 m 转向角α 20° -
为了验证放射源搜寻的可行性,本实验在Matlab 2016a平台上进行仿真。首先,选用500 m×500 m的平面地图,定义一个放射源。其次,移动机器人搭载辐射剂量计数器采集观测点辐射剂量值,并通过粒子滤波算法估计源参数。然后,利用人工势场规划机器人行进轨迹,并且前进n个步长。最后,不断重复源参数估计与路径规划,直到找到源。
-
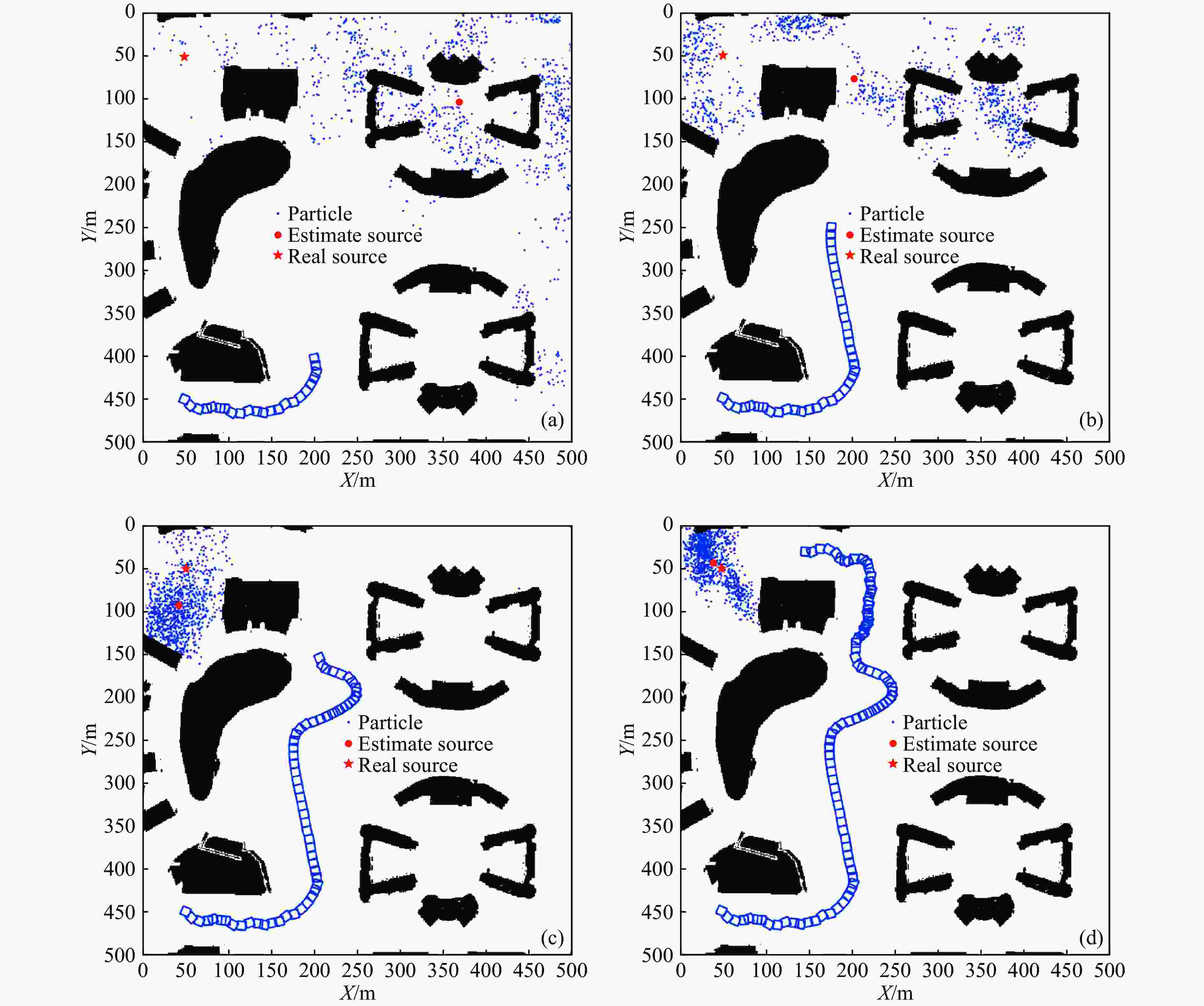
设置机器人的起始位置是(50 m, 450 m),放射源的放置位置是(50 m, 50 m),阈值D为2 m,放射源剂量计数值
${\phi _{\rm{s}}}$ 约为180 000 cps,粒子滤波生成的粒子数目N=2 000,本底辐射剂量计数值${\mu _{\rm b}}{\rm{ = 1\,cps}}$ ,辐射探测器的辐射暴露时间${\tau _k} = 5\,{\rm{s}}$ ,设置障碍物的衰减因子${\beta _{{{ks}}}}$ 为0.03。机器人的位置在矩形中心,前进步长定义为矩形中心到下一个矩形中心的长度,因受转向角的影响,因此步长并非定值。图5表示放射源的搜寻过程,经过粒子滤波定位和路径规划之后可得以下结果。机器人在搜寻的过程中需要对观测点进行测量,一般来说,观测点的数目越多粒子滤波效果越好。在开始寻源过程中,由于观测值较少,粒子滤波得到的源估计位置与实际位置相差较大,但其能够提供大致的寻源方向。随着机器人的逐步前进可以获得更多的观测点,位置估计也会变得越来越准确,直到找到源位置。
-
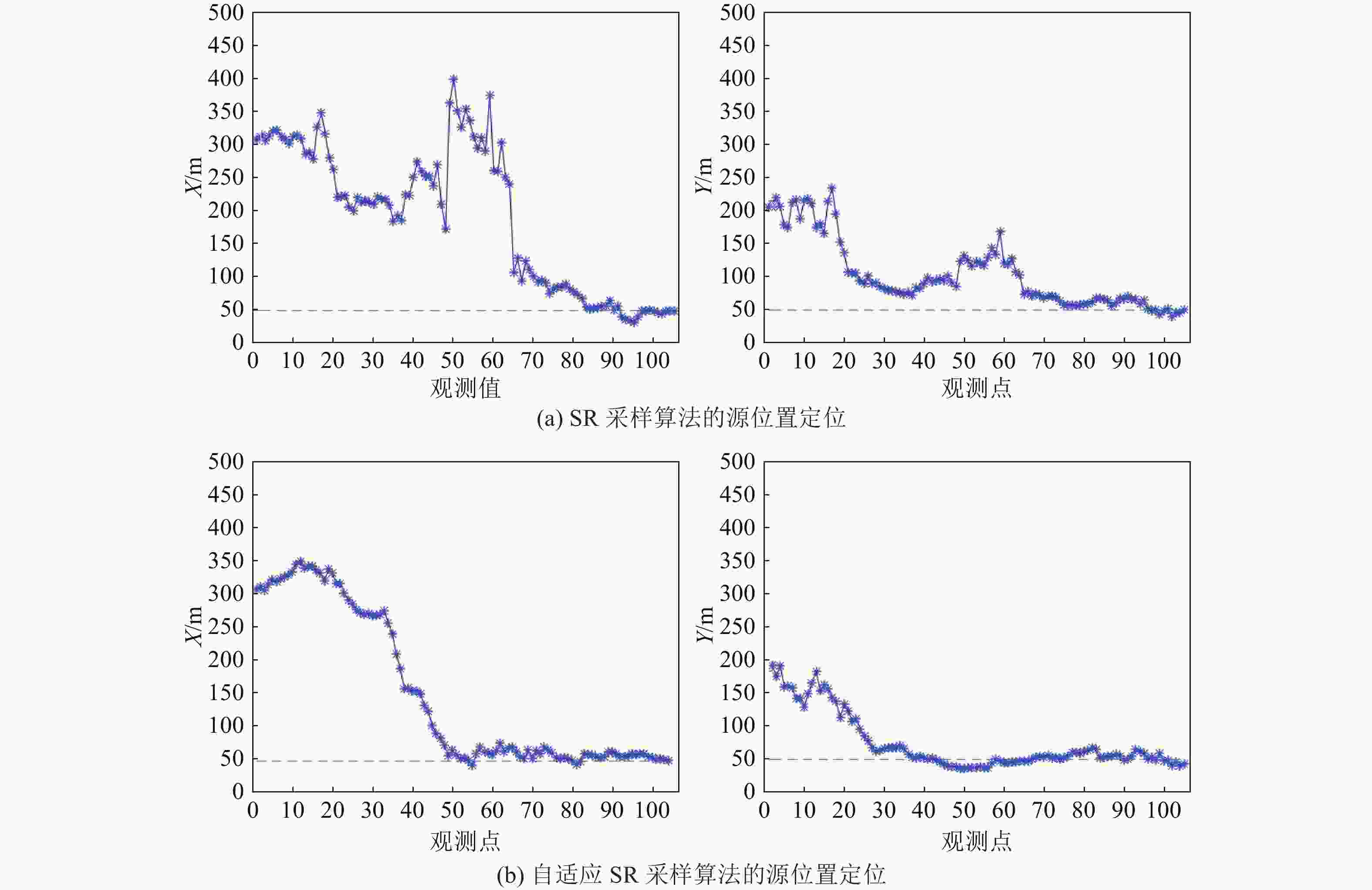
为了进一步研究不同观测值数目对于源定位的影响,在图6研究了不同观测值数目下SR采样算法与自适应SR采样算法对放射源位置定位算法稳定性的影响。其中,横坐标代表观测点的数目,纵坐标表示源估计位置(X和Y方向上的坐标)参数。
从图6可以看出,随着观测点数目的增多,SR采样算法将逐渐向放射源位置(50 m, 50 m)收敛,但算法稳定性较差使得定位波动较大,最终得到的源的估计位置也会受到影响。改进后的粒子滤波加入了粒子自适应更新粒子的思想,在粒子数目不变的前提下保证了粒子的多样性,在经过多次观测值采集后,放射源位置估计总体上会逐渐趋于平缓。
分别对SR采样算法和自适应SR采样算法进行50次模拟,可得到两种算法下的定位误差,如表2所列。根据表2中数据可知,两种算法在X和Y方向上定位的最大误差相对较大,能达到10 m以上,而二者的最小误差相差较小,由此说明自适应SR算法比SR更加稳定。在精度方面,自适应SR算法的平均误差小于SR,表明自适应SR算法受到初始化粒子的影响更小,平均定位精度更高。
表 2 AR和自适应AR算法的定位误差
参数 最大误差/m 最小误差/m 平均误差/m SR 自适应SR SR 自适应SR SR 自适应SR X方向 12.764 5 3.235 4 1.251 4 0.951 1 6.632 1 1.562 4 Y方向 18.625 4 4.524 1 1.951 4 1.592 4 8.425 4 2.921 4 -
针对放射源搜寻难度大、定位精度低等问题,本文提出了一种移动机器人渐进式定位搜寻方法。该方法采用移动机器人搭载探测器采集观测点剂量值,进而实时进行放射源定位并规划机器人的路径。同时,渐进式搜寻能根据实际复杂的环境做出相应的调整,自适应SR采样算法提高了算法的稳定性和定位精度。下一步的工作是解决多源环境下源的定位搜寻问题。
Search Method of Radioactive Source Based on Particle Filter and Artificial Potential Field
-
摘要: 针对放射源搜寻过程中难度大、定位精度低等问题,提出了一种适用于移动机器人的自主寻源方法。该方法利用移动机器人搭载辐射探测器采集的剂量计数值,根据γ射线的衰减规律建立辐射衰减模型;在机器人前进的过程中利用粒子滤波算法对放射源的参数进行实时估计;采用高斯分布函数对重采样后的粒子进行自适应更新,保证重采样后的粒子具有多样性;根据辐射环境创建机器人路径规划模型,采用人工势场法规划机器人的自主寻源路径。实验在Matlab下进行了仿真验证,结果表明,该方法在有遮挡环境下能够搜寻到未知的单点源,同时自适应更新能够提高算法的稳定性,缩小寻源误差。Abstract: In order to solve the problems of difficulty and low positioning accuracy in the process of radioactive source search, an autonomous source finding method suitable for mobile robot is proposed. In this method, the radiation counting value collected by the mobile robot equipped with the radiation detector is used to establish the radiation attenuation model according to the attenuation law of the gamma ray, and the particle filter algorithm is used to estimate the parameters of the radiation source in real time. The Gaussian distribution function is used to adaptively update the resampled particles to ensure the diversity of the resampled particles. The robot path planning model is established according to the radiation environment, and the artificial potential field law is used to draw the automatic source-seeking path of the robot. Experiments are carried out under matlab, and the results show that the method can find unknown single point source in the occluded environment, and the adaptive updating can improve the stability of the algorithm and reduce the source search error.
-
表 1 参数设定
仿真参数 值/单位 引力增益系数Kat 300 000 斥力增益系数Kre 260 000 斥力影响最大距离ρ0 500 m 障碍物最小安全距离da 1 m 转向角α 20° 表 2 AR和自适应AR算法的定位误差
参数 最大误差/m 最小误差/m 平均误差/m SR 自适应SR SR 自适应SR SR 自适应SR X方向 12.764 5 3.235 4 1.251 4 0.951 1 6.632 1 1.562 4 Y方向 18.625 4 4.524 1 1.951 4 1.592 4 8.425 4 2.921 4 -
[1] 张敏, 邓力. 科学技术创新, 2018(31): 189. doi: 10.3969/j.issn.1673-1328.2018.31.115 ZHANG Min, DENG Li. Scientific and Technological Innovation, 2018(31): 189. (in Chinese) doi: 10.3969/j.issn.1673-1328.2018.31.115 [2] 窦义芳. 环境与可持续发展, 2017, 42(05): 77. doi: 10.3969/j.issn.1673-288X.2017.05.022 DOU Yifang. Environment and Sustainable Development, 2017, 42(05): 77. (in Chinese) doi: 10.3969/j.issn.1673-288X.2017.05.022 [3] 石家磊, 何宇浩, 徐思倩. 科技经济导刊, 2019, 27(16): 132. SHI Jialei, HE Yuhao, XU Siqian. Technology and Economic Guide, 2019, 27(16): 132. (in Chinese) [4] 青云. 生命与灾害, 2019(05): 36. Qing Yun. Life and Disaster, 2019(05): 36. (in Chinese) [5] MASABUMI K, KAZUYA N, SHOJI H. Environmental Pollution, 2019, 255: 2. [6] 周勋. 设备管理与维修, 2019(14): 30. ZHOU Xun. Equipment Management and Maintenance, 2019(14): 30. (in Chinese) [7] 刘新华, 李冰, 吴德强. 辐射防护通讯, 2002(05): 11. doi: 10.3969/j.issn.1004-6356.2002.05.003 LIU Xinhua, LI Bing, WU Deqiang. Radiation Protection Newsletter, 2002(05): 11. (in Chinese) doi: 10.3969/j.issn.1004-6356.2002.05.003 [8] 左国平, 谭军文, 周剑良, 等. 原子能科学技术, 2017, 51(03): 515. ZUO Guoping, TAN Junwen, ZHOU Jianliang, et al. Atomic Energy Science and Technology, 2017, 51(03): 515. (in Chinese) [9] 王明生, 肖宇峰, 刘冉, 等. 测控技术, 2019, 38(06): 44. WANG Mingsheng, XIAO Yufeng, LIU Ran, et al. Measurement Control Technology, 2019, 38(06): 44. (in Chinese) [10] HMAM H. IEEE Trans on Aerospace and Electronic Systems, 2007, 43(1): 36. doi: 10.1109/TAES.2007.357153 [11] 何友, 孙顺, 董凯, 等. 控制与决策, 2017, 32(07): 1293. HE You, SUN Shun, DONG Kai, et al. Control and Decision, 2017, 32(07): 1293. (in Chinese) [12] 倪诗翔, 王伟强, 苏衍宇, 等. 机械与电子, 2015(09): 67. doi: 10.3969/j.issn.1001-2257.2015.09.017 NI Shixiang, WANG Weiqiang, SU Yanyu, et al. Machinery and Electronics, 2015(09): 67. (in Chinese) doi: 10.3969/j.issn.1001-2257.2015.09.017 [13] RISTIC B, GUNATILAKA A, RUTTEN M. An Information Gain Driven Search for a Radioactive Point Source[C]// International Conference on Information Fusion, IEEE, 2007. [14] 汤彬, 葛良全, 方方, 等. 核辐射测量原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2011: 93. TANG Bin, GE Liangquan, FANG Fang, et al. Principle of nuclear radiation measurement[M].Harbin: Harbin Engineering University Press, 2011: 93. (in Chinese) [15] MORAL P D. Markov Processes & Related Fields, 1996, 2(4): 555. [16] 王明生. 基于移动机器人的放射源搜寻方法研究[D].西南科技大学, 2019: 19. WANG Mingsheng. Research on Radioactive Source Search Method Based on Mobile Robot[D]. Southwest University of Science and Technology, 2019. (in Chinese) [17] 范澎湃, 隋立芬, 牟忠凯. 粒子滤波常用重采样算法分析比较[C]//通信理论与信号处理学术年会. 2008. FAN Pengpai, SUI Lifen, MOU Zhongkai. Analysis and Comparison of Resampling Algorithms Commonly Used in Particle Filter[C]//Annual Meeting of Communication Theory and Signal Processing, 2008. (in Chinese) [18] KHATIB O. International Journal of Robotics Research, 1986, 5(1): 90. doi: 10.1177/027836498600500106 -





 下载:
下载:





















































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号