原子核裂变的发现深刻地改变了人类社会，一直是核物理研究的一个重要关注点。核裂变数据是很多核技术和核工程应用的重要基础数据^[1]。例如在核能、国防、核辐射屏蔽、核废料处理和稀有同位素的生产中，裂变产额均是重要的基础数据。在合成超重元素^[2-3]，中子星并和过程中的r-process^[4]，以及反应堆中微子等研究中，核裂变过程也是不可或缺的。特别是高精度的锕系核区的裂变产物产额分布很有应用价值。利用对裂变产物产额的系统分析，还可以进一步认识原子核结构以及核动力学的演化^[5-7]，但是因为中子不带电，实验上很难给出入射中子能量连续变化的诱发裂变产物产额的实验值。现有个别能量点的实验测量数据但往往不完整。在国际上主流核数据库中，如中国的CENDL^[8]，美国的ENDF/B-VII.1^[9]，日本的JENDL-3.3^[10]，和欧洲的JEFF-3.1.1^[11]等，只有在热中子(0.025 eV左右)，0.5和14 MeV等三个能量点的中子诱发裂变的完整产额分布。而走向未来的核能—快中子反应堆需要精确的能量相关的裂变数据。因此对未知的不同中子能量的裂变产额进行高精度的预测和评价是非常急需的。

原子核裂变过程是一种复杂的量子多体系统的大幅度集体运动，对核裂变可观测量的精确描述仍是核物理最具有挑战性的课题之一^[12]。发展时间相关的微观裂变动力学模型(Time- Dependent- Hartree-Fock- Bogoliubov^[13]和Time-Dependent-Generate-Coordinate-Method^[14-15])可以更好地理解裂变机制，但离定量计算还有较大的距离。虽然准微观的裂变模型可以与某些原子核的现有实验数据符合得很好^[16]，但裂变模式也会随质子数中子数的不同而演化。所以准微观裂变模型和唯像裂变模型的预测能力很有限。裂变可观测量的计算主要取决于复杂的多维的势能面^[12]。随着激发能的增加，复合核裂变所涉及的量子效应逐渐减弱^{[3, 17]}。因此对复合核裂变产物的产额^[17-18]和发射中子后裂变产物的产额^[19]的能量依赖关系的描述将更为复杂。此外，针对核理论模型的不确定性的量化研究是近年来很受关注的问题^[20]。

目前人工智能与不同学科的交叉融合获得了广泛的成功和关注。在学习复杂的大数据并作出预测方面，机器学习是一个强有力的工具。神经网络深度学习^[21]是机器学习的一个分支，通过构造多层神经网络来训练大量数据，可以模拟复杂的物理关联。传统的神经网络很难给出预测结果的不确定性，而贝叶斯神经网络(BNN)的网络连接参数为概率分布，能够自然地给出逆向回归问题的不确定度^[22]。对于不同激发能的核裂变产物产额，有大量的但不完整的实验测量数据。因此，BNN是描述复杂的裂变观测量和分析复合核裂变统计特性的理想工具。近年来BNN已被广泛用于核物理，包括预测远离稳定线核区的结合能^[22-25]，模拟核反应截面^[26-27]，状态方程^[28]以及高能核核碰撞^[29]等。虽然高斯过程也可以求解回归问题，但侧重于局部关联^[22]。而传统的核裂变评价模型，如Brosa模型^[30]等，主要基于唯像模型的参数拟合^[31]。这种评价方法，在实验数据点很少的时候可能不适用，且不能给出不确定度分析。本文的主要目的是提出基于BNN方法对不完整裂变产物进行评价^[32]，展示BNN在描述裂变碎片产额上的初步能力，比较不同BNN结构的差异。BNN通过学习复杂的裂变数据进行预测和分析，有可能包含目前裂变理论模型之外的潜在关联，从而揭示在裂变过程中一些新的机制。

BNN将神经网络权重参数设定为概率分布^[33]，而不是传统神经网络设定的固定数值。BNN将网络参数的概率函数视作先验分布，利用贝叶斯公式训练后得到后验分布，通过后验分布对多维的网络权重参数进行马尔科夫链-蒙特卡洛积分，得到预测均值和不确定度。通过对给定的训练样本数据进行有限的训练步骤，BNN可以对包含预测均值的预测概率分布分析得到置信区间，从而可以定量描述不确定性。BNN还可以对特定问题采用不同的先验分布，从而引入惩罚函数避免过拟合问题。另一方面，与贝叶斯统计不同的经典统计的目的是通过无限次采样后获得精确的参数值。

BNN模型采用的前向神经网络的网络函数为

其中：$H$为隐藏层神经元个数；$l$为网络中输入参数个数；$\theta = \left\{ {a,{b_j},{c_j},{d_{ij}}} \right\}$为模型参数集。该公式描述了单隐藏层的神经网络。对于多层神经网络，每层的输入${x_i}$都是下一层的网络函数的输出。根据数据集的规模来确定神经元的个数，进而决定了网络的复杂性。目前模型采用了一层隐藏层，为了尽量避免在复杂网络中有的网络参数未被激活利用。网络的输入数据集为${x_i} = \{ {Z_i}, $$ {N_i},{A_i},{E_i} \}$，其中${Z_i}$为裂变核的电荷数；${N_i}$为裂变核的中子数；${A_i}$为裂变碎片的质量数；${E_i} = {e_i} + {S_i}$为复合核的激发能(其中${e_i}$和${S_i}$分别是中子入射能量和中子分离能)。选择裂变核的激发能作为输入可以与激发能为0的自发裂变进行区别。网络模型输出每个碎片的独立产额而不是所有产额的分布，但是总的裂变产额在2%的误差内非常接近总产额的归一化的期望值2.0。因此总产额的归一化不存在问题，采用后验归一化已经足够好。BNN网络的似然函数$p\left( {\left. D \right|\theta } \right)$和目标函数${\chi ^2}$由下式给出：

其中$D = \{ {x_i},{t_i}\} $网络数据；${x_i}$为输入数据；${t_i}$为输出裂变产额；$\Delta {t_i}$为对应的噪声强度^{[22-23, 25]}。后验分布$p\left( {\theta \left| {x,t} \right.} \right)$可由下式得到：

其中$p\left( \theta \right)$为设定的先验参数分布^[33]，一般采用高斯分布。网络参数学习实际上是一个应用随机梯度朗之万动力学方法，采样搜索后验分布的极大值的过程^[30]。随机梯度朗之万动力学方法，即在梯度下降算法的基础上，在导数中加入期望值为0并与学习速率相关的噪声项。基于给定的网络函数$f\left( {{x_n},\theta } \right)$可以得到新输入数据${x_n}$的预测结果。由于网络函数是一个概率分布，BNN网络的均值预测涉及高维积分，可以使用马尔可夫链-蒙特卡洛采样积分得到：

当进一步加入新的实验数据${D_n}$时，后验分布可以依据下式更新：

通过对后验分布的更新，可以对新的不完整的实验数据进行评价。

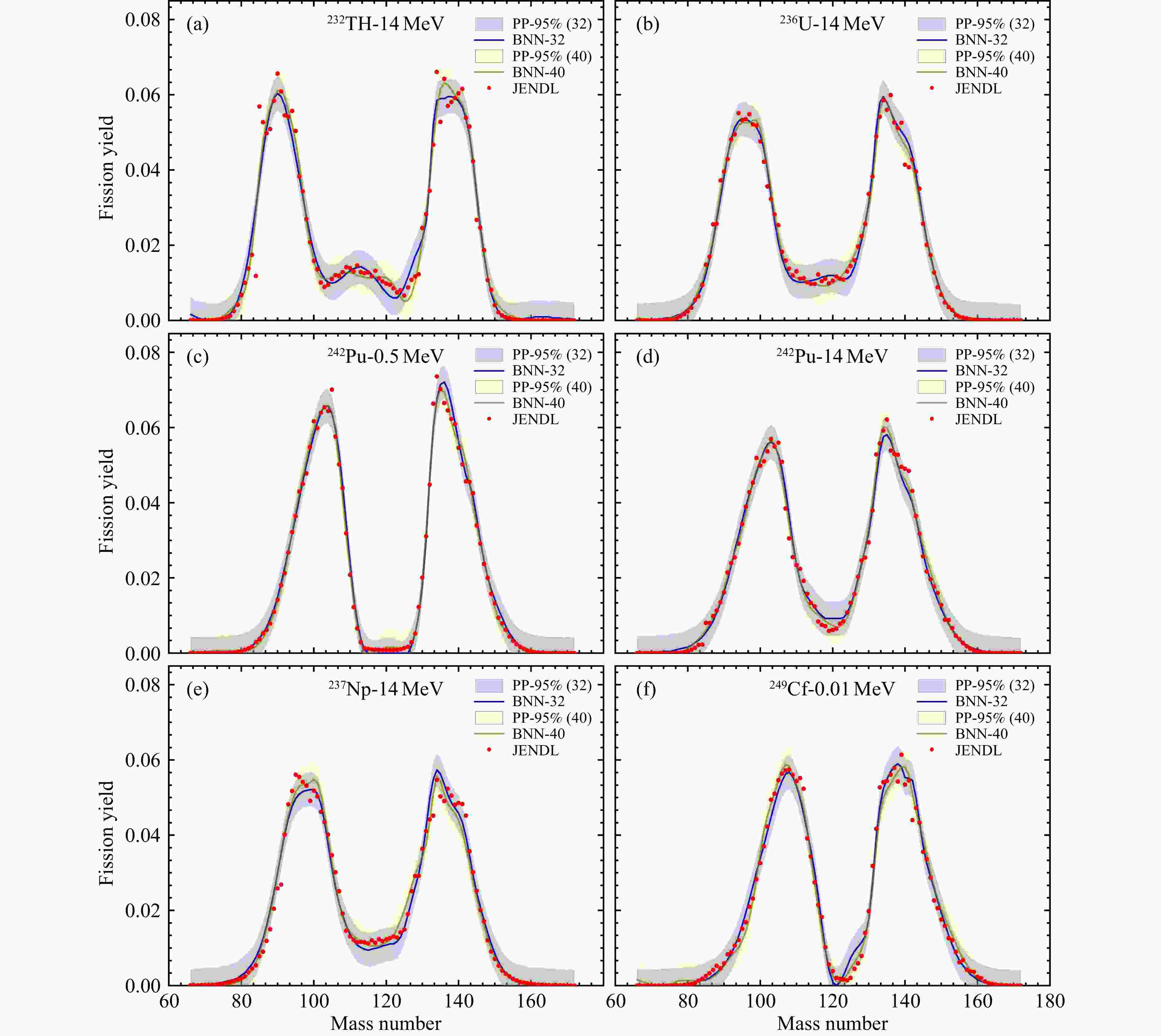
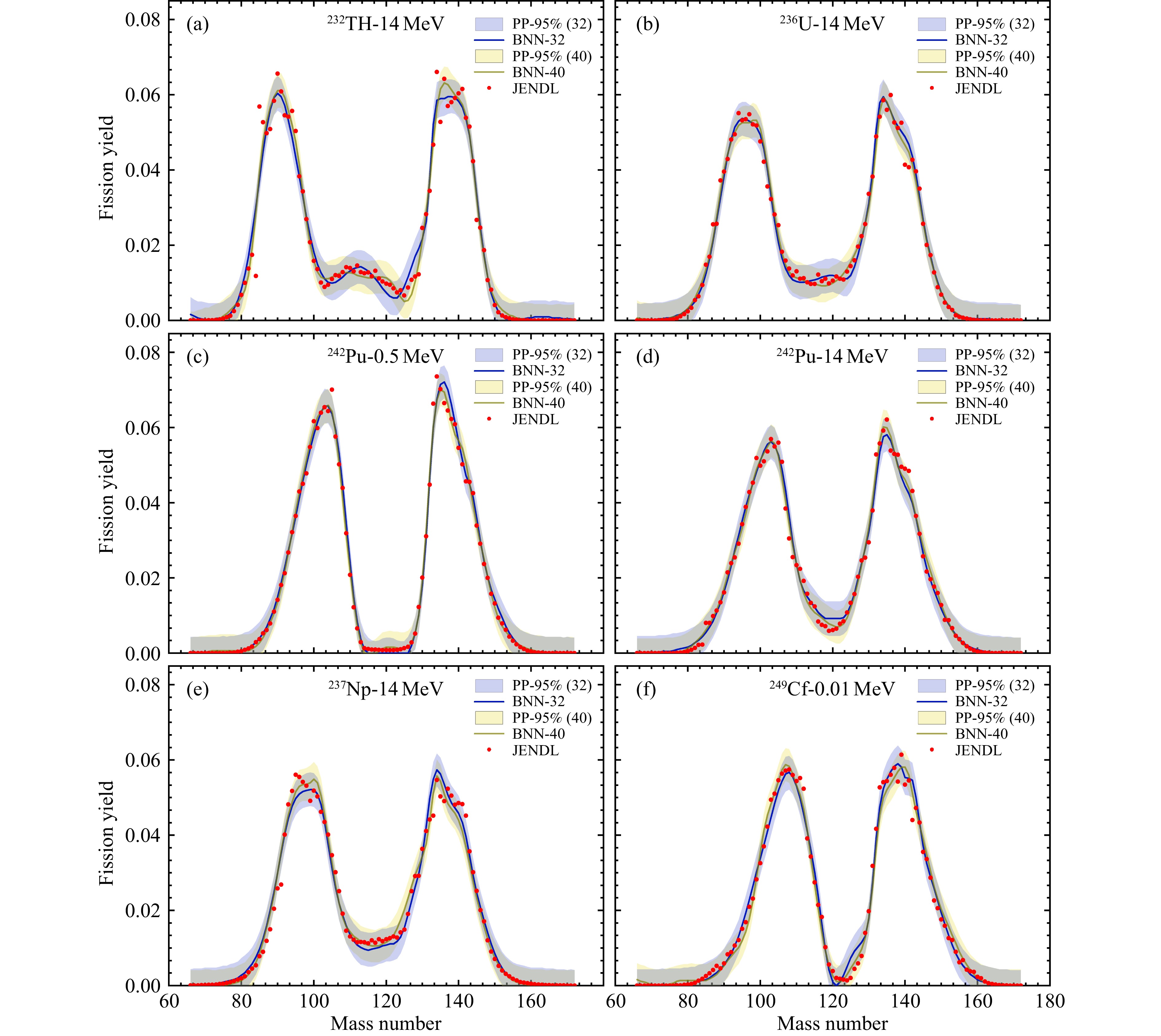
为了训练BNN模型，我们首先将日本的JENDL核数据库^[10]中的30个核(例如^227,229,232Th，²³¹Pa，^{232,233,234,235,236,237,238}U，^237,238Np，^{238,239,240,241,242}Pu，^241,243Am，^{242,243,244,245,246,248}Cm，^249,251Cf，²⁵⁴Es，²⁵⁵Fm)的中子诱发裂变数据加入训练数据集中。BNN网络训练的总误差定义为$\chi _N^2 = \sum\nolimits_i {{{\left[ {{t_i} - f({x_i})} \right]}^2}} /N$。一般认为全局优化和过拟合是神经网络模型中的两个最具有挑战性的问题。复杂网络结构的BNN可能存在训练的数值收敛问题^[22]。BNN模型需要足够的采样训练来达到数值收敛，这将耗费较长的运算时间。神经网络对包含30个核的5 350个数据点的训练数据集分别应用了32个和40个神经元的隐藏层。该训练数据量大于应用在原子核质量的BNN模型的数据量^{[22-23, 25]}。本文所有的网络训练均应用了100 000次采样学习。图1给出BNN网络的部分训练结果。从图中可以看出，BNN模型的训练结果基本上重现了裂变产额的分布，给出了正确的裂变产额的位置分布和能量依赖特征。对于不同核，BNN模型也给出了不同裂变模式，²³⁶U，²⁴²Pu和²³⁷Np均能很好地重现实验值。其原因是训练数据集中包含了U和Pu各同位素的数据。同样可以注意到，²³²Th和²⁴⁹Cf的训练结果略有偏离，这是因为训练数据集中这些核的邻近核的裂变数据比较少。图1显示训练结果对应的95%置信区间比较小，可以合理反映BNN模型的描述能力。

图  1  (在线彩图)BNN学习JENDL数据库的部分结果

除了训练数据集以外，神经网络的架构也可能影响模型的性能。图1也给出了隐藏层分别为32神经元和40神经元的BNN模型的训练结果的对比。40神经元在质量数为125~135的附近有较好表现。采用40神经元的95%置信区间没有明显减小。总体上，40神经元训练结果与32神经元训练结果并没有显著差距。在本文的网络架构下，随着隐藏层神经元数量上升，BNN方法所需的运算时间增加，而且可能导致预测值会有更大的不确定性。进一步，表1给出不同模型方法的验证能力的对比。表1中包含了应用TALYS程序的结果，包含Brosa和GEF模型的TALYS程序被广泛应用于裂变数据的评估。基于发展物理模型与神经网络融合的目的，我们采用了TALYS-1.9中GEF模型计算的初始裂变产额，使用BNN模型学习其残差。表1的结果表明BNN模型较TALYS程序有大幅度改进，然而由于TALYS程序的误差很大，结合TALYS程序的BNN模型比仅使用BNN的模型并没有明显变好的结果。目前我们正在研究多隐藏层的BNN，采用双隐藏层的BNN结果对比单隐藏层结果会有明显的改善。但值得一提的是，BNN结合微观核质量模型是十分成功的^{[22-23, 25]}，因此可以展望未来BNN结合微观裂变模型能够有很好的预测能力。

应用BNN模型的关键动机，是在学习现有完整裂变产额实验数据的基础上，对特定核不完整裂变产额的实验数据进行评价，并推断出完整的裂变产额。在学习JENDL的裂变产额数据后，BNN模型对²³⁵U,²³⁸U,²³⁹Pu在部分能量中子诱发下的不完整实验数据^[33]的评估结果由图2给出。现有数据库中没有相应的完整评估。从图2(c)和(e)可以发现，在包括了这些实验数据后^[33]，BNN模型可以对裂变产额给出相当合理的完整评估。这可以部分归因于1.37 MeV的能量颇为接近训练数据集中已经包含的0.5 MeV能量的数据。而当能量处于0.5和14 MeV之间时，完整评价是具有挑战性的。如图2(b)，(d)和(f)所示，BNN在远离0.5 MeV能量处的评估结果也比较合理。观察图2(c)，评估结果在质量数为110附近存在不合理的裂变产额分布接近负值，但包括不完整的实验数据点后，负值问题可以被避免。此外通过加入惩罚约束也可以避免负值问题。

图  2  (在线彩图)²³⁵U, ²³⁸U, ²³⁹Pu在部分能量中子诱发裂变的不完整实验数据的评估结果

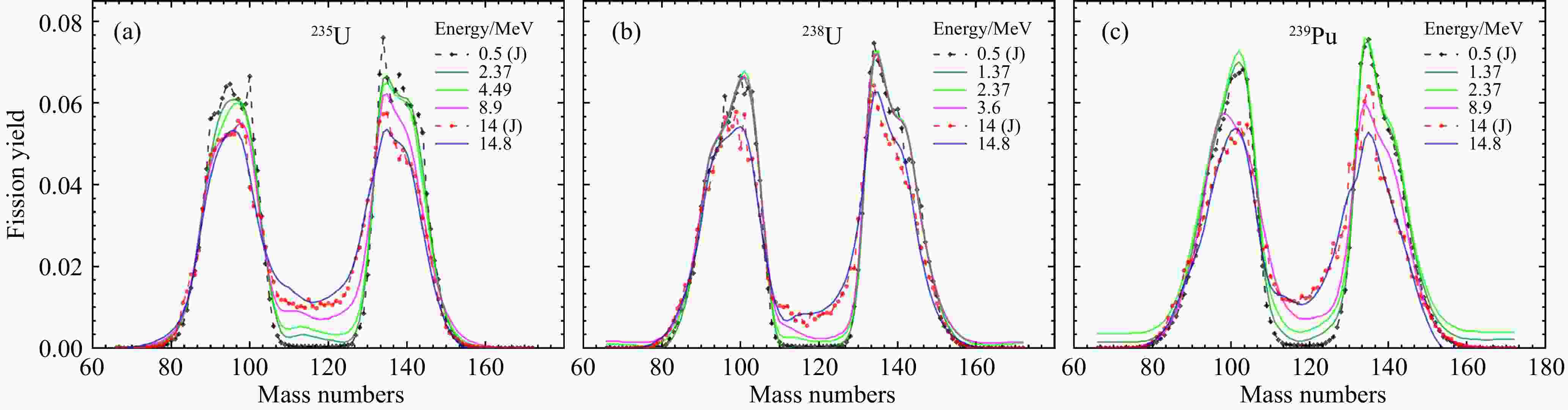
基于不同能量中子诱发裂变的不完整实验数据的评价，图3给出²³⁵U,²³⁸U,²³⁹Pu在不同能量的不完整实验数据的评估汇总。分别包含²³⁵U在2.37，4.49，8.9，14.8 MeV，²³⁸U在1.37，2.37，3.6，14.8 MeV和²³⁹Pu在1.37，2.37，8.9，14.8 MeV时的中子激发能评估曲线。可以注意到，在质量数为110~130附近的谷底，裂变产额随着能量单调上升。同时，随着激发能量的上升，非对称裂变模式对应的两个峰值也逐渐减小。一般认为，随着激发能的增加，对称裂变模式将逐渐占据主导，非对称裂变模式逐渐减退^{[17-18, 34]}。因此可以说明，BNN评价基本上合理地描述了裂变产额能量依赖的特征。

图  3  (在线彩图)²³⁵U, ²³⁸U, ²³⁹Pu在不同能量中子诱发裂变产额的不完整实验数据的评价结果

总体上BNN评价可以合理地给出置信区间作为不确定性的度量。BNN方法预测裂变产额的峰值分布位置是可靠的。虽然峰值附近的细致结构并不十分精确，但BNN方法对于单个核裂变的细致结果是精确的。通常，裂变产额是通过唯象模型来评估的，而唯象模型在只有少数实验数据点可用的情况下是无法可靠应用的，且无法给出不确定度。在这方面，BNN方法对有较大误差和有分歧的实验数据进行融合评价和进行量化误差分析有独特的优势。另外，通过在学习集中加入更多的实验测量数据，并优化神经网络的结构，可以进一步改进目前的网络模型。也可以引入其他辅助的物理量，例如，电荷分布的奇偶效应和壳效应等来进一步改进神经网络。最近我们基于改进的BNN对²³⁹U复合核裂变的电荷产额进行了推断，得到了可以与GEF模型相比较的高精度的评价数据^[35]。在未来可以融合微观裂变模型或者利用先验物理规律指导神经网络也是值得期待的。

本文应用BNN模型来研究和评价锕系区原子核在不同入射中子能量下的诱发裂变产额，这是一个新的方向。在很多情况下，中子诱发裂变产额分布的实验数据是不完整的。基于所获得的信息，对不完整的裂变产额数据进行BNN评价有广泛的应用前景。对裂变产额的分布位置和能量依赖关系，BNN的结果是令人满意的，而唯象评价模型在实验数据很少的情况下很难应用。此外，贝叶斯神经网络模型可以自然地给出置信区间来合理地估计预测的不确定性。今后我们将应用多隐藏层的BNN，发展与微观裂变模型的融合，评价其他的裂变观测量，以及分析裂变后的各种观测量之间的关联为发展裂变理论提供线索。BNN模型的进一步改进可以在未来提供更可靠和更精确的核裂变数据的评价，有望满足核能和核工程领域对应用级核数据的实际需求。