-
CiADS直线加速器是一台高功率超导质子直线加速器，其总体布局如图1所示。该加速器输出能量为500 MeV，束流平均流强为5 mA，由常温段与超导段组成。常温段包括离子源(ECR)、低能传输段(LEBT)、射频四极加速器(RFQ)、中能传输段(MEBT)。常温段能将质子束加速到2.1 MeV，超导段能将质子束加速至500 MeV，然后束流通过高能传输段(HEBT)至靶上[1-2]。
束流负载效应是指当束流通过超导腔被加速时，会在腔内激励起电磁场。对后续束团来说，其感受到的加速场为束流感应场与功率源建场的相量叠加[3]。高流强束流的负载效应对超导腔幅相稳定性的影响非常严重。通常连续束流的负载效应可被高频低电平反馈环路补偿，但脉冲束流的瞬态束流负载效应则因为反馈环路的时延而不能完全补偿，需增加前馈补偿环路[4-6]进一步进行补偿。
前馈补偿技术是在脉冲束流前沿通过超导腔的时刻，低电平产生一个与束流反相的脉冲信号加载于腔上与束流脉冲相抵消，从而保持腔中电场的稳定。不同于反馈环路的自动调整机制，由于前馈环路是预设式的，当束流脉冲发生不可预测的偏差时，前馈环路无法自动调整，所以需要评估束流各项偏差因素对前馈补偿的影响。
本文通过Simulink软件[7]对高频超导腔系统进行建模，仿真分析束流负载效应的影响，并在C-ADS注入器II上对该模型进行了实验验证。最后选取CiADS超导腔典型设计参数，评估脉冲长度、前馈的时序抖动和束流抖动等因素对超导腔幅相稳定度的影响，得出满足CiADS幅相稳定性设计要求的误差边界。
图 1 (在线彩图) CiADS直线加速器总体布局
-
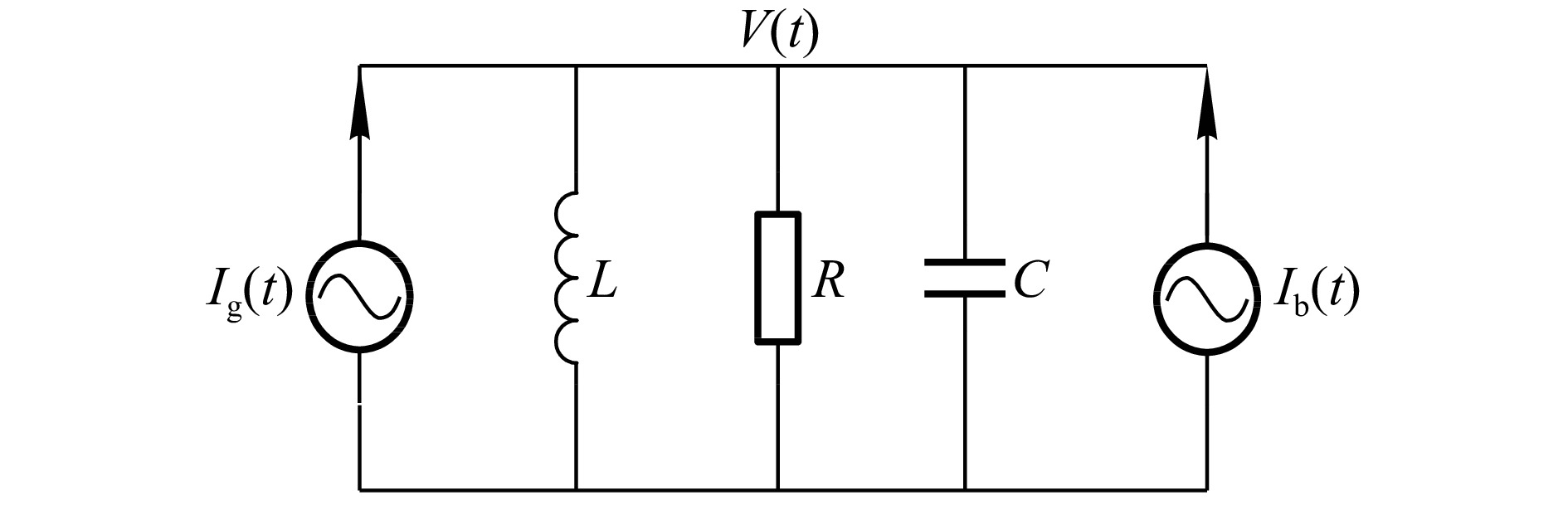
加速器高频系统可用RLC并联谐振电路来进行等效[8-9]，如图2所示。其中，
${I_{\rm{b}}}$ 和${I_{\rm{g}}}$ 分别是束流和功率源的等效电流；L和C分别是超导腔等效电感和等效电容；R是高频腔有载分路阻抗。
图 2 加速器高频系统等效电路图
对图2的并联谐振电路利用基尔霍夫电流定律(KCL)可以得到：
$$ I(t) = \frac{V(t)}{R}+\frac{1}{L}\int V(t)\,{\rm d}t +C\frac{\rm d}{{\rm d}t}V(t) {\text{。}} $$ (1) 对式(1)两边进行求导可以得到：
$$C\frac{{{{\rm{d}}^2}}}{{{\rm{d}}{t^2}}}V(t) + \frac{1}{R}\frac{{\rm{d}}}{{{\rm{d}}t}}V(t) + \frac{1}{L}V(t) = \frac{{\rm{d}}}{{{\rm{d}}t}}I(t),$$ (2) 谐振腔的特性参数与等效电路参数的对应关系为
$$ L = \frac{R}{{{\omega _0}{Q_L}}},\quad C = \frac{{{Q_L}}}{{{\omega _0}R}}{\text{。}} $$ (3) 其中
$ \omega_0 $ 表示腔体谐振频率；$ Q_L $ 表示腔体有载品质因素。利用谐振参数表述腔压振荡方程：$$\frac{{{{\rm{d}}^2}}}{{{\rm{d}}{t^2}}}V(t) + \frac{2}{\tau }\frac{{\rm{d}}}{{{\rm{d}}t}}V(t) + {\omega _0}^2V(t) = \frac{{{\omega _0}R}}{{{Q_L}}}\frac{{\rm{d}}}{{{\rm{d}}t}}I(t)$$ (4) 为了对腔压进行时域仿真计算，将时间离散化为
$ n(t) $ ，t为时间间隔。假设在n时刻腔内的电压为
$ V_{n} $ ，则在第n+1时刻，$${V_{c,n + 1}} = {V_n}{{\rm{e}}^{ - t/\tau }}{\text{。}}$$ (5) 当t时间较短时，
$ I(t) $ 可以近似为不变，此时间内等效电流在腔内建立的电压为$${V_{I,n + 1}} = {I_n}R(1 - {{\rm{e}}^{ - t/\tau }}){\text{。}}$$ (6) 根据式(5)~(6)，在第n+1时刻腔内的总电压为
$$ V_{n+1} = V_{c,n+1}+ V_{I,n+1} = V_n {\rm e}^{-t/\tau}+I_n R(1-{\rm e}^{-t/\tau}) {\text{。}} $$ (7) 假设t = mT,则有
$$ V_{n+1} = V_n {\rm e}^{-mT/\tau}+I_n R(1-{\rm e}^{-mR/\tau}) , $$ (8) 其中
${I_n} = {I_{{\rm{b}},n}} + {I_{{\rm{g}},n}}$ 表示n时刻功率源与束流等效电流之和，T表示一个射频周期。根据式(8)，在Simulink中建立束流负载效应的迭代仿真程序，该仿真程序主要由腔体电压迭代模块、束流脉冲生成模块、前馈控制单元、PI反馈控制单元等部分组成，如图3所示。
图 3 束流负载效应仿真结构图
为了便于仿真计算，定义建立电场
${V_{\rm{c}}}$ 所需的功率源输出等效电流${I_{\rm g0}} = \frac{{{V_{\rm{c}}}}}{R}$ ，并对脉冲束流等效流强进行归一化处理：$$I_{\rm{b}}' = \frac{{{I_{\rm{b}}}}}{{{I_{{\rm g}0}}}}{\text{。}}$$ (9) 定义功率源为补偿束流负载效应额外的输出电流为
${I_{{\rm{gb}}}}$ ，归一化额外输出电流为$I_{{\rm{gb}}}'$ ，此时功率源总输出的等效电流为$${I_{\rm{g}}} = {I_{{\rm{g}}0}} + {I_{{\rm{gb}}}}{\text{。}}$$ (10) 所以归一化后超导腔内等效电流为
$$I' = I_{\rm{b}}' + I_{{\rm{gb}}}' + 1{\text{。}}$$ (11) 由式(11)可知，当归一化后等效束流
$ I_{\rm{b}}' $ 越大，越容易对超导腔内电场幅相稳定性产生影响；利用前馈对束流负载效应进行补偿时$ I_{\rm{b}}' = - I_{{\rm{gb}}}' $ ，此时腔内等效电流为$ I' = 1 $ ，腔内电场维持不变。束流流强
$ I_{\rm{b}} $ 、腔体运行电压$ V_{\rm{c}} $ 、腔体的特征参数如：分路阻抗$ R $ 与品质因数$ Q $ 等是评估束流负载效应的重要参数，在仿真过程中这些参数需采用实际测量值或运行值。同时在仿真过程中暂未考虑失谐角的影响。在迭代计算的过程中，需合理选择射频周期数m，首先要与PI反馈环路的实际响应速度相匹配，其次要兼顾计算精度和计算所需时间。例如，对于CiADS，162.5 MHz超导腔，m不超过100，即时间长度大约不超过0.1 μs比较合适。
-
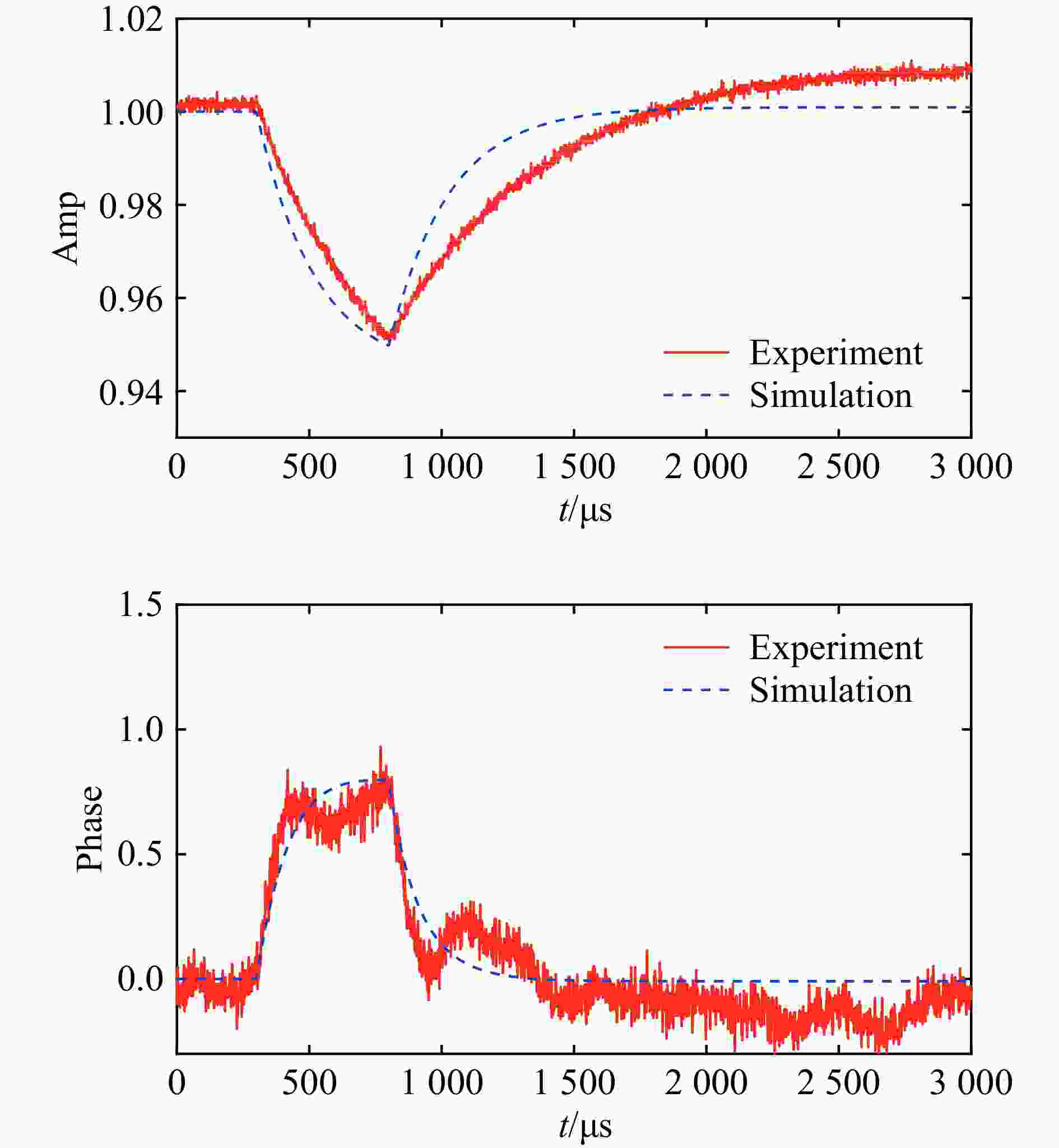
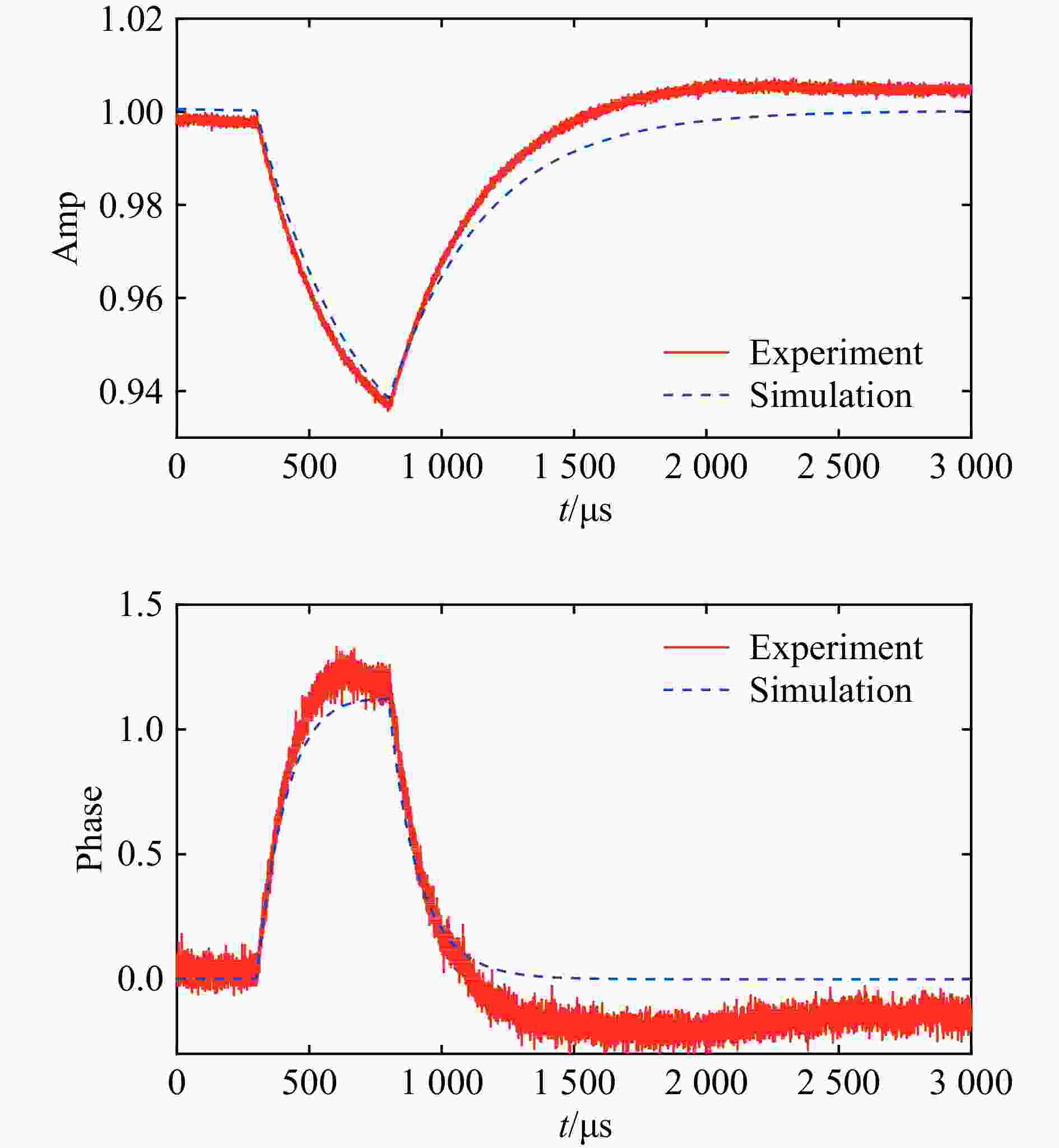
在无前馈补偿的情况下，对束流流强为1 mA，脉宽为500 μs的质子束通过超导腔时引起的束流负载效应进行了仿真计算，其中腔体主要高频参数采用了目前C-ADS注入器II上该腔型的运行参数，如表1。并在C-ADS注入器II上采用相同的运行值进行了实验验证，测量与仿真结果如图4、5所示。
表 1 C-ADS注入器II HWR010-3、HWR010-4等腔体高频参数
腔号 f/MHz FHBW/Hz TTF R/Q/$\Omega$ $ Q_L $ Vc/MeV HWR010-3 162.5 160 0.65 113 5.1E5 0.27 HWR010-4 162.5 184 0.73 113 4.4E5 0.25 
图 4 (在线彩图) HWR010-3 束流负载效应仿真与实验结果
图 5 (在线彩图) HWR010-4 束流负载效应仿真与实验结果
从图中腔体电压的幅相波形变化可以看出，由于反馈调节系数较大，相位偏移在束流未完全离开时便开始下降。同时幅值和相位在恢复时，会出现过冲现象。又因为仿真所采用的有载品质因素
$ Q_{L} $ 的测量值与真实值之间可能存在误差，所以仿真结果幅相恢复速度与实验结果存在误差。并且在实验测量过程中，由其他因素如氦压波动所造成的腔压抖动，尤其是相位的抖动也会造成实验和仿真结果的误差。仿真和实验腔压变化曲线大致吻合，仿真和实验结果幅相变化的一致性误差如表2所示。该结果表明，在不考虑其他因素的影响下，该模型可以较好地仿真束流负载效应对超导腔幅相稳定性的影响。表 2 C-ADS注入器II HWR010-3、HWR010-4束流负载效应对幅相稳定度仿真与实验结果的一致性误差
腔号 幅值一致性误差 相位一致性误差 HWR010-3 0.1% 0.01° HWR010-4 0.2% 0.03° -
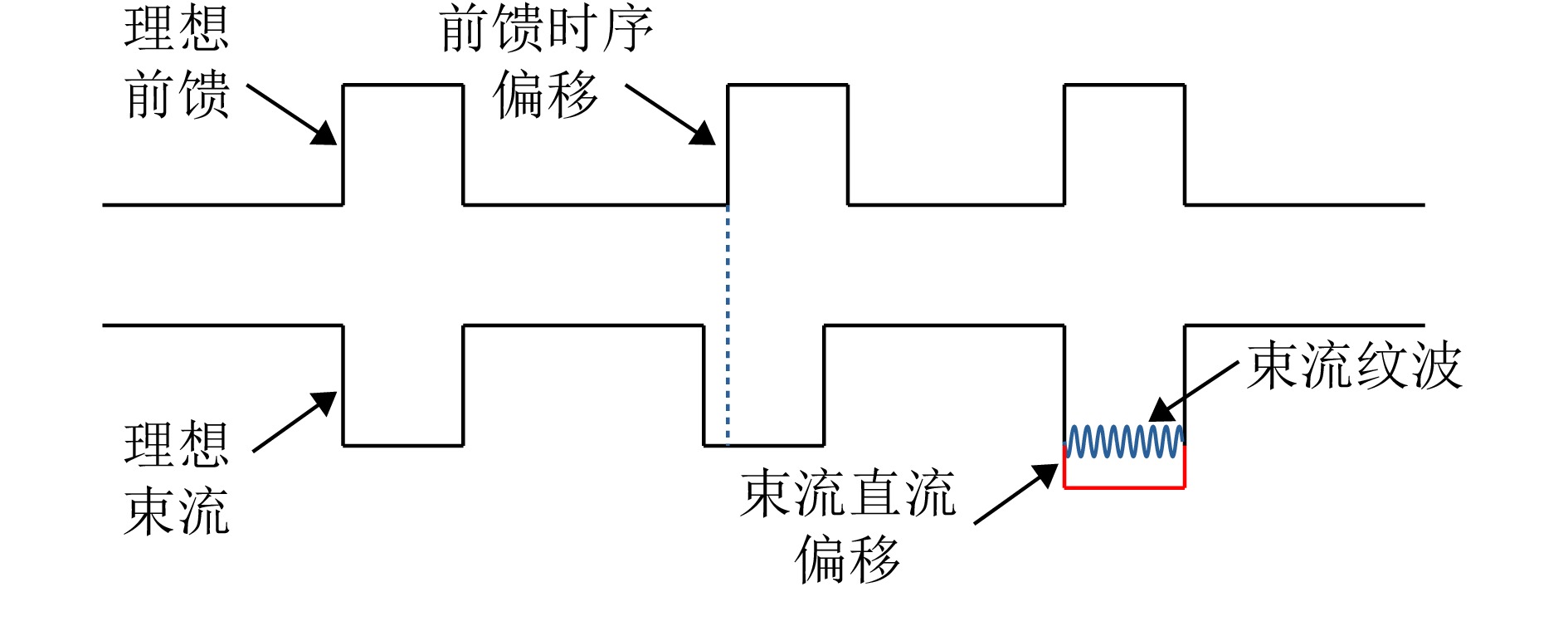
在束流运行的过程中，连续束的束流负载效应可被低电平反馈系统补偿，但在调束过程中采用脉冲束流，需利用前馈对束流负载效应进行补偿。然而通过预设前馈来补偿束流负载效应，可能会因为束流纹波以及前馈时序偏移等因素对腔压幅相稳定性造成影响。如图6所示，在理想情况下，即当前馈补偿量的等效电流和束流反相且大小相同时，束流负载引起的腔压变化将被完全补偿；当前馈系统补偿的时序发生偏移或束流存在随机性纹波时，前馈与束流的作用无法完全抵消，会造成腔压幅相不稳定。
图 6 (在线彩图)前馈时序抖动与束流纹波作用机制
在Simulink中对CiADS超导腔HWR010、HWR019、Spoke042、Ellip062、Ellip082等腔型的束流各项偏差进行评估，各腔型所采用的典型高频参数如表3所列。
表 3 CiADS各腔型典型参数
腔型 f/MHz FHBW/Hz TTF $R/Q\,/\Omega$ $ Q_L $ Vc/MV $ \varphi $ ${I_{\rm{b}}}{\rm{/mA}}$ $ I_{\rm{b}}' $ HWR010 162.5 130 0.73 115 6.25E5 0.71 –39 1 0.119 HWR019 162.5 100 0.77 214 8.13E5 2.6 –64 1 0.107 Spoke042 325 160 0.34 337 1.0E6 4.06 –30 1 0.092 Ellip062 650 120 0.64 328 2.7E6 6 –22 1 0.185 Ellip082 650 110 0.51 474 2.9E6 14.31 –23 1 0.121 -
当束流的流强与脉冲长度较小时，所引起的束流负载效应较小。为了得到在调束过程中满足幅相稳定性设计要求的束流标准，我们针对CiADS调束过程中可能运行的典型束流流强，在不同的束流脉宽下所引起的束流负载效应进行仿真，得到了不同腔型满足幅相设计要求的束流最大脉宽，如表4所列。
表 4 CiADS满足幅相稳定性的最大束流脉宽
腔型 1 mA 2 mA 3 mA 4 mA 5 mA HWR010 11 μs 5 μs 3 μs 2.5 μs 2 μs HWR019 17 μs 8 μs 5.5 μs 4 μs 3 μs Spoke042 20 μs 9.5 μs 6 μs 4.5 μs 3.7 μs Ellip062 5.5 μs 3.5 μs 2 μs 1.5 μs 1 μs Ellip082 11 μs 6 μs 3.5 μs 2.5 μs 2 μs 从表中可以看出，Eliip062腔型对束流脉冲长度的要求最为严格。这是因为在该参数下，Ellip062型超导腔的等效束流流强
$ I_{\rm{b}}' $ 最大，所导致的束流负载效应最为严重，而Spoke042腔内束流负载效应最小。因此在脉冲束调试过程中，可以采用Ellip062型超导腔的束流脉宽作为边界，此时利用反馈环路即可补偿束流负载效应的影响，无需进行前馈补偿，可以提高调束效率。 -
考虑到前馈补偿系统时序可能会发生漂移，我们在束流的流强为1 mA 脉宽为1 000 μs情况下，对HWR010超导腔前馈时序抖动进行了仿真评估，其中仿真结果如图7所示。
图 7 (在线彩图) HWR010前馈补偿时序抖动的影响
从图中可以看出，当前馈时序未发生偏移时，腔压幅值和相位保持不变。随着时序偏移逐渐增大，超导腔腔压幅值和相位的偏移也逐渐变大。当前馈时序偏移量小于1.4 μs时，前馈时序抖动所引起的幅值最大偏移为0.1%，相位最大偏移为
$ 0.04^{\circ} $ ，满足CiADS幅相稳定的设计要求。对其余四类超导腔利用相同的方法进行评估，结果如表5所列。表 5 CiADS前馈时序抖动对腔压幅相稳定性的影响
腔型 Timing jitter/μs Amp error/% Phase error/° HWR010 1.4 0.1 0.04 HWR019 1.75 0.09 0.06 Spoke042 1.24 0.09 0.06 Ellip062 0.79 0.1 0.03 Ellip082 1.36 0.09 0.02 从表中可以看出，Ellip062型超导腔因为束流负载效应的影响较其余腔型大，所以对前馈时序抖动的偏差要求最为严格。因此选用Ellip062腔型的时序要求作为CiADS时序系统的边界，即CiADS时序系统前馈时序抖动不能大于0.79 µs，该要求对目前的时序系统而言较为宽松。
-
考虑到超导腔运行的实际情况，离子源发射出来的束流存在随机性纹波，当纹波的频率为0 Hz时，称为直流偏差。因为前馈补偿值是预置的，无法补偿束流纹波引起的随机性偏差，所以需要评估束流抖动对超导腔幅相稳定性的影响。
假设束流出现纹波时，纹波流强
${I_w}$ ：$${I_w} = {I_0}\sum\limits_n {{A_n}} \cos ({\omega _n}t0),$$ (12) 此时束流流强
$ I_{\rm b} $ ：$${I_{\rm b}} = {I_0}[1 + \sum\limits_n {{A_n}} \cos ({\omega _n}t0)]$$ (13) A为纹波的相对幅值，
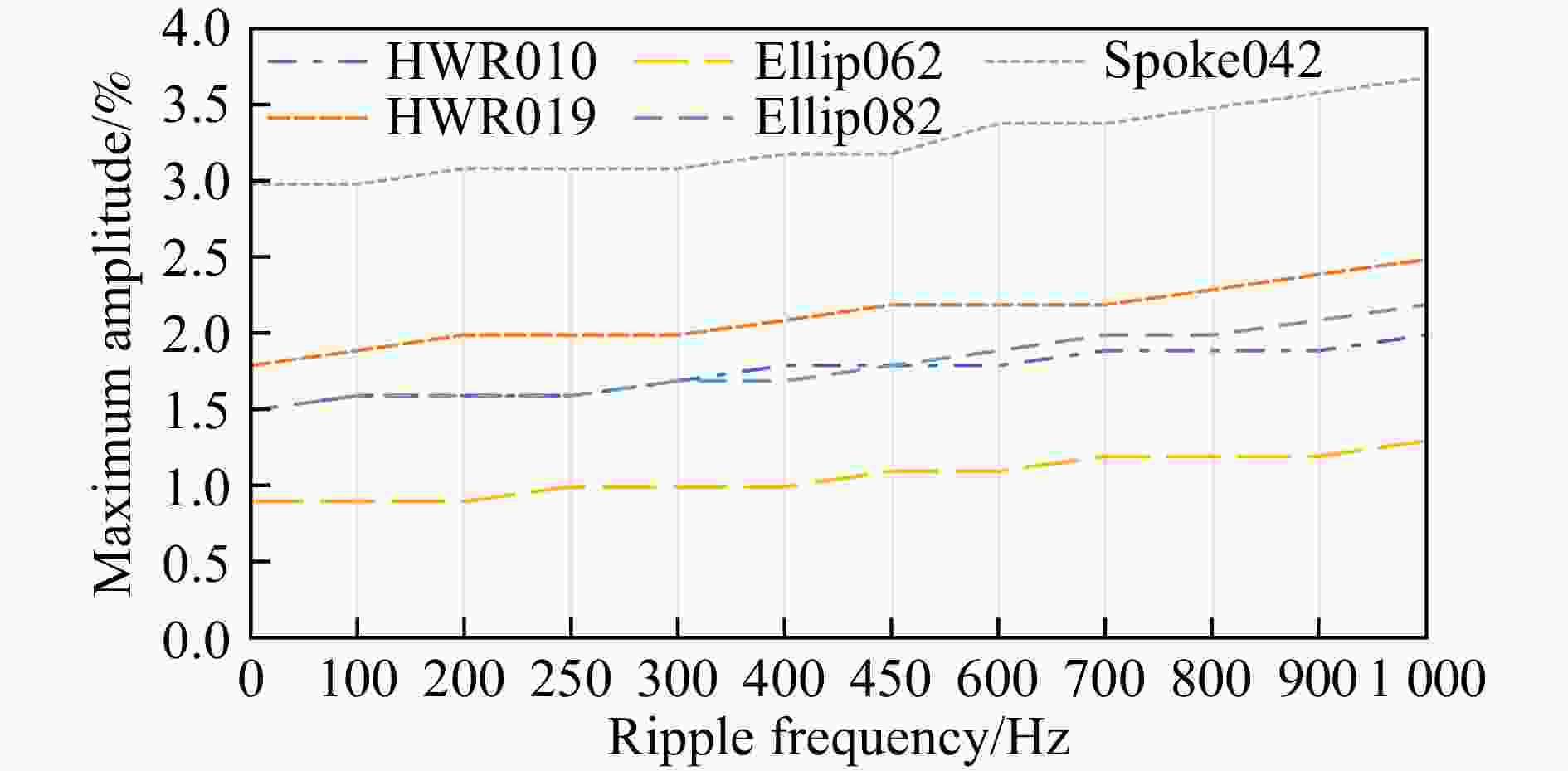
$ \omega $ 为纹波的振荡频率。利用固定量前馈补偿束流负载效应，仿真分析束流纹波在不同抖动频率下，满足CiADS要求的最大幅值抖动，结果如图8所示。
图 8 (在线彩图) CiADS超导腔束流纹波在不同频率下的最大幅值
仿真结果显示，随着束流纹波频率的增加，各腔型可容忍的最大束流纹波也逐渐提高。这表明束流低频纹波对超导腔幅相稳定的影响高于高频纹波，此外因为各腔型束流负载因子不同，Elip062腔型对束流品质的要求远高于其它腔型，而Spoke042对束流品质的要求则较为宽松。因此采用Elip062的值作为设计边界，即束流直流偏差不能大于0.9%。由于Elip062腔段目前的设计参数较为显著的降低了整个加速器对束流纹波的容忍度，在后续的加速器设计优化过程中，将考虑对该腔段物理参数进行适当调整。
-
本文建立了超导腔的时域迭代模型，并在C-ADS注入器II上对模型进行了验证。根据CiADS超导腔幅相稳定性的设计要求，利用该模型研究了束流负载效应以及前馈补偿偏差对腔体稳定性的影响。仿真结果表明，当束流的等效归一化流强越大，束流负载效应对腔内电场稳定性的影响越严重。在无前馈补偿的情况下，得到了CiADS超导腔不同流强下的最大束流脉宽，该结果可以为CiADS脉冲束调试提供帮助；在有前馈补偿的情况下，得到了不同腔型前馈时序的最大偏移量，以及不同纹波频率所允许的最大幅值偏移。并选取了Ellip062腔型的结果作为边界值，该结果可为CiADS相关子系统技术指标的设计提供数据支持。同时因为Ellip062腔型目前设计参数显著降低了整个加速器对各项误差的容忍度，所以在后续加速器的设计优化中，计划对该腔型的参数进行调整优化。
-
摘要: 在高功率超导质子直线加速器中，束流负载效应是影响超导腔幅相稳定性的一个重要因素。本工作基于谐振腔建场模型，开发了超导腔系统束流负载效应的时域仿真程序，分析了束流负载效应对超导腔幅相稳定性的影响，并在C-ADS注入器II上通过相关实验测量对仿真结果进行了验证。利用该程序，评估了CiADS超导直线加速器脉冲束流的脉冲长度，以及前馈补偿的时序抖动和束流纹波等因素对腔中电磁场幅相稳定度的影响。仿真结果表明：在当前CiADS直线加速器设计参数下，为满足超导腔中电磁场0.1%与
$0.1^{\circ}$ 的幅相稳定度指标，前馈时序抖动的偏差不能超过0.79 μs，束流流强的直流偏差不能超过0.9%，并且给出了束流纹波的最大抖动幅值与纹波频率之间的关系。这些结果将为CiADS超导直线加速器相关子系统技术指标的确定提供依据。Abstract: For a high power superconducting proton linac, the transient beam loading effect is an important factor affecting the amplitude and phase stability of the electromagnetic field in a superconducting cavity. Based on the resonant cavity field model, a time-domain simulation code for the beam loading effect in a superconducting cavity was developed, and the simulation results were verified in the prototype injector II of C-ADS. It was then evaluated the influence of pulse width, feedforward timing jitter and beam ripple for CiADS. The simulation results, to meet the design specification, showed that the Radio frequency(RF) fluctuations for each cavity should be less than 0.1% in amplitude and$0.1^{\circ}$ in phase. And the feedforward timing jitter should not exceed 0.79 µs, the beam DC deviation should not exceed 0.9%. The relationship between the maximum ripple amplitude and the ripple frequency was given. These results will provide a basis for determining technical specifications of relevant sub-systems of CiADS.-
Key words:
- CiADS /
- superconducting proton linac /
- beam loading /
- feedforward /
- error evaluation
-
表 1 C-ADS注入器II HWR010-3、HWR010-4等腔体高频参数
腔号 f/MHz FHBW/Hz TTF R/Q/$\Omega$ $ Q_L $ Vc/MeV HWR010-3 162.5 160 0.65 113 5.1E5 0.27 HWR010-4 162.5 184 0.73 113 4.4E5 0.25 
下载: 导出CSV
表 2 C-ADS注入器II HWR010-3、HWR010-4束流负载效应对幅相稳定度仿真与实验结果的一致性误差
腔号 幅值一致性误差 相位一致性误差 HWR010-3 0.1% 0.01° HWR010-4 0.2% 0.03°
下载: 导出CSV
表 3 CiADS各腔型典型参数
腔型 f/MHz FHBW/Hz TTF $R/Q\,/\Omega$ $ Q_L $ Vc/MV $ \varphi $ ${I_{\rm{b}}}{\rm{/mA}}$ $ I_{\rm{b}}' $ HWR010 162.5 130 0.73 115 6.25E5 0.71 –39 1 0.119 HWR019 162.5 100 0.77 214 8.13E5 2.6 –64 1 0.107 Spoke042 325 160 0.34 337 1.0E6 4.06 –30 1 0.092 Ellip062 650 120 0.64 328 2.7E6 6 –22 1 0.185 Ellip082 650 110 0.51 474 2.9E6 14.31 –23 1 0.121
下载: 导出CSV
表 4 CiADS满足幅相稳定性的最大束流脉宽
腔型 1 mA 2 mA 3 mA 4 mA 5 mA HWR010 11 μs 5 μs 3 μs 2.5 μs 2 μs HWR019 17 μs 8 μs 5.5 μs 4 μs 3 μs Spoke042 20 μs 9.5 μs 6 μs 4.5 μs 3.7 μs Ellip062 5.5 μs 3.5 μs 2 μs 1.5 μs 1 μs Ellip082 11 μs 6 μs 3.5 μs 2.5 μs 2 μs
下载: 导出CSV
表 5 CiADS前馈时序抖动对腔压幅相稳定性的影响
腔型 Timing jitter/μs Amp error/% Phase error/° HWR010 1.4 0.1 0.04 HWR019 1.75 0.09 0.06 Spoke042 1.24 0.09 0.06 Ellip062 0.79 0.1 0.03 Ellip082 1.36 0.09 0.02
下载: 导出CSV
-
[1] WANG Z, HE Y, HUANG G, et al. The Status of CiADS Superconducting LINAC[C]//10th International Particle Accelerator Conference, May 19-24, 2019, Melbourne, Australia. Geneva: JACoW Publishing, 2019: MOPTS059. [2] LIU S, HE Y, WANG Z. Beam Dynamics Design of CiADS Superconducting Section[C]// Proceedings of the 13th Symposium on Accelerator Physics, August 28-30, 2018, Jishou, Hunan. Geneva: JACoW Publishing, 2018: MOPH34. [3] ROBINSON K W. STABILITY OF BEAM IN RADIOFREQUENCY SYSTEM[R]. Oak Ridge, TN: Office of Scientific and Technical Information (OSTI), 1964. [4] KERNS Q A, FLOOD W S. Stabilization of Accelerating Voltage Under High-intensity Beam Loading[R]. San Francisco: Lawrence Berkeley National Laboratory, 1965. [5] LI S, FANG Z, FUTATSUKAWA K, et al. Nucl Instr and Meth A, 2019, 945: 162612. [6] GAO Z, HE Y, WANG X W, et al. Chinese Physics C, 2016, 40(5): 057005. doi: 10.1088/1674-1137/40/5/057005 [7] WORKS M. Simulink: Model Based and System Based Design[M]. Natick, Massachusetts: MathWorks Inc, 2002. [8] WILSON P B, GRIFFIN J E. High Energy Electron Linacs, Application to Storage Ring RF Systems and Linear Colliders[C]//AIP Conference Proceedings. New York: American Institute of Physics, 1982, 87(1): 450. [9] WANGLER T P. RF Linear Accelerators[M]. 2ed. Weinheim: Wiley, 2008. -
点击查看大图
图(8) / 表 (5)
计量
- 文章访问数: 829
- HTML全文浏览量: 275
- PDF下载量: 45
- 被引次数: 0
甘公网安备 62010202000723号