-
The interplay between nuclear structure and reaction dynamics has aroused more interest in multinucleon transfer (MNT) reactions to produce more neutron-rich nuclei around neutron shell closure
$ N $ =126[1-2]. The properties of these nuclei are extremely important to explore the production of nuclei around mass number$ A $ =195 in the abundance distribution in stellar nucleosynthesis[3].$ N $ =126 region below the doubly magic 208Pb has become accessible experimentally in fragmentation process[4]. The experimentally deduced cross sections in 136Xe+198Pt demonstrated that the MNT route is a more promising path to produce the neutron-rich isotopes$ N $ =126 in comparing with those measured in the fragmentation of a 1 GeV/nucleon 208Pb beam on a Be target[2]. In the prediction for the optimum projectile-target combinations, the low-energy collisions of 136Xe+208Pb were proposed because of the stabilizing effect of the closed neutron shell in both nuclei,$ N $ =82 and$ N $ =126[5]. The calculation based on multi-dimensional Langevin equations suggested that more than 50 unknown nuclei around$ N $ =126 might be produced with cross sections of not less than 1 μb. Cross sections for products heavier than 208Pb were measured and found sensibly larger than the theoretical predictions[1].The striking measurements inspire different theoretical methods to be used to calculate the production of neutron-rich nuclei in system 136Xe+208Pb. GRAZING model was adequate for describing the yields of nuclei near the projectile or target, but grossly underestimated the observed cross sections by orders of magnitude in more nucleons transfer[6]. The calculated cross sections based on dinuclear system (DNS) model showed a similar scenario[7-9]. The method of using the improved quantum molecular dynamics model and the statistical decay code GEMINI (ImQMD+GEMINI) is suitable to calculate the isotopic production cross sections for
$ \Delta{}Z$ =$-3 $ to 0[9]. Time-dependent Hartree-Fock (TDHF)+GEMINI reproduced the absolute value of the cross section for proton-stripping channels[10-11]. There remain discrepancies between the measurements and the calculated cross sections for proton-pickup processes, indicating a limit of the theoretical framework that works with a single mean-field potential[11]. In recent years, progresses were achieved in the development of theoretical methods by considering different mechanisms. With employing the quantal diffusion, the stochastic mean-field approach provided a better result of the primary fragment distribution of 136Xe+208Pb at$ E_{\rm{c.m.}} $ =526 MeV[12]. The dinuclear system model with considering dynamical deformations of two interacting nuclei improve the description of the potential energy surface and products distribution[13].To clarify the process of nucleons transfer, the effect of
$ Q $ -value on fusion reactions and MNT reactions had been analyzed[14-21]. Sequential transfers with negative$ Q $ -value led to a broad barrier distribution[22] and the intermediate neutron transfer channels with positive$ Q $ -value enhanced the fusion cross section at sub-barrier energies in 40,48Ca+48Ca[23]. However, a systematic comparison of the reduced excitation functions demonstrated that the influence of transfer channels on the fusion of Sn+Ni and Te+Ni was very weak. It was in contrast to a number of measurements that showed large fusion enhancements in correlation with increased positive$ Q $ -value transfer channels in lighter systems[18, 24-25]. The relationship between the cross sections for different produced isotopes and$ Q $ -value was analyzed experimentally in several nucleons transfer reactions[26-28]. Due to a large number of degrees of freedom, such as nucleon transfer, deformations of two interacting nuclei, and different types of separation of composite system being involved in MNT reactions, the effect of$ Q $ -value on the process of MNT is still unclear, especially for much more nucleons transfer. It is necessary to apply the microscopic dynamical methods to investigate the underlying mechanisms. The ImQMD model is suitable to study the reaction mechanism because the dissipation from nucleonic potential and nucleon-nucleon collisions, diffusion and correlation effects from classical N-body system are included[29-36]. In this work, ImQMD is applied to simulate the system 136Xe+208Pb at$ E_{\rm{c.m.}} $ =617 MeV with different impact parameters. The effect of$ Q $ -value on nucleons transfer is proposed to be considered in ImQMD model. The calculated results of ImQMD with and without$ Q $ -value effect are compared with the experimental data. The effect of$ Q $ -value on the distribution of total kinetic energy lost, mass distribution of fragments, lifetime of composite systems and the production of neutron-rich isotopes with neutron number$ N $ =126 are discussed. -
In ImQMD model, each nucleon is represented by a coherent state of a Gaussian wave packet. The time evolution of the coordinate and momentum of each nucleon is determined by the mean field part which is described by Hamiltonian equations and the nucleon-nucleon collision part. The Hamiltonian includes kinetic energy, nuclear potential energy and the Coulomb energy. The nuclear potential energy is an integration of the Skyrme type potential energy density functional, which reads
$$ \begin{split} V_{\rm{loc}} =& \frac{\alpha}{2}\frac{\rho^{2}}{\rho_{0}}+\frac{\beta}{\gamma+1} \frac{\rho^{\gamma+1}}{\rho _{0}^{\gamma}}+\frac{g_{0}}{2\rho _{0}}\left(\nabla\rho\right)^{2}+\\&\frac{c_{s}}{2\rho_{0}}\big[\rho^{2}-\kappa_{s}(\nabla\rho)^{2}\big]\delta^{2}+g_{\tau}\frac{\rho^{\eta+1}}{\rho_{0}^{\eta}}, \end{split}$$ (1) where
$ \rho = \rho_{\rm n}+\rho_{\rm p} $ is the nucleon density and$ \delta = (\rho_{\rm n}-\rho_{\rm p})/(\rho_{\rm n}+\rho_{\rm p}) $ .$ \rho_{\rm n} $ ,$ \rho_{\rm p} $ are neutron and proton density, respectively. The Coulomb energy in the Hamiltonian is written as a sum of the direct and the exchange contribution:$$ \begin{split} U_{\rm{Coul}} =& \frac{1}{2}\iint{{ \rho _{\rm p}({{r}})\frac{e^{2}}{|{{{r}}-{{r}}} ^{\prime }|}\rho _{\rm p}({{r}}^{\prime }){\rm d}{{r}}{\rm d}{{r}}^{\prime }-}}\\ & e^{2}\frac{3}{4}\left( \frac{3}{\pi }\right) ^{1/3}\int{{ \rho _{\rm p}^{4/3}{\rm d}{{r}}}}. \end{split}$$ (2) In the collision term, the isospin-dependent in-medium nucleon-nucleon scattering cross sections are applied, and the Pauli blocking effects are treated as in Ref. [30]. The phase space occupation number constraint method[37] is adopted in this model. The model parameters as those used in Ref. [31] are listed in Table 1. More detailed description of the ImQMD model and its applications can be found in Refs. [31, 33-34].
Table 1. The model parameters.
Parameter Values Parameter Values α/MeV –356 $g_{\tau}$/MeV 12.5 β/MeV 303 $\eta$ 2/3 $\gamma$ 7/6 $c_{\rm s}$/MeV 32 g0/(MeV·fm2) 7.0 $\kappa_{\rm s}$/fm2 0.08 $\rho_0$/fm–3 0.165 In this work, the binding energy per nucleon and deformation of 136Xe and 208Pb are taken from Ref. [38]. The orientations of the initial projectile and target in all events are sampled randomly with an equal probability. The cross section for the primary fragment with charge number
$ Z $ , mass number$ A $ , excitation energy$ E^* $ , angular momentum$ J $ is calculated by$$ \sigma(Z,A,E^*,J) = \sum\limits_{b = 0}^{b_{\rm{max}}}2\pi{}b\Delta{}b\frac{N_{\rm{frag}}(Z,A,b,E^*,J)}{N_{\rm{tot}}(b)}. $$ (3) Here
$ b $ is the impact parameter,$ N_{\rm{frag}}(Z,A,b,E^*,J) $ is the number of events in which a fragment$ (Z,A,E^*,J) $ is formed at a given impact parameter$ b. $ The excitation energy$ E^* $ for the fragment with charge number$ Z $ and mass number$ A $ is obtained by subtracting the corresponding ground-state energy[38] from the total energy of the excited fragment in its rest frame. The total energy of the fragment is calculated by the Hamiltonian. Angular momentum$ J $ of primary fragment is calculated by the coordinates and momentums of all nucleons in the rest frame of fragment. Both excitation energy and angular momentum of primary fragment are related with incident energy, impact parameters and nucleons transfer, etc.$ N_{\rm{tot}}(b) $ is the total event number at a given impact parameter$ b $ . The maximum impact parameter is taken to be$ b_{\rm{max}} $ =13 fm, and the impact parameter step is$ \Delta{b} $ =0.1 fm. The initial distance between the centers of mass of projectile and target is taken to be 30 fm. 10 000 events for each impact parameter are simulated in this work.The system 136Xe+208Pb is special because of the closed neutron shell in projectile and doubly magic target. The structure effect of two interacting nuclei, which may be partly missed in ImQMD model, should be significant in the reaction. For simply considering this effect,
$ Q $ -value is proposed to be considered in ImQMD model from the point of view based on the experimental results, in which the exponential dependence of the cross sections for products on$ Q $ -value was observed in multinucleon transfer reactions 232Th, 197Au+16O[39]. In ImQMD model, the motion of each nucleon can be tracked. In the small time step of simulation, the transfer of only several nucleons occurs in the area of neck. The neck area is defined by the density configuration of system. The experimentally observed dependence of transfer of several nucleons on$ Q $ -value is introduced in the process of nucleons transfer. In this work, whether the motion of transferred nucleons in neck area will be affected by$ Q $ -value is determined by the probability distribution of$ Q $ -value$P_i=f_i[Q^{(i)}_{\rm gg}]/\sum\limits_if_i[Q^{(i)}_{\rm gg}]$ for all possible transfer of nucleons. Here$ f_i[Q^{(i)}_{\rm gg}] $ =$ C_i\exp[Q^{(i)}_{\rm gg}] $ . The momentum component along the axis connecting the centers-of-mass of two interacting nuclei for each transferred nucleon changes to the opposite direction while the$ P_i $ is not selected by the random number. That is, the transfer of nucleons with larger$ Q $ -value is more likely to happen.$ Q^{(i)}_{\rm gg} $ is the mass difference between before and after nucleons transfer to produce$ i $ -th combination of projectile-like and target-like parts.$ C_i $ should be related with many factors, such as the structure properties, the deformation and the excitation of system, etc. It is still unclear and needs to be studied further. Here we simply set$C_i$ =1. Therefore, the motion of nucleons are determined by Hamiltonian equations, nucleon-nucleon collision part and the effect of$ Q $ -value. It is named ImQMD+$ Q $ .Multinucleon transfer reaction 136Xe+208Pb at
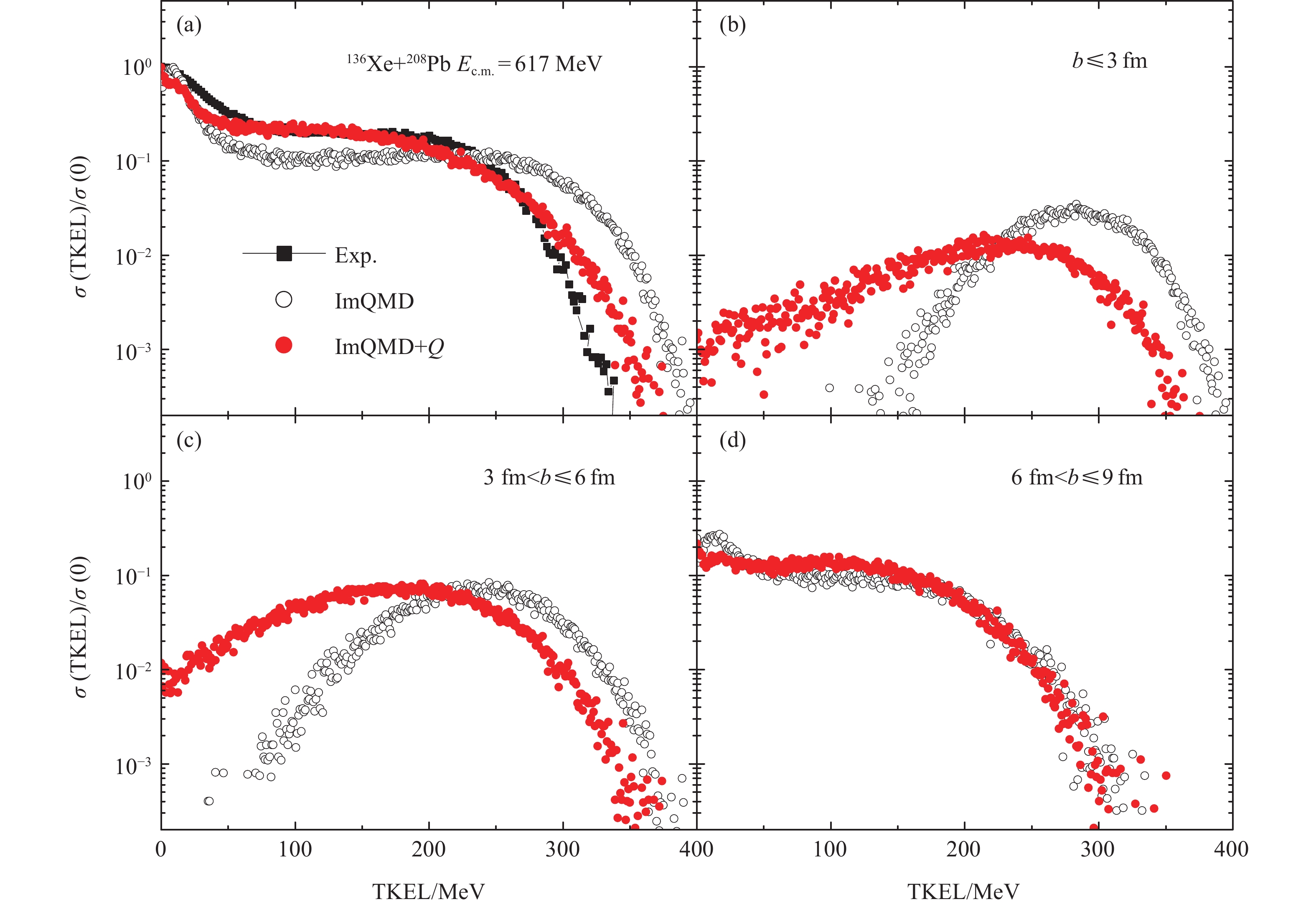
$ E_{\rm{c.m.}} $ =617 MeV is simulated by ImQMD and ImQMD+$ Q $ . The incident energy is about 40 percent over Bass barrier[40]. For comparing with experimental data deduced from different measured distributions[1], the angles of primary fragments are calculated according to the momenta of fragments in ImQMD and ImQMD+$ Q $ . The decays of primary fragments are considered by statistical evaporation model (HIVAP code)[41-42]. The matching time to apply HIVAP code is determined by the decay process of primary fragments calculated in ImQMD model. Over a period of time after the separation of composite system, the probability of forming a fragment decreases with a constant slope, which means that the fragment almost completely enters into the statistical decay stage. We take this time as the matching time to calculate the decay of primary fragments by HIVAP code. In the de-excitation of primary fragments through evaporation of$ \gamma $ , n, p and$ \alpha $ particle, we assume that the emitting angle of the fragments remains unchanged. The corresponding coincident binary fragments over experimentally detected angular range 25°~70° in the laboratory frame are identified. The distributions of total kinetic energy lost calculated by ImQMD and ImQMD+$ Q $ are plotted and compared with experimental data in Fig. 1(a). TKEL is normalized to the count number or cross sections at TKEL=0 for comparison. The open and solid circles represent the calculation results of ImQMD and ImQMD+$ Q $ , respectively. The data denoted by the solid squares are generally better reproduced by the results of ImQMD+$ Q $ .$ Q $ -value effect significantly decreases the contribution of larger TKEL in comparing with those of ImQMD. The effects of$ Q $ -value on TKEL from different impact parameters are shown in panels (b~d). The difference between the results of ImQMD and ImQMD+$ Q $ mainly occurs in the events at lower impact parameters ($ b\leqslant $ 6 fm). The energy transfer from collective motion to internal excitation decreases due to the effect of$ Q $ -value. It leads to a larger probability of producing primary fragments with smaller excitation energies.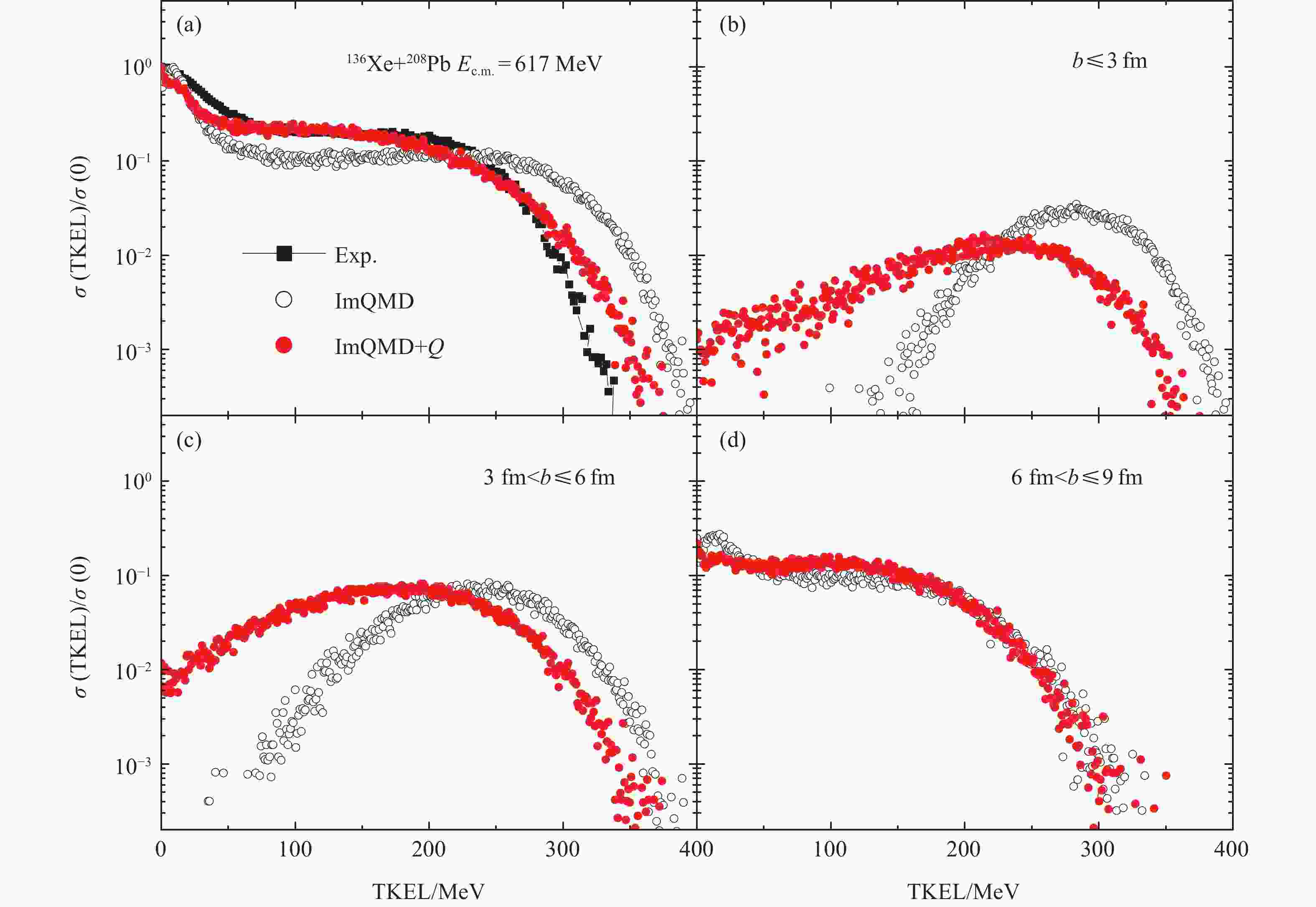
Figure 1. (color online)TKEL distribution of 136Xe+ 208Pb for binary events at
$E_{\rm{c.m.}}$ =617 MeV. Open and solid circles are the results of ImQMD and ImQMD+$Q$ , respectively. The data denoted by solid squares are taken from Ref. [1]. The calculated TKEL are compared with the data in panel (a). Panels (b~d) represent the contributions to TKEL from different impact parameters.The primary fragments produced in the binary events in Fig. 1 are selected with energy losses greater than 40 MeV. Mass distributions of those fragments are plotted in Fig. 2(a) for comparing with experimental data[1]. The open and solid circles represent the same meanings as Fig. 1. The experimental data denoted by solid squares are also better generally reproduced by the results of ImQMD+
$ Q $ than those of ImQMD. ImQMD provides a larger cross section in massive transfer between two nuclei. The effect of$ Q $ -value in ImQMD+$ Q $ leads to the suppression in the transfer of more than ten nucleons. The peaks of experimental mass distribution and the mass number of projectile and target are denoted by arrows and dashed lines, respectively. The peaks of mass distribution in ImQMD locate at the mass number of projectile and target. A large number of primary fragments in ImQMD+$ Q $ drift away from the entrance channel mass-asymmetry to the peaks of experimental mass distribution. It can be understood by positive$ Q $ -value in the maximum$ Q $ -value$ Q_{\rm gg} $ for each mass number of fragments in panel (b). The transfer of less than about ten nucleons are obviously driven by the effect of$ Q $ -value.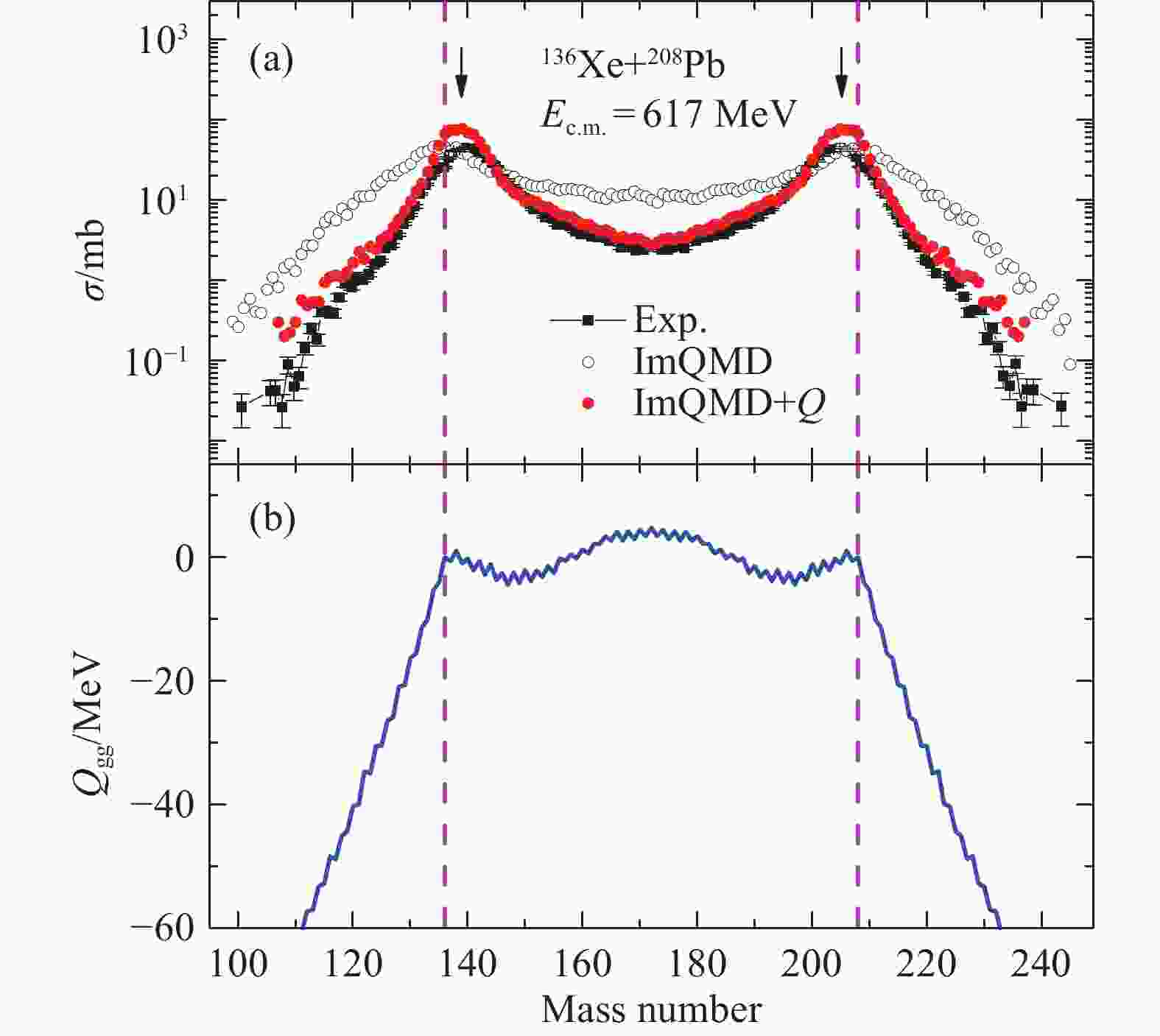
Figure 2. (color online) Mass distribution and
$Q_{\rm{gg}}$ distribution of 136Xe+208Pb. (a) Mass distribution for binary events with energy losses greater than 40 MeV. Open and solid circles are the results of ImQMD and ImQMD+$Q$ , respectively. The data denoted by solid squares are taken from Ref. [1]. The peak positions in experimental data and two colliding nuclei are represented by arrows and dashed lines, respectively. (b) Distribution of maximum$Q_{\rm{gg}}$ for all possible mass transfers.$Q_{\rm{gg}}$ =$M_{\rm{P}}$ +$M_{\rm{T}}$ –$M_{\rm{PLF}}$ –$M_{\rm{TLF}}$ , where$M_{\rm{P}}$ and$M_{\rm{T}}$ are the masses of projectile and target.$M_{\rm{PLF}}$ and$M_{\rm{TLF}}$ are the masses of the projectile-like and target-like fragments.Multinucleon transfer and the energy transfer from collective motion to internal excitation are strongly related with the lifetime of composite system. The comparison between the average lifetimes of composite system calculated by ImQMD and ImQMD+
$ Q $ for different impact parameters is shown in Fig. 3. With increasing the impact parameters, the larger angular momentum decreases the average lifetime of composite system. The effect of$ Q $ -value obviously decreases the average lifetime of composite system at lower impact parameters$ b\leqslant $ 5 fm. It explains the increase of lower TKEL at lower impact parameters in Fig. 1 and the suppression of cross sections for the fragments produced in the transfer of massive nucleons in Fig. 2. The smaller lifetime of composite system caused by the effect of$ Q $ -value provides the smaller probability for multinucleon transfer.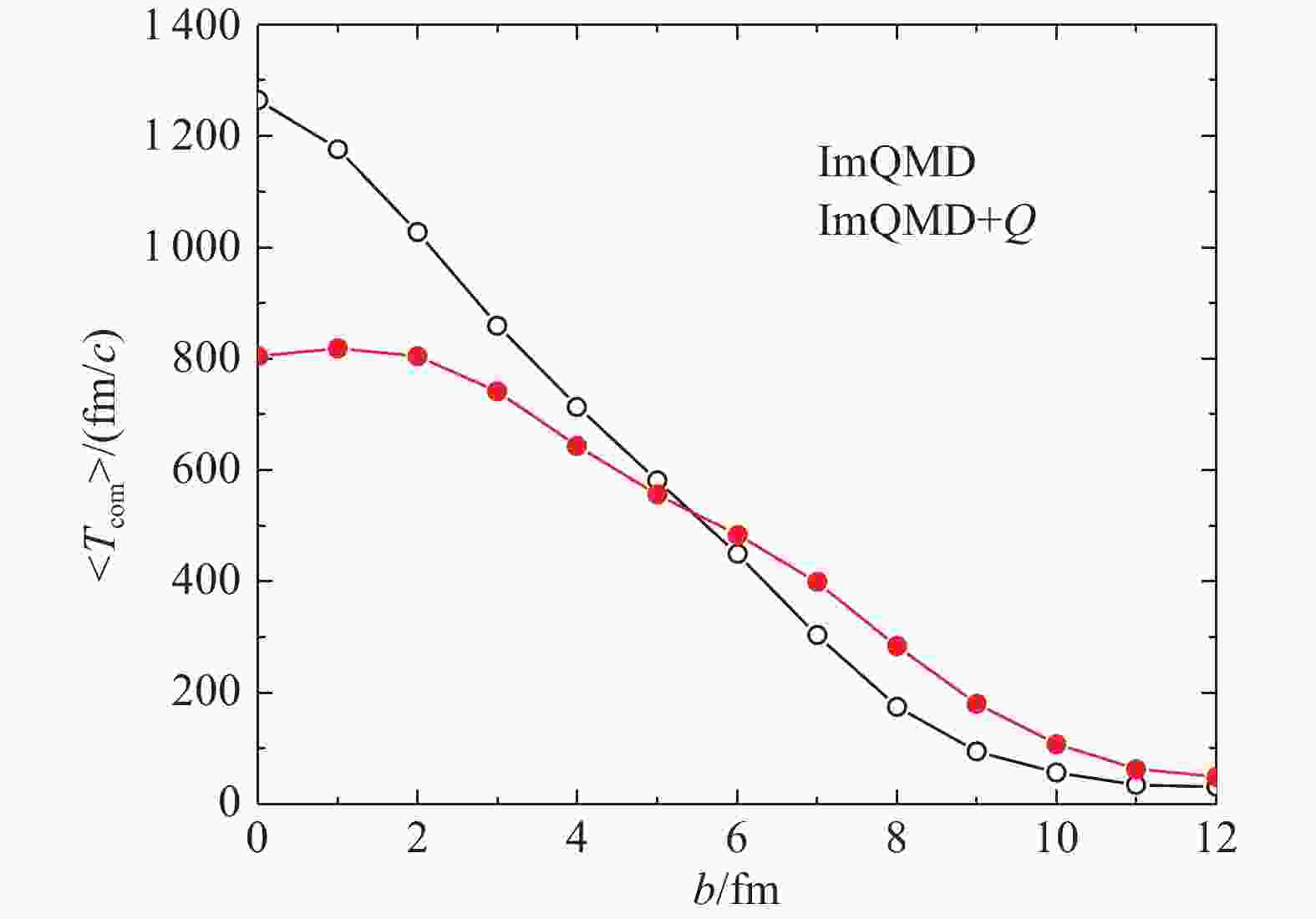
Figure 3. (color online) The average lifetime of composite system calculated by ImQMD and ImQMD+
$Q$ for different impact parameters. The meaning of the symbols is the same as Fig. 1.The system 136Xe+208Pb has aroused a great interest in the production of more neutron-rich nuclei with neutron number
$ N $ =126. The effect of$ Q $ -value on the production of these primary isotopes is shown in Fig. 4. ImQMD+$ Q $ provides larger cross sections for neutron-rich isotopes produced in protons transfer from target to projectile. It originates from the effect of$ Q $ -value in the comparison between the results of ImQMD and ImQMD+$ Q $ .$ Q $ -value describes the properties of nuclei in their ground states. The result implies that the production of those isotopes is still related with$ Q $ -value effect (or quantum effect) in 136Xe+208Pb even at 40 percent over bass barrier.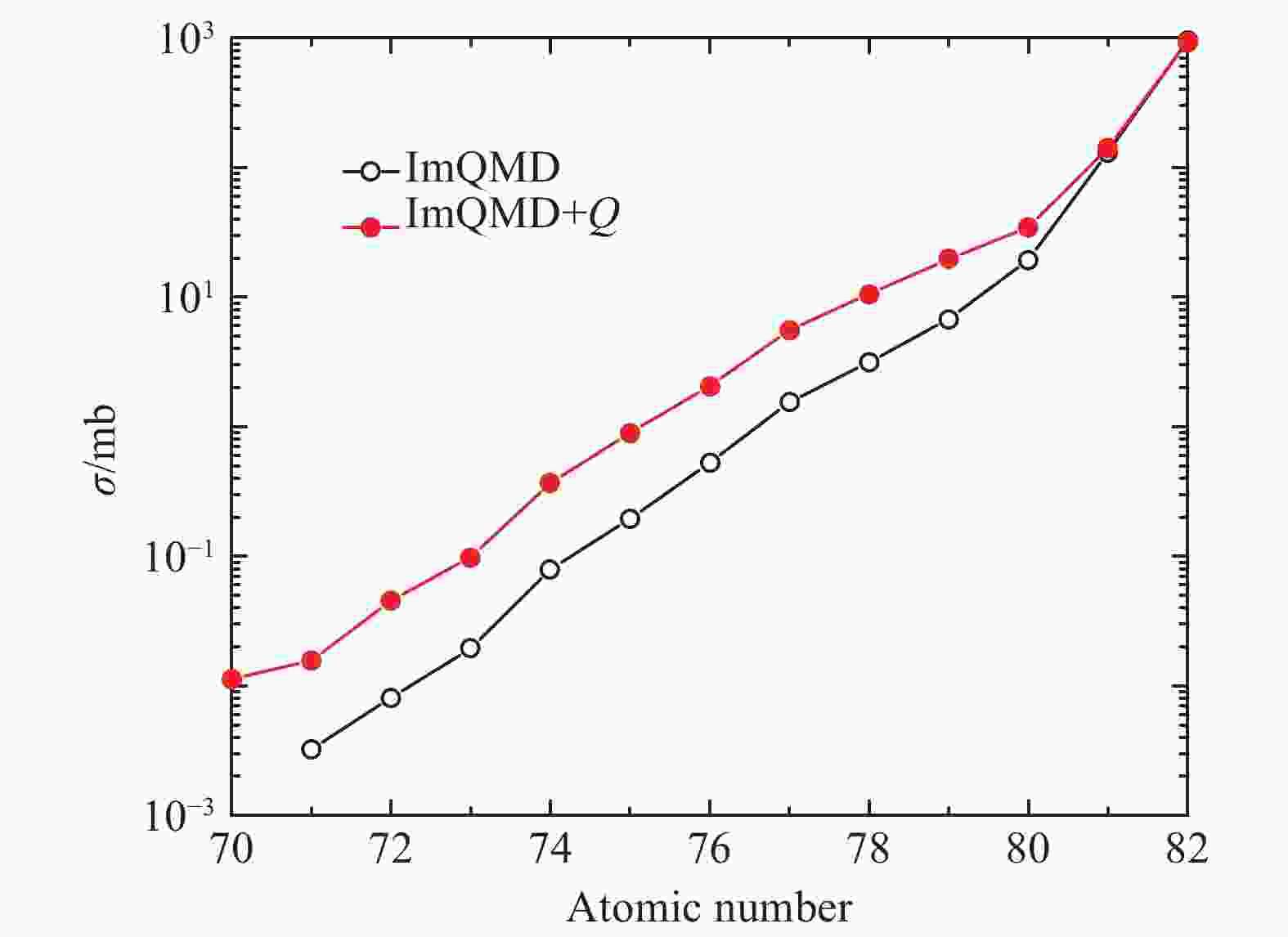
Figure 4. (color online) The cross sections for primary isotopes with neutron number
$N$ =126 in ImQMD and ImQMD+$Q$ . The meaning of the symbols is the same as Fig. 1. -
The effect of
$ Q $ -value on nucleons transfer between two interacting nuclei of system 136Xe+208Pb at$ E_{\rm{c.m.}} $ =617 MeV is proposed to be considered in ImQMD model. In the comparison between the results of ImQMD and ImQMD+$ Q $ , the transfer of less than ten nucleons is found to be obviously driven by$ Q $ -value effect, in which the nucleons transfer can be directly understood by the$ Q $ -value. Cross sections for primary fragments produced in the transfer of a large number of nucleons are suppressed. The transfer of these nucleons is related with not only$ Q $ -value but also dynamical processes (including the deformation and excitation of system). The experimental mass distribution and distribution of total kinetic energy lost are generally better reproduced by the results with considering the effect of$ Q $ -value. The drift of peaks in experimental mass distribution is also shown in the results of ImQMD+$ Q $ . The cross sections for primary fragments with$ N $ =126 calculated by ImQMD+$ Q $ are larger than those of ImQMD. The results suggest that the effect of$ Q $ -value be considered in the choice of projectile-target combination for the production of more neutron-rich nuclei in the multinucleon transfer reactions.Acknowledgements We acknowledge computing support by Supercomputer Center of HIRFL at Institute of Modern Physics, Chinese Academy of Sciences and National Supercomputer Center TianHe-1(A) in Tianjin, China.
-
摘要: 基于改进的量子分子动力学(ImQMD)模型,模拟了136Xe+208Pb在质心系入射能量为
$E_{\rm{c.m.}}$ =617 MeV的多核子转移反应。为了研究这个特殊的反应体系,将不同核子数转移前后形成的类弹与类靶对应的$Q$ 值的指数概率分布引入模型中考虑$Q$ 值效应,并将计算结果与实验探测的总动能损失分布和质量分布进行了比较。我们发现考虑$Q$ 值效应后的计算结果更好地再现了实验数据。在少于10个核子的转移过程中,核子的转移明显受到了$Q$ 值效应的驱动。在更多的核子转移过程中,$Q$ 值效应明显压低了反应产物的生成截面。这是因为大量的核子转移主要发生在小碰撞参数,对应的复合体系的寿命由于$Q$ 值效应明显减小。在ImQMD与ImQMD+Q的计算结果比较中,我们还发现,$Q$ 值效应明显增加了比208Pb更丰中子的中子数为126的初级碎块生成截面。Abstract: Multinucleon transfer reaction 136Xe+208Pb at$E_{\rm{c.m.}}$ =617 MeV is simulated by improved quantum molecular dynamics (ImQMD) model with and without considering the effect of$Q$ -value. The calculation results of ImQMD including the effect of$Q$ -value (ImQMD+$Q$ ) generally better reproduce the experimental mass distribution and distribution of total kinetic energy lost (TKEL).$Q$ -value effect is found to drive the transfer of less than ten nucleons and suppress more nucleons transfer. It also decreases the average lifetime of composite systems in the events at lower impact parameters. In the production of more neutron-rich isotopes with neutron number$N$ =126,$Q$ -value effect enhances the cross sections for these isotopes in the comparison between the results of ImQMD and ImQMD+$Q$ .-
Key words:
- multinucleon transfer reaction /
- Q-value effect /
- ImQMD model
-
Figure 1. (color online)TKEL distribution of 136Xe+ 208Pb for binary events at
$E_{\rm{c.m.}}$ =617 MeV. Open and solid circles are the results of ImQMD and ImQMD+$Q$ , respectively. The data denoted by solid squares are taken from Ref. [1]. The calculated TKEL are compared with the data in panel (a). Panels (b~d) represent the contributions to TKEL from different impact parameters.Figure 2. (color online) Mass distribution and
$Q_{\rm{gg}}$ distribution of 136Xe+208Pb. (a) Mass distribution for binary events with energy losses greater than 40 MeV. Open and solid circles are the results of ImQMD and ImQMD+$Q$ , respectively. The data denoted by solid squares are taken from Ref. [1]. The peak positions in experimental data and two colliding nuclei are represented by arrows and dashed lines, respectively. (b) Distribution of maximum$Q_{\rm{gg}}$ for all possible mass transfers.$Q_{\rm{gg}}$ =$M_{\rm{P}}$ +$M_{\rm{T}}$ –$M_{\rm{PLF}}$ –$M_{\rm{TLF}}$ , where$M_{\rm{P}}$ and$M_{\rm{T}}$ are the masses of projectile and target.$M_{\rm{PLF}}$ and$M_{\rm{TLF}}$ are the masses of the projectile-like and target-like fragments.Figure 3. (color online) The average lifetime of composite system calculated by ImQMD and ImQMD+
$Q$ for different impact parameters. The meaning of the symbols is the same as Fig. 1.Figure 4. (color online) The cross sections for primary isotopes with neutron number
$N$ =126 in ImQMD and ImQMD+$Q$ . The meaning of the symbols is the same as Fig. 1.Table 1. The model parameters.
Parameter Values Parameter Values α/MeV –356 $g_{\tau}$ /MeV12.5 β/MeV 303 $\eta$ 2/3 $\gamma$ 7/6 $c_{\rm s}$ /MeV32 g0/(MeV·fm2) 7.0 $\kappa_{\rm s}$ /fm20.08 $\rho_0$ /fm–30.165 -
[1] KOZULIN E M, VARDACI E, KNYAZHEVA G N, et al. Phys Rev C, 2012, 86: 044611. doi: 10.1103/PhysRevC.86.044611 [2] WATANABE Y X, KIM Y H, JEONG S C, et al. Phys Rev Lett, 2015, 115: 172503. doi: 10.1103/PhysRevLett.115.172503 [3] BURBIDGE K M, BURBIDGE G R, FOWLER W A, et al. Rev Mod Phys, 1957, 29: 547. doi: 10.1103/RevModPhys.29.547 [4] KURTUKIAN-NIETO T, BENLLIURE J, SCHMIDT K H, et al. Phys Rev C, 2014, 89: 024616. doi: 10.1103/PhysRevC.89.024616 [5] ZAGREBAEV V, GREINER W. Phys Rev Lett, 2008, 101: 122701. doi: 10.1103/PhysRevLett.101.122701 [6] BARRETT J S, LOVELAND W, YANEZ R, et al. Phys Rev C, 2015, 91: 064615. doi: 10.1103/PhysRevC.91.064615 [7] FENG Z Q. Phys Rev C, 2017, 95: 024615. doi: 10.1103/PhysRevC.95.024615 [8] ZHU L, WEN P W, LIN C J, et al. Phys Rev C, 2018, 97: 044614. doi: 10.1103/PhysRevC.97.044614 [9] LI C, ZHANG F, LI J J, et al. Phys Rev C, 2016, 93: 014618. doi: 10.1103/PhysRevC.93.014618 [10] JIANG X, WANG N. Phys Rev C, 2020, 101: 014604. doi: 10.1103/PhysRevC.101.014604 [11] SEKIZAWA K. Phys Rev C, 2017, 96: 014615. doi: 10.1103/PhysRevC.96.014615 [12] AYIK S, YILMAZ B, YILMAZ O, et al. Phys Rev C, 2019, 100: 014609. doi: 10.1103/PhysRevC.100.014609 [13] GUO S Q, BAO X J, ZHANG H F, et al. Phys Rev C, 2019, 100: 054616. doi: 10.1103/PhysRevC.100.054616 [14] WANG B, WEN K, ZHAO W J, et al. At Data Nucl Data Tables, 2017, 114: 281. doi: 10.1016/j.adt.2016.06.003 [15] SCAMPS G, SARGSYAN V V, ADAMIAN G G, et al. Phys Rev C, 2015, 91: 024601. doi: 10.1103/PhysRevC.91.024601 [16] STEFANINI A M, MONTAGNOLI G, ESBENSEN H, et al. Phys Lett B, 2014, 728: 639. doi: 10.1016/j.physletb.2013.12.048 [17] KOLATA J J, ROBERTS A, HOWARD A M, et al. Phys Rev C, 2012, 85: 054603. doi: 10.1103/PhysRevC.85.054603 [18] KOHLEY Z, LIANG J F, SHAPIRA D, et al. Phys Rev Lett, 2011, 107: 202701. doi: 10.1103/PhysRevLett.107.202701 [19] LIANG J F, SHAPIRA D, BEENE J R, et al. Phys Rev C, 2007, 75: 054607. doi: 10.1103/PhysRevC.75.054607 [20] JIA H M, LIN C J, YANG L, et al. Phys Lett B, 2016, 755: 43. doi: 10.1016/j.physletb.2016.01.058 [21] LIU Z H, BAO J D. Phys Rev C, 2006, 74: 057602. doi: 10.1103/PhysRevC.74.057602 [22] ROWLEY N, THOMPSON I J, NAGARAJAN M A. Phys Lett B, 1992, 282: 276. doi: 10.1016/0370-2693(92)90638-K [23] ZAGREBAEV V I. Phys Rev C, 2003, 67: 061601(R). doi: 10.1103/PhysRevC.67.061601 [24] JIANG C L, REHM K E, ESBENSEN H, et al. Phys Rev C, 1998, 57: 2393. doi: 10.1103/PhysRevC.57.2393 [25] LESKO K T, HENNING W, REHM K E, et al. Phys Rev C, 1986, 34: 2155. doi: 10.1103/PhysRevC.34.2155 [26] COCKS J F C, BUTLER P A, CANN K J, et al. Phys G: Nucl Part Phys, 2000, 26: 23. [27] MIJATOVIĆ T, SZILNER S, CORRADI L, et al. Phys Rev C, 2016, 94: 064616. doi: 10.1103/PhysRevC.94.064616 [28] RAFFERTY D C, DASGUPTA M, HINDE D J, et al. Phys Rev C, 2016, 94: 024607. doi: 10.1103/PhysRevC.94.024607 [29] WANG N, GUO L. Phys Lett B, 2016, 760: 236. doi: 10.1016/j.physletb.2016.06.073 [30] WANG N, WU X, LI Z. Phys Rev C, 2003, 67: 024604. doi: 10.1103/PhysRevC.67.024604 [31] ZHAO K, LI Z, WU X, et al. Phys Rev C, 2013, 88: 044605. doi: 10.1103/PhysRevC.88.044605 [32] TIAN J, WU X, ZHAO K, et al. Phys Rev C, 2008, 77: 064603. doi: 10.1103/PhysRevC.77.064603 [33] ZHAO K, WU X, LI Z. Phys Rev C, 2009, 80: 054607. doi: 10.1103/PhysRevC.80.054607 [34] WANG N, LI Z, WU X. Phys Rev C, 2002, 65: 064608. doi: 10.1103/PhysRevC.65.064608 [35] WANG N, LI Z, WU X, et al. Phys Rev C, 2004, 69: 034608. doi: 10.1103/PhysRevC.69.034608 [36] LI C, WEN P, LI J, et al. Phys Lett B, 2018, 776: 278. doi: 10.1016/j.physletb.2017.11.060 [37] PAPA M, MARUYAMA T, BONASERA A. Phys Rev C, 2001, 64: 024612. doi: 10.1103/PhysRevC.64.024612 [38] MÖLLER P, NIX J R, MYERS W D, et al. At Data Nucl Data Tables, 1995, 59: 185. doi: 10.1006/adnd.1995.1002 [39] ARTUKH A G, AVDEICHIKOV V V, ERÖ J, et al. Nucl Phys A, 1971, 160: 511. doi: 10.1016/0375-9474(71)90093-5 [40] BASS R. Nuclear Reactions with Heavy Ions[M]. Berlin: Springer Verlag, 1980. [41] SHEN C, KOSENKO G, ABE Y. Phys Rev C, 2002, 66: 061602(R). doi: 10.1103/PhysRevC.66.061602 [42] REISDORF W, HESSBERGER F P, HILDENBRAND K D, et al. Nucl Phys A, 1985, 444: 154. doi: 10.1016/0375-9474(85)90296-9 -











 下载:
下载:





























































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号