-
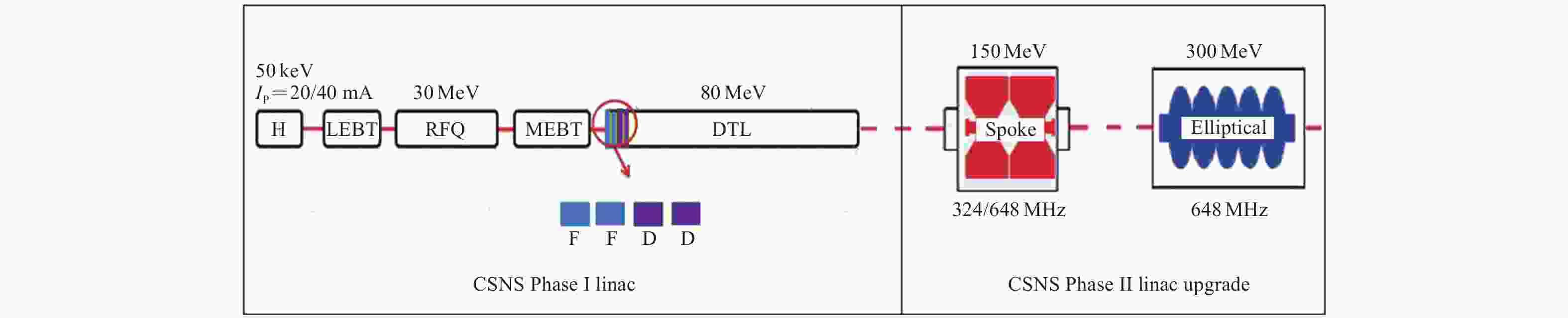
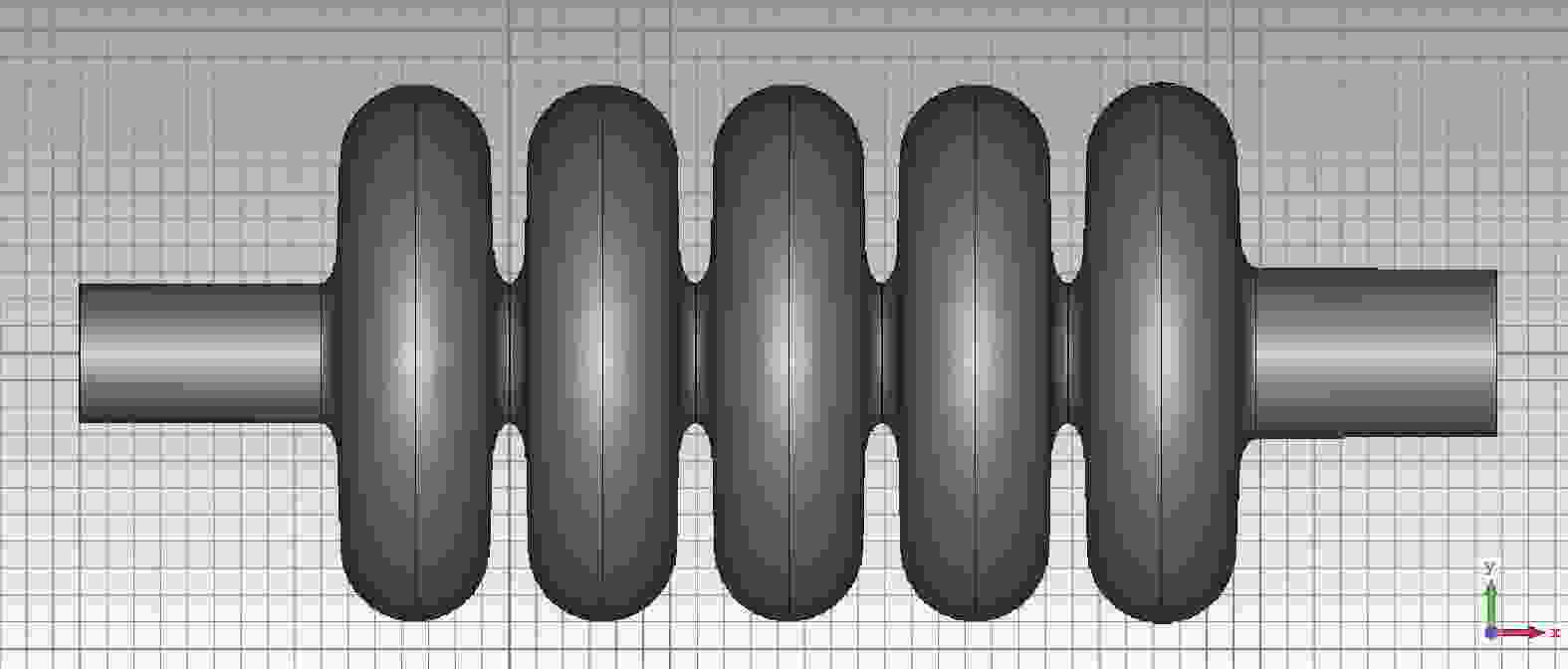
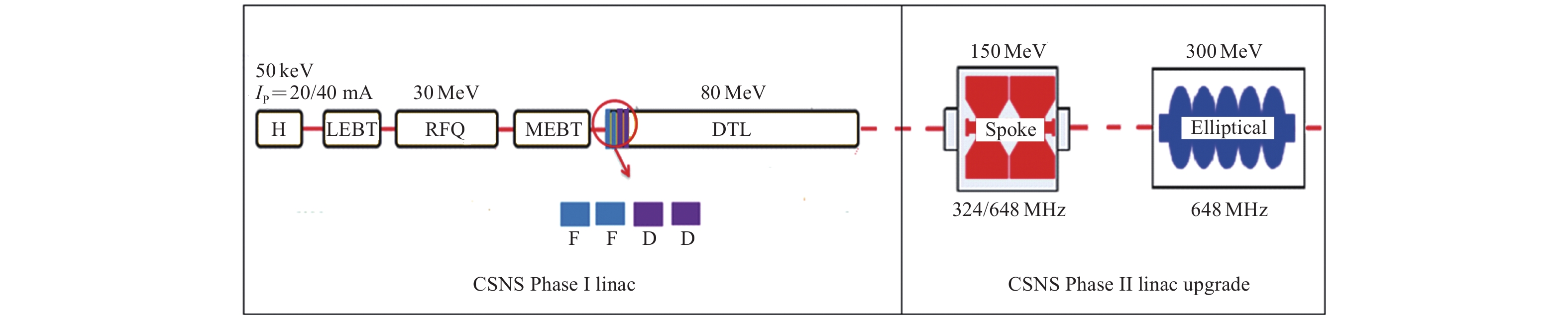
建设于东莞的中国散裂中子源(China Spallation Neutron Source, CSNS)一期设计束流功率为100 kW,目前已达到设计指标100 kW运行,二期(CSNS-II)计划升级束流功率到500 kW[1-2]。直线加速器H-的加速能量由现在的80 MeV提高到300 MeV以上,升级方案是在漂移管加速器(Drift Tube Linac, DTL)后接超导Spoke腔和椭球腔来提高能量。在150~300 MeV能量段拟采用技术相对成熟的中β超导椭球腔结构,椭球腔机械结构简单、加工及表面后处理相对容易、束管孔径大、束损小,且可以有非常高的加速梯度。另外,超导椭球腔已有较多的腔体运行经验、且其附属配件功率耦合器,调谐器及恒温器设计制造也相对成熟,工程风险较低[3]。CSNS-II的椭球腔采用5-cell结构,工作频率648 MHz,几何βg取0.60。
-
刚度较弱是椭球腔的一个弱势,因此,由氦压波动、机械振动及洛伦兹力等产生的失谐分析是研制椭球腔的必要环节。采用COMSOL Multiphysics[5]软件和CST[6]软件对氦压波动和洛伦兹力失谐进行分析,对于CSNS-II 的648 MHz 5-cell椭球纯铌腔,腔体所用铌材的机械特性如表1所列。
表 1 铌材特性
参量 值 杨氏模量/GPa 123 泊松比 0.38 密度/(kg/m3) 8.57×103 壁厚/mm 3.8 -
氦压的波动会引起超导椭球腔的形状变化,进而引起腔体本征频率的漂移。本征频率的偏移量∆f与氦压的变化量∆P满足式(1)[7]:
$$\Delta f = {K_{\rm{P}}} \bullet \Delta P,$$ (1) 其中KP定义为氦压敏感性系数,用来表征超导椭球腔对氦压波动的响应。
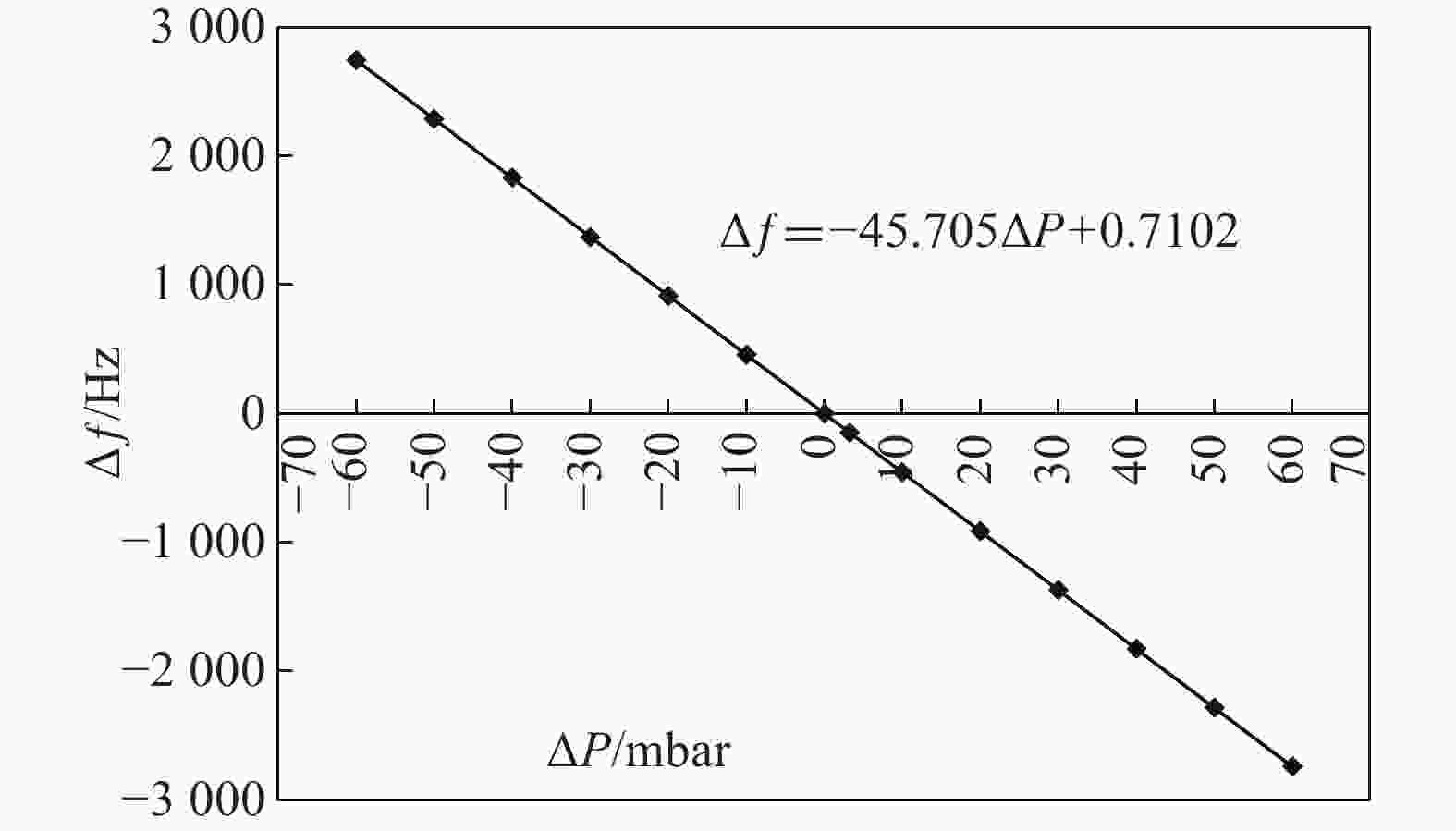
在两端束管端口固定边界条件下,对没带加强环的CSNS-II椭球腔,利用软件COMSOL Multiphysics计算其在不同氦压偏移量下的本征频率偏移,拟合曲线如图3所示,KP为-45.705 Hz/mbar。
-
洛伦兹力是由腔体内电磁场产生,作用于腔体的内表面上,导致腔体产生形变失谐,力的大小由式(2)计算得到[8]:
$$P = \frac{1}{4}({\mu _0}{H^2} - {\varepsilon _0}{E^2}),$$ (2) 其中: μ0是真空磁导率;ε0是真空介电常数;H和E分别是腔体内表面磁场强度和内表面电场强度,它们的大小与超导腔的加速梯度Eacc呈正比关系。
洛伦兹力导致腔体的形变失谐称为洛伦兹力失谐,洛伦兹力失谐量由式(3)给出:
$$\frac{{\Delta f}}{{{f_0}}} = \frac{1}{{4W}}\int_{\Delta V} {({\varepsilon _0}{E^2} - {\mu _0}{H^2})} {\rm{d}}V,$$ (3) 其中:
$$W = \frac{1}{4}\int_V {({\varepsilon _0}{E^2} + {\mu _0}{H^2})} {\rm{d}}V,$$ (4) W是超导腔内的高频储能,与腔的加速梯度Eacc有关,f0是超导腔原有的谐振频率。
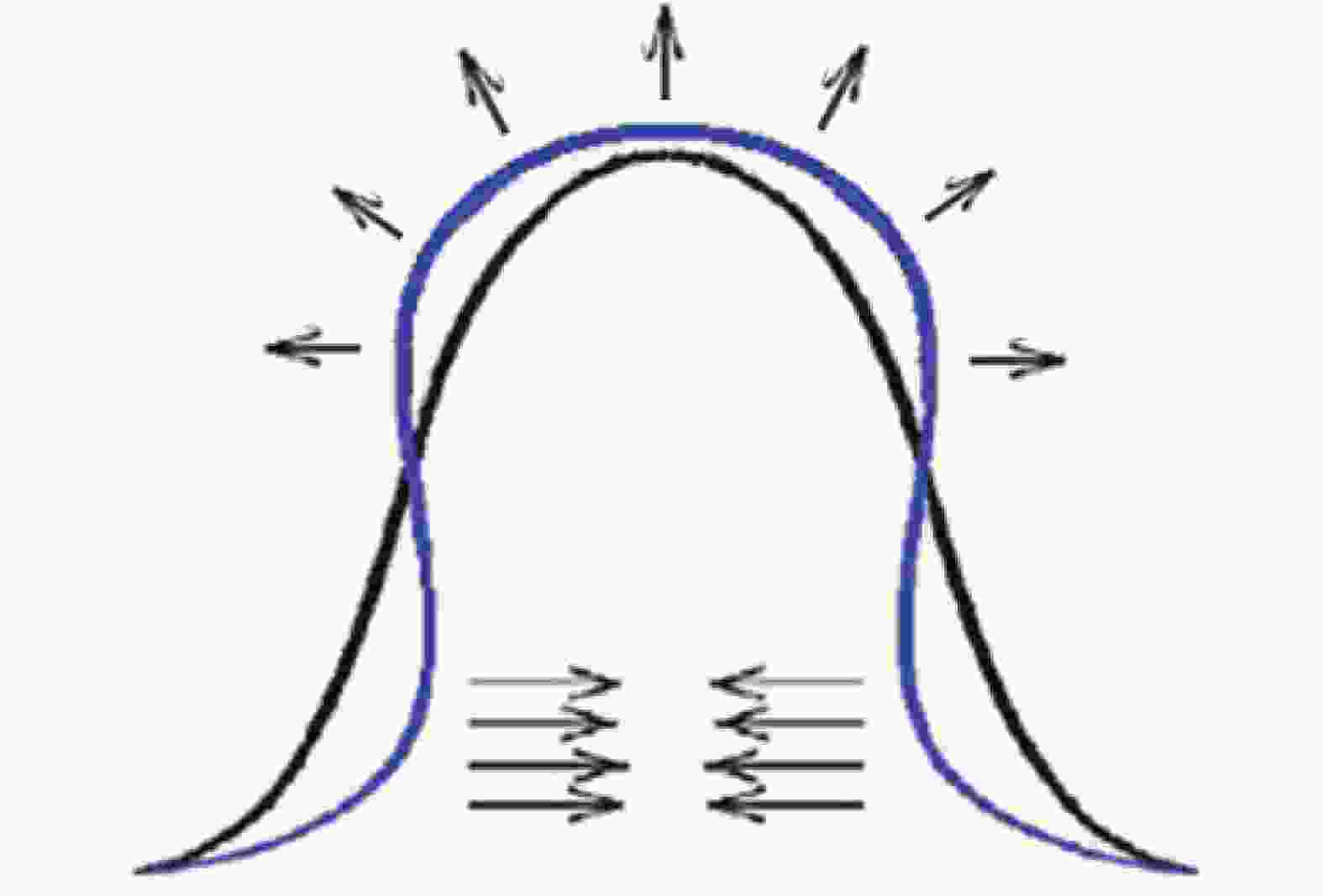
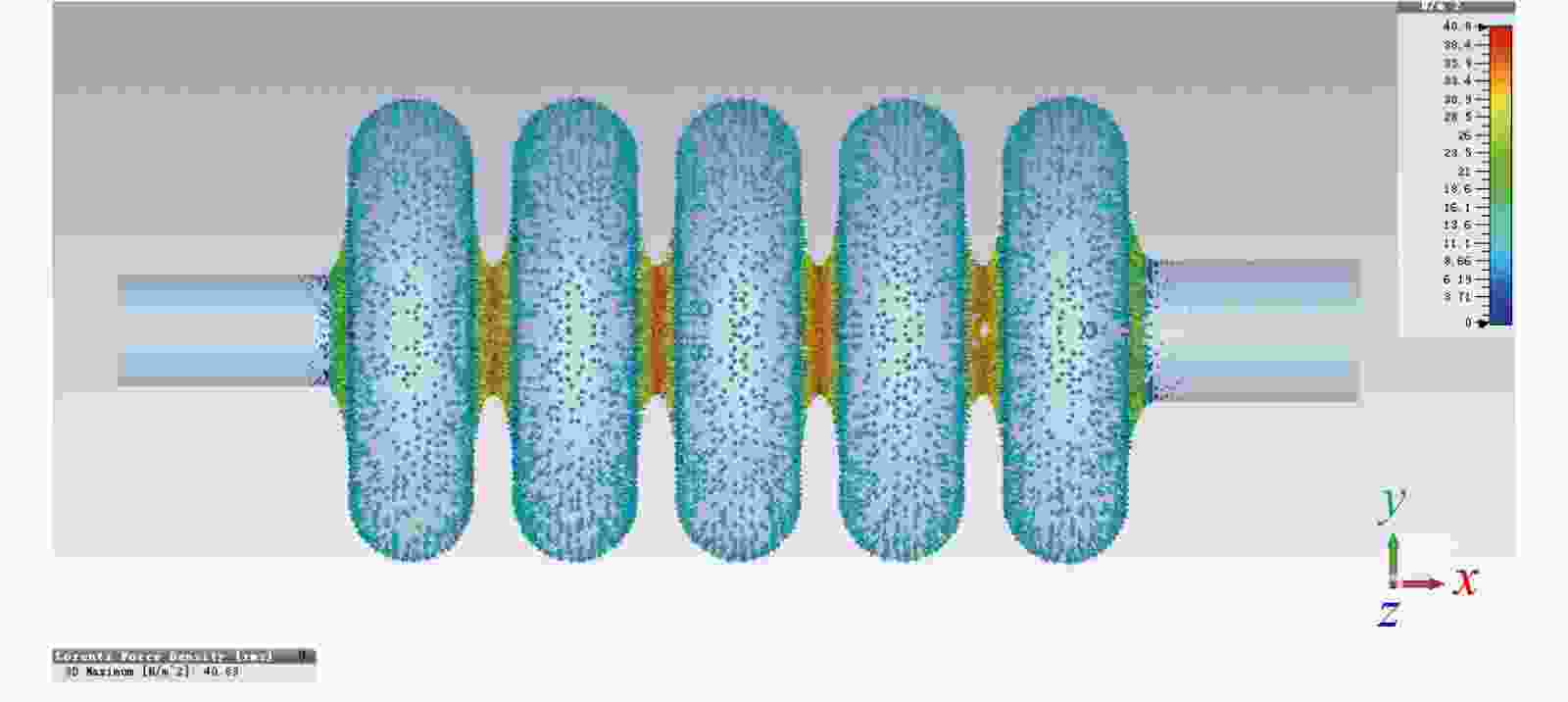
洛伦兹力对椭球腔的作用效果如图4所示[9],磁场区向外形变,电场区向内形变。Eacc为1.61 MV/m时,CST仿真计算的洛伦兹力分布如图5所示,腔颈处洛伦兹力最大,峰值为40 N/m2,赤道椭球面的力约10 N/m2。
根据式(2),在不同的Eacc下,洛伦兹力产生的腔体形变和频率偏移量不同,频率偏移量∆f与腔体加速梯度平方
$E_{{\rm{acc}}}^2$ 成正比关系[10-11]:$$\Delta f = {K_{\rm{L}}} \bullet E_{{\rm{acc}}}^2,$$ (5) 其中KL称为洛伦兹力失谐因子,是一个衡量腔在洛伦兹力下机械稳定性的参量,KL越小,说明超导腔越不易产生洛伦兹力失谐。
在两端束管端口固定边界条件下,用软件COMSOL Multiphysics计算超导椭球腔的洛伦兹力失谐量随Eacc的变化,如图6所示,拟合曲线计算KL为1.574 Hz/(MV/m)2,当设计工作加速梯度为10 MV/m时,腔体的洛伦兹失谐量为157.4 Hz。
-
改善超导椭球腔的机械强度一般不采用增加腔壁厚度,增加壁厚会影响超导腔体的导热性能[12],而采用在椭球单元之间增加加强环的方案。
-
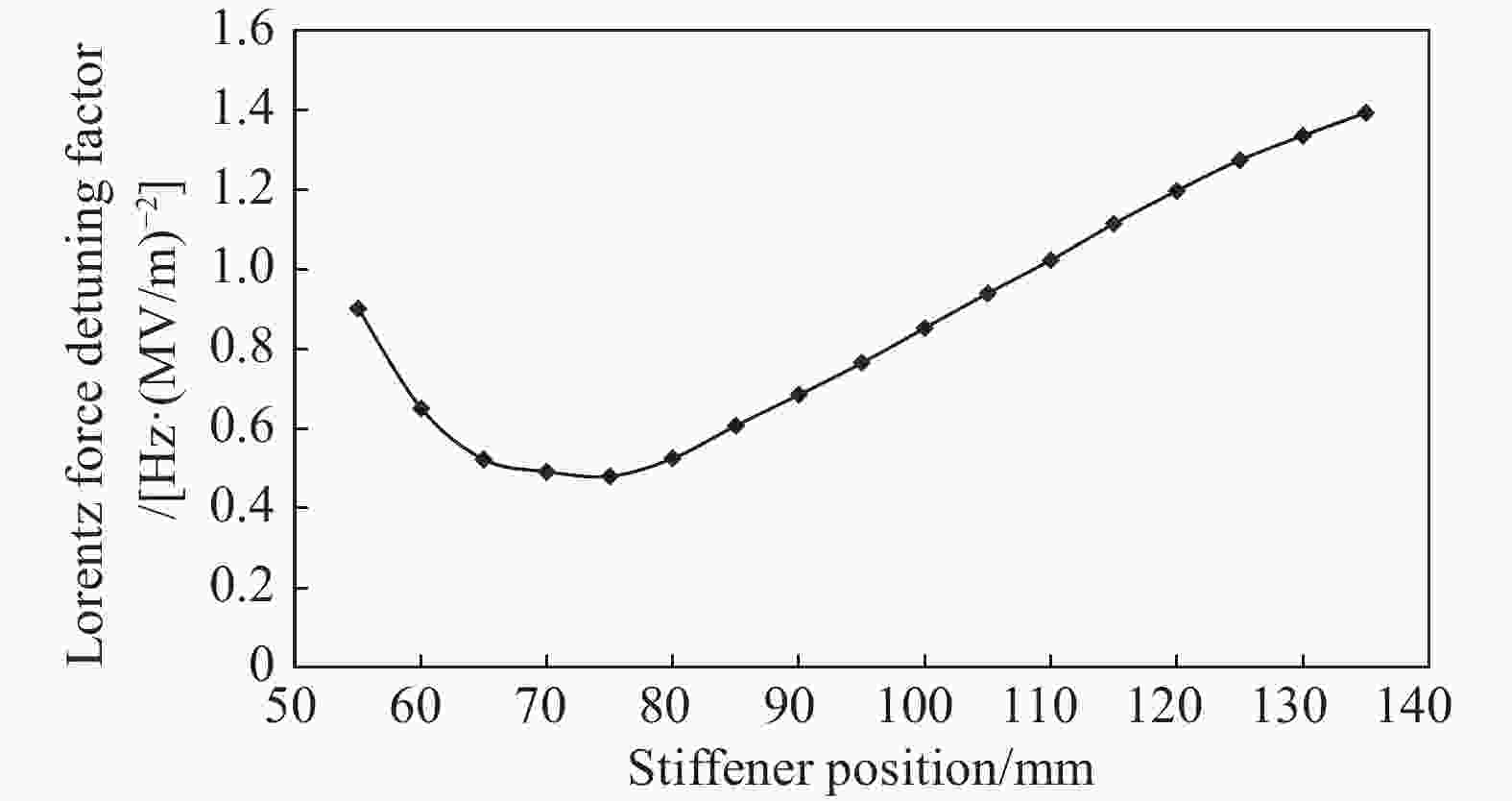
加强环的位置对氦压敏感性系数和洛伦兹失谐因子有较大的影响,在两端固定的边界条件下,使用单加强环方案,仿真计算了[55 mm, 140 mm]区间氦压敏感性系数和洛伦兹失谐因子随加强环位置的变化,如图7和8所示。
加强环位置在110 mm处,氦压波动对腔体失谐影响最小,75 mm处,对洛伦兹失谐抑制最佳,因此,提出采用双加强环方案。75 mm处放置1#加强环抑制洛伦兹失谐,由于1#加强环的存在,2#加强环的位置放在了120 mm处,抑制氦压波动,模型如图9所示,氦压敏感性系数KP=6 Hz/mbar,洛伦兹力失谐因子KL=0.43 Hz/(MV/m)2。
-
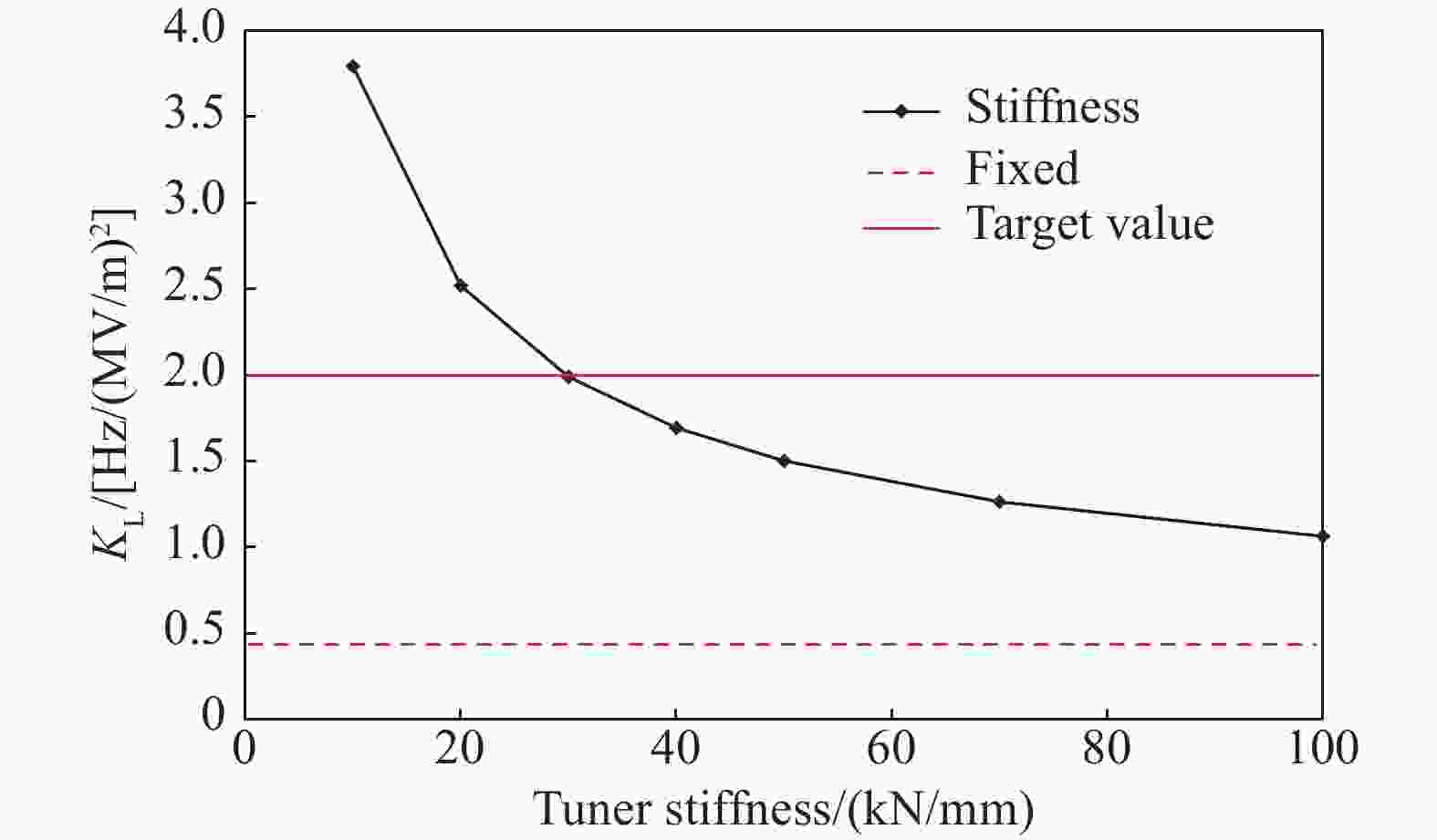
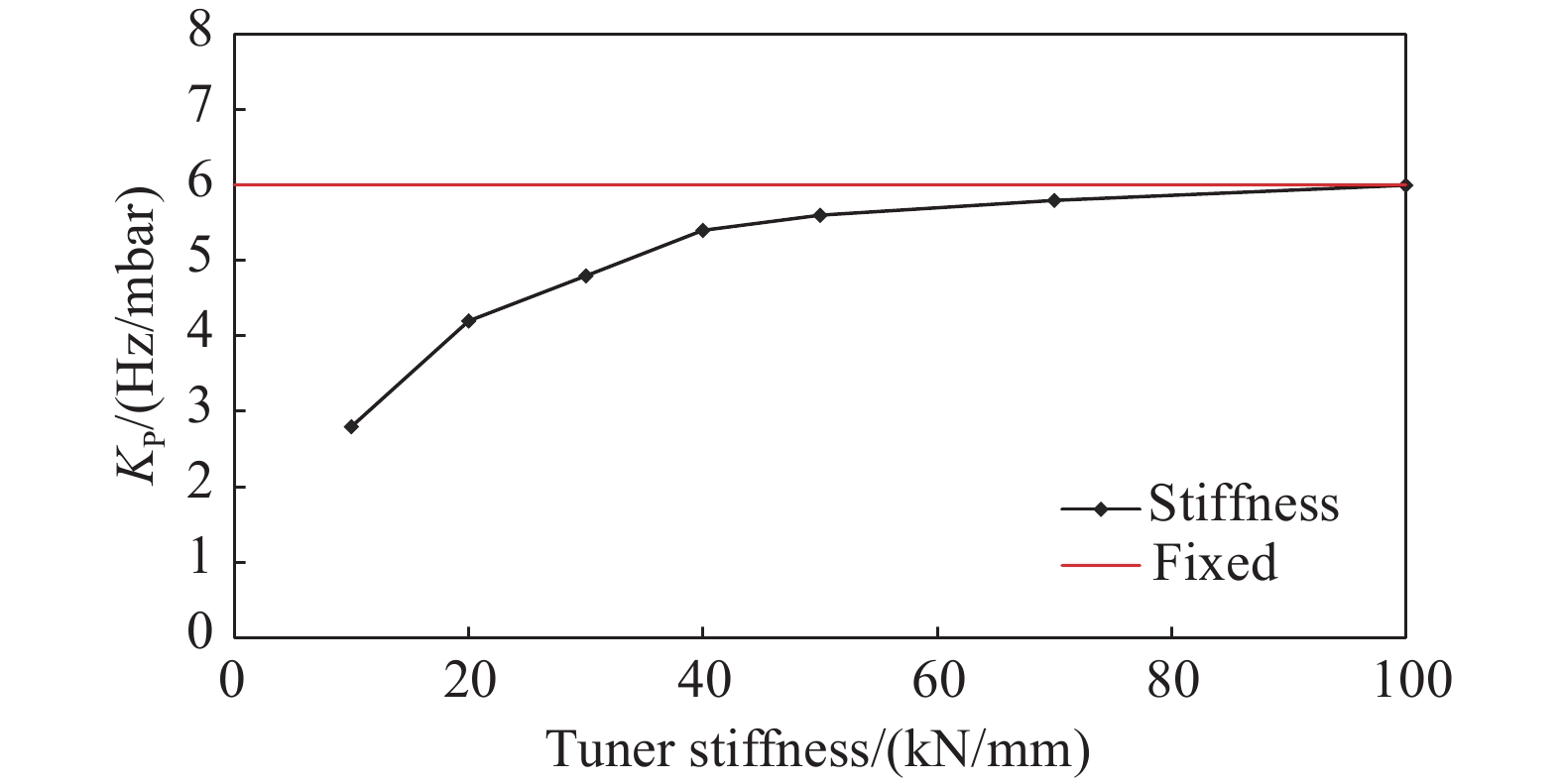
为了更准确地计算出椭球腔的失谐因子及其他机械参数,仿真边界条件引入调谐刚度,一般在调谐端设置30 kN/mm左右的刚度进行计算[13-14]。如图10是洛伦兹力失谐因子随调谐刚度的变化,调谐刚度30 kN/mm时,洛伦兹力失谐因子KL=1.99 Hz/(MV/m)2,满足设计要求。
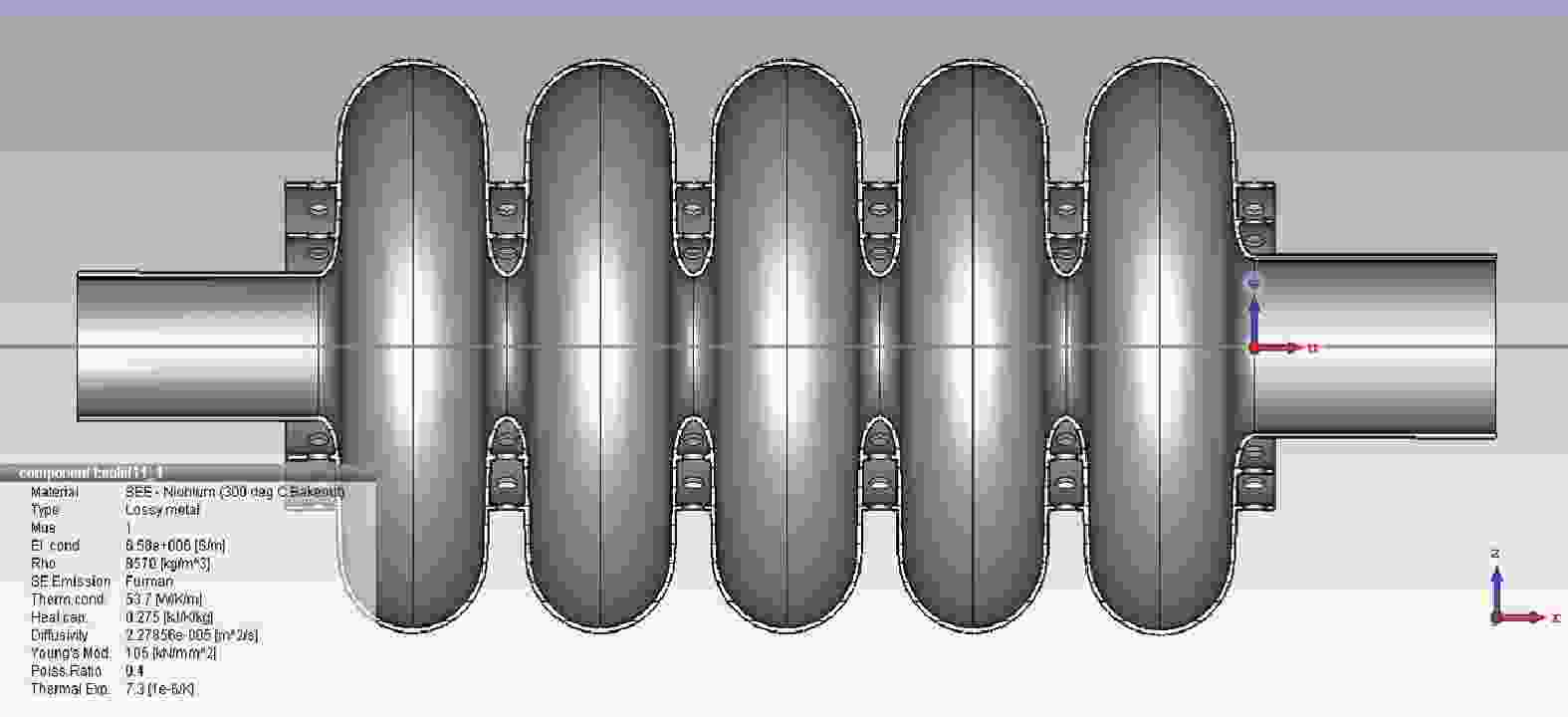
在计算氦压波动时,设计了氦槽模型,如图11所示是氦槽的四分之一计算模型,氦压敏感性系数随调谐刚度的变化如图12所示,调谐刚度30 kN/mm时,氦压敏感性系数KP=4.8 Hz/mbar,满足设计要求。
-
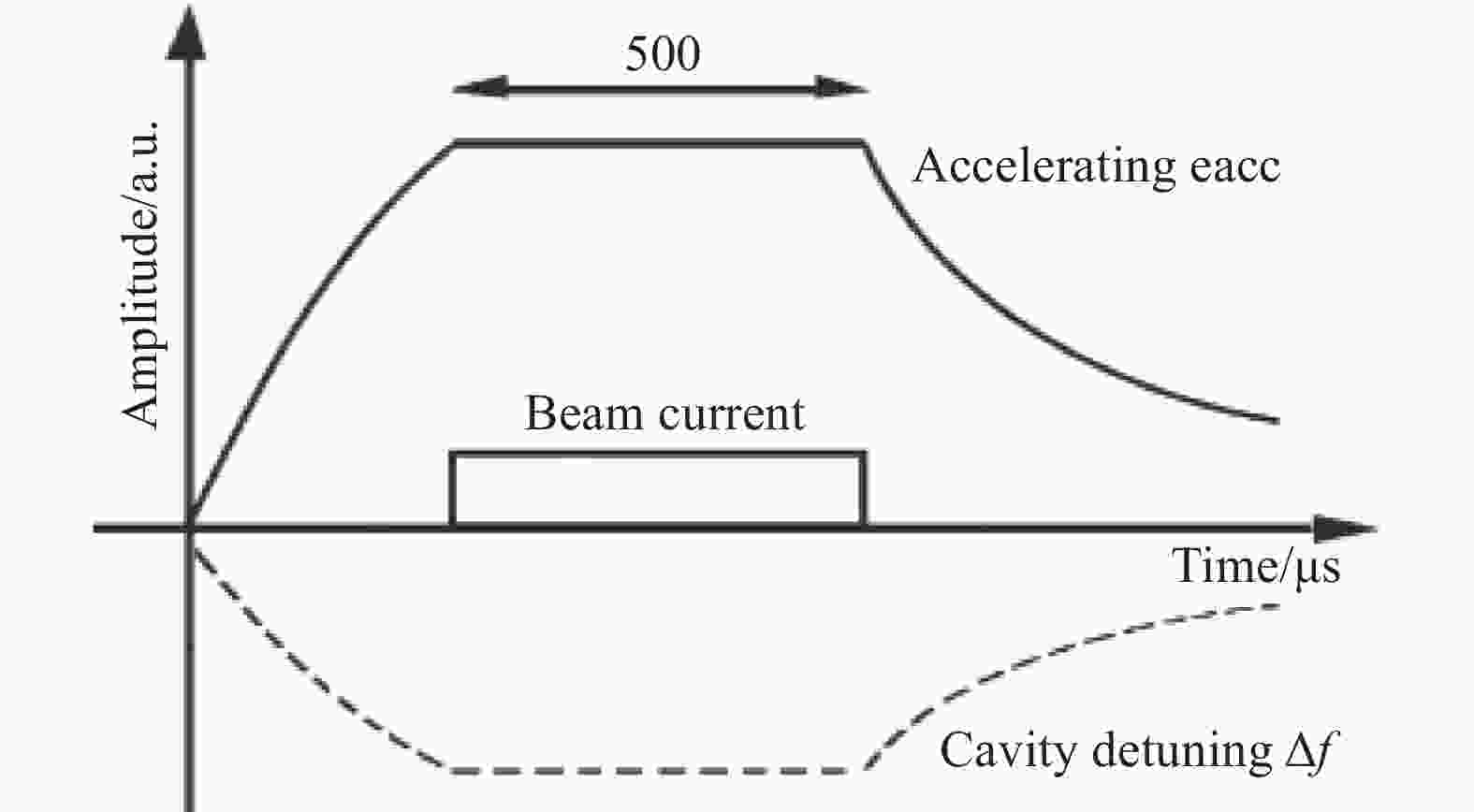
超导椭球腔如果在脉冲模式下工作,受到的是脉冲高频的作用,产生脉冲式动态洛伦兹力失谐[13, 15]。CSNS-II超导椭球腔的RF功率脉冲结构如图13实线所示,设计脉内加速梯度Eacc为10 MV/m,束流脉宽500 μs,相应的RF平顶宽度为500 μs。图13中虚线是RF脉冲激励对应的洛伦兹力失谐量,在脉冲平顶处产生的最大洛伦兹力失谐量为199 Hz,脉冲结束,失谐消失,洛伦兹力失谐是一个与RF脉冲同步的过程,频率为25 Hz。
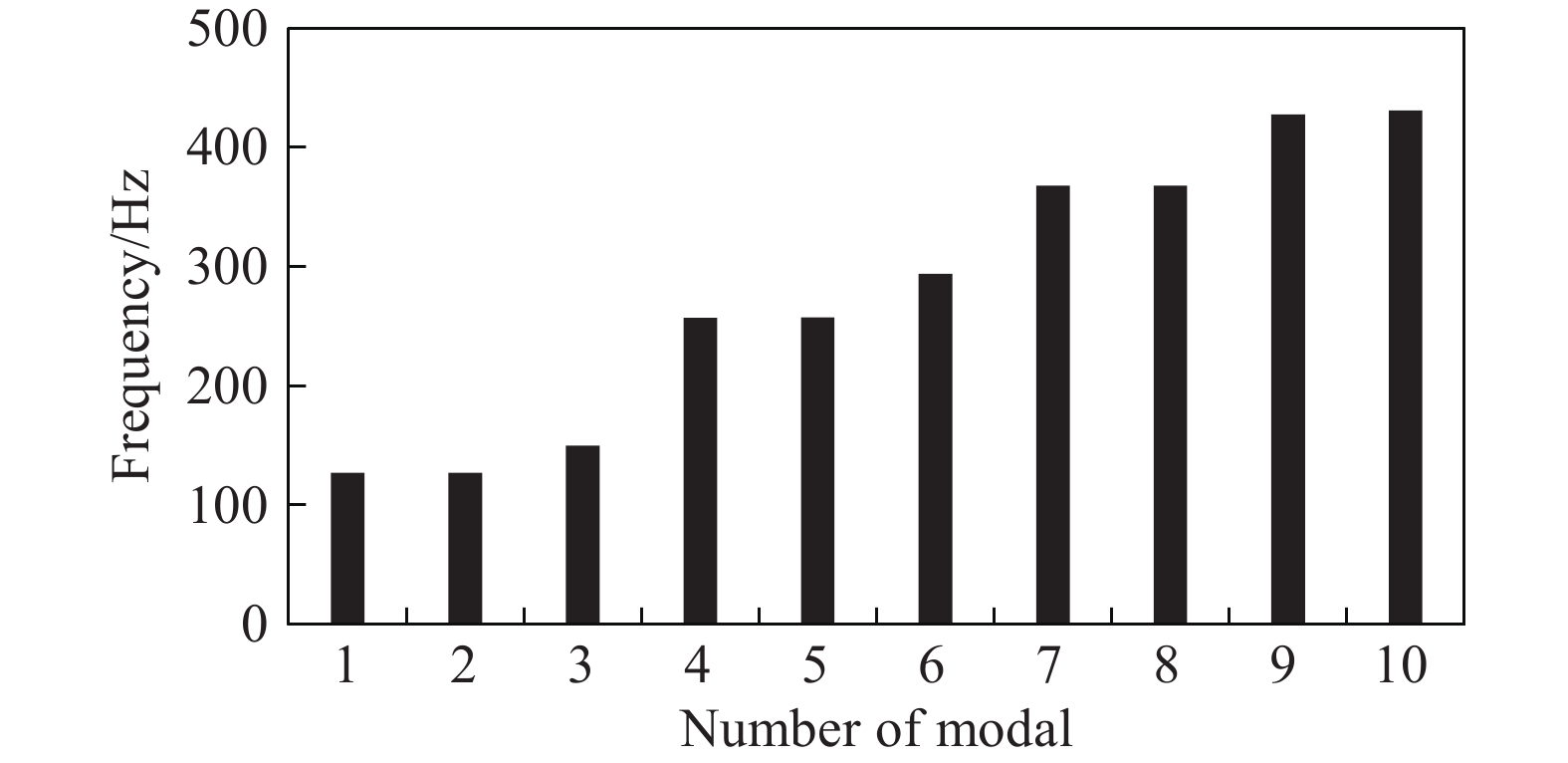
利用Workbench的Modal模块[16],在固定腔体两端的情况下,计算了腔体的10个振动本征频率,如图14所示。腔体的振动本征频率都远高于射频脉冲重复频率25 Hz,不会产生洛伦兹力失谐动态共振。
超导椭球腔动态洛伦兹失谐属于频率的快变化,因此,脉冲模式下运行的超导腔应配有快调谐系统进行调谐,一般采用压电陶瓷的频控环进行调谐,调谐量越小越好实现,本文超导腔加固以后的失谐量为199 Hz,能够达到快调谐的要求。
-
超导椭球腔结构简单,后处理容易,但结构强度偏弱,存在失谐的问题,本文分析了CSNS-II 648MHz βg=0.60 5-cell椭球腔的氦压波动失谐和洛伦兹力失谐,计算了氦压波动敏感性系数KP和洛伦兹失谐因子KL。设计优化了75 mm+120 mm的双加强环结构加固椭球腔,氦压波动敏感性系数KP=4.8 Hz/mbar,洛伦兹力失谐因子KL=1.99 Hz/(MV/m)2,满足要求。另外,初步分析了脉冲工作模式下椭球腔的动态洛伦兹力影响,为CSNS-II椭球腔的研制提供了理论数据支持,下一步还需要对动态洛伦兹失谐及调谐尝试进行仿真分析。
致谢 感谢王云同志在COMSOL Multiphysics软件应用中给予的帮助。
Detuning Analysis of the Superconducting Elliptical Cavity for CSNS-II Linac
-
摘要: 中国散裂中子源二期束流功率升级到500 kW,直线加速器H-的能量增益由现在的80 MeV提高到300 MeV以上,其中150 ~ 300 MeV能量段采用648 MHz βg=0.60的5-cell超导椭球腔结构。超导椭球腔具有加速梯度高、结构简单、后处理容易等优点,缺点是结构强度弱、易失谐。本文主要研究该椭球腔的失谐特性。利用COMSOL Multiphysics软件进行了计算分析,在两端固定边界条件下,裸腔的氦压敏感性系数KP=–45.705 Hz/mbar(1 mbar=100 Pa),洛伦兹力失谐因子KL=1.574 Hz/(MV/m)2。增加加强环并优化其位置来改善氦压敏感性系数和洛伦兹力失谐因子,通过计算分析最终确定选择双加强环方案来减小椭球腔的失谐。两个加强环位置分别取在75和120 mm的位置,腔体失谐的改善最大,KP=6 Hz/mbar,KL=0.43 Hz/(MV/m)2。为了更准确地计算椭球腔的氦压敏感性系数和洛伦兹力失谐因子,本文引入调谐刚度边界条件进行失谐分析,在椭球腔调谐器端设置30 kN/mm边界条件,另一端固定,计算得到氦压敏感性系数为4.8 Hz/mbar,洛伦兹力失谐因子1.99 Hz/(MV/m)2,满足工程要求。另外,用CST软件对椭球腔的动态洛伦兹力失谐进行了初步分析,用软件Workbench计算了椭球腔的振动本征频率,结果显示,振动本征频率离射频脉冲重复频率及环境振动频率较远,不易发生共振失谐。Abstract: China Spallation Neutron Source(CSNS) beam power will upgrade to 500 kW(CSNS-II), energy gain of H- linac will up to 300 MeV from 80 MeV, and the 648 MHz βg=0.6 5-cell superconducting elliptical cavity will be adopted to accelerate the H- from 150 to 300 MeV. Accompanied with the advantage of high accelerating gradient, simple structure, easy post-processing, weak stiffeness and detuning is the shortcoming of elliptical cavity, this study analysis detuning characteristic of the elliptical cavity. With code COMSOL Multiphysics, helium pressure sensitivity coefficient KP and lorentz force detuning factor KL of bare cavity was calculated under two end fixed conditions, KP=–45.705 Hz/mbar(1 mbar=100 Pa) and KL=1.574 Hz/(MV/m)2. Stiffener ring was designed and optimized to reduce the Helium pressure sensitivity coefficient and lorentz force detuning factor, and double ring was chosen to improve the detuning of elliptical cavity at last by vast calculation and analysis, the position of stiffener ring was optimized at 75 and 120 mm under two end fixed boundary, Helium pressure sensitivity coefficient drop down to KP=6 Hz/mbar, lorentz force detuning factor drop down to KL=0.43 Hz/(MV/m)2. Moreover, elastic boundary was used to analyze helium pressure sensitivity coefficient and lorentz force detuning factor, more realistic results were got under tuner end 30 kN/mm boundary and the other end fixed condition, KP=4.8 Hz/mbar and KL=1.99 Hz/(MV/m)2, meet engineering requirements. In addition, dynamic lorentz force detuning was analyzed qualitatively with code CST. And natural frequency of cavity was calculated by code Workbench, results show that nature frequency is far from RF pulse repetition rate and ambient vibration frequency, no resonance happen.
-
表 1 铌材特性
参量 值 杨氏模量/GPa 123 泊松比 0.38 密度/(kg/m3) 8.57×103 壁厚/mm 3.8 -
[1] WANG Sheng, FANG Shouxian, FU Shinian, et al. Chinese Physics C, 2009, 33(s2): 1. doi: 10.1088/1674-1137/33/S2/001 [2] WEI Jie, FU Shinian, TANG Jingyu, et al. Chinese Physics C, 2009, 33(11): 1033. doi: 10.1088/1674-1137/33/11/021 [3] 温良剑. ADS中β强流超导加速腔物理研究[D]. 兰州: 中国科学院近代物理研究所, 2016: 36. WEN Liangjian. Study of Medium Beta High-Current Superconduting Accelerating[D]. Lanzhou: Institute of Modern Physics, Chinese Academy of Sciences, 2016: 36. (in Chinese) [4] 李波, 刘华昌, 王云, 等. 核技术, 2019, 42(8): 080201. doi: 10.11889/j.0253-3219.hjs.42.080210 LI Bo, LIU Huachang, WANG Yun, et al. Nuclear Techniques, 2019, 42(8): 080201. (in Chinese) doi: 10.11889/j.0253-3219.hjs.42.080210 [5] COMSOL学习中心[EB/OL].[2020-01-08]. http://cn.comsol.com/learning-center. [6] 张敏. CST微波工作室用户全书究[M]. 成都: 电子科技大学出版社. 2004: 250. ZHANG Min. CST Microwave Studio Instruction[M]. Chengdu: University of Electronic Science and technology of China Publishing House, 2004: 250. (in Chinese) [7] POSEN S, LIEPE M. Physical Review Special Topics-accelerators and Beams, 2012, 15: 022002. doi: 10.1103/PhysRevSTAB.15.022002 [8] AUNE B, BANDELMANN R, BLOESS D, et al. Phys Rev ST Accel Beams, 2000, 516: 2. doi: 10.1103/PhysRevSTAB.3.092001 [9] KUMAR A, JANA A R, KUMAR V. Nucl Instr and Meth A, 2014, 750: 69. doi: 10.1016/j.nima.2014.03.005 [10] PLEITE E C, AMORIM A, SWIESZEK J S, et al. Numerical Evaluation of the Tuning, Pressure Sensitivity and Lorentz Force Detuning of RF Superconducting Crab Cavities[R]. European Organization for Nuclear Research, Laussane, 2018. [11] SIMROCK S N. Lorentz Force Compensation of Pulsed SRF Cavities[C]. Proceedings of LINAC 2002, 2002: 555. [12] 葛明骐, 赵升初. 高能物理与核物理, 2005, 29(4): 413. doi: 10.3321/j.issn:0254-3052.2005.04.016 GE Mingqi, ZHAO Shengchu. High Energy Physics and Nuclear Physics, 2005, 29(4): 413. (in Chinese) doi: 10.3321/j.issn:0254-3052.2005.04.016 [13] MITCHELL R, MATSUMOTO K, CIOVATI G, et al. Lorentz Force Detuning Analysis of the Spallation Neutron Source(SNS) Accelerating Cavities[C]. Proceedings of the 10th Workshop on RF Superconducty, 200: 236. [14] DEVANZ G, BAZIN N, DESMONS, et al. Ess Elliptical Cavities and Cryomodules[C]. Proceedings of SRF2013, 2013: 1218. [15] CARCAGNO R, BRANLARD J, CHASE B, et al. First Fermilab Results of SRF Cavity Lorentz Force Detuning Compensation Using a Piezo Tuner[C]. Proceedings of SRF2007, 2007: 259. [16] 浦广益. ANSYS Workbench 12 基础教程与实例详解[M]. 北京: 中国水利水电出版社. 2010: 117. PU Guangyi. ANSYS Workbench 12 Basic Courses and Examples[M]. Beijing: China Water & Power Press, 2010: 117.(in Chinese) -





 下载:
下载:










 甘公网安备 62010202000723号
甘公网安备 62010202000723号