-
The high energy hadronic collisions producing the large transverse momentum dileptons play a fundamental role in high energy physics. Since dileptons do not participate in strong interactions, it is relatively easy to probe the dilepton information emitted from the hard scattering[1-2]. The cold dileptons produced from the initial parton collisions can verify the correctness of the standard model and identify the dynamical mechanism in the different stage of the relativistic heavy ion collisions[3].
The PHENIX experiments indecate that the transverse momentum spectra of the dileptons in the Au-Au collisions for the different mass bins are in agreement with the expectation of the cocktail, the charm decays and the direct contributions when the transverse momentum is greater than 1 GeV[4]. However the spectra of the cocktail and the charm decays can not explain the experimental data if the transverse momentum is less than 1 GeV. The semi-coherent photon-photon interaction was considered to be the best theoretical candidate to explain the experimental data at low transverse momentum[5].
Recently, the STAR experiments present new results of the dilepton continuum in Au-Au collisions at low transverse momentum (< 0.15 GeV) of the dilepton pair. The experiments find a large excess at all masses that is particularly clear in the peripheral centrality bin. The coherent photon-photon scattering is proposed as a potential source of this excess[6].
The photon-photon collisions produce only small transverse momentum dileptons. In this paper, we consider the large transverse momentum dileptons produced from the photon-nucleon collisions. In the inelastic nucleon collisions, the high energy photon is emitted from the charged nucleons or partons due to the bremsstrahlung. The dileptons can be produced by the interaction
$ \gamma(\gamma^{*})n\rightarrow l^{+}l^{-} X $ . In the perturbative QCD (pQCD) the transverse momentum of dileptons can arise by the photon-parton hard scattering. If the momentum transfers are large, the calculations of the interactions can be calculated perturbatively. -
The conventional large transverse momentum
$ (P_{\rm T}) $ dilepton can be directly produced by the hard parton scattering in the relativistic heavy ion collisions. The leading order subprocesses are the quark anti-quark annihilation ($ q\bar{q}\rightarrow g l^{+}l^{-} $ ) and Compton processes ($ qg\rightarrow q l^{+}l^{-} $ ). According to the perturbative QCD factorization approach, the cross section of the leading order dileton production$A+B\rightarrow $ $ l^{+}l^{-}+X $ (Fig. 1) can be written as[3]$$\begin{split} \frac{{{\rm{d}}{\sigma _{{\rm{lea}}}}}}{{{\rm{d}}{M^2}{\rm{d}^2}{P_{\rm{T}}}{\rm{d}}y}} =& \displaystyle\int_{x_a^{\min }}^1 {{\rm{d}}{x_a}} {f_{a/A}}({x_a},{Q^2}){f_{b/B}}({x_b},{Q^2}) \times \\ &\frac{{{x_a}{x_b}}}{{{x_a} - {x_1}}}\frac{{{\rm{d}}\hat \sigma }}{{{\rm{d}}{M^2}{\rm{d}}\hat t}}(ab \to {l^ + }{l^ - }d), \end{split}$$ (1) where
$ {\rm d}\hat{\sigma}/{\rm d}M^{2}{\rm d}\hat{t} $ are the cross section of the subprocesses of parton collisions, and$$\begin{split} \frac{{{\rm{d}}\hat \sigma }}{{{\rm{d}}{M^2}{\rm{d}}\hat t}}(ab \to {l^ + }{l^ - }d) =& \frac{\alpha }{{3\pi {M^2}}}\sqrt {1 - \frac{{4m_l^2}}{{{M^2}}}} \left( {1 + \frac{{2m_l^2}}{{{M^2}}}} \right) \times \\ &\frac{{{\rm{d}}\hat \sigma }}{{{\rm{d}}\hat t}}(ab \to {\gamma ^*}d,\hat s,\hat u,\hat t),\\[-15pt] \end{split}$$ (2) where
$ \alpha $ is the QED coupling constant,$ M $ is the invariant mass of the dilepton pair and$ m_{\rm l} $ is the lepton mass. These subprocesses are given by the leading order QCD calculations of the interactions$ q\bar{q}\rightarrow g \gamma^{*} $ and$ qg\rightarrow q \gamma^{*} $ [7].The Mandelstam variables of these subprocesses are
$ \hat{s} = x_{a}x_{b}s $ ,$ \hat{u} = M^{2}-sx_{b}x_{1} $ and$ \hat{t} = M^{2}-sx_{a}x_{2} $ . The momentum fractions of the parton$ a $ and$ b $ of the nucleons$ A $ and$ B $ are defined as$ x_{a}^{\min} = (x_{1}-\tau)/ $ $(1-x_{2}) $ and$ x_{b} = (x_{a}x_{2}-\tau)/(x_{a}-x_{1}) $ , where$ \tau = M^{2}/ $ s,$ x_{1} = (P_{\rm T}^{2}+M^{2})^{1/2}{\rm e}^{y}/\sqrt{s} $ and$ x_{2} = (P_{\rm T}^{2}+M^{2})^{1/2}{\rm e}^{-y}/ $ $\sqrt{s} $ .$ \sqrt{s} $ is the center-of-mass energy of the colliding nucleons.The parton distribution function
$ f_{a/A}(x,Q^{2}) $ including the iso-spin effect of the nucleon is in the form$${f_{a/A}}(x,{Q^2}) \!=\! R(x,{Q^2},A)\!\left[ {\frac{Z}{A}p(x,{Q^2}) \!\!+\!\! \frac{{A \!-\! Z}}{A}n(x,{Q^2})} \right],$$ (3) where
$ R(x,Q^{2},A) $ is the nuclear modification factor[8],$ Z $ is the proton number of the nucleus and$ A $ is the nucleon number.$ p(x,Q^{2}) $ is the proton's parton distribution function, and$ n(x,Q^{2}) $ is the neutron's parton distribution function[9]. The scale of the transverse momentum is$ P_{\rm T}^{2} = Q^{2} $ .In the hard parton scattering, the final states
$ c $ of hard parton collisions$ ab\rightarrow cd $ can smash into dileptons by using the Born approximation of the virtual photon bremsstrahlung$ c\rightarrow c \gamma^{*} $ ($ \gamma^{*}\rightarrow l^{+}l^{-} $ )(Fig. 1). The cross section of the fragmentation dileptons is$$\begin{split} \frac{{{\rm{d}}{\sigma _{{\rm{fra}}}}}}{{{\rm{d}}{M^2}{\rm{d}^2}{P_{\rm{T}}}{\rm{d}}y}} =& \displaystyle\int_{x_a^{\min }}^1 {{\rm{d}}{x_a}} \int_{x_b^{\min }}^1 {{\rm{d}}{x_b}} {f_{a/A}}({x_a},{Q^2}) \times \\ &{f_{b/B}}({x_b},{Q^2})\frac{{{\rm{d}}\hat \sigma }}{{{\rm{d}}\hat t}}(ab \to cd) \times \\ &\frac{1}{{{z_c}}}{D_{{l^ + }{l^ - }/c}}({z_c},{Q^2}), \end{split}$$ (4) where the momentum fractions are
$ x_{a}^{\min} = x_{1}/(1-x_{2}) $ ,$ x_{b}^{\min} = x_{a}x_{2}/(x_{a}-x_{1}) $ and$ z_{c} = (x_{a}x_{2}+x_{b}x_{1})/x_{a}x_{b} $ . The cross sections$ {\rm d}\hat{\sigma}/{\rm d}\hat{t}(ab\rightarrow cd,\hat{s},\hat{u},\hat{t}) $ of the subprocesses of the hard parton collisions ($ qq'\rightarrow qq' $ ,$ q\bar{q}'\rightarrow q\bar{q}' $ ,$ qq\rightarrow qq $ ,$ q\bar{q}\rightarrow q'\bar{q}' $ ,$ q\bar{q}\rightarrow q\bar{q} $ ,$ gg\rightarrow q\bar{q} $ ,$ qg\rightarrow qg $ ,$ q\bar{q}\rightarrow gg $ and$ gg\rightarrow gg $ ) can be found in Ref. [7]. Here the Mandelstam variables are$ \hat{s} = x_{a}x_{b}s $ ,$ \hat{u} = -sx_{b}x_{1}/z_{c} $ and$ \hat{t} = -sx_{a}x_{2}/z_{c} $ . The full QCD evolution of the dilepton fragmentation function$ D_{l^{+}l^{-}/c}(z_{c},Q^{2}) $ of quarks and gluons is studied in Ref. [10]. -
The electron-proton deep inelastic scattering at HERA reveals the parton structure of the photon and the nucleon. Since the leading order
$ \gamma n\rightarrow X $ is the QED processes, the photon-nucleon collisions play an important role at HERA[11-12]. However, leading dilepton production from the central heavy ion collisions is in the order of$ \alpha\alpha_{s} $ , the photoproduction processes is in the order of$ \alpha^{2}\alpha_{s} $ . The QED coupling constant reduces the contribution of the photon-nucleon collisions in the central heavy ion collisions[13-14].In the peripheral heavy ion collisions, the average number of binary nucleon-nucleon collisions
$ (\langle N_{\mathrm{coll}}\rangle $ ) of the leading QCD processes is decreased. However, because of the electromagnetic interaction is a kind of the long range interaction, all of the nucleons in the ion can participate in the photon-nucleon collisions. In the overlap area of the two colliding ions, high energy photons are emitted from the charged partons in the nucleon due to the inelastic scattering of nucleons. In the non-overlap area the photons emitted from the protons of the ion. -
In the Weizsäcker-Williams approximation (WWA), the electromagnetic field emitted from the high energy charged nucleon A may be treated as a flux of nearly-real photons[15-16]. The cross section of dileptons produced from the interaction of high energy photon
$ \gamma $ and the nucleon$ B $ (Fig. 2) is given by the following
Figure 2. The sketches of the dilepton production from the photon-nucleon and resolved photon-nucleon collisions.
$$\begin{split} \frac{{{\rm{d}}\sigma _{\gamma - {\rm{nucl}}}^{{\rm{proton}}}}}{{{\rm{d}}{M^2}{\rm{d}^2}{P_{\rm{T}}}{\rm{d}}y}} =& \displaystyle\int_{{z_{\min }}}^1 {{\rm{d}}z} {F_{\gamma /A}}(z){f_{b/B}}({x_b},{Q^2})\frac{{z{x_b}}}{{z - {x_1}}} \times \\ &\frac{{{\rm{d}}\hat \sigma }}{{{\rm{d}}{M^2}{\rm{d}}\hat t}}(\gamma b \to {l^ + }{l^ - }d),\\[-15pt] \end{split}$$ (5) where
$ F_{\gamma/A} $ is the photon distribution function from the proton, and we have,$$\begin{split} {F_{\gamma /A}}(z) =& \frac{\alpha }{{2\pi }}\left[\frac{{1 + {{(1 - z)}^2}}}{z}\ln \frac{{P_{\max }^2}}{{P_{\min }^2}} - \right.\\ &2m_{\rm p}^2z\left.\left(\frac{1}{{P_{\min }^2}} - \frac{1}{{P_{\max }^2}}\right)\right], \end{split}$$ (6) where
$ z $ denotes the fraction of the proton energy taken by the photon. The kinematic limits are$ P^{2}_{\max} = z^{2}s/4 $ and$ P^{2}_{\min} = m^{2}_{\rm p}z^{2}/(1-z) $ ,$ m_{\rm p} $ is the mass of proton. The momentum fractions are defined as$ z_{\min} = (x_{1}-\tau)/(1-x_{2}) $ and$ x_{b} = (zx_{2}-\tau)/(z-x_{1}) $ .In the subprocesses of the photon-nucleon collisions, the real photon emitted from the charged nucleon
$ A $ interacts with the parton$ b $ of nucleon$ B $ by the QED Compton process$ q\gamma\rightarrow q\gamma^{*} $ . The Mandelstam variables of the subprocesses$ {\rm d}\hat{\sigma}/{\rm d}\hat{t} $ $(\gamma b\!\rightarrow\!\! \gamma^{*}d,\hat{s},\hat{u},\hat{t}) $ are$ \hat{s} = zx_{b}s $ ,$ \hat{u} = M^{2}-sx_{b}x_{1} $ and$ \hat{t} = M^{2}-szx_{2} $ . One can find the cross sections of subprocess of$ q\gamma\rightarrow q\gamma^{*} $ in the Ref. [7].The Heisenberg's uncertainty principle allows the flux of the high energy photons to fluctuate into a quark-antiquark pairs. In such interactions, the photons emitted from the charged nucleons can be regarded as an extended object consisting of quarks and also gluons. These photons are the so-called resolved photons[11-12]. In the factorization approach, the structure of the resolved photon can be defined by the photon parton distribution function. In stead of the QED subprocess(
$ q\gamma\rightarrow q\gamma^{*} $ ) of the real photon-nucleon collisions, the subprocesses of the resolved photon-nucleon collisions are the hard parton scattering$( q\bar{q}\rightarrow g \gamma^{*} $ and$ qg\rightarrow q \gamma^{*} $ ).The cross section of dileptons from the resolved photon-nucleon collisions (Fig. 2) can be written in the form
$$\begin{split} \frac{{{\rm{d}}\sigma _{{\rm{res}}\gamma - {\rm{nucl}}}^{{\rm{proton}}}}}{{{\rm{d}}{M^2}{{\rm d}^2}{P_{\rm{T}}}{\rm{d}}y}} = &\displaystyle\int_{{z_{\min }}}^1 {{\rm{d}}z} \int_{x_{a'}^{\min }}^1 {{\rm{d}}{x_{a'}}} {F_{\gamma /A}}(z){f_{a'/\gamma }}({x_{a'}},{Q^2}) \times \\ &{f_{b/B}}({x_b},{Q^2})\frac{{z{x_{a'}}{x_b}}}{{z{x_{a'}} - {x_1}}}\times \\ &\frac{{{\rm{d}}\hat \sigma }}{{{\rm{d}}{M^2}{\rm{d}}\hat t}}(a'b \to {l^ + }{l^ - }d),\\[-15pt] \end{split}$$ (7) where
$ f_{a'/\gamma}(z_{a'},Q^{2}) $ is the parton distribution function of the resolved photon[17]. The momentum fractions are$ z_{\min} = (x_{1}-\tau)/(1-x_{2}) $ and$ x_{a'}^{\min} = (x_{1}-\tau)/ $ $z(1-x_{2}) $ .The Mandelstam variables of the cross sections
$ {\rm d}\hat{\sigma}/{\rm d}\hat{t}(a'b\rightarrow \!\!\gamma^{*}d,\hat{s},\hat{u},\hat{t}) $ are$ \hat{s} = zx_{a'}x_{b}s $ ,$\hat{u} = M^{2}- $ $ sx_{b}x_{1} $ and$ \hat{t} = M^{2}-szx_{a'}x_{2} $ . In the subprocesses$ a'b\rightarrow \!\!\gamma^{*}d $ of the resolved photon-nucleon collisions, the parton$ a'( = q,g) $ is from the resolved photon. The hard scattering of parton$ a' $ and$ b $ are the quark anti-quark annihilation ($ q\bar{q}\rightarrow g \gamma^{*} $ ) and QCD Compton$( qg\rightarrow q \gamma^{*} )$ processes. -
In the inelastic nucleon-nucleon collisions, high energy photons can be emitted from the charged partons. The cross section of dileptons produced from the interaction of high energy photon
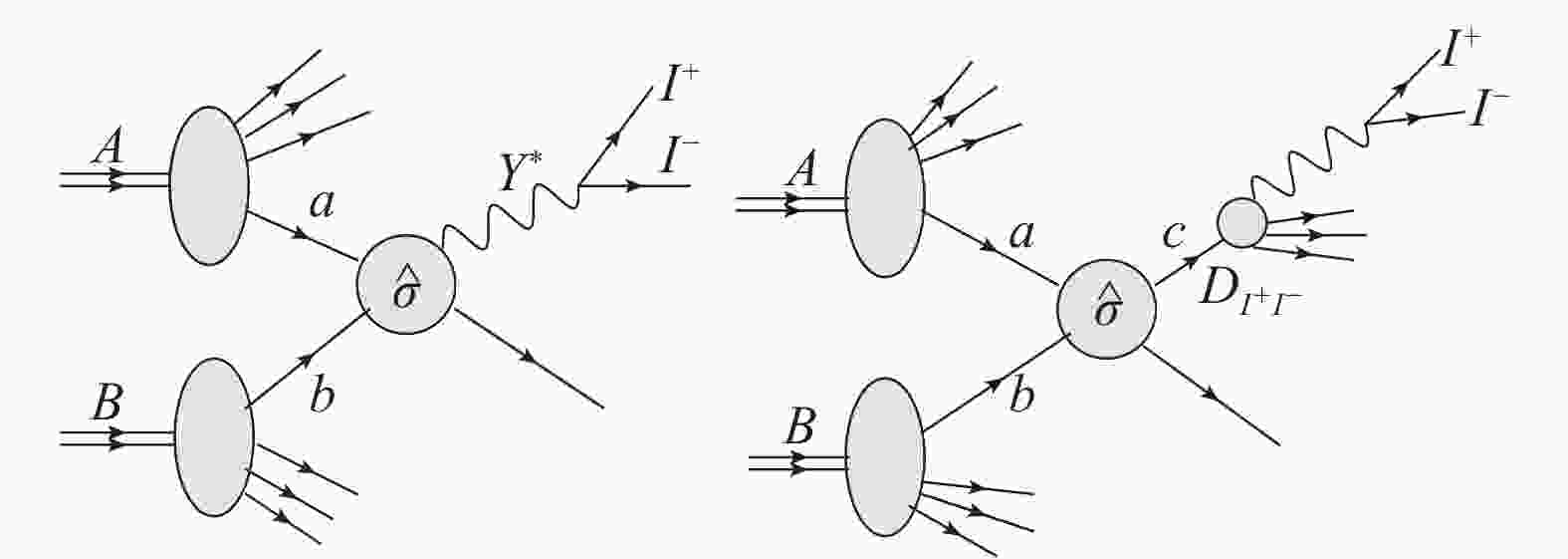
$ \gamma $ and the nucleon$ B $ (Fig. 3) is given by the following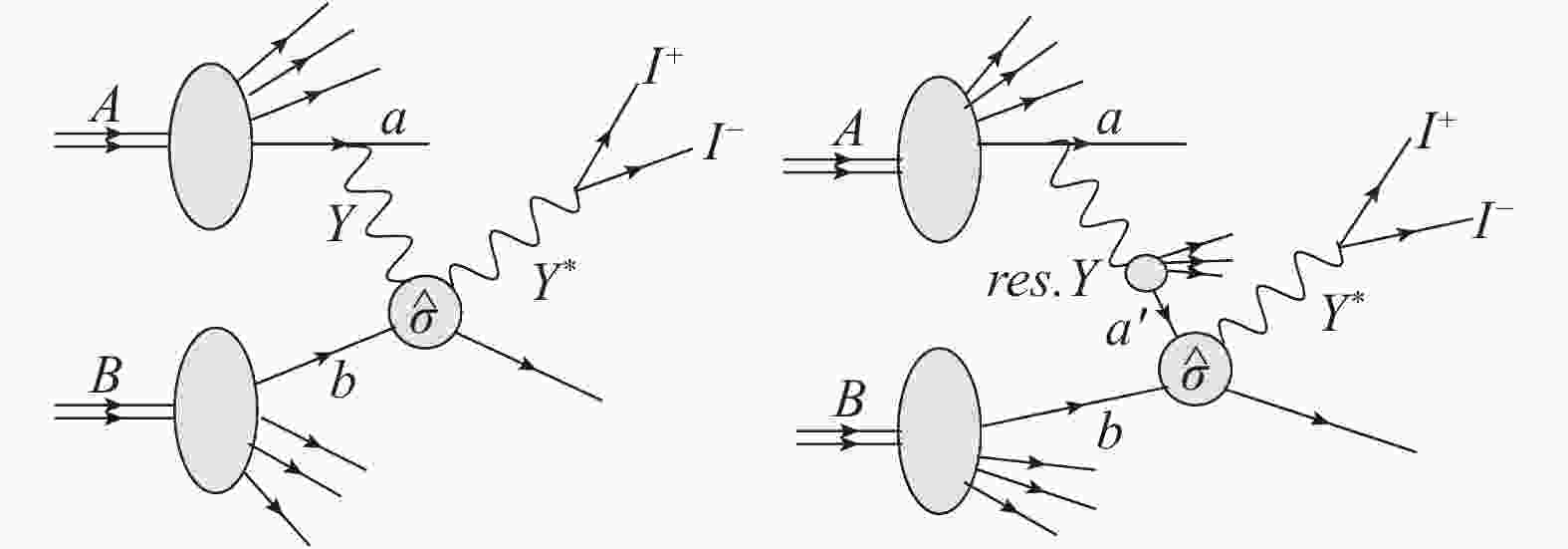
Figure 3. The sketches of the photon and resolved photon-nucleon collisions, but the photons is from the charged partons.
$$\begin{split} \frac{{{\rm{d}}\sigma _{\gamma - {\rm{nucl}}}^{{\rm{parton}}}}}{{{\rm{d}}{M^2}{\rm{d}^2}{P_{\rm{T}}}{\rm{d}}y}} =& \frac{2}{\pi }\int_{x_a^{\min }}^1 {{\rm{d}}{x_a}} \int_{x_b^{\min }}^1 {{\rm{d}}{x_b}} {f_{a/A}}({x_a},{Q^2}) \times \\ &{F_{\gamma /a}}({x_a},{z_a}){f_{b/B}}({x_b},{Q^2}) \times \\ &\frac{{{x_a}{x_b}{z_a}}}{{{x_a}{x_b} - {x_a}{x_2}}}\frac{{{\rm{d}}\hat \sigma }}{{{\rm{d}}{M^2}{\rm{d}}\hat t}}(\gamma b \to {l^ + }{l^ - }d), \end{split}$$ (8) where the photon distribution function from the charged parton in the nucleon is
$$\begin{split} {F_{\gamma /a}}({x_a},{z_a}) =& \frac{{\alpha e_a^2}}{{2\pi }}\left[\frac{{1 + {{(1 - {z_a})}^2}}}{{{z_a}}}\ln \frac{{P_{\max }^2}}{{P_{\min }^2}} -\right. \\ &2m_a^2{z_a}\left.\left(\frac{1}{{P_{\min }^2}} - \frac{1}{{P_{\max }^2}}\right)\right], \end{split}$$ (9) where
$ e_{a} $ is the charge of the charged parton, here the kinematic limits are$ P^{2}_{\max} = (x_{a}z_{a})^{2}s/4 $ and$ P^{2}_{\min} = m^{2}_{a}z_{a}^{2}/(1-z_{a}) $ ,$ m_{a} $ is the mass of the quark. The momentum fractions are defined as$ x_{a}^{\min} = (x_{1}-\tau)/(1-x_{2}) $ ,$ x_{b}^{\min} = (x_{a}x_{2}-\tau)/(x_{a}-x_{1}) $ and$ z_{a} = (x_{b}x_{1}-\tau)/(x_{a}x_{b}-x_{a}x_{2}) $ . The Mandelstam variables of the subprocesses$ {\rm d}\hat{\sigma}/{\rm d}\hat{t}(\gamma b\!\rightarrow\!\! \gamma^{*}d,\hat{s},\hat{u},\hat{t}) $ are$ \hat{s} \!=\! x_{a}x_{b}z_{a}s $ ,$ \hat{u} \!=\! M^{2}\!-\!sx_{b}x_{1} $ and$ \hat{t}\! =\! M^{2}\!-\!sx_{a}x_{2}z_{a} $ .The cross section of dileptons from the resolved photon-nucleon collisions (Fig. 3) can be written in the form
$$\begin{split} \frac{{{\rm{d}}\sigma _{{\rm{res}}\gamma - {\rm{nucl}}}^{{\rm{parton}}}}}{{{\rm{d}}{M^2}{\rm{d}^2}{P_{\rm{T}}}{\rm{d}}y}}\! =\! & \frac{2}{\pi }\!\displaystyle\int_{x_a^{\min }}^1\! {{\rm{d}}{x_a}} \!\int_{x_b^{\min }}^1 \!{{\rm{d}}{x_b}} \!\int_{z_{a'}^{\min }}^1 \!{{\rm{d}}{z_{a'}}} {f_{a\!/\!A}}({x_a},{Q^2}) \times \\ &{F_{\gamma /a}}({x_a},{z_a}){f_{a'/\gamma }}({z_{a'}},{Q^2}){f_{b/B}}({x_b},{Q^2}) \times \\ &\frac{{{x_a}{x_b}{z_a}{z_{a'}}}}{{{x_a}{x_b}{z_{a'}} - {x_a}{z_{a'}}{x_2}}}\frac{{{\rm{d}}\hat \sigma }}{{{\rm{d}}{M^2}{\rm{d}}\hat t}}(a'b \to {l^ + }{l^ - }d), \end{split}$$ (10) where the momentum fractions are
$ x_{a}^{\min} = (x_{1}-\tau)/ $ $(1-x_{2}) $ and$ x_{b}^{\min} = (x_{a}x_{2}-\tau)/(x_{a}-x_{1}) $ ,$ z_{a'}^{\min} = $ $ (x_{b}x_{1}-\tau)/(x_{a}x_{b}-x_{a}x_{2}) $ and$ z_{a} = (x_{b}x_{1}-\tau)/(x_{a}x_{b}z_{a'}- $ $x_{a}z_{a'}x_{2}) $ . The Mandelstam variables of the cross sections$ {\rm{d}}\hat{\sigma}/{\rm{d}}\hat{t}(a'b\rightarrow \!\!\gamma^{*}d,\hat{s},\hat{u},\hat{t}) $ are$ \hat{s} = x_{a}x_{b}z_{a}z_{a'}s $ ,$ \hat{u} = M^{2}-sx_{b}x_{1} $ and$ \hat{t} = M^{2}-sx_{a}x_{2}z_{a}z_{a'} $ . -
The production yield of dileptons can be scaling by the total cross section of the inelastic nucleon-nucleon collisions
$ \sigma_{\mathrm{inel}}^{\rm nn} $ and the average number of binary nucleon-nucleon collisions$ \langle N_{\mathrm{coll}}\rangle $ in the form$$\frac{{{\rm{d}}N}}{{{\rm{d}}{M^2}{\rm{d}^2}{P_{\rm{T}}}{\rm{d}}y}} = \frac{{\langle {N_{{\rm{coll}}}}\rangle }}{{\sigma _{{\rm{inel}}}^{{\rm{nn}}}}}\frac{{{\rm{d}}\sigma }}{{{\rm{d}}{M^2}{\rm{d}^2}{P_{\rm{T}}}{\rm{d}}y}},$$ (11) in this paper we discuss the 20%~40% centrality collsions. In the overlap area of the colliding ions, the component of partons inside the nucleons is important, the WWA photon is from the charged parton(Eq. (9)). The binary nucleon-nucleon collision numbers are
${\langle {N_{{\rm{coll}}}}\rangle _{20\% \sim 40\% }}$ = 297 at RHIC[18] and 438 at LHC[19]. We use$ \sigma_{\mathrm{inel}}^{nn} $ = 40 mb at RHIC[20] and 72 mb at LHC[20]. In the non-overlap area, there is no parton scattering of the nucleons, the interaction of nucleons is photon-nucleon inelastic scattering. Here the WWA photon is emitted from the proton(Eq. (6)), the corresponding binary nucleon-nucleon collision numbers are${\langle {N_{{\rm{coll}}}}\rangle _{b = 0}} - {\langle {N_{{\rm{coll}}}}\rangle _{20\% \sim 40\% }}$ , where$ \langle N_{\mathrm{coll}}\rangle_{b = 0} $ = 975 at RHIC and 1670 at LHC[20]. Finally, the production yield of photon-nucleon collisions can be expressed as$$\begin{split} &\frac{{{\rm{d}}{N_{\gamma - {\rm{nucl}}}}}}{{{\rm{d}}{M^2}{\rm{d}^2}{P_{\rm{T}}}{\rm{d}}y}} = \frac{{{{\langle {N_{{\rm{coll}}}}\rangle }_{20\% \sim 40\% }}}}{{\sigma _{{\rm{inel}}}^{{\rm{nn}}}}}\frac{{{\rm{d}}\sigma _{\gamma - {\rm{nucl}}}^{{\rm{parton}}}}}{{{\rm{d}}{M^2}{\rm{d}^2}{P_{\rm{T}}}{\rm{d}}y}} + \\ &\frac{{{{\langle {N_{{\rm{coll}}}}\rangle }_{b = 0}} - {{\langle {N_{{\rm{coll}}}}\rangle }_{20\% \sim 40\% }}}}{{\sigma _{{\rm{inel}}}^{{\rm{nn}}}}}\frac{{{\rm{d}}\sigma _{\gamma - {\rm{nucl}}}^{{\rm{proton}}}}}{{{\rm{d}}{M^2}{\rm{d}^2}{P_{\rm{T}}}{\rm{d}}y}}, \end{split}$$ (12) we have taken into account the effective proton number of Eq. (6) as
$ Z/A $ in this calculation. The calculation of resolved photon-nucleon collisions is similar to the above formula.In Figs. 4 and 5 we plot the large
$ P_{\rm T} $ distribution of the dileptons produced from the photon-nucleon collisions at RHIC and LHC energies. In order to avoid the influence of dilepton decays of the narrow vector mesons such as$ \phi $ and$ \omega $ , we choose the invariant mass of the dilepton pair as$ M $ = 500 MeV. The numerical results show that the resolved photon-nucleon collisions is more important than the real photon-nucleon collisions. In Eq. (5) and (8) the subprocesses$ q\gamma \rightarrow q\gamma^{*} $ is the QED interaction, and the coupling constant is$ \alpha^{2} $ . The coupling constants of the QCD subprocesses$ q\bar{q}\rightarrow g\gamma^{*} $ and$ qg \rightarrow q\gamma^{*} $ in Eq. (7) and (10) are$ \alpha \alpha_{s} $ . Since$ \alpha_{s}>\alpha $ the QCD subprocesses is more prominent in the photon-nucleon collisions.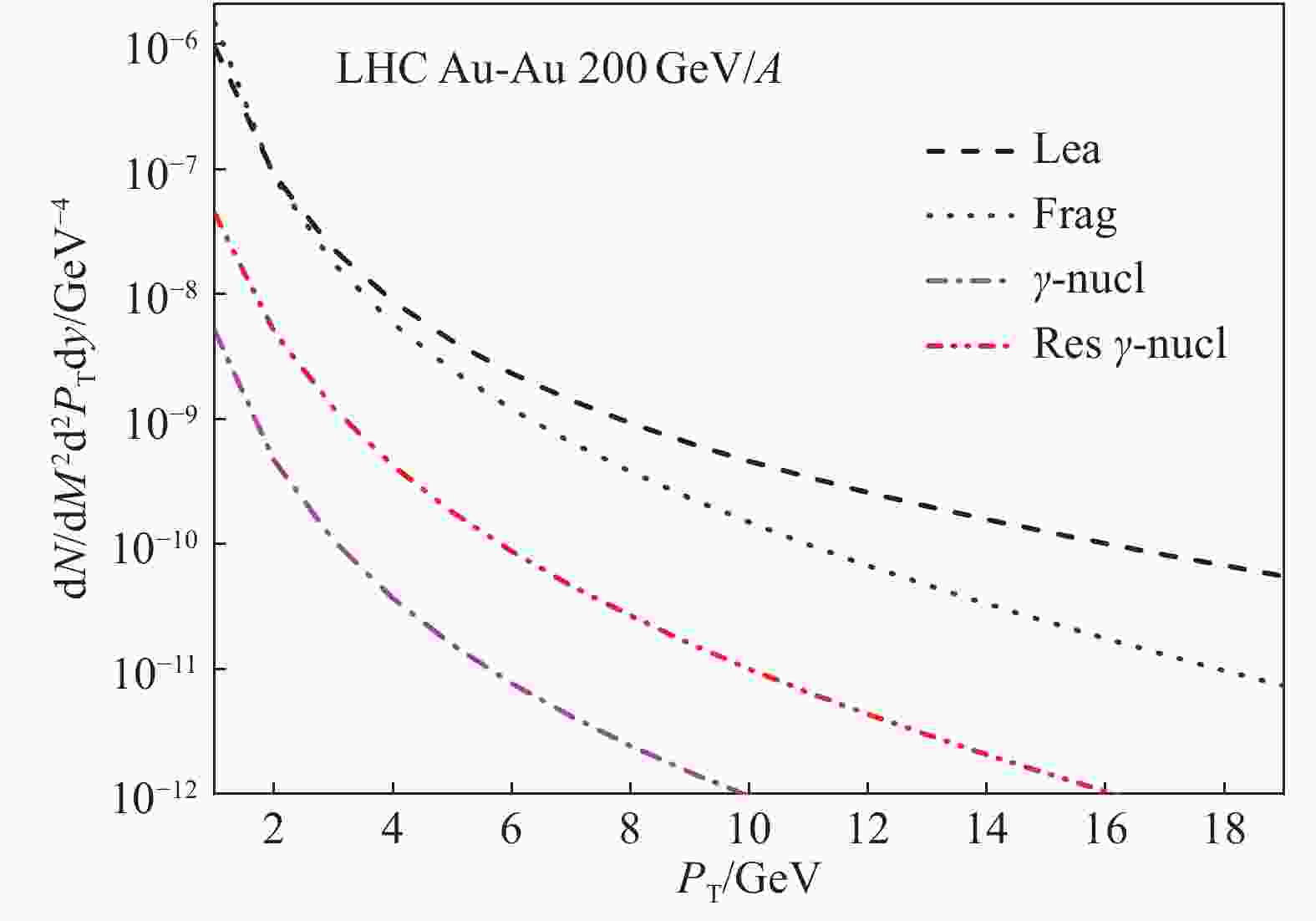
Figure 4. (color online)The large transverse momentum dilepton spectra in the Au-Au collisoins for
$\sqrt{s}$ = 200 GeV, M = 500 MeV and$y$ = 0. The dash line and dot line denote the leading and fragmentation dilepton production, respectively. The dileptons produced from the real photon-nucleon collisions (dash-dot line) and resolve photon-nucleon collisions (dash-dot-dot line) are also shown.
Figure 5. (color online)The large transverse momentum dilepton spectra in the Pb-Pb collisions for
$\sqrt{s}$ = 5.5 TeV, M = 500 MeV and$y$ = 0.The spectra of the photon-nucleon collisions is at least one order of magnitude less than the leading and fragmentation processes (Fig. 4) at RHIC. The role of the photon-nucleon collision is negligible in Au-Au 200 GeV/
$ A $ collisions at RHIC. In Fig. 5 we plot the large transverse momentum dilepton distribution for the mass bins 300 MeV$ <M< $ 500 MeV and 500 MeV$ <M< $ 750 MeV. The solid line denotes the sum of the hadronic decays and the contribution of leading and fragmentation dilepton production. The results of the hadronic decay cocktail and charmed meson decay are from Ref. [4]. The numerical results agree with the experimental data, the contribution of the photon-nucleon collisions is indeed negligible at RHIC energies. The transverse momentum spectra of dileptons for a mass bin in Fig. 6 can be calculated by the integral: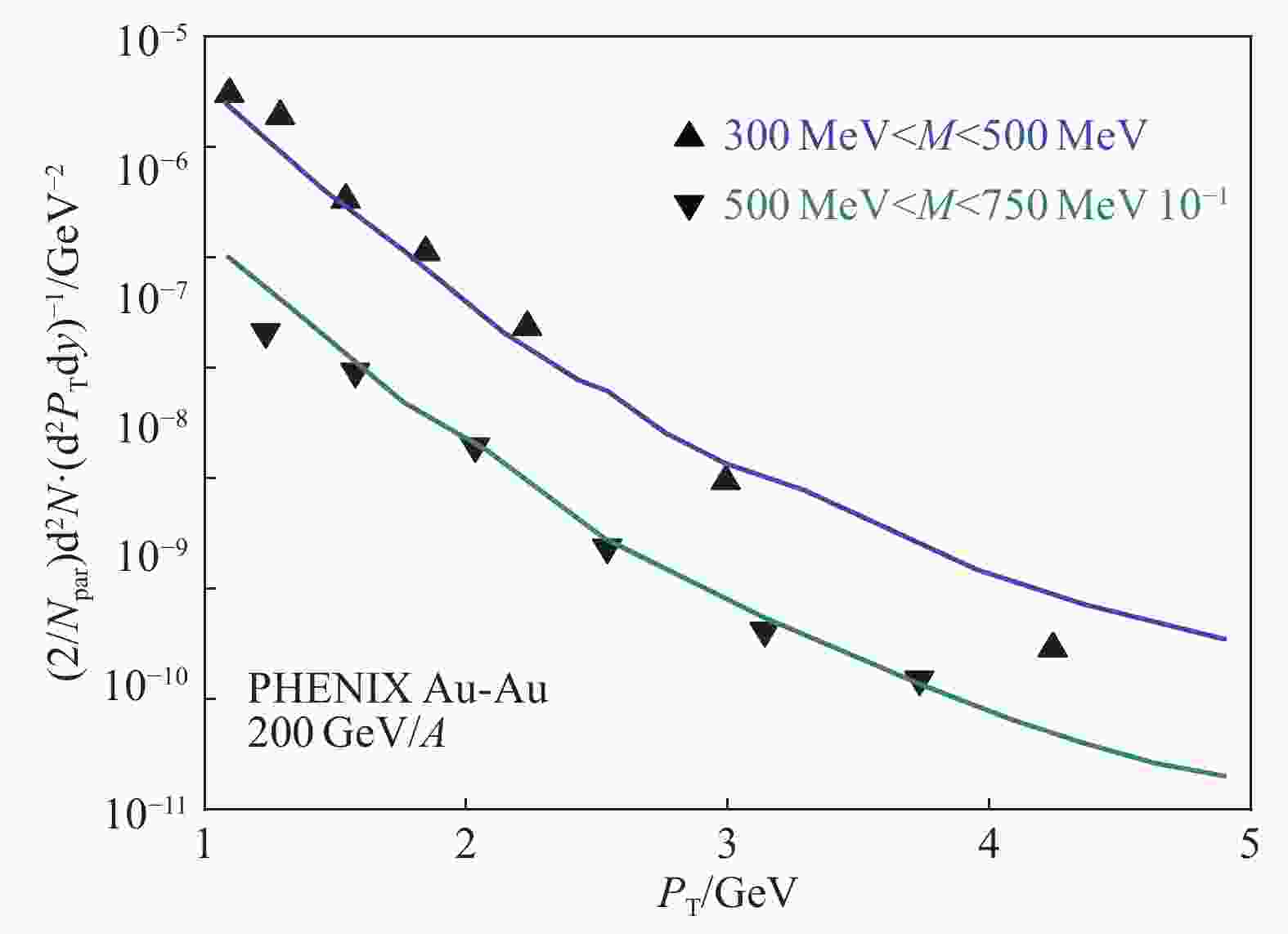
Figure 6. (color online)The
$P_{\rm T}$ spectra of dilepton in Au-Au 200 GeV/$A$ collisions at RHIC. The solid line is the sum of the leading and fragmentation contribution and the the hadronic decays. The data are from the PHENIX experiments[4].$$\frac{{{\rm{d}}N}}{{{\rm{d}^2}{P_{\rm{T}}}{\rm{d}}y}} = \int_{{M_1}}^{{M_2}} {\frac{{2M{\rm{d}}N}}{{{\rm{d}}{M^2}{\rm{d}^2}{P_{\rm{T}}}{\rm{d}}y}}} {\rm{d}}M,$$ (13) where
$ M_{1} $ and$ M_{2} $ are the lower and upper limits of the mass bins.The dilepton production mechanism of the photon-nucleon collisions becomes important in the Pb-Pb 5.5 TeV/
$ A $ collisions at LHC (Fig. 5). We note that the dilepton yield from the resolved photon-nucleon collisions and the leading processes are comparable in the region of$ P_{\rm T}\lesssim $ 2 GeV. The contribution of the photon-nucleon collisions may be probed by the enhancement effect in the large transverse momentum spectra at LHC energies. The enhancement rate due to the photon-nucleon collision is about 10% for the 20%~40% centrality Pb-Pb collisions. -
In conclusion, the dilepton production from the photon-nucleon collisions in the peripheral heavy ion collisions is studied. The photon-nucleon collisions include the real photon and resolved photon-nucleon collisions. We also calculate the dilepton production of the leading processes (Compton scattering and quark anti-quark annihilation) and fragmentation processes (hard parton scattering) for the comparation. The numerical results of 20%~40% centrality collisions of heavy ion at RHIC and LHC energies show that the photon-nucleon collisions could be an important dilepton source of peripheral heavy ion collisions in the large transverse momentum region at LHC.
Large Transverse Momentum Dilepton Production from the Photon-nucleon Collisions at RHIC and LHC
-
摘要: 研究了RHIC和LHC能区的Au-Au和Pb-Pb周边重离子碰撞中,来自光子-核子相互作用产生的大横动量双轻子。利用微扰QCD 参数化和Weizsäcker-Williams近似计算了双轻子的产率。经过与领头阶和碎裂过程的双轻子产生数值计算结果相比较,光-核碰撞过程产生的大横动量双轻子在RHIC能区是可忽略的。但是在LHC能区,光-核碰撞在大横动量区域是周边重离子碰撞的一个重要的双轻子源。Abstract: We study the large transverse momentum dilepton produced by the photon-nucleon interactions in the peripheral Au-Au collisions at RHIC and Pb-Pb collisions at LHC. We calculate the dilepton production yield by using the perturbative QCD factorization approach and the Weizsäcker-Williams approximation. The numerical results indicate that the photon-nucleon collision processes is negligible by comparing with the conventional large transverse momentum dilepton production at RHIC energies. However, in the large transverse momentum region, the photon-nucleon collision could be an important large transverse momentum dilepton source in the peripheral heavy ion collisions at LHC.
-
Figure 4. (color online)The large transverse momentum dilepton spectra in the Au-Au collisoins for
$\sqrt{s}$ = 200 GeV, M = 500 MeV and$y$ = 0. The dash line and dot line denote the leading and fragmentation dilepton production, respectively. The dileptons produced from the real photon-nucleon collisions (dash-dot line) and resolve photon-nucleon collisions (dash-dot-dot line) are also shown.Figure 6. (color online)The
$P_{\rm T}$ spectra of dilepton in Au-Au 200 GeV/$A$ collisions at RHIC. The solid line is the sum of the leading and fragmentation contribution and the the hadronic decays. The data are from the PHENIX experiments[4]. -
[1] KANG Z B, QIU J W, VOGELSANG W. Phys Rev D, 2009, 79: 054007. doi: 10.1103/PHYSREVD.79.054007 [2] KANG Z B, QIU J W, VOGELSANG W. Nucl Phys A, 2009, 830: 571. doi: 10.1016/j.nuclphysa.2009.10.051 [3] FIELD R D. Applications of Perturbative QCD[M]. Boston: AddisonWesley Publishing Company, 1989: 186. [4] ADARE A, AFANASIEV S, AIDALA C, et al. Phys Rev C, 2010, 81: 034911. doi: 10.1103/PhysRevC.81.034911 [5] FU Y P, LI Y D. Chin Phys C, 2011, 35: 109; FU Y P, LI Y D. Nucl Phys Rev, 2012, 29: 238. [6] CAMPBELL S. Nucl Phys A, 2017, 967: 177. doi: 10.1016/j.nuclphysa.2017.05.099 [7] OWENS J F. Rev Mod Phys, 1987, 59: 465. doi: 10.1103/RevModPhys.59.465 [8] ESKOLA K J, PAUKKUNEN H, SALGADO C A. J High Energy Phys, 2009, 0904: 065. doi: 10.1088/1126-6708/2009/04/065 [9] PUMPLIN J, STUMP D R, HUSTON J, et al. J High Energy Phys, 2002, 0207: 012. doi: 10.1088/1126-6708/2002/07/012 [10] ESKOLA K J, WANG X N. Phys Rev D, 1994, 49: 4532. doi: 10.1103/PhysRevD.49.4532 [11] NISIUS R. Phys Rep, 2000, 332: 165. doi: 10.1016/S0370-1573(99)00115-5 [12] KRAWCZYK M, ZEMBRZUSKI A, STASZEL M. Phys Rep, 2001, 345: 265. doi: 10.1016/S0370-1573(00)00105-8 [13] FU Y P, LI Y D. Phys Rev C, 2011, 84: 044906. doi: 10.1103/PhysRevC.84.044906 [14] YU G M, LI Y D. Phys Rev C, 2015, 91: 044908. doi: 10.1103/PhysRevC.91.044908 [15] EBOLI O J P, GONZALEZ G M C, NOVAES S F. Phys Rev D, 1994, 49: 91. doi: 10.1103/PhysRevD.49.91 [16] DREES M, GODBOLE R M, NOWAKOWSKI M, et al. Phys Rev D, 1994, 50: 2335. doi: 10.1103/PhysRevD.50.2335 [17] GlÜCK M, REYA E, VOGT A. Phys Rev D, 1992, 46: 1973. doi: 10.1103/PhysRevD.46.1973 [18] DAHMS T. arXiv: 0810.3040 [nucl-ex]. [19] ADAM J, ALICE Collaboration. Phys Lett B, 2016, 754: 235. doi: 10.1016/j.physletb.2016.01.020 [20] TURBIDE S, GALE C, JEON S, et al. Phys Rev C, 2005, 72: 014906. doi: 10.1103/PhysRevC.72.014906 -





 下载:
下载:





































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号