-
自从超重核“稳定岛”[1]被预言以来,在过去的几十年里核物理实验及理论工作者们对超重核的合成做了大量的研究。德国重离子研究中心(GSI)通过以Pb或Bi作为靶的“冷熔合”反应成功合成了Z=107~112的超重元素[2-7]。但是发现随着复合核电荷数的增加,产生截面呈现指数下降。在2004年,日本理化学研究所(RIKEN)通过
$ ^{70}{\rm{Zn}}+^{{\rm{209}}}{\rm{Bi}} $ 的“冷熔合”反应合成了超重核Z=113[8-9],但是产生截面仅仅只有0.03 pb,达到了当时实验探测技术的极限。而俄罗斯杜布纳联合核子研究所(Dubna)采用了48Ca束流和锕系靶的“热熔合”方式成功合成了Z=114~118的超重核[10-14]。至此,元素周期表的第七周期被全部填满。为了产生Z>118的超重核素,国际上的一些实验室做了许多的尝试。2009年,Dubna曾尝试利用反应$ ^{58}{\rm{Fe}} + ^{{\rm{244}}}{\rm{Pu}} $ 来合成120号超重元素[15],但是没有观测到相应的$ \alpha $ 衰变链。2016年,GSI也曾试图通过反应$ ^{54}{\rm{Cr}} + ^{{\rm{248}}}{\rm{Cm}} $ 来合成120号超重元素[16],并且观察到了与$ ^{299}120 $ 相关的3个$ \alpha $ 衰变和自发裂变事件,然而这只是一个随机事件[17],不能证明合成了Z=120的新元素。因此,如果想要合成Z>118的核素,不仅需要更加先进的探测及鉴别技术,也需要找到合适的合成方法和反应体系。为了更好地描述超重核熔合过程,基于大量的实验数据理论上发展了许多模型方法,提出了对熔合机制不同的理解。其中有两步模型(the two-step model)[18-19]、核子集体化模型(nucleon collectivization model)[20-22]、核扩散模型(fusion-by-diffusion(FBD) model)[23-25]、唯象经验方法[26-28]和双核系统模型(the dinuclear system(DNS) model)[29-34]等,并且这些模型在计算超重核的产生截面时都得到了不错的结果。同时这些理论方法也给出了许多关于
$ Z> $ 118元素的预言。本文运用的理论模型为双核系统模型,目标是希望通过比较不同模型对$ Z> $ 118超重核的计算及预言结果,从而为关注超重核合成的实验及理论工作者们提供一定的参考。本文的结构安排如下:在第二部分我们简略地介绍双核系统模型和其他模型,然后在第三部分通过对不同模型计算结果的对比来分析合成
$ Z> $ 118超重核的最佳反应体系,最后在第四部分给出结论。 -
在双核系统模型的概念中,超重核合成的物理过程被分成三步。首先,弹核和靶核克服库仑位垒到达势袋底部形成双核系统,这就是系统的俘获过程。接着,双核系统通过核子的转移形成复合核,即熔合过程,在这一过程中会伴随着准裂变参与竞争而阻碍复合核的形成。最后处于激发态的复合核会通过蒸发粒子、发射
$ \gamma $ 射线或裂变进行退激,而超重核主要通过激发态的复合核蒸发中子形成,同时裂变也会参与竞争从而减小形成蒸发剩余核的截面,即存活过程。根据上述物理思想,在质心系入射能量$ E_{\rm{c.m.}} $ 下形成超重核的蒸发剩余截面可以写成[35-36]:$$ \begin{split}\sigma_{\rm{ER}}\left(E_{\rm{c.m.}}\right) =& \frac{\pi \hbar^{2}}{2 \mu E_{\rm{c.m.}}} \sum\limits_{J}(2 J+1) T\left(E_{\rm{c.m.}}, J\right)\times \\ & P_{\rm{CN}}\left(E_{\rm{c.m.}}, J\right) W_{\rm{sur}}\left(E_{\rm{c.m.}}, J\right)\text{,}\end{split} $$ (1) 式中:
$ \hbar $ 、$ \mu $ 和$ J $ 分别为约化普朗克常数、碰撞系统的约化质量和入射角动量,$ T\left(E_{\rm{c.m.}}, J\right) $ 是碰撞核克服库仑位垒形成双核系统的穿透几率,$ P_{\rm{CN}}\left(E_{\rm{c.m.}}, J\right) $ 是熔合几率,$ W_{\rm{sur}}\left(E_{{\rm{cm}}. }, J\right) $ 是复合核经过裂变和蒸发中子的竞争后的存活几率[37]。俘获截面$ \sigma_{\rm{cap}} $ 可以用下面的式子表示:$$ \sigma_{\rm{cap}}\left(E_{\rm{c.m.}}\right) = \frac{\pi \hbar^{2}}{2 \mu E_{{\rm{c}} . {\rm{m}}.}} \sum\limits_{J}(2 J+1) T\left(E_{\rm{c.m.}}, J\right)\text{,}$$ (2) 其中穿透几率写为
$$ T\left(E_{\rm{c.m.}}, J\right) = \int f(B) T\left(E_{\rm{c.m.}}, B, J\right) {\rm d} B\text{,}$$ (3) 这里
$ B $ 表示弹靶核的库仑位垒,$ f(B) $ 是位垒分布函数,可以写为反高斯形式并由下式给出:$$ f(B) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{N}\exp \left[ { - {{\left( {\dfrac{{B - {B_{\rm{m}}}}}{{{\Delta _1}}}} \right)}^2}} \right],}&\!\!\!{B\! <\! {B_{\rm{m}}}}\\ {\dfrac{1}{N}\exp \left[ { - {{\left( {\dfrac{{B - {B_{\rm{m}}}}}{{{\Delta _2}}}} \right)}^2}} \right],}&\!\!\!{B \!>\! {B_{\rm{m}}}} \end{array}} \right.\text{,}$$ (4) 其中:
$ B_{\rm m} $ =$ \frac{B_{\rm s}+B_{0}}{2} $ ,$ B_{\rm s} $ 和$ B_0 $ 分别为形变鞍点处的位垒高度和在腰-腰碰撞下的库仑位垒高度。分布宽度$ \Delta_{2} =$ $ \frac{B_{0}-B_{\rm s}}{2} $ (MeV),$ \Delta_{1} $ =$ \Delta_{2} - $ 2 (MeV)。归一化常数N由$ \int f(B) {\rm d} B $ =1得出。此外式(3)中$ T\left(E_{\rm{c.m.}}, B, J\right) $ 表示为$$ \begin{split} T({E_{\rm c.m.}},B,J) =& \bigg\{ 1 + \exp \bigg[ - \frac{{2\pi }}{{\hbar \omega (J)}}({E_{\rm c.m.}} - B-\\ &\frac{{{\hbar ^2}}}{{2\mu R_B^2(J)}}J(J + 1))\bigg]{\bigg\} ^{ - 1}}\text{,} \end{split}$$ (5) 式中
$ \hbar \omega(J) = \left.\hbar \sqrt{-\frac{1}{\mu} \frac{\partial^{2} V}{\partial R^{2}}}\right|_{R = R_{\rm B}} $ 表示库仑位垒抛物线的宽度,$ R_{\rm B} $ 是库仑位垒处两碰撞核的相对距离。在双核系统模型中,质子数$ Z_1 $ ,中子数$ N_1 $ ,激发能$ E_1 $ 的碎片在$ t $ 时刻的分布几率$ P\left(Z_{1}, N_{1}, E_{1}, t\right) $ 由以下主方程得出:$$ \begin{split} &\frac{{\rm d} P\left(Z_{1}, N_{1}, E_{1}, t\right)}{{\rm d} t} \\ =&\sum\limits_{Z_{1}^{\prime}} W_{Z_{1}, N_{1}; Z_{1}^{\prime}, N_{1}}(t)\left[d_{Z_{1}, N_{1}} P\left(Z_{1}^{\prime}, N_{1}, E_{1}^{\prime}, t\right)\right.-\\ &\left.d_{Z_{1}^{\prime}, N_{1}} P\left(Z_{1}, N_{1}, E_{1}, t\right)\right] +\\ &\sum\limits_{N_{1}^{\prime}} W_{Z_{1}, N_{1};Z_{1}, N_{1}^{\prime}}(t)\left[d_{Z_{1}, N_{1}} P\left(Z_{1}, N_{1}^{\prime}, E_{1}^{\prime}, t\right)\right.-\\ &\left.d_{Z_{1}, N_{1}^{\prime}} P\left(Z_{1}, N_{1}, E_{1}, t\right)\right]- \\ &\left[\Lambda_{\rm{qf}}(\Theta(t))+\Lambda_{\rm {fis }}(\Theta(t))\right] P\left(Z_{1}, N_{1}, E_{1}, t\right) \text{,} \end{split}$$ (6) 这里
$ W_{Z_{1}, N_{1}; Z_{1}^{\prime}, N_{1}} $ 是从($ Z_1 $ ,$ N_1 $ )向($ {Z'}_1 $ ,$ N_1 $ )态的跃迁几率[38],维度$ d_{Z_{1}, N_{1}} $ 表示碎片在宏观状态($ Z_1 $ ,$ N_1 $ )时包含的微观状态数目,求和是对碎片($ Z_1 $ ,$ N_1 $ )能取到的所有状态进行的,$ \Lambda_{\rm{qf}} $ 和$ \Lambda_{\rm{fis}} $ 分别表示准裂变几率和裂变几率[39]。双核系统在核子转移过程中受势能曲面[40]的影响,势能曲面由下式给出:$$ \begin{aligned} U(Z_{1}, N_{1} ;\, Z_{2}, N_{2}, R) =& E_{\rm B}\left(Z_{1}, N_{1}\right)+E_{\rm B}\left(Z_{2}, N_{2}\right)- \\ &E_{\rm B}(Z, N)+V_{\rm C}(R)+V_{\rm N}(R)\text{,} \end{aligned} $$ (7) 这里
$ E_{\rm B}\left(Z_{i}, N_{i}\right) $ 和$ E_{\rm B}\left(Z,N\right) $ 分别表示碎片i和复合核的结合能。在双核系统的概念里,核子转移过程发生在势袋底部,所以我们只考虑势能曲面的质量不对称度$ \eta $ 自由度,此时势能曲面便成了驱动势,其中$ \eta = \left(A_{\rm P}- A_{\rm T}\right) / \left(A_{\rm P}+A_{\rm T}\right) $ ,$ A_{\rm P} $ 和$ A_{\rm T} $ 分别是弹核与靶核的质量数。具有足够内部激发能的双核系统越过内部熔合位垒后便可形成复合核,驱动势的最高点叫做B.G.(Businaro Gallone)点,所有越过B.G.点的碎片对质量分布几率进行求和就可以得到熔合几率[41]:
$$ P_{\rm{CN}}\left(E_{\rm{c.m.} }, J\right) = \int f(B) P_{\rm{CN}}\left(E_{\rm{c.m.} }, J, B\right) {\rm d} B\text{,}$$ (8) 这里的积分上下限分别为
$ B_{\rm m}+3\Delta_{2} $ 和$ B_{\rm m}-3\Delta_{1} $ ,$ P_{\rm{CN}}(E_{\rm{c.m.}}, J, B)$ 由下式给出:$$ \begin{split} &P_{\rm{CN}}\left(E_{\rm{c.m.}},J,B\right)\\ =& \sum\limits_{Z_{1} = 1}^{Z_{\rm{B.G.}}} \sum\limits_{N_{1} = 1}^{N_{\rm{B.G.}}} P\left[Z_{1},N_{1}, E_{1},\tau_{\rm{int}}\left(E_{\rm{c.m.}}, J, B\right)\right]\text{,} \end{split} $$ (9) 其中
$ Z_{\rm{B.G.}} $ 和$ N_{\rm{B.G.}} $ 分别表示B.G.点的质子数和中子数,$ \tau_{\rm {int}}\left(E_{\rm{c.m.}}, J, B\right) $ 是相互作用时间[42]。处于激发态的复合核通常发射粒子或$ \gamma $ 射线来进行退激。对于超重元素的合成,我们只考虑裂变与中子蒸发之间的竞争[43]。发射n个中子的存活几率可写成:$$ \begin{array}{l} {W_{\rm {sur }}\left(E_{\rm{CN}}^{*}, x, J\right)} { = P\left(E_{\rm{CN}}^{*}, x, J\right) \prod\limits_{i = 1}^{x}\left[\frac{\Gamma_{n}\left(E_{i}^{*}, J\right)}{\Gamma_{n}\left(E_{i}^{*}, J\right)+\Gamma_{f}\left(E_{i}^{*}, J\right)}\right]}\text{,}\end{array} $$ (10) 在这个式子里,
$ E_{\rm{CN}}^{*} $ 表示复合核的激发能,可以通过$ E_{\rm{CN}}^{*} = E_{\rm{c.m.}}+Q $ 来进行计算,$ J $ 是复合核的自旋。$ E_{i}^{*} $ 是复合核蒸发$ i $ 个中子前的激发能,用$ E_{i + 1}^* = E_i^* - B_i^n - 2{T_i} $ 来计算,这里会用到初始条件$ E_{1}^{*} = E_{\rm{CN}}^{*} $ ,$ T_{i} $ 是蒸发第$ i $ 个中子前的核温度并且满足关系$ E_{i}^{*} = a T_{i}^{2}-T_{i} $ 。$ B_{i}^{n} $ 是第$ i $ 个中子的分离能,$ P\left(E_{\rm{CN}}^{*}, x, J\right) $ 是蒸发$ x $ 中子的实现几率[44]。 -
对于重离子碰撞形成复合核的机制的解释有两种观点:其中一种认为弹靶接触后会很快失去它们原有的特性,所有核子集体化形成一个很大形变的原子核。随着时间的演化这个形变的核逐渐变成一个球形核,这时认为发生了熔合反应,但是如果形变越来越大的话就会发生准裂变。另一种观点认为弹靶接触后会保持各自原有的特性,随着时间的演化在两核之间发生核子转移,当一个核所有的核子全部转移到另一个核时复合核就形成了,即熔合过程。核子集体化模型的观点则介于这两者之间[20],认为在两原子核碰撞后会有越来越多的价核子成为体系的共用核子,而两核心仍然具有各自的独立性。共用原子核的个数会逐渐增多,当所有的核子都变成共用核子时复合核形成,认为发生了熔合反应,否则将发生准裂变现象。
-
核扩散模型[23]认为,在弹靶越过库仑位垒形成双核系统后,越过鞍点(相当于克服内部熔合位垒)到形成复合核的过程可以假设是一维布朗粒子的扩散过程,粒子沿着拉伸自由度在粘滞流体中做布朗运动。熔合几率由下式给出:
$$ P_{\rm{fus}} = \frac{1}{2}(1-{\rm{erf} }\sqrt{H / T})\text{,} $$ (11) 式中:
$ H $ 为鞍点与熔合起始点之间的能量差,$ T $ 为熔合系统的温度。 -
在重体系的熔合反应中,存在准裂变与熔合过程的竞争,以致大质量反应核的熔合过程受到了阻碍。对这种现象人们给出了两种解释:一个解释是在弹靶核克服库仑位垒的过程中初始入射动能的耗散[45];另一个解释是碰撞形成的形变体系逐渐变成一个球形复合核过程中集体动能的耗散[46]。这两种机制发生在不同的反应阶段(俘获和熔合),而两步模型结合了这两种机制,认为在两个反应阶段中都有能量的耗散,并将这两个阶段合并成一个阶段,最后再结合存活几率的计算便可得到蒸发剩余截面。在两步模型中超重核的产生截面可以表示为[19]
$$ \begin{split} \sigma^{}_{\rm{ER}} = &\frac{\pi \hbar^{2}}{2 \mu E_{\rm{c.m.}}} \sum\limits_{J}(2 J+1) \times P_{\rm {fusion }}\left(E_{\rm{c.m.}}, J\right) W_{\rm{sur}}\left(E^{*}\!, J\right){\text{。}} \end{split}$$ (12) -
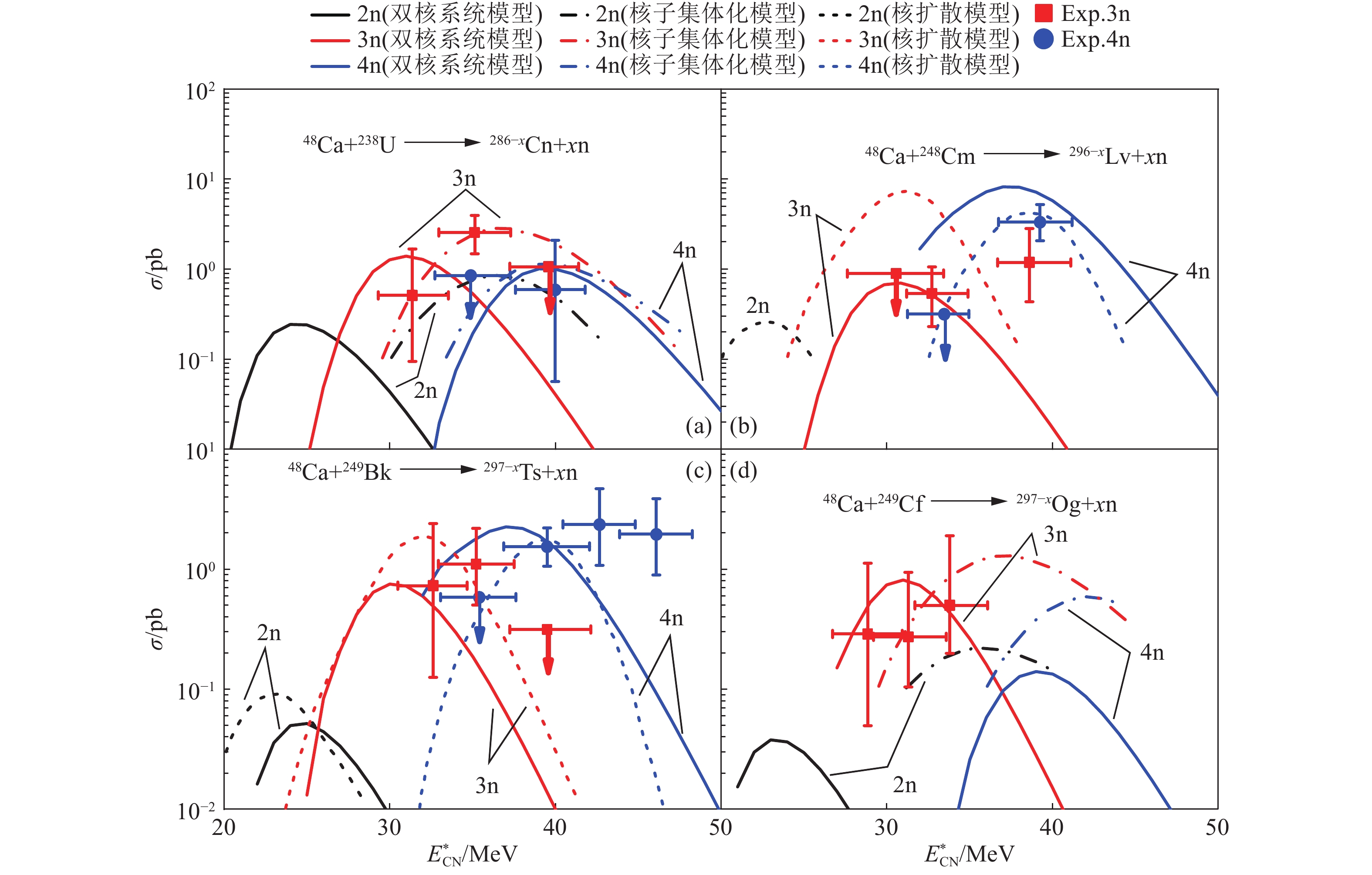
为了检验各个理论模型预测超重核产生截面的可靠性,图1中展示了合成112号元素Cn、116号元素Lv、117号元素Ts、118元素Og各模型计算的产生截面与实验数据的对比。由图可知,无论是理论值还是实验值最大的产生截面都出现在3n或4n反应道上,主要是因为“热熔合”的激发能高,所以容易在3n及4n出射道中出现最大截面。从图1(a)中可以看到双核系统模型和核子集体化模型计算的反应
$ ^{48}{\rm{Ca}} + ^{{\rm{238}}}{\rm{U}} $ 的2n反应道激发曲线的峰位都在实验值的峰位附近,峰位都与实验值相差2~3 MeV左右,另外核子集体化模型计算的反应$ ^{48}{\rm{Ca}} + ^{{\rm{238}}}{\rm{U}} $ 的2n与3n出射道的激发曲线的峰位非常接近,这与常规的实验规律有点不符,因为一般来说蒸发一个中子需要克服5~6 MeV的中子分离能。同时通过图1(b)、(c)可以知道双核系统模型与核扩散模型的各个反应道的激发曲线峰位基本都比较接近,但峰值差了几倍。由图1(b)、(c)、(d)还能够看出,随着靶核质子数的增加,最终的产生截面的大小总体在变小,这是由于弹核与靶核的库仑排斥在变大从而具有更高的库仑位垒所致。总的来说,在实验误差内各个模型计算的截面与实验数据都是符合得不错的。不过仅仅这样的比较还不足以说明哪个模型更好,因为目前可用的有关超重核的实验数据还是太少,而超重核的实验数据又不容易获得,所以我们认为不同模型对超重核的合成都具备一定的预测能力。
-
基于上面的分析可知,各个理论模型对于超重核合成的产生截面都是具有一定预言能力的,各模型所预言的最佳反应体系及其最大截面如表1所列,表中所列出的合成各个核素的最佳反应体系及其最大截面值取自所引文章的图表,下面我们将对比和分析不同模型对Z=119与Z=120超重核合成的预言结果。
表 1 不同模型对合成Z=119和Z=120超重核的最佳反应体系(最大截面/fb)预测的比较
核素 双核系统模型[50] 核子集体化模型[21, 51] 核扩散模型[25] 两步模型[52] 唯象经验方法[53-54] $^{289}119$ $^{40}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$(1270) $-$ $-$ $-$ $-$ $^{291}119$ $^{42}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$(1710) $-$ $-$ $-$ $-$ $^{293}119$ $^{44}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$(4320) $-$ $-$ $-$ $-$ $^{294}119$ $-$ $-$ $-$ $^{50}{\rm{Ti}} + ^{{\rm{247}}}{\rm{Bk}}$(43) $-$ $^{295}119$ $^{44}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$(2130) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$(57) $^{48}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$(44) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$(14) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$(41) $^{296}119$ $-$ $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$(39) $^{48}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$(200) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$(29) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$(105) $^{297}119$ $^{46}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$(3600) $-$ $^{48}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$(79) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$(19) $^{48}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$(952) $^{298}119$ $^{46}{\rm{Ca}} + ^{{\rm{255}}}{\rm{Es}}$(610) $^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$(234) $^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$(16) $-$ $^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$(155) $^{299}119$ $^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$(1670)) $^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$(300) $-$ $-$ $^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$(722) $^{290}120$ $^{50}{\rm{Cr}} + ^{{\rm{242}}}{\rm{Cm}}$(100) $-$ $-$ $-$ $-$ $^{292}120$ $^{46}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$(240) $-$ $-$ $-$ $-$ $^{293}120$ $^{40}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$(170) $-$ $-$ $-$ $-$ $^{294}120$ $^{40}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$(1240) $-$ $-$ $-$ $-$ $^{295}120$ $-$ $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$(45) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$(6) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$(2) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$(2) $^{296}120$ $^{42}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$(290) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$(42) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$(6) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$(3) $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$(103) $^{297}120$ $-$ $-$ $-$ $^{50}{\rm{Ti}} + ^{{\rm{250}}}{\rm{Cf}}$(5) $-$ $^{298}120$ $^{44}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$(1040) $^{54}{\rm{Cr}} + ^{{\rm{248}}}{\rm{Cm}}$(25) $-$ $^{50}{\rm{Ti}} + ^{{\rm{250}}}{\rm{Cf}}$(8) $^{54}{\rm{Cr}} + ^{{\rm{248}}}{\rm{Cm}}$(5) $^{299}120$ $-$ $^{54}{\rm{Cr}} + ^{{\rm{248}}}{\rm{Cm}}$(14) $-$ $^{50}{\rm{Ti}} + ^{{\rm{252}}}{\rm{Cf}}$(12) $^{54}{\rm{Cr}} + ^{{\rm{248}}}{\rm{Cm}}$(15) $^{300}120$ $^{46}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$(500) $-$ $-$ $^{50}{\rm{Ti}} + ^{{\rm{252}}}{\rm{Cf}}$(7) $-$ $^{302}120$ $^{48}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$(460) $-$ $-$ $-$ $-$ 通过表1我们可以发现不同的模型对Z=119和Z=120超重核合成的预言结果是不完全一样的。首先,不同模型预言的截面值相差几倍甚至1~2个量级,如双核系统模型预言的截面值在
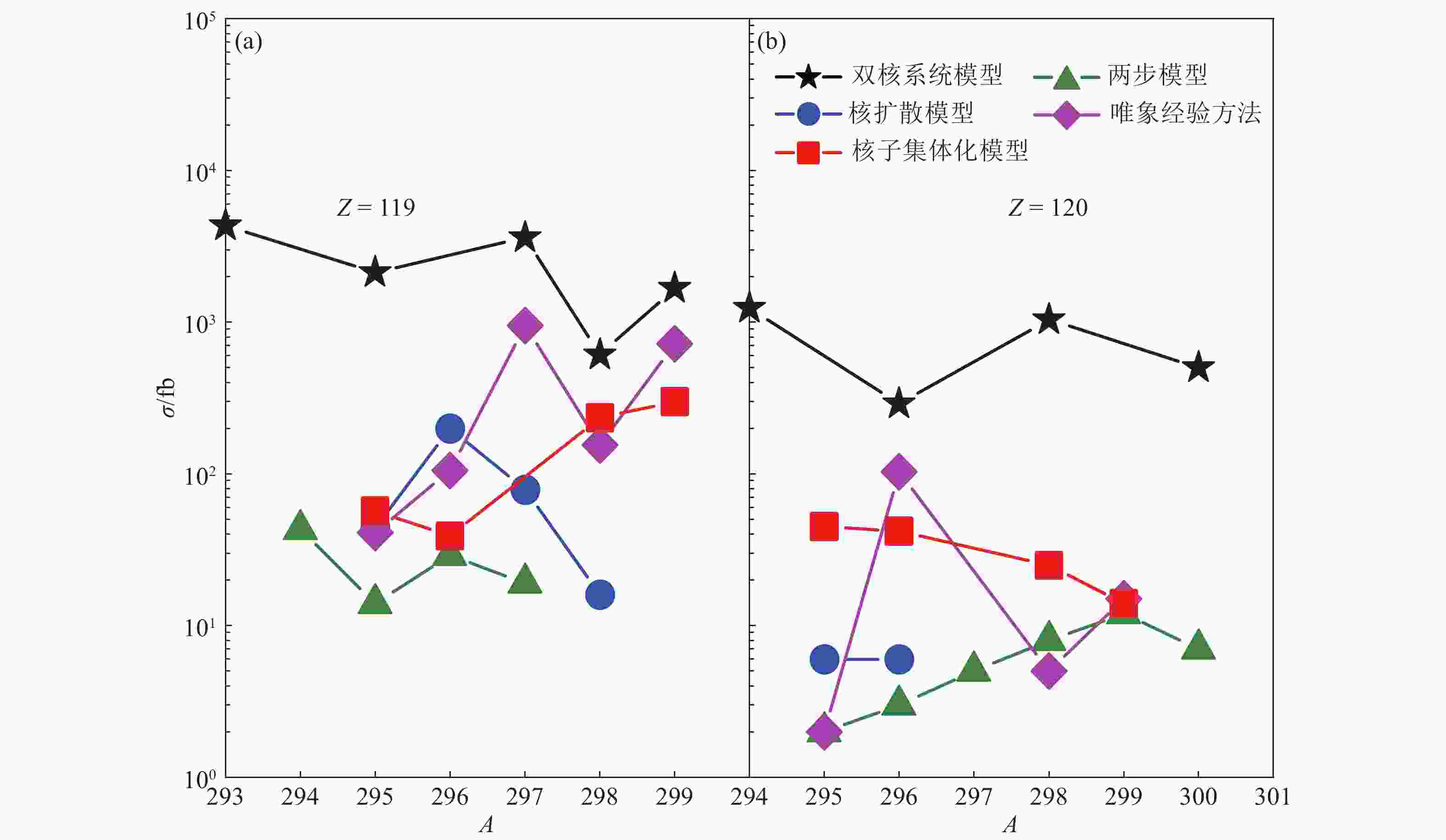
$ 10^2\sim10^3 $ fb量级,而两步模型的却只有$ 10^0\sim10^1 $ fb量级,可能是因为不同模型中使用了不同的参数,说明将不同模型的截面值拿来比较是完全没有意义的,同一模型中各个反应体系的产生截面值的相对大小才是我们需要关注的,所以从表中我们可以看到,双核系统模型、核子集体化模型、核扩散模型、两步模型和唯象经验方法合成 Z=119 超重核预言的最佳反应体系分别为反应$ ^{44}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}} $ 、$ ^{48}{\rm{Ca}}+ ^{{\rm{254}}}{\rm{Es}} $ 、$ ^{48}{\rm{Ca}}+ ^{{\rm{252}}}{\rm{Es}} $ 、$ ^{50}{\rm{Ti}}+^{{\rm{247}}}{\rm{Bk}} $ 和$ ^{48}{\rm{Ca}}+ ^{{\rm{252}}}{\rm{Es}} $ ,合成 Z=120 超重核预言的最佳反应体系分别为反应$ ^{40}{\rm{Ca}}+ ^{{\rm{257}}}{\rm{Fm}} $ 、$ ^{50}{\rm{Ti}}+^{{\rm{249}}}{\rm{Cf}} $ 、$ ^{50}{\rm{Ti}}+ ^{{\rm{249}}}{\rm{Cf}} $ 、$ ^{50}{\rm{Ti}}+^{{\rm{252}}}{\rm{Cf}} $ 和$ ^{50}{\rm{Ti}}+ ^{{\rm{249}}}{\rm{Cf}} $ 。其次,从表中还可以看出,对于同一核素的合成,不同模型有时会给出不太一样的预言结果,有时也会给出一样的预言结果。比如对于核素$ ^{297}119 $ 来说,双核系统模型和两步模型预言的最佳反应体系分别为反应$ ^{46}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}} $ 和$ ^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}} $ ,而核扩散模型与唯象经验方法的结果为反应$ ^{48}{\rm{Ca}}+ ^{{\rm{252}}}{\rm{Es}} $ 。对于核素$ ^{299}119 $ 和$ ^{295}120 $ 来说,不同模型预言的结果相同,所预言的最佳反应体系分别为反应$ ^{48}{\rm{Ca}}+^{{\rm{254}}}{\rm{Es}} $ 和$ ^{50}{\rm{Ti}}+ ^{{\rm{249}}}{\rm{Cf}} $ 。再次,我们可以看到,双核系统模型预言合成$ ^{294}120 $ 和$ ^{302}120 $ 超重核的最佳弹靶组合分别为反应$ ^{40}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}} $ 和$ ^{48}{\rm{Ca}}+ ^{{\rm{257}}}{\rm{Fm}} $ 。虽然它们的靶核相同,但是它们的截面值却相差了几倍,主要是由于反应$ ^{40}{\rm{Ca}}+ ^{{\rm{257}}}{\rm{Fm}} $ 有更大的质量不对称度而使其有了更大的熔合几率。值得一提的是,在被预言的最佳弹靶组合中,许多的弹核都是像48Ca这样的双幻核,因为它是一个非常丰中子的核,使得复合核能更容易蒸发中子,从而更有利于超重核的合成。为了更加直观地比较不同模型的预言结果,图2展示了合成Z=119和Z=120超重核的不同模型预测的最大截面值与质量数的关系。从图中可以看出,不管是对于哪一个模型,合成Z=119超重核的产生截面都要明显高于Z=120的,说明在将来的实验条件下Z=119的超重元素很有可能会是Z>118的元素中首先被实验合成的。
表2和表3列出了合成超重核
$ Z $ =119, 120的不同预言结果和我们计算的最大产生截面及对应的出射道与入射能量。由表2我们可以看到反应$ ^{48}{\rm{Ca}}+^{{\rm{252}}}{\rm{Es}} $ 是大部分理论研究认为更为可行的合成超重核$ Z $ =119的弹靶组合,这也和我们的计算结果是一致的。通过比较表2和表3可知,超重核$ Z $ =120合成的截面总体要比超重核$ Z $ =119小一些,然而,我们计算的反应$ ^{40}{\rm{Ca}}+ ^{{\rm{257}}}{\rm{Fm}} $ $ \rightarrow $ $ ^{297-x}{\rm{120}} $ +$ x{\rm n} $ 的最大截面达到了16 313 fb,这个截面甚至比我们计算的超重核$ Z $ =119合成中最大的截面$ \sigma_{\rm{ER}}^{\max}(^{48}{\rm{Ca}}+ ^{{\rm{252}}}{\rm{Es}}) $ =2 673 fb还要大一个量级,可见弹靶组合的选择对新核素的合成影响非常大,所以我们认为在选择好合适弹靶组合的情况下,超重核$ Z $ =120也是有可能要比超重核$ Z $ =119更早地被实验合成的,但是当下的实验条件也是需要考虑的因素,257Fm靶目前在实验上较难获得,可以在将来实验设备提高后进行尝试。为了说明反应$ ^{40}{\rm{Ca}}+ ^{{\rm{257}}}{\rm{Fm}} $ 的截面为何这么高,我们在图3中展示了反应$ ^{40}{\rm{Ca}}+ ^{{\rm{257}}}{\rm{Fm}} $ 和$ ^{46}{\rm{Ti}}+^{{\rm{251}}}{\rm{Cf}} $ 的俘获截面、熔合几率和蒸发剩余截面。表 2 合成超重核Z=119的不同预言结果和我们计算的最大产生截面及对应的出射道与入射能量
文献 反应体系 其他工作 本工作 出射道 $\sigma_{\rm{ER}}^{\max}/{\rm{fb}}$ $E_{\rm{c.m.}}/{\rm{MeV}}$ 出射道 $\sigma_{\rm{ER}}^{\max}/{\rm{fb}}$ $E_{\rm{c.m.}}/{\rm{MeV}}$ [50] $^{44}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$ $3{\rm n}$ 4320 $204$ $3{\rm n}$ 1288 $203$ [26] $^{48}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$ $4{\rm n}$ $960$ $221$ 3n 2673 214 [55] $4{\rm n}$ 3160 $227$ [53] $3{\rm n}$ $952$ $216$ [25] $4{\rm n}$ $200$ $220$ [56] $^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$ $3{\rm n}$ 4040 $211$ $3{\rm n}$ 2459 $211$ [52] $^{50}{\rm{Ti}} + ^{{\rm{247}}}{\rm{Bk}}$ $3{\rm n}$ $43$ $230$ $2{\rm n}$ $69$ $217$ [57] $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$ $4{\rm n}$ $110$ $234$ 2n 1510 221 [58] $3{\rm n}$ $480$ $226$ 表 3 合成超重核Z=120的不同预言结果和我们计算的最大产生截面及对应的出射道与入射能量
文献 反应体系 其他工作 本工作 出射道 $\sigma_{\rm{ER}}^{\max}$/fb $E_{\rm{c.m.}}$/MeV 出射道 $\sigma_{\rm{ER}}^{\max}$/fb $E_{\rm{c.m.}}$/MeV [50] $^{40}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$ $3{\rm n}$ 1240 $206$ $3{\rm n}$ 16313 $199$ [55] $^{48}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$ $5{\rm n}$ $88$ $234$ $3{\rm n}$ $56$ $213$ [59] $^{46}{\rm{Ti}} + ^{{\rm{251}}}{\rm{Cf}}$ $2{\rm n}$ 6200 $207$ $2{\rm n}$ 2547 $213$ [26] $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$ $4n$ $29$ $240$ 2n 93 226 [54] $3{\rm n}$ $103$ $226$ [25] $3{\rm n}/4{\rm n}$ $6$ $229/240$ [56] $^{50}{\rm{Ti}} + ^{{\rm{251}}}{\rm{Cf}}$ $3{\rm n}$ $120$ $232$ 3n 78 233 [57] $3{\rm n}$ $250$ $227$ [58] $^{50}{\rm{Ti}} + ^{{\rm{252}}}{\rm{Cf}}$ $3{\rm n}$ $570$ $227$ $3{\rm n}$ $43$ $232$ [60] $^{54}{\rm{Cr}} + ^{{\rm{248}}}{\rm{Cm}}$ $3{\rm n}$ 7860 $237$ $3{\rm n}$ $2$ $244$ 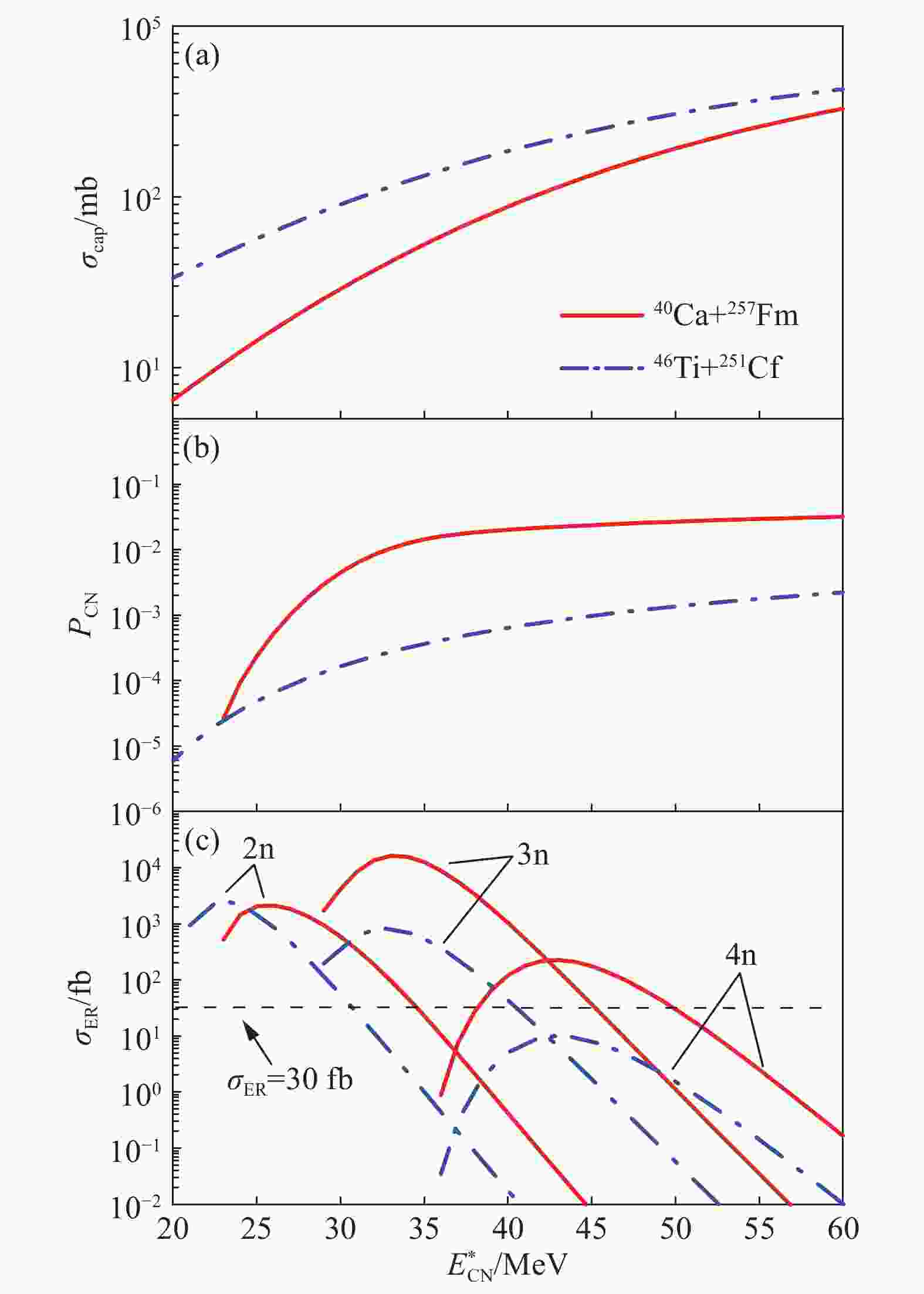
图 3 (在线彩图)
$^{40}{\rm{Ca}}+^{{\rm{257}}}{\rm{Fm}}$ 和$^{46}{\rm{Ti}}+^{{\rm{251}}}{\rm{Cf}}$ 计算的俘获截面$\sigma_{\rm cap}$ (a)、熔合几率$P_{\rm cn}$ (b) 和蒸发剩余截面$\sigma_{\rm{ER}}$ (2n、3n、4n反应道)(c)反应
$ ^{40}{\rm{Ca}}+^{{\rm{257}}}{\rm{Fm}} $ 和$ ^{46}{\rm{Ti}}+^{{\rm{251}}}{\rm{Cf}} $ 的复合核都是$ ^{297}120^{*} $ 。从图3中我们可以看到,两个反应的俘获截面和熔合几率都是随着激发能$ E^{*}_{\rm{{CN}}} $ 的增加而增大的,这是因为克服库仑位垒和内部熔合位垒的几率在增加。在激发能$ E^{*}_{\rm{CN}} = 33 $ MeV附近反应$ ^{40}{\rm{Ca}}+ ^{{\rm{257}}}{\rm{Fm}} $ 的俘获截面比反应$ ^{46}{\rm{Ti}}+ ^{{\rm{251}}}{\rm{Cf}} $ 小几倍,而反应$ ^{40}{\rm{Ca}}+^{{\rm{257}}}{\rm{Fm}} $ 的熔合几率却要比反应$ ^{46}{\rm{Ti}}+^{{\rm{251}}}{\rm{Cf}} $ 大1~2个量级,这是因为反应$ ^{40}{\rm{Ca}}+ ^{{\rm{257}}}{\rm{Fm}} $ 的内部熔合位垒低于反应$ ^{46}{\rm{Ti}}+ ^{{\rm{251}}}{\rm{Cf}} $ ,而它们熔合位垒的不同是由于$ ^{40}{\rm{Ca}}+^{{\rm{257}}}{\rm{Fm}} $ 体系的质量不对称度要比46Ti+251Cf大一些($ ^{40}{\rm{Ca}}+ ^{{\rm{257}}}{\rm{Fm}} $ 的$ \eta_{i} $ =–0.731,$ ^{46}{\rm{Ti}}+^{{\rm{251}}}{\rm{Cf}} $ 的$ \eta_{i}{'} $ =–0.690)。由此可见,熔合几率对最终蒸发剩余截面影响非常大。 -
人们除了对Z=119和Z=120的超重元素做了大量的研究以外,同时也对Z=121和Z=122的超重元素非常感兴趣,做了许多相关的尝试。为了合成Z=121和Z=122的元素,如果还使用48Ca作为弹核的话,那么就要求Z>100的锕系元素作为靶核,但是目前实验室上还不能够搜集足够多数量的Z>100的核素做成靶用来进行熔合反应,所以人们希望可以通过Ti、V、Cr、Fe、Ni、As、Se、Zr这些弹核去合成那些更重的超重元素。
对于Z=121超重元素的合成,Manjunatha等[61]提出合成超重核Z=121的最佳弹靶组合为V+Cf,而有最大蒸发剩余截面的是反应
$ ^{48}{\rm{V}}+^{{\rm{254}}}{\rm{Cf}} $ ,在$ E^{*}_{ \rm{CN}} $ =17 MeV处合成核素$ ^{300}121 $ 的截面为$ \sigma_{\rm{ER}}(2{\rm n}) = 2.6 $ pb,并且认为299-304121超重核具有足够长的半衰期从而能够被实验上探测到。考虑到不稳定的弹核会污染实验设备以及更长寿命的靶核会更有利于核反应实验的进行,我们挑选了稳定核50,51V和半衰期大于15 d的248-254Cf[62] 作为弹靶组合来计算它们合成超重核Z=121的蒸发剩余截面值,图4是反应$ ^{50}{\rm{V}} + ^{{\rm{248}}}{\rm{Cf}} $ 和$ ^{50}{\rm{V}} + ^{{\rm{251}}}{\rm{Cf}} $ 的激发曲线。从图中可以看出计算出的蒸发剩余截面仍在目前的实验检测能力范围内。反应截面最大的反应体系是$ ^{50}{\rm{V}}+^{{\rm{248}}}{\rm{Cf}} $ ,产生截面为131.6 fb,其中248Cf的半衰期为330.50 d,尽管248Cf的寿命足够长可以用来做靶核,但是目前去搜集它仍非常困难并且也会比较昂贵,而251Cf的半衰期为898.00 a,所以反应$ ^{50}{\rm{V}}+^{{\rm{251}}}{\rm{Cf}} $ 也值得考虑用来合成超重核Z=121。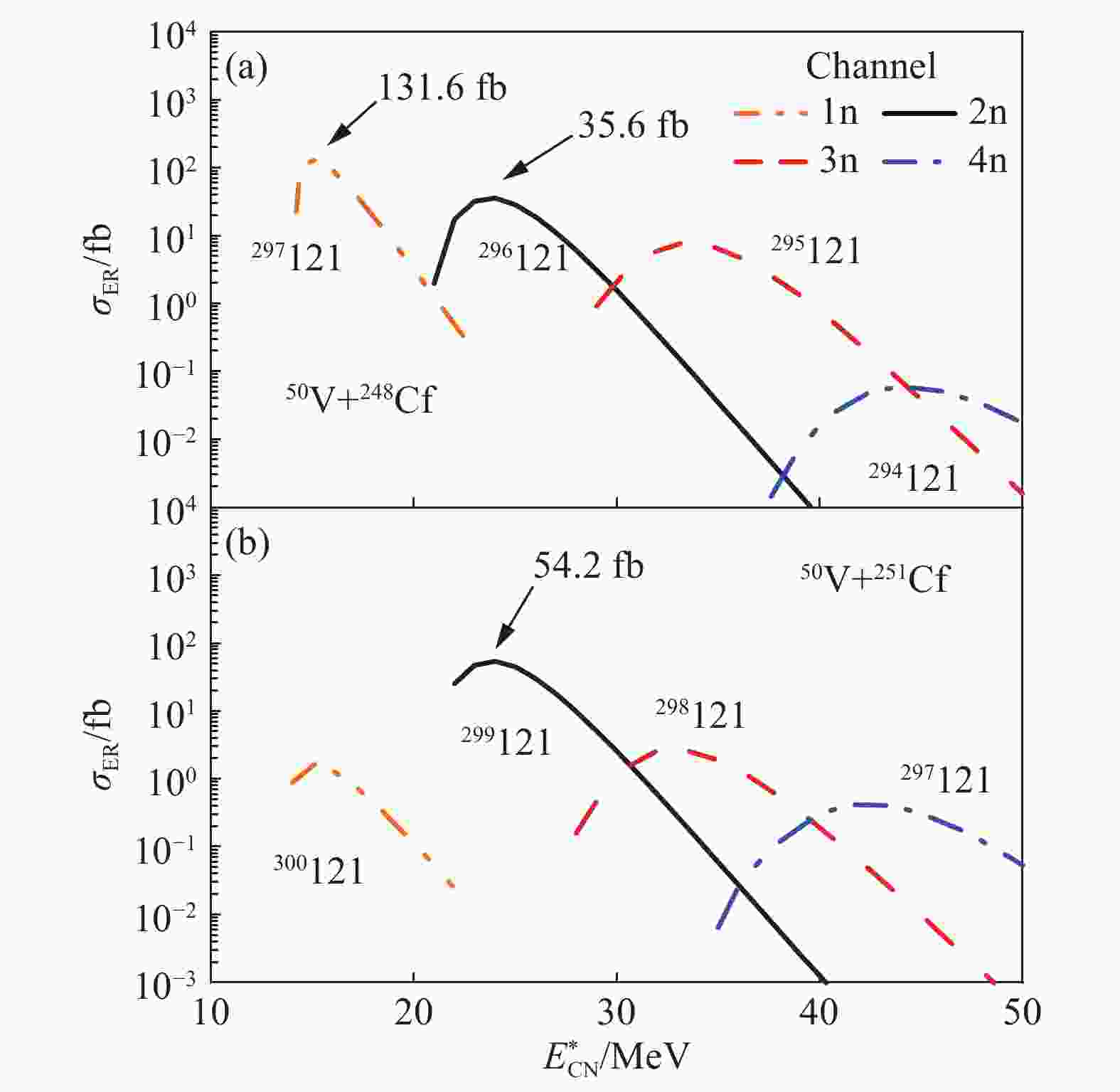
图 4 (在线彩图)反应
$^{50}{\rm{V}}+^{{\rm{248}}}{\rm{Cf}}$ (a)和$^{50}{\rm{V}}+ ^{{\rm{251}}}{\rm{Cf}}$ (b)合成超重核Z=121的蒸发剩余激发函数,箭头指示了截面值大于30 fb的各出射道最大蒸发剩余截面值对于Z=122超重元素的合成,理论上已经预言了许多的最佳反应体系,其中包括反应
$ ^{54}{\rm{Cr}}+ ^{{\rm{249}}}{\rm{Cf}} $ [21, 27]、$ ^{58}{\rm{Fe}}+ ^{{\rm{248}}}{\rm{Cm}} $ [63-65]、$ ^{64}{\rm{Ni}}+ ^{{\rm{242}}}{\rm{Pu}} $ [64]和$ ^{64}{\rm{Ni}} + ^{{\rm{244}}}{\rm{Pu}} $ [63]等。在图5中我们计算了反应$ ^{54}{\rm{Cr}}+^{{\rm{249}}}{\rm{Cf}} $ 和$ ^{58}{\rm{Fe}} + ^{{\rm{248}}}{\rm{Cm}} $ 的激发函数。对于反应$ ^{54}{\rm{Cr}}+ ^{{\rm{249}}}{\rm{Cf}} $ ,在激发能$ E_{ \rm{CN}}^{*} $ =33 MeV处3n道的最大蒸发剩余截面值为$ 4.6\times10^{-2} $ fb。对于反应$ ^{58}{\rm{Fe}}+^{{\rm{248}}}{\rm{Cm}} $ ,在$ E_{ \rm{CN}}^{*} $ =22 MeV处合成304122新核素的截面为$ \sigma_{\rm{ER}}(2{\rm n}) = 3.1\times10^{-3} $ fb,我们发现它们的产生截面都很小。因为随着弹核电荷数的增加,入射道的库仑位垒增大,而且反应体系的质量不对称度减小导致熔合几率降低。由于合成超重核Z=122的产生截面远小于实验测量的极限(30 fb),因此只有在将来提高实验设备后才能进行实验。 -
本文首先比较了双核系统模型、核子集体化模型、核扩散模型对
$ Z\leqslant118 $ 元素的计算结果与实验数据的符合情况,证明了不同模型对超重核的合成具备一定的预测能力。然后对比分析了双核系统模型、核子集体化模型、核扩散模型、两步模型和唯象经验方法对Z=119和Z=120超重核的预言结果,我们认为合成超重核Z=119和Z=120的最佳弹靶组合分别为反应$ ^{48}{\rm{Ca}}+^{{\rm{252}}}{\rm{Es}} $ 和$ ^{40}{\rm{Ca}}+ ^{{\rm{257}}}{\rm{Fm}} $ ,在将来的实验条件下Z=119的超重元素很有可能会是Z>118的元素中首先被合成的。最后,由于实验上Z>100锕系靶的限制,使用48Ca作为弹核来合成Z=121和Z=122的超重核会存在困难,所以人们正尝试使用Ti、V、Cr、Fe、Ni、As、Se、Zr这些更重的弹核去合成Z=121和Z=122的超重核。我们可以考虑通过反应V+Cf来合成Z=121的超重核素,而合成超重核Z=122的截面已经很小,要求我们将来在实验上提高探测及鉴别技术。我们希望文中的一些结果与讨论能够在将来给实验及理论核物理工作者们提供一些参考。
Progess on Synthesis of Superheavy Nuclei Z=119~122 with Predictions from Different Theoretical Models
-
摘要: 通过双核系统模型与其他模型对
$Z\leqslant$ 118元素的计算结果与实验数据的比较,证明了不同模型预测超重核的产生截面是可靠的。对比分析了不同模型对Z=119和Z=120超重核的预言结果,我们认为合成超重核Z=119和Z=120的最佳弹靶组合分别为反应$^{48}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$ 和$^{40}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$ ,并且Z=119新核素很有可能会先于Z=120新核素在实验上被合成。由于实验上Z>100锕系靶的限制,人们正尝试寻找比48Ca更重的弹核来合成超重核Z=121和Z=122,超重核Z=121可以通过反应V+Cf来合成,而超重核Z=122的产生截面已经非常小,要求将来在实验上提高探测及鉴别技术。希望本文的讨论可以在将来为实验及理论核物理工作者们提供一些参考。Abstract: In this paper, the calculated results of elements$Z\leqslant$ 118 based on the dinuclear system model and other models are compared with the experimental data. It is proved that different models are reliable in predicting the production cross sections of superheavy nuclei. The prediction results of superheavy nuclei$Z=119$ and$Z=120$ by different models are compared and analyzed. It is found that the optimal projectile-target combinations to synthesize superheavy nuclei$Z$ =119 and$Z$ =120 are$^{48}{\rm{Ca}}+ ^{{\rm{252}}}{\rm{Es}}$ and$^{40}{\rm{Ca}}+^{{\rm{257}}}{\rm{Fm}}$ , respectively, and it is likely that the new isotopes$Z$ =119 will be synthesized in the experiment before the new isotopes$Z$ =120. Because of the lack of target with$Z>$ 100 in the laboratory, attempts are being made to find heavier projectiles than 48Ca to synthesize superheavy nuclei$Z$ =121 and$Z$ =122. The superheavy nuclei$Z$ =121 can be synthesized by reactions V+Cf. However, the production cross sections of superheavy nuclei$Z$ =122 are very small, which requires us to improve the detection and identification techniques in the future. We hope that the discussion in this paper can provide some guidances for experimental and theoretical nuclear physicists in the future. -
表 1 不同模型对合成Z=119和Z=120超重核的最佳反应体系(最大截面/fb)预测的比较
核素 双核系统模型[50] 核子集体化模型[21, 51] 核扩散模型[25] 两步模型[52] 唯象经验方法[53-54] $^{289}119$ $^{40}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$ (1270)$-$ $-$ $-$ $-$ $^{291}119$ $^{42}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$ (1710)$-$ $-$ $-$ $-$ $^{293}119$ $^{44}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$ (4320)$-$ $-$ $-$ $-$ $^{294}119$ $-$ $-$ $-$ $^{50}{\rm{Ti}} + ^{{\rm{247}}}{\rm{Bk}}$ (43)$-$ $^{295}119$ $^{44}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$ (2130)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$ (57)$^{48}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$ (44)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$ (14)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$ (41)$^{296}119$ $-$ $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$ (39)$^{48}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$ (200)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$ (29)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$ (105)$^{297}119$ $^{46}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$ (3600)$-$ $^{48}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$ (79)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$ (19)$^{48}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$ (952)$^{298}119$ $^{46}{\rm{Ca}} + ^{{\rm{255}}}{\rm{Es}}$ (610)$^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$ (234)$^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$ (16)$-$ $^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$ (155)$^{299}119$ $^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$ (1670))$^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$ (300)$-$ $-$ $^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$ (722)$^{290}120$ $^{50}{\rm{Cr}} + ^{{\rm{242}}}{\rm{Cm}}$ (100)$-$ $-$ $-$ $-$ $^{292}120$ $^{46}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$ (240)$-$ $-$ $-$ $-$ $^{293}120$ $^{40}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$ (170)$-$ $-$ $-$ $-$ $^{294}120$ $^{40}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$ (1240)$-$ $-$ $-$ $-$ $^{295}120$ $-$ $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$ (45)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$ (6)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$ (2)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$ (2)$^{296}120$ $^{42}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$ (290)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$ (42)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$ (6)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$ (3)$^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$ (103)$^{297}120$ $-$ $-$ $-$ $^{50}{\rm{Ti}} + ^{{\rm{250}}}{\rm{Cf}}$ (5)$-$ $^{298}120$ $^{44}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$ (1040)$^{54}{\rm{Cr}} + ^{{\rm{248}}}{\rm{Cm}}$ (25)$-$ $^{50}{\rm{Ti}} + ^{{\rm{250}}}{\rm{Cf}}$ (8)$^{54}{\rm{Cr}} + ^{{\rm{248}}}{\rm{Cm}}$ (5)$^{299}120$ $-$ $^{54}{\rm{Cr}} + ^{{\rm{248}}}{\rm{Cm}}$ (14)$-$ $^{50}{\rm{Ti}} + ^{{\rm{252}}}{\rm{Cf}}$ (12)$^{54}{\rm{Cr}} + ^{{\rm{248}}}{\rm{Cm}}$ (15)$^{300}120$ $^{46}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$ (500)$-$ $-$ $^{50}{\rm{Ti}} + ^{{\rm{252}}}{\rm{Cf}}$ (7)$-$ $^{302}120$ $^{48}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$ (460)$-$ $-$ $-$ $-$ 表 2 合成超重核Z=119的不同预言结果和我们计算的最大产生截面及对应的出射道与入射能量
文献 反应体系 其他工作 本工作 出射道 $\sigma_{\rm{ER}}^{\max}/{\rm{fb}}$ $E_{\rm{c.m.}}/{\rm{MeV}}$ 出射道 $\sigma_{\rm{ER}}^{\max}/{\rm{fb}}$ $E_{\rm{c.m.}}/{\rm{MeV}}$ [50] $^{44}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$ $3{\rm n}$ 4320 $204$ $3{\rm n}$ 1288 $203$ [26] $^{48}{\rm{Ca}} + ^{{\rm{252}}}{\rm{Es}}$ $4{\rm n}$ $960$ $221$ 3n 2673 214 [55] $4{\rm n}$ 3160 $227$ [53] $3{\rm n}$ $952$ $216$ [25] $4{\rm n}$ $200$ $220$ [56] $^{48}{\rm{Ca}} + ^{{\rm{254}}}{\rm{Es}}$ $3{\rm n}$ 4040 $211$ $3{\rm n}$ 2459 $211$ [52] $^{50}{\rm{Ti}} + ^{{\rm{247}}}{\rm{Bk}}$ $3{\rm n}$ $43$ $230$ $2{\rm n}$ $69$ $217$ [57] $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Bk}}$ $4{\rm n}$ $110$ $234$ 2n 1510 221 [58] $3{\rm n}$ $480$ $226$ 表 3 合成超重核Z=120的不同预言结果和我们计算的最大产生截面及对应的出射道与入射能量
文献 反应体系 其他工作 本工作 出射道 $\sigma_{\rm{ER}}^{\max}$ /fb$E_{\rm{c.m.}}$ /MeV出射道 $\sigma_{\rm{ER}}^{\max}$ /fb$E_{\rm{c.m.}}$ /MeV[50] $^{40}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$ $3{\rm n}$ 1240 $206$ $3{\rm n}$ 16313 $199$ [55] $^{48}{\rm{Ca}} + ^{{\rm{257}}}{\rm{Fm}}$ $5{\rm n}$ $88$ $234$ $3{\rm n}$ $56$ $213$ [59] $^{46}{\rm{Ti}} + ^{{\rm{251}}}{\rm{Cf}}$ $2{\rm n}$ 6200 $207$ $2{\rm n}$ 2547 $213$ [26] $^{50}{\rm{Ti}} + ^{{\rm{249}}}{\rm{Cf}}$ $4n$ $29$ $240$ 2n 93 226 [54] $3{\rm n}$ $103$ $226$ [25] $3{\rm n}/4{\rm n}$ $6$ $229/240$ [56] $^{50}{\rm{Ti}} + ^{{\rm{251}}}{\rm{Cf}}$ $3{\rm n}$ $120$ $232$ 3n 78 233 [57] $3{\rm n}$ $250$ $227$ [58] $^{50}{\rm{Ti}} + ^{{\rm{252}}}{\rm{Cf}}$ $3{\rm n}$ $570$ $227$ $3{\rm n}$ $43$ $232$ [60] $^{54}{\rm{Cr}} + ^{{\rm{248}}}{\rm{Cm}}$ $3{\rm n}$ 7860 $237$ $3{\rm n}$ $2$ $244$ -
[1] SOBICZEWSKI A, GAREEV F A, KALINKIN B N. Phys Lett, 1966, 22(4): 500. doi: 10.1016/0031-9163(66)91243-1 [2] MÜNZENBERG G, HOFMANN S, HEßBERGER F P, et al. Zeitschrift für Physik A Atoms and Nuclei, 1981, 300(1): 107. doi: 10.1007/BF01412623 [3] MÜNZENBERG G, ARMBRUSTER P, FOLGER H, et al. Zeitschrift für Physik A Atoms and Nuclei, 1984, 317(2): 235. doi: 10.1007/BF01421260 [4] MÜNZENBERG G, ARMBRUSTER P, HEßBERGER F P, et al. Zeitschrift für Physik A Atoms and Nuclei, 1982, 309(1): 89. doi: 10.1007/BF01420157 [5] HOFMANN S, NINOV V, HEßBERGER F P, et al. Zeitschrift für Physik A Hadrons and Nuclei, 1995, 350(4): 277. doi: 10.1007/BF01291181 [6] HOFMANN S, NINOV V, HEßBERGER F P, et al. Zeitschrift für Physik A Hadrons and Nuclei, 1995, 350(4): 281. doi: 10.1007/BF01291182 [7] HOFMANN S, NINOV V, HEßBERGER F P, et al. Zeitschrift für Physik A Hadrons and Nuclei, 1996, 354(3): 229. doi: 10.1007/BF02769517 [8] MORITA K, MORIMOTO K, KAJI D, et al. Journal of the Physical Society of Japan, 2004, 73(10): 2593. doi: 10.1143/jpsj.73.2593 [9] MORITA K, MORIMOTO K, KAJI D, et al. Journal of the Physical Society of Japan, 2007, 76(4): 045001. doi: 10.1143/JPSJ.76.045001 [10] OGANESSIAN Y T, YEREMIN A V, POPEKO A G, et al. Nature, 1999, 400(6741): 242. doi: 10.1038/22281 [11] OGANESSIAN Y T, ABDULLIN F S, DMITRIEV S N, et al. Phys Rev C, 2013, 87(1): 014302. doi: 10.1103/PhysRevC.87.014302 [12] OGANESSIAN Y T, UTYONKOV V K, LOBANOV Y V, et al. Phys Rev C, 2000, 63(1): 011301. doi: 10.1103/PhysRevC.63.011301 [13] OGANESSIAN Y T, ABDULLIN F S, BAILEY P D, et al. Phys Rev Lett, 2010, 104(14): 142502. doi: 10.1103/PhysRevLett.104.142502 [14] OGANESSIAN Y T, UTYONKOV V K, LOBANOV Y V, et al. Phys Rev C, 2006, 74(4): 044602. doi: 10.1103/PhysRevC.74.044602 [15] OGANESSIAN Y T, UTYONKOV V K, LOBANOV Y V, et al. Phys Rev C, 2009, 79(2): 024603. doi: 10.1103/PhysRevC.79.024603 [16] HOFMANN S, HEINZ S, MANN R, et al. European Physical Journal A, 2016, 52(6): 180. doi: 10.1140/epja/i2016-16180-4 [17] HEßBERGER F P, ACKERMANN D. European Physical Journal A, 2017, 53(6): 123. doi: 10.1140/epja/i2017-12307-5 [18] ABE Y, MARCHIX A, SHEN C, et al. International Journal of Modern Physics E, 2007, 16(02): 491. doi: 10.1142/S0218301307005922 [19] SHEN C, ABE Y, BOILLEY D, et al. International Journal of Modern Physics E, 2008, 17(supp01): 66. doi: 10.1142/S0218301308011768 [20] ZAGREBAEV V I. Phys Rev C, 2001, 64(3): 034606. doi: 10.1103/PhysRevC.64.034606 [21] ZAGREBAEV V, GREINER W. Phys Rev C, 2008, 78(3): 034610. doi: 10.1103/PhysRevC.78.034610 [22] ZAGREBAEV V I, GREINER W. Nucl Phys A, 2015, 944: 257. doi: 10.1016/j.nuclphysa.2015.02.010 [23] SWIATECKI W J, SIWEK-WILCZYNSKA K, WILCZYNSKI J. Phys Rev C, 2005, 71(1): 014602. doi: 10.1103/PhysRevC.71.014602 [24] LIU Z H, BAO J D. Phys Rev C, 2009, 80(5): 054608. doi: 10.1103/PhysRevC.80.054608 [25] SIWEK-WILCZYNSKA K, CAP T, KOWAL M, et al. Phys Rev C, 2012, 86(1): 014611. doi: 10.1103/PhysRevC.86.014611 [26] ZHU L, XIE W J, ZHANG F S. Phys Rev C, 2014, 89(2): 024615. doi: 10.1103/PhysRevC.89.024615 [27] GHAHRAMANY N, ANSARI A. European Physical Journal A, 2016, 52(9): 287. doi: 10.1140/epja/i2016-16287-6 [28] SANTHOSH K P, SAFOORA V. European Physical Journal A, 2018, 54(5): 80. doi: 10.1140/epja/i2018-12512-8 [29] ADAMIAN G G, ANTONENKO N V, SCHEID W. Nucl Phys A, 1997, 618(1-2): 176. doi: 10.1016/S0375-9474(97)88172-9 [30] ADAMIAN G G, ANTONENKO N V, SCHEID W, et al. Nucl Phys A, 1998, 633(3): 409. doi: 10.1016/S0375-9474(98)00124-9 [31] FENG Z Q, JIN G M, LI J Q, et al. Nucl Phys A, 2009, 816: 33. doi: 10.1016/j.nuclphysa.2008.11.003 [32] ZHU L, FENG Z Q, LI C, et al. Phys Rev C, 2014, 90(1): 014612. doi: 10.1103/PhysRevC.90.014612 [33] ZHU L, FENG Z Q, ZHANG F S. Journal of Physics G: Nuclear and Particle Physics, 2015, 42(8): 085102. doi: 10.1088/0954-3899/42/8/085102 [34] ZHANG G, SOKHNA C A T, LIU Z, et al. Phys Rev C, 2019, 100(2): 024613. doi: 10.1103/PhysRevC.100.024613 [35] ANTONENKO N V, CHEREPANOV E A, NASIROVET A K, et al. Phys Rev C, 1995, 51: 2635. doi: 10.1103/PhysRevC.51.2635 [36] LI W, WANG N, JIA F, et al. Journal of Physics G: Nuclear and Particle Physics, 2006, 32(8): 1143. doi: 10.1088/0954-3899/32/8/006 [37] ZUBOV A S, ADAMIAN G G, ANTONENKO N V, et al. Phys Rev C, 2002, 65(2): 024308. doi: 10.1103/PhysRevC.65.024308 [38] AYIK S, SCHÜRMANN B, NÖRENBERG W. Zeitschrift für Physik A Atoms and Nuclei, 1976, 277(3): 299. doi: 10.1007/BF01415605 [39] GRANGE P, JUN-QING L, WEIDENMULLER H A. Phys Rev C, 1983, 27(5): 2063. doi: 10.1103/PhysRevC.27.2063 [40] SCHMIDT K H, MORAWEK W. Reports on Progress in Physics, 1991, 54(7): 949. doi: 10.1088/0034-4885/54/7/002 [41] FENG Z Q, JIN G M, LI J Q, et al. Phys Rev C, 2007, 76(4): 044606. doi: 10.1103/PhysRevC.76.044606 [42] LI J Q, WOLSCHIN G. Phys Rev C, 1983, 27(2): 590. doi: 10.1103/PhysRevC.27.590 [43] FENG Z Q, JIN G M, FU F, et al. Nucl Phys A, 2006, 771: 50. doi: 10.1016/j.nuclphysa.2006.03.002 [44] JACKSON J D. Canadian Journal of Physics, 1956, 34(8): 767. doi: 10.1139/p56-087 [45] FROBRICH P, STRACK B, DURAND M. Nucl Phys A, 1983, 406(3): 557. doi: 10.1016/0375-9474(83)90377-9 [46] SWIATECKI W J. Physica Scripta, 1981, 24(1B): 113. doi: 10.1088/0031-8949/24/1B/007 [47] OGANESSIAN Y T, UTYONKOV V K, LOBANOV Y V, et al. Phys Rev C, 2004, 70(6): 064609. doi: 10.1103/PhysRevC.70.064609 [48] OGANESSIAN Y T, ABDULLIN F S, ALEXANDER C, et al. Phys Rev C, 2013, 87(5): 054621. doi: 10.1103/PhysRevC.87.054621 [49] VOINOV A A, OGANESSIAN Y T, ABDULLIN F S, et al. Study of the 249-251Cf+48Ca Reactions: Recent Results and Outlook[C]. Journal of Physics: Conference Series. IOP Publishing, 2018, 966(1): 012057. [50] LI F, ZHU L, WU Z H, et al. Phys Rev C, 2018, 98(1): 014618. doi: 10.1103/PhysRevC.98.014618 [51] ZAGREBAEV V I, KARPOV A V, GREINER W. Phys Rev C, 2012, 85(1): 014608. doi: 10.1103/PhysRevC.85.014608 [52] LIU L, SHEN C, LI Q, et al. European Physical Journal A, 2016, 52(2): 35. doi: 10.1140/epja/i2016-16035-0 [53] SANTHOSH K P, SAFOORA V. Phys Rev C, 2017, 96(3): 034610. doi: 10.1103/PhysRevC.96.034610 [54] SANTHOSH K P, SAFOORA V. Phys Rev C, 2016, 94(2): 024623. doi: 10.1103/PhysRevC.94.024623 [55] DEVARAJA H M, GAMBHIR Y K, GUPTA M, et al. Phys Rev C, 2016, 93(3): 034621. doi: 10.1103/PhysRevC.93.034621 [56] BAO X J, GAO Y, LI J Q, et al. Phys Rev C, 2015, 91(1): 011603. doi: 10.1103/PhysRevC.91.011603 [57] WANG N, ZHAO E G, SCHEID W, ZHOU S G. Phys Rev C, 2012, 85(4): 041601. doi: 10.1103/PhysRevC.85.041601 [58] ZHANG J, WANG C, REN Z. Nucl Phys A, 2013, 909: 36. doi: 10.1016/j.nuclphysa.2013.04.010 [59] SRIDHAR K N, MANJUNATHA H C, RAMALINGAM H B. Nucl Phys A, 2019, 983: 195. doi: 10.1016/j.nuclphysa.2018.11.032 [60] NASIROV A K, GIARDINA G, MANDAGLIO G, et al. Phys Rev C, 2009, 79(2): 024606. doi: 10.1103/PhysRevC.79.024606 [61] SRIDHAR K N, MANJUNATHA H C, RAMALINGAM H B. Phys Rev C, 2018, 98(6): 064605. doi: 10.1103/PhysRevC.98.064605 [62] Nuclear Map[EB/OL].[2020-01-08]. http://nrv.jinr.ru/nrv/webnrv/map/. [63] LITNEVSKY V L, KOSENKO G I, IVANYUK F A. Phys Rev C, 2016, 93(6): 064606. doi: 10.1103/PhysRevC.93.064606 [64] CHOPRA S, GUPTA R K. Physl Rev C, 2017, 95(4): 044603. doi: 10.1103/PhysRevC.95.044603 [65] MANJUNATHA H C, SRIDHAR K N, SOWMYA N. Phys Rev C, 2018, 98(2): 024308. doi: 10.1103/PhysRevC.98.024308 -
















 下载:
下载:










































































































































































































































































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号