-
On August 17th 2017 the first gravitational wave (GW) signal from binary neutron star (BNS) merger was recorded by LIGO and VIRGO detectors[1]. This event was the first one long sought gravitational wave signal coming from, at that time, only theorized neutron star collision. Such type of events was long awaited since it allows to study both gravitational aspects of such a phenomenon as well as dynamical properties of matter contained in neutron star interiors. Neutron stars are assumed to be the densest stable objects in the universe with central core densities reaching several times nuclear saturation densities. An additional gravitational and dynamical compression created by the merger creates an even more extreme environment where temperatures may reach up to
$ T\sim 100 $ MeV. At such conditions the matter properties are described by the theory of strong interactions – Quantum Chromodynamics (QCD).The QCD theory itself is well established, but direct calculations are rather problematic – the theory suffers calculation problems: the large coupling constant disfavors perturbative methods and the numerical sign problem prevents lattice (LQCD) calculations at finite densities. Usage of phenomenological models for description of QCD matter is well accepted, but effective theories always rely on experimental observations and first-principle calculations. QCD phenomenology suggests a rather rich phase diagram of QCD matter[2-6], however no consensus on the structure of the phase diagram is reached yet. A big scientific interest is attracted to the hypothesis of a phase transition, attributed to the quark deconfinement. Even though the transition is much discussed in the QCD community, no indications of a first-order phase transition are yet found either experimentally or proved theoretically. Various indications of the transition were suggested: high-density nuclear Mach shock phenomena[7], studies of angular distributions of emitted particles[8-10], and signals in particle number fluctuations[11]. Recently it was proposed to measure such a transition by gravitational wave detections[12]. However, no convincing signal was detected yet.
The measurements of gravitational waves emitted from a binary neutron star merger allow to study regions of QCD phase diagram which were not experimentally accessible earlier. The QCD phase diagram is rigorously studied in laboratories by relativistic heavy ion collisions (HIC). In the experiments the large energy is deposited in a small space-time volume by two colliding nuclei, this creates an extremely compressed and heated strongly-interacting system – an expanding fireball. The fireball consists of many hadronic species at densities so large that a description in terms of a continuous fluid is appropriate. The particles in this fluid are so energetic that the system reaches temperatures
$ T>100 $ MeV. Such a system is successfully modeled by means of ideal relativistic hydrodynamics[13] which do not contain any QCD physics and require an additional input which encodes properties of the described matter – an equation of state (EOS).Even though the HIC simulations strongly depend on the equation of state, the extraction of the EOS from experimental data is rather a nontrivial procedure. Recently a usage of deep learning techniques was proposed to tackle the extraction task. It was proved that supervised learning with a deep convolutional neural network is able to identify the EOS used in simulations of heavy ion collisions by analysis of particle spectra[14]. In a more detailed study[15] a hadronic phase, which is EOS independent, was imposed on the simulations after the hydrodynamic stage of HIC. The study proved that deep convolutional neural network can identify on the event-by-event basis the EOS even if the system goes through multiple rescatterings in the hadronic phase. Spinodal clumping, an enhanced signal of a phase transition in high energy nuclear collisions[16], was proved to be detectable by machine learning methods[17]. The density clumping in coordinate space is detectable by the method in nearly every event, however in momentum distributions clumping is not observable.
Neutron star mergers are modeled theoretically by means of general relativistic hydrodynamic calculations. There the dynamics of matter govern hydrodynamic evolution, but contrary to heavy ion collisions, in the presence of a non-flat space-time metric which is generated by the binary neutron star system. Such a theoretical description is at the same time different and similar to heavy ion collisions. The QCD matter present in these systems is the same, but exists in rather different conditions. The hydrodynamic description is appropriate for both systems, but merging neutron stars require gravity to be taken into account. The other distinct difference comes from the size-scales:
$\sim\! 10\; {\rm{fm}} \!=\! 10^{-14}\; {\rm{m}}$ in heavy ion collisions, and$\sim\!10\; {\rm{km}} \!=\! 10^4\; {\rm{m}}$ in neutron stars, yielding in$ 18 $ orders of magnitude difference.On Fig. 1 the trajectories of hydrodynamic evolution over the phase diagram are presented in
$ \rho-T $ plane. The plot illustrates that the hot matter created in low energy heavy ion collisions and in neutron star mergers probes the same type of QCD matter, namely temperatures of$ T \!=\! 50\sim 60 $ MeV and densities of$ \rho \!=\! 1\sim 2\,\rho_0 $ . This hot hadronic corona is the region which is probed in the early stage of both HIC and BNS mergers and is created by the initial compression of the matter. Then this hot matter is cooled down due to the hydrodynamic evolution. However, there is another region of the phase diagram which is probed by BNS mergers but prohibited in HIC – the cold and dense matter. This one represents a rather slow compression of the NS core during the merger, where the already dense cores of neutron stars are slowly compressed during the merger with increase of density but the temperature increases only moderately. This region of cold dense core matter probes the part of QCD diagram where the hypothetical transition to deconfined matter occurs.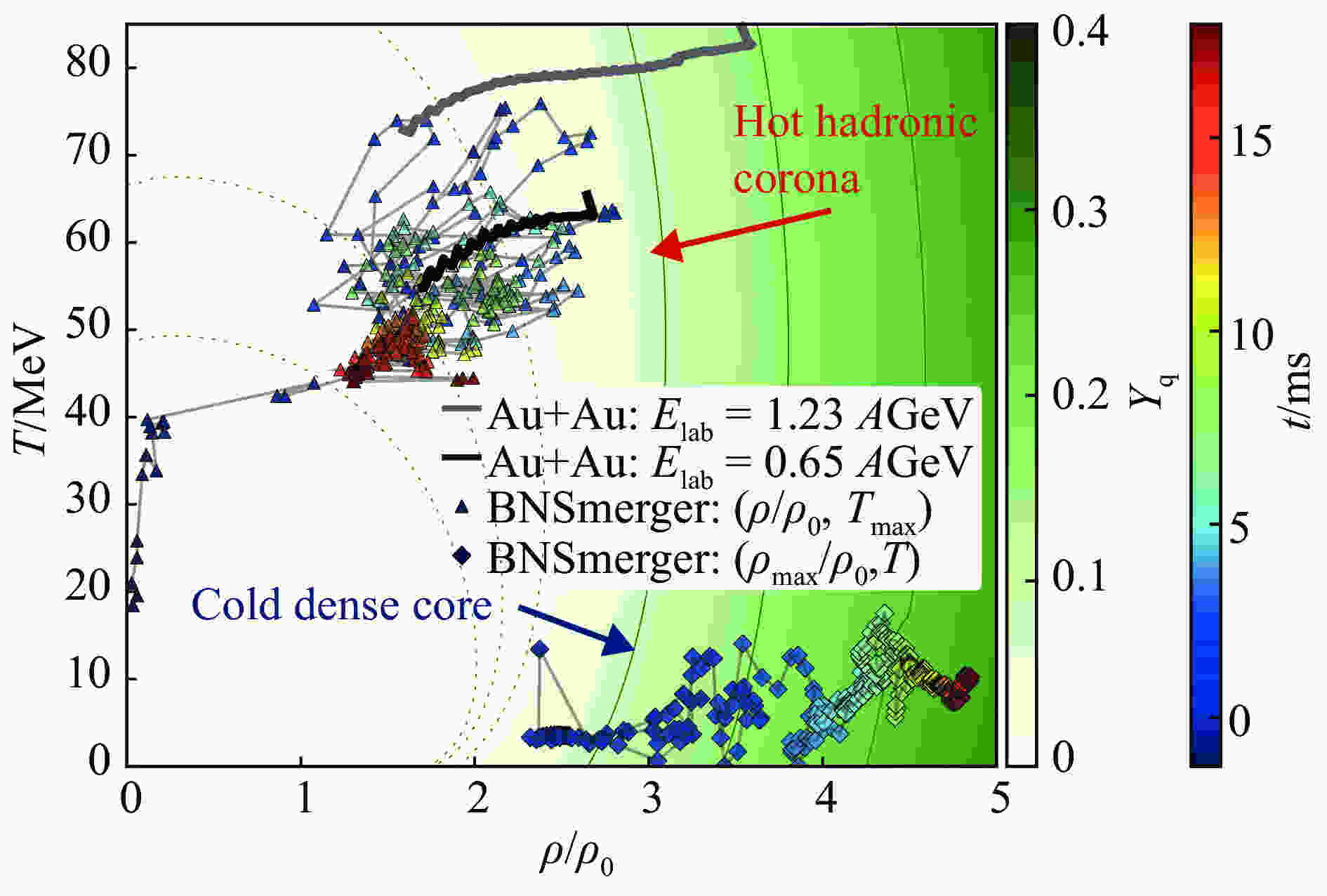
Figure 1. (color online) The maximum value of the temperature (triangles) and rest-mass density (diamonds) during the evolution of the hypermassive hybrid star using the simulation results of the LS220-M135 run (for details, see Refs. [18-19]). The color coding of triangles/diamonds indicate the time of the simulation after the merger in milliseconds (see the colorbar at the right border of the figure). The gray and black curves show the trajectories of hydrodynamic simulation of heavy-ion collision at energies
$E_{\rm{lab}}\! =\! 1.23$ AGeV and$E_{\rm{lab}} \!= \!0.65$ AGeV within the CMF model. The colorbar right next to the picture displays the quark fraction$Y_{\rm q}$ of the corresponding hot and dense matter within the CMF model. Contour lines indicate constant values of quark fraction at$Y_{\rm q}\!=\![0.0001, 0.001, 0.01]$ (green dotted lines) and$Y_{\rm q} \!= \![0.1, 0.2, 0.3]$ (green solid lines). Adapted from Ref. [20].In the present paper we will discuss how two theoretical concepts, hydrodynamic evolution and QCD matter EOS, allow to model HIC and BNS mergers, and which experimental signals of QCD matter can be found in such systems.
-
Here we present a phenomenological approach for the QCD equation of state, the Chiral
$ SU(3) $ -flavor parity-doublet Polyakov-loop Mean Field (CMF) model[21-24]. The CMF model can be used to calculate an EOS which describes nuclear matter properties at low temperatures and agrees with LQCD data at high temperatures and vanishing baryon density[23]. The CMF model is based on the main aspects of QCD phenomenology and includes the following concepts:● Interactions among baryons of the groundstate octet (nucleons,
$ \Lambda $ ,$ \Sigma $ , and$ \Xi $ baryons) are carried via mesonic mean fields according to the SU(3)$_{\rm f}$ chiral lagrangian$ {{\cal{L}}_{\cal{B}}} $ [25]:$$\begin{split} {{\cal{L}}_{\cal{B}}} =& \sum\limits_i (\bar{B_i} {\rm i} {\partial\!\!\!/} B_i) + \sum\limits_i \left(\bar{B_i} m^*_i B_i \right)+\\& \sum\limits_i \left(\bar{B_i} \gamma_\mu (g_{\omega i} \omega^\mu + g_{\rho i} \rho^\mu + g_{\phi i} \phi^\mu) B_i \right), \end{split}$$ (1) where the various coupling constants
$ g^{(j)}_i $ are determined by nuclear matter properties, here baryon effective masses read as:$$\begin{split} m^*_{i\pm} =& \sqrt{ \left[ (g^{(1)}_{\sigma i} \sigma + g^{(1)}_{\zeta i} \zeta )^2 + (m_0+n_s m_s)^2 \right]} \pm\\& g^{(2)}_{\sigma i} \sigma \pm g^{(2)}_{\zeta i} \zeta . \end{split}$$ (2) The repulsion among the baryons is mediated by the vector meson fields:
$ \omega $ meson field provides repulsion at finite baryon densities, the$ \rho $ meson field provides repulsion at finite isospin densities, and the$ \phi $ vector meson field generates repulsion when a finite strangeness density is generated.● Parity doubling among groundstate octet baryons which assumes that baryons with same quantum numbers but opposite parity are degenerate in mass at chirally restored phase, while at chirally broken phase (which is at lower energy densities) the mass gap between them is generated by non-strange and strange chiral mean fields
$ \sigma $ and$ \zeta $ , respectively[26-29]. The baryon parity determines 'plus' or 'minus' sign in Eq. (2);● The CMF model explicitly includes quark degrees of freedom similar to the Polyakov-loop-extended Nambu Jona-Lasinio (PNJL) model[30], where the quark thermal contribution is controlled by the Polyakov Loop order parameter
$ \Phi $ and the quark masses are dynamically generated by$ \sigma $ and$ \zeta $ fields[23]:$$\begin{split} P_{\rm q} =& T \sum\limits_{i\in Q}\frac{d_i}{(2 \pi)^3}\int{{\rm d}^3k} \frac{1}{N_c}\ln\left(1+3\Phi {\rm e}^{-\left(E_i^*-\mu_i\right)/T}+\right.\\&\left.3\bar{\Phi}{\rm e}^{-2\left(E_i^*-\mu^*_i\right)/T} +{\rm e}^{-3\left(E_i^*-\mu_i\right)/T}\right).\\[-15pt] \end{split}$$ (3) The sums run over all light quark flavors (u, d, and s),
$ d_i = 2\times3 $ being the quark degeneracy factor,$ E^*_i = \sqrt{m^{*2}_i+p^2} $ is the quark energy. The effective masses$ m^{*}_i $ of the light quarks are generated by the$ \sigma $ field, the mass of the strange quark is generated by the$ \zeta $ field. The small explicit mass terms are$ \delta m_{\rm q} = 5 $ MeV, and$ \delta m_{\rm s} = 150 $ MeV for the strange quark, and$ m_{0{\rm q}} = 253 $ MeV which corresponds to an explicit mass term which does not originate from chiral symmetry breaking:$$ \begin{split}& m_{\rm q}^* = -g_{{\rm q}\sigma}\sigma+\delta m_{\rm q} + m_{0{\rm q}},\\& m_{\rm s}^* = -g_{{\rm s}\zeta}\zeta+\delta m_{\rm s} + m_{0{\rm q}}. \end{split} $$ (4) The Polyakov-loop order parameter
$ \Phi $ effectively describes the gluon contribution to the thermodynamic potential and is controlled by the temperature dependent potential[23]:$$ \begin{split} U_{\rm{Pol}}(\Phi,\overline{\Phi},T) =& -\frac12 a(T)\Phi\overline{\Phi} + b(T)\log \Big[1-\\&6\Phi\overline{\Phi} + 4(\Phi^3+\overline{\Phi}^{3})-3(\Phi\overline{\Phi})^2\Big], \\ a(T) =& a_0 T^4+a_1 T_0 T^3+a_2 T_0^2 T^2, \\ b(T) =& b_3 T_0^4. \end{split} $$ (5) ● The CMF model includes full PDG list of hadrons[31] to provide a description of the QCD thermodynamics at intermediate temperatures
$ T \lesssim 160 $ MeV where meson and hadron resonances contribute significantly to the thermodynamics in the form of hadron resonance gas (HRG)[32-33]. The hadrons in the CMF model are attributed a finite size within excluded-volume (EV) model which mimics hard-core repulsion among hadrons[34-35]. This interaction mechanism allows to suppress the hadronic degrees of freedom at higher energy densities where quarks are expected to be dominant. Within the EV approach all particle densities, including quarks, read as:$$ \rho_i = \frac{\rho^{\rm{id}}_i (T, \mu^*_i - v_i\,p)}{1+\sum\limits_{j{ \epsilon {\rm{HRG}}}} v_j \rho^{\rm{id}}_j (T, \mu^*_j - v_j\,p)}, $$ (6) the
$ v_j $ are the eigenvolume parameters for the hadron species.$ p $ is total system pressure,$ \mu^* $ is the chemical potential of the hadron. In the standard CMF parameterization the$ v $ is assumed to be$ v_{\rm B} \!=\! 1 $ fm3 for (anti-) baryons,$ v_{\rm M} \!=\! 1/8 $ fm3 for mesons, and is set to zero$ v_{\rm q} \!=\! 0 $ for quarks.In the CMF model quarks appear smoothly so there is no deconfinement phase transition, the transition to quark matter is of crossover type. Note, there are also earlier implementations of the CMF model where quarks appear abruptly due to a phase transition[36-37] in the following we dub this model as
$ {\rm{CMF}}_{\rm{Q}} $ . In the$ {\rm{CMF}}_{\rm{Q}} $ model hadrons are treated as point-like particles and parity-doubling is not considered, the high density QCD transition is caused by coupling of Polyakov loop order parameter$ \Phi $ to the baryon and quark effective masses.The CMF model has two critical points. The first one is due to the established nuclear liquid-vapor phase transition[38], the critical endpoint of this transition is located at low temperature
$ T\approx 17 $ MeV and chemical potential close to the mass of the nucleon$ \mu_{\rm B}\approx 900 $ MeV. The second transition is attributed to the sudden vanishing of the chiral field. The endpoint of this transition is also located at low temperature$ T\approx 17 $ MeV but at higher values of the chemical potential$ \mu_ {\rm B}\approx 1\,400 $ MeV. The second critical point comes from the baryon parity pairing, this was also found in a similar model with only hadronic degrees of freedom[39]. None of these critical points are attributed to the quark deconfinement.The phase structure of QCD matter can be studied experimentally in HIC by measuring hadronic fluctuations[11] which are assumed to be sensitive to the proximity of the QCD critical point[40]. Usually fluctuations of
$ i $ -th conserved charge are measured by means of$ n $ -th order charge susceptibilities$ \chi^i_n $ which are theoretically calculated as derivatives of pressure with respect to the corresponding chemical potential:$ \chi^i_n = \frac{\partial^n P/T^4}{\left(\partial \mu_i/T \right)^n} $ . Significant interest is attributed to the third and fourth order baryon number fluctuations measures, namely skewness$ S \sigma = \chi^3_{\rm B}/\chi^2_{\rm B} $ and kurtosis$ \kappa \sigma^2 = \chi^4_{\rm B}/\chi^2_{\rm B} $ . The recent measurements by the STAR collaboration[41] at RHIC collider and by the HADES collaboration[42] at SIS18 accelerator present findings of rather large proton numbter fluctuations at low energy heavy ion collisions. These findings may be attributed to a critical behavior due to QCD interactions, however dynamical effects, e.g. centrality selection, finite particle acceptance, etc., are not yet ruled out.In the vicinity of the freeze out region the CMF model suggests that fluctuations are dominated by the remnants of the nuclear liquid-vapor phase transition. The chiral transition takes place at much higher chemical potentials and is located in the region which is reachable by BNS mergers.
The kurtosis values at Fig. 2 (a) suggests that the CMF model has 3 critical regions, with two of them having a critical endpoint at
$ T\approx17 $ MeV, so at$ T\gtrsim 17 $ MeV all transitions are smooth crossovers. Fig. 1 (b) indicates that quarks appear in the CMF model smoothly without a phase transition attributed to the deconfinement.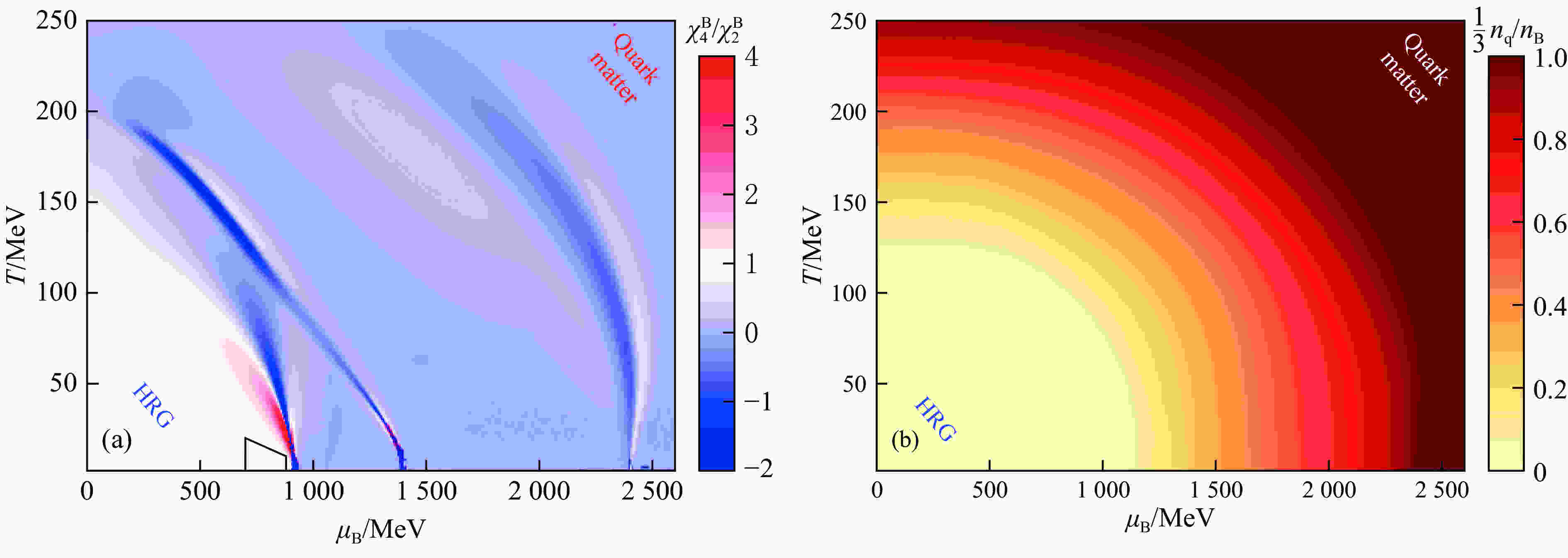
Figure 2. (color online) (a): Ratios of the CMF baryon number susceptibilities
$\chi_4^{\rm{B}}/\chi_2^{\rm{B}}$ kurtosis in the baryon chemical potential -$\mu_{\rm{B}}$ and temperature -$T$ plane. Note the 3 distinct critical regions, with their remnants reaching from$T\!=\!0$ up to$T>200$ MeV. (b): The quark fraction$\frac13{n_ {\rm q}}/{n_{\rm B}}$ of the CMF model in baryon chemical potential$\mu_{\rm{B}}$ and temperature$T$ plane. Note that the deconfinement smoothly appears only at higher energy densities/chemical potentials.We illustrate which regions of the phase diagram are probed in heavy ion collisions at low and moderate energies by using the one dimensional Taub adiabat model[43-45]. This model describes the expansion by lines of constant entropy per baryon
$ S/A = \, $ const (isentropes). These lines describe the isentropic matter evolution of ideal fluid dynamics at different collision energies. The input to the hydro simulations is the initial stage produced in a rapid and violent nuclear collision. In the initial state the entropy is produced by a violent shock compression[46]. While the system cools down during the expansion, the entropy increases only moderately due to a rather small viscosity[47-48], thus an isentropic expansion scenario is a reasonable approximation[49].The isentropic expansion of the equilibrated matter continues until the system becomes so dilute that the chemical freezeout occurs and the chemical composition is fixed.
We calculate initial entropy per baryon (
$ S/A $ ) assuming a 1-dimensional stationary scenario of central HIC – two colliding slabs of cold nuclear matter[44, 46, 50-54]. The relativistic Rankine-Hugoniot equation which results in Taub adiabat (RRHT)[43, 45], provides conservation of the baryon number, energy and momentum across the shock front. The initial state thermodynamics (density, temperature and entropy) of the hot, dense participant matter is obtained from RRHT as a function of the collision energy. The known initial entropy yields the lines of constant entropy which leads to the trajectories of the heavy ion collisions in the phase diagram.The predicted isentropic expansion trajectories are shown in the
$\mu_ {\rm B}-T$ phase diagram in Fig. 3.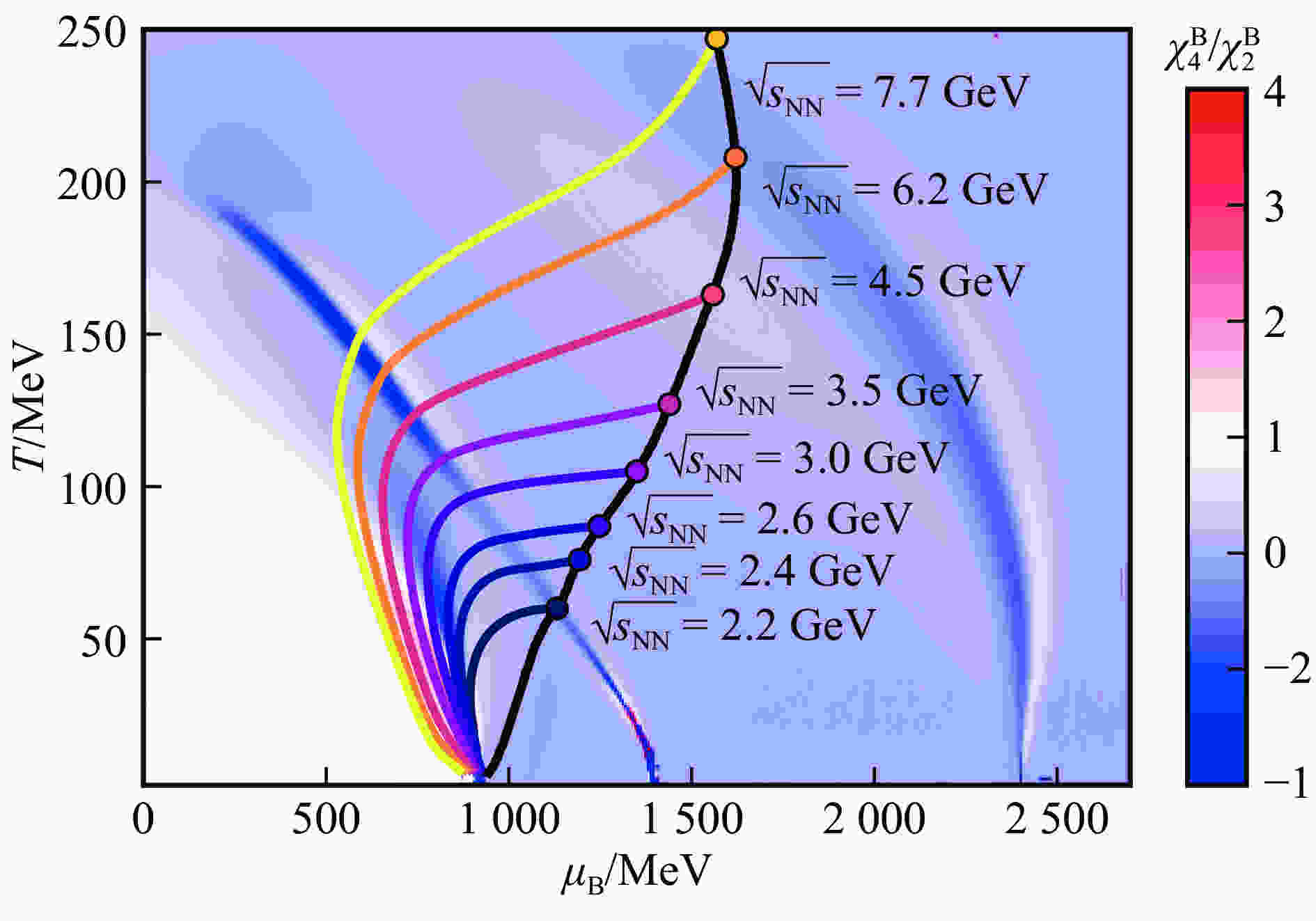
Figure 3. (color online) Evolution of heavy-ion collisions in the high baryon density region of the
$T-\mu_ {\rm B}$ phase diagram for different collision energies. Black line - Taub adiabat which describes the initial state of heavy ion collisions as an implicit function of$\sqrt{s_{\rm{NN}}}$ . Colored lines - isentropic lines of constant entropy per baryon$S/A$ at different bombarding energies$\sqrt{s_{\rm {NN}}}$ respectively.The RRHT-adiabat scenario predicts a very strong compression and heating already at an intermediate lab (fixed target) bombarding energies. The hot and dense system passes the chiral transition predicted by the present CMF model already at
$ E_{\rm{lab}}\approx 2 $ AGeV, i.e. at energies available at GSI's SIS18 accelerator facility. Here the total entropy is predicted to reach$ S/A\approx 3 $ , in accord with previous RMF-calculations[54] which also used the 1-D RRHT-scenario. The$\mu_ {\rm B}-T$ values,$ T\approx 70 $ MeV,$\mu_{\rm B}\approx 1.2$ GeV, with net baryon densities$ n_{\rm B}/n_0\approx 3 $ , reached here in HIC, coincide with the$\mu_{\rm B}-T$ values reached in binary NS collisions, as recent general relativistic fully 3+1-dimensional megneto-hydrodynamical calculations have confirmed[12, 55] for the gravitational wave event GW170817. At these temperatures and densities,$ T\approx 70 $ MeV and$n_{\rm B}/n_0\approx 3$ , the RRHT model predicts that there are about 20% of the dense matter is already transformed to quarks.Heavy ion fixed target experiments of SIS at FAiR and SPS at CERN as well as STAR BES program at RHIC probe temperatures from
$ 50<T<280 $ MeV and chemical potentials from$ 500<\mu_{\rm B}<1\,700 $ MeV for the collision energy range$ \sqrt{s_{\rm{NN}}}<10 $ GeV considered here. In this region the CMF model shows not an additional phase transition, but the remnants of the nuclear liquid-vapor transition at$ T \approx 20 $ MeV. The chiral transition at larger chemical potentials may influence the dynamical evolution as well. The present results suggest that heavy-ion collisions mostly probe regions where the nuclear matter liquid-vapor critical point dominates, there the observed baryon fluctuations are mostly due to remnants of the nuclear liquid-vapor phase transition. This had been suggested also in previous works[22, 56-60]. The CP associated with the chiral symmetry restoration in the CMF model lies at$\mu_{\rm B} \approx 1.4$ GeV and$ T \approx 17 $ MeV and is strongly affected by baryon parity doubling. This high density region is, to the best of our knowledge, reachable in the interiors of NS and in binary general relativistic NS mergers[ 12, 20, 61-64].The resulting CMF EOS at
$ T = 0 $ is used as input for the Tolman-Oppenheimer-Volkoff (TOV) equation, so a relation between the mass and the radius can be obtained for any static, spherical, gravitationally bound object[65-66], here a static NS. The outer NS layers presumably consist of mostly neutron rich nuclei and clusters in chemical and$ \beta $ -equilibrium. Those nuclei are not yet a part of the CMF model. Therefore, we use a classical crust-EOS[67] matched additionally to the CMF-EOS at$n_{\rm B}\approx 0.05\; {{\rm{fm}}^{-3}}$ . The NS mass-radius relation obtained using the TOV equation with the CMF EOS is presented in Fig. 4. The discussion of the quark and hadron content of the stars is presented in Refs. [23, 68]. Note that an unstable branch in the mass radius diagram is created by stars with the quark contribution to the baryon density$ 30\% $ and more. The central densities of the stable stars can not exceed$n_{\rm{B}} = 6\,n_0$ , where the maximum mass indicates the "last stable star". The continuous monotonous transition from NS matter to a deconfined quark phase provides a smooth appearance of quarks in the star structure and prevents a "second family" of stable solutions. Therefore there is no strict separation between a quark core and the hadronic interior of the star. This is a CMF result due to the Polyakov loop implementation of the deconfinement mechanism and no vector repulsion among quarks[70]. Though LQCD data disfavors repulsive forces for quarks, there are currently active discussions concerning vector repulsion in dense baryonic matter in NS interiors[71-72]. We present the resulting dimensionless tidal deformability coefficient$ \varLambda $ in Fig. 4, see Ref. [23] for discussion.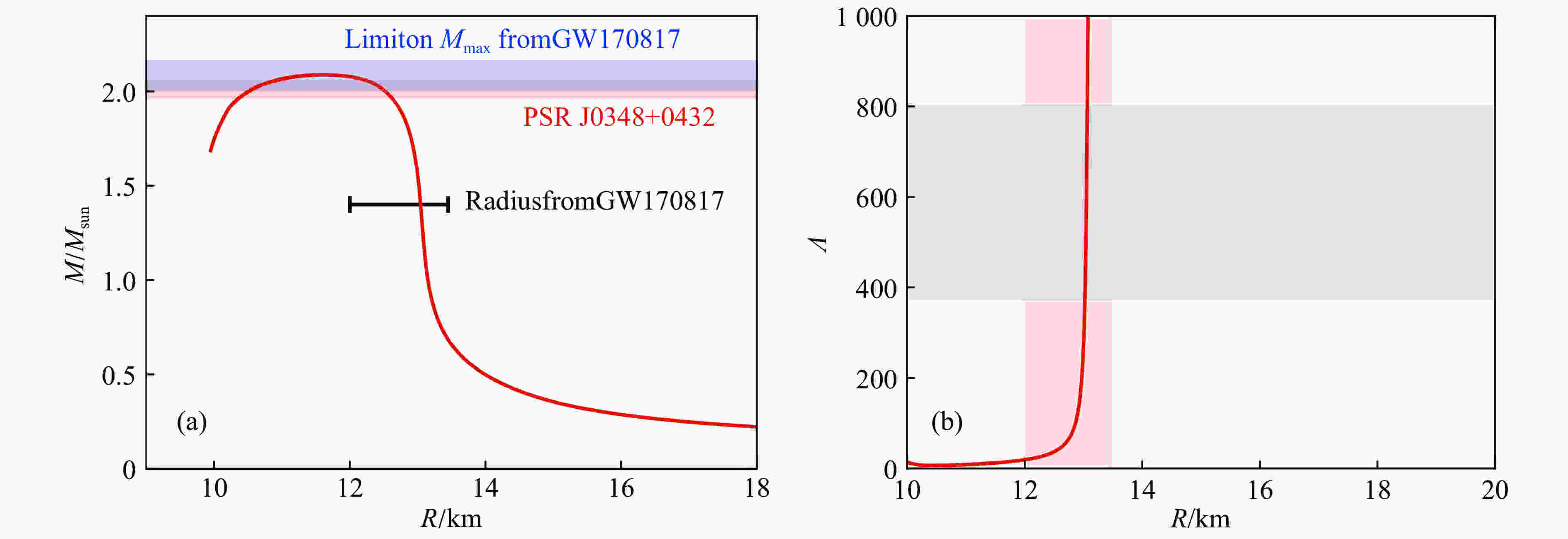
Figure 4. (color online) Neutron star mass-radius diagram (a) and tidal deformability
$\Lambda$ as function of NS radii (b) as calculated in the CMF model. In figure (b) blue bands correspond to$\Lambda$ constraints of NS with$M\!=\!1.4\sim M_{\rm{sun}}$ , and red bands- constraints on radius of NS with$M\!=\!1.4\sim M_{\rm{sun}}$ [69]. -
In the previous section the properties of MAGIC-matter at high densities and temperatures have been analyzed by using the results of relativistic collisions of heavy ions. In high-energy heavy-ion collision experiments the phase structure of the isospin-symmetric QCD equation of state is determined and it was shown that there is a large impact of the EOS on the properties of neutron stars. In this section we will take a deeper look at the signatures of the hadron-quark phase transition (HQPT) in a BNS merger scenario.
Before we will present the results obtained within two different EOSs which contains a HQPT, we will briefly focus on a conventional BNS merger simulation, e.g. using the temperature dependent, Lattimer Swesty
$ {\texttt{LS220}}$ EOS[73] with an initial mass of$ M = 1.35\,M_{\odot} $ (see Fig. 1 and Refs. [18, 74-75]). After the violent, transient post merger phase of the hypermassive neutron star (HMNS), two high temperature hot spots emerge. The high temperature values ($ T > 40 $ MeV) are reached in regions where the density is in a range of$1 \sim 2.5 \rho_{0}$ , while the maximum density values are always located in the center at moderate temperatures$ T < 20 $ MeV. The dynamics of the underlying fluid can be visualized using tracer particle (for details see Ref. [76]). Some of the tracer particles circulate around the high temperature hot spots, others populate the low temperature high dense inner region and some are moving in the outer surface of the HMNS within the low density regime. At later post merger times the HMNS reaches a quasi stable configuration and the temperature hot spots will smear out to become a ring like structure, the 'peanut' shape of the density distribution will dissolve and the area populated in the ($ T $ -$ \rho $ ) plane will populate only a small quasi stable region. The specific shape of the populated area in the ($ T $ -$ \rho $ ) plane depends on the total mass of the system and on the underlying EOS, however, if one assumes an EOS without a HQPT, the qualitative behavior of the HMNS in the post-merger phase is EOS-independent[20]. The unusual temperature hot spots and, at later times, the temperature ring-like structure are closely related with the rotation profile$ \Omega $ of the differentially rotating HMNS ($ \Omega = \alpha\; v^\phi\; - \; \beta^\phi $ , where$ v^\phi $ and$ \beta^\phi $ describes the$ \phi $ -component of the three-velocity and shift vector (see Ref. [18] for details).In the following the results of a hypermassive hybrid star (HMHS) will be discussed by focusing on a BNS merger simulation performed using the
$ {\rm{CMF}}_{\rm{Q}} $ EOS. In contrast to chiral SU(3)-flavor parity-doublet polyakov-loop quark-hadron mean-field model described in Sec. 2, the$ {\rm{CMF}}_{\rm{Q}} $ model has implemented a strong HQPT (for details see Ref. [12]). In the following we will discuss the BNS merger simulation of an initial mass of$M \!=\! 1.40\,M_{\odot}$ . For late post-merger times ($ t > 12 $ ms), the central value of the density within the HMHS reaches the phase transition boundary and a large amount of deconfined quarks appear. As a result of this transition, the EOS gets softer and the star dynamically reacts in increasing its temperature and density in the quark-hadron coexisting phase. A complicated dynamical oscillation starts as the differentially rotating HMHS decreases its radius and spins up. Within the used$ {\rm{CMF}}_{\rm{Q}} $ EOS stable hybrid stars are not possible and the matter rapidly collapses. Fig. 5 shows the last simulation snapshot ($ t \!=\! 15.26 $ ms) before the apparent horizon finder of the simulation program has detected the formation of a Kerr black hole. During the collapse of the HMHS to a Kerr black hole the color degrees of freedom of the pure quark core get macroscopically confined by the formation of the event horizon. The shape of the populated area in the ($ T $ -$ \rho $ ) plane (see Fig. 5 bottom) looks similar to a shape of a strange bird①. The hot head of the strange bird contains a high amount of deconfined strange quark matter, its thin neck is composed of mixed phase matter and follows the phase transition boundary, while its hot wings (local temperature maxima) contain mostly hadronic matter at much lower densities. The maximum temperature and density points correspond to the head of the strange bird where strangeness is present. Due to the stiffening of the EOS in the pure quark phase region, the temperature stops rising and the high pressure in the central region pushes against the large gravitational force.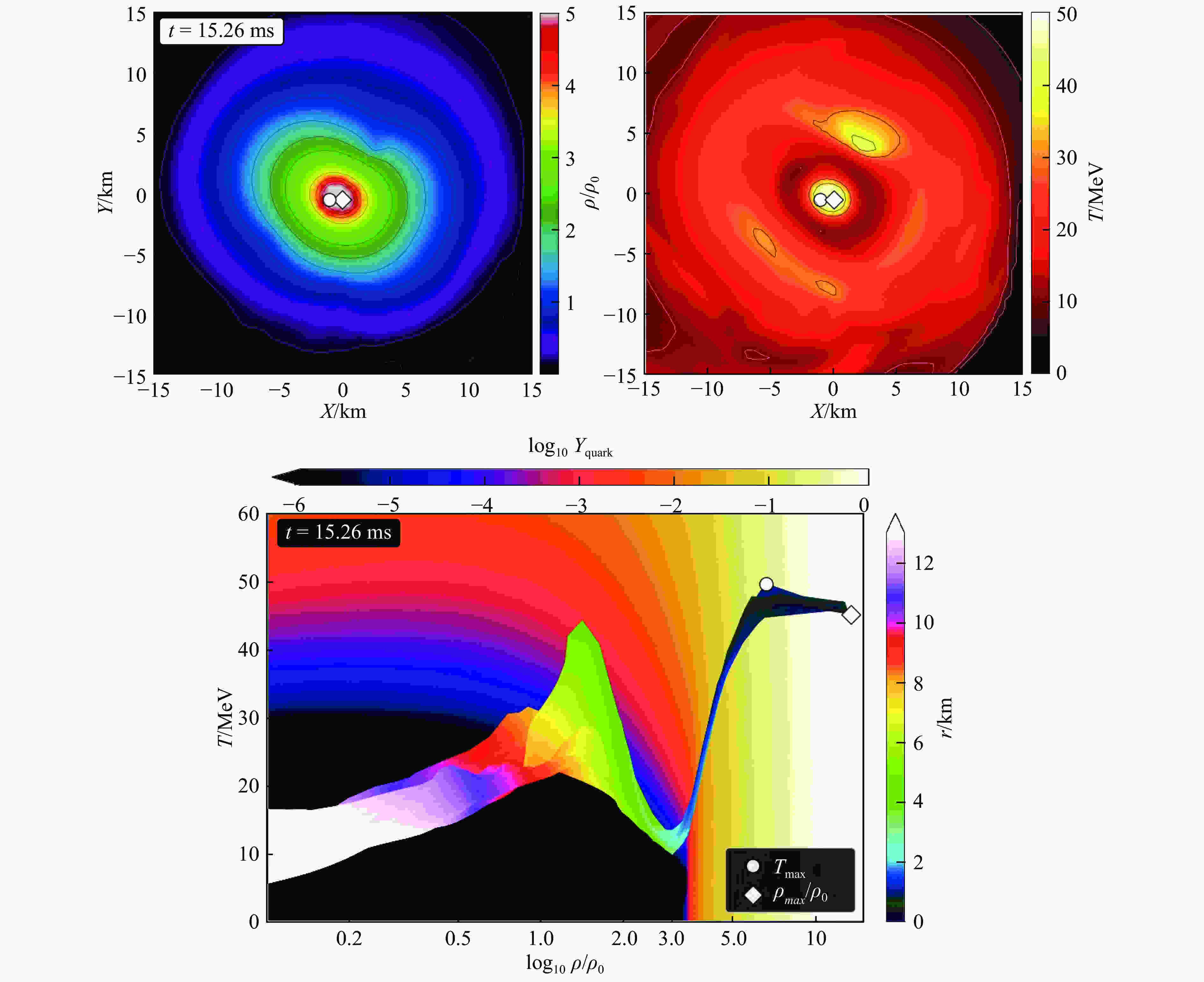
Figure 5. (color online) Upper panel: Spatial distribution of the rest-mass density
$\rho$ (left) and temperature$T$ (right) of the HMHS using the${\rm{CMF}}_{\rm{Q}}$ EOS with an initial masses of$M\!=\!1.40\,M_{\odot}$ at$t\!=\!15.26$ ms after merger. The white circles/diamonds mark the maximum values of temperature/density. Lower panel: Density-temperature profiles inside the inner region of the HMHS in the style of a$T$ -$\rho$ QCD phase diagram. The color-coding displayed on the right side indicates the radial position$r$ of the corresponding fluid element inside the HMHS, while the colorbar on the top displays the logarithm of the quark fraction$Y_{\rm q}$ which is displayed in the background of the figure.Can we detect the HQPT? In future GW detections of BNS merger systems it might be possible to detect the high density QCD phase transition by analyzing the spectrum of the emitted GW during the merger and post-merger phase. The post-merger gravitational-wave signatures of phase transitions in binary mergers of compact stars have been recently systematically analyzed[78]. While the prompt phase transition (PPT) scenario was already presented in Ref. [63], the recent work[78] focuses on the delayed phase transition (DPT) scenario. The scenario discussed so far is the so called phase-transition triggered collapse (PTTC) scenario, as the onset of the phase transition in the interior of the HMHS triggered a collapse.
The PPT scenario was presented in Ref. [63] where a temperature-dependent, hadron-quark hybrid (DD2F-SF) model[79] had been used in a BNS merger simulation. In contrast to the EOS of the
$ {\rm{CMF}}_{\rm{Q}} $ model, stable hybrid stars, containing both hadrons and quarks are realizable within the DD2F-SF EOS. In Ref. [63] it was shown that the dominant post-merger GW frequency$ f_{\rm{peak}} $ exhibit a significant deviation from the empirical relation between$ f_{\rm{peak}} $ and the tidal deformability$ \Lambda $ , if a strong first-order phase transition leads to the formation of a gravitationally stable extended quark matter core in the post-merger remnant. Such a shift of the dominant post-merger GW frequency might be revealed by future GW observations using second- and third-generation GW detectors.Finally in Ref. [78] the DPT scenario had been realized by constructing a hybrid EOS, where the relativistic mean-field model FSU2H[80-81] had been used for the cold hadronic part of the EOS and the HQPT was implemented with the use of two additional pieces of the EOS, following a polytropic dependence (FSU2H-PT model). During the collapse of the merger remnant the density in the interior region of this HMHS increases rapidly and the star spins up and, as a result, the emitted instantaneous GW frequency increases. In contrast to the results obtained within the
$ {\rm{CMF}}_{\rm{Q}} $ EOS, the collapse of the HMHS within the FSU2H-PT model will end in a quasistable differentially rotating hybrid star configuration. Due to the large stiffness of the pure quark phase for$ \rho \gtrsim 4\,\rho_0 $ the collapse is hindered and for later post-merger times ($ t > 4 $ ms) large macroscopic oscillations of the HMHS are present. During these oscillations, the density maxima reached in the center of the HMHS ($ \rho_{{\rm{max}}} $ ) and the minima of the lapse function$ \alpha_{{\rm{min}}} $ are in phase and the oscillations are accompanied by a change of the differential rotation profile of the HMHS. The maxima of$ \rho_{{\rm{max}}} $ additionally coincide with the maxima of the instantaneous GW frequency. At the moments when the density of the HMHS reach their maximal values, the HMHS is more compact and spins faster and as a result, the emitted GW frequency reaches its maxima[82]. -
In this article we have discussed an approach for hot and dense matter by focusing on chiral SU(3)-flavor parity-doublet polyakov-loop quark-hadron mean-field model, CMF. The similarity of dynamics of heavy ion collisions and neutron star mergers was discussed. We summarized these similarities in the title: Matter in Astrophysics, Gravitational waves, and Ion Collisions. The similarities between these macroscopically different systems come from the applicability of hydrodynamic description. We presented that HIC and BNS mergers probe the same regions of QCD phase diagram and, moreover, BNS mergers probe a region of cold and dense QCD matter which is not accessible by HIC. This region probed by cold dense core is suitable for reaching the state of deconfined matter where quarks may become free. In future gravitational wave detections of BNS mergers it might be possible to detect the QCD transition to deconfined state by analyzing the spectrum of the post-merger GW of the differentially rotating HMHS.
Firstly, by using the results of fully general-relativistic hydrodynamic simulations and employing the
$ {\rm{CMF}}_{\rm{Q}} $ EOS (PPTC scenario), we have demonstrated that during the collapse of the HMHS to a Kerr black hole the color degrees of freedom of the pure quark core gets macroscopically confined by the formation of the event horizon. During this collapse, the phase transition leads to a very hot and dense quark core that, when it collapses to the black hole, produces a ringdown signal different from the hadronic one.Secondly, in the DPT scenario (FSU2H-PT EOS) we have shown that the collapse of the HMHS to the black hole can be hindered by a formation of a differentially rotating HMHS. As the collapse from the HMNS to the HMHS takes place at late post-merger times and the FSU2H-PT model allows stable solution of hybrid stars, the observational signature of a HQPT, in the DPT scenario, are more distinct than in all other scenarios. It was demonstrated that the instantaneous GW frequency emitted during the collapse increases, and after the formation of the HMHS, large oscillations occur which are due to the overall macroscopic dynamics of the HMHS. The amplitude and frequency of these oscillations are mainly determined by the properties of the mixed phase and pure quark matter phase of the underlying EOS (e.g. extent of the mixed phase region and sound speed of the pure quark phase). Future second- and third-generation GW detectors might therefore be able to identify specific properties of deconfined strange quark matter.
Acknowledgments The authors thank HIC for FAIR, HGS-HIRe for FAIR, BMBF, and DFG for support. J.S. appreciates the support of the SAMSON AG, WGG-Forderverein, and the C.W. Acknowledgments Fück-Stiftungs Prize 2018. H.St. acknowledges the support through the Judah M. Eisenberg Laureatus Chair at Goethe University, and the Walter Greiner Gesellschaft, Frankfurt. Computational resources have been provided by the Center for Scientific Computing (CSC) at the J. W. Goethe-University, Frankfurt and the SuperMUC and SuperMUC-NG clusters at the LRZ in Garching. We would like to thank Elias R. Most, L. Jens Papenfort, and Veronica Dexheimer for performing the simulations within the
$ {\rm{CMF}}_{\rm{Q}} $ EOS. Additionally, we would like to give a special thanks to Luciano Rezzolla. Without his profound knowledge and his comprehensive expertise in the field of numerical relativity and general relativistic hydrodynamics, this article and the simulations herein would not have been possible.
-
摘要: 通过相对论性磁流体力学的计算知道,由双中子星合并产生的引力波对中子星内部是否存在夸克物质以及QCD物质状态方程的硬度度非常敏感。这些天文学上创造的热力学极限在20%以内跟某些快度、碰撞参数等条件下的相对论重离子碰撞产生的温度和密度相当。本文结合相对论模拟双中子星系统及实验室中重离子碰撞的结果,从而确定高密物质的状态方程和相结构。讨论了中子星合并后残留物的引力波发射,这将有助于了解夸克强子过渡的性质。Abstract: The gravitational waves emitted from a binary neutron star merger, as predicted from general relativistic magneto-hydrodynamics calculations, are sensitive to the appearance of quark matter and the stiffness of the equation of state of QCD matter present in the inner cores of the stars. These astrophysically created extremes of thermodynamics do match, to within 20%, the values of densities and temperatures which are found in relativistic heavy ion collisions, if though at quite different rapidity windows, impact parameters and bombarding energies of the heavy nuclear systems. In this article we combine the results obtained in general relativistic simulations of binary neutron star systems with ones from heavy ion collisions in the lab to pin down the EOS and the phase structure of dense matter. We discuss that the postmerger gravitational wave emission of the neutron star merger remnant might give, in the near future, insides about the properties of the hadron quark transition.
-
Key words:
- QCD matter /
- heavy ion collision /
- neutron star /
- binary neutron star mergers
-
Figure 1. (color online) The maximum value of the temperature (triangles) and rest-mass density (diamonds) during the evolution of the hypermassive hybrid star using the simulation results of the LS220-M135 run (for details, see Refs. [18-19]). The color coding of triangles/diamonds indicate the time of the simulation after the merger in milliseconds (see the colorbar at the right border of the figure). The gray and black curves show the trajectories of hydrodynamic simulation of heavy-ion collision at energies
$E_{\rm{lab}}\! =\! 1.23$ AGeV and$E_{\rm{lab}} \!= \!0.65$ AGeV within the CMF model. The colorbar right next to the picture displays the quark fraction$Y_{\rm q}$ of the corresponding hot and dense matter within the CMF model. Contour lines indicate constant values of quark fraction at$Y_{\rm q}\!=\![0.0001, 0.001, 0.01]$ (green dotted lines) and$Y_{\rm q} \!= \![0.1, 0.2, 0.3]$ (green solid lines). Adapted from Ref. [20].Figure 2. (color online) (a): Ratios of the CMF baryon number susceptibilities
$\chi_4^{\rm{B}}/\chi_2^{\rm{B}}$ kurtosis in the baryon chemical potential -$\mu_{\rm{B}}$ and temperature -$T$ plane. Note the 3 distinct critical regions, with their remnants reaching from$T\!=\!0$ up to$T>200$ MeV. (b): The quark fraction$\frac13{n_ {\rm q}}/{n_{\rm B}}$ of the CMF model in baryon chemical potential$\mu_{\rm{B}}$ and temperature$T$ plane. Note that the deconfinement smoothly appears only at higher energy densities/chemical potentials.Figure 3. (color online) Evolution of heavy-ion collisions in the high baryon density region of the
$T-\mu_ {\rm B}$ phase diagram for different collision energies. Black line - Taub adiabat which describes the initial state of heavy ion collisions as an implicit function of$\sqrt{s_{\rm{NN}}}$ . Colored lines - isentropic lines of constant entropy per baryon$S/A$ at different bombarding energies$\sqrt{s_{\rm {NN}}}$ respectively.Figure 4. (color online) Neutron star mass-radius diagram (a) and tidal deformability
$\Lambda$ as function of NS radii (b) as calculated in the CMF model. In figure (b) blue bands correspond to$\Lambda$ constraints of NS with$M\!=\!1.4\sim M_{\rm{sun}}$ , and red bands- constraints on radius of NS with$M\!=\!1.4\sim M_{\rm{sun}}$ [69].Figure 5. (color online) Upper panel: Spatial distribution of the rest-mass density
$\rho$ (left) and temperature$T$ (right) of the HMHS using the${\rm{CMF}}_{\rm{Q}}$ EOS with an initial masses of$M\!=\!1.40\,M_{\odot}$ at$t\!=\!15.26$ ms after merger. The white circles/diamonds mark the maximum values of temperature/density. Lower panel: Density-temperature profiles inside the inner region of the HMHS in the style of a$T$ -$\rho$ QCD phase diagram. The color-coding displayed on the right side indicates the radial position$r$ of the corresponding fluid element inside the HMHS, while the colorbar on the top displays the logarithm of the quark fraction$Y_{\rm q}$ which is displayed in the background of the figure. -
[1] ABBOTT B P, ABBOTT R, ABBOTT T D, et al. Phys Rev Lett, 2017, 119(16): 161101. doi: 10.1103/PhysRevLett.119.161101 [2] RAJAGOPAL K. Nucl Phys, 1999, A661: 150. doi: 10.1016/S0375-9474(99)85017-9 [3] ALFORD M G. Nucl Phys Proc Suppl, 2003, 117: 65. doi: 10.1016/S0920-5632(03)01411-7 [4] BUBALLA M. Phys Rept, 2005, 407: 205. doi: 10.1016/j.physrep.2004.11.004 [5] SCHÄFER T. arXiv:hep-ph/0304281. [6] FUKUSHIMA K, HATSUDA T. Rept Prog Phys, 2011, 74: 014001. doi: 10.1088/0034-4885/74/1/014001 [7] HOFMANN J, STOECKER H, HEINZ U W, et al. Phys Rev Lett, 1976, 36: 88. doi: 10.1103/PhysRevLett.36.88 [8] STOECKER H, MARUHN J A, GREINER W. Phys Rev Lett, 1980, 44: 725. doi: 10.1103/PhysRevLett.44.725 [9] NARA Y, STEINHEIMER J, STOECKER H. Eur Phys J, 2018, A54(11): 188. doi: 10.1140/epja/i2018-12626-y [10] NARA Y, STOECKER H. Phys Rev, 2019, C100(5): 054902. doi: 10.1103/PhysRevC.100.054902 [11] KOCH V. Hadronic Fluctuations and Correlations[M/OL]//STOCK R. Relativistic Heavy Ion Physics. 2010. http://materials.springer.com/lb/docs/sm_lbs_978-3-642-01539-7_20. [12] MOST E R, PAPENFORT L J, DEXHEIMER V, et al. Phys Rev Lett, 2019, 122(6): 061101. doi: 10.1103/PhysRevLett.122.061101 [13] RISCHKE D H, BERNARD S, MARUHN J A. Nucl Phys, 1995, A595: 346. doi: 10.1016/0375-9474(95)00355-1 [14] PANG L G, ZHOU K, SU N, et al. Nature Commun, 2018, 9(1): 210. doi: 10.1038/s41467-017-02726-3 [15] DU Y L, ZHOU K, STEINHEIMER J, et al. arXiv: 1910. 11530, 2019. [16] STEINHEIMER J, RANDRUP J. Phys Rev Lett, 2012, 109: 212301. doi: 10.1103/PhysRevLett.109.212301 [17] STEINHEIMER J, PANG L, ZHOU K, et al. JHEP, 2019, 12: 122. doi: 10.1007/JHEP12(2019)122 [18] HANAUSKE M, TAKAMI K, BOVARD L, et al. Phys Rev D, 2017, 96(4): 043004. doi: 10.1103/PhysRevD.96.043004 [19] BOVARD L, MARTIN D, GUERCILENA F, et al. Phys Rev, 2017, D96(12): 124005. doi: 10.1103/PhysRevD.96.124005 [20] HANAUSKE M, STEINHEIMER J, MOTORNENKO A, et al. Particles, 2019, 2(1): 44. doi: 10.3390/particles2010004 [21] STEINHEIMER J, SCHRAMM S, STOECKER H. J Phys G, 2011, 38: 035001. doi: 10.1088/0954-3899/38/3/035001 [22] MUKHERJEE A, STEINHEIMER J, SCHRAMM S. Phys Rev C, 2017, 96(2): 025205. doi: 10.1103/PhysRevC.96.025205 [23] MOTORNENKO A, STEINHEIMER J, VOVCHENKO V, et al. Phys Rev C, 2020, 101(3): 034904. doi: 10.1103/PhysRevC.101.034904 [24] MOTORNENKO A, STEINHEIMER J, VOVCHENKO V, et al. arXiv:2002.01217. [25] PAPAZOGLOU P, SCHRAMM S, SCHAFFNER-BIELICH J, et al. Phys Rev C, 1998, 57: 2576. doi: 10.1103/PhysRevC.57.2576 [26] DETAR C E, KUNIHIRO T. Phys Rev D, 1989, 39: 2805. doi: 10.1103/PhysRevD.39.2805 [27] ZSCHIESCHE D, TOLOS L, SCHAFFNER-BIELICH J, et al. Phys Rev C, 2007, 75: 055202. doi: 10.1103/PhysRevC.75.055202 [28] AARTS G, ALLTON C, DE BONI D, et al. JHEP, 2017, 06: 034. doi: 10.1007/JHEP06(2017)034 [29] SASAKI C. Nucl Phys A, 2018, 970: 388. doi: 10.1016/j.nuclphysa.2018.01.004 [30] FUKUSHIMA K. Phys Lett B, 2004, 591: 277. doi: 10.1016/j.physletb.2004.04.027 [31] TANABASHI M, HAGIWARA K, HIKASA K, et al. Phys Rev D, 2018, 98(3): 030001. doi: 10.1103/PhysRevD.98.030001 [32] BORSANYI S, FODOR Z, HOELBLING C, et al. Phys Lett B, 2014, 730: 99. doi: 10.1016/j.physletb.2014.01.007 [33] BAZAVOV A, BHATTACHARYA T, DETAR C, et al. Phys Rev D, 2014, 90: 094503. doi: 10.1103/PhysRevD.90.094503 [34] RISCHKE D H, GORENSTEIN M I, STOECKER H, et al. Z Phys C, 1991, 51: 485. doi: 10.1007/BF01548574 [35] STEINHEIMER J, SCHRAMM S, STOECKER H. Phys Rev C, 2011, 84: 045208. doi: 10.1103/PhysRevC.84.045208 [36] DEXHEIMER V, SCHRAMM S. Astrophys J, 2008, 683: 943. doi: 10.1086/589735 [37] DEXHEIMER V A, SCHRAMM S. Phys Rev C, 2010, 81: 045201. doi: 10.1103/PhysRevC.81.045201 [38] POCHODZALLA J, MOHLENKAMP T, RUBEHN T, et al. Phys Rev Lett, 1995, 75: 1040. doi: 10.1103/PhysRevLett.75.1040 [39] MOTOHIRO Y, KIM Y, HARADA M. Phys Rev C, 2015, 92(2): 025201. doi: 10.1103/PhysRevC.92.025201 [40] STEPHANOV M A. Phys Rev Lett, 2009, 102: 032301. doi: 10.1103/PhysRevLett.102.032301 [41] ADAM J, ADAMCZYK L, ADAMS J R, et al. arXiv: 2001.02852. [42] ADAMCZEWSKI-MUSCH J, ARNOLD O, BEHNKE C, et al. arXiv: 2002.08701. [43] TAUB A H. Phys Rev, 1948, 74: 328. doi: 10.1103/PhysRev.74.328 [44] STOECKER H, GREINER W, SCHEID W. Z Phys A, 1978, 286: 121. doi: 10.1007/BF01434620 [45] THORNE K S. Astrophys J, 1973, 179: 897. doi: 10.1086/151927 [46] STOECKER H, GREINER W. Phys Rept, 1986, 137: 277. doi: 10.1016/0370-1573(86)90131-6 [47] CSERNAI L P, KAPUSTA J, MCLERRAN L D. Phys Rev Lett, 2006, 97: 152303. doi: 10.1103/PhysRevLett.97.152303 [48] ROMATSCHKE P, ROMATSCHKE U. Phys Rev Lett, 2007, 99: 172301. doi: 10.1103/PhysRevLett.99.172301 [49] STEINHEIMER J, BLEICHER M, PETERSEN H, et al. Phys Rev C, 2008, 77: 034901. doi: 10.1103/PhysRevC.77.034901 [50] BAUMGARDT H G, SCHOTT J U, SAKAMOTO Y, et al. Z Phys A, 1975, 273: 359. doi: 10.1007/BF01435578 [51] STOECKER H, GRAEBNER G, MARUHN J A, et al. Phys Lett B, 1980, 95: 192. doi: 10.1016/0370-2693(80)90467-0 [52] STOECKER H, OGLOBLIN A A, GREINER W. Z Phys A, 1981, 303: 259. doi: 10.1007/BF01421522 [53] STOECKER H, GYULASSY M, BOGUTA J. Phys Lett B, 1981, 103: 269. doi: 10.1016/0370-2693(81)90222-7 [54] HAHN D, STOECKER H. Nucl Phys A, 1988, 476: 718. doi: 10.1016/0375-9474(88)90332-6 [55] HANAUSKE M, STEINHEIMER J, BOVARD L, et al. J Phys Conf Ser, 2017, 878(1): 012031. doi: 10.1088/1742-6596/878/1/012031 [56] FUKUSHIMA K. Phys Rev C, 2015, 91(4): 044910. doi: 10.1103/PhysRevC.91.044910 [57] VOVCHENKO V, GORENSTEIN M I, STOECKER H. Phys Rev Lett, 2017, 118(18): 182301. doi: 10.1103/PhysRevLett.118.182301 [58] VOVCHENKO V, JIANG L, GORENSTEIN M I, et al. Phys Rev C, 2018, 98(2): 024910. doi: 10.1103/PhysRevC.98.024910 [59] STEINHEIMER J, WANG Y, MUKHERJEE A, et al. Phys Lett B, 2018, 785: 40. doi: 10.1016/j.physletb.2018.07.068 [60] YE Y, WANG Y, STEINHEIMER J, et al. Phys Rev C, 2018, 98(5): 054620. doi: 10.1103/PhysRevC.98.054620 [61] DIETRICH T, BERNUZZI S, UJEVIC M, et al. Phys Rev D, 2015, 91(12): 124041. doi: 10.1103/PhysRevD.91.124041 [62] RADICE D, BERNUZZI S, DEL POZZO W, et al. Astrophys J, 2017, 842(2): L10. doi: 10.3847/2041-8213/aa775f [63] BAUSWEIN A, BASTIAN N U F, BLASCHKE D B, et al. Phys Rev Lett, 2019, 122(6): 061102. doi: 10.1103/PhysRevLett.122.061102 [64] HANAUSKE M, BOVARD L, MOST E, et al. Universe, 2019, 5(6): 156. doi: 10.3390/universe5060156 [65] TOLMAN R C. Phys Rev, 1939, 55: 364. doi: 10.1103/PhysRev.55.364 [66] OPPENHEIMER J R, VOLKOFF G M. Phys Rev, 1939, 55: 374. doi: 10.1103/PhysRev.55.374 [67] BAYM G, PETHICK C, SUTHERLAND P. Astrophys J, 1971, 170: 299. doi: 10.1086/151216 [68] MOTORNENKO A, STEINHEIMER J, VOVCHENKO V, et al. PoS, 2019, CORFU2018: 150. doi: 10.22323/1.347.0150 [69] MOST E R, WEIH L R, REZZOLLA L, et al. Phys Rev Lett, 2018, 120(26): 261103. doi: 10.1103/PhysRevLett.120.261103 [70] STEINHEIMER J, SCHRAMM S. Phys Lett B, 2014, 736: 241. doi: 10.1016/j.physletb.2014.07.018 [71] BENIC S, BLASCHKE D, ALVAREZ-CASTILLO D E, et al. Astron Astrophys A, 2015, 577: 40. doi: 10.1051/0004-6361/201425318 [72] SONG Y, BAYM G, HATSUDA T, et al. arXiv: 1905.01005. [73] LATTIMER J M, SWESTY F D. Nucl Phys A, 1991, 535: 331. doi: 10.1016/0375-9474(91)90452-C [74] HANAUSKE M, STEINHEIMER J, BOVARD L, et al. Journal of Physics: Conference Series, 2017, 878: 012031. [75] HANAUSKE M, BOVARD L, STEINHEIMER J, et al. Journal of Physics: Conference Series. IOP Publishing, 2019, 1271: 012023. [76] BOVARD L, REZZOLLA L. Classical and Quantum Gravity, 2017, 34(21): 215005. [77] MOST E R, PAPENFORT L J, DEXHEIMER V, et al. arXiv: 1910.13893, 2019. [78] WEIH L R, HANAUSKE M, REZZOLLA L. arXiv: 1912. 09340, 2019. [79] FISCHER T, BASTIAN N U F, WU M R, et al. Nature Astronomy, 2018, 2: 980. doi: 10.1038/s41550-018-0583-0 [80] TOLOS L, CENTELLES M, RAMOS A. Astrophys J, 2017, 834: 3. doi: 10.3847/1538-4357/834/1/3 [81] TOLOS L, CENTELLES M, RAMOS A. Publ Astron Soc Austral, 2017, 34: e065. doi: 10.1017/pasa.2017.60 [82] WEIH L R. et al. to be published. -









 下载:
下载:


















































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号