-
Light nuclei at drip-lines exhibit phenomena absent from the valley of stability. The fundamental feature of drip-line nuclei is their low particle-emission threshold. The close vicinity of the continuum can generate halo structure in drip-line nuclei, of one-nucleon and two-nucleon character[1-2]. The most studied halo nuclear states can be found at neutron drip-line, where one-neutron halos exist, such as in 11Be, and two-neutron halos can develop in nuclear ground states, such as in 6He and 11Li[2-3]. While not as numerous, one-proton halos also exist, with for example the ground state of 8B[2]. Moreover, drip-nuclei generally possess very few bound states, so that the largest part of their spectrum is made of unbound resonance states. Consequently, both continuum coupling and inter-nucleon correlations must be present at theoretical level if one aims at precisely describing these nuclear states.
While the most dramatic features occurring at drip-lines can be found in
$ p $ -shell nuclei,$ sd $ -shell nuclei also present unique phenomena. They are due to the strong Coulomb force and complex inter-nucleon interactions involving all partial waves for which$ \ell \leqslant 2 $ . Moreover, recent studies of the neutron-rich isotopes$ ^{26-28}{\rm{ O}}$ have shown that the energy saturation occurring at neutron drip-line is due to three-body forces[4]. Pairing energy is indeed not sufficiently strong to bind neutron-rich even-even oxygen isotopes, as 26O[5-6], and very probably 28O[7], are very loosely unbound. The consideration of the mirror counterparts of oxygen isotopes, i.e. of the isotones of 16O, could exhibit the subtle interplay between continuum coupling, Coulomb and three-body forces at proton drip-line[4]. It was indeed noticed that competing effects arise, as continuum coupling tend to generate extended nuclear densities, while the Coulomb force confines protons in the nuclear region[4]. Added to that, the repulsive character of three-body forces is comparatively stronger in proton-rich nuclei than in neutron-rich nuclei. Indeed, the effects of three-body forces are enhanced by the cancellations occurring between the attractive two-body nucleon-nucleon and repulsive Coulomb interactions[4].The 17O and 17F nuclei have been studied in the low energy region in Refs. [8-10]. 17O and 17F spectra have a low-lying nucleon emission threshold, so that most of their eigenstates are either weakly bound or unbound[11]. They are thus very good candidates to exhibit important information related to the nucleon-nucleon interaction in the unbound nuclear region. As 17O and 17F possess one added nucleon compared to 16O, their lowest positive-parity states correspond to single-particle (s.p.) states, as their first
$ 5/2^+_1 $ ,$ 1/2^+_1 $ , and$ 3/2^+_1 $ mainly consist of an occupied$ 0d_{5/2} $ ,$ 1s_{1/2} $ or$ 0d_{3/2} $ bound or resonance one-body state above a 16O core. One can note that the first$ 1/2^+_1 $ eigenstate of 17F is a one-proton halo[2]. A proton halo can arise therein because of the low binding energy of the 17F$ 1/2^+_1 $ eigenstate, of only 0.105 MeV, on the one hand, and of the absence of centrifugal barrier, on the other hand. As the 17O and 17F nuclei are mirror nuclei, isospin-symmetry breaking can be directly assessed from their spectra. 17O has its neutron-emission threshold at 4.143 MeV, while 17F is more weakly bound, as its proton-emission threshold can be found at 0.6 MeV. Moreover, 17F eigenstates strongly depend on the Coulomb barrier therein, while the Coulomb interaction is unimportant in the asymptotic region of the neutron-unbound eigenstates of 17O. Consequently, the Thomas-Ehrmann shift[12-13], i.e. the different excitation energies arising in mirror nuclei due to the different proton-emission and neutron-emission thresholds therein, can be expected to be sizable in 17O and 17F. Another interesting aspect of the 17O and 17F nuclei is that they can be conveniently studied in a shell model picture[9-10]. While this is immediately seen in their aforementioned s.p. states, it is also the case for the negative-parity states and reasonably high-lying positive-parity states of 17O and 17F. Indeed, they are mainly built from configurations bearing one or two holes in the 16O core. Consequently, the presence of both s.p. and correlated many-body states in the spectrum of 17O and 17F, as well as the isospin mixing generated by the proximity of the continuum, makes 17O and 17F very interesting from a theoretical point of view.However, a full ab-initio description of 17O and 17F has never been attempted with realistic Hamiltonians. Indeed, the no-core shell model in the continuum (NCSMC)[14-21] cannot handle nuclear systems bearing more than 11 nucleons[22]. While 17O and 17F have been studied in the context of the Coupled-Cluster (CC) model[8], only their
$ 5/2^+_1 $ ,$ 1/2^+_1 $ , and$ 3/2^+_1 $ s.p. states have been investigated. While the energies and widths of the$ 5/2^+_1 $ ,$ 1/2^+_1 $ , and$ 3/2^+_1 $ eigenstates obtained with CC compare well with experiment[8], one cannot infer useful information about the low-lying negative-parity states and other positive-parity states of 17O and 17F. Hence, one has to recur to effective Hamiltonians to study 17O and 17F. A particularly successful approach for that matter is that provided by the shell model embedded in the continuum (SMEC)[9-10, 23]. A very good description of the spectra of 17O and 17F, as well as 16O(p,p) elastic and 16O(p,$ \gamma $ ) radiative capture cross sections, could be obtained with SMEC[9-10]. Nevertheless, two different interactions were used in SMEC[9-10]. The part of the Hamiltonian acting in the resonant space was built from standard$ psd $ shell model interactions, while that related to the non-resonant continuum consisted of a Woods-Saxon (WS) potential fitted on experimental data, to which a schematic zero-range density-dependent force was added[9-10]. This separation in terms of shell model (internal) and continuum (external) degrees of freedom allowed to tune the Hamiltonian parameters so as to reproduce experimental data[10]. However, it is still not clear whether the 17O and 17F nuclei can be satisfactorily described using the same Hamiltonian in resonant and non-resonant many-body spaces.The aim of this paper is then to devise an effective Hamiltonian which can describe structure and reaction observables associated to 17O and 17F, without considering separately the resonant and non-resonant degrees of freedom of the Hamiltonian. For this, one will use the newly developed coupled-channel Gamow shell model (GSM-CC)[24-27]. GSM-CC is based on the GSM model, originally devised to describe nuclear structure at drip-lines (see Ref. [28] for a review of the GSM model), and which has been extended recently to GSM-CC to be able to calculate reaction observables. Indeed, one can use a core+valence particle approach therein, hence with small model space dimensions, so that this scheme is numerically tractable. Moreover, effective interactions able to reproduce experimental data of light nuclei at structure and reaction level have been devised in GSM[29], by making use of the Furutani-Horiuchi-Tamagaki (FHT) residual nucleon-nucleon interaction[30-31]. Therefore, we will study the spectrum of 17O and 17F and excitation functions of the 16O(p,p) reaction with GSM-CC using a WS potential mimicking the effect of the core, while the inter-nucleon correlations will be described by the FHT interaction in the valence space.
The paper is structured as follows. The basic features of GSM-CC, as well as the model and Hamiltonian used, will be firstly stated in Sec. 2. Results, consisting of the spectra of 17O, 17F and 16O(p,p) excitation functions, will be depicted in Sec. 3. Conclusion will be presented in Sec. 4.
-
One considers the core + valence particle approach, where 16O is the core and the valence space consists of
$ spdf $ proton and neutron partial waves. The Hamiltonian used consists of a potential mimicking the effect of the core and of the FHT interaction in the$ spdf $ valence space:$$ H = \sum\limits_i \left( \frac{{ {p_i}}^2}{2 m_i} + \hat{U}^{(i)}_{\rm{core}} \right) + \sum\limits_{i<j} \hat{V}_{ij} , $$ (1) where
$ m_i $ is the effective mass of the nucleon,$ \hat{U}^{(i)}_{\rm{core}} $ is the WS potential of the core acting on the$ i $ -th nucleon, and$ \hat{V}_{ij} $ is the residual interaction, containing the FHT interaction, the Coulomb interaction, and the recoil effects induced by the finite mass of the core[29].The negative-parity states of 17O and 17F are mainly built from 1p-1h excitations from the
$ 0p_{1/2} $ orbitals to the$ sd $ shell, while positive-parity states besides s.p. states mainly consist of 2p-2h excitations from$ 0p_{1/2} $ orbitals to the$ sd $ shell. Consequently, in order to have a sizable configuration mixing, while still dealing with small model space dimensions, one included configurations with up to 3p-3h excitations from$ 0p_{1/2} $ shells. However, this creates a double-counting of nucleon-nucleon correlations in$ H $ (see Eq. (1)), as$ \hat{U}^{(i)}_{\rm{core}} $ mimics the effect of the 16O core when core shells are fully occupied. This spurious effect can be removed with standard correction formulas[32]. The expressions of Ref. [32] are cumbersome, however, so that one has introduced a simplified removal procedure of double-counting terms. We use the following potential, denoted as$ \hat{U}_{dc} $ , which is subtracted from the one-body part of Eq. (1):$$\begin{split} \left\langle {f|{{\hat U}_{dc}}|i} \right\rangle =& \sum\limits_{s \in {\rm{core}},J} {\sqrt {1 \!+\! {\delta _{is}}} } \sqrt {1 \!+\! {\delta _{fs}}}\times\\& \left( {\frac{{2J \!+\! 1}}{{2{j_s} \!+\! 1}}} \right)\left\langle {sf|\hat V|s{i_J}} \right\rangle ,\end{split}$$ (2) where
$ \left| i \right\rangle $ and$ \left| f \right\rangle $ are basis one-body states and$ s $ runs over the active shells of the core, i.e. on proton and neutron$ 0p_{1/2} $ shells. Eq. (2) removes the spurious energy generated by the nuclear interaction already taken care of by$ \hat{U}^{(i)}_{\rm{core}} $ . In fact,$ \hat{U}_{dc} $ resembles the part of the spherical Hartree-Fock potential generated by$ H $ involving fully occupied proton and neutron$ 0p_{1/2} $ shells (see Eqs. (1,2)). Note that$ {\left\langle {si|\hat V|si} \right\rangle _J} = 0$ by definition if$ s,i \in {\rm{core}} $ , as one considers that this matrix element is already included in$ \hat{U}^{(i)}_{\rm{core}} $ .Continuum coupling enters 17O and 17F wave functions only via the coupled channels of GSM-CC (see Sec. 2.2), while 16O target states are well bound. Hence, 16O target states will be built from HO states in our model. For this, one takes the first 5, 4, 4 and 3 HO one-body states of the
$ spdf $ partial waves, respectively, from which the$ 0s_{1/2} $ and$ 0p_{3/2} $ shells are removed as they are inert shells of the core. The harmonic oscillator length is fixed at b = 2 fm. Moreover, Slater determinants can have only one proton or neutron occupied in HO one-body states verifying$ 2n + \ell \geqslant 3 $ . As the resonance spectrum of 17O and 17F is unbound by nucleon emission only, the presented truncation scheme recaptures the main structure of the considered many-body eigenstates of 17O and 17F. -
In GSM-CC, one decomposes the many-body Hamiltonian eigenstates in a basis of reaction channels:
$$\left| {c,r} \right\rangle = \widehat {\cal A}\left| {\{ \left| {\Psi _T^{{J_T}}} \right\rangle \otimes \left| {r\;\ell \;j} \right\rangle \} _{{M_A}}^{{J_A}}} \right\rangle ,$$ (3) $$\left| \Psi \right\rangle = \sum\limits_c {\int_0^{ + \infty } {\left( {\frac{{{u_c}(r)}}{r}} \right)} } {r^2}\left| {c,r} \right\rangle \;{\rm{d}}r ,$$ (4) where
$ c $ denotes the channel quantum numbers,$ \widehat {\cal A}{\rm{ }}\left| {\{ \left| {\Psi _T^{{J_T}}} \right\rangle \otimes \left| {r\;\ell \;j} \right\rangle \} } \right\rangle $ is an antisymmetrized tensor product of the target state$ \left| {\Psi _T^{{J_T}}} \right\rangle $ and projectile state$ \left| {r\;\ell \;j} \right\rangle $ , where$ { {J_A}} = { {J_T}} + { {j}} $ , and$ u_{ c } (r) $ is the radial wave function to determine.Starting from the Schrödinger equation
$ H \left| \Psi \right\rangle = E\left| \Psi \right\rangle $ , one derives the coupled-channel equations to solve in GSM-CC:$$ \!\sum\limits_{c}\int_{0}^{\infty} \!\!\! r^{ 2 } \left( H_{ cc' } (r , r') - E N_{ cc' } (r , r') \right) \left( \frac{ { u }_{ c } (r) }{ r } \right) \; {\rm d}r = 0\,, $$ (5) where
$ H_{ cc' } (r,r') $ and$ N_{ cc' } (r,r') $ arise from the integration of the Schrödinger equation over all degrees of freedom except$ r $ :$$ \begin{split} H_{ cc' } (r , r') =& \frac{ { \hbar }^{ 2 }}{ 2 m_p} \left( -\frac{ { d }^{ 2 }}{ {\rm d} r^{ 2 }} + \frac{\ell(\ell + 1)}{r^2} + E_{ T } +\right.\\& { U_{\rm{basis}}} (r) \left) \frac{ \delta (r - r') }{ r r' } { \delta }_{ cc' } \right. + { \tilde{ V }}_{ cc' } (r , r') \,, \\ N_{ cc' } (r , r') = & \frac{ \delta (r - r') }{ r r' } { \delta }_{ cc' } + \Delta N_{ cc' } (r , r') \,, \end{split} $$ (6) where
$ U_{\rm{basis}} (r) $ is the basis-generating potential, of WS type, and$ \tilde{ V }_{ cc' } $ ,$ \Delta N_{ cc' } (r , r') $ consist of the residual short-range terms of the Hamiltonian and norm kernels, respectively. As target states are expressed with a basis of Slater determinants, matrix elements involving target states are straightforward to compute using HO shell model (HO-SM) formulas.Eq. (5) is, in fact, a generalized eigenvalue problem, due to the presence of the norm kernel
$ N_{ cc' } (r , r') $ . The antisymmetry requirement between projectile and target indeed generates non-orthogonality between compound target-projectile basis states. A convenient method to solve generalized eigenvalue problems consists to apply a unitary transformation to the Hamiltonian so that one obtains a standard eigenvalue problem. For this, one introduces the overlap operator$ \hat{O} $ . The demanded standard eigenvalue problem equivalent to Eq. (5) then reads:$$ \sum\limits_c {\int_0^\infty {\rm{d}} } r\;{r^2}\left\langle {c',r'|{{\hat H}_m} - E|c,r} \right\rangle \left( {\frac{{{w_c}(r)}}{r}} \right) = 0,\;\;\; $$ (7) where
$ \hat{H}_{m} = \hat{O}^{ - \frac{1}{2} } \hat{H} \hat{O}^{ - \frac{1}{2}} $ is the modified Hamiltonian and where:$${w_c}(r) = \frac{{\left\langle {c,r|{{\hat O}^{\frac{1}{2}}}|\Psi } \right\rangle }}{r}{\mkern 1mu} .$$ (8) Thus, the
$ {w}_{c} (r) $ radial wave functions are firstly calculated from the standard eigenvalue problem of Eq. (7). The$ {u}_{c} (r) $ radial wave functions of Eq. (5) are then straightforward to recover from$ {w}_{c} (r) $ and the overlap operator$ \hat{O} $ . Once the$ {u}_{c} (r) $ radial wave functions are obtained, cross sections can be calculated from standard reaction theory. Indeed, besides kinetic and angular-momentum recoupling terms, cross sections are functions of the phase shifts of the$ {u}_{c} (r) $ radial wave functions, which are straightforward to obtain from the asymptotic form of$ {u}_{c} (r) $ functions.The coupled-channel representation of the Schrödinger equation of Eq. (7) will be solved using the Berggren basis[33]. It consists of resonant and scattering one-body states generated by a finite-depth potential[33]:
$$ \sum\limits_{n} u_{n}(r) \; u_{n}(r') + \int_{L^{+}} u(k,r) \; u(k,r') \; {\rm d}k = \delta(r - r')\,, $$ (9) where
$ u_n(r) $ and$ u(k,r) $ are resonant and scattering states, respectively, and$ L^+ $ is the contour of scattering states in the complex plane, which encompasses unbound$ u_n(r) $ states. All one-body states have the same angular quantum numbers, so that the three-dimensional completeness relation is recovered by summing over all partial waves. In numerical calculations, the scattering part of Eq. (9) is discretized using the Gauss-Legendre quadrature[34]:$$ \sum\limits_{n = 1}^{N} u^{(n)}(r) \; u^{(n)}(r') \simeq \delta(r - r')\,, $$ (10) where
$ N $ is the number of resonant and discretized scattering states, and$ u^{(n)}(r) $ is either a resonant$ u_n(r) $ wave function or the renormalized scattering$ \sqrt{w_n} \; u(k_n,r) $ function, with$ k_n $ and$ w_n $ the Gauss-Legendre abscissa and weight on the$ L^+ $ discretized contour, respectively. The latter renormalization is necessary to replace the initial Dirac delta normalization of$ u(k,r) $ functions in Eq. (9) by a Kronecker delta normalization.Let us firstly consider the calculation of bound and resonance many-body states.
$ { { u }_{ c }(r) } $ (see Eq. (5)) can be expanded in the basis of coupled-channel Berggren basis states arising from Eq. (10). The obtained matrix problem is formally identical to that of GSM, where a basis of Slater determinants is utilized, so that bound and resonance eigenstates can be calculated using the Jacobi-Davidson and overlap methods devised in GSM[28].Scattering eigenstates can be conveniently implemented by making use of the Hamiltonian Green's function[27]. For this, one uses the basis-generating Hamiltonian, whose eigenvector at the considered scattering energy
$ E $ is denoted as$\left| {{\Psi ^{(b)}}} \right\rangle $ . One can then separate$ \hat{H} $ and$ \left| {\Psi _{{M_A}}^{{J_A}}} \right\rangle $ into two parts, involving the basis-generating Hamiltonian,$ \left| {{\Psi ^{(b)}}} \right\rangle $ , and a rest part:$$ \hat{H} = t + \hat{U}_{\rm{basis}} + \hat{H}_{\rm{rest}}\,, $$ (11) $$\left| {\Psi _{{M_A}}^{{J_A}}} \right\rangle = \left| {{\Psi ^{(b)}}} \right\rangle + \left| {{\Psi _{{\rm{rest}}}}} \right\rangle . $$ (12) Using Eqs. (11, 12), one obtains:
$$ (\hat H - E)\left| {{\Psi _{{\rm{rest}}}}} \right\rangle = - {\hat H_{{\rm{rest}}}}\left| {{\Psi ^{(b)}}} \right\rangle . $$ (13) All values entering Eq. (13) are finite-ranged, so that they can be represented with a Berggren basis. Eq. (13) then becomes a linear system in the Berggren coupled-channel basis representation. Note that Eq. (13) is not invertible on the real energy axis. In order to avoid this problem, the contour of Berggren basis states is defined so that their complex energy always has a non-zero imaginary part[27]. This procedure is, in fact, equivalent to the standard replacement of
$ E $ by$ E + i \epsilon $ , with$ \epsilon \rightarrow 0^+ $ , which imposes an outgoing wave function character for$ \left| {{\Psi _{{\rm{rest}}}}} \right\rangle $ on all outgoing channels[27].As a consequence, the calculation of bound, resonance and scattering states in GSM-CC is handled with standard eigenvalue problems and linear systems, respectively, so that the determination of the solutions of Eqs. (5, 7) in GSM-CC is both fast and numerically stable.
-
The parameters of the Hamiltonian
$ H $ (see Eq. (1)) are firstly fitted at the level of HO-SM on the low-lying spectrum of 17O and 17F. The parameters of the WS potential of the core common to all partial waves read$ d $ = 0.65 fm for diffuseness,$ R_0 = 3.2 $ fm for radius, and$ V_{\rm so} $ = 7.5 MeV fm2 for spin-orbit strength. The WS central depth, denoted as$ V_o $ , is$ \ell $ -dependent and reads for protons: 50.022 MeV ($ \ell $ = 0), 37.214 MeV ($ \ell = 1 $ ), 47.800 MeV ($ \ell $ = 2), 39.705 MeV ($ \ell = 3 $ ), and for neutrons: 49.902 MeV ($ \ell $ = 0), 36.438 MeV ($ \ell $ = 1), 48.603 MeV ($ \ell = 2 $ ) and 38.998 MeV ($ \ell = 3 $ ).The FHT interaction is the sum of three Gaussian terms, depicting the central, spin-orbit and tensor components of the nucleon-nucleon interaction[30-31]. The parameters of the FHT interaction were fitted in Ref. [29] for
$ A \leqslant 9 $ nuclei. One could see therein that four parameters were very constrained, whereas the remaining three parameters bore large statistical errors[29]. Consequently, one fitted only the first four parameters, namely the central terms$ V_c^{00},V_c^{10},V_c^{01} $ and the tensor term$ V_T^{10} $ , where the two superscripts equal to 0 or 1 refer to the spin$ S $ and isospin$ T $ of the two nucleons[29]. The other three parameters are put to zero. Note that this choice is not arbitrary, as neglected parameters are of higher order compared to well constrained parameters[35]. The fitted parameters read:$ V_c^{00} = $ 14.351 MeV,$ V_c^{10} = - $ 8.263 MeV,$ V_c^{01} = - $ 8.723 MeV and$ V_T^{10} = - $ 0.089 MeV fm-2.The precision of the fit at HO-SM level is rather low, of the order of 500 keV (see Figs. (1, 2, 3, 4). Continuum coupling is indeed necessary to reproduce experimental data. It is included in GSM-CC, where one uses Eq. (5) to generate many-body nuclear states. For this, all the eigenstates of 16O of excitation energy smaller than 10 MeV are used as target pseudo-states in Eq. (3). As model spaces are not identical at HO-SM and GSM-CC levels, one multiplied the two-body nucleon-nucleon interaction of Eq. (1) by a corrective factor depending on the angular momentum
$ J $ and parity$ \pi $ of the many-body state in GSM-CC. Moreover, in order to remove spurious energy dependence in the calculated cross sections as much as possible, corrective factors have been devised so that the low-lying eigenstates of 17F reproduce experimental data (see Figs. (1, 2). The corrective factors therein are of the order of 2%~4%, nevertheless, so that the overall features of the Hamiltonian fitted at HO-SM level still remain in GSM-CC.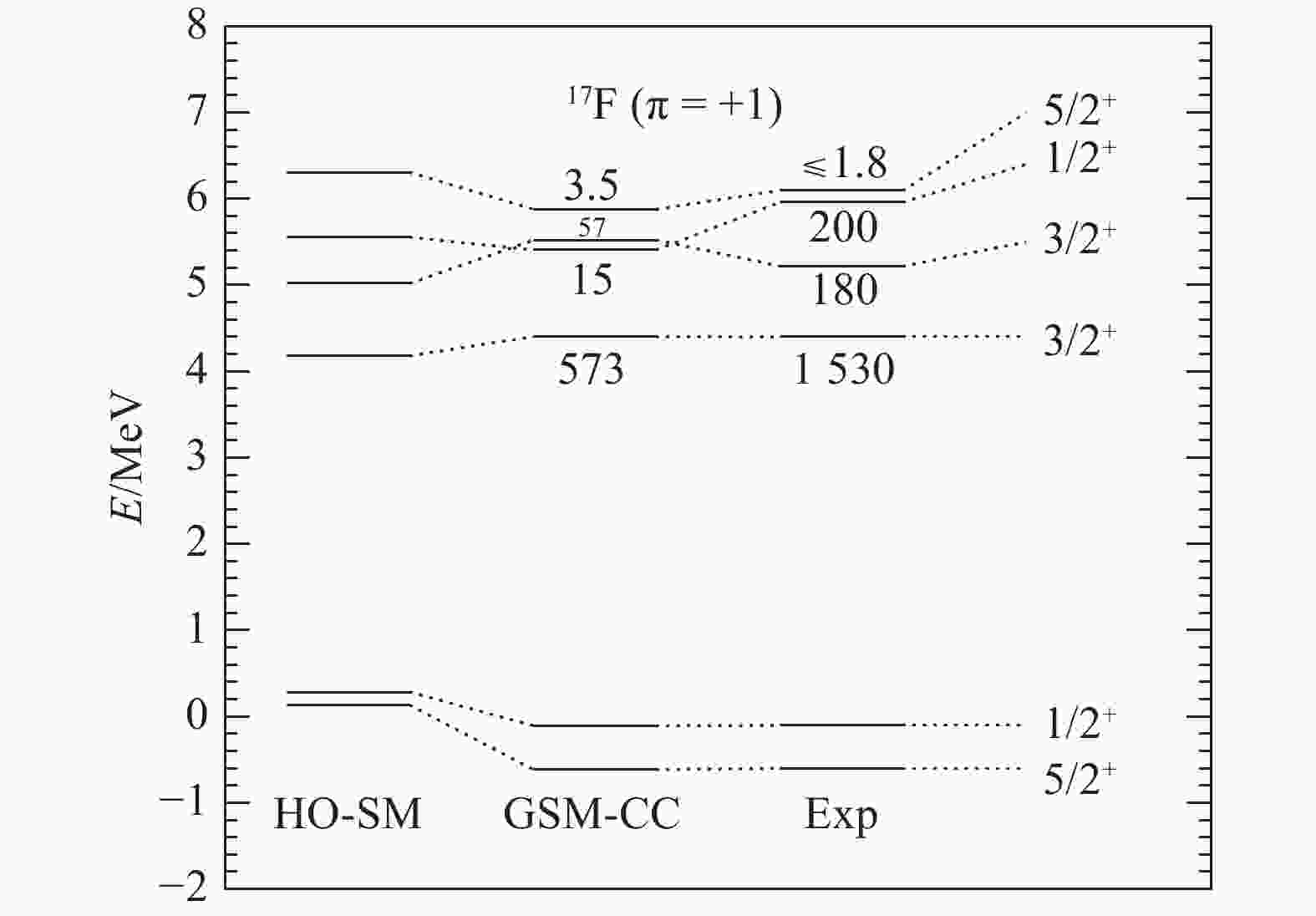
Figure 1. Low-lying energy spectrum of 17F calculated with HO-SM and GSM-CC and compared with experimental data (Exp). Positive-parity states only are depicted in this figure. Energies are given with respect to the 16O ground state and are given in units of MeV. The proton-emission width of unbound states is written next to their energy and is given in keV. Experimental data are taken from Ref. [11].
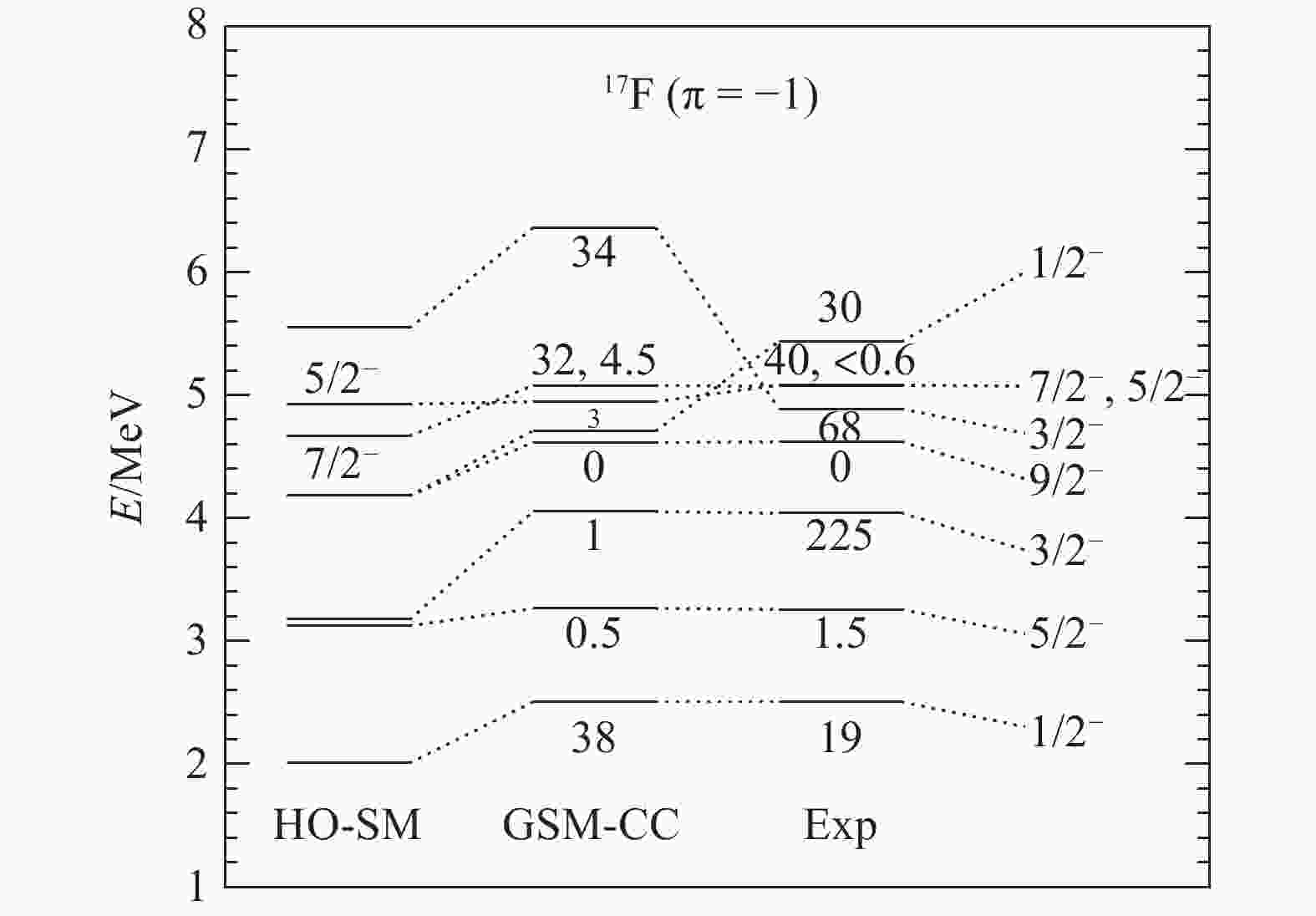
Figure 2. Same as Fig. 1, but for negative-parity states.
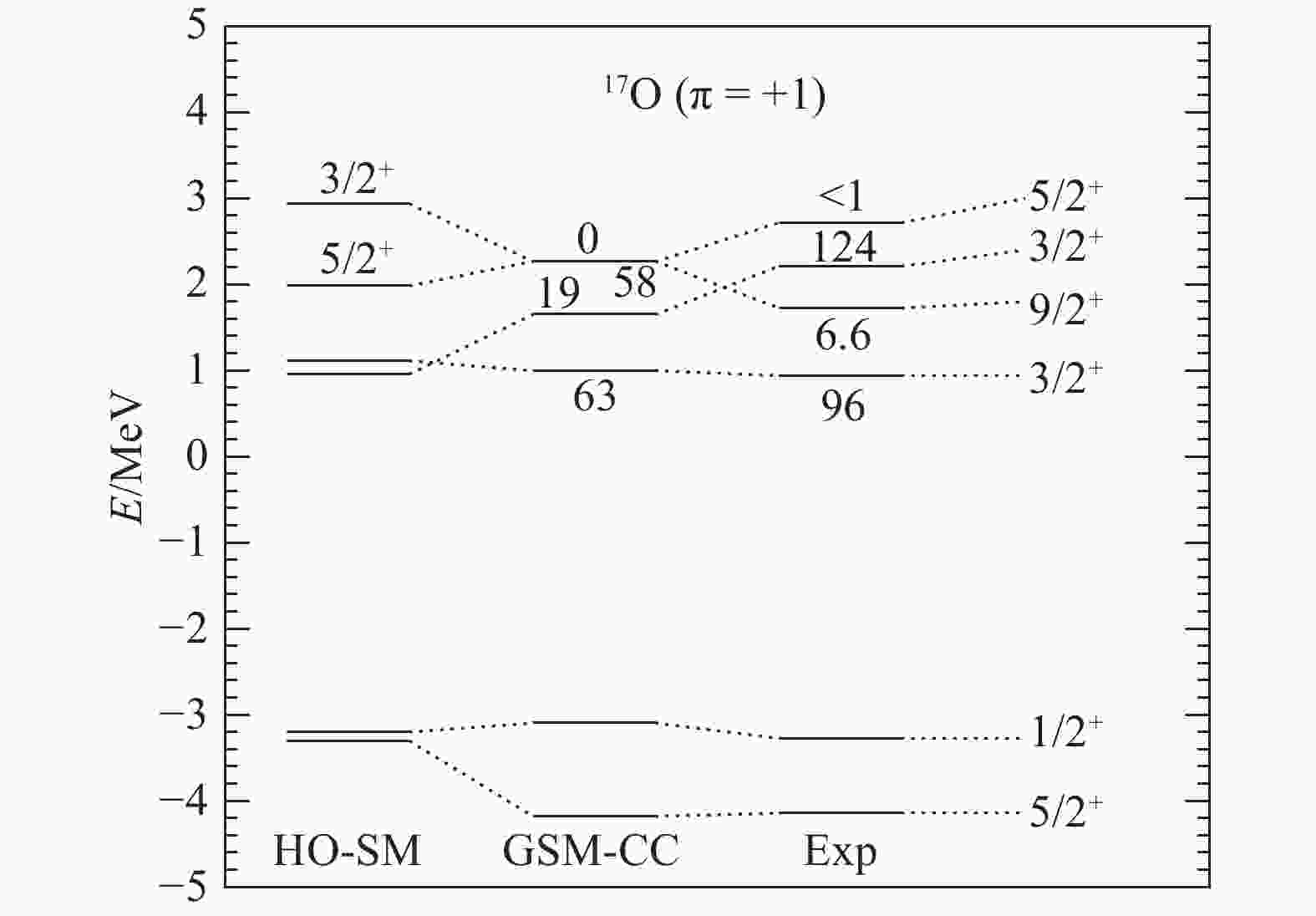
Figure 3. Same as Fig. 1, but for 17O positive-parity states, and where neutron-emission widths are depicted.
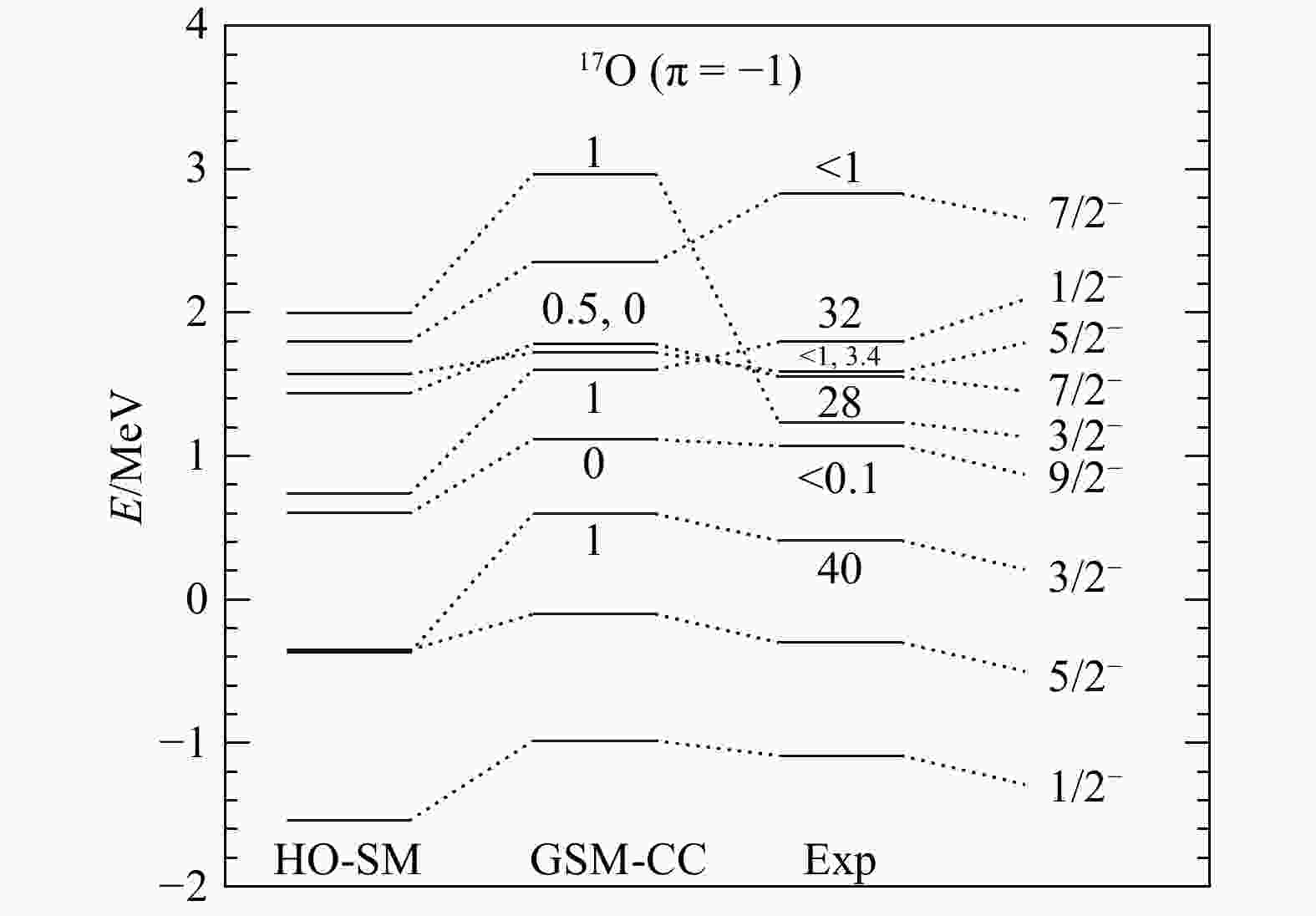
Figure 4. Same as Fig. 3, but for negative-parity states.
Let us consider the particle-emission widths of the eigenstates of 17F (see Figs. (1, 2). One can see that they are well reproduced in general, as they typically differ by a factor at most equal to three. However, discrepancies arise in the
$ 1/2^+_2 $ ,$ 1/2^-_1 $ and, especially$ 3/2^-_1 $ , eigenstates. Indeed, the experimental width of the$ 3/2^-_1 $ , eigenstate is equal to 225 keV, while its theoretical value is 1 keV. The widths of the$ 1/2^+_2 $ and$ 1/2^-_1 $ eigenstates differ by about a factor 7~10 from experimental widths, which is, however, not excessive due to their rather small values. Otherwise, the energies of the high-lying excited states of 17F usually differ by a few hundreds of keV, with the exception of the$ 3/2^-_2 $ eigenstate, differing by almost 2 MeV.The low-lying spectrum of 17O is depicted in Figs. (3, 4). All the 17O states mirroring the fitted eigenstates of 17F fairly reproduce experimental data, by 200~300 keV at most. In particular, the
$ 1/2^+_1 $ state of 17O is about 1.1 MeV above the$ 5/2^+_1 $ ground state of 17O, in good agreement with the experimental value of 0.87 MeV. The Thomas-Ehrmann shift is indeed rather large therein, as the$ 1/2^+_1 $ state of 17F has an excitation energy of 0.495 MeV with respect to the ground state of 17F. One can also note that the neutron-emission width of the s.p.$ 3/2^+_1 $ state of 17O, of 63 keV, is very close to the experimental value of 96 keV. Thus, continuum coupling, which is included in GSM-CC, accounts for the Thomas-Ehrmann shift occurring in 17O and 17F. Otherwise, one can notice that the$ 3/2^-_2 $ eigenstate is too high in energy, as was the case with 17F, and that the$ 7/2^-_2 $ eigenstate of 17O is too low by about 500 keV compared to experimental data. While the widths of the positive-parity states of 17O compare well with experiment, by a factor 10 at most, the widths of negative-parity states are all of the order of 1 keV, when experimental widths can reach 40 keV.As the main discrepancies with experimental data in the low-lying spectra of 17O and 17F arise above 5 MeV, one can consider that the devised Hamiltonian can be expected to provide sound reaction observables in this region. Moreover, no fine tuning of the Hamiltonian parameters has been effected from experimental cross sections, so that the following results are fully predictive. One calculated excitation functions of the 16O(p,p) elastic scattering reaction at the angles
$ \theta = 140.76^\circ $ and$ \theta = 166.75^\circ $ [see Figs. (5, 6)].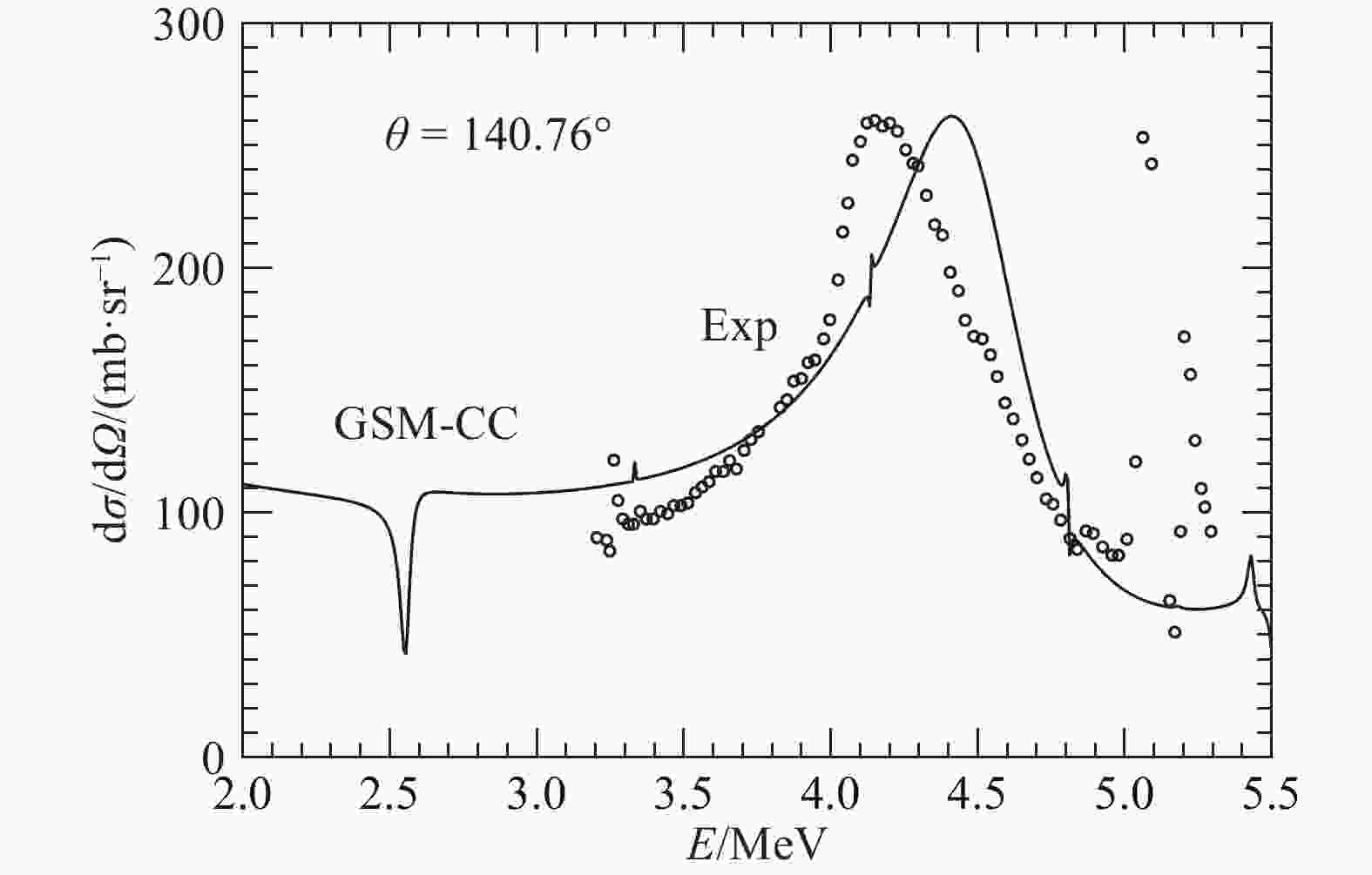
Figure 5. Excitation function of the 16O(p,p) elastic scattering reaction calculated with GSM-CC at
$ \theta = 140.76^\circ $ . Experimental data are taken from Ref. [36]. Energies and angles are given in the center of mass frame.
Figure 6. Same as Fig. 5, but with
$ \theta = 166.75^\circ $ .The excitation function calculated with GSM-CC at
$ \theta = 140.76^\circ $ is very close to experimental data (see Fig. 5). The only noticeable difference is that of the maximum of the cross section, which differs from its experimental value by about 300 keV. Nevertheless, the 16O(p,p) elastic scattering reaction at$ \theta = 140.76^\circ $ is not very sensitive to the details of nuclear structure, as the peak in Fig. 5 is almost entirely due to the s.p.$ 3/2^+_1 $ , eigenstate of 17F, so that its consideration is not sufficient to fully assess the ability of the Hamiltonian to describe reaction observables.Hence, we will study the 16O(p,p) excitation function for
$ \theta = 166.75^\circ $ (see Fig. 6). This angle is indeed sufficiently large for the excitation function to have a stringent dependence on the nuclear structure of 17F. The excitation function calculated at$ \theta = 166.75^\circ $ with GSM-CC bears an overall good agreement with the experimental cross section, as the magnitude of the theoretical excitation function is only about 50~100 mb/sr too large compared the experimental excitation function (see Fig. 6). However, one can see that it is not well reproduced around 4 MeV. Note that the sudden decrease of the excitation function around 4 MeV is difficult to obtain at theoretical level, as it is due to 17F negative-parity states, whose theoretical energy and widths must be very close to experimental data for the excitation function to be well described therein. Indeed, the same excitation function calculated in Ref. [9] in the SMEC model, where the most advanced shell model interactions were used for the resonant part of the Hamiltonian is similar to ours. In fact, the experimental excitation function at$ \theta = 166.75^\circ $ could be well reproduced only in Ref. [10], where the Zuker-Buck-Mc Grory (ZBM) shell model interaction[37], fitted from nuclei in the vicinity of 16O, had to be used for the resonant part of the Hamiltonian. The origin of this discrepancy is clearly due to the width of the$ 3/2^-_1 $ eigenstate, which is almost zero in our calculations, whereas it is 225 keV experimentally. This width was indeed sufficiently large in the SMEC calculations of Ref. [10], as it was around 100 keV. The energy of the$ 3/2^-_1 $ eigenstate plays no role therein, as it is well reproduced with both GSM-CC (see Fig. 2) and SMEC in Ref. [10].Note also that the decrease of the theoretical excitation function obtained in GSM-CC at
$ E = 4.5 $ MeV, which is too steep, seems to arise from the$ 3/2^-_2 $ eigenstate, which is too high in energy by about 2 MeV in GSM-CC compared to experimental data. Indeed, the SMEC excitation function fairly reproduces experimental data around this energy[10], which is probably due to the fact that the$ 3/2^-_2 $ eigenstate calculated with SMEC has an energy close to its experimental value[10]. -
The study of structure and reaction observables in a unified theoretical framework is a challenge of nuclear physics. Great progress has been made recently with the developments of realistic theoretical approaches including continuum degrees of freedom, such as NCSMC[14-21], CC[8, 34, 38], and GSM, GSM-CC[24-28]. Indeed, both spectra and reaction cross sections have been successfully calculated with NCSMC, CC and GSM in the domain of light nuclei. However, considering nuclei with more than 11 nucleons seems very difficult for NCSMC due to current computational capabilities[22], while CC cannot handle nuclei with more than two particles or holes above closed shells[39]. Therefore, it seems that GSM and GSM-CC are the tools of choice to study drip-line nuclei close in the whole nuclear chart, at both structure and reaction level.
Even though the spectrum of 17O and 17F, as well as 16O(p,p) excitation functions at low energy, are experimentally accessible, they are seldom studied from a theoretical point of view. The most successful studies for that matter remain those done in the SMEC formalism[9-10], where both spectra and cross sections could be quantitatively reproduced. However, this success could be achieved at the price of a highly phenomenological account of the physics of nuclear systems at drip-line. Indeed, shell model and continuum degrees of freedom were separated therein and fitted independently, thus hindering a possible unification of the structure and reaction aspects of nuclear quantum systems.
Consequently, due to the recent developments of GSM and GSM-CC, it has been attempted for the first time to study the low-energy spectrum of 17O and 17F and 16O(p,p) excitation functions using a unique Hamiltonian in that framework. For this, the low-energy spectrum of 17F has been fitted in a core + valence nucleon picture, with which the 17O and 17F spectra and 16O(p,p) excitation functions could be analyzed. While an overall agreement with experimental data could be achieved, one is still far from a quantitative reproduction of structure and reaction observables at low energy. It has indeed been noticed that it is necessary to reproduce the experimental low-lying spectrum of 17F almost exactly for both energy and width to achieve this goal. Indeed, the shell model interaction of the early SMEC calculation of Ref. [9] was providing with too strong a configuration mixing among resonant many-body states, which was preventing from obtaining a very good reproduction of 16O(p,p) excitation functions at large angles. On the contrary, the introduction of the ZBM interaction[37] for that matter in Ref. [10] could phenomenologically solve this problem. Thus, it appears that the question pondered in this paper, i.e. whether a unique theoretical Hamiltonian can reproduce structure and reaction observables associated to 17O and 17F, does not have a definitive answer yet. It seems that only the use of the ab-initio GSM framework developed in Ref. [40] could help solving this problem, as then both continuum coupling and a realistic account of the nucleon-nucleon interaction can be included consistently in the same theoretical approach.
Calculations of the 17O and 17F Spectra and 16O(p,p) Reaction Cross Sections in the Coupled-channel Gamow Shell Model
-
摘要: 利用耦合道Gamow壳模型计算了17O和17F的低激发能谱以及16O(p,p)反应的低能弹性散射截面。结果表明,17O和17F中非束缚共振态能级的核子发射宽度的计算需要合理地考虑连续态耦合效应。计算得到的17O和17F的低激发能谱以及16O(p,p)反应的低能弹性散射激发函数都与实验数据吻合较好。这说明基于现实核力的计算可更好地描述16O(p,p)反应的低能弹性散射截面。Abstract: We apply the coupled-channel Gamow shell model to calculate the spectra of 17O and 17F, as well as 16O(p,p) elastic cross sections at low energies. It is shown that continuum coupling is necessary to account for the particle-emission width of the unbound eigenstates of 17O and 17F. The low-lying spectrum of 17O and 17F and 16O(p,p) excitations functions are in fair agreement with experimental data. Nevertheless, it is also shown that the use of a realistic nuclear Hamiltonian is needed to have an optimal reproduction of 16O(p,p) elastic cross sections in the low-energy region.
-
Figure 1. Low-lying energy spectrum of 17F calculated with HO-SM and GSM-CC and compared with experimental data (Exp). Positive-parity states only are depicted in this figure. Energies are given with respect to the 16O ground state and are given in units of MeV. The proton-emission width of unbound states is written next to their energy and is given in keV. Experimental data are taken from Ref. [11].
Figure 2. Same as Fig. 1, but for negative-parity states.
Figure 3. Same as Fig. 1, but for 17O positive-parity states, and where neutron-emission widths are depicted.
Figure 4. Same as Fig. 3, but for negative-parity states.
Figure 5. Excitation function of the 16O(p,p) elastic scattering reaction calculated with GSM-CC at
$ \theta = 140.76^\circ $ . Experimental data are taken from Ref. [36]. Energies and angles are given in the center of mass frame.Figure 6. Same as Fig. 5, but with
$ \theta = 166.75^\circ $ . -
[1] RIISAGER K. Rev Mod Phys, 1994, 66: 1105. doi: 10.1103/RevModPhys.66.1105 [2] AL-KHALILI, J. The Euroschool Lectures on Physics with Exotic Beams[M]. Berlin Heidelberg: Springer, 2004: 77. DOI: 10.1007/978-3-540-44490-93 [3] ZHUKOV M V, DANILIN B V, FEDOROV D V, et al. Phys Rep, 1993, 231: 151. doi: 10.1016/0370-1573(93)90141-Y [4] MICHEL N, LI J G, XU F R, et al. Phys Rev C, 2019, 100: 064303. doi: 10.1103/PhysRevC.100.064303 [5] KOHLEY Z, BAUMANN T, BAZINET D, et al. Phys Rev Lett, 2013, 110: 152501. doi: 10.1103/PhysRevLett.110.152501 [6] KONDO Y, NAKAMURA T, TANAKA R,et al. Phys Rev Lett, 2016, 116: 102503. doi: 10.1103/PhysRevLett.116.102503 [7] VOLYA A, ZELEVINSKY V. Phys Rev Lett, 2005, 94: 052501. doi: 10.1103/PhysRevLett.94.052501 [8] HAGEN G, PAPENBROCK T, HJORTH-JENSEN M. Phys Rev Lett, 2010, 104: 182501. doi: 10.1103/PhysRevLett.104.182501 [9] BENNACEUR K, NOWACKI F, OKOLOWICZ J, et al. Nucl Phys A, 2000, 671: 203. doi: 10.1016/S0375-9474(99)00851-9 [10] BENNACEUR K, MICHEL N, NOWACKI F, et al. Phys Lett B, 2000, 488: 75. doi: 10.1016/S0370-2693(00)00843-1 [11] Evaluated Nuclear Structure Data File[EB/OL].[2020-03-01]http://www.nndc.bnl.gov/ensdf. [12] THOMAS, R G. Phys Rev, 1952, 88: 1109. doi: 10.1103/PhysRev.88.1109 [13] EHRMAN, J B. Phys Rev, 1951, 81: 412. doi: 10.1103/PhysRev.81.412 [14] QUAGLIONI S, NAVRATIL P. Phys Rev C, 2009, 79: 044606. doi: 10.1103/PhysRevC.79.044606 [15] NAVRATIL P, QUAGLIONI S, HUPIN G, et al. Phys Scr, 2016, 91: 053002. doi: 10.1088/0031-8949/91/5/053002 [16] HUPIN G, QUAGLIONI S, NAVRATIL P. Phys Rev Lett, 2015, 114: 212502. doi: 10.1103/PhysRevLett.114.212502 [17] RAIMONDI F, HUPIN G, NAVRATIL P, et al. Phys Rev C, 2016, 93: 054606. doi: 10.1103/PhysRevC.93.054606 [18] NAVRATIL P, ROTH R, QUAGLIONI S. Phys Rev C, 2010, 82: 034609. doi: 10.1103/PhysRevC.82.034609 [19] QUAGLIONI S, NAVRATIL P. Phys Rev Lett, 2008, 101: 092501. doi: 10.1103/PhysRevLett.108.042503 [20] HUPIN G, LANGHAMMER J, NAVRATIL P, et al. Phys Rev C, 2013, 88: 054622. doi: 10.1103/PhysRevC.88.054622 [21] HUPIN G, QUAGLIONI S, NAVRATIL P. Nature Communications, 2019, 10: 351. [22] BONACCORSO A, CAPPUZZELLO F, CARBONE D, et al. Phys Rev C, 2019, 100: 024617. doi: 10.1103/PhysRevC.100.024617 [23] BENNACEUR K, NOWACKI F, OKOLOWICZ J, et al. Nucl Phys A, 1999, 651: 289. doi: 10.1016/S0375-9474(99)00133-5 [24] JAGANATHEN Y, MICHEL N, PLOSZAJCZAK M, et al. Phys Rev C, 2014, 89: 034624. doi: 10.1103/PhysRevC.89.034624 [25] DONG G X, MICHEL N, FOSSEZ K, et al. J Phys G Nucl Part Phys, 2017, 44: 045201. doi: 10.1088/1361-6471/aa5f24 [26] FOSSEZ K, MICHEL N, PLOSZAJCZAK M, et al. Phys Rev C, 2015, 91: 034609. doi: 10.1103/PhysRevC.91.034609 [27] MERCENNE A, MICHEL N, PLOSZAJCZAK M, et al. Phys Rev C, 2019, 99: 044606. doi: 10.1103/PhysRevC.99.044606 [28] MICHEL N, NAZAREWICZ W, PLOSZAJCZAK M, et al. J Phys G Nucl Part Phys, 2009, 36: 013101. doi: 10.1088/0954-3899/36/1/013101 [29] JAGANATHEN Y, ID BETAN R M, MICHEL N, et al. Phys Rev C, 2017, 96: 054316. doi: 10.1103/PhysRevC.96.054316 [30] FURUTANI H, HORIUCHI H, TAMAGAKI R. Prog Theor Phys, 1979, 62: 981. doi: 10.1143/PTP.62.981 [31] FURUTANI H, KANADAi H, KANEKO T, et al. Prog Theor Phys Supp, 1980, 68: 193. doi: 10.1143/PTPS.68.193 [32] BRINK D M, SATCHLER G R. Nuovo Cim, 1956, 4: 549. doi: 10.1007/BF02745378 [33] BERGGREN T. Nucl Phys A, 1968, 109: 265. doi: 10.1016/0375-9474(68)90593-9 [34] HAGEN G, HJORTH-JENSEN M, MICHEL N, et al. Phys Rev C, 2006, 73: 064307. doi: 10.1103/PhysRevC.73.064307 [35] MAO X, ROTUREAU J, NAZAREWICZ W, et al. Phys Rev C, 2020, 102: 024309. doi: 10.1103/PhysRevC.102.024309 [36] HARRIS R W, PHILLIPS G C, JONES C M. Nucl Phys, 1962, 38: 259. doi: 10.1016/0029-5582(62)91033-7 [37] ZUKER A P, BUCK B, MCGRORY J B. Phys Rev Lett, 1968, 21: 39. doi: 10.1103/PhysRevLett.21.39 [38] TSUKIYAMA K, HJORTH-JENSEN M, HAGEN G, et al. Phys Rev C, 2009, 80: 051301. doi: 10.1103/PhysRevC.80.051301 [39] JANSEN G R, HJORTH-JENSEN M, HAGEN G, et al. Phys Rev C, 2011, 83: 054306. doi: 10.1103/PhysRevC.83.054306 [40] HU B S, WU Q, LI J G, et al. Phys Lett B, 2020, 802: 135206. doi: 10.1016/j.physletb.2020.135206 -




 下载:
下载:


































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号