-
核物质状态方程描述了核物质的比结合能、压强、密度、中子-质子数目密度差异等宏观量之间的关系。对比原子核的液滴模型,对一个核物质体系,其零温时的状态方程可以表示成比结合能E与密度和同位旋非对称度的函数:
$$ E\left(\rho ,\delta \right)={E}_{0}\left(\rho \right)+{E}_{\mathrm{s}\mathrm{y}\mathrm{m}}\left(\rho \right){\mathrm{\delta }}^{2}+{\cal{O}}\left({\delta }^{4}\right), $$ (1) 式中:
$ \rho \!=\!{\rho }_{\mathrm{n}}+{\rho }_{\mathrm{p}} $ 表示中子和质子的总密度;$ \delta \!=\!\frac{{\rho }_{\mathrm{n}}-{\rho }_{\mathrm{p}}}{\rho } $ 表示同位旋不对称度(isospin asymmetry)。其中的第一项E0给出对称核物质贡献,此处的对称意味着中子数和质子数密度相等。第二项的系数Esym(ρ) 表征对称能的密度依赖关系,最后一项为高阶项。对于对称核物质,尽管存在一些争议,但人们普遍认为,核物质可压缩性系数偏小,具有“软”的性质[1-2]。而当前人们不太清楚而又非常重要的一个问题是极端条件下非对称核物质性质,亦对称能的密度依赖关系Esym(ρ)[3]。通过重离子实验和理论研究确定大密度范围内Esym(ρ) 是当代中能重离子物理的一个新的前沿[3-5]。由式(1)可见,对称能项的贡献对同位旋非对称度存在二次依赖关系。当δ较大,即体系中的中子数远大于质子数时,对称能项的贡献逐渐显著。这一物理量对于正确认识弱束缚晕核和近滴线核基本性质并进一步发展适用于远离稳定线的核结构理论有非常重要的科学意义。同时,它对于检验各种核多体理论方法和确定非对称核介质中有效核子-核子相互作用的同位旋依赖性至关重要[6]。在构建中子星的结构性质和演化特征等研究中,对称能与中子星的塌陷与介子凝聚、D-Urca冷却机制、壳芯转化密度、转频突变以及质量-半径关联等现象紧密关联[7-8]。尤其是2017年,LIGO和VIRGO合作组发现了两个中子星并合产生引力波事件GW170817[9-10],该事件也提供了一个约束高密区对称能随密度依赖的途径。当两个中子星绕旋至相互靠近时,会产生潮汐形变 (tidal deformability),同时引起引力波频率和强度的变化,LIGO的引力波探测器对引力波频率和强度变化敏感,故能给出潮汐极化的大小。由于潮汐形变度Λ与中子星半径R和质量M的关系满足
$ \varLambda \!\propto\! {\left(\frac{R}{M}\right)}^{5} $ ,而R/M的比值取决于中子星物质的状态方程。因此,通过中子星并合引力波的观测可以提取对称能的密度依赖Esym(ρ)[11-12]。最近,Xie等[13]通过引入贝叶斯分析方法,得到了2倍饱和密度区附近的对称能的可能取值范围。对称能也会影响原子核的一些结构性质以及核反应的动力学演化特征。对于球形重原子核,其外层表面的中子皮厚度与低密区的对称能性质具有紧密关系,并建立起中子皮厚度与饱和点附近对称能随密度变化的斜率参数L之间的关联。此外,在重离子核反应中,尤其是在Fermi能区的重离子核反应中,人们已经找到了一些可以用来约束对称能的物理量,例如同位旋扩散[14-17]、同位旋标度[18]、Pb核中子皮厚度和极化度[19-20]、同位素链的巨单极共振强度变化[21]、碎片产物N/Z比[22]和原子核结合能系统性[23]等物理量,通过和模型的对比,得到了饱和密度点附近对称能的值S和斜率参数L。文献[24-25]总结了近年来饱和点附近的对称能约束的近似结果,即
$ S\!\approx \!(32\pm 3)\,\mathrm{M}\mathrm{e}\mathrm{V} $ ,$ L\!\approx\! (59\pm 25)\,\mathrm{M}\mathrm{e}\mathrm{V} $ 。从结果可见,饱和点附近的对称能的值约束较好,斜率参数的范围也给出了大致的约束,但不确定度略大。对称能随密度依赖行为,已成为当前世界上几个大型核物理实验室以及天体观测装置的主要研究目标之一。例如,美国NASA国际空间站上的一个X-射线望远镜项目NICER (Neutron Star Interior Composition Exploer),可以精确测量中子星的半径和质量,通过它们的R-M关系来对Esym(ρ)进行更为精确的约束[26-28]。
在重离子核反应中,对称能主要影响了反应过程中质子和中子的不同输运行为,因此,同位旋自由度在反应中的驰豫特性,可能携带对称能效应的敏感信息[29],因此,研究重离子反应中的同位旋自由度的输运属性,进而提出敏感的对称能探针,是提高对称能约束准确度的一把钥匙。本文主要讨论了费米能区重离子核反应中同位旋自由度驰豫的实验观测和相应的对称能约束结果,此外,对于今后定量观测同位旋自由度驰豫时标以及寻找新的对称能约束探针,也做了简单讨论。本文的结构如下:第2部分给出重离子反应中同位旋自由度弛豫与时标方面的实验结果,以及同位旋驰豫时标测量方面的实验现状,第3部分讨论了用氘核直接反应约束亚饱和密度区对称能一些理论上的考虑,第4部分是文章的小结。
-
在重离子核反应过程中,对称能通过两种机制影响同位旋自由度的驰豫,一个是同位旋扩散(Isospin diffusion),另一个是同位旋漂移 (Isospin drift)。在同位旋扩散机制作用下,中子和质子的粒子流差异表示如下:
$$ {j}_{\mathrm{n}\mathrm{p}}^{I}={j}_{\mathrm{n}}^{I}-{j}_{\mathrm{p}}^{I}=-\left({D}_{\mathrm{n}}^{I}-{D}_{\mathrm{p}}^{I}\right)\nabla I, $$ (2) 式中角标n,p分别表示中子和质子;
$ I=\frac{N-Z}{N+Z} $ 表示反应体系的同位旋非对称度,即中子和质子数相对差异。此式表明,中子和质子的粒子流差异由体系N/Z的分布非均匀性驱动。例如当丰中子弹核与缺中子靶核碰撞时,多余的中子会从弹核往靶核输运。上式右边的比例系数正比于对称能,即$$ {D}_{\mathrm{n}}^{I}-{D}_{\mathrm{p}}^{I}\propto \rho {E}_{\mathrm{s}\mathrm{y}\mathrm{m}}\left(\rho \right){\text{。}} $$ (3) 而在同位旋漂移机制作用的情形下,中子和质子的粒子流差异则由体系的密度分布梯度
$ \nabla \rho $ 驱动,如下式所示:$$ {j}_{\mathrm{n}\mathrm{p}}^{I}={j}_{\mathrm{n}}^{\rho }-{j}_{\mathrm{p}}^{\rho }=-\left({D}_{\mathrm{n}}^{\rho }-{D}_{\mathrm{p}}^{\rho }\right)\nabla \rho {\text{。}} $$ (4) 比例系数正比于对称能随密度的变化率
$$ {D}_{\mathrm{n}}^{\rho }-{D}_{\mathrm{p}}^{\rho }\propto I\frac{\partial }{\partial \rho }{E}_{\mathrm{s}\mathrm{y}\mathrm{m}}\left(\rho \right){\text{。}} $$ (5) 在核反应过程中,实验上很难完全区分这两种机制的影响,这两种机制是叠加在一起发生作用的。但依然有一些观测量,人们认为某一种机制会起主要贡献。例如,在同位旋非对称体系的周边碰撞中,同位旋扩散机制对类弹碎片同位旋组成的影响占有主要贡献。例如前面已经提及,Tsang等[15]通过在
$ {}^{\mathrm{112,124}}\mathrm{S}\mathrm{n}+{}^{\mathrm{112,124}}\mathrm{S}\mathrm{n} $ 四个反应体系中构造同位旋扩散的观测量,结合输运模型的计算,给出了对称能随密度依赖的约束[16-17]。 -
我们首先考察同位旋自由度在重离子核反应中的驰豫过程。同位旋输运在核反应中有一些观测效应,例如由于对称能的密度依赖效应,核反应中的中子更容易被排斥到气相而质子更容易聚集到液相中,从而出现同位旋相分化现象[30]。当入射能较低时,研究表明同位旋自由度是一个最快达到驰豫平衡的自由度[31-34],随着入射能量升高,同位旋自由度驰豫的时标变化较慢而动量驰豫的时标急剧下降,导致同位旋自由度的驰豫很可能达不到平衡[35-38]。在周边和近周边反应中,人们用类弹碎片的出射动能来表征耗散程度或耗散时间,通过观察类弹碎片的N/Z随出射动能的关系,并在不同的实验中均观察到了由同位旋扩散机制(下面有述)导致的驰豫过程[14, 39-40]。从这些丰富的结果可以看出,同位旋自由度在核反应中驰豫与否,和反应条件及物理过程可能紧密相关。最近的一些实验结果表明,当同位旋漂移机制发生作用时,同位旋自由度的驰豫可能持续更长时间,可以超过
$ {10}^{3}\,\mathrm{f}\mathrm{m}/c $ [41-42]。在兰州重离子研究装置 (HIRFL) 上的大散射筒终端上,人们测量了35 MeV/u Ar+Au反应中出射的裂变碎片和符合轻粒子。采用六块大面积的PPAC用来测量反应中出射的裂变碎片。沿着束流线的周围,对称放置了两圈共12个Si-BGO望远镜探测器,用来测量反应中出射的类弹碎片。在不同的角度处放置了六块三叠层的半导体望远镜,用来测量与裂变碎片或者类弹碎片符合的轻粒子。实验中的一类触发条件是两个裂变碎片和一个望远镜点火的事件。从关联的碎片速度可以求得裂变前类靶核的速度,从而得到非完全熔合过程中的线性动量转移以及裂变碎片的质量非对称度。探测器布局的详情可以参阅文献[43]。在六块轻粒子望远镜中,80°和158°处的两块望远镜,可以实现清楚的同位素鉴别,对比两个探测器的粒子计数结果发现,中前角区的轻粒子的中子丰度相对更高。
为了定量地解释不同同位旋轻粒子产额随角度的分布,我们采用多源模型拟合能谱。图1显示的是80°和158°处的Z=1轻粒子在不同裂变碎片非对称性区间内的能谱,曲线是拟合曲线,图中η为裂变碎片的非对称度。在拟合中假设粒子来源于3个运动源,在每个源的本体坐标系中,粒子能谱满足Maxwell分布。这三个源分别是动力学发射期间的中速源 (IV),非完全熔合核源,或简称复合核源 (CN) 和晚期发射的裂变碎片源 (FF)。在后角区,粒子能谱可以由CN源很好地描述,如图1(上)的三个框图结果所示。但是在中前角区,如图1(下)所示,IV源和FF源的贡献很显著。对于IV源,由于温度较高,主要贡献在高能端,而FF源因为激发能已经降得很低,且有显著的运动学效应,主要贡献在能谱的低能端。
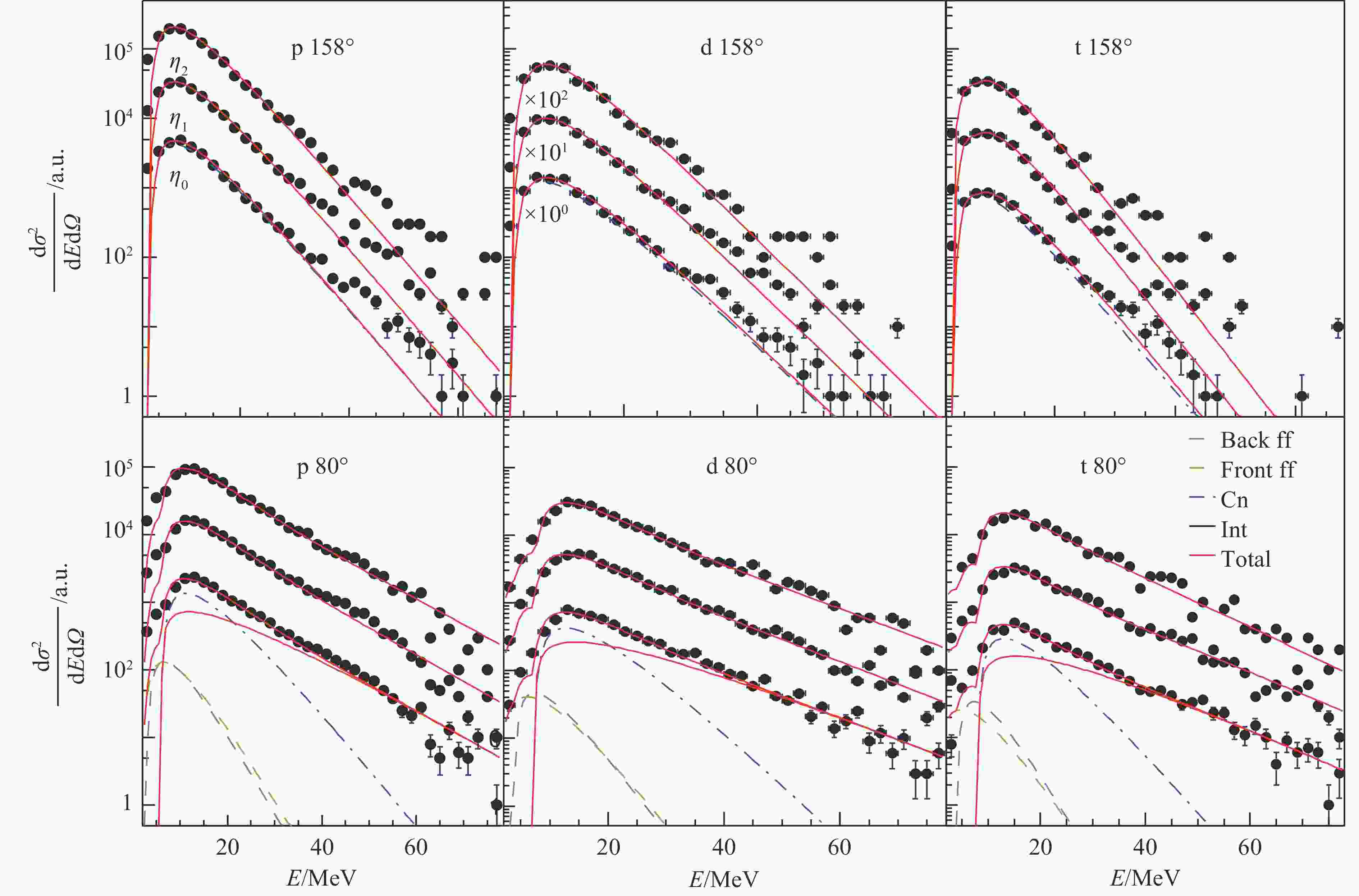
图 1 (在线彩图)不同裂变碎片质量非对称度条件下,记录的158°(上)和 80°(下)处的能谱,不同源的贡献也已标出,图选自文献[43]
多源模型的拟合参数较多,为了尽量避免因为参数关联造成的拟合不确定度,引入了最小χ2分析方法来寻找各个参数的最优值。结果如图2所示。图中的横坐标是裂变碎片质量的非对称度η,可以反映裂变过程的动力学效应或者裂变时标的大小,而纵坐标分别是IV源和FF源相对于CN源的粒子多重性比值。由图可见,在用CN源做了归一之后,IV源中的丰中子核素t的产额相对更高,而FF源中的质子产额相对更高。考虑到IV源对应于早期的动力学发射,FF源对应于断点之后的裂变碎片发射,这一结果意味着,粒子发射呈现出同位旋依赖的发射次序,即丰中子轻粒子相比缺中子粒子,发射相对更早[43]。

图 2 (在线彩图)不同裂变碎片质量非对称度条件下,IV源(a)和FF源(b)的粒子多重性相对CN源粒子多重性的比值,图选自文献[43]
-
由于只有两个角度的轻粒子能谱结果,再加上多源模型的分析本身由于参数较多具有较大的不确定度,因此上述分析未能给出对称能的约束。然而,同位旋相关的粒子发射次序结果告诉我们,轻粒子的中子丰度随实验室系的角度分布能够反映不同阶段粒子发射的同位旋组成。这就意味着,在大角度范围内出射粒子中子丰度的变化趋势,可以定性表征同位旋自由度的驰豫过程。考虑到对称能对密度的导数是粒子从高密液相向低密气相输运的驱动力,可以推测,出射粒子中子丰度的角分布可能携带有对称能软硬属性的信息。输运模型的计算支持这一推测,即改变对称能的密度依赖参数γ,得到不同粒子中子丰度的角分布。
$\gamma $ 越大,即对称能越硬,轻粒子中子丰度随实验室角度下降的趋势越显著[44]。我们在HIRFL-RIBLL1实验终端,完成了另一轮 30 MeV/u Ar+Au的实验[45]。同样的,裂变碎片用PPAC测量,此外在实验室19°~165°的范围内,安放了11块三叠层硅望远镜测量与碎片符合的轻粒子。图3显示的是其中部分角度的粒子能谱的双源模型拟合结果,为了清楚地显示出射角度对粒子出射时间的定性依赖,我们只选取了两个发射源,即IV和CN源。图3(a)显示了几个典型角度37°, 70°和74°处的能谱拟合结果,图3(b) 显示了IV 源和CN 源的粒子产额随角度的变化关系。当所有角度处IV源和CN源多重性参数均作为自由参数时,结果如实线所示,而当所有角度的两源多重性参数统用全局的参数来拟合时,得到的结果如虚线所示。这一分布特征和文献[46] 报道的中等质量碎片结果是一致的,说明本次实验数据的可靠性。从图3(b)可见,由于运动学效应,两个源的粒子产额随角度的变化趋势不同,当对两个源的粒子发射时标τ1和τ2做加权平均来求粒子的平均出射时标时,可以得到如图3(c)所示的分布。结果表明,大范围实验室系角度分布可以定性反映物理量的时间分布特性。
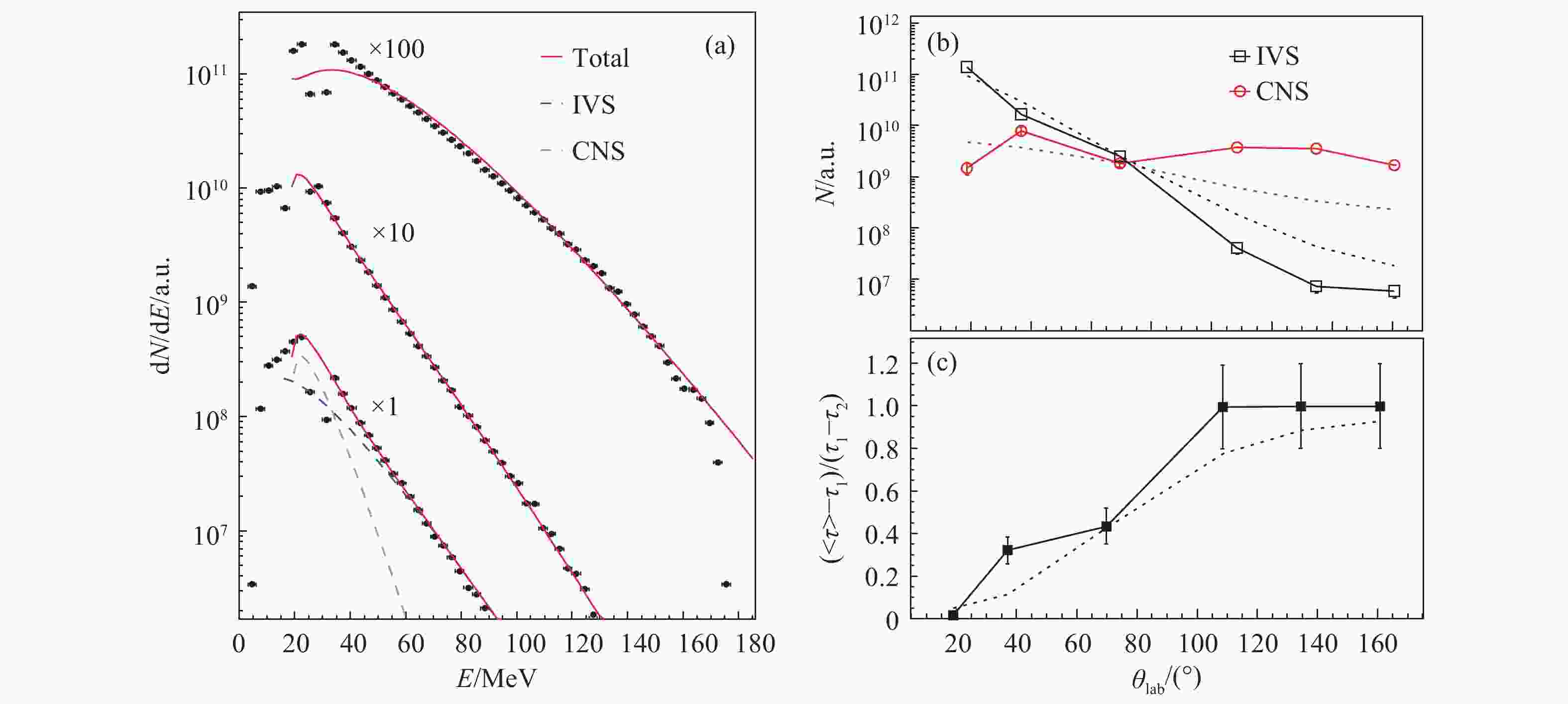
图 3 (在线彩图)37°, 70°和74°不同角度处的能谱双源模型拟合结果(a), IV 源和CN源的多重性随角度的分布(b)及粒子的平均时标随角度的变化关系(c), 图选自文献[45]
图4给出了轻粒子相对中子丰度随角度的变化关系。此处相对中子丰度的定义为所有轻粒子中的中子富裕度与电荷总数的比值,即
$$ {Y}_{\mathrm{n},\mathrm{e}\mathrm{x}}/{Y}_{\mathrm{p},\mathrm{C}\mathrm{I}}=\frac{\sum _{i}{y}_{i}\left({N}_{i}-{Z}_{i}\right)}{\sum _{i}{y}_{i}{Z}_{i}}, $$ (6) 式中:yi代表Z=1,2的某种粒子产额;Ni和Zi为相应的中子数和质子数。由图可见,随着实验室系出射角度
$ {\theta }_{\mathrm{l}\mathrm{a}\mathrm{b}} $ 的增大,轻粒子的相对中子丰度逐渐下降,和图2实验中得到的结果定性相符。这一结果表明,轻粒子的同位旋组成随角度或者出射的平均时间在发生变化。考虑到后角区对应的主要来自统计蒸发阶段的贡献,这一结果表明同位旋漂移的驰豫机制可能是一个长时标的过程。这就意味着,当我们讨论同位旋自由度驰豫平衡与否的问题时,一定要针对具体的物理过程来分析。而一般条件下笼统地去问同位旋自由度驰豫平衡与否,可能没有一个确定的结论。此外,图4(a)中曲线表示输运模型和统计蒸发模型联合计算的结果,不同的线型表示采用了不同的对称能密度依赖参数γ。由图可见$ \gamma =0.5 $ 时理论计算和实验结果符合最好。值得注意的是,图中不同曲线之间在纵轴上的值似乎存在一个上下的偏置,这可能是因为输运模型对碎片产额模拟存在低估的缺陷,因此直接对比理论预言的中子丰度和实验结果,具有一定的风险。为此,我们假设输运模型低估碎片产额的这一缺陷对所有角度都相同,用100°以内数据点的斜率来表征中子丰度随角度的变化率,或者定性表达其随出射时间的变化率,可以明显看到,不同的对称能软硬属性对斜率具有显著影响。图中的小框是斜率值k的实验和理论结果的对比,从图中的对比可以看出,较软的对称能模拟结果和实验符合较好。通过对比计算和实验结果,在95%的扩展不确定度下,我们得到了饱和点密度附近的对称能斜率参数为$ L\!=\!(47\pm 14)\,\mathrm{M}\mathrm{e}\mathrm{V} $ 。计算中我们没有考虑饱和点对称能值的变化,即S固定于$ S\!=\!28.3\,\mathrm{M}\mathrm{e}\mathrm{V} $ [45]。考虑S和L之间最新的关联关系[47],这一斜率参数和文献中由其他观测量提取的结果一致[24-25]。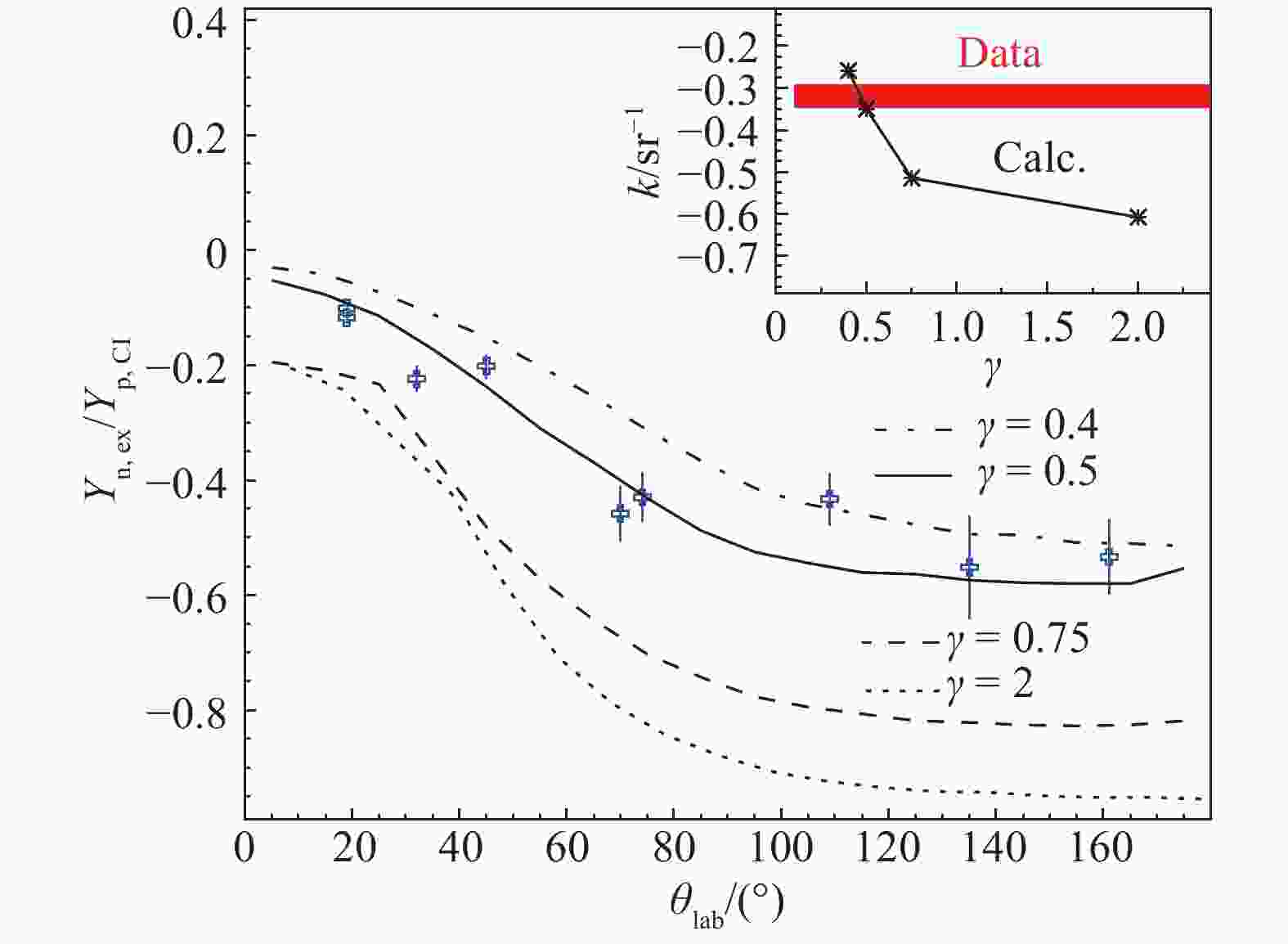
图 4 (在线彩图)30 MeV/u Ar+Au 反应中轻粒子中子相对丰度随角度的变化关系,内插图显示的是角度分布斜率的实验和理论对比,图选自文献[45]
-
轻粒子相对中子丰度的角分布虽然定性地反映了同位旋自由度的驰豫快慢,但是不能给出驰豫时标的定量结果。驰豫时标的定量结果,需要测量不同同位旋粒子的发射时标。在核反应中,由于反应持续的时间极短,大约在
$ {10}^{-21}\,\mathrm{s} $ 量级,因此不能够直接测量,需要借助一些特殊方法。20世纪50年代,Hanbury-Brown和Twiss发明了一种强度干涉学的方法,通过测量来自遥远的天狼星的两束光线的短基线关联(或者小角关联)函数,可以计算出该星的角半径[48]。后来,这一方法被引进到重离子核反应中,可以测量粒子出射的发射源时空信息[49-51]。值得注意的是,由于核反应过程的短暂性,与天文学应用不同的是,两个粒子的关联函数不仅与发射源的大小有关,还与粒子的出射时标有关。Koonin[52]发展了这一方法的理论描述。2002年,我们在实验中测量到,在
$ {}^{40}\mathrm{A}\mathrm{r}+{}^{\mathrm{112,124}}\mathrm{S}\mathrm{n} $ 两个反应体系中,由于发射源N/Z的差异,中等质量碎片发射时标也表现出差异。结果表明,在指数衰减发射规律的假设下,这一方法对粒子发射时标的测量精度可以达到$ 30\!\sim\! 50\;\mathrm{f}\mathrm{m}/c $ [53]。为了定量测量同位旋自由度的驰豫时标,我们搭建了一套小型的重离子实验谱仪(Compact Spectrometer for Heavy IoN Experiment, CSHINE)。该实验采用大面积三叠层的硅条望远镜阵列来测量轻粒子,用平行板雪崩计数器 (PPAC) 来测量裂变碎片。其中三块PPAC探测器的灵敏面积为
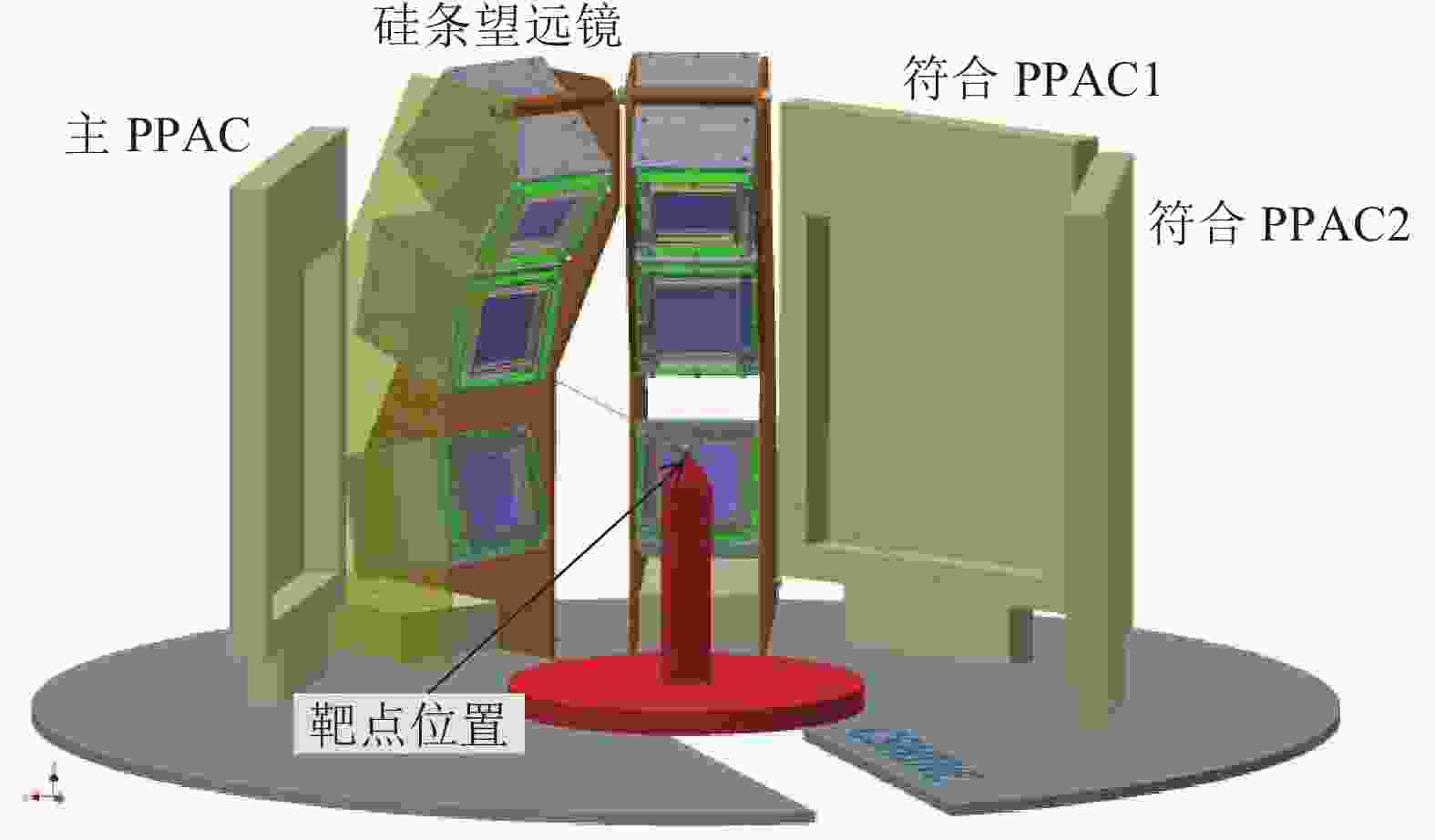
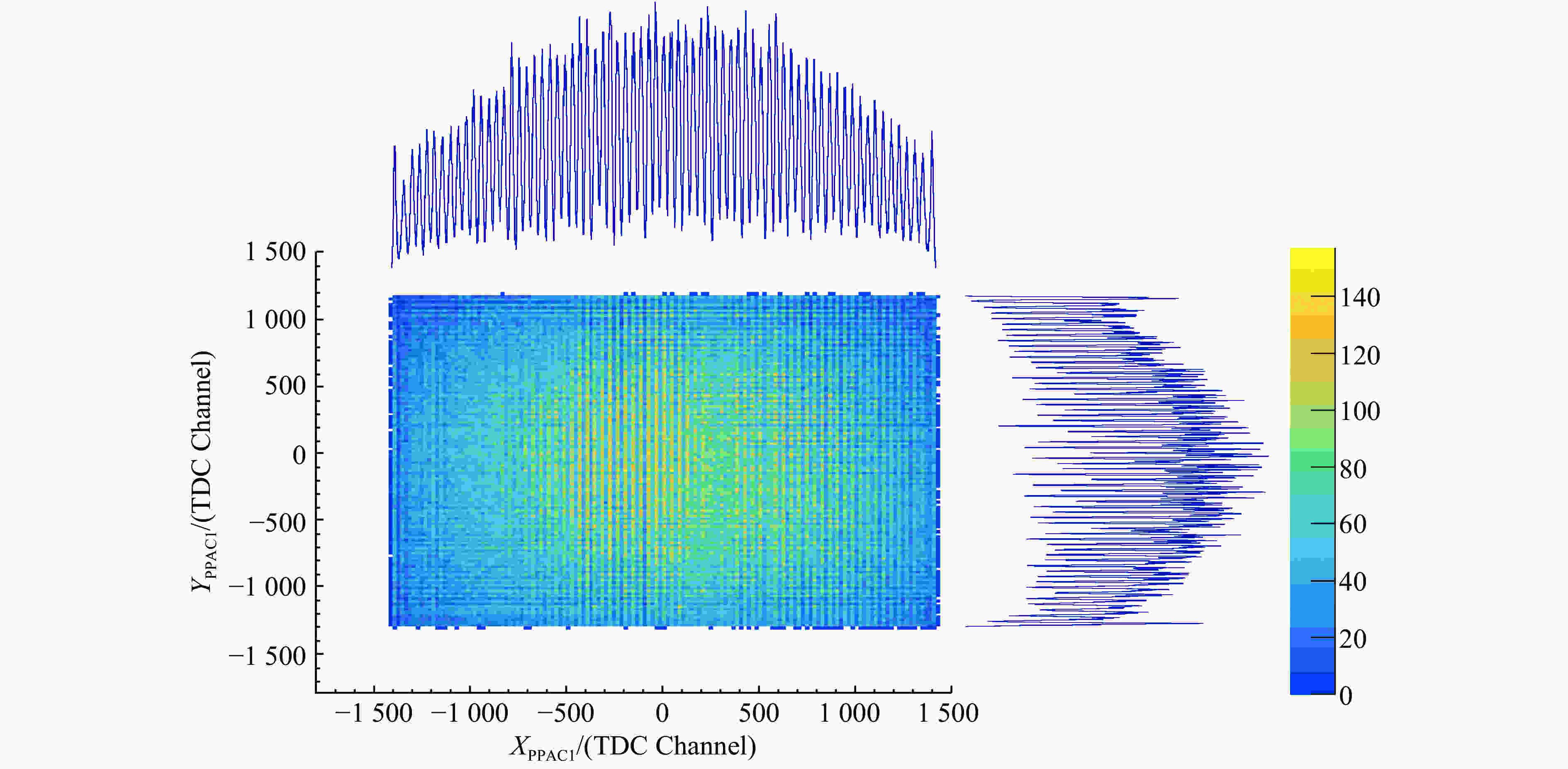
$24\;\mathrm{c}\mathrm{m}\!\times \!28\;{\mathrm{c}\mathrm{m}}^{}$ ,放置在中心离靶点约为40 cm的地方,第一块PPAC是主裂变碎片探测器,第二块和第三块PPAC则置于束流的另一侧,为符合碎片探测器。如图5所示。为了测量和裂变碎片符合的轻粒子,CSHINE还计划安装6套硅条望远镜,分别固定在两个塔上,每个塔上安装3套望远镜。每一套硅条望远镜包含一层一维的薄硅条探测器,一层双维的厚硅条探测器和一层CsI晶体组成的能量探测器阵列。CsI晶体探测器为一个$ 3\times 3 $ 单元的阵列,每个单元厚度为5 cm,均采用光二极管读出,记录轻带电粒子穿透硅条后在CsI内沉积的总能量。硅条探测器选用的是Micron公司的BB7型单维或者双维探测器,灵敏面积均为$64\;\mathrm{m}\mathrm{m}\!\times \!64\;\mathrm{m}\mathrm{m}$ ,条宽为2 mm,厚度可以根据需要选装。利用这一装置,我们重新完成了30 MeV/u Ar+Au的反应实验和新的25 MeV/u Kr+Pb的实验。在前一个实验中,安装了2套硅条望远镜,两层硅条探测器的厚度分别为65和1 500 μm。而在后一个的实验中,安装了4套硅条望远镜,两层硅条探测器的厚度分别为$ 100\!\sim\! 300$ μm 和$ 500\!\sim \!1\,000$ μm,越在前角,探测器厚度可以越厚。图5显示的是CSHINE的结构示意图。PPAC的感应阳极丝间距为0.5 mm,四根丝合并一个信号输出,因此相邻的点火信号之间相差4 mm。PPAC工作气体为异丁烷,实验中的工作电压为460~490 V。此时裂变碎片的测量效率接近100% 而轻粒子则不能产生点火信号[54]。图6显示的是30 MeV/u Ar+Au反应中,主PPAC探测器中裂变碎片的二维位置分布和向X和Y方向(本体坐标系)的投影。从投影的位置分布可以看出,每一组丝可以清晰分辨,这表明PPAC的位置分辨可已达到
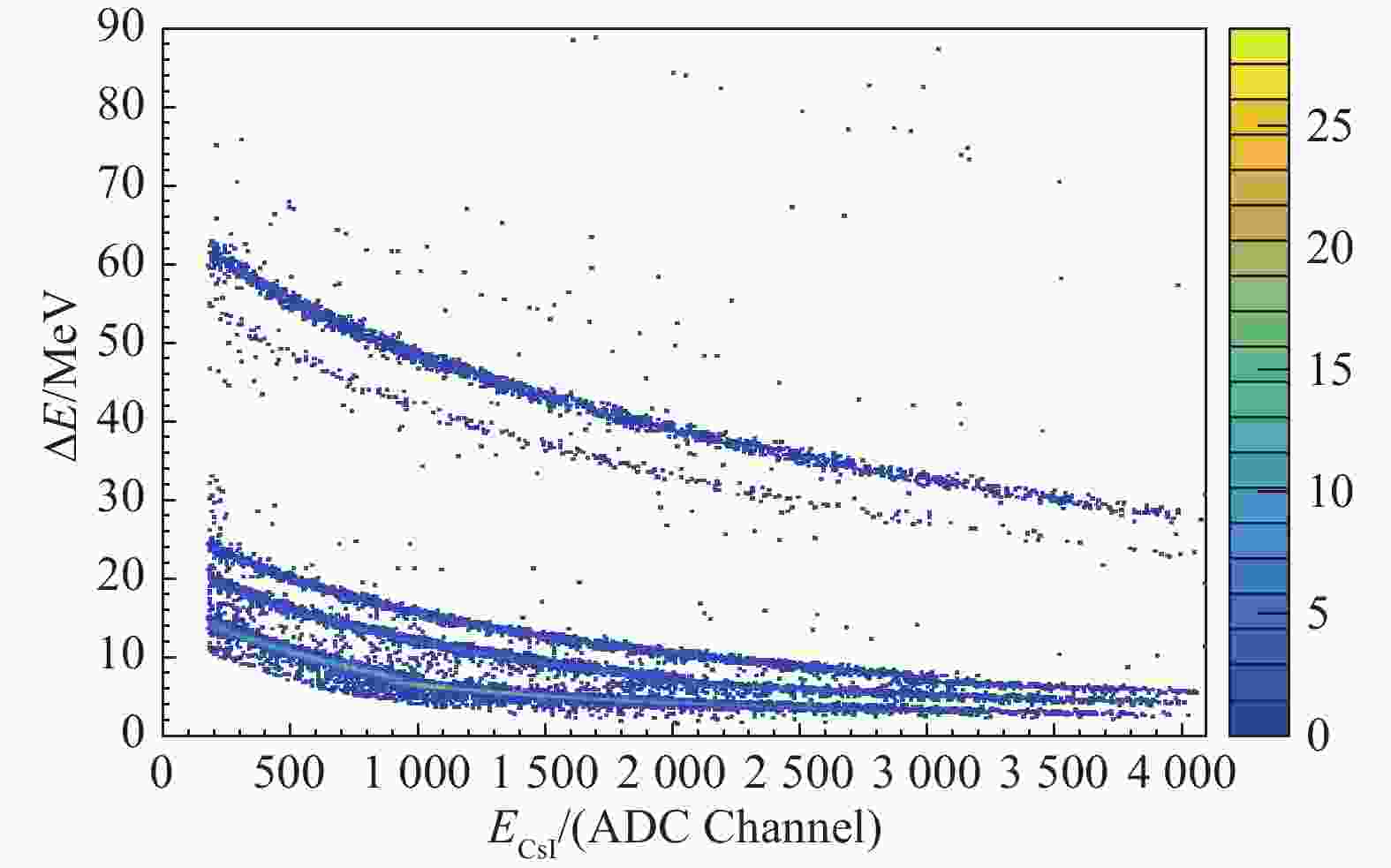
$4/\sqrt{12}\;\mathrm{m}\mathrm{m}$ ,对应实验室系角分辨优于1°。图7显示的是30 MeV/u Ar+Au反应中1号硅条望远镜的探测器的
$ \Delta E–{E}_{\mathrm{C}\mathrm{s}\mathrm{I}} $ 关联散点图。由于每一套硅条探测器立体角都接近$ 50\,\mathrm{m}\mathrm{s}\mathrm{r} $ ,两粒子同时点火几率较高。图中的散点图是挑选的单粒子入射事件画出的,32条硅条的结果叠加在一起。由图可见$ Z\!\leqslant\! 2 $ 的轻粒子可以清楚鉴别,且同位素带非常细。由于第二层硅条厚度达到$ 1\,500$ μm,穿透的高能质子也能够被记录下来。硅条探测器采用放射源和脉冲发生器联合方法完成刻度,而CsI的光输出响应则通过图7中每种粒子的
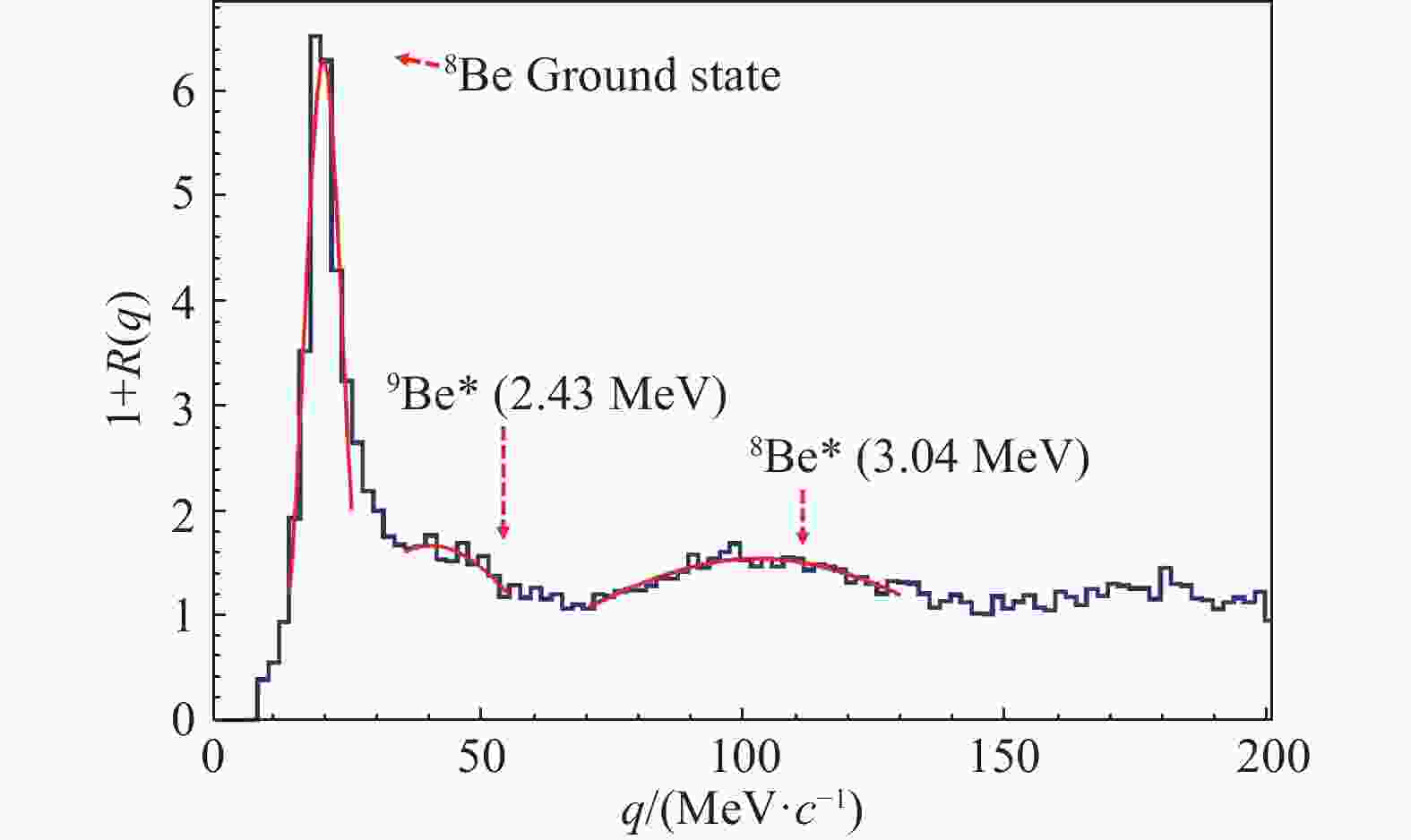
$ \Delta E–{E}_{\mathrm{C}\mathrm{s}\mathrm{I}} $ 曲线,采用能损反推的方法完成刻度。刻度的结果可以通过$ \mathrm{\alpha }–\mathrm{\alpha } $ 动量关联函数加以检验。反应中出射的$ \mathrm{\alpha } $ 粒子可能来源于8Be基态或者激发态 ($ {E}^{*}\!= 3.04\,\mathrm{M}\mathrm{e}\mathrm{V} $ ) 的破裂以及9Be激发态 ($ {E}^{*}\!=\!2.43\,\mathrm{ }\mathrm{M}\mathrm{e}\mathrm{V} $ ) 的两个$ \mathrm{\alpha } $ 粒子破裂道。由于两个α粒子的相干性,该关联函数不能用来提取发射源的时空信息,但是可以用来检验探测器的刻度情况。图8显示的是30 MeV/u Ar+Au反应中硅条望远镜测量到的$ \mathrm{\alpha }–\mathrm{\alpha } $ 动量关联函数。图中箭头标出上述不同状态下$ \mathrm{\alpha }–\mathrm{\alpha } $ 相对动量的预期位置,曲线是对局部峰域的高斯拟合。由图可见,实验测量的三个峰的位置和预期的位置重合,这表明探测器的能量刻度正常。在此基础上,我们将得到不同粒子对的关联函数,并借助三体弹道模型提取不同粒子的发射时标。但是,探测器的测量效率对关联函数上升沿的影响非常敏感。为了从关联函数准确提取时标,探测器对两粒子关联的效率曲线需要确定,这方面的数据正在处理中。在已完成的25 MeV/u 的Kr+Pb实验中,实验的目标和文献[43, 45]是一致的,即研究裂变事件中,中间快度区 (即颈部) 出射的轻粒子和中等质量碎片的N/Z随角度和粒子能量的关系。但在文献[43]中,由于只有80°和158° 两个角度的轻粒子数据,未能从丰中子的颈部发射结果提取对称能的密度依赖参数。新的实验中则安装了四块硅条望远镜,图9显示是25 MeV/u 的Kr+Pb反应中硅条望远镜
$ \theta –\phi $ 关联分布的Geant4 模拟结果,可见探测器可以连续覆盖实验室系15°~60°的范围。根据量子分子动力学 (ImQMD)的模拟结果,如文献[44]中的图6所示,在实验室系前角区,轻粒子的N/Z随角度的变化对饱和点密度处的对称能依赖是最敏感的。在文献[45]中,即图4显示的结果,显示的是从单举的望远镜数据中得到的粒子同位旋随角度的变化关系,对比新的实验中,由于望远镜的覆盖立体角增加了几十倍,我们会有足够的数据统计来研究与裂变碎片符合的轻粒子N/Z的演化,在给定反应几何的条件下考察同位旋自由度的输运行为并提取对称能的密度依赖关系。目前数据正在刻度中。 -
我们知道,从重离子核反应过程中提取可以约束对称能的物理量,需要依赖与输运模型的计算结果做对比。这是因为,非对称核物质的状态方程并不是一个直接观测量,它的效应是通过影响重离子碰撞的输运过程表现出来的,并在最终的观测量上体现。在输运模型的计算中,除了状态方程的参数是输入量之外,还有一些其它的参数以及数值处理的技术,都会影响最后的计算结果。进一步的研究还发现,输运模型中的众多参数,可能存在关联,它们对观测量的效应是叠加在一起的,这样就增加了从重离子反应中提取对称能参数的不确定性[55]。近年来,国际同行开展了暗盒计算(box calculations)或者限制相同条件做重离子碰撞模拟,来比较不同的输运模型之间的差异[56-58], 有关ImQMD输运模型对重离子碰撞模拟的最新综述,请参考文献[59]。
而另一方面,我们也可以尝试考虑用其它的实验途径来约束对称能。与剧烈的重离子中心碰撞相比,直接反应中参与反应的自由度较少,许多核子的自由度被冻结,故直接反应通常可以采用量子力学框架处理,因此有可能提供精确约束对称能的探针。如果考虑质子和中子分别同原子核的近周边散射过程,不难理解,由于核势中同位旋矢量势的存在,中子和质子的散射角分布是不一样的。输运模型计算表明,它们各自的散射角分布,可以用来探测对称能[60]。在光学模型的框架下,这是因为中子和质子在与原子核散射的过程中,全局光学势存在差异。而最近的理论研究表明,根据Hugenholtz–Van Hove定理,中子、质子全局光学势的差异可以解析导出饱和密度附近的对称能值及其密度依赖斜率[61]。只是在相同探测设备上,同时完成中子束流和质子束流实验,存在不小的技术困难。
为了解决这一困难,或许可以通过某种方式将中子和质子“绑”在一起完成上述散射实验。氘核是一种非常特殊的原子核,由一个质子和一个中子组成,总自旋为1,核子空间波函数偏离球形,呈现出轴向对称的特点[62]。其结合能很小,只有2.2 MeV,在高能散射中结合能的影响可以忽略。因此,可以考虑采用氘核与原子核的散射,通过测量弹核弹性破裂后中子和质子的分布特性来提取对称能参数。
中子和质子除了所受核势不一样之外(体现在核势的同位旋矢量部分),其库仑势也有巨大的差异。由于质子带电,在氘核与重核的散射过程中,氘核容易受到极化作用,使得质子远离靶核而中子靠近靶核,这一效应被称为库仑极化,它在核反应中的效应最早由Oppenheimer等[63-64]发现,近年来在丰质子不稳定核的散射实验中也有报道[65]。同样的道理,当考虑同位旋矢量势时,这一部分作用势对质子产生吸引作用而对中子产生排斥作用,除了会导致重离子反应中的同位旋相分化现象之外,在氘核散射过程中,这一差异会对氘核加上一个力矩作用,使之产生额外的转动。如果氘核进一步产生破裂,这一额外的转动效应,将会对中子和质子的角分布产生影响[66],如图10所示。
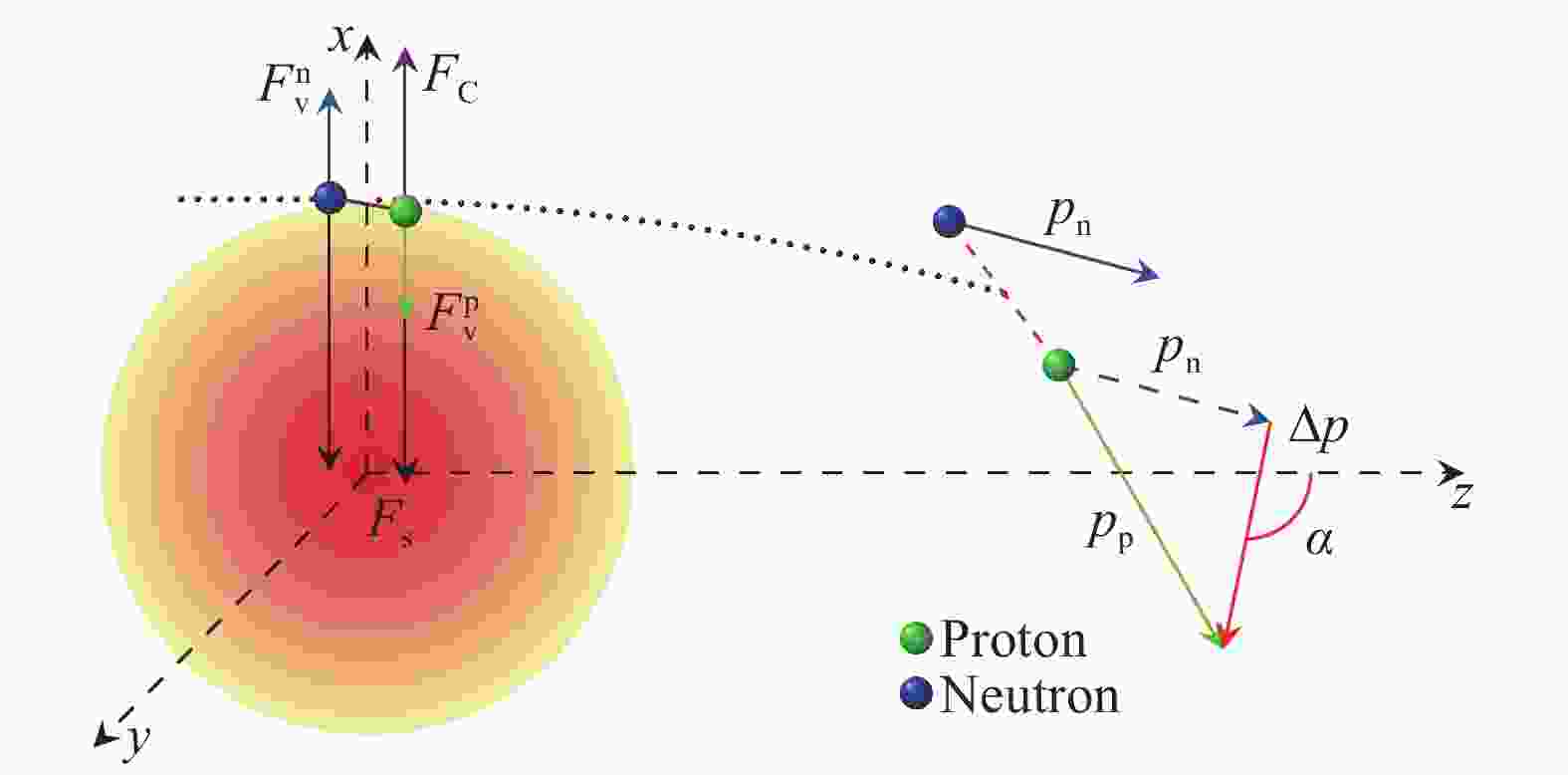
图 10 (在线彩图)极化氘核与重核散射时的同位旋矢量极化效应示意图,图选自文献[66]
在输运模型的框架下,我们计算了氘核与124Sn原子核的周边散射过程。为了降低氘核结合能的影响,氘核的入射能量取为100 MeV以上。为了减少初始氘核随机取向的影响,计算中假设氘核是矢量极化的。极化氘核束流在世界上几个重要的实验室都能够获得,并且极化度很高[67-68]。此处,矢量极化意味着,其自旋在束流轴上投影的
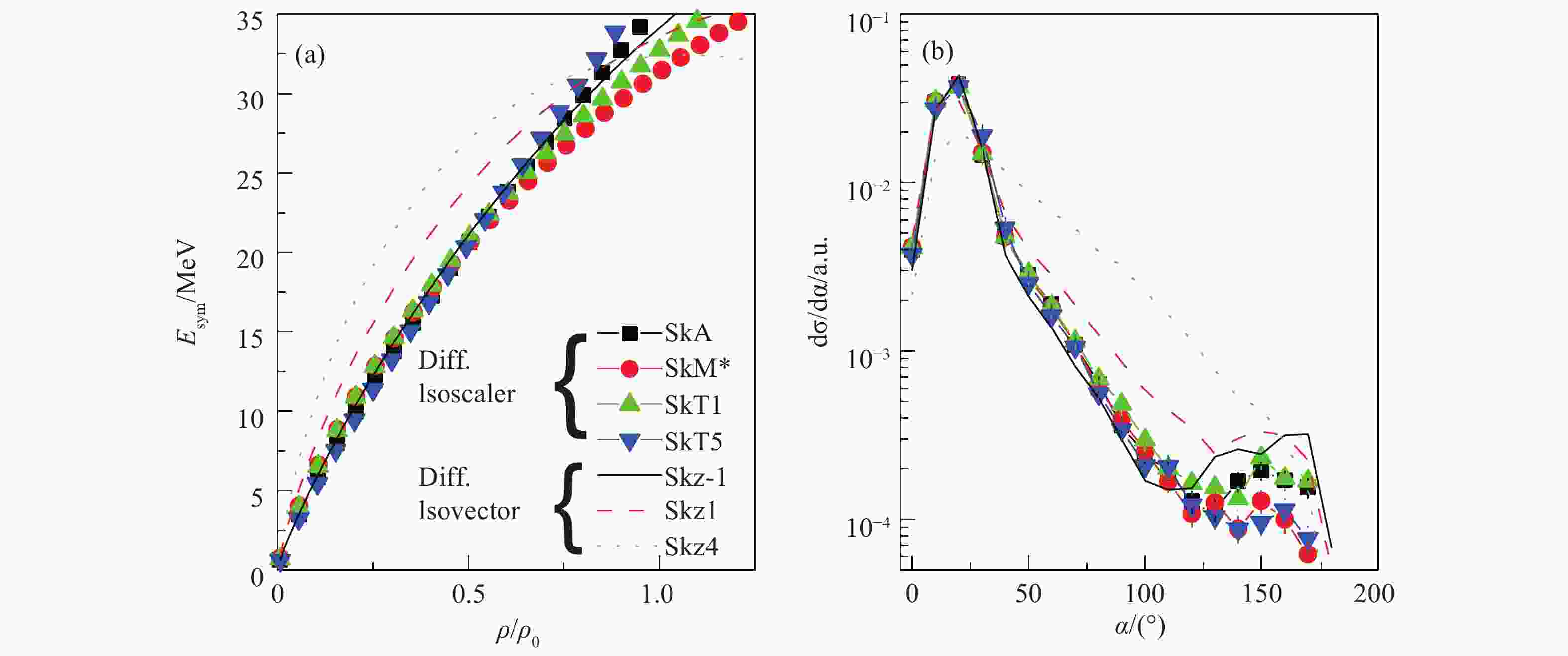
$ {m}_{z}\!=\!1 $ 分量可以确定。此时,中子-质子连线方向与束流轴平行,但中子和质子仍然具有交换对称性。在计算中,我们采用了7套Skyrme势参数来模拟极化氘核的同位旋矢量极化和破裂过程,这7套Skyrme势参数包括SkA[69],SkT5,SkT1[70],SkM*[71],Skz-1,Skz1和 Skz4[72],由这7套参数给出的对称能随密度依赖的关系如图11(a)所示。由图可见,前四套参数的同位旋矢量势相近,而同位旋标量势差异较大,后三套参数的同位旋标量势相近而同位旋矢量势差异较大。为了找到敏感依赖于对称能的观测量,我们在氘核的破裂道中,提取中子和质子的相对动量的夹角α,如图11 (b)所示。从图中可以看出,α的分布对SkA,SkT5,SkT1和SkM* 这4套参数没有显著的差异,而对Skz-1,Skz1,和 Skz4等3套参数具有显著的依赖性。可见破裂中子和质子的关联角α对同位旋矢量势的密度变化具有敏感依赖,而对同位旋标量势不敏感。计算发现,这一效应主要发生在周边碰撞区域,对应的核物质密度在
$ 0.5{\rho }_{0} $ 附近,因此,极化氘核与重核散射时的同位旋矢量极化效应,是低密区对称能的一个敏感探针。最近的模拟结果表明,在氘核与重核的散射过程中,中子和质子各自的散射角分布,对低密区对称能也具有敏感依赖性,这实际上降低了实验上符合测量的要求,有利于实验的进行[73]。在量子力学的框架下,基于含时基展开的方法,人们计算了仅考虑库仑作用的情况下氘核和重核散射时的波函数演化行为,重现了氘核空间波函数的库仑极化效应[74]。 -
重离子核反应是研究核物质状态方程的有效手段,也蕴含了丰富的动力学演化信息。核物质状态方程,尤其是对称能随密度的依赖性质,对人们理解奇异核结构与核反应、核素图边界以及致密天体过程的物理,均具有重要意义。在HIRFL大科学装置上,完成了费米能区的 Ar+Au 的实验,观测到同位旋自由度的长时标弛豫特征,揭示了同位旋依赖的粒子发射次序,在固定
$ {S}_{0}\!=\!28.3\,\mathrm{M}\mathrm{e}\mathrm{V} $ 时,从中得到对称能在饱和点的斜率参数$ L\!=\!(47\pm 14)\,\mathrm{M}\mathrm{e}\mathrm{V} $ 。在此基础上,搭建了一套具有裂变碎片和带电粒子符合测量的高性能探测器阵列CSHINE,对轻粒子能够实现同位素分辨,并能够精确测量轻粒子的HBT关联函数,从而具备给核反应中的粒子发射过程“摄像”的能力,将在费米能区的核反应研究中提供更多的有关同位旋自由度驰豫过程的新数据。经历近二十年在对称能约束方面的实验和理论进展,尤其是最近基于GW170817事件的Bayesian分析结果,人们逐渐意识到,不同的观测量对
$ {E}_{\mathrm{s}\mathrm{y}\mathrm{m}}\left(\rho \right) $ 敏感的密度区间互有差异。重离子反应能够制备的核物质密度与反应条件密切相关,因此对于某一个给定的观测量,应考察其敏感的密度区间并得到该区间内的对称能参数。自然地,要在大范围内更精确地约束对称能的密度依赖关系,实验上需要进一步寻找新的探针,覆盖宽广的密度范围并提高实验精度。理论上,则可能需要全局考虑不同能区的实验和观测量,追求在同一理论框架下实现多观测量的拟合,从而得到自洽的对称能行为。用高密区观测量导出饱和点附近的对称能密度依赖,或者用饱和点密度附近的参数来外推远离饱和密度的结果,都是具有一定风险的。不管在高密区还是低密区,对称能的效应本质上都是影响同位旋自由度在核反应这一非平衡过程中的输运行为,因此,测量同位旋自由度的输运性质,深入理解核反应过程的动力学效应,对于我们获取对称能的约束这一特定的目标,也具有很重要的意义。重离子反应观测量需要依赖于输运模型方可以提取对称能的信息,而输运模型对于反应过程的完整描述依赖于众多的参数,包括核子有效质量劈裂和NN反应截面等信息,也依赖于对物理过程的处理方法,不同参数之间的关联性较大。为了改善这种状况,一方面,贝叶斯关联分析方法可以引入到重离子反应的数据分析中,以研究不同参数之间的关联并得到敏感参数的最可几取值,另一方面,在参与反应自由度较少、可用基于量子力学框架描述且模型可调参数较少的直接反应中寻找对称能的新探针,也会是对称能研究的一个方向。氘核的同位旋矢量极化效应,可能提供一个新的利用直接反应约束非对称核物质状态方程的手段,这一效应,本质上反映的正是中子和质子与重核光学势之间的差异,根据Hugenholtz–Van Hove定理,由该差异有望导出低密区的对称能。
全文HTML
2.1. 同位旋相关的粒子发射次序
2.2. 轻粒子中子丰度角分布和对称能的约束
2.3. 同位旋自由度驰豫时标的定量测量和新实验项目
 2019-CNPC63.pdf
2019-CNPC63.pdf
|

|









 下载:
下载:






















































 甘公网安备 62010202000723号
甘公网安备 62010202000723号