-
Simulations of lattice quantum chromodynamics(QCD) predict that when the temperature of the system reaches up to about
$ 155 $ MeV[1-3], the quark and gluon degrees of freedom that are usually confined in normal nuclear matter are liberated, and a new state of matter called quark-gluon plasma (QGP) can be formed. Such hot and dense deconfined QGP matter has existed in early Universe a few microseconds after the Big Bang, when the temperature of the Universe is so high that quarks and gluons cannot combine to form hadrons due to their violent thermal motions. QGP can also be created in the laboratories via colliding heavy nuclei at ultra-relativistic energies, such as those performed at the Relativistic Heavy-Ion Collider (RHIC) and the Large Hadron Collider (LHC). The primary goal of high-energy heavy-ion collisions is to probe the novel properties of QGP and explore the phase structure of strong-interaction QCD matter at various conditions of temperatures and/or densities. Comprehensive experimental and theoretical studies have shown that the highest temperature achieved at RHIC and the LHC is about 350~480 MeV[4-8], which is well above the phase transition temperature ($ \sim 155 $ MeV) between normal nuclear matter and deconfined QGP.Relativistic heavy-ion collision is a dynamically-evolving many-body process. It starts from the collision of two heavy ions which have been accelerated to ultra-relativistic energies. The energetic ion collision deposits a lot of energy and produces a large amount of entropy and particles. After a short pre-equilibrium stage, the system arrives at a nearly thermal equilibrium state, i.e., the hot and dense QGP. The fireball then expands and cools until the temperature reaches down to the phase transition temperature when the system hadronizes into hadrons. The produced hadrons continue to interact with each other until the kinetic freeze-out. Finally, all produced particles fly to the detectors. One important task of relativistic heavy-ion collisions is, by studying the observed distributions and correlations of produced particles, to infer the evolution dynamics of the collisions and probe the macroscopic and microscopic properties of QGP.
In this review, we discuss two most important probes of QGP, soft and hard probes, in relativistic heavy-ion collisions. Soft probes refer to the collective properties of soft bulk matter, which consists of more than 99% of particles produced in collisions. Here we focus on anisotropic collective flows of the QGP. Hard probes mainly refer to the particles carrying large transverse momenta (
$ p^{}_{\rm{T}} $ ), which are usually originated from early hard collisions. Here we focus on high$ p^{}_{\rm{T}} $ and heavy flavor hadrons and jets. We will also discuss the collectivity in small collision systems. -
One of the most important evidences of QGP formation in relativistic heavy-ion collisions is the strong collective flow[9-12], which is anisotropic in the plane transverse to the beam. In a typical nucleus-nucleus collision, the produced QGP matter is anisotropic in the transverse plane due to the intrinsic collision geometry and the fluctuations of the initial states[13-25]. The initial geometric anisotropy can be quantified by the so-called eccentricity
$ \epsilon_n $ , defined as follows[20-22]:$$ {\cal{E}}_n = \epsilon_n {\rm{e}}^{{\rm i}n\Psi_n} = \frac{\{ r_\perp^m {\rm{e}}^{{\rm i}n\varphi} \}}{\{ r_\perp^m \}}, $$ (1) where
$ m $ =3 for$ n $ =1 and$ m\!=\!n $ for$ n \geqslant 2 $ .$ \Psi_n $ is the orientation of the$ n $ -order eccentricity$ \epsilon_n $ ,$ \{ \cdots \} $ represents the average over the entropy (energy) density profile, and$ (r_\perp, \varphi) $ represents the polar coordinates. Due to the strong interaction among QGP constituents, the initial geometric anisotropy can be translated into the final state anisotropy of particle momentum distribution. The momentum anisotropy can be quantified via the Fourier decomposition of the spectrum as follows:$$ \frac{{\rm{d}}N}{{\rm{d}}p^{}_{\rm{T}} {\rm{d}}y {\rm{d}}\phi} \propto 1 + \sum_n 2v_n(p^{}_{\rm{T}}, y) \cos\Big[\phi - \Phi_n(p^{}_{\rm{T}}, y)\Big], $$ (2) where
$ v_n $ is the flow coefficient and$ \Phi_n $ is the corresponding orientation angle. One can combine$ v_n $ and$ \Phi_n $ together and define a vector notation:$$ {\rm{V}}_n = v_n {\rm{e}}^{{\rm i}n\Phi_n} = \{{\rm{e}}^{{\rm i}n\phi}\}. $$ (3) Here
$ \{ ...\} $ represents the average over the particle momentum distribution. The dynamical evolution of the bulk matter and the observed anisotropic flows can be successfully described by relativistic hydrodynamics simulations. This implies that the hot and dense QGP matter produced in the heavy-ion collisions at RHIC and the LHC is a strongly-coupled QGP and behaves like a relativistic fluid[4-8].Relativistic hydrodynamics is based on the conservation law of energy and momentum,
$ \partial_\mu T^{\mu\nu}\!=\!0 $ , where$ T^{\mu\nu} $ is the energy-momentum tensor. One can decompose$ T^{\mu\nu} $ as follows:$$ T^{\mu\nu} = e u^\mu u^\nu + (P + \Pi) \Delta^{\mu\nu} + \pi^{\mu\nu}, $$ (4) where
$ e $ ,$ P $ ,$ u^{\mu} $ are local energy density, pressure and flow velocity of the fluid, respectively,$ \Delta^{\mu\nu}\!=\! g^{\mu\nu} - u^\mu u^\nu $ is the projector transverse to the flow velocity$ u $ ,$ \pi^{\mu\nu} $ and$ \Pi $ are shear tensor and bulk pressure whose evolution equations can be obtained with the help of the entropy principle or kinetic theory[26-32]. For Israel-Steward hydrodynamics, we have the following equations for$ \pi^{\mu\nu} $ and$ \Pi $ [26-27]:$$ \begin{split} &\dot{\Pi} = -\frac{1}{\tau_{\Pi}} \left[ \Pi + \zeta \theta + \Pi \zeta T \partial_\mu \left( \frac{\tau_\Pi}{2\zeta T} u^\mu \right) \right], \\ &\Delta^\mu_\alpha \Delta^\mu_\beta \dot{\pi}^{\alpha\beta} \!=\! -\frac{1}{\tau_{\pi}} \left[ \pi^{\mu\nu} \!-\! 2 \eta \sigma^{\mu\nu} \!+\! \pi^{\mu\nu} \eta T \partial_\alpha \left( \frac{\tau_\pi}{2\eta T} u^\alpha \right) \right], \end{split} $$ (5) where
$ \dot{X}\!=\!DX\!=\!(u\cdot \partial) X $ is the comoving derivative on$ X $ ,$ \theta\!=\!\partial \cdot u $ ,$ \sigma^{\mu\nu}\!=\!\frac{1}{2}(\nabla^\mu u^\nu + \nabla^\nu u^\mu) - \frac{1}{3} (\nabla \cdot u) \Delta^{\mu\nu} $ ,$ \nabla^\mu\!=\!\Delta^{\mu\nu}\partial_\nu $ ,$ \zeta $ and$ \eta $ are the bulk and shear viscosities,$ \tau_{\Pi} $ and$ \tau_{\pi} $ are the corresponding relaxation times. To solve the hydrodynamic equations, the equation of state (EOS)$ P\!=\!P(e) $ , which relates the energy density to the pressure, has to be supplemented. The EOS is usually taken from lattice QCD. The production of particles (particlization) from relativistic hydrodynamics is usually performed via Cooper-Frye description[33]. The produced hadrons continue to interact with each other until the kinetic freeze-out. The hadronic interaction may be simulated via hadron cascade models, such as UrQMD[34].There are two important factors in the initial states responsible for the final state anisotropic flows of the particle momentum distribution. The first is the intrinsic collision geometry which is usually an almond shape for a typical non-central collision. Another is the quantum fluctuations of the initial states, which generate various shapes and their combinations for the produced QGP. The initial spatial anisotropies can generate the anisotropies (flows) for the momentum distribution via hydrodynamic evolution. The intrinsic collision geometry is one of the main driving forces to generate elliptic flow
$ v_2 $ and other even-order anisotropic flows. The initial state fluctuations not only contributes to even-order harmonic flows, but most importantly can generate triangular flow$ v_3 $ and other odd-order anisotropic flows[18-22]. The elliptic flow$ v_2 $ , triangular flow$ v_3 $ and other higher-order harmonic flows can be well understood by initial state fluctuations and relativistic hydrodynamics, which can not only describe the event-averaged value of$ v_n $ , but also the event-by-event distributions of flow$ v_n $ and the correlations between flows of different orders.Various studies have suggested that the event-by-event fluctuations of flow
$ {{V}}_n $ ($ v_n $ ) can be approximately described by two-dimensional Gaussian distribution (Bessel-Gaussian distribution)[35-38]. Recently, the deviation of$ v_n $ distributions from the Bessel-Gaussian baseline has been studied using the higher-order moments of$ v_n $ and the comparisons of multi-particle$ v_n $ 's[39-41]. It has been shown by hydrodynamic calculations that the event-averaged$ v_2 $ and$ v_3 $ are linearly correlated with the initial state$ \epsilon_2 $ and$ \epsilon_3 $ . However, higher-order$ v_n $ 's originate from a combination of initial anisotropy$ \epsilon_n $ and the non-linear response of lower-order flow$ v_m (m<n) $ . For example,$ v_4 $ has a non-linear relation to$ v_2 $ [42-43]. Another interesting observation is the negative correlation between$ v_3 $ and$ v_2 $ [42-43], which can be understood from the initial correlation between$ \epsilon_2 $ and$ \epsilon_3 $ . Not only the flow magnitudes$ v_n $ 's of different orders are correlated[44], their orientations$ \Phi_n $ 's are also correlated with each other[45-49]. Detailed studies on the event-by-event fluctuations of flow$ v_n $ and the correlations of$ {{V}}_n $ with$ {{V}}_m $ are helpful to achieve more precise determination of the transport properties of QGP.In heavy-ion collisions, the initial density profiles fluctuate not only in the transverse plane, but also in the longitudinal direction. The longitudinal fluctuations can lead to the fluctuations and decorrelations of flow
$ v_n $ 's along the pseudorapidity direction[50-61]. To quantify the effect of longitudinal decorrelations, one may define the following correlation function[55, 58]:$$ r(\eta)[n,k] = \frac{\langle {{V}}_n(\eta) {{V}}_n(\eta_{\rm{ref}}) \rangle}{\langle {{V}}_n(-\eta) {{V}}_n(\eta_{\rm{ref}})\rangle}, $$ (6) where
$ \eta_{\rm{ref}} $ is the reference rapidity. Similarly, one may also define the correlation functions$ r_M(\eta)[n,k] $ and$ r_\Phi(\eta)[n,k] $ using flow magnitude$ v_n $ and orientation$ \hat{\rm{V}}_n $ [59]. Since the above correlation function is, to the leading order, a linear function of$ \eta $ , one may simply use its slope to quantify the decorrelation effect. According to the expression$ r[n,k](\eta) \approx 1 - 2 f[n,k] \eta $ , one can define the slope parameter as follows:$$ f[n,k] = \frac{\sum_i(1 - r[n,k](\eta_i))\eta_i}{2\sum_i \eta_i^2}. $$ (7) Similarly, one may also define the slope parameters
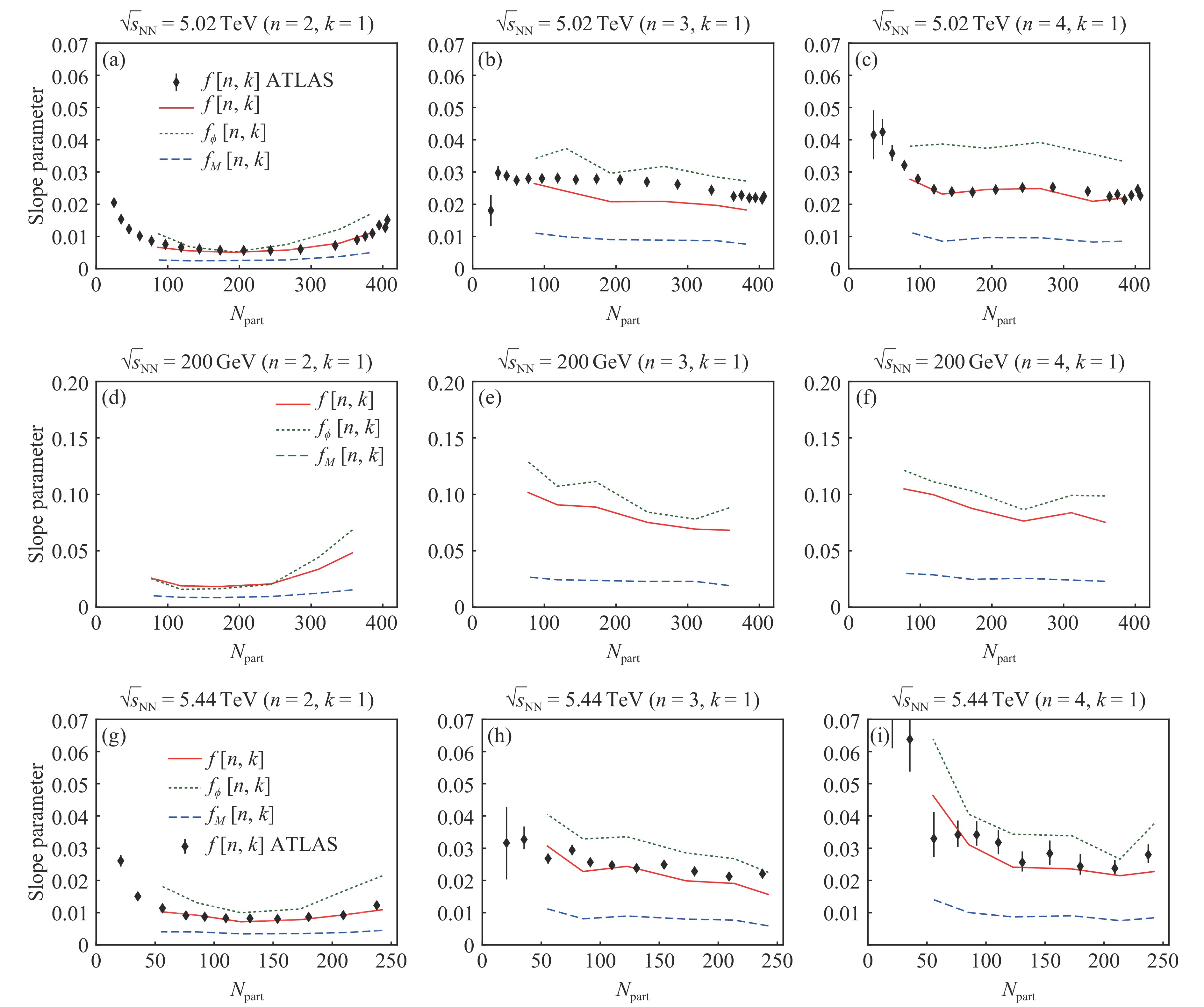
$ f_M[n,k] $ and$ f_\Phi[n,k] $ for$ r_M(\eta)[n,k] $ and$ r_\Phi(\eta)[n,k] $ .In Fig. 1[61], we show the effect of longitudinal decorrelation (in terms of the slope parameter
$ f $ ,$ f_M $ and$ f_\Phi $ ) for Pb+Pb collisions at 5.02$ A $ TeV at the LHC (upper panel) and Au+Au collisions at 200$ A $ GeV at RHIC (middle panel) from a (3+1)-dimensional hydrodynamics calculation using the AMPT[62] initial conditions. It is interesting to note that within the full AMPT model, significant amount of elliptic flow may come from the escape mechanism[63]. From Fig. 1, one can see that the longitudinal decorrelation effect is larger at RHIC than at the LHC (see Ref. [64] for STAR result), which may be traced back to the longitudinal structures of the initial states. Since RHIC has lower collision energy and thus has a larger violation of longitudinal boost invariance, the lengths of the initial string structures (in the AMPT model) is smaller than those at the LHC. In the lower panel of Fig. 1, we show our prediction for longitudinal decorrelations in Xe-Xe collisions at 5.44$ A $ TeV at the LHC[65], which agrees with recent ATLAS data[66] quite well.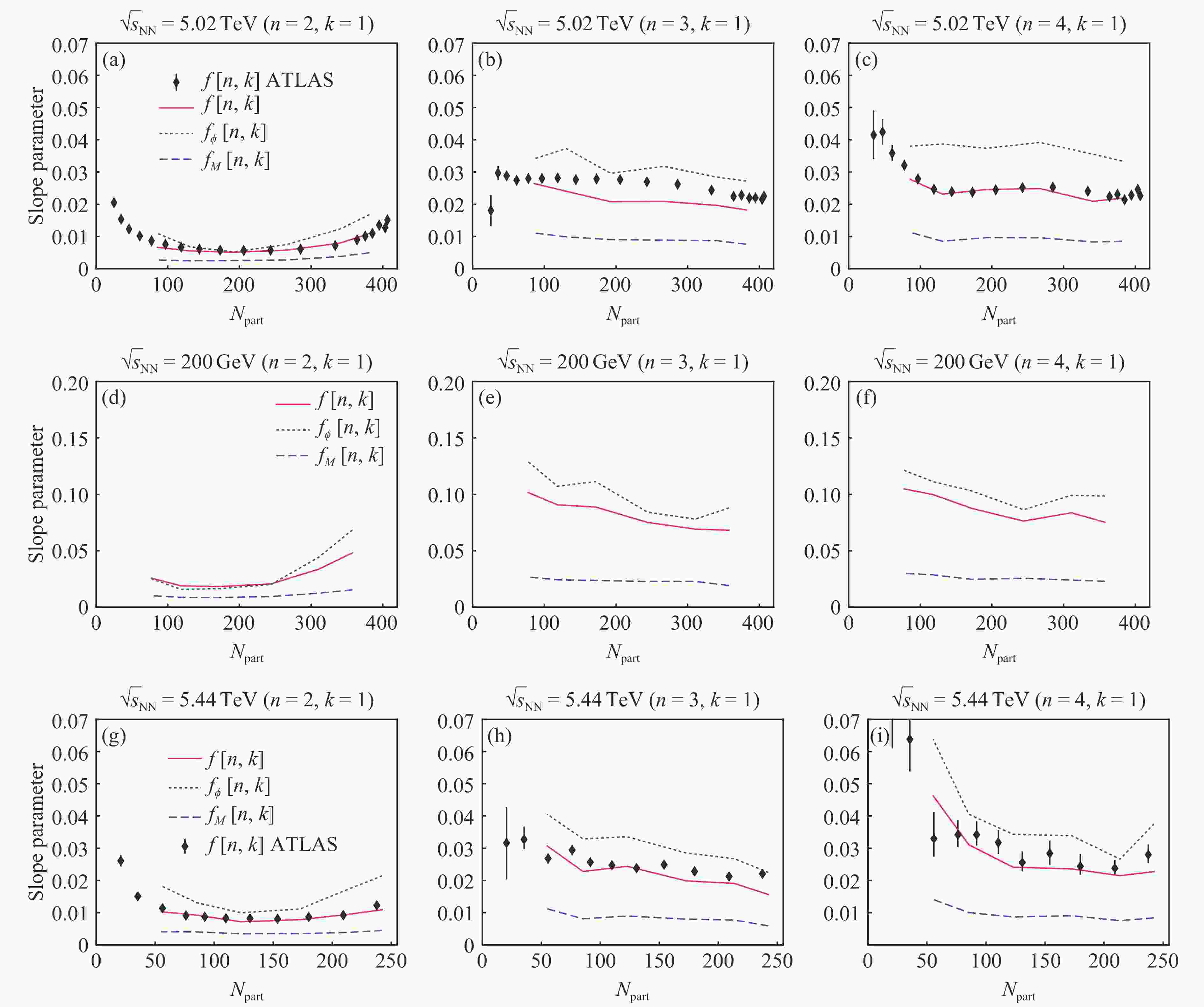
Figure 1. (color online) The slope parameters
$f[n, k]$ ,$f_M[n, k]$ and$f_\Phi[n, k]$ (with$n\!=\!2,3,4$ and$k\!=\!1$ ) of the longitudinal decorrelation functions as a function of centrality in Pb+Pb collisions at 5.02$A{\rm TeV}$ (upper panel)[61], Au+Au collisions at 200$A{\rm GeV}$ (middle panel)[61], and Xe+Xe collisions at 5.44$A{\rm TeV}$ (lower panel)[65]. The ATLAS data[58, 66] are compared.It is worth noting that machine learning and Bayesian analysis have recently been applied to the study of relativistic heavy-ion collisions. Ref. [67] builds a deep convolutional neural network to identify QCD equation of state employed in relativistic hydrodynamics simulations using the simulated final-state particle spectra. Ref. [68] applies Bayesian analysis to a dynamical collision model and a wide variety of experimental data, and simultaneously extracts the estimates of the temperature-dependent specific shear and bulk viscosities. It is found that the specific viscosity of QGP is at least an order of magnitude smaller than that of most common fluids, which implies that QGP behaves like a nearly perfect fluid[4-8].
-
Jets that are produced in early hard scatterings have been regarded as valuable probes of QGP in relativistic heavy-ion collisions. During their passage through QGP, jets interact with QGP via elastic and inelastic interactions, and lose some energy during the processes. Such phenomenon is usually called jet quenching[69-70]. One consequence of jet energy loss is the suppression of large
$ p^{}_{\rm{T}} $ hadrons and jets in nucleus-nucleus collisions as compared to the expectation from independent nucleon-nucleon collisions. To quantify such jet quenching effect, one may define the nuclear modification factor$ R_{\rm{AA}} $ as follows:$$ R_{\rm{AA}} = \frac{{\rm{d}}N_{\rm{AA}} /{\rm{d}}p^{}_{\rm{T}} {\rm{d}}y}{\langle N_{\rm{coll}} \rangle {\rm{d}}N_{\rm{pp}}/{\rm{d}}p^{}_{\rm{T}} {\rm{d}}y}, $$ (8) where
$ N_{\rm{coll}} $ is the number of binary nucleon-nucleon collisions. Various experimental results have shown that$ R_{\rm{AA}} $ for high$ p^{}_{\rm{T}} $ hadrons and jets are significantly below unity, which means that jet quenching is mainly due to parton energy loss caused by the final-state interaction between hard jets and hot QGP medium.To study parton energy loss and jet quenching in relativistic heavy-ion collisions, various theoretical formalisms have been developed for calculating radiative energy loss[71-76] and collisional energy loss[77-81] experienced by jet partons inside the dense nuclear matter. Recently, many studies have been performed to improve various approximations used in previous approaches. For example, Ref. [82] extends the Arnold-Moore-Yaffe formalism to include the finite size effect on radiative energy loss. Ref. [83] studies the next-to-eikonal corrections within the path integral formalism. Refs. [84-86] extend the higher-twist formalism by going beyond collinear rescattering expansion and soft gluon emission approximation. Refs. [87-88] reinvestigate the Gyulassy-Levai-Vitev formalism by relaxing soft gluon emission approximation. Refs. [89-90] calculate the correction to multiple soft scattering limit in the Baier-Dokshitzer-Mueller-Peigne-Schiff-Zakharov formalism. In addition, the interference between sequential gluon emissions has also been investigated in Refs. [91-92].
The general framework for the phenomenological studies of jet quenching is based on perturbative QCD factorization theorem, which states that processes involving large momentum transfer can be factorized as the convolution of parton distribution functions (PDFs), hard partonic scattering process, and fragmentation function (FF). For single inclusive high-
$ p^{}_{\rm{T}} $ hadron production in proton-proton collisions, the cross section can be expressed as follows[93-94]:$$ {\rm{d}}\sigma_{pp \to hX} = \sum_{abc} f(x_a) \otimes f(x_b) \otimes {\rm{d}}\sigma_{ab\to c} \otimes D_{h/c}(z_c), $$ (9) where
$ f(x_a) $ ,$ f(x_b) $ are PDFs,$ {\rm d}\sigma_{ab \to c} $ is the parton scattering cross section, and$ D_{h/c}(z_c) $ is FF. To study single inclusive high-$ p^{}_{\rm{T}} $ hadron production in heavy-ion collisions, we need to take into account two additional effects. The first is the cold nuclear matter effect due to the modification of PDFs in nuclei. Another is the hot nuclear matter effect caused by the final state jet-medium interaction. Here we provide some details on a linearized Boltzmann transport (LBT) model[95-101], a quite general framework for simulating heavy and light flavor jet quenching in heavy-ion collisions.In LBT model, one essentially solves the following Boltzmann equation using Monte-Carlo method:
$$ p \cdot \partial f({{x}}, {{p}}, t) = E ({\cal{C}}_{\rm{el}} + {\cal{C}}_{\rm{inel}}), $$ (10) where
$ C_{\rm{el}} $ and$ C_{\rm{inel}} $ represent the collision integrals for elastic and inelastic processes. The elastic scattering between jet partons and medium is simulated using the differential scattering rate calculated from the leading order perturbative QCD matrix elements. The inelastic radiative process for jet partons is simulated using the higher-twist energy loss formalism[76, 102-103].Fig. 2 shows the numerical results on nuclear modification factor
$ R_{\rm{AA}} $ from Ref. [101], which combines the LBT model with relativistic hydrodynamics to study the energy loss and nuclear modifications of heavy and light flavor jets in the LHC heavy-ion collisions. A next-to-leading order perturbative QCD framework is utilized in order to consistently take into account the contributions from both quarks and gluon to light and heavy flavor hadron productions in high-energy nuclear collisions[93-94]. The CTEQ5 parameterization[104] is used for PDFs and the EPS09 parameterization[105] is used for nuclear shadowing effect. The FFs of charged hadrons,$ D $ meson and$ B $ mesons are taken from Refs. [106-108], respectively. We can see that by including both quark and gluon contributions to light and heavy flavor hadron productions, Ref. [101] obtains a satisfactory description of the$ R_{\rm AA} $ data[109-112] for light hadrons,$ D $ mesons,$ B $ mesons and$ B $ -decayed$ D $ mesons simultaneously over a wide range of$ p^{}_{\rm{T}} $ (8~300 GeV). Below 30~40 GeV,$ B $ meson is less suppressed than charged hadrons and$ D $ mesons due to the large masses of$ b $ quarks. Above 30~40 GeV, Ref. [101] predicts that charged hadrons,$ D $ mesons and$ B $ mesons all have similar$ R_{\rm{AA}} $ 's, which may be tested in the future measurements.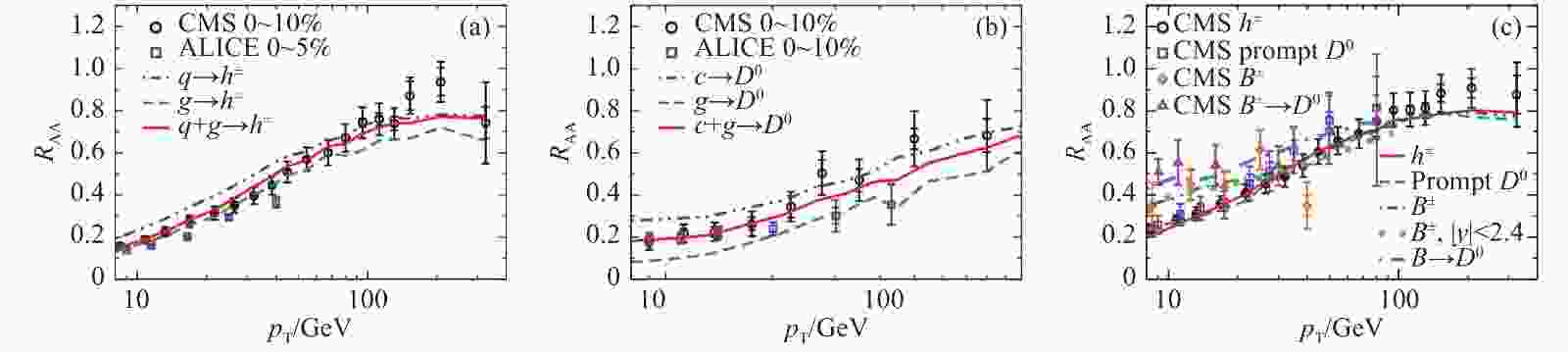
Figure 2. (color online) Nuclear modification factor
$R_{\rm{AA}}$ for charged hadrons (a) and$D$ mesons (b) in central 0~10% and 0~80% Pb+Pb collisions at 5.02$A{\rm TeV}$ . Also shown are$R_{\rm{AA}}$ for hadrons initiated by quarks and gluons[101]. (c) Nuclear modification factor$R_{\rm{AA}}$ for charged hadrons,$D$ mesons,$B$ mesons and$B$ -decayed$D$ mesons in central 0~80% (or minimum bias) Pb+Pb collisions at 5.02$A{\rm TeV}$ [101]. The CMS[109-112] and ALICE[113-114] data are compared.While high-
$ p^{}_{\rm{T}} $ heavy hadrons can be utilized to probe the flavor dependence of jet quenching[98, 101, 115-121], low and intermediate$ p^{}_{\rm{T}} $ heavy hadrons are ideal for studying the hadronization of heavy quarks in heavy-ion environment. Various studies have demonstrated that the coalescence mechanism, in which heavy quarks combine with the thermal partons from the QGP medium to form hadrons, plays important roles for heavy flavor hadron production at low and intermediate$ p^{}_{\rm{T}} $ regime[122-127]. In particular, coalescence is essential to understand the non-monotonic$ p^{}_{\rm{T}} $ dependence of$ D $ meson$ R_{\rm{AA}} $ from low to intermediate$ p^{}_{\rm{T}} $ [128-129]. Recently, experiments have observed a strong enhancement for$ \varLambda_c $ and$ D_s $ meson yields as compared to that of$ D^0 $ mesons in heavy-ion collisions[130-132]. Various studies have been performed to explain such enhancement effect[133-138].In Ref. [138], a comprehensive coalescence model has been developed including a complete set of both
$ s $ and$ p $ -wave hadronic states. Such advanced hadronization scheme is then combined with a Langevin-hydrodynamics model[126-127], which describes elastic and inelastic energy loss of heavy quarks inside the realistic QGP medium. In Figs. 3(a, b), we show the numerical results for$ \varLambda_c/D^0 $ and$ D_s/D^0 $ ratios from Ref. [138]. One can see that the$ p^{}_{\rm{T}} $ differential$ \varLambda_c/D^0 $ and$ D_s/D^0 $ ratios can be described quite well by the coalescence model in Ref. [138]. It is also found that the radial flow of the QGP is essential to understand the chemical composition of the charmed hadrons observed in the experiments. In Fig. 3(c), we show our prediction for the$ B_s/B^+ $ ratio in Pb+Pb collisions at 5.02$ A $ TeV[139], which agrees with recent CMS data[140] very well.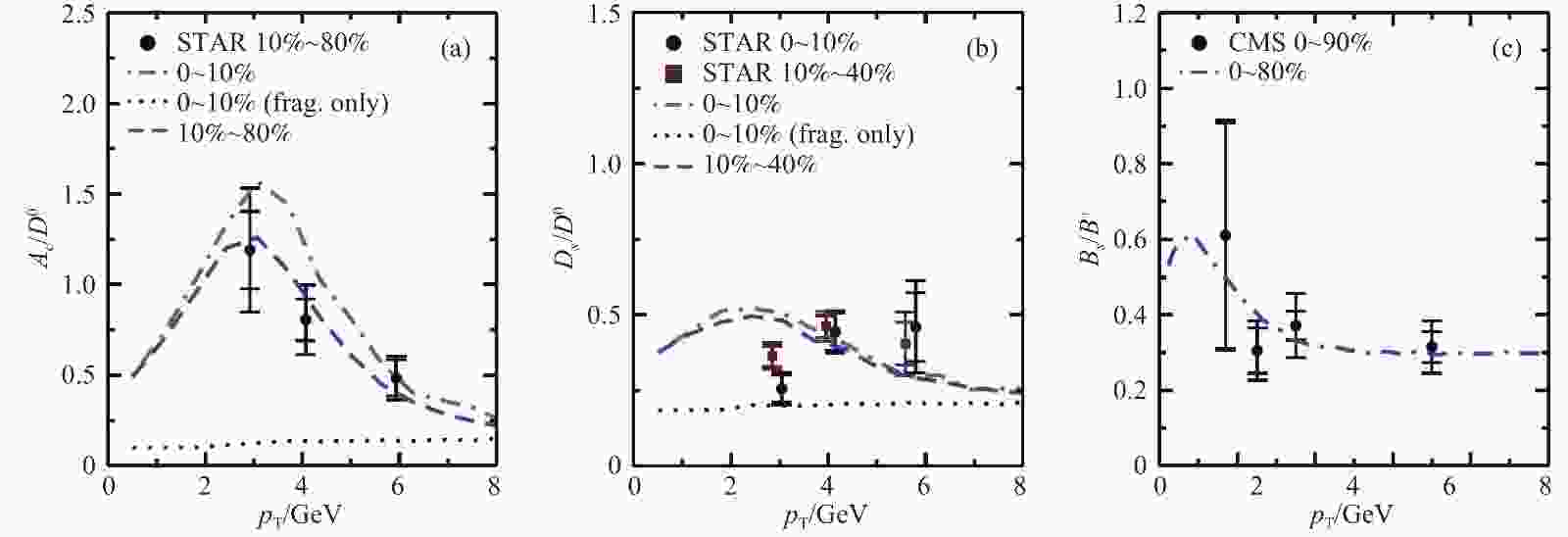
Figure 3. (color online) (a, b)
$\varLambda_c/D^0$ and$D_s/D^0$ ratios as a function of$p^{}_{\rm{T}}$ in Au+Au collisions at 200$A{\rm GeV}$ at RHIC. The results with only fragmentation contribution are also shown[138]. (c)$B_s/B^+$ ratio as a function of$p^{}_{\rm{T}}$ in Pb+Pb collisions at 2.76$A{\rm TeV}$ at the LHC[139]. The STAR data[131-132] and CMS data[140] are compared.In the last decade, fully reconstructed jets have become a hot topic in jet quenching studies in heavy-ion collisions[141-150]. For full jets, one needs to consider not only the in-medium evolution and energy loss of the leading parton, but also how the shower (radiated) partons interact with the medium and where they go in the final state. For full jet energy loss, one may decompose it into the following components[144, 150-152]:
$$ \Delta E_{\rm{loss}} = \Delta E_{\rm{rad, out}} + \Delta E_{\rm{scatt, out}} + (E_{\rm{th}} - E_{\rm{th, in}}). $$ (11) First, only the out-of-cone radiation is considered as full jet energy loss. Second, some energy inside jet cone may be scattered out of jet cone by elastic interactions. Third, jet partons can deposit energy into the medium or soft shower partons of the jet may thermalize into the medium. Note that some deposited or thermalized energy flows to large angles away from the jets, and some energy is still inside the jet cone. To study the internal structure of full jets, one of the most interesting observables is jet shape function, which describes the energy distribution in the radial
$ r $ direction,$$ \rho(r) = \frac{{\rm{d}}}{{\rm{d}}r}\left[\frac{\sum_{i\in J} p^{}_{{\rm{T}}, i} \theta(r-r_i)}{\sum_{i\in J} p^{}_{{\rm{T}}, i} \theta(R-r_i)}\right], $$ (12) where
$ R $ is jet radius and$ r \!=\! \sqrt{(\phi \!-\! \Phi_J)^2 \!+\! (\eta - \eta_J)^2} $ , with$ \Phi_J $ and$ \eta_J $ being the azimuthal angle and the pseudorapidity of the jet.In Refs. [151-153], a coupled jet-fluid model has been developed to study the interaction of full jet shower with the dynamically-evolving QGP medium and the nuclear modification of full jet observables in heavy-ion collisions. In this calculation, the evolution of full jet shower is obtained by solving the following Boltzmann equation for the three-dimensional momentum distribution of partons inside the jets
$ f(\omega, k_\perp^2, t)\!=\!{\rm{d}}N(\omega, k_\perp^2,t )/{\rm{d}}\omega {\rm{d}}k_\perp^2 $ as follows:$$ \frac{\partial f(\omega, k_\perp^2, t)}{\partial t} = \hat{e} \frac{\partial f}{\partial \omega} + \frac{1}{4} \hat{q} \nabla_{k_\perp}^2 f + \left.\frac{\partial f}{\partial t}\right|_{\rm{rad}}. $$ (13) In the above equation, the first and second terms describe the elastic energy loss and transverse momentum broadening effects, respectively, with
$ \hat{e} $ and$ \hat{q} $ being the elastic energy loss rate and transverse momentum broadening rate. The third term describes the contribution from medium-induced radiation (splitting). To simulate the medium response to jet-deposited energy and momentum, the hydrodynamic equation with the source term is solved:$$ \partial T_{\rm{fluid}}^{\mu\nu} (x) = J^\nu(x) = - \frac{{\rm{d}}P_{\rm{jet}}^\nu}{{\rm{d}}^4x}, $$ (14) where the source term
$ J^\nu(x) $ may be constructed from the solution of Boltzmann equation.Fig. 4 shows the numerical results for full jet shape function and its nuclear modification factor from Refs. [152-153]. One can see that jet-induced medium excitation dominates jet shape function at large
$ r $ , which means that a lot of jet-deposited energy flows to large angles away from the jet direction. Similar result has also been obtained by other calculations[100, 154-156]. Another interesting result is that for both inclusive jets and$ \gamma $ -tagged jets, the nuclear modification of jet shape function for jet$ p^{}_{\rm{T}} > $ 120 GeV is a non-monotonic function of$ r $ , i.e., an enhancement at larger$ r $ and a dip at$ r\sim (0.1\thicksim0.15) $ , while the modification factor for$ p^{}_{\rm{T}} > $ 30 GeV is a monotonic function of$ r $ , i.e., an enhancement at larger$ r $ and a dip at$ r \sim 0 $ . This implies that the nuclear modification of$ \rho(r) $ has a weak dependence on jet flavors (quark or gluon), but has a strong dependence on jet energies. Such finding may be tested by future measurements with lower energy inclusive jets or high energy$ \gamma $ -tagged jets.
Figure 4. (color online) (a) jet shape function
$\rho(r)$ in Pb+Pb collisions at 2.76$A{\rm TeV}$ at the LHC. The contributions from jet shower and hydrodynamic response are also shown[152]. (b, c) nuclear modification factor of$\rho(r)$ for single inclusive jets and$\gamma$ -tagged jets with two different jet energies in Pb+Pb collisions at 5.02$A{\rm TeV}$ at the LHC[153]. The CMS data[157-159] are compared.Jet fragmentation function is another interesting observable, describing the distribution of the fractional energy carried by the hadrons inside the jets[160-161]. Recently, extensive studies have been performed on jet substructure in relativistic heavy-ion collisions. For example, by removing the soft components of the jets using jet grooming algorithms[162-164], one may reconstruct two hard branches that satisfy certain conditions. One interesting observable is the momentum sharing
$ z_{\rm{g}} $ distribution of two subjets, which provides a unique opportunity to study the first hard splitting of the partonic jet in hot and dense QGP and directly probe the medium-induced jet splitting function[165-175]. In Fig. 5, we show our calculation of the nuclear modification factor for the groomed jet momentum sharing distribution$ p(z_{\rm{g}}) $ in Pb+Pb collisions at 5.02$ A{\rm TeV} $ [176] for two different jet radius sizes ($ R $ =0.2 and$ 0.4 $ ) and for two different$ z_{\rm{cut}} $ values:$ z_{\rm{cut}} $ =0.1 (a) and$ z_{\rm{cut}} $ =0.2 (b) compared to recent ALICE data[177]. -
Small collision systems such as proton-proton and proton-nucleus collisions have been regarded as the references for studying various signatures and properties of QGP in nucleus-nucleus collisions. Intriguingly, strong collectivity has been observed in proton-lead[178-180], deuteron-gold[181], and even high multiplicity proton-proton collisions[182]. The origin of the collectivity in small collision systems has now become one of the most interesting and important topics in heavy-ion physics. The final answer to it may significantly affect our understanding of the collective behaviors and transport properties of the dense QCD matter produced in nucleus-nucleus collision systems.
One of the most popular explanations of the collectivity in small collision systems is the hydrodynamics approach, in which the anisotropic flows are viewed as a final state effect generated from relativistic hydrodynamic evolution of the fireball with initial state fluctuations and anisotropies[183-189]. It is usually assumed by hydrodynamics approach that the QGP fluid is formed. However, no jet quenching has been observed in small collision systems so far, which may be understood since the size of the QGP fireball is small. Another alternative explanation is based on the color glass condensate (CGC) framework or the saturation dynamics which shows that the correlations between the partons originated from the projectile proton and the dense gluons inside the target nucleus can also provide significant collectivity for light hadrons[190-193].
Recently, experiments at the LHC have also observed sizable collectivity for charm quarks in small collision systems: large elliptic flow
$ v_2 $ for both$ D^0 $ and$ J/\Psi $ mesons in proton-lead collisions[194-196], though the$ v_2 $ values are smaller than$ v_2 $ of light hadrons. While the final state effect from hydrodynamics evolution can provide successful description for light hadron$ v_2 $ in small collision systems, it is usually difficult for hydrodynamics to generate large collectivity for heavy mesons. This is simply because: heavy quarks with large masses in general do not flow as much as light quarks and gluons. As shown by Ref. [197], the final state effects caused by the formation of an expanding QGP medium cannot account for the large$ v_2 $ values for$ J/\Psi $ observed in the LHC proton-lead collisions.In Ref. [198], the elliptic flow
$ v_2 $ of$ J/\Psi $ is studied within a simplified model based on the color evaporation model and the dilute-dense factorization in the CGC framework. It considers a gluon and a quark originated from the projectile proton, with the quark serving as the reference whereas the gluon splitting into a pair of heavy quarks. During their passage through the target nucleus, the incoming partons interact with the dense gluons in the nucleus, which generates correlations between the heavy quark pair and the accompanying reference quark. As a result, a significant amount of elliptic flow$ v_2 $ for$ J/\Psi $ can be generated due to the correlations between$ J/\Psi $ and light quarks (hadrons), as shown in Fig. 6. This calculation also predicts that heavier$ \Upsilon $ has similar$ v_2 $ values as$ J/\Psi $ , which may be tested in the future measurements.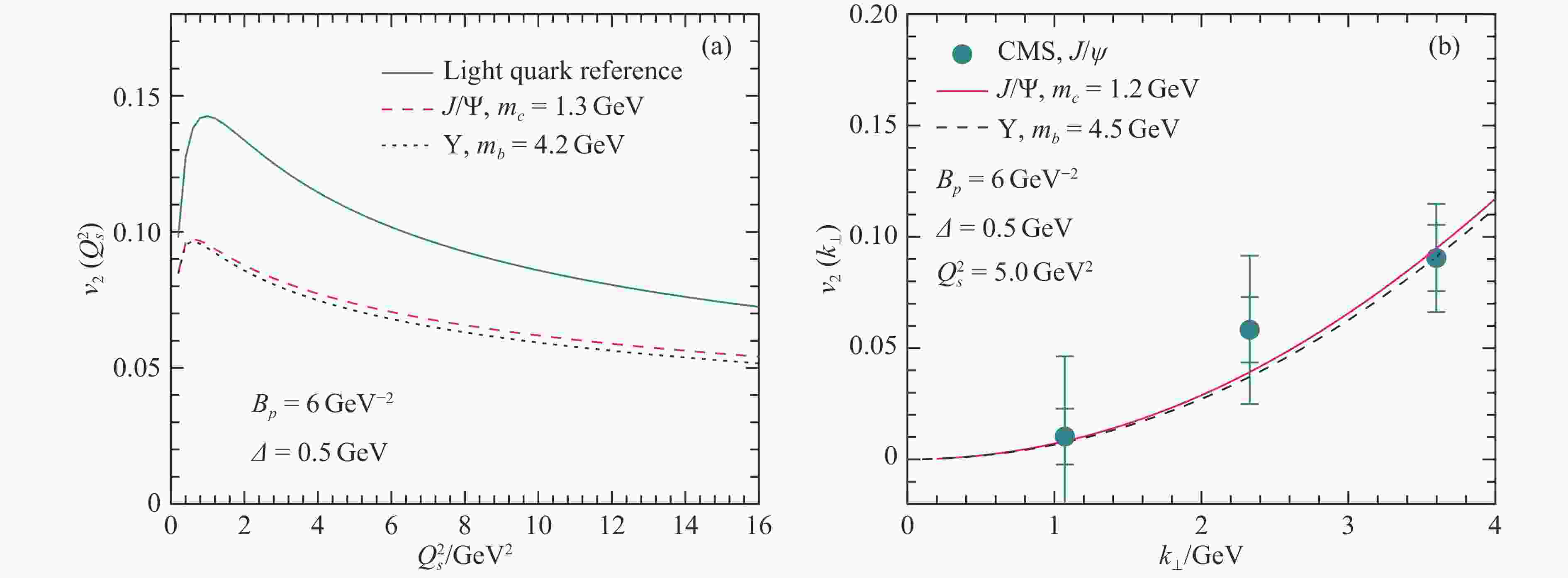
Figure 6. (color online) The integrated
$v_2$ of$J/\Psi$ and$\Upsilon$ compared to the reference light quark$v_2$ as a function of the saturation scale$Q_{\rm s}^2$ (a) and the transverse momentum dependence of$v_2$ of$J/\Psi$ and$\Upsilon$ (b) in p+Pb collisions at$\sqrt{s^{}_{\rm{NN}}}$ = 8.16 TeV at the LHC[198]. The CMS data[199] are compared. -
One of the main purposes of relativistic heavy-ion collisions is to create the strong-interaction matter at various temperatures and densities, and to study the novel properties of quark-gluon plasma. In the last decades, tremendous progresses have been made in the field of high-energy nuclear collisions. In this paper, we have reviewed some of the recent developments in the soft and hard probes of QGP related to the heavy-ion experiments at RHIC and the LHC. Our main focus was given to anisotropic collective flows and jet quenching, which have been regarded as two most important signatures of QGP in relativistic heavy-ion collisions.
For collective behaviors of the QCD matter, we have discussed initial-state fluctuations, hydrodynamical evolution and final-state flows, correlations and longitudinal decorrelations. One important direction is to utilize the advanced statistical tools to analyze various bulk observables for various collision systems at various energies, which can help us to obtain more precise determination of the transport properties, such as the viscosities, of the QGP. Regarding hard probes of the QGP, we have discussed the energy and flavor dependences of jet quenching, heavy quark hadronization, full jet structure/substructure and medium response. With more realistic simulation of jet-medium interaction and more detailed analysis of jet-related observables, one should be able to probe the properties and internal structure of the QCD matter at various energy and length scales. For collectivity in small collision systems, we have discussed the observed collective flows of light and heavy flavor hadrons in proton-nucleus collisions. One future task is to disentangle the contribution from initial state correlations and that from the final state interactions, which is also essential for understanding the origins of anisotropic flows in large nucleus-nucleus collision systems. The ultimate goal is to map out the novel properties and phase structures of the QCD matter at various conditions and achieve a comprehensive understanding on the non-equilibrium dynamics of high-energy nuclear collisions.
-
摘要: 简要回顾了高能核碰撞中夸克胶子等离子体的软探针和硬探针的一些最新进展,主要内容集中在相对论重离子对撞机和大型强子对撞机实验中各向异性集体流和喷注淬火的理论和唯象研究,对小系统中集体流的来源也做了简要的讨论。对于软探针,讨论了初态三维涨落和碰撞几何各向异性、相对论流体力学演化、末态各向异性集体流以及集体流的涨落、关联和纵向去关联等。通过与实验数据作系统的比较,可以探测重离子碰撞中夸克胶子等离子体的动力演化和各种输运性质。对于硬探针,集中讨论了部分子能量损失和喷注淬火对部分子味道的依赖性、重味夸克在夸克胶子等离子体中的强子化、整体喷注在核介质中的演化以及核介质对喷注的响应等。细致分析相关的观测量,可以帮助我们更全面地了解相对论核碰撞中喷注与核介质的相互作用以及重味粒子的生成。对于小系统,讨论初态和末态效应在解释小系统中轻强子和重味强子的集体流方面的贡献,这有助于我们理解大碰撞系统中集体流的起源成因。Abstract: We provide a short review on some recent developments in the soft and hard probes of quark-gluon plasma(QGP) in high-energy nuclear collisions. The main focus is on the theoretical and phenomenological studies of anisotropic collective flow and jet quenching related to the Relativistic Heavy-Ion Collider(RHIC) and the Large Hadron Collider(LHC). The origin of the collectivity in small collision systems is also briefly discussed. For soft probes, we discuss initial-state fluctuations and geometric anisotropy, the hydrodynamic evolution of the fireball, and final-state anisotropic flows, flow fluctuations, correlations and longitudinal decorrelations. Systematic comparison to experimental data may infer the evolution dynamics and various transport properties of the QGP produced in heavy-ion collisions. For hard probes, we focus on the flavor dependence of parton energy loss and jet quenching, the hadronization of heavy quarks in QGP, full jet evolution in nuclear medium and medium response. Detailed analysis of related observables can help us achieve more comprehensive understanding of jet-medium interaction and heavy flavor production in relativistic nuclear collisions. For small systems, we discuss how initial-state and final-state effects explain the observed collective flows of light and heavy flavor hadrons in proton-nucleus collisions, which is helpful in understanding the origin of the collectivity in large collision systems.
-
Key words:
- Quark-Gluon plasma /
- heavy-ion collisions /
- anisotropic flow /
- jet quenching /
- small systems
-
Figure 1. (color online) The slope parameters
$f[n, k]$ ,$f_M[n, k]$ and$f_\Phi[n, k]$ (with$n\!=\!2,3,4$ and$k\!=\!1$ ) of the longitudinal decorrelation functions as a function of centrality in Pb+Pb collisions at 5.02$A{\rm TeV}$ (upper panel)[61], Au+Au collisions at 200$A{\rm GeV}$ (middle panel)[61], and Xe+Xe collisions at 5.44$A{\rm TeV}$ (lower panel)[65]. The ATLAS data[58, 66] are compared.Figure 2. (color online) Nuclear modification factor
$R_{\rm{AA}}$ for charged hadrons (a) and$D$ mesons (b) in central 0~10% and 0~80% Pb+Pb collisions at 5.02$A{\rm TeV}$ . Also shown are$R_{\rm{AA}}$ for hadrons initiated by quarks and gluons[101]. (c) Nuclear modification factor$R_{\rm{AA}}$ for charged hadrons,$D$ mesons,$B$ mesons and$B$ -decayed$D$ mesons in central 0~80% (or minimum bias) Pb+Pb collisions at 5.02$A{\rm TeV}$ [101]. The CMS[109-112] and ALICE[113-114] data are compared.Figure 3. (color online) (a, b)
$\varLambda_c/D^0$ and$D_s/D^0$ ratios as a function of$p^{}_{\rm{T}}$ in Au+Au collisions at 200$A{\rm GeV}$ at RHIC. The results with only fragmentation contribution are also shown[138]. (c)$B_s/B^+$ ratio as a function of$p^{}_{\rm{T}}$ in Pb+Pb collisions at 2.76$A{\rm TeV}$ at the LHC[139]. The STAR data[131-132] and CMS data[140] are compared.Figure 4. (color online) (a) jet shape function
$\rho(r)$ in Pb+Pb collisions at 2.76$A{\rm TeV}$ at the LHC. The contributions from jet shower and hydrodynamic response are also shown[152]. (b, c) nuclear modification factor of$\rho(r)$ for single inclusive jets and$\gamma$ -tagged jets with two different jet energies in Pb+Pb collisions at 5.02$A{\rm TeV}$ at the LHC[153]. The CMS data[157-159] are compared.Figure 6. (color online) The integrated
$v_2$ of$J/\Psi$ and$\Upsilon$ compared to the reference light quark$v_2$ as a function of the saturation scale$Q_{\rm s}^2$ (a) and the transverse momentum dependence of$v_2$ of$J/\Psi$ and$\Upsilon$ (b) in p+Pb collisions at$\sqrt{s^{}_{\rm{NN}}}$ = 8.16 TeV at the LHC[198]. The CMS data[199] are compared. -
[1] BAZAVOV A, DING H T, HEGDE P, et al(HotQCD Collaboration). Phys Lett B, 2019, 795: 15. doi: 10.1016/j.physletb.2019.05.013 [2] BORSANYI S, FODOR Z, HOELBLING C, et al(Wuppertal-Budapest Collaboration). JHEP, 2010, 1009: 073. doi: 10.1007/JHEP09(2010)073 [3] BHATTACHARYA T, BUCHOFF M I, CHRIST N H, et al. Phys Rev Lett, 2014, 8(113): 082001. doi: 10.1103/PhysRevLett.113.082001 [4] ROMATSCHKE P, ROMATSCHKE U. arXiv: 1712.05815 [nucl-th]. [5] RISCHKE D H, BERNARD S, MARUHN J A. Nucl Phys A, 1995, 595: 346. doi: 10.1016/0375-9474(95)00355-1 [6] HEINZ U, SNELLINGS R. Ann Rev Nucl Part Sci, 2013, 63: 123. doi: 10.1146/annurev-nucl-102212-170540 [7] GALE C, JEON S, SCHENKE B. Int J Mod Phys A, 2013, 28: 1340011. doi: 10.1142/S0217751X13400113 [8] HUOVINEN P. Int J Mod Phys E, 2013, 22: 1330029. [9] OLLITRAULT J Y. Phys Rev D, 1992, 46: 229. doi: 10.1103/PhysRevD.46.229 [10] ADLER S S, AFANASIEV S, AIDALA C, et al. Phys Rev Lett, 2003, 91: 182301. doi: 10.1103/PhysRevLett.91.182301 [11] ADAMS J, ADLER C, AGGARWAL M M, et al. Phys Rev Lett, 2004, 92: 052302. doi: 10.1103/PhysRevLett.92.052302 [12] AAMODT K, ABELEV B, ABRAHANTES-QUINTANA A, et al(ALICE Collaboration). Phys Rev Lett, 2010, 105: 252302. doi: 10.1103/PhysRevLett.105.252302 [13] GYULASSY M, RISCHKE D H, ZHANG B. Nucl Phys A, 1997, 613: 397. doi: 10.1016/S0375-9474(96)00416-2 [14] AGUIAR C E, HAMA Y, KODAMA T, et al. Nucl Phys A, 2002, 698: 639. doi: 10.1016/S0375-9474(01)01447-6 [15] BRONIOWSKI W, BOZEK P, RYBCZYNSKI M. Phys Rev C, 2007, 76: 054905. doi: 10.1103/PhysRevC.76.054905 [16] ANDRADE R P G, GRASSI F, HAMA Y, et al. Phys Rev Lett, 2008, 101: 112301. doi: 10.1103/PhysRevLett.101.112301 [17] HIRANO T, NARA Y. Phys Rev C, 2009, 79: 064904. doi: 10.1103/PhysRevC.79.064904 [18] ALVER B, ROLAND G. Phys Rev C, 2010, 81: 054905. Erratum: [Phys Rev C, 2010, 82: 039903.] [19] PETERSEN H, QIN G Y, BASS S A, et al. Phys Rev C, 2010, 82: 041901. doi: 10.1103/PhysRevC.82.041901 [20] QIN G Y, PETERSEN H, BASS S A, et al. Phys Rev C, 2010, 82: 064903. doi: 10.1103/PhysRevC.82.064903 [21] STAIG P, SHURYAK E. Phys Rev C, 2011, 84: 034908. doi: 10.1103/PhysRevC.84.034908 [22] TEANEY D, YAN L. Phys Rev C, 2011, 83: 064904. doi: 10.1103/PhysRevC.83.064904 [23] SCHENKE B, JEON S, GALE C. Phys Rev Lett, 2011, 106: 042301. doi: 10.1103/PhysRevLett.106.042301 [24] MA G L, WANG X N. Phys Rev Lett, 2011, 106: 162301. doi: 10.1103/PhysRevLett.106.162301 [25] QIU Z, HEINZ U W. Phys Rev C, 2011, 84: 024911. doi: 10.1103/PhysRevC.84.024911 [26] ISRAEL W. Annals Phys, 1976, 100: 310. doi: 10.1016/0003-4916(76)90064-6 [27] ISRAEL W, STEWART J M. Annals Phys, 1979, 118: 341. doi: 10.1016/0003-4916(79)90130-1 [28] BAIER R, ROMATSCHKE P, SON D T, et al. JHEP, 2008, 0804: 100. [29] ROMATSCHKE P. Class Quant Grav, 2010, 27: 025006. doi: 10.1088/0264-9381/27/2/025006 [30] EL A, XU Z, GREINER C. Phys Rev C, 2010, 81: 041901. doi: 10.1103/PhysRevC.81.041901 [31] DENICOL G S, NIEMI H, MOLNAR E. Phys Rev D, 2012, 85: 114047. Erratum: [Phys Rev D, 2015, 91(3): 039902.] [32] JAISWAL A, BHALERAO R S, PAL S. Phys Rev C, 2013, 87: 2, 021901. doi: 10.1103/PhysRevC.87.021901 [33] COOPER F, FRYE G. Phys Rev D, 1974, 10: 186. [34] BASS S A, BELKACEM M, BLEICHERET M, et al. Prog Part Nucl Phys, 1998, 41: 255. doi: 10.1016/S0146-6410(98)00058-1 [35] AAD G, ABAJYAN T, ABBOTT B, et al. JHEP, 1311: 183. doi: 10.1007/JHEP11(2013)183 [36] GALE C, JEON S, SCHENKE B, et al. Phys Rev Lett, 2013, 110(1): 012302. doi: 10.1103/PhysRevLett.110.012302 [37] NIEMI H, DENICOL G S, HOLOPAINEN H, et al. Phys Rev C, 2013, 87(5): 054901. doi: 10.1103/PhysRevC.87.054901 [38] RENK T, NIEMI H. Phys Rev C, 2014, 89(6): 064907. doi: 10.1103/PhysRevC.89.064907 [39] SIRUNYAN A M, TUMASYANL A. Phys Lett B, 2019, 789: 643. doi: 10.1016/j.physletb.2018.11.063 [40] GIACALONE G, YAN L, NORONHA-HOSTLER J, et al. Phys Rev C, 2017, 95(1): 014913. doi: 10.1103/PhysRevC.95.014913 [41] BHALERAO R S, GIACALONE G, OLLITRAULT J Y. Phys Rev C, 2019, 99(1): 014907. doi: 10.1103/PhysRevC.99.014907 [42] QIAN J, HEINZ U. Phys Rev C, 2016, 94(2): 024910. doi: 10.1103/PhysRevC.94.024910 [43] MOHAPATRA S. Nucl Phys A, 2014, 931: 959. doi: 10.1016/j.nuclphysa.2014.10.029 [44] ADAM J, ADAMOVÁ D, AGGARWAL M M, et al. Phys Rev Lett, 2016, 117: 182301. doi: 10.1103/PhysRevLett.117.182301 [45] BHALERAO R S, LUZUM M, OLLITRAULT J Y. Phys Rev C, 2011, 84: 034910. doi: 10.1103/PhysRevC.84.034910 [46] QIN G Y, MULLER B. Phys Rev C, 2012, 85: 061901. doi: 10.1103/PhysRevC.85.061901 [47] JIA J, MOHAPATRA S. Eur Phys J C, 2013, 73: 2510. doi: 10.1140/epjc/s10052-013-2510-y [48] QIU Z, HEINZ U. Phys Lett B, 2012, 717: 261. doi: 10.1016/j.physletb.2012.09.030 [49] ACHARYA S, ADAMOVÁ D, ADOLFSSON J, et al. Phys Lett B, 2017, 773: 68. doi: 10.1016/j.physletb.2017.07.060 [50] ADAM J, ADAMOVÁ D, AGGARWALET M M, et al. Phys Lett B, 2016, 762: 376. doi: 10.1016/j.physletb.2016.07.017 [51] PETERSEN H, BHATTACHARYA V, BASS S A. Phys Rev C, 2011, 84: 054908. doi: 10.1103/PhysRevC.84.054908 [52] XIAO K, LIU F, WANG F. Phys Rev C, 2013, 87(1): 011901. doi: 10.1103/PhysRevC.87.011901 [53] JIA J, HUO P. Phys Rev C, 2014, 90(3): 034905. doi: 10.1103/PhysRevC.90.034905 [54] PANG L G, QIN G Y, ROY V, et al. Phys Rev C, 2015, 91(4): 044904. doi: 10.1103/PhysRevC.91.044904 [55] KHACHATRYAN V, SIRUNYAN A M, TUMASYAN A, et al. Phys Rev C, 2015, 92(3): 034911. doi: 10.1103/PhysRevC.92.034911 [56] PANG L G, PETERSEN H, QIN G Y, et al. Eur. Phys. J A, 2016, 52(4): 97. doi: 10.1140/epja/i2016-16097-x [57] JIA J, ZHOU M, TRZUPEK A. Phys Rev C, 2017, 96(3): 034906. doi: 10.1103/PhysRevC.96.034906 [58] AABOUD M, AAD G, ABBOTT B, et al. Eur Phys J C, 2018, 78(2): 142. doi: 10.1140/epjc/s10052-018-5605-7 [59] BOZEK P, BRONIOWSKI W. Phys Rev C, 2018, 97(3): 034913. doi: 10.1103/PhysRevC.97.034913 [60] PANG L G, PETERSEN H, WANG X N. Phys Rev C, 2018, 97(6): 064918. doi: 10.1103/PhysRevC.97.064918 [61] WU X Y, PANG L G, QIN G Y, et al. Phys Rev C, 2018, 98(2): 024913. doi: 10.1103/PhysRevC.98.024913 [62] LIN Z W, KO C M, LI B A, et al. Phys Rev C, 2005, 72: 064901. doi: 10.1103/PhysRevC.72.064901 [63] HE L, EDMONDS T, LIN Z W, et al. Phys Lett B, 2016, 753: 506. doi: 10.1016/j.physletb.2015.12.051 [64] YE Z. Nucl Phys A, 2019, 982: 29. doi: 10.1016/j.nuclphysa.2018.09.086 [65] WU X Y, PANG L G, QIN G Y, et al. in Preparation. [66] AAD G.arXiv: 2001.04201[nucl-ex]. [67] PANG L G, ZHOU K, SU N, et al. Nature Commun, 2018, 9(1): 210. doi: 10.1038/s41467-017-02726-3 [68] BERNHARD J E, MORELAND J S, BASS S A. Nature Phys, 2019, 15(11): 1113. doi: 10.1038/s41567-019-0611-8 [69] WANG X N, GYULASSY M. Phys Rev Lett, 1992, 68: 1480. doi: 10.1103/PhysRevLett.68.1480 [70] QIN G Y, WANG X N. Int J Mod Phys E, 2015, 24(11): 1530014. doi: 10.1142/S0218301315300143 [71] BAIER R, DOKSHITZER Y L, MUELLER A H, et al. Nucl Phys B, 1997, 483: 291. doi: 10.1016/S0550-3213(96)00553-6 [72] ZAKHAROV B G. JETP Lett, 1996, 63: 952. doi: 10.1134/1.567126 [73] GYULASSY M, LEVAI P, VITEV I. Nucl Phys B, 2000, 571: 197. doi: 10.1016/S0550-3213(99)00713-0 [74] WIEDEMANN U A. Nucl Phys B, 2000, 588: 303. doi: 10.1016/S0550-3213(00)00457-0 [75] ARNOLD P B, MOORE G D, YAFFE L G. JHEP, 2002, 0206: 030. [76] WANG X N, GUO X F. Nucl Phys A, 2001, 696: 788. doi: 10.1016/S0375-9474(01)01130-7 [77] BJORKEN J D. FERMILAB-PUB-82-059-THY, FERMILAB-PUB-82-059-T. [78] BRAATEN E, THOMA M H. Phys Rev D, 1991, 44(9): R2625. doi: 10.1103/PhysRevD.44.R2625 [79] DJORDJEVIC M. Phys Rev C, 2006, 74: 064907. doi: 10.1103/PhysRevC.74.064907 [80] QIN G Y, RUPPERT J, GALE C, et al. Phys Rev Lett, 2008, 100: 072301. doi: 10.1103/PhysRevLett.100.072301 [81] SCHENKE B, GALE C, QIN G Y. Phys Rev C, 2009, 79: 054908. doi: 10.1103/PhysRevC.79.054908 [82] CARON-HUOT S, GALE C. Phys Rev C, 2010, 82: 064902. doi: 10.1103/PhysRevC.82.064902 [83] APOLINÁRIO L, ARMESTO N, MILHANO J G, et al. JHEP, 2015, 1502: 119. [84] ZHANG L, HOU D F, QIN G Y. Phys Rev C, 2018, 98(3): 034913. doi: 10.1103/PhysRevC.98.034913 [85] ZHANG L, HOU D F, QIN G Y. Phys Rev C, 2019, 100(3): 034907. doi: 10.1103/PhysRevC.100.034907 [86] ZHANG Y Y, QIN G Y, WANG X N. Phys Rev D, 2019, 100(7): 074031. doi: 10.1103/PhysRevD.100.074031 [87] BLAGOJEVIC B, DJORDJEVIC M, DJORDJEVIC M. Phys Rev C, 2019, 99(2): 024901. doi: 10.1103/PhysRevC.99.024901 [88] SIEVERT M D, VITEV I, YOON B. Phys Lett B, 2019, 795: 502. doi: 10.1016/j.physletb.2019.06.019 [89] MEHTAR-TANI Y. JHEP, 2019, 1907: 057. [90] TYWONIUK K, BLOK B. Eur Phys J C, 2019, 79(7): 560. doi: 10.1140/epjc/s10052-019-7061-4 [91] ARNOLD P, IQBAL S. JHEP, 2015, 1504: 070. Erratum: [JHEP, 2016, 1609: 072.] [92] CASALDERREY-SOLANA J, PABLOS D, TYWONIUK K. JHEP, 2016, 1611: 174. [93] JAGER B, SCHAFER A, STRATMANN M, et al. Phys Rev D, 2003, 67: 054005. doi: 10.1103/PhysRevD.67.054005 [94] AVERSA F, CHIAPPETTA P, GRECO M, et al. Nucl Phys B, 1989, 327: 105. doi: 10.1016/0550-3213(89)90288-5 [95] WANG X N, ZHU Y. Phys Rev Lett, 2013, 111(6): 062301. doi: 10.1103/PhysRevLett.111.062301 [96] HE Y, LUO T, WANG X N, et al. Phys Rev C, 2015, 91: 054908, Erratum: [Phys Rev C, 2018, 97(1): 019902.] [97] CAO S, LUO T, QIN G Y, et al. Phys Rev C, 2016, 94(1): 014909. doi: 10.1103/PhysRevC.94.014909 [98] CAO S, LUO T, QIN G Y, et al. Phys Lett B, 2018, 777: 255. doi: 10.1016/j.physletb.2017.12.023 [99] CHEN W, CAO S, LUO T, et al. Phys Lett B, 2018, 777: 86. doi: 10.1016/j.physletb.2017.12.015 [100] LUO T, CAO S, HE Y, et al. Phys Lett B, 2018, 782: 707. doi: 10.1016/j.physletb.2018.06.025 [101] XING W J, CAO S, QIN G Y, XING H. Phys Lett B, 2020, 805: 135424. doi: 10.1016/j.physletb.2020.135424 [102] ZHANG B W, WANG E, WANG X N. Phys Rev Lett, 2004, 93: 072301. doi: 10.1103/PhysRevLett.93.072301 [103] MAJUMDER A. Phys Rev D, 2012, 85: 014023. doi: 10.1103/PhysRevD.85.014023 [104] PUMPLIN J, STUMP D R, HUSTON J, et al. JHEP, 2002, 0207: 012. [105] ESKOLA K J, PAUKKUNEN H, SALGADO C A. JHEP, 2009, 0904: 065. [106] KRETZER S. Phys Rev D, 2000, 62: 054001. doi: 10.1103/PhysRevD.62.054001 [107] KNEESCH T, KNIEHL B A, KRAMER G, et al. Nucl Phys B, 2008, 799: 34. doi: 10.1016/j.nuclphysb.2008.02.015 [108] B A KNIEHL, G KRAMER, I SCHIENBEIN, H SPIESBERGER. Phys Rev D, 2008, 77: 014011. doi: 10.1103/PhysRevD.77.014011 [109] KHACHATRYAN V, SIRUNYAN A M, TUMASYAN A, et al. JHEP, 2017, 1704: 039. doi: 10.1007/JHEP04(2017)039 [110] SIRUNYAN A M, TUMASYAN A, ADAM M, et al. Phys Lett B, 2018, 782: 474. doi: 10.1016/j.physletb.2018.05.074 [111] SIRUNYAN A M, TUMASYAN A, ADAM M, et al. Phys Rev Lett, 2017, 119(15): 152301. doi: 10.1103/PhysRevLett.119.152301 [112] SIRUNYAN A M, TUMASYAN A, ADAM M, et al. Phys Rev Lett, 2019, 123(2): 022001. doi: 10.1103/PhysRevLett.123.022001 [113] ACHARYA S, ACOSTA F T, ADAMOVÁ D, et al. JHEP, 2018, 1811: 013. [114] ACHARYA S, ACOSTA F T, ADAMOVÁ D, et al. JHEP, 2018, 1810: 174. [115] WICKS S, HOROWITZ W, DJORDJEVIC M, et al. Nucl Phys A, 2007, 784: 426. doi: 10.1016/j.nuclphysa.2006.12.048 [116] QIN G Y, MAJUMDER A. Phys Rev Lett, 2010, 105: 262301. doi: 10.1103/PhysRevLett.105.262301 [117] BUZZATTI A, GYULASSY M. Phys Rev Lett, 2012, 108: 022301. doi: 10.1103/PhysRevLett.108.022301 [118] DJORDJEVIC M. Phys Rev Lett, 2014, 112(4): 042302. doi: 10.1103/PhysRevLett.112.042302 [119] CAO S, QIN G Y, WANG X N. Phys Rev C, 2016, 93(2): 024912. doi: 10.1103/PhysRevC.93.024912 [120] KANG Z B, RINGER F, VITEV I. JHEP, 2017, 1703: 146. [121] CAO S, MAJUMDER A, QIN G Y, et al. Phys Lett B, 2019, 793: 433. doi: 10.1016/j.physletb.2019.05.020 [122] SONG J, LI H H, SHAO F L. Eur Phys J C, 2018, 78(4): 344. doi: 10.1140/epjc/s10052-018-5817-x [123] ZHENG L, ZHANG C, SHI S S, et al. Phys Rev C, 2020, 101(3): 034905. doi: 10.1103/PhysRevC.101.034905 [124] HE M, FRIES R J, RAPP R. Phys Rev C, 2012, 86: 014903. doi: 10.1103/PhysRevC.86.014903 [125] SONG T, BERREHRAH H, CABRERA D, et al. Phys Rev C, 2015, 92(1): 014910. doi: 10.1103/PhysRevC.92.014910 [126] CAO S, QIN G Y, BASS S A. Phys Rev C, 2013, 88: 044907. doi: 10.1103/PhysRevC.88.044907 [127] CAO S, QIN G Y, BASS S A. Phys Rev C, 2015, 92(2): 024907. doi: 10.1103/PhysRevC.92.024907 [128] XIE G. PoS HardProbes, 2018, 2018: 142. [129] ADAM J, ADAMCZYK L, ADAMS J R, et al. Phys Rev C, 2019, 99(3): 034908. doi: 10.1103/PhysRevC.99.034908 [130] ACHARYA S, ACOSTA F T, ADAMOVÁ D, et al. Phys Lett B, 2019, 793: 212. doi: 10.1016/j.physletb.2019.04.046 [131] ADAM J, ADAMCZYK L, ADAMS J R, et al. arXiv: 1910.14628[nucl-ex]. [132] ZHOU L. Nucl Phys A, 2017, 967: 620. doi: 10.1016/j.nuclphysa.2017.05.114 [133] PLUMARI S, MINISSALE V, DAS S K, et al. Eur Phys J C, 2018, 78(4): 348. doi: 10.1140/epjc/s10052-018-5828-7 [134] ZHAO J, SHI S, XU N, et al. arXiv: 1805.10858[hep-ph]. [135] GOSSIAUX P B, BIERKANDT R, AICHELIN J. Phys Rev C, 2009, 79: 044906. doi: 10.1103/PhysRevC.79.044906 [136] OH Y, KO C M, LEE S H, et al. Phys Rev C, 2009, 79: 044905. doi: 10.1103/PhysRevC.79.044905 [137] HE M, RAPP R. Phys Rev Lett, 2020, 124(4): 042301. doi: 10.1103/PhysRevLett.124.042301 [138] CAO S, SUN K J, LI S Q, et al. arXiv: 1911.00456[nucl-th]. [139] CAO S, SUN K J, LI S Q, et al. in Preparation. [140] TAKAKI D T (for the CMS Collaboration). CMS HeavyIon Physics Program: Recent Results and Future Plans[C]// Hard Probes 2020, Austin: University of Texas at Austin, USA. [141] QIN G Y, MAJUMDER A, SONG H, et al. Phys Rev Lett, 2009, 103: 152303. doi: 10.1103/PhysRevLett.103.152303 [142] NEUFELD R B, MULLER B. Phys Rev Lett, 2009, 103: 042301. doi: 10.1103/PhysRevLett.103.042301 [143] VITEV I, ZHANG B W. Phys Rev Lett, 2010, 104: 132001. doi: 10.1103/PhysRevLett.104.132001 [144] QIN G Y, MULLER B. Phys Rev Lett, 2011, 106: 162302. Erratum: [Phys Rev Lett, 2012, 108: 189904.] [145] CASALDERREY-SOLANA J, MILHANO J G, WIEDEMANN U A. J Phys G, 2011, 38: 035006. doi: 10.1088/0954-3899/38/3/035006 [146] LOKHTIN I P, BELYAEV A V, SNIGIREV A M. Eur Phys J C, 2011, 71: 1650. doi: 10.1140/epjc/s10052-011-1650-1 [147] YOUNG C, SCHENKE B, JEON S, et al. Phys Rev C, 2011, 84: 024907. doi: 10.1103/PhysRevC.84.024907 [148] RENK T. Phys Rev C, 2012, 85: 064908. doi: 10.1103/PhysRevC.85.064908 [149] FISTER L, IANCU E. JHEP, 2015, 1503: 082. [150] QIN G Y. Eur Phys J C, 2014, 74: 2959. doi: 10.1140/epjc/s10052-014-2959-3 [151] CHANG N B, QIN G Y. Phys Rev C, 2016, 94(2): 024902. doi: 10.1103/PhysRevC.94.024902 [152] TACHIBANA Y, CHANG N B, QIN G Y. Phys Rev C, 2017, 95(4): 044909. doi: 10.1103/PhysRevC.95.044909 [153] CHANG N B, TACHIBANA Y, QIN G Y. Phys Lett B, 2020, 801: 135181. doi: 10.1016/j.physletb.2019.135181 [154] V KHACHATRYAN, SIRUNYAN A M, TUMASYAN A, et al. JHEP, 2016, 1611: 055. doi: 10.1007/JHEP11(2016)055 [155] PARK C, JEON S, GALE C. Nucl Phys A, 2019, 982: 643. doi: 10.1016/j.nuclphysa.2018.10.057 [156] KUNNAWALKAM ELAYAVALLI R, ZAPP K C. JHEP, 2017, 1707: 141. [157] BREWER J, RAJAGOPAL K, SADOFYEV A, et al. JHEP, 2018, 1802: 015. [158] SIRUNYAN A M, TUMASYAN A, ADAM W, et al. JHEP, 2018, 1805: 006. [159] SIRUNYAN A M, TUMASYAN A, ADMA W, et al. Phys Rev Lett, 2019, 122(15): 152001. doi: 10.1103/PhysRevLett.122.152001 [160] CHATRCHYAN S, KHACHATRYAN V, SIRUNYAN A M, et al. Phys Rev C, 2014m, 90(2): 024908. doi: 10.1103/PhysRevC.90.024908 [161] AAD G, ABBOTT B, ABDALLAH J, et al. Phys Lett B, 2014, 739: 320. doi: 10.1016/j.physletb.2014.10.065 [162] BUTTERWORTH J M, DAVISON A R, RUBIN M, et al. Phys Rev Lett, 2008, 100: 242001. doi: 10.1103/PhysRevLett.100.242001 [163] LARKOSKI A J, MARZANI S, SOYEZ G, et al. JHEP, 2014, 1405: 146. [164] LARKOSKI A J, MARZANI S, THALER J. Phys Rev D, 2015, 91(11): 111501. doi: 10.1103/PhysRevD.91.111501 [165] SIRUNYAN A M, TUMASYAN A, ADAM W, et al. Phys Rev Lett, 2018, 120(14): 142302. doi: 10.1103/PhysRevLett.120.142302 [166] K KAUDER. Nucl Part Phys Proc, 2017, 289-290: 137. doi: 10.1016/j.nuclphysbps.2017.05.028 [167] CHIEN Y T, VITEV I. Phys Rev Lett, 2017, 119(11): 112301. doi: 10.1103/PhysRevLett.119.112301 [168] MEHTAR-TANI Y, TYWONIUK K. JHEP, 2017, 1704: 125. [169] CHANG N B, CAO S, QIN G Y. Phys Lett B, 2018, 781: 423. doi: 10.1016/j.physletb.2018.04.019 [170] MILHANO G, WIEDEMANN U A, ZAPP K C. Phys Lett B, 2018, 779: 409. doi: 10.1016/j.physletb.2018.01.029 [171] LI H T, VITEV I. Phys Lett B, 2019, 793: 259. doi: 10.1016/j.physletb.2019.04.052 [172] CHIEN Y T, KUNNAWALKAM ELAYAVALLI R. arXiv: 1803.03589[hep-ph]. [173] CAUCAL P, IANCU E, SOYEZ G. JHEP, 2019, 1910: 273. [174] CASALDERREY-SOLANA J, MILHANO G, PABLOS D, et al. JHEP, 2020, 2001: 044. [175] KANG Z B, LEE K, LIU X, et al. JHEP, 2020, 2002: 054. [176] CHANG N B, CAO S, QIN G Y. in Preparation. [177] MAO Y X (for the ALICE Collaboration). ALICE Overview: Recent (selected) Results and Future Plans[C]//Hard Probes 2020, Austin: University of Texas at Austin, USA [178] ABELEV B, ADAM J, ADAMOVA D, et al. Phys Lett B, 2013, 719: 29. doi: 10.1016/j.physletb.2013.01.012 [179] AAD G, ABAJYAN T, ABBOTT B, et al. Phys Rev Lett, 2013, 110(18): 182302. doi: 10.1103/PhysRevLett.110.182302 [180] CHATRCHYAN S, KHACHATRYAN M, SIRUNYAN A M, et al. Phys Lett B, 2013, 724: 213. doi: 10.1016/j.physletb.2013.06.028 [181] ADARE A, AIDALA C, AJITANAND N N, et al. Phys Rev Lett, 2013, 111(21): 212301. doi: 10.1103/PhysRevLett.111.212301 [182] KHACHATRYAN V, SIRUNYAN A M, TUMASYAN A, et al. JHEP, 2010, 1009: 091. doi: 10.1007/JHEP09(2010)091 [183] BOZEK P, BRONIOWSKI W. Phys Rev C, 2013, 88(1): 014903. doi: 10.1103/PhysRevC.88.014903 [184] BZDAK A, SCHENKE B, TRIBEDY P, et al. Phys Rev C, 2013, 87(6): 064906. doi: 10.1103/PhysRevC.87.064906 [185] QIN G Y, MÜLLER B. Phys Rev C, 2014, 89(4): 044902. doi: 10.1103/PhysRevC.89.044902 [186] WERNER K, BLEICHER M, GUIOT B, et al. Phys Rev Lett, 2014, 112(23): 232301. doi: 10.1103/PhysRevLett.112.232301 [187] BOZEK P, BRONIOWSKI W, TORRIERI G. Phys Rev Lett, 2013, 111: 172303. doi: 10.1103/PhysRevLett.111.172303 [188] NAGLE J L, ADARE A, BECKMAN S, et al. Phys Rev Lett, 2014, 113(11): 112301. doi: 10.1103/PhysRevLett.113.112301 [189] SCHENKE B, VENUGOPALAN R. Phys Rev Lett, 2014, 113: 102301. doi: 10.1103/PhysRevLett.113.102301 [190] DUSLING K, VENUGOPALAN R. Phys Rev Lett, 2012, 108: 262001. doi: 10.1103/PhysRevLett.108.262001 [191] DUSLING K, MACE M, VENUGOPALAN R. Phys Rev Lett, 2018, 120(4): 042002. doi: 10.1103/PhysRevLett.120.042002 [192] MACE M, SKOKOV V V, TRIBEDY P, et al. Phys Rev Lett, 2018, 121(5): 052301. Erratum: [Phys Rev Lett, 2019, 123(3): 039901.] [193] DAVY M K, MARQUET C, SHI Y, et al. Nucl Phys A, 2019, 983: 293. doi: 10.1016/j.nuclphysa.2018.11.001 [194] ACHARYA S, ADAMOVÁ D, ADOLFSSON J, et al. Phys Lett B, 2018, 780: 7. doi: 10.1016/j.physletb.2018.02.039 [195] CMS Collaboration. CMS-PAS-HIN-18-010. [196] SIRUNYAN A M, TUMASYAN A, ADAM W, et al. Phys Rev Lett, 2018, 121(8): 082301. doi: 10.1103/PhysRevLett.121.082301 [197] DU X, RAPP R. JHEP, 2019, 1903: 015. [198] ZHANG C, MARQUET C, QIN G Y, et al. Phys Rev Lett, 2019, 122(17): 172302. doi: 10.1103/PhysRevLett.122.172302 [199] SIRUNYAN A M, TUMASYAN A, ADAM W, et al. Phys Lett B, 2019, 791: 172. doi: 10.1016/j.physletb.2019.02.018 -












 下载:
下载:








































































































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号