-
近几十年,人们对中高能重离子碰撞进行了广泛的研究[1-12],其中通过重离子反应过程中产生的可观测到的碎裂反应截面有助于我们理解核结构在重离子反应中的作用。现在,核碎裂已经应用到了天体物理学、辐射生物学和辐射治疗中[13-14],精确的碎裂反应截面在辐射生物学和辐射治疗中是至关重要的。因此,核碎裂产生截面的反应机制和反应原理的研究对核碎裂反应过程的描述是非常重要的。
目前已经有许多实验[15-19]和理论[20-26]运用于碎裂现象的研究。核碎裂对带电粒子的分布、粒子发射和碎块分布进行了研究[2, 15-16, 27-30]。实验测量结果表明,弹核碎裂过程中电荷碎裂反应分截面表现出明显的奇偶效应[17-18, 28, 31],即电荷数为偶数的碎裂产生截面要比相邻的电荷数为奇数的碎裂产生截面大,并且这种现象与弹核和末态碎块的同位旋有关[15, 32]。Iancu等[32]在研究400 AMeV 36Ar 和40Ar的核碎裂时,指出弹核的同位旋
$ T_{Z} $ =0时的奇偶效应比$ T_{Z} $ =2时的奇偶效应明显。Knott等[15]在研究碎裂的产生截面和同位旋关系时指出: 碎块质量数为偶数的$ T_{Z} $ =0的分截面和碎块质量数为奇数的$ T_{Z} $ =0.5的分截面比其它的碎块分截面大。理论上也有一些模型对核碎裂进行研究[ 25-26, 33-36],secondary algorithms中弹核碎裂的总反应截面随靶核质量数的增加而增加,但是反应产生的分截面却不能重现实验结果[37]。abrasion-ablation模型重现了奇偶效应,但是比实验值高[38]。目前,对弹核碎裂反应中产生的奇偶性质的研究还不够充分。本小组在前期的研究中对弹核碎裂的反应截面进行了研究[17, 39-41]。我们对400 AMeV 20Ne与C、Al、CH
$ _{2} $ 靶的碎裂反应截面进行了实验测量,20Ne的弹核碎裂反应截面呈现出明显的奇偶效应[17]。运用改进的量子分子动力学模型(ImQMD)[42]和GEMINI统计衰变模型[43]对400 AMeV 20Ne、36Ar、40Ar 弹核碎裂反应截面的奇偶效应进行了初步的理论分析,结果表明,奇偶效应的产生与碰撞参数有关,主要发生在擦边碰撞中[39];36Ar($ T_{Z} $ =0)弹核碎裂反应截面的奇偶效应强于40Ar($ T_{Z} $ =2)的奇偶效应[40]。在稳定核素中,中子、质子有各自成对相处的趋势。当成对的同类核子相距很近时,它们的空间波函数对称而自旋波函数反对称,这样的成对核子有很强的吸引作用,这种作用称为对能。同类核子成对相处时,附加的对能使结合能增大。本文在前期研究的基础上对400 AMeV 36Ar与C、Al、Cu、Pb的弹核碎裂反应截面中出现的奇偶效应进行进一步的理论研究,分析对能在奇偶效应中的作用。 -
ImQMD模型和GEMINI统计衰变模型的具体介绍可见文献[42-43],其中ImQMD模型描述动力学演化过程,GEMINI统计衰变模型描述处于激发态的初级碎块的退激发过程[44]。在本文中,我们选取Skyrme相互作用势的参数见表1,在动力学演化过程基本完成时,利用Coalescence模型对核子进行成块判断,
$ R_{0}\!=\!4.5 $ fm,$ P_{0}\!=\!300 $ MeV/$ c $ ,同时计算出该初级碎块的能量$ E(Z,A) $ 。表 1 ImQMD 模型中的相互作用势采用的参数
α/MeV β/MeV γ g0/(MeV·fm2) gτ/MeV η CS/MeV κs/fm2 ρ0/fm–3 –356 303 7/6 7.0 12.5 2/3 32.0 0.08 0.165 利用结合能公式:
$$ B(Z,A)\!=\!Z\Delta(^{1} {\rm { H}})+(A-Z)\Delta( {\rm{n}})-{\text{Δ}}(Z,A), $$ (1) 其中:
$ B(Z,A) $ 指的是电荷数为 Z、质量数为 A的核素的结合能;$ \Delta(Z,A) $ 是质量过剩所对应的能量,进一步计算出初级碎块的激发能$ E^{*}(Z,A) $ =$E(Z,A)- B(Z,A)$ 。从动力学演化过程到统计衰变过程的转换时间$t_{\rm sw}\!=\! 250$ fm/$ c $ [44]。在统计衰变模型中,对能表示为[45]:
$${E_{{\rm{pairing}}}}\!=\!\left\{ {\begin{array}{*{20}{l}} {{{\bar \Delta }_{\rm{p}}} + {{\bar \Delta }_{\rm{n}}} - {\delta _{{\rm{np}}}},}&{(N{\rm{,}}\;Z\;{\rm{odd}})}\\ {{{\bar \Delta }_{\rm{n}}},}&{(N\;{\rm{even}},Z\;{\rm{odd}})}\\ {{{\bar \Delta }_{{\rm{p}},}}}&{(N\;{\rm{odd}},Z\;{\rm{even}})}\\ {0,}&{(N\;{\rm{and}}\;Z\;{\rm{even}})} \end{array}} \right.$$ 其中
$ \bar{\Delta }_{\rm n} $ 是平均中子对能隙,$ \bar{\Delta }_{\rm p} $ 是平均质子对能隙,$ \delta_{\rm np} $ 是平均中子-质子相互作用能。$$ \bar{\Delta }_{\rm n}\!=\!\frac{r_{\rm mac}B_{S}}{N^{1/3}}, $$ (2) $$ \bar{\Delta }_{\rm p}\!=\!\frac{r_{\rm mac}B_{S}}{Z^{1/3}}, $$ (3) $$ \delta_{\rm np}\!=\!\frac{h}{B_{S}A^{2/3}}, $$ (4) 式中:
$ Z $ 是电荷数;$ N $ 是中子数;$ A $ 是质量数;$ r_{\rm mac} $ =4.80 MeV;$ h $ =6.6 MeV;$ B_{S}\!=\!\frac{A^{-2/3}}{4\pi r_{0}^{2}}\int_{S}{\rm d}S $ 是相对表面能,即原子核的真实表面积与原子核的球形表面积的比值。 -
弹核碎裂电荷反应截面
$ \sigma(Z) $ 通过下式进行计算:$$ \sigma(Z)\!=\!2\pi\int\nolimits_{0}^{\;b_{\rm max}}bP(Z,b){\rm d}b{\text{。}} $$ (5) 其中:
$ b $ 是碰撞参数;$ P(Z,b) $ 是电荷数为 Z,碰撞参数为$ b $ 时的反应几率;$ b_{\rm max} $ 是最大碰撞参数。在弹核碎裂反应截面的研究[40]中,实验测量结果[32]与理论计算结果进行了比较,ImQMD+GEMINI复合模型的理论计算结果与实验测量结果符合得较好,在电荷数 Z=5~16有明显的奇偶效应。在这里我们重现了ImQMD模型和ImQMD+GEMINI复合模型计算的400 AMeV 36Ar与C、Al、Cu、Pb靶的弹核碎裂电荷反应截面的结果,如图1所示。在图1中,用ImQMD计算的弹核碎裂产生的初级碎块的电荷反应截面没有表现出奇偶效应,而ImQMD+GEMINI 的理论计算结果使弹核碎裂的电荷反应截面表现出了明显的奇偶效应,与实验结果[32]一致。由此可知:400 AMeV 36Ar与C、Al、Cu、Pb靶的弹核碎裂电荷反应截面的奇偶效应是在初级碎块的退激发过程中产生的。
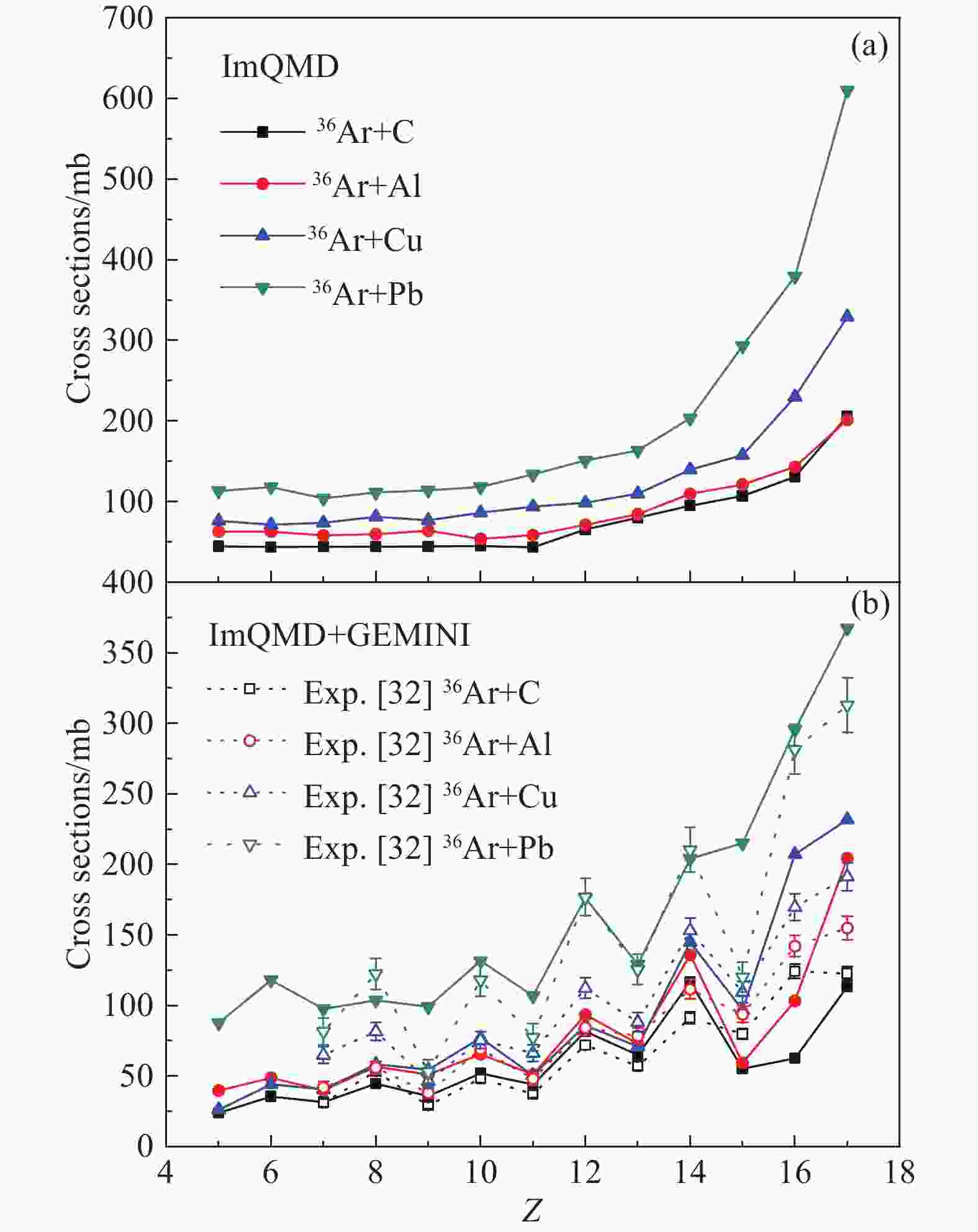
图 1 (在线彩图) 400 AMeV 36Ar与C、Al、Cu、Pb靶的弹核碎裂电荷反应截面,(a) 为ImQMD的计算结果,(b) 为ImQMD+GEMINI的计算结果和实验测量结果[32]
在动力学反应过程中,系统处于高激发态,对能的作用很小,所以在动力学过程中没有考虑对能的作用。在动力学反应过程完成之后,用GEMINI统计衰变模型模拟激发态的初级碎块的退激发过程。它包含有n, p, d, t, 3He,
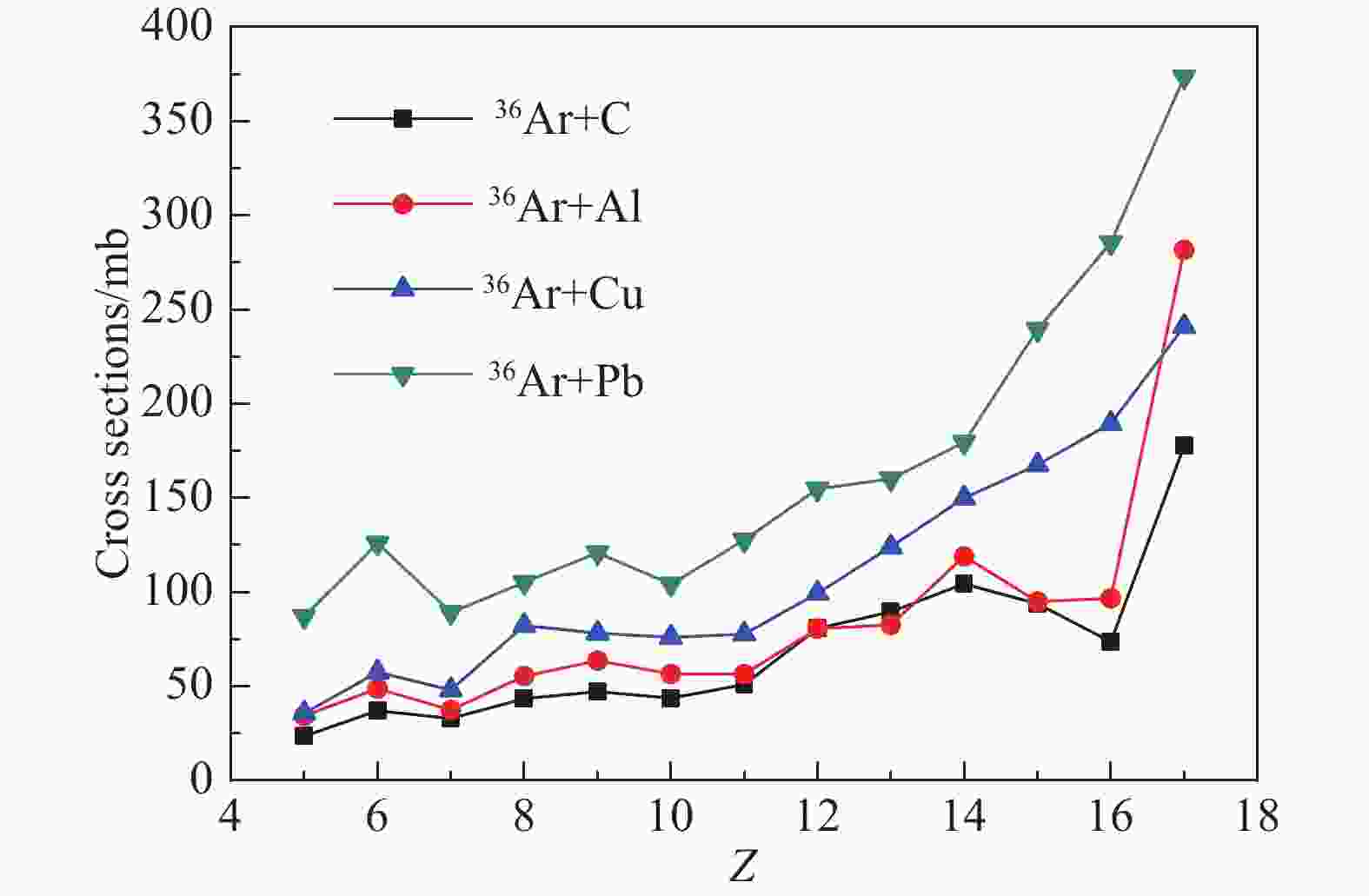
$ \alpha $ 等轻粒子的蒸发,复合核的衰变以及$ \gamma $ 射线的发射,直至再不可能发生任何衰变为止。在稳定核素中,同类核子有各自成对相处的趋势,所以退激发过程中考虑了对能。为了与在对能情况下的反应机制进行比较,我们先在没有对能的情况下计算了400 AMeV 36Ar与C、Al、Cu、Pb靶的弹核碎裂电荷反应截面,如图2所示。很明显,在退激发过程中不考虑对能的作用时,弹核碎裂电荷反应截面的奇偶效应消失。这也意味着对能对弹核碎裂电荷反应截面的奇偶效应起着重要的作用。 -
为了更好地表达弹核碎裂电荷反应截面的奇偶效应,引入了
$ V(Z) $ [32]:$$ V(Z)\!=\!\frac{2\sigma(Z)}{\sigma(Z+1)+\sigma(Z-1)}{\text{,}} $$ (6) 其中Z 是碎块的电荷数。用
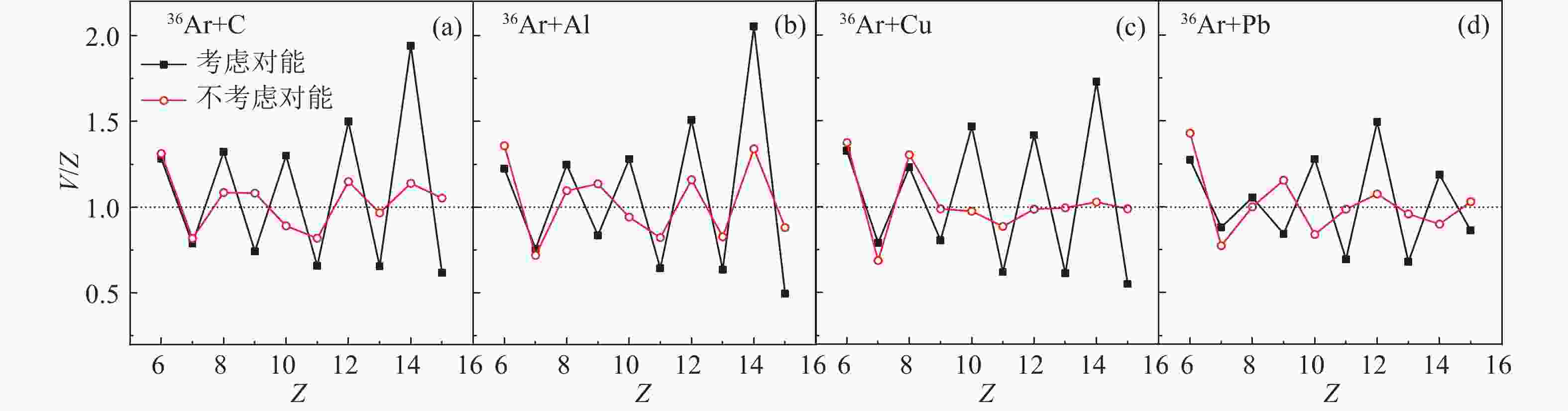
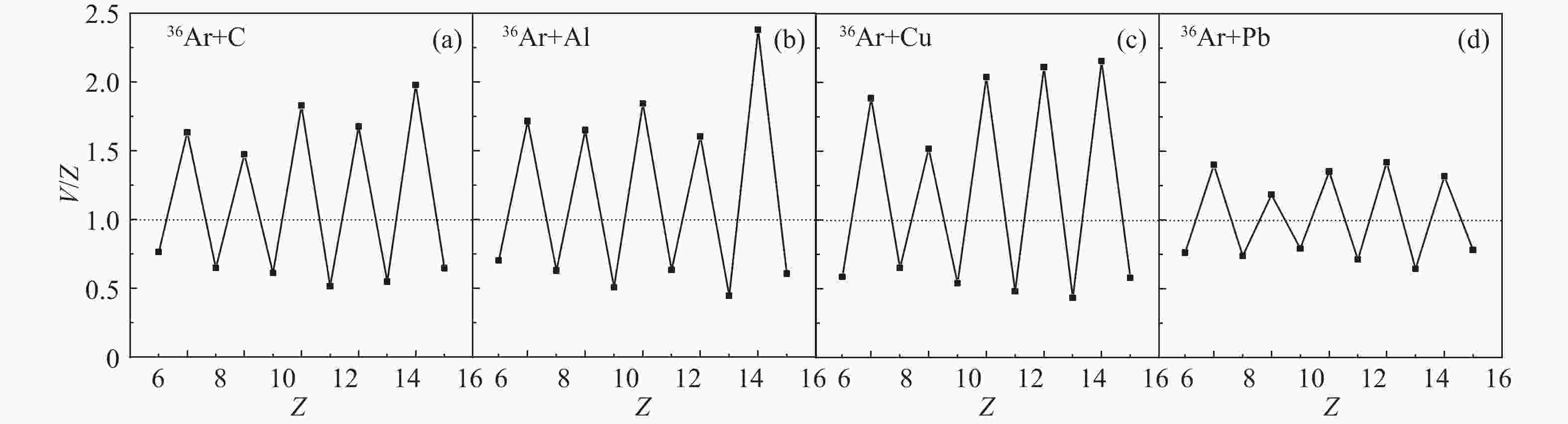
$ V(Z) $ 描述奇偶效应时,当$ Z $ 为奇数,$ V(Z)< $ 1;当$ Z $ 为偶数,$ V(Z)> $ 1。400 AMeV 36Ar与C、Al、Cu、Pb靶的弹核碎裂反应截面的奇偶效应用$ V(Z) $ 表示,如图3所示。图中的虚线表示$ V(Z)\!=\!1 $ 。在退激发过程中考虑对能时,弹核碎裂电荷反应截面表现出明显的奇偶效应,其中Pb靶的奇偶效应最弱。这是因为随着靶核中子数的增加,产生的初级碎块在退激发的过程中将发射出更多的中子,因此质子数的奇偶效应就不那么明显了。而不考虑对能作用时,弹核碎裂电荷反应截面的奇偶效应消失。在弹核碎裂电荷反应截面的研究[40]中指出,电荷反应截面的奇偶效应主要来自于同位旋
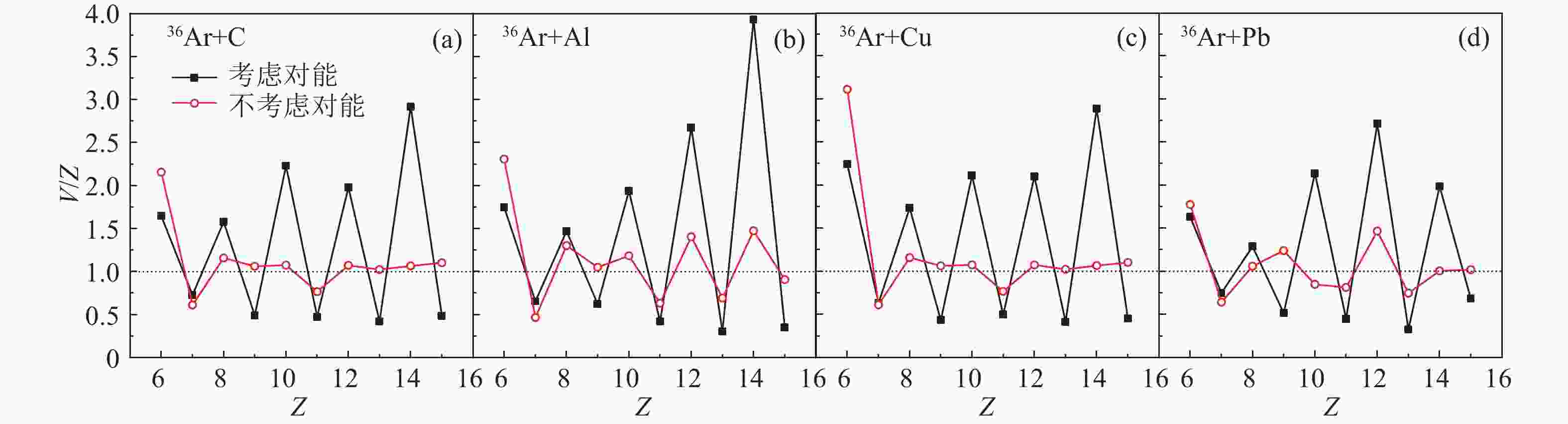
$ T_{Z} $ =0的碎块。我们比较了$ T_{Z} $ =0时在两种情况下的$ V(Z) $ 值,如图4 所示。在考虑对能的情况下,36Ar的弹核碎裂电荷反应截面表现出了明显的奇偶效应。不考虑对能时,弹核碎裂电荷反应截面的奇偶效应减弱甚至于完全消失。同时,通过图3和图4,我们发现两种情况下的$ V(Z)(Z\!=\!6,7,8) $ 都具有奇偶效应。这是因为12C和16O的比结合能较大,而且$ E_{\rm pairing} $ =0。由于对能的作用,不仅使弹核碎裂的电荷反应截面表现出奇偶效应,中子反应截面也表现出了奇偶效应,我们用
$ V(N) $ 来表示弹核碎裂中子反应截面的奇偶效应,类似于式(7),$$ V(N)\!=\!\frac{2\sigma(N)}{\sigma(N+1)+\sigma(N-1)}, $$ (7) 其中 N 是碎块的中子数,
$ \sigma(N) $ 是弹核碎裂中子反应截面,$$ \sigma(N)\!=\!2\pi\int\nolimits_{0}^{\;b_{\rm max}}bP(N,b){\rm d}b{\text{。}} $$ (8) $ P(N,b) $ 是中子数为 N,碰撞参数为$ b $ 时的反应几率。如图5所示。通过图3和图5可以看出,中子反应截面的奇偶效应强于电荷反应截面的奇偶效应。由于没有库仑位垒的作用,中子衰变要比质子衰变简单,中子更容易发射。比如Pb靶,在衰变过程中有更多的中子发射出来,这时中子的奇偶效应比较明显。如图6所示,初级碎块的中质比(
$ <N>/Z $ )斜率大于退激发后的中质比斜率,也就是说退激发后的同位素分布宽度小于初级碎块的同位素分布宽度。退激发后的C、Al、Cu靶的碎块分布主要集中在$ <N>/Z\!=\!1 $ 的附近,这也体现了弹核碎块反应截面在$ T_{Z}\!=\!0 $ 时奇偶效应最强;Pb靶的碎块中质比的斜率最大,电荷数较小时的丰中子核素较多,这体现了中子对能的作用,因此Pb靶的弹核碎裂电荷反应截面在电荷数较小时的奇偶效应较弱。这与其他结果一致[46-47]。 -
本文运用ImQMD和GEMINI统计衰变模型分别描述弹核碎裂的动力学反应过程和初级碎块的退激发过程,分析了400 AMeV 36Ar与 C、Al、Cu、Pb靶的弹核碎裂电荷反应截面的奇偶效应。弹核碎裂电荷反应截面的奇偶效应产生在初级碎块的退激发过程中。对能的作用使弹核碎裂反应截面在质子数和中子数中都表现出了明显的奇偶效应。
Effect of Pairing Energy for Projectile Fragmentation Cross Sections
-
摘要: 运用改进的量子分子动力学(ImQMD)模型嫁接GEMINI统计衰变模型对400 AMeV 36Ar与C、Al、Cu、Pb的弹核碎裂反应截面的奇偶效应进行了理论分析。分析结果表明,弹核碎裂电荷反应截面的奇偶效应产生在初级碎块的退激发过程中,而且退激发过程中的对能在奇偶效应的产生中起着重要作用。如果不考虑对能,弹核碎裂电荷反应截面的奇偶效应将消失。同时由于对能的作用使得弹核碎裂的中子反应截面也表现出明显的奇偶效应。Abstract: The improved quantum molecular dynamics(ImQMD) model plus the GEMINI statistical decay model are used to analyze the odd-even effect of fragmentation cross sections for reactions 36Ar beams on C, Al, Cu, Pb targets at 400 AMeV. The result shows that the odd–even effect is appeared in the de-excitation process of primary fragments, and the pairing energy plays an important role. The odd–even effect of fragmentation cross sections disappears when the pairing energy is removed from the de-excitation process. The odd–even effect in neutron of fragmentation cross section is significantly.
-
Key words:
- fragmentation /
- odd-even effect /
- pairing energy
-
图 1 (在线彩图) 400 AMeV 36Ar与C、Al、Cu、Pb靶的弹核碎裂电荷反应截面,(a) 为ImQMD的计算结果,(b) 为ImQMD+GEMINI的计算结果和实验测量结果[32]
表 1 ImQMD 模型中的相互作用势采用的参数
α/MeV β/MeV γ g0/(MeV·fm2) gτ/MeV η CS/MeV κs/fm2 ρ0/fm–3 –356 303 7/6 7.0 12.5 2/3 32.0 0.08 0.165 -
[1] MOCKO M, TSANG M B, ANDRONENKO L, et al. Phys Rev C, 2006, 74: 054612. doi: 10.1103/PhysRevC.74.054612 [2] GOLOVCHNKO A N, SIHVER L, OTA S, et al. Radiat Meas, 2010, 45(7): 856. doi: 10.1016/j.radmeas.2010.03.006 [3] MEI B, TU X L, WANG M, et al. Nucl Instr and Meth A, 2010, 624(1): 109. doi: 10.1016/j.nima.2010.09.001 [4] ZHANG X H, SUN Z Y, CHEN R F, et al. Phys Rev C, 2012, 85: 024621. doi: 10.1103/PhysRevC.85.024621 [5] YANG J C, XIA J W, XIAO G Q, et al. Nucl Instr and Meth B, 2013, 317: 263. doi: 10.1016/j.nimb.2013.08.046 [6] BAUMANN T, HAUSMANN M, SHERRILL B M, et al. Nucl Instr and Meth B, 2016, 376: 33. doi: 10.1016/j.nimb.2016.02.057 [7] LI J S, ZHANG D H, CHENG J X, et al. Chin J Phys, 2016, 54: 314. doi: 10.1016/j.cjph.2016.05.003 [8] LEHMANN E, PURI R K, FAESSLER A, et al. Phys Rev C, 1995, 51(4): 2113. doi: 10.1103/PhysRevC.51.2113 [9] SINGH J, KUMAR S, PURI R K. Phys Rev C, 2000, 62: 044617. doi: 10.1103/PhysRevC.62.044617 [10] GAUTAM S, CHUGH R, SOOD A D, et al. J Phys G: Nucl Part Phys, 2010, 37: 085102. doi: 10.1088/0954-3899/37/8/085102 [11] ALCANTARA-NUNEZ J, BENLLIURE J, PARADELA C, et al. Phys Rev C, 2015, 92: 024607. doi: 10.1103/PhysRevC.92.024607 [12] MEI B, TU X L, WANG M. Phys Rev C, 2018, 97: 044619. doi: 10.1103/PhysRevC.97.044619 [13] PETTI P L, ARLENE J. Annu Rev Nucl Part Sci, 1994, 44: 155. doi: 10.1146/annurev.ns.44.120194.001103 [14] 杨建设, 李文建, 金晓东, 等. 中国科学G辑: 物理学 力学 天文学, 2005, 35(6): 561. doi: 10.1360/2005-35-6-561 YANG J S, LI W J, JIN X D, et al. Science China Physics, Mechanics & Astronomy, 2005, 35(6): 561. (in Chinese) doi: 10.1360/2005-35-6-561 [15] KNOTT C N, ALBERGO S, CACCIA Z, et al. Phys Rev C, 1997, 56(1): 398. doi: 10.1103/PhysRevC.56.398 [16] ZEITLIN C, FUKUMURA A, GUETERSLOH S B, et al. Nucl Phys A, 2007, 784: 341. doi: 10.1016/j.nuclphysa.2006.10.088 [17] CHENG J X, ZHANG D H, YAN S W, et al. Chin Phys C, 2012, 36(1): 37. doi: 10.1088/1674-1137/36/1/006 [18] 李俊生, 党英华, 张东海. 原子核物理评论, 2017, 34(3): 545. doi: 10.11804/NuclPhysRev.34.03.545 LI J S, DANG Y H, ZHANG D H. Nucl Phys Rev, 2017, 34(3): 545. (in Chinese) doi: 10.11804/NuclPhysRev.34.03.545 [19] HUO L D, WANG L H, ZHU J H, et al. Chin J Phys, 2019, 60: 88. doi: 10.1016/j.cjph.2019.04.022 [20] WILSON J W, SHINN J L, TOWNSEND L W, et al. Nucl Instr and Meth B, 1994, 94: 95. doi: 10.1016/0168-583X(94)95662-6 [21] CUMMINGS J R, BINNS W R, GARRARD T L, et al. Phys Rev C, 1990, 42(6): 2530. doi: 10.1103/PhysRevC.42.2530 [22] TSAO C H, SILBERBERG R, BARGHOUTY A F, et al. Phys Rev C, 1993, 47(3): 1257. doi: 10.1103/PhysRevC.47.1257 [23] ONO A, HORIUCHI H, MARUYAMA T, et al. Phys Rev Lett, 1992, 68(19): 2898. doi: 10.1103/PhysRevLett.68.2898 [24] FELDMEIER H. Nucl Phys A, 1990, 515(1): 147. doi: 10.1016/0375-9474(90)90328-J [25] SU J, ZHANG F S and BIAN B A. Phys Rev C, 2011, 83: 014608. doi: 10.1103/PhysRevC.83.014608 [26] ZHANG X H. Nucl Phys A, 2013, 915: 59. doi: 10.1016/j.nuclphysa.2013.06.013 [27] ZEITLIN C, HEILBRONN L, MILLER J, et al. Phys Rev C, 1997, 56(1): 388. doi: 10.1103/PhysRevC.56.388 [28] MEI B, XU H S, ZHANG Y H, et al. Phys Rev C, 2016, 94: 044615. doi: 10.1103/PhysRevC.94.044615 [29] ZHANG D H, SHI R, LI J S, et al. Nucl Instr and Meth B, 2018, 435: 174. doi: 10.1016/j.nimb.2018.05.045 [30] WANG L H, HUO L D, ZHU J H, et al. Nucl Sci Tech, 2019, 30: 186. doi: 10.1007/s41365-019-0704-1 [31] ZEITLIN C, MILLER J, GUETERSLOH S, et al. Phys Rev C, 2011, 83: 034909. doi: 10.1103/PhysRevC.83.034909 [32] IANCU G, FLESCH F, HEINRICH W. Radiat Meas, 2005, 39(5): 525. doi: 10.1016/j.radmeas.2004.10.011 [33] OLMI A, PIANTELLI S. Eur Phys J A, 2015, 51: 154. doi: 10.1140/epja/i2015-15154-4 [34] HARTNACK C, LI Z X, NEISE L, et al. Nucl Phys A, 1989, 495: 303. doi: 10.1016/0375-9474(89)90328-X [35] NILSEN B S, WADDINGTON C J, CUMMINGS J R, et al. Phys Rev C, 1989, 52(6): 3277. doi: 10.1103/PhysRevC.52.3277 [36] VERMANI Y K, DHAWAN J K, GOYAL S, et al. J Phys G: Nucl Part Phys, 2010, 37: 015105. doi: 10.1088/0954-3899/37/1/015105 [37] GOYAL S, PURI R K. Phys Rev C, 2011, 83: 047601. doi: 10.1103/PhysRevC.83.047601 [38] RICCIARDI M, IGNATYUK A, KELI A, et al. Nucl Phys A, 2004, 733(3): 299. doi: 10.1016/j.nuclphysa.2004.01.069 [39] CHENG J X, JIANG X, YAN S W, et al. J Phys G: Nucl Part Phys, 2012, 39: 055104. doi: 10.1088/0954-3899/39/5/055104 [40] CHENG J X, TIAN J L, ZHANG D H. J Phys G: Nucl Part Phys, 2015, 42: 015102. doi: 10.1088/0954-3899/42/1/015102 [41] 王立春, 程锦霞, 李彦晶, 等. 原子核物理评论, 2013, 30(2): 107. doi: 10.11804/NuclPhysRev.30.02.107 WANG L C, CHENG J X, LI Y J, et al. Nuclear Physics Review, 2013, 30(2): 107. (in Chinese) doi: 10.11804/NuclPhysRev.30.02.107 [42] WANG N, LI Z X, WU X Z. Phys Rev C, 2002, 65(6): 064608. doi: 10.1103/PhysRevC.65.064608 [43] CHARITY R J, JING K X, BOWMAN D R, et al. Nucl Phys A, 1990, 511(1): 59. doi: 10.1016/0375-9474(90)90027-J [44] 程锦霞, 张东海, 李贤, 等. 原子核物理评论, 2015, 32(1): 36. doi: 10.11804/NuclPhysRev.32.01.036 CHENG J X, ZHANG D H, LI X, et al. Nuclear Physics Review, 2015, 32(1): 36. (in Chinese) doi: 10.11804/NuclPhysRev.32.01.036 [45] MOLLER P, NIX J, MYERS W, et al. Atom Data Nucl Data Tables, 1995, 59(2): 185. doi: 10.1006/adnd.1995.1002 [46] LOMBARDO I, AGODI C, AMORINI F, et al. Phys Rev C, 2011, 84(2): 024613. doi: 10.1103/PhysRevC.84.024613 [47] PIANTELLI S, CASINI G, MAURENZIG P R, et al. Phys Rev C, 2013, 88(6): 064607. doi: 10.1103/PhysRevC.88.064607 -





 下载:
下载:







































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号