-
核耗散对深度非弹性散射、熔合等低能核-核碰撞过程均有重要影响。近年来,它在理解激发核衰变机制[1-2],尤其是在裂变性质中所起的关键作用引起了广泛的关注。实验测量表明:高激发能下的断前粒子多重性[3-5]和蒸发剩余截面[6-8]明显偏离标准统计模型的预测值。这被认为是由于裂变过程中的摩擦效应引起的。通过分析裂变几率和蒸发剩余截面 这些被认为仅敏感于鞍点前摩擦的观测量可以严格地约束小形变处的摩擦强度[6, 8-11],然而关于大形变处(鞍点后)的摩擦强度仍有明显的差异[12-14]。在这种情况下,为了探索裂变过程中核摩擦对形变的依赖性,获得鞍点后摩擦强度的精确信息就变得非常紧迫和十分必要。目前,这方面的研究较少。
不同于仅对鞍点前摩擦敏感的裂变几率和蒸发剩余截面,轻粒子可以在整个裂变路径上发射,它们也因此会受到鞍点后摩擦的影响。此外,鞍点后的粒子发射是裂变系统质量数的增函数。因此重裂变系统的轻粒子多重性被广泛地用于探测鞍点后的耗散性质[4-5, 12]。
目前,实验上主要是基于熔合反应形成的激发核来研究核裂变过程中的耗散性质。当通过这种方式来产生重的复合系统(A~240)时,熔合-裂变道和准裂变道都会出现[15-17]。由于这两个不同反应道产生的碎片特征有些相似,这导致用重裂变系统的粒子多重性数据 来提取核摩擦强度时会存在较大的不确定性[18-21]。进而,入射能量的增加也会引起更强的准裂变道与熔合-裂变道之间的竞争[15, 18-19]。因此,为了使用断前粒子发射来可靠地研究核耗散的特性,通过熔合反应途径产生的重裂变系统通常会限制在较低的激发能区域。
在实验方面,除熔合反应外,中能重离子碰撞[22-26]和质子引起的散裂反应[27-28]也被用来产生高激发的核系统。熔合产生的复合核通常具有较低的激发能(
$ < $ 70 MeV),而对后面两种实验方式,它们产生的核系统的激发能可以达到~500 MeV[22]和~1 GeV[27-28]。为了更好地指导实验探索,本工作致力于研究何种条件可以增强重裂变系统的粒子(特别是轻带电粒子)多重性对鞍点后摩擦的敏感性。为此,我们将在Langevin模型的框架内考察激发能和角动量对该敏感性的影响。大量研究[12-14, 29-33]已表明 随机模型是研究激发核裂变的合适途径。
-
热核系统的驱动力不仅仅是裸势的负梯度,它还应该包含热力学修正[12, 34]。因此,在Langevin方程中,熵被用于描述裂变系统的动力学演化。我们用下面的一维Langevin方程进行动力学轨道计算:
$$ \begin{split} \frac{{\rm d} q}{{\rm d} t} = \frac{p}{m}, \;\;\;\;\frac{{\rm d} p}{{\rm d} t} = K -\beta p + \sqrt{m\beta T}\varGamma(t){\text{。}}\end{split} $$ (1) 其中:t是时间变量;q是无量纲形变坐标,表示未来裂变碎片质心间距离的一半(以复合核半径为单位);p是其共轭动量;m是惯性质量参数;
$ \beta $ 和T分别表示耗散强度和温度。$ \varGamma(t) $ 表示涨落力,满足$ <\varGamma(t)> $ =0和$ <\varGamma(t)\varGamma(t')> $ =2$ \delta(t-t') $ 。方程(1)中的驱动力K通过在恒定激发能下的熵
$ S(q) $ 对q的导数来获得:$$ K = T\frac{{\rm d} S}{{\rm d} q}\; {\text{。}} $$ (2) 熵
$ S(q) $ 可由Fermi-gas模型[12]得到:$$ S(q) = 2\sqrt{a(q)\big[E^*-V(q)-E_{\mathrm{coll}}\big]}, $$ (3) 其中
$ E^* $ 为裂变系统的总激发能,$ E_{\mathrm{coll}} $ 为系统集体自由度的动能。有限力程液滴势能$ V(q) $ [35]包含了形变依赖的表面能、库仑能和转动能项。构建熵
$ S(q) $ 时,使用了Ignatyuk等[36]的方法来计算形变相关的能级密度参数:$$ a(q) = 0.073 A + 0.095 A^{2/3} B_{\rm s}(q), $$ (4) 式中:A为原子核的质量数;
$ B_{\rm s}(q) $ 是描述原子核表面形状的无量纲参数[12]。轻粒子的衰变宽度用Blann的参数化公式[37]计算:
$$ \begin{split} \varGamma_{\rm \nu} =& (2s_{\nu}+1)\frac{m_{\nu}}{\pi^2 \hbar^2 \rho_{\rm c}(E^*_{\mathrm{intr}})}\times \\ & \int\nolimits_{0}^{E^*_{\mathrm{intr}}-B_{\nu}} {\rm d}\varepsilon_{\nu} \rho_{\rm R}(E^*_{\mathrm{intr}}-B_{\nu}-\varepsilon_{\nu})\varepsilon_{\nu}\sigma_{\mathrm{inv}}(\varepsilon_{\nu}),\end{split}$$ (5) 这里,
$ s_{\nu} $ 是被发射粒子$ \nu $ (=n, p,$ ^{2}{\rm H} $ ,$ ^{3}{\rm H} $ ,$ ^{3}{\rm He} $ ,$ \alpha $ )的自旋,$ m_{\nu} $ 是其相对于蒸发余核的约化质量。系统内部的激发能是$ E^*_{\mathrm{intr}}\big[ = E^*-V(q)-E_{\mathrm{intr}}-E_{\mathrm{evap}}(t)\big] $ ,其中$ E_{\mathrm{evap}}(t) $ 代表在时间t之前所有被蒸发粒子所带走的能量。$ \rho_{\rm c}(E^*_{\mathrm{intr}}) $ 和$ \rho_{\rm R}(E^*_{\mathrm{intr}}-B_{\nu}-\varepsilon_{\nu}) $ 是母核和子核的能级密度[38]。$ B_{\nu} $ 和$ \varepsilon_{\nu} $ 分别表示被发射粒子$ {\nu} $ 的结合能和动能。$ \sigma_{\mathrm{inv}}(\varepsilon_{\nu}) $ 为逆反应截面[37]。本文采用离散化的方式[12-13, 33]处理轻粒子发射。首先计算每个时间步长
$ \tau $ 时的轻粒子衰变宽度;然后在时间步长$ \tau $ 内判断一个随机数$ \zeta $ ($ 0\leqslant\zeta\leqslant1 $ )是否小于$ \tau/\tau_{\mathrm{dec}} $ ;如是,则粒子被允许发射,并根据$ \varGamma_{\nu}/\varGamma_{\mathrm{part}} $ 权重通过Monte Carlo方法挑选出被发射粒子的种类。这里,$ \tau_{\mathrm{dec}} \!=\! \hbar/\varGamma_{\mathrm{part}} $ ,$ \varGamma_{\mathrm{part}} $ 代表所有轻粒子衰变宽度的和。粒子发射会引起衰变系统角动量的损失。本工作中假定如下[12-13]:发射一个中子、一个质子、一个$ \alpha $ 粒子和一个$ \gamma $ 光子分别带走角动量1$ \hbar $ 、1$ \hbar $ 、2$ \hbar $ 和1$ \hbar $ 。在粒子发射以后,Langevin方程中的内能$ E^*_{\mathrm{intr}} $ 、势能$ V(q) $ 和熵将会被重新计算并继续进行动力学方程的演化。当动力学轨道从基态越过鞍点到达断点,它就被视作一次裂变事件。断前粒子多重性是通过计算在裂变轨道中蒸发的粒子数获得的。进而,通过记录粒子发射时的形变坐标q并比较其与鞍点位置的大小来判断该粒子是来自鞍点内还是来自鞍点外,从而得到鞍点前、后的粒子多重性。
-
在本工作中,重裂变系统240Am蒸发的轻粒子多重性被用于研究大形变处的耗散性质。为了更好地揭示鞍点后的摩擦效应,计算中选用了不同的鞍点后摩擦强度(
$ \beta $ )。此外,根据近期的理论估计和实验分析[12-13, 39-42],鞍点前的摩擦强度取为4$ \times10^{21} $ s–1。图1展示了在角动量
$ \ell \!=\! 50 $ $ \hbar $ 和激发能$ E^* \!=\! 60,\; 120,\; 250 $ MeV时,240Am在鞍点后蒸发的轻粒子多重性随$ \beta $ 的演化。可以看到粒子发射是摩擦强度的敏感函数。原因是核摩擦阻尼了裂变。随着$ \beta $ 的增加,裂变过程变长,这能提供更多的时间用于粒子发射,从而导致粒子多重性随着摩擦的增强而上升。
图 1 (在线彩图)在激发能
$E^* \!=\! 60,\; 120,\; 250$ MeV和角动量$\ell \!=\! 50\;\hbar$ 时,240Am核在鞍点后蒸发的中子(a),质子(b)和$\alpha$ 粒子(c)多重性随鞍点后摩擦强度($\beta$ )的变化从图1中能观察到,激发能越高,鞍点后粒子多重性越大。原因是粒子蒸发时间在高激发能时变短。此外,因强摩擦而延长的裂变时间也有利于粒子在高能时的发射。这些因素都导致了粒子多重性随
$ E^* $ 的升高而增加。在低$ E^* $ 时,不但粒子发射弱,而且 因为不同衰变道之间的竞争,较强的中子发射也会进一步抑制质子和$ \alpha $ 粒子的 发射。因此,轻带电粒子的发射在低能时非常小,这降低了它们对摩擦的敏感度。但对于高能情况,较强的粒子发射表明摩擦效应会随着$ E^* $ 的增加而变强。此外,从图中还能看到激发能强烈地影响了鞍点后粒子多重性对
$ \beta $ 的敏感性。具体来说,对于中子,$ E^*\! =\! 250 $ MeV时,鞍点后中子多重性$ M_{\rm n}^{\mathrm{post}} $ 随$ \beta $ 变化曲线的斜率明显陡于$ E^* \!=\! 60 $ MeV时的情形。这表明在高$ E^* $ 时,中子发射对$ \beta $ 有很强的敏感性。然而对于轻带电粒子,在$ E^* \!=\! 60 $ MeV时,鞍点后质子多重性$ M_{\rm p}^{\mathrm{post}} $ 和鞍点后$ \alpha $ 粒子多重性$ M_{\alpha}^{\mathrm{post}} $ 几乎不随$ \beta $ 变化。也就是说,它们不敏感于摩擦。但在$ E^* \!=\! 120 $ MeV时,$ M_{\rm p}^{\mathrm{post}} $ 和$ M_{\alpha}^{\mathrm{post}} $ 对$ \beta $ 的敏感度变大。当在$ E^* $ 上升到250 MeV时,增强的轻带电粒子发射增加了它们对$ \beta $ 的敏感性。这意味着使用高激发能条件下测量的粒子多重性(包括质子和$ \alpha $ 粒子)会有利于更严格地约束鞍点后摩擦的强度。为了研究鞍点后的耗散性质,目前实验的测量主要集中在通过低能熔合反应提供的重裂变核的中子发射上[3-4]。这样做的原因是:同带电粒子相比,中子是主要的衰变道。此外,轰击能量的增加会引起准裂变道的干扰[15, 18-19]。因此,通过熔合-裂变反应测得的来自重核蒸发的粒子多重性一般都局限在较低的能量范围内。因为这些原因,对于由熔合反应产生的重裂变核,其轻带电粒子发射是非常弱的。从图1(b)和1(c)可以看到,当
$ E^* \!=\! 60 $ MeV时,质子和$ \alpha $ 粒子的多重性非常小。这表明,如果在低能条件下研究鞍点后的摩擦强度,轻带电粒子不是好的观测量。然而图1指出,在高$ E^* $ 时,不但$ M_{\rm n}^{\mathrm{post}} $ ,而且$ M_{\rm p}^{\mathrm{post}} $ 和$ M_{\alpha}^{\mathrm{post}} $ 也都会明显地增加,它们对$ \beta $ 的变化也相当敏感。这说明在高$ E^* $ 的条件下,重裂变系统蒸发的轻带电粒子也是一个对鞍点后摩擦十分敏感的探针。同熔合反应相比,入射能量从几十到几百MeV每核子的中能重离子碰撞能产生各种不同激发能和角动量的重核系统。例如,近心碰撞能产生高激发能、低角动量的热核,而周边碰撞可以产生激发能超过200 MeV、角动量50
$ \hbar $ 左右的激发核[22-24]。通过裂变碎片的折叠角技术[22-23],实验上能很好地确定不同碰撞参数(如近心、半周边、周边碰撞)所引起的裂变事件,同时也能方便地提取[24-26] 裂变源的质量数A、电荷数Z、激发能$ E^* $ 等实验信息。此外,采用多源模型方法可以从实验上获得与裂变碎片符合的轻粒子多重性。该方法已经被广泛地用在熔合-裂变[3-4]和 中能重离子引起的裂变反应中[22-23, 25-26]。因此,通过测量由中能核反应产生的高激发重裂变核发射的轻粒子多重性来研究鞍点后的摩擦强度是非常合适的。另外,从图1中可以发现,当使用粒子多重性(尤其是轻带电粒子)来探测鞍点后的摩擦强度时,中能重离子碰撞能够提供比低能熔合反应更有利的实验条件。除了激发能,角动量也是一个对激发核退激模式有重要影响的参数。因此,我们在图2中展示了在角动量
$ \ell \!=\! 10,\; 35,\; 55\;\hbar $ 下的计算结果。可以看到$ \ell $ 越大,鞍点后发射的粒子多重性对$ \beta $ 的敏感度就越大。原因是增加角动量会降低裂变位垒,这有利于裂变。也就是说,在高$ \ell $ 的情况下,裂变几率变大,鞍点前发射降低,这为鞍点后的粒子发射留下了更多的能量,从而增加了鞍点后的粒子多重性。一个大的鞍点后粒子多重性增强了它对$ \beta $ 的敏感性。在中能重离子周边碰撞中,产生的激发核可以拥有一个较高的角动量[22, 24-26]。图2的结果表明,当选择轻粒子多重性来探测鞍点后的耗散特性时,利用中能重离子周边碰撞产生的裂变系统可以提供更优化的条件,也因此能对鞍点后的摩擦强度施加更严格的约束。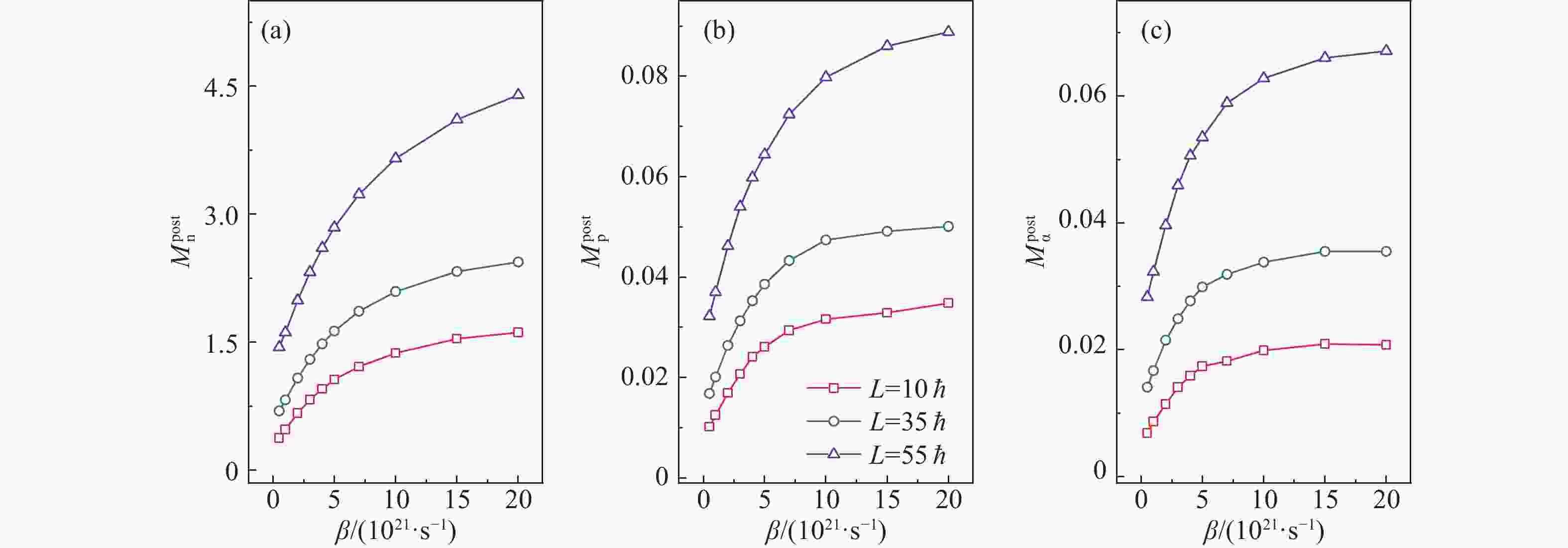
图 2 (在线彩图)在角动量
$\ell \!=\! 10,\; 35,\; 55\; \hbar$ 和激发能$E^* \!=\! 150$ MeV时,240Am核在鞍点后蒸发的中子(a),质子(b)和$\alpha$ 粒子(c)多重性随鞍点后摩擦强度($\beta$ )的变化如前所述,由于准裂变道的竞争,利用熔合机制很难产生高
$ E^*(>$ 200 MeV)和 大$ \ell $ (~50$ \hbar $ )的重裂变核,而中能核反应能产生相当高激发能的重衰变系统。为了进一步考察这两种不同的实验途径在探索热核的衰变特征(尤其是通过粒子发射来研究裂变过程中的耗散性质)的差异,我们在条件(i)($ E^* \!=\! 70 $ MeV,$ \ell \!=\! 50 $ $ \hbar $ )和条件(ii)($ E^* \!=\! 250 $ MeV,$ \ell \!=\! 15 $ $ \hbar $ )下计算了裂变核240Am在鞍点后发射的粒子多重性随$ \beta $ 的变化。条件(i)和(ii)分别对应由熔合反应和中能重离子近心碰撞所产生的重裂变系统所具有的初始条件。从图3(a)可以看出,在条件(i)和(ii)下,鞍点后的中子发射对
$ \beta $ 的敏感度相当;但对轻带电粒子,差异则很大,见图3(b)和3(c)。在条件(i)下,$ M_{\rm p}^{\mathrm{post}} $ 和$ M_{\rm {\alpha}}^{\mathrm{post}} $ 随$ \beta $ 的变大仅有微小的改变。这表明对由熔合反应产生的重裂变核,其发射的带电粒子不是鞍点后摩擦强度好的观测量。但是,条件(ii)下的质子和$ \alpha $ 粒子对$ \beta $ 有很大的敏感性。
图 3 (在线彩图)在不同初始条件(
$E^*$ = 70 MeV,$\ell \!=\! 50\; \hbar$ ),($E^*\! =\! 250$ MeV,$\ell \!=\! 15\; \hbar$ )和($E^* \!=\! 200$ MeV,$\ell \!=\! 50\; \hbar$ )下,240Am核在鞍点后蒸发的中子(a),质子(b)和$\alpha$ 粒子(c)多重性随$\beta$ 的变化在中能反应中,通过近心碰撞可以产生高
$ E^* $ 和低$ \ell $ 的激发核,而周边碰撞能形成高$ E^*(>200 $ MeV)和高$ \ell $ ($ \sim50\; \hbar $ )的裂变系统[24]。图3中展示了在$ E^* \!=\! 200 $ MeV和$ \ell \!=\! 50\; \hbar $ 条件下的计算结果。从图中可以看到,$ M_{\rm p}^{\mathrm{post}} $ 和$ M_{\alpha}^{\mathrm{post}} $ 随$ \beta $ 的增加快速上升,$ M_{\rm n}^{\mathrm{post}} $ 随$ \beta $ 变化的速度也快于条件(i)下的情形。这说明高$ E^* $ 和高$ \ell $ 条件有利于用轻粒子发射来探测鞍点后的摩擦强度。因此,测量中能周边重离子碰撞产生的重核在裂变过程中的粒子发射能为更强地 约束鞍点后的摩擦强度提供有力的工具。 -
在耦合了粒子统计发射的Langevin方程框架内,我们研究了激发能和角动量对用重裂变系统的粒子多重性来探测鞍点后摩擦强度(
$ \beta $ )的影响。结果表明,在高激发能和高角动量的情况下,鞍点后粒子多重性对$ \beta $ 的敏感性显著增强。此外,相比于低激发能和高角动量条件,在高激发能和低角动量条件下的轻带电粒子对$ \beta $ 更为敏感。这两种条件分别对应于熔合反应和中能重离子碰撞所形成的重裂变核的特征。因此,在实验方面,当通过测量轻粒子多重性来更准确地提取鞍点后的摩擦强度时,可以选择由中能重离子碰撞产生的高激发重裂变核系统。
-
摘要: 基于考虑了粒子发射的随机Langevin模型,计算了重裂变核240Am在 鞍点后发射的中子、质子和
$ \alpha $ 粒子多重性作为鞍点后摩擦强度($ \beta $ )的函数。结果表明在高激发能($ E^* $ )和高角动量($ \ell $ )条件下,这些轻粒子发射对摩擦的敏感性变强。进而,比较了在(高$ E^* $ ,低$ \ell $ )和(低$ E^* $ ,高$ \ell $ )这两个不同初始条件下,240Am核在鞍点后蒸发的粒子随$ \beta $ 的演化。发现前者不但能增强核摩擦对粒子发射的影响,也显著提高了带电粒子对$ \beta $ 的敏感性。在实验方面,我们建议可以用中能重离子碰撞的方式产生高激发的重裂变系统,来更精确地用粒子发射(尤其是轻带电粒子)来探测鞍点后的摩擦强度。Abstract: The stochastic Langevin model is applied to calculate the evolution of postsaddle emitted neutrons, protons and$ \alpha $ particles of heavy 240Am nuclei with the postsaddle friction strength($ \beta $ ). A significantly enhanced sensitivity of these particles to$ \beta $ has been observed at a high energy($ E^* $ ) and a large angular momentum($ \ell $ ). Moreover, the postsaddle emission as a function of$ \beta $ is compared under two contrasting initial conditions of (high$ E^* $ , low$ \ell $ ) and (low$ E^* $ , high$ \ell $ ) for the populated 240Am system. It is shown that for the former type of conditions, the influence of friction on particle evaporation is amplified and the sensitivity of light charged particles to friction is significantly increased. These results suggest that in experiment, to precisely probe the postsaddle friction through the measurement of particle multiplicity, in particular light charged-particle multiplicities, it is best to choose intermediate-energy heavy-ion collisions to produce highly excited heavy fissioning nuclei. -
-
[1] JACQUET D, MORJEAN M. Prog Part Nucl Phys, 2009, 63: 155. [2] ANDREYEV A N, NISHIO K, SCHMIDT K H. Rep Prog Phys, 2018, 81: 016301. doi: 10.1088/1361-6633/aa82eb [3] HINDE D J, HILSCHER D, ROSSNER H, et al. Phys Rev C, 1992, 45: 1229. doi: 10.1103/PhysRevC.45.1229 [4] HILSCHER D, ROSSNER H. Ann Phys (Paris), 1992, 17: 471. doi: 10.1051/anphys:01992001706047100 [5] PAUL P, THOENNESSEN M. Annu Rev Nucl Part Sci, 1994, 44: 55. doi: 10.1146/annurev.ns.44.120194.000433 [6] BACK B B, BLUMENTHAL D J, DAVIDS C N, et al. Phys Rev C, 1999, 60: 044602. doi: 10.1103/PhysRevC.60.044602 [7] PRASAD E, VARIER K M, MADHAVAN N, et al. Phys Rev C, 2011, 84: 064606. doi: 10.1103/PhysRevC.84.064606 [8] SANDAL R, BEHERA B R, SINGH V, et al. Phys Rev C, 2015, 91: 044621. doi: 10.1103/PhysRevC.91.044621 [9] YE W, WANG N. Phys Rev C, 2013, 87: 014610. doi: 10.1103/PhysRevC.87.014610 [10] BANERJEE T, NATH S, JHINGAN A, et al. Phys Rev C, 2017, 96: 014618. doi: 10.1103/PhysRevC.96.014618 [11] SCHMITT C, SCHMIDT K H, KELIĆ A, et al. Phys Rev C, 2010, 81: 064602. doi: 10.1103/PhysRevC.81.064602 [12] FRÖBRICH P, GONTCHAR I I. Phys Rep, 1998, 292: 131. doi: 10.1016/S0370-1573(97)00042-2 [13] NADTOCHY P N, ADEEV G D, KARPOV A V. Phys Rev C, 2002, 65: 064615. doi: 10.1103/PhysRevC.65.064615 [14] KRAPPE H J, POMORSKI K. Theory of Nuclear Fission, Lecture Notes in Physics[M]. Berlin: Springer, 2012: 83. [15] WILLIAMS E, HINDE D J, DASGUPTA M, et al. Phys Rev C, 2013, 88: 034611. doi: 10.1103/PhysRevC.88.034611 [16] CHATTERJEE A, NAVIN A, KAILAS S, et al. Phys Rev C, 1995, 52: 3167. doi: 10.1103/PhysRevC.52.3167 [17] SHEN W Q, ALBINSKI J, GOBBI A, et al. Phys Rev C, 1987, 36: 115. doi: 10.1103/PhysRevC.36.115 [18] SIWEK-WILCZYNSKA K, WILCZYNSKI J, LEEGTE H K W, et al. Phys Rev C, 1993, 48: 228. doi: 10.1103/PhysRevC.48.228 [19] SIWEK-WILCZYNSKA K, WILCZYNSKI J, SIEMSSEN R H, et al. Phys Rev C, 1995, 51: 2054. doi: 10.1103/PhysRevC.51.2054 [20] SAXENA A, CHATTERJEE A, CHOUDHURY R K, et al. Phys Rev C, 1994, 49: 932. doi: 10.1103/PhysRevC.49.932 [21] SHAW N P, DIÓSZEGI I, MAZUMDAR I, et al. Phys Rev C, 2000, 61: 044612. doi: 10.1103/PhysRevC.61.044612 [22] HILSCHER D, ROSSNER H, CRAMER B, et al. Phys Rev Lett, 1989, 62: 1099. doi: 10.1103/PhysRevLett.62.1099 [23] KNOCHE K, LÜDEMANN L, SCOBEL B, et al. Phys Rev C, 1995, 51: 1908. doi: 10.1103/PhysRevC.51.1908 [24] ECKERT E M, KÜHMICHEL A, POCHODZALLA J, et al. Phys Rev Lett, 1990, 64: 2483. doi: 10.1103/PhysRevLett.64.2483 [25] WANG R S, ZHANG Y, XIAN Z G, et al. Phys Rev C, 2014, 89: 064613. doi: 10.1103/PhysRevC.89.064613 [26] WU Q, ZHANG Y, XIAO Z, et al. Phys Rev C, 2015, 91: 014617. doi: 10.1103/PhysRevC.91.014617 [27] BENLLIURE J, ARMBRUSTER P, BERNAS M, et al. Nucl Phys A, 2002, 700: 469. doi: 10.1016/S0375-9474(01)01331-8 [28] LOTT B, GOLDENBAUM F, BOHM A, et al. Phys Rev C, 2001, 63: 034616. doi: 10.1103/PhysRevC.63.034616 [29] YE W, WU F, YANG H W. Phys Lett B, 2007, 647: 118. doi: 10.1016/j.physletb.2007.01.065 [30] WANG N, YE W. Phys Lett B, 2020, 801: 135138. doi: 10.1016/j.physletb.2019.135138 [31] ARITOMO Y, CHIBA S, IVANYUK F, et al. Phys Rev C, 2014, 90: 054609. doi: 10.1103/PhysRevC.90.054609 [32] RANDRUP J, MÖLLER P. Phys Rev Lett, 2011, 106: 132503. doi: 10.1103/PhysRevLett.106.132503 [33] SCHMITT C, MAZUREK K, Nadtochy P N. Phys Rev C, 2018, 97: 014616. doi: 10.1103/PhysRevC.97.014616 [34] LESTONE J P, MCCALLA S G. Phys Rev C, 2009, 79: 044611. doi: 10.1103/PhysRevC.79.044611 [35] KRAPPE H J, NIX J R, SIERK A J. Phys Rev C, 1979, 20: 992. doi: 10.1103/PhysRevC.20.992 [36] IGNATYUK A V, ITKIS M G, OKOLOVICH V N, et al. Sov J Nucl Phys, 1975, 2: 612. [37] BLANN M. Phys Rev C, 1980, 21: 1770. doi: 10.1103/PhysRevC.21.1770 [38] BOHR A, MOTTELSON B R. Nuclear Structure[M]. London: Benjamin, 1975: 2. [39] JURADO B, SCHMITT C, SCHMIDT K H, et al. Phys Rev Lett, 2004, 9: 072501. doi: 10.1103/PhysRevC.93.072501 [40] RYABOV E G, KARPOV A V, NADTOCHY P N, et al. Phys Rev C, 2008, 78: 044614. doi: 10.1103/PhysRevC.78.044614 [41] TIAN J, YE W. Phys Rev C, 2016, 94: 021601(R). doi: 10.1103/PhysRevC.94.021601 [42] RODRÍGUEZ-SÁNCHEZ J L, BENLLIURE J, PARADELA C, et al. Phys Rev C, 2016, 94: 034605. doi: 10.1103/PhysRevC.94.034605 -

















 下载:
下载:












































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号