-
近年来,随着放射性核束技术的快速发展,远离β稳定线的奇特原子核的结构引起了人们的普遍关注。在这些奇特原子核中,呈现出许多新的现象,如晕(皮)、集团自组织、非线性多中子关联、连续态耦合、能级反转、幻数移动等新物理现象。自从1985年Tanihata等[1]第一次发现11Li中的晕现象以来,奇特核的研究引起了广泛关注,核实验及理论工作者就此做了大量的研究[2-6]。近期,文献[7]利用形变的相对论Hartree-Bogoliubov模型探讨了22C中晕的形成、形变效应、能级反转以及壳层的演化。
由于奇特核的中子或质子费米面非常接近零势能面,连续阈附近弱束缚和非束缚态的贡献变得十分重要。恰当地处理连续阈附近弱束缚和非束缚态的贡献,尤其是连续谱中共振态的贡献,是一个理论能否成功描述奇特核的关键[6]。因此,物理学家们已经发展了很多研究单粒子共振态的方法,包括散射相移方法[8]、Jost 函数方法[9-10]、格林函数方法[11-12]、耦合常数解析延拓方法[13-15]、实稳定化方法[16-17]以及复标度方法[18-19]。这些理论方法在描述奇特核方面取得了一定成功,但仍存在缺陷。因此,我们建立了复动量 (CMR) 表象方法[20],采用CMR方法,不仅能够统一描述束缚态、共振态和连续谱,而且能够很好地描述窄共振和宽共振[21]。最近,我们进一步发展了复动量表象(CMR)方法,获得了其它方法难以获得的连续阈附近低轨道角动量宽共振的信息。并且在非相对论框架下采用CMR方法计算得到单粒子能量、单粒子态的主要组分占比随四极形变系数β2变化的关系以及径向密度分布等,解释了实验上已经发现的31Ne[22]和19C[23]中的晕现象,还预测了几个比37Mg[24]更重的核(77Fe、75Cr和53Ar)中也存在不同的晕结构。
-
为了研究晕核的单粒子共振态,我们首先将哈密顿量表示为
$$H = T + V,$$ (1) 这里动量算符
$T = {{{{{p}}^2}} / {2m}}$ ,其中,${{p}} = \hbar {{k}}$ (${{k}}$ 是波矢),根据文献[25],相互作用势V由中心势、形变势以及自旋轨道耦合势三部分组成:$$\begin{split} &{V_{{\rm{cent}}}}(r) = {V_0}f(r), \\ & {V_{{\rm{def}}}}(r) = - {\beta _2}k(r){Y_{20}}(\vartheta ,\varphi ), \\ & {V_{sl}}(r) = - 4{V_0}{\Lambda ^2}\frac{1}{r}\frac{{{\rm{d}}f(r)}}{{{\rm{d}}r}}(s \cdot l), \\ \end{split} $$ (2) 上式中
$\Lambda $ 是核子的约化康普顿波长${\hbar / {{m_r}}}c$ ,$${\text{且}}\qquad\qquad\qquad\begin{array}{l} f(r) = \dfrac{1}{{1 + {{\rm e}^{\frac{{r - R}}{a}}}}}, \\ k(r) = {V_0}r\dfrac{{{\rm{d}}f(r)}}{{{\rm{d}}r}}{\text{。}} \\ \end{array} \qquad\qquad\qquad\qquad$$ 和文献[26]类似,参数
$a\!=\!0.67\;{\rm{fm}}$ ,$R\!=\!{r_0}{A^{{1 / 3}}}$ ,${r_0}\!=\! $ $1.27\;{\rm{fm}}$ 。为了获得共振态,我们将薛定谔方程转到动量空间,可以同时得到束缚态、共振态和连续谱:
$$\int {\rm{d}} {{k}}'\left\langle {{{k}}\left| H \right|{{k}}'} \right\rangle \psi ({{k}}') = E\psi ({{k}}),$$ (3) 对于轴对称形变核,宇称
$\pi $ 以及总角动量的第三个分量是个好量子数,动量波函数$\psi ({{k}})$ 用径向和角向部分来表达,故$$\psi ({{k}}) = {\psi _{{m_j}}}({{k}}) = \sum\limits_{lj} {{f^{lj}}(k)} {\phi _{lj{m_j}}}({\Omega _k}),$$ (4) 这里
${f^{lj}}(k)$ 是波函数的径向分量。波函数的角向部分表示为$${\phi _{lj{m_j}}}({\Omega _k}) = \sum\limits_{{m_s}} {\left\langle {\left. {lm\frac{1}{2}{m_s}} \right|} \right.} \left. {j{m_j}} \right\rangle {Y_{lm}}({\Omega _k}){\chi _{{m_s}}},$$ (5) 将上述的波函数代入薛定谔方程,我们可以得到:
$$\begin{split} & \frac{{{\hbar ^2}k_a^2}}{{2M}}{f^{lj}}({k_a}) + \sum\limits_b {{w_b}} k_b^2{V_s}(l,j,{k_a},{k_b}){f^{lj}}({k_b}) - \\ & {\beta _2}\sum\limits_{l'j'} {\sum\limits_b {{w_b}} k_b^2{V_d}(l,j,l',j',{k_a},{k_b}){f^{l'j'}}({k_b})} = E{f^{lj}}({k_a}), \\ \end{split} $$ (6) 式(6)中的矩阵是不对称的,为了简便计算,我们变为对称矩阵
$$\begin{split} &\frac{{{\hbar ^2}k_a^2}}{{2M}}{F^{lj}}({k_a}) + \sum\limits_b {\sqrt {{w_a}{w_b}} {k_a}{k_b}} {V_s}(l,j,{k_a},{k_b}){F^{lj}}({k_b}) - \\ &{\beta _2}\sum\limits_b {\sum\limits_{l'j'} {\sqrt {{w_a}{w_b}} {k_a}{k_b}} } {V_d}(l,j,l',j',{m_j},{k_a},{k_b}){F^{l'j'}}({k_b}) =\\ &E{F^{lj}}({k_a}) {\text{。}} \\[-12pt] \end{split} $$ (7) 至此,通过求解对称矩阵的本征解就可以解出薛定谔方程,获得束缚态和共振态的能量,为了获得坐标空间波函数,做如下变换:
$$\psi ({ r}) = {\psi _{{m_j}}}({ r}) = \frac{1}{{{{(2\pi )}^{3/2}}}}\displaystyle\int {{\rm{d}}{{k}}{{\rm e}^{{\rm{i}}{{k}} \cdot {{r}}}}} {\psi _{{m_j}}}({{k}}){\text{。}}$$ (8) 假设
${\psi _{{m_j}}}({{k}})$ 具有如下形式$${\psi _{{m_j}}}( { r} ) = \sum\limits_{lj} {{f^{lj}}} (r){\phi _{lj{m_j}}}({\Omega _r}),$$ (9) 则得到波函数的径向部分
$${f^{lj}}(r) = {i^l}\sqrt {\frac{2}{p}} \sum\limits_{a = 1}^N {\sqrt {{w_a}} } {k_a}{j_l}({k_a}r){F^{lj}}({k_a}),$$ (10) 和径向密度分布
$$ {\rho _{{m_j}}}(r) = \sum\limits_{lj} {{f^{lj*}}} (r){f^{lj}}(r)\text{。} $$ (11) -
基于上面的理论公式,我们对31Ne进行了计算[22]。值得指出的是,2012年文献[27]采用复标度方法对31Ne进行过研究,2014年文献[15]在相对论平均场框架下采用耦合常数的解析延拓方法亦对31Ne中的晕现象进行了深入的研究。在图1中我们展示了采用CMR方法计算得到的31Ne单粒子能量随四极形变参数β2的变化情况,在该Nilsson能级图中共振态和束缚态分别用虚线和实线标记,β2=0代表球形核。
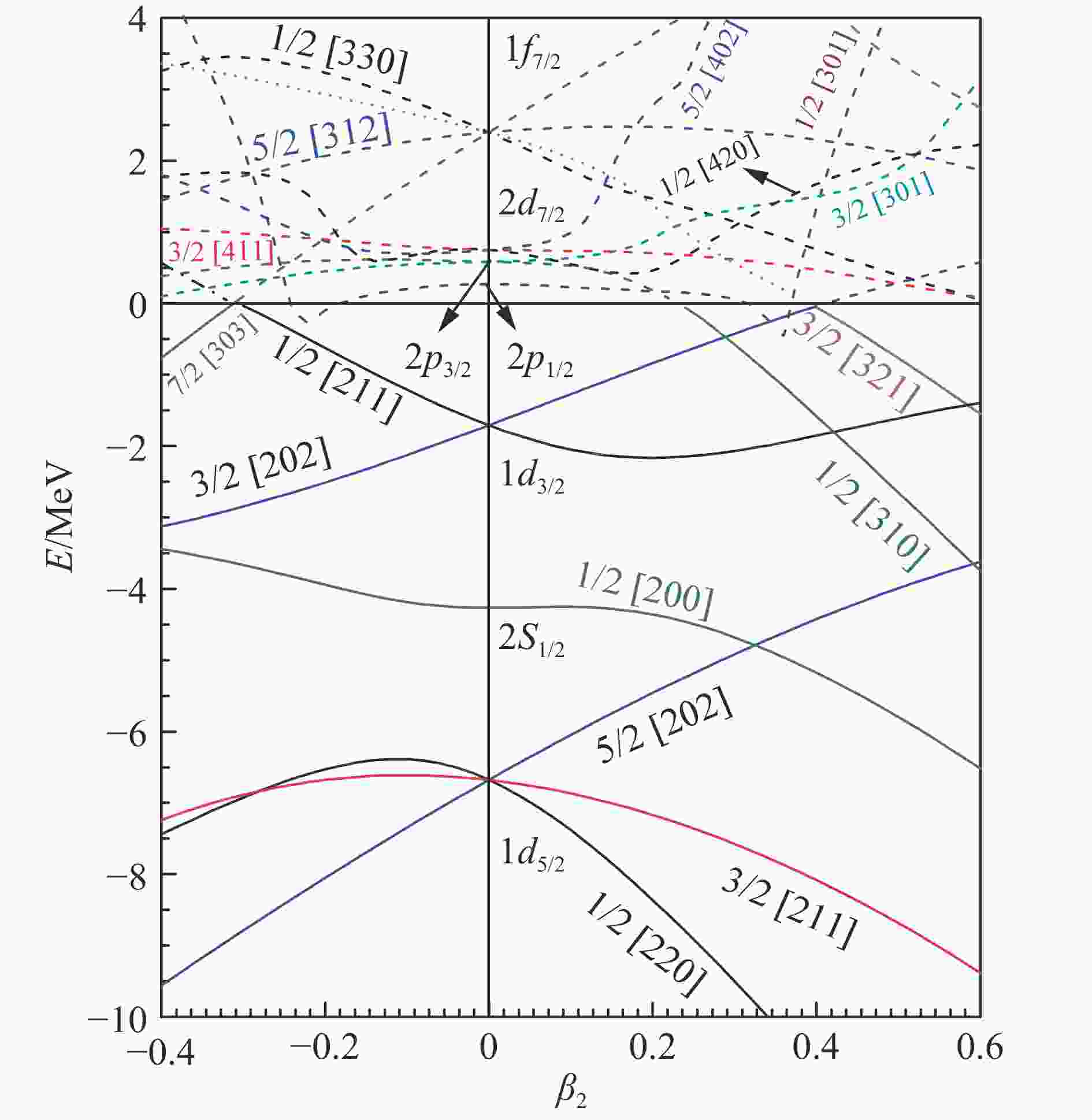
图 1 (在线彩图)计算得到的随四极形变系数β2变化的单粒子能量,本图取自文献[22]
我们可以看到所有的束缚态和文献[26]完全相同。对于共振态,在散射相移计算[26]中只得到1f7/2能级,在复标度计算[27]中得到了1f7/2, 1f5/2和1g9/2等共振能级,却仍未得到能级2p3/2, 2p1/2和2d5/2。在CMR模型的计算结果下,我们可以看到,当β2=0时,共振能级2p3/2,2p1/2和2d5/2的顺序排列与我们所熟知的壳模型结构顺序不同,即产生了p-f反转。核的能级次序与晕态的形成有关,晕态的形成使弱束缚态核子的低轨道角动量降低,形成能级反转。遗憾的是,1/2[301]和5/2[402]轨道由于计算数值的不收敛导致轨道反常增高。由于能级发生了反转,使得31Ne的最后一个中子占据在p轨道上,满足了晕形成的必要条件之一。当β2不等于0的时候,可以看到31Ne的第21个中子在不同的形变范围下分别占据不同的能级。考虑到单中子分离能的实验值,我们发现,31Ne的第21个中子在0.20
$\leqslant $ β2$\leqslant $ 0.29和0.40$\leqslant $ β2$\leqslant $ 0.59时分别占据在3/2[321]以及1/2[310]能级。为了进一步确定31Ne是否为晕核,我们画出了单粒子态1/2[310]和3/2[321]的主要组分占比与形变参数的关系。由图2可知,1/2[310]能级的波函数主要是由p3/2轨道贡献的,其占据几率高达64%。在图3中可以明显地观察到能级3/2[321]主要是由f7/2和p3/2轨道构成,p3/2轨道贡献依然很大。晕结构是由于具有较低分离能的价核子占据在l=0或l=1的轨道形成的,所以当价核子占据在能级1/2[310]和3/2[321]可能会形成晕。

图 2 (在线彩图)单粒子态1/2[310]的主要组分的占比与形变参数的变化关系,本图取自文献[22]
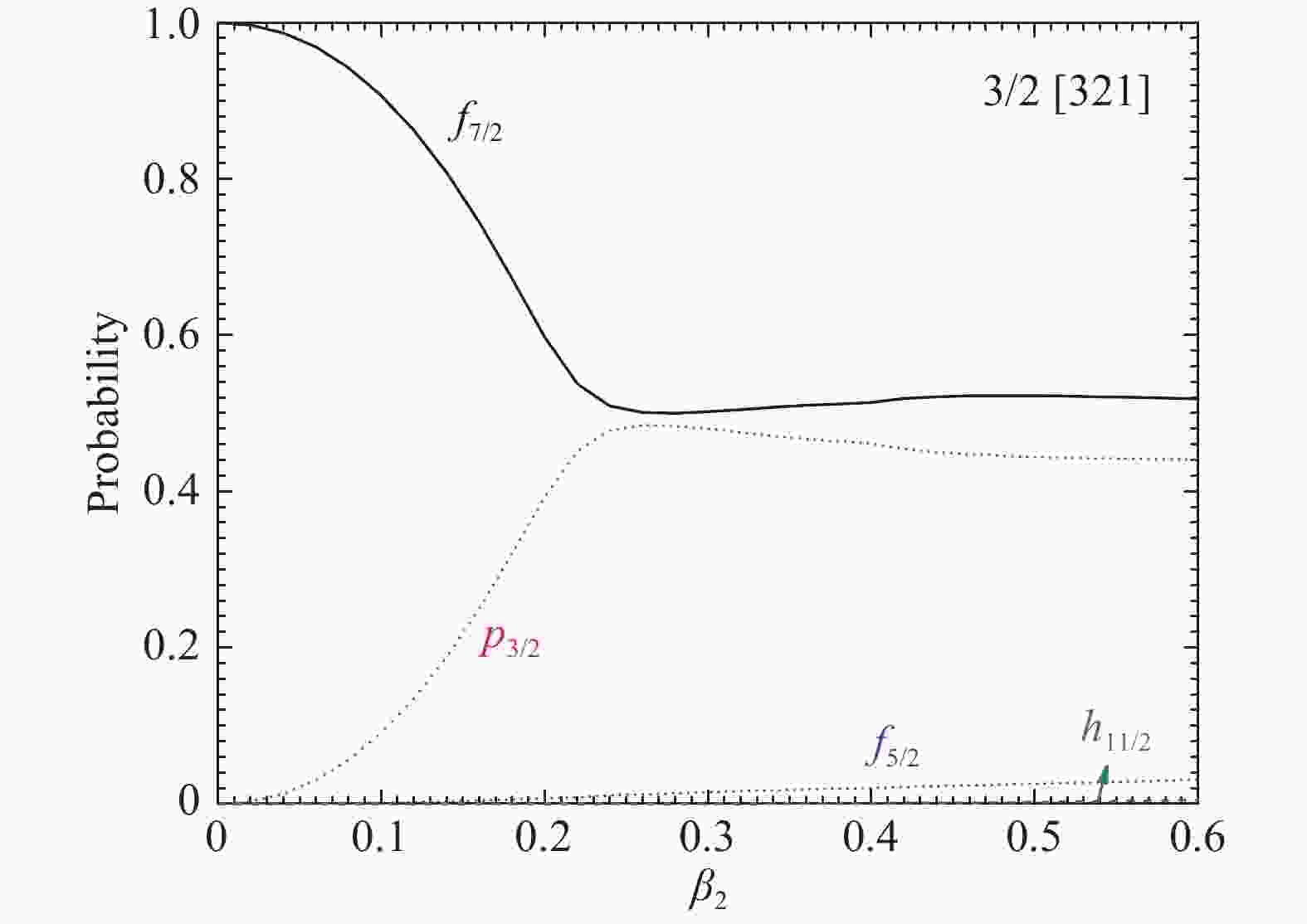
图 3 (在线彩图)单粒子态3/2[321]的主要组分的占比与形变参数的变化关系,本图取自文献[22]
在图4中我们还展示了坐标空间内不同积分路径下单粒子态1/2[310]的径向密度分布随半径的变化曲线。路径1代表k=0.0 fm–1,k=0.5–i0.2 fm–1,k=1.0 fm–1,k=3.0 fm–1四点构成的三角形路径。路径2代表k=0.0 fm–1,k=0.2–i0.6 fm–1,k=1.0 fm–1,k=3.0 fm–1四点构成的三角形路径。路径3代表k=0.0 fm–1,k=0.5–i0.6 fm–1,k=1.0 fm–1,k=3.0 fm–1四点构成的三角形路径。路径4代表k=0.0 fm–1,k=0.8–i0.6 fm–1,k=1.0 fm–1,k=3.0 fm–1四点构成的三角形路径。我们观察到,径向密度分布并不依赖于计算过程中的积分路径。考虑到31Ne的第21个中子在0.40
$\leqslant $ β2$\leqslant $ 0.59时占据1/2[310]能级,因此,单粒子态1/2[310]的形变参数β2定为0.25。我们发现此时的1/2[310]的径向密度分布较为弥散,这说明当最后一个粒子占据1/2[310]时,晕现象的出现是合理的。而单粒子态3/2[321]的径向密度也有类似的性质,详情可参看文献[22]。综上所得,31Ne可能是0.20$\leqslant $ β2$\leqslant $ 0.29或0.40$\leqslant $ β2$\leqslant $ 0.59的形变p波晕核。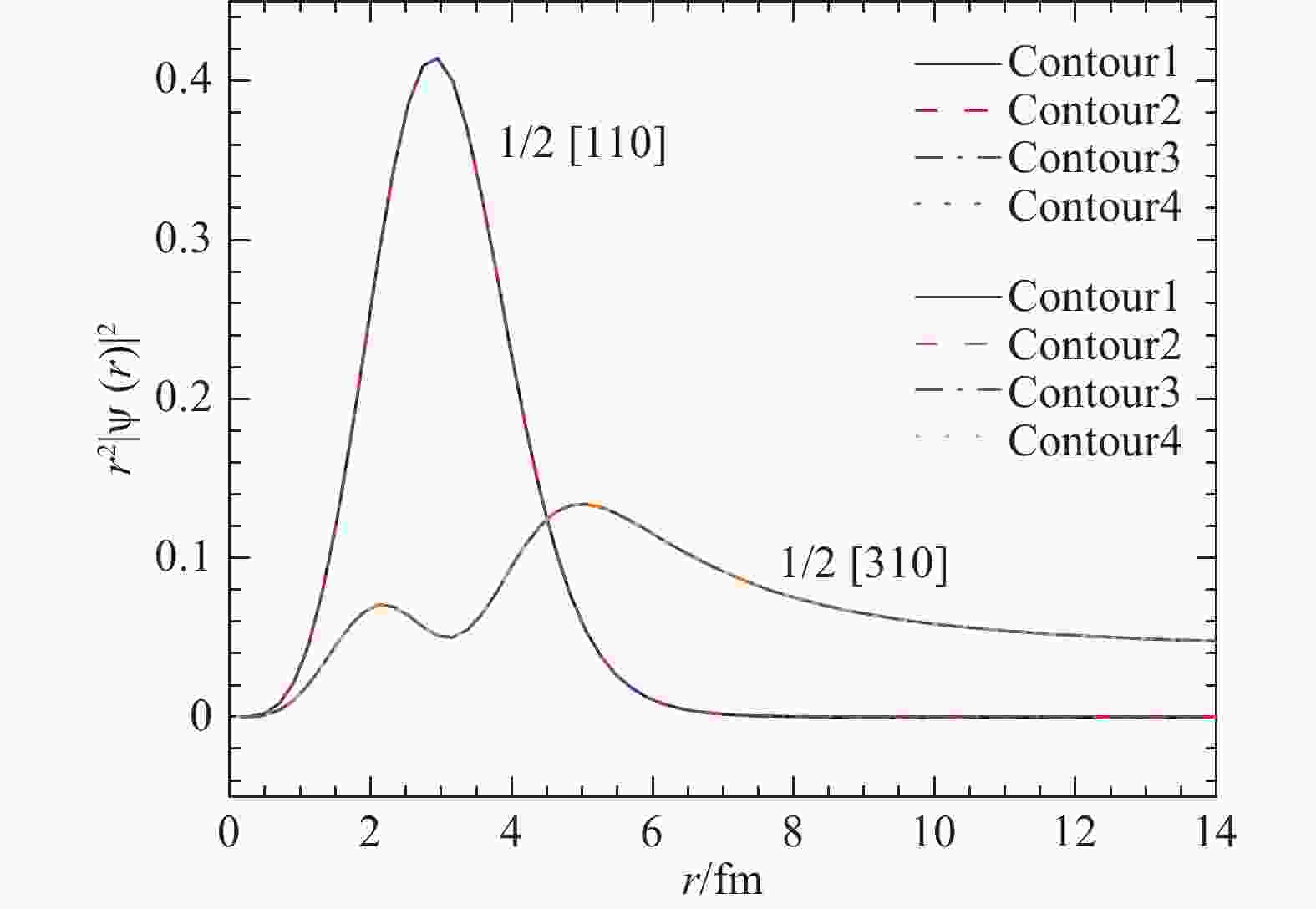
图 4 (在线彩图)单粒态1/2 [110]和1/2 [310]的径向密度随
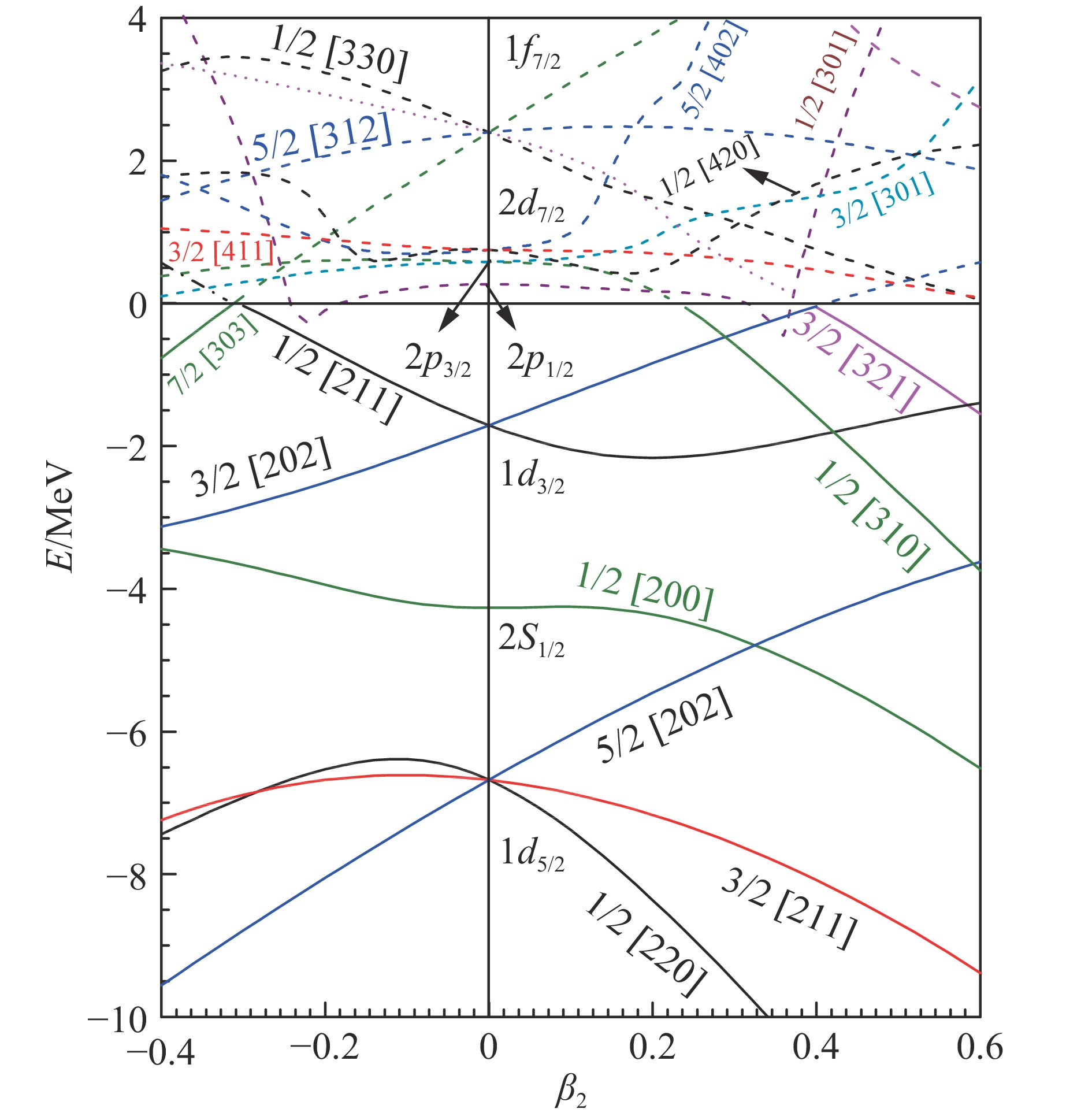
$r$ 的变化曲线,本图取自文献[22]采用上述分析方法,我们也研究了丰中子核19C,得到束缚态及共振态的能量随形变参数的变化关系、单粒子态主要组分的占比、密度分布及单中子分离能,结果表明19C的最后一个中子最有可能占据在0.20
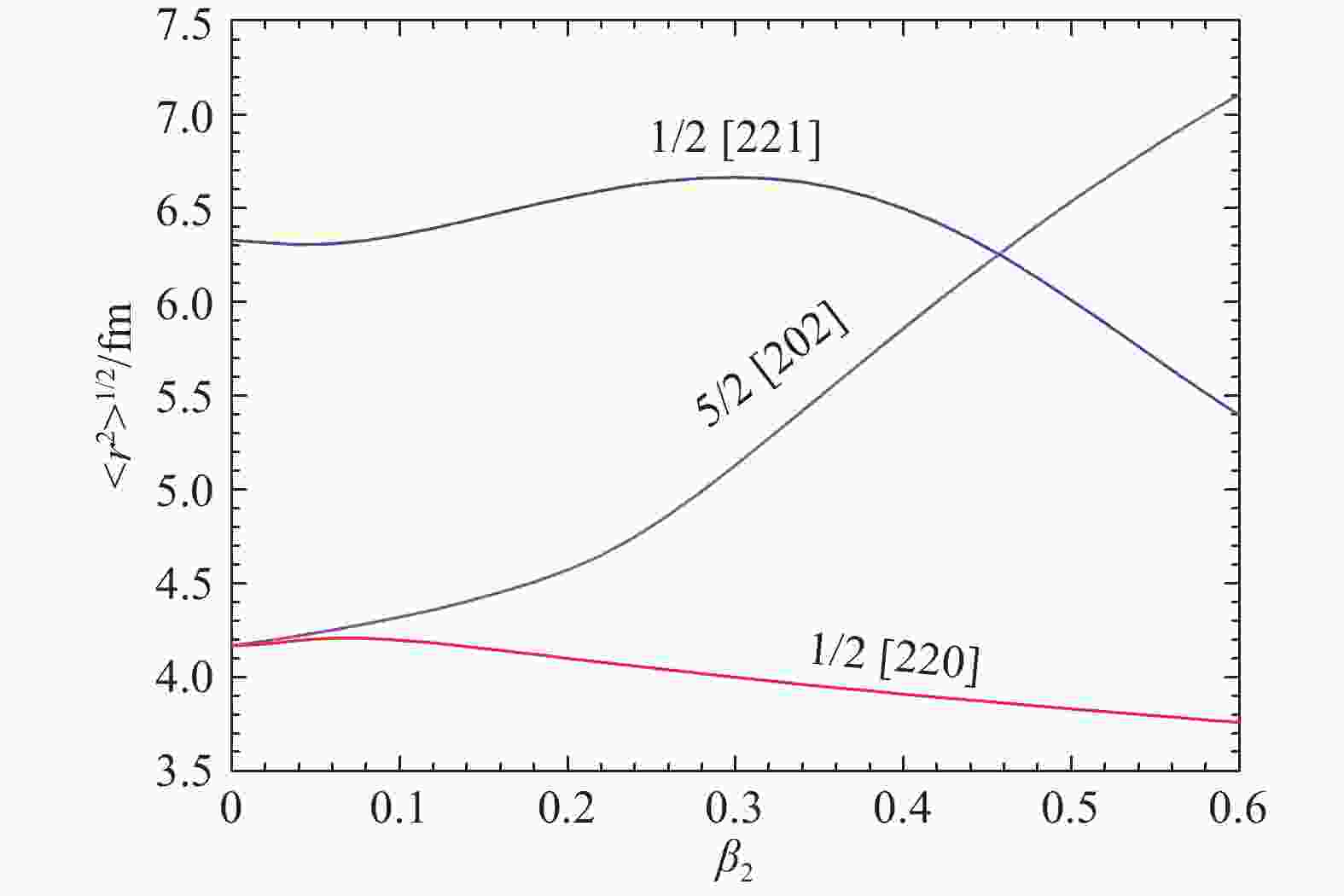
$\leqslant $ β2$\leqslant $ 0.40时的1/2 [211]能级。另外我们还在图5中展示了19C 中1/2 [211], 5/2[202], 1/2[220]能级的均方根半径随形变参数β2的变化情况。从图5我们发现1/2 [211]的方均根半径随着形变参数β2的变大略有降低,但在0.20$\leqslant $ β2$\leqslant $ 0.40形变范围内,其值均超过6.49 fm,远大于相邻能级方均根半径。综合考虑,19C最有可能是个β2介于0.2与0.4之间的长椭形变s波晕核,这与实验结果以及其它理论方法计算的结果相吻合。详细分析过程参考文献[23]。 -
目前,37Mg是实验上发现的最重的晕核,预测比37Mg更重的晕核得到了很多核理论工作者的关注。文献[28] 将坐标空间的对关联引入到相对论Hartree-Bogoliubov (RHB)计算,在计算中考虑连续谱的贡献,预言在Zr同位素中子滴线附近存在巨晕现象。文献[29]利用Woods-Saxon基发展了考虑连续谱贡献的形变RHB模型,很好地描述了形变晕等奇特现象,并预言了晕与核芯的形状退耦现象[29-30]。和稳定核相比,我们知道晕核具有一些特点,如:较大的物质均方根半径,较弥散的密度分布,离心势垒较低,价核子具有较小的分离能,反应总截面较大等。结合单中子分离能的实验结果进行分析,可以在核素图上寻找单中子分离能较小的丰中子核。然后通过详尽分析寻找可能存在的中子晕核。通过初步分析,我们发现77Fe、75Cr和53Ar这三个原子核具备晕核的一些特征。
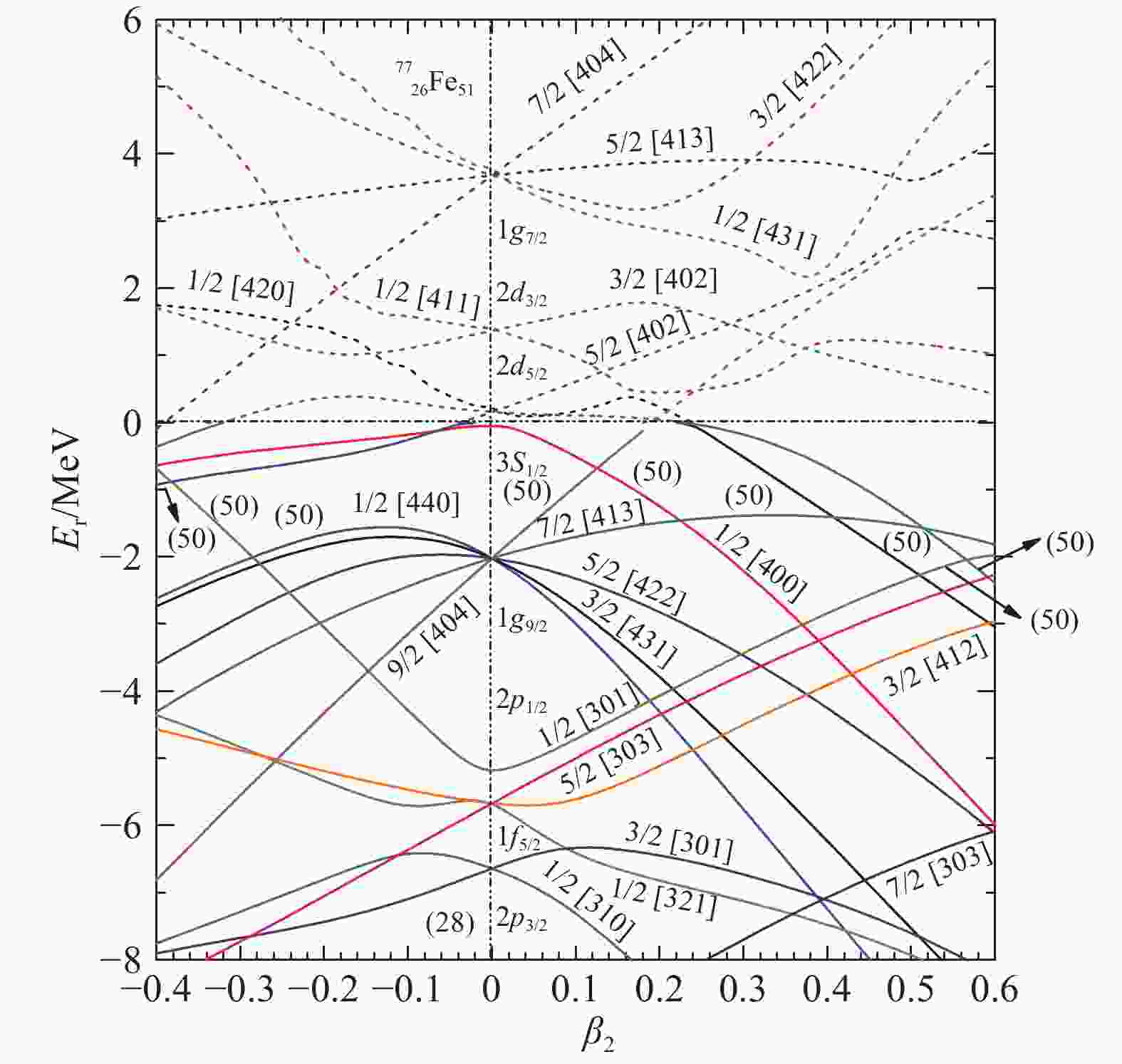
为了确定77Fe到底是不是晕核?我们经过计算得到了77Fe的Nillison能级图、单粒子态主要组分的占比和能级密度分布。从实验数据推测,77Fe的单中子分离能较小。另外根据图6,最后一个(第51个)中子占据在N=50(幻数)的壳的上方。这些让我们判定77Fe是个较好的候选晕核。而通过详尽分析,我们发现当-0.06
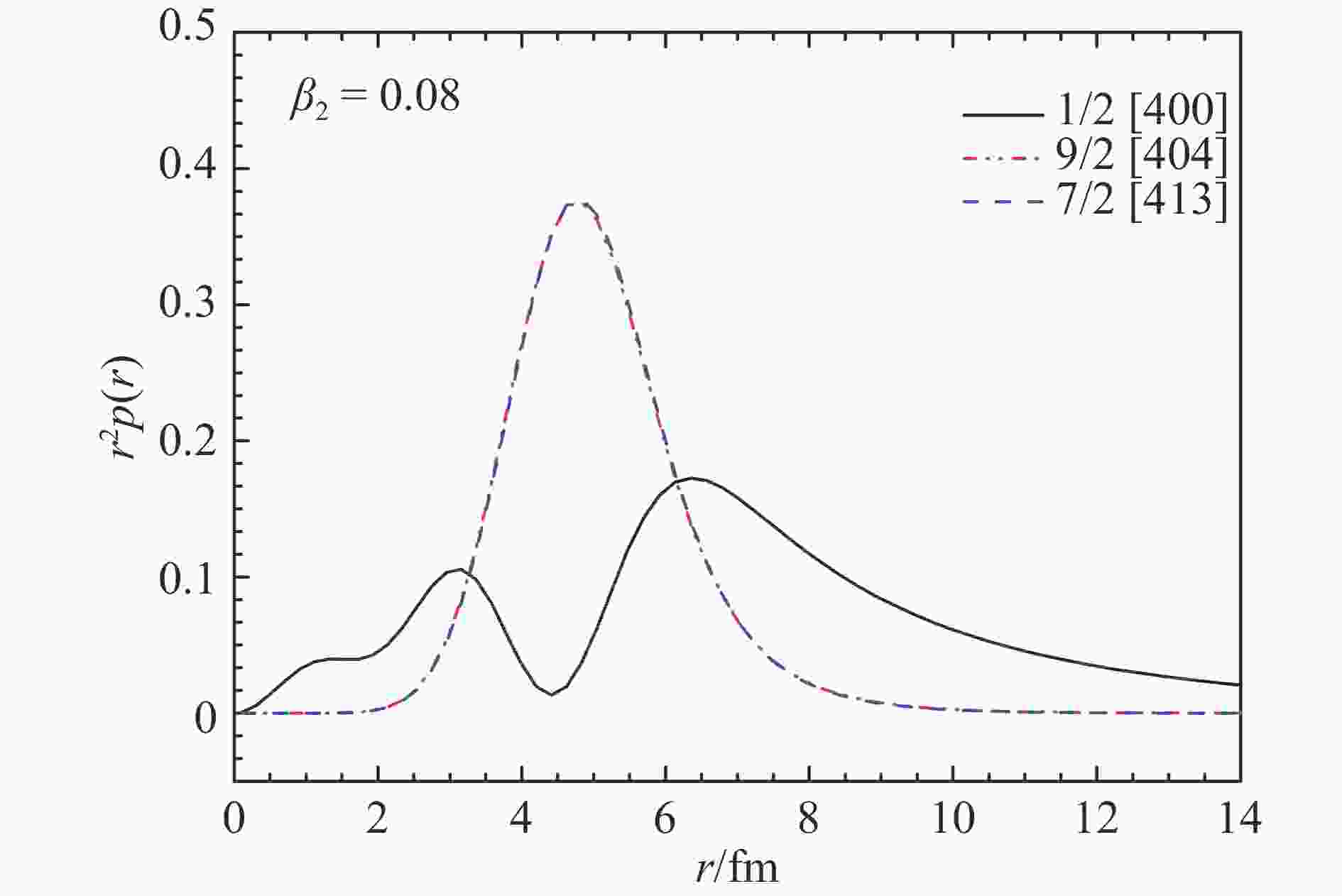
$\leqslant $ β2$\leqslant $ 0.13时,最后一个中子占据1/2[400],单中子分离能小于1.0 MeV,满足晕形成的条件。另外从图7中可以看见,与相邻束缚态9/2[404]和7/2 [413]比较,1/2[400]的径向密度更为弥散。这表明当价核子占据弱束缚能级1/2[400]时,晕的形成是很有可能的。而在其它形变区间,由于各种各样的原因,譬如说:分离能过大,单粒子能级主要组分轨道角动量较大,单粒子态的密度分布收敛较快等,不能满足晕的形成条件。75Cr和77Fe相比只是少了两个质子,它们之间的能级结构很相似。75Cr的最后一个中子在–0.12
$\leqslant $ β2$\leqslant $ 0.12范围内是占据在能级1/2[400]上的。我们分析75Cr可能是一个s波晕核。对于53Ar而言,在0$\leqslant $ β2$\leqslant $ 0.13时,最后一个中子占据1/2[321],单中子分离能小于1.0 MeV,满足晕形成的条件。而在其它形变区间,因为种种原因,不能满足晕的形成条件。更为细节的分析过程,可以参考文献[24]。 -
本文概述了采用复动量表象方法(CMR)方法对共振态的研究。给出了详细理论公式,计算获得了31Ne、19C以及比37Mg更重的核(77Fe、75Cr和53Ar)的单粒子能级图,以及单粒子态主要组分的占比随形变参数β2变化的曲线以及径向密度分布。揭示了31Ne和19C晕形成的物理机制,预测了比37Mg更重的核(77Fe、75Cr和53Ar)可能形成的晕结构。31Ne最后一个中子在0.20
$\leqslant $ β2$\leqslant $ 0.29或0.40$\leqslant $ β2$\leqslant $ 0.59区间内是占据在1/2[310]能级或3/2 [321]能级上,支持p波晕的形成。在19C最后一个中子在0.2$\leqslant $ β2$\leqslant $ 0.4形变范围内是占据在1/2[211]能级上的,从能级成分占比可以判定其为s波晕。接下来,还预测77Fe、75Cr和53Ar可能存在的晕结构。得到77Fe(75Cr)可能是在–0.06$\leqslant $ β2$\leqslant $ 0.13(–0.12$\leqslant $ β2$\leqslant $ 0.12)的s波晕核,而53Ar可能是0.09$\leqslant $ β2$\leqslant $ 0.13的p波晕核。这一预测对在实验中寻找较重的晕核具有一定的参考价值。下一步,我们计划发展原子核中的协变密度泛函理论(CDFT),将CMR和CDFT结合,建立统一描述束缚态、共振态和连续谱的CDFT-CMR理论,研究原子核的单粒子运动,获得单粒子共振态的信息,揭示奇特核的壳层结构及其演化规律;进一步考虑对关联,考虑束缚态和共振态的耦合,探索形变、对关联、共振态及其与束缚态的耦合在奇特现象的形成中所扮演的角色,弄清晕、能级反转、幻数移动等奇特现象的物理机制。
Study on Halo Phenomenon in Exotic Nuclei by Complex Momentum Representation Method
-
摘要: 晕现象的研究使人们对核结构有了新的认识。连续谱,尤其是连续谱中的共振态在其中扮演着重要角色。复动量表象(CMR)方法不仅能够统一描述束缚态、共振态和连续谱,而且能够很好地描述窄共振和宽共振。本文介绍了CMR方法对原子核共振态的研究。给出了31Ne和19C等核的束缚态和共振态的单粒子能量随形变参数β2的变化规律,分析了19C和31Ne中单中子晕形成的物理机制和在中子数N=20附近能级反转的原因,并预测了比37Mg重的核中的单中子晕现象,这一预测结果对在实验中寻找较重的晕核具有一定的参考价值。这些研究表明CMR 方法不仅适用于描述稳定核,也适用于描述具有弥散物质分布的奇特核。Abstract: The study of halo phenomenon gives us a new understanding of nuclear structure, in which the continuum, especially the resonance in the continuum, plays an important role. The complex momentum representation (CMR) method can not only describe the bound state, resonant state and continuous spectrum uniformly, but also describe the narrow and wide resonance well. In this paper, the CMR method is introduced for the study of nuclear resonance. The single particle energy of bound state and resonance state of 31Ne and 19C with deformation parameter β2 is given. The physical mechanism of halo formation in 19C and 31Ne and the reason of energy level inversion near the neutron number N=20 are analyzed. The halo phenomenon in nuclei heavier than 37Mg is predicted. The result of this prediction is helpful to find heavier halo nuclei in experiments. These studies show that the CMR method is suitable for describing not only stable nuclei, but also exotic nuclei with diffuse material distribution.
-
图 1 (在线彩图)计算得到的随四极形变系数β2变化的单粒子能量,本图取自文献[22]
图 2 (在线彩图)单粒子态1/2[310]的主要组分的占比与形变参数的变化关系,本图取自文献[22]
图 3 (在线彩图)单粒子态3/2[321]的主要组分的占比与形变参数的变化关系,本图取自文献[22]
图 4 (在线彩图)单粒态1/2 [110]和1/2 [310]的径向密度随
$r$ 的变化曲线,本图取自文献[22] -
[1] TANIHATA I, HAMAGAKI H, HASHIMOTO O, et al. Phys Rev Lett, 1985, 55: 2676. doi: 10.1103/PhysRevLett.55.2676 [2] MENG J, TOKI H, ZHOU S G, et al. Prog Part Nucl Phys, 2006, 57(2): 470. doi: 10.1016/j.ppnp.2005.06.001 [3] 孟杰, 郭建友, 李剑, 等. 物理学进展, 2011, 31: 1. MENG J, GUO J Y, LI J, et al. Prog Phys, 2011, 31: 1. (in Chinese) [4] TANIHATA I, SAVAJOLS H, KANUNGO R. Prog Part Nucl Phys, 2013, 68: 215. doi: 10.1016/j.ppnp.2012.07.001 [5] MENG J, ZHOU S G. Journal of Physics G: Nuclear and Particle Physics, 2015, 42(9): 093101. doi: 10.1088/0954-3899/42/9/093101 [6] MENG J, TOKI H, ZENG J Y, et al. Phys Rev C, 2002, 65: 041302. doi: 10.1103/PhysRevC.65.041302 [7] SUN X X, ZHAO J, ZHOU S G. Phys Lett B, 2018, 785: 530. doi: 10.1016/j.physletb.2018.08.071 [8] HAMAMOTO I. Phys Rev C, 2016, 93(5): 054328. doi: 10.1103/PhysRevC.93.054328 [9] LU B N, ZHAO E G, ZHOU S G. Phys Rev Lett, 2012, 109(7): 072501. doi: 10.1103/PhysRevLett.109.072501 [10] LU B N, ZHAO E G, ZHOU S G. Phys Rev C, 2013, 88(2): 024323. doi: 10.1103/PhysRevC.88.024323 [11] MATSUO M. Nucl Phys A, 2001, 696(3-4): 371. doi: 10.1016/S0375-9474(01)01133-2 [12] SUN T T, ZHANG S Q, ZHANG Y, et al. Phys Rev C, 2014, 90(5): 054321. doi: 10.1103/PhysRevC.90.054321 [13] TANAKA N, SUZUKI Y, VARGA K. Phys Rev C, 1997, 56(1): 562. doi: 10.1103/PhysRevC.56.562 [14] ZHANG S S, SMITH M S, ARBANAS G, et al. Phys Rev C, 2012, 86(3): 032802. doi: 10.1103/PhysRevC.86.032802 [15] ZHANG S S, SMITH M S, KANG Z S, et al. Phys Lett B, 2014, 730: 30. doi: 10.1016/j.physletb.2014.01.023 [16] ZHANG L, ZHOU S G, MENG J, et al. Phys Rev C, 2008, 77(1): 014312. doi: 10.1103/PhysRevC.77.014312 [17] ZHOU S G, MENG J, ZHAO E G. Phys B: At, Mol Opt Phys, 2009, 42(24): 245001. doi: 10.1088/0953-4075/42/24/245001 [18] MYO T, KIKUCHI Y, MASUI H, et al. Prog Part Nucl Phys, 2014, 79: 1. doi: 10.1016/j.ppnp.2014.08.001 [19] GUO J Y, FANG X Z, JIAO P, et al. Phys Rev C, 2010, 82(3): 034318. doi: 10.1103/PhysRevC.82.034318 [20] LI N, SHI M, GUO J Y, et al. Phys Rev Lett, 2016, 117(6): 062502. doi: 10.1103/PhysRevLett.117.062502 [21] 郭建友, 刘泉, 牛中明, 等. 原子核物理评论, 2018, 35(4): 401. doi: 10.11804/NuclPhysRev.35.04.401 GUO J Y, LIU Q, NIU Z M. Nucl Phys Rev, 2018, 35(4): 401. (in Chinese) doi: 10.11804/NuclPhysRev.35.04.401 [22] TIAN Y J, LIU Q, HENG T H, et al. Phys Rev C, 2017, 95: 064329. doi: 10.1103/PhysRevC.95.064329 [23] CAO X N, LIU Q, GUO J Y. J Phys G, 2018, 45: 085105. doi: 10.1088/1361-6471/aad0bf [24] CAO X N, LIU Q, GUO J Y. Phys Rev C, 2019, 99: 014309. doi: 10.1103/PhysRevC.99.014309 [25] HAMAMOTO I. Phys Rev C, 2005, 72(2): 024301. doi: 10.1103/PhysRevC.72.024301 [26] HAMAMOTO I. Phys Rev C, 2010, 81(2): 021304. doi: 10.1103/PhysRevC.81.021304 [27] LIU Q, GUO J Y, NIU Z M, et al. Phys Rev C, 2012, 86(5): 054312. doi: 10.1103/PhysRevC.86.054312 [28] MENG J, RING P. Phys Rev Lett, 1998, 80(3): 460. doi: 10.1103/PhysRevLett.80.460 [29] ZHOU S G, MENG J, RING P, et al. Phys Rev C, 2010, 82(1): 011301. doi: 10.1103/PhysRevC.82.011301 [30] LI L, MENG J, RING P, et al. Phys Rev C, 2012, 85(2): 024312. doi: 10.1103/PhysRevC.85.024312 -





 下载:
下载:




























































 甘公网安备 62010202000723号
甘公网安备 62010202000723号