-
To investigate properties of nuclei far from stability and neutron-star-like objects in heaven, the concept asymmetric nuclear matter holding unequal numbers of neutron and proton is frequently mentioned. To describe the properties of asymmetric nuclear matter, the equation of state of nuclear matter is frequently used. The equation of state (EoS) of nuclear matter at density
$ \rho $ and isospin asymmetry$ \delta $ ($ \delta=(\rho_{\rm n}-\rho_{\rm p})/(\rho_{\rm n}+\rho_{\rm p}) $ ) usually reads as[1-3]$$ \begin{array}{l} E(\rho ,\delta ) = E(\rho ,0)+E_{\rm{sym}}(\rho )\delta ^{2}+{\cal{O}} (\delta ^{4}), \end{array} $$ (1) where
$ E_{\rm{sym}}(\rho) $ is the nuclear symmetry energy. Apparently, the nuclear symmetry energy describes the change of the single nucleonic energy of nuclei or nuclear matter when replacing protons with neutrons. The EoS of isospin symmetric nuclear matter$ E(\rho, 0) $ is relatively well constrained[4] while the EoS of isospin asymmetric nuclear matter, especially the high-density symmetry energy, as shown in Fig. 1, is still a subject of debate[5-11].The nuclear symmetry energy not only plays crucial roles in nuclear physics[2-3] but also, in a density range of 0.1~10 times nuclear saturation density, affects the birth of neutron stars and supernova neutrinos[12], the cooling rates and the thickness of the crust of neutron stars, the mass-radius relationship and the moment of inertia of neutron stars[13-17]. The nuclear symmetry energy also plays important roles in the evolution of core-collapse supernova[18] and astrophysical r-process nucleosynthesis[19-22], the gravitational-wave frequency[23-24] and the gamma-ray bursts[25] in neutron star mergers[26-27].
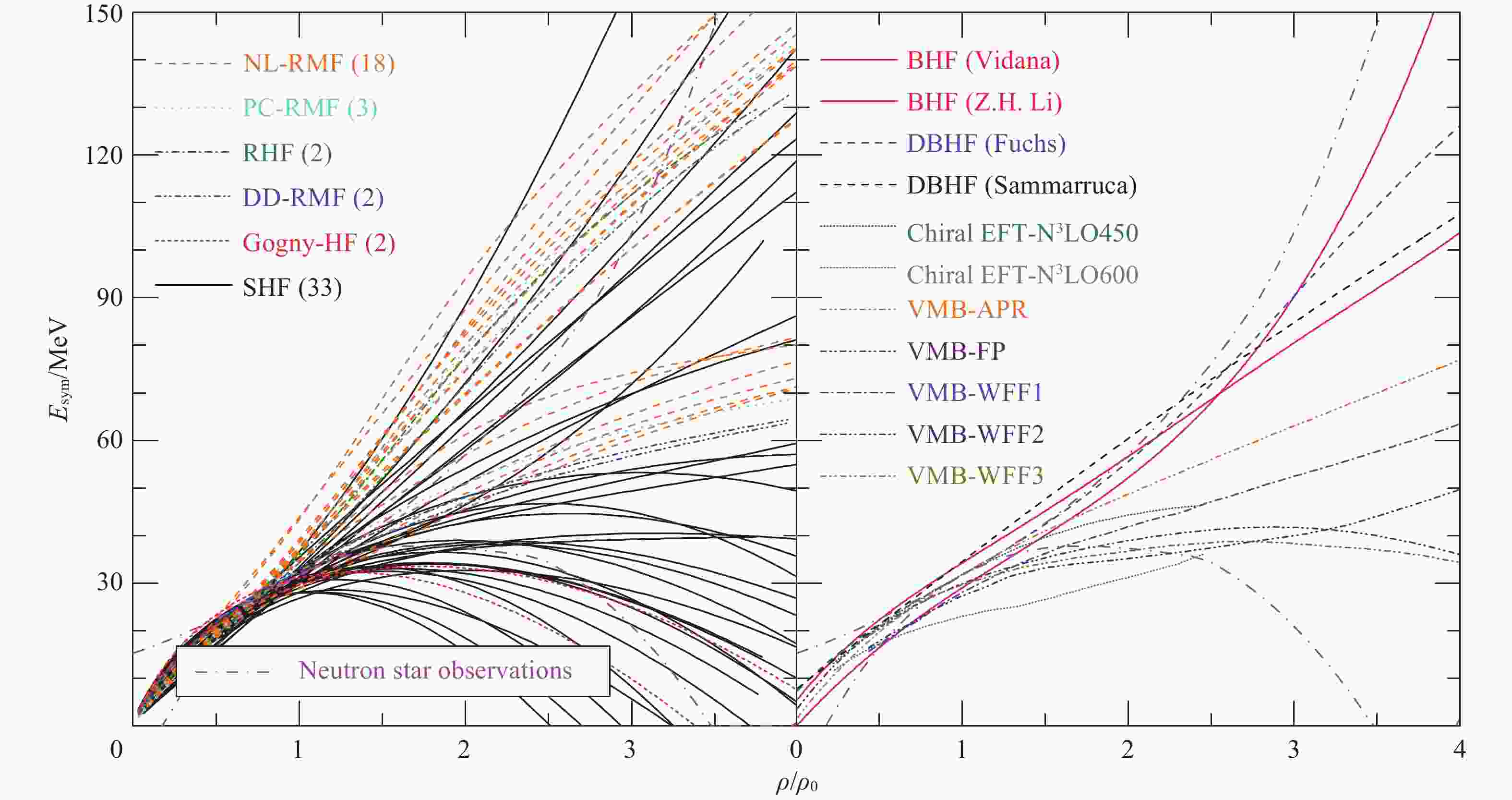
Figure 1. (color online)Nuclear symmetry energy given by different nuclear many-body approaches in comparison with the constraining boundaries extracted from studying properties of neutron stars. Taken from Ref. [6].
Around saturation density both the value of the nuclear symmetry energy [about (31.7±3.2) MeV] and the magnitude of its slope [about (58.7±28.1) MeV] have been roughly determined from a series of concerning analyses[28-29]. While recent studies on nuclear experimental measurements from the FOPI and FOPI-LAND by different groups give divergent high-density symmetry energies[30-35]. The in-medium effects[36-38], the isospin dependence of strong interactions[39], the short-range correlations[40-41] may affect the interpretation of nuclear experimental data by transport models.
The high-density symmetry energy could be roughly constrained by studying neutron-star merger event GW1760817 since it plays a role in the deformation of dense nuclear matter in neutron-star merger event[6]. To confine the high-density symmetry energy more directly, currently many terrestrial experiments are being carried out using a wide variety of advanced facilities, as done at the GSI Facility for Antiproton and Ion Research (FAIR) in Germany[42], the Cooling Storage Ring on the Heavy Ion Research Facility HIRFL-CSR at IMP in China[43] and the Facility for Rare Isotope Beams (FRIB) in the Untied States[44], the Radioactive Isotope Beam Facility (RIBF) at RIKEN in Japan[45-47] and the Rare Isotope Science Project (RISP) in Korea[48].
-
The Boltzmann-Uehling-Uhlenbeck (BUU) equation denotes time evolution of single particle phase space distribution function
$ f({{r}},{{p}},t) $ , which reads[49]$$ \begin{aligned} \frac{\partial f}{\partial t}+\nabla_{{{p}}}E\cdot\nabla_{{{r}}}f-\nabla_{{{r}}}E\cdot\nabla_{{{p}}}f = I_{\rm c}. \end{aligned} $$ (2) The left-hand side of Eq. (2) describes time evolution of the particle phase space distribution function due to its transport and mean field, and the right-hand side accounts for the modification of the phase space distribution function by elastic and inelastic two body collisions.
$ E $ denotes a particle's total energy, which is equal to kinetic energy$ E_{\rm kin} $ plus its average potential energy$ U $ . The mean-field potential$ U $ of the single particle depends on its position and momentum of the particle as well as its local asymmetry of medium and is given self-consistently by its phase space distribution function$ f({{r}},{{p}},t) $ . The BUU model is one of the most extensively used transport models which describes nucleus-nucleus collisions at different energy regions. At intermediate energies, its main ingredients are single particle potential and particle-particle scattering cross sections as well as pauli-blockings of fermions.To study the effects of symmetry energy in heavy-ion collisions, isospin dependence is extensively involved into different parts of the BUU transport model. The isospin- and momentum-dependent single nucleon mean-field potential reads[2, 50]
$$ \begin{aligned} U(\rho,\delta,{{p}},\tau) =& A_u(x)\frac{\rho_{\tau'}}{\rho_0}+A_l(x)\frac{\rho_{\tau}}{\rho_0}+\\ &B\Big(\frac{\rho}{\rho_0}\Big)^{\sigma}(1-x\delta^2)-8x\tau\frac{B}{\sigma+1} \frac{\rho^{\sigma-1}}{\rho_0^\sigma}\delta\rho_{\tau'}+\\ &\frac{2C_{\tau,\tau}}{\rho_0} \int {\rm d}^3\,p'\frac{f_\tau({{r}},{{p^{'}}})}{1+({{p}}-{{p^{'}}})^2/\Lambda^2}+\\ &\frac{2C_{\tau,\tau'}}{\rho_0} \int {\rm d}^3\,p'\frac{f_{\tau'}({{r}},{{p^{'}}})}{1+({{p}}-{{p^{'}}})^2/\Lambda^2}, \\[-17pt]\end{aligned} $$ (3) where
$ \rho_0 $ denotes the saturation density,$ \tau, \tau' $ =1/2(−1/2) is for neutron (proton).$ \rho_{\rm n} $ ,$ \rho_{\rm p} $ denote neutron and proton densities, respectively. The parameter values$ A_u(x) $ =33.037–125.34$ x $ MeV,$ A_l(x) $ =–166.963+ 125.34$ x $ MeV,$ B $ =141.96 MeV,$ C_{\tau,\tau} $ =18.177 MeV,$ C_{\tau,\tau'} $ =–178.365 MeV,$\sigma$ =1.265, and$\Lambda$ =630.24 MeV/c. With these settings, the empirical values of nuclear matter at normal density are reproduced, i.e., the saturation density$ \rho_{0} $ =0.16 fm–3, the binding energy$ E_{0} $ = –16 MeV, the incompressibility$ K_{0} $ = 230 MeV[29, 51], the isoscalar effective mass$m_{\rm s}^{*} = 0.7\; m$ [52], the single-particle potential$ U^{0}_{\infty} $ =75 MeV at infinitely large nucleon momentum at saturation density in symmetric nuclear matter, the symmetry energy$E_{\rm sym}(\rho_0)$ =30 MeV[53]. In Eq. (3), different symmetry energy's stiffness parameters$ x $ can be used in different density regions to mimic different density-dependent symmetry energies. Fig. 2 shows the used symmetry energy derived from the single particle potential Eq. (3) with different$ x $ parameters at low and high densities.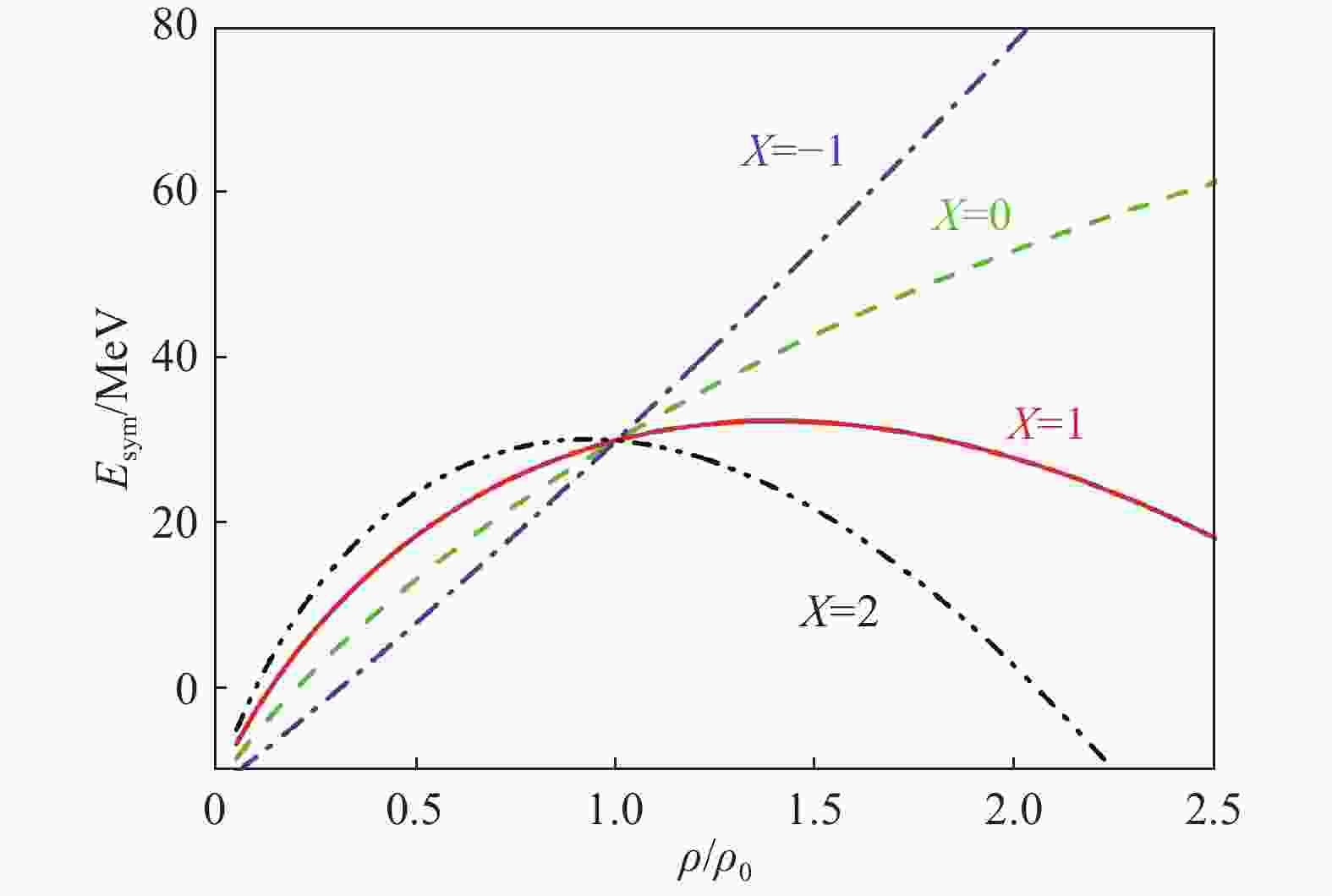
Figure 2. (color online)Density-dependent symmetry energy with different
$ x $ parameters. Taken from Ref. [53].The isospin-dependent baryon-baryon (BB) scattering cross section in medium
$ \sigma _{\rm BB}^{\rm medium} $ is reduced compared with their free-space value$ \sigma _{\rm BB}^{\rm free} $ by a factor of[53-54]$$ \begin{split} R^{\rm BB}_{\rm medium}(\rho,\delta,{{p}})\equiv & \sigma _{{\rm BB}_{\rm elastic, inelastic}}^{\rm medium}/\sigma _{{\rm BB}_{\rm elastic, inelastic}}^{\rm free}\\ =& (\mu _{\rm BB}^{\ast }/\mu _{\rm BB})^{2}, \end{split} $$ (4) where
$ \mu _{\rm BB} $ and$ \mu _{\rm BB}^{\ast } $ are the reduced masses of the colliding baryon pairs in free space and medium, respectively. The effective mass of baryon in isospin asymmetric nuclear matter is expressed as[53]$$ \begin{aligned} \frac{m_{\rm B}^{\ast }}{m_{\rm B}} = 1\Big/\Big(1+\frac{m_{\rm B}}{p}\frac{ {\rm d} U}{{\rm d} p}\Big). \end{aligned} $$ (5) More details on the present used model can be found in Ref. [53].
-
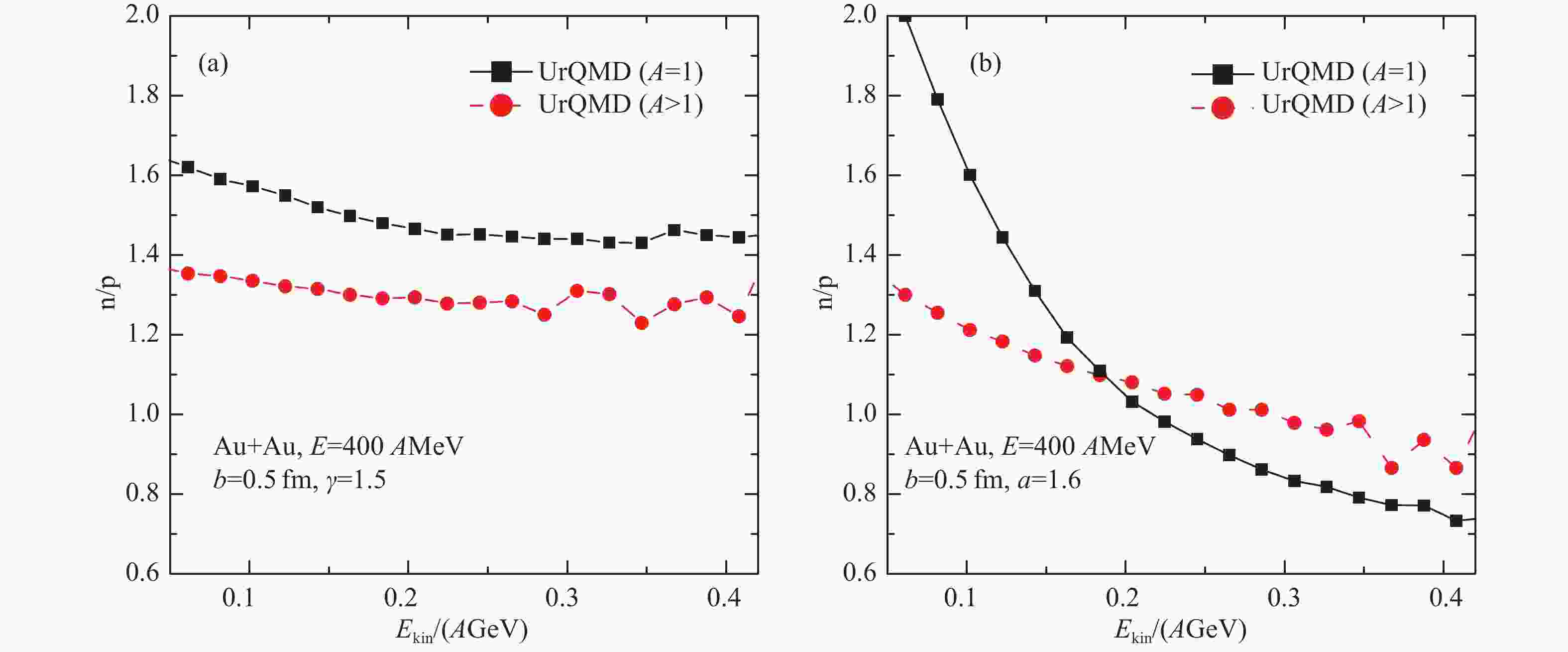
To constrain the density-dependent symmetry energy by heavy-ion collisions, symmetry energy sensitive probes are usually used as counterparts to compare with relevant experimental data. Since the symmetry potential has opposite actions for neutrons and protons and the value of symmetry potential is always quite small compared to the isoscalar potential, to enlarge the effects of symmetry energy, most observables in fact use differences or ratios of isospin multiplets of baryons, mirror nuclei and mesons, such as the neutron/proton ratio, neutron-proton differential flow, neutron-proton correlation function, t/3He,
$ \pi ^{-}/\pi ^{+} $ ,$ \Sigma ^{-}/\Sigma ^{+} $ and$ K^{0}/K^{+} $ ratios, etc[2-3].Squeezed-out nucleons emitted in the direction of perpendicular to the reaction plane in semi-central heavy-ion collisions carry more information on the property of dense matter. Fig. 3 demonstrates transverse momentum dependent neutron/proton ratio of mid-rapidity nucleons emitted in the direction perpendicular to the reaction plane[55]. It is seen in panel (b) that the symmetry energy effect on the n/p ratio increases with the increasing transverse momentum
$ p_{\rm t} $ and the effect can be as high as 40% at high transverse momenta. The high$ p_{\rm t} $ nucleons most likely originate from the high density region in the early stage in heavy-ion collisions thus is more sensitive to the high-density symmetry energy. The n/p ratio of free nucleons at mid-rapidity without azimuthal angle cut (shown in panel (a)) is much less sensitive to the symmetry energy[55].It is practically difficult to measure observables involving neutrons. One question frequently being asked is whether the triton-3He (t-3He) pair may carry the information of nuclear symmetry energy. It is normally difficult to extract reliable information about the symmetry energy from the individual flows of triton and 3He clusters. To decrease effects of the isoscalar potential while enhancing effects of the isovector potential are helpful. Fig. 4 shows the triton-3He relative and differential flows as a function of rapidity[56]. From panel (a) of Fig. 4, it is shown that the triton-3He relative flow is very sensitive to the symmetry energy. Effects of the symmetry energy on the differential flow are shown in panel (b), is relatively small. Therefore triton-3He relative flow is a potential probe used to detect the symmetry energy in heavy-ion collisions.
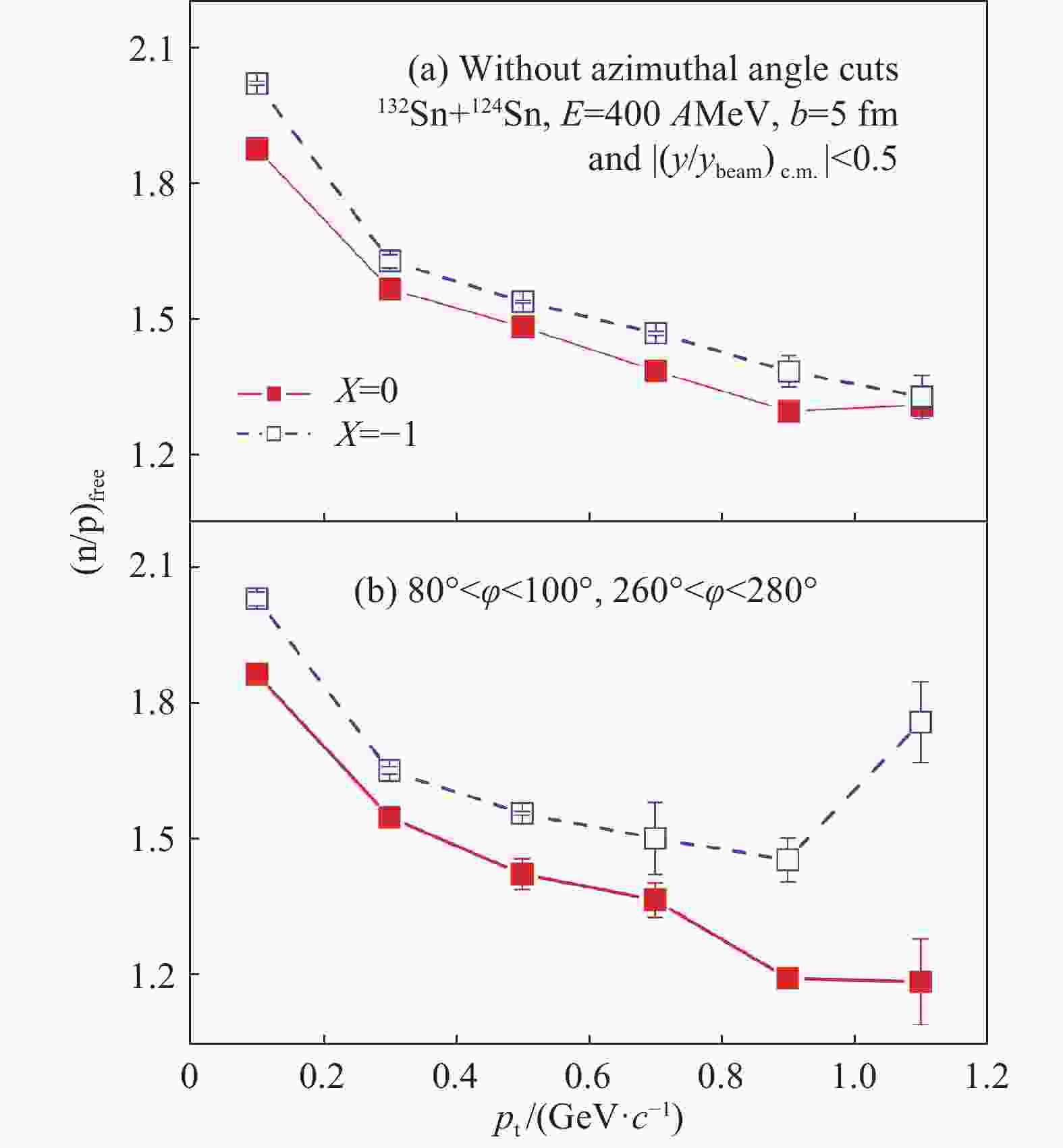
Figure 3. (color online)Effects of symmetry energy on the non-squeezed-out (panel (a)) and squeezed-out (panel (b)) neutron to proton ratios in 132Sn+124Sn reaction at
$ 400 $ AMeV. Taken from Ref. [55]. 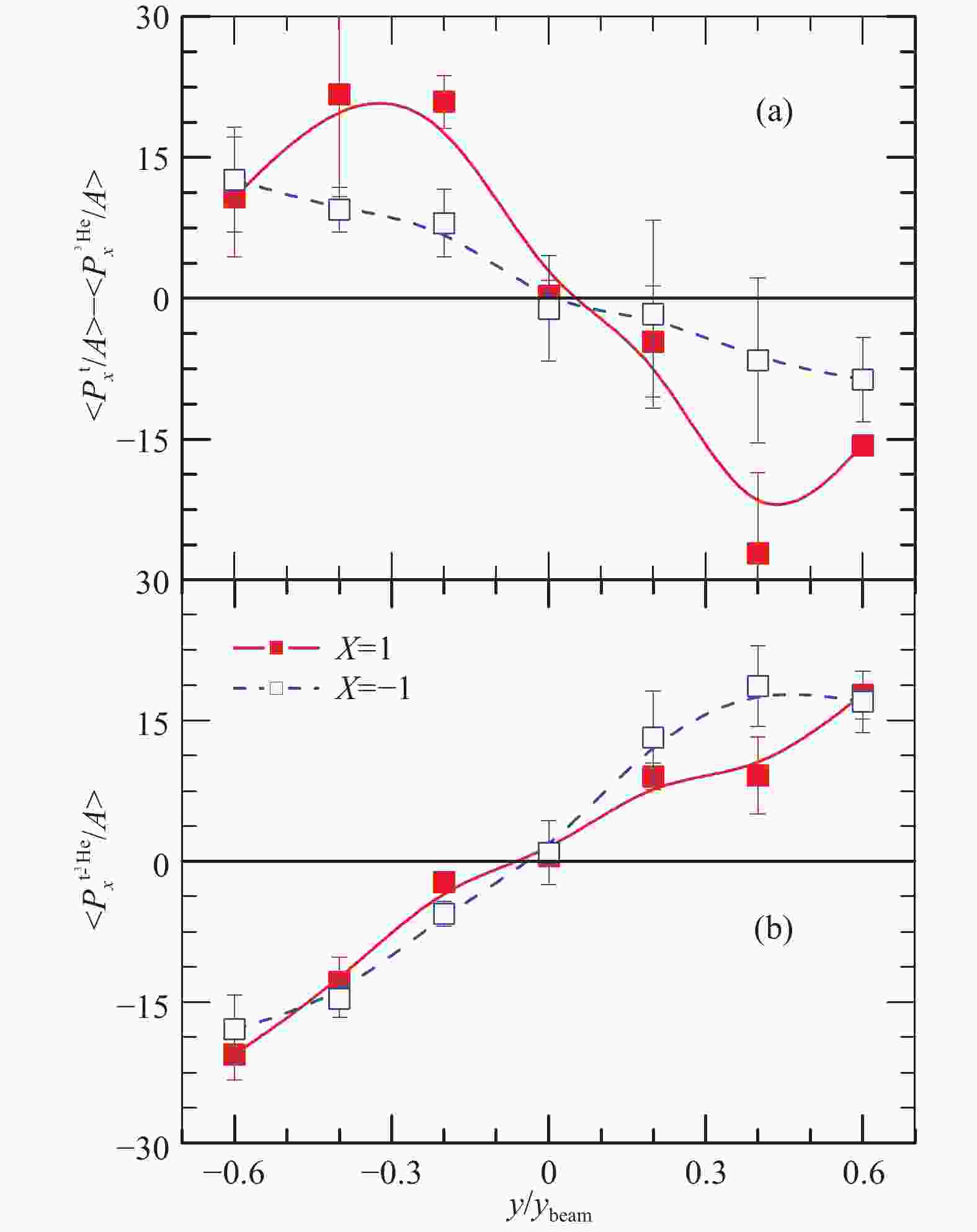
Figure 4. (color online)Effects of symmetry energy on the triton-3He relative (panel (a)) and differential (panel (b)) flows as a function of rapidity in the semi-central reaction of 132Sn+124Sn at 400 AMeV. Taken from Ref. [56].
Charged
$ \pi^-/\pi^+ $ ratio is another sensitive probe of nuclear symmetry energy. Shown in Fig. 5 is$ (\pi^-/\pi^+)_{\rm like} $ ratio (=$ \frac{\pi^-+\Delta^-+\frac{1}{3}\Delta^0} {\pi^++\Delta^{++}+\frac{1}{3}\Delta^+} $ ) as a function of time[57]. Due to more neutron-neutron scatterings than that of proton-proton when two neutron skins start overlapping at the beginning of the reaction, the value of the$ (\pi^-/\pi^+)_{\rm like} $ ratio soars in the early stage of the reaction. The$ (\pi^-/\pi^+)_{\rm like} $ ratio saturates at about 25 fm/$ c $ indicating that a chemical freeze-out stage has been reached. The sensitivity to the symmetry energy is clearly shown in the final$ \pi^-/\pi^+ $ ratio.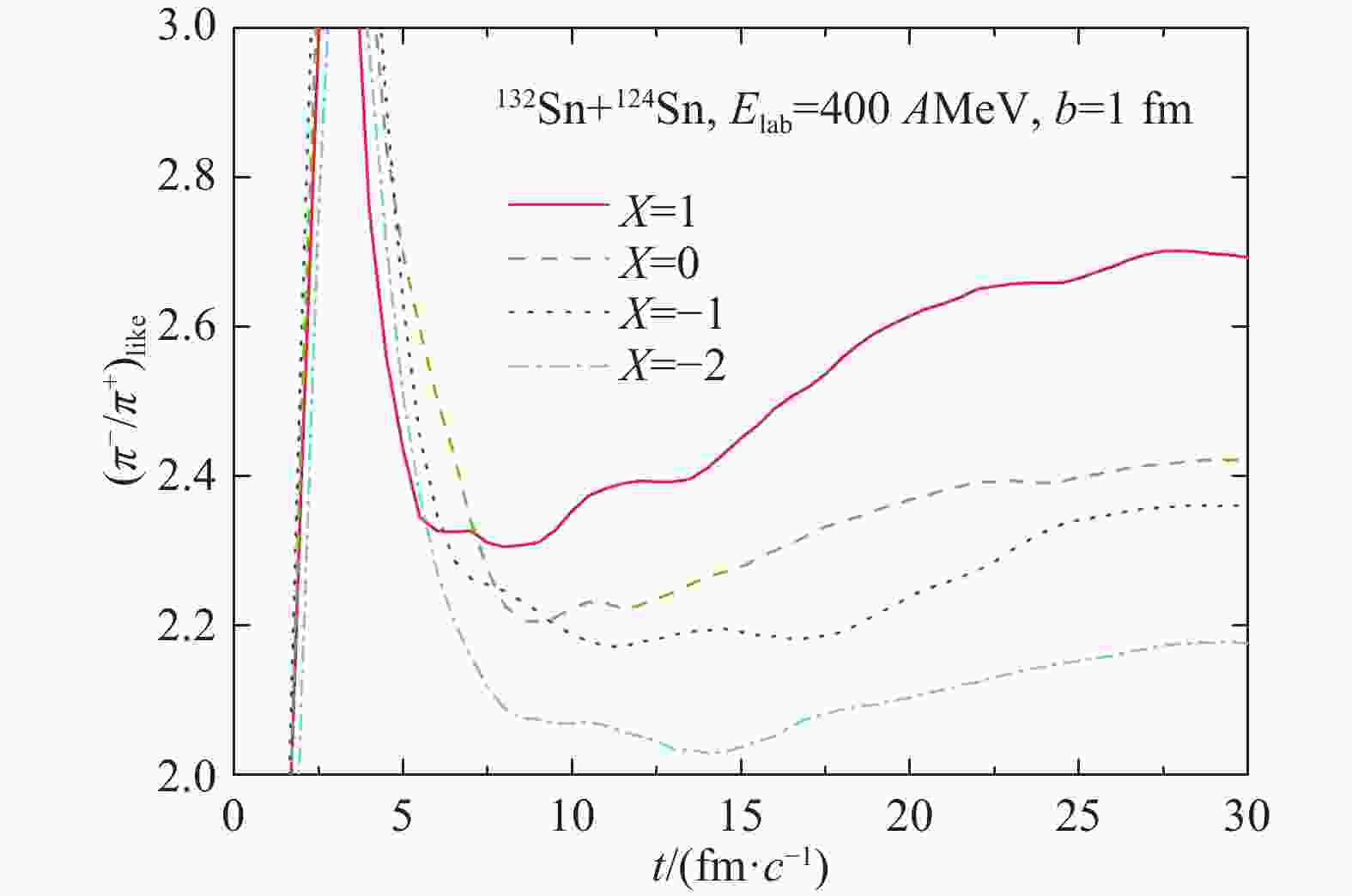
Figure 5. (color online)Effects of symmetry energy on the
$ (\pi^-/\pi^+)_{\rm like} $ ratio in the central 132Sn+124Sn reaction at 400AMeV. Taken from Ref. [57]. The hadronic probes usually suffer from distortions due to the strong interactions in the final state. It is preferable to get more clean ways to probe the symmetry energy especially at supranormal densities. Fig. 6 shows the spectra ratio
$ R_{1/2}(\gamma) $ of hard photons with$ p^a_{\gamma}( = 1.55\times10^{-3}\times\frac{1}{\varepsilon_{\gamma}}(\beta_{i}^{2}+\beta_{f}^{2})) $ and$ p^b_{\gamma} $ ($ =\! 2.1\!\times\!10^{-6}\frac{(1-y^{2})^{\alpha}}{y} $ ,$ y\! =\! \varepsilon_{\gamma}/E_{\max} $ ,$ \alpha \!=\! 0.7319\!-\!0.5898\beta_i $ ,$ \beta_{\rm i} $ and$ \beta_{\rm f} $ are the initial and final velocities,$ E_{\max} $ is the energy available in the center of mass) production forms[58]. It is first seen that calculations with$ p^a_{\gamma} $ and$ p^b_{\gamma} $ and in-medium NN cross sections all lead to about the same$ R_{1/2}(\gamma) $ within statistical errors as expected. The effect of the in-medium NN cross sections is canceled out in the spectra ratio. Free from the uncertainties of elementary photon production and the NN cross sections, the observable$ R_{1/2}(\gamma) $ could be considered as a robust probe of the symmetry energy. Comparing the calculations with soft and stiff symmetries both using the$ p^b_{\gamma} $ , it is seen that the$ R_{1/2}(\gamma) $ is very sensitive to the symmetry energy especially for energetic photons.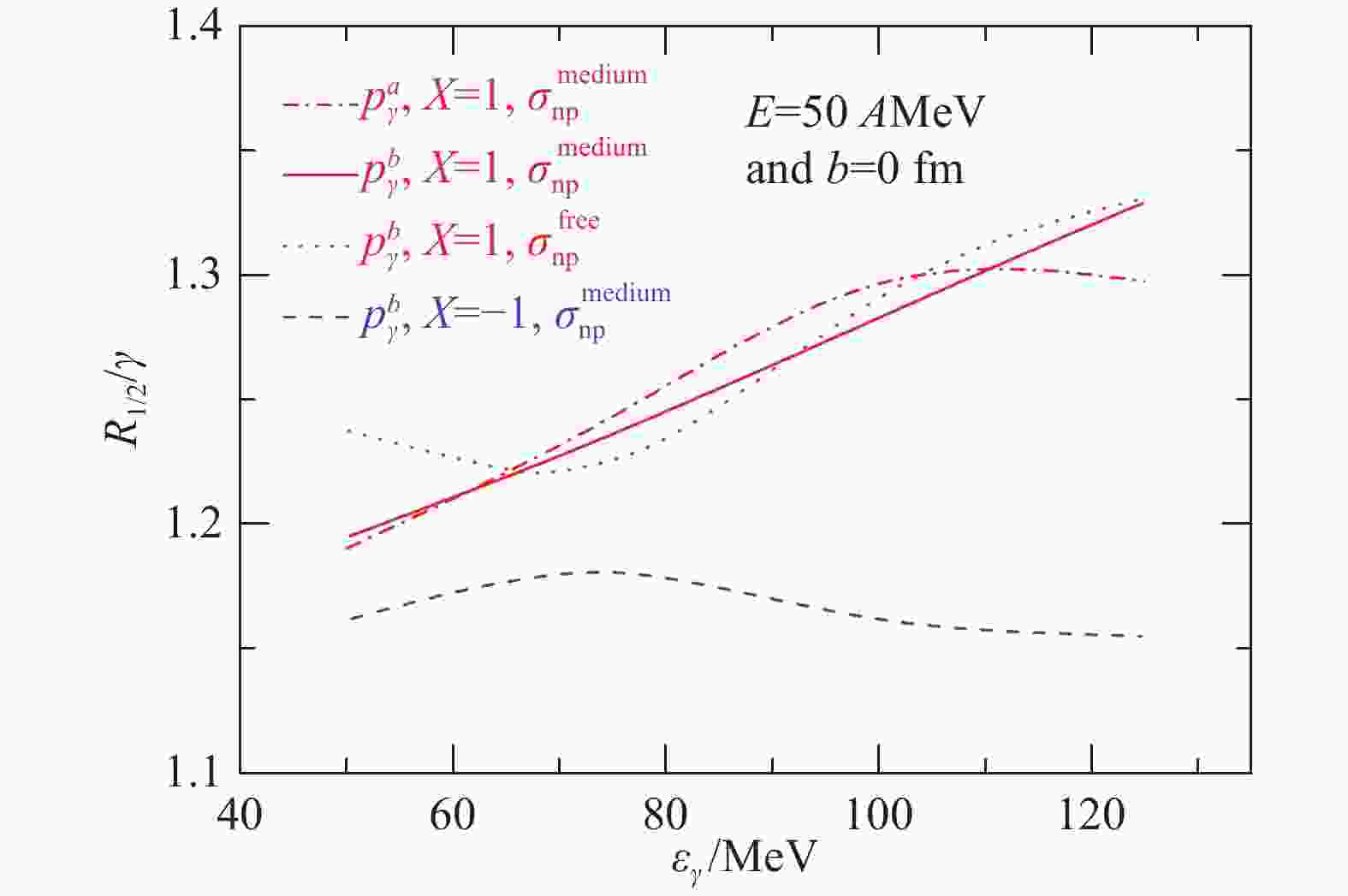
Figure 6. (color online)Effects of symmetry energy on the spectra ratio of hard photons in reactions of 132Sn+124Sn and 112Sn+112Sn at 50
AMeV, see text for details. Taken from Ref. [58]. In the light of sensitivity of the
$ \pi^-/\pi^+ $ ratio to the symmetry energy at subthreshold energies, the multiplicity of$ \eta $ production as a function of incident beam energy is also examined especially below its production threshold. Compared to pions,$ \eta $ mesons experience weaker final state interactions due to hidden strangeness. Fig. 7 shows$ \eta $ multiplicity as a function of beam energy in Au+Au reaction with soft ($ x $ =0) and stiff ($ x $ =–2) symmetry energies[59]. One can see that the multiplicity of$ \eta $ declines with decreasing beam energy, especially for the soft symmetry energy. And it saturates at incident energy of about 10 AGeV. The effect of nuclear symmetry energy on the$ \eta $ production is much more evident than the$ \pi^-/\pi^+ $ ratio especially in the deeper sub-threshold region.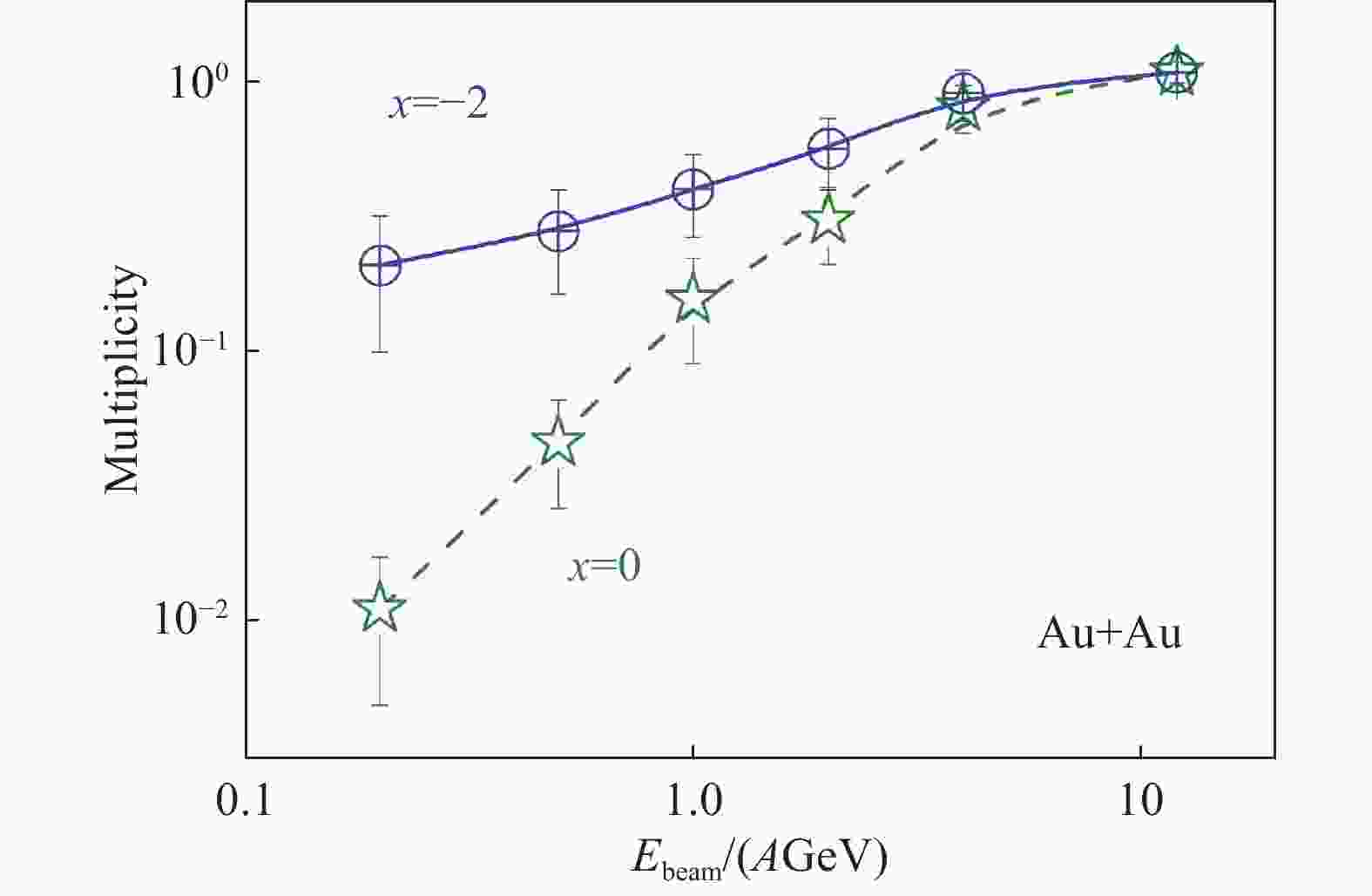
Figure 7. (color online)Effects of symmetry energy on the multiplicity of
$ \eta $ production as a function of incident beam energy in Au+Au reactions. Taken from Ref. [59]. -
Based on the chemical equilibrium condition of nuclear matter[60], if the symmetry energy does not change with density, the liquid-gas phase transition cannot occur. Therefore, in case the symmetry energy is less density-dependent, the effects of symmetry energy on the final-state observable may disappear.
To show the blind spots of probing the high-density symmetry energy, the neutron to proton ratio ratio in the central Au+Au reaction at 300 AMeV is used as an example[61]. In the used transport model, the effects of neutron-proton short-range-correlations are taken into account[53, 62]. Also the transition momentum of the proton is set to be the same as that of neutron[63]. The in-medium inelastic baryon-baryon collisions and the pion in-medium transport are included as well[64-65]. For initialization, nucleon density distribution in colliding nuclei is calculated using the Skyrme-Hartree-Fock with Skyrme
$ M^{\ast} $ force parameters[65]. And the proton and neutron momentum distributions with high-momentum tails in initial nucleus are reproduced[53, 62, 66-68].Since below saturation density, the symmetry energy is roughly constrained[69-70], we simulate the low-density symmetry energy with parameter
$ x $ =1. From Fig. 8, it is seen that with parameter$ x $ =1 the simulated symmetry energy is well consistent with the current constraints. In the study, we vary the high-density symmetry energy with parameter$ x $ in the range of$ x $ =–1, 1, 2, which cover the current uncertainties of the high-density symmetry energy[5, 70].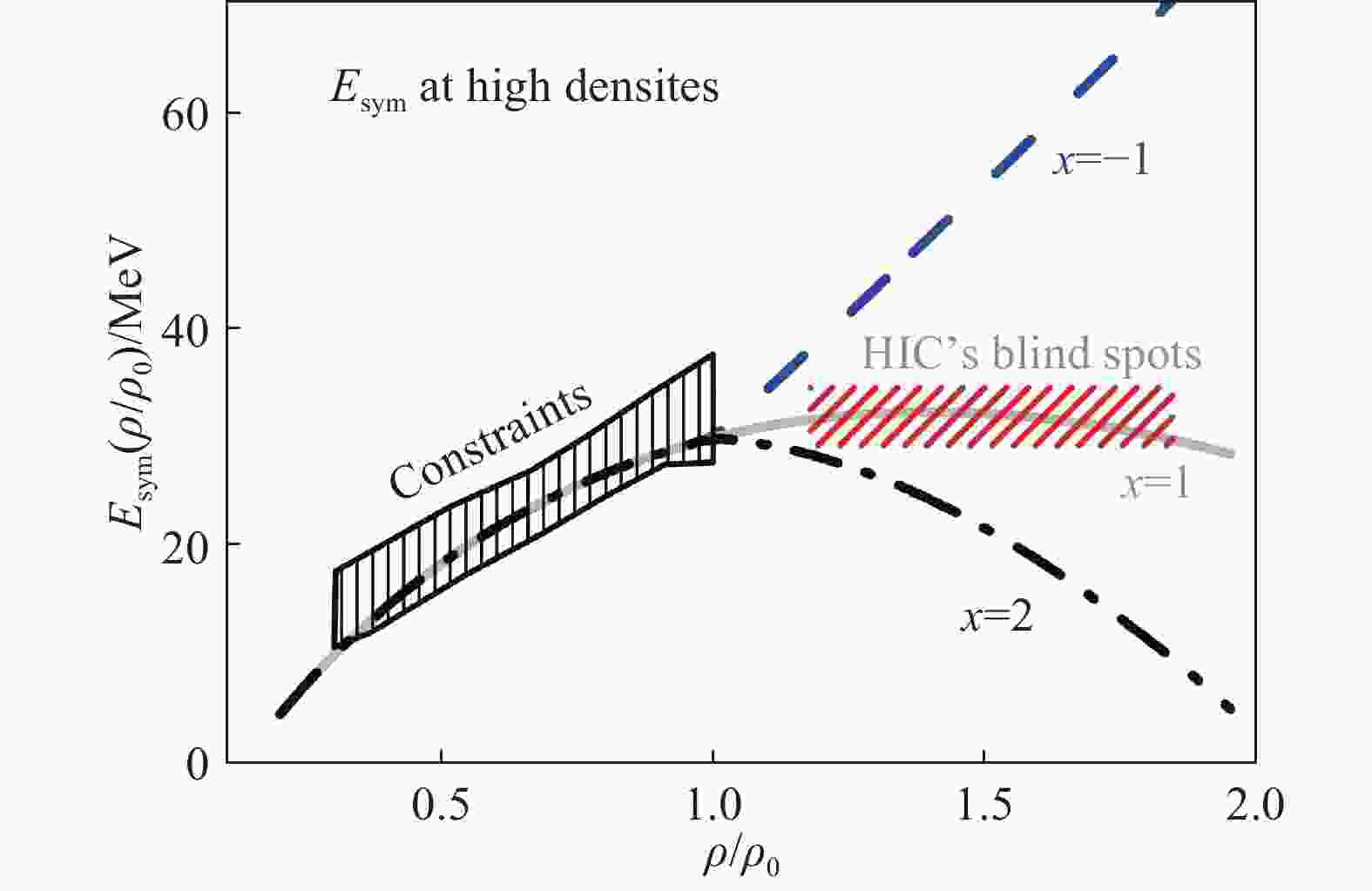
Figure 8. (color online)The density-dependent symmetry energy at low and high densities. The symmetry energy below saturation density is fixed as experimental constraints while the high-density symmetry energy is alterable. Taken from Ref. [61].
Fig. 9 shows the effects of high-density symmetry energy on the neutron to proton ratio n/p of dense matter formed in central Au+Au reaction at 300 AMeV. In the study, the same low-density symmetry energy as shown in Fig. 8 is used. From Fig. 9(a) and (c), one sees that the stiffer/soft high-density symmetry energy causes a smaller/large asymmetry of dense matter. While from Fig. 9(b), it is seen that the less density-dependent high-density symmetry energy (
$ x $ =1, shown in Fig. 8) almost does not affect the asymmetry of dense matter. For isospin-fractionation, there is a chemical equilibrium condition[60, 71-74]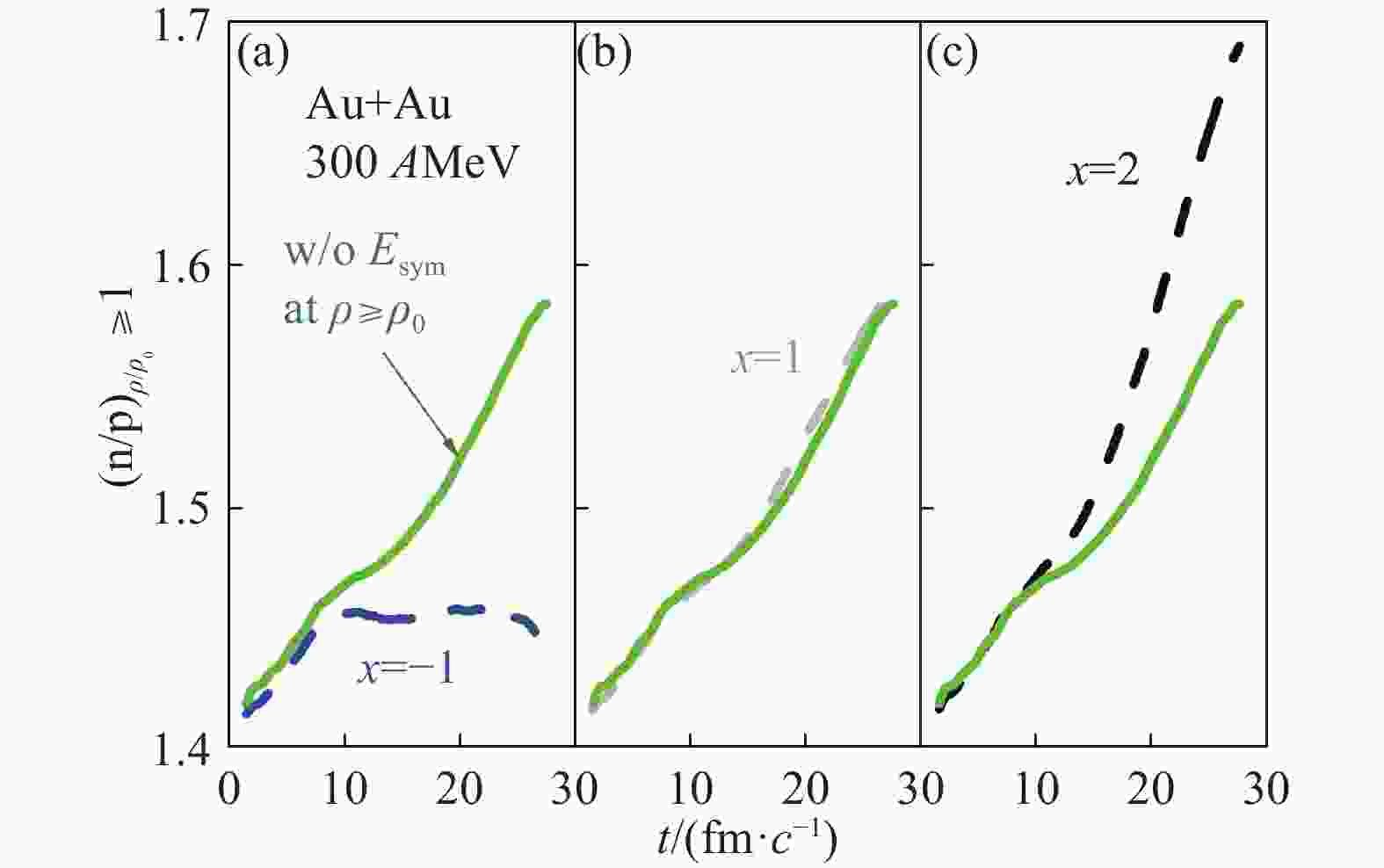
Figure 9. (color online)Effects of the high-density symmetry energy on the neutron to proton ratio n/p in dense matter (
$ \rho/\rho_{0}\geqslant $ 1) as a function of time in central Au+Au reaction at 300AMeV. The solid line denotes the case without high-density symmetry energy, panels (a), (b), (c) indicate cases with stiff, soft and super-soft symmetry energies, respectively. Taken from Ref. [61]. $$ \begin{array}{l} E_{\rm sym}(\rho_1)\delta_1 = E_{\rm sym}(\rho_2)\delta_2, \end{array} $$ (6) where
$ E_{\rm sym}(\rho_1), E_{\rm sym}(\rho_2) $ denote symmetry energies at different density regions and$ \delta_1, \delta_2 $ are, respectively, their asymmetries. In nuclear matter there is a dynamical process of nucleon movement determined by Eq. (6) according to the density dependent symmetry energy. Since the high-density symmetry energy with parameter$ x $ =1,$ E_{\rm sym}(\rho_1) $ $ \approx $ $ E_{\rm sym}(\rho_2) $ , the asymmetry of dense matter$ \delta_1 $ $ \approx $ $ \delta_2 $ . One thus sees in Fig. 9(b), the less density-dependent high-density symmetry energy almost does not affect the asymmetry of dense matter formed in heavy-ion collisions.Since the symmetry potential acts directly on nucleons, the neutron/proton ratio n/p of nucleon emissions may be one of the best observables to probe the symmetry energy[75-76]. Fig. 10 shows the effects of high-density symmetry energy on the kinetic energy distribution of the free neutron to proton ratio n/p in central Au+Au reaction at 300 AMeV. From Fig. 10(a), (c), it is seen that the stiffer/soft high-density symmetry energy causes a larger/small n/p ratio. While from Fig. 10(b) one sees that the less density-dependent high-density symmetry energy almost does not affect the free n/p ratio. Therefore, the less density-dependent high-density symmetry energy cannot be probed effectively in heavy-ion collisions.
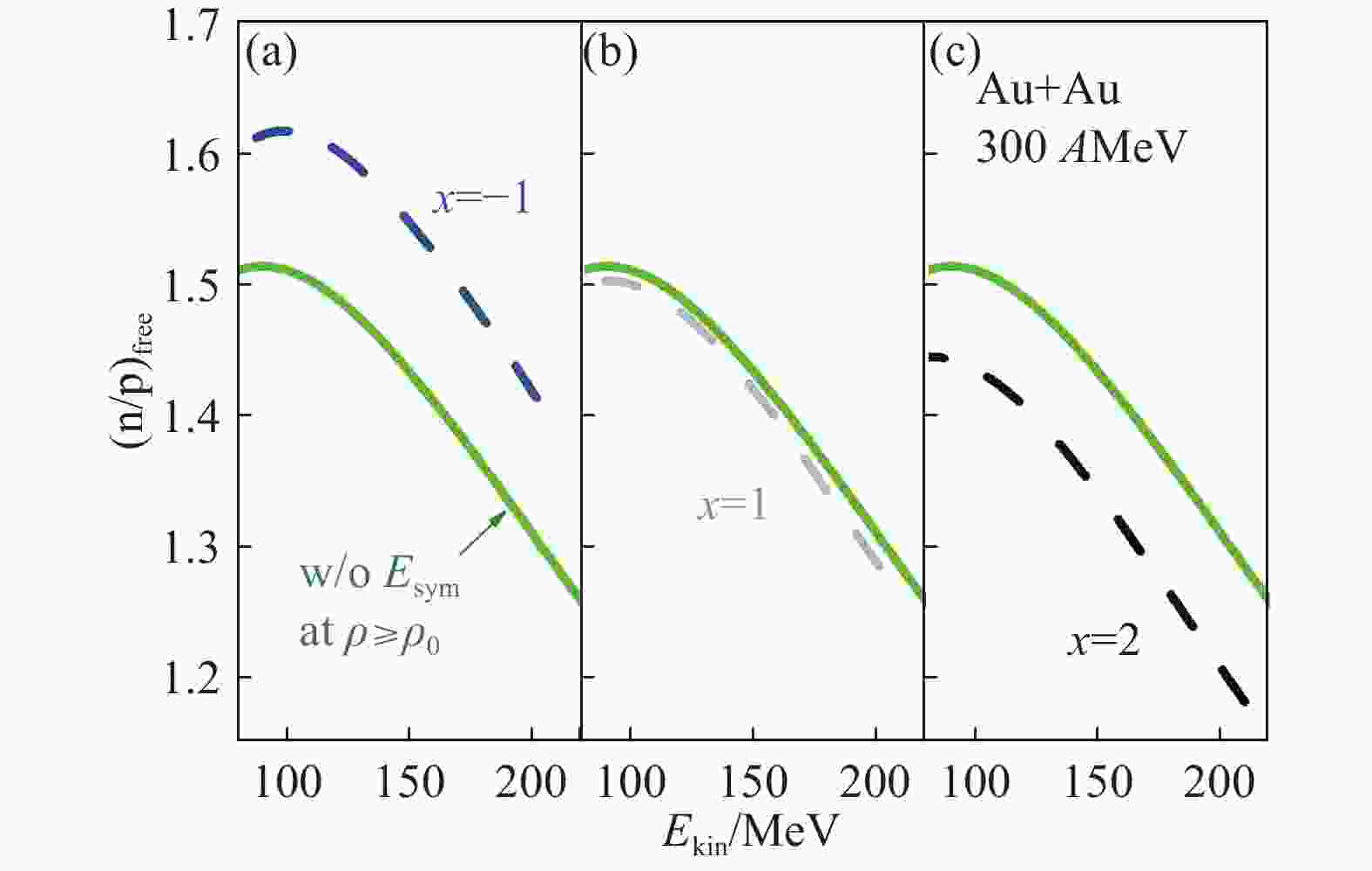
Figure 10. (color online)Effects of high-density symmetry energy on the free neutron to proton ratio n/p as a function of kinetic energy in central Au+Au reaction at 300 AMeV. The solid line denotes the case without high-density symmetry energy, panels (a), (b), (c) indicate cases with stiff, soft and super-soft symmetry energies, respectively. Taken from Ref. [61].
-
There are many factors affecting nuclear reaction transport simulation, e.g., the initialization, the nucleon-nucleon interaction or single nucleon potential, the nucleon-nucleon scattering cross sections, and the framework of transport models. It is thus necessary to make a study among different models, to see how large the differences are on the values of isospin sensitive observables.
Within the frameworks of isospin-dependent transport models Boltzmann-Uehling-Uhlenbeck (IBUU04)[57] and Ultrarelativistic Quantum Molecular Dynamics (UrQMD)[77-78], the model dependences of frequently used isospin-sensitive observables
$ \pi^{-}/\pi^{+} $ ratio and n/p ratio of free nucleons have been demonstrated[79]. Fig. 11 shows the n/p ratio of free nucleons and$ \pi^-/\pi^+ $ ratio as a function of kinetic energy in the 197Au+197Au reaction at a beam energy of 400 AMeV simulated by the IBUU and the UrQMD models. From panel (a) one can see that both models give the same trend of n/p ratio as a function of nucleonic kinetic energy. The result of the UrQMD model is overall larger than that of the IBUU model due to their different forms of symmetry potential[79]. From panel (b) of Fig. 11, one can see that there is a cross between the$ \pi^-/\pi^+ $ ratios from the UrQMD model and that from the IBUU model. At lower kinetic energies, the value of$ \pi^-/\pi^+ $ ratio from the UrQMD is much larger than that from the IBUU model. And from panel (a) of Fig. 12, one can see that nucleonic transverse flow given by the IBUU model shows large isospin effect than that with the UrQMD model. From panel (b) of Fig. 12, it is seen that the slope of neutron-proton differential flow is evidently larger for the UrQMD model than that for the IBUU model.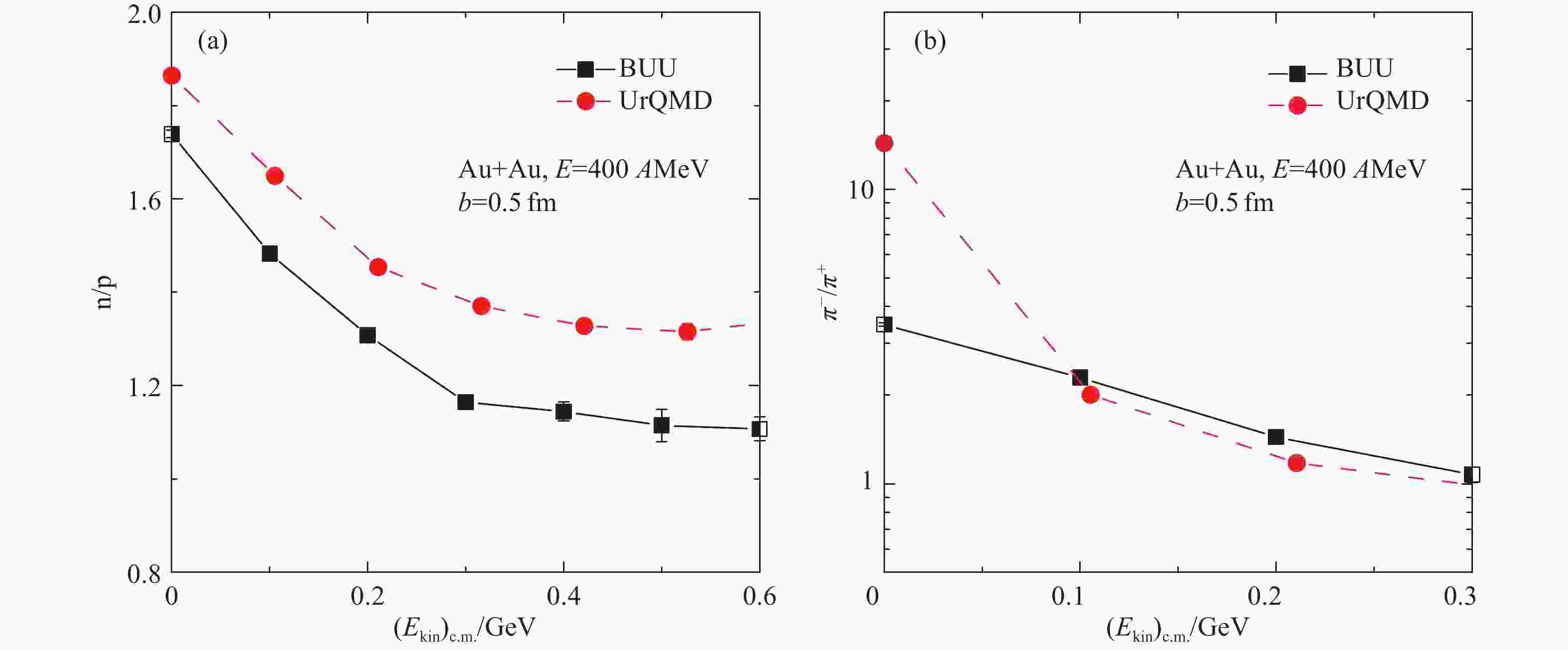
Figure 11. (color online)Model dependence of n/p ratio of free nucleons and
$ \pi^-/\pi^+ $ ratio as a function of kinetic energy in 197Au+197Au at 400AMeV. Panels (a) and (b) show n/p and $ \pi^-/\pi^+ $ ratio cases, respectively. Taken from Ref. [79].Since most observables of the symmetry energy are model dependent, on the first step, what is crucially needed currently is a qualitative observable to probe whether the symmetry energy at high densities is stiff or soft.
Fig. 13 shows nucleon kinetic energy distribution of n/p ratios of free (gas) and bound (liquid) nucleons in the central 197Au+197Au reaction at 400 AMeV with positive and negative symmetry potentials at supra-saturation densities given by the IBUU transport model[5]. From panel (a), it is seen that the value of n/p of nuclear gas phase is larger than that of liquid phase in the whole kinetic energy distribution with the positive symmetry potential. However, it is interesting to see that the value of n/p of gas phase is smaller than that of liquid phase at higher kinetic energies with the negative symmetry potential at high densities. The same situation is demonstrated in Fig. 14 with the UrQMD model. The only discrepancy is that the kinetic energy of transition point given by the UrQMD model is lower than that given by the IBUU model. With positive/negative symmetry potential at high densities, for energetic nucleons, the value of neutron to proton ratio of free nucleons is larger/smaller than that of bound nucleon fragments. Compared with extensively studied quantitative observables of the nuclear symmetry energy, the normal or abnormal isospin-fractionation of energetic nucleons can be a qualitative probe of nuclear symmetry energy at high densities.
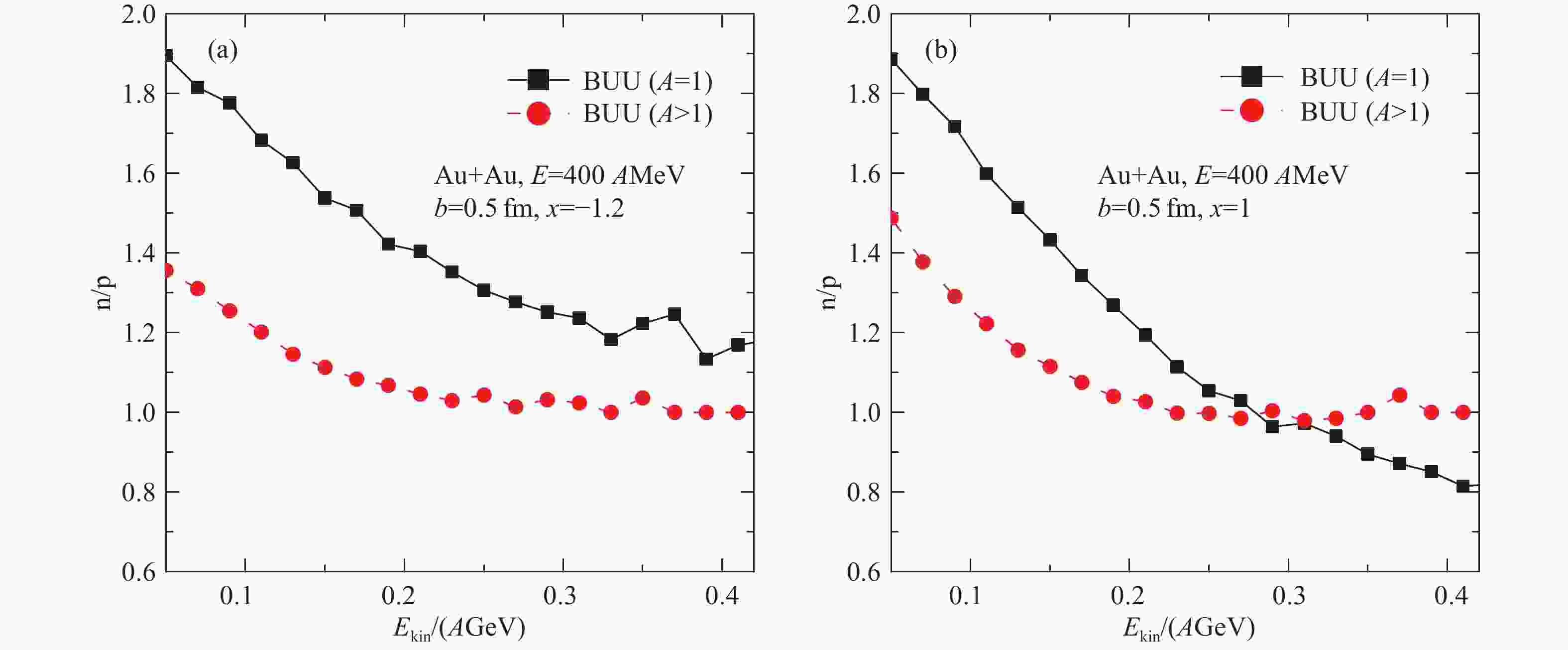
Figure 13. (color online)kinetic energy distribution of neutron to proton ratio n/p of free (panel (a)) and bound nucleons (panel (b)) in the central 197Au+197Au reaction at 400
AMeV with positive (left, $ x $ =–1.2) and negative (right,$ x $ =1) symmetry potentials at supra-saturation densities. Given by the IBUU transport model. Taken from Ref. [5]. -
To investigate the symmetry energy at high densities, the
$ \pi^-/\pi^+ $ ratio has been frequently proposed in the literature[57, 80-81]. Aiming at probing the high-density symmetry energy by the$ \pi^-/\pi^+ $ ratio, Sn+Sn reactions at about 270 AMeV experiments are being carried out at RIKEN in Japan[46, 82-83]. Does the$ \pi^-/\pi^+ $ ratio in heavy-ion collisions at intermediate energies always probe the symmetry energy above saturation density? Alternatively, in what conditions does the$ \pi^-/\pi^+ $ ratio probe the symmetry energy at high densities?To answer the above questions, we studied the decomposition of the sensitivity of the symmetry energy observables. From Fig. 15(a), it is demonstrated that, in the medium-mass nuclei 132Sn+124Sn central reaction at 300 AMeV, the effects of the symmetry energy in the densities below 0.5
$ \rho_{0} $ are larger than that in the densities above 1.5$ \rho_{0} $ . Below saturation density the effects of the symmetry energy are roughly equal to that above saturation density. However, from Fig. 15(b), one can see that, the effects of the symmetry energy in the densities below 0.5$ \rho_{0} $ are obviously smaller than that in the densities above 1.5$ \rho_{0} $ . The effects of the symmetry energy below saturation density are obviously smaller than that above saturation density. Therefore, to probe the high-density symmetry energy by the$ \pi^-/\pi^+ $ ratio, heavy system and at relatively higher incident beam energies is a preferable.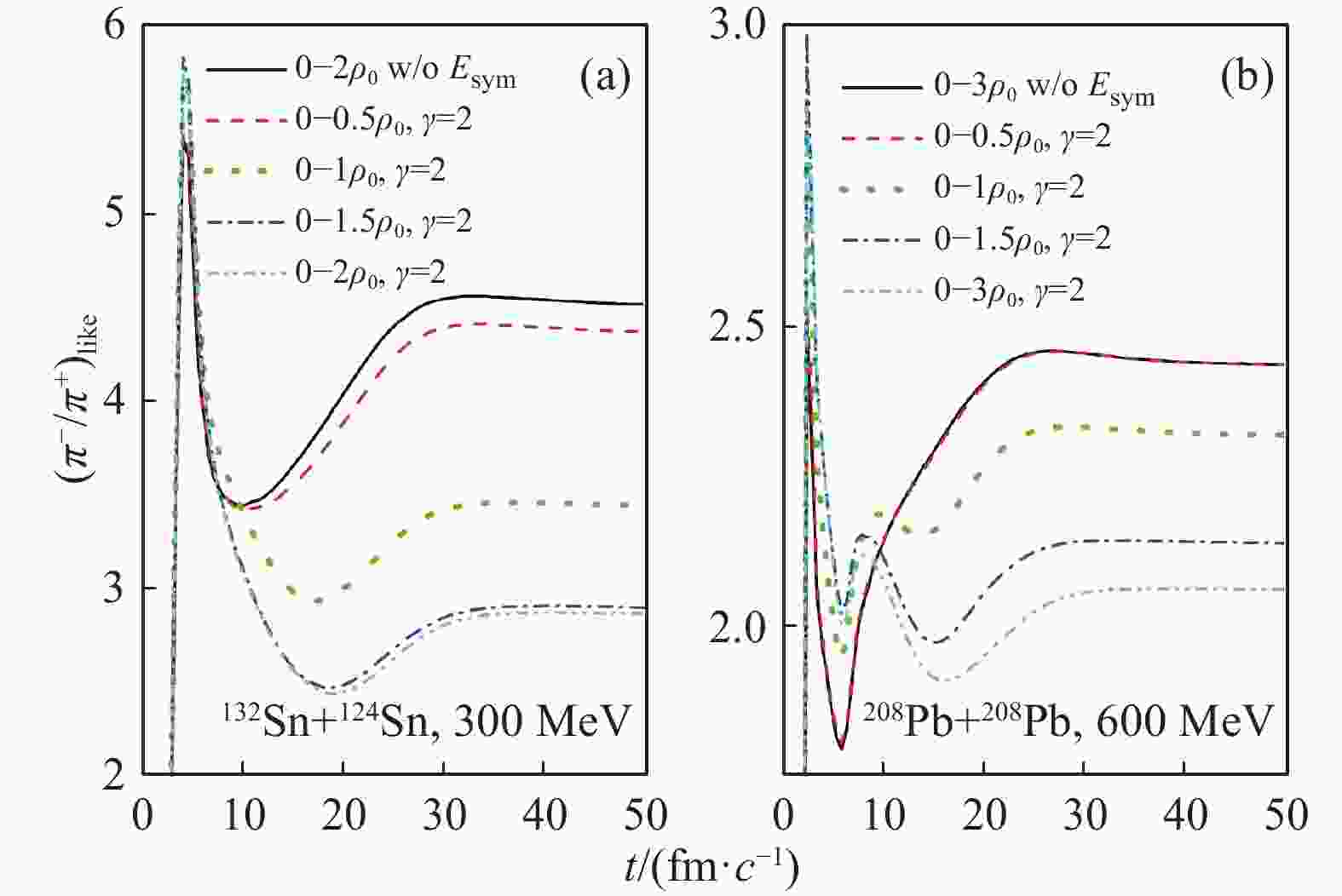
Figure 15. (color online)Evolution of the relative sensitivity of the symmetry energy observable
$ (\pi^-/\pi^+)_{\rm like} $ ratio in 132Sn+124Sn at 300AMeV (panel (a)) and 208Pb+208Pb at 600 AMeV (panel (b)). Taken from Ref. [84]. Similar studies were also carried out for some other frequently discussed observables[85]. The symmetry energy sensitive observable n/p ratio in the 132Sn+124Sn reaction at 0.3 AGeV is shown to be sensitive to the symmetry energy below
$ 1.5\rho_0 $ . Nucleon elliptic flow can probe the symmetry energy from low to high densities when changing the beam energies from 0.3 to 0.6 AGeV in the semi-central 132Sn+124Sn reaction. And nucleon transverse and elliptic flows in the semi-central 197Au+197Au reaction at 0.6 AGeV are more sensitive to the high-density symmetry energy. -
Recent proton-removal experiments showed that only about 80% nucleons participate in the independent particle motion[66, 86-87]. Also it is shown that nucleons in nuclei can form pairs with larger relative momenta and smaller center-of-mass momenta[88-89]. This is interpreted by the nucleon-nucleon short-range tensor interaction[90-91]. The nucleon-nucleon short-range correlations (SRC) in nuclei cause a high-momentum tail (HMT) in single-nucleon momentum distribution above Fermi momentum[92-96]. And the high-momentum tail's shape is almost identical for all nuclei[97-100], i.e., roughly exhibits a
$ C/k^{4} $ distribu tion[67, 101-103].The short-range correlations in nuclei surely affect
$ \pi $ ,$ K $ ,$ \eta $ and nucleon emission in heavy-ion collisions. Fig. 16 shows$ \pi^{+} $ production as a function of high-momentum tail cutoff parameter$ \lambda $ in Au+Au collisions at 0.4 and 1 AGeV incident beam energies[68]. Larger high-momentum cutoff parameter causes larger nucleon average kinetic energy, especially proton average kinetic energy, thus more$ \pi^{+} $ 's are produced. As incident beam energy increases, the initial movement of nucleons in nuclei becomes less important in nucleus-nucleus collisions.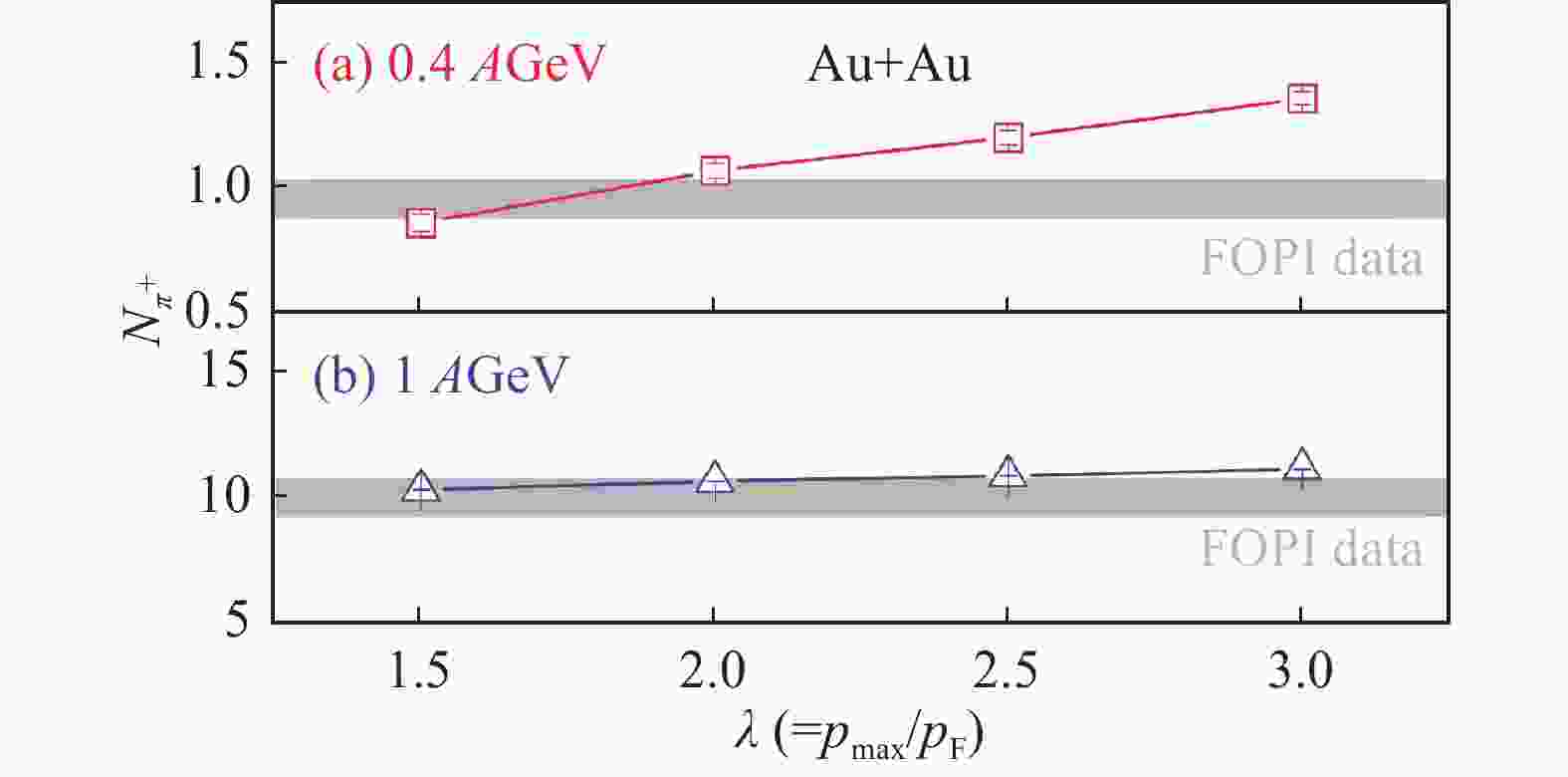
Figure 16. (color online)Effects of short-range correlations on the number of produced
$ \pi^{+} $ meson production in Au+Au collisions at 0.4 (panel (a)) and 1 AGeV (panel (b)) beam energies. Taken from Ref. [68].Fig. 17 shows effects of short-range correlations on the kinetic energy distributions of
$ \pi^{-} $ ,$ \pi^{+} $ as well as$ \pi^{-}/\pi^{+} $ ratio in the semi-central reaction 197Au+197Au at 400 AMeV[104]. It is clearly demonstrated that the kinetic energy distributions of both$ \pi^{-} $ and$ \pi^{+} $ are sensitive to the HMT. The ratio of$ \pi^{-}/\pi^{+} $ is sensitive to the HMT except in the high kinetic energy region. The short-range corrections increase kinetic energies of neutrons and protons, thus more pion's are produced. With the short-range correlations, protons have a larger probability than neutrons to have larger momenta, one thus sees a lower value of the$ \pi^{-}/\pi^{+} $ ratio with the HMT. From Fig. 18, one can see that the effects of the HMT on the difference of neutron and proton elliptic flows ($ v_{2}^{\rm n}-v_{2}^{\rm p} $ ) is also crucial[104].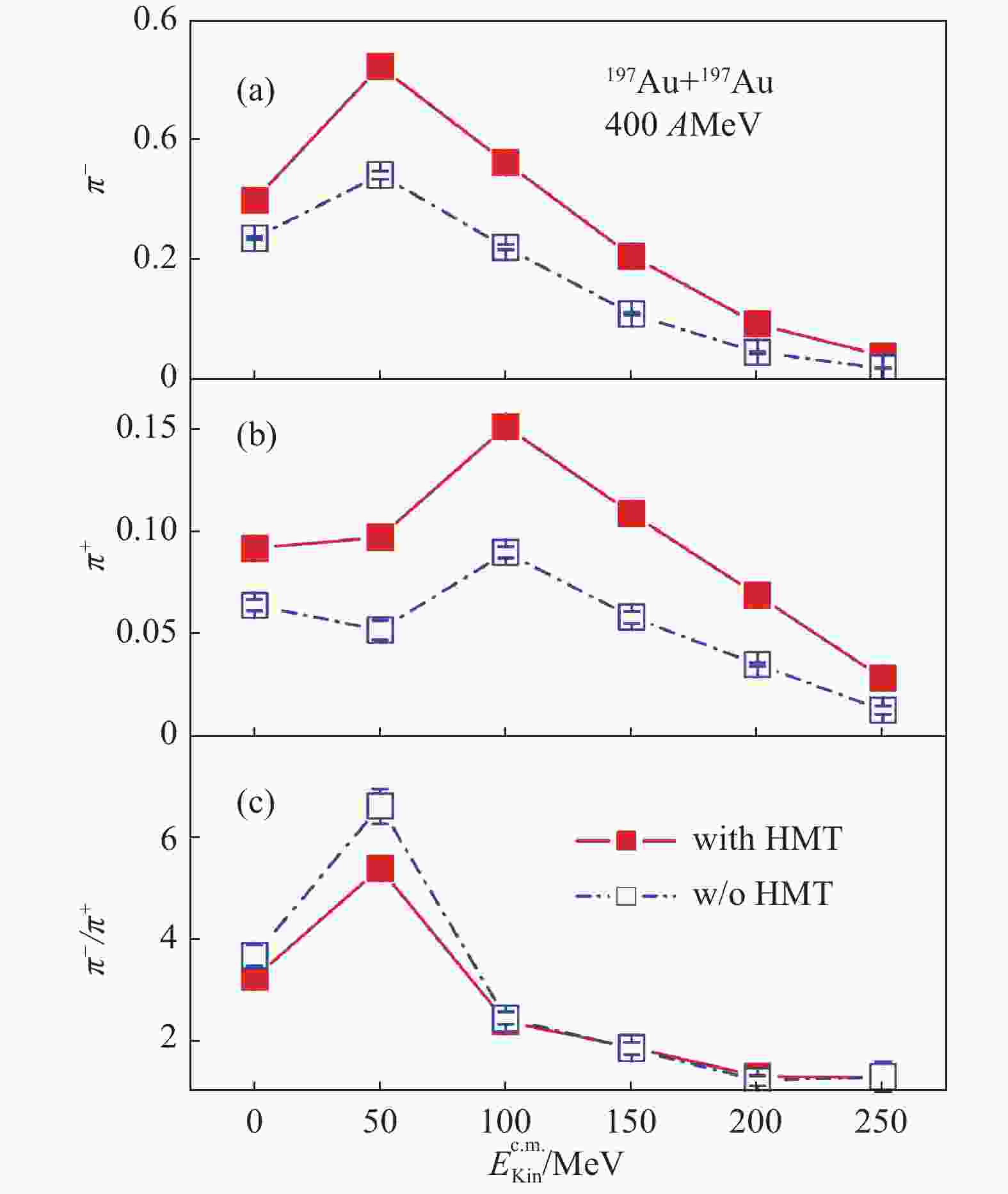
Figure 17. (color online)Effects of short-range correlations on the kinetic energy distributions of
$ \pi^{-} $ (panel (a)),$ \pi^{+} $ (panel (b)) and$ \pi^{-}/\pi^{+} $ ratio (panel (c)) in the reaction of$ ^{197}\rm {Au}+^{197}\rm {Au} $ at 400AMeV. Taken from Ref. [104]. 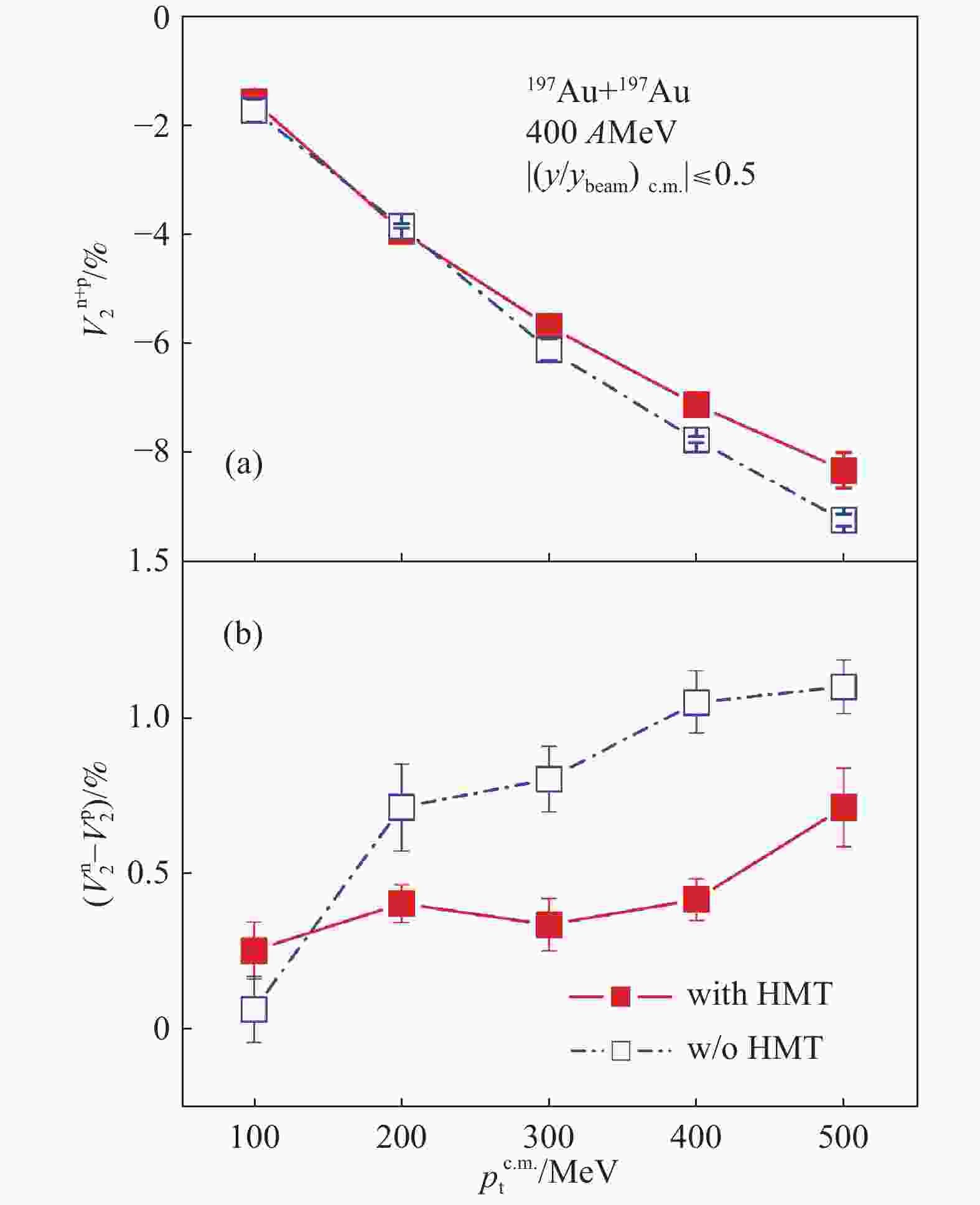
Figure 18. (color online)Effects of short-range correlations on the nucleon elliptic flow (panel (a)) and the difference of neutron and proton elliptic flow (panel (b)) in the semi-central reaction of
$ ^{197}\rm {Au}+ ^{197}\rm {Au} $ at 400AMeV. Taken from Ref. [104]. In neutron-rich matter, neutron and proton may have very different Fermi momenta. If each correlated neutron and proton have
$ 1/k^{4} $ distributions starting from their respective Fermi momenta, based on the n-p dominance model[67], the correlated neutron and proton cannot have the same momentum magnitude. It is thus reasonable to think that in neutron-rich matter proton has the same transition momentum as that of neutron. Fig. 19 shows nucleon momentum distribution in 48Ca. One can see that a HMT above the nuclear Fermi momentum is produced. Proton has greater probability than neutron to have momenta greater than the nuclear Fermi momentum. Compared case A with case B, it is seen that with the starting point of neutron Fermi momentum, proton has even more greater probability to have high momenta. The dynamics of heavy-ion collisions could be affected by proton momentum gap. Fig. 20 demonstrates the ratio of$ \pi^{-}/\pi^{+} $ in 132Sn+124Sn reactions with different proton starting momenta in the HMT. As expected, there is an evident decline of the value of$ \pi^{-}/\pi^{+} $ ratio when varying the starting momentum of proton in the HMT. From the inserted figure, it is seen that mainly the$ \pi^{+} $ production is affected. To interpret related experiments at Radioactive Isotope Beam Facility (RIBF) at RIKEN in Japan[46-82], it is necessary to study how the$ \pi^{-}/\pi^{+} $ ratio is affected by the proton momentum gap.
Figure 19. (color online)Momentum distribution of nucleon with different starting points of protons in 48Ca. Panels (a), (b) show cases without and with proton momentum gap in nucleon momentum distributions, respectively. Taken from Ref. [63].

Figure 20. (color online)The ratio of
$ \pi^{-}/\pi^{+} $ in 132Sn+124Sn reactions at 300AMeV with different proton starting momenta in the HMT. Taken from Ref. [63]. -
Since the constraints on the symmetry energy are always model dependent, it is instructive to make cross-check of the symmetry energy using different probes. Fig. 21 shows the
$ \pi^{-}/\pi^{+} $ ratio given by the IBUU model. It is seen that larger$ \pi^{-}/\pi^{+} $ ratio corresponds softer symmetry energy. One can also see that both the short-range correlations and in-medium cross section affect the value of$ \pi^{-}/\pi^{+} $ ratio evidently. From Fig. 21, it is concluded that the FOPI pion data supports a softer symmetry energy ($ x $ =1, 2, even$ x $ =3).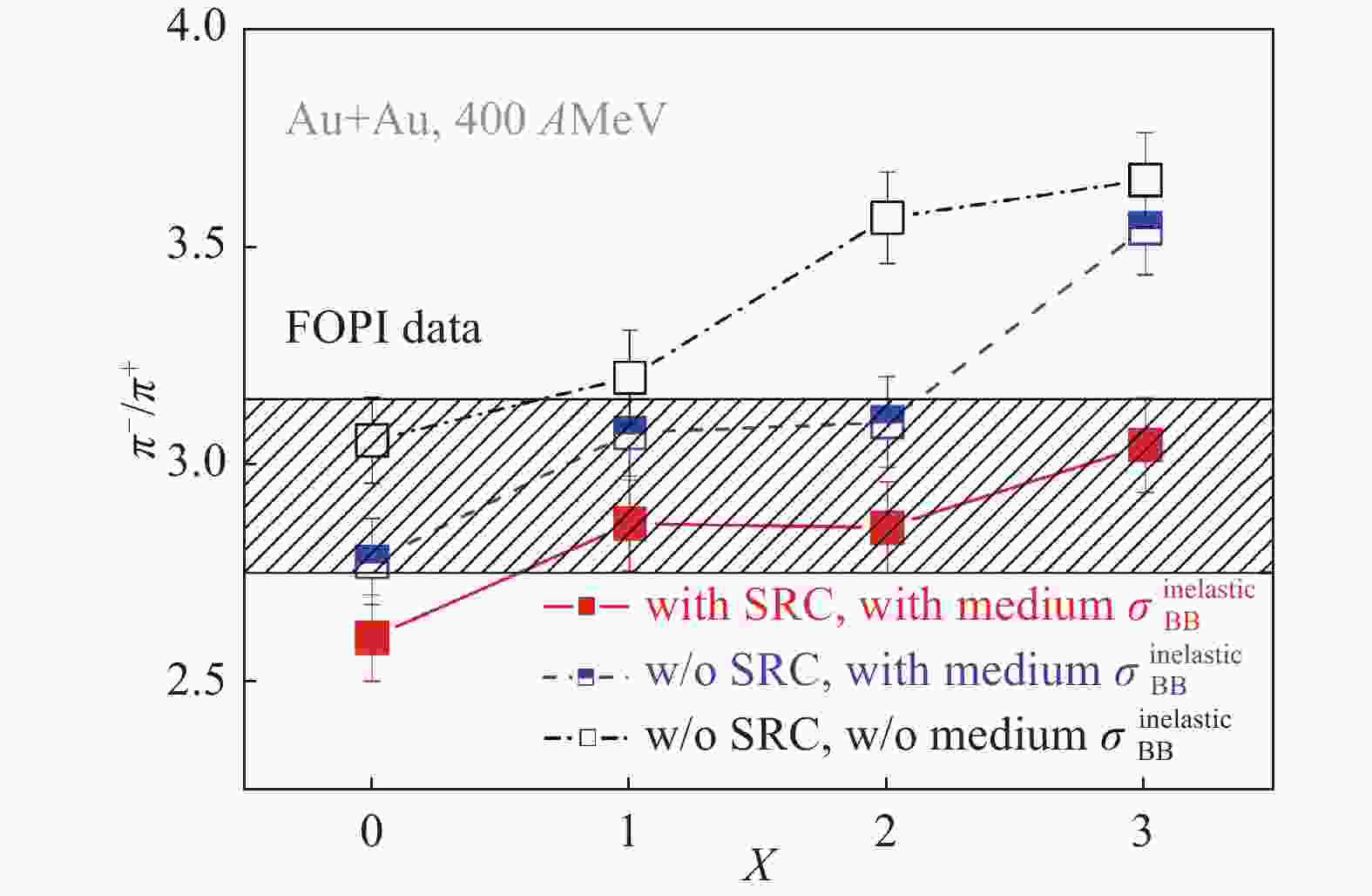
Figure 21. (color online)Effects of symmetry energy on the
$ \pi^{-}/\pi^{+} $ ratio in Au+Au reaction at 400AMeV with different short-range correlations and in-medium cross section. Taken from Ref. [64]. Fig. 22 shows comparison of simulated nucleon elliptic flow and experimental data. Since stiffer symmetry energy generally causes more neutrons to emit in the direction perpendicular to the reaction plane, larger values of elliptic flow ratios of neutron and proton
$ v_{2}^{\rm n}/v_{2}^{\rm p} $ are seen with stiffer symmetry energies. With the SRC of nucleon-nucleon, values of the$ v_{2}^{\rm n}/v_{2}^{\rm p} $ ratio are larger than that without the SRC. Fig. 22 indicates the FOPI-LAND elliptic flow experimental data does not favor very soft symmetry energy ($ x $ =2, 3). Combining the studies of nucleon elliptic flow and$ \pi^{-}/\pi^{+} $ ratio, one can roughly obtain the symmetry energy stiffness parameter$ x $ =1, i.e., a mildly soft density-dependent symmetry energy at supra-saturation densities is obtained as shown in Fig. 2.
Figure 22. (color online)Effects of symmetry energy on the ratio of neutron and proton elliptic flows
$ v_{2}^{\rm n}/v_{2}^{\rm p} $ in Au+Au reaction at 400AMeV. Taken from Ref. [64]. -
The density-dependent symmetry energy at saturation can be Taylor expanded as[105],
$$ \begin{aligned} E_{\rm sym}(\rho) = E_{\rm sym}(\rho_0)+L\left(\frac{\rho-\rho_0}{3\rho_0}\right) +\frac{K_{\rm sym}}{2}\left(\frac{\rho-\rho_0}{3\rho_0}\right)^2, \end{aligned} $$ (7) where
$ E_{\rm sym}(\rho_0) $ is the value of the symmetry energy at saturation and the quantities$ L $ ,$ K_{\rm sym} $ are, respectively, its slope and curvature at saturation,$$ \begin{aligned} {L = 3\rho_0\frac{\partial E_{\rm sym}(\rho)}{\partial \rho} \Big |_{\rho = \rho_0}} \ , \,\,\,\, {K_{\rm sym} = 9\rho_0^2\frac{\partial^2E_{\rm sym}(\rho)}{\partial \rho^2} \Big |_{\rho = \rho_0}}. \end{aligned} $$ (8) The most probable magnitude
$ E_{\rm sym}(\rho_0) $ =(31.7$ \pm $ 3.2) MeV and slope$ L $ =(58.7±28.1) MeV of the nuclear symmetry energy at saturation have been obtained[28-29]. While the curvature$ K_{\rm{sym}} $ is still unknown, probably to be in the range of$ -400 $ $ \leqslant $ $ K_{\rm{sym}} $ $ \leqslant $ 100 MeV[106-107]. Fig. 23 shows density-dependent symmetry energies derived from single nucleon potential (Eq. (3)) in the transport model and that of Taylor expansion (Eq. (7)). It is seen that the symmetry energies obtained from different combinations of slope values with$ L = $ 40, 60, 80 MeV and curvatures$ K_{\rm sym} = - $ 4 000 MeV cover current uncertain range of the high-density symmetry energy as shown in Fig. 1. The curvature of nuclear symmetry energy not only connects with the high-density symmetry energy, but also closely related to the incompressibility of neutron-rich matter, while it still remains an open problem[105, 108].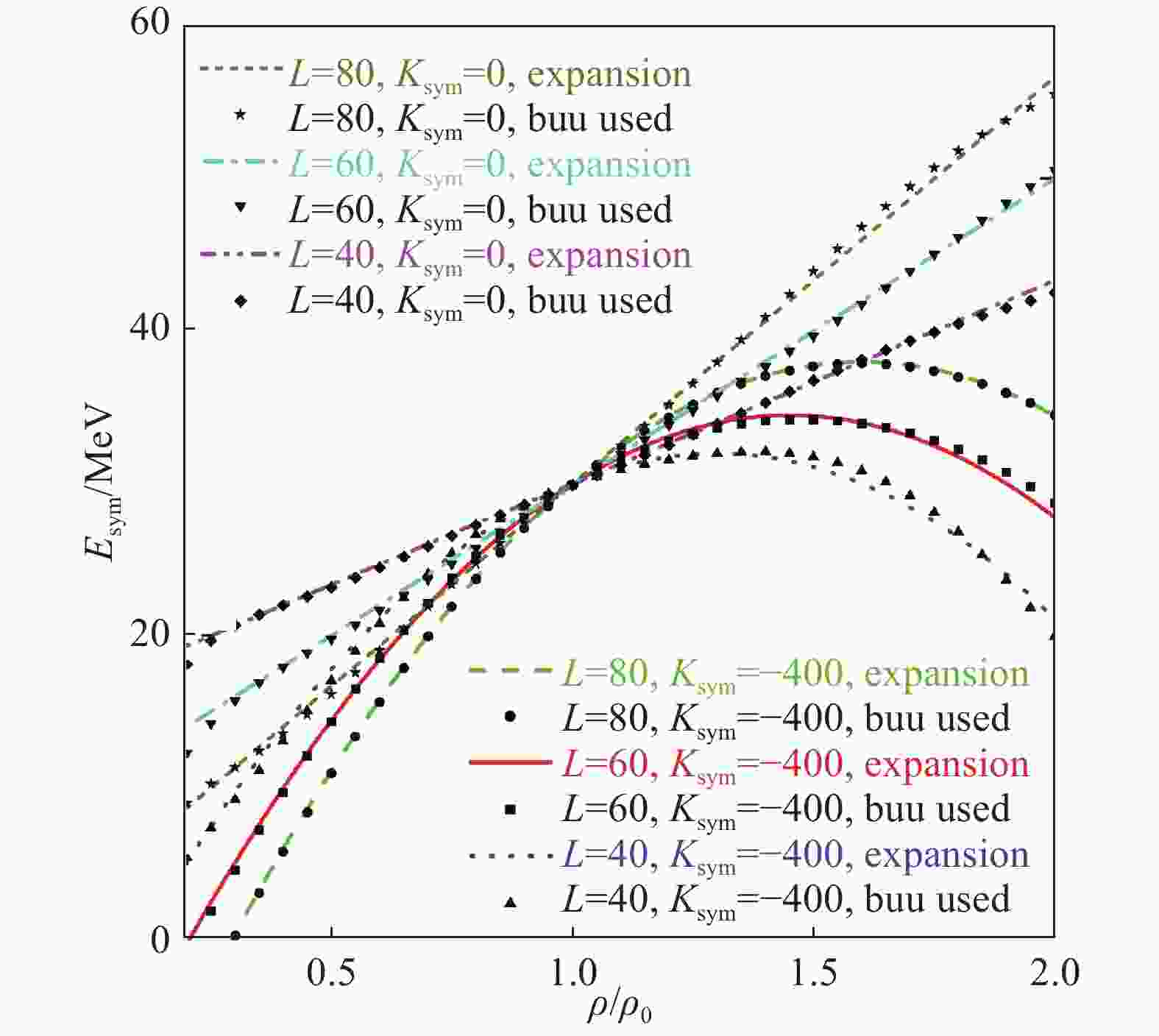
Figure 23. (color online)Density-dependent symmetry energies for six combinations of curvatures
$ K_{\rm sym} = $ $ -4\,000 $ MeV and slopes$ L $ = 40, 60, 80 MeV obtained from single nucleon potential Eq. (3) (symbols) and Taylor expansion Eq. (7) (lines).Squeezed-out nucleon, which emitted in the direction perpendicular to the reaction plane in semi-central collisions, is known to carry direct information about the high density phase[4, 49, 55, 109-112]. Fig. 24 shows the squeezed-out neutron to proton ratio in Au+Au at 400 (panel (a)) and 600 (panel (b)) AMeV[113]. It is demonstrated that the effects of the curvature of the symmetry energy on the squeezed-out neutron to proton ratio n/p are quite evident, especially at high transverse momenta. The values of the squeezed-out n/p with
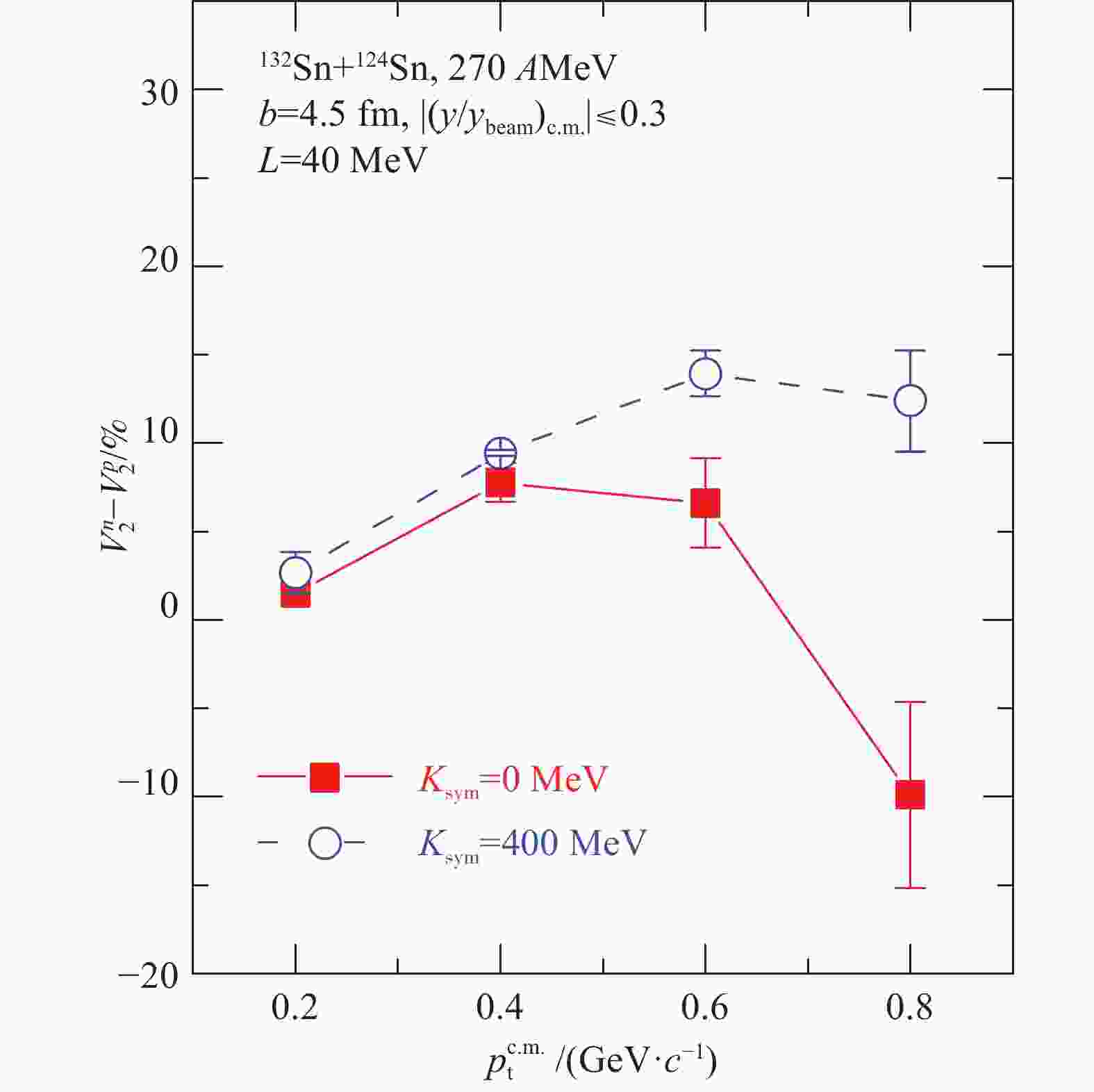
$ K_{\rm sym} = $ 0 are higher than that with$ K_{\rm sym} = - $ 400 MeV. It is also seen that, the effects of the curvature of the symmetry energy on the squeezed-out n/p are much larger than the ratio of integrating neutron and proton elliptic flows[114]. Fig. 25 shows the effects of the curvature of nuclear symmetry energy on the difference of neutron and proton elliptic flow in the semi-central reaction of$ ^{132}\rm {Sn}+^{124}\rm {Sn} $ at 270 AMeV. It is clearly seen that the difference of neutron and proton elliptic flow is also quite sensitive to the curvature of nuclear symmetry energy. The isospin-dependent squeezed-out nucleon emission thus may be one potential probe of the high-density symmetry energy.
Figure 24. (color online)Effects of the curvature of nuclear symmetry energy on the squeezed-out neutron to proton ratio in the semi-central reaction of Au+Au at 400 (panel (a)) and 600 (panel (b))
AMeV. The bandwidths denote uncertainties of the slope L. Taken from Ref. [113]. -
Nuclear symmetry energy is an old but fundamental and critical physical quantity in isospin nuclear physics, especially in astrophysics relating to neutron stars's production, evolution and merger, etc. Due to small asymmetry of compressed nuclear matter formed in general heavy-ion collisions in terrestrial laboratory, the effects of nuclear symmetry energy on many observables are generally less than 10% or 20%. Therefore uncertainties from transport models or some other unclear physical inputs inevitably affect interpretation of nuclear symmetry energy from experimental data. Topics on model dependence, qualitative observables, sensitive probes, many-observable cross-constraints, probed density-region of sensitive observables and the effects of short-range correlations should be demonstrated before constraining the density-dependent symmetry energy from experimental data comparisons.
Besides constraining the nuclear symmetry energy from heavy-ion collisions[42, 64], the symmetry energy could be also determined via the studies of neutron star merger[115-116]. It is fascinating to see the match of constraints of the high-density symmetry energy from heaven[117] and earth[118-119] in the near future.
Acknowledgments We thank Lie-Wen Chen, Xiao-Hua Fan, Yuan Gao, Wen-Mei Guo, Bao-An Li, Qing-Feng Li, Gao-Feng Wei, Yong-Jia Wang, Zu-Xing Yang, Fang Zhang, Hong-Fei Zhang and Wei Zuo for collaborations. Also the National Natural Science Foundations of China under Grants No. 11775275, 11375239 and No. 11435014 are greatly acknowledged.
Probing High-density Symmetry Energy Using Heavy-ion Collisions at Intermediate Energies
-
摘要: 用于描述核物质中子质子单粒子能量之差的对称能,最近20年得到了核物理学界的广泛关注。在饱和核密度附近,对称能的数值及斜率基本得到约束,然而其高密行为至今仍具有很大的不确定性。当前,探测对称能的研究计划正在世界范围内能够提供放射性束流的实验室展开。伴随着对称能相关实验的规划、进行,发展更加先进的同位旋依赖的输运理论模型变得非常必要。我们将核子-核子短程关联及介质中同位旋依赖的重子-重子非弹性散射截面等研究的新进展融入到了同位旋依赖的输运模型里面;探索了新的敏感于高密对称能的可观测量,比如挤出核子的中质比、光子、轻碎片,以及包含奇异隐奇异夸克的介子产生等;提出了高密对称能探测盲点的问题并给出解决办法;对于常见的对称能敏感观测量的模型预言的不确定性进行了彻底细致的研究;提出采用定性观测量,比如高能出射粒子的中质比,将高密对称能进行定性约束;率先提出并研究了对称能敏感观测量的探测密度区间问题,指出对称能敏感观测量的探测密度往往小于核反应最大压缩密度;发现核子-核子短程关联明显削弱观测量的对称能效应;考虑到饱和点处对称能斜率的约束范围,基于输运模型,提出通过探测对称能的曲率来约束高密对称能。除了利用重离子碰撞约束高密对称能之外,人们也可以通过与中子星相关的大量天体观测来间接约束高密对称能。Abstract: The nuclear symmetry energy, which describes the energy difference of per proton and neutron in nuclear matter, has been extensively studied within the last two decades. Around saturation density, both the value and the slope of the nuclear symmetry energy have been roughly constrained, its high-density behavior is now still in argument. Probing high-density symmetry energy at terrestrial laboratories is being carried out at facilities that offer radioactive beams worldwide. While relevant experiments are being conducted, we theoretically developed more advanced isospin-dependent transport model including new physics such as nucleon-nucleon short-range correlations and in-medium isospin-dependent baryon-baryon scattering cross section. New sensitive probes of the high-density symmetry energy are provided, such as squeezed-out neutron to proton ratio, photon and light cluster as well as the production of mesons with strangeness or hidden strangeness. The blind spots of probing the high-density symmetry energy by sensitive observable are demonstrated. Model dependences of frequently used sensitive probes of the symmetry energy have been studied thoroughly based on different transport models. A qualitative observable of neutron to proton ratio at high kinetic energy is proposed to probe the high-density symmetry energy qualitatively. The probed density regions of the symmetry energy by some observables are first studied and usually lower probed density regions comparing with maximum compression density are obtained. Nucleon-nucleon short-range correlations usually reduce values of sensitive observables of the symmetry energy. Probing the curvature of the symmetry energy by involving the slope information of the symmetry energy at saturation point in the transport model is proposed. Besides constraining the high-density symmetry energy by using heavy-ion collisions, a lot of neutron-star related observations from heaven may also be used to constrain the high-density symmetry energy.
-
Key words:
- heavy-ion collision /
- high-density symmetry energy /
- sensitive observable
-
Figure 1. (color online)Nuclear symmetry energy given by different nuclear many-body approaches in comparison with the constraining boundaries extracted from studying properties of neutron stars. Taken from Ref. [6].
Figure 2. (color online)Density-dependent symmetry energy with different
$ x $ parameters. Taken from Ref. [53].Figure 3. (color online)Effects of symmetry energy on the non-squeezed-out (panel (a)) and squeezed-out (panel (b)) neutron to proton ratios in 132Sn+124Sn reaction at
$ 400 $ AMeV. Taken from Ref. [55]. Figure 4. (color online)Effects of symmetry energy on the triton-3He relative (panel (a)) and differential (panel (b)) flows as a function of rapidity in the semi-central reaction of 132Sn+124Sn at 400 AMeV. Taken from Ref. [56].
Figure 5. (color online)Effects of symmetry energy on the
$ (\pi^-/\pi^+)_{\rm like} $ ratio in the central 132Sn+124Sn reaction at 400AMeV. Taken from Ref. [57]. Figure 6. (color online)Effects of symmetry energy on the spectra ratio of hard photons in reactions of 132Sn+124Sn and 112Sn+112Sn at 50
AMeV, see text for details. Taken from Ref. [58]. Figure 7. (color online)Effects of symmetry energy on the multiplicity of
$ \eta $ production as a function of incident beam energy in Au+Au reactions. Taken from Ref. [59].Figure 8. (color online)The density-dependent symmetry energy at low and high densities. The symmetry energy below saturation density is fixed as experimental constraints while the high-density symmetry energy is alterable. Taken from Ref. [61].
Figure 9. (color online)Effects of the high-density symmetry energy on the neutron to proton ratio n/p in dense matter (
$ \rho/\rho_{0}\geqslant $ 1) as a function of time in central Au+Au reaction at 300AMeV. The solid line denotes the case without high-density symmetry energy, panels (a), (b), (c) indicate cases with stiff, soft and super-soft symmetry energies, respectively. Taken from Ref. [61]. Figure 10. (color online)Effects of high-density symmetry energy on the free neutron to proton ratio n/p as a function of kinetic energy in central Au+Au reaction at 300 AMeV. The solid line denotes the case without high-density symmetry energy, panels (a), (b), (c) indicate cases with stiff, soft and super-soft symmetry energies, respectively. Taken from Ref. [61].
Figure 11. (color online)Model dependence of n/p ratio of free nucleons and
$ \pi^-/\pi^+ $ ratio as a function of kinetic energy in 197Au+197Au at 400AMeV. Panels (a) and (b) show n/p and $ \pi^-/\pi^+ $ ratio cases, respectively. Taken from Ref. [79].Figure 13. (color online)kinetic energy distribution of neutron to proton ratio n/p of free (panel (a)) and bound nucleons (panel (b)) in the central 197Au+197Au reaction at 400
AMeV with positive (left, $ x $ =–1.2) and negative (right,$ x $ =1) symmetry potentials at supra-saturation densities. Given by the IBUU transport model. Taken from Ref. [5].Figure 15. (color online)Evolution of the relative sensitivity of the symmetry energy observable
$ (\pi^-/\pi^+)_{\rm like} $ ratio in 132Sn+124Sn at 300AMeV (panel (a)) and 208Pb+208Pb at 600 AMeV (panel (b)). Taken from Ref. [84]. Figure 16. (color online)Effects of short-range correlations on the number of produced
$ \pi^{+} $ meson production in Au+Au collisions at 0.4 (panel (a)) and 1 AGeV (panel (b)) beam energies. Taken from Ref. [68].Figure 17. (color online)Effects of short-range correlations on the kinetic energy distributions of
$ \pi^{-} $ (panel (a)),$ \pi^{+} $ (panel (b)) and$ \pi^{-}/\pi^{+} $ ratio (panel (c)) in the reaction of$ ^{197}\rm {Au}+^{197}\rm {Au} $ at 400AMeV. Taken from Ref. [104]. Figure 18. (color online)Effects of short-range correlations on the nucleon elliptic flow (panel (a)) and the difference of neutron and proton elliptic flow (panel (b)) in the semi-central reaction of
$ ^{197}\rm {Au}+ ^{197}\rm {Au} $ at 400AMeV. Taken from Ref. [104]. Figure 19. (color online)Momentum distribution of nucleon with different starting points of protons in 48Ca. Panels (a), (b) show cases without and with proton momentum gap in nucleon momentum distributions, respectively. Taken from Ref. [63].
Figure 20. (color online)The ratio of
$ \pi^{-}/\pi^{+} $ in 132Sn+124Sn reactions at 300AMeV with different proton starting momenta in the HMT. Taken from Ref. [63]. Figure 21. (color online)Effects of symmetry energy on the
$ \pi^{-}/\pi^{+} $ ratio in Au+Au reaction at 400AMeV with different short-range correlations and in-medium cross section. Taken from Ref. [64]. Figure 22. (color online)Effects of symmetry energy on the ratio of neutron and proton elliptic flows
$ v_{2}^{\rm n}/v_{2}^{\rm p} $ in Au+Au reaction at 400AMeV. Taken from Ref. [64]. Figure 24. (color online)Effects of the curvature of nuclear symmetry energy on the squeezed-out neutron to proton ratio in the semi-central reaction of Au+Au at 400 (panel (a)) and 600 (panel (b))
AMeV. The bandwidths denote uncertainties of the slope L. Taken from Ref. [113]. -
[1] BOMBACI I, LOMBARDO U. Phys Rev C, 1991, 44: 1892. doi: 10.1103/PhysRevC.44.1892 [2] LI B A, CHEN L W, KO C M. Phys Rep, 2008, 464: 113. doi: 10.1016/j.physrep.2008.04.005 [3] BARAN V, COLONNA M, GRECO V, et al. Phys Rep, 2005, 410: 335. doi: 10.1016/j.physrep.2004.12.004 [4] DANIELEWICZ P, LACEY R, LYNCH W G. Science, 2002, 298: 1592. doi: 10.1126/science.1078070 [5] GUO W M, YONG G C, WANG Y J, et al. Phys Lett B, 2002, 738: 397. doi: 10.1016/j.physletb.2014.10.011 [6] LI B A, KRASTEV P G, WEN D H, et al. Euro Phys J A, 2019, 55: 117. doi: 10.1140/epja/i2019-12780-8 [7] CHEN L W. Nuclear Physics Review, 2014, 31: 273. doi: 10.11804/NuclPhysRev.31.03.273 [8] LI A, HU J N, BAO S S, et al. Nuclear Physics Review, 2019, 36: 1. (in Chinese) doi: 10.11804/NuclPhysRev.36.01.001 [9] YONG G C, LI B A, CHEN L W. Nuclear Physics Review, 2009, 26: 85. (in Chinese) doi: 10.11804/NuclPhysRev.26.02.085 [10] XU C. Nuclear Physics Review, 2017, 34: 46. doi: 10.11804/NuclPhysRev.34.01.046 [11] ZHANG Y X, LU X H, ZHAO K, et al. Nuclear Physics Review, 2011, 28: 377. (in Chinese) doi: 10.11804/NuclPhysRev.28.04.377 [12] SUMIYOSHI K, SUZUKI H, TOKI H. Astron Astrophys, 1995, 303: 475. [13] SUMIYOSHI K, TOKI H. Astrophys J, 1994, 422: 700. doi: 10.1086/173763 [14] LATTIMER J M, PRAKASH M. Science, 2004, 304: 536. doi: 10.1126/science.1090720 [15] STEINER A W, PRAKASH M, LATTIMER J M, et al. Phys Rep, 2005, 411: 325. doi: 10.1016/j.physrep.2005.02.004 [16] LATTIMER J M, STEINER A W. Eur Phys J A, 2014, 50: 40. doi: 10.1140/epja/i2014-14040-y [17] WEN D H, JING Z Z. Nuclear Physics Review, 2015, 32: 161. (in Chinese) doi: 10.11804/NuclPhysRev.32.02.161 [18] FISCHER T. Eur Phys J A, 2014, 50: 46. doi: 10.1140/epja/i2014-14046-5 [19] NIKOLOV N, SCHUNCK N, NAZAREWICZ W, et al. Phys Rev C, 2011, 83: 034305. doi: 10.1103/PhysRevC.83.034305 [20] GORIELY S, BAUSWEIN A, JANKA H T. Astrophys J, 2011, 738: 32. doi: 10.1088/0004-637X/738/1/32 [21] BAUSWEIN A, GORIELY S, JANKA H T. Astrophys J, 2013, 773: 78. doi: 10.1088/0004-637X/773/1/78 [22] WANAJO S, SEKIGUCHI Y, NISHIMURA N, et al. Astrophys J, 2014, 789: 39. doi: 10.1088/0004-637X/789/1/39 [23] MASELLI A, GUALTIERI L, FERRARI V. Phys Rev D, 2013, 88: 104040. doi: 10.1103/PhysRevD.88.104040 [24] BAUSWEIN A, STERGIOULAS N, JANKA H T. Phys Rev D, 2014, 90: 023002. doi: 10.1103/PhysRevD.90.023002 [25] LASKY P D, HASKELL B, RAVI V, et al. Phys Rev D, 2014, 89: 047302. doi: 10.1103/PhysRevD.89.047302 [26] ROSSWOG S. International Journal of Modern Physics D, 2015, 24: 1530012. [27] ABBOTT B P, ABBOTT R, ACERNESEET T D, et al. Phys Rev Lett, 2017, 119: 161101. doi: 10.1103/PhysRevLett.119.161101 [28] LI B A, HAN X. Phys Lett B, 2013, 727: 276. doi: 10.1016/j.physletb.2013.10.006 [29] OERTEL M, HEMPEL M, KLAHN T, et al. Rev Mod Phys, 2017, 89: 015007. doi: 10.1103/RevModPhys.89.015007 [30] XIAO Z G, LI B A, CHEN L W, et al. Phys Rev Lett, 2009, 102: 062502. doi: 10.1103/PhysRevLett.102.062502 [31] FENG Z Q, JIN G M. Phys Lett B, 2010, 683: 140. doi: 10.1016/j.physletb.2009.12.006 [32] RUSSOTTO P, WU P Z, ZORIC M, et al. Phys Lett B, 2011, 697: 471. doi: 10.1016/j.physletb.2011.02.033 [33] COZMA M D, LEIFELS Y, TRAUTMANN W, et al. Phys Rev C, 2013, 88: 044912. doi: 10.1103/PhysRevC.88.044912 [34] XIE W J, SU J, ZHU L, et al. Phys Lett B, 2013, 718: 1510. doi: 10.1016/j.physletb.2012.12.021 [35] WANG Y J, GUO C C, LI Q F, et al. Phys Rev C, 2014, 89: 044603. doi: 10.1103/PhysRevC.89.044603 [36] XU J, CHEN L W, KO C M, et al. Phys Rev C, 2013, 87: 067601. doi: 10.1103/PhysRevC.87.067601 [37] GUO W M, YONG G C, ZUO W. Phys Rev C, 2015, 91: 054616. doi: 10.1103/PhysRevC.91.054616 [38] HONG J, DANIELEWICZ P. Phys Rev C, 2014, 90: 024605. doi: 10.1103/PhysRevC.90.024605 [39] YONG G C, ZUO W, ZHANG X C. Phys Lett B, 2011, 705: 240. doi: 10.1016/j.physletb.2011.10.020 [40] PANDHARIPANDE V R, GARDE V K. Phys Lett B, 1972, 39: 608. doi: 10.1016/0370-2693(72)90009-3 [41] XU C, LI B A. http://arxiv.org/abs/1104.2075, arXiv: 1104. 2075. [42] RUSSOTTO P. Phys Rev C, 2016, 94: 034608. doi: 10.1103/PhysRevC.94.034608 [43] LU L M. Sci China-Phys Mech Astron, 2017, 60: 012021. doi: 10.1007/s11433-016-0342-x [44] BOLLEN G. AIP Conf Proc, 2010, 1224: 432. [45] Symmetry Energy Project[EB/OL].[2019-12-15]. https://groups.nscl.msu.edu/hira/sepweb/pages/home.html. [46] SHANE R. Nucl Instr and Meth A, 2015, 784: 513. doi: 10.1016/j.nima.2015.01.026 [47] YANO Y. Nucl Instr and Meth B, 2007, 261: 1009. doi: 10.1016/j.nimb.2007.04.174 [48] TSHOO K. Nucl Instr and Meth B, 2013, 317: 242. doi: 10.1016/j.nimb.2013.05.058 [49] BERTSCH G F, DAS GUPTA S. Phys Rep, 1988, 160: 189. doi: 10.1016/0370-1573(88)90170-6 [50] DAS C B, DAS GUPTA S, GALE C, et al. Phys Rev C, 2003, 67: 034611. doi: 10.1103/PhysRevC.67.034611 [51] KHAN E, MARGUERON J, VIDANA I. Phys Rev Lett, 2012, 109: 092501. doi: 10.1103/PhysRevLett.109.092501 [52] DANIELEWICZ P. Nucl Phys A, 2000, 673: 375. doi: 10.1016/S0375-9474(00)00083-X [53] YONG G C. Phys Rev C, 2017, 96: 044605. doi: 10.1103/PhysRevC.96.044605 [54] LI B A, CHEN L W. Phys Rev C, 2005, 72: 064611. doi: 10.1103/PhysRevC.72.064611 [55] YONG G C, LI B A, CHEN L W. Phys Lett B, 2007, 650: 344. doi: 10.1016/j.physletb.2007.05.050 [56] YONG G C, LI B A, CHEN L W, et al. Phys Rev C, 2009, 80: 044608. doi: 10.1103/PhysRevC.80.044608 [57] LI B A, YONG G C, ZUO W. Phys Rev C, 2005, 71: 014608. doi: 10.1103/PhysRevC.71.014608 [58] YONG G C, LI B A, CHEN L W. Phys Lett B, 2008, 661: 82. doi: 10.1016/j.physletb.2008.02.013 [59] YONG G C, LI B A. Phys Lett B, 2013, 723: 388. doi: 10.1016/j.physletb.2013.05.059 [60] LI B A. Nucl Phys A, 2002, 708: 365. doi: 10.1016/S0375-9474(02)01018-7 [61] YONG G C. Phys Lett B, 2018, 786: 422. doi: 10.1016/j.physletb.2018.10.018 [62] YONG G C, LI B A. Phys Rev C, 2017, 96: 064614. doi: 10.1103/PhysRevC.96.064614 [63] YONG G C. Phys Lett B, 2018, 776: 447. doi: 10.1016/j.physletb.2017.11.075 [64] YONG G C. Phys Rev C, 2016, 93: 044610. doi: 10.1103/PhysRevC.93.044610 [65] FRIEDRICH J, REINHARD P G. Phys Rev C, 1986, 33: 335. doi: 10.1103/PhysRevC.33.335 [66] SUBEDI R(HALL A. Collaboration). Science, 2008, 320: 1476. [67] HEN O(The CLAS Collaboration). Science, 2014, 346: 614. [68] YONG G C. Phys Lett B, 2017, 765: 104. doi: 10.1016/j.physletb.2016.12.013 [69] HOROWITZ C J, BROWN E F, KIM Y. J Phys G Nucl Part Phys, 2014, 41: 093001. doi: 10.1088/0954-3899/41/9/093001 [70] CHEN L W. Nuclear Physics Review, 2017, 34: 20. doi: 10.11804/NuclPhysRev.34.01.020 [71] MULLER H, SEROT B D. Phys Rev C, 1995, 52: 2072. doi: 10.1103/PhysRevC.52.2072 [72] LI B A, KO C M. Nucl Phys A, 1997, 618: 498. doi: 10.1016/S0375-9474(97)00124-3 [73] BARAN V, LARIONOV A, COLONNA M, et al. Nucl Phys A, 1998, 632: 287. doi: 10.1016/S0375-9474(98)00006-2 [74] SHI L, DANIELEWICZ P. Euro Phys Lett, 2000, 49: 34. doi: 10.1209/epl/i2000-00116-1 [75] LI B A, CHEN L W, YONG G C, et al. Phys Lett B, 2006, 634: 378. doi: 10.1016/j.physletb.2006.02.003 [76] LI B A, KO C M, REN Z Z. Phys Rev Lett, 1997, 78: 1644. doi: 10.1103/PhysRevLett.78.1644 [77] BASS S A, HARTNACK C, STOECKER H, et al. Phys Rev C, 1995, 51: 3343. [78] LI Q F, SHEN C W, GUO C C, et al. Phys Rev C, 2011, 83: 044617. doi: 10.1103/PhysRevC.83.044617 [79] GUO W M, YONG G C, WANG Y J, et al. Phys Lett B, 2013, 726: 211. doi: 10.1016/j.physletb.2013.07.056 [80] LI B A. Phys Rev Lett, 2002, 88: 192701. doi: 10.1103/PhysRevLett.88.192701 [81] YONG G C, LI B A, CHEN L W, ZUO W. Phys Rev C, 2006, 73: 034603. doi: 10.1103/PhysRevC.73.034603 [82] OTSU H. Nucl Instr Meth B, 2016, 376: 175. doi: 10.1016/j.nimb.2016.02.056 [83] JHANG G. Journ Of the Kor Phys Soc, 2016, 69: 144. doi: 10.3938/jkps.69.144 [84] YONG G C, GAO Y, WEI G F, et al. J Phys G Nucl Part Phys, 2019, 46: 105105. doi: 10.1088/1361-6471/ab3772 [85] FAN X H, YONG G C, ZUO W. Phys Rev C, 2018, 97: 034604. doi: 10.1103/PhysRevC.97.034604 [86] LAPIKAS L. Nucl Phys A, 1993, 553: 297. doi: 10.1016/0375-9474(93)90630-G [87] KELLY J. Adv Nucl Phys, 1996, 23: 75. [88] PIASETZKY E, SARGSIAN M, FRANKFURT L, et al. Phys Rev Lett, 2006, 97: 162504. doi: 10.1103/PhysRevLett.97.162504 [89] SHNEOR R. Phys Rev Lett, 2007, 99: 072501. doi: 10.1103/PhysRevLett.99.072501 [90] SARGSIAN M M, ABRAHAMYAN T V, STRIKMAN M I, et al. Phys Rev C, 2005, 71: 044615. doi: 10.1103/PhysRevC.71.044615 [91] SCHIAVILLA R, WIRINGA R B, PIEPER S C, et al. Phys Rev Lett, 2007, 98: 132501. doi: 10.1103/PhysRevLett.98.132501 [92] BETHE H A. Ann Rev Nucl Part Sci, 1971, 21: 93. doi: 10.1146/annurev.ns.21.120171.000521 [93] ANTONOV A N, HODGSON P E, PETKOV I Z. Nucleon Momentum and Density Distributions in Nuclei[M]. Oxford: Clarendon Press, 1988. [94] RIOS A, POLLS A, DICKHOFF W H. Phys Rev C, 2009, 79: 064308. doi: 10.1103/PhysRevC.79.064308 [95] YIN P, LI J Y, WANG P, et al. Phys Rev C, 2013, 87: 014314. doi: 10.1103/PhysRevC.87.014314 [96] CIOFI DEGLI ATTI C. Phys Rep, 2015, 590: 1. doi: 10.1016/j.physrep.2015.06.002 [97] CIOFI DEGLI ATTI C. SIMULA S, Phys Rev C, 1996, 53: 1689. doi: 10.1103/PhysRevC.53.1689 [98] FANTONI S, PANDHARIPANDE V R. Nucl Phys A, 1984, 427: 473. doi: 10.1016/0375-9474(84)90226-4 [99] PIEPER S C, WIRINGA R B, PANDHARIPANDE V. Phys Rev C, 1992, 46: 1741. doi: 10.1103/PhysRevC.46.1741 [100] EGIYAN K. Phys Rev C, 2003, 68: 014313. doi: 10.1103/PhysRevC.68.014313 [101] HEN O, WEINSTEIN L B, PIASETZKY E, et al. Phys Rev C, 2003, 92: 045205. doi: 10.1103/PhysRevC.92.045205 [102] HEN O, LI B A, GUO W J, et al. Phys Rev C, 2015, 91: 025803. doi: 10.1103/PhysRevC.91.025803 [103] CAI B J, LI B A. Phys Rev C, 2015, 92: 011601. [104] ZHANG F, YONG G C. Eur Phys J A, 2016, 52: 350. doi: 10.1140/epja/i2016-16350-4 [105] VIDANA I. Phys Rev C, 2009, 80: 045806. doi: 10.1103/PhysRevC.80.045806 [106] TEWS I, LATTIMER J M, OHNISHI A, K, et al. Astrophys J, 2009, 848: 105. doi: 10.3847/1538-4357/aa8db9 [107] ZHANG N B, CAI B J, LI B A, et al. Nucl Sci Tech, 2017, 28: 181. doi: 10.1007/s41365-017-0336-2 [108] PIEKAREWICZ J, CENTELLES M. Phys Rev C, 2009, 79: 054311. doi: 10.1103/PhysRevC.79.054311 [109] STOCKER H, GREINER W. Phys Rep, 1986, 137: 277. doi: 10.1016/0370-1573(86)90131-6 [110] CASSING W, METAG V, MOSEL U, et al. Phys Rep, 1990, 188: 363. doi: 10.1016/0370-1573(90)90164-W [111] AICHELIN J. Phys Rep, 1991, 202: 233. doi: 10.1016/0370-1573(91)90094-3 [112] REISDORF W, RITTER H G. Annu Rev Nucl Part Sci, 1997, 47: 663. doi: 10.1146/annurev.nucl.47.1.663 [113] GUO Y F, YONG G C. Phys Rev C, 2019, 100: 014617. doi: 10.1103/PhysRevC.100.014617 [114] COZMA M D. Eur Phys J A, 2018, 54: 40. doi: 10.1140/epja/i2018-12470-1 [115] ZHANG N B, LI B A. Eur Phys J A, 2019, 55: 39. doi: 10.1140/epja/i2019-12700-0 [116] TSANG C Y, TSANG M B, DANIELEWICZ P, et al. arXiv, 2019, 1901.07673. [117] ABBOTT B P[LIGO+Virgo Collaborations]. Phys Rev Lett, 2017, 119: 161101. [118] The 2015 U.S. Long Range Plan for Nuclear Science, Reaching for the Horizon[EB/OL].[2020-02-05]. https://science.energy.gov/~/media/np/nsac/pdf/2015LRP/2015_LRPNS_091815.pdf. [119] The Nuclear Physics European Collaboration Committee (NuPECC) Long Range Plan 2017, Perspectives in Nuclear Physics[EB/OL].[2020-02-05]. http://www.esf.org/fileadmin/user_upload/esf/Nupecc-LRP2017.pdf. -




 下载:
下载:



























































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号