-
BRing作为强流重离子加速器HIAF(High Intensity heavy-ion Accelerator Facility)[1]的增强器,具有加速质子到铀离子的能力。由于质子和重离子的注入能量低,例如238U35+的注入能量为17 MeV,回旋频率为0.099 MHz,低于高频加速腔的最低工作频率。为满足高频加速腔的带宽要求,需要采用高次谐波进行加速。加速完成后,采用单圈快引出方式[2]将束流引出到实验装置,因此需要将多个束团合为一个。将多个束团合为单个束团,通常有两种方法:散束再聚束和束团合并[3]。散束再聚束是将高频电压降至零后,多个束团散成漂移束,再使用一次谐波将漂移束俘获成单个束团。在漂移束状态时,束流动量分散很小,容易受到纵向空间电荷效应或环中元件阻抗的影响而产生微波不稳定性[4]。同时,束流在尾场的影响下所损失的能量无法通过高频电压补偿,导致束流同步能量的下降。束团合并采用多个高频谐波,在合并过程中,高次谐波电压逐渐降低,低次谐波(多为前一高次谐波的二分频)逐渐上升,直至最后1次谐波将束流俘获成单个束团。束团合并过程中,束团始终处于高频电压的控制下从而避免产生微波不稳定性和同步能量下降,因此HIAF-BRing采用束团合并的方式将多个束团合为单个束团。
BRing中采用磁合金加载腔[5]对束流进行加速。与铁氧体腔[6]相比,磁合金加载腔具有加速梯度高、频率覆盖宽等特点。采用磁合金加载腔能够在不占用过多空间的情况下提供高的加速电压,满足BRing快循环的要求。同时磁合金加载腔的频率范围宽,能够在不添加调谐模块的情况下覆盖重离子加速过程中的频率变化。由于高频腔存在较大阻抗,束流在通过高频腔体时,会产生尾场。尾场电压与高频功率源在腔体激发的电压叠加后作用到束流上,影响束流的品质,严重时会引起束流损失。因此需要高频功率源提供额外的功率来补偿束流尾场电压,这就是束流负载效应。表1为BRing及其高频系统的部分参数。BRing中共6个磁合金加载腔提供最高270 kV的高频电压。
BRing中单次加速的238U35+的粒子数(particles per pulse,ppp)达到1
$ \times 10^{11} $ ,因此需要确定尾场对束流造成的影响。线密度为高斯分布的束团的尾场电压分布为[7]$$ \begin{split} V(\tau ) =& \frac{{q{\omega _r}{R_{\rm{s}}}}}{{2Q\cos (\theta )}}{\rm{Real}}\left\{ {{{\rm e}^{{\rm{i}}\theta - {\tau ^2}/(2\sigma _\tau ^2)}} \times } \right.\\ &\left. {f\left(\frac{{{\sigma _\tau }{\omega _r}{{\rm e}^{{\rm{i}}\theta }}}}{{\sqrt 2 }} + \frac{{{\rm{i}}\tau }}{{\sqrt 2 {\sigma _\tau }}}\right)} \right\}, \end{split} $$ (1) 式中:
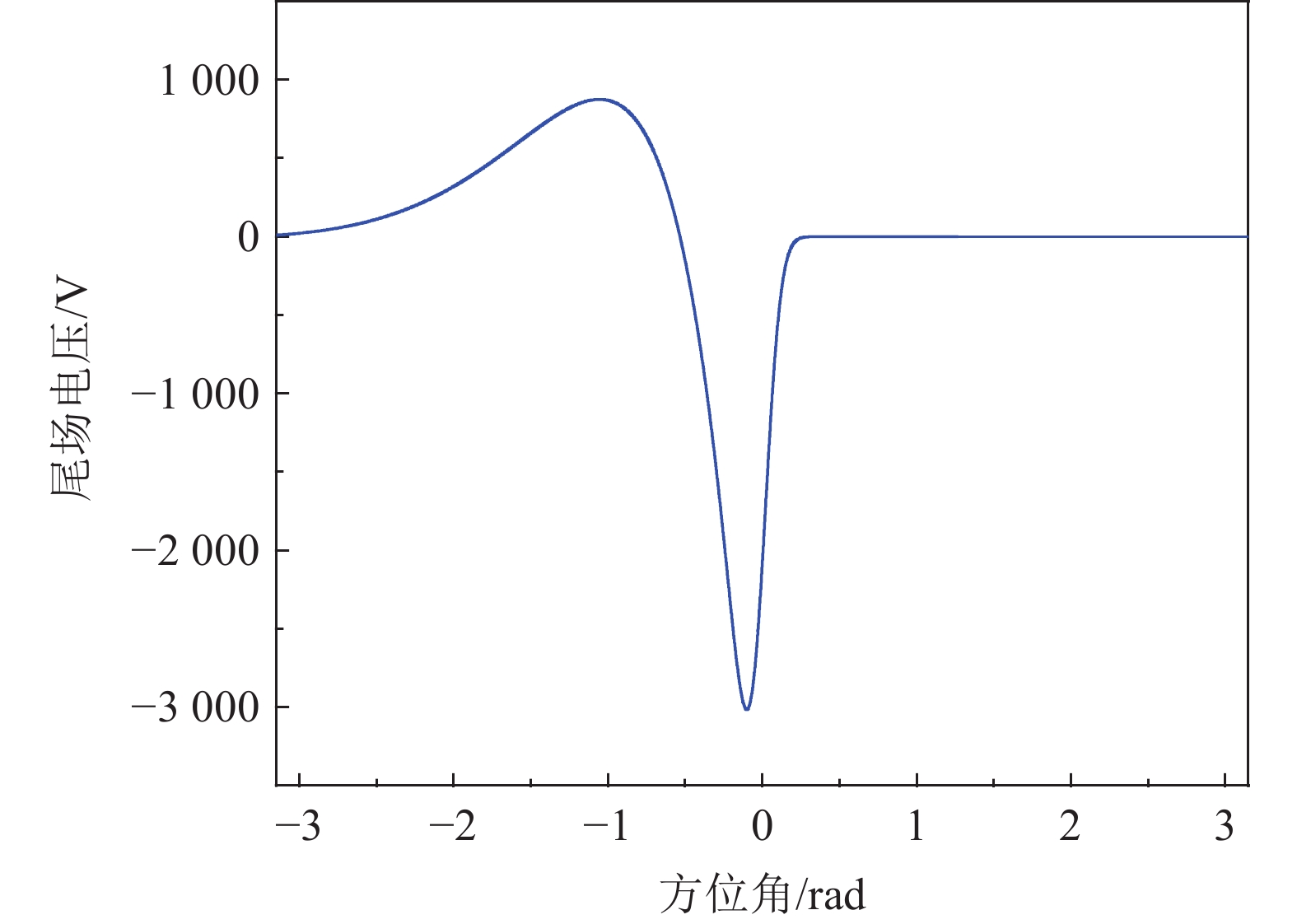
$ q $ 为束团所带电荷数;$ \omega_r $ 为腔体的谐振频率;$ R_{\rm s} $ 为腔体的分路阻抗;$ Q $ 为腔体$ Q $ 值;$ \theta\equiv\arccos (\sqrt{|1-1/(4Q^2)|}) $ ;Real为取复数实部;$ f $ 为复误差函数;$ \tau $ 为时间;$ \sigma_\tau $ 为束团的RMS时间长度。用方位角替代时间作为变量,BRing中采用4次谐波加速过程尾场电压达到最大值时, 单个束团的尾场分布如图1所示,束团中心处于方位角为0的位置。尾场在距离束团中心较近处为负值,距离超过0.5 rad后变为正值。BRing最高采用4次谐波加速,而距离束团中心$ (2\pi)/4 $ 处的尾场电压约为幅值的20%。因此BRing中的束流负载效应主要体现为瞬态效应,束团主要感受到其本身产生的尾场电压。但是在束团合并过程中,两个束团中心的间距逐渐减小,当距离过小时,即会出现束团间的耦合效应,合并的两个束团中运动靠前的束团产生的尾场会对与之合并的另一个束团产生影响。这种束团耦合效应会引起合束后束团中心的振荡和束流纵向发射度的增长,需要研究确定其影响大小并在必要时采用前馈系统进行补偿。表 1 BRing及高频系统部分参数
参数 数值 周长C 569.1 m 转变能$ {\rm{\gamma}}_{\rm t} $ 7.645 85 动量接收度 ±0.005 分路阻抗$ R_{\rm s} $ 2.8~3.7 kΩ $Q$值 0.45~0.6 谐振频率$f_r$ 1.0 MHz 最大峰值电压$V_{\rm RF,\,max} $ 270 kV 本文介绍了对BRing中典型粒子束流238U35+纵向跟踪模拟的结果,并结合理论对模拟结果进行分析,针对结果提出了相应的补偿措施,对补偿结果进行对比和分析,最后提出了HIAF-BRing束团合并过程对前馈系统的参数要求。
-
为了研究BRing中束流负载效应的影响,对典型的粒子束流238U35+进行了纵向跟踪模拟。模拟采用的纵向动力学跟踪程序LPTC (Longitudinal Particle Tracking Code)是针对操作复杂和采用低
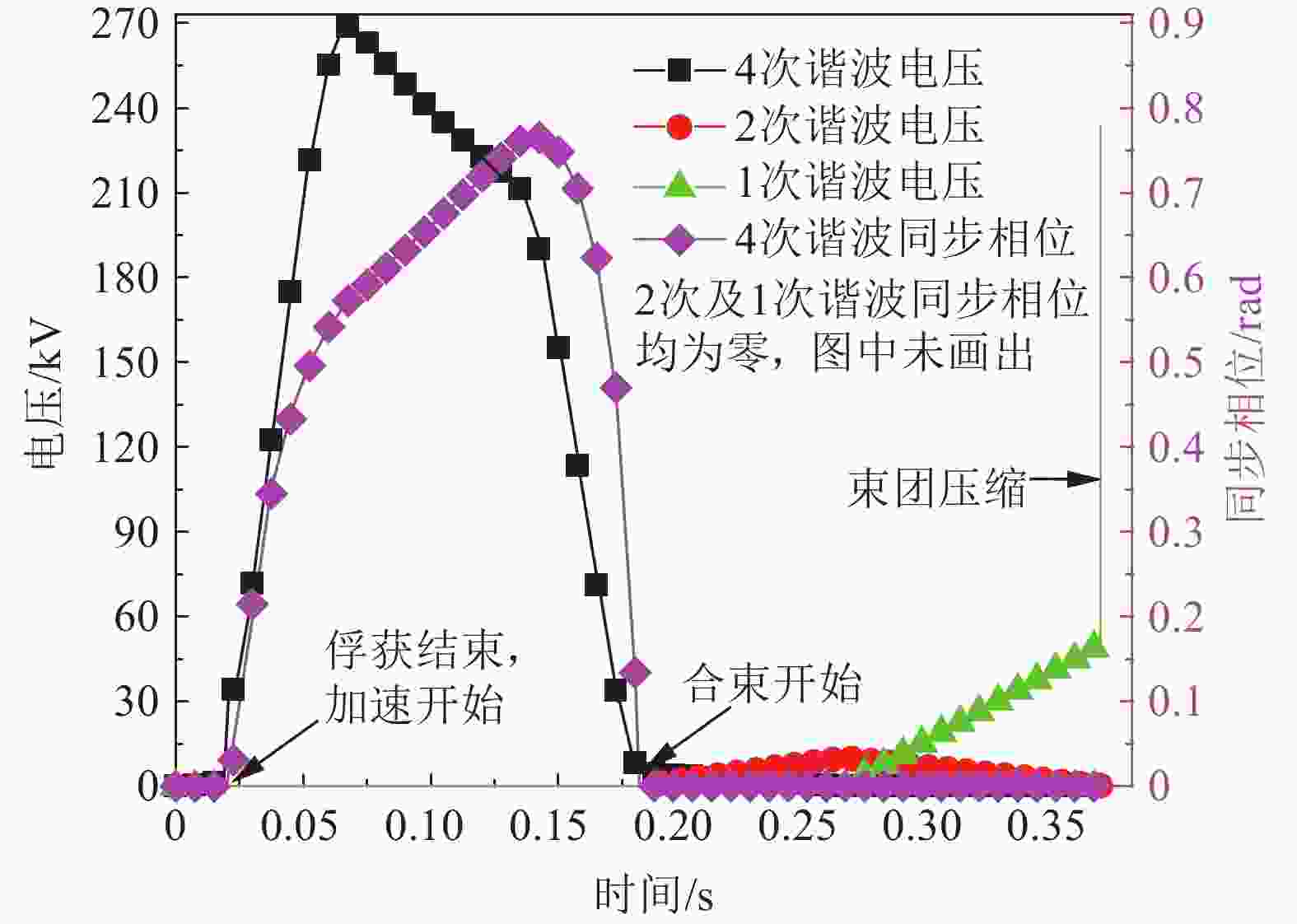
$ Q $ 值磁合金加载腔的重离子加速器而开发的,能在时域模拟$ Q $ 值小于0.5的高频腔体引起的尾场。图2是模拟采用的高频加速电压及同步相位曲线,表2是模拟采用的束流参数。束流注入到BRing后为漂移束状态,快引出模式下,经过俘获阶段、加速阶段及束团合并阶段,最终得到单个束团进行引出。俘获和加速阶段采用4次谐波以满足高频系统的下频率边带要求。束团合并采用4次、2次和1次谐波。加速结束后,4次谐波开始下降,2次谐波上升,4次谐波降至零时2次谐波上升到最大值,束团个数由4个合并为2个。此后2次谐波开始下降直至零,1次谐波逐渐上升,束团由2个合并为1个。合束时间过短会造成合束过程中的发射度稀释[8],为降低BRing合束过程中束流发射度的稀释,两次合束时间均大于10倍同步振荡周期,模拟结果表明,没有束流负载效应时的束流发射度稀释小于3%。图中1次谐波电压在加速周期末尾处快速上升,是为了通过束团非绝热压缩[9]来获得短束团。表 2 粒子跟踪模拟所采用的束流参数
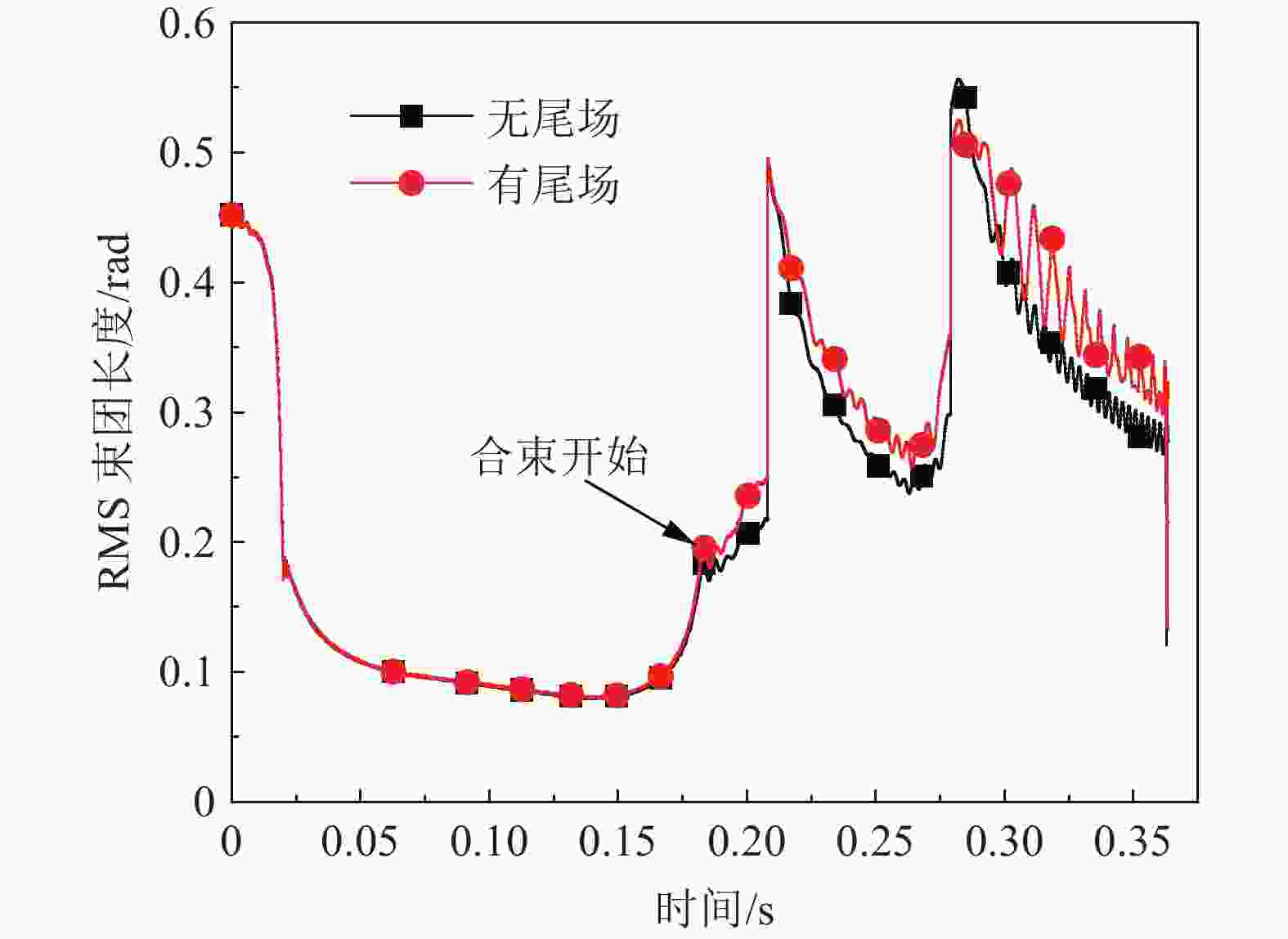
参数 数值 粒子种类 238U35+ 注入能量$E_{\rm inj} $ 17 MeV/u 引出能量$E_{\rm ext} $ 800 MeV/u 谐波数h 4, 2, 1 注入动量分散(3$\sigma$) $\delta$ ±0.002 束流流强 1×1011 ppp (55~249 mA) 回旋频率$F_{\rm rev} $ 0.099~0.444 MHz 图3是单个运行周期的束流动量分散统计结果(均方根差,即RMS,下同)。可以看出,在加速阶段束流的动量分散受尾场影响很小。从束团合并开始,尾场的存在使得束流的动量分散有所增加,在束团压缩之前相对于无尾场情况增加了10.7%。图4是束团长度统计结果。在加速阶段尾场的影响较小。束团合并开始后,由于尾场的存在,束团长度有所增长,束团长度的振荡幅度更大。在束团压缩之前束团长度震荡幅度增长80%,束团长度(以其振荡中心计算)相对于无尾场情况增长14.5%。
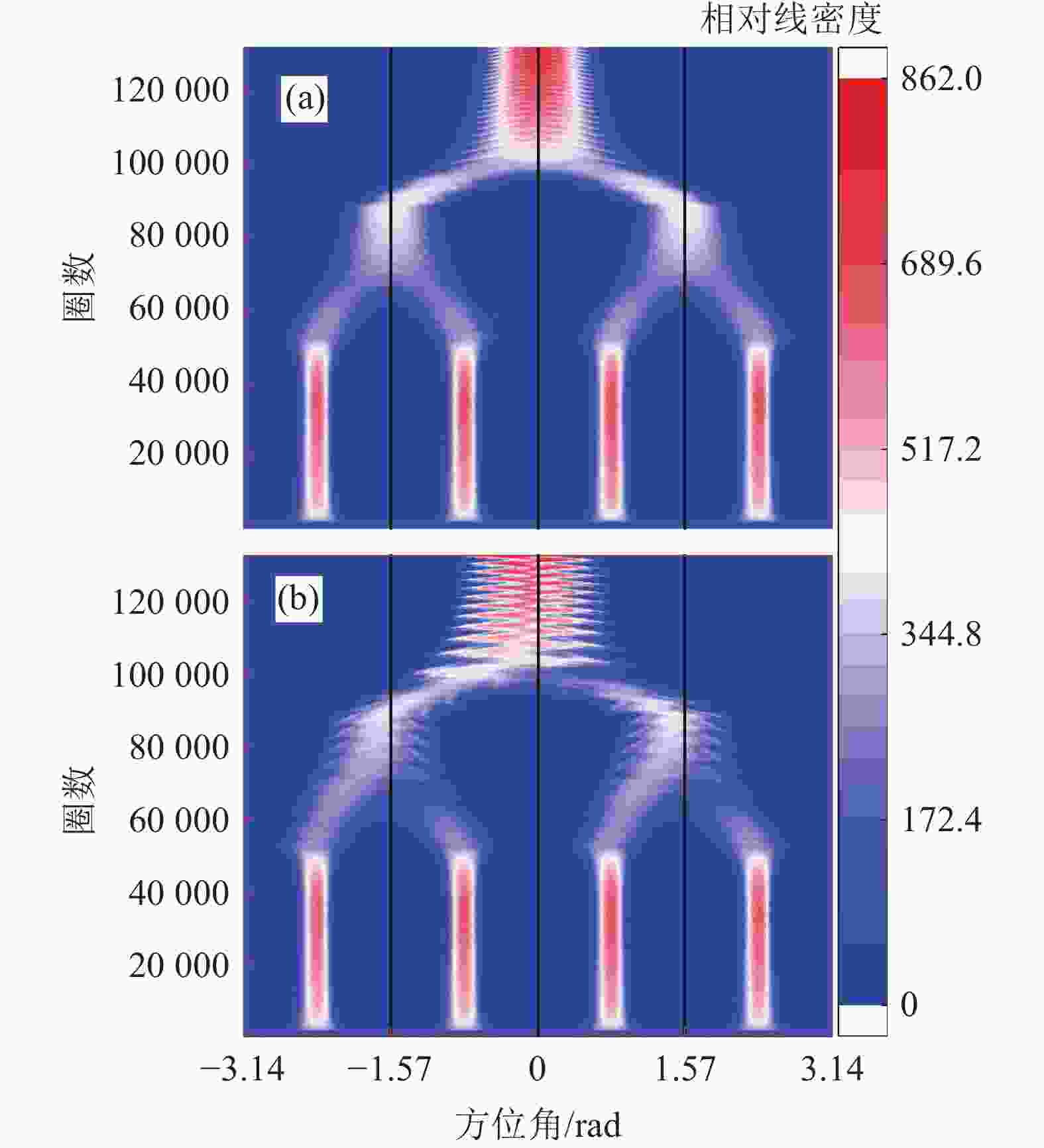
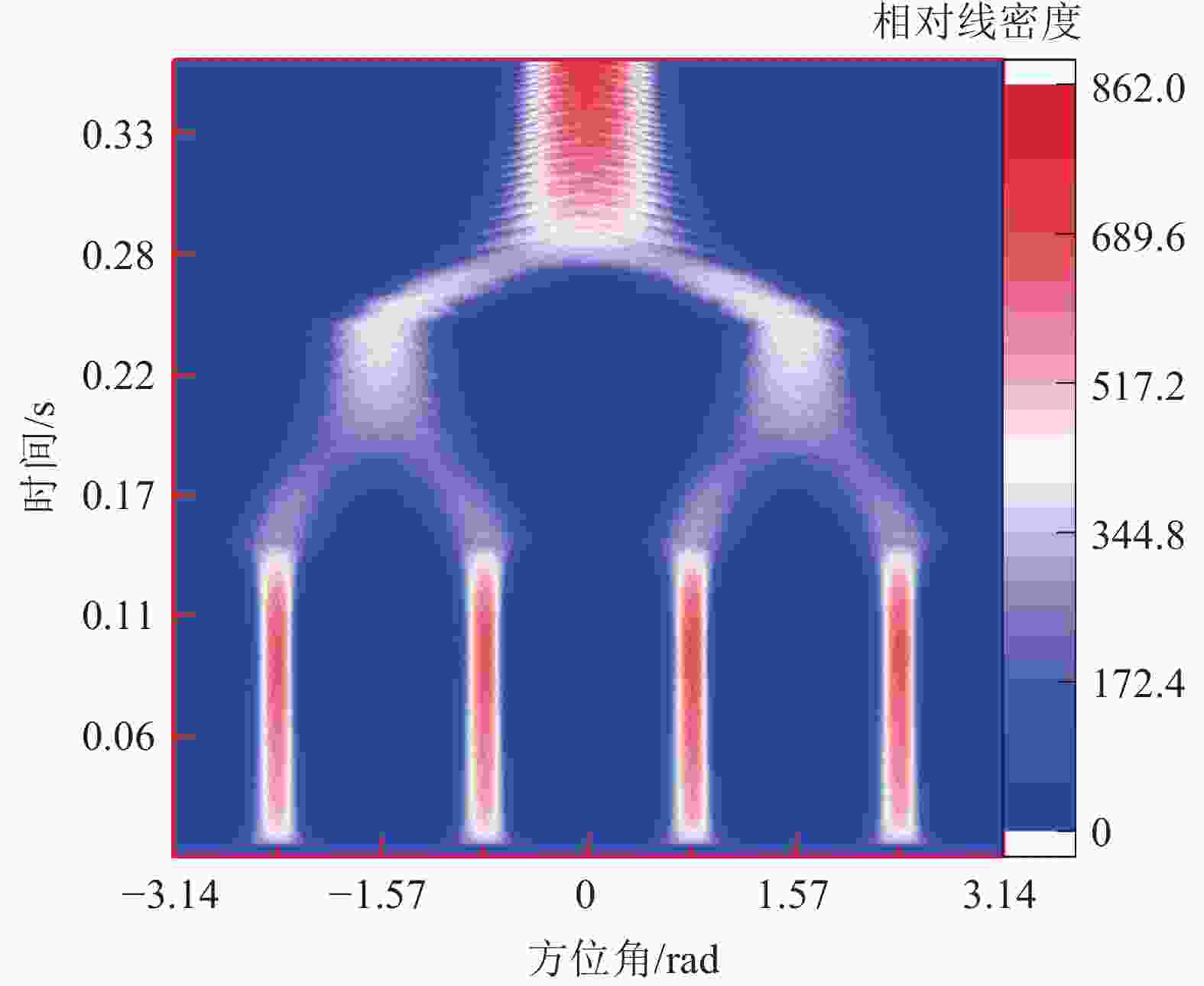
图5是束流分布的热图。由图可见,在进行束团合并之前,尾场对束团中心位置无明显影响。4次谐波到2次谐波束团合并过程中,尾场的存在导致束团的中心出现小幅震荡,同时束团的中心所处方位角小于无尾场情况,即在环中运动时与无尾场情况相比,束团中心相对落后,所对应的高频相位更大,束团从高频场中获得更多能量与尾场引起的能量损失达到平衡。合并为单个束团后,束团的中心位置出现明显振荡,且振荡的中心所处方位角同样小于无尾场时的情况。束团合并的过程中可以看到,合并的两个束团的运动轨迹并不是对称的。以上几种情况均表明,束流在束团合并过程中受到尾场的影响,同时由于束团中心的靠近,束团之间出现较强耦合现象。
-
尾场引起的不稳定性的阈值,可以结合束流负载因子进行判定[10]。对比BRing加速过程中动量分散和束团长度的变化可以看到,尾场引起的束团长度的振荡比动量分散更明显,且振幅随时间有减小趋势,这表明尾场的主要影响是引起了势阱畸变而不是不稳定性。采用尾场电压与高频系统建立的最大电压的比值来衡量势阱畸变的大小,可以用来分析束流负载效应影响的大小。图6是单个运行周期内的尾场电压及尾场电压与腔体内最大高频电压之比。在俘获阶段,尾场电压与高频电压的比值较大但此时尾场电压小,随着高频俘获电压升高,尾场的影响快速下降。在加速阶段,尾场电压相对于高频电压很小,因此对束流的影响也比较小。在束团合并阶段,尾场电压较大,且与高频电压之比快速增大,最大值达到0.35,此时尾场的影响不可忽略。
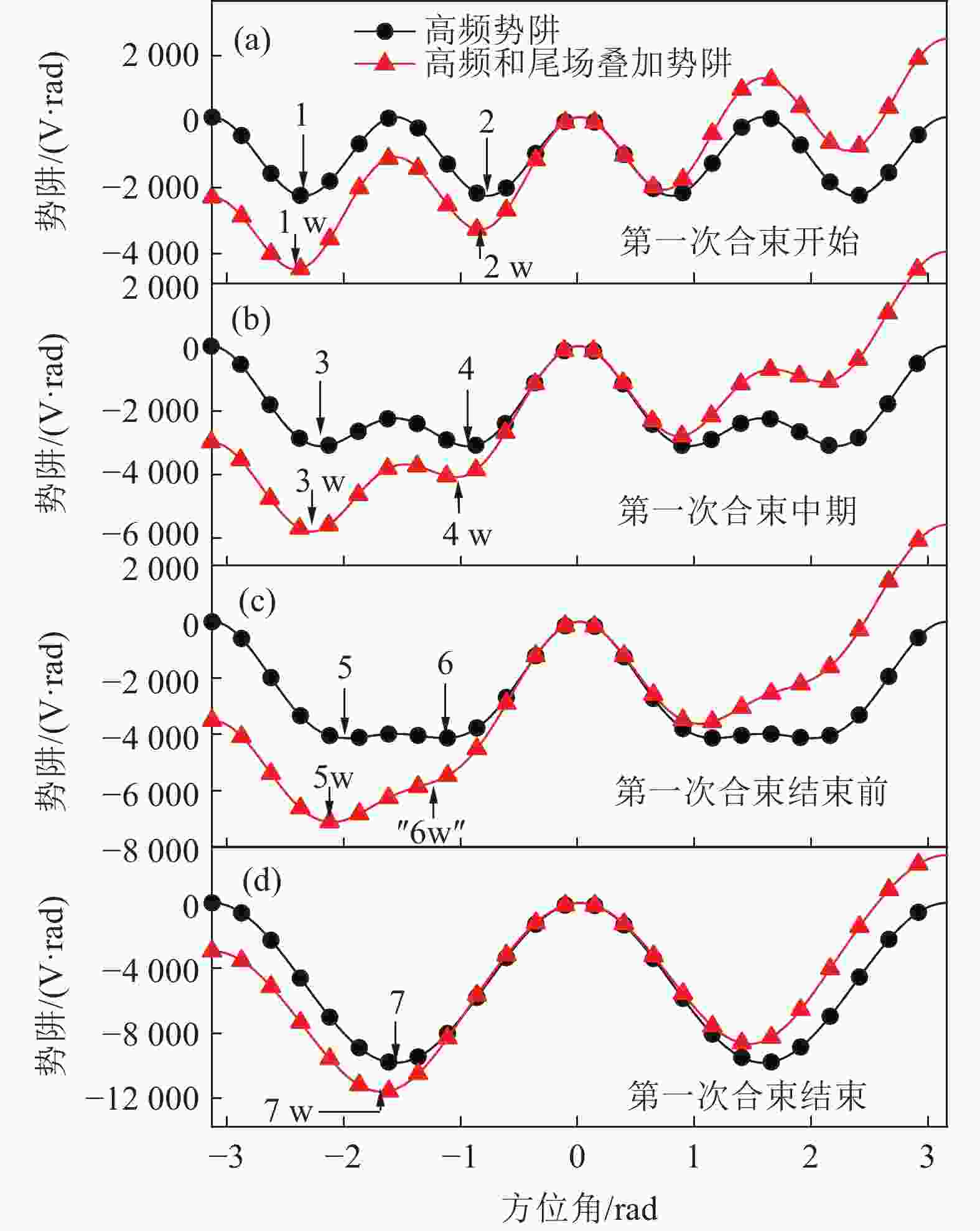
图7为第一次束团合并过程的势阱变化。以左侧两个势阱为例分析尾场对势阱的影响。图中标注1表示高频电压在该处形成的势阱,势阱1w表示势阱1受尾场电压影响而形成的新势阱,箭头所指区域为对应势阱的最低处,下同。第一次束团合并开始时,由于尾场的存在,势阱1w向左(向左表示对应方位角偏小,对应的高频相位偏大,下同)偏移了0.06 rad,同时势阱2w深度降低了约10%。束团合并中期,尾场的存在使得势阱3w加深而势阱4w变浅。第一次束团合并结束前随着4次谐波电压下降,2次谐波电压上升,在无尾场情况下势阱5和势阱6即将消失,其之间存在较小的势垒,两个势阱中的束团的等效中心在此势垒处,即-
$ \pi /2 $ 处。由于束团间距离减小,尾场存在时,原本处于势阱6w处的束团的尾场电压抵消了高频电压在势阱5和势阱6之间形成的势垒,势阱6w消失,在势阱5w处形成一个单独的势阱,使得原本处于势阱6处的粒子向左运动到5w处。此时势阱的不对称会导致束团分布的不对称。到第一次束团合并结束,4次谐波电压降为0,2次谐波电压形成势阱7,原本处于势阱5和势阱6处的2个束团被势阱7俘获,形成1个束团,其中心仍处于–$ \pi /2 $ 。有尾场的情况下,束团的中心位置由势阱5w附近移动到势阱7w附近,相位短时间内幅度变化过大,同时束团分布不对称,从而引起束团中心的振荡。第二次束团合并的过程和第一次相同,但振幅更大,有两个原因:一是此时单束团流强增大,尾场电压更大,导致束团偏离同步相位幅度更大。二是第一次束团合并过程引起的振荡部分叠加到第二次束团合并过程中。图8为束流纵向压缩前的纵向相空间分布,与无尾场情况相比,有尾场时束团中心明显偏移。束团合并过程中的势阱畸变导致束流在相空间的丝化,引起束流纵向发射度的增长。
-
由于尾场的存在,束团合并后中心振荡过大,不利于束流的引出,同时束流动量分散和束团长度有一定增长。为了提供高品质稳定单束团引出,需要对束流尾场进行补偿。瞬态束流负载效应的补偿有多种方式[7],采用磁合金加载腔引起的瞬态束流负载效应,需要在扫频状态下补偿多个谐波频率下的尾场,可以采用多谐波前馈系统[11]进行补偿。其主要过程可由以下两个等式说明:
$$ V(h\omega) = Z(h\omega)\times I(h\omega), $$ (2) $$ V(t) = \Sigma_{h\in A} \bar{V}(h\omega) \sin(h\omega t+ \phi_h), $$ (3) 式(2)中
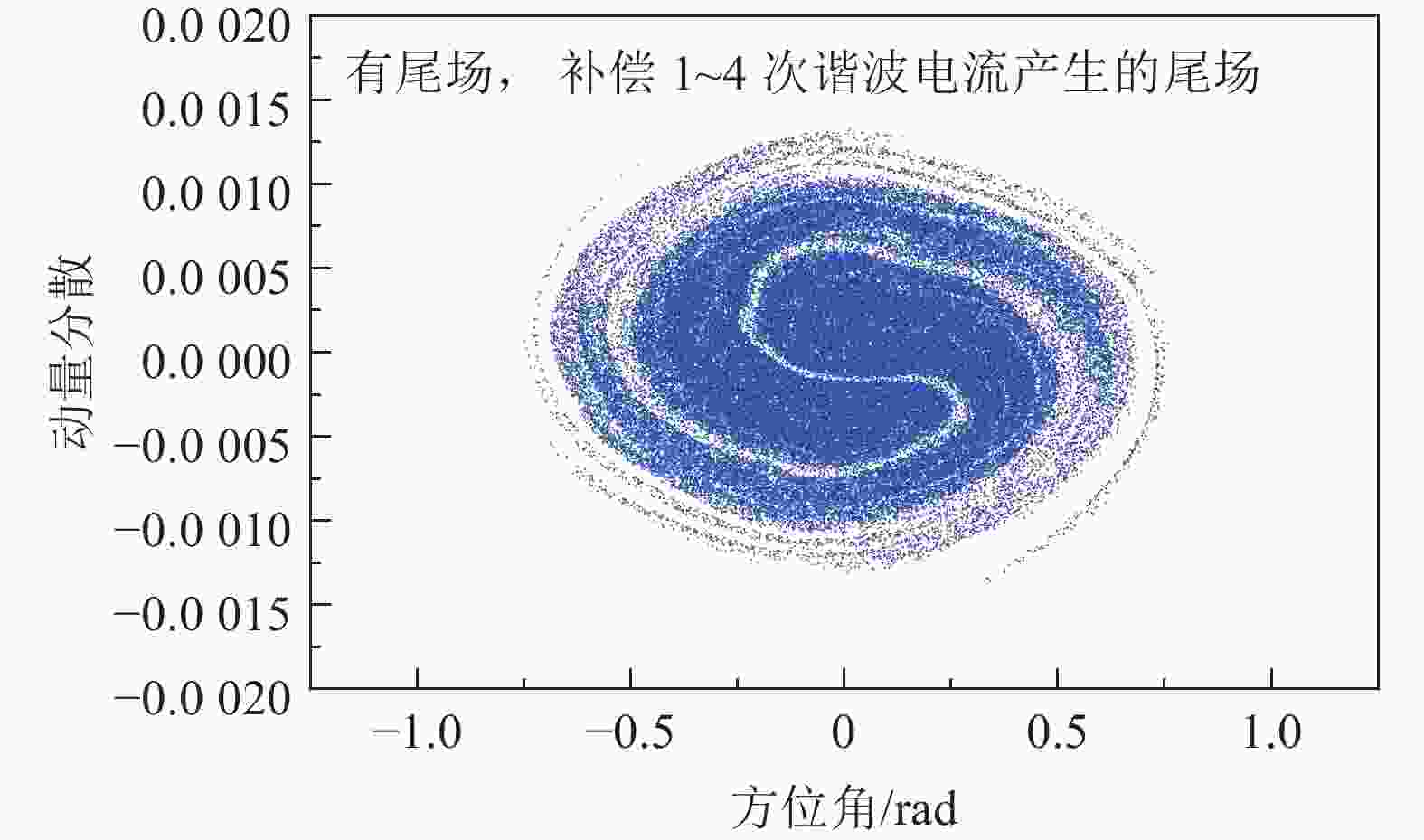
$ I(h\omega) $ 为束流在频域中频率为$ h $ 倍循环角频率$ \omega $ 处的谐波电流,由壁电流探测器得到的信号经过模数转换后再经过I/Q调制得到,$ Z(h\omega) $ 为该频率对应的高频腔体的阻抗,$ V(h\omega) $ 是对应谐波电流和阻抗激发的谐波电压。式(3)中,$ \bar{V}(h\omega) $ 和$ \phi_h $ 分别是$ V(h\omega) $ 的幅值和相位,$ A $ 为需要补偿的谐波数的集合,$ V(t) $ 即需要补偿的尾场电压。对前馈系统来说,需要确定的参数包括系统的延迟时间、需要补偿的谐波个数、需要覆盖的带宽以及补偿需要的功率。由于从前馈系统采集束流信号到完成补偿需要一定时间,即前馈系统延迟时间。该时间包括系统进行分析计算的时间和信号传输时间,因此补偿信号通常需要延迟束流循环周期的整数倍(约2~3),具体的相位需要在机器调试期间进行测试得到。由于纵向工作点约$ 10^{-3} $ ,采用2~3圈前的束流信号补偿当前的束流负载效应的影响可以忽略。图9为束团合并过程各次谐波电流的最大值及高频腔体的阻抗。加速过程中采用了4,2和1次谐波,因此对应谐波电流较大。3次谐波电流幅值同样较大,在第一次束团合并过程中4次谐波向2次谐波转变时达到最大值。另外,高频腔体的谐振频率为1.0 MHz,谐波1~4距离谐振频率较近,对应的阻抗也更大,因此首先考虑补偿。图10和图11分别是补偿1~4次谐波后的束流分布的热图以及进行纵向压缩前的相空间分布图,可以看到束流的分布与无尾场情况基本相同。统计得到的束流的动量分散和束团长度相对于无尾场情况增长小于1%。补偿1~4次谐波时,前馈系统的频率覆盖范围为0.444~1.332 MHz。束流纵向压缩过程时束团长度最小,尾场电压达到最大值约8 kV。考虑到用于压缩的高频电压为240 kV,而高频系统设计最大电压为270 kV,在束团合并阶段为了补偿束流负载效应没有超过高频系统最大功率。
-
为了研究束流负载效应在HIAF-BRing合束过程中的影响,对典型粒子束流238U35+进行了纵向跟踪模拟。模拟结果表明,在加速阶段束流负载效应影响较小,在束团合并阶段,束流负载效应引起束流动量分散和束团长度的增长,导致束团长度和束团中心的振荡。通过对模拟结果分析可知,束团的尾场会引起束团同步相位的偏移,并且在合并过程中随着束团中心的靠近,束团间尾场的耦合导致势阱的畸变增大,势阱所处相位在短时间变化幅度过大,引起束团中心位置的振荡。由于第一次束团合并的影响以及单束团流强的增大,第二次束团合并时束团中心振荡幅度更大。势阱畸变同时也引起束流在相空间的丝化,最终导致发射度的增长。通过前馈系统补偿1~4次谐波电流引起的尾场电压之后,束流负载效应在束团合并过程中的影响基本消除。前馈系统需要覆盖的频率范围为0.444~1.332 MHz,需要补偿的最大尾场电压为8 kV。
Simulation Study of the Beam Loading Effects During the Bunch Merging in HIAF-BRing
-
摘要: 强流重离子加速器HIAF-BRing在加速完成后进行束团合并,为研究BRing中的束流负载效应对束团合并的影响,对238U35+束流进行了粒子跟踪模拟。模拟结果显示,在束团合并过程中,束流负载效应引起束团长度和束团中心位置的振荡,导致束流动量分散和束团长度的增长。束团合并过程中尾场电压以及不同束团间尾场的耦合导致的势阱畸变,是引起束团长度和束团中心振荡及束流发射度增长的原因。为了降低束流负载效应的影响,采用多谐波前馈系统进行补偿,达到了补偿束团合并过程中的束流负载效应的目的,从而确保了BRing中引出束流的品质,同时根据模拟结果确定了前馈系统需要覆盖的频率范围和需要补偿的最大尾场电压。
-
关键词:
- HIAF-BRing /
- 尾场 /
- 束流负载效应 /
- 束团合并 /
- 势阱畸变
Abstract: In the booster ring (BRing) of the High Intensity heavy-ion Accelerator Facility (HIAF), the multi-bunch should be merged into single bunch after the acceleration. To study the influence of the beam loading effects during the bunch merging, the simulations of particle tracking with 238U35+ beam are carried out. According to the simulation results, during the bunching merging, the beam loading effects can result in the growth of the momentum spread and the bunch length as well as the oscillation of the bunch length and the bunch center. The potential well distortion induced by the wake voltage and wake field coupling during the bunch merging are the reasons why the bunch center oscillates and the emittance of the beam grows. To reduce the influence of the beam loading effects, the multi-harmonic feed-forward system is employed to compensate the wake voltage. With the feed-forward system, the beam loading effects can be compensated during the bunching merging. The feed-forward system is able to guarantee the high quality of the beam for extraction in the BRing. The frequency range to be covered and the largest wake voltage to be compensated by the feed-forward system are determined according to the simulation results.-
Key words:
- HIAF-BRing /
- wake field /
- beam loading effect /
- bunch merging /
- potential well distortion
-
表 1 BRing及高频系统部分参数
参数 数值 周长C 569.1 m 转变能 $ {\rm{\gamma}}_{\rm t} $ 7.645 85 动量接收度 ±0.005 分路阻抗 $ R_{\rm s} $ 2.8~3.7 kΩ $Q$ 值0.45~0.6 谐振频率 $f_r$ 1.0 MHz 最大峰值电压 $V_{\rm RF,\,max} $ 270 kV 表 2 粒子跟踪模拟所采用的束流参数
参数 数值 粒子种类 238U35+ 注入能量 $E_{\rm inj} $ 17 MeV/u 引出能量 $E_{\rm ext} $ 800 MeV/u 谐波数h 4, 2, 1 注入动量分散(3 $\sigma$ )$\delta$ ±0.002 束流流强 1×1011 ppp (55~249 mA) 回旋频率 $F_{\rm rev} $ 0.099~0.444 MHz -
[1] YANG J C, XIA J W, XIAO G Q, et al. Nucl Instr and Meth B, 2013, 317: 263. doi: 10.1016/j.nimb.2013.08.046 [2] RUAN S, YANG J, ZHANG J, et al. , Nucl Instr and Meth A, 2018, 892: 53. doi: 10.1016/j.nima.2018.02.052 [3] GAROBY R. Bunch Merging and Splitting Techniques in the Injectors for High Energy Hadron Colliders[R/OL].CERN/PS 98-048 (RF), 1998[2019-10-25]. http://cds.cern.ch/record/367499/files/ps-98-048.pdf. [4] SACHERER F J. IEEE Trans Nucl Sci, 1977, 24(3): 1393. doi: 10.1109/TNS.1977.4328955 [5] MORI Y, FUJIEDA M, KOBA K, et al. EPAC, 1998: 299. [6] FAY C E. Proceedings of the IRE, 1956, 44(10): 1446. doi: 10.1109/JRPROC.1956.274989 [7] NG K Y. Physics of Intensity Dependent Beam Instabilities[M]. Hackensack: World Scientific, 2006: 270. [8] BOZSIK I, HOFMANN I, JAHNKE A, et al. Numerical Investigation of Bunch-merging in a Heavy-ion-synchrotron[M]. Berlin: Springer, 1984: 128. [9] SPILLER P, BLASCHE K, BOINE-FRANKENHEIM O, et al. Generation of High Power Heavy Ion Beams at GSI[C]. IEEE Particle Accelerator Conference, 1999: 1788. [10] PEDERSEN F. IEEE Trans Nucl Sci, 1975, 22(3): 1906. doi: 10.1109/TNS.1975.4328024 [11] TAMURA F, YAMAMOTO M, OHMORI C, et al. Phys Rev Accel Beams, 2011, 14(5): 051004. doi: 10.1103/PhysRevSTAB.14.051004 -






 下载:
下载:












































 甘公网安备 62010202000723号
甘公网安备 62010202000723号