Structural Investigation in A ≈ 90 Mass Region and Comparison in Its Vicinity

0.   Introduction

Atomic nuclei near the $A = 90$ mass region with few protons above the $Z = 38$ subshell and few neutrons (holes) above the $N = 50$ closure shell have become a great interesting topics in nuclear physics^[1-40]. More and more interesting phenomena, e.g., single-particle excitation^[2-21], isomeric states^[8-16], core breaking^[2-36], and seniority symmetry breaking^[27] have been found in this mass region. Investigations of the level structures in these nuclei may provide information on the particle-hole exciting mechanism. For these nuclei with several valence protons (neutrons) above the closed shell, the low-lying levels generate from aligning the spins of the valence protons (neutrons) and the high spin levels stem from promoting protons (neutrons) across (sub)shell closure to the higher shells.

In recent studies of $N > 50$ nuclei^[34-45], some of the nuclei were investigated by the shell model with the truncation spaces, i.e., the $h_{11/2}^{}$ neutron orbital was neglected^{[19, 22, 34-35]}. Nevertheless, the $h_{11/2}^{}$ neutron orbit plays a major role in $N > 50$ nuclei, where the low and intermediate spins are interpreted as proton excitation ($f_{5/2}^{}$, $p_{3/2}^{}$, $p_{1/2}^{}$)$\rightarrow$$g_{9/2}^{}$ and neutron excitation $d_{5/2}^{}$ $\rightarrow$ ($g_{7/2}^{}$, $h_{11/2}^{}$), and the high spins involve the core excitation $\nu$$g_{9/2}^{}$$\rightarrow$$\nu$($d_{5/2}^{}$, $g_{7/2}^{}$). An interesting phenomenon was observed that the sudden deviations from the systematic characteristics emerge as the numbers of protons and neutrons change. For instance, the discontinuous separation energy of two protons (neutrons) and the abrupt increase of energy of the $2 _{1}^{+}$ state at certain proton (neutron) numbers may be attributed to the appearance of magic numbers. In addition, the evolution of shell with proton and neutron numbers can be such evident that one observes the fragmentation and vanishment of the conventional magic number or the appearance of new magic number in those exotic systems.

1.   Evolution Characteristics of the N = 50 neutron-core excited states

We studied the $^{91-93} {\rm{Nb}}$ nuclei by the $^{82} {\rm{Se}}$+$^{14} {\rm{N}}$ reaction^{[9, 17, 34-35]} as well as $^{89} {\rm{Zr}}$ and $^{91} {\rm{Mo}}$ by $^{89} {\rm{Y}}$+$^{6} {\rm{Li}}$ reactions^[46]. The level structures of these nuclei were explicated by the shell model calculations with $\pi$($f_{5/2}^{}$, $p_{3/2}^{}$, $p_{1/2}^{}$, $g_{9/2}^{}$)$\otimes$$\nu$($p_{1/2}^{}$, $g_{9/2}^{}$, $g_{7/2}^{}$, $d_{5/2}^{}$) model space. The results of calculations manifest that the proton core-excited across the $Z = 38$ subshell and neutron core-excited across the $N = 50$ closed shell are indispensable to explicate the high-spin levels. However, neutron core-excited states of the $N = 50$ nuclei were reported in lower-spin states. In order to understand neutron core-excitation of the low spin states, the systematic surveys of the $N = 50$ even-even isotones $^{86} {\rm{Kr}}$^[47], $^{88} {\rm{Sr}}$^[32-33], $^{90} {\rm{Zr}}$^[6], $^{92} {\rm{Mo}}$^[20-23], $^{94} {\rm{Ru}}$^[26-28], and odd-$A$ isotones $^{85} {\rm{Br}}$^[48], $^{87} {\rm{Rb}}$^[48], $^{89} {\rm{Y}}$^[1-3], $^{91} {\rm{Nb}}$^[17-19], $^{93} {\rm{Tc}}$^[24-25], are displayed in Fig. 1. As indicated in Fig. 1(a), the first 23/2⁺ levels in $^{87} {\rm{Rb}}$ and $^{89} {\rm{Y}}$ nuclei with $Z < 40$ are interpreted as the $N = 50$ neutron core breaking. The first 23/2⁺ states of the $^{91} {\rm{Nb}}$ and $^{93} {\rm{Tc}}$ nuclei with $Z > 40$ are interpreted by moving protons across the $Z = 40$ subshell, rather than neutron core breaking.

Figure  1.  Partial energy levels in $N = 50$ nuclei. (a) odd-$A$ isotones $^{85} {\rm{Br}}$, $^{87} {\rm{Rb}}$, $^{89} {\rm{Y}}$, $^{91} {\rm{Nb}}$, $^{93} {\rm{Tc}}$, $^{95} {\rm{Rh}}$, and (b) even-even isotones $^{86} {\rm{Kr}}$, $^{88} {\rm{Sr}}$, $^{90} {\rm{Zr}}$, $^{92} {\rm{Mo}}$, $^{94} {\rm{Ru}}$, $^{96} {\rm{Pd}}$. The neutron core-excited states from the $N = 50$ core are denoted by quadrilaterals, and the proton excited across the $Z = 40$ subshell are denoted by circles.

DownLoad: Full-Size Img PowerPoint

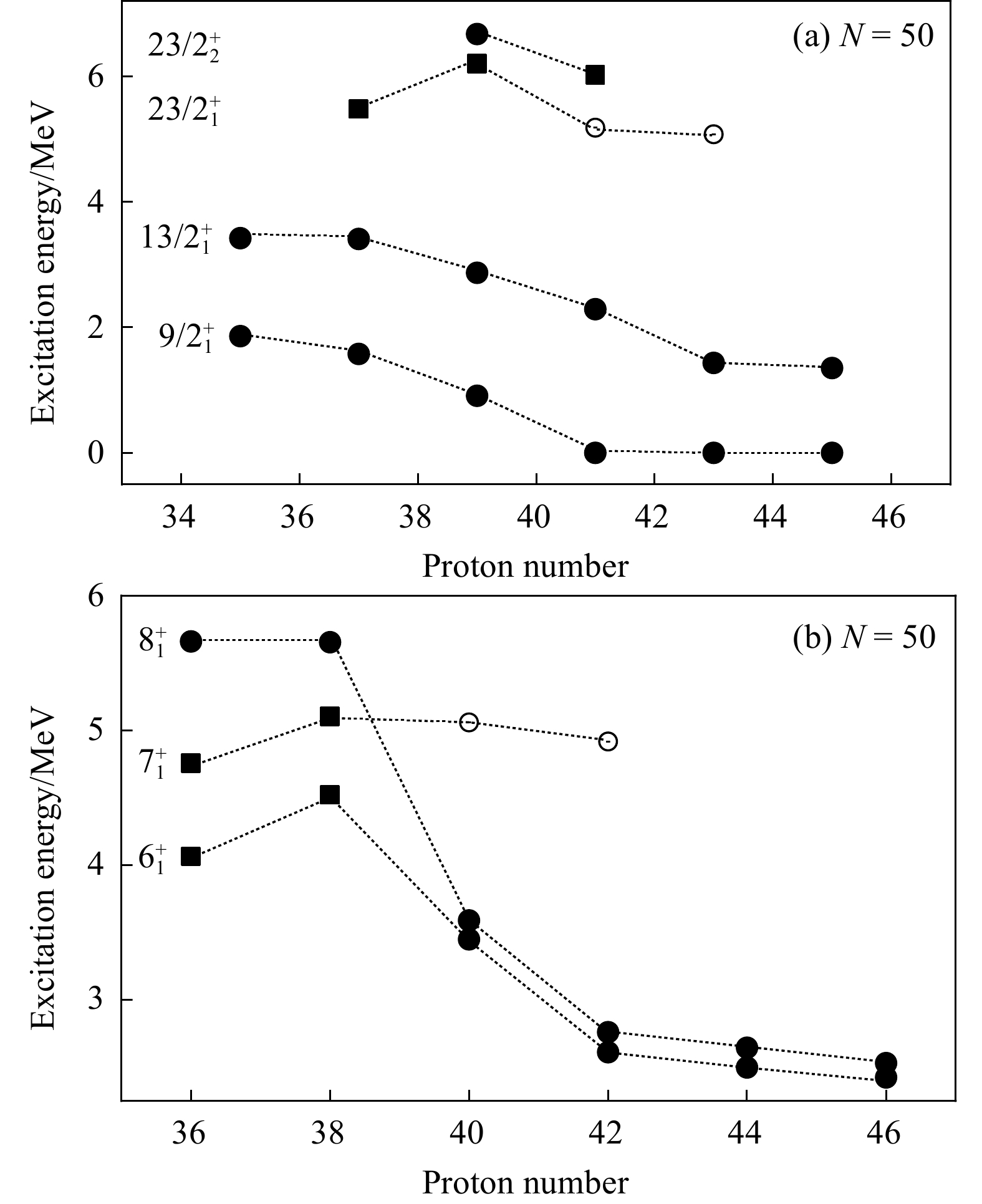
As shown in Fig. 1(b), in $^{86} {\rm{Kr}}$ and $^{88} {\rm{Sr}}$ nuclei, the $N = 50$ neutron core breaking is also observed at the first 6⁺ and 7⁺ levels, However in $^{90} {\rm{Zr}}$, $^{92} {\rm{Mo}}$, $^{94} {\rm{Ru}}$ and $^{96} {\rm{Pd}}$ nuclei, the first 6⁺ states originate from the proton configurations. This phenomenon may be associated with the shifts of the proton Fermi surface. As the number of proton increases, the proton Fermi surface gradually closes to the $g_{9/2}^{}$ orbit, which facilitates the proton core excitations ($(fp)\rightarrow g_{9/2}^{}$). And note that, the $N = 50$ neutron core breaking is easier than promoting proton across $Z = 40$ subshell in the $6 _{1}^{+}$ and $7 _{1}^{+}$ states as the proton number decreases, as displayed in Fig. 1(b). Notably, the excitation energies of the first 8⁺ state in $^{90} {\rm{Zr}}$ are much higher than those of the $^{92} {\rm{Mo}}$, $^{94} {\rm{Ru}}$ and $^{96} {\rm{Pd}}$ nuclei. It is generally known that $^{90} {\rm{Zr}}$ is a quasimagic nucleus with the $N = 50$ neutron shell closure and $Z = 40$ subshell closure which, in spherical nuclei, represents the filling of the $fp$ shell with the $g_{9/2}^{}$ shell empty above. The first 8⁺ state in the $^{90} {\rm{Zr}}$ nucleus is generated by promoting protons from the $p_{1/2}^{}$ orbital across the $Z = 40$ subshell to the $g_{9/2}^{}$ orbit, which has seniority ν = 2. The first 8⁺ states in $^{92} {\rm{Mo}}$, $^{94} {\rm{Ru}}$ and $^{96} {\rm{Pd}}$ are suggested as the $\pi$($g_{9/2}^{}$)ⁿ (n = 2, 4, 6) configurations, which are not referring to proton excitation.

2.   The high-j intruder orbital

Recently, we studied the $^{89} {\rm{Sr}}$^[49] and $^{93} {\rm{Mo}}$^[50] nuclei by the shell-model calculations, which were carried out with $\pi$($f_{5/2}^{}$, $p_{3/2}^{}$, $p_{1/2}^{}$, $g_{9/2}^{}$)$\otimes$$\nu$($g_{9/2}^{}$, $g_{7/2}^{}$, $d_{5/2}^{}$, $d_{3/2}^{}$, $s_{1/2}^{}$, $h_{11/2}^{}$) model space. It is worth emphasizing that promoting the neutron from $\nu d_{5/2}^{}$ orbit across $N = 56$ subshell into the $\nu h_{11/2}^{}$ orbit is necessary to explicate the level structure of $^{89} {\rm{Sr}}$ and $^{93} {\rm{Mo}}$ nuclei. In addition, the $h_{11/2}^{}$ neutron orbit plays a vital role in shaping the level structures in $N > 50$ nuclei. For example, the abrupt deformation near $Z = 40$ ($N = 60$) was explicated as the filled with $\pi g_{9/2}^{}$ orbit protons cooperated with the occupation of the neutron in $h_{11/2}^{}$ orbit and diminution of neutrons in the $\nu g_{9/2}^{}$ orbits^[51-53].

To further illustrate the characteristics of the neutron core excitations across the $N = 56$ subshell, the low spin structures of the $N = 51$ nuclei from the $^{85} {\rm{Se}}$ to $^{97} {\rm{Pd}}$ are surveyed^[24-30]. The energies of the $11/2 _{1}^{-}$ levels are not markedly changed, that result from the excitation of a single neutron from the $\nu d_{5/2}^{}$ orbit across $N = 56$ subshell into the $\nu h_{11/2}^{}$ orbit. The similar features is found in the $N = 51$ odd-odd nuclei^{[7, 17, 30]}. In these nuclei, the excitation energies of 10^- states are known to be around 2 MeV. These may be due to the depletion radial overlap between the $\pi g_{9/2}^{}$ orbit and the $\nu h_{11/2}^{}$ orbit which diminishes the interplay between the two orbits and results in a similar variation of binding energy between them. One would expect that promoting the neutron from $\nu d_{5/2}^{}$ orbit across the $N = 56$ subshell into the $\nu h_{11/2}^{}$ orbit may be validated by the future experiments and play an important role in the level structures of nuclei with $N = 51$ in the $A = 90$ mass region.

3.   Isomers in N = 50 (51) isotones

The lifetimes are considerably longer for isomers than for common excited states. The characteristics of isomers play a significant role in comprehending the nuclear structure because they provide rigorous tests for nuclear models. To our knowledge, high-spin isomers in the nuclei around the shell closure appear when the neutron number and/or the proton number outside the closed shell is an odd number^[54].

In $N = 51$ isotones, the neutron number is around the magic number 50 and proton number is near semimagic number 40. In Ref. [15], the characteristics of the isomeric states in $^{90} {\rm{Y}}$^[13], $^{91} {\rm{Zr}}$^[14], $^{92} {\rm{Nb}}$^[15], $^{93} {\rm{Mo}}$^[15], $^{94} {\rm{Tc}}$^[17], $^{95} {\rm{Ru}}$^[18], $^{96} {\rm{Rh}}$^[19], and $^{97} {\rm{Pd}}$^[19], originated from the same excitation mechanism, were investigated. As an example, the 21/2⁺ isomer in $^{93} {\rm{Mo}}$ has the predominant configuration $\pi g_{9/2}^{2}\otimes$$\nu d_{5/2}^{}$, and the neutron–proton interaction may be the physical origin of its long lifetime. On the other hand, the isomers in $^{144} {\rm{Pm}}$, $^{145} {\rm{Sm}}$, $^{146} {\rm{Eu}}$ and $^{147} {\rm{Gd}}$ nuclei with $N = 83$ were investigated systematically^[55]. Their lifetimes range from 10 ns to μs, such as the halflife of 49/2⁺ isomer (8.6 MeV level) in $^{147} {\rm{Gd}}$ is 510 ns. These isomers are dominated by the configuration of $\pi h_{1/2}^{2}\otimes$$\nu f_{7/2}^{}h_{9/2}^{}i_{13/2}^{}$^[15]. According to analogous analysis of configurations of isomers between $N = 83$ and $N = 51$ isotones, specifically high-spin isomers in $N = 51$ isotones are predicted to be dominated by [$\pi g_{9/2}^{2}\otimes \nu d_{5/2}^{}g_{7/2}^{}h_{11/2}^{}$]$_{39/2^{-}}^{}$ for odd-A nuclei, and [$\pi p_{1/2}^{-1}g_{9/2}^{2}\otimes \nu d_{5/2}^{}g_{7/2}^{}h_{11/2}^{}$]$_{20^{+}}^{}$ for odd-odd nuclei.

As shown in Fig. 2, the experimental lifetimes of the isomers in $N = 50$ nuclei with odd number of protons (no valence neutron), $^{89} {\rm{Y}}$, $^{91} {\rm{Nb}}$, $^{93} {\rm{Tc}}$, $^{95} {\rm{Rh}}$ and $^{97} {\rm{Ag}}$ are investigated. The $^{91} {\rm{Nb}}$, $^{93} {\rm{Tc}}$, $^{95} {\rm{Rh}}$ and $^{97} {\rm{Ag}}$ nuclei also show a 21/2⁺ isomer. For example, the 21/2⁺ isomer in $^{93} {\rm{Tc}}$ is associated with the configuration $\pi g_{9/2}^{3}$. In addition, the isomeric states 17/2⁻ in $^{91} {\rm{Nb}}$, $^{93} {\rm{Tc}}$ and $^{95} {\rm{Rh}}$ nuclei are interpreted by configuration $\pi p_{1/2}^{}$$\otimes$$g_{9/2}^{2}$. The results may indicate that the isomeric states in odd-mass nuclei are interpreted as a spin-aligned configuration in which a single neutron or proton couples with a fully aligned proton pair in the $g_{9/2}^{}$ orbit.

Figure  2.  Experimental systematics of isomers in $N = 50$ isotones.

DownLoad: Full-Size Img PowerPoint

4.   The weak coupling model in A ≈ 90

Figure 3(a) exhibits the systematics of the $0 _{1}^{+}$, $2 _{1}^{+}$, $4 _{1}^{+}$, $6 _{1}^{+}$ and $8 _{1}^{+}$ in $^{90} {\rm{Zr}}$, $^{92} {\rm{Mo}}$, $^{94} {\rm{Ru}}$ and $^{96} {\rm{Pd}}$ even-even nuclei^{[6, 21, 26, 35, 37]} as well as the $9/2 _{1}^{+}$, $13/2 _{1}^{+}$, $17/2 _{1}^{+}$, $21/2 _{1}^{+}$ and $25/2 _{1}^{+}$ states in $^{91} {\rm{Nb}}$, $^{93} {\rm{Tc}}$, $^{95} {\rm{Rh}}$ and $^{97} {\rm{Ag}}$ odd-$A$ nuclei^{[17, 24, 56- 57]}. The level structures between the $N = 50$ even-even nuclei and the neighboring odd-$A$ nuclei, shown for comparison in Fig. 3(a), are similar up to the $4 _{1}^{+}$ state. For example, the level energies of $13/2 _{1}^{+}$ and $17/2 _{1}^{+}$ levels in $^{93} {\rm{Tc}}$ are close to the energies of $2 _{1}^{+}$ and $4 _{1}^{+}$ levels in the $^{92} {\rm{Mo}}$($^{94} {\rm{Ru}}$) core. The systematic of the energy levels in the $N = 48$ odd-$A$ and the even-even isotones is presented in Fig. 3(b). The $13/2 _{1}^{+}$ and $17/2 _{1}^{+}$ states in $^{89} {\rm{Nb}}$^[4], $^{91} {\rm{Tc}}$^[6], $^{93} {\rm{Rh}}$^[58] and $^{95} {\rm{Ag}}$^[59] are close in energies with the $2 _{1}^{+}$ and $4 _{1}^{+}$ states in $^{88} {\rm{Zr}}$^[5], $^{90} {\rm{Mo}}$^[60], $^{92} {\rm{Ru}}$ and $^{94} {\rm{Pd}}$^[61], respectively. The above features could be explicated by the weak coupling model. Based on the weak coupling simplification of expressions, the low spins of an odd-$A$ nucleus can be interpreted as a nucleon in a single-$j$ orbit coupled to an even-even core. The $\psi_I^{\dagger} | 0 \rangle$ denotes the wave function of the low level $I_1^{+}$ ($E_I^{}$) of the even-even core. The $\psi_I^{\dagger} | 0 \rangle$ coupled to the single nucleon $a_j^{\dagger}$ can generate the multiplet states with spin $J$ for the odd-mass nucleus:

Figure  3.  (a) The low-energy levels in the $N = 50$ isotones; (b) the same as (a) but for $N = 48$ isotones.

DownLoad: Full-Size Img PowerPoint

where $J = |I-j|,|I-j|+1,\cdots,I+jI+j$, represents the angular momentum, We employ $E_J^{}(I,j)$ to represent the excitation energies of the multiplet states. The relation between $E_I^{}$ and $E_J^{}(I,j)$ is expressed by

The configuration $\pi$$g_{9/2}^{}$$\otimes$($2 _{1}^{+}$, $^{92} {\rm{Ru}}$) could generate multiplet states with $5/2 _{1}^{+}$ (621-keV), $7/2 _{1}^{+}$ (240-keV), $9/2 _{2}^{+}$ (1630-keV), $11/2 _{1}^{+}$ (894-keV) and $13/2 _{1}^{+}$ (852-keV) in $^{93} {\rm{Rh}}$. Using Eq. (2), the calculated energy of $2 _{1}^{+}$ level in $^{92} {\rm{Ru}}$ is 892-keV, which is consistent with the experimental one (865-keV). It is noteworthy that high spins are not in compliance with the results of the weak coupling framework, for example the energy of the $8 _{1}^{+}$ state in $^{88} {\rm{Zr}}$ is much higher than the $25_{1}^{+}$ state in $^{89} {\rm{Nb}}$. This might be due to the fact that the core excitations in high-spins of the even-even core may not be negligible, and configuration admixtures become increasingly significant.

5.   Systematics of nuclear structure characteristics near A = 90

Figure 4(a) displays the evolutions of the $2 _{1}^{+}$ levels in Zr^[60-58], Mo^[61-68], Ru^[61-69], Pd^[62-70] isotopes from $N = 44$ to $N = 60$. As shown in Fig. 4(a), the Zr, Mo, and Sr isotopes with neutron $N \leqslant 58$ show near-spherical features, whereas, nuclei with $N > 58$ nuclei show deformation characteristics. This may be attributed to the fact that the $Z = 40$ subshell weakens abruptly in the Sr, Zr, and Mo at $N = 60$. Figure 4(b) displays the evolutions of the $13/2 _{1}^{+}$ states in Nb^[71-77], Tc^[72-78], and Rh^[73-80] isotopes from $N = 50$ to $N = 60$. We also note that, the level energies of first 2⁺ (13/2⁺) states in $^{90} {\rm{Zr}}$ ($^{91} {\rm{Nb}}$) and $^{96} {\rm{Zr}}$ ($^{97} {\rm{Nb}}$) nuclei are significantly higher than that in other Zr (Nb) isotopes, which reveals that $N = 56$ is a good subshell closure, whereas the $2 _{1}^{+}$ energy peaks are only found at $N = 50$ in Mo, Ru and Cd isotopes chains. It is observed that the energy of $2 _{1}^{+}$ in the $^{96} {\rm{Zr}}$ nucleus is 1 750-keV, whereas the 2⁺ energies in $^{98} {\rm{Mo}}$, $^{100} {\rm{Ru}}$, and $^{102} {\rm{Pd}}$ nuclei are only 787-, 540-, 556-keV, respectively. The low energies in $2 _{1}^{+}$ levels for the $N = 56$ isotones are incompatible with that in the spherical nuclei. Such disparate behavior with proton number of $Z \geqslant 42$ may be attributed to the vanishing of the $N = 56$ subshell.

Figure  4.  The evolution of the first 2⁺ states in the $N = 44$ to $N = 60$. Zr (circles), Mo (squares), Mo (solid circles) and Ru (pentagons) isotopes; (b) The evolution of the first 13/2⁺ states in the $N = 44$ to $N = 60$, Nb (squares), Tc (solid circles), Rh (circles).

DownLoad: Full-Size Img PowerPoint

As compared to Zr and Mo, the Nb (Z = 41) nucleus may be in the intermediate regime where the $N = 56$ shell effect is prominent ($Z = 40$) and evanescent ($Z \geqslant 42$). Figure 5 indicates that the values of ${\rm{R}} _{4_{1}^{+}/2_{1}^{+}}^{}$ in $^{90-98} {\rm{Zr}}$ are less than 2, showing the steadiness of the $Z = 40$ subshell. The ${\rm{E}} _{4_{1}^{+}}^{}$/${\rm{E}} _{2_{1}^{+}}^{}$ value increases dramatically in $^{100} {\rm{Zr}}$, and the low lying level structure shows the deformation onset in Zr isotopes with $N \geqslant 60$. The $^{92} {\rm{Mo}}$, $^{94} {\rm{Ru}}$, $^{96} {\rm{Pd}}$, and $^{98} {\rm{Cd}}$ as well as $^{90} {\rm{Zr}}$, $^{92} {\rm{Zr}}$, $^{94} {\rm{Zr}}$, $^{96} {\rm{Zr}}$, and $^{98} {\rm{Zr}}$ nuclei have ${\rm{R}} _{4_{1}^{+}/2_{1}^{+}}^{}$ ratios around 1.5, which indicates the representative features of spherical nuclei. As shown in Fig. 5, the ${\rm{R}} _{4_{1}^{+}/2_{1}^{+}}^{}$ in the Mo and Ru isotopic chains show a similar tendency, but notable differences from the Zr isotopic chain. The decrease of ${\rm{R}} _{4_{1}^{+}/2_{1}^{+}}^{}$ from $N = 60$ to $N = 50$, followed by a drop toward $N = 50$, is observed. In general, nuclear deformation can be reflected by $2 _{1}^{+}$ energies (${\rm{R}} _{4_{1}^{+}/2_{1}^{+}}^{}$) towards the rotational limits. Figure 6(a) shows the excitation energies of $2 _{1}^{+}$ to 1$0 _{1}^{+}$ states in $N = 56$ isotones, Zr^[67], Mo^[68], Ru^[69], Pd^[70], and Cd^[80]. As displayed in Fig. 6(a), the excited energies of the $2 _{1}^{+}$ to 1$0 _{1}^{+}$ states in $^{96} {\rm{Zr}}$ nucleus are noticeably higher than that in other $N = 56$ isotones. This may be because the $^{96} {\rm{Zr}}$ nucleus is near spherical character, originating from the double-subshell closure at $Z = 40$ and $N = 56$. The double subshell closure is testified by the high excitation energy and low collectivity of the first 2⁺ state. The level energies of the $2 _{1}^{+}$ to 1$0 _{1}^{+}$ states in $^{98} {\rm{Mo}}$, $^{100} {\rm{Ru}}$, $^{102} {\rm{Pd}}$ and $^{104} {\rm{Cd}}$ nuclei are very close. The $2 _{1}^{+}$, $4 _{1}^{+}$, $6 _{1}^{+}$ and $8 _{1}^{+}$ levels originate from the seniority $\nu$ = 2 states in the seniority scheme^[81]. The angular momenta stem from the coupling of the two unpaired protons in the $g_{9/2}^{}$ orbit.

Figure  5.  The evolutionary trends of the ratios of $4_{1}^{+}$ to $2_{1}^{+}$ with neutron number.

DownLoad: Full-Size Img PowerPoint

Figure 6(b) shows the $9/2 _{1}^{+}$ to $25/2 _{1}^{+}$ states in the $N = 56$ isotones Nb^[75], Tc^[76], Rh^[77], Ag^[78], and In^[79]. The low-energy spectra for $^{96} {\rm{Zr}}$^[65] and $^{98} {\rm{Mo}}$^[66], shown in Fig. 6(a), are similar to the ones for $^{97} {\rm{Nb}}$^[75] and $^{99} {\rm{Tc}}$^[76], respectively. These similarities can also be explicated using the weak coupling theory. When moving to the $^{101} {\rm{Rh}}$ and $^{103} {\rm{Ag}}$ nuclei^[77-78], the ground states display a sudden transition from 9/2⁺ to 1/2^- and 7/2⁺, respectively, which may indicate the onset of deformation in $^{101} {\rm{Rh}}$ and $^{103} {\rm{Ag}}$ nuclei because of the sudden weakening (vanishing) of the $Z = 40$ subshell in $N = 56$ nuclei.

Figure  6.  The evolution of positive parity states in even-even N = 56 isotones $^{96} {\rm{Zr}}$, $^{98} {\rm{Mo}}$, $^{100} {\rm{Ru}}$, $^{102} {\rm{Pd}}$, and $^{104} {\rm{Cd}}$; The evolution of positive parity states in odd-A N = 50 isotones $^{97} {\rm{Nb}}$, $^{99} {\rm{Tc}}$, $^{101} {\rm{Rh}}$, $^{103} {\rm{Ag}}$, and $^{105} {\rm{In}}$.

DownLoad: Full-Size Img PowerPoint

Additionally, it has been reported that the nuclei with $N$ = 48 and 49, specifically $^{83} {\rm{Br}}$, $^{85} {\rm{Rb}}$, and $^{87} {\rm{Y}}$ nuclei with $N = 48$, exhibit the strong ${\rm{E}}2$ and ${\rm{M}}1$ transitions^[32]. These nuclei show the electric quadrupole transitions strengths of $B({\rm{E}}2)$ are about 15 Weisskopf units (W.u.) up to 17/2⁺, while the higher-spin states display the $\Delta I$ = 1 sequences, in which the $B({\rm{M}}1)$ values are up to $\approx$ 1 W.u. Similar characteristics are reported in $N = 49$ isotones $^{85} {\rm{Kr}}$ and $^{86} {\rm{Rb}}$. In these nuclei, the strong ${\rm{E}}2$ transitions are ascribed to the proton excitations coupled to the unpaired ${\rm{g}} _{9/2}^{}$ neutron, and the M1 transitions are construed as the neutron core excitations across the $N = 50$ closed shell^[82].

To survey systematically the $N = 50$ nuclei and probe the mechanisms for generating the strong ${\rm{E}}2$ and ${\rm{M}}1$ transitions, the shell-model calculations for the $^{90} {\rm{Zr}}$, $^{91} {\rm{Nb}}$, $^{92} {\rm{Mo}}$, $^{93} {\rm{Tc}}$, $^{94} {\rm{Ru}}$ and $^{96} {\rm{Pd}}$ nuclei are performed with proton and neutron core excitations across the $^{88} {\rm{Sr}}$ core. The shell-model calculations were carried out with the NUSHELLX code^[83]. We employed the $\pi$($p_{3/2}^{}$, $f_{5/2}^{}$, $p_{1/2}^{}$, $g_{9/2}^{}$)$\otimes$$\nu$($p_{1/2}^{}$, $g_{9/2}^{}$, $g_{7/2}^{}$, $d_{5/2}^{}$, $d_{3/2}^{}$, $s_{1/2}^{}$) configuration space and GWBXG effective interaction. The calculated results are generally coincident with experimental ones. The $N = 50$ nuclei $^{89} {\rm{Y}}$, $^{90} {\rm{Zr}}$, $^{93} {\rm{Tc}}$, and $^{94} {\rm{Ru}}$ display the large $B(\rm E2)$ values at low and moderate spins, which are believed to be a result of proton recoupling in the $pfg$ orbits (1$p_{3/2}^{}$, $0 f_{5/2}^{}$, 1$p_{1/2}^{}$, $0 g_{9/2}^{}$). The high spin states display strong ${\rm{M}}1$ transitions, which are explicated as proton excitation from the $pf$ shells (1$p_{3/2}^{}$, $0 f_{5/2}^{}$, 1$p_{1/2}^{}$) to the $0 g_{9/2}^{}$ orbit, coupling to a neutron excitation from the $g_{9/2}^{}$ orbit to the $d_{5/2}^{}$ orbit. For example, in the $^{91} {\rm{Nb}}$ nucleus, the E2 transitions $21/2 _{1}^{+}$$\rightarrow$$17/2 _{1}^{+}$, $17/2 _{1}^{+}$$\rightarrow$$13/2 _{1}^{+}$, and $13/2 _{1}^{+}$$\rightarrow$$9/2 _{1}^{+}$ are is ascribed to the excitation of protons from $f_{5/2}^{}p$ orbits to $g_{9/2}^{}$ orbit. The calculations $B$(E2) values are 100.7, 287.8 and 152.9 $\rm{ e^{2}fm^{4} }$, respectively. However, for the transitions $23/2_{4}^{+}$$\rightarrow$1$9/2 _{2}^{+}$ and $25/2 _{3}^{+}$$\rightarrow$$21/2 _{2}^{+}$, the calculations predict $B$(E2) values decrease abruptly. The difference could be related to the forbidden $23/2 _{4}^{+}$$\rightarrow$1$9/2 _{2}^{+}$ and $25/2 _{3}^{+}$$\rightarrow$$21/2 _{2}^{+}$ transitions from neutron core-excited to pure proton states. Whereas rather strong M1 transitions $31/2 _{1}^{+}$$\rightarrow$$29/2 _{1}^{+}$, $33/2_{1}^{+}$$\rightarrow$$31/2_{1}^{+}$, whose $B$(M1) values are in the range of 1.1 - 2.6 $\mu_{N}^{2}$, are ascribed to the recouplings of the two unpaired neutrons, i.e, the $g_{9/2}^{}$ neutron hole and the $d_{5/2}^{}$ neutron. Figure. 7 displays the comparisons between the calculated $B({\rm{E}}2)$ values and experimental ones in $^{90} {\rm{Zr}}$, $^{92} {\rm{Mo}}$, $^{94} {\rm{Ru}}$ and $^{96} {\rm{Pd}}$ as well as $^{91} {\rm{Nb}}$ and $^{93} {\rm{Tc}}$. As shown in Fig. 7, the $B(\rm{E}2)$ values of calculation are generally consistent with that of the experiments (except $B({\rm{E}}2$; 2⁺$\rightarrow$0⁺) of $^{94} {\rm{Ru}}$ and $^{96} {\rm{Pd}}$, and $B({\rm{E}}2$; 13/2⁺$\rightarrow$ 9/2⁺)). The overestimation of the $B({\rm{E}}2$; 2⁺$\rightarrow$0⁺) for $^{94} {\rm{Ru}}$ ($^{96} {\rm{Pd}}$) and $B({\rm{E}}2$; 13/2⁺$\rightarrow$ 9/2⁺) for $^{93} {\rm{Tc}}$ with the GWBXG effective interaction is conspicuous. It is worth mentioning that some pure-proton space models fail to reproduce the $B({\rm{E}}2)$ values well because they cannot provide the amount of seniority mixing^[84-85].

Figure  7.  Experimental $B({\rm{E}}2)$ strengths(circle) and the shell model predictions(solid circle) in the proton($f_{5/2}^{}$, p, $g_{9/2}^{}$) model space.

DownLoad: Full-Size Img PowerPoint

6.   Summary

We survey the systematics of the lower energy levels in the $A \approx 90$ mass region. The results indicate that the lower energy levels of the odd-A nucleus can be interpreted by its neighboring even-even core coupled to a valence nucleon, whereas the weak-coupling model is not applicable for the description of the high spin states. The excitation energies of the $2 _{1}^{+}$ levels in even-even isotopes are investigated systematically, which shows the competition between particle and collective excitation at high-spin states in the nuclei with $N = 46$ (47). For $N = 48$ (49) nuclei, there are still some evidences of collective motion, even at low-spin states. For $N = 50$ nuclei, level structures show the property of single particle excitations at high-spin states. To better understand the level structures of $N > 50$ nuclei, it is necessary to consider the neutron core excitations from $d_{5/2}^{}$ neutron orbit across the $N = 56$ subshell into $h_{11/2}^{}$ orbit. In addition, the evolution of the first 2⁺ states and the energy ratios of $4 _{1}^{+}$ to $2 _{1}^{+}$ in the $N = 50$ to $N = 60$ nuclei indicate that the $N = 56$ subshell closure appears at $Z = 40$ (41) and disappears for the $Z > 42$ nuclei.