Shell-Model Explanation on Some Newly Discovered Isomers

1.   Introduction

Isomeric states are of great importance for nuclear structure investigations. For example, the isomeric states in nuclei around doubly magic nuclei, so called the shell-model isomers, often provide the first spectroscopic properties in the extreme neutron-rich and neutron-deficient nuclei in the medium and heavy mass region and include a plenty of information, such as the proton-neutron interaction and its role in shell evolution. Recent years, many isomeric states are newly discovered in extreme neutron-rich and neutron-deficient nuclei around doubly magic, ¹⁰⁰Sn, ¹³²Sn, and ²⁰⁸Pb. Because of relatively long half-lives, the properties of the isomeric states are easier to be observed and provide the first spectroscopic properties. Just in the year of 2019, discoveries on isomeric states are firstly reported in ¹⁰¹In^[1], ^123,125Ag^[2], ¹³⁴In^[3], and ²¹⁸Pa^[4].

Fruitful discussions are made on the underlying physics behind the observed isomeric states. The strong neutron configuration mixing between the $0g_{7/2}$ and $1d_{5/2}$ orbitals is introduced to explain the similarity among the excitation energies of the newly observed $1/2^{-}$ isomeric states in ¹⁰¹In and those in odd-$A$ In isotopes, ^103-109In^[1]. A six-nucleon noncollective isomeric state is found beyond a chiral-like pair band of ¹²⁰I^[5]. Many isomeric states are found in ¹²²I and the corresponding configurations are identified by comparing with the calculations^[6]. The evolution of the isomeric states from ¹¹⁷Ag to ¹²³Ag is found to be caused by the tensor part of the nuclear interaction^[2]. The isomeric state in ¹³⁴In is suggested to be $5^-$^[3] because its decay energy and reduced transition rate are close to the previous shell-model prediction on a $5^-$ isomeric state^[7]. Based on the observations and shell-model calculations, the spin and parity of the ground states and the isomeric states are suggested to be inverted from ²¹⁶Ac to ²¹⁸Pa due to the proton-neutron interaction and the proton configuration mixing^[4].

In the present work, the nuclear shell model is used to provide more detailed investigations on the newly discovered isomeric states in ¹⁰¹In, ^123,125Ag, and ²¹⁸Pa, including Type I and II shell evolution and configuration mixing. A brief introduction is presented in Section 2 on the shell model and Hamiltonians used to investigate these isomeric states. The isomeric states in ¹⁰¹In, ^123,125Ag, and ²¹⁸Pa are discussed in Sections 3, 4, 5, respectively. The present work is concluded in Section 6.

2.   Nuclear shell model and hamiltonians

The nuclear shell model solves the many body Schrodinger equations with the full considerations of the configuration mixing in a truncated model space. It provides nice descriptions on the spectroscopic properties of the atomic nuclei, such as the binding energies (relative to the core), the levels, the electromagnetic properties, the $\beta$ transitions, and the spectroscopic factors. Because the shell model is implemented in a truncated model space, it is of great importance to choose a proper model space and the corresponding Hamiltonian. During decades, a lot of shell model Hamiltonians are suggested for many model spaces. For example, the USD family provides the wonderful Hamiltonians for the $sd$ region. But if the mirror nuclei are considered, the modified USD family with the weakly bound effect should be used to describe the mirror energy differences in the nuclei around $A \!=\! 20$^[8], which further explain the recent observations on the decay properties of ²²Si^[9], ²⁶P^[10], and ²⁷S^[11-12].

The phenomenological nuclear force, the monopole based universal interaction ${V}_{\rm{MU}}$^[13] plus the M3Y spin-orbit interaction^[14], is used as the cross shell interaction for the $psd$ region^[15], the ¹³²Sn region^[7], and the ²⁰⁸Pb^[16] region. The $psd$ Hamiltonian, YSOX, provides nice descriptions on the levels and the spectroscopic properties of ¹¹Be^[17], the cross-shell components in ¹²Be^[18-19], the levels and the transition rates of ¹⁴C^[20], and the spectroscopic factors of C isotopes^[21-22]. The Hamiltonian for the southeast region of ¹³²Sn, jj46Y16, predicted an isomeric state in ¹³⁴In, which is found in a recent work in RIKEN^[3].

Encouraged by the nice performance of ${V}_{\rm{MU}}$ plus the M3Y spin-orbit interaction, it is possible to use it not only as the cross-shell interaction, but also as the full parts of the Hamiltonian. It is found in the previous works that one central part of ${V}_{\rm{MU}}$, C10 with T, S = 1, 0, should be enhanced by $15\%$ for the proton-proton interaction and $5\%$ for the neutron-neutron interaction^[23-24]. The original ${V}_{\rm{MU}}$ plus the M3Y spin-orbit interaction with the modified proton-proton and neutron-neutron parts is used to calculate the Hamiltonian for investigations of ¹⁰¹In, ^123,125Ag, and nearby nuclei, while the one for ¹⁰¹In has been slightly modified. The model space for investigating ¹⁰¹In and ^123,125Ag includes the proton $0f_{5/2}$, $1p_{3/2}$, $1p_{1/2}$, $0g_{9/2}$ orbitals and the neutron $0g_{7/2}$, $1d_{5/2}$, $1d_{3/2}$, $2s_{1/2}$, $0h_{11/2}$ orbitals.

The isomeric states of ²¹⁸Pa and the $N\!=\! 127$ isotopes are examined through the KHPE Hamiltonian^[25], which is based on the Kuo-Herling interaction^[26-27]. KHPE is recently used to identify the spin and parity of the ground state of ²²³Np. The model space includes the proton $0h_{9/2}$, $1f_{7/2}$, $1f_{5/2}$, $2p_{3/2}$, $2p_{1/2}$, $0i_{13/2}$ orbitals and the neutron $0i_{11/2}$, $1g_{9/2}$, $1g_{7/2}$, $2d_{5/2}$, $2d_{3/2}$, $3s_{1/2}$, $0j_{15/2}$ orbitals. All the shell-model calculations are performed through the code KSHELL^[28]. It should be noted that all calculations in the present work do not take into account the uncertainty of the shell-model Hamiltonians. Some uncertainty analyses are performed for the liquid drop model^[29-30]. Although there are some analyses on the shell-model uncertainty^{[23, 31]}, they are still preliminary and need further investigations.

3.   ¹⁰¹In

Recently, an isomeric $1/2^{-}$ state in ¹⁰¹In is observed^[1]. Compared through the previously observed data, the excitation energies of the isomeric $1/2^{-}$ states in odd-$A$ isotopes, ^101-109In, are close to each other. For the ^101-109In isotopes, the $9/2^{+}$ ground state corresponds to a proton hole in the $0g_{9/2}$ orbital, while the $1/2^{-}$ isomeric state corresponds to a proton hole in the $1p_{1/2}$ orbital. From the single particle states of ¹⁰¹Sn, It is found that the neutron $0g_{7/2}$ and $1d_{5/2}$ orbitals locate just beyond the $N \!=\! 50$ magic number, while the other three orbitals, $1d_{3/2}$, $2s_{1/2}$, and $0h_{11/2}$ locate much higher^[32]. The excitation energies of isomeric $1/2^{-}$ states in odd-$A$ isotopes reflect the proton $Z \!=\! 40$ subshell evolution as the function of neutron numbers.

It should be noted that the shell evolution is generally induced by the proton-neutron interactions. As discussed in Ref. [13], the $j = l\pm1/2$ neutron generally attracts the $j' = l'\mp1/2$ proton more than the $j'' = l''\pm1/2$ proton, where $j$, $j'$, $j''$ are the total angular momentum of certain orbitals and $l$, $l'$, $l''$ are orbital angular momentum of certain orbitals. For example, the $1d_{5/2}$ ($0g_{7/2}$) neutron attracts the $1p_{1/2}$ ($0g_{9/2}$) proton more than the $0g_{9/2}$ ($1p_{1/2}$) proton. The occupancy of the $1d_{5/2}$ ($0g_{7/2}$) neutron increases (decreases) the $Z \!=\! 40$ subshell gap and the excitation energies of the isomeric $1/2^{-}$ states. Such analysis is supported by the shell-model calculation^[1]. Thus, the similar excitation energies of the isomeric $1/2^{-}$ states among the odd-$A$ In isotopes, ^101-109In, are caused by the strong neutron configuration mixing between the $0g_{7/2}$ and $1d_{5/2}$ orbitals. The neutrons occupy both these two orbitals with the increasing neutron number, which changes little on the $Z \!=\! 40$ subshell gap.

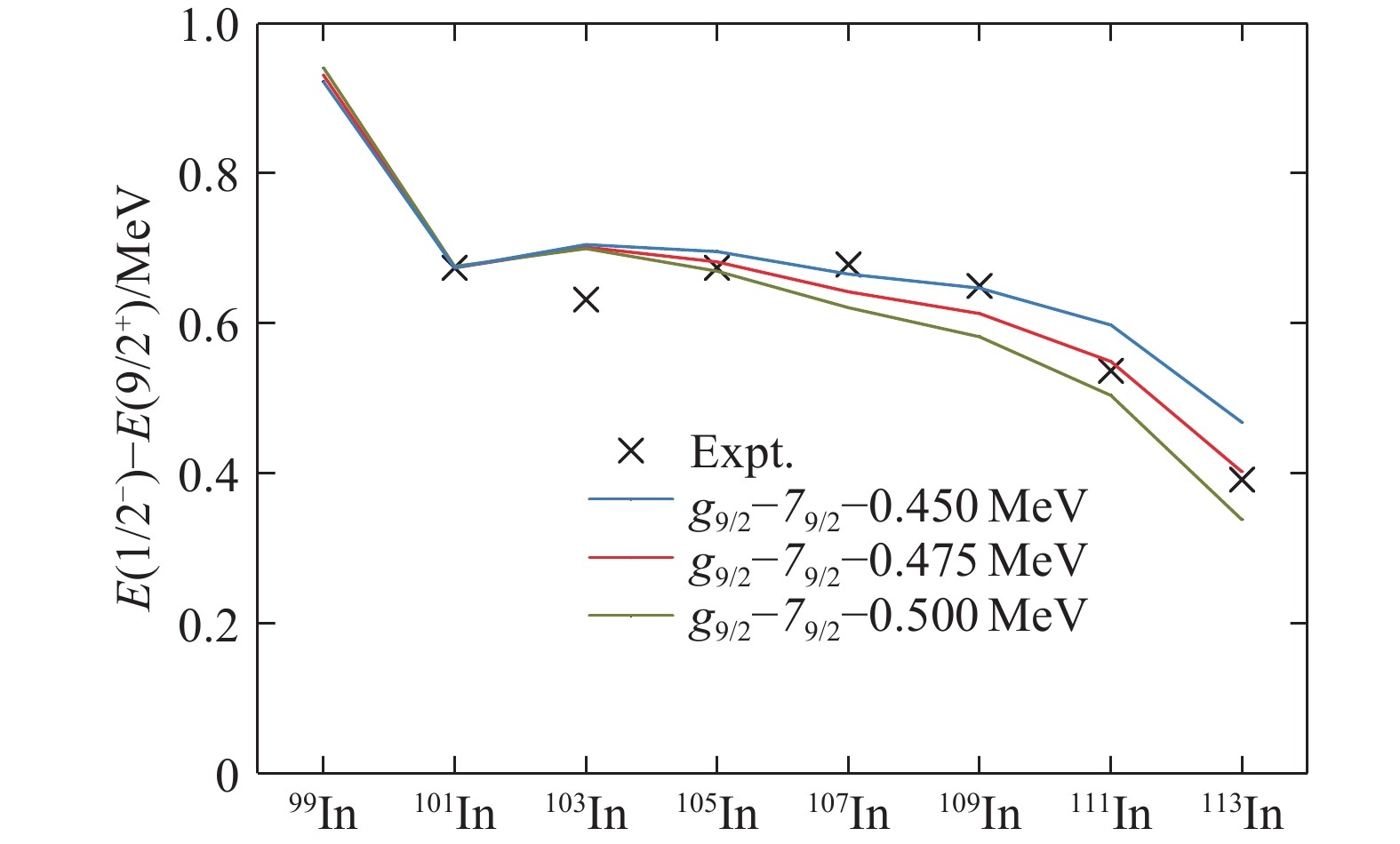
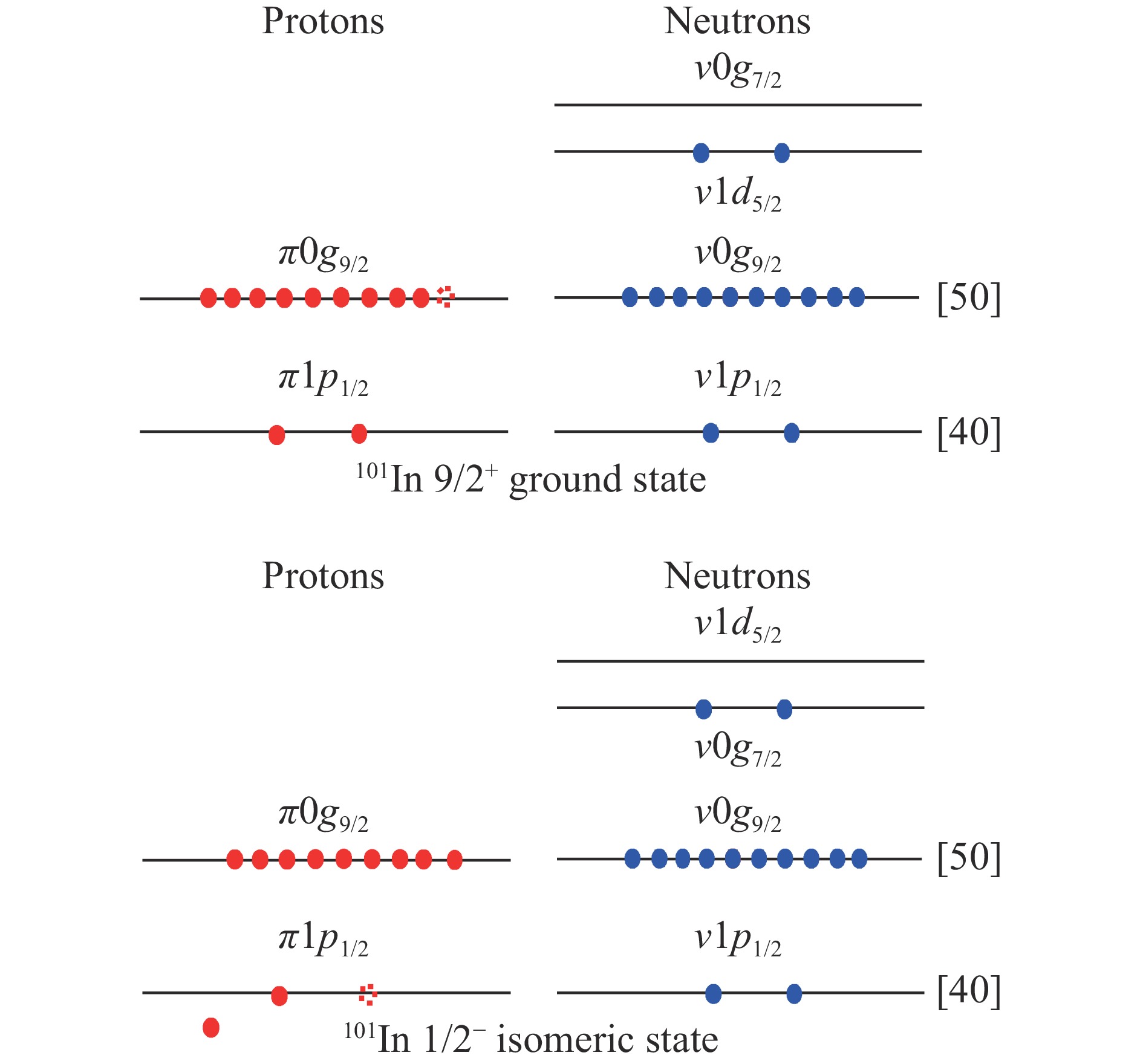
On the other hand, the change of the proton configuration can induce the neutron shell evolution. A schematic picture is presented in Fig. 1 for the type II shell evolution in ¹⁰¹In. The two neutrons above the $N \!=\! 50$ shell are schematically presented for simplicity because they have strong configuration mixing between the $0g_{7/2}$ and $1d_{5/2}$ orbitals. The $1p_{1/2}$ $(0g_{9/2})$ proton attracts the $1d_{5/2}$ ($0g_{7/2}$) neutron more than the $0g_{7/2}$ ($1d_{5/2}$) neutron. From the $9/2^{+}$ ground state to the $1/2^{-}$ isomeric state in odd-$A$ In isotopes, a proton moves from the $1p_{1/2}$ orbital to the $0g_{9/2}$ orbital. One more proton on the $0g_{9/2}$ orbital decreases the shell gap between the neutron $0g_{7/2}$ and $1d_{5/2}$ orbitals, while one less proton on the $1p_{1/2}$ orbital has a similar effect. Due to the proton-neutron interactions among four orbitals, it is thus expected that the shell gap between the neutron $0g_{7/2}$ and $1d_{5/2}$ orbitals can change a lot or even invert from the $9/2^{+}$ ground state to the $1/2^{-}$ isomeric state in the odd-$A$ In isotopes. The shell-model calculations show that the neutrons occupy more on the $1d_{5/2}$ orbital in the $9/2^{+}$ ground state but more on the $0g_{7/2}$ orbital in the $1/2^{-}$ isomeric state^[1]. From the calculated effective single particle energies (ESPE) of ^99-105In, the $0g_{7/2}$ orbital locates higher than the $1d_{5/2}$ orbital in the $9/2^{+}$ ground state and lower in the $1/2^{-}$ isomeric state^[1]. It is called type I shell evolution that the proton (neutron) shell evolves as the function of the neutron (proton) number. The proton (neutron) shell evolution in different states with different configurations in one nuclei is called type II shell evolution, which is suggested in ⁶⁸Ni firstly^[33] and identified in some neutron-rich even-even and odd-odd nuclei, such as ⁹⁶Zr^[34] and ⁷⁰Co^[35]. The discovery of isomeric state in ¹⁰¹In and the corresponding analysis on the possible type II shell evolution in a odd-$A$ neutron-deficient nucleus provide a unique and novel candidate for type II shell evolution, of which the inversion of two neutron orbitals is induced by a single proton movement.

Figure  1.  (color online)Schematic configurations for $9/2^{+}$ ground state and $1/2^{-}$ isomeric state of ¹⁰¹In.

DownLoad: Full-Size Img PowerPoint

Following above analysis, the excitation energies of the isomeric states in the odd-$A$ In isotopes are rather sensitive to the proton-neutron interaction. As shown in Fig. 2, the monopole term between the proton $0g_{9/2}$ orbital and the neutron $0g_{7/2}$ orbital strongly affects the excitation energies of the isomeric states in the odd-$A$ In isotopes with increasing neutron number. Only a $0.025$ MeV change on this monopole results a change more than $0.5$ MeV on the excitation energy of the isomeric state in ¹¹³In when that in ¹⁰¹In is fixed. The flat energies from ¹⁰¹In to ¹⁰⁹In are induced by the balance of four proton-neutron interactions among the proton $1p_{1/2}$, $0g_{9/2}$ orbitals and the neutron $0g_{7/2}$, $1d_{5/2}$ orbitals. The Hamiltonian discussed in Section 2 can not exactly describe the balance. The mentioned monopole term between the $0g_{9/2}$ proton and the $0g_{7/2}$ neutron is modified to be $0.475$ MeV more attractive, where the relative single particle energy between the proton $1p_{1/2}$ and the $0g_{9/2}$ are fitted to reproduce the excitation energy of the isomeric state in ¹⁰¹In. Although it is difficult to judge which term of the proton-neutron interaction should be modified based on the present observables, the preset work provides a possible modification to reproduce the observed data and shows the sensitivity between the interaction and the levels.

Figure  2.  (color online)The excitation energies of the isomeric states in the odd-A In isotopes, ^101-113In. The proton-neutron interaction between the proton $0g_{9/2}$ orbital and the neutron $0g_{7/2}$ orbital is modified to be 0.450, 0.475, and 0.500 MeV more attractive, respectively, than the Hamiltonian described in Section 2.

DownLoad: Full-Size Img PowerPoint

4.   ^123,125Ag

Nuclei around the ¹³²Sn region are of great interest because of their importance in both the fission products and the $r$-process. Recently, the level of ¹⁴⁰Te^[36] is analysed based on the $\beta$ decay of ¹⁴⁰I^[37] through the EURICA collaboration. As discussed in Ref. [2], the ground states and the isomeric states are $9/2^{+}$ and $1/2^{-}$, respectively, in the odd-$A$ Ag isotopes, ^99-103Ag. But for the odd-$A$ Ag isotopes, ^105-117Ag, inversions are found while the ground states and the isomeric states become $1/2^{-}$ and $9/2^{+}$, respectively. Similar to the discussions in the odd-$A$ In isotopes, the $9/2^{+}$ and $1/2^{-}$ states correspond to proton holes in $0g_{9/2}$ and $1p_{1/2}$ orbitals, respectively. But the situation is more complicated in the Ag isotopes because of their three proton holes rather than the one proton hole in the In isotopes. The spin-parities of the ground states and the isomeric states with their energy differences reflect the size of the $Z \!=\! 40$ subshell gap in the odd-$A$ Ag isotopes. The $Z \!=\! 40$ subshell exists in ^99-103Ag because of the $9/2^{+}$ ground states and the $1/2^{-}$ isomeric states. The $Z \!=\! 40$ subshell disappears with the almost degenerate $1/2^{-}$ ground states and $9/2^{+}$ isomeric states in ^105-117Ag. It should be noted that it is difficult to identify the $Z \!=\! 40$ subshell gap purely from the $9/2^{+}$ and $1/2^{-}$ states because the $9/2^{+}$ state can be obtained by both the proton $(0g_{9/2})^{-3}$ and $(0g_{9/2})^{-1}(1p_{1/2})^{-2}$ configurations, while the proton firstly occupy the $1p_{1/2}$ orbital in the former case and the $0g_{9/2}$ orbital in the latter case. Both from the observed data and the shell-model calculations, the odd-$A$ Ag isotopes always have a rather low lying or even ground $7/2^{+}$ states, which can not be coupled by the proton $(0g_{9/2})^{-1}(1p_{1/2})^{-2}$ configuration. It is thus concluded that the $9/2^{+}$ and the $1/2^{-}$ states in odd-$A$ Ag isotopes are dominated by the $(0g_{9/2})^{-3}$ and the $(0g_{9/2})^{-2}(1p_{1/2})^{-1}$ configurations, respectively. The $(0g_{9/2})^{-3}$ configuration becomes more favourable when the $Z \!=\! 40$ subshell exists. The $(0g_{9/2})^{-2}(1p_{1/2})^{-1}$ configuration becomes more favourable when the $Z \!=\! 40$ subshell disappears.

It is of great interest to know whether the $Z \!=\! 40$ subshell exists or not in the neutron-rich odd-$A$ Ag isotopes, such as ^123,125Ag. The answer is found that the isomeric states in ^123,125Ag are discovered to be $1/2^{-}$ states but with rather small excitation energies^[2]. The $Z \!=\! 40$ subshell recovers with a small shell gap in ^123,125Ag. An inversion between the $1p_{1/2}$ and $0g_{9/2}$ orbitals is found from ¹¹⁷Ag to ¹²³Ag. A schematic picture of the shell evolution is presented in Fig. 3 for comparison between ¹¹⁷Ag and ¹²³Ag. The shell-model calculations with the Hamiltonian discussed in Section 2 well reproduce the levels of ^123,125Ag^[2]. ESPE are calculated with and without the tensor interaction to further investigate which part of the nuclear interaction contributes to the inversion of the proton $1p_{1/2}$ and $0g_{9/2}$ orbitals around $N \!=\! 72$. It is found that the $1p_{1/2}$ orbital locates always below $0g_{9/2}$ orbital without the tensor interaction, while with the tensor interaction it locates above $0g_{9/2}$ orbital around $N \!=\! 68$ and below $0g_{9/2}$ orbital around $N = 76$. The tensor interaction is the key reason to explain the inversion of the two orbitals around $N \!=\! 72$.

Figure  3.  (color online)Schematic configurations for $1/2^{-}$ and $9/2^{+}$ ground states of ¹¹⁷Ag and ¹²³Ag, resepctively.

DownLoad: Full-Size Img PowerPoint

As mentioned in Section 3, the $j = l\pm1/2$ neutron generally attracts the $j' = l'\mp1/2$ proton more than the $j'' = l''\pm1/2$ proton. The $0h_{11/2}$ neutron attracts more the $1p_{1/2}$ proton rather than the $0g_{9/2}$ proton. From ¹¹⁷Ag to ¹²³Ag, the neutrons mainly occupy the $0h_{11/2}$ orbital, which is the reason for the recovery of the $Z \!=\! 40$ subshell. As observed and discussed in Ref. [2], the $Z\! =\! 40$ subshell recovers with a small shell gap, which is because of the neutron configuration mixing between the $0h_{11/2}$ and $1d_{3/2}$ orbitals. The occupancy of the neutron $1d_{3/2}$ orbital has an opposite effect on the $Z \!=\! 40$ subshell gap to that of the neutron $0h_{11/2}$ orbital. From ¹¹⁷Ag to ¹²³Ag, the neutrons mainly occupy the $0h_{11/2}$ orbital but with certain mixing occupancy on the $1d_{3/2}$ orbital, which explains the recovery of the small $Z \!=\! 40$ subshell gap.

It is worth using the present Hamiltonian for the further investigations on the astrophysical interested $N \!=\! 82$ isotones because of its nice description on ^123,125Ag. Fig. 4 presents the low lying levels of the even $N \!=\! 82$ isotones from ¹³⁰Cd to ¹²⁰Sr. It is clearly seen that the excitation energies of the $2^+$, $4^+$, $6^+$, $8^+$, $4^-$, and $5^-$ states increase as the proton number decreases, while those of the $0^+_2$ states decrease from ¹³⁰Cd to ¹²²Zr. If only the proton $1p_{1/2}$ and $0g_{9/2}$ orbitals are considered, the $2^+$, $4^+$, $6^+$, and $8^+$ states can only be coupled by the even protons on the $0g_{9/2}$ orbital and the $4^-$ and $5^-$ states can only be coupled by the odd protons on the $0g_{9/2}$ orbital and the single proton on the $1p_{1/2}$ orbital. The ground state and the $0^+_2$ state are from different configuration mixing between the proton pairs on these two orbitals. The results in Fig. 4 show that the protons favour to couple to pairs with zero angular momentum. Actually, the protons also remove from the $1p_{3/2}$ orbital and even the $0f_{5/2}$ orbital from ¹³⁰Cd to ¹²⁰Sr. The proton $1p_{1/2}$ and $0g_{9/2}$ orbitals still have considerable occupancies of $0.678$ and $2.251$ in the ground state of ¹²⁰Sr, respectively. The $Z \!=\! 38$ and $40$ subshell gaps are not kept in the extreme neutron rich $N \!=\! 82$ isotones, such as ¹²²Zr and ¹²⁰Sr, based on the present study.

Figure  4.  (color online)Observed (points) and calculated (lines) levels of the even $N \!=\! 82$ isotones from ¹³⁰Cd to ¹²⁰Sr.

DownLoad: Full-Size Img PowerPoint

5.   ²¹⁸Pa

A $1^{-}$ ground state and a high spin isomeric state are observed along the odd-odd $N \!=\! 127$ isotones, ²¹⁰Bi, ²¹²At, ²¹⁴Fr, and ²¹⁶Ac^[32]. In these odd-odd $N\! =\! 127$ isotones, both the $1^{-}$ ground state and the high spin isomeric state are from the multiplet coupled by the odd $0h_{9/2}$ protons and the single $1g_{9/2}$ neutron. Recently the isomeric state in ²¹⁸Pa is discovered for the first time^[4]. It is not possible to identify the spin-parity of both the ground state and the isomeric state due to the limited statistics of the data. It is very natural to assume that the ground state is a $1^{-}$ state and the isomeric state is a high spin state following the systematics of the other $N \!=\! 127$ isotones.

However, some facts from the observations and the shell-model calculations show deviations from such assumptions. Firstly, the excitation energies of the high spin isomers decrease from ²¹⁰Bi to ²¹⁶Ac. The newly discovered isomeric state in ²¹⁸Pa has a larger excitation energy than that of ²¹⁶Ac, which deviates from the systematic trend of the odd-odd $N \!=\! 127$ isotones^[4]. Secondly, the shell-model calculations reproduce the observed spins and parities of the ground states and the isomeric states of ²¹⁰Bi, ²¹²At, ²¹⁴Fr, and ²¹⁶Ac but predict a $8^{-}$ ground state for ²¹⁸Pa. Following the $\alpha$ decay properties and the shell-model calculations, the ground state and isomeric state of ²¹⁸Pa are suggested to be $8^{-}$ state and $1^{-}$ state, respectively^[4].

It is worth investigating further the mechanism which induces the evolution of the ground states and the isomeric states among $N \!=\! 127$ isotones. As shown in Fig. 5, constrained calculations, of which protons are constrained with $(0h_{9/2})^n$ configuration or with $(0h_{9/2}1f_{7/2}0i_{13/2})^n$ configuration, are performed to identify the important configurations for the evolution. Along the $N \!=\! 127$ isotones from ²¹⁰Bi to ²¹⁸Pa, the increasing protons mainly occupy the $0h_{9/2}$ orbital. However, if only the $0h_{9/2}$ protons are included in the model space while the other proton orbitals are excluded, it is found from Fig. 5 that the excitation energies of the high spin isomer decrease very quickly and become the ground state in ²¹⁴Fr. It should be noted that KHPE interaction fixed the proton-neutron interaction to reproduce the multiplet in ²¹⁰Bi, while the evolution from ²¹⁰Bi should be investigated. From ²¹⁰Bi to ²¹⁸Pa, the proton-neutron particle-particle interaction in the $(0h_{9/2})^{1}(1g_{9/2})^{1}$ configuration changes to the proton-neutron hole-particle interaction in the $(0h_{9/2})^{-1}(1g_{9/2})^{1}$ configuration when the protons only occupy the $0h_{9/2}$ orbital. The transition from the particle-particle interaction to the hole-particle interaction drives the decreasing energy between the high spin $8^{-}$ state and the $1^{-}$ state but much more quickly than the observations. If the $0h_{9/2}$, $1f_{7/2}$, and $0i_{13/2}$ orbitals are included in the model space, the calculated results are rather close to the calculations with the full model space. From ²¹⁰Bi to ²¹⁸Pa, the protons occupy not only the $0h_{9/2}$ orbital but also the $1f_{7/2}$ and $0i_{13/2}$ orbitals. The protons on the $1f_{7/2}$ and $0i_{13/2}$ orbitals generally couple to pairs which contribute little on the spin but some on the energy.

Figure  5.  (color online)Observed (points) and calculated (lines) levels of the odd-odd $N \!=\! 127$ isotones from ²¹⁰Bi to ²¹⁸Pa.

DownLoad: Full-Size Img PowerPoint

6.   Conclusion

In summary, the newly discovered isomeric states in ¹⁰¹In, ^123,125Ag, and ²¹⁸Pa are well reproduced by the shell-model calculations, which provides a nice basis to investigate the underlying physics in these isomeric states.

The neutron configuration mixing is introduced to explain the similar excitation energies of the isomeric states in the odd-$A$ In isotopes, ^101-109In. The type II shell evolution is suggested for these isotopes that the relative positions between neutron $1d_{5/2}$ and $0g_{7/2}$ orbitals are different in the ground $9/2^+$ states and the isomeric $1/2^-$ states in these In isotopes. The shell-model calculations also show strong sensitivity between the proton-neutron interaction and the excitation energies of the isomeric states.

The newly discovered isomeric states in ^123,125Ag indicate the recovery of the $Z \!=\! 40$ subshell. The tensor interaction is found to be the key components in the nuclear interaction to reproduce the $Z \!=\! 40$ subshell evolution from ¹¹⁷Ag to ¹²³Ag. Based on the nice description on ^123,125Ag, the same Hamiltonian is used to investigate the levels of the $N \!=\! 82$ isotones. The $Z \!=\! 38$ and $40$ subshell are found to be not kept in the extreme neutron-rich $N \!=\! 82$ isotones.

Based on the observed $\alpha$ decay properties and the shell-model calculations, the ground state and the newly discovered isomeric state of ²¹⁸Pa are suggested to be the $8^-$ and $1^-$ states, respectively, which differ from the previous observed odd-odd $N \!=\! 127$ isotones ²¹⁰Bi to ²¹⁶Ac with the ground $1^-$ states and the high spin isomeric states. The transition of the proton-neutron interaction from the particle-particle type to the hole-particle type is found to be the key interaction contributed to the rapid evolution between the ground states and the isomeric states in the odd-odd $N \!=\! 127$ isotones. The configuration mixing from the other two proton orbitals, $1f_{7/2}$ and $0i_{13/2}$, slows the evolution and reproduces well the observed data.

It is expected that ${V}_{\rm{MU}}$ plus the M3Y spin-orbit interaction can provide a universal interaction for the nuclear structure study, which are preliminarily investigated in the present work and Refs. [23-24]. It is more reliable to perform the shell-model calculations based on one effective interaction, while the Gogny interaction is also a potential one^[38-39].

Acknowledgement Prof. Zhang Yuhu, Prof. Wang Meng, Prof. Xu Xing, Prof. Yang Huabin, and Prof. Zhang Zhiyuan from the Institute of Modern Physics, CAS and Prof. Li Zhihuan, Prof. Hua Hui, and Dr. Chen Zhiqiang from Peking University are appreciated for their helpful discussions.