Hypernuclear Structure in $ {_\Lambda^{16}} {\rm\bf{O}}$ and Its Dependence on Hyperon's Coupling Strengths with the Relativistic Hartree-Fock Theory
-
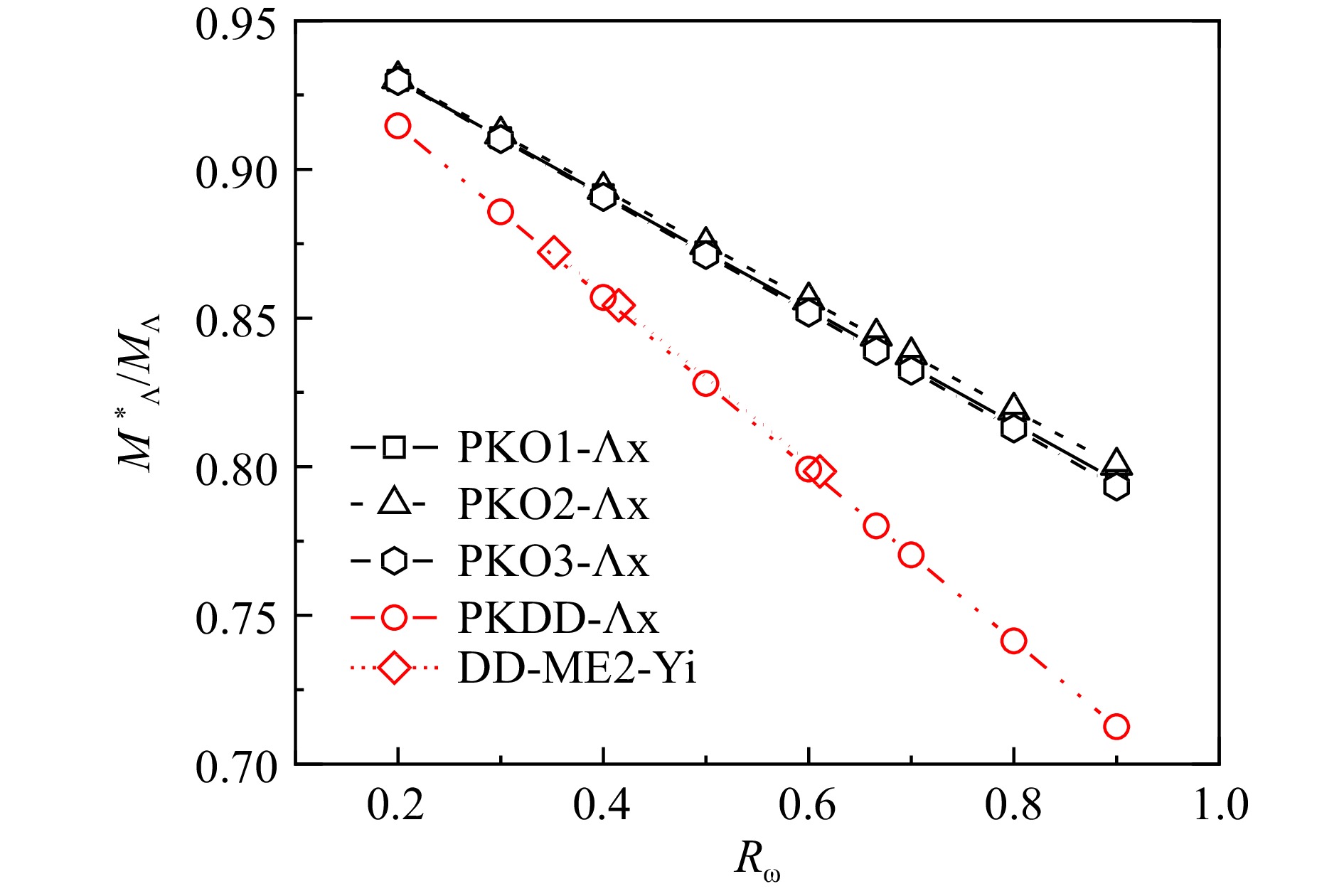
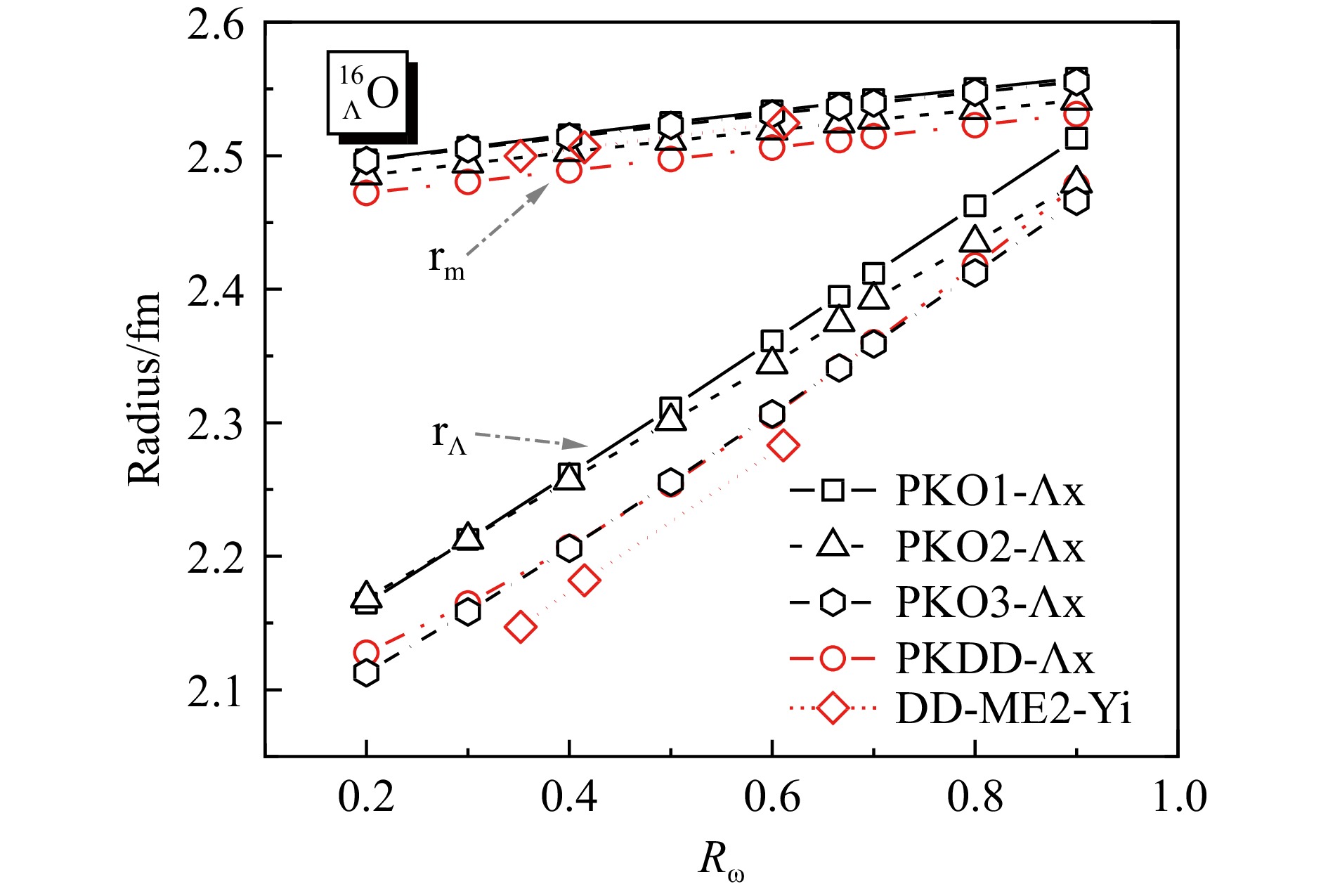
摘要: 超核物理研究为揭示重子-重子相互作用的核介质中特性以及理解原子核与中子星内部结构提供了关键信息。基于密度依赖的相对论Hartree-Fock (RHF)理论，拟合单$\Lambda$超核中超子分离能实验数据得到模型中$\Lambda \rm { N}$有效相互作用。交换项的引入改变了超子道中有效核力的动力学平衡，导致不同于相对论平均场模型的介子-超子耦合强度，进而影响超子自旋-轨道劈裂的描述。考虑到模型中有效核力取值的不确定性，进一步研究了单$\Lambda$超核的粗块及单粒子性质对于超子耦合强度的依赖，探索约束其取值范围的可能方法。具体以$^{16}_{\Lambda} \rm{O}$超核为例，通过改变同位旋标量道超子耦合强度，系统分析了超核能量泛函中核介质与交换项效应。结果显示，超子自旋-轨道劈裂、Dirac有效质量以及超核特征半径等与超子耦合强度比值可能存在一定的线性关联。因此，通过实验或理论对这些物理量做出约束，有望对核介质中超子相关的有效核力给出更强的限制。Abstract: The research in hypernuclear physics provides crucial information for uncovering the characteristics of baryon-baryon interactions in the nuclear medium and understanding the internal structure of atomic nuclei and neutron stars. Based on the density-dependent relativistic Hartree-Fock (RHF) theory, the $\Lambda \rm{N}$ effective interaction in the model is obtained by fitting experimental data of hyperon separation energies for single-$\Lambda$ hypernuclei. The inclusion of the Fock term alters the dynamic equilibrium of the effective nuclear force in the hyperon channel, resulting in a meson-hyperon coupling strength that differs from the relativistic mean-field model and influences the description of hyperon spin-orbit splitting. Considering the uncertainty in the values of the effective nuclear force within the model, further research is conducted to explore the dependence of hypernuclear bulk and single-particle properties on the hyperon coupling strength, aiming to identify possible ways to constrain its range of values. Taking the $^{16}_{\Lambda}\rm{O}$ hypernucleus as an example, the effects of the nuclear medium and Fock terms are systematically analyzed by adjusting the hyperon coupling strength in the isoscalar channel within the hypernuclear energy functional. The results suggest a possible linear relationship between the ratio of hyperon coupling strength and quantities such as hyperon spin-orbit splitting, Dirac effective mass, and hypernuclear characteristic radius. Therefore, by constraining these quantities through experimental or theoretical means, it is possible to impose stronger limitations on the effective nuclear force associated with hyperons in the nuclear medium.
-
0. 引言
由于Z=38 亚壳与N = 50幻数壳的存在，A~90，N~50核区的核素大多具有近球形核结构，低激发态主要表现出单粒子运动的特性[1]。对于N = 50和56之间的核结构，通常理解为这些壳层之上核子的单粒子激发[2-5]。随着中子数的增加，A≈100的原子核一般会经历从球形向形变核的转变，当中子数超过56时，这个质量区域的原子核形状会发生快速的形状转变，价核子数目的增多和激发能的增加更可能会使原子核的高自旋态出现集体运动和核芯激发现象。
通过本组之前对A~90质量区Nb同位素的研究发现，对于N>50的稳定线以及稳定线附近的92, 93Nb核[4-5]，中等自旋能级可由Z = 38的核芯激发或N = 56的亚壳层激发形成，更高自旋的能级会涉及N = 50的核芯激发。然而，由于实验的困难，稳定线右侧的丰中子Nb同位素高自旋态信息非常缺乏。Bucurescu等[1]利用82Se(16O, 1p2n)95Nb反应，16O束流能量为48 MeV，布局了95Nb的高自旋态，由于入射粒子能量较低，所得纲图信息较少，并未对高自旋能级进行指定。
因此，进一步扩展丰中子侧Nb同位素能级纲图，揭示其单粒子激发和集体运动的共存和竞争，是很有意义的。本文将详细介绍95Nb高自旋态的实验研究结果，在扩展其能级纲图的基础上，通过把实验结果和壳模型计算结果相比较，探讨95Nb的激发机制。
1. 实验和数据分析
在HI-13串列加速器上，利用中国联合伽马探测阵列，最多可放置40个Ge探测器，BGO和HPGe探测器分别与法兰相连，径向距离可通过螺杆调节，如图1所示。采用82Se(18O, 1p4n)95Nb熔合蒸发反应，18O束流能量为82和88 MeV，对95Nb的能级结构进行研究,平均束流强度为90 nA，靶由厚度为0.85 mg/cm2的82Se和4.45 mg/cm2厚的金衬组成。探测系统是由28台带反康的高纯锗(或Clover)探测器和1 台小平面探测器组成。其中6 台探测器放置在与束流夹角为150°的方向，7台探测器放置在60°方向，90°和120°方向各8台。
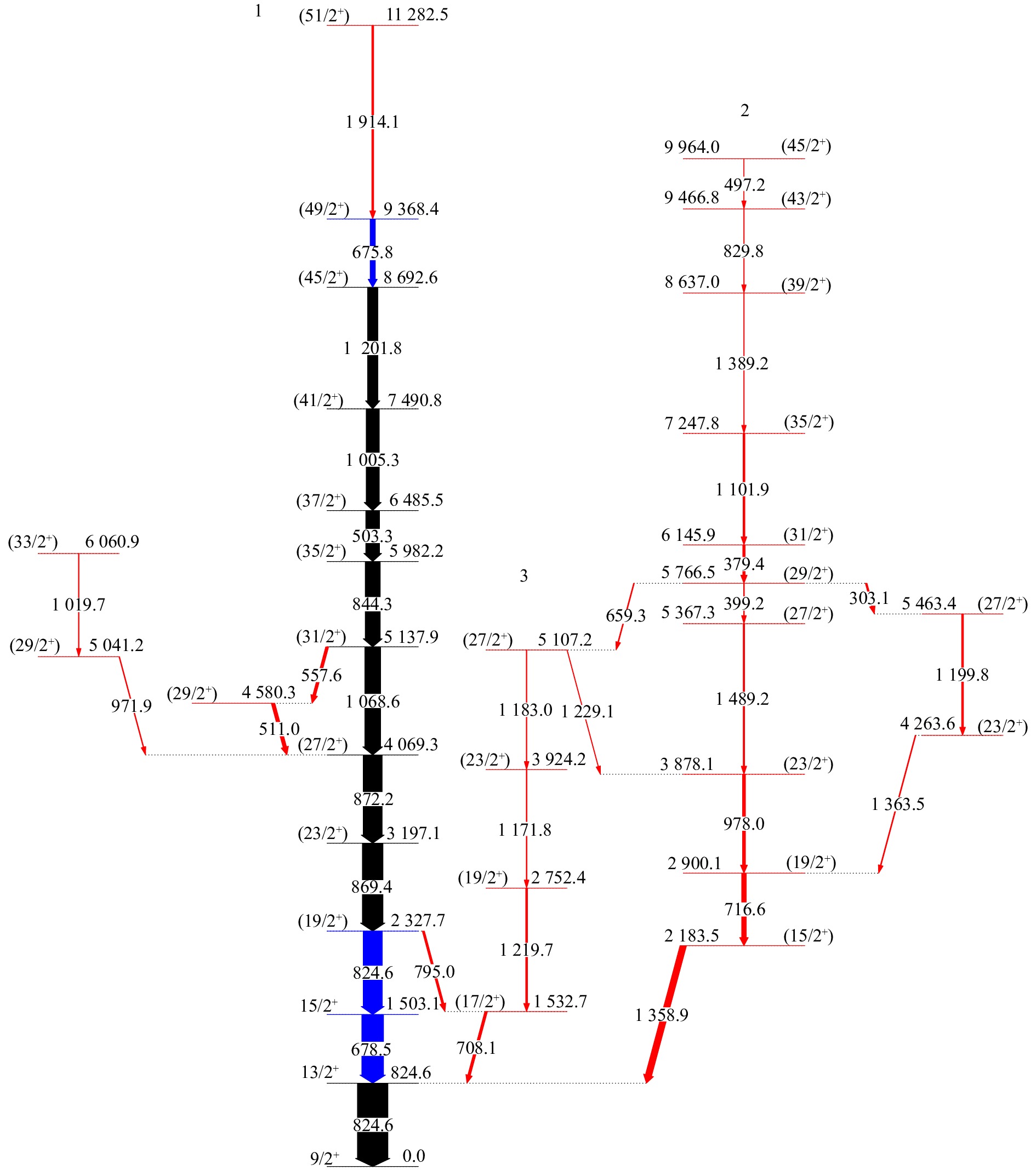
用60Co，133Ba和152Eu标准放射源对探测器进行了能量和效率刻度。将实验数据离线反演成γ-γ二维对称矩阵，用于分析γ-γ符合关系，提取γ跃迁的强度和建立能级纲图。处理实验数据后得到的95Nb纲图，如图2所示，图中标红射线是在此次实验中新发现的射线，标蓝射线调整了摆放顺序。
为进一步确定新发现能级的自旋，利用90°和150°方向上的探测器构建二维γ-γ DCO矩阵， DCO比例系数为
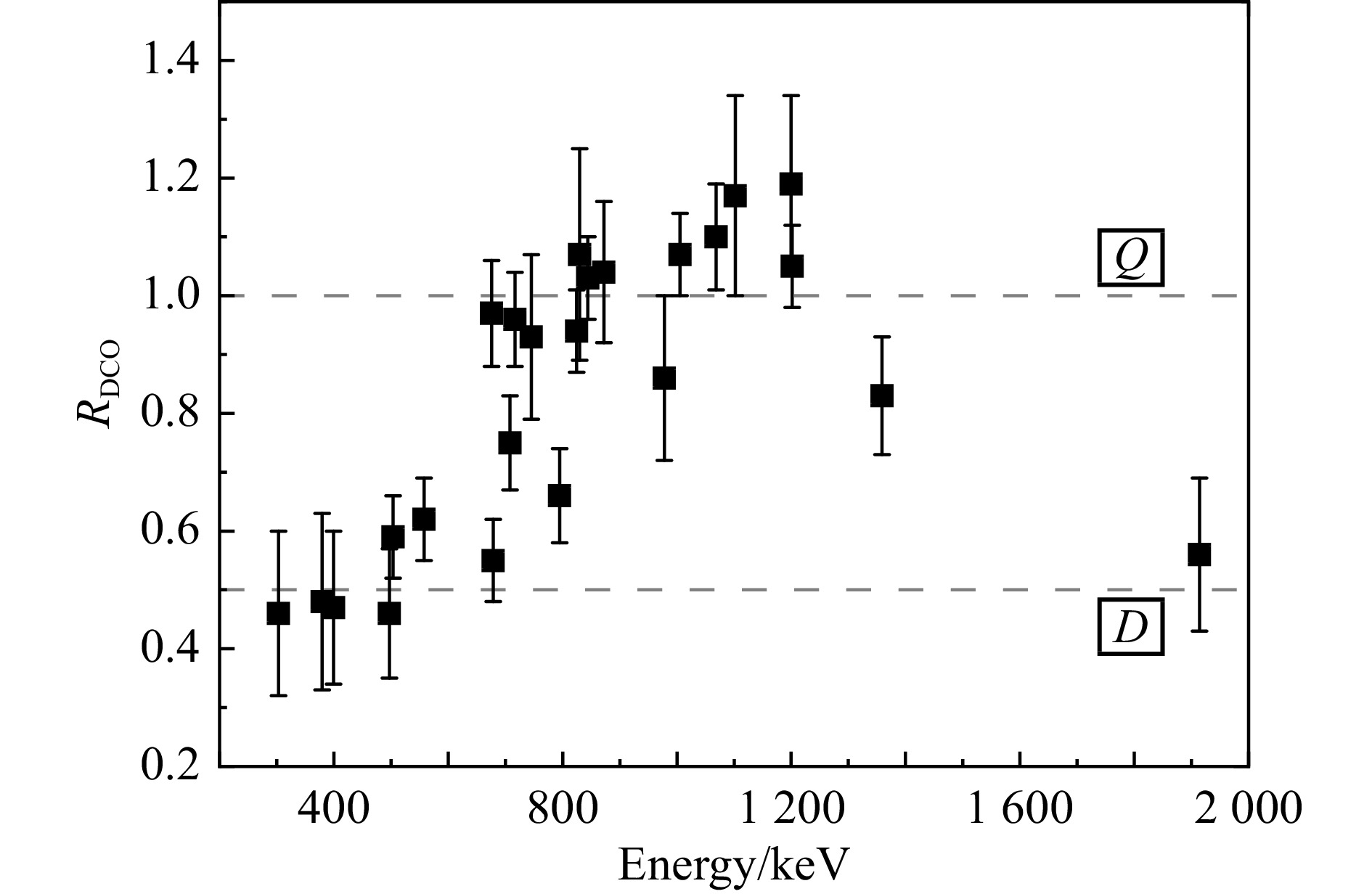
$$ {{R}}_{{\rm{DCO}}} = \frac{{I_\theta ^{{\gamma _1}}({\text{gated by }} {\gamma _2} {\text{ at }} {{90}^ \circ })}}{{I_{{{90}^ \circ }}^{{\gamma _1}}({\text{gated by }} {\gamma _2} {\text{ at }} \theta )}}\frac{{\varepsilon _\theta ^{{\gamma _1}}\varepsilon _{{{90}^ \circ }}^{{\gamma _2}}}}{{\varepsilon _{{{90}^ \circ }}^{{\gamma _1}}\varepsilon _\theta ^{{\gamma _2}}}} \text{，} $$ (1) 其中：γ2是用来开窗的，已知极性的电四极(ΔI=2)跃迁，与该跃迁存在符合关系的纯四极跃迁的RDCO值在1.0附近，而纯偶极跃迁的值在0.5附近；公式中$I_\theta ^{{\gamma _1}}$和$I_{90^\circ }^{{\gamma _1}}$分别是在150°和90°方向上开窗射线γ2得到的射线γ1的强度；θ为小角度方向150°；ε为90°或150°方向不同能量跃迁的探测器效率。
此外，本工作还利用线极化测量方法确定γ跃迁的电磁特性。利用放置在90°的分辨率较好的Clover探测器测量平行和垂直方向的康普顿散射事件来确定入射光子的极化度(非对称度)，把符合事件处理为平行散射事件矩阵和垂直散射事件矩阵。非对称度公式[6]为
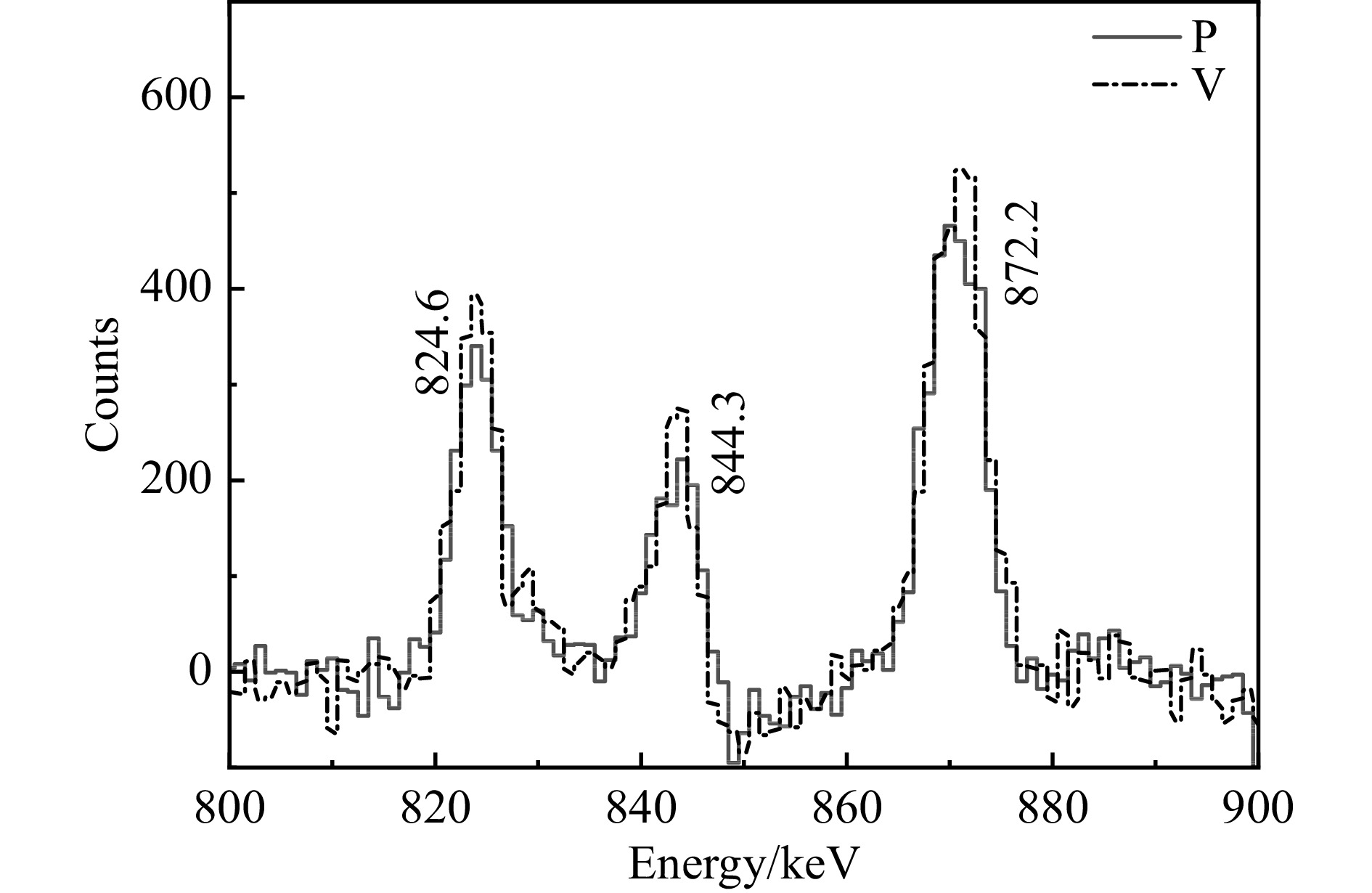
$$ A(\theta ) = \frac{{a(E_\gamma ){N_ \bot } - {N_\parallel }}}{{a(E_\gamma ){N_ \bot } + {N_\parallel }}} \text{，} $$ (2) 其中：a($E_\gamma $)为极化效率刻度曲线，是Clover探测器对平行和垂直散射的γ跃迁探测效率的比值；N⊥和$N_\parallel$分别为实验测量的与反应平面垂直和平行的康普顿散射光子的计数。每个Clover探测器可以分为4块晶体，利用90°方向上的Clover探测器(此方向A(θ)有最大值)。实验时伽马射线入射到任意一晶体上，与之相邻的两个晶体探测到的康普顿散射光子被认定分别对应于垂直和平行的康普顿事件。此外，四块晶体探测效率不同，需要对探测器的效率进行修正。作极化探测效率刻度曲线时，使用没有被极化的放射源133Ba和152Eu进行刻度，选取水平和垂直事件进行计算，公式定义为：a($E_\gamma $) = N||/N⊥，将得到的不同能量下的a($E_\gamma $)进行直线拟合。拟合公式为：$a({E_\gamma }) = 0.995\,17 - 2.662\,62{{\rm e}^{ - 5}} \times {E_\gamma }$。A(θ)的计算值若为正，该跃迁为电跃迁，若为负，则为磁跃迁。图3为利用824 keV伽马跃迁开门得到的824.6，844.3和872.2 keV跃迁在垂直(V)和平行方向(P)的能谱，从图中可以看到，824.6，844.3和872.2 keV的水平方向计数明显小于垂直方向计数，为电跃迁。结合之前的DCO测量结果，γ跃迁DCO比值如图4所示，可判断它们三者均为电四极跃迁，以此类推可得到其他γ跃迁的电磁特性。
2. 结果与讨论
2.1 能级纲图
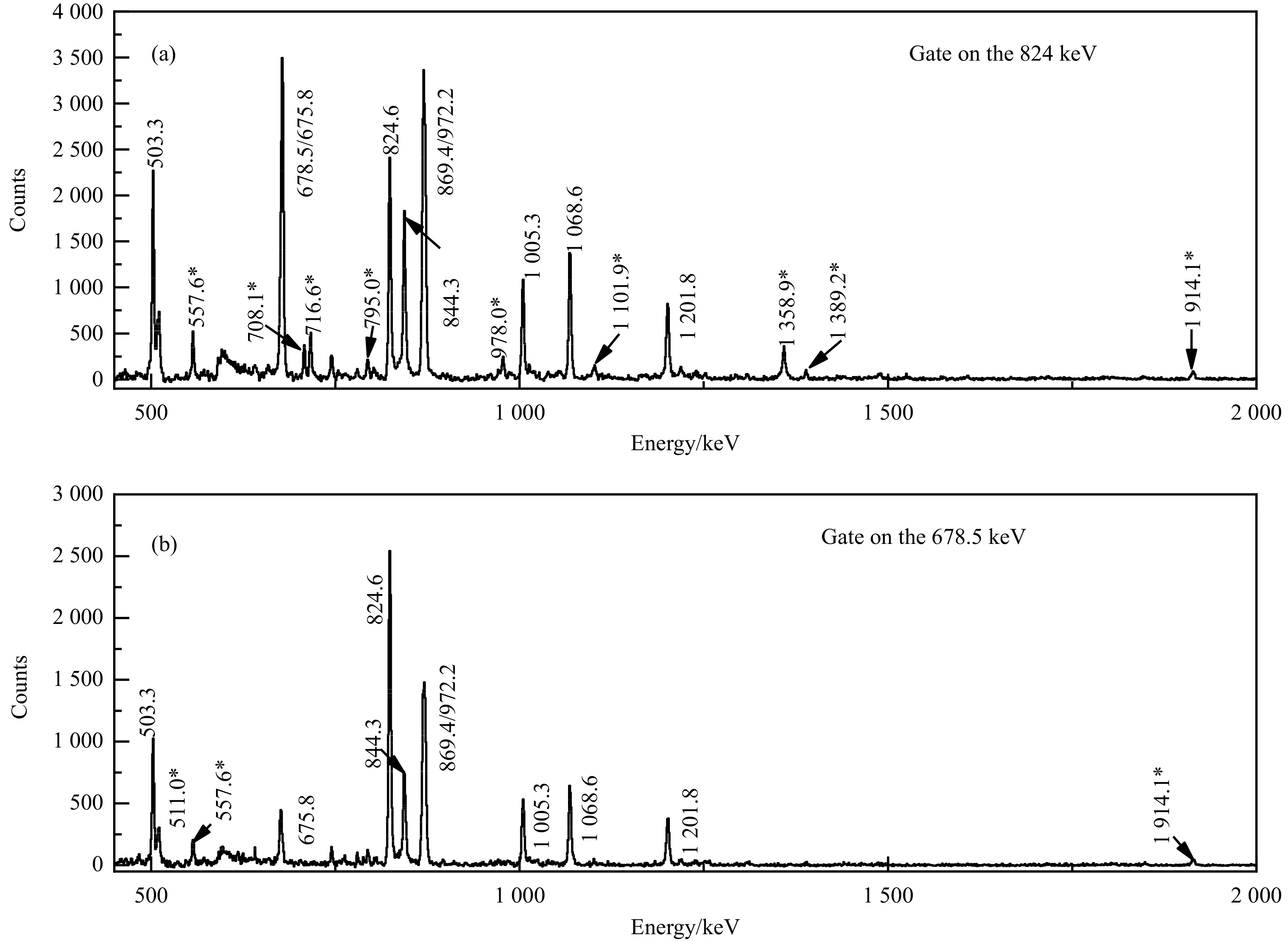
本工作之前，Bucurescu等[1]利用82Se (16O, 1p2n) 95Nb反应，将95Nb自旋和能量推高至33/2 ћ态和8.7 MeV。如图2所示，我们用已知的γ射线开窗寻找新的γ射线，在其基础上发现了约25条新的γ射线、21个新的能级，建立了2个新的序列(序列2和3)，自旋推高到了51/2 ћ，激发能约11 MeV；此外，根据符合和强度关系调整了部分能级位置的摆放。图5为此次基态跃迁能量824 keV开窗谱和678.5 keV开窗谱。
在本次实验的678.5 keV开窗谱中，如图5(b)所示，发现了675.8 keV，并且872.2 keV与自身没有级联关系，利用708.1 keV和795.0 keV的级联加和关系和能量强度，修改了678.5 keV的位置在两条824.2 keV之间，并且根据能量强度关系，确定675.8 keV在能级8 692.6 keV之上。在序列1不同γ跃迁的开窗谱中，发现了更高自旋态49/2+之上的1 914.1 keV跃迁。在能级4 069.3 keV之上，分别发现了557.6，511.0，971.9，1 019.7 keV的退激序列。
在本次实验824.2 keV的开窗谱中，如图5(a)所示，可以观测到1 358.9，716.6 keV的正宇称退激序列，通过级联关系、强度关系和级联加和关系确定了716.6 keV往上的两条退激路径。与此同时，在708.1 keV开窗谱中，发现了1 219.7, 1 171.8, 1 183.0和659.3 keV的级联顺序，且它们的级联加和关系和序列2相呼应。这增加了序列3的合理性。对于基态跃迁，708.1和1 358.9 keV只与824.6 keV有级联关系，这能够从实验上确定824.6 keV为基态跃迁。
2.2 壳模型计算
为了解释95Nb的激发能级的实验观测值，我们利用壳模型程序Nushellx[7]对95Nb的激发能级进行计算。选取的壳模型空间为GWB，相互作用势为GWBXG[8]。壳模型空间总共由10 条轨道组成：π(f5/2，p3/2，p1/2，g9/2)，ν(p1/2，g9/2，g7/2，d5/2，d3/2，s1/2)。每条轨道所对应的单粒子能量分别为：−5.322，−6.144，−3.941，−1.250，−0.696，−2.597，5.159，1.830，4.261和1.741 MeV。考虑到壳模型计算的复杂性和耗时性，对计算的组态空间进行截断，只将各态的主要组态成分考虑进去，而其他次要的组态成分则忽略。实验结果和壳模型计算结果如图6所示。
95Nb费米能级为πg9/2和νd5/2，相对于Z = 38和N = 50的核心外面有三个价质子和四个价中子。由于质子高jg9/2轨道单粒子激发能较低，而中子高jg7/2轨道的激发能较高，所以95Nb低位能级主要由π(p1/2 g9/2)轨道激发。正如壳模型的计算结果所给出的那样，基态9/2+由质子轨道1g9/2上未成对的质子表示。随着自旋的增加，23/2+及以上开始涉及质子轨道2p1/2质子对向轨道1g9/2激发，例如，31/2+和35/2+态，它们的质子组态都为π(1g9/2)3。当自旋更高时，将涉及中子轨道d5/2上的中子跨56亚壳向更高能量的3s1/2轨道激发，例如，35/2+态，中子组态为ν(1g7/2)1(2d5/2)2(3s1/2)1。在高自旋态时，如39/2+和45/2+态时，涉及质子轨道1f5/2上的质子跨Z = 38壳的核芯激发，质子组态为π(1f5/2)5(2p1/2)1(1g9/2)3。
从图6中可以看出，壳模型计算整体符合较好，对于高自旋能级，实验能级和计算结果相差较大。通常情况下，特定能级的计算值与实验值的偏差程度取决于被忽略的组态成分对这一能级波函数的贡献程度。忽略了特定能级的重要组态成分将会导致这条能级的计算值比实验值大很多。对于本工作中的壳模型计算结果在高激发态出现的明显差异，最主要原因可能是在GWB相互作用空间没有考虑h11/2轨道。因此，进一步进行壳模型计算的意义在于，能够揭示其中子激发与质子激发的竞争和相互作用。
3. 总结
利用熔合蒸发反应82Se (18O, p4n) 95Nb布居了95Nb的高自旋态，扩展了95Nb的能级方案，对95Nb核的高自旋态能级纲图做了重要修改，新发现了25条γ跃迁和21条能级。利用DCO和线极化测量方法，确定了部分能级的自旋和宇称。为了更好地理解95Nb的能级结构，使用Nushellx程序进行了壳模型计算，结果表明，95Nb较低自旋能级组态的主要成分由若干个πg9/2和νd5/2价核子构成，随着自选增加出现π(p1/2→g9/2)激发，在较高自旋能级中，将涉及ν(d5/2→g7/2，s1/2)激发，当自旋大于39/2+和45/2+出现了质子跨Z = 38的核心激发。
致谢 本工作是在中国原子能科学研究院串列加速器上完成的，感谢加速器运维组为实验提供了束流，同时感谢各位老师同学对实验各方面的帮助。
-
![]()
图 2 采用RHF有效相互作用PKO1-$\Lambda$x、PKO2-$\Lambda$x和PKO3-$\Lambda$x计算的$^{16}_{\Lambda}$O超核中核子与超子道交换项与直接项能量泛函比值$ \chi $随$R_{\omega}$的变化
![]()
图 3 含超子核物质中超子$M_{\Lambda}^{\star}/M_{\Lambda}$随矢量耦合强度比值$R_{\omega}$的变化(在线彩图)
结果基于RHF有效拉氏量PKO1-$\Lambda$x，PKO2-$\Lambda$x，PKO3-$\Lambda$x以及RMF有效拉氏量PKDD-$\Lambda$x，DD-ME2-Y$ i $计算得到。
![]()
图 4 采用RHF有效相互作用PKO1-$\Lambda$x，PKO2-$\Lambda$x，PKO3-$\Lambda$x(黑色)以及RMF有效相互作用PKDD-$\Lambda$x，DD-ME2-Y$ i $(红色)计算给出的$^{16}_{\Lambda}$O超核物质半径及$\Lambda$超子半径随矢量耦合强度比值$R_{\omega}$的变化(在线彩图)
表 1 在不同的介子-超子与介子-核子耦合强度比值$ R_{\omega} $下，拟合$^{16}_{\Lambda}$O、$^{40}_{\Lambda}$Ca和$^{208}_{\Lambda}$Pb超子分离能实验值得到的系列CDF有效相互作用[9]，部分数据取自文献[53]
$ R_{\omega} $ 0.200 0.300 0.400 0.500 0.600 0.666 0.700 0.800 0.900 PKO1-$\Lambda$x $ R_{\sigma} $ 0.262 0.334 0.405 0.477 0.549 0.596 0.621 0.692 0.764 $ \varDelta_{1} $ 0.851 0.601 0.357 0.121 0.107 0.254 0.328 0.539 0.642 $ \varDelta_{2} $ 1.610 1.335 1.088 0.877 0.715 0.646 0.623 0.615 0.681 PKO2-$\Lambda$x $ R_{\sigma} $ 0.263 0.334 0.404 0.474 0.545 0.591 0.614 0.685 0.755 $ \varDelta_{1} $ 0.933 0.694 0.458 0.228 0.046 0.144 0.252 0.436 0.647 $ \varDelta_{2} $ 1.480 1.245 1.049 0.904 0.858 0.802 0.779 0.849 0.940 PKO3-$\Lambda$x $ R_{\sigma} $ 0.259 0.331 0.403 0.475 0.546 0.594 0.618 0.690 0.762 $ \varDelta_{1} $ 0.491 0.250 0.013 0.221 0.450 0.598 0.673 0.889 1.096 $ \varDelta_{2} $ 1.760 1.536 1.348 1.227 1.133 1.100 1.093 1.103 1.155 PKDD-$\Lambda$x $ R_{\sigma} $ 0.241 0.322 0.403 0.485 0.566 0.620 0.647 0.729 0.810 $ \varDelta_{1} $ 0.969 0.799 0.615 0.421 0.219 0.083 0.012 0.194 0.401 $ \varDelta_{2} $ 1.099 0.992 0.884 0.781 0.690 0.641 0.622 0.588 0.614 注：其中$ \varDelta_{1} $表示$^{16}_{\Lambda}$O超子分离能的均方根偏差，$ \varDelta_{2} $表示系列超核$^{12}_{\Lambda}$C、$^{13}_{\Lambda}$C、$^{16}_{\Lambda}$O、$^{28}_{\Lambda}$Si、$^{40}_{\Lambda}$Ca、$^{51}_{\Lambda}$V、$^{89}_{\Lambda}$Y、$^{139}_{\Lambda}$La、$^{208}_{\Lambda}$Pb的均方根偏差。 
下载: 导出CSV
表 2 $^{16}_{\Lambda}$O超核中超子$ 1p $伙伴态自旋-轨道劈裂$\varDelta E_{{\rm{SO}}}^{\Lambda}$随$R_{\omega}$的变化
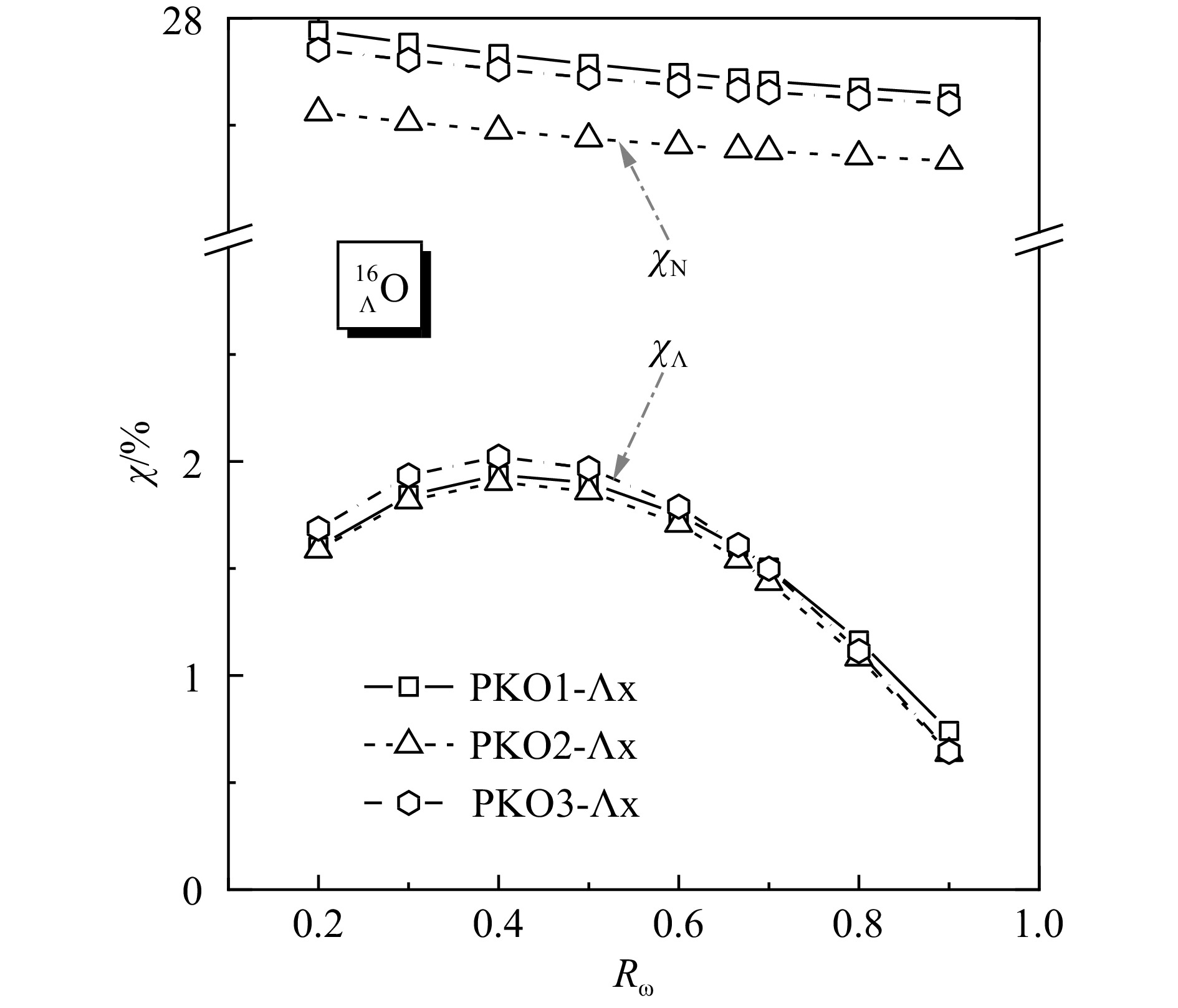
$^{16}_{\Lambda}$O $R_{\omega}$ 0.200 0.300 0.400 0.500 0.600 0.666 0.700 0.800 0.900 $\varDelta E_{{\rm{SO}}}^{\Lambda}$ PKO1-$\Lambda$x 0.426 0.573 0.720 0.868 1.015 1.111 1.161 1.305 1.447 PKO2-$\Lambda$x 0.438 0.585 0.733 0.882 1.033 1.127 1.174 1.322 1.464 PKO3-$\Lambda$x 0.427 0.575 0.722 0.868 1.011 1.105 1.152 1.290 1.424 PKDD-$\Lambda$x 0.525 0.742 0.959 1.176 1.390 1.528 1.599 1.801 1.994 注：结果采用有效相互作用PKO1-$\Lambda$x、PKO2-$\Lambda$x、PKO3-$\Lambda$x以及PKDD-$\Lambda$x计算得到，部分数据取自文献[53]。
下载: 导出CSV
-
[1] YAMAMOTO Y, MOTOBA T, HIMENO H, et al. Progress of Theoretical Physics Supplement, 1994, 117: 361. DOI: 10.1143/ptp.117.361
[2] GIBSON B F, HUNGERFORD E V. Phys Rept, 1995, 257(6): 349. DOI: 10.1016/0370-1573(94)00114-I
[3] EPELBAUM E, HAMMER H W, MEIẞNER U G. Rev Mod Phys, 2009, 81: 1773. DOI: 10.1103/RevModPhys.81.1773
[4] PRAKASH M, BOMBACI I, PRAKASH M, et al. Phys Rept, 1997, 280(1): 1. DOI: 10.1016/S0370-1573(96)00023-3
[5] TOLOS L, FABBIETTI L. Prog Part Nucl Phys, 2020, 112: 103770. DOI: 10.1016/j.ppnp.2020.103770
[6] BURGIO G F, SCHULZE H J, VIDAÑA I, et al. Prog Part Nucl Phys, 2021, 120: 103879. DOI: 10.1016/j.ppnp.2021.103879
[7] HASHIMOTO O, TAMURA H. Prog Part Nucl Phys, 2006, 57(2): 564. DOI: 10.1016/j.ppnp.2005.07.001
[8] FELICIELLO A, NAGAE T. Reports on Progress in Physics, 2015, 78(9): 096301. DOI: 10.1088/0034-4885/78/9/096301
[9] GAL A, HUNGERFORD E V, MILLENER D J. Rev Mod Phys, 2016, 88: 035004. DOI: 10.1103/RevModPhys.88.035004
[10] SAITO T R, DOU W, DROZD V, et al. Nature Reviews Physics, 2021, 3: 803. DOI: 10.1038/s42254-021-00371-w
[11] ABOONA B E, ADAM J, ADAMS J R, et al. Phys Rev Lett, 2023, 130: 212301. DOI: 10.1103/PhysRevLett.130.212301
[12] MA Y G. Nuclear Science and Techniques, 2023, 34(6): 97. DOI: 10.1007/s41365-023-01248-6
[13] VIDAÑA I. Universe, 2021, 7(10): 376. DOI: 10.3390/universe7100376
[14] HIYAMA E, KAMIMURA M, MIYAZAKI K, et al. Phys Rev C, 1999, 59: 2351. DOI: 10.1103/PhysRevC.59.2351
[15] HIYAMA E, YAMADA T. Progress in Particle and Nuclear Physics, 2009, 63(2): 339. DOI: 10.1016/j.ppnp.2009.05.001
[16] GAL A, MILLENER D. Phys Lett B, 2011, 701(3): 342. DOI: 10.1016/j.physletb.2011.05.069
[17] GAZDA D, GAL A. Phys Rev Lett, 2016, 116: 122501. DOI: 10.1103/PhysRevLett.116.122501
[18] WIRTH R, ROTH R. Phys Rev Lett, 2016, 117: 182501. DOI: 10.1103/PhysRevLett.117.182501
[19] MAREŠ J, JENNINGS B K. Phys Rev C, 1994, 49: 2472. DOI: 10.1103/PhysRevC.49.2472
[20] LU B N, HIYAMA E, SAGAWA H, et al. Phys Rev C, 2014, 89: 044307. DOI: 10.1103/PhysRevC.89.044307
[21] ZHOU X R, HIYAMA E, SAGAWA H. Phys Rev C, 2016, 94: 024331. DOI: 10.1103/PhysRevC.94.024331
[22] SUN T T, HIYAMA E, SAGAWA H, et al. Phys Rev C, 2016, 94: 064319. DOI: 10.1103/PhysRevC.94.064319
[23] XING X Y, HU J N, SHEN H. Phys Rev C, 2017, 95: 054310. DOI: 10.1103/PhysRevC.95.054310
[24] XIA H, WU X, MEI H, et al. Science China Physics, Mechanics & Astronomy, 2023, 66: 252011. DOI: 10.1007/s11433-022-2045-x
[25] DING S Y, YANG W, SUN B Y. Chin Phys C, 2023, 47(12): 124103. DOI: 10.1088/1674-1137/acf91e
[26] MENG J. Relativistic Density Functional for Nuclear Structure[M/OL]. World Scientific, 2016. https://doi.org/10.1142/9872.
[27] SUGAHARA Y, TOKI H. Progress of Theoretical Physics, 1994, 92(4): 803. DOI: 10.1143/ptp/92.4.803
[28] LONG W H, SUN B Y, HAGINO K, et al. Phys Rev C, 2012, 85: 025806. DOI: 10.1103/PhysRevC.85.025806
[29] XIA H J, MEI H, YAO J M. Sci China-Phys Mech Astron, 2017, 60: 102021. DOI: 10.1007/s11433-017-9048-2
[30] RONG Y T, TU Z H, ZHOU S G. Phys Rev C, 2021, 104: 054321. DOI: 10.1103/PhysRevC.104.054321
[31] KOHRI H, AJIMURA S, HAYAKAWA H, et al. Phys Rev C, 2002, 65: 034607. DOI: 10.1103/PhysRevC.65.034607
[32] MOTOBA T, LANSKOY D E, MILLENER D J, et al. Nuclear Physics A, 2008, 804(1): 99. DOI: 10.1016/j.nuclphysa.2008.01.026
[33] JENNINGS B K. Phys Lett B, 1990, 246(3): 325. DOI: 10.1016/0370-2693(90)90607-8
[34] BROCKMANN R, TOKI H. Phys Rev Lett, 1992, 68: 3408. DOI: 10.1103/PhysRevLett.68.3408
[35] WEI B, ZHAO Q, WANG Z H, et al. Chin Phys C, 2020, 44(7): 074107. DOI: 10.1088/1674-1137/44/7/074107
[36] LONG W H, VAN GIAI N, MENG J. Phys Lett B, 2006, 640(4): 150. DOI: 10.1016/j.physletb.2006.07.064
[37] GENG J, XIANG J, SUN B Y, et al. Phys Rev C, 2020, 101: 064302. DOI: 10.1103/PhysRevC.101.064302
[38] JIANG L J, YANG S, SUN B Y, et al. Phys Rev C, 2015, 91: 034326. DOI: 10.1103/PhysRevC.91.034326
[39] ZONG Y Y, SUN B Y. Chin Phys C, 2018, 42(2): 024101. DOI: 10.1088/1674-1137/42/2/024101
[40] WANG Z H, ZHAO Q, LIANG H Z, et al. Phys Rev C, 2018, 98: 034313. DOI: 10.1103/PhysRevC.98.034313
[41] LONG W H, NAKATSUKASA T, SAGAWA H, et al. Phys Lett B, 2009, 680(5): 428. DOI: 10.1016/j.physletb.2009.09.034
[42] LI J J, MARGUERON J, LONG W H, et al. Phys Lett B, 2016, 753: 97. DOI: 10.1016/j.physletb.2015.12.004
[43] LIANG H Z, VAN GIAI N, MENG J. Phys Rev Lett, 2008, 101: 122502. DOI: 10.1103/PhysRevLett.101.122502
[44] NIU Z M, NIU Y F, LIANG H Z, et al. Phys Rev C, 2017, 95: 044301. DOI: 10.1103/PhysRevC.95.044301
[45] LONG W H, RING P, GIAI N V, et al. Phys Rev C, 2010, 81: 024308. DOI: 10.1103/PhysRevC.81.024308
[46] SUN B Y, LONG W H, MENG J, et al. Phys Rev C, 2008, 78: 065805. DOI: 10.1103/PhysRevC.78.065805
[47] LI A, HU J N, SHANG X L, et al. Phys Rev C, 2016, 93: 015803. DOI: 10.1103/PhysRevC.93.015803
[48] GENG J, LI J J, LONG W H, et al. Phys Rev C, 2019, 100: 051301. DOI: 10.1103/PhysRevC.100.051301
[49] LIU J, NIU Y F, LONG W H. Phys Lett B, 2020, 806: 135524. DOI: 10.1016/j.physletb.2020.135524
[50] YANG S, SUN X D, GENG J, et al. Phys Rev C, 2021, 103: 014304. DOI: 10.1103/PhysRevC.103.014304
[51] LONG W H, GENG J, LIU J, et al. Communications in Theoretical Physics, 2022, 74(9): 097301. DOI: 10.1088/1572-9494/ac70ae
[52] XIA C J, SUN B Y, MARUYAMA T, et al. Phys Rev C, 2022, 105: 045803. DOI: 10.1103/PhysRevC.105.045803
[53] DING S Y, QIAN Z, SUN B Y, et al. Phys Rev C, 2022, 106: 054311. DOI: 10.1103/PhysRevC.106.054311
[54] SUN X D, MIAO Z Q, SUN B Y, et al. The Astrophysical Journal, 2023, 942(1): 55. DOI: 10.3847/1538-4357/ac9d9a
[55] WANG X S, SANG H Y, WANG J H, et al. Communications in Theoretical Physics, 2013, 60(4): 479. DOI: 10.1088/0253-6102/60/4/16
[56] LONG W H, SAGAWA H, MENG J, et al. Phys Lett B, 2006, 639(3): 242. DOI: 10.1016/j.physletb.2006.05.065
计量
- 文章访问数: 148
- HTML全文浏览量: 32
- PDF下载量: 32
甘公网安备 62010202000723号