-
摘要: 本工作通过引入原子核的形变改进了用于计算单质子放射性半衰期的Gamow-like模型。计算结果显示,相比于原Gamow-like模型,形变Gamow-like模型能够更好地再现单质子放射性实验数据。此外,通过研究单质子放射性半衰期实验值的对数形式和穿透概率计算值的对数形式之间的线性关系,证实了形变Gamow-like模型的可靠性。作为应用,使用形变Gamow-like模型预测了形变核的单质子放射性半衰期,预测的结果能够很好地符合Geiger-Nuttall定律。最后,通过研究轨道角动量与计算半衰期的关系,给出了母核109I和131Eu的角动量参考值,以获取更加准确的单质子放射性理论半衰期。这项工作有利于对质子滴线的研究以及新的单质子放射性半衰期的准确测量。
-
关键词:
- 单质子放射性 /
- 半衰期 /
- 形变 /
- Gamow-like模型
Abstract: In this work, the Gamow-like model for calculating the one-proton radioactivity half-life is improved by introducing the deformation of the nucleus. The calculations show that the deformed Gamow-like model can reproduce the experimental data better than the Gamow-like model. In addition, the reliability of the deformed Gamow-like model is confirmed by studying the linear relationship between the logarithmic form of the experimental half-life and the logarithmic form of the theoretical penetration probability. As an application, the one-proton radioactivity half-life of the deformed nucleus is predicted using the deformed Gamow-like model, and the predictions are able to comply well with the Geiger-Nuttall law. Finally, by studying the relationship between the orbital angular momentum and the calculated half-life, the reference values of the orbital angular momentum of 109I and 131Eu are given to obtain a more accurate theoretical half-life for one-proton radioactivity.-
Keywords:
- one-proton radioactivity /
- half-life /
- deformation /
- Gamow-like model
-
0. 引言
众所周知,我们的可见世界是由原子构成的,原子由原子核和电子构成,原子核由质子和中子组成,质子和中子由夸克组成。从这个意义来说,原子核是物质结构的一个重要微观层次,介于原子和核子之间,可以认为是由质子和中子组成的束缚态集团。核力是基于核子自由度,理解丰富多彩的核物理现象的根本出发点。此外,核力也和核天体物理、奇特强子态,超出标准模型的新物理等息息相关。
1919年卢瑟福发现质子[1],1932年查德威克发现中子之后[2],人们就开始思考到底是什么力将质子和中子束缚在10 fm大小的空间内。由于要克服质子间的强大库仑斥力,所以这个力必须非常强,这就是强相互作用力名称的来源。1935年,日本学者汤川秀树提出π介子交换理论[3],开启了对核力的微观研究。20世纪五六十年代,随着π介子以及一系列更重的介子(如ρ, ω)的实验发现,人们发展了单玻色子交换模型[4−6],可以定性描述核力乃至氘核的性质。20世纪70年代,物理学家们建立了描述强相互作用的基本理论–量子色动力学(QCD),其基本自由度是夸克和胶子。因而,科研人员尝试从夸克层次描述核力,发展了各种类型的夸克模型[7−23]。然而,总体上这类基于夸克自由度的核力模型还是唯象的,其与QCD的联系并不明晰。
对核力的研究在1990年取得了一个重大突破,诺贝尔物理学奖得主温伯格提出,可以利用从QCD发展而来的手征有效场论(Chiral Effective Field Theory, ChEFT)描述核力,即手征核力,这也是现代微观核力的开端[24−26]。有关核力发展的早期历史及文献,可以参考综述[27−29]。温伯格手征核力经过30多年的发展,获得了巨大成功,成为了第一性原理核物理研究的标准输入,也开创了基于有效场论方法研究非微扰强相互作用的先河。值得注意的是,温伯格手征核力是非相对论的。
温伯格手征核力在获得巨大成功的同时,也遇到了很多问题,如收敛速度慢、不满足重整化群不变性、三体力处理的自洽性等等。为了解决这些问题,研究人员做了各种各样的尝试。如发展不显含π介子的手征核力[30],考虑激发态Δ(1232)的贡献[31−44],考虑重整化群不变性发展新的计阶规则[45−48],发展相对论手征核力[49−53]等等。本文将主要介绍近期北航课题组及合作者在发展相对论手征核力方面所做的努力和取得的进展。
本文主要包含以下内容:在第1节将简单介绍手征有效场论的基本思想,并详细介绍非相对论手征核力的发展现状,以及其在应用于第一性原理计算中遇到的问题。在第2节简略介绍协变计阶规则及相对论手征核力的构建。在第3节将展示次次领头阶相对论手征核力对散射数据的描述效果。最后在第4节,进行简单总结,并对未来工作进行展望。
1. 手征核力
1979年,温伯格在有效场论的基础上提出,描述低能下强相互作用最一般形式的拉氏量应满足所有已知的QCD的对称性,特别是破缺的手征对称性[54]。手征对称性的自发破缺产生无质量的Goldstone玻色子。而后,这种利用有效场论描述Goldstone玻色子动力学的方法就被称为手征有效场论。由此可见,手征有效场论与描述强相互作用的基本理论QCD通过手征对称性紧密联系。手征有效场论在介子系统,特别是u、d两味系统中获得了巨大成功[55−56]。
手征有效场论在用于重子系统时,原有的(基于介子系统)发展计阶规则会因为手征极限下不为零的重子质量而遭到破坏。这是因为非零的重子质量使得对于重子场的协变微商不再是一个严格的小量[57]。Jenkins等[58]提出重重子近似(heavy baryon scheme),将作为硬能标的核子质量从核子外腿动量中分离,从而实现与介子系统类似的计阶规则。重重子手征有效场论(HB ChEFT)由此而来。然而,重重子方法本身破坏洛伦兹协变性,其对四动量的非相对论展开破坏了重子传播子的解析性,从而导致非物理的发散[59]。为了解决这一问题,人们提出了协变的计阶规则恢复方案,包括红外正规化方法(Infared Regularization, IR)[59]以及拓展的在壳重整化方案(Extended On Mass Shell, EOMS)[60]。这两种方法结合了相对论性以及重重子方法的优点,同时避免了两者的不足(前者破坏计阶规则,后者收敛性有问题)[61]。
1.1 非相对论手征核力
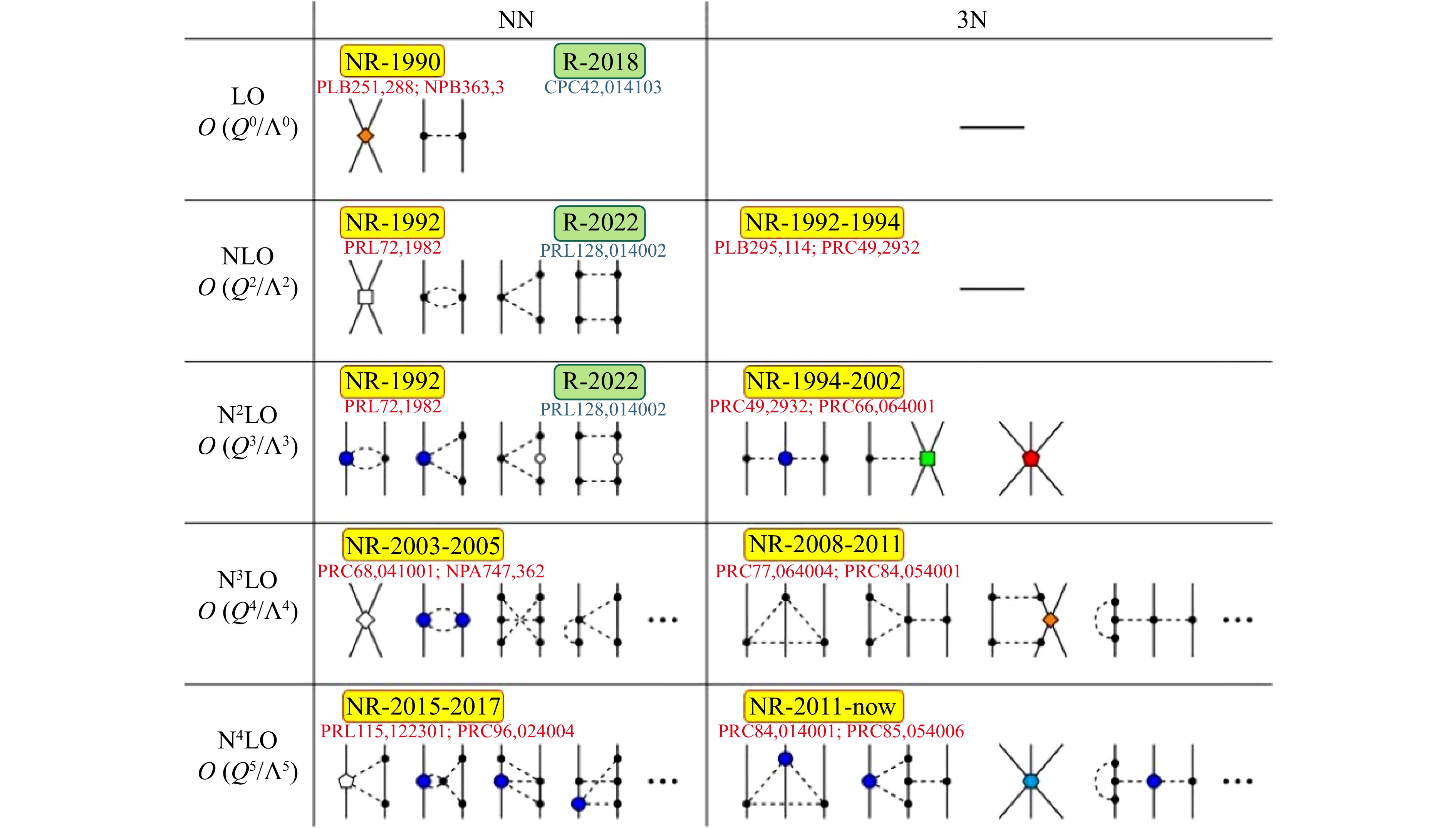
1990年,温伯格率先指出,可以利用手征有效场论来描述核子间相互作用[24−26],标志着现代核力研究的开端。他提出,我们可以首先按照手征阶数展开,微扰地计算核力,然后代入到Lippmann-Schwinger(LS)方程中考虑非微扰效应。这种基于重重子手征有效场论发展而来的核力就是温伯格手征核力。与唯象模型(如AV18[62],Reid93[63]以及CD-Bonn[64])不同,温伯格手征核力与强相互作用基本理论QCD联系紧密。在手征有效场论中,借由计阶规则,可以先验地对核力中某一部分的相对大小进行估计,从而实现系统的逐阶计算,提供了按照手征阶数逐阶提高描述精度以及系统估计理论误差的方法[27, 65−66]。此后30余年,经过众多物理学家的不懈努力,非相对论手征核力获得了长足的发展。图1展示了按照温伯格基于朴素维度分析的计阶规则,到手征阶数第5阶(N4LO)的各阶核力的贡献。该图同时给出了北航课题组及合作者发展的相对论手征核力的情况。
温伯格首先构建了领头阶(LO)的手征核力[24−25]。在LO,手征核力包含长程的单π介子交换项(OPE),即著名的Yukawa相互作用[3]以及短程的接触项。在此之后,Ordonez 等[31−32]基于时序(time ordered)手征有效场论将手征核力推进到次次领头阶(NNLO)。在次领头阶(NLO)以及次次领头阶,除新的短程相互作用项外,还包含中程的两π交换(TPE)以及相对论修正项。Kaiser等[67]则采用另一种方法,即维数正规化(Dimensional Regularization, DR)重新计算了TPE的贡献,发现新方法对高角动量分波的描述更好,不过其未考虑非微扰效应。Epelbaum等[68−69]的研究则指出,基于时序手征有效场论得到的核力依赖于入射核子的能量,并基于幺正变换提出了新的NNLO核力方案。在2003年Epelbaum等[70−71]利用谱函数正规化(spectrum function regularization)进一步改进了这一核力方案的收敛性。几乎与此同时,Entem等[72和Epelbaum等[73]分别将核力研究推进到了次次次领头阶(N3LO)。两种核力依据相同的计阶规则,均拟合了质子-质子、质子-中子的相移,不同之处主要在于采用了不同的正规化方案:前者采用维数正规化,后者则采用谱函数正规化。在这一阶,出现了新的短程接触项、两圈图的TPE、三π交换项以及相应的相对论修正项。也是在这一阶,非相对论手征核力对于核子-核子散射可观测量的描述精度达到了唯象核力的程度,实现了“高精度”的目标。在2014年,Epelbaum等[74]进一步改进了N3LO的手征核力,提出利用坐标空间的局域正规化因子取代动量空间正规化因子来改善短程贡献以及收敛性,并提出了基于手征有效场论收敛性质的理论不确定度估计方法。最近,Saha教授等[75]构建完成了坐标空间的局域N3LO手征核力。
从图1中我们可以看到,随着手征阶数的不断升高,核力的计算变得越来越复杂。第5阶(N4LO)的手征核力在2015—2017年分别由Machleidt与Epelbaum教授构建完成[76−79]。两种核力区别主要在于正规化方案,Machleidt教授采用谱函数正规化方法处理圈图,并采用非局域形状因子消除发散。Epelbaum教授则采用一种新的局域形状因子处理长程的π交换,并指出N3LO的短程相互作用中包含冗余的低能常数,这些冗余可以通过恰当的幺正变换消除,这简化了低能常数的拟合,并使得核力更软。在第6阶(N5LO),Machleidt教授给出了部分重要的长程贡献[80]。到N5LO,核力的计算已经极其繁杂,目前尚未有完整的N5LO手征核力。
上面提到的核力研究均不包含核子激发态Δ(1232)。但是必须指出,Δ(1232)的质量仅比核子质量高约300 MeV,其在核子-核子散射过程中可能起到重要的作用。上面提到的不考虑Δ(1232)的核力,其实际上是将其贡献作为高能部分吸收到了相关的πN低能常数。关于πN以及NN散射过程的研究表明,明确考虑Δ(1232)自由度将有效地加速手征展开的收敛速度[34, 81],从而在较低阶实现对散射过程的更好描述。Kolck教授在构建NNLO核力时已考虑Δ(1232)的贡献[32],Kaiser教授在微扰框架下讨论了Δ(1232)的贡献[33],Epelbaum教授在他们的NNLO核力中同样讨论了Δ(1232)的贡献,但并不完整[69]。在2007年,Epelbaum教授进行了系统的计算,证明Δ(1232)的贡献可以通过NLO的πN低能常数吸收掉[34],由此显著改善了收敛性,不过未考虑非微扰效应。在考虑Δ(1232)的情况下,NLO的TPE贡献将超过NNLO(在不考虑Δ(1232)时,NNLO的TPE比NLO的大,这实际上表明收敛性有瑕疵[69]。)在此之后,Piarulli等[36]进一步发展了包含Δ(1232)贡献的“minimally nonlocal”的NNLO手征核力,并在2016年约化为纯粹的局域核力[82]。Ekstroem等[37, 83]在2017-2020年完整地计算了包含Δ(1232)的NNLO手征核力并对核物质与有限核进行了计算,发现Δ自由度的引入显著改善了对核物质与有限核的描述。然而,Nosyk等[39]在之后的研究中指出,其低能常数的拟合考虑了有限核及核物质的性质,使得对两体相移的描述,特别是在P波及混合角严重偏离了实验值。考虑Δ(1232)同样会使得核力的计算更加复杂,目前尚未有完整的N3LO的考虑Δ(1232)的手征核力。
手征有效场论的计阶规则可以自洽地包含三体乃至四体相互作用。值得一提的是,这些所谓“多体核力”,其本质实际体现了核子并非是点状的基本粒子,而是具有内部结构的复合粒子[84]。此外,有效场论中被积分掉的高能自由度也会显示为多体力[85]。按照温伯格计阶规则,NLO的三体相互作用被严格抵消[26],因此非零的最低阶三体核力出现在NNLO[40, 86]。在NNLO,三体相互作用包含短程的接触项、中程的单π交换项以及长程的两π交换项。在2007年,对于三体核力的计算推进到了N3LO[87−89],并在2011年前后完成了N4LO长程、中程以及部分短程贡献的计算[90−92],但目前尚不完整。另一方面,考虑了Δ(1232)的三体核力已被完整地计算至NNLO[40, 42]。其与无Δ(1232)三体核力最大的不同在于,最低阶贡献出现在NLO。这表明,无Δ(1232)核力可能低估了三体核力的大小,因而产生收敛速度慢等一系列问题。目前,N3LO阶包含Δ(1232)的三体核力的长程部分已构建完成[44],但中程、短程部分仍尚未得到充分研究。
最低阶的四体相互作用出现在N3LO[93−94],文献[95]进一步讨论了四体相互作用在4He中的作用。目前尚未有关于N4LO四体相互作用的研究。
1.2 非相对论手征核力遇到的问题
非相对论手征核力发展至今已非常成熟,然而在其发展以及其应用于第一性原理计算过程中,也遇到了一系列的问题。首要问题在于计阶规则或收敛速度。非相对论手征核力基于重重子手征有效场论,这种对重子传播子进行非相对论展开的处理,使得其按照温伯格朴素维度分析(naive dimensional analysis)的计阶规则收敛速度过慢。Epelbaum[96]教授指出,中子-氘核(n−d)散射过程的准确描述至少需要用到N4LO的手征核力。Machleidt[97]教授在最近关于手征核力与核物理第一性原理计算的评论中指出,手征核力在N3LO的精度不足以满足第一性原理计算的要求,理想的精度有望在N4LO实现。然而,手征有效场论在高阶的复杂程度随手征阶数的增长急速膨胀。到N4LO,除了数量庞大的两体、三体贡献外,还将包含第二阶的四体相互作用。这将使得手征核力的计算及其在第一性原理中的应用变得十分困难。针对温伯格计阶规则,物理学家们陆续提出了不同的改进方案[46, 98−101],但有研究[102]指出,这样的改进并没有显著的必要性。
事实上,对于计阶规则的讨论通常与 LS 方程的重整化问题以及重整化群不变性(Renormalization group invariance)联系在一起。前文提到的计阶规则改进方案大都基于重整化群分析。问题的本质是 LS 方程截断到手征展开的某一阶时是不可重整的。散射振幅中圈图的紫外发散无法被截断到某一阶的低能常数完全吸收[103],部分物理学家由此认为温伯格计阶规则并不完备,即其对可观测量的描述不满足重整化群不变性。相关讨论可以参考Kolck教授的综述文章[66]。Kaplan[104]教授提出,可以通过微扰地考虑π交换贡献实现重整化,但该方案的收敛性存在问题。Epelbaum与Gegelia则指出,在协变框架下,非微扰的OPE是可重整的,但是高阶贡献仍需微扰处理[105]。目前这一问题尚未有妥善的解决方案。
温伯格计阶规则定性地解释了三体核力的贡献要比两体核力小很多,其原因在于最低阶三体核力出现在N2LO[27−28]。尽管很多核物理可观测量的描述不需要引入三体核力,仅用两体核力就可以进行很好的描述[106],但是作为自洽计算,计阶规则要求引入对应阶的三体相互作用。而且,实际计算也表明,三体核力的确在有限核以及核物质性质的描述中发挥着关键作用[84, 107],因此,目前的第一性原理计算通常包含三体核力。然而,目前三体核力的引入存在自洽性问题,即基于维数正规化得到的三体核力(N3LO的圈图贡献)在应用于基于动量截断的散射方程(Faddeev equation)时,破坏了手征对称性(一次迭代过程中产生的发散无法被手征对称性约束的中程相互作用吸收)。这一问题在Epelbaum以及Machleidt教授的很多文章中被反复强调[96−97, 102, 108]。实际上,由于存在无法被重整化的发散项,目前所有引入N3LO三体核力的第一性原理计算均存在不可控的误差,因而是不可靠的。因此,在自洽地解决三体核力的正规化问题之前,可靠的预言只能依据LO,NLO以及N2LO手征核力(首个非零的三体核力出现在N2LO,在此阶不存在上文提及的自洽性问题)。
除此之外,引入三体核力的自洽性问题也体现在其与对应阶两体核力的结合方面。前文提到,在N3LO的两体核力中,短程的相互作用存在冗余的低能常数[79],这些冗余的低能常数可以通过特定的幺正变换消除。然而,当这些幺正变换作用于完整的相互作用哈密顿量时,除了产生吸收冗余的两体算符外,还同时产生了同一阶(N3LO)的三体算符[109]。这些三体算符都是短程贡献,实际上对应于接触项。这与按照温伯格计阶规则,N3LO三体核力不存在短程相互作用的认识相悖。这些“等效”的三体短程相互作用提供了新的低能常数,有助于解决n−d散射过程中著名的“$ A_y $疑难”(低能区n−d可观测量$ A_y $的描述与实验不符)[110]。然而,目前的计算仍不是自洽的(唯象两体核力+有效三体手征核力),这一问题有待进一步研究。
目前,非相对论手征核力已成为核物理第一性原理计算的标准微观输入,广泛应用于核结构、核物质、核反应以及核天体物理的研究中,并取得了巨大的成功。相关研究可以参考综述文献[84]。然而,以目前的手征核力作为输入的第一性原理计算结果对于所描述的可观测量、核素以及核力的细节十分敏感。目前还没有一种核力,在具备系统的手征展开收敛性的同时,还能够在误差范围内准确预言整个核素图上所有核素的少体与多体可观测量。核物理学家迫切需要进一步发展手征核力,能够正确地再现已知原子核和核物质的性质,并能以可靠和受控的方式预言核素图中尚未观测到的核素的性质。目前,两体核力及其在第一性原理中的应用已清晰明确,但三体核力本身以及其应用均面临很大的挑战。
值得一提的是,为了适应不同的多体方法,人们基于手征核力,进一步发展了各种优化或软化的核力,包括NNLOsat[111],NNLOopt[106],NNLOsim[112]等等,其不同之处在于确定NN,3N以及πN低能常数的方法以及是否引入多体可观测量进行约束。软化核力的技术则基于相似重整化群方法[113−115],其大致思想在于通过对哈密顿量进行一系列的幺正变换,将哈密顿量中的高能部分与低能部分退耦,以此来软化核力。应该注意,这样会引入等效的三体核力。
2. 相对论手征核力
考虑到非相对论手征核力遇到的问题,特别是收敛性慢、不满足重整化群不变性等问题,我们提出依据协变重子手征有效场论的协变计阶规则[49],发展相对论手征核力。这种方法借鉴了单重子系统中用于恢复计阶规则的EOMS方案。不同于重重子手征有效场论,其保留了协变手征有效拉氏量中完整的狄拉克旋量以及克利福德代数,并且通过求解相对论的散射方程处理非微扰效应。这种相对论框架下的手征有效场论已被广泛应用于单重子系统(重子质量[116−120]、sigma项[121−122]、磁矩[123−126]、πN散射[127]、超子弱辐射衰变[128]等等),并表现出了比非相对论框架更快的收敛速度。而且,目前基于Dirac-Brueckner-Hartree-Fock(DBHF)框架的研究表明,相对论框架下的核多体计算对可观测量的描述显著优于非相对论框架Brueckner-Hartree-Fock (BHF)[129],有望实现核物质以及有限核性质的同时描述。然而相对论核多体方法无法采用温伯格手征核力作为输入,我们发展的相对论手征核力填补了这一空白。
2.1 协变计阶规则及手征有效拉氏量
为了构建相对论框架下的手征核力,我们需要NN接触项拉氏量,其对应核力的短程部分。描述核子-核子短程相互作用的接触项拉氏量已被构建至$ {\cal{O}}(p^4) $阶(N3LO)[50]。相对论框架下,手征有效拉氏量的构建应遵循以下几个原则:手征有效拉氏量应为洛伦兹标量,应满足手征对称性、宇称变换、电荷共轭变换、厄米共轭变换以及时间反演不变性。其构建应该满足一定的计阶规则,从而可以预先估计每一项的相对大小并保证到手征展开的某一阶手征有效拉氏量的项数是有限的。
满足上面几点要求的协变拉氏量的一般形式为
$$ \frac{1}{\left(2m\right)^{N_d}} \left(\bar{\psi} i \overleftrightarrow {\partial}{}^{\alpha} i\overleftrightarrow {\partial}{}^{\beta} \cdots \varGamma_A \psi\right) \partial^{\lambda} \partial^{\mu} \cdots \left(\bar{\psi} i \overleftrightarrow {\partial}{}^{\sigma} i\overleftrightarrow {\partial}{}^{\tau} \cdots \varGamma_B \psi\right), $$ (1) 上式中,微分$ \overleftrightarrow {\partial}{}^{\alpha} = \overrightarrow{\partial}^{\alpha} - \overleftarrow{\partial}^{\alpha} $,$ \varGamma $指代克利福德代数,即$\varGamma \in \{{\bf{1}},\, \gamma_5,\; \gamma^{\mu},\; \gamma_5 \gamma^{\mu},\; \sigma^{\mu\nu},\; g^{\mu\nu},\; \epsilon^{\mu\nu\rho\sigma}\}$。在上面的表达式中,$ N_d $表示拉氏量中微分的个数(包括$ \overleftrightarrow {\partial}{} $以及$ \partial $),m指代核子手征极限质量。因子$ 1/(2m)^{N_d} $的引入保证了拉氏量中每一项的低能常数都有统一的量纲。洛伦兹指标$\alpha,\; \beta,\; \sigma,\; \tau,\; \cdots$必须缩并以保证拉氏量的每一项是洛伦兹标量。
下一步,我们应明确规定手征有效拉氏量各个构成单元的手征阶数,以构建自洽的计阶规则。相对论框架下,核子双线性结构、微分算符、狄拉克矩阵、以及 Levi-Civita 张量的手征阶数,及它们在宇称($ {\cal{P}} $)、电荷共轭($ {\cal{C}} $)、以及厄米共轭(h.c.)变换下的性质如表1所列。
表 1 核子双线性结构、微分算符、狄拉克矩阵Levi-Civita张量的手征阶数以及它们在宇称($ {\cal{P}} $)、电荷共轭($ {\cal{C}} $)、以及厄米共轭(h.c.)变换下的性质组成单元 1 $ \gamma_5 $ $ \gamma_\mu $ $ \gamma_5\gamma_\mu $ $ \sigma_{\mu\nu} $ $ \epsilon_{\mu\nu\rho\sigma} $ $ \overleftrightarrow \partial_{\mu} $ $ \partial_{\mu} $ $ {\cal{P}} $ + − + − + − + + $ {\cal{C}} $ + + − + − + − + h.c. + − + + + + − + 手征阶数$ {\cal{O}} $ 0 1 0 0 0 − 0 1 微分算符$ \partial $作用于整个核子双线性结构时手征阶数为$ {\cal{O}}(p^1) $,而作用于其內部时,由于出现核子质量,记为$ {\cal{O}}(p^0) $。狄拉克矩阵γ5被记为$ {\cal{O}}(p^1) $,因为它将核子旋量的大小分量混合在一起。与 n 个微分算符缩并的Levi-Civita张量$ \epsilon_{\mu \nu \rho \sigma} $作用于双线性结构内部时将提升$ n-1 $阶。此外,如果双线性结构内部的微分算符$ \overleftrightarrow \partial $与不属于同一双线性结构的狄拉克矩阵γ5γμ或者是$ \sigma^{\mu\nu} $缩并时, 手征阶数为$ {\cal{O}}(q^1) $。这个结果可以由运动方程(EOM)得到。因此,在计阶规则的每一阶,拉氏量中只包含有限个微分算符$ \partial $或Levi-Civita张量$ \epsilon_{\mu\nu\rho\sigma} $。然而,原则上,缩并的微分算符允许以下面的形式在给定阶数的拉氏量中存在任意数量:
$$ \begin{split} {\widetilde{{\cal{O}}}_{{\varGamma}_A {\varGamma}_B}^{(n)}}= & \frac{1}{(2m)^{2n}} {\left(\bar{\psi} {\mathrm{i}} \overleftrightarrow{\partial}^{{\mu}_1} {\mathrm{i}} \overleftrightarrow{\partial}^{{\mu}_2} \cdots {\mathrm{i}} \overleftrightarrow{\partial}^{{\mu}_n} {\varGamma}_{A}^{\alpha} {\psi} \right)} \times \\ &{\left(\bar{\psi} {\mathrm{i}} \overleftrightarrow{\partial}_{{\mu}_1} {\mathrm{i}} \overleftrightarrow{\partial}_{\mu_2} \cdots {\mathrm{i}} \overleftrightarrow{\partial}_{{\mu}_n} {\varGamma}_{B {\alpha}} {\psi} \right)。} \end{split} $$ (2) 因为此结构的手征阶数为$ {\cal{O}}(p^0) $。但是,考虑到
$$ \frac{\left[\left(p_1+p_3\right) \cdot \left(p_2+p_4\right)\right]^{n}}{\left(2m\right)^{2n}}, $$ (3) 可以被重新表示为
$$ \left[1+\frac{\left(s-4m^2\right)-u}{4m^2}\right]^{n}, $$ (4) 式中$ s-4m^2=-(p_1-p_2)^2=-(p_3-p_4)^2 \sim {\cal{O}}(p^2) $,$ u=(p_1- p_4)^2\sim {\cal{O}}(p^2) $,可以看出,因为$ n>2 $的项并不提供新的结构,在$ {\cal{O}}(p^0) $,只有$n=0,\; 1,\; 2$的项是必需的。类似的,在$ {\cal{O}}(p^2) $,只有$n=0,\; 1$是必需的,在$ {\cal{O}}(p^4) $中,则只有$ n=0 $的项是必需的。
基于以上规则,我们可以写出相对论框架下的$ {\cal{O}}(p^0) $、$ {\cal{O}}(p^2) $以及$ {\cal{O}}(p^4) $的有效拉氏量。然而,这样构建的拉氏量并不都是彼此独立的。运动方程可以消除冗余的项。在领头阶,核子的运动方程即狄拉克方程:
$$ \cancel{\partial}\psi = \gamma^\mu \partial_\mu \psi = - {\mathrm{i}} m \psi + {\cal{O}}(p) \,, $$ (5) 及其厄米共轭。由此可见,在忽略高阶贡献的情况下,我们可以将$ \cancel{\partial}\psi $替换为$ - {\mathrm{i}} m \psi $,以及将$ \bar \psi \overleftarrow{\cancel{\partial}} $替换为$ {\mathrm{i}} m \bar \psi $。基于狄拉克矩阵的分解关系[50],我们可以推导一系列的运动方程,并将$ {\cal{O}}(p^4) $的拉氏量简化为表2所列的40项,包括领头阶的4项,次领头阶的13项以及次次次领头阶的23项。核力的短程接触相互作用可以由此拉氏量自然得到。
表 2 至$ {\cal{O}}(p^4) $阶核子-核子接触项协变手征有效拉氏量低能常数 手征有效拉氏量 低能常数 手征有效拉氏量 $ \widetilde{{O}}_{1} $ $ \left(\bar{\psi} \psi\right)\left(\bar{\psi} \psi\right) $ $ \widetilde{{O}}_{21} $ $ \frac{1}{16m^4}\left(\bar{\psi} {\rm{i}}\overleftrightarrow{\partial}^{ \mu} \psi\right) \partial^{2} \partial^{\nu}\left(\bar{\psi} \sigma_{\mu\nu} \psi\right) $ $ \widetilde{{O}}_{2} $ $ \left(\bar{\psi} \gamma^{\mu} \psi\right)\left(\bar{\psi} \gamma_{\mu} \psi\right) $ $ \widetilde{{O}}_{22} $ $ \frac{1}{16m^4}\left(\bar{\psi} \sigma^{\mu \alpha} \psi\right) \partial^{2} \partial_{\alpha}\partial^{\nu}\left(\bar{\psi} \sigma_{\mu\nu} \psi\right) $ $ \widetilde{{O}}_{3} $ $ \left(\bar{\psi} \gamma_5 \gamma^{\mu} \psi\right)\left(\bar{\psi} \gamma_5 \gamma_{\mu} \psi\right) $ $ \widetilde{{O}}_{23} $ $ \frac{1}{16m^4}\left(\bar{\psi} \sigma^{\mu\nu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right) \partial^{\beta} \partial_{\nu}\left(\bar{\psi} \sigma_{\alpha \beta} {\rm{i}}\overleftrightarrow{\partial}_{ \mu} \psi\right) $ $ \widetilde{{O}}_{4} $ $ \left(\bar{\psi} \sigma^{\mu\nu} \psi\right)\left(\bar{\psi} \sigma_{\mu\nu} \psi\right) $ $ \widetilde{{O}}_{24} $ $ \frac{1}{16m^4}\left(\bar{\psi} \psi\right) \partial^{4}\left(\bar{\psi} \psi\right) $ $ \widetilde{{O}}_{5} $ $ \left(\bar{\psi} \gamma_5 \psi\right)\left(\bar{\psi} \gamma_5 \psi\right) $ $ \widetilde{{O}}_{25} $ $ \frac{1}{16m^4}\left(\bar{\psi} \gamma^{\mu} \psi\right) \partial^{4} \left(\bar{\psi} \gamma_{\mu} \psi\right) $ $ \widetilde{{O}}_{6} $ $ \frac{1}{4m^2}\left(\bar{\psi} \gamma_5 \gamma^{\mu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right)\left(\bar{\psi} \gamma_5 \gamma_{\alpha} {\rm{i}}\overleftrightarrow{\partial}_{ \mu} \psi\right) $ $ \widetilde{{O}}_{26} $ $ \frac{1}{16m^4}\left(\bar{\psi} \gamma_5 \gamma^{\mu} \psi\right) \partial^{4} \left(\bar{\psi} \gamma_5 \gamma_{\mu} \psi\right) $ $ \widetilde{{O}}_{7} $ $ \frac{1}{4m^2}\left(\bar{\psi} \sigma^{\mu\nu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right)\left(\bar{\psi} \sigma_{\mu\alpha} {\rm{i}}\overleftrightarrow{\partial}_{ \nu} \psi\right) $ $ \widetilde{{O}}_{27} $ $ \frac{1}{16m^4}\left(\bar{\psi} \sigma^{\mu\nu} \psi\right) \partial^{4} \left(\bar{\psi} \sigma_{\mu\nu} \psi\right) $ $ \widetilde{{O}}_{8} $ $ \frac{1}{4m^2}\left(\bar{\psi} {\rm{i}}\overleftrightarrow{\partial}^{ \mu} \psi\right)\partial^{\nu}\left(\bar{\psi} \sigma_{\mu\nu} \psi\right) $ $ \widetilde{{O}}_{28} $ $ \frac{1}{4m^2}\left(\bar{\psi} \gamma_5 {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right)\left(\bar{\psi} \gamma_5 {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} \psi\right)-\widetilde{O}_{5} $ $ \widetilde{{O}}_{9} $ $ \frac{1}{4m^2}\left(\bar{\psi} \sigma^{\mu \alpha} \psi\right)\partial_{\alpha}\partial^{\nu}\left(\bar{\psi} \sigma_{\mu\nu} \psi\right) $ $ \widetilde{{O}}_{29} $ $ \frac{1}{16m^4}\left(\bar{\psi} \gamma_5\gamma^{\mu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} {\rm{i}}\overleftrightarrow{\partial}^{ \beta} \psi\right)\left(\bar{\psi} \gamma_5\gamma_{\alpha} {\rm{i}}\overleftrightarrow{\partial}_{ \mu} {\rm{i}}\overleftrightarrow{\partial}_{ \beta} \psi\right)-\widetilde{O}_{6} $ $ \widetilde{{O}}_{10} $ $ \frac{1}{4m^2}\left(\bar{\psi} \psi\right) \partial^{2}\left(\bar{\psi} \psi\right) $ $ \widetilde{{O}}_{30} $ $ \frac{1}{16m^4}\left(\bar{\psi} \sigma^{\mu\nu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} {\rm{i}}\overleftrightarrow{\partial}^{ \beta} \psi\right)\left(\bar{\psi} \sigma_{\mu\alpha} {\rm{i}}\overleftrightarrow{\partial}_{ \nu} {\rm{i}}\overleftrightarrow{\partial}_{ \beta} \psi\right)-\widetilde{O}_{7} $ $ \widetilde{{O}}_{11} $ $ \frac{1}{4m^2}\left(\bar{\psi} \gamma^{\mu} \psi\right) \partial^{2} \left(\bar{\psi} \gamma_{\mu} \psi\right) $ $ \widetilde{{O}}_{31} $ $ \frac{1}{16m^4}\left(\bar{\psi} {\rm{i}}\overleftrightarrow{\partial}^{ \mu} {\rm{i}}\overleftrightarrow{\partial}^{ \beta} \psi\right) \partial^{\alpha}\left(\bar{\psi} \sigma_{\mu\alpha} {\rm{i}}\overleftrightarrow{\partial}_{ \beta} \psi\right)-\widetilde{O}_{8} $ $ \widetilde{{O}}_{12} $ $ \frac{1}{4m^2}\left(\bar{\psi} \gamma_5 \gamma^{\mu} \psi\right) \partial^{2} \left(\bar{\psi} \gamma_5 \gamma_{\mu} \psi\right) $ $ \widetilde{{O}}_{32} $ $ \frac{1}{16m^4}\left(\bar{\psi} \sigma^{\mu \alpha} {\rm{i}}\overleftrightarrow{\partial}^{ \beta} \psi\right)\partial_{\alpha} \partial^{\nu}\left(\bar{\psi} \sigma_{\mu\nu} {\rm{i}}\overleftrightarrow{\partial}_{ \beta} \psi\right)-\widetilde{O}_{9} $ $ \widetilde{{O}}_{13} $ $ \frac{1}{4m^2}\left(\bar{\psi} \sigma^{\mu\nu} \psi\right) \partial^{2} \left(\bar{\psi} \sigma_{\mu\nu} \psi\right) $ $ \widetilde{{O}}_{33} $ $ \frac{1}{16m^4}\left(\bar{\psi} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right)\partial^{2}\left(\bar{\psi} {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} \psi\right)-\widetilde{O}_{10} $ $ \widetilde{{O}}_{14} $ $ \frac{1}{4m^2}\left(\bar{\psi} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right)\left(\bar{\psi} {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} \psi\right)-\widetilde{O}_{1} $ $ \widetilde{{O}}_{34} $ $ \frac{1}{16m^4}\left(\bar{\psi} \gamma^{\mu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right)\partial^{2}\left(\bar{\psi} \gamma_{\mu} {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} \psi\right)-\widetilde{O}_{11} $ $ \widetilde{{O}}_{15} $ $ \frac{1}{4m^2}\left(\bar{\psi} \gamma^{\mu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right)\left(\bar{\psi} \gamma_{\mu} {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} \psi\right)-\widetilde{O}_{2} $ $ \widetilde{{O}}_{35} $ $ \frac{1}{16m^4}\left(\bar{\psi} \gamma_5\gamma^{\mu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right)\partial^{2}\left(\bar{\psi} \gamma_5\gamma_{\mu} {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} \psi\right)-\widetilde{O}_{12} $ $ \widetilde{{O}}_{16} $ $ \frac{1}{4m^2}\left(\bar{\psi} \gamma_5\gamma^{\mu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right)\left(\bar{\psi} \gamma_5 \gamma_{\mu} {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} \psi\right)-\widetilde{O}_{3} $ $ \widetilde{{O}}_{36} $ $ \frac{1}{16m^4}\left(\bar{\psi} \sigma^{\mu\nu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right)\partial^{2}\left(\bar{\psi} \sigma_{\mu\nu} {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} \psi\right)-\widetilde{O}_{13} $ $ \widetilde{{O}}_{17} $ $ \frac{1}{4m^2}\left(\bar{\psi} \sigma^{\mu\nu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right)\left(\bar{\psi} \sigma_{\mu\nu} {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} \psi\right)-\widetilde{O}_{4} $ $ \widetilde{{O}}_{37} $ $ \frac{1}{16m^4}\left(\bar{\psi} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} {\rm{i}}\overleftrightarrow{\partial}^{ \beta} \psi\right)\left(\bar{\psi} {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} {\rm{i}}\overleftrightarrow{\partial}_{ \beta} \psi\right)-2\widetilde{O}_{14}-\widetilde{O}_{1} $ $ \widetilde{{O}}_{18} $ $ \frac{1}{4m^2}\left(\bar{\psi} \gamma_5 \psi\right) \partial^{2}\left(\bar{\psi} \gamma_5 \psi\right) $ $ \widetilde{{O}}_{38} $ $ \frac{1}{16m^4}\left(\bar{\psi} \gamma^{\mu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} {\rm{i}}\overleftrightarrow{\partial}^{ \beta} \psi\right)\left(\bar{\psi} \gamma_{\mu} {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} {\rm{i}}\overleftrightarrow{\partial}_{ \beta} \psi\right)-2\widetilde{O}_{15}-\widetilde{O}_{2} $ $ \widetilde{{O}}_{19} $ $ \frac{1}{16m^4}\left(\bar{\psi} \gamma_5 \gamma^{\mu} {\rm{i}}\overleftrightarrow{\partial}^{\nu} \psi\right) \partial^{2} \left(\bar{\psi} \gamma_5 \gamma_{\nu} {\rm{i}}\overleftrightarrow{\partial}_{ \mu} \psi\right) $ $ \widetilde{{O}}_{39} $ $ \frac{1}{16m^4}\left(\bar{\psi} \gamma_5 \gamma^{\mu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} {\rm{i}}\overleftrightarrow{\partial}^{ \beta} \psi\right)\left(\bar{\psi} \gamma_5 \gamma_{\mu} {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} {\rm{i}}\overleftrightarrow{\partial}_{ \beta} \psi\right)-2\widetilde{O}_{16}-\widetilde{O}_{3} $ $ \widetilde{{O}}_{20} $ $ \frac{1}{16m^4}\left(\bar{\psi} \sigma^{\mu\nu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} \psi\right) \partial^{2} \left(\bar{\psi} \sigma_{\mu\alpha} {\rm{i}}\overleftrightarrow{\partial}_{ \nu} \psi\right) $ $ \widetilde{{O}}_{40} $ $ \frac{1}{16m^4}\left(\bar{\psi} \sigma^{\mu\nu} {\rm{i}}\overleftrightarrow{\partial}^{ \alpha} {\rm{i}}\overleftrightarrow{\partial}^{ \beta} \psi\right)\left(\bar{\psi} \sigma_{\mu\nu} {\rm{i}}\overleftrightarrow{\partial}_{ \alpha} {\rm{i}}\overleftrightarrow{\partial}_{ \beta} \psi\right)-2\widetilde{O}_{17}-\widetilde{O}_{4} $ 2.2 π介子交换贡献
为了描述核力中长程的单π介子交换以及中程的两π介子交换,我们需要πN相互作用的拉氏量,其形式为[130]
$$ {\cal{L}}^{(1)}_{\pi N} = \bar{\psi}({\mathrm{i}} \cancel{D}-m+\frac{g_A}{2}\cancel{u}\gamma_5)\psi , $$ (6) $$ \begin{split} {{\cal{L}}^{(2)}_{\pi N} = }&{c_1^{}\langle\chi_+\rangle\bar{\psi}\psi-\frac{c_2^{}}{4m^2}\langle\ u^\mu u^\nu \rangle(\bar{\psi}D_\mu D_\nu \psi+h.c.) +} \\ & {\frac{c_3^{}}{2}\langle\ u^2 \rangle \bar{\psi}\psi - \frac{c_4^{}}{4} \bar{\psi} \gamma^\mu\gamma^\nu[u_\mu,u_\nu] \psi 。} \end{split} $$ (7) 上式中,$ \bar{\psi} $以及$ \psi $为核子场,$ D_\mu $为协变微商,定义为$ D_\mu=\partial_\mu+\varGamma_\mu $,$ \varGamma_\mu=\frac{1}{2}(u^\dagger\partial_\mu u+u \partial_\mu u^\dagger) $,$u=\exp(\frac{{\rm i} \varPhi}{2f})$。$ \varPhi $指代2×2的矩阵:
$$ \varPhi=\left( \begin{array}{*{20}{cc}} {\pi^0} & {\sqrt{2}\pi^+} \\ {\sqrt{2}\pi^-} & {-\pi^0} \end{array} \right) 。 $$ (8) 轴矢流$ u_\mu $定义为$ u_\mu={\mathrm{i}}(u^\dagger\partial_\mu u-u \partial_\mu u^\dagger) $。手征对称性破缺项$ \chi_+=u^\dagger \chi u+u \chi u^\dagger $,$\chi={\rm{diag}}(m^2_\pi,\;m^2_\pi)$。$ g_A $为轴矢耦合常数,在实际计算中取为$ g_A=1.29 $,$c_{1,\,2,\,3,\,4}$为次领头阶πN相互作用的低能常数,通过拟合πN散射数据确定。我们采用同样在协变手征有效场论框架下拟合得到的值,c1 = −1.39,c2 = 4.01,c3 = −6.61 ,c4 = 3.92,单位均为GeV−1。计算中采用核子及π介子的物理质量,即mN = 0.939 GeV,mπ = 0.138 GeV。
按照计阶规则,各阶的π交换贡献如图1所示。在领头阶,π交换贡献仅包含单π交换贡献。在次领头阶,中程的两π介子交换开始贡献,此外,还包含OPE的单圈阶修正,不过此部分贡献可以被领头阶OPE的重整化吸收掉。在次次领头阶,第二阶的TPE开始贡献,其包含了NLO的πN散射低能常数。相关细节可参考文献[51−52]。
2.3 相对论框架下核子-核子散射
氘核的存在说明核子-核子相互作用包含显著的非微扰效应。为考虑此非微扰效应,我们求解了下面的相对论Blankenbecler-Sugar (BbS) 方程[131],
$$ \begin{split} T({\boldsymbol{p}}',\, {\boldsymbol{p}},\, s)= & V({\boldsymbol{p}}',\, {\boldsymbol{p}},\, s)+ \\ & \int\frac{{\rm{d}}^3{\boldsymbol{k}}}{(2\pi)^3}V({\boldsymbol{p}}',\, {\boldsymbol{k}},\, s)\frac{m^2}{E_k}\frac{1}{{\boldsymbol{q}}_{{\mathrm{cm}}}^2-{\boldsymbol{k}}^2-{\rm i}\epsilon}T({\boldsymbol{k}},\, {\boldsymbol{p}},\, s), \end{split}$$ (9) 上式中$ |{\boldsymbol{q}}_{{\mathrm{cm}}}|=\sqrt{s/4-m^2} $是质心系下的核子动量,V即为构建的手征核力。出射、入射以及中间过程的核子动量标记如图2所示。
为了避免紫外发散,在BbS方程重求和过程中,要对V进行动量截断。通常采用下面的正规化方法:
$$ V_{l'l}^{sj}({p}',\, {p}|\sqrt{s})=f_{R}({p})V({p}',\, {p}|\sqrt{s})f_{R}({p'}), $$ (10) 正规化因子取为
$$ f_{R}({p})=f_{R}^{ \rm{sharp}}({p})=\theta(\varLambda^2-p^2)。 $$ (11) 每个分波的S矩阵可以表示为散射振幅T的函数:
$$ S_{l'l}^{sj}({p}_{\rm{cm}}) = \delta_{l'l}^{sj} + 2\pi {\mathrm{i}} \rho T_{l'l}^{sj}({p}_{\rm{cm}}),\quad \rho=-\frac{|{p}_{\rm{cm}}|M^2}{16\pi^2E_{\rm{cm}}} $$ (12) 上式中,$ {p}_{\rm{cm}}=\sqrt{T_{\rm{lab}}M/2} $。
由分波散射过程的S矩阵,我们可以得到单道的分波相移:
$$ S_{jj}^{0j}= {\rm{exp}}{\left(2{\mathrm{i}}\delta_{j}^{0j}\right)},\quad S_{jj}^{1j}= {\rm{exp}}{\left(2{\mathrm{i}}\delta_{j}^{1j}\right)}, $$ (13) 上式中的$ \delta^{0j}_j $及$ \delta^{1j}_j $为相应分波的散射相移。类似地,对于耦合道,我们采用Stapp因子化[132]的S矩阵:
$$ \begin{split} {S=}&\left(\begin{array}{*{20}{cc}} S_{--}^{1j} & S_{-+}^{1j} \\ S_{+-}^{1j} & S_{++}^{1j} \end{array}\right)\\ =&\left(\begin{array}{*{20}{cc}} {\rm{exp}}{\left({\mathrm{i}}\delta_-^{1j}\right)} & 0 \\ 0 & {\rm{exp}}{\left({\mathrm{i}}\delta_+^{1j}\right)} \end{array}\right)\left(\begin{array}{*{20}{cc}} \cos(2\varepsilon) & {\mathrm{i}} \sin(2\varepsilon) \\ {\mathrm{i}} \sin(2\varepsilon) & \cos(2\varepsilon) \end{array}\right)\boldsymbol\cdot \\ & \left(\begin{array}{*{20}{cc}} {\rm{exp}}{\left({\mathrm i}\delta_-^{1j}\right)} & 0 \\ 0 & {\rm{exp}}{\left({\mathrm{i}}\delta_+^{1j}\right)} \end{array}\right)\\ =&\left(\begin{array}{*{20}{cc}} \cos(2\varepsilon) {\rm{exp}}{\left(2{\mathrm{i}}\delta_-^{1j}\right)} & {\mathrm{i}} \sin(2\varepsilon) {\rm{exp}}{\left({\mathrm{i}}\delta_-^{1j}+{\mathrm{i}}\delta_+^{1j}\right)} \\ {\mathrm{i}} \sin(2\varepsilon) {\rm{exp}}{\left({\mathrm{i}}\delta_-^{1j}+{\mathrm{i}}\delta_+^{1j}\right)} & \cos(2\varepsilon) {\rm{exp}}{\left(2{\mathrm{i}}\delta_+^{1j}\right)} \end{array} \right) \end{split} $$ (14) 上式中的下标"+"代表总自旋为j+1,“−”代表总自旋为j−1。
3. 结果与讨论
理论中待定的低能常数通过拟合分波散射相移确定。我们采用了跟非相对论手征核力研究中[31, 78]相同的拟合方法。具体来讲,我们拟合了取自Nijmegen合作组的所有角动量$ J\leqslant 2 $的质子-中子散射相移[133]。注意,在领头阶,因为接触项不对$ J=2 $的分波贡献,所以拟合中仅考虑$J=0,\;1$分波相移。对于每个分波,我们选取8个实验点,分别对应实验室系动能$T_{\rm{lab}}=1,\; 5,\; 10,\; 25,\; 50,\; 100,\; 150,\, 200 \;{\mathrm{MeV}}$。理论计算与实验数据的偏差函数$ \tilde{\chi}^2 $定义为
$$ \tilde{\chi}^2=\sum\limits_i(\delta^i-\delta^i_{\rm{PWA93}})^2, $$ (15) 上式中$ \delta^i $为理论计算得到的分波相移或混合角,$ \delta^i_{\rm{PWA93}} $是来自Nijmengen合作组分波分析的结果[133]。
3.1 领头阶相对论手征核力
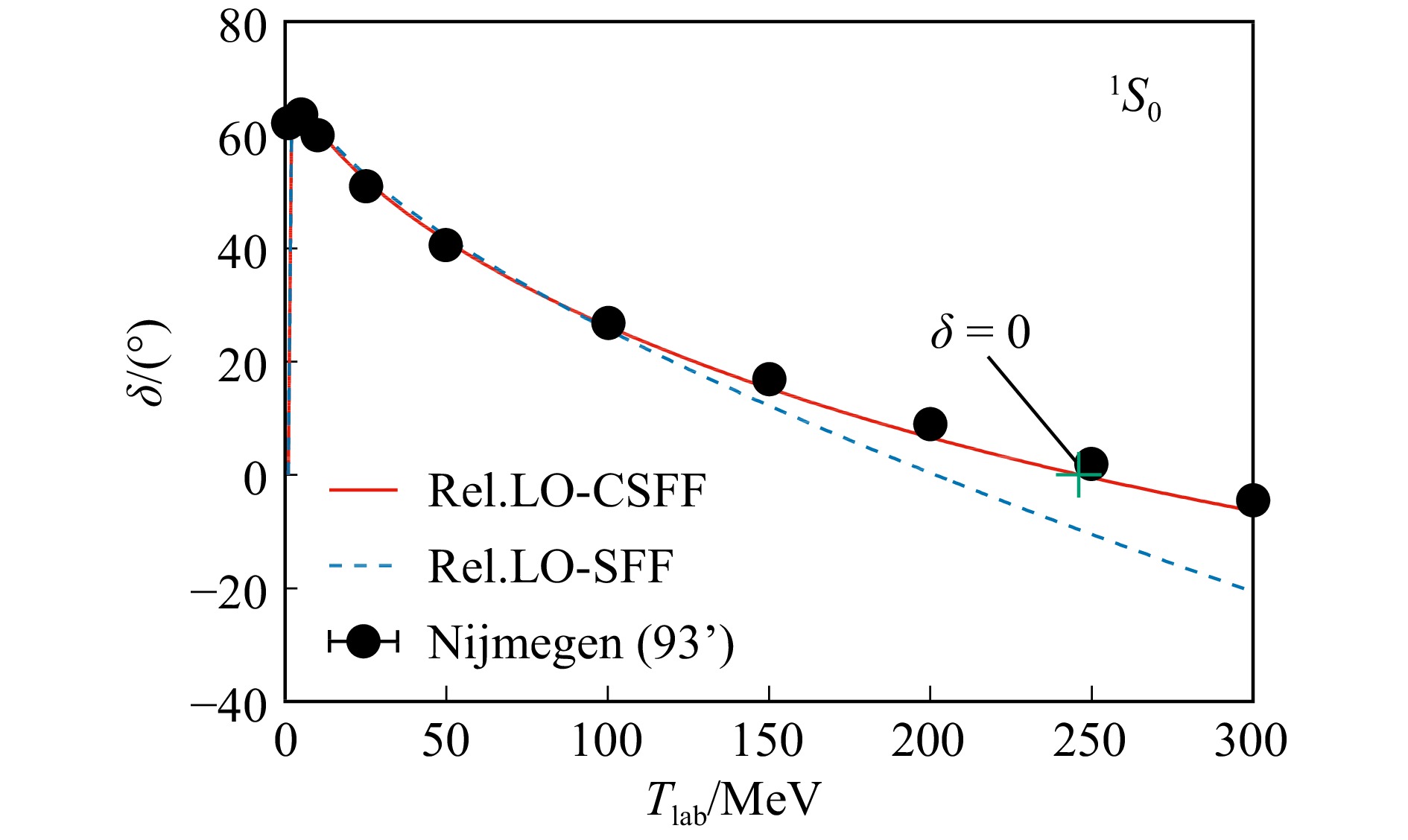
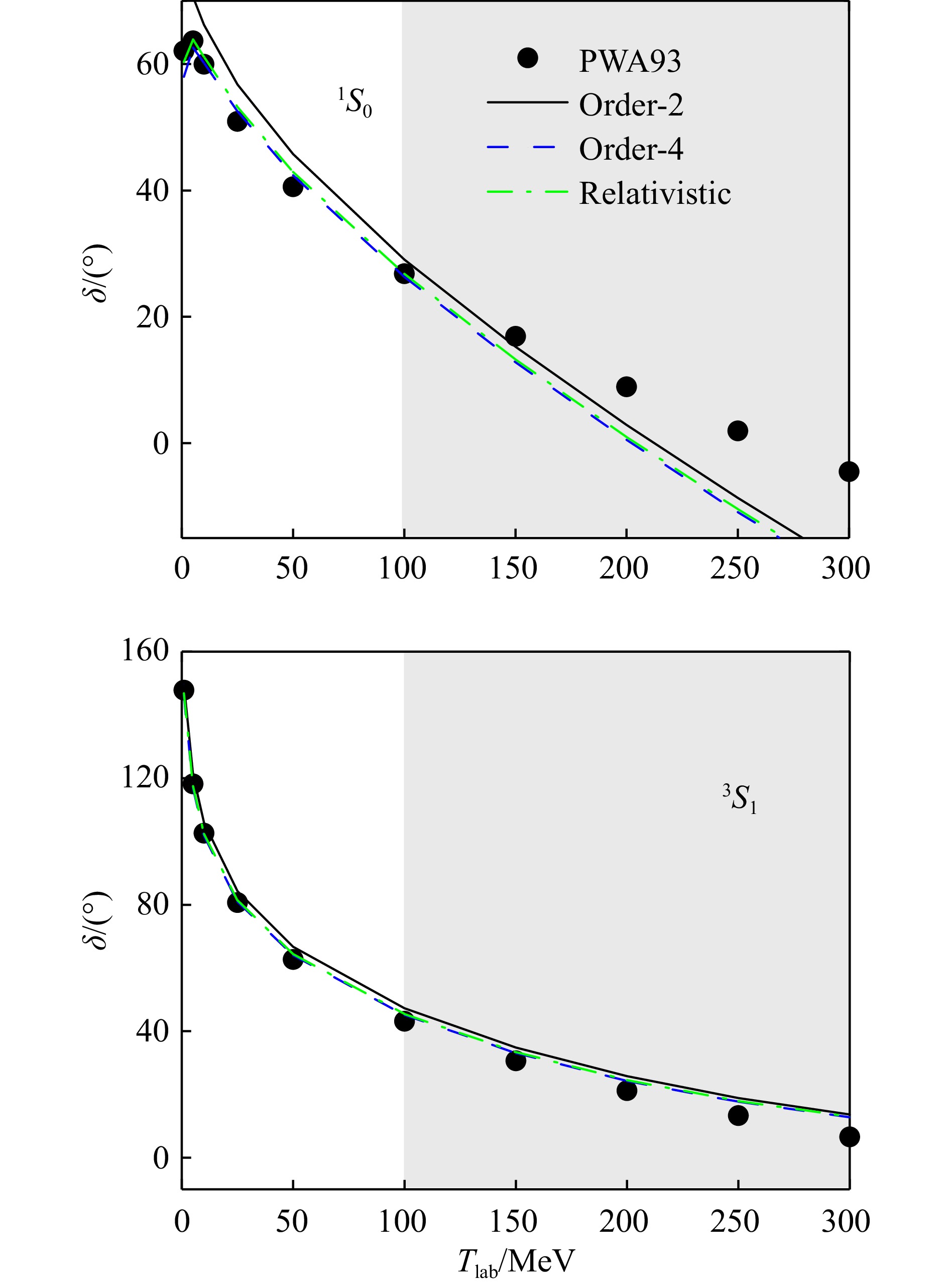
与非相对论手征核力相同,相对论手征核力在LO包含短程的接触相互作用与长程的OPE贡献。但是协变计阶规则使得相对论手征核力在LO就包含了非相对论手征核力NLO的算符结构,因而显著加快了手征展开的收敛速度。在领头阶,相对论手征核力对与总角动量$ J\leqslant 1 $的分波散射相移的描述效果已经与非相对论NLO的结果相当[49]。进一步地,我们基于领头阶相对论手征核力,详细研究了1S0分波的质子-中子散射数据[134],包括1S0分波的散射相移、散射过程中产生的虚态位置、散射长度、有效力程等,并讨论了不同正规化因子的影响。领头阶相对论手征核力对与1S0分波散射相移的描述见图3。与需要计算至NLO的非相对论手征核力相比,在领头阶就可以很好描述散射过程的大部分细节的相对论手征核力及其协变计阶规则,显然更符合我们对具有完备计阶规则的有效场论的期望。
![]() 图 3 1S0分波相移随实验室系能量Tlab的变化(在线彩图)红色实线以及蓝色虚线分别代表采用可分离的协变形状因子与非协变形状因子的领头阶相对论手征核力的结果,图中的十字标出了相移为0的位置。黑色实心圆点代表Nijmegen合作组的分波分析结果[133]。
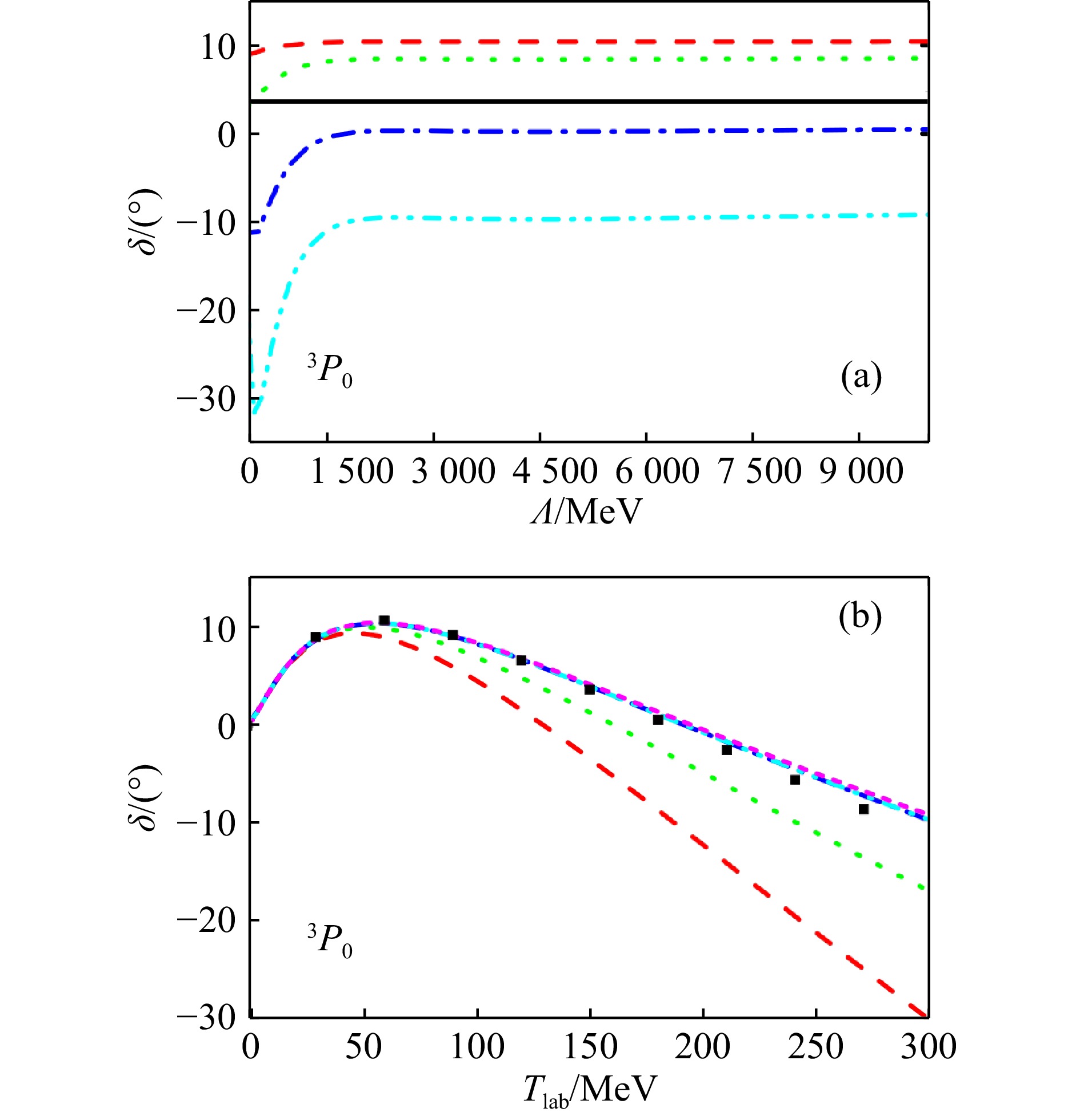
图 3 1S0分波相移随实验室系能量Tlab的变化(在线彩图)红色实线以及蓝色虚线分别代表采用可分离的协变形状因子与非协变形状因子的领头阶相对论手征核力的结果,图中的十字标出了相移为0的位置。黑色实心圆点代表Nijmegen合作组的分波分析结果[133]。一个具备完备计阶规则的有效场论应是满足重整化群不变性的,或者换句话说,其对可观测量的描述应不(显著)依赖于求解散射方程时引入的动量截断。然而,前文提到,非相对论手征核力对相移的描述并不满足重整化群不变性。但在相对论框架下,可观测量的重整化群演化行为获得了很大的改善[135]。我们发现,在协变计阶规则下,3S1、3D1、$ \epsilon_1 $、3P0、1P1分波相移自然地满足重整化群不变性。我们注意到,在3P0分波,基于温伯格计阶规则的非相对论手征核力不满足重整化群不变性,如图4。此外,我们进一步研究了相对论手征核力随π介子质量的演化[136−137],与格点合作组HALQCD[138]的结果符合得很好。
基于u、d、s三味空间的SU(3)对称性,我们的协变理论框架可以很自然地拓展到SU(3)味空间,构建完成了领头阶的超子-核子以及超子-超子相互作用,包括奇异数$ S=-1 $[139−141],$ S=-2 $[142],$ S=-3,\, -4 $[143],以及含粲重子的$ \varLambda_c N $相互作用[144−145]。最近,我们在相对论框架下,计算了超子-核子散射过程的动量关联函数[146],与ALICE合作组的结果[147−149]符合得很好。
3.2 次次领头阶相对论手征核力
虽然领头阶的相对论手征核力在对总角动量$ J\leqslant 1 $分波散射数据的描述效果几乎可以与非相对论次领头阶的结果相媲美,但其对更高角动量$ J >1 $的分波的描述精度尚嫌不足[49]。为了实现对核子-核子散射数据的高精度描述,我们在相对论框架下,将手征核力计算至了次次领头阶[53]。到次次领头阶,完整的相对论手征核力包含以下几部分贡献:
$$ V=V_{\rm{CT}}^{\rm{LO}}+V_{\rm{CT}}^{\rm{NLO}}+V_{\rm{OPE}}+V_{\rm{TPE}}^{\rm{NLO}}+V_{\rm{TPE}}^{\rm{NNLO}}-V_{\rm{IOPE}}, $$ (16) 依次为LO[$ {\cal{O}}(p^0) $]以及NLO[$ {\cal{O}}(p^2) $]的接触项相互作用,OPE项,第一阶及第二阶的TPE贡献。最后一项则减除了考虑非微扰效应时对OPE贡献的重复计算。
我们首先微扰地研究了TPE交换的贡献[51]及其对高分波散射相移(无低能常数)的描述,与非相对论手征核力的结果相比,考虑相对论效应使得对散射相移的描述有明显的改善。进一步地考虑非微扰效应,得到了相同的结论[52]。
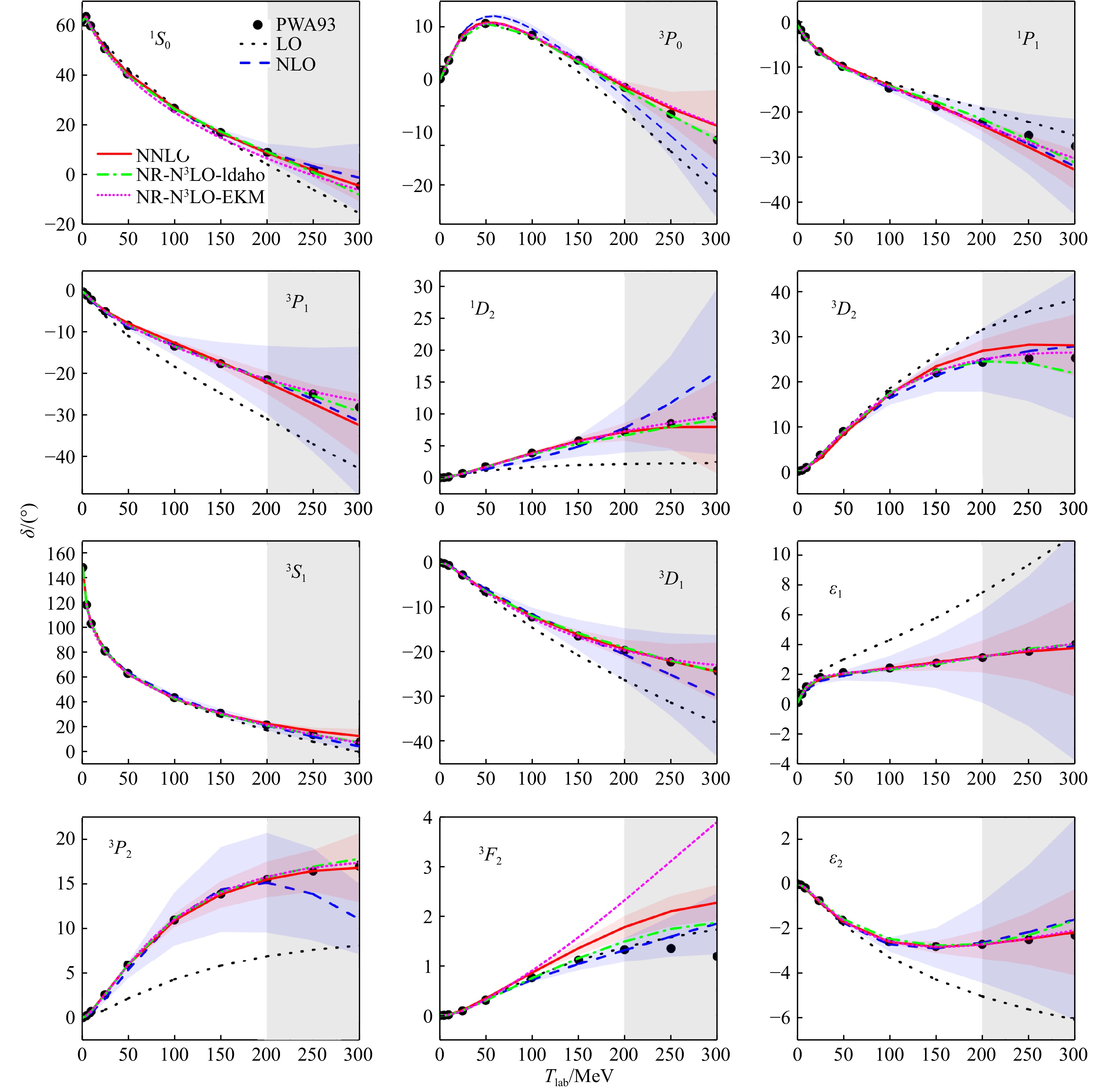
在通过拟合未知确定低能常数之后,次次领头阶相对论手征核力对散射相移的描述如图5所示。置信度68%的理论不确定度通过贝叶斯模型估计得到[150−152]。作为比较,我们同时给出了非相对论N3LO 采取不同正规化方案得到的结果,分别用“Idaho”[28, 72]以及“EKM”[74, 78]表示。
![]() 图 5 不同核力给出的$ J\leqslant 2 $分波散射相移(在线彩图)图中红色的实线为我们构建的相对论手征核力NNLO的结果,动量截断选为$ \varLambda=0.9 \;{\mathrm{GeV}} $。蓝色的虚线为相对论手征核力NLO的结果,动量截断选为$ \varLambda=0.6 \;{\mathrm{GeV}} $。相应的阴影区间为68%置信度的理论不确定度。作为比较,我们同时给出了相对论领头阶(黑色点线,动量截断$ \varLambda=0.6 \;{\mathrm{GeV}}$)以及两种非相对论N3LO手征核力的结果,分别是NR-N3LO-Idaho ($ \varLambda=0.5 \;{\mathrm{GeV}}$,绿色点虚线)[28, 72]以及 NR-N3LO-EKM ($ \varLambda=0.9 \;{\mathrm{fm}}$,紫色短点线)[74, 78]。黑色的实心点为Nijmegen合作组的分波分析结果[133]。
图 5 不同核力给出的$ J\leqslant 2 $分波散射相移(在线彩图)图中红色的实线为我们构建的相对论手征核力NNLO的结果,动量截断选为$ \varLambda=0.9 \;{\mathrm{GeV}} $。蓝色的虚线为相对论手征核力NLO的结果,动量截断选为$ \varLambda=0.6 \;{\mathrm{GeV}} $。相应的阴影区间为68%置信度的理论不确定度。作为比较,我们同时给出了相对论领头阶(黑色点线,动量截断$ \varLambda=0.6 \;{\mathrm{GeV}}$)以及两种非相对论N3LO手征核力的结果,分别是NR-N3LO-Idaho ($ \varLambda=0.5 \;{\mathrm{GeV}}$,绿色点虚线)[28, 72]以及 NR-N3LO-EKM ($ \varLambda=0.9 \;{\mathrm{fm}}$,紫色短点线)[74, 78]。黑色的实心点为Nijmegen合作组的分波分析结果[133]。首先我们注意到,在相对论框架下,NLO以及NNLO核力对散射相移的预言直到$ T_{\rm{lab}}=200 \;{\mathrm{MeV}} $都与实验数据非常接近,而且与非相对论N3LO的结果相差无几。特别是,相对论NLO对相移的描述效果与NNLO非常接近,而NNLO的结果与实验数据符合得更好。这一点证明了在相对论框架下手征展开的较快收敛速度。另一方面,在3F2分波,NLO的表现更好,这可能是因为NNLO的次领头阶TPE贡献较大,在对$ J=2 $所有分波的拟合中不得不牺牲3F2分波。当我们把D波与3P2-3F2分波参数之间的关联移除,即分别独立拟合D波与3P2-3F2分波,或略微调整动量截断的大小,描述效果都将获得显著改善。针对这一问题,我们注意到,在NR-N3LO-Idaho的工作中,为了更好地描述3F2分波相移,他们将πN散射低能常数作为半自由的参数进行了调整[72]。
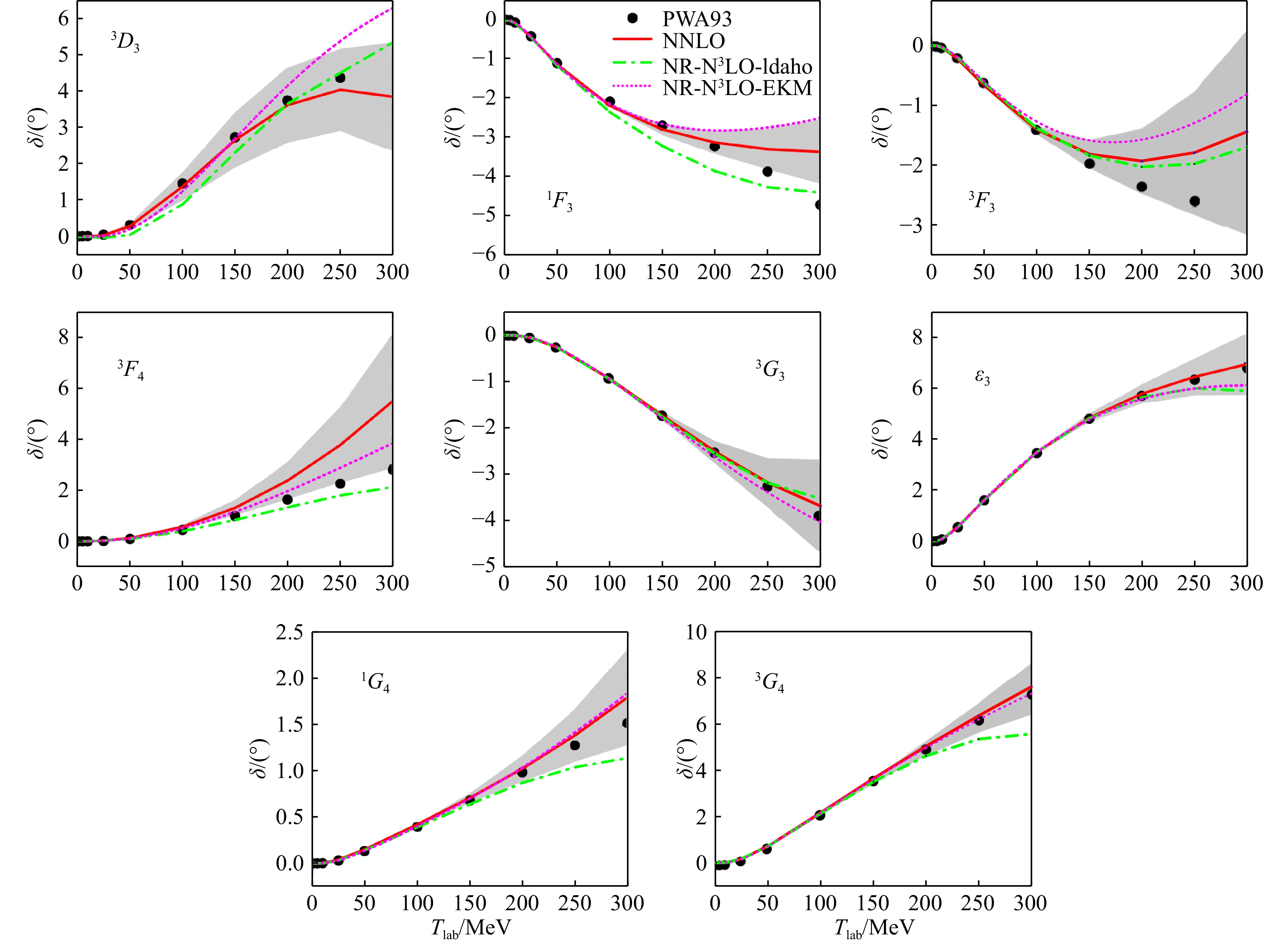
在图6中,我们进一步比较了非相对论NR-N3LO-Idaho[28, 72]、NR-N3LO-EKM[74, 78]手征核力与相对论NNLO手征核力得到的$ J\leqslant 4 $、$ L\leqslant4 $分波相移。更高角动量分波相移不再展示,因为在这些分波中,长程的OPE起主导作用。显然,在图6所示的分波中,相对论NNLO的结果在$ T_{\rm{lab}}\leqslant200 \; {\mathrm{MeV}}$范围内,与非相对论N3LO的结果差不多,对于部分分波,相对论的结果与实验数据符合得更好。相对论的结果仅在3F4分波略逊色。对于3D3与1F3分波,相对论NNLO结果与非相对论NR-N3LO-EKM都无法描述高动量区间的实验数据,而NR-N3LO-Idaho 的结果对于$ T_{\rm{lab}}\in $[100, 200] MeV的数据描述效果略差。对于3F3分波,三种核力都不能描述$ T_{\rm{lab}}=200 \; {\mathrm{MeV}} $以上的实验数据。其中,NR-N3LO-Idaho相对更好。对于3F4分波,过大的第二阶TPE贡献使得相对论结果明显高于Nijmegen的实验数据,NR-N3LO-Idaho 结果表现最好。对于G波以及混合角$ \epsilon_3 $,三种核力都能够很好地描述$ T_{\rm{lab}}\leqslant200 \; {\mathrm{MeV}} $范围的散射相移,但是NR-N3LO-Idaho的结果在高能区偏小。
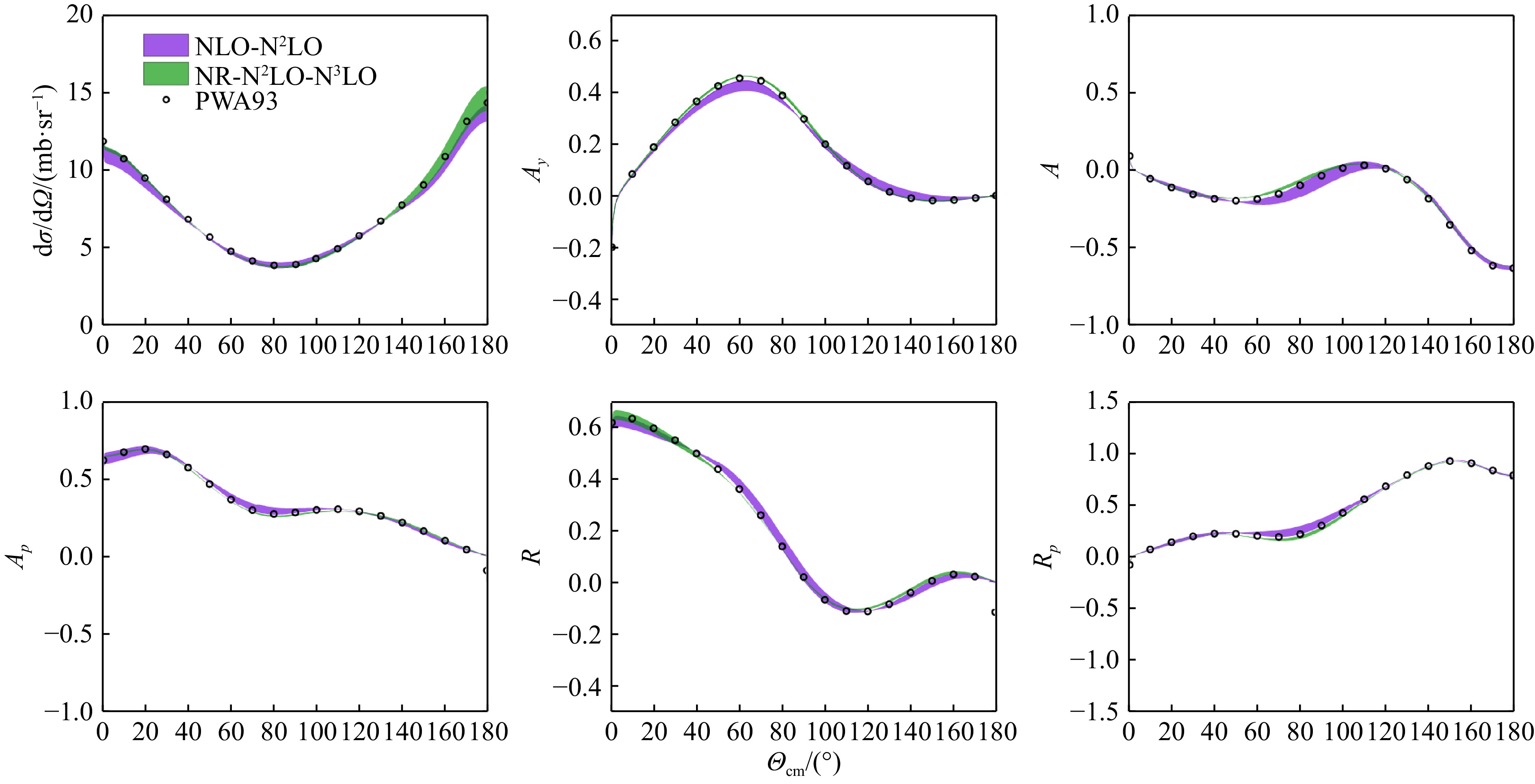
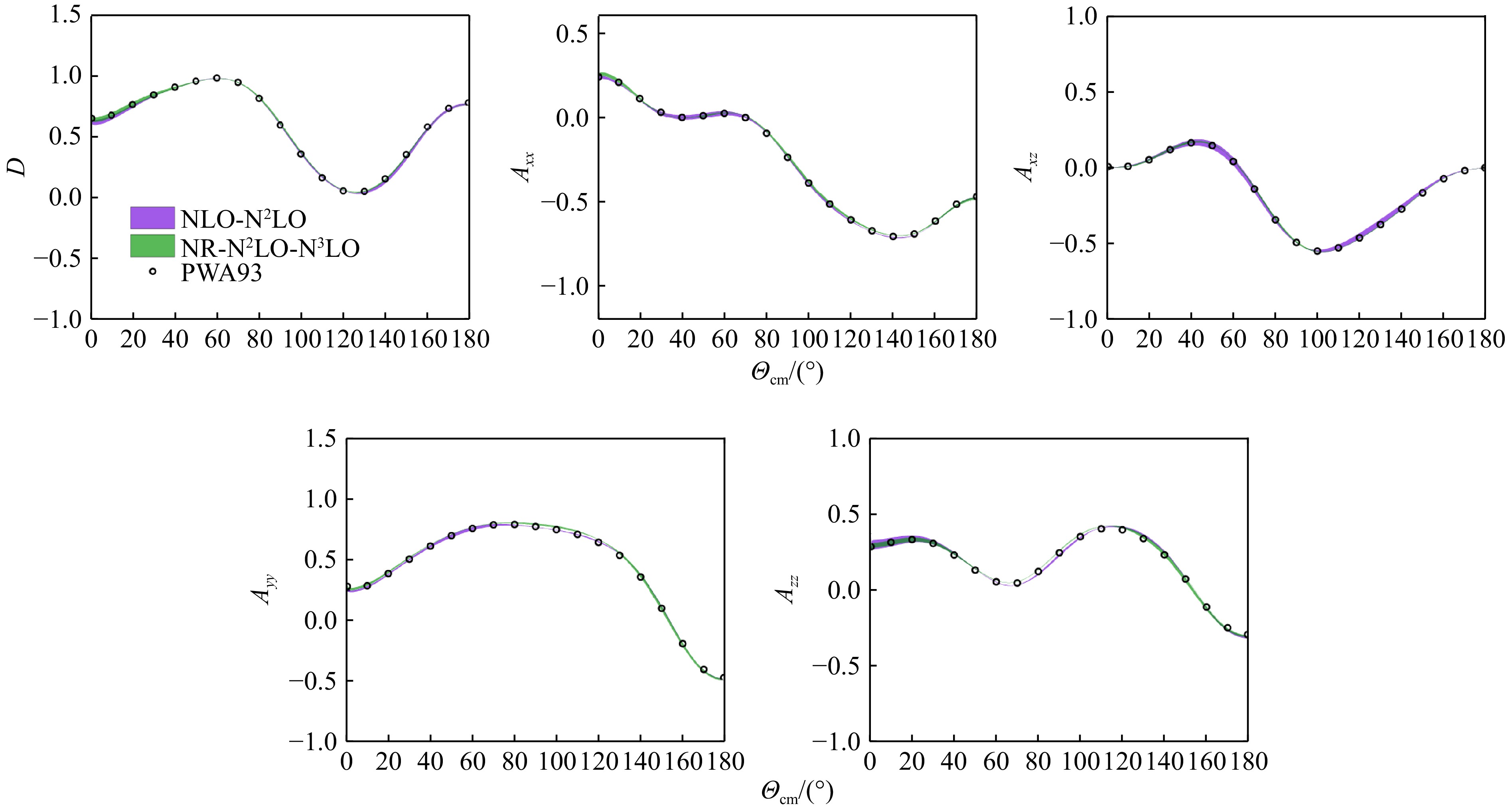
在图7、图8中我们给出了高精度的NNLO阶相对论手征核力与$ {\rm N}^{3} $LO阶非相对论手征核力对$ T_{\rm{lab}}= 100 \;{\mathrm{MeV}} $时微分散射截面(DSG)、极化($ A_y $)、退极化(D)、横向转动参数(A, $ A^{\prime} $)、纵向转动参数(R, $ R^{\prime} $)、自旋关联参数($ A_{xx} $, $ A_{yy} $, $ A_{zz} $, $ A_{zx} $)随质心系散射角演化的预言。作为对比,我们同时给出了Nijmegen的结果,其中紫色带状区表示NLO阶与NNLO阶相对论手征核力给出的结果,绿色带状区表示NNLO阶与N3LO阶非相对论手征核力给出的结果,黑色圆点表示Nijmegen的结果。如图所述,对于不同的实验室系能量,高精度的NNLO阶协变手征核力皆可以很好地描述这些可观测量。
3.3 非相对论约化
在次次领头阶,相对论手征核力已经能够很好地描述核子-核子散射相移,但是其复杂的形式及对能量的依赖很大程度上限制了其应用于传统的量子多体方法处理核多体问题。针对这一问题,我们期望对相对论手征核力进行一定程度的约化,在保证精度的前提下,将其约化为非相对论手征核力的形式,甚至是局域核力,方便其应用于目前大多基于非相对论框架或求解薛定谔方程的多体方法。
在初步的探索性研究中,我们首先针对领头阶相对论手征核力进行约化。考虑到在领头阶,长程的单π交换贡献形式,除核子旋量外与非相对论手征核力的OPE完全一致,我们暂时保留了相对论OPE的完整形式。但对于短程的接触项,我们进行了非相对论展开。非相对论手征核力的短程部分在领头阶只有常数项,而相对论手征核力的接触项由于包含来自旋量的能量、动量,不仅包含了非相对论次领头阶的贡献,也因为相对论的色散关系,包含了更高阶的相对论效应。
我们基于Thompson方程,采用指数形式的形状因子,在动量截断$ \varLambda=600 \; {\mathrm{MeV}} $时重新拟合了核子-核子散射相移。相应的低能常数如表3所列。在相同低能常数下,分别将1S0、3S1分波的短程接触项展开至$ {\cal{O}}(p^2) $以及$ {\cal{O}}(p^4) $,其对散射相移的描述如图9所示。在采用相同低能常数的情况下,我们发现,展开之后的$ {\cal{O}}(p^2) $阶的修正非常显著,到$ {\cal{O}}(p^4) $阶就已经与完整的相对论手征核力相差无几。这说明,按照协变计阶规则引入的高阶动量贡献,实际上对于描述相移非常重要。
表 3 基于Thompson方程,采用指数形状因子以及动量截断$ \varLambda=600\; {\mathrm{MeV}} $,拟合散射相移至100 MeV 得到的领头阶低能常数单位:GeV−2 $ C_1 $ $ C_2 $ $ C_3 $ $ C_4 $ −619.04 631.94 −198.56 −79.55 4. 总结与展望
在协变重子手征有效场论的基础上,我们将核子-核子相互作用计算至次次领头阶,构建了一种新的能够精确描述Nijmegen分波相移的相对论手征核力。在相对论框架下,NLO以及NNLO的结果对$ T_{\rm{lab}}\leqslant 200 \; {\mathrm{MeV}}$时散射相移的描述类似,但在高能区,NNLO的结果有明显改善。这证明了协变手征展开良好的收敛性。我们构建的相对论NNLO手征核力,为相对论第一性原理核物质与核结构研究提供了亟需的微观输入。
更快的收敛速度意味着在更低阶就可以实现理想的精度,因此相对论手征核力有望解决第一性原理计算中非相对论手征核力必需计算至N4LO这一问题。但在NNLO,相对论手征核力的精度尚不足以比拟N4LO的非相对论手征核力,因此有必要在相对论框架下将核力构建至N3LO。相对论手征核力更快的收敛速度使我们有理由相信,在N3LO相对论手征核力将与N4LO的非相对论手征核力相当。
然而,目前相对论手征核力的形式并不适用于当前主流的量子多体方法。其主要原因在于相对论手征核力包含对能量的显式依赖。针对这一问题,除开发自洽的相对论多体方法外,可能的解决办法包括在保证精度的前提下,进行非相对论约化,期望消除能量依赖甚至约化为与非相对论手征核力相似的形式(长程部分依赖相对动量,即局域势),以期适用于非相对论量子多体方法。
基于高精度的相对论手征核力,我们期望在以下几个方面,结合相对论多体方法,开展进一步的研究。
近年来,北京大学课题组基于DBHF[129],开展第一性原理研究有限核及核物质取得了重要进展。在有限核方面,他们从相对论的Bonn势出发,利用完全自洽的Dirac Woods-Saxon基求解DBHF方程,在不引入任何自由参数的情况下,实现了4He、16O、40Ca等原子核基态性质的相对论第一性原理计算[129]。此外,针对核物质的DBHF理论也取得了进一步的发展和完善,特别是两核子质心动量的严格处理在一定程度上改善了DBHF理论对核物质饱和性质的描述[153],而狄拉克基空间完备性的恢复解决了提取单粒子势场时遇到的不确定性问题[154]。这些发展意味着在相对论框架有可能实现核反应和核结构的自洽统一计算。然而,目前DBHF的计算采用的还是30年前发展的基于单玻色子交换的唯象Bonn势[155],不仅缺乏重要的理论基础,而且精度也不符合第一性原理计算的要求[97]。
密度泛函理论是目前唯一可行的能够描述整个核素图上中重质量原子核的理论方法[156−157]。与非相对论方法相比,协变密度泛函理论可以自洽包含自旋轨道相互作用;可以提供对赝自旋对称性的微观解释;可以更为自洽地处理奇时间场;可以在不显式考虑三体相互作用的情况下给出核物质的饱和性质;可以通过洛伦兹不变性的约束来减小自由参数的个数;可以提供与QCD更为紧密的联系[156]。总体上,协变密度泛函理论对中重核的描述是成功的,对结合能描述的精度在1~2 MeV,对半径的描述精度在0.01~0.02 fm。然而,如何进一步改进现有的密度泛函理论以及如何控制密度泛函理论外推至滴线区的系统误差是当前密度泛函理论研究必须解决的关键问题[158]。针对这一问题,物理学家正在探索构建基于有效场论思想的密度泛函理论,但是目前,这方面的研究主要集中于非相对论框架[159],相对论框架下的研究还较为有限[160−161]。
此外,中国原子能科学研究院马中玉研究员及其合作者基于DBHF方法构建了相对论核子-原子核光学势[162−164]。这种基于 DBHF 方法构建的同位旋依赖的相对论光学势从现实核力出发,结合先进的多体计算,其微观基础更为可靠,因此具备较强的预言能力,特别是对于缺乏实验数据、远离$ \beta $稳定线的核反应过程。然而,这一系列的工作与上文提及的基于DBHF方法开展的核结构研究存在同样的问题,其仍采用唯象的Bonn势,不符合第一性原理计算的要求。目前的微观光学势大多基于非相对论的手征核力[165−167],无法自洽地兼容相对论效应,因而无法应用于相对论形式的核反应计算。基于高精度相对论手征核力,发展一套微观光学势在兼容相对论效应的同时,又能扩宽其适用范围,使之能更为自洽地应用于相对论形式的核反应研究[168]。
致谢 本工作由国家自然科学基金项目(No.11735003,No.11975041)资助完成。陆俊旭博士感谢国家自然科学基金项目(No.12105006)的资助。肖杨博士感谢国家自然科学基金(No.12347113)的资助。
-
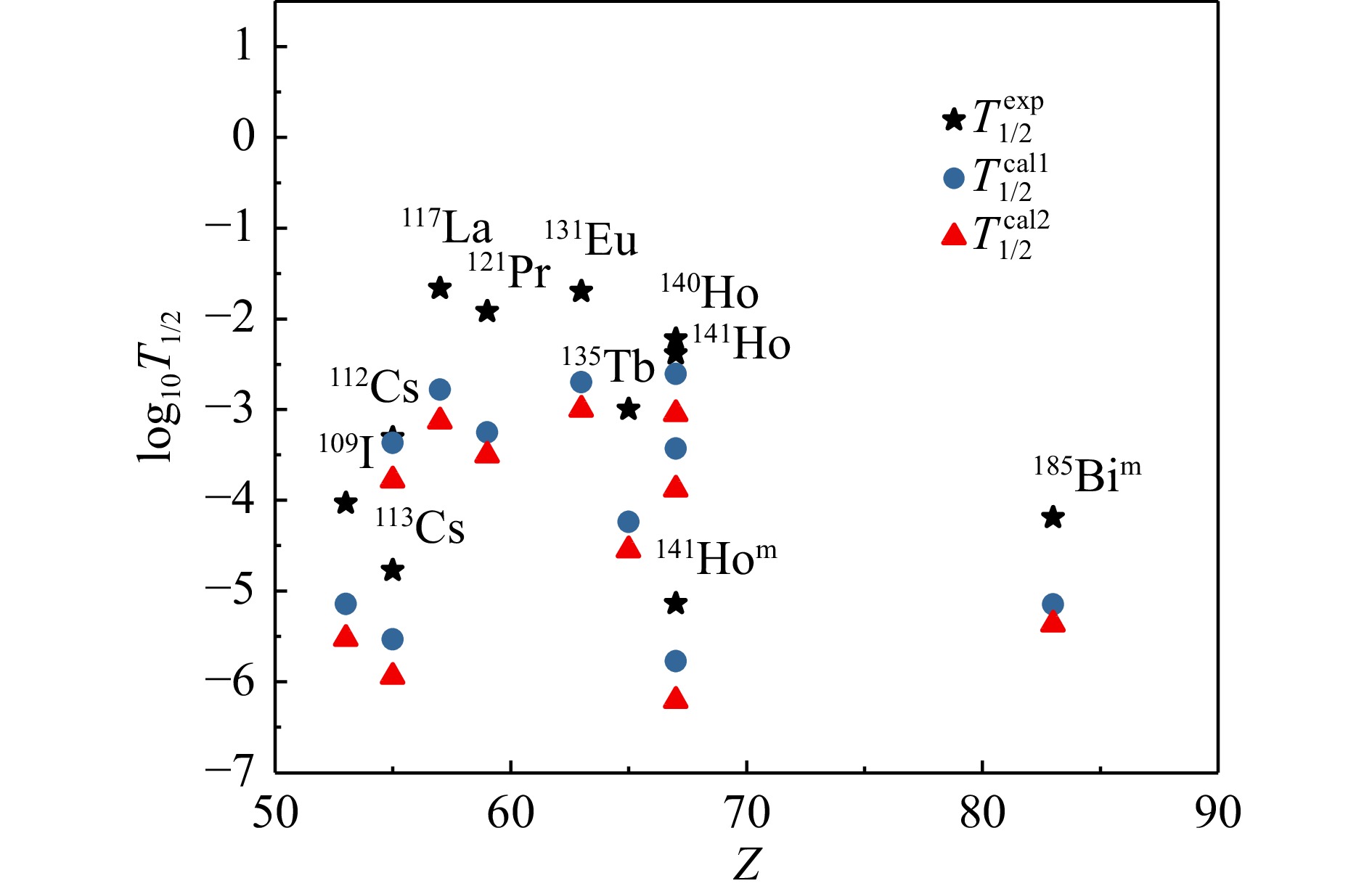
表 1 使用形变Gamow-like模型和Gamow-like模型计算得到的单质子放射性理论半衰期
Nucleus $Q_{\rm p}^{}/\rm{MeV}$ $l$ ${\rm{log}}_{10}^{}T_{1/2}^{\rm{exp}}$/s ${\rm{log}}_{10}^{}T_{1/2}^{\rm{cal1}}$/s ${\rm{log}}_{10}^{}T_{1/2}^{\rm{cal2}}$/s $^{109}{\rm{I}}$ 0.820 0 −4.032 −5.141 −5.522 $^{112}{\rm{Cs}}$ 0.816 2 −3.310 −3.368 −3.778 $^{113}{\rm{Cs}}$ 0.973 2 −4.771 −5.532 −5.943 $^{117}{\rm{La}}$ 0.820 2 −1.664 −2.783 −3.129 $^{121}{\rm{Pr}}$ 0.890 2 −1.921 −3.251 −3.503 $^{131}{\rm{Eu}}$ 0.947 2 −1.699 −2.699 −2.997 $^{135}{\rm{Tb}}$ 1.188 3 −2.996 −4.240 −4.545 $^{140}{\rm{Ho}}$ 1.106 3 −2.222 −2.610 −3.045 $^{141}{\rm{Ho}}$ 1.247 0 −5.137 −5.773 −6.207 $^{141}{\rm{Ho}}$ 1.177 3 −2.387 −3.432 −3.880 $^{144}{\rm{Tm}}$ 1.725 5 −5.569 −5.212 −5.862 $^{145}{\rm{Tm}}^m$ 1.736 5 −5.499 −5.606 −5.946 $^{146}{\rm{Tm}}$ 1.206 5 −1.137 −1.127 −1.474 $^{146}{\rm{Tm}}$ 0.896 0 −0.810 −0.662 −0.975 $^{147}{\rm{Tm}}$ 1.059 5 0.587 0.892 0.318 $^{147}{\rm{Tm}}^m$ 1.120 2 −3.444 −2.829 −3.423 $^{150}{\rm{Lu}}$ 1.290 2 −4.398 −4.340 −4.732 $^{150}{\rm{Lu}}$ 1.270 5 −1.347 −1.114 −1.642 $^{151}{\rm{Lu}}^m$ 1.301 2 −4.796 −4.413 −4.853 $^{151}{\rm{Lu}}^m$ 1.255 5 −0.896 −0.946 −1.494 $^{155}{\rm{Ta}}$ 1.453 5 −2.495 −2.124 −2.937 $^{156}{\rm{Ta}}^m$ 1.020 2 −0.826 −0.298 −0.823 $^{156}{\rm{Ta}}$ 1.110 5 0.933 1.588 0.783 $^{157}{\rm{Ta}}$ 0.935 0 −0.527 0.155 −0.252 $^{159}{\rm{Re}}^m$ 1.801 5 −4.665 −4.248 −5.170 $^{160}{\rm{Re}}$ 1.267 0 −3.163 −3.571 −4.142 $^{161}{\rm{Re}}^m$ 1.317 5 −0.678 −0.197 −1.143 $^{161}{\rm{Re}}$ 1.197 0 −3.306 −2.921 −3.344 $^{164}{\rm{I}}{\rm{r}}$ 1.844 5 −3.959 −4.353 −5.060 $^{165}{\rm{I}}{\rm{r}}^m$ 1.711 5 −3.433 −2.981 −4.146 $^{166}{\rm{I}}{\rm{r}}$ 1.152 2 −0.824 −0.967 −1.437 $^{166}{\rm{I}}{\rm{r}}$ 1.332 5 −0.076 −0.221 −0.801 $^{167}{\rm{I}}{\rm{r}}^m$ 1.070 0 −1.120 −0.677 −1.054 $^{167}{\rm{I}}{\rm{r}}$ 1.245 5 0.842 0.724 0.166 $^{170}{\rm{Au}}^m$ 1.472 2 −3.487 −3.607 −4.408 $^{170}{\rm{Au}}$ 1.752 5 −3.975 −2.578 −4.032 $^{171}{\rm{Au}}^m$ 1.702 5 −2.587 −2.227 −3.672 $^{171}{\rm{Au}}$ 1.448 0 −4.652 −4.423 −4.913 $^{176}{\rm{Tl}}^m$ 1.265 0 −2.208 −1.703 −2.415 $^{177}{\rm{Tl}}^m$ 1.963 5 −3.346 −3.608 −5.087 $^{177}{\rm{Tl}}$ 1.172 0 −1.178 −0.640 −1.347 $^{185}{\rm{Bi}}^m$ 1.607 0 −4.191 −5.148 −5.367 表 2 使用不同模型预测单质子放射性半衰期
Nucleus $Q_{\rm p}^{}/\rm{MeV}$ ${\rm{log}}_{10}^{}T_{1/2}^{\rm{UDLP}}$/s ${\rm{log}}_{10}^{}T_{1/2}^{\rm{CPPM}}$/s ${\rm{log}}_{10}^{}T_{1/2}^{\rm{DDM3Y}}$/s $^{111}{\rm{Cs}}$ 1.731 −9.862 −11.252 −11.431 $^{127}{\rm{Pm}}$ 0.781 −0.099 −0.166 −0.481 $^{137}{\rm{Tb}}$ 0.831 0.337 0.356 −0.031 $^{185}{\rm{Bi}}$ 1.523 −0.670 −0.610 −0.637 $^{185}{\rm{Bi}}^n$ 1.703 −0.859 −0.920 −0.861 Nucleus $Q_{\rm p}^{}/\rm{MeV}$ ${\rm{log}}_{10}^{}T_{1/2}^{\rm{NGNL}}$/s ${\rm{log}}_{10}^{}T_{1/2}^{\rm{TPA-SHF}}$/s ${\rm{log}}_{10}^{}T_{1/2}^{{\rm{This}}\ {\rm{work}}}$/s $^{111}{\rm{Cs}}$ 1.731 −10.101 −11.687 −11.242 $^{127}{\rm{Pm}}$ 0.781 0.286 −0.751 −0.520 $^{137}{\rm{Tb}}$ 0.831 0.739 −0.197 0.057 $^{185}{\rm{Bi}}$ 1.523 −0.350 −0.852 −0.533 $^{185}{\rm{Bi}}^n$ 1.703 −1.163 −1.036 −0.830 -
[1] JACKSON K, CARDINAL C, EVANS H, et al. Phys Lett B, 1970, 33(4): 281. DOI: 10.1016/0370-2693(70)90269-8
[2] XU C, REN Z Z. Nucl Phys Rev, 2006, 23(4): 433. DOI: 10.11804/NuclPhysRev.23.04.433
[3] CHEN J L, CHENG J H, DENG J G, et al. Nucl Phys Rev, 2018, 35(3): 257. DOI: 10.11804/NuclPhysRev.35.03.257
[4] QIAN Y B, REN Z Z. Eur Phys J A, 2016, 52: 1. DOI: 10.1140/epja/i2016-16068-3
[5] THOENNESSEN M. Nucl Phys Rev, 2016, 33(2): 117. DOI: 10.11804/NuclPhysRev.33.02.117
[6] ZHANG D M, QI L J, GUI H F, et al. Phys Rev C, 2023, 108: 024318. DOI: 10.1103/PhysRevC.108.024318
[7] KARNY M, RYKACZEWSKI K, GRZYWACZ R, et al. Phys Lett B, 2008, 664(1): 52. DOI: 10.1016/j.physletb.2008.04.056
[8] SANTHOSH K, SUKUMARAN I. Phys Rev C, 2017, 96: 034619. DOI: 10.1103/PhysRevC.96.034619
[9] DONG J M, ZHANG H F, ROYER G. Phys Rev C, 2009, 79: 054330. DOI: 10.1103/PhysRevC.79.054330
[10] BASU D N, CHOWDHURY P R, SAMANTA C. Phys Rev C, 2005, 72: 051601. DOI: 10.1103/PhysRevC.72.051601
[11] QIAN Y B, REN Z Z, NI D D, et al. Chin Phys Lett, 2010, 27(11): 112301. DOI: 10.1088/0256-307X/27/11/112301
[12] ZDEB A, WARDA M, PETRACHE C M, et al. Eur Phys J A, 2016, 52(10): 323. DOI: 10.1140/epja/i2016-16323-7
[13] XING F, QI H, CUI J, et al. Nucl Phys A, 2022, 1028: 122528. DOI: 10.1016/j.nuclphysa.2022.122528
[14] AZEEZ O K, YAHYA W A, SAEED A A. Phys Scripta, 2022, 97(5): 055302. DOI: 10.1088/1402-4896/ac619d
[15] ZHU D X, XU Y Y, LIU H M, et al. Eur Phys J A, 2022, 33(10): 122. DOI: 10.1007/s41365-022-01116-9
[16] CHEN J L, XU J Y, DENG J G, et al. Eur Phys J A, 2019, 55: 214. DOI: 10.1140/epja/i2019-12927-7
[17] XU C, REN Z Z. Phys Rev C, 2006, 73: 041301. DOI: 10.1103/PhysRevC.73.041301
[18] ISMAIL M, SEIF W, ADEL A, et al. Nucl Phys A, 2017, 958: 202. DOI: 10.1016/j.nuclphysa.2016.11.010
[19] REN Z Z, XU C. Mod Phys Lett A, 2008, 23(27n30): 2597. DOI: 10.1142/S0217732308029885
[20] TAKIGAWA N, RUMIN T, IHARA N. Phys Rev C, 2000, 61: 044607. DOI: 10.1103/PhysRevC.61.044607
[21] ISMAIL M, SEIF W, EL-GEBALY H. Phys Lett B, 2003, 563(1): 53. DOI: 10.1016/S0370-2693(03)00600-2
[22] ZHANG G L, LE X Y, LIU Z H. Chin Phys Lett, 2008, 25(4): 1247. DOI: 10.1088/0256-307x/25/4/023
[23] SOYLU A, KOYUNCU F, GANGOPADHYAY G, et al. Chin Phys C, 2021, 45(4): 044108. DOI: 10.1088/1674-1137/abe03f
[24] HUANG W, WANG M, KONDEV F, et al. Chin Phys C, 2021, 45(3): 030002. DOI: 10.1088/1674-1137/abddb0
[25] WANG M, HUANG W, KONDEV F, et al. Chin Phys C, 2021, 45(3): 030003. DOI: 10.1088/1674-1137/abddaf
[26] KONDEV F, WANG M, HUANG W, et al. Chin Phys C, 2021, 45(3): 030001. DOI: 10.1088/1674-1137/abddae
[27] BLANK B, BORGE M. Prog Part Nucl Phys, 2008, 60(2): 403. DOI: 10.1016/j.ppnp.2007.12.001
[28] MÖLLER P, SIERK A, ICHIKAWA T, et al. Atom Data Nucl Dat, 2016, 109-110: 1. DOI: 10.1016/j.adt.2015.10.002
[29] POENARU D N, PLONSKI I H, GREINER W. Phys Rev C, 2006, 74: 014312. DOI: 10.1103/PhysRevC.74.014312
[30] POENARU D N, GHERGHESCU R A, GREINER W. Phys Rev C, 2011, 83: 014601. DOI: 10.1103/PhysRevC.83.014601
[31] ADEL A, ABDULGHANY A R. Phys Scripta, 2021, 96(12): 125314. DOI: 10.1088/1402-4896/ac33f6
[32] QI C, XU F R, LIOTTA R J, et al. Phys Rev Lett, 2009, 103: 072501. DOI: 10.1103/PhysRevLett.103.072501
[33] QI C, XU F R, LIOTTA R J, et al. Phys Rev C, 2009, 80: 044326. DOI: 10.1103/PhysRevC.80.044326
[34] QI C, DELION D S, LIOTTA R J, et al. Phys Rev C, 2012, 85: 011303. DOI: 10.1103/PhysRevC.85.011303
[35] GHODSI O N, DAEI-ATAOLLAH A. Phys Rev C, 2016, 93: 024612. DOI: 10.1103/PhysRevC.93.024612
[36] GUO C L, ZHANG G L, LE X Y. Nucl Phys A, 2013, 897: 54. DOI: 10.1016/j.nuclphysa.2012.10.003
[37] DENG J G, LI X H, C J L, et al. Eur Phys J A, 2019, 55(4): 58. DOI: 10.1140/epja/i2019-12728-0
[38] CHENG J H, ZHANG Z, WU X J, et al. Chin Phys C, 2022, 46(10): 104104. DOI: 10.1088/1674-1137/ac7a99
[39] GEIGER H P D, NUTTALL J M B S. Philos Mag, 1911, 22(130): 613. DOI: 10.1080/14786441008637156
[40] WANG Y Z, WANG S J, HOU Z Y, et al. Phys Rev C, 2015, 92: 064301. DOI: 10.1103/PhysRevC.92.064301
[41] BROWN B A. Phys Rev C, 1992, 46: 811. DOI: 10.1103/PhysRevC.46.811
[42] REN Y J, REN Z Z. Phys Rev C, 2012, 85: 044608. DOI: 10.1103/PhysRevC.85.044608




 下载:
下载:
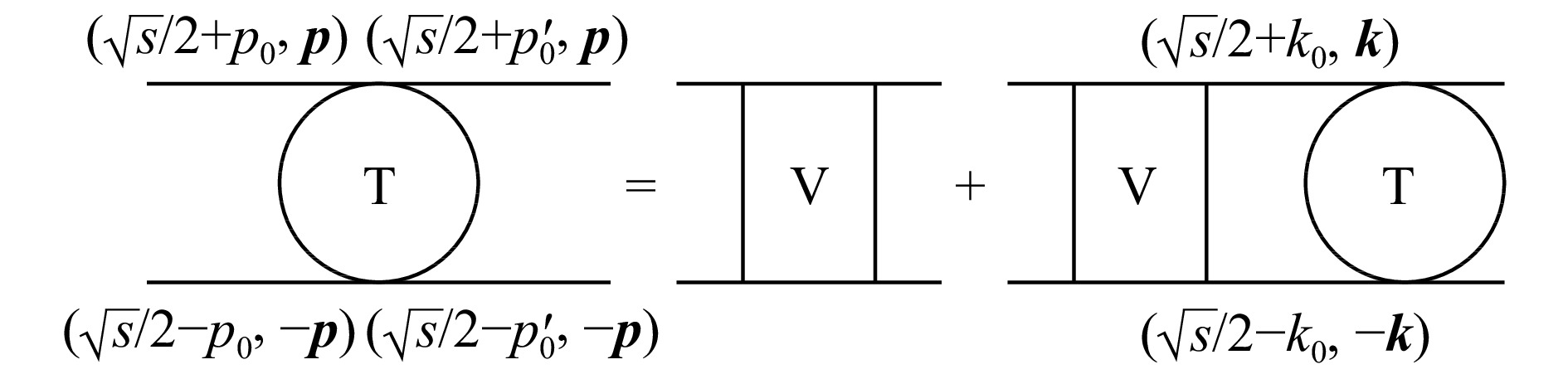
 甘公网安备 62010202000723号
甘公网安备 62010202000723号