The Influence of Gogny Nucleon-nucleon Interaction Potentials of AMD on Ground State Properties of Nuclei
-
摘要: 在反对称化的分子动力学(AMD)模型中，分别采用g0、g0as和g0ass三套Gogny相互作用参数研究了4He、6Li、12C、20Ne、40Ca和60Ni的结合能和均方根半径在自身平均场中随时间的涨落。系统地研究了原子序数从1到18的同位素的结合能，并与现有实验数据进行比较，发现g0的结果更接近实验值。这为利用AMD研究低能区的熔合和中能区的多重碎裂等核反应机制提供了基础。Abstract: In antisymmetrized molecular dynamics(AMD) model, the binding energies and root mean square (RMS) radii of 4He, 6Li, 12C, 20Ne, 40Ca and 60Ni in their own mean field were studied by three sets of Gogny interactions (g0, g0as and g0ass). The binding energies of isotopes with atomic numbers from 1 to 18 were studied systematically. Comparing with the experimental data, it is found that the result of g0 is the best. These investigations would provide clues to the study of the nuclear reaction mechanism such as fusion in low energy region and multi fragmentation in medium energy region by AMD.
-
Keywords:
- AMD /
- binding energy /
- root mean square
-
1. 引言
近几十年来，重离子核反应一直是研究核结构和核反应动力学性质的重要途径，例如奇异核的性质、核状态方程以及超重核特征[1–3]。我们除通过实验之外，理论模型也是非常重要的研究方式。目前应用广泛的输运模型[4-5]如下：分子动力学模型Boltzmann-Uehling-Uhlenbeck(BUU)[6]和Boltzmann-Nordheim-Vlasov (B-NV)[7]、量子分子动力学(QMD)[8-9]模型以及扩展版本的量子分子动力学(EQMD)[10-11]模型、约束分子动力学(CoMD)[12–14]模型、反对称化的分子动力学(AMD)[15]模型及费米子分子 动力学(FMD)[16]模型。每一个模型都有自己的成功之处和适用范围。分子动力学模型BUU和BNV等单体半经典输运模型在处理N体问题上取得了巨大的成就[6-7]。QMD在重离子核反应中从中高能量到高能量取得了成功，然而量子分子动力学模型在低能反应中缺乏核子的费米子特征[8-9]。为了解决这个问题，提出了一些修改的量子分子动力学模型，如EQMD模型和CoMD模型。EQMD模型试图通过引入泡利势来模拟费米子的特征，泡利势禁止具有相同自旋的核子在相空间中相互靠近，该模型具有稳定的基态和核物质饱和性质等优点[10-11]。CoMD模型成功地将费米子性质引入核多体系统，它能够用相同的参数重现稳定核的主要特征，然而在轻核结合能的理论预测与实验结果一致性上存在问题[12]。弹核和靶核的初始化对输运模型模拟的重离子观测结果有着较大影响。例如:初始核的中子皮厚度的不确定性可能影响中子/质子产率[17]、中子-质子微分流[18]、氘核/氚核产率[19]、
$ \pi $ +$ / $ $ \pi $ –比率[20]和其他可观测的[21]重离子碰撞中同位旋相关动力学。AMD模型用与时间相关的波函数描述核系统，在核反应随时间演化过程中严格遵从泡利阻塞。AMD模型广泛地应用于核反应和核结构领域中[22]，但往往忽略了不同Gogny核子-核子相互作用势对初始核的影响。本文利用AMD中不同核子- 核子相互作用势对原子核基态性质进行研究，这能够为使用AMD模型在研究核反应与核结构领域提供基础。2. AMD模型简介
AMD模型是量子分子动力学(QMD)的反对称化版本[23–26]。AMD模型中随时间演化的波函数能够描述核的量子效应，原子核稳定的基态是通过摩擦冷却方法构造的[27]。对于N个核子的反应系统，用斯莱特行列式(Slater determinant)表示N个高斯波包构成的波函数：
$$ \Phi (Z) = \det \left[\exp \left\{ - \nu {{({{r}_{j}}-{}^{{{Z}_{i}}}\!\!\diagup\!\!{}_{\sqrt{\nu }}\;)}^{2}} + \frac{1}{2}Z_i^2\right\} {\chi _{aj}}(j)\right], $$ (1) $ {\chi _{aj}}\left( j \right) $ 为自旋和同位旋波函数，即$ p\uparrow $ 、$ p\downarrow $ 、$ n\uparrow $ 和$ n\downarrow $ 四个状态。复变量$ Z \!=\! \left\{ {{Z_i}} \right.;i \!=\! 1,\cdots N\left. {} \right\}\ $ ，$ {Z_i} $ 表示波包质心,表示为$$ {Z_i} = \sqrt\nu {D_i} + {}^{i}\!\!\diagup\!\!{}_{2\hbar \sqrt{\nu }}\;{K_i}{\text{。}} $$ (2) AMD模型中，波包的宽度参数
$ \nu $ 被看作是恒定的常数，对于所有的波包都相同。通常选取$ \nu $ =0.16 fm–2。方程(1)给出的AMD波函数$ \Phi (Z) $ 是没有考虑多体关联效应，因此需要将有效相互作用与波函数结合起来一起使用。在AMD模型中，系统的有效哈密顿量包括动能和核子-核子相互作用势，表达式为$$ {\cal{H}} = \sum\limits_i {\frac{{p_i^2}}{{2M}}} + \sum\limits_{i < j} {{V_{ij}}}{\text{。}} $$ (3) Gogny核子-核子相互作用势由局域的两体相互作用和零程的密度相关项的和构成，表示为
$$ \begin{split} V_{\rm g0} =& \sum\limits_{i = 1,2}(W_{i}+B_{i}P_{\sigma }-H_{i}P_{\sigma }-M_{i}P_{\sigma}P_{\tau })\times \\&\exp\left[\frac{-(r-{r}')^{2}}{{\eta}_{i}^{2}}\right]+ \frac{t_{0}}{6}(W_{\rho}+B_{\rho}P_{\sigma }+\\&H_{\rho}P_{\tau}-M_{\rho }P_{\sigma }P_{\tau })\rho(r)^{\alpha }\delta (r-{r}'), \end{split} $$ (4) 其中：
$ {P_\tau} $ 为同位旋算符，$ {P_\sigma} $ 为自旋交换算符，$ \rho \left( r \right) $ 为坐标空间r处密度。根据对称能的密度依赖关系，Gogny核子-核子相互作用势有三套参数，即软(g0)[28]、硬的(g0as)、超硬(g0ass)，g0为式(4)所示，g0as和g0ass[29]通过改进g0得到：$$ V_{\rm{g0as(g0ass)}} = V_{\rm{g0}}-(1-x)t_{3}[\rho (r_{1})^{\frac{1}{3}}-\rho _{0}^{\frac{1}{3}}]P_{\sigma }\delta (r_{1}-r_{2}), $$ (5) 公式中
$ t_{3} $ 和$ \rho_{0} $ =0.16 fm–3为系数，$ x $ =$ -\frac{1}{2} $ (g0as)，$ x $ =$ -2 $ (g0ass)，其余参数在表1给出。表 1 Gogny核子-核子相互作用势参数表Interaction i $\eta$ W B H M $\alpha$ $t_0$/(MeV·fm–4) $\chi_0$ $W_\rho$ $B_\rho$ $H_\rho$ $M_\rho$ g0 1 0.7 $-402.4$ $-100.0$ $-496.2$ $-23.56$ 1/3 8 100 1 1 1 0 0 2 1.2 $-21.3$ $-11.77$ 37.27 $-68.81$ g0as 1 0.7 $-402.4$ $-100.0$ $-496.2$ $-23.56$ 1/3 8 100 1 1 $-0.5$ 0 0 2 1.2 $-21.3$ $-11.77$ 37.27 $ -68.81$ g0ass 1 0.7 $-402.4$ $-100.0$ $-496.2$ $-23.56$ 1/3 8 100 1 1 $-2$ 0 0 2 1.2 $-21.3 $ $-11.77$ 37.27 $-68.81$ 3. 结果与讨论
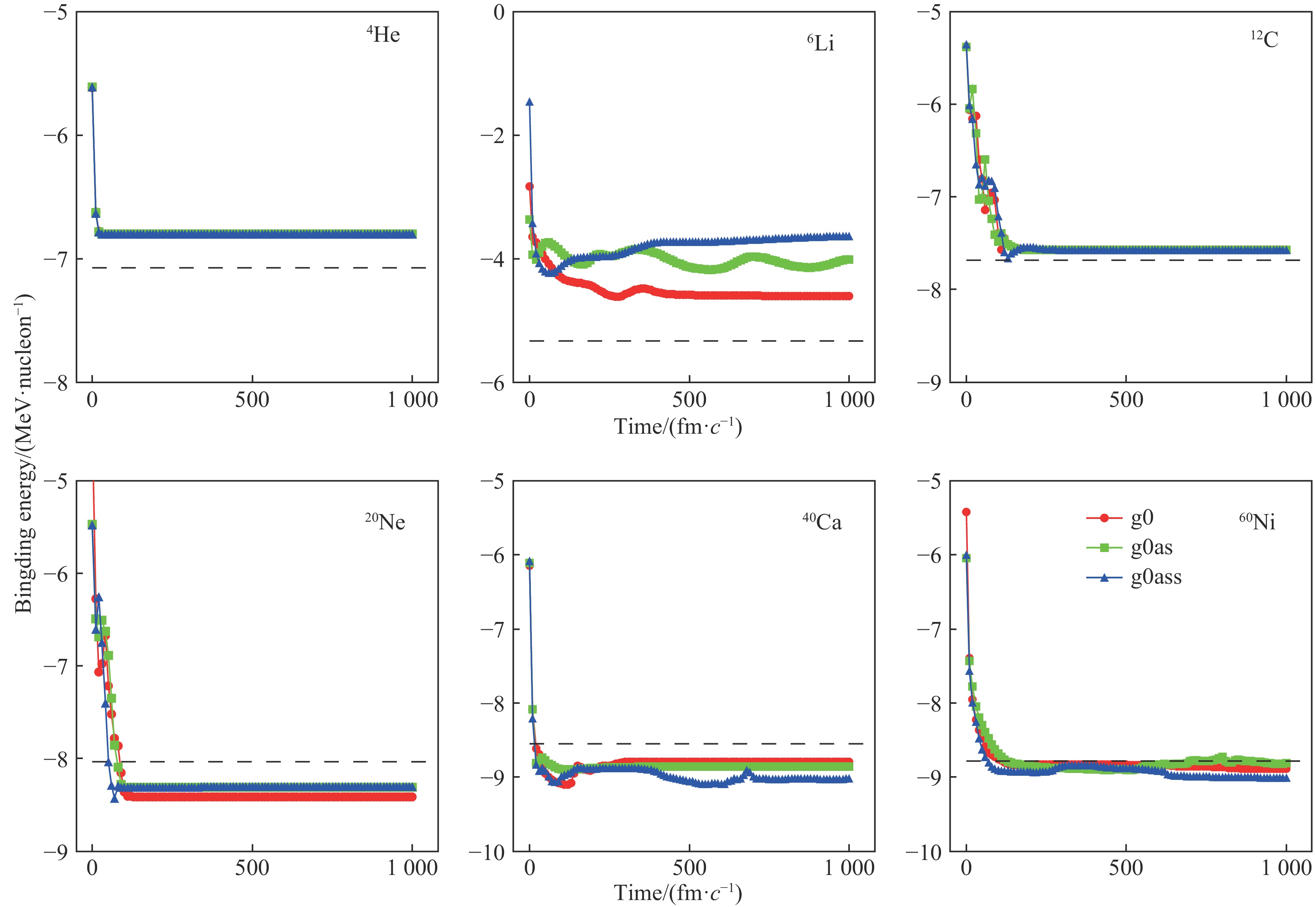
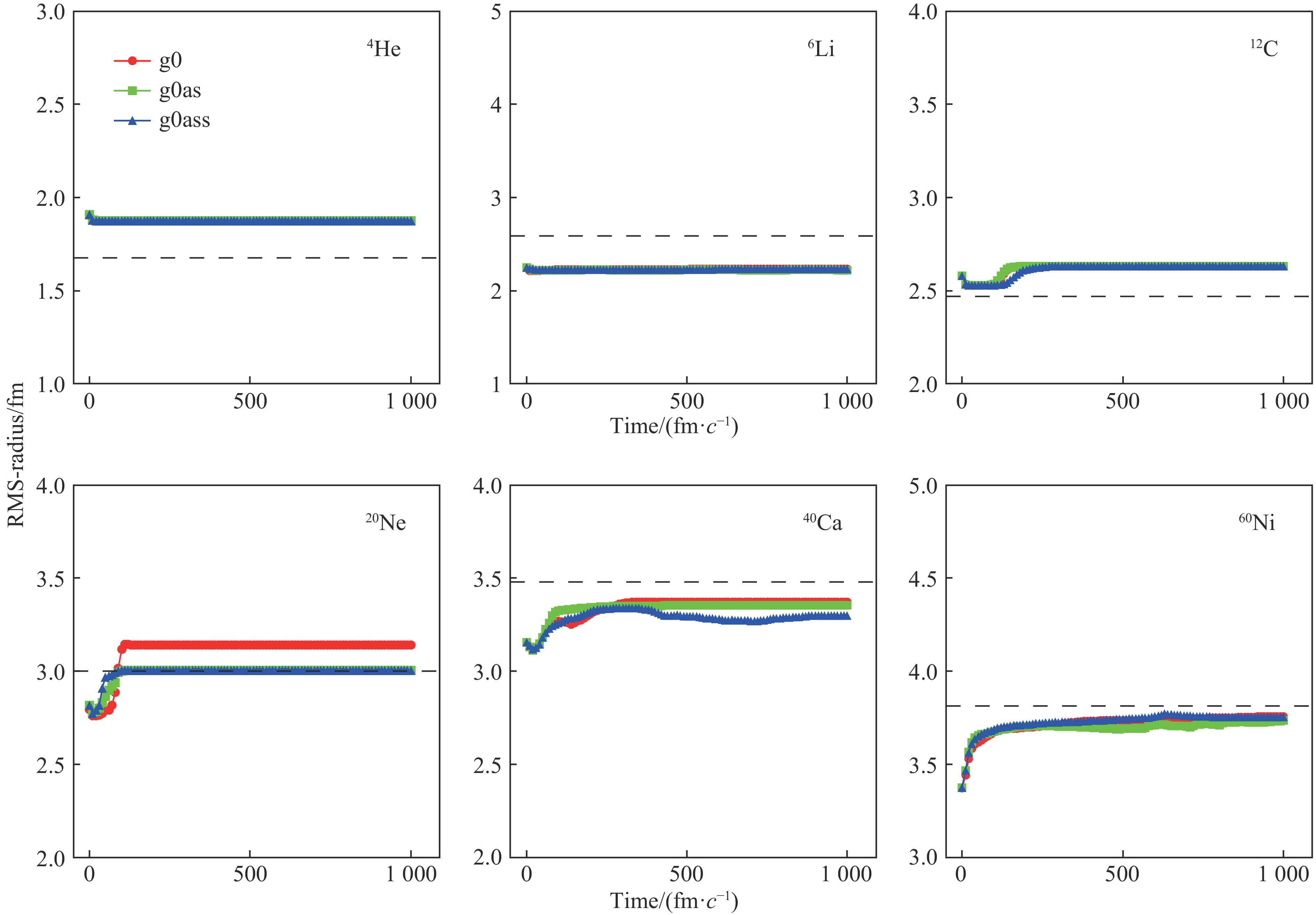
AMD模型在描述中低能核反应方面非常成功。为了验证AMD不同核子-核子相互作用势对原子核基态性质计算结果的可靠性。首先，计算了不同原子核结合能和方均根半径在自身平均场中随时间的演化，如图1和图2所示。可以看出，三种核子-核子相互作用势对几个稳定核结合能的计算结果随时间演化的涨落很小，最后都会趋于稳定值，如图1所示。其中6Li的三种核子-核子相互作用势结合能的计算值差别很大，其它几个稳定核计算结果在数值上基本相同。而对于方均根半径在自身平均场随时间的演化，如图2所示，可以看出，三种核子-核子相互作用势方均根半径随时间演化的涨落也很小，但三种核子-核子相互作用势对20Ne的计算值有一定差距。由上述几种稳定核的结合能及方均根半径的对比，AMD模型的三种核子- 核子相互作用势对几种不同稳定核结合能和方均根半径随时间自由演化过程的涨落方面给出了满意的描述。
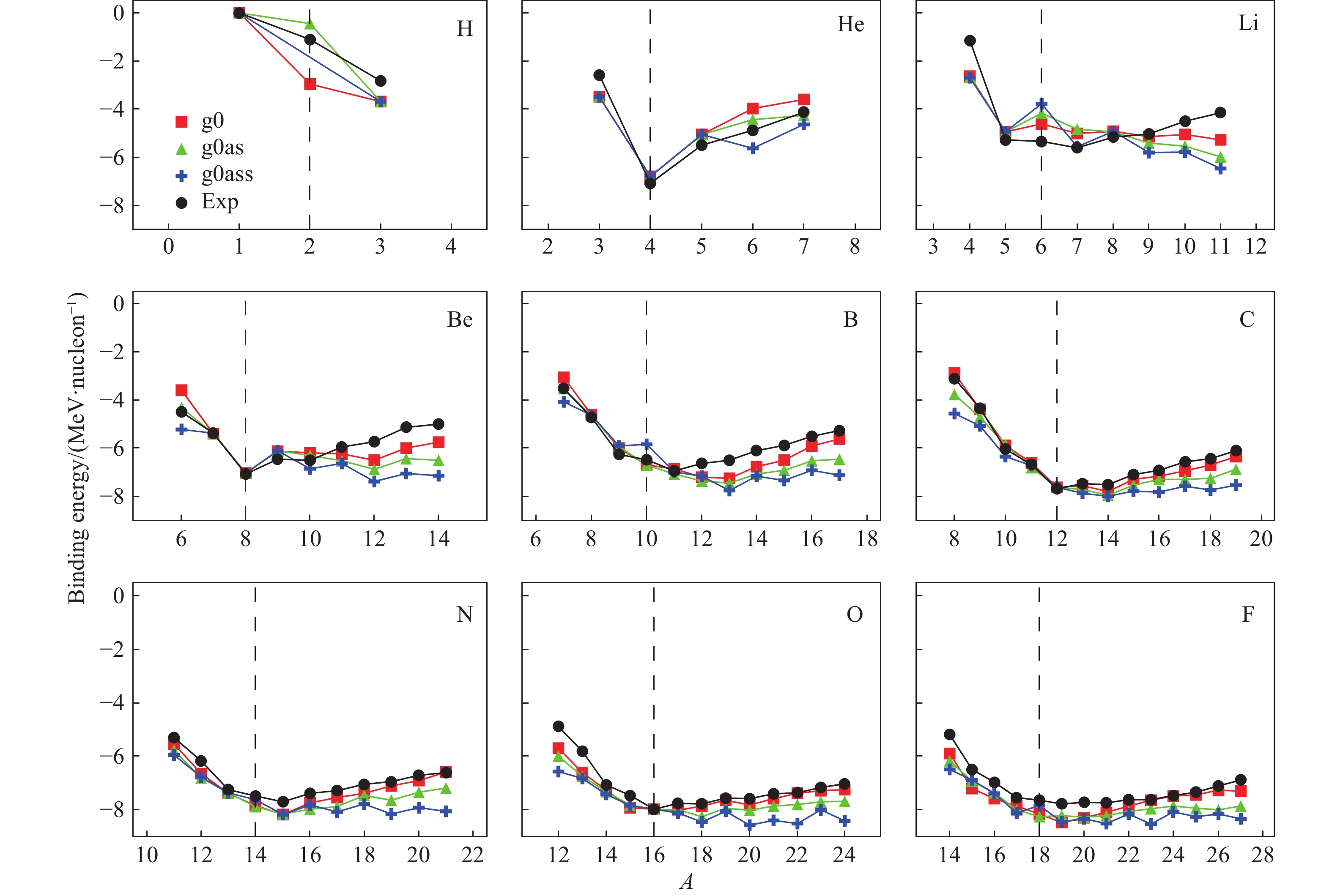
其次，计算了原子序数(Z)从1到18原子核的大量同位素结合能并与实验值对比，如图3和图4。三种核子-核子相互作用势无法很好地重现H、He和Li同位素依赖曲线，这是由于平均场方法对轻核描述是具有局限性导致的。对于实验值符合情况来看，对H和He的同位素g0as核子-核子相互作用势的结合能计算结果与实验值符合得更好。对Li(
$ Z \!= \!3 $ )到Ar($ Z \!=\! 18 $ )的同位素的结合能计算结果，g0核子-核子相互作用势的结合能计算结果要好于g0as和g0ass。我们用竖直虚线标记出质子数等于中子数的原子核，对Be($ Z \!=\! 4 $ )到Ar($ Z \!=\! 18 $ )原子核的同位素中，三种核子-核子相互作用势对丰质子和丰中子核结合能的计算值要小于实验值。对$ Z \!=\! 1 $ 到18原子核的同位素三种核子-核子相互作用势对丰质子核的结合能计算结果要好于丰中子核，对于质子数与中子数相差越大的核，三种核子-核子相互作用势的计算结果相差越大，但总满足$ BE_{\rm{g0}} $ $ > $ $ BE_{\rm{g0as}} $ $ > $ $ BE_{\rm{g0ass}} $ ，这是由于三种核子-核子相互作用势的对称能的密度依赖关系不同导致的。由上述可知，通过对比三种核子-核子相互作用势对$ Z \!=\! 1 $ 到$ Z \!=\! 18 $ 原子核的同位素结合能的计算值与实验值，综合来看g0符合得更好，且丰质子核对结合能的计算结果优于丰中子核。4. 结论
通过上面的计算结果可以看出，AMD模型中三种核子-核子相互作用势对几种稳定核的结合能和方均根半径在自身平均场中随时间的演化过程中涨落很小。另外，通过分别比较它们的
$ Z\! =\! 1\thicksim18 $ 同位素结合能的模拟计算值与实验值，发现g0结合能的计算值与实验值符合得更好。相对于丰中子核，丰质子核的结合能计算能够更好地再现实验数据。这能够为利用AMD模型研究中低能重离子核反应机制提供基础。致谢 感谢在本文研究过程中，四川大学林炜平副教授和田国玉博士的帮助和深入探讨。
-
表 1 Gogny核子-核子相互作用势参数表
Interaction i $\eta$ W B H M $\alpha$ $t_0$ /(MeV·fm–4)$\chi_0$ $W_\rho$ $B_\rho$ $H_\rho$ $M_\rho$ g0 1 0.7 $-402.4$ $-100.0$ $-496.2$ $-23.56$ 1/3 8 100 1 1 1 0 0 2 1.2 $-21.3$ $-11.77$ 37.27 $-68.81$ g0as 1 0.7 $-402.4$ $-100.0$ $-496.2$ $-23.56$ 1/3 8 100 1 1 $-0.5$ 0 0 2 1.2 $-21.3$ $-11.77$ 37.27 $ -68.81$ g0ass 1 0.7 $-402.4$ $-100.0$ $-496.2$ $-23.56$ 1/3 8 100 1 1 $-2$ 0 0 2 1.2 $-21.3 $ $-11.77$ 37.27 $-68.81$ 
下载: 导出CSV
-
[1] BECK C, SOUZA F A, ROWLEY N, et al. Phys Rev C, 2003, 67: 054602. DOI: 10.1103/PhysRevC.67.054602
[2] KEELEY N, RAABE R, ALAMANOS N, et al. Prog in Part and Nucl Phys, 2007, 59: 579. DOI: 10.1016/j.ppnp.2007.02.002
[3] CANTO L F, GOMES P R S, HUSSEIN M S, et al. Phys Rep, 2006, 424: 1. DOI: 10.1016/j.physrep.2005.10.006
[4] XU J. Progress in Particle and Nuclear Physics, 2019, 106: 312. DOI: 10.1016/j.ppnp.2019.02.009
[5] MA C W, ZHANG Y L, WANG S S, et al. Chin Phys Lett, 2015, 32: 072501. DOI: 10.1088/0256-307X/32/7/072501
[6] BERTSCH G F, GUPTA S D. Phys Rep, 1988, 160: 189. DOI: 10.1016/0370-1573(88)90170-6
[7] BONASERA A, GULMINELLI F, MOLITORIS J. Phys Rep, 1994, 1: 243.
[8] AICHELIN J, STÖCKER H. Phys Lett B, 1986, 176: 14. DOI: 10.1016/0370-2693(86)90916-0
[9] AICHELIN J. Phys Rep, 1991, 202: 233. DOI: 10.1016/0370-1573(91)90094-3
[10] 王闪闪, 曹喜光, 张同林, 等. 原子核物理评论, 2015, 32: 24. DOI: 10.11804/NuclPhysRev.32.01.024 WANG S S, CAO X G, ZHANG T L, et al. Nuclear Physics Review, 2015, 32: 24. (in Chinese) DOI: 10.11804/NuclPhysRev.32.01.024
[11] MARUYAMA T, NⅡTA K, IWAMOTO A. Phys Rev C, 1996, 53: 297. DOI: 10.1103/PhysRevC.53.297
[12] PAPA M, MARUYAMA T, BONASERA A, et al. Phys Rev C, 2001, 64: 024612. DOI: 10.1103/PhysRevC.64.024612
[13] ZHANG S, WANG J C, HUANG M R, et al. Chines Physics C, 2019, 43: 064102. DOI: 10.1088/1674-1137/43/6/064102
[14] ZHANG S, BONASERA A, HUANG M, et al. Phys Rev C, 2019, 99: 044605. DOI: 10.1103/PhysRevC.99.044605
[15] ONO A, HORIUCHI H. Phys Rev Lett, 1992, 68: 2898. DOI: 10.1103/PhysRevLett.68.2898
[16] FELDMEIER H. Nucl Phys A, 1990, 515: 147. DOI: 10.1016/0375-9474(90)90328-J
[17] SUN X Y, FANG D Q, MA Y G, et al. Phys Lett B, 2010, 682: 396. DOI: 10.1016/j.physletb.2009.11.031
[18] YONG G C, GAO Y, ZUO W, et al. Phys Rev C, 2011, 84: 034609. DOI: 10.1103/PhysRevC.84.034609
[19] DAI Z T, FANG D Q, MA Y G, et al. Phys Rev C, 2014, 89: 014613. DOI: 10.1103/PhysRevC.89.014613
[20] WEI G F, LI B A, XU J, et al. Phys Rev C, 2014, 90: 014610. DOI: 10.1103/PhysRevC.90.014610
[21] WEI G F. Phys Rev C, 2015, 91: 014616. DOI: 10.1103/PhysRevC.91.014616
[22] ONO A, HORIUCHI H. Phys Rev C, 1999, 59: 853. DOI: 10.1103/PhysRevC.59.853
[23] ONO A, HORIUCHI H, MARUYAMA T, et al. Phys Rev C, 1993, 48: 2946. DOI: 10.1103/PhysRevC.48.2946
[24] ONO A, HORIUCHI H. Phys Rev C, 1996, 53: 2341. DOI: 10.1103/PhysRevC.53.2341
[25] LIN W, LIU X, WADA R, et al. Phys Rev C, 2016, 94: 064609. DOI: 10.1103/PhysRevC.94.064609
[26] WADA R. Phys Rev C, 2000, 62: 034601. DOI: 10.1103/PhysRevC.62.034601
[27] ONO A, HORIUCHI H, MARUYAMA T, et al. Progress of Theoretical Physics, 1992, 87: 1185. DOI: 10.1143/ptp/87.5.1185
[28] DECHARGÉ J, GOGNY D. Phys Rev C, 1980, 21: 1568. DOI: 10.1103/PhysRevC.21.1568
[29] ONO A, DANIELEWICZ P, FRIEDMAN W A, et al. Phys Rev C, 2003, 68: 051601. DOI: 10.1103/PhysRevC.68.051601
[30] WANG M, AUDI G, KONDEV F G, et al. Chin Phys C, 2017, 41: 030003. DOI: 10.1088/1674-1137/41/3/030003
[31] ANGELI I, MARINOVA K P. Atomic Data and Nuclear Data Tables, 2013, 99: 69. DOI: 10.1016/j.adt.2011.12.006
计量
- 文章访问数: 870
- HTML全文浏览量: 180
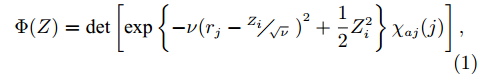
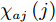
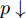
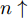
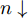
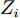
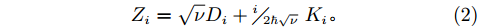
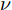
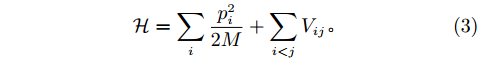
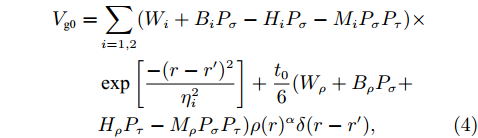
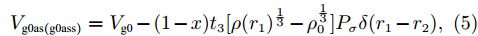
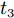
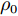
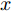
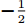
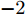
- PDF下载量: 48
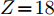
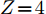
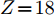
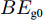
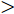
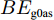
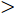
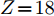
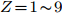
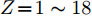
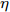
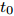
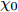
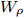
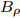
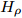
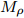
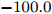
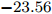
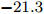
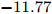
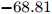
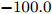
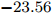
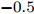
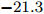
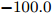
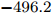
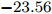
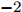
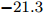
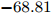
甘公网安备 62010202000723号