HTML
-
原子核质量(或结合能)和电荷半径是一个原子核的基本物理量。迄今为止,包括天然存在的近300种核素在内,实验室已经鉴别或合成了3 300多种核素[1-2],并测量了其中2 500多种核素的质量[3-4]和900多种核素的电荷半径[5]。根据理论模型预言,自然界的束缚核有7 000~12 000种[6-7],可见还有很多核素的质量和电荷半径等基本性质是未知的。这些结构性质所知甚少的核素主要集中在中重质量的丰中子区域,涵盖了宇宙中合成重元素关键核反应的某些路径,因此这些丰中子核素结构性质方面的数据是理解宇宙中合成重元素机制的关键参数。更重要的是,远离稳定线原子核的结构和反应机制是深入理解强相互作用低能极限以及全面认知原子核作为物质结构的一个基本层次所必需的。由于实验技术的限制,这些核素在可以预见的未来还不能全部被合成,相关结构性质的数据只能依赖理论模型的预言,因此从实验和理论两方面对中重质量丰中子原子核基态结构性质的研究是原子核物理一个长期的重要科学前沿课题。
原子核的质量是原子质量减去原子中所有电子质量的总和,再加上电子的结合能。中子数为N、质子数为Z的原子核质量
$ M(N, Z) $ 和结合能$ B(N, Z) $ 的关系为其中
$ M_{\rm n} $ 和$ M_{\rm p} $ 分别表示一个自由中子和一个自由质子的静止质量。实验上,由于通常不能剥离原子核外的所有电子,因此原子核的质量往往不能直接测量。然而电子静止质量是已知的,原子内电子结合能也可由很多方法相当准确地计算出来,因此人们习惯用原子质量代替原子核的质量 [计算时$ M_{\rm p} $ 取$ ^1_1 {\rm{H}}$ 原子质量、$ M(N, Z) $ 取相应原子质量,而与电子结合能相关的能量则基本抵消或间接地包含在理论模型参数中],例如,国际原子质量评估(Atomic Mass Evaluation, AME)数据表[3, 8-12]中就使用了原子质量。早期测量原子质量的常用仪器是质谱仪,其原理是让电离的原子通过电场和磁场加速偏转,根据偏转的曲率半径求出离子的质量。近几十年来,随着实验设备和技术的发展,对原子质量的测量已进入远离稳定线区域,目前主要的测量方法有飞行时间、储存环质谱术和离子阱等[13-14]。在理论方面,人们已经发展了很多原子核结合能模型[15]。20世纪30年代Gamow基于核力的饱和性提出了原子核结合能的液滴模型[16],在此基础上建立的Weizsäcker公式[17-18]提供了简单而直观的结合能物理图像,是一个宏观的半经验公式。Möller等[19-21]和Haustein[22]在液滴模型的基础上进一步考虑微观效应,提出了有限力程小液滴模型(the Finite-Range Droplet Model,FRDM)。这类模型被称为宏观-微观模型,类似的模型还有修正的Weizsäcker-Skyrme质量公式(WS公式)[23-27]和改进的宏观微观质量公式[28]等。从有效核子-核子相互作用出发,通过近似求解多体运动方程计算原子核结合能的方法被称为微观理论模型,例如,Skyrme-Hartree-Fock-Bogoliubov(SHFB)理论[29-34],相对论连续谱Hartree-Bogoliubov(RCHB)理论[7, 35]和形变相对论连续谱Hartree-Bogoliubov(DRHBc)理论[36-37]等。此外,也有一些直接研究分离能[38-40]或α衰变能[41-43]的半经验公式。
方便起见,人们通常把上述那些理论模型称为全局型(global)理论,而把建立在局域相互作用假设基础上的、联系相邻原子核物理量的关系式称为局域型(local)理论,把适用于某些特定区域内原子核物理量的关系式称为区域型(regional)理论。关于质量的局域型理论主要有Garvey-Kelson局域质量关系(GK关系)[44-45]、基于中子-质子相互作用的质量关系(
$ \delta V_{i {\rm n}-j {\rm p}} $ 关系)[46-49]以及在编辑AME数据表过程中发展的Audi-Wasptra外推方法[3, 8-12]等。局域型理论关注物理量的差分,并且这些差分之间具有局域相干性,因此,我们将具有这些特点的局域型理论统称为局域相干性差分法(Scheme of Local Interferential Difference, SOLID)。关于质量的区域型理论主要有同位旋多重态质量方程(Isobaric Multiplet Mass Equation, IMME)[50-55]和镜像核质量公式[56-61]等。此外,也有一些直接研究分离能[62-63]或α衰变能[64-67]的局域型或区域型理论。原子核电荷半径与这些物理量类似,既存在全局型理论的计算方法,如SHFB理论[29-34]和唯象的半经验公式[68-70]等,也发展出了一些局域型方法[71-74]和区域型方法[75-76]。全局型理论和局域型、区域型理论是相互补充的。全局型理论能够反映原子核基态性质的系统变化,在描述和预言远离已知实验数据区域核素的基态物理量方面比较有优势;而局域型、区域型理论基于实验数据,强调原子核基态性质的局域化、区域化特征,在描述已知实验数据方面比较有优势。在实验数据已知的区域,局域型或区域型理论的精度是最高的,例如,对质量数
$ A \geqslant 16 $ 核素的结合能,全局型的Duflo-Zuker(DZ)模型[77]描述实验数据的方均根偏差(Root-Mean-Squared Deviation,RMSD)大约为380 keV,而局域型$ \delta V_{i {\rm n}-j {\rm p}} $ 关系的RMSD大约为200 keV[49];对电荷半径,SHFB理论描述实验数据的RMSD大约为0.026 fm[33-34],半经验公式的RMSD大约为0.022 fm[70],而局域型或区域型理论的RMSD一般小于0.010 fm[71-76]。值得指出的是,数值实验表明,当预言未知区域的原子核质量或电荷半径时,在目标原子核处于核素图中的位置与已知实验数据的边界不超过三到五步的情况下,由局域型或区域型理论得到的预言结果精度往往也是最高的。不仅如此,局域型或区域型理论还有助于分析某些难以直接测量的相互作用成分,从而对确定原子核结构某些重要参量的数值发挥独特作用。除上述全局型和局域型、区域型理论外,近年来机器学习也被广泛应用于研究原子核质量和电荷半径等物理量[78-90]。机器学习通常以物理量实验值或已有理论模型给出的物理量理论值与其实验值的差值为训练集,经过各层训练直到输出结果满足一定要求,进而预言未知的物理量数据。目前主要的机器学习方法有贝叶斯神经网络、Levenberg-Marquardt神经网络、支持向量机和决策树等。此外,径向基函数(Radial Basis Function, RBF)[26-27, 66, 81, 91-94]和不确定度分析[95-98]等也有助于提高理论模型描述和预言原子核基态物理量的精度。
本文主要综合、总结原子核质量及其相关物理量(如分离能和α衰变能等)和电荷半径的系统规律,以及建立在这些规律上的关系式。本文还基于局域型关系的优势来确定唯象宏观质量模型中的对称能和Wigner能系数,并讨论原子核内质子之间的库仑能以及原子核低激发态的结构演化。作为附件(见科学数据银行)[99],本文整理了基于这些理论模型预言的部分原子质量剩余(或结合能)及其相关物理量和原子核电荷半径。
本文第1节讨论GK关系及其推广,第2节讨论中子-质子相互作用的系统规律及相关质量公式,第3节讨论结合能、衰变能和分离能的局域双重差分与GK关系的联系及相关外推方法,第4节讨论局域质量关系的系统规律对原子核对称能和Wigner能的约束,第5节讨论镜像核的质量公式及库仑能的奇偶性,第6节讨论原子核单(双)核子分离能与价核子数之间的关系以及单核子分离能的半经验公式,第7节讨论利用不同理论模型得到的、目前尚没有实验结果的原子核质量、α衰变能和单核子分离能,第8节讨论原子核电荷半径的局域型和区域型关系以及基于这些关系式得到的电荷半径预言结果,第9节为总结。本文第1~7节的所有计算都基于最新的原子质量评估AME2020数据表[3]中原子质量剩余(或结合能)的实验数据。
-
Garvey-Kelson局域质量关系(GK关系)因简单有效而为人所知,是典型的、无参数的局域相干性差分法(SOLID)。近年来有很多基于GK关系的研究工作,例如,GK关系与中子-质子相互作用的联系[100-101],利用GK关系外推预言的可靠性[102-103],用单核子分离能改写GK 关系以减小外推预言时误差的迭代[104],推广GK关系预言丰质子核的质量[105-107],在形式上参考GK关系描述并预言原子核电荷半径[71]等。本节回顾GK关系及与之相关的一些推广工作。
-
Garvey-Kelson局域质量关系假定原子核内的核子之间只有单体和两体相互作用,并且这些相互作用在核素图上邻近原子核的最后几个核子之间近似不变。GK关系包括两个联系相邻六个原子核质量的关系式[44-45],即
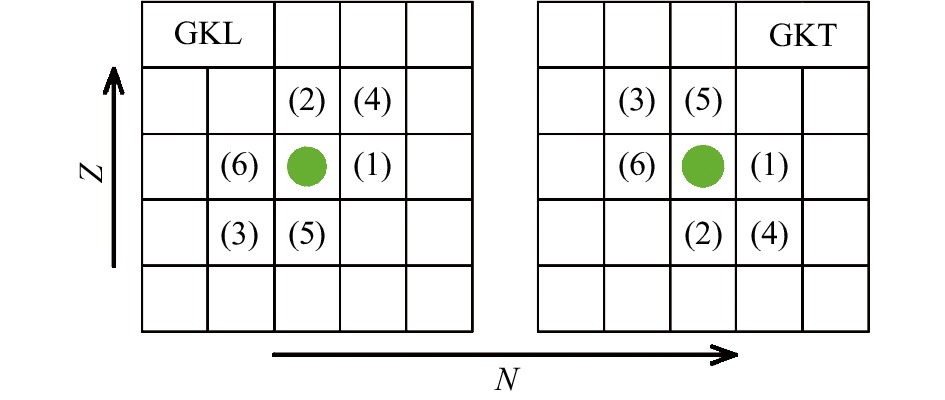
基于所涉及原子核在核素图上的分布形状与β稳定线的相对位置,式(2)和(3)分别表示纵向(longitudinal)的GK关系(简称GKL)和横向(transverse)的GK关系(简称GKT),其中
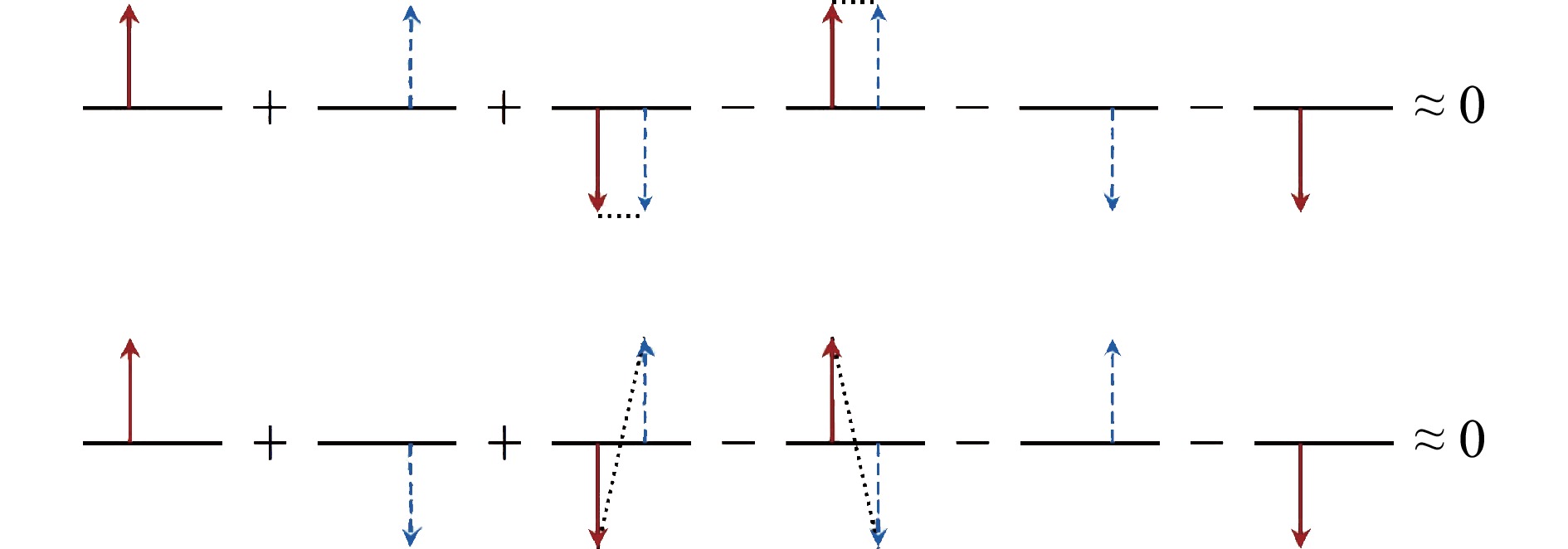
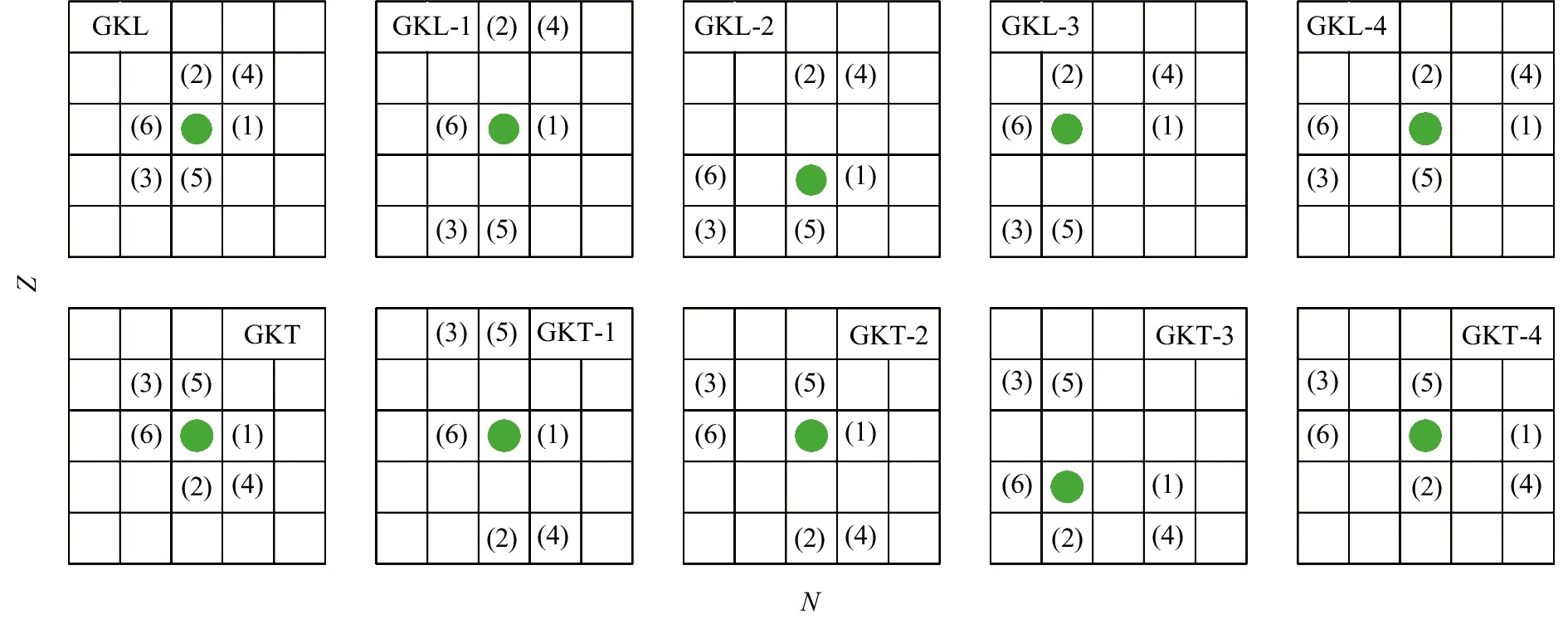
$ D_{\rm L} $ 和$ D_{\rm T} $ 分别表示GKL和GKT相对于零的偏离,$ M(N, Z) $ 表示中子数为N、质子数为Z的原子核质量。由于Wigner能(见第4.2节)的贡献,GK关系中涉及的六个原子核不能包含N=Z=奇数的情况;为保证与同位旋投影$ T_z =(N-Z)/2 $ 相关的剩余相互作用完全抵消,GKT中涉及的六个原子核不能分布在N=Z这条线两侧[45],因此通常要求GKT中不包含N < Z的原子核。图1为GKL和GKT的示意图,其中绿色实心圆对应参考核,即中子数为N、质子数为Z的原子核位置,(1)~(3)位置对应原子核质量前的符号为正号,(4)~(6)位置对应原子核质量前的符号为负号。图2为GKL(上)和GKT(下)所涉及六个原子核中各种相互作用的示意图,从左到右依次对应图1中(1)~(6)位置的原子核,黑色横线表示参考核
$ (N, Z) $ 的能量,向上或向下的红色实线(蓝色虚线)箭头分别对应比参考核的中子数N(质子数Z)+1或−1的单中子(单质子)能量,连接两种箭头的黑色点线表示中子-质子相互作用。根据GK关系的假定,从图2容易看出GKL和GKT所涉及六个原子核的单体和两体相互作用完全抵消[44-45],因此GK关系在很高的精度内近似为零。表1列出了在不同区域(质量数
$ A = N + Z \geqslant 16 $ 、$ A \geqslant 60 $ 和$ A \geqslant 120 $ )GKL和GKT的方均根偏差(标记为$ \sigma $ )。这里$ \sigma $ 的定义为区域 $\sigma$ GKL GKT $ A \geqslant 16 $ 229 221 $ A \geqslant 60 $ 173 180 $ A \geqslant 120 $ 146 159 其中
$ D(N, Z) $ 表示中子数为N、质子数为Z时公式的理论值相对于实验值的偏差,$ \mathcal{N} $ 是所有能计算到的$ D(N, Z) $ 的个数。以表1的第2~3列为例,式(4)中的$ D(N, Z) $ 分别对应式(2)和(3)的$ D_{\rm L}(N, Z) $ 和$ D_{\rm T}(N, Z) $ ,$\mathcal{N}$ 分别为基于AME2020数据表[3]中质量实验数据能够计算到的$ D_{\rm L}(N, Z) $ 和$ D_{\rm T}(N, Z) $ 的个数。从表1可以看到,随着质量数A的增加,GKL和GKT的方均根偏差$ \sigma $ 逐渐减小;除$ 16 \leqslant A < 60 $ 的区域外,GKL的精度略高于GKT。本文还涉及到另一种方均根偏差(标记为
$ \overline{\sigma} $ ),其定义为其中
$P^{\,\rm exp}_i$ 和$P^{\,\rm th}_i$ 分别表示第i个原子核的物理量P的实验值和理论值;$ \mathcal{N} $ 是理论能够计算出$P_i^{\,\rm th}$ 且同时存在相应实验值$P_i^{\,\rm exp}$ 的原子核个数。以使用式(2)[式(3)] 计算质量为例,若已知GKL(GKT)中所涉及任意5个原子核的质量,则可计算出剩下第6个原子核的质量。因此对于给定的第i个原子核,根据它与其它已知质量原子核不同的相对位置,GKL(GKT)最多有6种关于$ M_i $ 的计算结果,取所有计算结果的平均值作为该原子核质量的理论值,记为$M_i^{\,\rm th}$ 。若利用GKL(GKT)能够计算出$M_i^{\,\rm th}$ 且AME2020数据表[3]中存在相应实验值$M_i^{\,\rm exp}$ 的原子核个数为$ \mathcal{N} $ ,则根据式(5)计算的GKL(GKT)描述不同区域质量实验数据的方均根偏差$ \overline{\sigma} $ 和个数$ \mathcal{N} $ 在表2的第$ 2 \sim 3 $ 列(第$ 4 \sim 5 $ 列)给出。表2最后两列“GK”为同时使用GKL和GKT计算质量时的结果,在这种情况下$M_i^{\,\rm th}$ 最多由12种计算结果的平均值给出。由表2可知,GK关系以非常简单的形式高精度地描述了质量的绝大部分实验数据(AME2020数据表[3]中收录了2 484个$ A \geqslant 16 $ 的质量实验数据)。区域 GKL GKT GK $ \overline{\sigma} $ $ \mathcal{N} $ $ \overline{\sigma} $ $ \mathcal{N} $ $ \overline{\sigma} $ $ \mathcal{N} $ $A \geqslant 16$ 154 2 355 143 2 294 138 2 398 $A \geqslant 60$ 106 2 012 109 2 024 100 2 052 $ A \geqslant 120 $ 82 1 374 100 1 382 83 1 402 注:最后两列“GK”为同时使用GKL和GKT计算质量时的结果。 -
GK关系更一般的表示形式[45]可以写为
上式中每个
$ N_i $ 和$ Z_j $ ($ i, j = 1, 2, 3 $ )都出现了两次且对应质量前的符号相反,因此式(6)所涉及六个原子核的中子-中子和质子-质子相互作用完全抵消。由于原子核的中子-质子相互作用与中子数和质子数的乘积成正比,因此为抵消式(6)中的中子-质子相互作用,要求令
$ \varDelta N_i = N_2 - N_i $ 、$ \varDelta Z_j = Z_1 - Z_j $ ,从上式可得其中L为整数[45]。当L取1和−1时,容易验证式(6)分别对应式(2)的GKL和式(3)的GKT。
当式(7)中的L取±2时,由式(6)可构造出十个相互独立的、联系相邻六个原子核质量的关系式(其中正好包含了
$ L = \pm 1 $ 时的GKL和GKT),称为GKs关系[108]。图3为GKs关系的示意图(表示方式同图1),其中第一列为GKL和GKT;第一行的第2~5个公式与GKL类似,都沿着$ T_z $ 为常数的方向分布,所以将这四个公式分别标记为GKL-k($ k = 1, 2, 3, 4 $ ),将第一行的五个公式统称为GKLs;第二行的第2~5个公式与GKT类似,都沿着A为常数的方向分布,所以将这四个公式分别标记为GKT-k($ k = 1, 2, 3, 4 $ ),将第二行的五个公式统称为GKTs。与GK关系类似,GKs关系中涉及的六个原子核不能包含$ N = Z = $ 奇数的情况,GKTs中通常不包含$ N<Z $ 的原子核。表3 给出了不同区域GKL-k、GKT-k的方均根偏差
$ \sigma $ [见式(4)]和它们描述质量实验数据的方均根偏差$ \overline{\sigma} $ [见式(5)]。由表1~3可知,GKs关系的十个公式中GKL和GKT的$ \sigma $ 最小,然而当$ A \geqslant 120 $ 时GKL-2、GKL-3和GKL-4的$ \overline{\sigma} $ 都小于GKT的$ \overline{\sigma} $ 。表3最后一列“GKs”为同时使用GKs关系的十个公式计算质量时的$ \overline{\sigma} $ ,在这种情况下质量理论值最多由60种计算结果的平均值给出。可以看到,当$ A \geqslant 60 $ 和$ A \geqslant 120 $ 时GKs关系的$ \overline{\sigma} $ 小于GK关系的$ \overline{\sigma} $ (见表2第6列)。这说明在描述质量实验数据方面GKs关系是有竞争力的。区域 GKL-1 GKL-2 GKL-3 GKL-4 GKT-1 GKT-2 GKT-3 GKT-4 GKs $ \sigma $ $ \overline{\sigma} $ $ \sigma $ $ \overline{\sigma} $ $ \sigma $ $ \overline{\sigma} $ $ \sigma $ $ \overline{\sigma} $ $ \sigma $ $ \overline{\sigma} $ $ \sigma $ $ \overline{\sigma} $ $ \sigma $ $ \overline{\sigma} $ $ \sigma $ $ \overline{\sigma} $ $ \sigma $ $ \overline{\sigma} $ $ A \geqslant 16 $ 462 306 312 186 313 182 457 295 302 210 279 182 290 202 279 201 -- 171 $ A \geqslant 60 $ 242 160 206 110 207 109 221 145 233 140 219 121 221 129 216 133 -- 96 $ A \geqslant 120 $ 203 126 174 91 175 90 177 97 203 119 189 105 187 105 187 109 -- 75 注:最后一列“GKs”为同时使用 GKs 关系的十个公式计算质量时的$ \overline{\sigma} $。 -
根据文献[109-111],式(2)和(3)的GK关系[44-45]也可以表示为
其中运算符
$\varDelta^{i,\, j}$ 的定义为其中
$ C_1 $ 和$ C_2 $ 为常数。上式的通解[45]为其中点函数
$ f_i $ ($ i = 1, 2 $ )以及常数$ \lambda $ 和$ \mu $ 通过最小二乘法拟合质量实验数据确定。然而式(12)并不能很好地描述质量实验数据,其方均根偏差~2 MeV[112]。文献[112]在式(12)的基础上提出了一种新的外推方法,即在拟合时只考虑被计算原子核
$ (N_0, Z_0) $ 周围原子核$ (N, Z) $ 的质量实验值。这里要求其中
$ E = N - Z $ 、$ E_0 = N_0 - Z_0 $ 为中子过剩,L为正整数。由于GK关系是一种局域型理论,式(13)中L的取值不能太大;拟合需要足够多的实验数据,所以L的取值也不能太小。当L的取值令被计算原子核质量$ M(N_0, Z_0) $ 的理论不确定度$ \sigma_{\rm th} $ 最小时[112],对$ A \geqslant 16 $ 、$ A \geqslant 60 $ 和$ A \geqslant 120 $ 的情况($ N>Z $ 或$ N=Z $ 为偶数),式(12)描述质量实验数据的方均根偏差 [见式(5)] 分别为122, 94和76 keV,相比GK关系(见表2)有所降低。上述方法中质量理论不确定度
$ \sigma_{\rm th} $ 的计算步骤[20, 112]如下。给定$ \sigma_{\rm th} $ 的初始值,代入等式右边计算,从而得到一个新的
$ \sigma_{\rm th} $ ,再将新的$ \sigma_{\rm th} $ 代入上式右边计算,如此迭代循环直到得到的$ \sigma_{\rm th} $ 满足一定的精度要求。式(14)中$M_{\rm th}^{\,i}$ 、$M_{\rm exp}^{\,i}$ 和$\sigma_{\rm exp}^{\,i}$ 分别表示第i个原子核质量的理论计算值、实验值和实验误差,$ \alpha_i^2 $ 是计算第i个原子核质量时用到的所有质量实验值的误差平方和,$ \mathcal{N} $ 是理论能够计算出$M_{\rm th}^{\,i}$ 且同时存在相应质量实验值$M_{\rm exp}^{\,i}$ 的原子核个数 [注意计算中不包含被计算原子核$ (N_0, Z_0) $ ]。此外,Jänecke等[106, 109-111, 113-115]在式(12)的基础上通过分开处理丰中子核和丰质子核、引入非齐次项等方法,发展出了全局型的Jänecke公式。文献[91]通过同时考虑关于中子数N、质子数Z、质量数A和中子过剩E的点函数,并引入库仑能、对称能和对能项作为修正,改进了Jänecke公式,提高了其描述原子核质量实验数据的精度(考虑径向基修正后的方均根偏差约128 keV)。
-
中子-质子相互作用在许多现象(如集体性、组态混合、原子核形变和相变等)中起着关键作用[116-118]。通过相邻四个原子核结合能的双重差分,可以提取出中子-质子相互作用;根据中子-质子相互作用的系统规律,可以构造出一系列原子核质量公式[46-49]。这些公式都属于局域相干性差分法(SOLID),在国际原子核质量网站[119]上被称为“Nucleon Interaction”模型。相比GK关系,这些公式涉及的原子核个数更少,描述中重核区质量实验数据的精度更高,因此具有更好的外推性。
此外,Casten和Zamfir在20世纪80年代引入了
$ N_{\rm n}N_{\rm p} $ (价中子数$ N_{\rm n} $ 和价质子数$ N_{\rm p} $ 的乘积)替代经验的中子-质子相互作用来研究原子核低激发态的系统性,这对深入理解原子核集体运动演化的图像发挥了重要作用[120-122]。本文将原子核物理量与$ N_{\rm n}N_{\rm p} $ 的关系称为Casten经验公式。本节讨论中子-质子相互作用的系统规律,以及原子核物理量的双重差分与Casten经验公式的联系。 -
定义原子核最后i个中子和最后j个质子之间的中子-质子相互作用(标记为
$ \delta V_{i {\rm n}-j {\rm p}} $ )[46-49, 100-101, 123]为其中
$ B(N, Z) $ 是中子数为N、质子数为Z的原子核结合能。由于Wigner能(见第4.2节)的影响,计算中不能包含$ \delta V_{1 {\rm n}-1 {\rm p}} $ 非常大的$ N=Z $ 的原子核。$ \delta V_{2 {\rm n}-1 {\rm p}} $ 和$ \delta V_{1 {\rm n}-2 {\rm p}} $ 可以写为相邻两个$ \delta V_{1 {\rm n}-1 {\rm p}} $ 之和,即因此除了
$ N=Z $ 的原子核,在计算$ \delta V_{2 {\rm n}-1 {\rm p}} $ ($ \delta V_{1 {\rm n}-2 {\rm p}} $ )时也不能包含$ N-1=Z $ ($ N+1=Z $ )的原子核。图4给出了
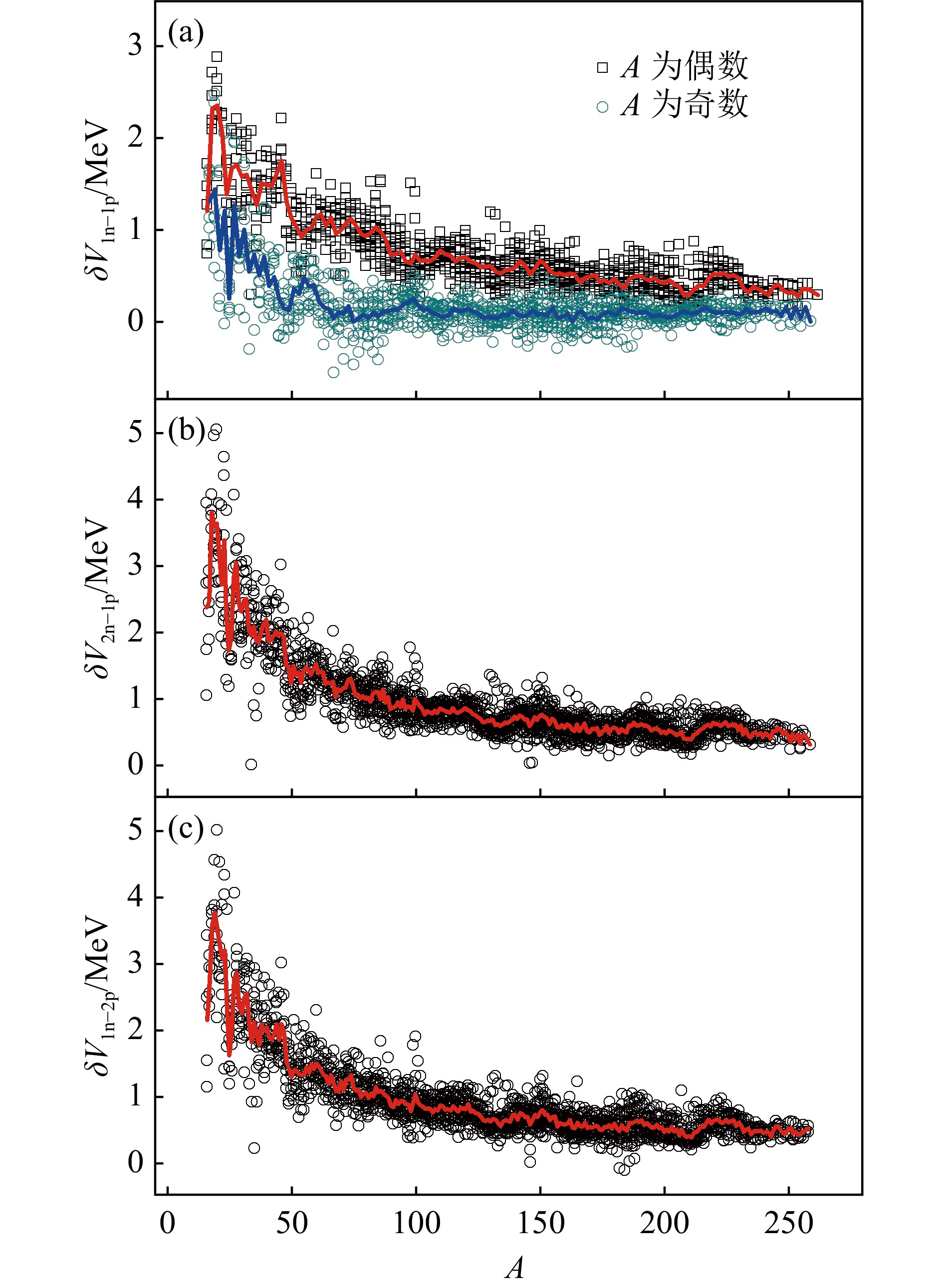
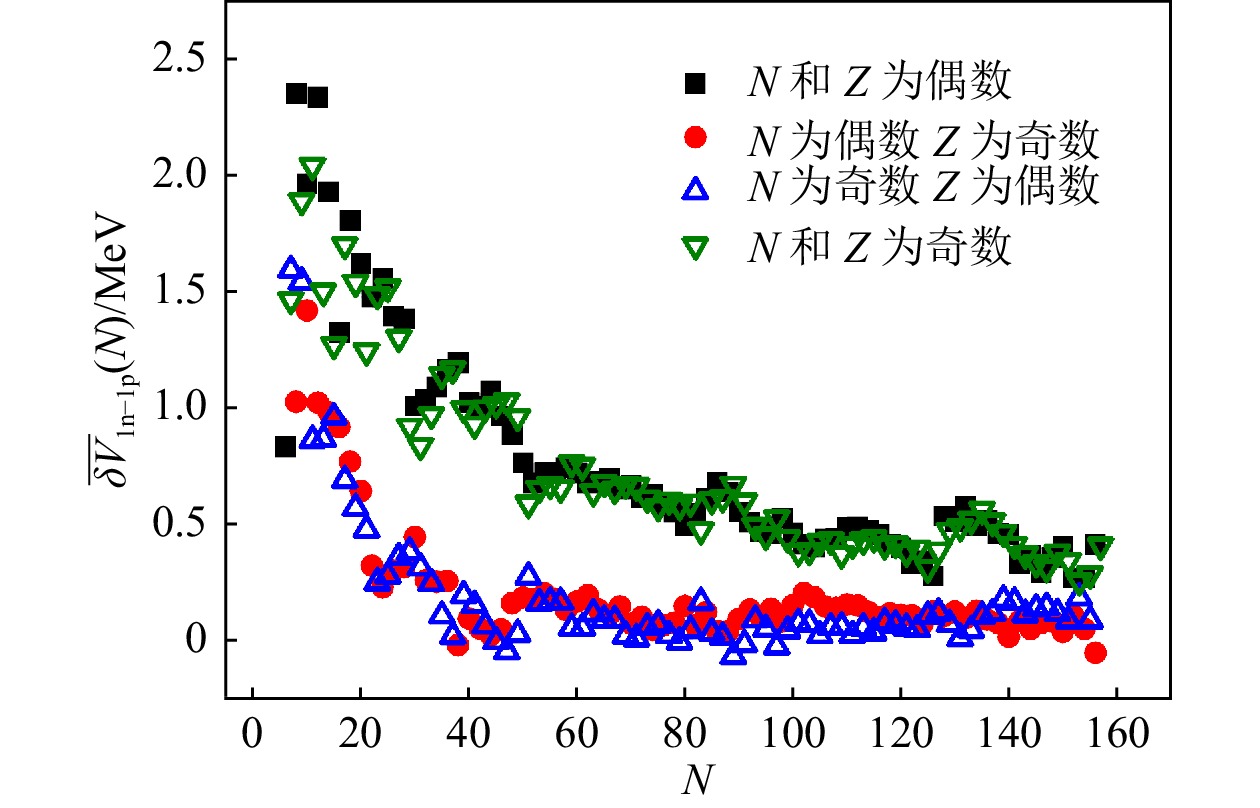
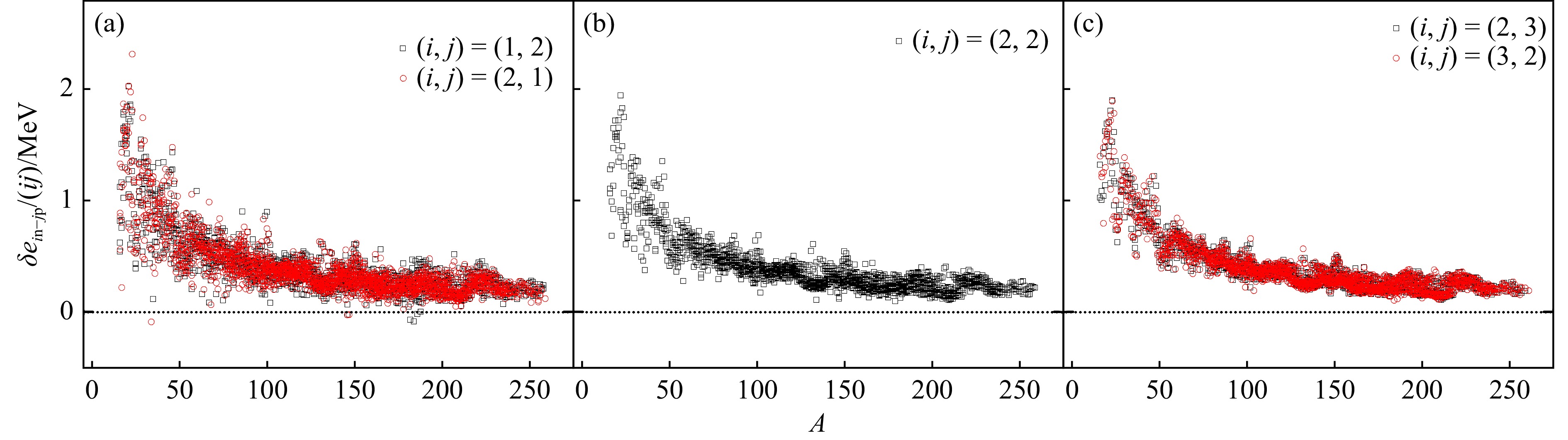
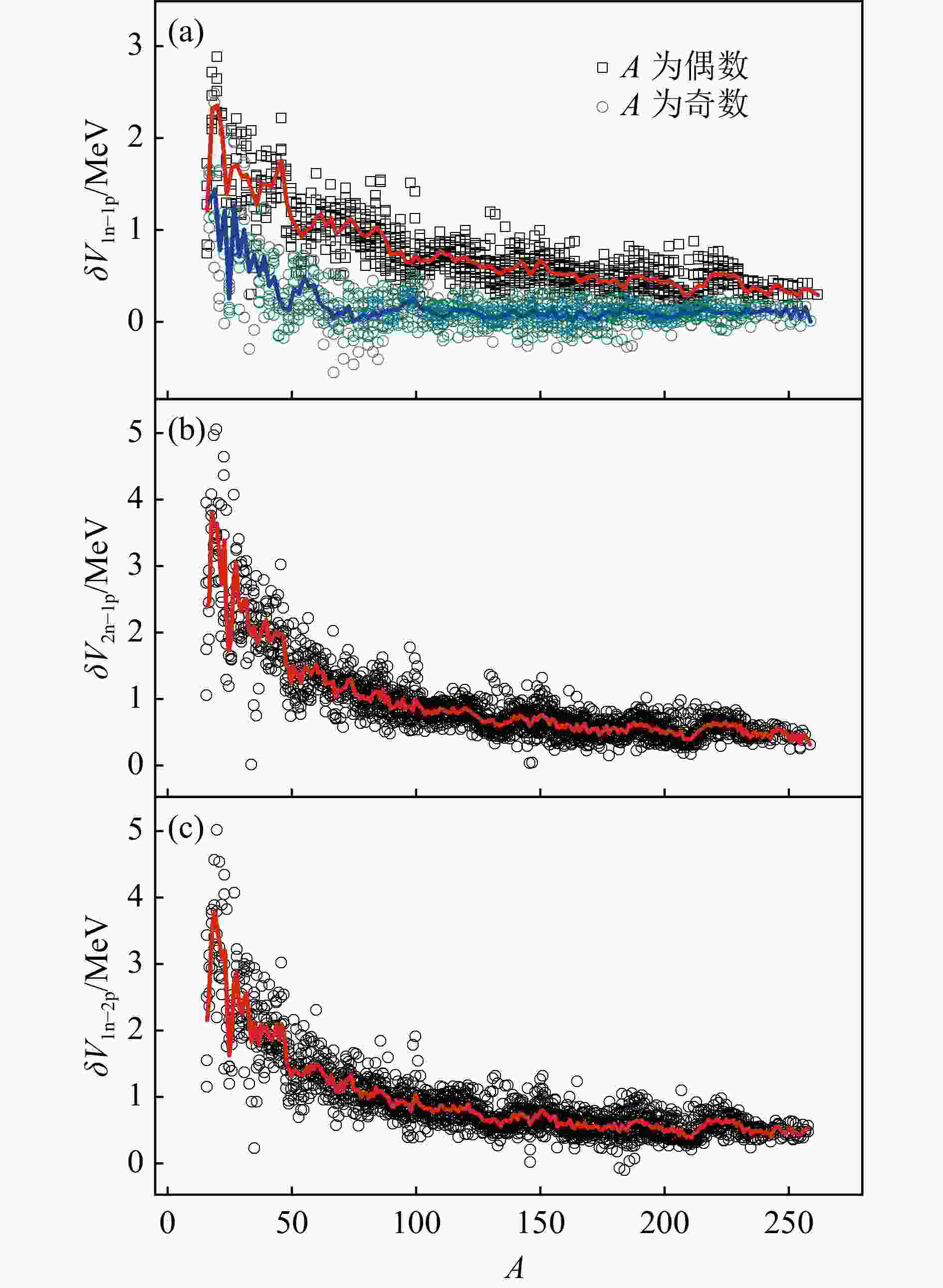
$ A \geqslant 16 $ 时$ \delta V_{i {\rm n}-j {\rm p}} $ [$ (i, j) $ $=(1, 1), (2, 1), (1, $ $2)] $ 与A的关系图,其中实线表示$ \delta V_{i {\rm n}-j {\rm p}} $ 关于A的平均值 [标记为$ \overline{\delta V}_{i {\rm n}-j {\rm p}}(A) $ ]。图4(a)中A为偶数和奇数的$ \delta V_{1 {\rm n}-1 {\rm p}} $ 分别用空心的黑色正方形和绿色圆形表示,相应的平均值$ \overline{\delta V}_{1 {\rm n}-1 {\rm p}}(A) $ 分别用红色和蓝色实线表示。从图4可以看到,$ \delta V_{i {\rm n}-j {\rm p}} $ 随A的增加整体呈下降趋势,且逐渐趋于平缓。此外,图4(a)中A为偶数和奇数的$ \delta V_{1 {\rm n}-1 {\rm p}} $ 有明显差别[124],这种奇偶效应主要是由对能所引起的[48]。考虑文献[23, 125]中对能
$ V_{\rm p} $ 的形式,即其中
$ a_{\rm p} $ 为拟合系数,$ I =(N-Z)/ A $ 是电荷不对称参数。考虑中重核区$ N>Z $ 的原子核,根据式(15)和(17)可得$ \delta V_{1 {\rm n}-1 {\rm p}} $ 中对能的贡献为$V_{\rm p} (N, Z)+ V_{\rm p} (N-1, Z-1)- V_{\rm p} (N-1, Z)- V_{\rm p} (N, $ $ Z- 1)\approx \pm a_{\rm p} I A^{-1/3} $ (A是偶数时为正,A是奇数时为负)。取$ a_{\rm p} = 5.44 $ MeV[24],则对能对$ \delta V_{1 {\rm n}-1 {\rm p}} $ 奇偶差值的贡献为$ 2 a_{\rm p} I A^{-1/3} \sim 330 $ keV,占了图4(a)中中重核区域$ \overline{\delta V}_{1 {\rm n}-1 {\rm p}}(A) $ 平均奇偶差值(~410 keV)的绝大部分[48]。根据文献[48],
$ A \geqslant 100 $ 的$ \delta V_{1 {\rm n}-1 {\rm p}} $ 呈现出两种不同的变化趋势,A为奇数时约等于一个常数,而A为偶数时随A的增加整体呈下降趋势,这种趋势上的不同还有待进一步研究。从图4(a)可得,$ A \geqslant 100 $ 且为奇数时$ \delta V_{1 {\rm n}-1 {\rm p}} $ 的平均值为84 keV,这一数值与图4(a)中$ \delta V_{1 {\rm n}-1 {\rm p}} $ 实验值的方均根偏差$ \sigma $ [见式(4)] 为119 keV;A为偶数时$ \delta V_{1 {\rm n}-1 {\rm p}} $ 可以用关于A的简单函数来描述,即这一结果与实验值的方均根偏差
$ \sigma $ 为148 keV。由此可见,$ \delta V_{1 {\rm n}-1 {\rm p}} $ 与A存在简单的经验关系,且精度比GK关系更高(见表1)。$ \delta V_{2 {\rm n}-1 {\rm p}} $ 和$ \delta V_{1 {\rm n}-2 {\rm p}} $ 作为相邻两个A分别为偶数和奇数的$ \delta V_{1 {\rm n}-1 {\rm p}} $ 之和 [见式(16)],不出所料也呈现出关于A的简单经验关系,且由于求和时对$ \delta V_{1 {\rm n}-1 {\rm p}} $ 奇偶效应有主要贡献的对能的抵消,图4(b)和(c)中$ \delta V_{2 {\rm n}-1 {\rm p}} $ 和$ \delta V_{1 {\rm n}-2 {\rm p}} $ 没有表现出关于A的奇偶效应[48]。为了尽可能准确地得到
$ \delta V_{i {\rm n}-j {\rm p}} $ 的理论值以便更好地利用式(15)描述和预言结合能,需将图4中的$ \overline{\delta V}_{i {\rm n}-j {\rm p}}(A) $ 作为初始值,再引入修正项[48]。由于体积能和表面能对$ \delta V_{i {\rm n}-j {\rm p}} $ 的贡献几乎为零,库仑能修正和对称能修正对提高$ \delta V_{i {\rm n}-j {\rm p}} $ 的精度作用很小[48],因此这里只讨论对中子-质子相互作用有主要影响的壳效应,称为$ \delta V_{i {\rm n}-j{\rm p}} $ 的壳修正。考虑壳修正后,$ \delta V_{i {\rm n}-j {\rm p}} $ 的理论计算值(标记为$ \delta V_{i {\rm n}-j {\rm p}}^{\rm th} $ )[49]为经验表明,当价质子和价中子在各自壳层的填充比例相近时,中子-质子相互作用更强[126]。受此启发,式(19)中壳修正的形式[48-49]可以表示为
其中
$ a_{\rm sh} $ 和$ b_{\rm sh} $ 是拟合系数;$ N_{\rm n} $ ($ N_{\rm p} $ )是价中子数(价质子数);中子(质子)为粒子型和空穴型时$ \delta_{\rm n} $ ($ \delta_{\rm p} $ )分别等于+1和−1。$ \Omega_{N} = \sum_{j_{N}}(j_{N} + 1/2) $ ,$ \Omega_{Z} = \sum_{j_{Z}}(j_{Z} + 1/2) $ ,其中$ j_{N} $ ($ j_{Z} $ )是价中子(价质子)的单粒子轨道自旋。根据图4中$ \delta V_{i {\rm n}-j {\rm p}} $ 的实验值拟合式(19),可得在不同壳层区域、A分别为偶数和奇数时的壳修正系数$ a_{\rm sh} $ 和$ b_{\rm sh} $ ,见表4。根据式(4),表5给出了式(19)在不同区域的方均根偏差$ \sigma $ 。区域 系数 A为偶数 A为奇数 $ 1 \leqslant Z< 28 $, $ 1 \leqslant N< 28 $ $ a_{\rm sh} $ 66.720 00 89.100 00 $ b_{\rm sh} $ −1.397 00 −3.850 00 $ 1 \leqslant Z< 28 $, $ 28 \leqslant N< 50 $ 或
$ 28 \leqslant Z< 50 $, $ 1 \leqslant N< 28 $$ a_{\rm sh} $ −15.040 00 −30.600 00 $ b_{\rm sh} $ −0.433 40 0.798 80 $ 28 \leqslant Z< 50 $, $ 28 \leqslant N< 50 $ $ a_{\rm sh} $ 162.300 00 −162.300 00 $ b_{\rm sh} $ −0.710 00 0.796 50 $ 28 \leqslant Z< 50 $, $ 50 \leqslant N< 82 $ 或
$ 50 \leqslant Z< 82 $, $ 28 \leqslant N< 50 $$ a_{\rm sh} $ 75.600 00 40.010 00 $ b_{\rm sh} $ −0.271 90 −0.112 60 $ 50 \leqslant Z< 82 $, $ 50 \leqslant N< 82 $ 或
$ 28 \leqslant Z< 50 $, $ 82 \leqslant N< 126 $$ a_{\rm sh} $ 88.680 00 −62.640 00 $ b_{\rm sh} $ −0.231 00 0.095 20 $ 50 \leqslant Z< 82 $, $ 82 \leqslant N< 126 $ 或
$ 82 \leqslant Z< 126 $, $ 50 \leqslant N< 82 $$ a_{\rm sh} $ 67.990 00 89.170 00 $ b_{\rm sh} $ −0.125 70 −0.236 08 $ 82 \leqslant Z< 126 $, $ 82 \leqslant N< 126 $ 或
$ 50 \leqslant Z< 82 $, $ 126 \leqslant N< 184 $$ a_{\rm sh} $ −5.672 00 10.030 00 $ b_{\rm sh} $ −0.089 87 −0.013 18 $ 82 \leqslant Z< 126 $, $ 126 \leqslant N< 184 $ $ a_{\rm sh} $ 40.280 00 −10.180 00 $ b_{\rm sh} $ −0.142 70 0.041 01 注:壳修正形式[48-49] 见式 (20)。第 3 列和第 4 列分别对应 A 为偶数和奇数时的拟合结果。 区域 $ \delta V_{1 {\rm n}-1 {\rm p}} $的$ \sigma $ $ \delta V_{2 {\rm n}-1 {\rm p}} $的$ \sigma $ $ \delta V_{1 {\rm n}-2 {\rm p}} $的$ \sigma $ $ A \geqslant 16 $ 177 214 221 $ A \geqslant 60 $ 134 147 158 $ A \geqslant 120 $ 114 126 137 将式(15)中的
$ \delta V_{i {\rm n}-j {\rm p}} $ 替换为式(19)中的$ \delta V^{\rm th}_{i {\rm n}-j {\rm p}} $ ,若已知式(15)中任意3个原子核的结合能,则可计算出剩下第4个原子核的结合能。因此对于给定的第i个原子核,根据它与其它已知结合能原子核不同的相对位置,每个$ \delta V_{i {\rm n}-j {\rm p}} $ 关系式最多有4 种关于$ B_i $ 的计算结果,取所有可能计算结果的平均值作为该原子核结合能的理论值$ B^{\rm th}_i $ ,则根据式(5)计算的$ \delta V_{i {\rm n}-j {\rm p}} $ 关系描述不同区域结合能实验数据的方均根偏差$ \overline{\sigma} $ 在表 6中给出,其中n是计算$ B^{\rm th}_i $ 时所有可能计算结果的个数。相比GK关系,式(15)的精度更高,且只涉及四个相邻原子核的结合能,这对提高外推预言结合能的理论精度是非常重要的。公式中涉及的原子核个数越少,外推迭代预言结合能的不确定度越小。区域 $ \overline{\sigma} $ $ n \geqslant 1 $ $ n \geqslant 4 $ $ n \geqslant 7 $ $ n \geqslant 8 $ $ n \geqslant 12 $ $ A \geqslant 16 $ 119 110 93 89 82 $ A \geqslant 60 $ 80 71 69 68 68 $ A \geqslant 120 $ 65 62 59 59 59 注:n为计算一个原子核结合能时所有可能计算结果的个数。 文献[127]进一步研究了
$ 104 \leqslant N \leqslant 126 $ 、$ 83 \leqslant Z \leqslant 93 $ 区域$ \delta V_{i {\rm n}-j {\rm p}} $ 关系[$ (i, j) $ =(1, 1), (2, 1), (1, 2)]的理论计算值$ \delta V_{i {\rm n}-j {\rm p}}^{\rm cal} $ 与实验值$ \delta V_{i {\rm n}-j {\rm p}}^{\rm exp} $ 的偏差,即由于
$ \delta V_{2{\rm n}-1 {\rm p}} $ 和$ \delta V_{1{\rm n}-2 {\rm p}} $ 在该区域关于A的变化趋势与$ \delta V_{1{\rm n}-1 {\rm p}} $ 基本相同[没有图4(a)中$ \delta V_{1{\rm n}-1 {\rm p}} $ 表现出的奇偶效应],因此式(21)中的$ \delta V_{i {\rm n}-j {\rm p}}^{\rm cal}(N, Z) $ 可以简单地表示为其中a和C为拟合系数(A为偶数和奇数的
$ \delta V_{1{\rm n}-1 {\rm p}} $ 需分开拟合)[127]。数值实验表明,偏差$ \varDelta V_{i {\rm n}-j {\rm p}}(N, Z) $ 与$\varDelta V_{i {\rm n}-j {\rm p}} (N-2, Z-2)$ 之间有近似的线性关系。假设$ \varDelta V_{i {\rm n}-j {\rm p}}(N, Z)= \lambda \varDelta V_{i {\rm n}-j {\rm p}}(N-2, Z-2) $ ,其中$ \lambda $ 为线性拟合系数,并令最终的理论计算值为则
$ \delta V_{i {\rm n}-j {\rm p}} $ 关系在该区域的方均根偏差$ \sigma $ [见式(4)] 有明显降低(~50%),仅有~30 keV[127]。 -
根据原子核最后两个中子和最后两个质子之间的中子-质子相互作用
$ \delta V_{\rm 2n-2p} $ ,平均每个中子和每个质子之间的相互作用$ \delta V_{\rm np}(N, Z) $ 可以经验地表示为$ \delta V_{\rm 2n-2p}(N+1, Z+1)/ 4 $ [123, 129]。通过对所有价核子的$ \delta V_{\rm np} $ 求和,可得价核子间总的中子-质子相互作用(标记为$ V_{\rm np} $ )[123, 130]为其中
$ N_0 $ 和$ Z_0 $ 分别为距离N和Z最近的幻数,中子(质子)为粒子型和空穴型时$ \delta_{\rm n} $ ($ \delta_{\rm p} $ )分别等于+1和−1,根据文献[123],在
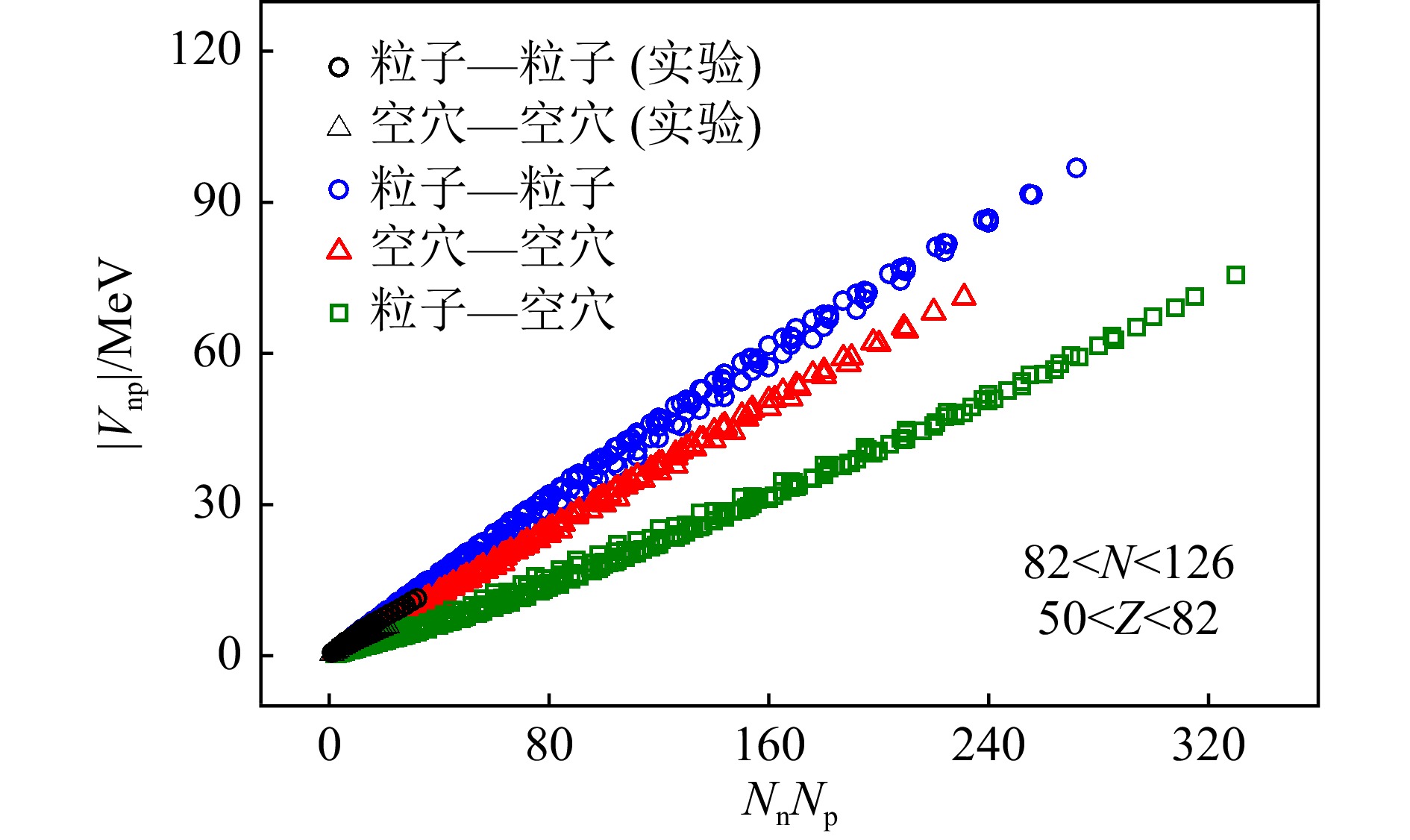
$ A \sim 100 $ 和$ 130 $ 区域绝对值$ |V_{\rm np}| $ 与价中子数和价质子数的乘积$ N_{\rm n}N_{\rm p} $ 之间有明显的线性关系。文献[128, 130]进一步在
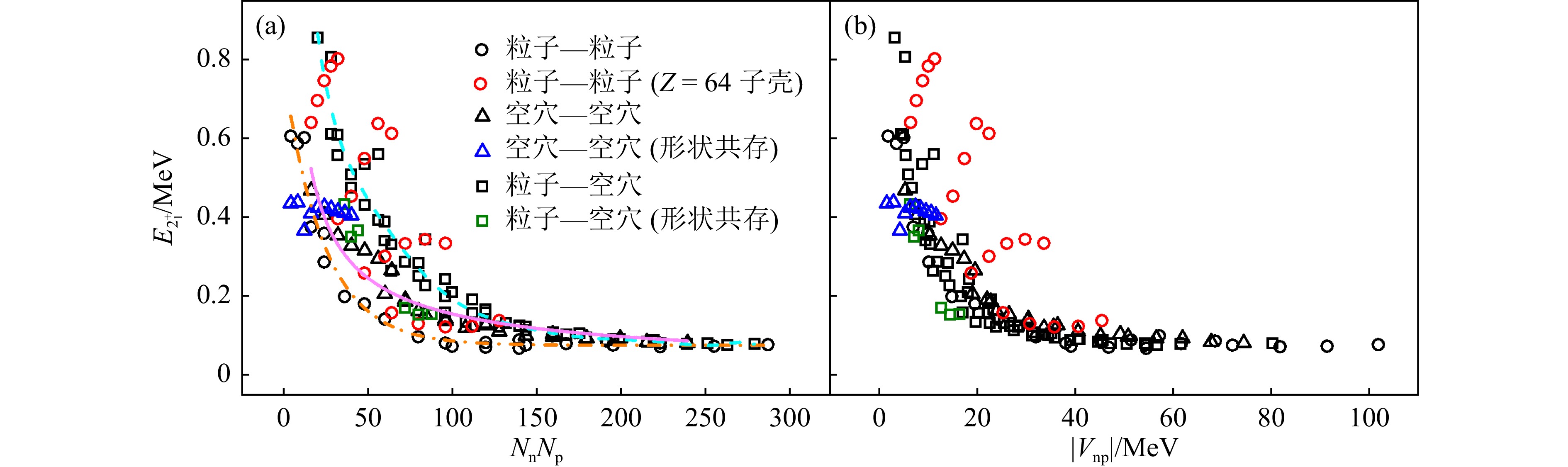
$ N_{\rm n}N_{\rm p} $ 的框架下研究了原子核集体运动演化与$ |V_{\rm np}| $ 的关联。以$ 82 < N < 126 $ 、$ 50 < Z < 82 $ 区域为例,图5给出了根据式(24)计算的$ |V_{\rm np}| $ 与$ N_{\rm n}N_{\rm p} $ 的关系图,其中圆形(三角形)对应价中子和价质子都是粒子型(空穴型)的情况,标记为“粒子-粒子”(“空穴-空穴”);正方形对应价中子为粒子型、价质子为空穴型的情况,标记为“粒子-空穴”。图5中黑色数据点表示用结合能实验值计算的$ |V_{\rm np}| $ ,彩色数据点则表示计算中包含了利用$ \delta V_{i {\rm n}-j {\rm p}} $ 关系 [见2.1节式(15)和(19)][49]基于AME2020数据表[3]外推得到的结合能预言值。可以看到,在考虑外推预言结果的情况下,$ |V_{\rm np}| $ 与$ N_{\rm n}N_{\rm p} $ 依然保持非常好的线性关系,并且这种线性关系的斜率对三种不同类型的原子核有明显差别,“粒子-粒子”型斜率最大,“空穴-空穴”型次之,“粒子-空穴”型最小。这种$ |V_{\rm np}| $ 与$ N_{\rm n}N_{\rm p} $ 线性关系斜率的变化,说明原子核集体演化对于同一主壳层内粒子型和空穴型的价空间会有所不同[128]。这种与价空间类型相关的差别也体现在
$ E_{2^+_1} $ (第一个2+态的激发能)、$ E_{4^+_1} $ (第一个4+态的激发能)和它们的比值$ R_{4/2} $ 与$ N_{\rm n}N_{\rm p} $ 的关系[131]中。以$ 82 < N < 126 $ 、$ 50 < Z < 82 $ 区域的$ E_{2^+_1} $ 为例,图6(a)和(b)分别给出了$ E_{2^+_1} $ 的实验值[4]与$ N_{\rm n}N_{\rm p} $ 和$ |V_{\rm np}| $ [见式(24),计算涉及结合能的实验值和外推预言值] 的关系图,其中圆形、三角形和正方形分别对应“粒子-粒子”、“空穴-空穴”和“粒子-空穴”型的原子核,它们在图(a)中的变化趋势分别用橙色点划线、粉色实线和青色虚线表示。从图6(a)可以看出,除了受原子核结构演化影响的彩色异常点之外,$ E_{2^+_1} $ 表现出关于$ N_{\rm n}N_{\rm p} $ 的系统性;随着$ N_{\rm n}N_{\rm p} $ 的增加,$ E_{2^+_1} $ 的演化速率对粒子型和空穴型的价空间有所差别,“粒子-粒子”型原子核的$ E_{2^+_1} $ 下降得最快,其次是“空穴-空穴”型,“粒子-空穴”型最慢,这与图5中的结果一致。有意思的是,由于横坐标$ |V_{\rm np}| $ 合理地考虑了中子-质子相互作用的强度,因此图6(b)中不同价空间类型原子核$ E_{2^+_1} $ 的演化趋势(不含彩色异常点)基本一致[128]。需要明确的是,这里用于计算
$ |V_{\rm np}| $ 的结合能外推预言值的不确定度<1 MeV[49],而$ |V_{\rm np}| $ 最大可达$ \sim 100 $ MeV(见图5),因此即使采用其它理论模型预言的结合能,图5中$ |V_{\rm np}| $ 与$ N_{\rm n} N_{\rm p} $ 以及图6(b)中$ E_{2_1^+} $ 与$ |V_{\rm np}| $ 之间的系统规律依然成立[128]。 -
定义原子核某一物理量F的局域双重差分为
其中
$ i, j = 1, 2 $ 。当F为原子核结合能B时,式(26)即为2.1节讨论的$ \delta V_{i {\rm n}-j {\rm p}} $ 关系 [见式(15)]。这种局域双重差分不仅能用于计算结合能,也能用于计算原子核的其它物理量[132-134],如$ \alpha $ 衰变能[66](见第3.2节)、分离能[135](见第3.3节)和电荷半径[72-73](见第8.1节)等,这些都是局域相干性差分法的应用实例。文献[132]指出,Casten经验公式[120-122]实际上是的特殊情况,满足Casten经验公式的物理量[如
$ B(\rm{E2}) $ 和$ E_{2^+_1} $ ][120-122, 136-139]都满足式(27),但满足式(27)的物理量不一定满足Casten经验公式(如$ \alpha $ 衰变能和分离能)。文献[133]进一步讨论了式(27)与Casten经验公式之间的联系。在局部区域内,可将式(26)中的N和Z分别替换为
$ N_{\rm n} $ 和$ N_{\rm p} $ 。假设物理量F是$ N_{\rm n} $ 和$ N_{\rm p} $ 的函数,则将式(26)中的F泰勒展开到二阶项并代入式(27),可得上式的通解为
其中
$ f_{\rm n} $ 和$ f_{\rm p} $ 分别是关于$ N_{\rm n} $ 和$ N_{\rm p} $ 的任意函数。式(29)说明,任何满足式(27)的物理量在局部区域内都可以写为中子部分贡献和质子部分贡献之和。如果F是关于
$ N_{\rm n} N_{\rm p} $ 的光滑函数,则式(28)可以改写为该方程的解为
其中
$ c_1 $ 和$ c_2 $ 为任意常数。显然式(31)是式(29)的特殊情况,即$ f_{\rm n} $ 和$ f_{\rm p} $ 分别为$ N_{\rm n} $ 和$ N_{\rm p} $ 的等系数对数函数。系数相等说明质子和中子对F演化规律的贡献是一致的,这也是核力电荷无关性的体现[133]。在上述这种情况下,满足式(27)的物理量同时也满足Casten经验公式(即物理量表现出关于$ N_{\rm n} N_{\rm p} $ 的系统性),因此Casten经验公式可视为局域双重差分为零的特殊情况。另一方面,同时满足Casten 经验公式和式(27)的物理量,必然满足式(31),这在一定程度上给出了Casten 经验公式的普适解析形式,说明了$ N_{\rm n} N_{\rm p} $ 数值演化规律的鲁棒性[133]。 -
根据式(1)~(3)和式(15),GKL和GKT可以用
$ \delta V_{1 {\rm n}-1 {\rm p}} $ 改写为根据式(32),相邻原子核
$ \delta V_{1{\rm n}-1{\rm p}} $ 之间的差异会导致GK关系展现出规律性特征。本节讨论的内容正是基于$ \delta V_{1{\rm n}-1{\rm p}} $ 的差异所导致的GK关系的奇偶性[108, 140-141],以及通过抵消这种奇偶性构造出的原子核$ \alpha $ 衰变能的局域关系[66],同时本节回顾联合衰变能、分离能的局域双重差分和GK关系的外推方法[135]。 -
文献[108, 140-141]观察到GK关系中存在一些有趣的奇偶现象。根据中子和质子的奇偶性,可将图1中GK关系的参考核
$ (N, Z) $ 分为偶偶核(N和Z都为偶数,标记为“ee”)、偶奇核(N为偶数,Z为奇数,标记为“eo”)、奇偶核(N为奇数,Z为偶数,标记为“oe”)和奇奇核(N和Z都为奇数,标记为“oo”)四种情况。根据式(2)和(3),
$ A \geqslant 16 $ 时对上述四种奇偶情况$ D_{\rm L} $ 和$ D_{\rm T} $ 的平均值分别为$ \overline{D}_{\rm L}({\rm ee})= -41 $ keV、$ \overline{D}_{\rm L}({\rm eo})= -54 $ keV、$ \overline{D}_{\rm L}({\rm oe})= 42 $ keV、$ \overline{D}_{\rm L}({\rm oo})= 20 $ keV和$\overline{D}_{\rm T}({\rm ee})= 39$ keV、$ \overline{D}_{\rm T}({\rm eo})= 28 $ keV、$ \overline{D}_{\rm T}({\rm oe})= -26 $ keV、$ \overline{D}_{\rm T}({\rm oo})= -65 $ keV。由此可见,GKL和GKT相对于零的偏离$ D_{\rm L} $ 和$ D_{\rm T} $ 不是完全随机的,它们的平均值$ \overline{D}_{\rm L} $ 和$ \overline{D}_{\rm T} $ 对不同奇偶类型的参考核有明显差别[140]。$ \overline{D}_{\rm L} $ 和$ \overline{D}_{\rm T} $ 的这种奇偶性与对能有关[140]。结合式(2)~(3)和式(17)给出的对能形式,并取$ a_{\rm p} = 5.44 $ MeV[24],可得$ A \geqslant 16 $ 时对偶偶核、偶奇核、奇偶核、奇奇核这四种情况$ \overline{D}_{\rm L} $ 和$ \overline{D}_{\rm T} $ 中对能的贡献分别为−27, −47, 59, 15 keV和77, −6, −45, −31 keV。这些结果与上述四种奇偶类型的$ \overline{D}_{\rm L} $ 和$ \overline{D}_{\rm T} $ 实验值的正负号基本一致 [除了$ \overline{D}_{\rm T}({\rm eo}) $ ],数值上较为接近,因此式(17)的对能形式可以定性地解释GK关系相对于零的偏离[140]。文献[108]进一步讨论了GK关系的这种奇偶性。由上述计算结果可知,
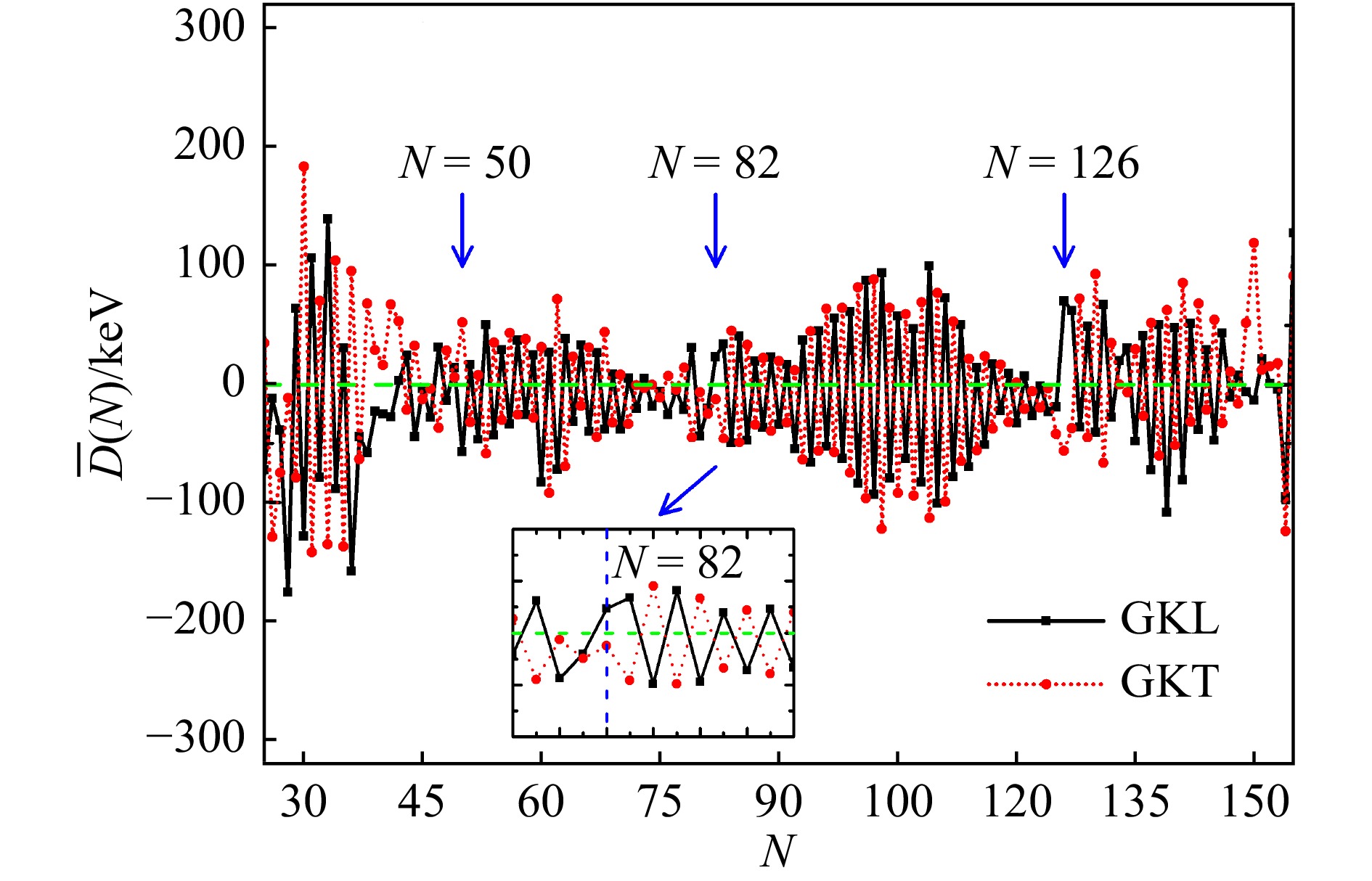
$ \overline{D}_{\rm L} $ 和$ \overline{D}_{\rm T} $ 的正负与中子数N有关,N为偶数时$ \overline{D}_{\rm L} $ 为负,N为奇数时$ \overline{D}_{\rm L} $ 为正;$ \overline{D}_{\rm T} $ 与$ \overline{D}_{\rm L} $ 相反,N为偶数时为正,N为奇数时为负。图7给出了$ D_{\rm L} $ 和$ D_{\rm T} $ 关于N的平均值 [分别标记为$ \overline{D}_{\rm L}(N) $ 和$ \overline{D}_{\rm T}(N) $ ],其中黑色实线和红色点线分别对应GKL和GKT,绿色虚线标记纵轴为零的位置。从图7可以看到,$ \overline{D}_{\rm L}(N) $ 和$ \overline{D}_{\rm T}(N) $ 在零附近随着N的变化表现出奇偶振荡现象,且$ \overline{D}_{\rm L}(N) $ 和$ \overline{D}_{\rm T}(N) $ 的正负号基本相反[108]。图7中还标记了N为幻数的位置,在幻数附近$ \overline{D}_{\rm L}(N) $ 和$ \overline{D}_{\rm T}(N) $ 的正负表现出异常(见$ N=82 $ 附近局部放大图)[108]。图7中GK关系的这种奇偶振荡现象与
$ \delta V_{1 {\rm n}-1 {\rm p}} $ 的奇偶性有关[108]。图8给出了在不同奇偶情况下$ \delta V_{1 {\rm n}-1 {\rm p}} $ 关于中子数N的平均值 [标记为$ \overline{\delta V}_{1 {\rm n}-1 {\rm p}}(N) $ ],其中黑色正方形、红色圆形、蓝色上三角和绿色下三角分别对应偶偶核、偶奇核、奇偶核和奇奇核。图8中$ \overline{\delta V}_{1 {\rm n}-1 {\rm p}}(N) $ 存在两种奇偶性:一是A为偶数的$ \overline{\delta V}_{1 {\rm n}-1 {\rm p}}(N) $ 明显大于A为奇数的$ \overline{\delta V}_{1 {\rm n}-1 {\rm p}}(N) $ ;二是$ N \leqslant 132 $ 时偶偶核的$ \overline{\delta V}_{1 {\rm n}-1 {\rm p}}(N) $ 略大于其相邻奇奇核的$ \overline{\delta V}_{1 {\rm n}-1 {\rm p}}(N) $ ,偶奇核的$ \overline{\delta V}_{1 {\rm n}-1 {\rm p}}(N) $ 略大于其相邻奇偶核的$ \overline{\delta V}_{1 {\rm n}-1 {\rm p}}(N) $ 。因此根据式(32),偶偶核和偶奇核这两种N为偶数时的$ \overline{D}_{\rm L}(N) $ 应为负,奇偶核和奇奇核这两种N为奇数时的$ \overline{D}_{\rm L}(N) $ 应为正;$ \overline{D}_{\rm T}(N) $ 与$ \overline{D}_{\rm L}(N) $ 相反,N为偶数时应为正,N为奇数时应为负[108]。这一结果与图7中反映出的GK关系的奇偶振荡现象基本一致。GK关系的奇偶性在描述质量实验数据的方均根偏差中也有所体现[141]。依次将图1中GKL(GKT)的位置(1)~(6)作为参考核
$ (N, Z) $ ,相应的等式分别标记为$ R_1 $ ~$ R_6 $ ($ R_7 $ ~$ R_{12} $ )。如果GK关系的偏差平均为0且是随机的,那么由更多等式平均给出的质量理论值$ M^{\rm th} $ 应该更接近实验值[142, 143]。表2中的数据似乎也证实了这一说法,相比单独使用GKL或GKT时的方均根偏差$ \overline{\sigma} $ ,同时使用GKL和GKT这两个关系式计算给出的$ M^{\rm th} $ 与实验值之间的$ \overline{\sigma} $ 更小。若只考虑$ M^{\rm th} $ 由GKL和GKT全部12个等式计算结果的平均值给出的情况,对$ A \geqslant 16 $ 、$ A \geqslant 60 $ 和$ A \geqslant 120 $ 的原子核,其$ \overline{\sigma} $ [见式(5)] 分别为86、77和67 keV,相比表2中第6列“GK”的$ \overline{\sigma} $ 又有所降低。但是由于GK关系中奇偶效应的存在,这12个等式$ R_i(i = 1, 2, \cdots, 12) $ 之间有很强的相关性,因此由全部12个等式平均给出的$ M^{\rm th} $ 与实验值之间的$ \overline{\sigma} $ 并不是最小的[141]。以等式个数
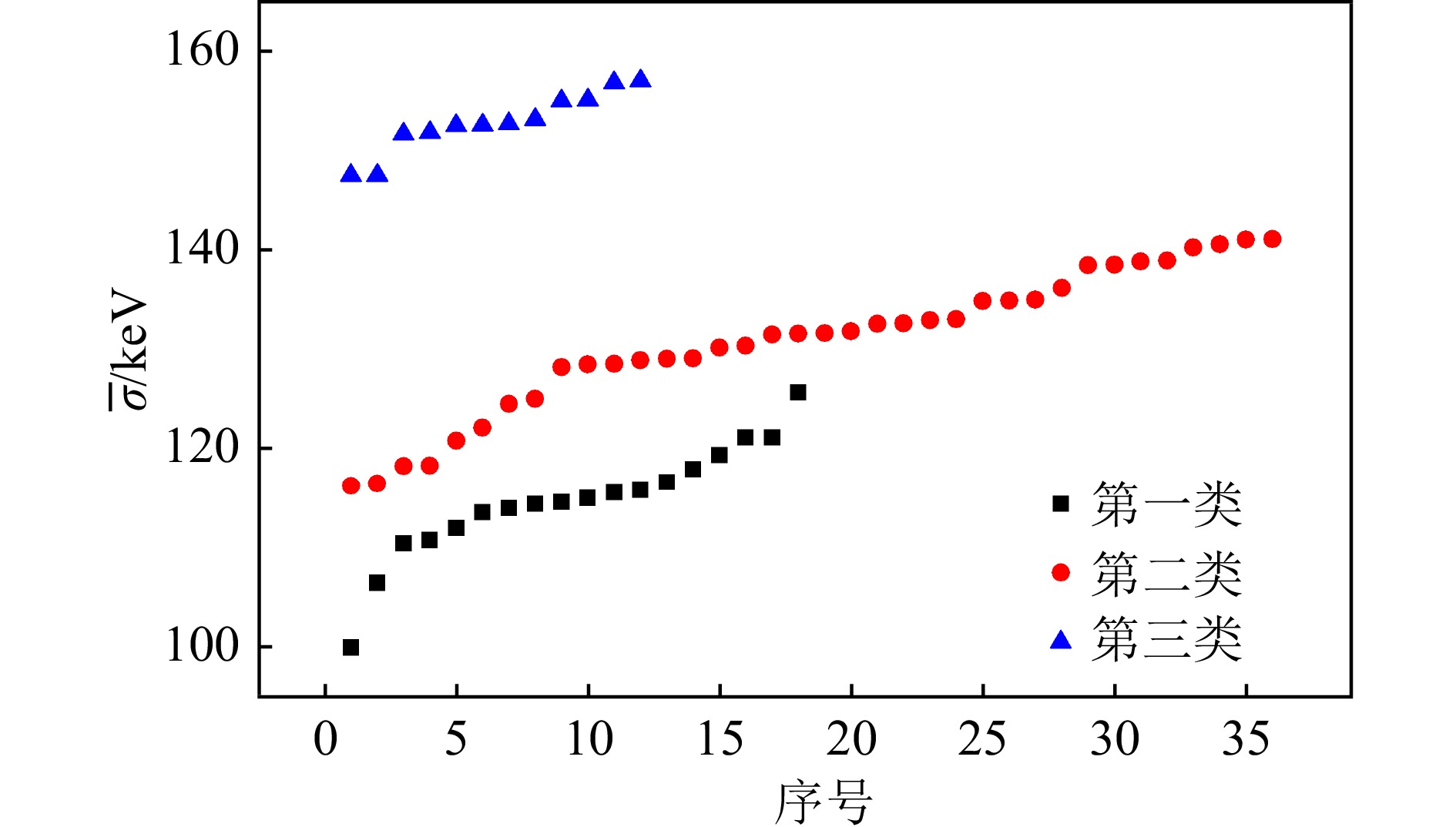
$ n=2 $ 的情况为例。从上述12个等式$ R_i $ 中任意选取2个计算质量,共有$ C^2_{12}=66 $ 种组合方式。按照奇偶性,可以将这些组合分为三类[141]。根据式(32),如果这2个等式中一个等式相对于零的偏离$ D_i = \delta V_{1 {\rm n}-1 {\rm p}}({\rm ee})- \delta V_{1 {\rm n}-1 {\rm p}}({\rm oo}) $ 、另一个等式的偏离$D_{i'} = \delta V_{1 {\rm n}-1 {\rm p}}({\rm oo})- \delta V_{1 {\rm n}-1 {\rm p}}({\rm ee})$ ($ i, i' = 1, 2, \cdots, 12 $ ),或者$D_i = \delta V_{1 {\rm n}-1 {\rm p}}({\rm eo})- \delta V_{1 {\rm n}-1 {\rm p}}({\rm oe})$ 、$ D_{i'} = \delta V_{1 {\rm n}-1 {\rm p}}({\rm oe})- \delta V_{1 {\rm n}-1 {\rm p}}({\rm eo}) $ ,则该组合为第一类。利用这类组合给出的$ M^{\rm th} $ 与实验值的偏差为$ (D_i+D_{i'})/2 $ ,因此原本GK关系中因$ \delta V_{1 {\rm n}-1 {\rm p}} $ 的奇偶性造成的偏差[108]在这2个等式相加取平均后抵消,由此得到的$ M^{\rm th} $ 会更加精确。第三类组合与第一类相反,2个等式的偏离$ D_i $ 和$ D_{i'} $ 都属于$ \delta V_{1 {\rm n}-1 {\rm p}}({\rm ee})- \delta V_{1 {\rm n}-1 {\rm p}}({\rm oo}) $ 或者$ \delta V_{1 {\rm n}-1 {\rm p}}({\rm eo})- \delta V_{1 {\rm n}-1 {\rm p}}({\rm oe}) $ ,则相加之后奇偶性叠加,由此得到的$ M^{\rm th} $ 与实验值的方均根偏差$ \overline{\sigma} $ 会更大。第二类组合为介于第一类和第三类之间的其它情况,即奇偶性没有完全抵消也没有完全叠加,相应的$ \overline{\sigma} $ 也基本介于第一类和第三类的$ \overline{\sigma} $ 之间。图9给出了
$ n=2 $ 时GK关系的66种组合方式描述$ A \geqslant 60 $ 区域质量实验数据的方均根偏差$ \overline{\sigma} $ [见式(5)],其中黑色正方形、红色圆形和蓝色三角形分别对应上述的第一类、第二类和第三类组合(每一类中的组合按$ \overline{\sigma} $ 从小到大排序)。图9中18种第一类组合的$ \overline{\sigma} $ 都比较小,其中最小的是组合$(R_1, R_6)$ ,它们描述1 534个质量实验数据的$ \overline{\sigma} $ 为100 keV;12种第三类组合的$ \overline{\sigma} $ (148 keV~157 keV)明显大于第一类和第二类组合的$ \overline{\sigma} $ ;36种第二类组合的$ \overline{\sigma} $ 基本介于第一类和第三类组合的$ \overline{\sigma} $ 之间[141]。表7列出了
$ n = 1, 2, \cdots, 12 $ 时描述$ A \geqslant 60 $ 区域质量实验数据精度最高的等式组合,以及相应的方均根偏差$ \overline{\sigma} $ [见式(5)] 和描述质量实验数据的个数$ \mathcal{N} $ 。表7中$ \overline{\sigma} $ 最小的是$ n = 8 $ 的组合,这8个等式可以分为4组,即($ R_1 $ ,$ R_6 $ )、($ R_2 $ ,$ R_5 $ )、($ R_7 $ ,$ R_{12} $ )和($ R_8 $ ,$ R_{11} $ ),每一组都是上述讨论的$ n=2 $ 时的第一类组合。类似地,表7中所有n为偶数时的最优组合都可以分为$ n/2 $ 组第一类组合。这说明通过抵消奇偶性可以有效降低GK关系描述质量实验数据的方均根偏差[141]。此外表7中$ n = 4 $ ~11时最优组合的$ \overline{\sigma} $ 都小于或等于$ n = 12 $ 时的$ \overline{\sigma} $ ,这表明在GK关系的应用中利用一些n比较小的组合可以得到更精确的质量计算结果[141]。n 组合$ \alpha $ $ \overline{\sigma} $ $ \mathcal{N} $ 1 $ R_3 $ 173 1 690 2 $ R_1 $, $ R_6 $ 100 1 534 3 $ R_2 $, $ R_7 $, $ R_{12} $ 90 1 395 4 $ R_2 $, $ R_5 $, $ R_7 $, $ R_{12} $ 75 1 350 5 $ R_2 $, $ R_5 $, $ R_6 $, $ R_7 $, $ R_{12} $ 77 1 347 6 $ R_1 $, $ R_2 $, $ R_5 $, $ R_6 $, $ R_7 $, $ R_{12} $ 72 1 346 7 $ R_1 $, $ R_2 $, $ R_5 $, $ R_6 $, $ R_7 $, $ R_8 $, $ R_{12} $ 73 1 310 8 $ R_1 $, $ R_2 $, $ R_5 $, $ R_6 $, $ R_7 $, $ R_8 $, $ R_{11} $, $ R_{12} $ 70 1 277 9 $ R_1 $, $ R_2 $, $ R_4 $, $ R_5 $, $ R_6 $, $ R_7 $, $ R_8 $, $ R_{11} $, $ R_{12} $ 73 1 276 10 $ R_1 $, $ R_2 $, $ R_3 $, $ R_4 $, $ R_5 $, $ R_6 $, $ R_7 $, $ R_8 $, $ R_{11} $, $ R_{12} $ 73 1 272 11 $ R_1 $, $ R_2 $, $ R_3 $, $ R_4 $, $ R_5 $, $ R_6 $, $ R_7 $, $ R_8 $, $ R_9 $, $ R_{11} $, $ R_{12} $ 76 1 225 12 $ R_1 $, $ R_2 $, $ R_3 $, $ R_4 $, $ R_5 $, $ R_6 $, $ R_7 $, $ R_8 $, $ R_9 $, $ R_{10} $, $ R_{11} $, $ R_{12} $ 77 1 178 注:最后一列为该最优组合描述质量实验数据的个数$ \mathcal{N} 。$ 综上所述,GK关系相对于零的偏离不完全随机(与对能有关),而是存在与
$ \delta V_{1 {\rm n}-1 {\rm p}} $ 相关联的奇偶性,并且通过抵消这种奇偶性可以有效降低GK关系描述质量实验数据的方均根偏差。 -
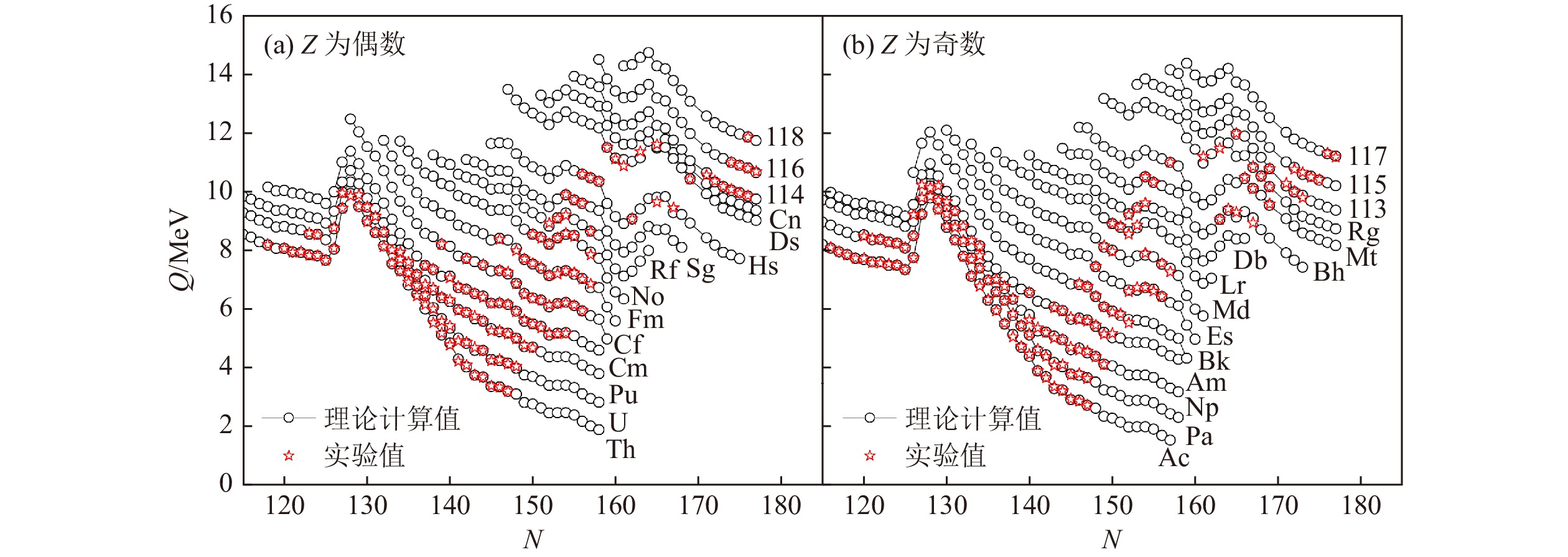
$ \alpha $ 衰变能局域关系式的构造[66]是GK关系奇偶性[108, 141]的一个重要应用。作为重核和超重核区域不稳定核最重要的衰变方式之一,$ \alpha $ 衰变在原子核结构及超重元素的研究中发挥着重要作用[144-147]。$ \alpha $ 衰变能是预言重核寿命的关键参量,其数值在极大程度上影响着半衰期[148-154]计算。中子数为N、质子数为Z的原子核$ \alpha $ 衰变能$Q_{\alpha}(N, Z)$ 的定义为根据式(33),
$ \alpha $ 衰变能可以由结合能实验值或各理论模型给出的结合能预言值计算得到[7, 49, 148-158]。此外也有一些直接研究$ \alpha $ 衰变能的全局型半经验公式[41-43] 和局域型[66]、区域型理论(如基于邻近$ \alpha $ 衰变能之间关联的预言方法[64-65]、$ \alpha $ 衰变能与价核子数的线性关系[67]等)。文献[66]通过抵消3.1节中讨论的GK关系的奇偶性[108]构造了
$ \alpha $ 衰变能的局域关系式,由其给出的$ \alpha $ 衰变能预言值与近期一些实验测量结果[159-161]吻合得很好。由式(32)给出的GKL与$ \delta V_{1 {\rm n}-1 {\rm p}} $ 的关系可知,$ D_{\rm L}({\rm ee})= \delta V_{1 {\rm n} - 1 {\rm p}}({\rm oo})- \delta V_{1 {\rm n} - 1 {\rm p}}({\rm ee}) $ 、$D_{\rm L}({\rm oo})= \delta V_{1 {\rm n} - 1 {\rm p}}({\rm ee})- \delta V_{1 {\rm n} - 1 {\rm p}}({\rm oo})$ ,因此$ D_{\rm L}({\rm ee})\approx -D_{\rm L}({\rm oo}) $ 。类似地,可得$ D_{\rm L}({\rm eo})\approx -D_{\rm L}({\rm oe}) $ 。由此可见,相邻不同奇偶类型$ D_{\rm L} $ 的数值大小基本相同,但正负号有所区别。因此通过对相邻两个不同奇偶性的GKL求和,即可以抵消GK关系中的奇偶效应[66]。
将式(2)的GKL代入上式,并结合式(33)给出的
$ \alpha $ 衰变能的定义以及式(1)给出的结合能与质量的关系,可得[66]这是一种局域相干性差分法。由于GK关系奇偶效应的抵消,
$ \delta Q_{\rm 1n-1p} $ 具有很高的精度。此外,类比式(16)将式(35)重复应用于相邻原子核,可得[66]表8 给出了式(35)~(37)的方均根偏差
$ \sigma $ [见式(4)]。这里$ A < 270 $ 的原子核$ \alpha $ 衰变能的实验数据由式(33)给出,其中结合能实验值取自AME2020数据表[3];$ A \geqslant 270 $ 的原子核$ \alpha $ 衰变能的实验数据来自文献[3]中的表III。若已知式(35)[或式(36)、(37)] 中所涉及任意3个原子核的$ \alpha $ 衰变能,则可计算出剩下第4个原子核的$ \alpha $ 衰变能。因此对于给定的第i个原子核,根据它与其它已知$ \alpha $ 衰变能原子核不同的相对位置,式(35)[或式(36)、(37)] 最多有4种关于$Q_{\alpha, i}$ 的计算结果,取所有计算结果的平均值作为该原子核$ \alpha $ 衰变能的理论值$Q^{\rm th}_{\alpha, i}$ ,则根据式(5)计算的描述不同区域$ \alpha $ 衰变能实验数据的方均根偏差$ \overline{\sigma} $ 也在表8中给出。表8最后一列“组合”为同时使用式(35)~(37)计算$ \alpha $ 衰变能时的结果,在这种情况下$ Q^{\rm th}_{\alpha, i} $ 最多由12种计算结果的平均值给出。由表8可知,$ \delta Q_{i {\rm n}-j {\rm p}} $ 关系 [$ (i, j) $ =(1, 1), (2, 1), (1, 2)] 的精度很高,尤其是$ \delta Q_{\rm 1n-1p} $ ,它在超重核区的$ \overline{\sigma} $ 只有47 keV;同时使用式(35)~(37)能有效提高$Q^{\rm th}_{\alpha}$ 的精度,对$ A \geqslant 200 $ 的原子核,其描述$ \alpha $ 衰变能实验数据的$ \overline{\sigma} $ 只有73 keV。区域 $ \delta Q_{\rm 1n-1p} $ $ \delta Q_{\rm 2n-1p} $ $ \delta Q_{\rm 1n-2p} $ 组合 $ \sigma $ $ \overline{\sigma} $ $ \sigma $ $ \overline{\sigma} $ $ \sigma $ $ \overline{\sigma} $ $ \sigma $ $ \overline{\sigma} $ $ A \geqslant 280 $ 54 47 59 55 64 70 -- 44 $ A \geqslant 200 $ 119 80 145 82 157 109 -- 73 注:最后一列“组合”为同时使用式(35)~(37) 计算$ \alpha $衰变能时的$ \overline{\sigma} 。$ -
文献[135]将式(27)局域双重差分为零的等式分别应用于双中子分离能
$ S_{\rm 2n} $ 、双质子分离能$ S_{\rm 2p} $ 、$ \alpha $ 衰变能$Q_{\alpha}$ 和双β衰变能$Q_{2 \beta}$ ,同时结合GK关系,给出了一种新的结合能外推方法。这里中子数为N、质子数为Z的原子核k中子分离能$ S_{k \rm n}(N, Z) $ 、k质子分离能$ S_{k \rm p}(N, Z) $ 和双β衰变能$Q_{2 \beta}(N, Z)$ 的定义分别为根据式(26),分别将
$ i=j=1 $ 时$ S_{2 \rm n} $ 、$ S_{2 \rm p} $ 和$Q_{2 \beta}$ 的局域双重差分代入式(27),可得[135]$Q_{\alpha}$ 的定义和$ \delta Q_{\rm 1n-1p} $ 关系[66]分别由式(33)和(35)给出。根据式(33)和式(38)~(39)给出的
$Q_{\alpha}$ 和$ S_{\rm 2n} $ 、$ S_{\rm 2p} $ 的定义以及式(1)给出的结合能与质量的关系,式(2)的GKL可以改写为同理,根据式(1)和式(38)~(40)给出的
$ S_{\rm 2n} $ 、$ S_{\rm 2p} $ 、$Q_{2 \beta}$ 的定义,式(3)的GKT可以改写为类比3.2节中计算
$Q^{\rm th}_{\alpha}$ 的方式,根据式(35)和(41),可以得到最多由4种计算结果的平均值给出的$Q_{\alpha}$ 、$ S_{\rm 2n} $ 、$ S_{\rm 2p} $ 和$Q_{2 \beta}$ 的理论值,将它们代入式(42)~(47),若已知式中任一原子核的结合能,则可计算出另一个原子核的结合能[135]。因此给定一个原子核,式(42)~(47)最多有12种关于其结合能的计算结果,取所有计算结果的平均值作为该原子核结合能的理论值,相应的外推预言结果将在7.1节中讨论。 -
对称能和Wigner能的参量数值反映了原子核内核子之间强相互作用的特性,是原子核物理的基础性问题之一。受中子-质子相互作用系统性和局域质量关系的启发,文献[162-163]利用“实验”对称能的双重差分和1.2节中的GKs关系分别研究了对称能和Wigner 能。这些局域差分在很大程度上消除了多个唯象相互作用项所带来的不确定性,从而得到精确度很高的对称能系数和Wigner能系数。这是原子核基态局域系统规律研究的一个副产品。本节回顾上述从局域质量关系提取对称能系数和Wigner能系数的方法。
-
对称能是原子核物理和核天体物理领域的热点问题之一,在核反应的动力学演化、中子星结构等问题中起着重要作用[147, 164-174]。近年来有许多工作通过对不同理论模型的参数化处理来确定对称能项中的体对称能系数
$ c_2^{\rm(v)} $ 和面对称能系数$ c_2^{\rm(s)} $ (或它们的比值$ \kappa_{\rm s/v} = c_2^{\rm(s)} / c_2^{\rm(v)} $ )[20, 27, 162, 174-186]。本节讨论从中子-质子相互作用出发来确定对称能系数的方法[162],这种方法取得了很好的效果[187-194]。中子-质子相互作用随着质量数A相对平滑地变化(见图4),这说明相邻四个原子核结合能的双重差分能够抵消质量模型中一些具有很大不确定性的成分,尤其是壳修正项。图10给出了FRDM[21](黑色正方形)和WS4公式[27](红色圆形)中的壳修正项
$ E_{\rm sh} $ 和它们在$ \delta V_{2 {\rm n}-2 {\rm p}} $ [见式(15)]中的贡献$ \delta E_{\rm sh} $ 与N的变化关系。相比图10(a)中的$ E_{\rm sh} $ ,图10(b)中双重差分后的壳修正项$ \delta E_{\rm sh} $ 的不确定性大幅降低。另一方面,中子-质子相互作用和对称能紧密关联。计算表明,对于$ A \geqslant 100 $ 核素的$ \delta V_{2 {\rm n}-2 {\rm p}} $ 来说,在结合能Weizsäcker公式[17]的主导项中,体积能和对称能的贡献基本为零,库仑能、表面能和Wigner能的贡献很小(分别为$ \sim 100 $ keV、$ \sim 20 $ keV和$\sim -10$ keV),而对称能的贡献则高达$ \sim 1\,100$ keV,因此对称能的贡献在中子-质子相互作用中是关键性的主导部分。由于中子-质子相互作用具有很好的系统性,且与对称能紧密关联,因此可以被用于确定对称能的系数[162]。这种方法可分为三步:第一步是提取原子核对称能的“实验值”。根据修正的Bethe-Weizsäcker质量公式[24],将结合能实验值减去体积能
$ B_{\rm v} $ 、表面能$ B_{\rm s} $ 、库仑能$ E_{\rm c} $ 、对能$ V_{\rm p} $ 和Wigner能$ E_{\rm W} $ 贡献后的剩余部分标记为对称能的“实验值” [用$ e(N, Z) $ 表示][162],其形式为其中
$ \delta_{\rm np} $ 由式(18)给出,$ a_i $ 为拟合系数(数值取自文献[24]中表I的最后一列)。上式中Wigner能$ E_{\rm W} $ 的形式可以取[24]或[195]
其中
$ C_0 $ 和W为拟合系数。虽然这样得到的对称能“实验值”不是精确的,不过不失为一个合理的近似结果,作为核素图上很大区域系统研究的数据是合适的。第二步是计算上述对称能“实验值”
$ e(N, Z) $ 的双重差分[162],即图11为
$ \delta e_{i {\rm n}-j {\rm p}} /(ij) $ 与A的关系图,其中黑色虚线标记$ \delta e_{i {\rm n}-j {\rm p}} = 0 $ 的位置。图11(a)(c)中黑色正方形和红色圆形分别对应$ (i, j)=(1, 2) $ 和$ (2, 1) $ [$ (i, j)=(2, 3) $ 和$ (3, 2) $ ],图11(b)中黑色正方形对应$ (i, j)=(2, 2) $ 。从图11可以看到,$ \delta e_{i {\rm n}-j {\rm p}} /(ij) $ 与A有很好的相关性;与图4(b)~(c)中的$ \delta V_{i {\rm n}-j {\rm p}} $ 关系($ ij = 2 $ )类似,$ \delta e_{i {\rm n}-j {\rm p}} /(ij) $ 没有表现出明显的奇偶差别。由于对称能“实验值”的双重差分中很好地抵消了壳修正项,人们期望基于$ \delta e_{i {\rm n}-j {\rm p}} /(ij) $ 的系统规律提取出的体对称能系数$ c_2^{\rm(v)} $ 和面对称能系数$ c_2^{\rm(s)} $ 具有很高的精度。第三步是拟合"实验值"得到对称能系数
$ c_2^{\rm(v)} $ 和$ c_2^{\rm(s)} $ 。令$ e(N, Z)= a_{\rm sym} I^2 A = -(c_2^{\rm(v)} - c_2^{\rm(s)} A^{-1/3}) I^2 A $ [18, 196],则由式(51)可得[162]其中
根据第一步和第二步,由式(48)和式(51)计算
$ \delta e_{i {\rm n}-j {\rm p}} $ 作为其"实验值",并利用式(52)对它进行拟合,即可得对称能系数$ c_2^{\rm(v)} $ 和$ c_2^{\rm(s)} $ [162]。基于
$ A \geqslant 16 $ 核素的结合能实验值,表9列出了$ c_2^{\rm(v)} $ 和$ c_2^{\rm(s)} $ 的拟合结果以及它们的比值$ \kappa_{\rm s/v} $ ,其中第2~4列和第5~7列分别对应取式(49)和(50)作为式(48)中Wigner能$ E_{\rm W} $ 的形式,最后一行为同时拟合$ (i, j)=(1, 2) $ , (2, 1), (2, 2), (2, 3)和(3, 2)的$ \delta e_{i {\rm n}-j {\rm p}} $ 所得到的结果。表9中的最佳拟合结果为$ c_2^{\rm(v)} = (31.37 \pm 0.16 )$ MeV、$ c_2^{\rm(s)} = (51.88 \pm 0.56 )$ MeV、$\kappa_{\rm s/v} = 1.65 \pm 0.02$ 或$c_2^{\rm(v)} = (32.48 \pm 0.16)$ MeV、$ c_2^{\rm(s)} =( 59.93 \pm 0.53) $ MeV、$\kappa_{\rm s/v} = 1.85 \pm 0.02$ ,这些结果与原有数值相比不确定度大幅降低,且与FRDM[21]给出的体对称能系数$ c_2^{\rm(v)} = (32.5 \pm 0.5) $ MeV[188]和面对称能系数$ c_2^{\rm(s)} = 58.16 $ MeV[187]非常接近。e的双重差分 $ E_{\rm W} $取式(49)的形式 $ E_{\rm W} $取式(50)的形式 $ c_2^{\rm(v)} $ $ c_2^{\rm(s)} $ $ \kappa_{\rm s/v} $ $ c_2^{\rm(v)} $ $ c_2^{\rm(s)} $ $ \kappa_{\rm s/v} $ $ \delta e_{2 {\rm n}-1 {\rm p}} $ $ 32.24 \pm 0.50 $ $ 55.87 \pm 1.66 $ 1.73 $ \pm $ 0.06 $ 32.80 \pm 0.48 $ $ 60.53 \pm 1.58 $ 1.85 $ \pm $ 0.06 $ \delta e_{1 {\rm n}-2 {\rm p}} $ $ 32.31 \pm 0.50 $ $ 56.32 \pm 1.65 $ 1.74 $ \pm $ 0.06 $ 32.84 \pm 0.48 $ $ 60.76 \pm 1.58 $ 1.85 $ \pm $ 0.06 $ \delta e_{2 {\rm n}-2 {\rm p}} $ $ 31.65 \pm 0.39 $ $ 53.15 \pm 1.29 $ 1.68 $ \pm $ 0.05 $ 32.58 \pm 0.36 $ $ 60.19 \pm 1.21 $ 1.85 $ \pm $ 0.04 $ \delta e_{3 {\rm n}-2 {\rm p}} $ $ 30.91 \pm 0.35 $ $ 49.85 \pm 1.21 $ 1.61 $ \pm $ 0.04 $ 32.23 \pm 0.34 $ $ 59.04 \pm 1.16 $ 1.83 $ \pm $ 0.04 $ \delta e_{2 {\rm n}-3 {\rm p}} $ $ 31.36 \pm 0.34 $ $ 51.73 \pm 1.17 $ 1.65 $ \pm $ 0.04 $ 32.59 \pm 0.33 $ $ 60.56 \pm 1.13 $ 1.86 $ \pm $ 0.04 $ \delta e_{i {\rm n}-j {\rm p}} $ $ 31.37 \pm 0.16 $ $ 51.88 \pm 0.56 $ 1.65 $ \pm $ 0.02 $ 32.48 \pm 0.16 $ $ 59.93 \pm 0.53 $ 1.85 $ \pm $ 0.02 注:第2~4列和第5~7列分别对应Wigner能$E_{\rm W}$取式(49)和(50)的形式。最后一行“$\delta e_{i {\rm n}-j {\rm p}}$”为同时拟合$(i, j)=(1, 2)$, (2, 1), (2, 2), (2, 3)和(3, 2)的$\delta e_{i {\rm n}-j {\rm p}}$所得到的结果。 从表9可以看到,当Wigner能
$ E_{\rm W} $ 取式(49)的形式时$ \kappa_{\rm s/v} $ 更小,$ c_2^{\rm(v)} $ 和$ c_2^{\rm(s)} $ 随着$ ij $ 的增加有缓慢减小的趋势;而当Wigner能$ E_{\rm W} $ 取式(50)的形式时$ c_2^{\rm(v)} $ 和$ c_2^{\rm(s)} $ 则比较稳定,不同$ ij $ 给出的拟合结果相差不大,这似乎表明在质量公式中指数形式的Wigner能更加合适[162]。值得指出的是,由这两种Wigner能形式给出的拟合结果的不确定度都随着$ ij $ 的增加而降低,这与图11的结果一致,即$ \delta e_{3 {\rm n}-2 {\rm p}} $ 和$ \delta e_{2 {\rm n}-3 {\rm p}} $ 关于A的系统性最好,$ \delta e_{2 {\rm n}-2 {\rm p}} $ 次之,$ \delta e_{2 {\rm n}-1 {\rm p}} $ 和$ \delta e_{1 {\rm n}-2 {\rm p}} $ 则相对较差[162]。文献[197]进一步研究了原子核对称能高阶项的可能贡献。一方面对称能体积项、表面项和曲率项的大小会随着I 2和
$ A^{-1/3} $ 阶数的增加而迅速减小,另一方面体对称能和面对称能中的二阶(I 2)和四阶(I 4)项在有限核对称能中起着重要作用[197]。此外,文献[198-199]讨论了有限核对称能中的I 4项对理论模型的依赖性。数值实验表明,从不同全局型质量模型提取的有限核对称能中I 4项的系数与该模型质量理论值和质量实验值之间的方均根偏差,以及在核素图上该模型计算到质量的束缚核个数之间都存在较强的线性关联[198-199]。需要注意的是,根据这种线性关联外推得到的对称能I 4项系数大于预期[199]。考虑
$ I^4 $ 项后,对称能$ e(N, Z) $ 可以写为其中
$ c_4^{\rm(v)} $ 和$ c_4^{\rm(s)} $ 分别表示体对称能和面对称能中$ I^4 $ 项的系数[197]。将上式代入式(51),可得对称能“实验值”的双重差分为其中
$ X_2^{\rm(v)} $ 和$ X_2^{\rm(s)} $ 的计算公式分别见式(53)和(54),$ X_4^{\rm(v)} $ 和$ X_4^{\rm(s)} $ 的计算公式见文献[197]附录。根据式(48)和式(51),由$ A \geqslant 16 $ 核素的结合能实验值得到对称能“实验值”的双重差分$ \delta e_{i {\rm n}-j {\rm p}} $ ,并利用式(56)同时对$ (i, j)=(1, 2) $ , (2, 1), (2, 2), (2, 3)和(3, 2)的$ \delta e_{i {\rm n}-j {\rm p}} $ 进行拟合,得到的对称能系数见表10,其中第2~3行和第4~5行分别对应取式(49)和(50)作为式(48)中Wigner能$ E_{\rm W} $ 的形式,第2行和第4行为假设$ c_4^{\rm(s)} = 0 $ 时的拟合结果。$ E_{\rm W} $ $ c_2^{\rm(v)} $ $ c_2^{\rm(s)} $ $ c_4^{\rm(v)} $ $ c_4^{\rm(s)} $ 式(49) $ 31.75 \pm 0.15 $ $ 59.44 \pm 0.55 $ $ 8.26 \pm 0.20 $ $ - $ $ 25.91 \pm 0.27 $ $ 41.02 \pm 0.88 $ $ 40.63 \pm 1.26 $ $ 94.29 \pm 3.62 $ 式(50) $ 32.66 \pm 0.15 $ $ 63.60 \pm 0.55 $ $ 4.01 \pm 0.21 $ $ - $ $ 26.24 \pm 0.27 $ $ 43.36 \pm 0.89 $ $ 39.58 \pm 1.27 $ $ 103.59 \pm 3.65 $ 注:第2~3行和第4~5行分别对应 Wigner 能EW取式(49)和(50)的形式,第 2 行和第 4 行为假设c4(s) =0时的拟合结果。 从表10以及表9的最后一行可以看到,当
$ c_4^{\rm(s)} = 0 $ 时四阶体对称能项的引入对$ c_2^{\rm(v)} $ 拟合数值的影响很小,且$ c_4^{\rm(v)} $ 远小于$ c_2^{\rm(v)} $ ,这与文献[169, 200-201]中的结果一致,即核物质状态方程的同位旋相关部分中二阶体对称能项的贡献远大于其它项的贡献;而当$ c_4^{\rm(s)} \neq 0 $ 时,$ c_2^{\rm(v)} $ 和$ c_2^{\rm(s)} $ 的拟合数值相比没有引入对称能高阶项时有明显降低,这与文献[202]中表1的结果是一致的,此外$ c_4^{\rm(v)} $ 的拟合数值相比$ c_4^{\rm(s)} = 0 $ 时的结果增加了一个数量级,相应的不确定度也有所增加,即四阶面对称能项的引入会造成对称能拟合系数的不稳定[197]。值得注意的是,用上述方法提取出的$ c_4^{\rm(v)} $ [197]计算得到的核物质四阶对称能$ E_{\rm sym, 4}(\rho_0)\sim 20 $ MeV($ \rho_0 $ 为饱和密度)[203],远大于根据平均场模型得到的结果(普遍小于2 MeV)[200, 204],但在不考虑高阶同位旋相关的表面张力的情况下(有限核四阶对称能中有高阶表面项的贡献,而无限的核物质没有表面),几个MeV的$ c_4^{\rm(v)} $ 不一定会导致这么大的$ E_{\rm sym, 4}(\rho_0) $ [205]。由此可见,四阶对称能$ E_{\rm sym, 4}(\rho_0) $ 的大小是一个有争议的话题,需进一步深入探讨。总而言之,如果考虑体对称能中的
$ I^4 $ 项并采用式(50)的Wigner能形式,由局域双重差分拟合得到的对称能系数见表10第4行,即$ c_2^{\rm(v)} = (32.66 \pm 0.15) $ MeV,$ c_2^{\rm(s)} = (63.60 \pm 0.55) $ MeV,$ c_4^{\rm(v)} = (4.01 \pm 0.21) $ MeV。 -
由于中子-质子配对关联,
$ N=Z $ 原子核中有额外的结合能——Wigner能。Wigner能最早是1937年Wigner在SU(4)自旋-同位旋对称的框架下引入研究的[206-207],它有多种数学形式,除了式(49)和(50)外,还有一种常见形式,即其中
$ W(A) $ 和$ d(A) $ 是质量数A的函数,$ \pi_{\rm np} $ 对奇奇核和其它奇偶类型的原子核分别取1和0[164]。这几种Wigner能在形式上差别较大,但对I比较小的情况,式(49)、(50)和(57) 可分别近似为这时这三种Wigner能的数值差别不大。
本节考虑式(57)的Wigner能形式。提取Wigner能中
$ W(A) $ 和$ d(A) $ 的方法有很多,例如,利用近似抵消了对称能贡献的$ \delta V_{\rm 2n-2p} $ 的差值来提取[164],基于价中子-质子对的数目来估计[208],通过双β衰变能来获得[165, 170]等。本节主要讨论文献[163]中提出的从局域质量关系出发提取$ W(A) $ 和$ d(A) $ 的方法。将
$ W(A) $ 泰勒展开到一阶项,可得考虑
$ N=Z=A/2 $ 为偶数的情况,将式(57)和(60)代入1.2节图3给出的GKT-k($ k=1, 2, 3, 4 $ )关系,若令图3中"(5)"的位置为参考核$ (N, Z) $ ,则GKT-k关系相对于零的偏差$ D_l $ ($ l = k $ )为若令图3中"(6)"的位置为参考核
$ (N, Z) $ ,则其中
$ l = k+4 $ [163]。类比式(32),文献[209]通过对两个
$ \delta V_{\rm 1n-1p} $ [见式(15)] 作差,构造了三个联系相邻八个原子核结合能的局域关系式,即考虑
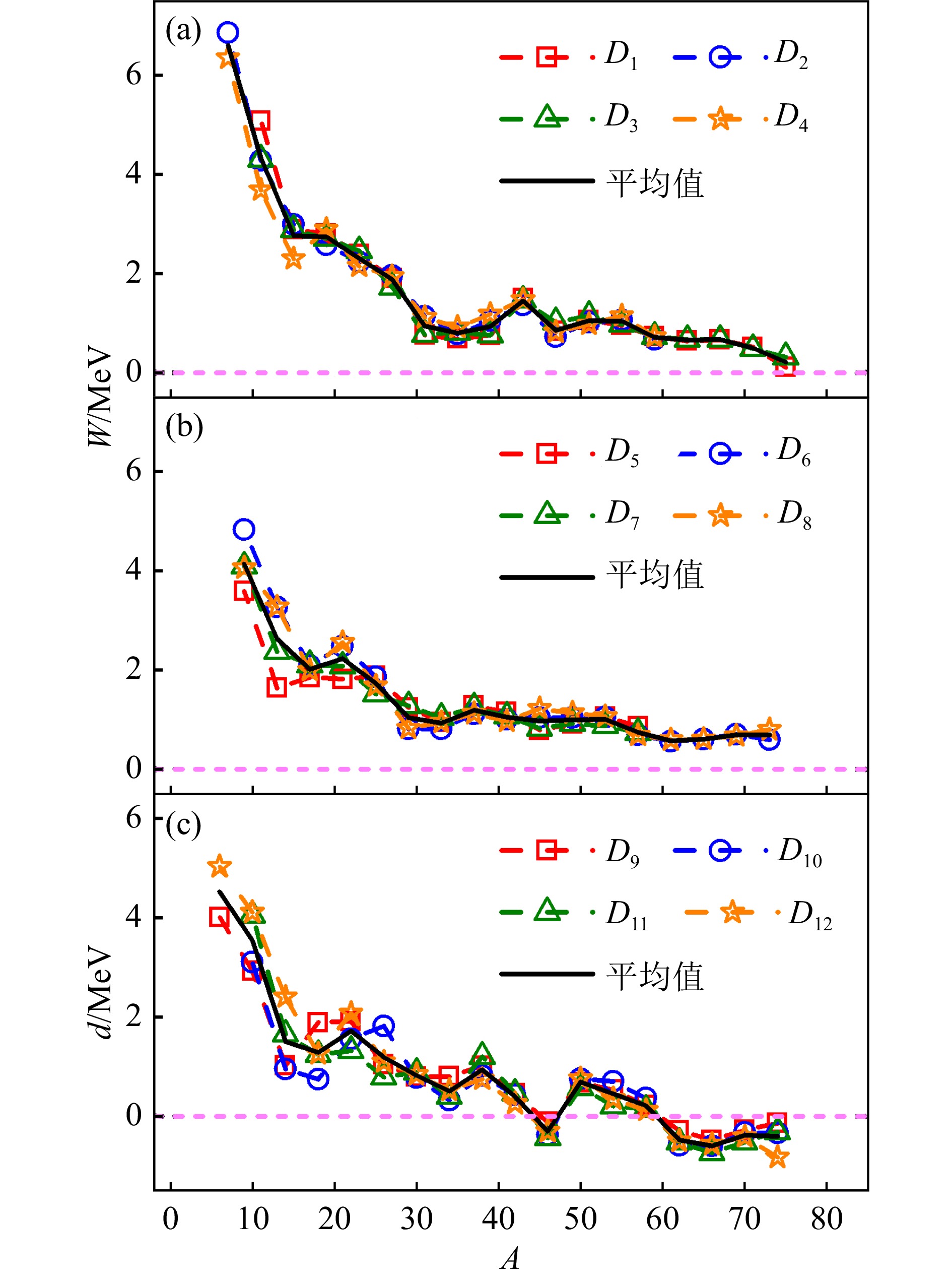
$ N=Z=A/2 $ 为奇数的情况,将式(57)和(60)分别代入式(63)~(65)和图3给出的GKT关系 [取"(3)"的位置为参考核$ (N, Z) $ ],可得式(63)、(64)、(65)和GKT关系相对于零的偏差$ D_l $ (l依次取9,10,11和12)为[163]图12(a)、(b)和(c)分别给出了利用式(61)、(62)和(66)计算得到的W和d与A的关系图,其中黑色实线为相应图中四种W或d计算结果的平均值,粉色虚线标记W或d等于0的位置。由于式(61)和(62)中要求
$ A/2 $ 为偶数,因此图12(a)和(b)中只涉及奇A核的W;根据式(66),图12(c)中只涉及$ N=Z $ 的奇奇核的d。从图12可以看到,A较小时W和d远大于零。但是在$ 10 \leqslant A \leqslant 80 $ 区域,当所有用于计算的原子核都满足$ N>Z $ 时,$ \frac{1}{8} \sum^4_{l = 1} D_l(N, Z)= 0 $ 、$ \frac{1}{8} \sum^8_{l = 5} D_l(N, Z)= 0 $ [系数$ \frac{1}{8} $ 源于对4个$ D_l $ 的平均以及式(61)和(62)中的系数2]和$ \frac{1}{4} \sum^{12}_{l = 9} D_l(N, Z)= 0 $ 的方均根偏差$ \sigma $ [见式(4)] 分别只有201, 198和300 keV。这是因为在这种情况下,Wigner能 [见式(57)] 中的第二项$ E^{\,(d)}_{\rm W} $ 为0,并且第一项中的$ W(A) $ 在式(60)给出的一阶近似条件下相互抵消[163]。由此可见,在轻核区GKTs关系和式(63)~(65)相对于零的偏差$ D_l $ ($ l = 1, 2, \cdots, 12 $ )大部分来源于Wigner能,当Wigner能抵消时这些关系式的方均根偏差有明显降低(见文献[163]的表I)。定义偶A核的
$ W(A) $ 为相邻两个奇A核$ W(A) $ 的平均值[163],即其中
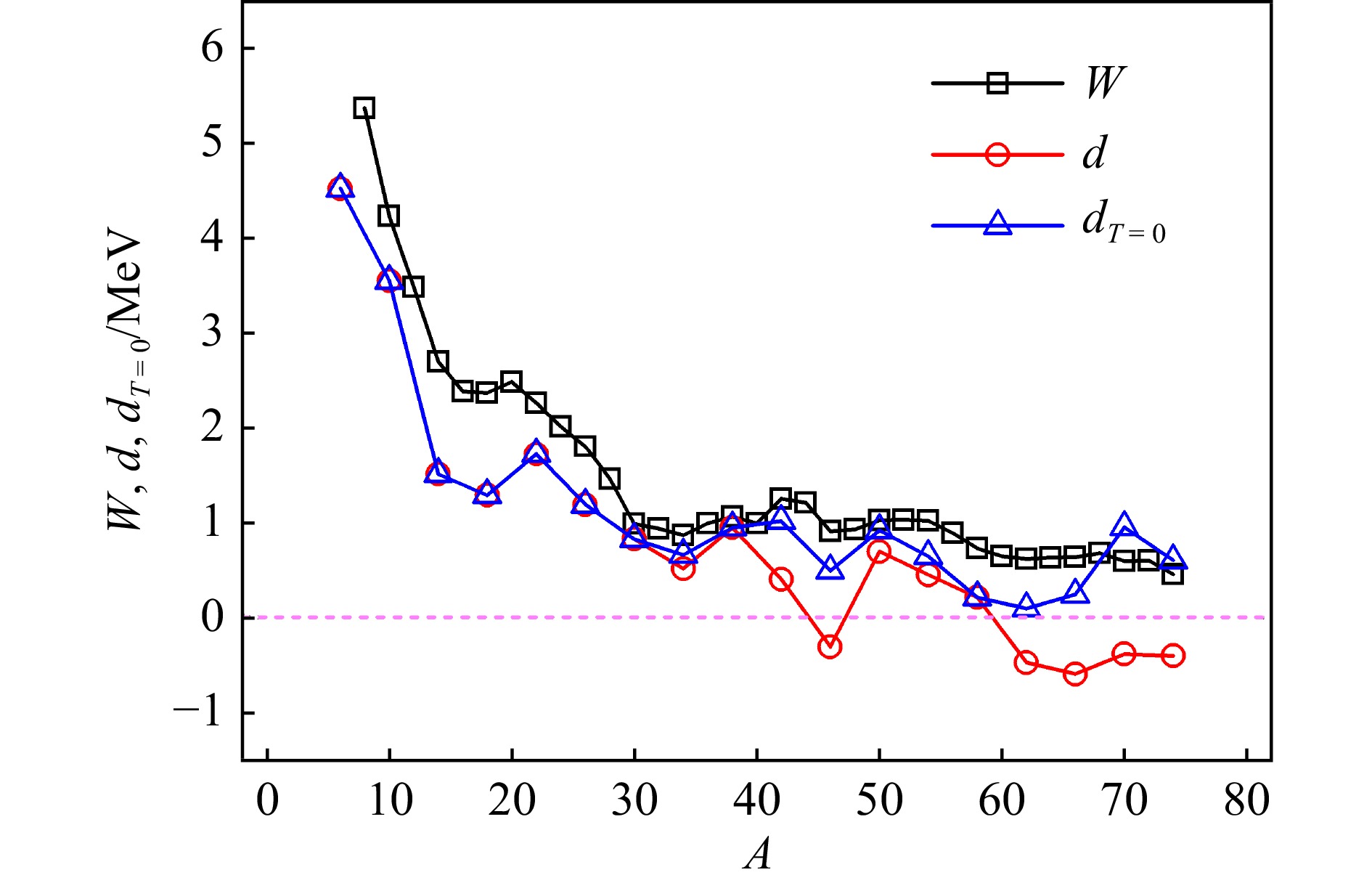
$ \overline{W}(A-1) $ 和$ \overline{W}(A+1) $ 为图12(a)和(b)中由黑色实线给出的平均值。图13给出了偶A核的W和$ N=Z $ 的奇奇核的d [即图12(c)中由黑色实线给出的平均值] 与A的关系图,分别用黑色正方形和红色圆形表示,粉色虚线标记纵轴为零的位置。根据SU(4)对称性,W和d应为正值,且大小相近[210]。但从图13可以看出,当$ A>40 $ 时d相对W有明显偏离,且出现了$ d<0 $ 的情况,这些异常是由于$ N=Z $ 的奇奇核(包括$ ^{34}{\rm{Cl}} $ )的基态同位旋从$ T=0 $ 演变成了T = 1[164]。将$ ^{34}{\rm{Cl}} $ 以及$ A>40 $ 且$ T=1 $ 原子核的基态能量替换为相应$ T=0 $ 态的最低能量(排除基态$ T=0 $ 的$ ^{58}{\rm{Cu}} $ )[4],则根据式(66)四种计算结果给出的d的平均值(标记为$ d_{T=0} $ )在图13中用蓝色三角形表示。显然所有$ d_{T=0} $ 都为正,且大小与W相近。如图13所示,随着A的增加W和
$ d_{T=0} $ 整体呈下降趋势。假设$ W(A)= a_W / A $ ,$ d_{T=0}(A)= a_d / A $ ,其中$ a_W $ 和$ a_d $ 为拟合系数。分别拟合图12(a)、(b)中奇A核的W和图13中$ N=Z $ 的奇奇核的$ d_{T=0} $ ,可得$ a_d / a_W = 0.67 $ 。这一结果与文献[208]中给出的$a_W = (43 \pm 5)$ MeV、$a_d / a_W = 0.56 \pm 0.27$ ,以及文献[170]中给出的$ a_W =(42.5 \pm 1.2) $ MeV都比较接近。采用式(57)的Wigner能形式以及式(68)和(69)给出的拟合系数,按照4.1节中提取对称能系数的计算步骤,利用式(52)同时对
$ (i, j)=(2, 2) $ , (2, 3)和(3, 2)的$ \delta e_{i {\rm n}-j {\rm p}} $ 进行拟合($ 10 \leqslant A \leqslant 80 $ )[163],可得$c_2^{\rm(v)} = (32.64 \pm 0.33)$ MeV、$ \kappa_{\rm s/v} = 1.68 \pm 0.03 $ ,这与4.1节表9中的拟合结果非常接近。 -
镜像核是指中子数N和质子数Z的大小互换的一对原子核。实验上,近年来我国基于兰州重离子研究装置(HIRFL)精确测量了多个短寿命丰质子核的质量[211],如
$ ^{65} {\rm{As}}$ [212]、$ ^{52-54} {\rm{Ni}}$ [213-215]、$ ^{44-45} {\rm{Cr}}$ [215-218]、$ ^{44-45}{\rm{V}} $ [217]和$ ^{27}{\rm{P}} $ [219]等。理论上,对于同量异位多重态,它们之间的能量差可以简单地用同位旋投影$ T_z $ 相关的同位旋多重态质量方程(IMME)来描述[50-55],即其中
$ a = M_0 + E_c^{(0)} - T(T + 1)E_c^{(2)} $ ,$ b = \varDelta E_{\rm np} - E_c^{(1)} $ ,$ c = 3E_c^{(2)} $ ,$ M_0 $ 是电荷无关的原子核质量,$ \varDelta E_{\rm np} = M_{\rm n} - M_{\rm p} \approx 0.782 $ MeV,$ E_c^{(0)} $ 、$ E_c^{(1)} $ 和$ E_c^{(2)} $ 分别是库仑能中的同位旋标量项、矢量项和张量项。此外,Kelson-Garvey质量关系及其推广[105-107]也适用于$ N = Z $ 线附近的镜像核,可以有效预言轻核区丰质子核的质量。本节讨论从原子核结合能的Weizsäcker公式[17]出发构造出的镜像核质量公式,并讨论库仑能的奇偶性[56-59, 61, 76]。方便起见,本节中约定$ N = Z $ ,$ A = N + Z = 2Z $ 。 -
根据Weizsäcker公式[17-18],
$ M(N, Z) $ 可以表示为其中
$ a_i $ 为拟合系数,$ \delta_{\rm pair} $ 对偶偶核、奇奇核和奇A核分别等于1、−1和0。上式中库仑能$ E_{\rm c} $ 的形式通常为若取
$ r_0 = 1.2 $ fm,则库仑能系数式中
$ N = Z $ ,$ A = N + Z $ ,$ \delta_{\rm c} = k(A-k)^{2/3} $ 。由于库仑能不能通过实验直接测量,因此可以将式(74)中的$ a_c $ 和$ k \varDelta E_{\rm np} \equiv C $ 都作为可调参数 [见式(75)][56]。文献[220]中基于同位素截面分布预言的7个丰质子核的质量($ k = 4 $ 或5)与式(75)吻合得很好。若在式(75)的基础上进一步考虑壳修正项$ a_{\rm sh}\delta_{\rm sh} $ [见6.2节式(113)的分离能半经验公式][56],则改进后公式描述108个$ \delta M(N, k) $ $( k = 1, 2, 3, 4) $ 的方均根偏差$ \sigma $ [见式(4)]为211 keV。这里$ a_{\rm sh} $ 为拟合系数,当N或Z在1~2, 3~8, 9~20, 21~28, 29~50和51~82的范围时,$ \delta_{\rm sh} $ 分别等于1, 2, 3, 4, 5和6[38-39]。文献[57]对上述工作进行了推广,定义
将式(75)代入上式可得
其中
$ k = 1 $ ~4,库仑项当
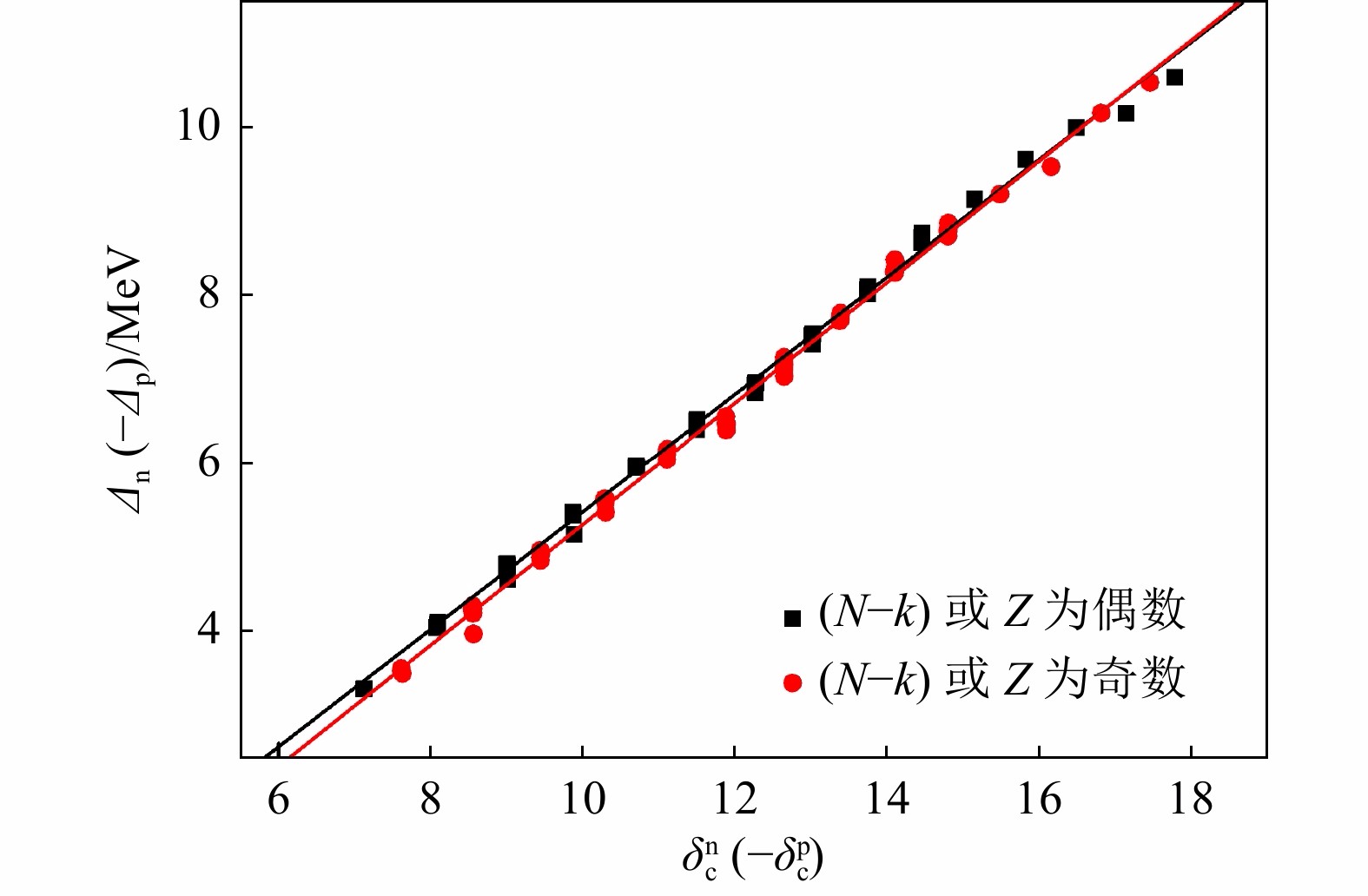
$ k=1 $ 时,容易验证$ \varDelta_{\rm p} (N-1, Z) $ 即为$ - \delta M(N, 1) $ 。$ \varDelta_{\rm n} $ 和$ \varDelta_{\rm p} $ 具有奇偶性[58]。图14给出了$ \varDelta_{\rm n} $ ($ - \varDelta_{\rm p} $ )与$ \delta^{\rm n}_{\rm c} $ ($ - \delta^{\rm p}_{\rm c} $ )的关系图,其中黑色正方形和红色圆形分别表示$ (N - k) $ (Z)为偶数和奇数时$ \varDelta_{\rm n} $ ($ - \varDelta_{\rm p} $ )的实验值,黑色和红色直线分别为相应实验值的拟合结果。由图14可知,黑色正方形和红色圆形具有很好的线性关系,因此文献[58]将式(77)中的$ \varDelta_{\rm n} $ 和$ \varDelta_{\rm p} $ 统一表示为对
$ \varDelta_{\rm n} $ 和$ \varDelta_{\rm p} $ ,上式中$ \delta'_{\rm c} $ 分别取式(78)中的$ \delta^{\rm n}_{\rm c} $ 和$ \delta^{\rm p}_{\rm c} $ ,C前的符号分别取负号和正号。$ N-k \geqslant 10 $ 时,对$ (N - k) $ 或Z为偶数和奇数的情况,式(79)的拟合系数、方均根偏差$ \sigma $ 和个数$\mathcal{N}$ [见式(4)] 在表11中给出。根据表11,式(79)对所有124个$ \varDelta_{\rm n} $ 和$ \varDelta_{\rm p} $ 的方均根偏差$ \sigma $ 为93 keV,相比$ \delta M $ 关系有明显降低。此外表11中$ a_{\rm c} $ 的拟合结果与式(73)给出的经验值720 keV非常接近,但$ |C| $ 的数值却远大于$ \varDelta E_{\rm np} $ 的实验值$ 782 $ keV,这一偏离在考虑质子的库仑自能项和质子之间的相互作用能贡献后可以较好地消除,详见5.4节。$ a_{\rm c} $ C $ \sigma $ $\mathcal{N}$ $ (N - k) $或Z为偶数 698 1 550 94 62 $ (N - k) $或Z为奇数 719 1 907 92 62 注:第 2、3 行分别为(N−k)或Z为偶数、奇数时的计算结果。 将式(77)改写为
其中系数
$ a_{\rm c} $ 和C取式(79)对$ (N - k) $ 或Z分奇偶拟合时的结果[58]。若已知式(80)或(81)等号右侧3个原子核的质量,则可给出等号左侧原子核质量的理论计算值,因此给定一个原子核最多有2种关于其质量的计算结果。取所有计算结果的加权平均值作为该原子核质量的理论值$ M^{\rm th} $ ,即其中
$ M^{\rm th}_1 $ 和$ M^{\rm th}_2 $ 分别为式(80)和(81)给出的原子核$ (N, Z) $ 的质量计算值,$ \sigma^2_{\rm pre1} $ 和$ \sigma^2_{\rm pre2} $ 为相应理论不确定度的平方[58]。由该方法给出的质量预言值与近期一些实验测量结果[218, 221]吻合得很好。 -
式(79)中的拟合系数C对不同奇偶的
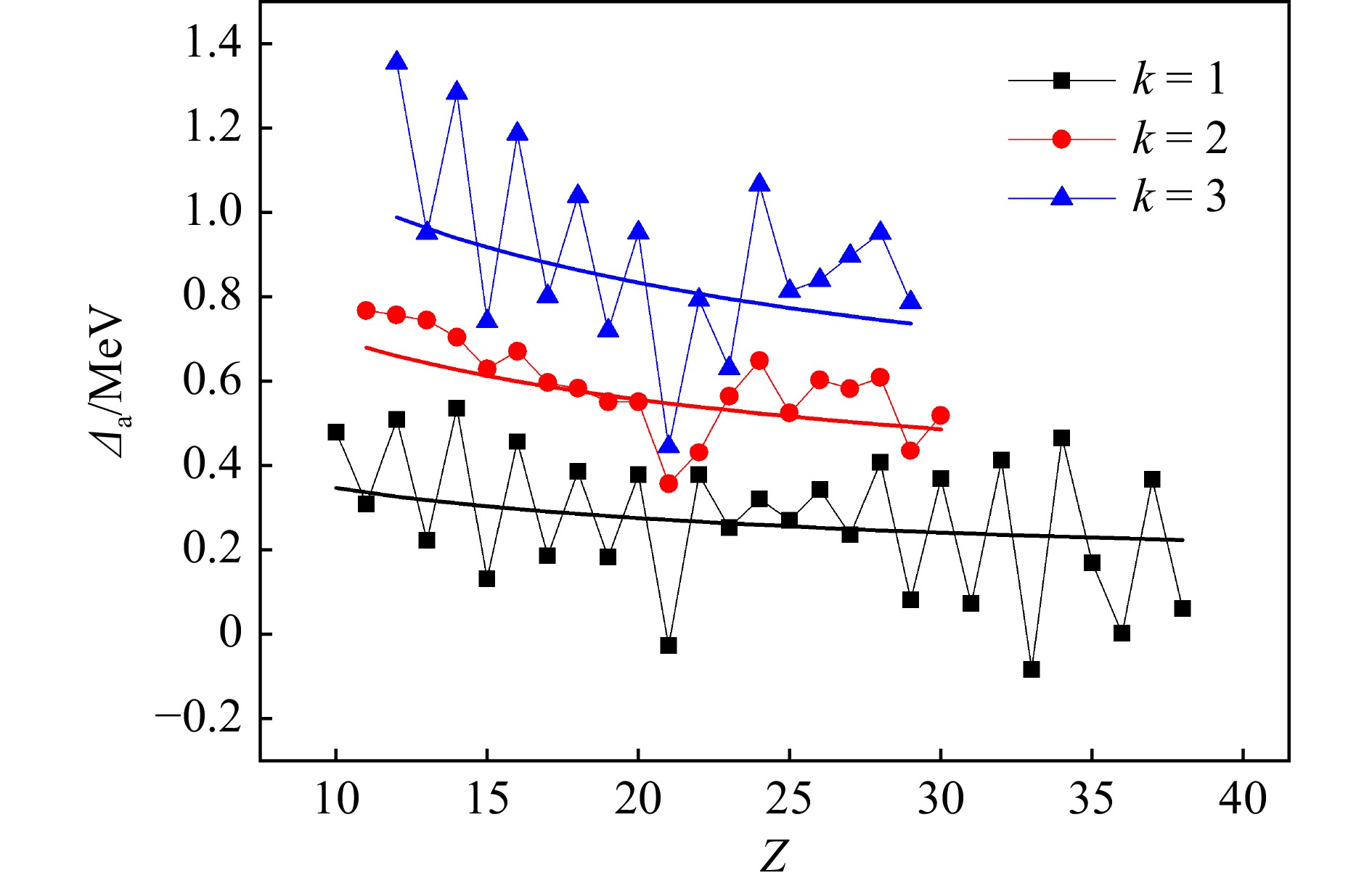
$ (N - k) $ 或Z有明显差别(见表11,大约0.4 MeV),这与库仑能中的奇偶性有关[58]。简单来说,库仑能的这种奇偶性源于质子配对关联[222-226],即如果两个质子的状态为自旋方向相反的配对状态,那么二者空间分布的重叠就很大。一方面质子之间的库仑相互作用相对于强相互作用而言要小得多,库仑排斥不足以对质子配对造成明显影响,另一方面库仑能取决于质子的空间分布,因此核子的配对关联导致了质子之间静电相互作用能呈现明显的奇偶性[58, 225]。文献[58]定义经验的库仑能奇偶差为
根据式(79),由
$ \varDelta_{\rm p} $ 给出的Z为偶数时库仑能的奇偶差,即图14中两条拟合直线之间的差值,可以表示为其中
$ a^{\rm e}_{\rm c} $ 和$ C^{\rm e} $ ($ a^{\rm o}_{\rm c} $ 和$ C^{\rm o} $ )分别取自表11第2行(第3行)的第2列和第3列,由此得到的$ k = 1 $ 时的$ \delta_{\rm cp} $ 与式(83)给出的经验值基本吻合[58]。文献[59]也讨论了库仑能的这种奇偶性。定义
则根据式(75)可得
当
$ k \ll 2N $ 时,上式可改写为即给定N或Z,
$ \varDelta_{\rm a} $ 近似与k成正比。图15给出了$ Z \geqslant 10 $ 时$ \varDelta_{\rm a} $ 与Z的关系图,其中黑色正方形、红色圆形和蓝色三角形分别表示$ k = 1 $ 、2和3时根据式(85)计算的$ \varDelta_{\rm a} $ 的实验值,相应颜色的曲线为式(86)给出的$ \varDelta_{\rm a} $ 的理论近似值,其中$ a_{\rm c} $ 取$ Z \geqslant 10 $ 时式(75)的拟合结果。由图15可知,$ k=1 $ 和3时$ \varDelta_{\rm a} $ 的实验值关于Z表现出了明显的奇偶振荡现象[59]。这种奇偶性可以用库仑相互作用的辛弱数模式来解释[59, 117, 223, 227]。对一个辛弱数为0或1的全同粒子体系,其基态两体相互作用的期望值[117, 227]可以表示为
其中j为单粒子态的角动量,n为价核子数,
$ \; {V} $ 为闭合壳层内的相互作用,$ \epsilon_j $ 为有效单粒子能量,$ [n/2] $ 表示不超过$ n/2 $ 的最大整数,α和β的大小取决于两体相互作用的矩阵元[227]。根据式(75)和(87),$ \varDelta_{\rm a}(N-k, Z) $ 中库仑相互作用的贡献为其中n、
$ n-1 $ 、$ n-k $ 和$ n-k-1 $ 分别为$ \varDelta_{\rm a} $ 所涉及四个原子核的价质子数。式(88)中$ \varDelta_{\rm a} $ 主要包含两项,第一项与k成正比,这与式(86)的结论一致;第二项对应图15中k为奇数时$ \varDelta_{\rm a} $ 关于Z(或N)的奇偶效应[59]。由上述讨论可知,库仑能存在源于质子配对关联的奇偶性[222-226],且这种奇偶性可以从镜像核质量公式中提取出来[58-59, 224-226]。
-
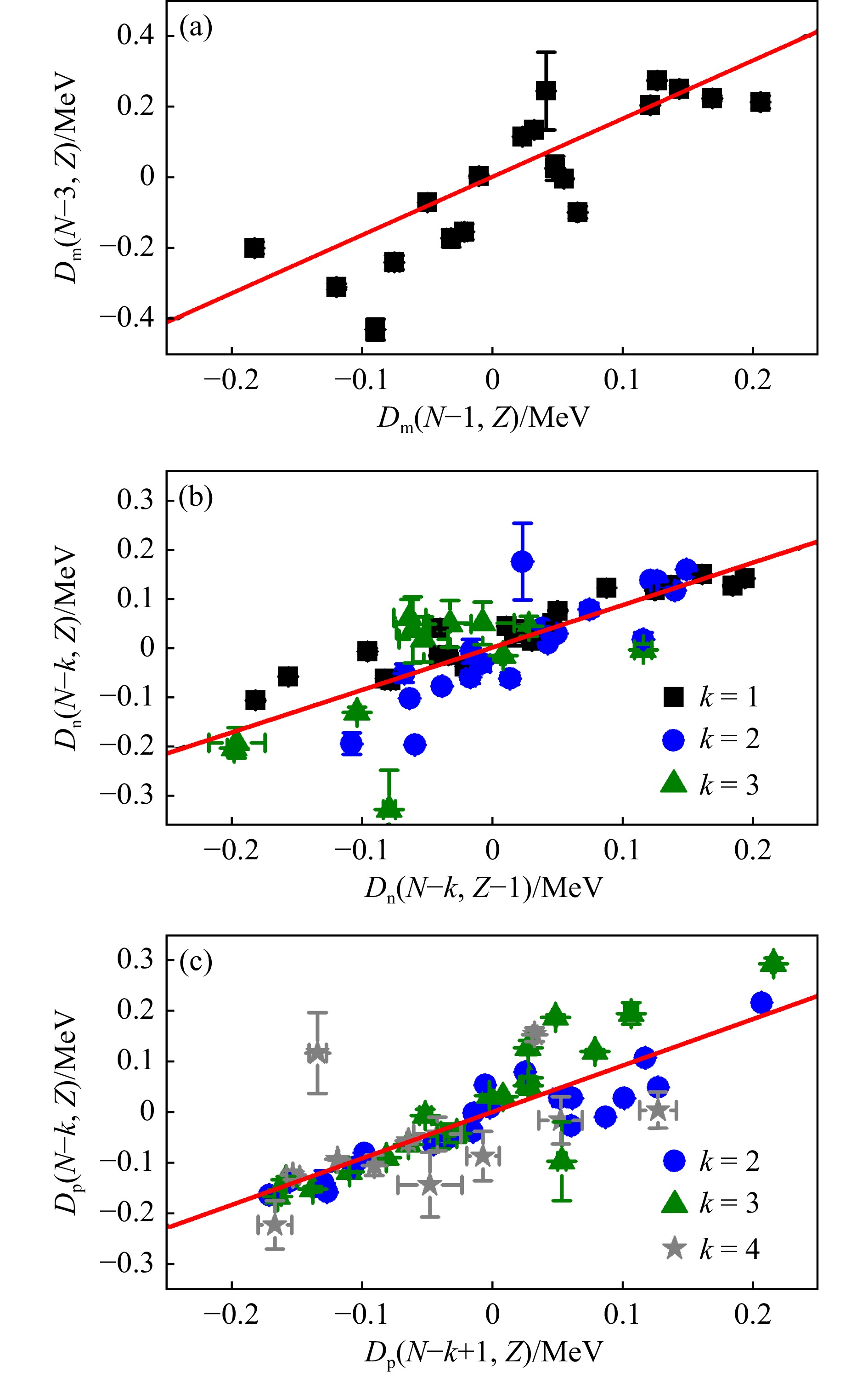
文献[59]进一步研究了式(75)和(76)与其实验值(用上标"exp"标记)的偏差,定义
对
$ D_{\rm m}(N-k, Z) $ 和$ D_{\rm p}(N-k, Z) $ ,k的取值范围是$ 1 \sim 4 $ ,$ a_{\rm c} $ 和C取$ N-k \geqslant 8 $ 时$ \delta M $ 和$ \varDelta_{\rm p} $ 的拟合系数;对$ D_{\rm n}(N-k, Z) $ ,k的取值范围是$ 0 \sim 3 $ ,$ a_{\rm c} $ 和C取$ N-k > 8 $ 时$ \varDelta_{\rm n} $ 的拟合系数。图16(a)、(b)和(c)分别给出了
$ D_{\rm m}(N-3, Z) $ 与$ D_{\rm m}(N-1, Z) $ 、$ D_{\rm n}(N-k, Z) $ 与$ D_{\rm n}(N-k, Z-1) $ 和$ D_{\rm p}(N-k, Z) $ 与$ D_{\rm p}(N-k+1, Z) $ 的关系图以及计算这些物理量时所涉及到的质量实验误差的方均根,其中黑色正方形、蓝色圆形、绿色三角形和灰色星形分别对应$ k = 1 $ , 2, 3和4。由于库仑相互作用贡献中β项的抵消 [见式(88)],这样的三对D之间存在相互关联[59],它们的线性拟合$( y = \lambda x )$ 结果在图16中用红色直线表示。图16(a)、(b)和(c)中的拟合斜率$ \lambda $ 分别为1.647, 0.864和0.920,相应的方均根偏差$ \sigma $ [见式(4)] 分别为119, 66和66 keV,由此可见,这三对D之间有很好的线性关系,若在计算中排除误差较大的质量实验数据(实验误差大于155 keV的$ ^{28}{\rm{S}} $ 和$ ^{55}{\rm{Cu}} $ ),相应的$ \sigma $ 会进一步降低[59]。在式(80)和(81)给出的
$ M(N-k-1, Z) $ 和$ M(N- k, Z) $ 的基础上,考虑上述线性修正,即并代入式(82)计算,可进一步提高理论计算值的精度,其中
$ \lambda_1 $ 和$ \lambda_2 $ 分别为$ D_{\rm n}(N-k, Z) $ 与$ D_{\rm n}(N-k, Z-1) $ 以及$ D_{\rm p}(N-k, Z) $ 与$ D_{\rm p}(N-k+1, Z) $ 之间线性关系的斜率 [见图16(b)和(c)]。 -
文献[61]进一步将镜像核质量公式推广应用于质子滴线外的非束缚系统,即
$ S_{\rm p} $ 或$ S_{\rm 2p} $ 小于零的情况。考虑包含自能项$ E_{\rm c}^{\rm s} $ 和交换项$ E_{\rm c}^{\rm e} $ 的库仑能[223-224],即其中
$ \delta_{\rm c}^{\rm m} = A^{2/3} - 0.808 - A^{-1/3} $ ,$ a_{\rm c} $ 、$ C' $ 和β是拟合系数,$ a' $ 和α是小于100 keV的小量[61]。根据式(93),式(77)中的$ \varDelta_{\rm n} $ 和$ \varDelta_{\rm p} $ 可分别改写为[61]其中
$ a_{\rm c} $ 和$ C' $ 分别由式(94)和(95)给出,根据式(38)和(39)中分离能的定义,以及式(77)和(97),可得[61]
其中
$ S_{\rm n}(N, Z-k) $ 取实验值。类似地,若定义[61]则有
其中
$ S_{\rm 2n}(N, Z-k) $ 取实验值,表12中给出了式(93)、(96)和(97)、(100)和(102)的拟合系数以及方均根偏差
$ \sigma $ [见式(4)]。可以看到,这些公式的$ \sigma $ 都很小,且$ C' $ 与$ \varDelta E_{\rm np} $ 的实验值相差不大(α很小)。值得注意的是,方均根偏差$ \sigma $ 和拟合系数$ a' $ 、α、β都具有很好的鲁棒性,即使用AME2012数据表[9]或AME2016数据表[8]得到的计算结果与表12基本一致[61]。公式 $ \sigma $ $ a' $ α β $ \delta M' $ 147 $ -20 \pm 2 $ $ 67 \pm 24 $ $1\,276 \pm 329$ $ \Delta'_{\rm n} $& $\Delta'_{\rm p}$ 96 $ -16 \pm 2 $ $ 105 \pm 24 $ $1\,473 \pm 150$ $ S_{\rm p} $ 96 $ -18 \pm 3 $ $ 70 \pm 31 $ $1\,500 \pm 175$ $ S_{\rm 2p} $ 151 $ -19 \pm 3 $ $ 67 \pm 28 $ $ - $ 对于质子滴线外的非束缚系统,文献[61]唯象地将质子分布近似地分为两部分,内部是质子密度正常分布的核芯,外部的质子密度则相对较小。令
$ R_1 $ 和$ R_2 $ 分别表示内、外部的半径,则式(92)的库仑能可改写为其中
$ \epsilon =(R_2 - R_1)/ R_2 $ ,$ k' = c k_{\rm n} +(1-c)k_{\rm p} $ 表示“正常”核芯外的有效质子数,$ k_{\rm n} $ ($ k_{\rm p} $ )是在核素图上与处于质子滴线的同位素(同中子异核素)之间的距离[61]。其中
$ a' $ 、α和β的数值沿用描述质子滴线内原子核的系数(见表12第2行),假设
$ \epsilon = a A + b $ ,则a、b和c的优化结果分别为$ -0.024 \pm 0.005 $ 、$ 0.553 \pm 0.070 $ 和$ 0.872 \pm 0.077 $ [61]。这里由于库仑位垒一般会随着质量数(和质子数)的增加而变高,从而导致$ R_1 $ 与$ R_2 $ 的相对差异变小,因此$ a<0 $ 的结果是容易理解的。式(105)描述质子滴线外丰质子系统质量的方均根偏差$ \sigma $ [见式(4)] 为183 keV,若排除具有奇异结构的中子晕核$ ^{11}{\rm{Li}} $ 的实验数据,则$ \sigma $ 减小为 164 keV[61]。 -
分离能作为研究快中子和快质子俘获过程的关键输入参数,对天体物理学和宇宙学具有重要意义,并且通过中子(质子)分离能可以有效判断原子核内中子(质子)的壳层结构。根据式(38)和(39)给出的k核子分离能定义,可由AME2020数据表[3]中结合能的实验值(理论模型给出的质量或结合能的计算值)得到
$ S_{k {\rm n}} $ 和$ S_{k {\rm p}} $ 的实验值(计算值)。本节讨论两种直接描述和预言分离能的工作,包括单(双)核子分离能与价核子数的线性关系[62-63]以及全局型的单核子分离能半经验公式[38-40]。 -
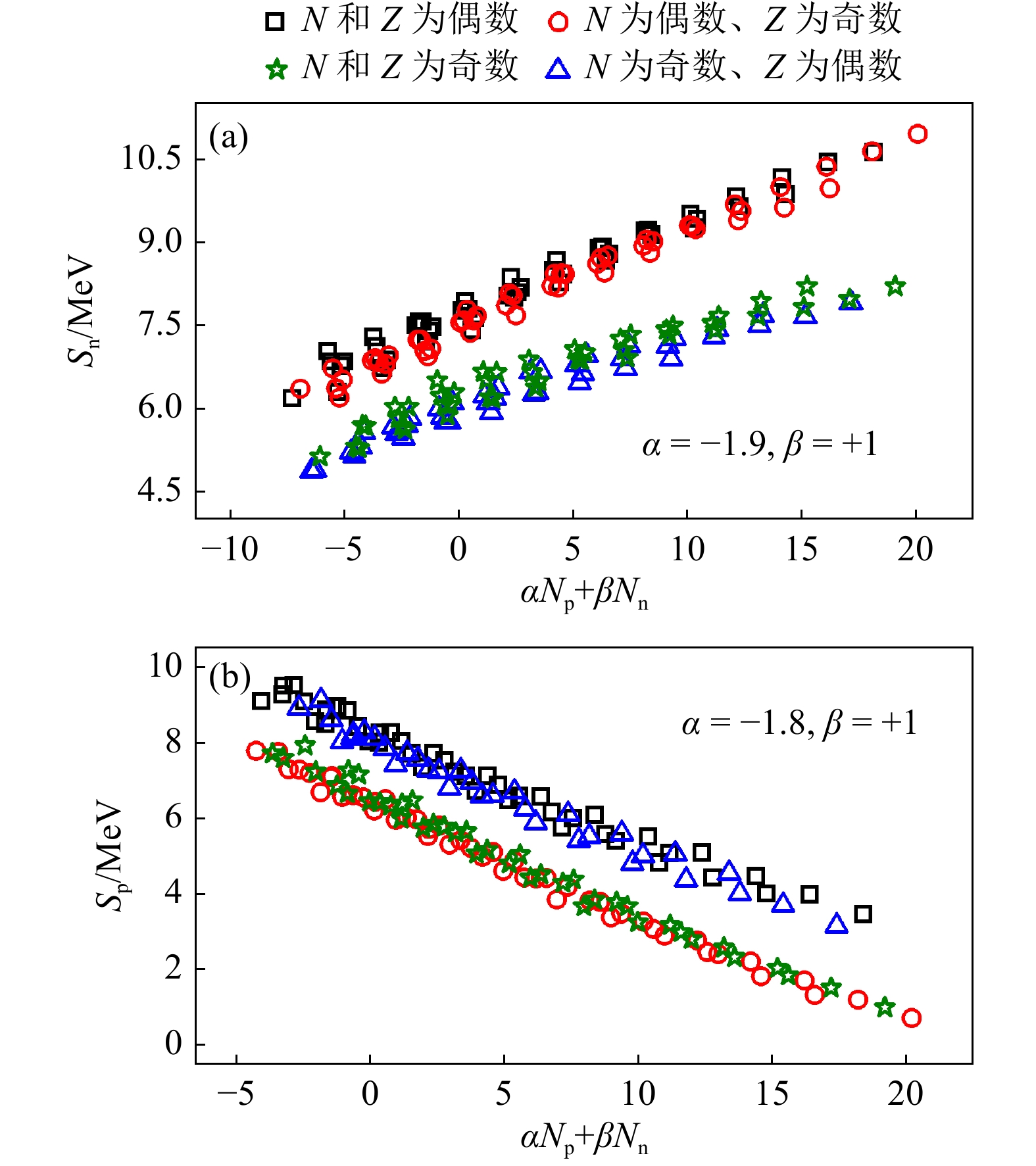
在半壳中偶偶核的单中子分离能
$ S_{\rm n} $ 和单质子分离能$ S_{\rm p} $ 与$ \alpha N_{\rm p} + \beta N_{\rm n} $ 有很好的线性关系[62],其中α为拟合系数(粒子型为正、空穴型为负),β对粒子型和空穴型分别取−1和+1。以$ S_{\rm n} $ 为例,这种线性关系可以表示为其中K和C为拟合系数(需排除所有单满壳、双满壳以及
$ N = Z $ 的原子核)。文献[63]通过数值实验进一步说明这种线性关系不仅适用于偶偶核的单核子分离能,也适用于其它奇偶类型的单核子分离能以及双核子分离能。这种价关联机制对于研究核素图中不同区域各种物理量的演化非常有用。图17(a)和(b)分别给出了在
$ 104 \leqslant N \leqslant 125 $ 、$ 66 \leqslant $ $ Z \leqslant $ 81的半壳区域内,$ S_{\rm n} $ 和$ S_{\rm p} $ 与$ \alpha N_{\rm p} + \beta N_{\rm n} $ 的关系图,其中黑色正方形、红色圆形、蓝色三角形和绿色星形分别对应偶偶核、偶奇核、奇偶核和奇奇核,根据式(106)拟合得到的α和β也在图中给出。图17中$ S_{\rm n} $ 和$ S_{\rm p} $ 与$ \alpha N_{\rm p} + \beta N_{\rm n} $ 有很好的线性关系,且表现出了两种奇偶性:第一种是N(Z)为偶数的$ S_{\rm n}( S_{\rm p}) $ 明显高于其相邻N(Z)为奇数的$ S_{\rm n}(S_{\rm p}) $ ,这种奇偶性与对能有关,已被人们所熟知;第二种是A为偶数的$ S_{\rm n}( S_{\rm p}) $ 略高于其相邻A为奇数的$ S_{\rm n}(S_{\rm p}) $ 。分离能的这两种奇偶性可以用结合能半经验公式中的对能和对称能来解释[63]。以
$ A>100 $ 时的$ S_{\rm n} $ 为例,考虑WS公式中的对能形式 [见式(17)] 和对称能:并取
$ a_{\rm p} = 5.44 $ MeV、$ c_{\rm sym} = -29.16 $ MeV、$ \kappa = 1.35 $ [23]。假设$ N > Z $ ,则$ S_{\rm n}(N, Z)- S_{\rm n}(N-1, Z) $ 中对能的贡献约为对称能的贡献约为
类似地,假设
$ N > Z+1 $ 则$ S_{\rm n}(N, Z)- S_{\rm n}(N, Z-1) $ 中对能和对称能的贡献分别为$ a_{\rm p} A^{-4/3} |N-Z| $ 和$ -2 c_{\rm sym}(A^{-1} - \kappa A^{-4/3} ) $ 。式(108)的第一项很大(
$ A = 188 $ 时~1.90 MeV),第二项相对较小且对偶数和奇数的Z有微小差别,如对$ ^{188}_{76} {\rm{Os}} _{112} $ 和$ ^{189}_{77} {\rm{Ir}} _{112} $ 分别为$ A = 188 $ 时由式(109)给出的对称能贡献$ \sim -0.16 $ MeV。综合上述两项可得,N为偶数的$ S_{\rm n} $ 平均比其相邻N为奇数的$ S_{\rm n} $ 高$ \sim 1.23 $ MeV($ A \geqslant 100 $ 时WS公式[23]中其它项的贡献$ \leqslant 25 $ keV,可忽略),与图17(a)中的结果基本吻合。同样地,对第二种奇偶性,(以
$ ^{188}_{76} {\rm{Os}} _{112} $ 和$ ^{189}_{77} {\rm{Ir}} _{112} $ 为例)对能的贡献$ \sim 5.44 \times 189^{-4/3} \times(112-77)\approx 0.18 $ MeV,(以$ A = 188 $ 为例)对称能的贡献$ \sim 2 \times 29.16 \times(188^{-1} - 1.35 \times 188^{-4/3} )\approx 0.24 $ MeV,则A为偶数的$ S_{\rm n} $ 平均比其相邻A为奇数的$ S_{\rm n} $ 高$ \sim 0.42 $ MeV,这与图17(a)中的结果也基本吻合。此外根据式(15)的$ \delta V_{\rm 1n-1p} $ 关系和式(38)~(39)给出的k核子分离能的定义,可得因此,图17中
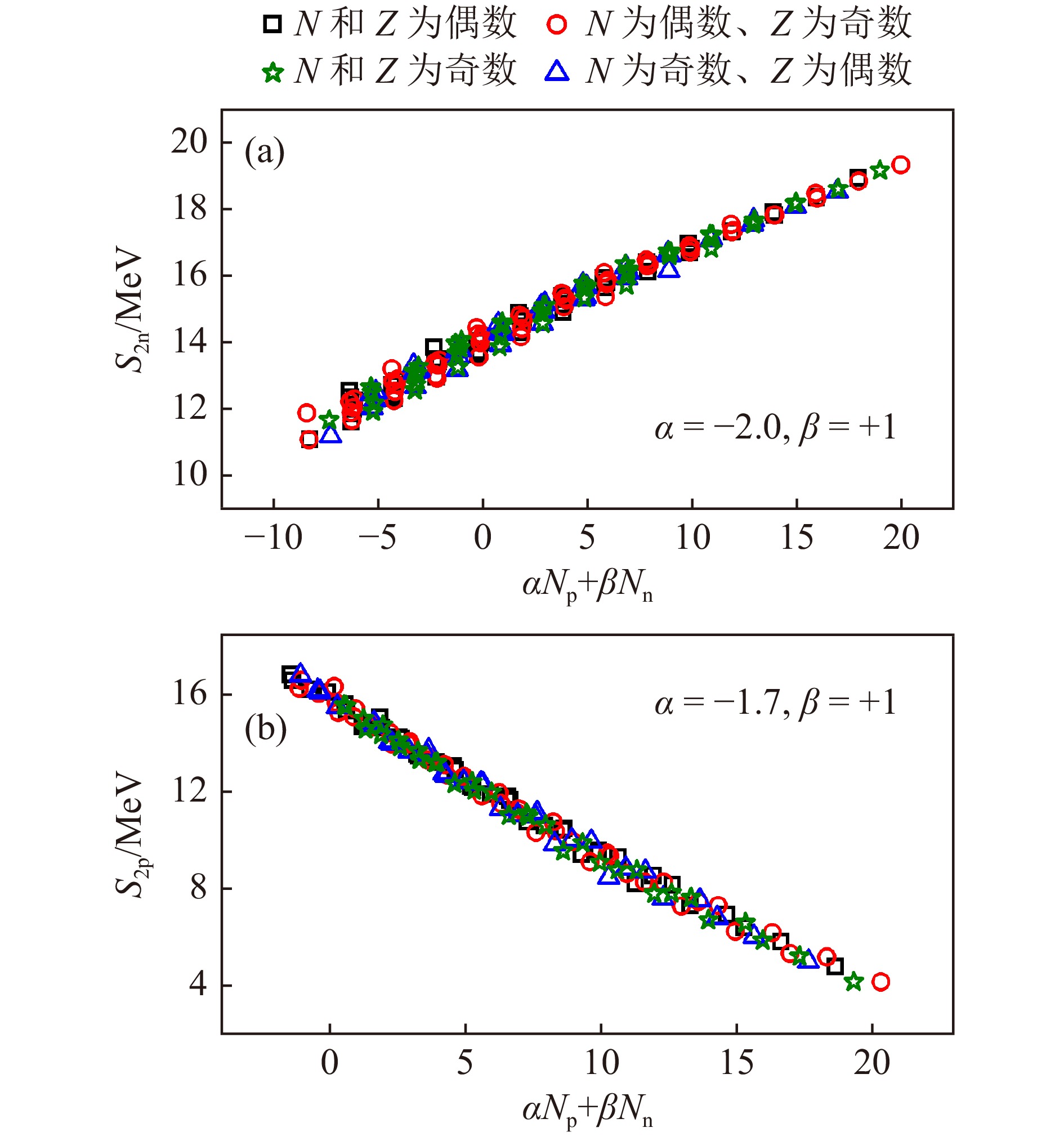
$ S_{\rm n} $ 和$ S_{\rm p} $ 的第二种奇偶性与图4(a)中$ \delta V_{\rm 1n-1p} $ 关系表现出的奇偶性一致[63],即A为偶数的$ \delta V_{\rm 1n-1p} $ 大于其相邻A为奇数的$ \delta V_{\rm 1n-1p} $ (约410 keV,见2.1节)。双核子分离能也有类似的线性关系,以
$ 104 \leqslant N \leqslant 125 $ 、$ 66 \leqslant Z \leqslant 81 $ 的半壳区域为例,图18(a)和(b)分别给出了$ S_{\rm 2n} $ 和$ S_{\rm 2p} $ 与$ \alpha N_{\rm p} + \beta N_{\rm n} $ 的关系图及相应α和β的拟合结果,其中黑色正方形、红色圆形、蓝色三角形和绿色星形分别对应偶偶核、偶奇核、奇偶核和奇奇核。由于单核子分离能中的奇偶性在相加时有所抵消,因此图18中
$ S_{\rm 2n} $ 和$ S_{\rm 2p} $ 没有表现出明显的奇偶差异。以
$ S_{\rm 2n} $ 为例,令$ \delta S_{\rm 2n}(N, Z)= S_{\rm 2n}(N, Z)- S_{\rm 2n}(N-1, Z) $ ,同样考虑WS公式中的对能 [见式(17)] 和对称能 [见式(107)][23],可得$ A > 100 $ 时$ \delta S_{\rm 2n}(N, Z) $ 中对能的贡献约为对称能的贡献约为
若考虑
$ ^{188}_{76} {\rm{Os}} _{112} $ 和$ ^{189}_{77} {\rm{Ir}} _{112} $ 的$ \delta S_{\rm 2n} $ ,则式(111)给出的对能贡献分别为$ -0.01 $ 和$ -0.02 $ MeV,式(112)给出的对称能贡献为$ -0.33 $ MeV。因此$ A > 100 $ 时,$ S_{\rm 2n}(N, Z) $ 总是比$ S_{\rm 2n}(N-1, Z) $ 小$ \sim 0.3 $ MeV,并且这种能量差主要来源于对称能的贡献[63],这与图18(a)中的结果一致($ S_{\rm 2n} $ 的拟合斜率$ K \sim 0.29 $ MeV)。双核子分离能还有一种更微小的奇偶差异[63],即
$ A > 100 $ 时,N为偶数的$ \delta S_{\rm 2n} $ 总是比其相邻N为奇数的$ \delta S_{\rm 2n} $ 小$ \sim 0.06 $ MeV,这可能是由对能所引起的。例如,N和Z都为偶数时,平均$ \delta S_{\rm 2n}(N, Z)\sim -0.43 $ MeV、$ \delta S_{\rm 2n}(N-1, Z)\sim -0.37 $ MeV。对$ \delta S_{\rm 2p}(N, Z)= S_{\rm 2p}(N, Z)- S_{\rm 2p}(N, Z-1) $ 也有类似的结论[63]。 -
中子(质子)分离能会随着
$ N/Z $ ($ Z/N $ )的增加而减小,考虑对能和壳效应后,单中子分离能$ S_{\rm n} $ 和单质子分离能$ S_{\rm p} $ 的半经验公式[38]分别为其中
$ a_i $ 为拟合系数,$ \delta_{\rm coul} = Z^2 A^{-1/3} $ ,$ \delta_{\rm pair} = \pm a_{\rm p} A^{-1/2} $ (N或Z为偶数时取正、为奇数时取负),N或Z处于1~28, 29~50, 51~82, 83~126和$ \geqslant 127 $ 的范围时$ \delta_{\rm sh} $ 分别等于0, 1, 2, 3和4。式(113)不适用于N或Z为幻数的原子核、$ N=Z $ 的原子核,以及$ S_{\rm n} $ 中$ N-1 $ 为幻数或$ N-1 = Z $ 和$ S_{\rm p} $ 中$ Z-1 $ 为幻数或$ N +1= Z $ 的原子核。根据式(4),$ A > 40 $ 时式(113)给出的$ S_{\rm n} $ 和$ S_{\rm p} $ 的理论计算值与实验值的方均根偏差$ \sigma $ 分别为390 和424 keV。文献[39]将式(113)中的对能项
$ \delta_{\rm pair} $ 替换为式(17)的形式,同时进一步考虑对称能相关的修正,则改进后单中子分离能$ S_{\rm n} $ 和单质子分离能$ S_{\rm p} $ 的半经验公式[39]可分别表示为这里采用的对称能包括体积项
$ \delta_{\rm sv} = a_{\rm sv} |I| $ 和表面项$ \delta_{\rm ss} = a_{\rm ss} |I| A^{-1/3} $ 。引入对称能修正项的理论基础是分离能与对称能相关,虽然主导项$ Z/N $ 或$ N/Z $ 中已经包含了部分原子核对称能效应,然而无论$ Z/N $ 还是$ N/Z $ 都不足以表示对称能,因此文献[39]期望采用与对称能形式相同的修正项以提高理论计算分离能的精度。表13列出了基于单核子分离能实验数据得到的$ A > 40 $ 时式(114)和(115)的拟合系数、方均根偏差$ \sigma $ [见式(4)] 及拟合实验值的个数,可见改进后公式的精度有明显提高,描述$ S_{\rm n} $ 和$ S_{\rm p} $ 实验数据的$ \sigma $ 分别为325和352 keV。需要说明的是,由于主导项$ Z/N $ 或$ N/Z $ 中也包含了部分对称能效应,因此这里对称能修正项的系数$ a_{\rm sv} $ 和$ a_{\rm ss} $ 会与原子核对称能系数有很大不同,两者不能混淆。公式 $ a_{\rm 1} $ $ a_{\rm 2} $ $ a_{\rm 3} $ $ a_{\rm p} $ $ a_{\rm sh} $ $ a_{\rm sv} $ $ a_{\rm ss} $ $ a_{\rm c} $ $ \sigma $ $ \mathcal{N} $ $ S_{\rm n} $ 11.636 3.325 $ -10.561 $ 6.527 $ -1.557 $ 13.967 $ -30.562 $ $ - $ 0.325 1 883 $ S_{\rm p} $ 16.687 1.427 $ -6.975 $ 6.142 $ -1.192 $ $ -26.899 $ 24.399 $ -1.241 $ 0.352 1 818 根据式(114)和(115)给出的单核子分离能半经验公式,可以推导出6.1节中单核子分离能与价核子数的线性关系[39]。以
$ S_{\rm n} $ 为例,将$ N = N_0 + \delta_{\rm n} N_{\rm n} $ 和$ Z = Z_0 + \delta_{\rm p} N_{\rm p} $ 代入式(114),可得其中
$ N_0 $ 和$ Z_0 $ 分别为距离中子数和质子数最近的幻数,$ A_0 = N_0 + Z_0 $ 。对比上式和式(106),可得以
$ 104 \leqslant N \leqslant 125 $ 、$ 66 \leqslant Z \leqslant 81 $ 的半壳区域为例,式(117)和(118)给出的$ K\alpha = -0.27 $ MeV、$ K\beta = 0.14 $ MeV,与图17(a)的拟合结果($ K\alpha = -0.29 $ MeV、$ K\beta = 0.15 $ MeV)非常接近。文献[40]在式(114)和(115)的基础上进一步考虑了与对称能高阶项——四阶体对称能项
$ \delta'_{\rm sv} = a'_{\rm sv} |I|^3 $ 相关的修正 [这里不考虑四阶表面对称能项形式的修正,因为该项会导致拟合系数的不稳定(详见4.1节)[197]],同时在原有壳修正的基础上增加了一项壳修正$ a'_{\rm sh} \delta'_{\rm sh} $ ,其中$ \delta'_{\rm sh} $ 的形式在$ S_{\rm n} $ 和$ S_{\rm p} $ 的半经验公式中分别为N或Z为粒子型(空穴型)时取正(负),
$ x>0 $ 时$ {\rm Sgn} [x] = 1 $ ,$ x \leqslant 0 $ 时$ {\rm Sgn} [x] = 0 $ 。当N或Z最靠近的幻数为20, 28, 50, 82和126时,式(119)和(120)中的r分别等于4, 6, 8, 10和12。当N最靠近的幻数为20, 28, 50, 82和126时,式(119)中的c分别等于1, 2, 3, 2和1;当Z最靠近的幻数为20, 28, 50和82时,式(120)中的c分别等于1, 2, 2和1。此外文献[40]令式(114)和(115)中的$ \delta_{\rm pair} = 0 $ ,取而代之的是在拟合时将拟合系数$ a_1 $ 、$ a_2 $ 和$ a_3 $ 按照原子核的奇偶类型分为四类。改进后
$ S_{\rm n} $ 和$ S_{\rm p} $ 的半经验公式[40]分别表示为根据单核子分离能实验值得到的
$ A > 40 $ 时式(121)和(122)的拟合系数、方均根偏差$ \sigma $ [见式(4)] 及拟合实验值的个数在表14中给出。可以看到,文献[40]的改进有效提高了$ S_{\rm n} $ 和$ S_{\rm p} $ 半经验公式的精度。公式 $ a^{\rm ee}_{\rm 1} $ $ a^{\rm ee}_{\rm 2} $ $ a^{\rm ee}_{\rm 3} $ $ a^{\rm eo}_{\rm 1} $ $ a^{\rm eo}_{\rm 2} $ $ a^{\rm eo}_{\rm 3} $ $ a^{\rm oe}_{\rm 1} $ $ a^{\rm oe}_{\rm 2} $ $ a^{\rm oe}_{\rm 3} $ $ a^{\rm oo}_{\rm 1} $ $ a^{\rm oo}_{\rm 2} $ $ a^{\rm oo}_{\rm 3} $ $ S_{\rm n} $ 22 534 2 049 −15 297 21 055 2 235 −15 165 15 749 2 747 −15 244 17 182 2 450 −15 075 $ S_{\rm p} $ 14 828 1 940 −3 217 14 033 2 355 −7 627 14 840 2 012 −4 049 14 334 2 248 −7 022 公式 $ a_{\rm sh} $ $ a'_{\rm sh} $ $ a_{\rm sv} $ $ a'_{\rm sv} $ $ a_{\rm ss} $ $ a_{\rm c} $ $ \sigma $ $ \mathcal{N} $ $ S_{\rm n} $ −944 −27 20 405 −99 025 −7 995 − 273 1 883 $ S_{\rm p} $ −426 −48 −41 601 −55 941 82 408 −1 604 305 1 818 注:ai(i= 1, 2, 3)的上标 “ee”、“eo”、“oe” 和“oo” 分别对应偶偶核、偶奇核、奇偶核和奇奇核。 -
本节主要讨论第1~6节介绍的几种理论模型对原子核基态物理量的预言。基于已知实验数据,可根据理论模型计算得到原子核物理量的理论值,将其与最新数据表中新增的实验数据对比,相应的方均根偏差由式(5)计算给出。基于最新的AME2020数据表[3],本文在附件(见科学数据银行)[99]中给出了部分未知质量剩余(或结合能)、α衰变能和分离能的预言结果及相应不确定度(计算方法与文献[48]一致)。此外本节还讨论全局型质量模型预言结果相对实验数据的偏差(包括奇偶性和线性修正)。
-
本节讨论对原子核质量或结合能的预言。考虑两种外推情况,第一种是从AME2016数据表[8]到AME2020数据表[3]的外推,第二种是从AME2003数据表[10]到AME2020数据表[3]的外推,它们的预言方均根偏差(分别标记为
$ \sigma_1 $ 和$ \sigma_2 $ )和预言到的原子核质量个数见表15。表15第$ 2\sim3 $ 和12~13列“GK”对应1.1节中的式(2)~(3)[44-45],第4~5和14~15列"GKs"对应1.2节图3 中的10个关系式[108],第6~7和16~17列"GK + J"对应1.3节中基于式(12)的新外推方法[112],第8~9和18~19列"δV(in−jp)"对应2.1节中的式(15)和(19)[(i, j)=(1,1), (2,1)和(1, 2)][49],第10~11和20~21列"GK+δF(1n−1p)"对应3.3节中的式(42)~(47)[135]。区域 GK[44-45] GKs[108] GK + J[112] $ \delta V_{i {\rm n}-j {\rm p}} $[49] GK + $ \delta F_{\rm 1n-1p} $ GK[44-45] GKs[108] GK + J[112] $ \delta V_{i {\rm n}-j {\rm p}} $[49] GK + $ \delta F_{\rm 1n-1p} $[135] $ \sigma_1 $ $ \mathcal{N} $ $ \sigma_1 $ $ \mathcal{N} $ $ \sigma_1 $ $ \mathcal{N} $ $ \sigma_1 $ $ \mathcal{N} $ $ \sigma_1 $ $ \mathcal{N} $ $ \sigma_2 $ $ \mathcal{N} $ $ \sigma_2 $ $ \mathcal{N} $ $ \sigma_2 $ $ \mathcal{N} $ $ \sigma_2 $ $ \mathcal{N} $ $ \sigma_2 $ $ \mathcal{N} $ $ A \geqslant 16 $ 461 70 286 70 559 61 215 67 272 60 783 302 729 316 529 283 507 307 634 292 $ A \geqslant 60 $ 272 57 256 57 431 56 189 54 231 52 503 263 495 270 451 260 431 261 457 257 $ A \geqslant 120 $ 215 38 156 38 258 38 169 36 196 37 323 166 262 171 243 166 269 166 273 166 注:"GK"、"GKs"、"GK + J"、"$\delta V_{i {\rm n}-j {\rm p}}$"和"GK + $\delta F_{\rm 1n-1p}$"分别对应1.1节中的式(2)~(3)[44-45]、1.2节图3中的10个关系式[108]、1.3节基于式(12)的新外推方法[112]、2.1节的式(15)、(19)[$(i, j)=(1, 1)$, (2,1)和(1, 2)][49]和3.3节的式(42)~(47)[135]。$\sigma_1$和$\sigma_2$分别为从AME2016数据表[8]到AME2020数据表[3]和从AME2003数据表[10]到AME2020数据表[3]的外推预言方均根偏差。 对比表15中的预言结果可知,由于轻核区平均场不太稳定,原子核结构随核子数变化相对剧烈,因此这些基于局部区域内相互作用近似不变假设的局域型理论模型在轻核区的预言方均根偏差普遍较大,此外随着预言范围的增加方均根偏差明显变大,即
$ \sigma_2 $ 远大于$ \sigma_1 $ (除了"GK + J")。相比其它理论模型,"GK + J"预言已知数据附近的$ \sigma_1 $ 相对较大,而预言远离稳定线区域的$ \sigma_2 $ 较小($ A \geqslant 120 $ 区域的$ \sigma_2 $ 最小,其它区域仅次于"$ \delta V_{i {\rm n}-j {\rm p}} $ ")。有意思的是,"GK + J"的预言方均根偏差随预言范围增加的变化不大,甚至在轻核区和$ A \geqslant 120 $ 区域其$ \sigma_2 < \sigma_1 $ 。在$ A \geqslant 16 $ 和$ A \geqslant 60 $ 区域,"$ \delta V_{i {\rm n}-j {\rm p}} $ "的精度最高。相比GK关系,"GKs"和"GK +$ \delta F_{\rm 1n-1p} $ "的预言方均根偏差更小,且"GKs"能够预言到的原子核质量个数更多。"GK +$ \delta F_{\rm 1n-1p} $ "在$ 16 \leqslant A <120 $ 区域比较有优势,而"GKs"在$ A \geqslant 120 $ 区域的精度更高($ \sigma_1 $ 最小,$ \sigma_2 $ 仅次于"GK + J")。鉴于上述理论模型具有良好的预言效果,本文基于AME2020数据表[3]在附件[99]中列出了利用"GKs"、"GK + J"、"$ \delta V_{i {\rm n}-j {\rm p}} $ "和"GK +$ \delta F_{\rm 1n-1p} $ "这四种不同方法计算的部分原子结合能或质量剩余及其不确定度(限于1 000 keV)。对轻核区的丰质子核,考虑第5节中的镜像核质量公式,根据式(5),5.1节中式(80)~(82)[58]预言的7个和20个丰质子核质量的方均根偏差
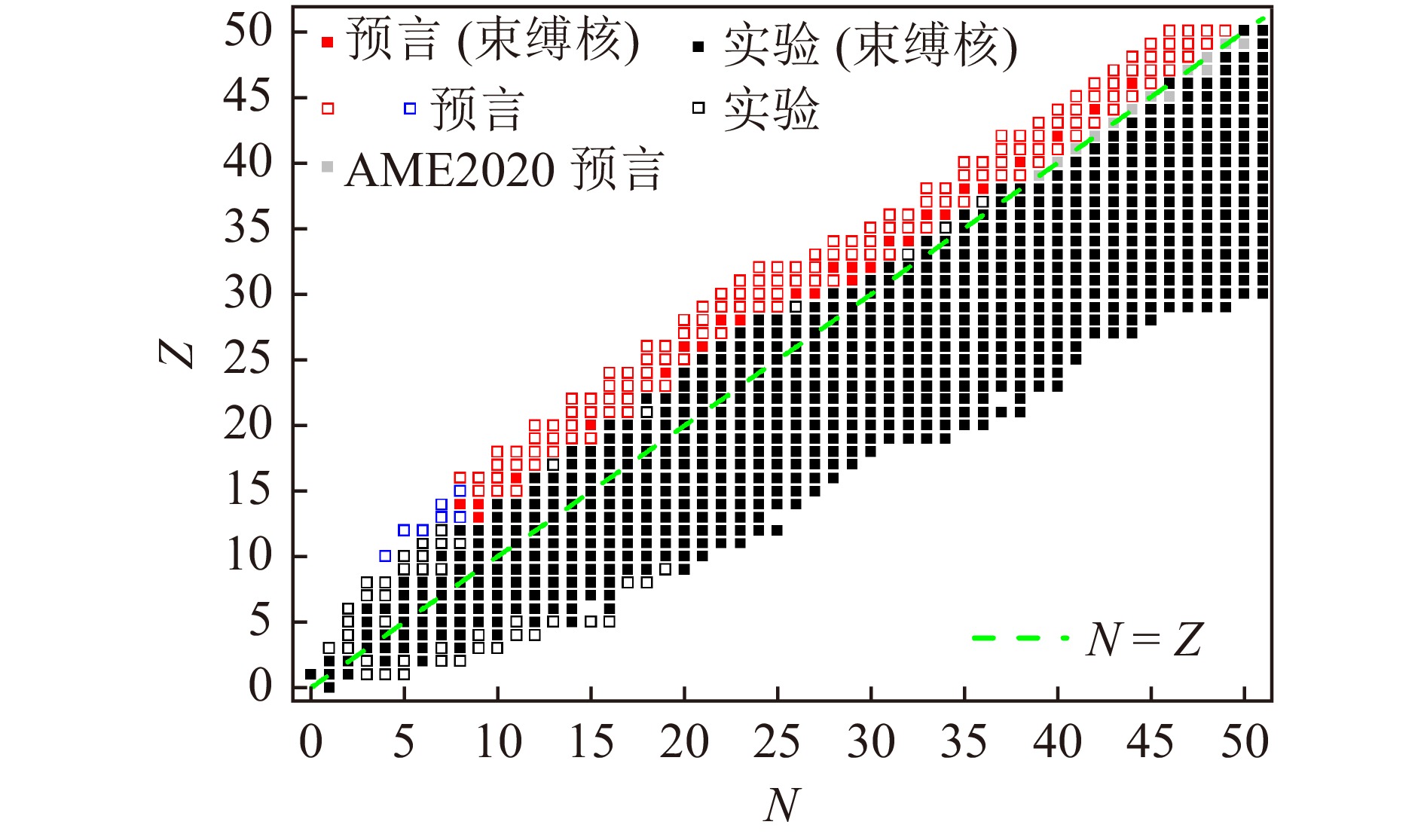
$ \sigma_1 $ 和$ \sigma_2 $ 分别为89 和118 keV,远小于相应GKs关系或$ \delta V_{i {\rm n}-j {\rm p}} $ 关系的预言方均根偏差。由于AME2016数据表[8]和AME2003数据表[10]中$ ^{44} {\rm{V}}$ 的质量实验值与AME2020数据表[3]中的实验值相差较大,因此在拟合式(80)和(81)时本文采用了AME2020数据表[3]中$ ^{44} {\rm{V}}$ 的质量作为已知实验数据。基于AME2020数据表[3],利用式(80)~(82)[58]预言的71个丰质子区($ k \leqslant 4 $ 且$ N \geqslant 10 $ )的原子质量剩余及其不确定度$ \sqrt{F} $ 在本文附件[99]中给出。若进一步考虑5.3节中对偏差的修正[59],则式(82)和式(90)~(91)预言6个和15个丰质子核质量的$ \sigma_1 $ 和$ \sigma_2 $ [见式(5)] 分别为65 和79 keV,可见这些预言结果的精度是非常高的。基于AME2020数据表[3](排除误差较大的
$ ^{28}{\rm{S}} $ 、$ ^{71}{\rm{Kr}} $ 和$ ^{75} {\rm{Sr}}$ 的质量实验数据)并考虑文献[61]中的库仑修正,利用式(96)~(105)预言的26个束缚核和136个非束缚系统的质量剩余以及部分单质子、双质子分离能,见本文附件[99]。图19中用红色($ A>21 $ )和蓝色($ A\leqslant 21 $ )正方形标记了这些预言到的束缚核和非束缚系统,其中黑色正方形表示AME2020数据表[3]中有质量实验值的原子核,灰色正方形表示AME2020数据表[3]中有质量预言值的原子核,实心正方形表示质子滴线内的束缚核,空心正方形表示质子滴线外的非束缚系统,绿色短划线标记$ N=Z $ 的位置。 -
文献[228-229]中指出一个有趣的事实,即A为偶数的原子核结合能在统计上大于其相邻A为奇数的原子核结合能[100, 230, 231],这些额外的能量导致单核子分离能表现出一定的奇偶效应,而一些流行的理论模型(如FRDM[19-22]、WS公式[23-27]、DZ模型[77]和SHFB理论[29-33]等)并没有很好地描述实验数据的这种奇偶性。
根据式(1)和式(38),利用AME2020数据表[3]中的结合能实验值和理论模型给出的结合能计算值,可分别得到单中子分离能的实验值
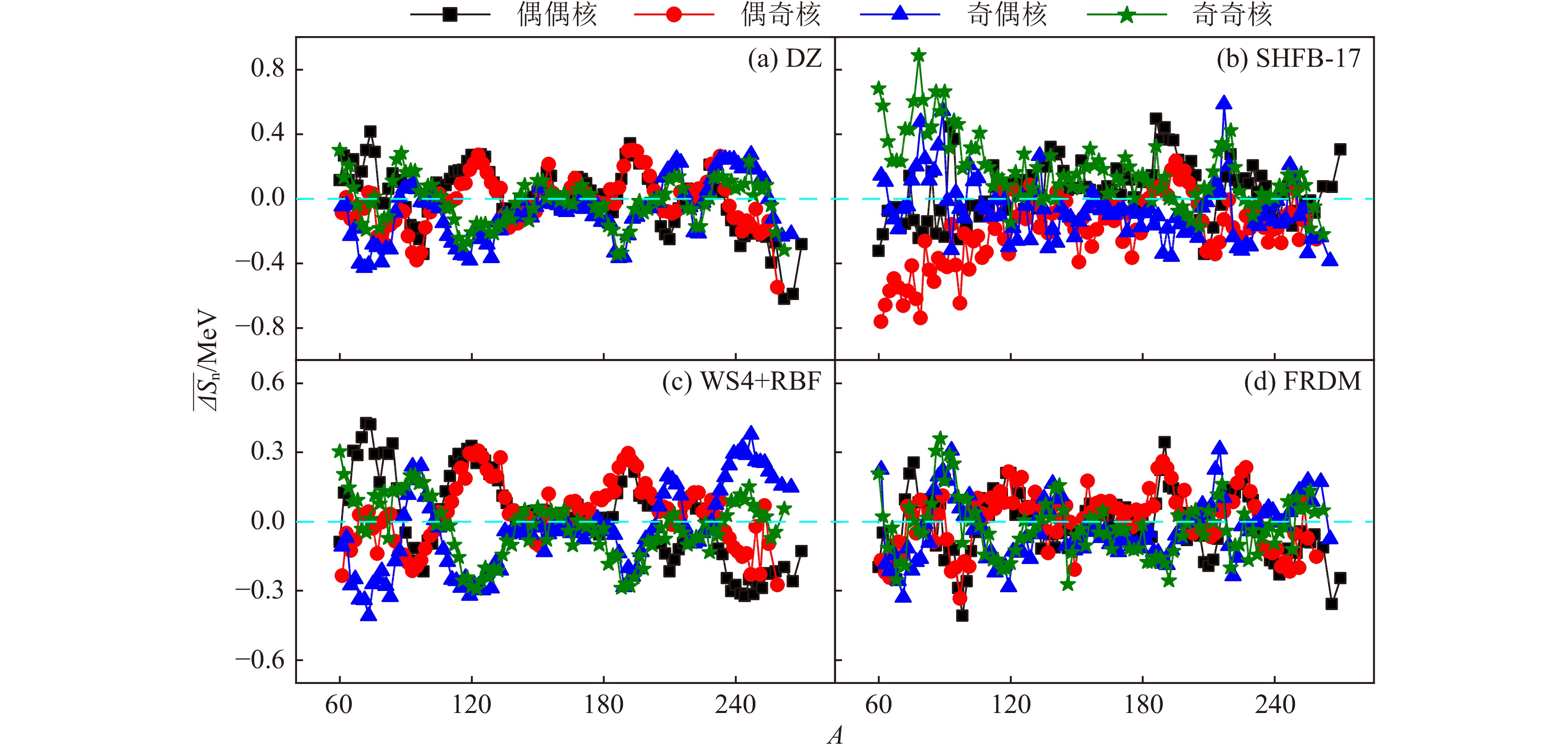
$ S^{\rm exp}_{\rm n} $ 和理论计算值$ S^{\rm th1}_{\rm n} $ 。图20给出了$ A \geqslant 60 $ 时,单中子分离能的理论计算值与其实验值的偏差$ \varDelta S_{\rm n} = S^{\rm exp}_{\rm n} - S^{\rm th1}_{\rm n} $ 关于质量数A的平均值(标记为$ \overline{\varDelta S}_{\rm n} $ ),其中(a)、(b)、(c)和(d)中涉及的$ S^{\rm th1}_{\rm n} $ 分别来自DZ模型[77]、SHFB-17模型[31]、考虑径向基的WS4公式(标记为"WS4+RBF")[27]和FRDM[21],黑色正方形、红色圆形、蓝色三角形和绿色星形分别对应偶偶核、偶奇核、奇偶核和奇奇核,青色虚线标记$ \overline{\varDelta S}_{\rm n} = 0 $ 的位置。图20中四种理论模型的
$ \overline{\varDelta S}_{\rm n} $ 都表现出明显的奇偶效应[228],尤其是在大部分区域 N为偶数的$ \overline{\varDelta S}_{\rm n} $ (黑色正方形和红色圆形)和N为奇数的$ \overline{\varDelta S}_{\rm n} $ (蓝色三角形和绿色星形)的正负号都是相反的。这种奇偶效应与2.1节图4(a)中$ \delta V_{\rm 1n-1p} $ 的奇偶效应[48, 124]以及文献[63, 230]中提到的单核子分离能中细微的奇偶效应(见6.1节)一致[228-229],都与原子核中的中子-质子相互作用有关[231]。将理论模型给出的质量计算值(标记为
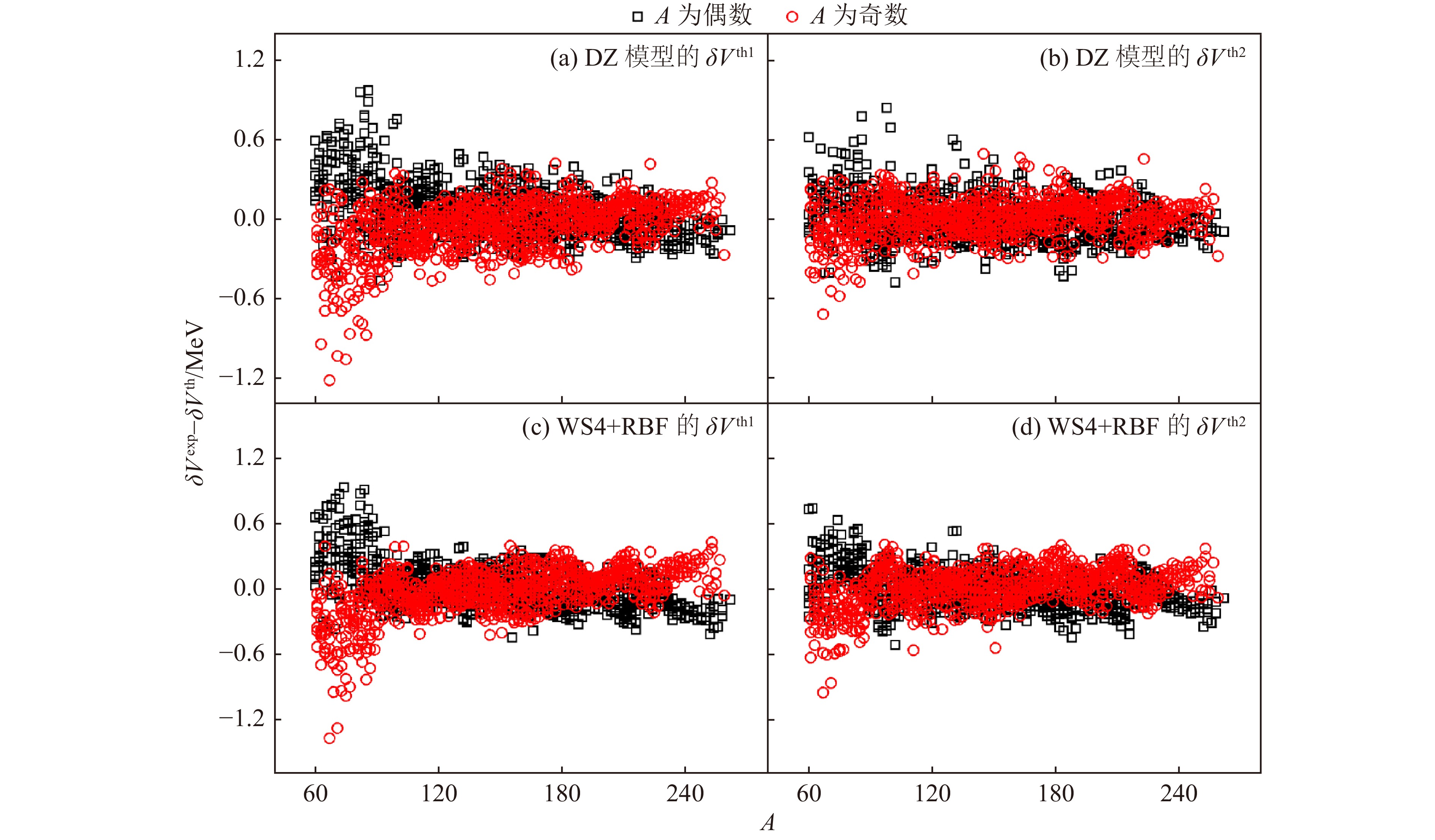
$ M^{\rm th1} $ )代入式(15),可得$ \delta V_{\rm 1n-1p} $ 的理论计算结果(标记为$ \delta V^{\rm th1} $ )。图21(a)和(c)分别给出了$ A \geqslant 60 $ 且$ N>Z $ 时DZ模型[77]和"WS4+RBF"[27]给出的$ \delta V^{\rm th1} $ 与基于AME2020数据表[3]计算得到的$ \delta V_{\rm 1n-1p} $ 的实验值(标记为$ \delta V^{\rm exp} $ )之间的偏差($ \delta V^{\rm exp} - \delta V^{\rm th1} $ ),其中黑色正方形和红色圆形分别对应A为偶数和奇数的情况。从图中可以看到,由这两种理论模型得到的$ \delta V^{\rm th1} $ 与其实验值的偏差对A为偶数和奇数的情况都有明显差别(尤其是在$ A \leqslant 100 $ 的区域),这说明DZ模型和"WS4+RBF"中存在未消除的奇偶效应[229]。若以简单的形式考虑该奇偶效应,则可提高这些理论模型的预言精度[228-229]。文献[229]通过引入同位旋相关的奇偶项,有效降低了结合能和单中子分离能的理论计算值与实验值之间的方均根偏差。令
其中
$ C_1 $ 、$ C_2 $ 、$ C'_1 $ 、$ C'_2 $ 、$C''_1$ 和$C''_2$ 为拟合系数。当$ A \geqslant 60 $ 且$ N>Z $ 时,基于AME2020数据表[3]得到的A为偶数和奇数时的拟合结果以及相应的方均根偏差 [见式(5)]在表16中给出,其中$ \sigma'_1 $ 和$ \sigma'_2 $ 分别为考虑奇偶修正前后("$ {\rm th1} $ "和"$ {\rm th2} $ ")的方均根偏差。M $ S_{\rm n} $ $ \delta V_{\rm 1n-1p} $ DZ[77] WS4+RBF[27] DZ[77] WS4+RBF[27] DZ[77] WS4+RBF[27] $ C_1({\rm e}) $ 2.328 0.385 $ C'_1({\rm e}) $ 0.787 0.940 $C''_1({\rm e})$ 1.873 1.825 $ C_2({\rm e}) $ −15.341 −2.288 $ C'_2({\rm e}) $ −4.764 −5.310 $C''_2({\rm e})$ −9.877 −10.567 $ C_1({\rm o}) $ 1.283 −0.543 $ C'_1({\rm o}) $ −1.276 −0.848 $C''_1({\rm o})$ −2.190 −1.868 $ C_2({\rm o}) $ −9.794 3.101 $ C'_2({\rm o}) $ 6.046 4.746 $C''_2({\rm o})$ 11.861 10.664 $ \sigma'_1 $ 0.547 0.157 $ \sigma'_1 $ 0.257 0.225 $ \sigma'_1 $ 0.207 0.214 $ \sigma'_2 $ 0.524 0.153 $ \sigma'_2 $ 0.247 0.217 $ \sigma'_2 $ 0.155 0.175 注:系数$C_i$、$C'_i$和$C''_i$($i = 1, 2$)括号内的"e"和"o"分别对应A为偶数和奇数的情况。式(123)~(125)中的同位旋相关修正有效提高了全局型理论模型的预言精度。 对比表16的最后2行可知,对M、
$ S_{\rm n} $ 和$ \delta V_{\rm 1n-1p} $ ,修正后DZ模型[77]的方均根偏差分别降低了23, 10和52 keV,"WS4+RBF"的方均根偏差分别降低了4, 8和39 keV。根据式(125)和表16中的拟合系数,图21(b)和(d)分别给出了修正后DZ模型[77]和"WS4+RBF"[27]的$ \delta V^{\rm th2} $ 与$ \delta V^{\rm exp} $ 之间的偏差($ A \geqslant 60 $ 且$ N>Z $ ),显然式(125)给出的同位旋相关修正有效减少了图21(a)和(c)中$ \delta V_{\rm 1n-1p} $ 的偏差关于A的奇偶差别。值得说明的是,这些修正项关于A有良好的鲁棒性,即如果将式(123)~(125)中的$ A^{-1/3} $ 和$ A^{-4/3} $ 分别替换为$ A^{-1/2} $ 和$ A^{-3/2} $ 或分别替换为$ A^{-1} $ 和$ A^{-2} $ ,得到的方均根偏差相比没有修正时的$ \sigma'_1 $ 同样有明显降低[229]。 -
文献[232]进一步讨论了7.2节中全局型理论模型的预言结果与实验数据的偏差,并提出可以通过线性修正简单有效地提高理论模型描述和预言原子核质量、单核子分离能以及电荷半径的精度。这种方法利用物理量理论预言值与实验值偏差之间的局域相关性来改进全局型理论模型的精度,效果显著。
以原子核质量为例,图22给出了
$ Z > 28 $ 时全局型理论模型给出的质量计算值$ M^{\rm th1} $ 与AME2012数据表[9]中质量实验值$ M^{\rm exp} $ 的偏差$ D(N, Z) $ 与$ D(N \pm 2, Z) $ 的关系图,其中黑色正方形和红色圆形分别对应丰中子核 [横坐标取$ D(N - 2, Z) $ ] 和丰质子核 [横坐标取$ D(N + 2, $ Z)][232]。图22(a)、(b)、(c)和(d)分别对应"WS4+RBF"[27]、"HFB-31"[34]、DZ模型[77]和相对论平均场(Relativistic Mean Field,RMF)质量模型[233]。从图22可以看到,$ D(N, Z) $ 和$ D(N \pm 2, Z) $ 之间存在线性关系($ y = \lambda x $ ),其拟合系数$ \lambda $ 和相应的皮尔森系数r见表17的第三列和第四列。考虑这种线性修正,即令理论模型 区域 $ \lambda $ r $ \sigma'_1 $ $ \sigma'_2 $ WS4+RBF 丰中子 0.75 0.75 150 104 丰质子 155 101 HFB-31 丰中子 0.76 0.74 464 318 丰质子 497 331 DZ 丰中子 0.78 0.67 400 305 丰质子 313 226 RMF 丰中子 0.97 0.93 1 840 843 丰质子 2 535 737 注:第三、四列分别为式(126)中的线性拟合系数$\lambda$和相应的皮尔森系数r,第五、六列分别为修正前后$M^{\rm th1}$和$M^{\rm th2}$在丰中子区和丰质子区的方均根偏差$\sigma'_1$和$\sigma'_2$ [见式(5),单位:keV]。 则在丰中子区和丰质子区,修正前后
$ M^{\rm th1} $ 和$ M^{\rm th2} $ 与相应实验数据的方均根偏差$ \sigma'_1 $ 和$ \sigma'_2 $ [见式(5)] 在表17的第五列和第六列给出,对比可知修正后的$ \sigma'_2 $ 相比$ \sigma'_1 $ 降低了24%~71%[232]。图23为
$ Z > 28 $ 时上述四种全局型理论模型给出的质量预言值与AME2020数据表[3]中新增质量实验数据的偏差及相应不确定度,其中黑色正方形和红色圆形分别表示线性修正前后,即$ M^{\rm th1} $ 和$ M^{\rm th2} $ 与实验数据的偏差。图23(a)、(b)、(c)和(d)分别对应"WS4+RBF"[27]、"HFB-31"[34]、DZ模型[77]和RMF质量模型[233],蓝色虚线标记偏差为零的位置。这里修正后质量不确定度$ \sigma_{\rm pre2} $ 的定义为其中
$ \sigma'_2 $ 为线性修正后式(126)给出的$ M^{\rm th2} $ 与实验数据的方均根偏差;$ \sigma_{\rm exp} $ 为相应原子核质量的实验误差。从图23可以看到,式(126)的线性修正可效提高全局型理论模型预言原子核质量的精度(方均根偏差比修正前降低了14%~76%,例如,在丰质子区DZ模型和RMF质量模型的预言方均根偏差分别从419和5 245 keV降低到306和1 256 keV)[232]。 -
本节通过数值实验讨论式(35)~(37)外推预言α衰变能的效果。数值实验所采用的实验数据有两个来源,原子核质量数
$ A < 270 $ 的α衰变能是根据式(33)的定义从AME2012数据表[9]中提取出来的,而$ A \geqslant 270 $ 的实验数据来自文献[234-239]。利用式(35)~(37)的$ \delta Q_{i {\rm n}-j {\rm p}} $ 关系 [$ (i, j)=(1, 1), (2, 1) $ 和(1, 2)][66]进行外推,得到的计算结果与近年新增39个实验数据($ A < 270 $ 和$ A \geqslant 270 $ 的α衰变能分别提取自AME2020数据表[3]和文献[3]中的表III)之间的方均根偏差 [见式(5)] 为189 keV。根据最新的α衰变能实验数据,图24给出了利用式(35)~(37)[66]预言的Z=89~118同位素链的α衰变能(用黑色圆形表示),其中图(a)和(b)分别为Z为偶数和奇数的情况。从图24可以看到,α衰变能的理论计算值与实验值(用红色五角星表示)吻合得很好。本文附件[99]中汇总了利用式(35)~(37)[66]外推预言的499个
$ A \geqslant 200 $ 且理论不确定度小于等于500 keV的α衰变能。 -
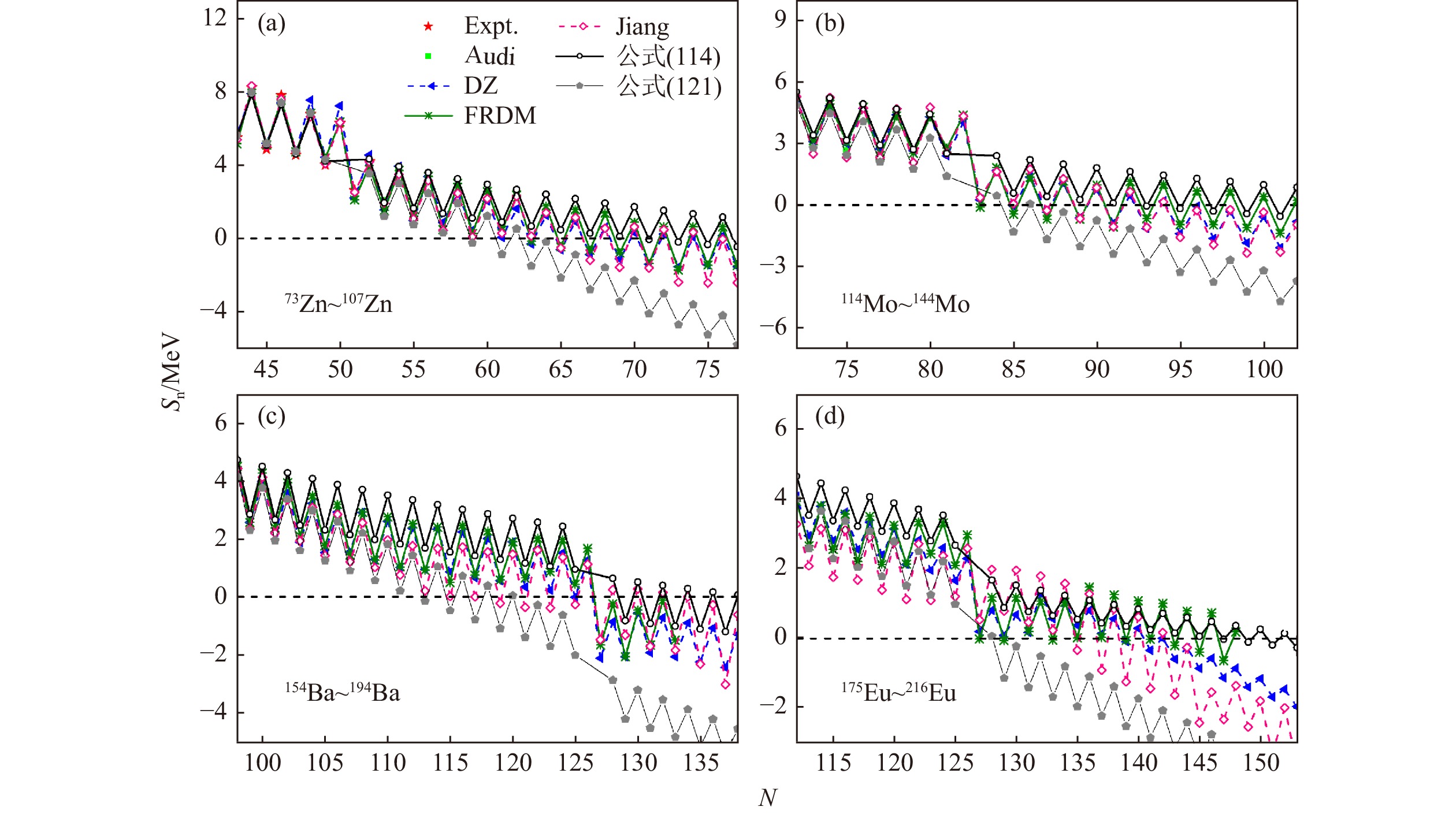
本节通过两组数值实验讨论对单核子分离能的预言,一是从AME2016数据表[8]到AME2020数据表[3]的预言,二是从AME2003数据表[10]到AME2020数据表[3]的预言,它们的预言方均根偏差分别标记为
$ \sigma_1 $ 和$ \sigma_2 $ 。对$ A > 40 $ 的原子核,从式(114)~(115)[39]或式(121)~(122)[40]出发,拟合已知实验数据得到参数来计算单核子分离能,得到的理论计算值与AME2020数据表[3]中新增实验数据的预言方均根偏差 [见式(5)] 在表18中给出。从表18可以看到,式(114)给出的$ S_{\rm n} $ 与实验值的方均根偏差更小,而式(122)预言的$ S_{\rm p} $ 精度更高。基于AME2020数据表[3],本工作利用式(114)~ (115)[39]和式(121)~(122)[40]计算的部分
$ S_{\rm n} $ 和$ S_{\rm p} $ 在本文附件[99]中给出。图25给出了Zn、Mo、Ba和Eu同位素链单中子分离能$ S_{\rm n} $ 的实验值和一些理论计算值,其中式(114)和式(121)的计算结果分别用黑色圆形和灰色五边形表示,根据AME2020数据表[3]中结合能实验值(预言值)计算出的$ S_{\rm n} $ 用红色星形(浅绿色正方形)表示,DZ模型[77]、FRDM[21]和"Jiang"[49]的计算结果分别用蓝色三角形、绿色星号和粉色菱形表示,黑色虚线标记$ S_{\rm n} = 0 $ 的位置。若
$ S_{\rm n}(N, Z)> 0 $ 且$ S_{\rm n}(N+1, Z)< 0 $ ,则N对应的位置即为中子滴线。从图25可以看出,在远离稳定线区域,由于考虑了四阶体对称能项的修正,式(121)给出的$ S_{\rm n} $ 比其它理论模型的$ S_{\rm n} $ 下降得更快,中子滴线对应的N普遍较小,而式(114)对应的N则普遍较大,总体上式(114)的结果与其它理论预言更接近。此外,图25(d)中不同理论模型给出的中子滴线之外的预言结果快速发散,这表明研究现状还不尽人意,有待进一步深入讨论。 -
原子核电荷半径和质量、自旋、宇称一样是原子核的基本性质,它描述了一个原子核的尺度,同时也能提供原子核结构演化的直观信息[240-241]。实验上,可以用高能电子散射和同位素位移等方法测量电荷半径,最新的CR2013数据表[5, 242]中包含了957个电荷半径的实验值。理论上,一些微观模型[7, 29-34, 37, 243-245]和宏观-微观模型[246-250]可以被用于计算电荷半径,近期基于RMF理论修正的电荷半径公式被证明可有效再现电荷半径在中子幻数处的转折特征以及关于中子数N的奇偶振荡现象[251-254]。电荷半径也可以用一些简单的经验公式来描述,例如
$ 1.2 A^{1/3} $ fm[255],其它唯象公式见文献[68-70, 256-259]。此外,还有一些原子核电荷半径的局域型和区域型公式,如电荷半径的双重差分与偶偶核四极形变参数之间的线性关系[74]和基于同位素链的电荷半径关系[260]等。本节讨论原子核电荷半径的两种关系,分别是局域型的电荷半径双重差分和区域型的同位素电荷半径差分关系。本节所有计算都基于CR2013数据表[5, 242]中电荷半径的实验值。 -
原子核电荷半径会随着质子数的增加而增加,同时随着中子数的变化中子-质子相互作用也会导致电荷半径的改变,因此文献[72]在独立粒子壳模型的框架下提出了电荷半径的局域双重差分关系,即
其中
$ R(N, Z) $ 是中子数为N、质子数为Z的原子核电荷半径。类比2.1节讨论的$ \delta V_{i {\rm n}- j {\rm p}} $ 关系,将式(127)重复应用于相邻原子核,可得[72-73]式(127)~(130)统称为
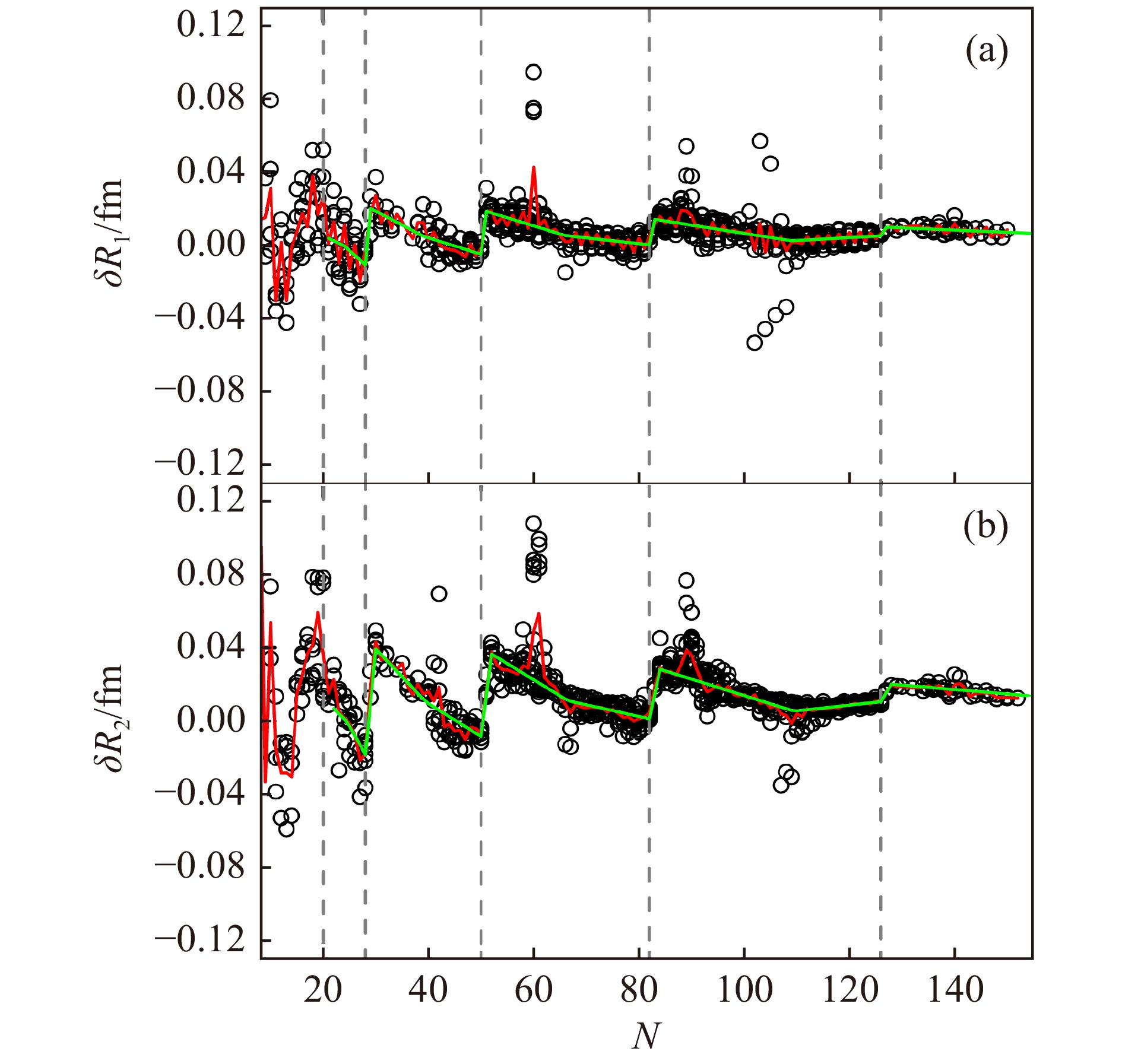
$ \delta R_{i{\rm n}-j{\rm p}} $ 关系,这些关系式都属于局域相干性差分法。$ N, Z \geqslant 8 $ 时式(127)~(130)的方均根偏差$ \sigma $ [见式(4)] 在表19的第2行给出。若已知式(127)[或式(128)、(129)和(130)] 中所涉及任意3个原子核的电荷半径,则可计算出剩下第4个原子核的电荷半径。因此对于给定的第i个原子核,根据它与其它已知电荷半径原子核不同的相对位置,式(127)[或式(128)、(129)和(130)]最多有4种关于电荷半径$ R_i $ 的计算结果,取所有计算结果的平均值作为该原子核电荷半径的理论值$R^{\,\rm th}_{i}$ ,则根据式(5)计算的描述$ N, Z \geqslant 8 $ 区域电荷半径实验数据的方均根偏差$ \overline{\sigma} $ 及个数$ \mathcal{N} $ 在表19的第3行给出,其中最后一列“组合”表示同时使用式(127)~(130)的计算结果,在这种情况下$ R^{\rm th}_{i} $ 最多由16种计算结果的平均值给出。由表19可知,$ \delta R_{\rm 1n-1p} $ 的精度最高;同时使用四个公式计算时,虽然其$ \overline{\sigma} $ 略大于$ \delta R_{\rm 1n-1p} $ 的$ \overline{\sigma} $ ,但能够计算到的电荷半径个数却比$ \delta R_{\rm 1n-1p} $ 多很多。文献[73]进一步讨论了
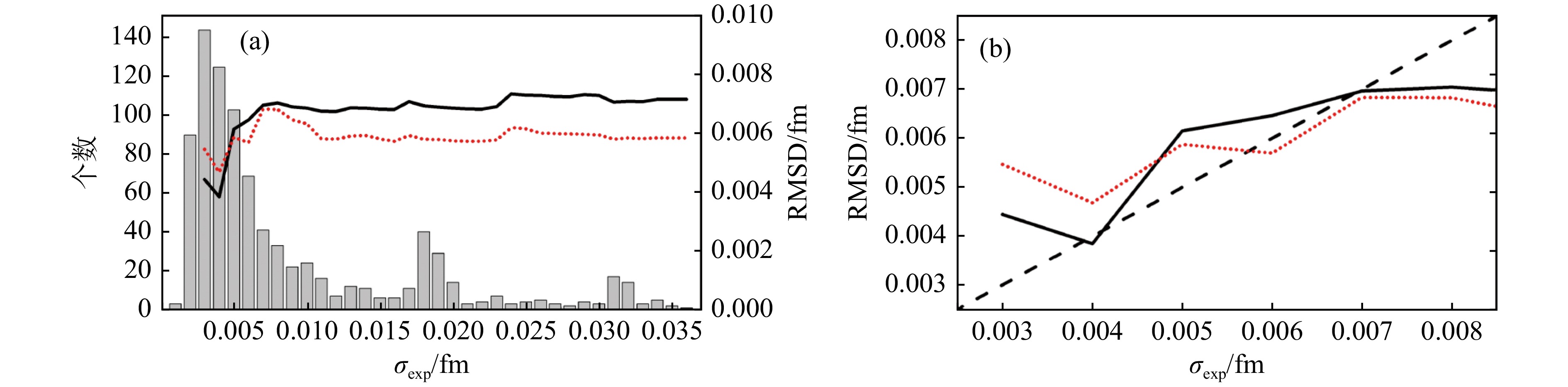
$ \delta R_{\rm 1n-1p} $ 的方均根偏差。图26给出了$ \delta R_{\rm 1n-1p} $ 的$ \sigma $ 和$ \overline{\sigma} $ 与电荷半径实验误差$ \sigma_{\rm exp} $ 的关系图。图26(a)中的柱状图表示给定实验误差$ \sigma_{\rm exp} $ 所对应的电荷半径实验数据个数,可以看到,大部分电荷半径的实验误差都小于0.1 fm。图26中的黑色实线和红色点线分别是描述实验误差小于等于给定$ \sigma_{\rm exp} $ 的电荷半径实验数据的$ \sigma $ 和$ \overline{\sigma} $ 。图26(b)中的黑色虚线标记方均根偏差等于$ \sigma_{\rm exp} $ 的情况,可以看到,如果只考虑$ \sigma_{\rm exp} \leqslant 0.007 $ fm的电荷半径实验数据,则$ \delta R_{\rm 1n-1p} $ 的$ \sigma $ 和$ \overline{\sigma} $ 基本与$ \sigma_{\rm exp} $ 相等,这说明$ \delta R_{\rm 1n-1p} $ 的理论计算精度可以和电荷半径的实验测量精度相比,如果进一步降低实验值的测量误差,$ \delta R_{\rm 1n-1p} $ 的精度可能会更高[73]。图27给出了利用式(127)~(130)计算的电荷半径理论值与相应实验值偏差的绝对值[75],其中图(a)、(b)、(c)和(d)分别对应
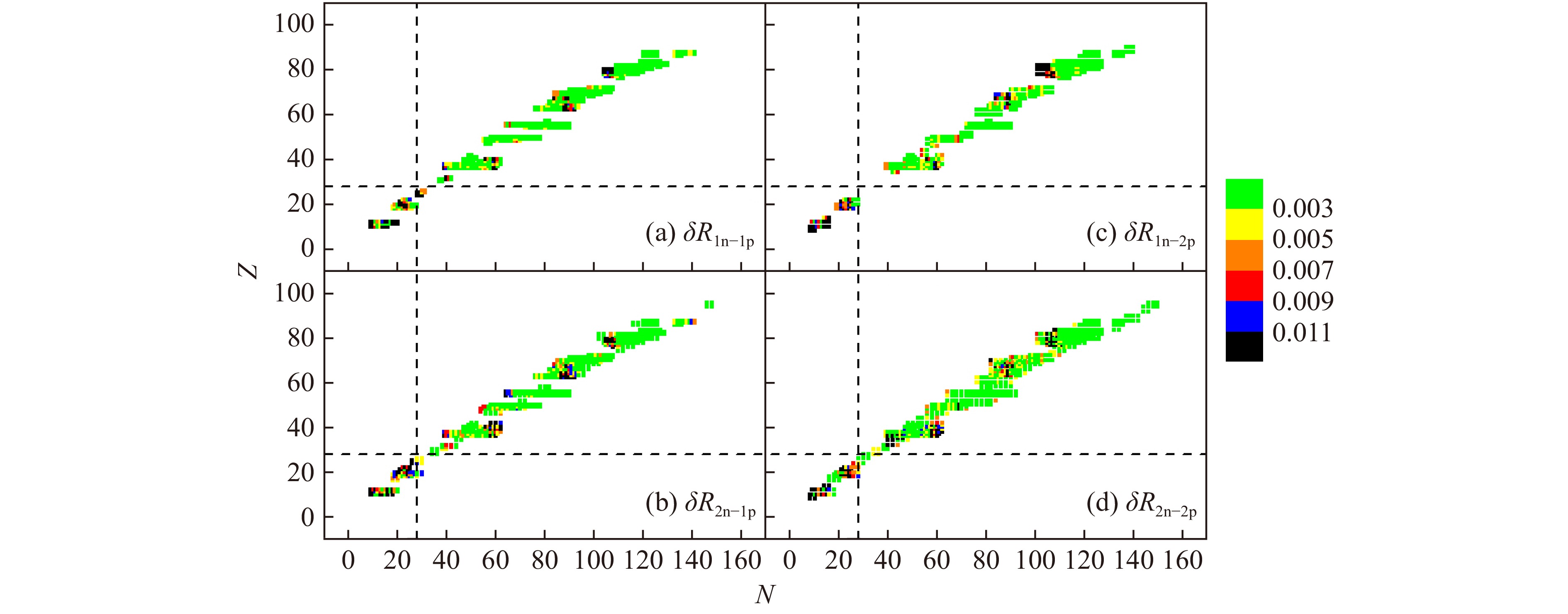
$ \delta R_{\rm 1n-1p} $ 、$ \delta R_{\rm 2n-1p} $ 、$ \delta R_{\rm 1n-2p} $ 和$ \delta R_{\rm 2n-2p} $ ,黑色虚线标记了$ N, Z = 28 $ 的位置。从图27可以看出,在$ N, Z<28 $ 区域$ \delta R_{i {\rm n}-j {\rm p}} $ 的偏差普遍较大,而$ N, Z \geqslant 28 $ 时大部分电荷半径偏差的绝对值都小于0.003 fm,偏差较大的主要集中在以下三个区域:(1)$ N \sim 60 $ 且$ Z \sim 38 $ ;(2)$ N \sim 90 $ 且$ \delta R_{\rm 1 n - 1 p} $ 和$ \delta R_{\rm 2 n - 1 p} $ 中$ Z \sim 63 $ 或$ \delta R_{\rm 1 n - 2 p} $ 和$ \delta R_{\rm 2 n - 2 p} $ 中$ Z \sim 67 $ ;(3)$ N \sim 108 $ 且$ Z \sim 80 $ [75]。在以上三个区域中出现的较大偏差都与原子核结构的演化有关:(1)原子核在$ N = 60 $ 、$ Z \sim 40 $ 处突然出现形变[261];(2)在$ N = 90 $ 、$ Z \sim 64 $ 附近存在形状相变[262];(3)在$ Z = 78 \sim 80 $ 、$ N \sim 104 $ 区域,原子核的四极形变参数和$ E_{2_1^+} $ 都表现出异常,这是由于靠近中子子壳的原子核可能存在形状共存态[137]。原子核的这些结构演化在其它物理量的局域型或区域型理论中也有所体现[139]。 -
文献[76]研究了两个同位素的电荷半径之差,定义
上式也可表示为
假设原子核是球形的,并且质子在原子核内是均匀分布的,那么原子核的电荷半径应该基本与Z1/3成正比关系[256-257],则根据式(131)
图28给出了
$ \delta R_1 $ 和$ \delta R_2 $ 与N的关系图[76],其中黑色圆形为$ \delta R_k $ ($ k = 1, 2 $ )的实验值,红色实线为$ \delta R_k $ 关于N的平均值 [标记为$ \overline{\delta R}_k(N) $ ]。可以看到,$ \overline{\delta R}_k(N) $ 在中子幻数处(用灰色虚线标记)有大幅增加,随后缓慢下降,且$ \delta R_2 $ 相对于零的偏差明显大于$ \delta R_1 $ 。此外由于形变或形状共存等因素,$ \delta R_k $ 在以下四个范围表现出异常:(1)$ N \leqslant 20 $ ;(2)$ N = 60 $ 且$ 37 \leqslant Z \leqslant 41 $ ;(3)$ 88 \leqslant N \leqslant 90 $ 且$ 62 \leqslant Z \leqslant 67 $ ;(4)$ N \leqslant 108 $ 且$ 78 \leqslant Z \leqslant 79 $ ,或$ N \leqslant 106 $ 且$ Z = 80 $ [76]。以上四个$ \delta R_k $ 的异常区域,与8.1节讨论的$ \delta R_{i {\rm n}-j {\rm p}} $ 的几个异常区域基本一致。根据式(4),
$ k = 1 $ 时式(133)的方均根偏差$ \sigma $ 为0.014 fm($ N>8 $ ),接近表19中$ \delta R_{i {\rm n}-j {\rm p}} $ 关系的精度;根据式(132),当$ k >1 $ 时$ \delta R_k $ 相对于零的偏差会变大。为了提高$ \delta R_k $ 的精度,文献[76]引入了关于N的修正,将$ k = 1 $ 时的式(133)改写为其中
$ N_0 $ 为半满壳时的中子数;$ a_1 $ 、$ a_2 $ 和b为拟合系数;对不同壳层的拟合结果在表20中给出。$ k>1 $ 时的$ \delta R_k $ 由式(132)和式(134)给出。图28中的绿色实线为式(132)和式(134)给出的$ k=1 $ 和2时$ \delta R_k $ 的理论计算值,若不考虑上述四个异常区域,$ \delta R_1 $ 和$ \delta R_2 $ 的方均根偏差$ \sigma $ [见式(4)] 分别为0.005 0和0.006 3 fm,相比式(133)有明显降低。参数 $ 21 \leqslant N \leqslant 28 $ $ 29 \leqslant N \leqslant 50 $ $ 51 \leqslant N \leqslant 82 $ $ 83 \leqslant N \leqslant 126 $ $N \geqslant 127$ $ a_1 $ $ -1.417 $ $ -1.520 $ $ -0.881 $ $ -0.449 $ $ -0.121 $ $ a_2 $ $ -2.577 $ $ -0.899 $ $ -0.317 $ $ 0.158 $ $ - $ b $ -0.150 $ $ 5.226 $ $ 5.548 $ $ 2.696 $ $ 6.744 $ -
本节考虑基于CR1999数据表[263]和CR2004数据表[264]的外推预言数值实验,相应的方均根偏差由式(5)给出,分别标记为
$ \sigma_{R1} $ 和$ \sigma_{R2} $ 。为了避免在数值实验中出现不当结果,本节将CR1999数据表[263]和CR2004数据表[264]中的实验值替换为CR2013数据表[5, 242]中相应的实验结果。图29给出了同时使用式(127)~(130)[73]得到的
$ N, Z \geqslant 8 $ 时原子核电荷半径的理论预言值与CR2013数据表[5, 242]中相应实验值的偏差,其中黑色数据点表示已知电荷半径实验值的原子核,图(a)和(b)分别是基于CR1999数据表[263]和CR2004数据表[264]的预言结果。可以看到,在这两种外推情况下,电荷半径的外推预言值与实验值偏差的大小基本都小于0.04 fm。图29(a)和(b)中两种外推预言的方均根偏差$ \sigma_{R1} $ 和$ \sigma_{R2} $ [见式(5)] 分别为0.022 4 和0.014 0 fm,相应预言到的电荷半径个数分别为530个和147个。基于最新的CR2013数据表[5, 242],利用式(127)~(130)[73]外推预言的1 031个不确定度(计算方法与文献[48]一致)小于等于0.03 fm的未知电荷半径见本文附件[99]。根据式(131),若已知
$ R(N-k, Z) $ 或$ R(N+k, Z) $ 的实验值,则可根据得到原子核
$ (N, Z) $ 的电荷半径计算值,其中$ \delta R^{\rm th} $ 可由式(132)和式(134)给出,也可通过其它理论模型给出[76]。因此给定一个原子核,考虑$ k = 1 $ ~15的情况,根据式(135)和(136)最多有30种关于其电荷半径的计算结果,选取其中理论不确定度最小的计算结果作为该原子核电荷半径的理论值$ R^{\rm th}(N, Z) $ ,相应的预言方均根偏差 [见式(5)] 在表21中给出,其中第2~6行分别为$ \delta R^{\rm th} $ 由式(132)和(134)[76]、"HFB-31"[34]、RCHB[7]、"RMF+ BCS"[244]和WS*公式[70]给出时的结果(计算时排除了8.2节中$ \delta R_k $ 异常的四个形状相变或形状共存区域)。这里根据式(135)和(136)计算的电荷半径的理论不确定度分别定义为其中
$ \sigma_{\rm exp} $ 为相应电荷半径的实验误差,$ \sigma_{\rm th1} $ 为$ \delta R^{\rm th}_1 $ 的理论不确定度,对"HFB-31"[34]、RCHB[7]、"RMF+BCS"[244]、WS*公式[70]和式(134)[76]分别取0.011, 0.005, 0.011, 0.006和0.005 fm[76]。由表21可知,基于式(132)和(134)[76]以及WS*公式[70]得到的电荷半径预言方均根偏差最小(RCHB[7]和“RMF+BCS”[244]的参数个数较少,且RCHB理论假设原子核具有球对称性)。基于CR2013数据表[5, 242],将这两种理论模型得到的预言结果的平均值作为最终的理论计算值
$ \delta R_k^{\rm th} $ 代入式(135)~(136)中计算,得到的1 647个不确定度小于等于0.03 fm的未知电荷半径在本文附件[99]中给出。这里电荷半径的不确定度为其中
$ R^{\rm th}_1 $ 和$ R^{\rm th}_2 $ 分别为式(132)和(134)[76]和WS*公式[70]给出的电荷半径理论计算值,$ \sigma_{\rm pre1} $ 和$ \sigma_{\rm pre2} $ 为相应计算结果的不确定度。 -
原子核是由质子和中子组成的复杂量子多体系统,迄今为止人们对核力的理解还不深入,核多体理论本身也不成熟,所以对原子核结构和反应机制的研究还面临着很多挑战,深入理解作为自然界基本层次之一的原子核还任重而道远。另一方面,原子核又呈现出许多简单性,人们能够基于这些系统规律寻找理解原子核结构和反应性质的线索。本文从不同角度讨论了原子核质量和原子核电荷半径的系统规律,这些系统规律具有图像直观、简单实用且精度较高的特点。
本文讨论了原子核质量局域相干性差分法(SOLID)的几个典型结果,包括基于中子-质子相互作用的
$ \delta V_{i {\rm n}-j {\rm p}} $ 关系[49]、Garvey-Kelson质量(GK)关系[44-45]、推广的GK(GKs)关系[108]和所谓的“GK + J”[112]、“GK +$ \delta F_{\rm 1n-1p} $ ”[135]外推方法。根据数值实验,$ \delta V_{i {\rm n}-j {\rm p}} $ 关系在$ A \geqslant 16 $ 和$ A \geqslant 60 $ 区域有明显优势,GKs关系在$ A \geqslant 120 $ 区域精度很高且能外推预言到更多的原子核质量,“GK + J”外推方法更适用于远离已知边界的区域,而“GK +$ \delta F_{\rm 1n-1p} $ ”在$ 16 \leqslant A < 120 $ 区域的方均根偏差较小。我们注意到GK关系有奇偶效应,利用这种奇偶性可以有效降低GK关系描述原子核质量的方均根偏差[41],此外GKs关系(除了GKL-4和GKT-4关系)的偏差[108]关于中子数N的平均值也表现出明显的奇偶振荡现象,这些奇偶效应与$ \delta V_{1 {\rm n}-1 {\rm p}} $ 关系中的奇偶性是一致的。本文基于区域型镜像核质量公式讨论了质子滴线附近质量数
$ A<115 $ 核素(甚至是质子滴线外非束缚系统)的质量[56-59]。我们利用镜像核质量差与相应库仑能之差的关系,大幅降低了库仑能理论计算所带来的不确定度;如果进一步考虑由核子配对效应所导致的库仑能奇偶性,则可构造出精度非常高的区域型原子核质量公式,这些公式的理论预言结果与后续实验测量结果在很高精度内一致。一些常见理论模型给出的多种物理量的计算结果与其实验数据存在系统性的偏离,最近人们注意到这些偏离存在简单的局域相关性[59, 127, 232],这种相关性为进一步提高理论模型计算结果和预言未知区域原子核物理量的精度提供了一个新途径。本文讨论了核子分离能与价核子数之间的区域型关系[63],同时也在改进核子分离能的全局型唯象
$ N/Z $ 或$ Z/N $ 半经验公式方面做了有益尝试[39-40]。关于α衰变能$ Q_{\alpha} $ 和电荷半径R,本文总结了近年来关于$ \delta Q_{i {\rm n}-j {\rm p}} $ 局域型关系[66]和$ \delta R_{i {\rm n}-j {\rm p}} $ 局域型关系[73]、$ \delta R_k $ 区域型关系[76]的主要结果。可以证明,满足局域双重差分为零的物理量在局部区域内可以表示为$ N_{\rm n} $ 和$ N_{\rm p} $ 的函数之和,而Csaten经验公式可看作局域双重差分为零的特殊情况。对于粒子型和空穴型的价空间,价中子-价质子之间的总相互作用与$ N_{\rm n}N_{\rm p} $ 相关性的差别反映了原子核在集体演化方面的差异。本文回顾了在利用原子核质量的双重差分和全局型质量公式[24]提取对称能系数[162]、利用局域型质量关系提取Wigner能系数[163]方面的研究。基于AME2020数据表[3]得到的对称能系数结果为
$ c_2^{\rm(v)} =(32.48 \pm 0.16) $ MeV、$ c_2^{\rm(s)} = (59.93 \pm 0.53) $ MeV、$\kappa_{\rm s/v} = 1.85 \pm 0.02$ ,Wig-ner能系数结果为$ a_W =(42.57 \pm 1.16) $ MeV、$ a_d =(28.66 \pm 1.52) $ MeV。我们基于最新版本的实验数据库(AME2020[3]中的原子质量剩余或结合能、文献[3]表III中
$ A\geqslant 270 $ 的α衰变能和CR2013数据表[5, 242]中的电荷半径),利用本文综述的多种方法得到了部分不确定度小于等于1 000 keV的原子质量剩余(或结合能)和单(双)核子分离能、不确定度小于等于500 keV的α衰变能以及不确定度小于等于0.03 fm的原子核电荷半径的预言结果,作为本文的附件(见科学数据银行)[99]。对于已知实验数据边界附近的原子核,不同理论模型给出的质量或电荷半径预言结果之间的差异一般并不太大。然而,原子核版图上依然存在着非常广阔的未知区域,特别是中等质量和重质量丰中子区域,人们对这些核素的性质所知甚少,不同理论模型预言的原子核质量之间存在很大的差异,此外我们对导致电荷半径关系异常的形状相变机制理解还不够深入,因此在未来相当长的时间内,从理论和实验两方面对质量、电荷半径等原子核基态结构性质的研究都将是原子核物理的重要前沿课题,包括鉴别或合成新核素、登陆超重稳定岛、探索远离稳定线区域的新物理等[147]。我们期望未来积累越来越多的原子核基态或激发态实验数据(尤其是中等质量区和重质量区的丰中子核素版图空白区域),以修正和完善现有理论模型,加深我们对核多体问题的认识和理解。
致谢 感谢有马朗人先生的指导和长期合作,感谢程奕源、傅冠健、何增、雷杨、李剑、林沫琼、刘敏、路毅、马畅、寿嵘、孙保华、王琨、王宁、尹鑫、虞瀚诚、张双全、宗瑶瑶等的合作,感谢陈列文、华辉、李宝安、马余刚、孟杰、任中洲、孙立杰、王猛、杨晓菲、张丰收、张鸿飞、张玉虎、R. F. Casten、P. V. Isacker、S. Pittel等人的有益讨论。








































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号 DownLoad:
DownLoad: