-
20世纪50年代，核物理学家根据已有的实验数据提出，原子核的形状可以偏离球形，从而能够产生与双原子分子转动谱类似的能谱[1]。自此以后，形变原子核的转动性质一直是核物理学重要的研究领域之一。实验上使原子核发生转动的方式主要有重离子熔合反应、库仑激发反应，锕系核的裂变反应等。由于实验条件的限制，早期关于转动原子核的研究主要局限于
$ \beta $ 稳定线附近原子核的低自旋态上。随着世界各地重离子加速器的建立以及探测技术的发展，科学家们进一步拓展了其研究范围。一方面，拓展到了远离$ \beta $ 稳定线的奇特核以及超铀核；另一方面，布居了原子核的高自旋态。当原子核高速转动时，会产生诸如回弯[2-3]、带终结[4-5]、超形变[6]、摇摆运动[7] 等一系列奇特的物理现象，吸引了大批国内外核物理学家的研究兴趣。锕系区是实验上能够布居原子核高自旋态最重的核区，目前在此质量区的原子核中已经观测到了 一系列的转动谱[8-9]，特别地，实验上于2012年还首次观测到超重核
$ ^{256}{\rm{Rf}} $ 的转动谱[10]。实验数据显示这个质量区的原子核都具有稳定形变，其四极形变$\beta\approx 0.28\pm 0.02$ [11]。由于形变效应，决定超重核区能级结构和质子幻数的若干关键的单粒子能级，例如质子$ 2f_{5/2} $ 和$2f_{7/2}^{}$ ，会降低到这些原子核的费米面附近。研究这些核的高自旋结构可以揭示其组态结构、壳层结构等诸多信息，从而一方面对现有的理论模型进行检验，另一方面有助于深入认识超重核性质。众所周知，形变原子核转动带中的回弯现象是由于高
$ j $ 低$ \Omega $ 轨道上一对粒子被拆散，从而使得这对粒子的角动量沿着转动轴顺排所导致的[12]。稀土区原子核的第一个回弯/上弯由一对$i_{13/2}^{}$ 中子顺排引起，第二个回弯/上弯由一对$ h_{11/2} $ 质子顺排引起[3]。对于U-Pu区的原子核，质子$i_{13/2}^{}$ 和中子$j_{15/2}^{}$ 轨道均位于其费米面附近，因此，这个质量区的回弯/上弯现象可以归结为由这两条高$ j $ 轨道上一对粒子的顺排引起。推转壳模型的计算表明，在这个质量区，质子$i_{13/2}^{}$ 和中子$j_{15/2}^{}$ 的能级交叉 频率非常接近，这导致很难分辨转动带中的回弯/上弯到底是质子还是中子的贡献，从而使得锕系核的顺排十分复杂。特别地，实验观测表明，这个质量区许多原子核的转动带中并未观测到中子$j_{15/2}^{}$ 引起的顺排，这与推转壳模型的计算矛盾。许多理论对此进行了解释，把此现象归结为对关联或者 高阶形变的影响等[13-14]。但是到目前为止，理论上对此现象尚未能够给出一个满意的解释。相较于偶偶核，奇$ A $ 核能够提供更为丰富的谱学信息。尤其是当奇质子占据$i_{13/2}^{}$ 轨道时，由于堵塞效应，质子$i_{13/2}^{}$ 对回弯/上弯没有贡献，这将有助于我们研究此质量区顺排的机制。本文将采用基于推转壳模型的粒子数守恒方法来研究实验上观测到的
$ ^{235}{\rm{Np}} $ 和$ ^{237}{\rm{Np}} $ 中的转动带[15-16]，分析其带头自旋以及组态构成，并理解其顺排机制。与传统的BCS(Bardeen-Cooper-Schrieffer)或者HFB(Hartree-Fock-Bogoliubov)方法不同，粒子数守恒方法在一个截断的多粒子组态空间中直接把多体哈密顿量对角化，从而保证在计算中粒子数严格守恒，并且能够精确考虑奇核子的堵塞效应。值得注意的是，本方法已经用来系统研究超镄核、超重核的基态以及高$ K $ 同核异能态的转动性质[17-23]。近年来，粒子数守恒方法已经得到了很大的发展，它已经被移植到许多理论模型中，例如total-Routhian-surface方法[24]、推转Skyrme-Hartree-Fock方法[25]以及推转协变密度泛函理论[26-27]。最近，He等[28]发展了包含八极形变的粒子数守恒方法 。此外，由于人们越来越重视如何更加精确地处理对关联，近些年发展出了许多类似的粒子数严格守恒的方法[29-34]。 -
包含对力的推转 Nilsson 哈密顿量[35]可以写为
$$ H_{\rm{CSM}}^{} = H_0^{} + H_{\rm{P}^{}} = H_{\rm Nil}^{}-\omega J_x^{} + H_{\rm{P}} ^{} \ , $$ (1) 其中：
$H_0 ^{}$ 为单体哈密顿量，包括Nilsson哈密顿量$H_{\rm Nil} ^{}$ 和Coriolis相互作用$-\omega J_x^{}$ ；$H_{\rm P}^{} = H_{\rm P}^{}(0) + H_{\rm P}^{}(2)$ 为对相互作用，包括单极对力和四极对力$$ H_{\rm P}^{}(0) = -G_{0}^{} \sum\limits_{\xi\eta}^{} a^\dagger_{\xi} a^\dagger_{\bar{\xi}} a_{\bar{\eta}}^{} a_{\eta}^{} \ , $$ (2) $$ H_{\rm P}^{}(2) = -G_{2}^{} \sum\limits_{\xi\eta}^{} q_{2}^{}(\xi)q_{2}^{}(\eta) a^\dagger_{\xi} a^\dagger_{\bar{\xi}} a_{\bar{\eta}}^{} a_{\eta}^{} \ 。 $$ (3) $\bar{\xi}(\bar{\eta})$ 表示Nilsson态$\xi(\eta )$ 的时间反演态，$q_{2}^{}(\xi) = \sqrt{{16\pi}/{5}} \times \langle \xi |r^{2}Y_{20}^{} | \xi \rangle$ ，$G_0 ^{}$ 和$G_2 ^{}$ 是单极和四极有效对力强度。在粒子数守恒方法中，通过采用多粒子组态截断，把推转壳模型哈密顿量
$ H_{\rm CSM} $ 在一个足够大的推转多粒子组态空间(CMPC)中直接对角化以后就可以得到哈密顿量基态以及低激发态足够精确的解[36-37]。研究表明，CMPC空间的维度取1 000已经足够满足对于重核的计算。对角化后，$H_{\rm{CSM}}^{}$ 的本征态$ |\Psi\rangle $ 具有确定的粒子数、宇称和旋称，并且计算中堵塞效应是自动而且严格考虑的。$ |\Psi\rangle $ 可以表示为$$ |\Psi\rangle = \sum\limits_{i} ^{}C_i | i \rangle \ , $$ (4) 其中
$ | i \rangle $ 是一个 CMPC，它是单体哈密顿量$H_0 ^{}$ 的本征态；$C_i^{}$ 是展开系数，为实数。在
$ | \Psi \rangle $ 态下，沿着$ x $ 方向的角动量$J_x ^{}$ 的期待值(角动量顺排)可以写为$$ \langle \Psi | J_x ^{}| \Psi \rangle = \sum\limits_i^{} C_i^2 \langle i | J_x^{} | i \rangle + 2\sum\limits_{i<j}^{}C_i ^{}C_j^{} \langle i | J_x^{} | j \rangle \ 。 $$ (5) 运动学转动惯量可以表示为
$$ J^{(1)} = \frac{1}{\omega} \langle\Psi | J_x^{} | \Psi \rangle \ 。 $$ (6) 由于
$J_x^{}$ 是一个单体算符，只有当两个CMPC$ |i\rangle $ 和$ |j\rangle $ 的占据相差1个粒子态时，$ \langle i | J_x | j \rangle $ ($ i\neq j $ )矩阵元才不为零。假设$ \mu $ 和$ \nu $ 为相差的单粒子态，其它粒子态的填布相同，$ |i\rangle $ 和$ |j\rangle $ 可写为$$ | i \rangle = | \cdots \mu \cdots \rangle \ , \quad | j \rangle = | \cdots \nu \cdots \rangle \ 。 $$ (7) 经过一系列产生算符的对易后，上式可化为
$$ \begin{split}| i \rangle = (-1)^{M_{i\mu}} | \mu \cdots \rangle \ , \quad | j \rangle = (-1)^{M_{j\nu}} | \nu \cdots \rangle \ ， \end{split} $$ (8) 其中
$M_{i\mu}^{}$ 和$M_{i\nu}^{}$ 是费米子的重排次数。由此可得角动量顺排可表示为$$ \langle \Psi | J_x^{} | \Psi \rangle = \sum\limits_{\mu}^{} j_x^{}(\mu) + \sum\limits_{\mu<\nu}^{} j_x^{}(\mu\nu) \ 。 $$ (9) 对角元和非对角元为
$$ \begin{split} j_x^{}(\mu) = &\langle \mu | j_{x}^{} | \mu \rangle n_{\mu} \ , \\ j_x^{}(\mu\nu) = & 2 \langle \mu | j_{x}^{} | \nu \rangle \sum\limits_{i<j}^{} (-1)^{M_{i\mu}^{}+M_{j\nu}^{}} C_{i}^{} C_{j}^{} \ ， \end{split} $$ (10) 其中：
$n_{\mu}^{} = \displaystyle\sum\limits_{i}^{} |C_{i}^{}|^{2} P_{i\mu}^{}$ 为推转Nilsson能级$ |\mu\rangle $ 的占据几率。当推转多粒子组态中的$ |\mu\rangle $ 被占据时$P_{i\mu}^{} = 1$ ，当$ |\mu\rangle $ 未被占据时$P_{i\mu}^{} = 0$ 。实验上，每一条转动带的运动学转动惯量
$ J^{(1)} $ 和转动频率$ \hbar\omega $ 可以按下式提取：$$ \begin{split} \frac{J^{(1)}(I)}{\hbar^2} = & \frac{2I+1}{E_{\gamma}^{}(I+1\rightarrow I-1)} \ , \\ \hbar\omega(I) = & \frac{E_{\gamma}^{}(I+1\rightarrow I-1)}{I_{x}^{}(I+1)-I_{x}^{}(I-1)} \ ,\end{split} $$ (11) 其中：
$I_{x}^{}(I) = \sqrt{(I+1/2)^{2}-K^{2}}$ ；$ I $ 为总角动量；$ K $ 为总角动量在对称轴$ z $ 轴上的投影。 -
Hurst等[16]在实验上观测到了
$ ^{235}{\rm{Np}} $ 的两条转动带，他们认为这 两条转动带是组态为$\pi5/2^+[642](i_{13/2}^{})$ 的旋称伙伴带 。此外，文献[16]中还提出，根据对顺排的分析，并不能排除这两条转动带的组态为$\pi5/ 2^-[523](h_{9/2}^{})$ 的可能性。值得注意的是，文献[16]的工作中并未观测到带1中78 keV与带2中101 keV的跃迁，因此在文献[16]的表1和图5中，把这两个跃迁用星号和括号进行了标记。这两个跃迁是1974年 Friedman等[38]在实验中观测到的。文献[16]猜测他们建立起的转动带结构基于文献[38]中观测到的低自旋能级，但缺乏实验证据。Afanasjev等[39]通过推转相对论平均场理论的计算，建议将文献[16]中观测到的转动带结构视为孤立的，并基于系统性重新建议了自旋宇称，即应当把带1中连接$ 9/2\rightarrow 5/2 $ 的78 keV的跃迁去掉，且其他能级所对应的自旋值应当降低1$ \hbar $ 。此外，他们还把这两条转动带的组态指定为$ \pi5/2^-[523] $ 。在下面的研究中，我们首先将确定这两条转动带的自旋及组态。吴崇试与曾谨言从Bohr哈密顿量出发，得到其近似的解析解，进而得到了描述转动带的
$ ab $ 公式[40]：$$ E_I^{} = a\left[ \sqrt{1+bI(I+1)} - 1 \right] \ , $$ (12) 其中
$a,\, b$ 为待定参数。此公式能够非常好地描述原子核的转动谱，并且在转动谱的自旋指定方面取得了很大的 成功[41-43]。根据$ ab $ 公式，由角动量$ I \rightarrow I-2 $ 的跃迁能量$ E_\gamma(I) $ 可以表示为$$ \begin{split} E_\gamma^{}(I) &\equiv E_\gamma^{}(I \rightarrow I-2) \\& = a\left[ \sqrt{1+bI(I+1)} - \sqrt{1+b(I-1)(I-2)} \right] \ 。 \end{split}$$ (13) 可以定义理论和实验值的均方根偏差
$ \sigma $ 以及相对均方根偏差$ \chi $ ：$$ \sigma = \left[ \frac{1}{n} \sum\limits_{i=1}^{n} | E_\gamma^{\rm exp}(I_i) - E_\gamma^{\rm cal}(I_i^{}) |^2 \right]^{1/2} \ , $$ (14) $$ \chi = \left[ \frac{1}{n} \sum\limits_{i = 1}^{n} \left( 1- \frac{E_\gamma^{\rm cal}(I_i^{})}{E_\gamma^{\rm exp}(I_i^{})} \right)^2 \right]^{1/2} \ , $$ (15) 其中：
$E_\gamma^{\rm exp}(I_i^{})$ 和$E_\gamma^{\rm cal}(I_i^{})$ 分别为跃迁能量的实验值和计算值；$ n $ 为拟合实验数据的个数。将实验观测到的跃迁能量用上述转动谱公式进行拟合，使均方根偏差$ \sigma $ 取极小值，就可以得到相应参数$ a $ 和$ b $ 的最佳取值。利用
$ ab $ 公式，我们可以通过指定不同带头自旋对这两条转动带的能谱进行拟合。与78 keV的跃迁相似，101 keV这个跃迁也非文献[16]的观测结果，将其归于带2同样缺乏实验证据，应当和78 keV的跃迁一同舍弃。因此，在以下的拟合中我们忽略了文献[16]带1中78 keV的跃迁以及带2中101 keV的跃迁。从图1中我们可以看到，当$ ^{235}{\rm{Np}} $ 带1的带头自旋指定为7/2，带2的带头自旋指定为9/2时拟合所得到的相对均方根偏差$ \chi $ 最小。需要注意的是，如果我们把实验上101 keV的跃迁放到带2的数据里进行拟合，得到的相应能级的自旋值保持不变。因此，本文通过另一种独立的理论手段，认为文献[39]的建议与我们的结果更相符。
表1中给出了
$ ab $ 公式对于$ ^{235}{\rm{Np}} $ 带1和带2的拟合结果。可以看到$ ab $ 公式能够很好地拟合$ ^{235}{\rm{Np}} $ 中的转动谱，除了在带1低自旋处的两个跃迁与实验偏差较大之外，其余均与实验符合得非常好，其均方根偏差约为$ 2\sim4 $ keV。需要注意的是，如果我们把实验上101 keV的跃迁放到带2的数据里进行拟合，得到的均方根偏差会增大至2.435 keV，并且拟合得到的该跃迁能量为95.7 keV，与实验值偏差较大，这说明此跃迁可能并不属于带2。表 1
$ ^{235}{\rm{Np}} $ 两条转动带跃迁能量$E_\gamma^{}(I \rightarrow I-2)$ 的实验值${E}{\,\rm^{exp}_{\gamma} }$ 以及利用$ ab $ 公式得到的计算值${E}^{\,ab}_{\gamma}$ ($ \sigma $ 为均方根偏差)带1 带2 $I_i\rightarrow ^{} I_f^{} /\hbar$ ${E}\rm^{\,exp}_{\gamma}$/keV ${E}^{\,ab}_{\gamma}$/keV $I_i^{}\rightarrow I_f^{} (\hbar)$ ${E}\rm^{\,exp}_{\gamma}$/keV ${E}^{\,ab}_{\gamma}$/keV 11/2$ \rightarrow $ 7/2 127.1 116.7 13/2$ \rightarrow $ 9/2 143.4 141.2 15/2$ \rightarrow $ 11/2 153.7 161.2 17/2$ \rightarrow $ 13/2 186.6 185.0 19/2$ \rightarrow $ 15/2 200.5 203.6 21/2$ \rightarrow $ 17/2 227.4 226.4 23/2$ \rightarrow $ 19/2 245.9 243.5 25/2$ \rightarrow $ 21/2 265.7 265.0 27/2$ \rightarrow $ 23/2 282.6 280.8 29/2$ \rightarrow $ 25/2 300.0 300.7 31/2$ \rightarrow $ 27/2 316.4 315.3 33/2$ \rightarrow $ 29/2 331.9 333.4 35/2$ \rightarrow $ 31/2 346.3 347.0 37/2$ \rightarrow $ 33/2 360.4 363.2 39/2$ \rightarrow $ 35/2 372.4 375.9 41/2$ \rightarrow $ 37/2 387.8 390.1 43/2$ \rightarrow $ 39/2 402.4 402.1 45/2$ \rightarrow $ 41/2 414.9 414.4 47/2$ \rightarrow $ 43/2 425.3 425.9 49/2$ \rightarrow $ 45/2 439.5 436.3 51/2$ \rightarrow $ 47/2 449.4 447.5 $ a\times10^{-3} $ /keV 9.826 9.177 $ b\times10^{3} $ 1.206 1.313 $ \sigma $ /keV 4.262 1.873 接下来，我们将采用粒子数守恒方法对
$^{235,\, 237}{\rm{Np}}$ 中的转动带进行进一步的研究。本工作中的Nilsson参数($ \kappa, \mu $ )取自文献[19]。通过拟合超镄核区原子核的单粒子能级，我们得到了一套轨道角动量依赖的Nilsson参数[19]，它可以很好地描述这个质量区原子核的低激发谱。锕系区原子核形变的实验数据非常少，并且不同理论模型预测的形变参数也不尽相同[13, 44-45]。在本工作中，形变参数取自文献[44]，对于$ ^{235}{\rm{Np}} $ ，$\varepsilon_2^{} = 0.200$ ，$\varepsilon_4^{} = -0.073$ ；对于$ ^{237}{\rm{Np}} $ ，$\varepsilon_2^{} = 0.200$ ，$\varepsilon_4^{} = -0.067$ 。计算中取质子$N = $ 4，5，6 壳以及中子$N = $ 6，7壳构建推转单粒子组态空间，对于质子和中子，推转多粒子组态空间均取为1 000维。单极和四极有效对力强度除了$ ^{235}{\rm{Np}} $ 质子的四极对力取为零外，其余均取自文献[19]，即$G_{\rm{p}^{}}$ = 0.25 MeV，$G_{\rm{2p}}^{}$ = 0.01 MeV，$G_{\rm{n}}^{}$ = 0.30 MeV，$G_{\rm{2n}}^{}$ = 0.02 MeV。图2展示了
$ ^{235}{\rm{Np}} $ 费米面附近(a)质子和(b)中子的推转Nilsson能级。其中，蓝色和红色的线分别代表宇称为正和负的能级，实线和虚线分别代表旋称$\alpha = +1/2$ 和$\alpha = -1/2$ 的能级。$ ^{237}{\rm{Np}} $ 的能级与此十分相似，因此我们只展示了$ ^{235}{\rm{Np}} $ 的结果。从图2(a)中可以看到，对于$^{235,\, 237}{\rm{Np}}$ ，其基态为$ \pi5/2^+[642] $ ，这与实验上观测到$ ^{237}{\rm{Np}} $ 的基态一致 [15]。质子$i_{13/2}^{}$ 和中子$j_{15/2}^{}$ 轨道均位于其费米面附近，其Nilsson组态分别为$ \pi5/2^+[642] $ 和$ \nu 7/2^-[743] $ 。
图 2
$^{235}{\rm{Np}}$ 费米面附近(a)质子和(b)中子的推转Nilsson 能级(在线彩图)图3展示了粒子数守恒方法计算得到的
$ ^{235}{\rm{Np}} $ 中组态为$ \pi 5/2^+[642] $ 和$ \pi5/2^-[523] $ 的转动惯量与实验值的比较。注意这里按照公式(11)提取转动惯量与转动频率的实验值时，自旋取自表1拟合得到的结果，且去掉了78 keV以及101 keV的跃迁。从图中可以看到，计算得到的组态为$ \pi 5/2^+[642] $ 的转动惯量有明显的旋称劈裂，而实验显示此条转动带的转动惯量在高自旋处没有旋称劈裂，这与$ \pi5/2^-[523] $ 组态的计算结果一致。实验上的转动惯量在低自旋处有旋称劈裂，这与$ \pi5/ 2^-[523] $ 组态的计算结果又不一致。从表1中可以看到，低自旋处$ ab $ 公式拟合的结果与实验的跃迁能量偏差较大，特别是正旋称带(带1)，这可能是由于这条转动带在低自旋处不是纯的集体转动，或者低自旋处的跃迁能量存疑，因此导致计算与实验不符。此外，从图中可以看出，整体来说组态$ \pi5/2^-[523] $ 转动惯量的计算结果与实验符合得更好。因此，粒子数守恒方法的计算表明，此条转动带的组态可能为$ \pi5/2^-[523] $ ，这与Afanasjev等[39]采用推转相对论平均场理论的计算结果一致。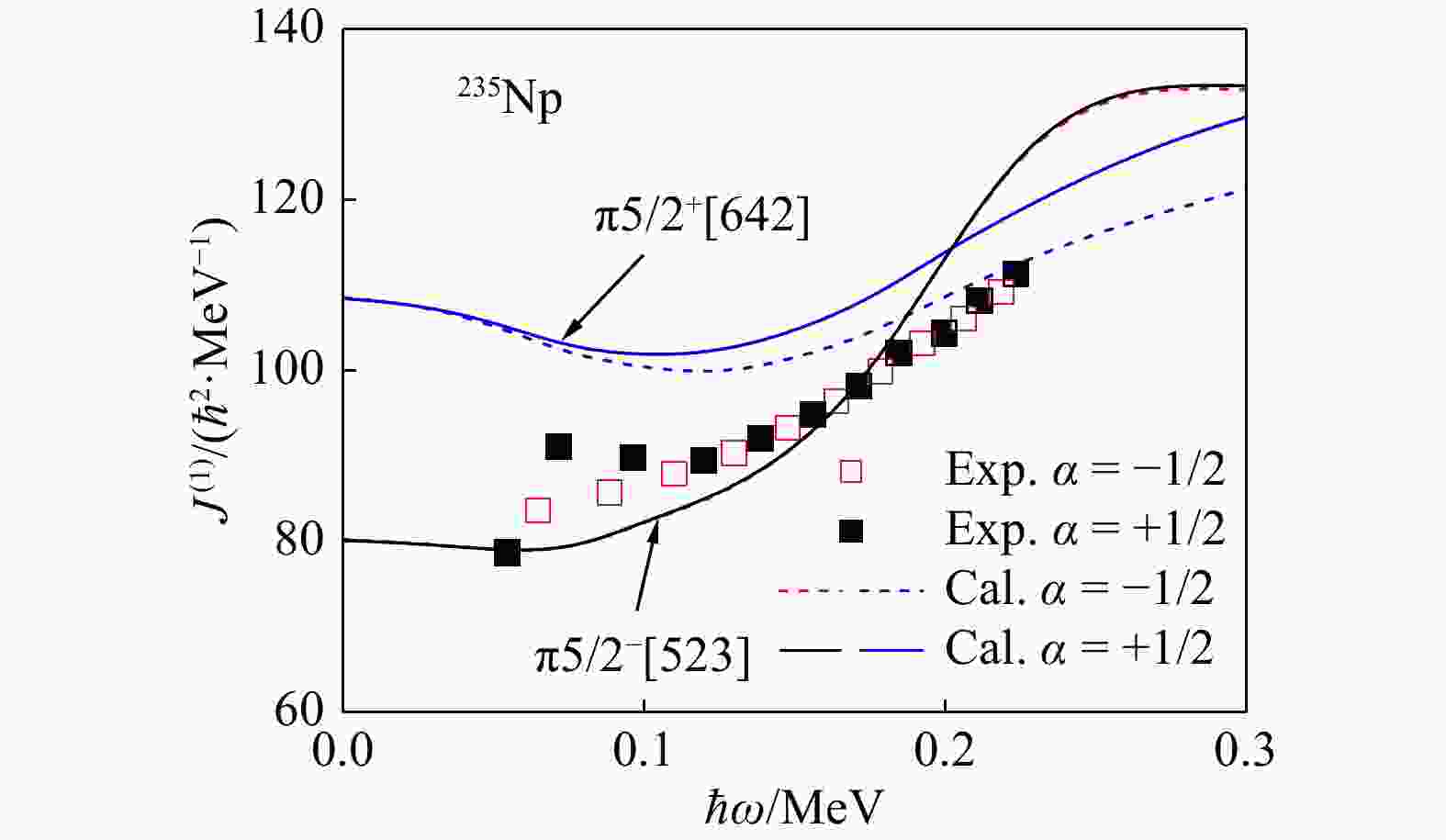
图 3 粒子数守恒方法计算得到的
$^{235}{\rm{Np}}$ 中组态为$\pi 5/2^+[642]$ 和$\pi5/2^-[523]$ 的转动惯量与实验值[16] 的比较(在线彩图)图4展示了粒子数守恒方法计算得到的
$ ^{237}{\rm{Np}} $ 中两条转动带转动惯量(图的上排)和顺排(图的下排)与实验值的比较。可以看到，计算能够很好地再现转动惯量与顺排的实验值。此外，计算能够很好地再现基态带$ \pi 5/2^+[642] $ 中的旋称劈裂。对于$ \pi5/2^+[642] $ ，由于质子$i_{13/2}^{}$ 轨道被堵塞，回弯只能来自于中子$j_{15/2}^{}$ 。从图4(a)和(c)中可以看到，对于这条转动带实验上并未观测到明显的上弯，只在$ \hbar\omega>0.2 $ MeV处出现了非常缓慢的上弯，这表明中子$j_{15/2}^{}$ 对上弯几乎没有贡献。对于$ \pi5/2^-[523] $ ，质子$i_{13/2} ^{}$ 轨道和中子$j_{15/2} ^{}$ 轨道均未被堵塞，因此这两条轨道都可以对$ \pi5/2^-[523] $ 中的上弯有贡献。从图4(b)和(d)中可以看到，这条转动带在$ \hbar\omega>0.2 $ MeV处的上弯也是十分平缓。然而，粒子数守恒方法计算得到的这两条转动带在转动频率$ \hbar\omega\approx0.2 $ MeV处的上弯要明显强于实验，且顺排增益要远大于实验值。对于$ ^{235}{\rm{Np}} $ 的计算结果与此十分相似(见图3)。此外，实验数据显示$ \pi5/2^-[523] $ 在上弯后出现了很明显的旋称劈裂，旋称$ \alpha=-1/2 $ 分支的上弯更加明显。而粒子数守恒方法对这条带两个旋称分支的计算结果几乎没有劈裂。这是由于这条能级在我们的计算中几乎是简并的[见图2(a)]。下面我们将对以上理论与实验的偏离进行详细的分析。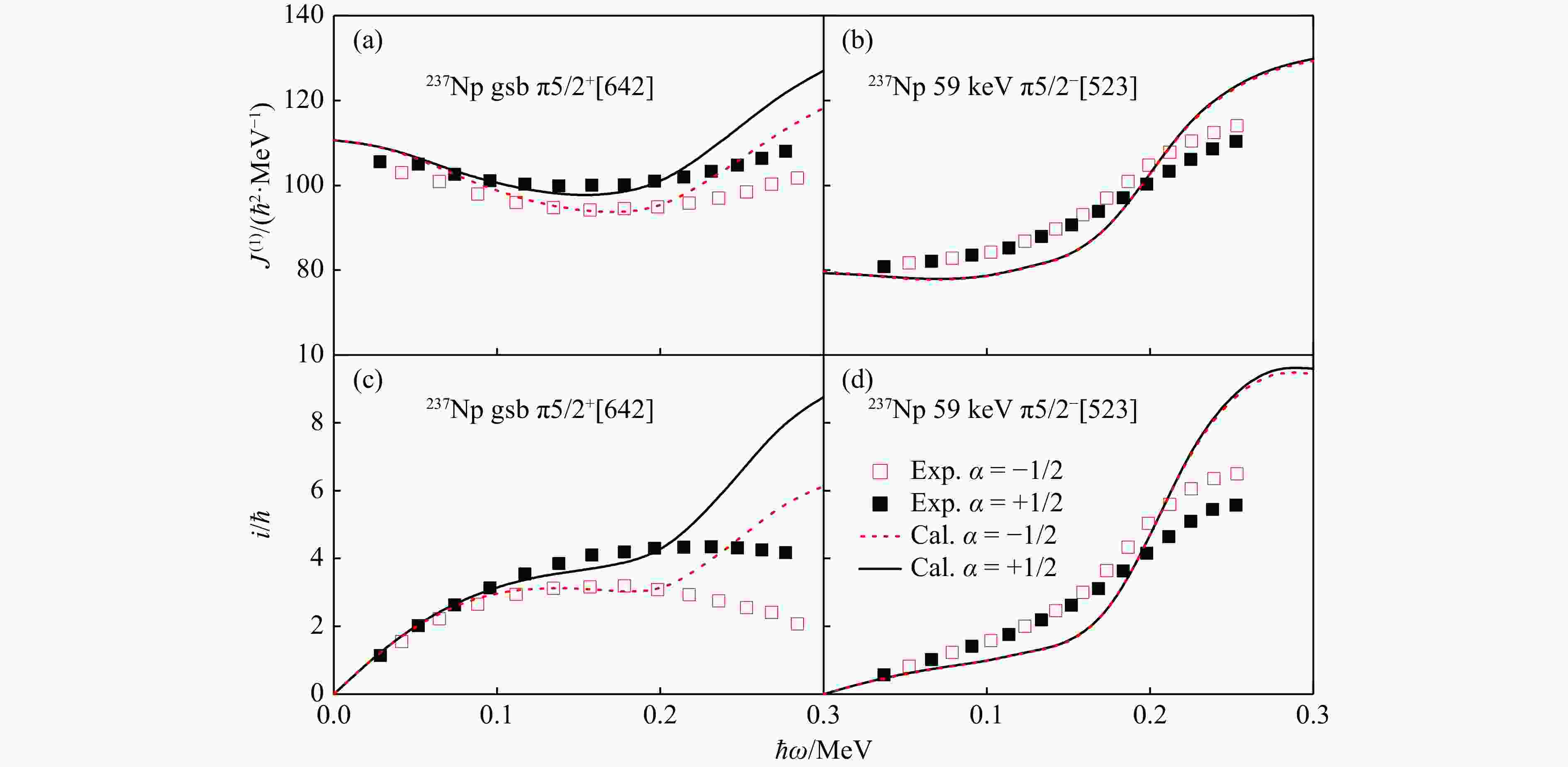
图 4 粒子数守恒方法计算得到的
$^{237}{\rm{Np}}$ 中两条转动带 转动惯量(图的上排)和顺排(图的下排)与实验值 [15]的比较(在线彩图)图5展示了粒子数守恒方法计算得到的
$ ^{237}{\rm{Np}} $ 中两条转动带角动量顺排$ J_x $ 与实验值的比较。与图4(c)和(d)不同，在此图当中没有扣掉Harris参考的平滑部分$\omega J_0^{} +\omega^3 J_1 ^{}$ 。对于基态带$ \pi5/2^+[642] $ ，由于质子$i_{13/2}^{}$ 轨道被堵塞，它不会对上弯有贡献。从图5(a)中可以看到，粒子数守恒方法计算得到的质子的$J_x ^{}$ 随着转动频率平缓地增加，而中子的$J_x^{}$ 在推转频率$\hbar\omega\approx 0.2$ MeV处有一个明显的增加，这表明粒子数守恒方法计算中出现的上弯来自于中子的贡献。更进一步的研究表明，此贡献主要来源于中子高$ j $ 轨道$j_{15/2}^{}$ 。对于$ \pi5/2^-[523] $ ，质子$i_{13/2} ^{}$ 轨道和中子$j_{15/2} ^{}$ 轨道均未被堵塞，它们均可以对上弯有贡献。从图5(b)中可以看到，对于这条转动带，粒子数守恒方法计算得到的质子和中子部分均对上弯有贡献，质子能级交叉的频率要小于中子。此外，质子对于上弯的贡献大于中子。这与其他推转模型得到的结果类似，即计算中出现了实验上未观测到的中子$j_{15/2} ^{}$ 的顺排，导致计算得到的上弯与实验不符。
图 5 粒子数守恒方法计算得到的
$^{237}{\rm{Np}}$ 中两条转动带角动量顺排$J_x$ 与实验值的比较(在线彩图)图6展示了粒子数守恒方法计算得到的
$ ^{237}{\rm{Np}} $ 中子$N = 6$ 壳和$N = 7$ 壳对角动量顺排的贡献，其中红色虚线表示公式(9)中$N = 7$ 壳对角元以及非对角元的贡献。可以看到，中子$N = 7$ 壳贡献了计算中出现的$ \hbar\omega>0.2 $ MeV处缓慢的上弯，并且，此贡献全部来源于$ N=7 $ 壳的非对角元。此前研究表明高阶形变$\varepsilon_6^{}$ 会影响费米面附近的高$ j $ 轨道的位置，从而影响计算中出现的回弯/上弯频率 [21, 47-48]。因此，我们还研究了高阶形变$\varepsilon_6 ^{}$ 对中子$N = 7$ 壳顺排的影响。插图表示当高阶形变$\varepsilon_6^{}$ 分别取−0.03、0.00以及0.03时$N = 7$ 对角动量顺排的贡献。可以看到，不同的$\varepsilon_6^{}$ 可以改变$ N=7 $ 壳顺排的强弱，因此它会在很大程度上影响中子$j_{15/2}^{}$ 的顺排。值得注意的是，此前我们在图4中看到，实验数据显示$ \pi5/2^-[523] $ 在上弯后出现了很明显的旋称劈裂，旋称$\alpha = -1/2$ 分支的上弯更加明显，这也可能是由于随着推转频率的增加，这两个旋称分支的$\varepsilon_6^{}$ 不同导致的。此外，我们知道对关联也会影响高$ j $ 轨道的顺排，因此若想对此问题进行进一步深入研究，还需要进行转动、形变以及对关联全部自洽的微观计算。
图 6
$^{237}{\rm{Np}}$ 中子$N=6$ 壳和$N=7$ 壳对角动量顺排的贡献(在线彩图) -
本文采用基于推转壳模型的粒子数守恒方法研究了实验上观测到的
$ ^{235}{\rm{Np}} $ 和$ ^{237}{\rm{Np}} $ 中转动带的性质，计算得到的转动惯量、角动量顺排等与实验符合。首先，通过描述转动谱的$ ab $ 公式确定了$ ^{235}{\rm{Np}} $ 中观测到的转动带的带头自旋，发现应当把实验带1中连接$ 9/2\rightarrow 5/2 $ 的 78 keV的跃迁去掉，且其他能级所对应的自旋值应当降低1$ \hbar $ ；带2中101 keV的跃迁也应当一同舍弃。此外，通过对比理论与实验上的转动惯量，确定了其组态为$ \pi 5/2^-[523] $ 。本工作确定的$ ^{235}{\rm{Np}} $ 中转动带的自旋及组态与Afanasjev等[39]采用推转相对论平均场理论的计算结果一致。随后，文章计算了$ ^{237}{\rm{Np}} $ 中两条转动带的转动惯量及顺排，分析了理论与实验偏离的原因，发现由于计算中出现了实验上未观测到的中子$j_{15/2}^{}$ 的顺排，导致计算得到的上弯与实验不符。此外，文章中讨论了高阶形变$\varepsilon_6^{}$ 对中子$j_{15/2}^{}$ 顺排的影响，解释了$^{235,\, 237}{\rm{Np}}$ 的转动带中产生上弯的机制。最后，本文还讨论了转动带$ \pi 5/2^-[523] $ 中旋称劈裂出现的可能原因，可能是由于这两个旋称分支上弯以后高阶形变$\varepsilon_6^{}$ 不同所导致的。
-
摘要: 锕系核的转动性质对于揭示
$A \approx 250 $ 质量区原子核的顺排机制、对关联性质、能级结构等十分重要，研究这些核的高自旋结构一方面可以对现有的理论模型进行检验，另一方面有助于深入认识超重核。本工作采用基于推转壳模型的粒子数守恒方法研究了实验上观测到的$^{235}{\rm{Np}}$ 和$^{237}{\rm{Np}}$ 中转动带的性质，计算得到的转动惯量、角动量顺排等与实验符合。首先，通过描述转动谱的$ab$ 公式确定了$^{235}{\rm{Np}}$ 中观测到的转动带的带头自旋。随后，通过对比理论与实验上的转动惯量，确定了其组态为$\pi 5/2^-[523]$ 。此外，也讨论了高阶形变$\varepsilon_6^{}$ 对中子$j_{15/2}^{}$ 顺排的作用，探索了在计算中出现而在实验上未观测到中子$j_{15/2}^{}$ 顺排的原因，从而解释了$^{235, 237}{\rm{Np}}$ 的转动带中产生上弯的机制。最后，还讨论了$^{237}{\rm{Np}}$ 的转动带$\pi 5/2^-[523]$ 中出现旋称劈裂的原因，发现可能是由于这个转动带的两个旋称分支上弯以后高阶形变$\varepsilon_6^{}$ 不同所导致的。Abstract: The rotational properties of the actinides are quite important for revealing the alignment mechanism, pairing correlations, level structure etc., of the nuclei in$A \approx 250$ mass region. On the one hand, investigation of the high-spin structures of these nuclei can provide benchmark for testing various theoretical models. On the other hand, it can help us to get more information about the superheavy nuclei. In this work, the particle-number conserving method based on the cranked shell model is adopted to investigate the rotational bands observed in$^{235}{\rm{Np}}$ and$^{237}{\rm{Np}}$ . The moments of inertia, alignments etc., are reproduced by the calculations. Firstly, the$ab$ formula which is used to investigate the rotational spectra, is adopted to determine the bandhead spin of the rotational bands observed in$^{235}{\rm{Np}}$ . Secondly, by comparing the experimental and calculated moments of inertia, the configuration for this signature partner band is assigned as$\pi 5/2^-[523]$ . Moreover, the influence of higher-order deformation$\varepsilon_6$ on the alignments of neutron$j_{15/2}$ is discussed. The appearance of the neutron$j_{15/2}$ alignment in the calculations, which is non-existent in experiment, is explored. The upbending mechanism in$^{235,\, 237}{\rm{Np}}$ is investigated. Finally, the possible reason for the signature splitting of the rotational band$\pi 5/2^-[523]$ in$^{237}{\rm{Np}} $ is explored, which may due to the different higher-order deformation$\varepsilon_6$ in these two signature branches of this band after upbending. -
图 2
$^{235}{\rm{Np}}$ 费米面附近(a)质子和(b)中子的推转Nilsson 能级(在线彩图)其中，蓝色和红色的线分别代表宇称为正和负的能级，实线和虚线分别代表旋称 $\alpha=+1/2$ 和 $\alpha=-1/2$ 的能级。
图 3 粒子数守恒方法计算得到的
$^{235}{\rm{Np}}$ 中组态为$\pi 5/2^+[642]$ 和$\pi5/2^-[523]$ 的转动惯量与实验值[16] 的比较(在线彩图)其中，黑色实线(红色虚线)代表组态$\pi5/2^-[523]$旋称为$\alpha= $$ +1/2$($\alpha=-1/2$)带的计算值，蓝色实线(蓝色虚线)代表组态 $\pi 5/2^+[642]$旋称为$\alpha=+1/2$($\alpha=-1/2$)带的计算值，黑色实心(红色空心)方块代表旋称为 $\alpha=+1/2$($\alpha=-1/2$)带的实验值。
图 4 粒子数守恒方法计算得到的
$^{237}{\rm{Np}}$ 中两条转动带 转动惯量(图的上排)和顺排(图的下排)与实验值 [15]的比较(在线彩图)其中，黑色实线(红色虚线)代表旋称为$\alpha=+1/2$($\alpha=-1/2$)带的计算值，黑色实心(红色空心)方块代表旋称为$\alpha=+1/2$($\alpha=-1/2$)带的实验值。顺排$i= \langle J_x \rangle -\omega J_0 -\omega^3 J_1$，其中 Harris 参数[46] $J_0 = 65\ \hbar^2 {{\rm{MeV}}}^{-1}$，$J_1 = 365\ \hbar^4 {{\rm{MeV}}}^{-3}$取自文献[15]。
图 5 粒子数守恒方法计算得到的
$^{237}{\rm{Np}}$ 中两条转动带角动量顺排$J_x$ 与实验值的比较(在线彩图)黑色实心(红色空心)方块代表旋称为$\alpha=+1/2$($\alpha=-1/2$)带的实验值，黑色(红色)实线代表旋称为 $\alpha=+1/2$($\alpha=-1/2$)带的计算值。虚线表示质子和中子分别对$J_x$的贡献。在此图当中没有扣掉 Harris参考的平滑部分$\omega J_0 +\omega^3 J_1$。
图 6
$^{237}{\rm{Np}}$ 中子$N=6$ 壳和$N=7$ 壳对角动量顺排的贡献(在线彩图)其中：红色虚线表示公式(9)中$N=7$壳对角元以及非对角元的贡献。插图表示当高阶形变$\varepsilon_6$分别取−0.03、0.00以及0.03时$N=7$壳对角动量顺排的贡献。
表 1
$ ^{235}{\rm{Np}} $ 两条转动带跃迁能量$E_\gamma^{}(I \rightarrow I-2)$ 的实验值${E}{\,\rm^{exp}_{\gamma} }$ 以及利用$ ab $ 公式得到的计算值${E}^{\,ab}_{\gamma}$ ($ \sigma $ 为均方根偏差)带1 带2 $I_i\rightarrow ^{} I_f^{} /\hbar$ ${E}\rm^{\,exp}_{\gamma}$/keV ${E}^{\,ab}_{\gamma}$/keV $I_i^{}\rightarrow I_f^{} (\hbar)$ ${E}\rm^{\,exp}_{\gamma}$/keV ${E}^{\,ab}_{\gamma}$/keV 11/2$ \rightarrow $ 7/2 127.1 116.7 13/2$ \rightarrow $ 9/2 143.4 141.2 15/2$ \rightarrow $ 11/2 153.7 161.2 17/2$ \rightarrow $ 13/2 186.6 185.0 19/2$ \rightarrow $ 15/2 200.5 203.6 21/2$ \rightarrow $ 17/2 227.4 226.4 23/2$ \rightarrow $ 19/2 245.9 243.5 25/2$ \rightarrow $ 21/2 265.7 265.0 27/2$ \rightarrow $ 23/2 282.6 280.8 29/2$ \rightarrow $ 25/2 300.0 300.7 31/2$ \rightarrow $ 27/2 316.4 315.3 33/2$ \rightarrow $ 29/2 331.9 333.4 35/2$ \rightarrow $ 31/2 346.3 347.0 37/2$ \rightarrow $ 33/2 360.4 363.2 39/2$ \rightarrow $ 35/2 372.4 375.9 41/2$ \rightarrow $ 37/2 387.8 390.1 43/2$ \rightarrow $ 39/2 402.4 402.1 45/2$ \rightarrow $ 41/2 414.9 414.4 47/2$ \rightarrow $ 43/2 425.3 425.9 49/2$ \rightarrow $ 45/2 439.5 436.3 51/2$ \rightarrow $ 47/2 449.4 447.5 $ a\times10^{-3} $ /keV 9.826 9.177 $ b\times10^{3} $ 1.206 1.313 $ \sigma $ /keV 4.262 1.873 
下载: 导出CSV
-
[1] RAINWATER J. Phys Rev, 1950, 79: 432. doi: 10.1103/PhysRev.79.432 [2] JOHNSON A, RYDE H, SZTARKIER J. Phys Lett B, 1971, 34: 605. doi: 10.1016/0370-2693(71)90150-X [3] LEE I Y, ALEONARD M M, DELEPLANQUE M A, et al. Phys Rev Lett, 1977, 38: 1454. doi: 10.1103/PhysRevLett.38.1454 [4] BENGTSSON T, RAGNARSSON I. Phys Scr, 1983, T5: 165. doi: 10.1088/0031-8949/1983/T5/031 [5] AFANASJEV A, FOSSAN D, LANE G, et al. Phys Rep, 1999, 322: 1. doi: 10.1016/S0370-1573(99)00035-6 [6] TWIN P J, NYAKO B M, NELSON A H, et al. Phys Rev Lett, 1986, 57: 811. doi: 10.1103/PhysRevLett.57.811 [7] ØDEGÅRD S W, HAGEMANN G B, JENSEN D R, et al. Phys Rev Lett, 2001, 86: 5866. doi: 10.1103/PhysRevLett.86.5866 [8] HERZBERG R D, GREENLEES P. Prog Part Nucl Phys, 2008, 61: 674. doi: 10.1016/j.ppnp.2008.05.003 [9] BLOCK M, LAATIAOUI M, RAEDER S. Prog Part Nucl Phys, 2021, 116: 103834. doi: 10.1016/j.ppnp.2020.103834 [10] GREENLEES P T, RUBERT J, PIOT J, et al. Phys Rev Lett, 2012, 109: 012501. doi: 10.1103/PhysRevLett.109.012501 [11] HERZBERG R D, AMZAL N, BECKER F, et al. Phys Rev C, 2001, 65: 014303. doi: 10.1103/PhysRevC.65.014303 [12] STEPHENS F S, SIMON R S. Nucl Phys A, 1972, 183: 257. doi: 10.1016/0375-9474(72)90658-6 [13] AFANASJEV A V, KHOO T L, FRAUENDORF S, et al. Phys Rev C, 2003, 67: 024309. doi: 10.1103/PhysRevC.67.024309 [14] HOTA S, CHOWDHURY P, KHOO T, et al. Phys Lett B, 2014, 739: 13. doi: 10.1016/j.physletb.2014.10.021 [15] ABU SALEEM K, JANSSENS R V F, CARPENTER M P, et al. Phys Rev C, 2004, 70: 024310. doi: 10.1103/PhysRevC.70.024310 [16] HURST A M, WU C Y, STOYER M A, et al. Phys Rev C, 2010, 81: 014312. doi: 10.1103/PhysRevC.81.014312 [17] HE X T, REN Z Z, LIU S X, et al. Nucl Phys A, 2009, 817: 45. doi: 10.1016/j.nuclphysa.2008.12.003 [18] ZHANG Z H, ZENG J Y, ZHAO E G, et al. Phys Rev C, 2011, 83: 011304(R). doi: 10.1103/PhysRevC.83.011304 [19] ZHANG Z H, HE X T, ZENG J Y, et al. Phys Rev C, 2012, 85: 014324. doi: 10.1103/PhysRevC.85.014324 [20] 张振华, 温凯, 贺晓涛, 等. 原子核物理评论, 2013, 30: 268. doi: 10.11804/NuclPhysRev.30.03.268 ZHANG Z H, WEN K, HE X T, et al. Nucl Phys Rev, 2013, 30: 268. (in Chinese) doi: 10.11804/NuclPhysRev.30.03.268 [21] ZHANG Z H, MENG J, ZHAO E G, et al. Phys Rev C, 2013, 87: 054308. doi: 10.1103/PhysRevC.87.054308 [22] LI Y C, HE X T. Sci China-Phys Mech Astron, 2016, 59: 672011. doi: 10.1007/s11433-016-0061-0 [23] HE X T, ZHAO S Y, ZHANG Z H, et al. Chin Phys C, 2020, 44: 034106. doi: 10.1088/1674-1137/44/3/034106 [24] FU X M, XU F R, PEI J C, et al. Phys Rev C, 2013, 87: 044319. doi: 10.1103/PhysRevC.87.044319 [25] LIANG W Y, JIAO C F, WU Q, et al. Phys Rev C, 2015, 92: 064325. doi: 10.1103/PhysRevC.92.064325 [26] SHI Z, ZHANG Z H, CHEN Q B, et al. Phys Rev C, 2018, 97: 034317. doi: 10.1103/PhysRevC.97.034317 [27] XIONG B W. Phys Rev C, 2020, 101: 054305. doi: 10.1103/PhysRevC.101.054305 [28] HE X T, LI Y C. Phys Rev C, 2020, 102: 064328. doi: 10.1103/PhysRevC.102.064328 [29] RICHARDSON R, SHERMAN N. Nucl Phys, 1964, 52: 221. doi: 10.1016/0029-5582(64)90687-X [30] PAN F, DRAAYER J, ORMAND W. Phys Lett B, 1998, 422: 1. doi: 10.1016/S0370-2693(98)00034-3 [31] VOLYA A, BROWN B A, ZELEVINSKY V. Phys Lett B, 2001, 509: 37. doi: 10.1016/S0370-2693(01)00431-2 [32] PILLET N, QUENTIN P, LIBERT J. Nucl Phys A, 2002, 697: 141. doi: 10.1016/S0375-9474(01)01240-4 [33] JIA L Y. Phys Rev C, 2013, 88: 044303. doi: 10.1103/PhysRevC.88.044303 [34] CHEN W C, PIEKAREWICZ J, VOLYA A. Phys Rev C, 2014, 89: 014321. doi: 10.1103/PhysRevC.89.014321 [35] NILSSON S G, TSANG C F, SOBICZEWSKI A, et al. Nucl Phys A, 1969, 131: 1. doi: 10.1016/0375-9474(69)90809-4 [36] WU C S, ZENG J Y. Phys Rev C, 1989, 39: 666. doi: 10.1103/PhysRevC.39.666 [37] MOLIQUE H, DUDEK J. Phys Rev C, 1997, 56: 1795. doi: 10.1103/PhysRevC.56.1795 [38] FRIEDMAN A M, KATORI K, ALBRIGHT D, et al. Phys Rev C, 1974, 9: 760. doi: 10.1103/PhysRevC.9.760 [39] AFANASJEV A V, ABDURAZAKOV O. Phys Rev C, 2013, 88: 014320. doi: 10.1103/PhysRevC.88.014320 [40] 吴崇试, 曾谨言. 高能物理与核物理, 1984, 8: 219. WU C S, ZENG J Y. HEP & NP, 1984, 8: 219. (in Chinese) [41] ZENG J Y, MENG J, WU C S, et al. Phys Rev C, 1991, 44: 1745(R). doi: 10.1103/PhysRevC.44.R1745 [42] WU C S, ZENG J Y, XING Z, et al. Phys Rev C, 1992, 45: 261. doi: 10.1103/PhysRevC.45.261 [43] 温凯, 张振华, 赵恩广, 等. 中国科学: 物理学 力学 天文学, 2012, 42: 22. doi: 10.1360/132011-1167 WEN K, ZHANG Z H, ZHAO E G, et al. Sci Sin-Phys Mech Astron, 2012, 42: 22. (in Chinese) doi: 10.1360/132011-1167 [44] MÖLLER P, NIX J. At Data and Nucl Data Tables, 1995, 59: 185-381. doi: 10.1006/adnd.1995.1002 [45] SOBICZEWSKI A, MUNTIAN I, PATYK Z. Phys Rev C, 2001, 63: 034306. doi: 10.1103/PhysRevC.63.034306 [46] HARRIS S M. Phys Rev, 1965, 138: B509. doi: 10.1103/PhysRev.138.B509 [47] LIU H L, XU F R, WALKER P M. Phys Rev C, 2012, 86: 011301(R). doi: 10.1103/PhysRevC.86.011301 [48] LIU H, XU F. Chin Sci Bull, 2014, 59: 11. doi: 10.1007/s11434-013-0004-9 -
点击查看大图
图(6) / 表 (1)
计量
- 文章访问数: 496
- HTML全文浏览量: 95
- PDF下载量: 79
- 被引次数: 0
甘公网安备 62010202000723号