Heavy ion collisions(HIC) are the only methods of artificially generating hot and dense nuclear matter. Their final products are usually compared with transport model analysis to extract information about the nuclear matter and further constrain the equation of state(EOS) of isospin-asymmetric matter. Such constraints via transport models require a good understanding of the density and momentum dependence of the single-nucleon mean-field potential. The momentum dependence of mean-field potential can be characterized by nucleon effective mass which was first introduced by Brueckner to describe the motion of nucleons^[1-2]. The nucleon effective mass is defined as $ \frac{m_{\tau }^{\ast }}{m_{\tau }} = \left\{ 1+\frac{m_{\tau }^{}}{p}\frac{{\rm{d}}U_{\tau }^{}}{{\rm{d}}p}\right\}^{-1} $, for $ p = p_{F}^{\tau} $, at fixed density^[3]. For asymmetric nuclear matter, the effective mass of proton and neutron may not be the same, and the difference is defined by effective mass splitting $ m_{\rm n-p}^{*} $ $ (m_{\rm n-p}^{*} \equiv m_{\rm n}^{*}-m_{\rm p}^{*}) $.

The study of neutron-proton effective mass splitting is crucial in nuclear physics. It has been known that the neutron-proton effective mass splitting would affect the in-medium nucleon–nucleon cross-sections, transport properties, and the liquid-gas phase transition in neutron-rich matter^[4]. It also plays a crucial role in astrophysics such as the equilibrium neutron-to-proton ratio^[5], hot proto-neutron stars formed in core-collapse supernovae^[6], and the properties of neutron stars^[7].

The neutron–proton effective mass splitting is determined by the momentum dependence of the symmetry potential, and it is not well understood because of the little knowledge of nucleon-nucleon interactions. Various microscopic and phenomenological models have been used to study the symmetry potential^[8-24]. However, there is no general consensus on which of the neutrons and protons have the larger effective mass. The non-relativistic Brueckner–Hartree–Fock(BHF) and relativistic Dirac–Brueckner-Hartree-Fork (DBHF)^[25-26] calculations predict that the effective mass of neutron is larger than that of proton in neutron-rich systems^[27-28]. In addition, the same results are obtained from the Landau-Fermi-liquid theory^[29], the optical model analysis of the nucleon-nucleon elastic scattering data^[30], and constraints on the symmetry energy from various terrestrial nuclear laboratory experiments and astrophysical observations based on the Hugenholtz–Van Hove theorem^[31].

On the contrary, the Dirac effective mass of neutron is smaller than that of proton in the relativistic mean-field(RMF) model based on nucleon-meson interactions^{[2, 8, 32]}. Furthermore, based on comparisons with calculations using improved quantum molecular dynamics(ImQMD) model, analyses of free neutron/proton double ratio from the National Superconducting Cyclotron Laboratory at Michigan State University(NSCL/MSU) seem to indicate that protons have a slightly larger effective mass than neutrons^[33]. All three cases ($ m_{\rm n}^{*} < m_{\rm p}^{*} $, $ m_{\rm n}^{*} = m_{\rm p}^{*} $, and $ m_{\rm n}^{*} > m_{\rm p}^{*} $) exist in Skyrme-Hartree-Fork calculations with different sets of Skyrme parameters^[8].

Since the original Skyrme interaction was introduced in the 1950s^[34], several hundred sets of Skyrme parameters have been fitted to predict a wealth of properties of atomic nuclei. In this work, we try to construct a self-consistent transport model based on Skyrme effective interactions and further extract the information of neutron-proton effective mass splitting with the NSCL experimental data. The article is organized as follows. In Sec. 2, the single-nucleon potential, in-medium nucleon-nucleon cross-section, and initial density distributions of nucleons are obtained from Skyrme interaction and used in IBUU04 code. In Sec. 3, the free neutron/proton double ratio is discussed with particular Skyrme parameters and compared with the NSCL experimental data.

The standard form of Skyrme effective interaction is^[34-35]

where $ t_{i}^{} $, $ x_{i}^{} $ $(i = 0,\, 1,\, 2, \,3)$, the power $ \alpha $ of density dependence, and the spin-orbit strength $ W_{0}^{} $ are Skyrme parameters of the interaction; $ P_{\sigma}^{} = \frac{1}{2}\left(1+\sigma_{1}^{} \cdot \sigma_{2}^{} \right) $ is the spin exchange operator; $ {\boldsymbol{R}} = ({\boldsymbol{r}}_{1}^{}+{\boldsymbol{r}}_{2}^{}) / 2 $ is the center-of-mass coordinate; $ {\boldsymbol{r}} = {\boldsymbol{r}}_{1}^{}-\mathbf{r}_{2}^{} $ is the relative coordinate of the two particles; $ \overrightarrow{k} = {\rm{i}}(\overrightarrow{\nabla}_{1}^{}-\overrightarrow{\nabla}_{2}^{}) / 2 $ and $ \overleftarrow{k} = {\rm i}(\overleftarrow{\nabla}_{1}^{}-\overleftarrow{\nabla}_{2}^{}) / 2 $ are the relative momentum operators acting on the right and on the left, respectively.

We begin with the Skyrme effective interaction and use mean-field Hartree-Fock approximation to obtain single-nucleon Hartree-Fork equation. In asymmetric nuclear matter with an asymmetry parameter $ \beta = (\rho_{\rm{n}}^{}-\rho_{\rm{p}}^{})/(\rho_{\rm{n}}^{}+\rho_{\rm{p}}^{}) $, the nucleon effective mass determined by the momentum dependence of single-nucleon potential is^[36]

where $ q = n $, $ \omega_{q}^{} = 1 $ for neutrons and $ q = p $, $ \omega_{q}^{} = -1 $ for protons. The simplified notation is

And the momentum-independent mean-field potential is

where the kinetic energy density $ \tau_{q}^{}({\boldsymbol{r}}) $ satisfies $ \tau({\boldsymbol{r}}) = \tau_{\rm{p}}^{}({\boldsymbol{r}})+\tau_{\rm{n}}^{}({\boldsymbol{r}}) $.

Generally, in the Boltzmann-Uehling-Uhlenbeck (BUU) model, the mean-field potential is expressed as a function of the (continuous) phase-space distribution, which is resolved in terms of a (large) number of discrete test particles as^[37]

where $ A $ is the number of nucleons, $ \widetilde{N} $ is the test particle number per nucleon (200 in this work), $ {\boldsymbol{r}}_{i}^{} $ and $ {\boldsymbol{p}}_{i}^{} $ are the coordinates and momenta of the individual test particles. The available volume is divided into sufficiently small cubes of side $ l $ which can be considered as uniform nuclear matter. Under the local density approximation of nuclear matter, the gradient term of the density and spin-orbit term of mean-field potential vanish.

Then the momentum-independent single-nucleon potential obtained from Eq. (4) is

and the momentum-dependent part is

The isospin- and momentum- depentent single-nucleon potential used in the BUU code is

where $ q = n $ for neutrons and $ q = p $ for protons.

For the BUU code, the kinetic energy density $ \tau_{q}^{}({\boldsymbol{r}}) $ in the above Eq. (6) is derived with the phase-space distribution function $f({\boldsymbol{r}}, \,{\boldsymbol{p}})$

Therefore, we have

where the summation represents the sum of all the protons ($ q = p $) or neutrons ($ q = n $) in the grid where they are located with coordinate $ {\boldsymbol{r}} $.

The symmetry energy can be obtained from the binding energy per nucleon $ E/A $^[38]

The initial density distributions of neutron and proton in nucleus are given by the Skyrme-Hartree-Fork calculations with corresponding Skyrme parameters. And we let the nucleon momentum distribution in the high-momentum-tail(HMT)^[39-41]

and

The isospin-dependent baryon–baryon(BB) scattering cross section in medium $ \sigma ^{\rm{medium}}_{\rm{BB}} $ is reduced compared with their free-space value $ \sigma ^{\rm free}_{\rm{BB}} $ by a factor of^[42-43]

where $ \mu_{\rm{B B}}^{} $ and $ \mu_{\rm{B B}}^{*} $ are the reduced masses of the colliding baryon-pair in free space and medium, respectively. The nucleon effective mass in the factor $ R_{\rm {medium }}^{} $ is obtained using the Skyrme interaction, see Eq. (2).

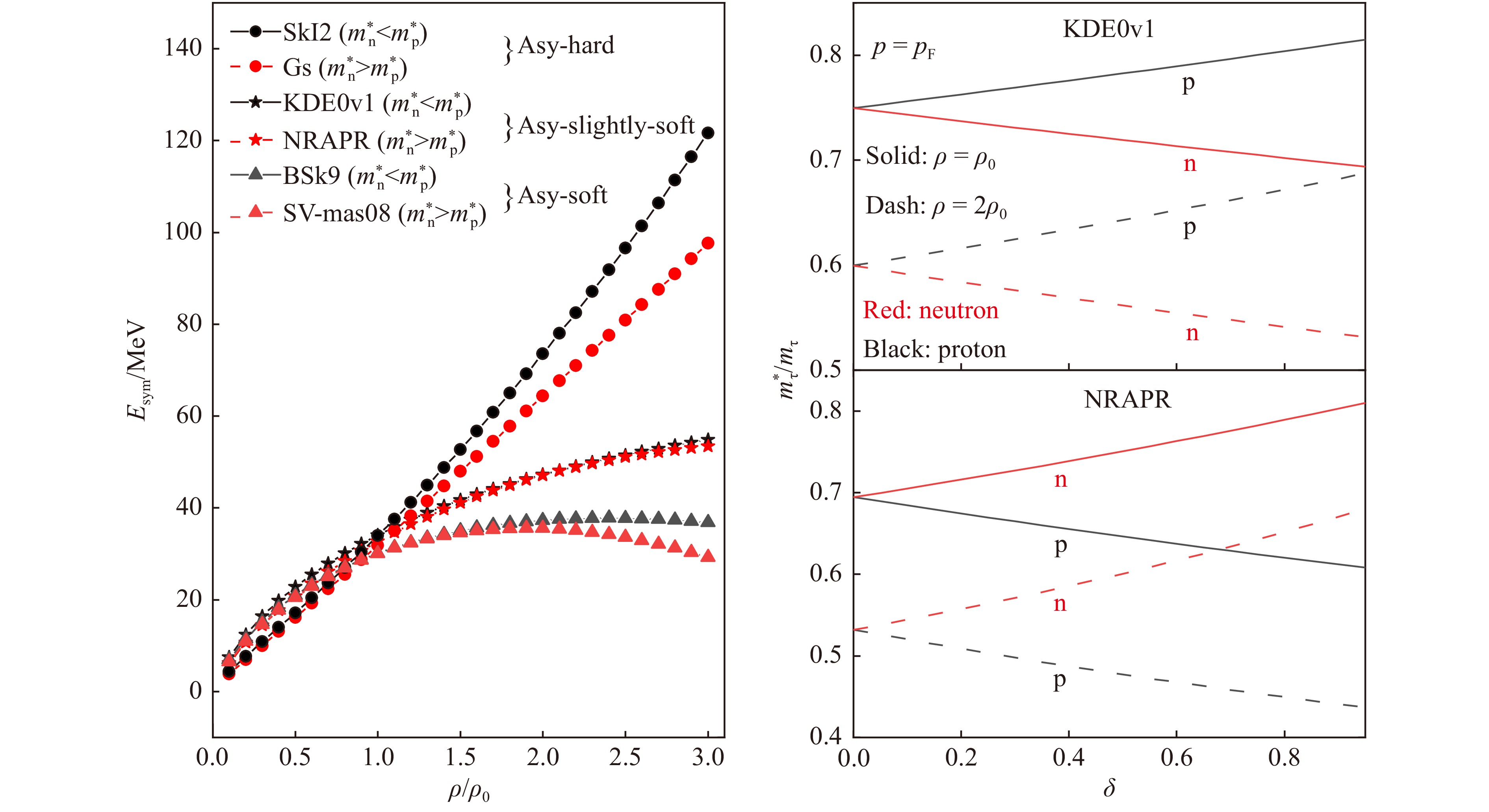
The neutron/proton double ratio has recently been used to study the effective mass splitting effect with NSCL experiments^[33-44], and we also need to consider the choice of symmetry energy because it's still unclear, especially in high-density regions^[45-48]. In this way, it is convincing that signals are mainly due to the neutron-proton effective mass splitting and not strictly depending on the choice of the stiffness of the symmetry energy. In this work, among the published 240 Skyrme interaction parameter sets in the Ref. [49], six Skyrme interactions predict the opposite choices of effective mass splitting for different stiffnesses of the symmetry energy (asy-hard, asy-sightly-soft, and asy-soft), as shown in Table 1. The corresponding two sets of Skyrme parameters selected with similar symmetry energy also predict very close saturation properties of nuclear matter, such as incompressibility $ K_0^{} $, the binding energy $ E_{0}^{} $ and isoscalar effective mass $ m^{*} $, with the exception that the effective mass splitting is opposite. The saturation properties of nuclear matter are determined by standard Skyrme parameter sets with 9 parameters $ \{t_0^{},\, t_1^{},\, t_2^{},\, t_3^{}, \,x_0^{}, \,x_1^{},\, x_2^{}, \, x_3^{},\, \alpha \}$. By the way, if we fix the symmetry energy coefficient $ S_{0}^{} $, its slope $ L $, and curvature $K_{\rm sym}^{}$, the trend of the symmetry energy is roughly determined. The density dependence of nuclear symmetry energy with selected Skyrme parameters is shown in the left panel of Fig. 1. And the right panel displays the effective mass of neutron and proton as a function of density ($ \rho = \rho_0^{} $, $ 2\rho_0^{} $) and isospin-asymmetry with the KDE0v1 and NRAPR interactions, respectively. It shows that the effective mass of proton is slightly larger than that of neutron for the KDE0v1 interaction and the opposite for NRAPR.

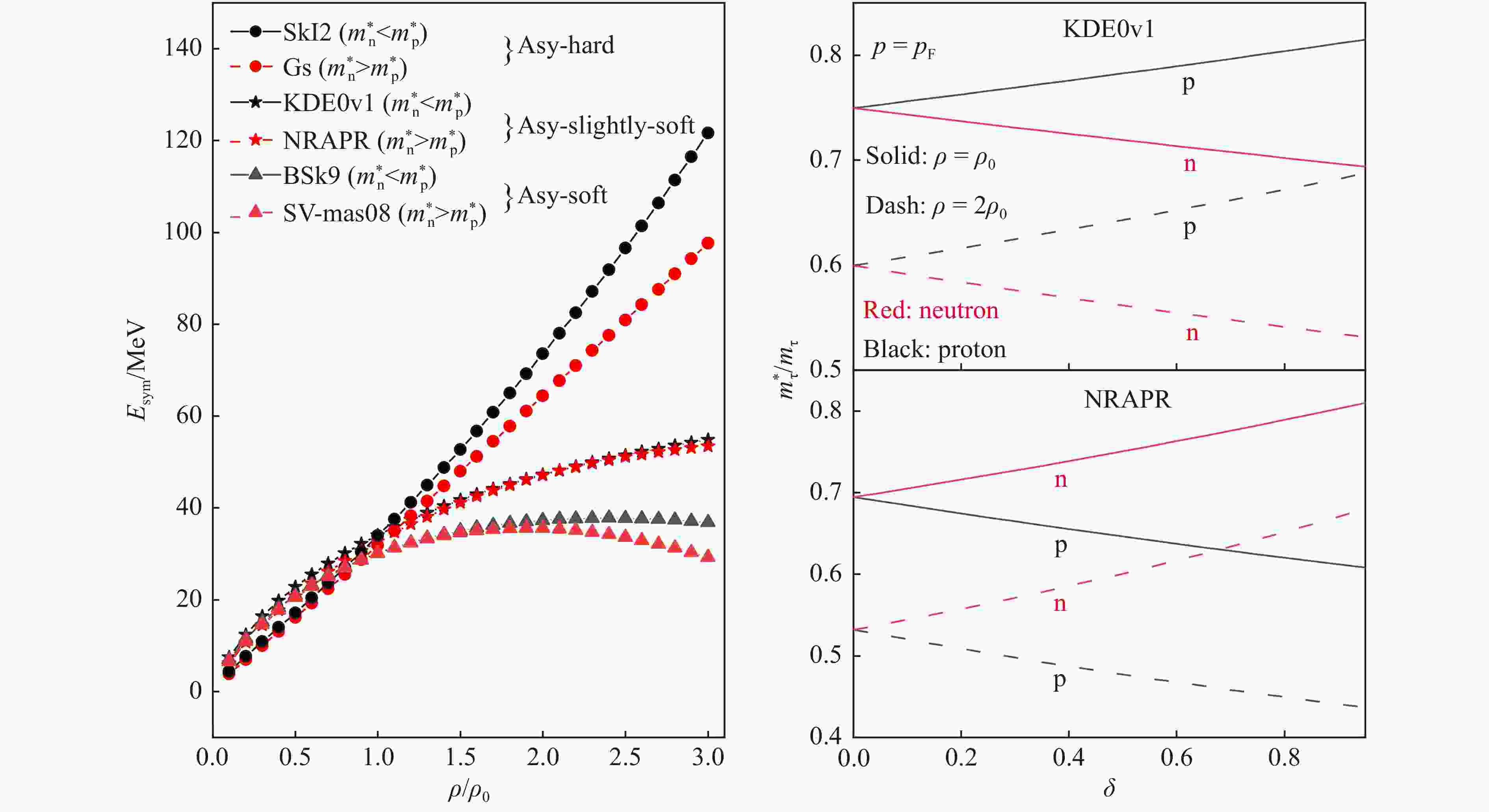
Figure 1.  Left panel: Density dependence of symmetry energy with different Skyrme parameter sets; Right panel: The effective mass of neutron and proton as a function of density at $ \rho = \rho_0^{},\, 2\rho_0^{} $ and isospin-asymmetry for the parameters KDE0v1 (upper window) and NRAPR (lower window) in cold asymmetric nuclear matter. (color online)

In cold asymmetric nuclear matter, the kinetic energy density of nucleon in the Eq. (6) can be written as $ \tau_{q}^{} = \frac{3}{5} k_{F_{q}^{}}^{2} \rho_{q}^{} $, and the symmetry potential can be obtained from the definition $ U_{\rm{sym}}^{} = (U_{\rm{n}}^{}-U_{\rm{p}}^{})/2\delta $. Where $ U_{\rm{n}}^{} $ ($ U_{\rm{p}}^{} $) is the single-nucleon mean-field potential of neutron (proton). The symmetry potentials as a function of density and momentum at isospin asymmetry $ \delta = 0.2 $ with the previously selected Skyrme parameters in cold asymmetric nuclear matter are shown in Fig. 2. The left panel shows the negative effective mass splitting for different stiffnesses of the symmetry energy predicted by the SkI2, KDE0v1, and BSk9 interactions while the corresponding positive effective mass splitting predicted by the Gs, NRAPR, SV-mas08 interactions are shown in the right, respectively. One can see that for the case of $ m_{\rm{n}}^{*} < m_{\rm{p}}^{*} $, the symmetry potential increases with momentum and increases more rapidly due to the squared term of momentum in the mean-field potential, while decreases for $ m_{\rm{n}}^{*} > m_{\rm{p}}^{*} $ case. Combining the Eq. (2), we can obtain the effective mass splitting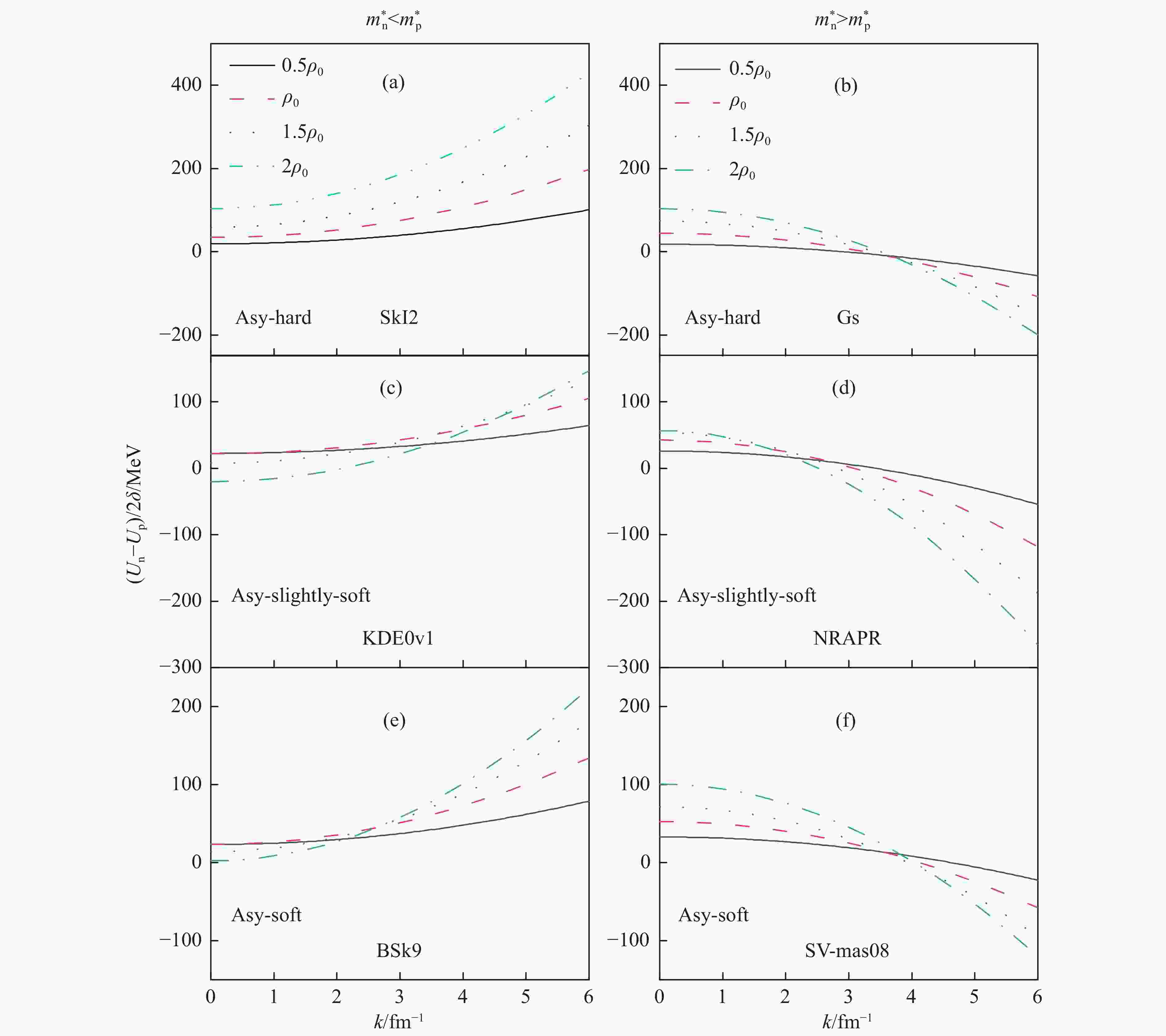

Figure 2.  The symmetry potential as a function of density and momentum with isospin asymmetry $ \delta = 0.2 $ in cold asymmetric nuclear matter; Different color lines represent different densities ($ \rho = 0.5\rho_{0}^{} $, $ \rho = \rho_{0}^{} $, $ \rho = 1.5\rho_{0}^{} $, $ \rho = 2\rho_{0}^{} $). (color online)

And combining the Eq. (8), we can obtain the momentum-dependent behavior of symmetry potential

From the Eq. (15) and Eq. (16), we can see the sign of the effective mass splitting is opposite to the momentum-dependent behavior of symmetry potential, and the sign is determined by the notation $ \xi_{\nu}^{} $. This is consistent with the previous analysis in Fig. 2. In this framework, the Skyrme force has a strong momentum-dependent behavior and it is also mentioned in Ref. [56].

Due to the opposite choices of effective mass splitting corresponding to symmetry potentials' different momentum-dependent behaviors, the symmetry potential is almost positive for the case of $ m_{\rm{n}}^{*} < m_{\rm{p}}^{*} $, but may have a cross-over (from positive to negative) at higher momentum and density for $ m_{\rm{n}}^{*} > m_{\rm{p}}^{*} $ case. This distinction will be a key entry point for the analysis of the following results.

In this work, we simulated the collisions of ¹²⁴Sn+¹²⁴Sn and >¹¹²Sn+¹¹²Sn reactions with beam energies of 50 MeV/nucleon and 120 MeV/nucleon at impact parameter $ 0 < b < 3 $ fm using the BUU code based on Skyrme effective interactions. The double ratio of pre-equilibrium emitted nucleons is shown in the Fig. 3 with angular cuts $ 70^\circ < \theta_{\rm{c.m.}}^{} < 110^\circ $ ($ \cos\theta = p_z^{}/\sqrt{p_{x}^2+p_{y}^2+p_{z}^2} $) from the above collision systems. A local density cut method is used to judge free nucleons, i.e., if the local density of a nucleon is less than 0.05 times saturation density, then it is a free nucleon. In the studies, we slightly change this criterion, and it's found that the double neutron/proton ratio is less affected. The free neutron/proton double ratio is roughly the same as that neutron/proton including light cluster $ A < 5 $, according to Figure 6 in the Ref. [57]. Compared to the neutron-proton single ratio, the double ratio can reduce the effect of Coulomb force and the systematic error caused by poor efficiency of detecting neutrons^{[45, 58]}. As shown in Fig. 3, due to the increase of nucleon-nucleon scattering, the neutron-proton double ratio of 120 MeV/nucleon beam energy in the right panel is smaller than the left one which is 50 MeV/nucleon, consistent with the Ref. [59]. First of all, it should be clarified that when the symmetry potential is positive, it exhibits attraction to protons and repulsion to neutrons. When the symmetry potential is negative, it repels protons and attracts neutrons. For windows (c) and (e) in Fig. 2, the symmetry potential decreases with increasing density before the crossover point and increases with increasing density after. And the symmetry potential increases with increasing kinetic energy. Before the crossover point, density- and momentum- dependent parts compete, after that, their contributions are consistent. However, for windows (d) and (f) in Fig. 2, the symmetry potential has the opposite behavior. For the two opposite choices of effective mass splitting, the symmetry potentials have a larger difference at higher momentum. Therefore, when the effective mass of neutron is smaller than that of proton, the almost always positive symmetry potential with increasing momentum causes neutrons to feel more repulsion at higher kinetic energy, and more neutrons are emitted, compared to the case of $ m_{\rm{n}}^{*} > m_{\rm{p}}^{*} $. As shown in Fig. 3, the distinctions caused by the effective mass splitting effect are mainly concentrated in higher momentum range. For lower kinetic energies, de-excitation of hot fragments in heavy-ion collisions becomes important, thus the effects of symmetry potential should be disturbed. Therefore, we don’t deduce the neutron-proton effective mass splitting from the lower kinetic part. Whereas for the nucleons at high kinetic energies, the effects of de-excitation of hot fragments in heavy-ion collisions would become smaller, hence symmetry potential or the neutron-proton effective mass splitting increasingly affects the neutron/proton ratio. Overall, the isospin effective mass splitting effect is more obvious at higher momentum, which is consistent with the Refs. [59-60].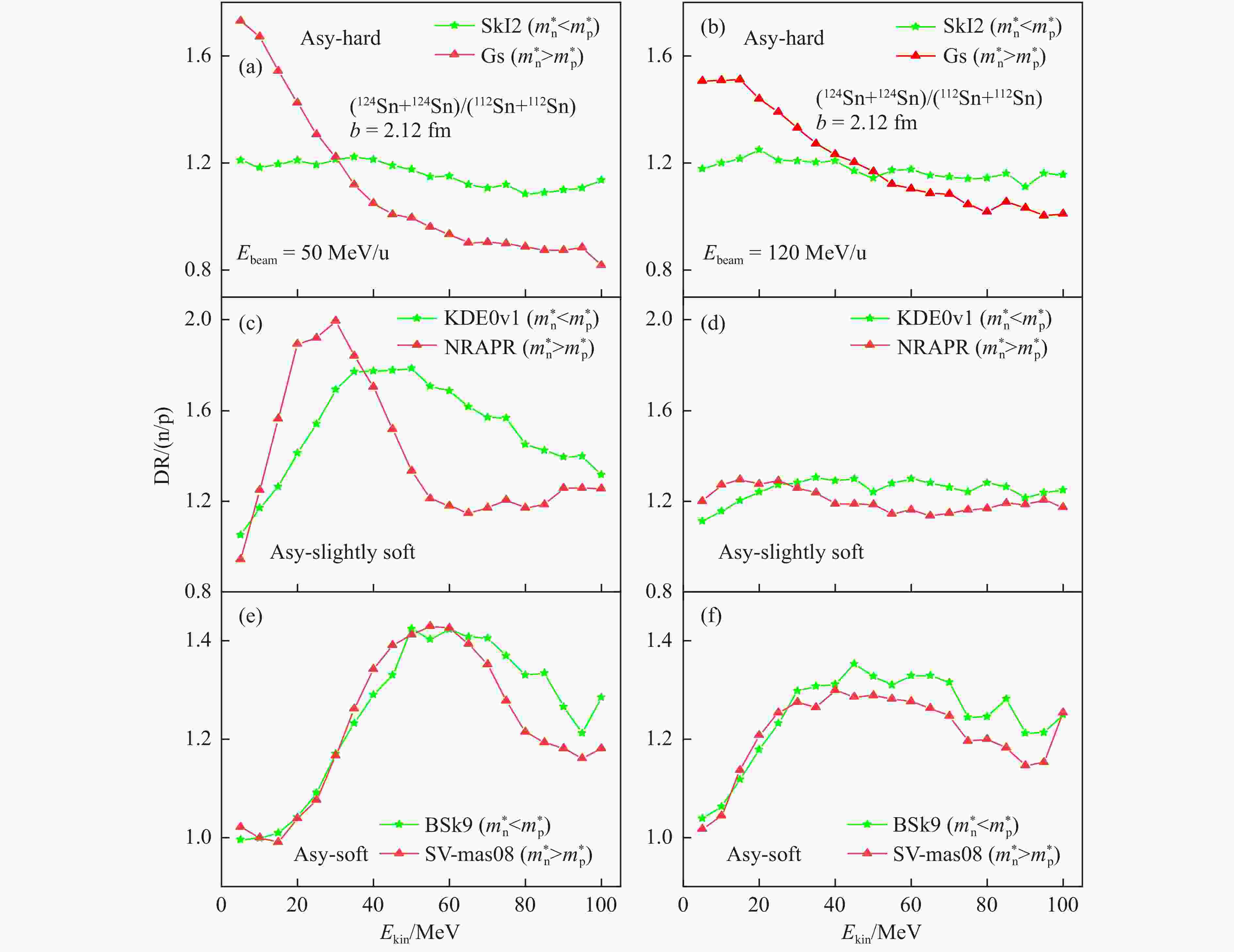

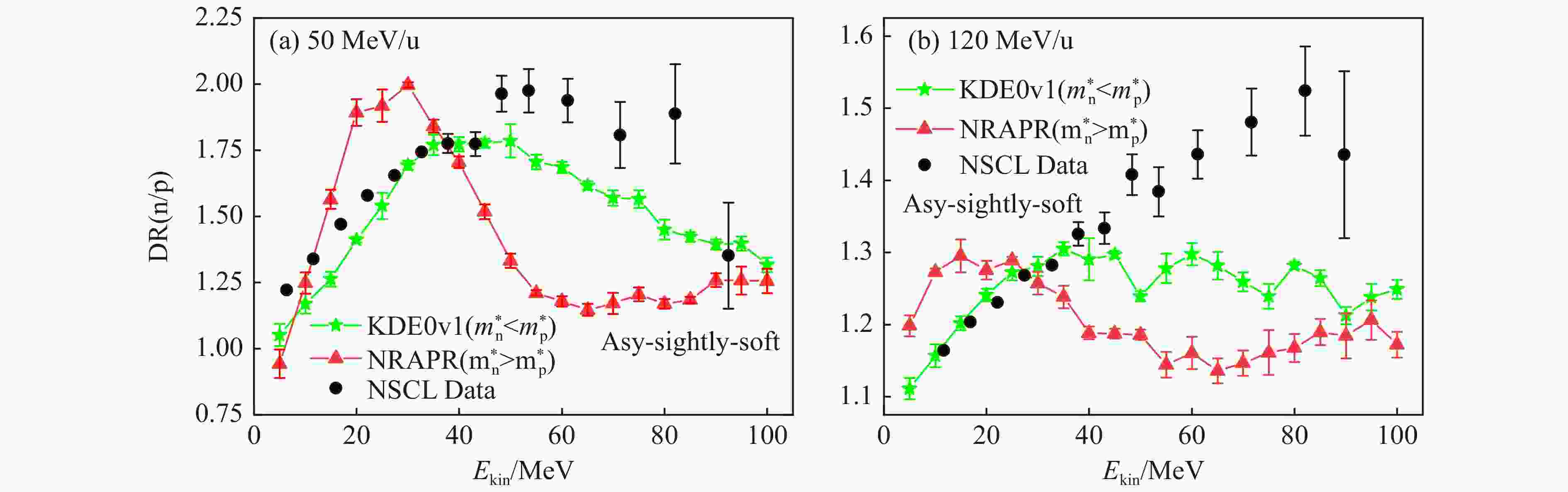
Figure 3.  The double neutron/proton ratio of free nucleons is taken from the reactions $ ^{124}{\rm Sn} $+$ ^{124}{\rm Sn} $ and $ ^{112}{\rm Sn} $+$ ^{112}{\rm Sn} $ at beam energies of 50 MeV/nucleon (left window) and 120 MeV/nucleon (right window) at impact parameter b = 2.12 fm with angular cuts $ 70^\circ < \theta_{\rm{c.m.}}^{} < 110^\circ $ ($ \cos\theta = p_z^{}/\sqrt{p_{x}^2+p_{y}^2+p_{z}^2} $), respectively; From top to bottom, the stiffnesses of the symmetry energy are asy-hard, asy-sightly-soft, and asy-soft; Green(Red) line for the effective mass splitting $ m_{\rm{n}}^{*} < m_{\rm{p}}^{*} $ ($ m_{\rm{n}}^{*} > m_{\rm{p}}^{*} $). (color online)

Shown in the left of Fig. 3, except for the asy-slightly-soft symmetry energy case, the maximum value of the neutron-proton double ratio that can be reached is around 1.4~1.6, while the NSCL experimental result can reach 2. The differences are indeed large relatively by comparisons. To avoid an overall depression caused by the inclusion of comparison with the experimental data, we only display the results of NRAPR and KDE0v1 compared with NSCL experimental data, as shown in Fig. 4. It can be seen that the kinetic-energy spectra of the neutron-proton double ratio results predicted by the KDE0v1 interaction are in relatively better agreement with the experiment, especially when the nucleus's kinetic energy is less than 40 MeV, and it's consistent with the trend of increasing and then decreasing experimental results. It should be noted that the results are still a little low compared to the experiment for nucleon kinetic energies between 40 and 80 MeV. On the whole, among the six sets of interactions, it seems to imply that the momentum- and density-dependent symmetry potential predicted by the KDE0v1 interaction is closer to that expected from NSCL experimental data.

Figure 4.  The same results of the slightly-soft symmetry energy in the previous Fig. 3, but compared with the NSCL experimental data^[33]. (color online)

In summary, the single-nucleon potential, in-medium nucleon-nucleon cross-section, and initial density distributions of nucleons are described by the Skyrme nucleon-nucleon effective interaction and used in BUU code to simulate heavy-ion collisions. Six sets of Skyrme parameter SkI2, Gs, KDE0v1, NRAPR, BSk9, and SV-mas08 are used for various stiffnesses of the symmetry energy with opposite choices of neutron-proton effective mass splitting in this work. We try to extract the information of effective mass splitting by free neutron/proton double ratio. It is found that distinctions caused by two opposite choices of effective mass splitting are mainly concentrated in the high momentum range. This can be explained by their different density- and momentum-dependent behaviors of the symmetry potential in Fig. 2. The comparison with NSCL experimental data indicates that double neutron-proton ratios corresponding to the KDE0v1 interaction seem closer to the experimental data, among the six sets of interactions. And it is planned to consider more situations by performing a covariance analysis of the neutron-proton effective mass splitting in the future, as done in Ref. [60].

Acknowledgments We thank Prof. Gao-Chan Yong for many fruitful discussions. This work was supported by the National Natural Science Foundation of China under Grant No. 11975282.