在粒子物理中，强子是由夸克与胶子构成的束缚态，有着复杂的内部结构。从原子核中最为常见的质子与中子，到种类繁多的其他重子和介子，众多的强子态为人们展示了复杂而多样的微观世界的一角，吸引科学家们开展对强相互作用的不懈探索。然而，一方面由于强相互作用的非微扰特性，使得传统的微扰方法在强子研究领域不再生效；另一方面色禁闭的存在也使得人们只能将结构复杂的强子整体进行研究，难以窥探强子内部的结构细节。因此，虽然原则上标准模型已经对于强子内部包含的基本粒子给出了很好的预言，不过实践中对其开展的研究仍然困难重重。目前，已经发展出很多非微扰的框架，例如格点量子色动力学(QCD)方法^[1]，已被广泛应用于对强相互作用的处理，但是强子的内部结构依旧是一个未曾解决的问题。即使是最常见的质子，有关其大小、自旋结构和寿命等性质的确定也仍然悬而未决^[2]。

质子的内部结构不仅仅是前沿科学家孜孜追求的研究方向之一，甚至对于回答很多最根本的物理问题都有巨大的意义和影响。例如，一个根本的问题就是：质子的寿命是不是无限的？科学家们曾试图从理论上和实验上解决这个问题。日本发现中微子振荡的超级神冈探测器^[3-4]，最初建造时的目的即为观测质子的衰变，不过很遗憾的是，在大量观测数据中^[5]并未探测到质子的衰变现象，因此可以确信质子的半衰期超过$ 3.3\times {10}^{33} $ a。理论上，从标准模型出发的话，如果要求重子数守恒不被破坏，那么质子作为最轻的重子的确无法自发衰变到其他重子。相应地，由于并不严格的同位旋对称性，上夸克与下夸克的质量不严格相等，故而中子和质子也具有微小的质量差，因此质量较大的中子可以衰变为质子。而质子比中子少的这一点点质量，恰好使得我们的宇宙中充满了大量的带正电的稳定质子，使电磁相互作用成为宇宙中普遍存在的现象。同时，中子的衰变率由中子与质子的质量差决定，而其衰变率又决定了质子和中子的丰度比。假使中子和质子的质量差变大或者变小一点点，那么中子衰变和核子聚变的平衡也将被打破，便无法形成各种各样的原子。另外，对于标准模型可能存在的修正和对大统一理论的探索也推动研究者们提出了一系列关于质子寿命的猜测^[6-7]。同时，在质子的寿命之外，质子的内部自旋结构和电荷分布半径(charge radius)同样作为物理学的基本问题之一受到人们的广泛关注。因此，对于核子内部结构的研究可以进一步加深人们对这个世界的理解，同时也能够为研究者们深入认识基本物理原理的迫切需求打开一扇窗口。

形状因子提供了对于强子内部结构的重要描述。通过形状因子可以计算出强子的电荷分布、电荷分布半径等一系列内部结构相关的参数。形状因子的理论计算和实验测量作为分析强子内部结构的重要手段，也一直受到粒子物理研究者们的关注^[8-9]。在过去的实验中，人们采用散射实验的手段来测量质子的形状因子，进而计算出其电荷分布半径，这种方法的误差大约在2%^[10-11]。进一步的实验采用了跃迁光谱的测量方法，可以将质子半径的计算精度提升约一倍^[12-14]。然而，在2010年使用$ \mathrm{\mu } $-氢原子进行的跃迁实验在更高精确度上测得了质子的电荷分布半径，并且与前述实验中得到的结果有较大的偏差^[2]。直到近几年，才有研究团队分别通过新的氢原子光谱实验^[15]与电子-质子的散射实验^[16]测得了与$ \mathrm{\mu } $-氢原子较为吻合的结果。随着实验的不断完善和取得进展，人们对于质子大小有着越来越具体的理解。不过，如何从理论上给出质子大小之谜的解答，并对其表现出的性质提出合理的预言，仍是理论物理学中重要的工作之一。

在当前处理非微扰理论最为有效的格点QCD框架下，理论上可以给出粒子的形状因子数值，这一计算也是相关研究的重点之一^[17-18]。然而在使用格点模拟来计算形状因子时，由于格子体积有限，因此在动量空间中动量参量均处于分立值，而全动量空间上的形状因子曲线只能通过拟合的办法得到数值解。另外，如果我们希望通过形状因子进一步求解电荷分布半径等数值，那么更感兴趣的部分往往是形状因子在低能区域的表现，而在这一区域中，有限体积效应带来的动量分立变得不可忽视.由于求解任意动量的形状因子仍然对于深入理解强子的内部组成和结构有着重要的意义，因此，我们试图研究有限体积效应对于形状因子计算的影响，并尝试探索一种更普遍的方法来处理形状因子计算中有限体积带来的问题。本文以$ \mathrm{{\text{π}} } $介子的形状因子为例寻找合理的插值方法，在压低有限体积效应带来的系统误差的同时，计算整个动量空间上的形状因子的数值结果。

本文关注的对象和工具是欧氏空间下$ \mathrm{{\text{π}} } $介子的强子函数$ {H}_{\phi }\left(x\right) $。一方面，通过格点QCD的手段，可以计算出一系列的关联函数，进而得到强子函数的数值。另一方面，强子函数反映了在特定时空点上电磁流与强子的相互作用，其中包含了形状因子的重要信息。${\text{π}} $介子的强子函数$ {H}_{\phi }\left(x\right) $定义为

在该矩阵元中，$ \left| {\text{π}} \left(\bf{0}\right) \right\rangle $代表初态为空间方向动量为0的$ \mathrm{{\text{π}} } $介子；$ \Phi \left(x\right) $为插入的场算符，其作用是湮灭一个$ {\text{π}} $介子；$ {J}_{\mu }\left(0\right) $为电磁场的流矢量。当我们所取的时间分量满足$ {t}'\ll 0\ll t $时，$ \mathrm{{\text{π}} } $介子激发态的贡献将被指数压低，因此可以只考虑基态$ \mathrm{{\text{π}} } $介子的不同动量本征态，并对空间坐标求和，由此建立强子函数与三点关联函数的联系：

式(2)左边为涉及场算符$ \Phi $与$ {\phi }_{{\text{π}} }^{\dagger } $的三点关联函数，$ {\phi }_{\mathrm{{\text{π}} }}^{\dagger } $为产生$ \mathrm{{\text{π}} } $介子的场算符，而右边第一个矩阵元$ \left\langle 0\right|\Phi \left(x\right)J\left(0\right)|{\text{π}} \left(\bf{0}\right)\rangle $即为强子函数，式中的$ {m}_{\mathrm{{\text{π}} }} $为$ \mathrm{{\text{π}} } $介子的静止质量。后一个矩阵元可以通过两点关联函数计算得到：

此处对于坐标的空间分量$ {x} $进行了求和。以上两式，建立了忽略激发态贡献时强子函数与三点关联函数$ \left.\left\langle 0\right|\Phi \left(x\right)J\left(0\right){\phi }_{\mathrm{{\text{π}} }}^{\dagger }\left({x}'\right)\left|0\right. \right\rangle $的联系。

强子的形状因子是定义在微观粒子的相互作用矩阵元中的洛伦兹标量，描述了粒子相互作用顶角的性质，反映了粒子的内部结构。形状因子可以描述为粒子内部电荷分布的傅立叶变换，其频域变量即为动量转移$ q\!=\!{p}_{1}\!-\!{p}_{2} $，通常记为$ {q}^{2} $的函数。其中，$ {p}_{2} $与$ {p}_{1} $分别为初态和末态的动量。

我们以$ \mathrm{{\text{π}} } $介子与光子的相互作用为例，根据Ward恒等式^[19]，矩阵元$ \left\langle {\text{π}} \left({{p}}_{\bf{1}}\right)\left|{J}_{\mu }\left(0\right)\right|{\text{π}} \left({{p}}_{\bf{2}}\right) \right\rangle $可以用形状因子表示为$ {{\left({p}_{1}+{p}_{2}\right)}_{\mu }F}_{{\text{π}} }\left({q}^{2}\right) $，其中$ {F}_{{\text{π}} }\left({q}^{2}\right) $为$ {\text{π}} $介子与光子相互作用的形状因子，$ {q}^{2}\!=\!{\left({p}_{1}\!-\!{p}_{2}\right)}^{2} $为动量转移。

文献[20]中的工作阐述了强子函数与形状因子之间直接的积分联系式：

其中：$ {j}_{0}\left(px\right) $为零阶球贝塞尔函数；$ {f}_{\mathrm{{\text{π}} }} $为$ \mathrm{{\text{π}} } $介子的衰变常数；$ E $为动量为$ p $的$ \mathrm{{\text{π}} } $介子具有的能量。上式左边实为强子函数的傅立叶变换$ \int {\mathrm{d}}^{3}{x}{\mathrm{e}}^{\mathrm{i}{p}\cdot {x}}H\left(t,{x}\right) $，由于上式右侧仅与空间动量的大小有关，与其方向无关，因此可以对上式左边的傅立叶变换进行各个方向上的平均，得到以$ {j}_{0}\left(px\right) $作为积分核的表达式。如果已知$ H\left(t,{x}\right) $的值，即可根据该式来数值求解不同动量转移下的形状因子。这也是目前常用的计算形状因子的方法。

量子色动力学(QCD)是在规范场论框架下，对于强相互作用进行描述的基本理论。而由于QCD的规范群是SU(3)的非阿贝尔群，故而QCD与量子电动力学仍然有着巨大差别。首先，QCD中传递相互作用的胶子与光子不同，其间可以发生相互作用；其次，这种差异表现在夸克具有“渐近自由”和“色禁闭”现象。因此，对于以强相互作用为代表的强耦合场论的处理，往往需要使用一些非常规的非微扰手段。而格点场论方法是目前以非微扰方法研究强耦合场论最为有效的手段。

格点QCD是在四维欧氏空间中，使用分立的时空格点定义出的非微扰QCD理论，是处理强相互作用的一种重要手段。其优势一方面在于非零格距给出自然的高能标截断，并将耦合常数吸收到了格距参数中，回避了紫外发散；另一方面在于格点QCD采用的算法易于实现，也易于推广到其他非微扰理论中。另外，格点QCD使用四维欧式时空，规避了闵氏空间中复指数震荡的作用量，故而计算效率得以大幅提高。格点计算中常用的Monte-Carlo方法与Metropolis算法运用了重要性采样^[21]，也使得计算当中绝大多数算力用于对主要区域的取样，因此可以高效地完成数值模拟计算。

在有限体积下的格点计算中，我们无法对$ H\left(t,{x}\right) $进行全空间的积分。因此对应到其傅立叶变换$ \tilde H\left(t,{p}\right) $上，便只能在分立的动量$ {p}=\frac{2{\text{π}} }{L}{n} $上得到结果。以常见的QCD格点点阵的大小为例，L的大小约为几fm，则可以计算得到动量空间的分立间隔约为几十到几百MeV。

对于格点计算方法来说，格距和有限体积是两个主要的系统误差来源。其中格距的限制在动量空间上给出了高能区域的动量截断，而有限体积的限制使得动量空间上只能计算分立点的数值。一般而言，不同的格点方案处理格距误差的方法各不相同，而有限体积带来的误差是所有格点方案都要面临的问题，同时其在动量空间中产生的分立效应也造成了计算电荷分布半径等物理量的困难。因此我们想要追求一种普适的、系统化的处理有限体积效应的方案，将动量空间上的形状因子计算平滑化并推广到整个动量空间上(不考虑格距带来的截断)，并尽可能降低有限体积的影响。

在格点QCD中，我们可以计算有限体积内强子函数$ {H}_{{\text{π}} }\left(x\right) $的数值，并通过强子函数计算得到动量空间上$ {p}=\frac{2{\text{π}} }{L}{n} $的格点上的形状函数数值。在连续的全空间极限下，形状函数与强子函数的关系为

上式中忽略了激发态粒子的贡献。在格点上，我们可以从强子函数的数值出发，在动量空间格点上定义未归一化的$ {\tilde H}^{\left(L\right)}(t,{p}) $：

式中：$ {\mathrm{O}}_{\mathrm{h}} $是三维立方格点满足的旋转反射对称群，其中的群元记作$ \widehat{\mathrm{R}} $，该群的阶记作$ {\mathrm{N}}_{\mathrm{R}} $。式中的$ {L}^{3} $为所有格点的集合，这里L为格点区域的尺寸。根据上式定义，在忽略格距作用的情况下，$ {\tilde H}^{\left(L\right)}\left(t,{p}\right) $与形状因子的关系为

注意到，在$ {\tilde H}^{\left(L\right)}\left(t,{p}\right) $的定义式中，由于有限体积的影响，动量只能定义在动量空间满足$ {p}=\frac{2{\text{π}} }{L}{n} $的分立点上，因此只能使用上式求得相应格点上动量对应的形状因子数值。后续的计算中，我们还将使用到$ q $与$ {p} $的下述关系：

在3.1节中，我们通过格点QCD的常规方法得到了形状因子在动量空间分立点上的取值。而想要得到全空间中的形状因子，在有限体积下的格点模拟中是不可能的。因此我们需要通过合理的内插方法，将这些分立的形状因子取值推广到整个动量空间上。在进行内插操作时，需要注意到形状因子$ {F}_{{\text{π}} }\left({q}^{2}\right) $仅与动量转移$ q $的大小有关，因此在动量空间具有O(3)的旋转对称性。故而要求在内插过程中需保持这一对称性，这对于可行的内插方法提出了一定的限制。

文献[22]讨论了四维欧式时空上格点算符的重整化，文中在对格点上的格林函数进行计算时，提出了一种在坐标空间下保持对称性的内插方法，以此来处理格点计算中非零格距的问题。由于坐标空间与动量空间具有对偶关系，我们猜测可以通过将类似的方法推广到动量空间上，以此来降低格点计算中普遍存在的有限体积效应的影响。同时，该方法在计算中保证了系统的旋转对称性不被破坏，因此要优于直接的线性内插。该方法首先将一维空间的线性内插推广至高维空间，以三维空间为例的内插公式可以写作：

其中$ a $为格距，$ {n}=\left(\left\lfloor \frac{x}{a} \right\rfloor ,\left\lfloor \frac{y}{a} \right\rfloor ,\left\lfloor \frac{z}{a} \right\rfloor \right) $ (其中$ \left\lfloor \frac{x}{a} \right\rfloor $为floor函数，表示不超过$ \frac{x}{a} $的最大整数，$ \left\lfloor \frac{y}{a} \right\rfloor ,\left\lfloor \frac{z}{a} \right\rfloor $同理)，$ {\Delta }_{\mu ,\nu } $定义为$ a\left({n}_{\mu }+1-\nu \right)-{x}_{\mu } $，其中$ \mu \!=\!1,2,3 $，$ \nu \!=\!i,j,k $。

在格点上，我们希望进行内插后得到的目标函数具有三维空间中的O(3)对称性，那么接下来需要将线性内插过程中破坏的O(3)对称性复原。故而，需要将内插得到的函数$ f(x,y,z) $按照全部方位角积分并取平均值：

我们将这一内插方法推广到动量空间中，对形状因子$ {F}_{{\text{π}} }\left({q}^{2}\right) $进行内插计算。首先，暂时不考虑O(3)对称性，采用

定义未归一化的形状因子$ {F}_{{\text{π}} }^{\left(L\right)}\left({p}\right) $为

其中t的选取有任意性，可以选择足够大的合适时间片段。易知形状因子$ {F}_{{\text{π}} }\left({q}^{2}\right) $与该定义中的$ {F}_{{\text{π}} }^{\left(L\right)}\left({p}\right) $具有的关系为

随后我们对上式中的$ {F}_{{\text{π}} }^{\left(L\right)}\left({p}\right) $进行内插，将$ {p} $的取值范围从分立点上推广到连续的动量空间。首先通过三维空间的线性插值得到：

接下来，我们对其进行平滑化处理，并将${F}_{{\text{π}} }^{\left(L\right)}\left[\frac{2{\text{π}} }{L}({n}+i{\widehat{e}}_{1}+j{\widehat{e}}_{2}+k{\widehat{e}}_{3})\right]$的表达式代入，得到：

其中，$ \left\lfloor \frac{{p}}{2{\text{π}} /L} \right\rfloor +\left(i,j,k\right) $是$\left(\left\lfloor \frac{{p}_{x}}{\frac{2{\text{π}} }{L}} \right\rfloor +i,\left\lfloor \frac{{p}_{y}}{\frac{2{\text{π}} }{L}} \right\rfloor +j, $$ \left\lfloor \frac{{p}_{z}}{\frac{2{\text{π}} }{L}} \right\rfloor +k\right)$的缩略写法，$ {E}_{{p},ijk} $定义为动量空间里分立动量$ \frac{2{\text{π}} }{L}\left[\left\lfloor \frac{{p}}{\frac{2{\text{π}} }{L}} \right\rfloor +\left(i,j,k\right)\right] $所对应的能量。

我们希望将对形状因子进行内插求解的结果以权重函数的形式表示出来，并且观察其在无穷体积极限下的行为。从3.2节得到的表达式中，我们可以直接抽出满足$ {\sum\nolimits}_{{x}\in {L}^{3}}{H}^{\left(L\right)}\left(x\right)\omega (x,{p})\!=\!{\widehat{F}}_{{\text{π}} }\left(\right|{p}\left|\right) $的权重函数$ \omega (x,{p}) $，其形式为

我们对其在无穷体积极限下的行为进行讨论。当$ L\to \mathrm{\infty } $时，在动量空间的分立最小单位$ \frac{2{\text{π}} }{L}\to 0 $。对于上式中的核心部分$\frac{{\rm e}^{{E}_{{p},ijk}t}}{{\rm e}^{{E}_{{p},ijk}t}+{m}_{\mathrm{{\text{π}} }}}\cos\Big\{\frac{2{\text{π}} }{L}\left[\left\lfloor \frac{{p}}{2{\text{π}} /L} \right\rfloor + \big(i,j,k\big)\right]\cdot $$ {x}\Big\}$中，floor运算$\left\lfloor \mathrm{\;}\cdot \mathrm{\;} \right\rfloor$对于数值的影响极小，因为$ \frac{{p}}{2{\text{π}} /L} $为正比于$ L $的无穷大量，因此floor操作的系统偏差$ \frac{\frac{{p}}{2{\text{π}} /L}-\left\lfloor \frac{{p}}{2{\text{π}} /L} \right\rfloor }{\frac{{p}}{2{\text{π}} /L}}\sim O\left(\frac{1}{L}\right) $，可以忽略。同理$ (i,j,k) $的贡献也在$ O\left(\frac{1}{L}\right) $量级。因此，该余弦函数在无穷体积近似下可以直接写作$\frac{{\rm e}^{{E}_{{p}}t}}{{\rm e}^{{E}_{{p}}t}+{m}_{\mathrm{{\text{π}} }}}\mathrm{c}\mathrm{o}\mathrm{s}({p}\cdot {x})$。另外由于线性内插的特性，有

因此，有

因此在全空间连续极限下，上式给出的权重函数$ \omega \left(x,{p}\right) $回归到经典连续系统下的积分因子${j}_{0}\big(\left|{p}\left|\right|{x}\right|\big)$的相同形式。

本节通过数值模拟的方式来对上文中的计算结果进行检验，并分析该内插方法的表现。在本节中，我们在假定形状因子的表达式已知的前提下，通过本节给出的内插公式计算生成全动量空间的形状因子数值，并与所假设的表达式相比对。

我们假定形状因子有VMD(Vector Meson Dominance)模型的形式，即

这里的$ {m}_{v} $为矢量介子的质量，我们在数值模拟中采用最轻的矢量介子$ \rho $介子的质量，即取$ {m}_{v} $=775 MeV。由$ {q}^{2} $与$ {{p}}^{2} $之间的关系$ {{p}}^{2}=\frac{{q}^{4}}{4{m}_{{\text{π}} }^{2}}-{q}^{2} $，我们可以将形状因子由$ {q}^{2} $的依赖关系改写为$ {{p}}^{2} $的依赖关系：

在模拟中，我们采用的数值为格距$ a\!=\!1\times {10}^{-3} $$ {\rm{Me{V}}}^{-1} $，坐标空间的尺寸$ L\!=\!Na $，$ N $为每个空间维度的格子数目，我们模拟中分别取值$ N\!=\!32, \mathrm{\;}48, $$ \mathrm{\;}64,\mathrm{\;}96,\mathrm{\;}128 $。用到的其他常数数值包括$ {m}_{\mathrm{{\text{π}} }}\!= \!135\mathrm{\,}\mathrm{M}\mathrm{e}\mathrm{V} $，$ {f}_{\mathrm{{\text{π}} }}\!=\!130\mathrm{\,}\mathrm{M}\mathrm{e}\mathrm{V} $。我们采用自然单位制，$ 1\!=\!\mathrm{\hslash }c\!=\!0.197 $$ \mathrm{\;}\mathrm{e}\mathrm{V}\cdot {\text μ }\mathrm{m} $，因此$ a\approx 0.2\mathrm{\,}\mathrm{f}\mathrm{m} $。时间维度上的格点数目固定为128。在动量空间，分立的动量之间的最小间隔为$ \Delta p\!=\!\frac{2{\text{π}} }{L} $，以N=64为例，$ \Delta p\!=\!\frac{2{\text{π}} }{64a}\approx 98.17\,\mathrm{M}\mathrm{e}\mathrm{V} $。

空间维度各个不同取值的格点数目所对应的参数如表1所列。

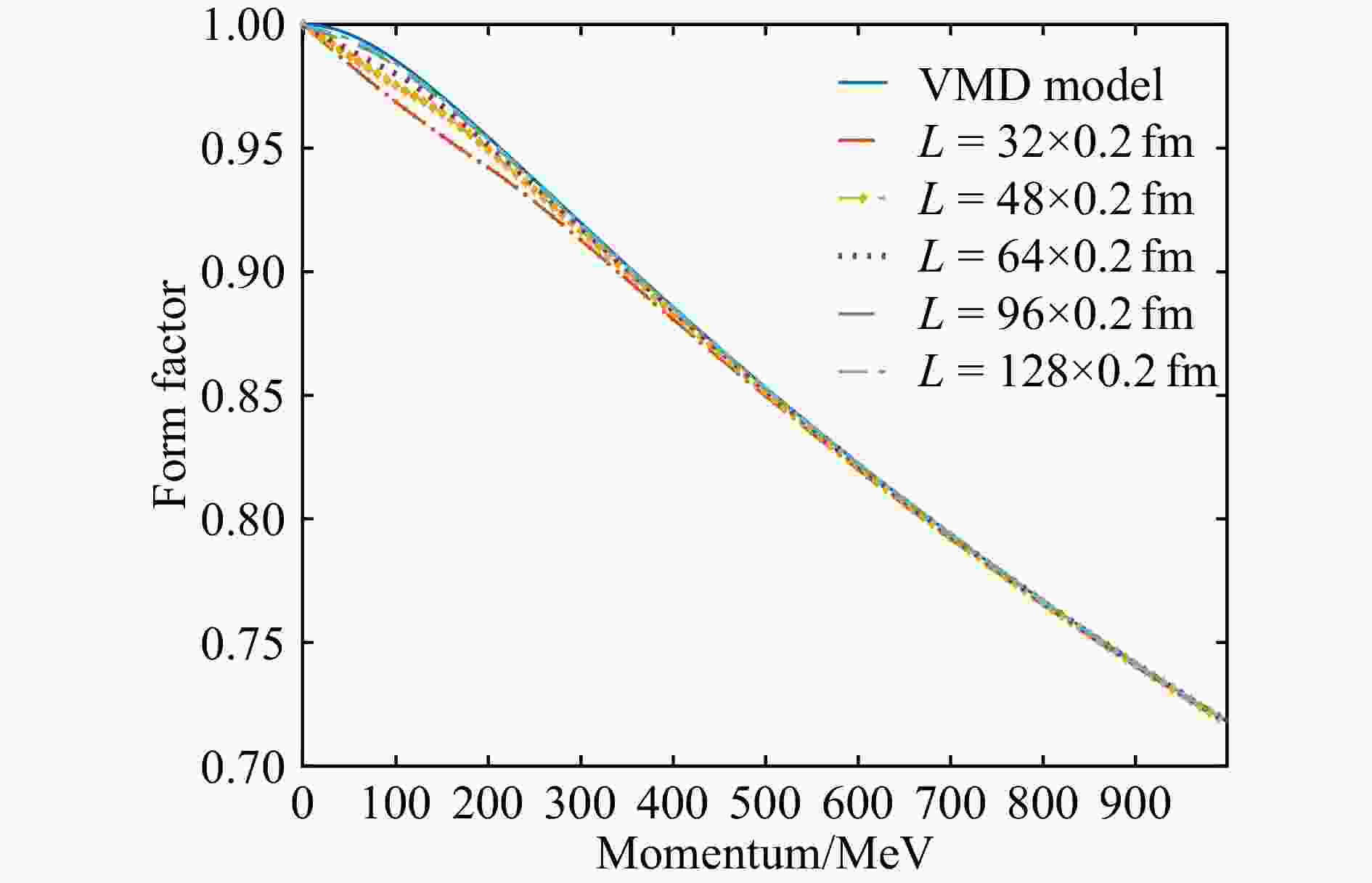
不同的格子数目N给出不同的动量空间最小间隔。由于格距a固定为$ 1\times {10}^{-3}\,\mathrm{M}\mathrm{e}{\mathrm{V}}^{-1} $，因此格距限制下的最大动量大小为$ \frac{{\text{π}} }{a}\approx 3.1\,\mathrm{G}\mathrm{e}\mathrm{V} $。我们计算形状因子仅使用动量范围0~1 000 MeV。

对于不同的格点空间尺寸L=Na，我们分别作出内插得到的形状因子$ {F}_{{\text{π}} }\left(\left|{p}\right|\right) $关于动量$ \left|{p}\right| $的图线，见图1。

图  1  (在线彩图)不同格点体积下内插得到的形状因子的动量依赖关系

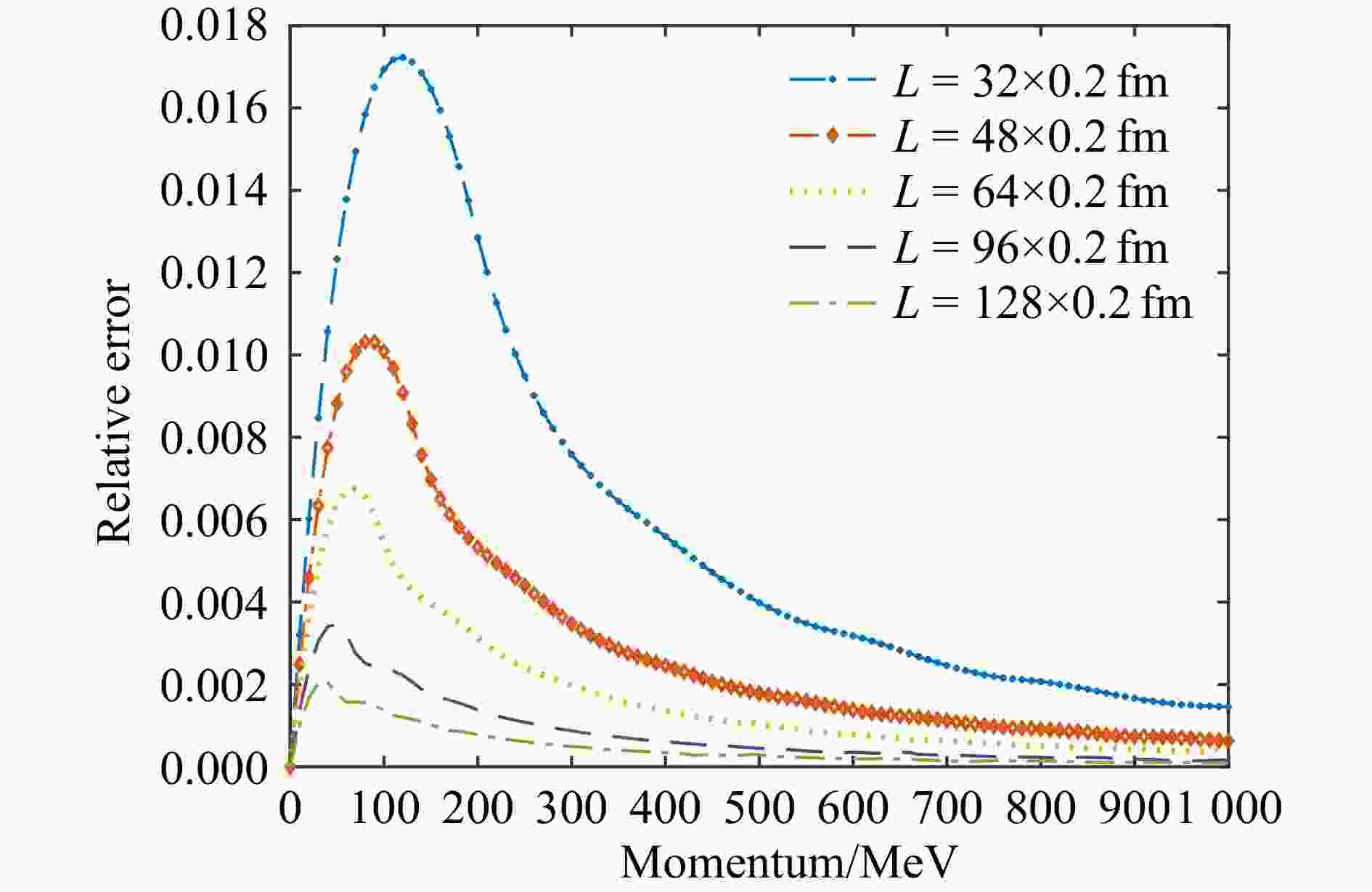
从图1中可以看出，一方面，随着格点空间体积的增加，内插得到的形状因子函数图像与所预设的形状因子动量依赖关系符合得更好。另一方面，在较大动量的区域(典型区域$ p>2\times \frac{2{\text{π}} }{L} $)，内插的结果比较理想，而在我们更感兴趣的较小动量区域(典型区域$ p<\frac{2{\text{π}} }{L} $)，内插结果呈现明显的线性特征，与在零点附近曲率较大的VMD模型符合得一般。我们可以进一步作出内插得到的形状因子的百分比相对误差(Relative Error)曲线，如图2所示。

图  2  (在线彩图)不同格点体积下内插的相对误差曲线

从图2中可看出，拟合的误差主要集中在小动量区域，同时在N取不同取值时，相对误差随着格点体积的增大而明显变小。图中相对误差的最大值以及出现最大误差的动量取值列在下表中。同时由于不同的空间体积下，动量空间具有不同的分辨率，因此我们也将出现最大误差的动量位置与动量空间的分辨率在表2中进行比较。

表2显示，最大误差位置往往出现于分立间隔的0.6~0.8倍处，同时最大误差大体上随着体积L的增加而以$ O\left(\frac{1}{L}\right) $的趋势减小，基本与理论预期相符。需要注意的是，在本节的数据模拟中尽管由于这些数值是在我们假定形状因子具备VMD模型形式的前提下进行插值模拟得到的，故而具有模型依赖关系，所计算得到的相对误差的大小与位置未必具有普适性；但是，表中的最大误差动量相对动量分立间隔的比值反映的是不同体积下插值系统本身的特性随着系统体积变化的变化模式，因此，该计算方法给出的误差对于任何实际的形状因子表达式均应有类似表现。一方面，在较大动量区域，特定动量附近对应的分立动量点变多，使得内插方法较容易给出更接近精确值的数值结果；而从另一方面来看，我们对于小动量区域，即$ {q}^{2} $在零点附近时形状因子的动量依赖关系更加感兴趣。因此，还需试图对这一插值方法进行进一步探索。

在4.1中通过线性内插之后进行球壳平均的方法，计算得到了形状因子的内插数值。在本节中，我们试图采用其他插值方法进行内插，并与4.1节中的结果进行比较。

在我们的模型中，处于特定分立动量值上的点，即$ {p}\!=\!\frac{2{\text{π}} }{L}{n} $的点上的形状因子数值可以通过格点数据直接计算出来。如果我们直接在三维动量空间采用插值算法，那么可以得到定义在全动量空间上的形状因子函数$ {\tilde F}_{{\text{π}} }\left({p}\right) $。不过从形状因子的定义角度而言，物理的形状因子$ {F}_{{\text{π}} }\left({q}^{2}\right) $在动量空间中应该有O(3)的旋转对称性，即其应该是动量大小的一维函数，${F}_{{\text{π}} }\left({q}^{2}\right)\!=\! {F}_{{\text{π}} }\left\{-2{m}_{{\text{π}} }\times $$ \left[E\left(\left|{p}\right|\right)-{m}_{{\text{π}} }\right]\right\}$。在第3节的模型中，我们的处理手段是在三维空间进行插值处理后，对每个动量大小对应的球壳上的形状因子取值作平均，从而得到仅与动量大小相关的形状因子$ {F}_{{\text{π}} }\left({q}^{2}\right) $。为了验证球壳平均的有效性，我们在这里可以采用另一种处理手段，即选取某个特定方向，以该方向上插值得到的形状因子数值作为对应动量的结果。我们在这里选取了三个特殊方向：

● 坐标轴方向，$(0,\mathrm{\,}0,\mathrm{\,}1)$；

● 面对角线方向，$(1,\mathrm{\,}0,\mathrm{\,}1)/\sqrt{2}$；

● 体对角线方向，$(1,\mathrm{\,}1,\mathrm{\,}1)/\sqrt{3}$。

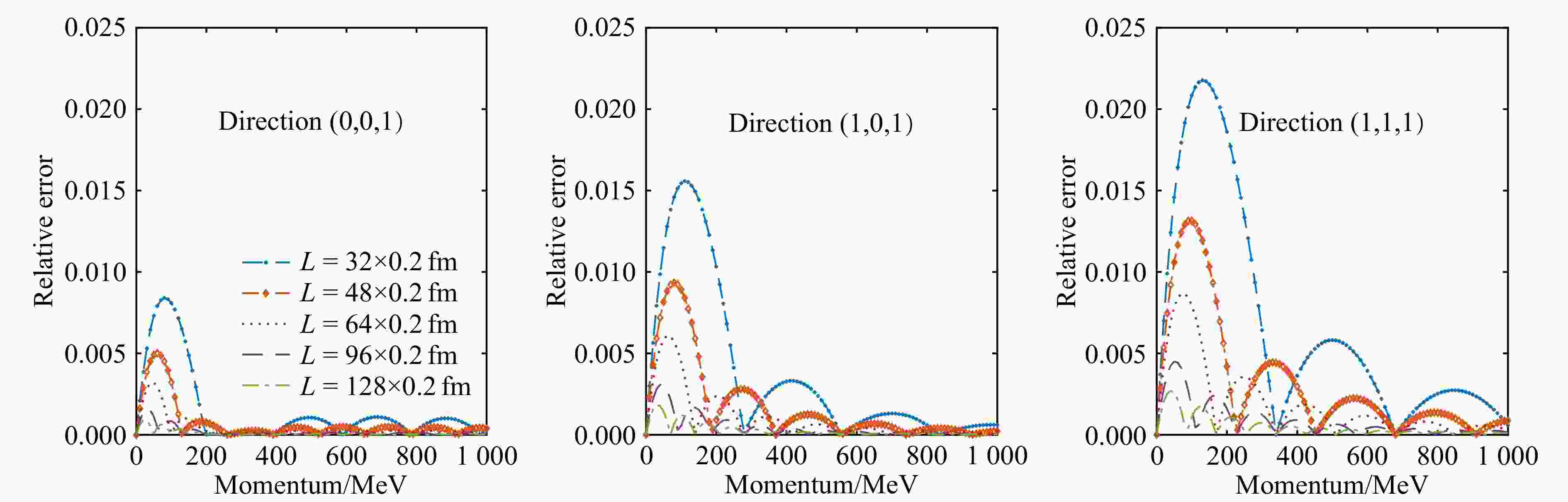
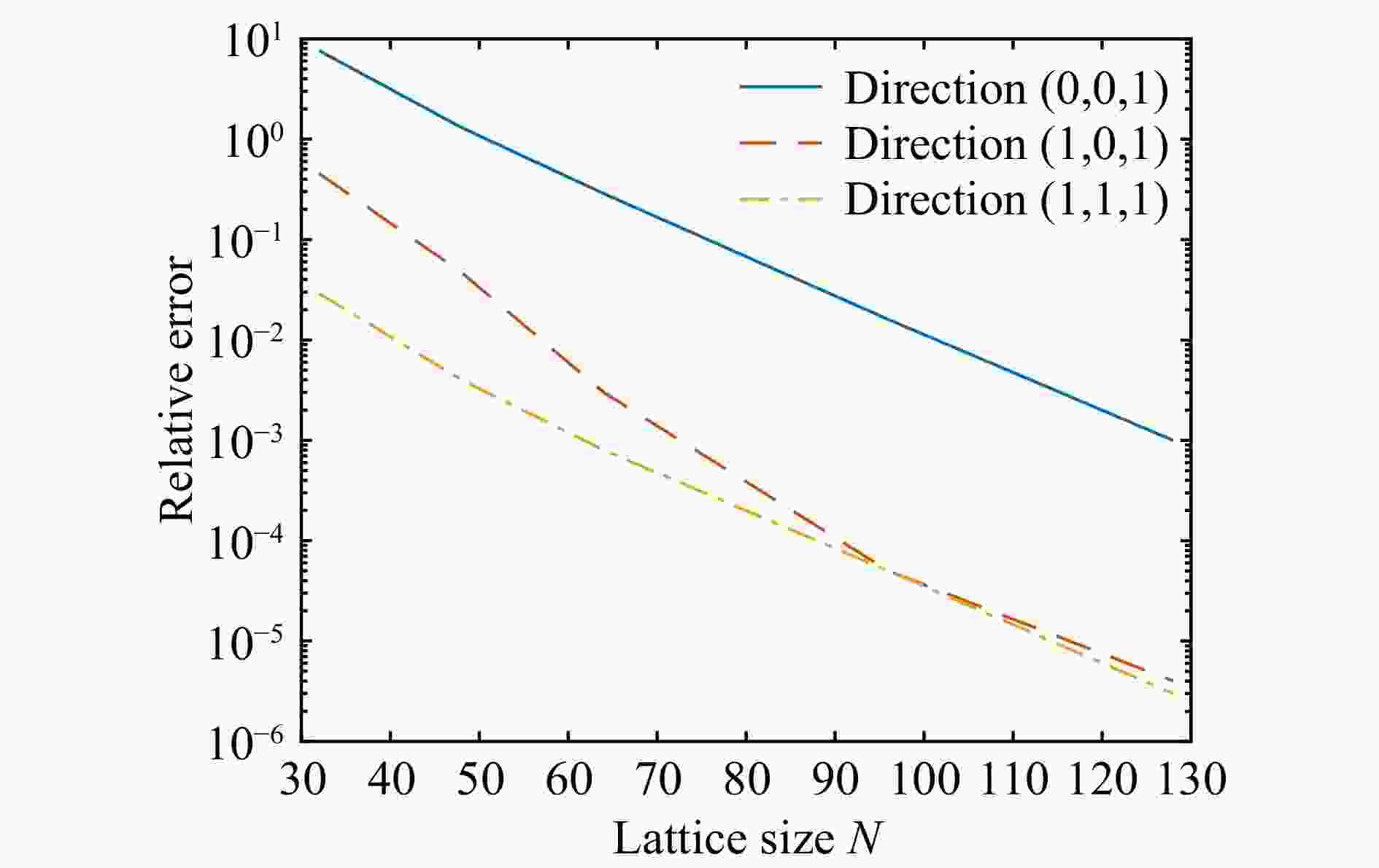
我们选取的三个方向均经过动量空间中已有数据的分立点，三个方向上与分立格点的交汇间隔之比为$ 1:\sqrt{2}:\sqrt{3} $。与上一节中的球壳平均方法不同的是，在已有数据的分立点上拟合出的数值应当与给出的确定值相同，故而可以预期对于在特定方向上进行的内插拟合来说，其误差将随着交汇间隔的增大而变大。我们同样作出不同动量下相对误差数值的图像，图像中各个方向上的相对误差-动量曲线与预计中的表现相同，如图3所示。

图  3  (在线彩图)沿特定方向内插时不同体积下的相对误差曲线

图中可见的图像节点为恰好已有数据的分立点，对于不同方向而言，途经的相邻节点的间距有所不同。我们可以通过上述计算结果来比较不同的内插方法的最大误差。各方法的误差分别列在表3~5中。

我们可以从表3~5中看出，沿方向(0, 0, 1)，即沿格点排布方向进行内插时，相对误差要明显小于沿其他两个方向(即沿格点面对角线及体对角线)进行内插时的误差。与我们在4.1节中采用的球壳平均方案进行对比，显然球壳平均的方案给出的相对误差介于本节中方向(0, 0, 1)与方向(1, 1, 1)上给出的误差之间。从数值模拟的算法来看，方向(0,0,1)的相邻交汇点的距离最小(即1倍的动量分立间隔)，而方向(1, 1, 1)上相邻交汇点距离最大(即$ \sqrt{3} $倍的动量分立间隔)，故而不同的误差表现即为符合预期的结果。考虑到系统具备的空间旋转对称性，仅取特定方向进行内插或许难以给出合理解释；而球壳平均方法在解决这个问题时，其他各个其他方向上更大的拟合误差会给出对于平均误差的贡献。因此系统误差的增加即可视作恢复系统的对称性时需要付出的代价。大致上，随着格点体积L的增大，这部分系统误差会以$ O\left(\frac{1}{L}\right) $的速度收敛。

在连续无穷大空间中，强子函数与形状因子的关系由式(4)给出。与此同时，对于格点QCD来说，我们需要将式(4)中的连续傅立叶变换转化为离散傅立叶变换(DFT)，即

如前所述，对于离散傅立叶变化，上式计算的空间动量需要位于分立点上，满足$ {p}=\frac{2{\text{π}} }{L}{n} $关系。接下来我们探索另外一种内插方式，使用推广的离散时间傅立叶变换(DTFT)代替离散傅立叶变换，应用在空间上离散的强子函数上，将其变换为动量空间上连续的频谱。

在进行DTFT变换时，需要可数并且平方可积的数据集。对于有限体积的格点系统中的强子函数来说，我们可以将格点体积之外的数据取作0来进行计算。由于强子函数随着空间尺度增大而具有指数衰减的性质，可以预期有限体积效应同样会随着体积增加而以指数形式衰减。我们尝试采用下式计算形状因子：

其中$ \tilde H\left(t,{p}\right) $未归一化，为强子函数的傅立叶变换${\sum\nolimits}_{{x}\in L}\mathrm{c}\mathrm{o}\mathrm{s}({p}\cdot {x})H\left(x\right)$。可以注意到，上式左侧的形状因子在时间$ t $足够大时不依赖于时间。我们在后续的数值计算中取$ t=9a $。另一方面，该方法受到有限体积效应的影响，不能完全保持系统的旋转对称性，故而我们需要选取特定方向，将动量的取值限定在某个维度上。与前述计算类似，我们仍然选取以下三个方向：

●坐标轴方向，$(0,\mathrm{\,}0,\mathrm{\,}1)$；

●面对角线方向，$(1,\mathrm{\,}0,\mathrm{\,}1)/\sqrt{2}$；

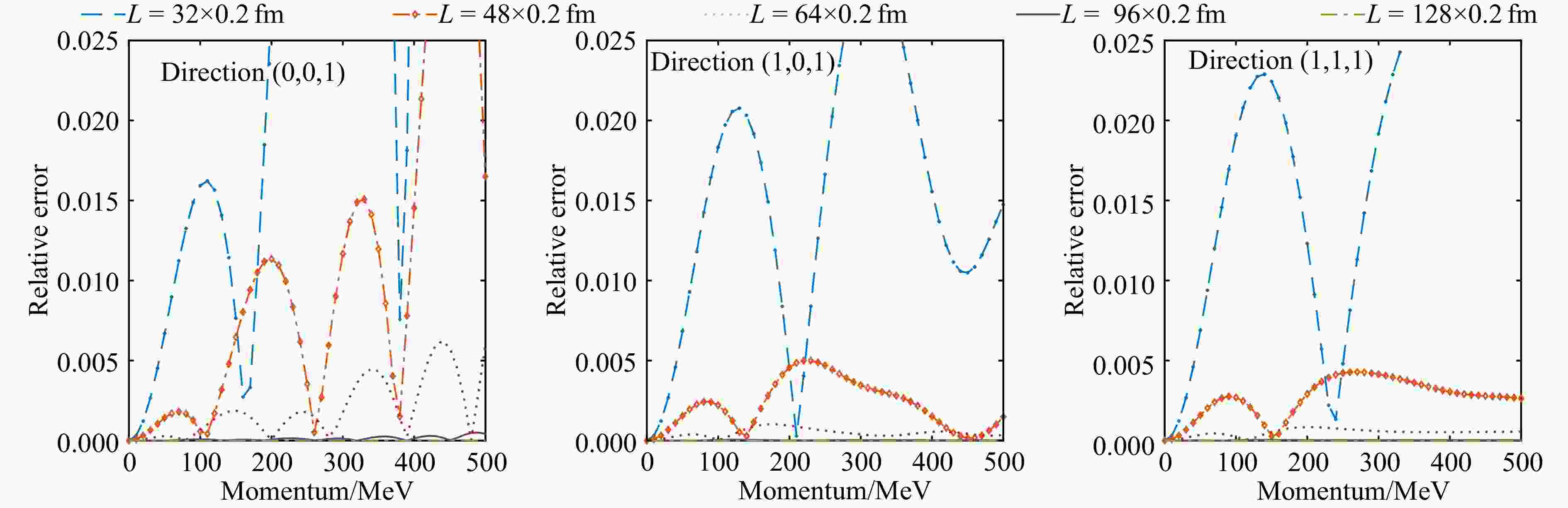
●体对角线方向，$(1,\mathrm{\,}1,\mathrm{\,}1)/\sqrt{3}$；

拟合结果的相对误差曲线见图4。

图  4  (在线彩图)采用傅立叶变换的连续化内插时，沿特定方向内插时不同体积下的相对误差曲线

从图4中可以看出，该方法在小体积或者中等体积的格点系统中表现较差，与前述的保持旋转对称性的内插算法相比，相对误差明显更大。但是我们注意到，一方面，这一算法的误差主要分布于较大动量的区域，另一方面，在较大体积的格点系统中，该方法的表现显著优于前述算法。这与我们的猜测相符，即误差随着格点系统尺度的增大而指数衰减。考虑到图4中，误差衰减的指数行为不易观察，因此为了验证这一猜测，我们将三个方向上的最大误差以对数坐标画出，如图5所示。

图  5  (在线彩图)最大相对误差关于格点系统尺度N的依赖关系

该方法相比前文提出的保持旋转对称性的内插算法，优点在于相对误差随格点系统尺度的增加的收敛速度更快，不过其劣势也很明显：一方面，在系统体积较小、误差较大的情况下，系统的旋转对称性无法保持；另一方面，对于目前的算力来说，我们很难高效地完成较大规模格点系统的快速计算。然而，使用这一算法得到的数值模拟结果能够展示出内插结果的偏差对于系统尺度的依赖关系，能够为格点计算中系统体积的合理选取提供参考，同时其快速收敛的特性也为后续的研究提供了有意义的方向。另外，随着硬件条件的进步以及未来可预期的算力提升，在更大尺度的格点系综上的计算也会使得基于这一思路的内插算法具备更高的应用价值。

接下来，我们使用格点QCD计算中得到的原始数据，从格点上的三点关联函数出发，进行形状因子的求解和计算拟合。本节中使用的数据来源于文献[20]中使用的24D组态。其格点数目为$ 24\times 24\times 24\times 64 $，格距$a\!=\!1.015\mathrm{\,}\mathrm{G}\mathrm{e}{\mathrm{V}}^{-1}$，$ {\text{π}} $介子的质量为$(141.2\pm 0.4)\,\mathrm{M}\mathrm{e}\mathrm{V}$。在本节的计算中，我们使用了该系综下生成的39个规范场组态下，由wall-source的$ {\text{π}} $介子生成算符$ {\phi }_{W,{\text{π}} }^{\dagger } $产生的三点函数$ \left\langle {A}_{4}\left(x\right){J}_{4}\left(0\right){\phi }_{W,{\text{π}} }^{\dagger }\left(-{t}_{{\text{π}} }\right) \right\rangle $的数值，这里时间间隔$ {t}_{{\text{π}} } $取值为$ {t}_{{\text{π}} }\!=\!10\times a $，以保证基态$ {\text{π}} $介子的贡献占主导地位。

根据第2节中的讨论，三点函数可以与强子函数H(x)建立联系：

式中，场算符$ \Phi $取为轴矢量算符的第四分量$ {A}_{4}= $$ \bar u{\gamma }_{4}{\gamma }_{5}d $，电磁流矢量算符同样取第四分量$ {J}_{4}\left(0\right) $。我们使用的数据中包含39个规范场组态，需要对其取平均值。我们采用刀切法(Jackknife)^[23]来对数据的均值和标准差给出无偏估计。另外，对于该实际格点系综而言，考虑格距效应，我们需要使用带格距修正的表达式进行形状因子的计算。我们使用文献[20]中的式(24)定义比值$ {M}^{\left(L\right)}(t,{p}) $：

上式中，$ {\tilde H}^{\left(L\right)}\left(t,{p}\right) $为强子函数的离散傅立叶变换

其中动量处于分立点上，满足$ {p}=\frac{2{\text{π}} }{L}{n} $。实际计算中，我们对强子函数直接作快速傅立叶变换(FFT)后取其实部。上式中解得的$ {M}^{\left(L\right)}\left(t,{p}\right) $在时间t足够大时便收敛到该动量点上的形状因子值$ {F}_{\mathrm{{\text{π}} }}\left({\widehat{q}}^{2}\right) $。后续计算中为了便于与第4节中的数值模拟作比照，我们仍采用空间动量$ {p} $作为形状因子$ {F}_{\mathrm{{\text{π}} }} $的参量。

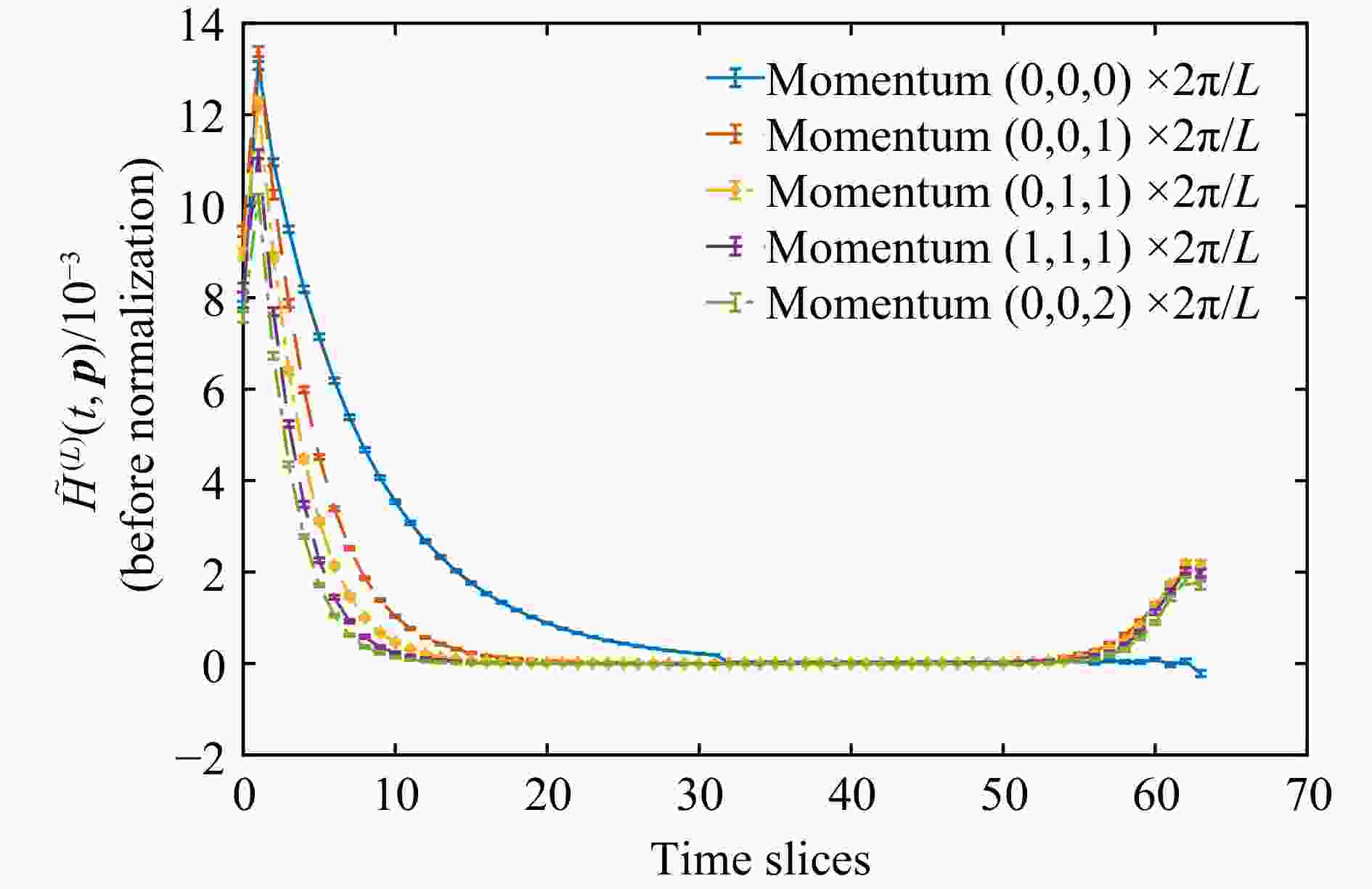
首先我们作出未归一化的强子函数的傅立叶变换$ {\tilde H}^{\left(L\right)}\left(t,{p}\right) $，前几个较小动量处的取值如图6所示。

图  6  (在线彩图)几个小动量点上的$ {\tilde H}^{\left(L\right)}\left(t,{p}\right) $

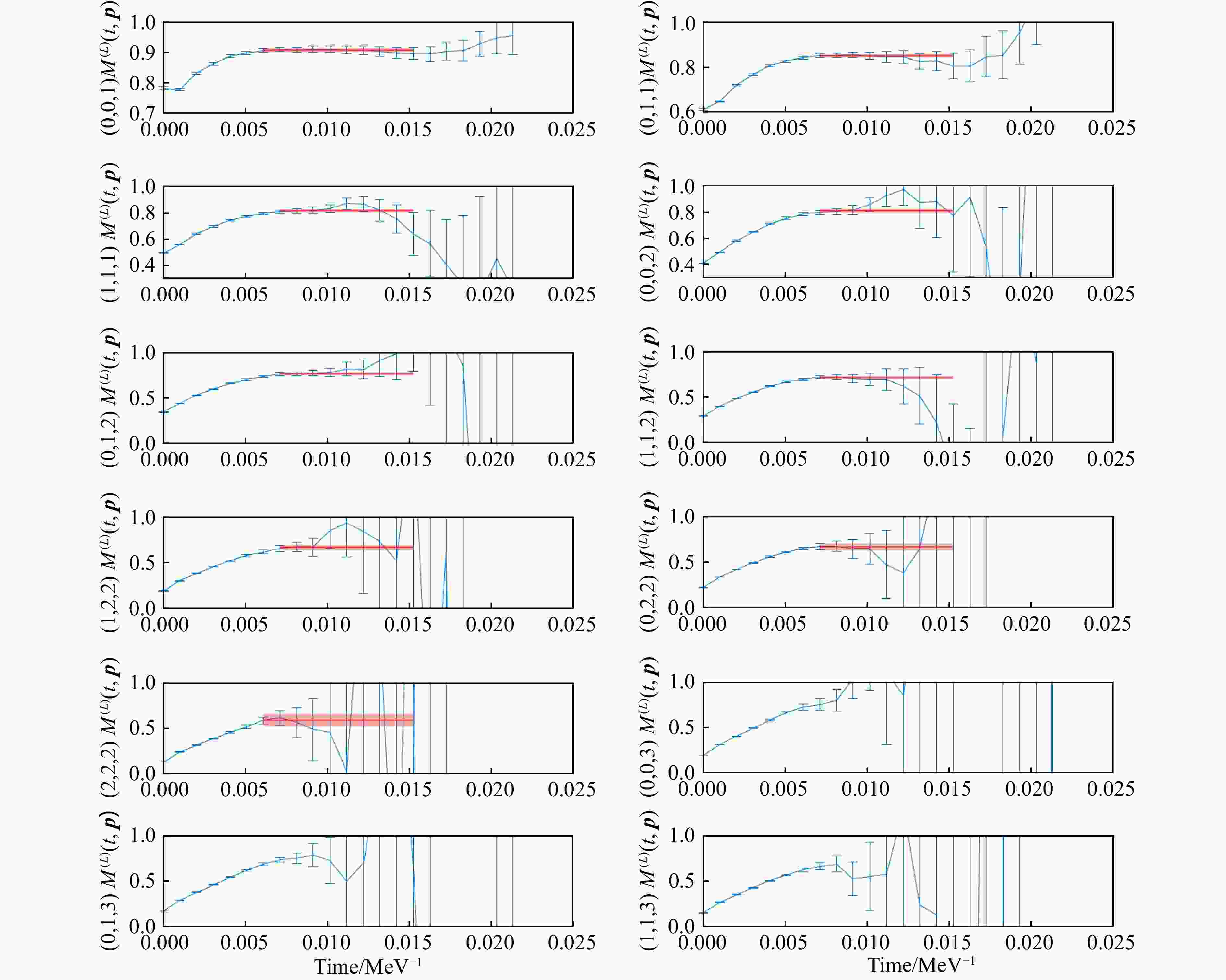
对于这几个动量较小的分立点，我们计算出各个时间片上$ {M}^{\left(L\right)}\left(t,{p}\right) $的取值，并使用前述方法进行内插计算。考虑到系统的立方群对称性，我们对群轨道上的所有$ {M}^{\left(L\right)}\left(t,{p}\right) $的数值进行平均后，将前12个分立动量上的$ {M}^{\left(L\right)}\left(t,{p}\right) $在图7中给出。

图  7  (在线彩图)前12个动量点上经过立方群平均的$ {M}^{\left(L\right)}\left(t,{p}\right) $

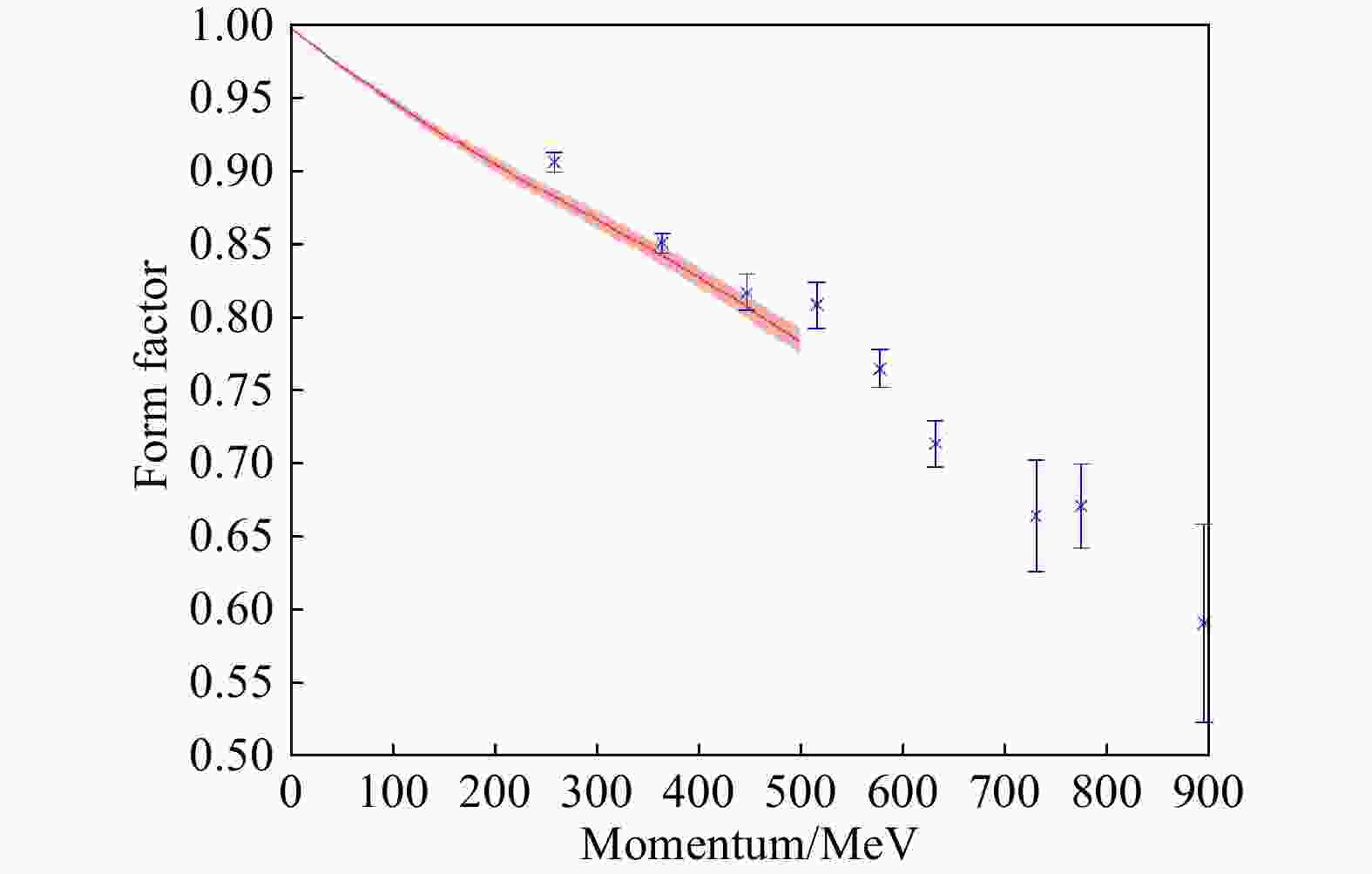
由图7可见，前面几个动量较小的子图中可以较为清晰地找到$ {M}^{\left(L\right)}\left(t,{p}\right) $的平台区域，进而给出形状因子的取值；而后面几个动量较大的图中$ {M}^{\left(L\right)}\left(t,{p}\right) $的行为更加异常，对形状因子取值估计的偏差也会迅速增大。我们采用$ {\chi }^{2} $的拟合方法求得了前面9个小动量对应的形状因子拟合值及其对应的标准差，如图中水平的红色线段所示。在该格点系综中，动量的分立间隔约为$ 252\mathrm{\;}\mathrm{M}\mathrm{e}\mathrm{V} $，我们进行拟合的动量范围取在$0\leqslant \left|{p}\right|\leqslant $$ 500 \mathrm{\,}\mathrm{M}\mathrm{e}\mathrm{V}$，因此任一空间方向上仅需要不超过2倍动量分立间隔处的数据。

我们使用前9个小动量进行形状因子的数值拟合，拟合得到的结果如图8所示(注意内插拟合的范围为球对称的全部空间，故需要用到更大动量处的分立数据点)。

图  8  (在线彩图)形状因子的取值在动量0~500 MeV范围的拟合结果。

从图8中可以看出，最小的动量点(即(0, 0, 1)位置及其在立方群群轨道上的等价点)所给出的形状因子与拟合的结果偏离较大，而其余动量点上的形状因子与拟合结果较为吻合，这与我们在第4节中数值模拟部分给出的结论一致。由于我们采用的格点体积相对较小，因此该部分的偏离在结果中体现得较为明显，而随着计算使用的格点体积的增大，该偏差将被按比例压低。因此，上述方法可以自然地推广到体积更大的格点系综中，并且在有限体积导致的动量空间分立化的情况下给出合理的平滑化拟合结果。

本文主要讨论了在计算强子的形状因子的过程中，有限体积效应对所得结果的影响。以$ \mathrm{{\text{π}} } $介子为例，从格点QCD中计算得到的三点函数出发，可以得到$ \mathrm{{\text{π}} } $介子对应的强子函数，进而计算出动量空间中的形状因子，而有限体积效应使得我们只能得到分立动量上的值。本文给出的算法可以在强子函数的基础上计算得到全动量空间上的形状因子，并且在假设形状因子具有VMD模型的前提下，给出了其拟合结果。进一步，我们使用格点系综上的实测数据，通过前文分析的内插算法得到了形状因子在动量空间的连续化取值，从而证实了文中提出方法的可靠性和可操作性。上述方法可以推广到任意有限体积的格点系统中，并且可以用于不同强子的形状因子计算。同时，本文初步探索了另一种对傅立叶变换进行连续化的內插方法，并展示了该方法的拟合误差随着格点尺度增加而指数衰减的依赖关系。该方法在系统尺度较小时表现差于第一种内插算法，然而随着系统尺度增加，误差衰减的速度会远远快于前一种算法，因此在格点体积足够大时，该方法有着更广阔的应用潜力和研究意义。一方面，上述两种方法给出的计算结果在一定程度上提供了强子形状因子的更多信息，有助于人们加深对于强子内部结构的理解；另一方面，也给出了其内插结果相对于真实结果的偏差与系统体积的依赖关系，有助于格点计算中体系尺度的合理选取，也为内插算法的进一步探索提供了有潜力的方向。

致谢 本文内容为作者在攻读硕士研究生期间，在导师冯旭研究员指导下完成的工作。本文能够得以完成，离不开导师的悉心指导和北京大学物理学院诸位老师的教育与培养。在此，作者谨对导师以及其他在过去几年间不吝赐教的师友致以诚挚的感谢。