下载:
-
等单元长度多间隙加速结构是一种非常重要且应用广泛的加速结构：质子超导直线加速器和重离子直线加速器的超导腔大都采用这种结构，能量大于100 MeV的常温质子加速结构如CCL结构[1-2]，也大都采用这种结构。随着人们对清洁能源的重视，近年来许多国家都在进行用于加速器驱动的次临界系统(ADS)的大功率强流质子直线加速器的设计及研制[3-5]。在强流质子直线加速器的超导腔中，理论上，随着质子速度的增加，加速腔的尺寸应该随之变化，但是考虑到制造工艺、成本等因素，在工程实践中，通常我们将整台加速器分为若干段，每一段使用同样的加速腔，也就是采用等单元长度多间隙加速结构。在高能段，粒子在单个腔体中的速度变化相对于粒子的平均速度是非常小的，在单个加速腔中的速度可以认为是不变的，故可以采用相同的加速腔[6]。在常温直线加速器中，低能质子直线加速器在治疗癌症、辐射加固等领域的应用广泛，需求大。等单元长度多间隙加速结构既可以满足输出束流的品质要求，又建造方便，节约成本，因而在低能质子直线加速器中也有采用该结构的趋势[7]。
粒子在高频腔体中的能量增益是直线加速器设计的一个关键参数，简单而又准确地计算粒子在单个腔体中的能量增益对直线加速器的设计非常重要。当粒子能量较大(>100 MeV)，且粒子在单个加速腔中的能量增益较小时(<10 MeV)，这时在单个加速腔中粒子速度的变化是非常小的，可以近似认为粒子在单个加速腔中的速度是不变的。此时，粒子在单腔中的能量增益可简单地表示为[8]
$$ \Delta W=q{V}_{0}T{\rm{cos}}\phi , $$ (1) 其中V0为腔体的等效电压，定义为
$$ {V}_{0}={\int }_{0}^{L}\left|E\left({0,0},z\right)\right|{\rm{d}}z, $$ 其中：E(0,0,z)为腔内驻波电磁场电场峰值沿腔体轴线的分布；z为相对于腔体入口的纵向坐标；L为腔体长度；
$ \phi $ 为粒子的同步相位，定义为粒子在加速间隙中心时的高频相位。如果认为粒子的速度在整个腔体内为常数，则其相位沿腔体为线性变化，如果腔体中心对应于加速间隙中心，则同步相位与粒子在腔体入口相位$ {\phi }_{\rm{in}} $ 、出口相位$ {\phi }_{\rm{out}} $ 间的关系满足$$ \phi =({\phi }_{\rm{in}}+{\phi }_{\rm{out}})/2{\text{。}} $$ (2) T为渡越时间因子，考虑粒子以有限速度经过一定长度的加速结构所伴随的渡越时间效应，是表征单元结构加速效率的特征量。其定义为：将加速结构看作一个间隙时，余弦因子的电场的加权平均值
$$ T=\frac{{\int }_{-L/2}^{L/2}E\left({0,0},z\right){\rm{cos}}\omega t\left(z\right){\rm{d}}z}{{\int }_{-L/2}^{L/2}E\left({0,0},z\right){\rm{d}}z}, $$ 对于等单元长度多间隙加速结构，如果假设该腔体工作在π模，即相邻单元的电场相位差为π，且电场沿轴线的分布可以表示为正弦(或余弦)函数，则其渡越时间因子可表示为[9]
$$\begin{split}& T=\frac{\Delta W}{q{\rm{cos}}\phi {V}_{0}}=\\& \left\{\begin{array}{c}{\left(-1\right)}^{\frac{N-1}{2}}\dfrac{{\left(\frac{\beta }{{\beta }_{\rm{S}}}\right)}^{2}}{N\left[{\left(\frac{\beta }{{\beta }_{\rm{S}}}\right)}^{2}-1\right]}\cos\left[\frac{N\pi }{2\frac{\beta }{{\beta }_{\rm{S}}}}\right]\;\;\;\;\;\left(N{\text{为奇数}}\right)\\ {\left(-1\right)}^{\frac{N+2}{2}}\dfrac{{\left(\frac{\beta }{{\beta }_{\rm{S}}}\right)}^{2}}{N\left[{\left(\frac{\beta }{{\beta }_{\rm{S}}}\right)}^{2}-1\right]}\sin\left[\frac{N\pi }{2\frac{\beta }{{\beta }_{\rm{S}}}}\right]\;\;\;\;\;\left(N{\text{为偶数}}\right)\end{array}\right., \end{split} $$ (3) N为单腔中加速单元的个数，β为实际粒子速度，βS为腔体设计的同步粒子速度。当粒子速度等于同步粒子速度时，式(3)分母为零，此时渡越时间因子可以通过求解式(3)极限获得，为π/4。从式(3)可以看出，渡越时间因子与单元数及粒子速度和同步粒子速度的比值有关。对于给定的渡越时间因子，随着腔体单元数的增加，粒子速度接受度(粒子达一定加速效率的速度范围或能量范围)减小。对于单元数较少的加速腔，例如N等于3，相比于同步结构，其具有更大的能量接受范围。
利用式(1)~(3)，原则上我们可以得到粒子在单个腔体中的能量增益。但是在粒子能量比较低或电场梯度较大时，粒子在单个加速单元中的能量增益相对于粒子能量不再是一个小量时，粒子在单个加速腔中的速度变化就变得不可忽视。此时为了正确描述粒子在加速结构中的束流动力学行为，就必须考虑到粒子速度变化的影响。本文将通过推导严格的粒子纵向运动方程，来研究粒子在非同步加速结构中的动力学行为，以便对这类加速器的动力学设计提供帮助。
-
考虑参考粒子沿腔体轴线的运动。由于只有电场对粒子的能量改变产生影响，因此可以不考虑磁场的作用。如果假设电场沿腔体轴线的分布为
$$\begin{split} {E}_{z}\left(0, 0, z,t\right)=&E\left(0, 0, z\right){\rm{cos}}\left(\omega t+{\phi }_{0}\right)\\=&E\left(0, 0, z\right){\rm{cos}}\phi \left(z\right), \end{split}$$ 其中：
$ \phi \left(z\right)=\omega t+{\varphi }_{0} $ 为粒子在位置z时的高频相位；$ {\varphi }_{0} $ 为初始相位。根据牛顿运动定律，粒子从z到z+dz的过程中能量的改变量为$$ {\rm{d}}W=qE\left(0, 0, z\right){\rm cos}\phi \left(z\right){\rm{d}}z, $$ 由此可得粒子能量对空间位置z的微分
$$\tag{4-1} {{W'}}=\frac{{\rm{d}}W}{{\rm{d}}z}=qE\left(0, 0, z\right){\rm{cos}}\phi \left(z\right){\text{。}} $$ 由于
$$ \phi \left(z\right)=\omega t+{\varphi }_{0}={\varphi }_{0}+{\int }_{0}^{z}\frac{2\pi }{\beta \left(s\right)\lambda }{\rm{d}}s, $$ 其中：
$ \lambda =c/f $ 为电磁场的真空波长；c为真空光速；f为电磁场频率；$ \beta \left(s\right)=v\left(s\right)/c $ 为粒子在s处的归一化速度。上式两端对z进行微分可得$$\tag{4-2} {\phi '}\left(z\right)=\frac{2\pi }{\beta \left(z\right)\lambda }, $$ 其中
$ \beta \left(z\right) $ 是粒子能量的函数，即$$\tag{4-3} W\left(z\right)=\left(\gamma -1\right){m}_{0}{c}^{2}=\left[\frac{1}{\sqrt{1-{\beta }^{2}\left(z\right)}}-1\right]{m}_{0}{c}^{2}, $$ 其中
$ {m}_{0} $ 为粒子的静止质量。对具有任意轴线上电场分布的任意加速结构，只要给定了粒子初始相位及能量，通过方程(4-1)、(4-2)、(4-3)，原则上就可以确定粒子在位置z处的能量及相位。 -
对于工作在π模的等单元长度多间隙加速结构，通常电场分布为关于间隙中心对称的正弦(或余弦)函数，如果假设沿腔体轴线的电场分布为
$$ {E}_{z}={E}_{0}\sin\left(2\pi z/{\beta }_{\rm{s}}\lambda \right), $$ (5) 将其带入公式(4-1)，就可以确定严格的束流纵向运动的微分方程组。
对于任意初始状态的粒子，通过方程(4)，我们就可以得到其运动状态随时间的演化规律，其在相空间中对应于一条确定的相运动轨道。当初始状态为同步粒子
$ \left({W}_{\rm{s}}, {\phi }_{\rm{s}}\right) $ 时，得到的为同步粒子的相轨迹；当初始状态为任意$ \left(W, \phi \right) $ 时，所得相轨迹即为任意非同步粒子的相轨迹。根据加速器物理的惯例，我们对任意粒子相对于同步粒子的运动更感兴趣，通过将两条相轨迹对应点相减，即可得到任意粒子相对于同步粒子的运动。在直线加速器中，对粒子纵向运动的描述主要基于薄透镜近似得到，即认为粒子只是在加速间隙中心时才受到射频电磁场的作用，能量发生跳变，在加速结构的其它地方粒子以恒定速度漂移。在该方法中，粒子的高频相位为粒子在加速间隙中心时的高频相位。当认为粒子在单个加速间隙的能量增益为小量时，可以假定粒子速度足够接近同步粒子的速度，认为其与同步粒子具有相同的渡越时间因子，任意粒子相对于同步粒子的能量增益及相位可以由相空间运动轨迹的方程给出[8]：
$$\begin{split}& {\left\{ \begin{aligned} &w = \frac{{W - {W_{\rm s}}}}{{{m_0}{c^2}}}\\ &A = \frac{{2\pi }}{{\gamma _{\rm{s}}^3\beta _{\rm{s}}^3\lambda }}\\ &B = \frac{{q{E_0}T}}{{{m_0}{c^2}}} \end{aligned}\right.,}\\ & \frac{A{w}^{2}}{2}+B\left({\rm{sin}}\varphi -\varphi {\rm{cos}}{\varphi }_{\rm{s}}\right)={H}_{\varphi }{\text{。}} \end{split} $$ (6) 其中：
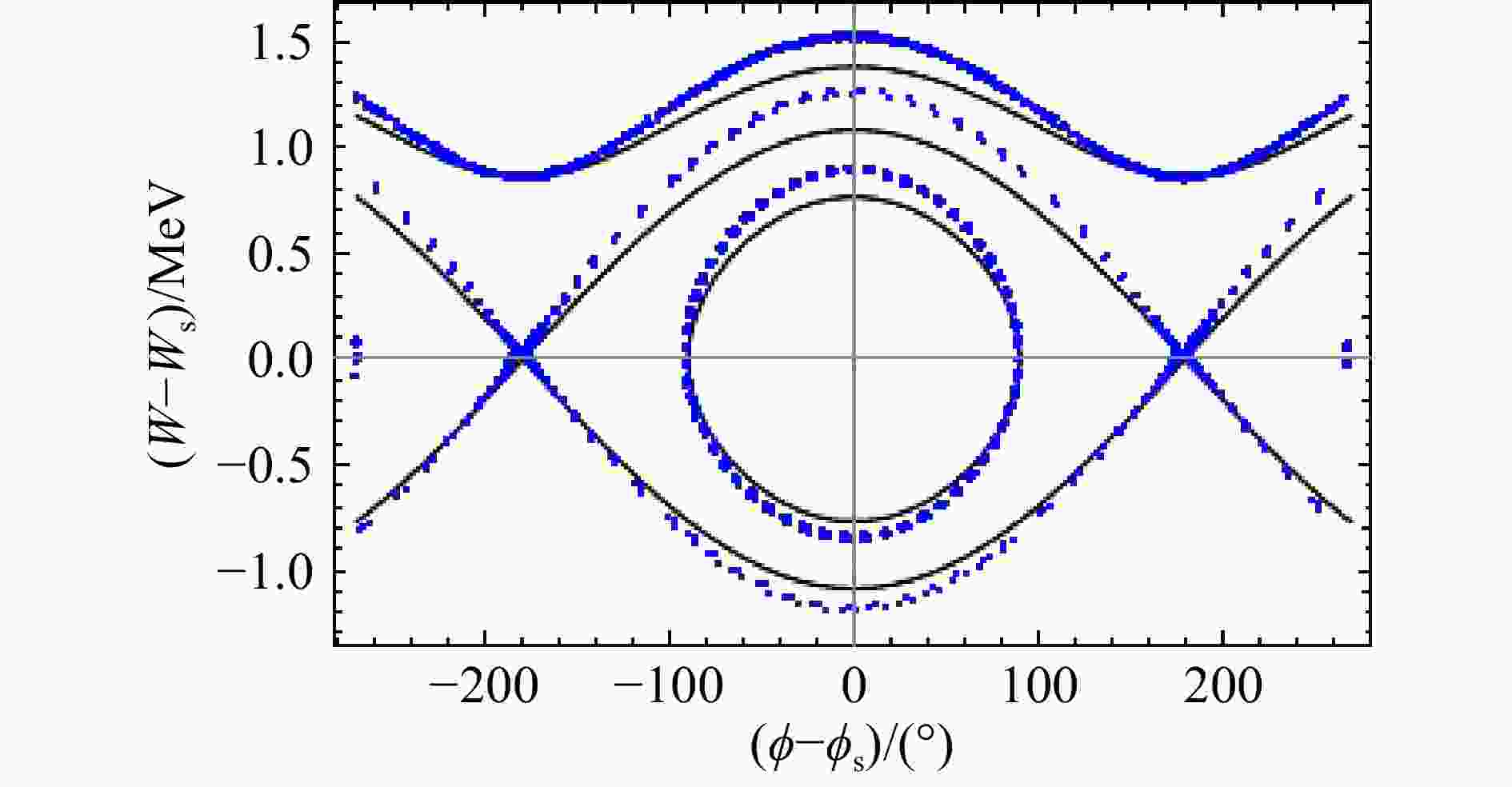
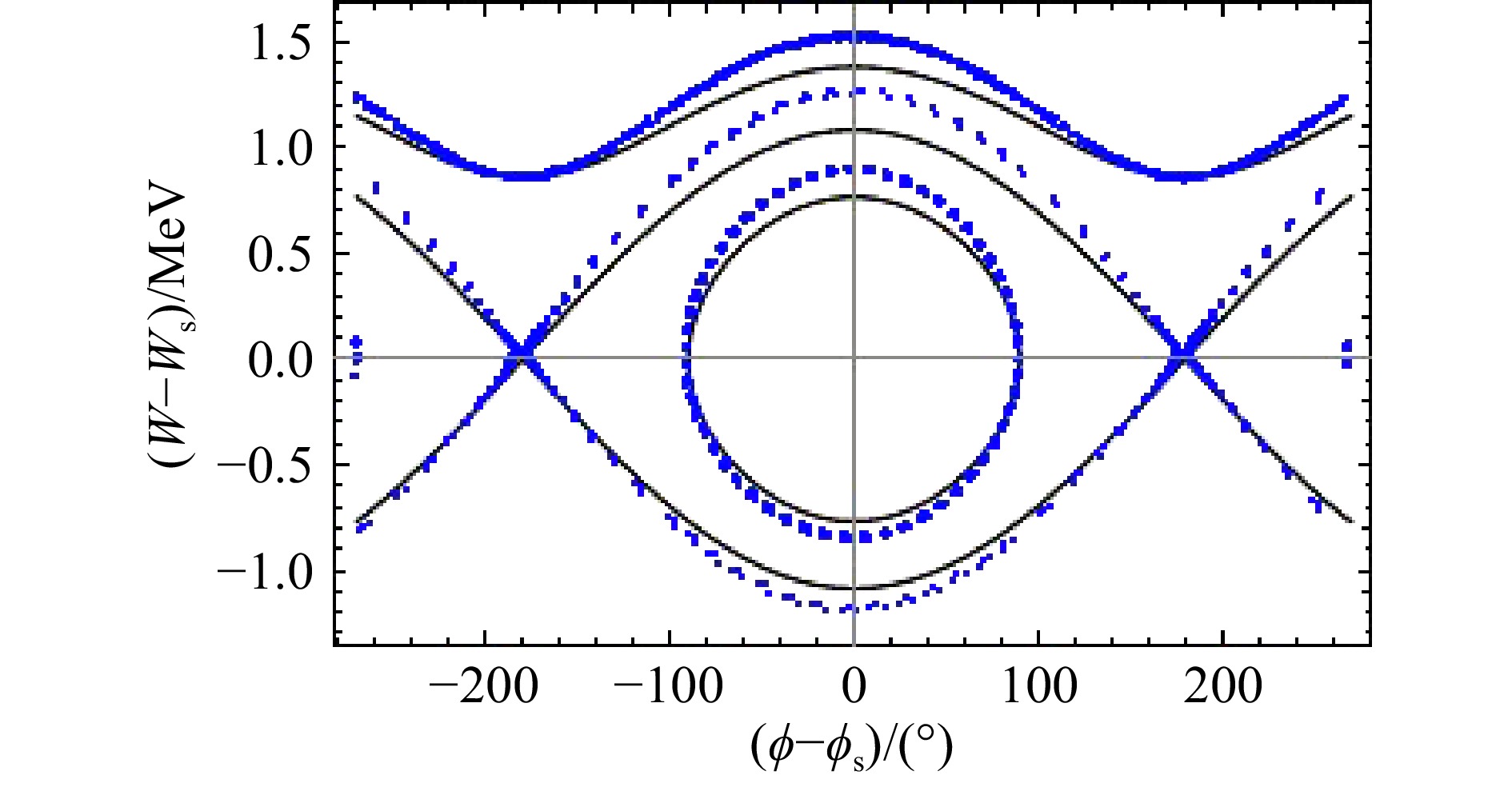
$ {\beta }_{\rm{s}},\;{\gamma }_{\rm{s}} $ 分别为同步粒子的归一化速度和相对论参数。每一个$ {H}_{\varphi } $ 对应着一组w和φ的函数关系也就是一条相运动轨迹，通过取不同的$ {H}_{\varphi } $ 值就可以得到方程(6)对应的相图。方程(6)是基于薄透镜近似理论的束流纵向运动方程，方程(4)是由运动方程推导的严格束流纵向运动方程。在等单元长度多间隙这种结构中，同步粒子在结构中的能量增益为零，同步相位$ {\varphi }_{\rm{s}}\!=\!-90° $ ，以同步相位作为粒子的入口相位，取加速腔的$ {\beta }_{\rm{s}}\!=\!0.12 $ ，场梯度$ {E}_{0}\!=\!25\,{\rm{ MV}}/{\rm{m}} $ ，高频频率$ f\!=\! $ 3 GHz，$\lambda \!=\!c/f\!= $ $ 0.1\,{\rm{m}}$ 。方程(6)对应的相运动轨迹如图1中黑色曲线。方程(4)对应的相运动轨迹如图1中蓝色曲线。由图1可以看出，相较于方程(6)描述的相运动轨迹，方程(4)描述的相运动轨迹的纵向高度差更大，也就是在相同的相位变化范围内，方程(4)求解的粒子能量变化量更大，且在相稳定区边界上，两方程描述的相运动轨迹的高度差最大。这里相稳定区边界的纵向高度可以用$ \varphi \!=\!{\varphi }_{\rm{s}} $ 处，具有周期运动特性的非同步粒子与同步粒子所具有的最大能量差，也就是相稳定区边界的最大高度来表示。方程(6)稳定区边界由$ (w\!=\!0, \varphi \!=\!-{\varphi }_{\rm{s}}\!=\!\pi /2) $ 的粒子轨迹决定，利用该条件可以确定此时系统能量为
图 1 (在线彩图)方程(4)和(6)对应的相运动轨迹对比图
$$ {H}_{-{\varphi }_{\rm{s}}=\pi /2}=B{\text{。}} $$ 该粒子当相位等于同步相位时，其能量增益为
$$ {w}_{\rm{max}}=\frac{\Delta {W}_{\rm{max}}}{m{c}^{2}}=\sqrt{\frac{2q{E}_{0}{\beta }_{\rm s}^{3}{\gamma }_{\rm s}^{3}\lambda }{\pi m{c}^{2}}}{\text{。}} $$ (7) 将公式(7)中的
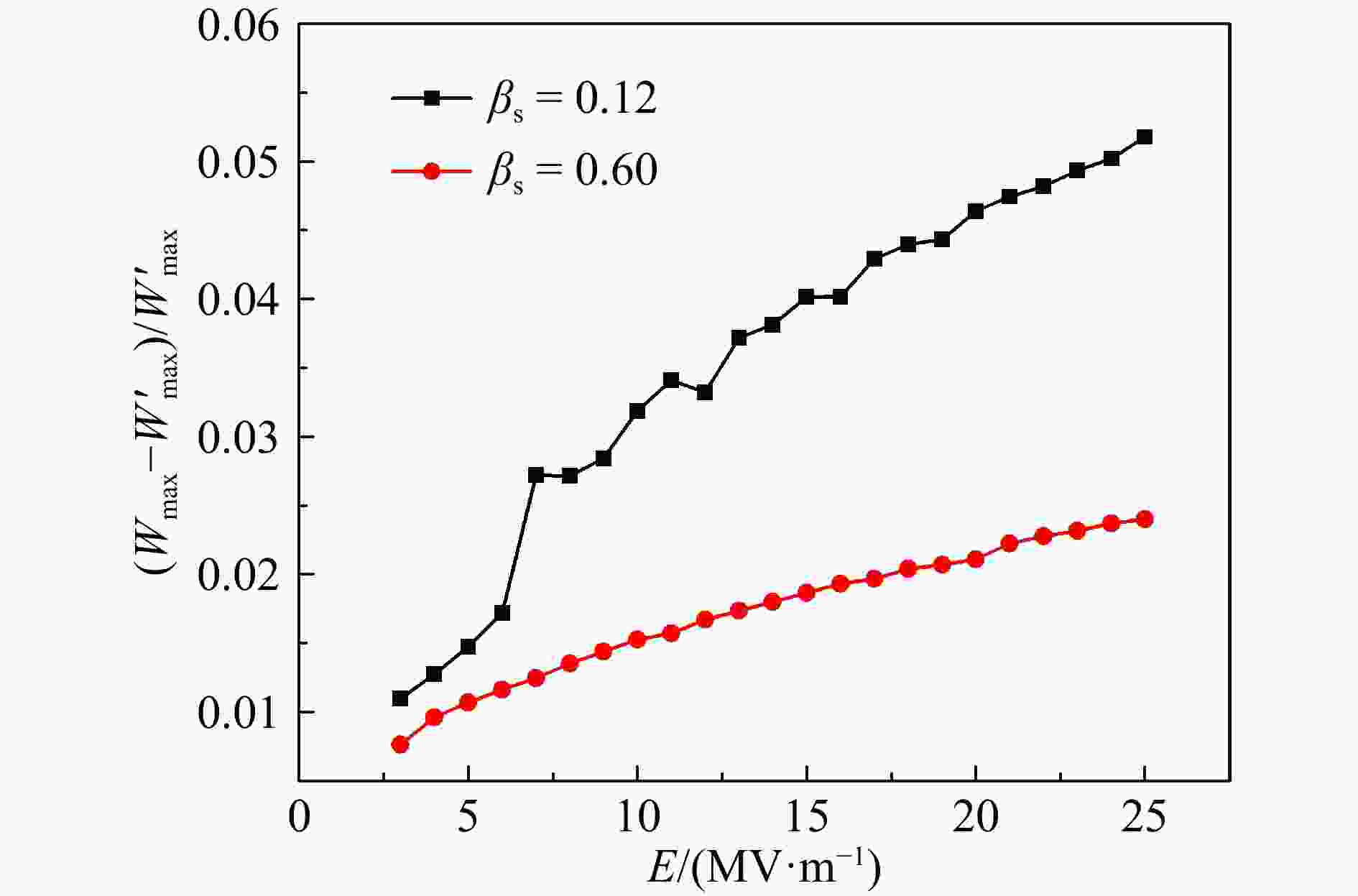
$ \Delta {W}_{\rm{max}} $ 记为$ {W}_{\rm{max}}^{'} $ ，方程(4)描述相轨迹中相稳定区的边界高度记为$ {W}_{\rm{max}} $ ，方程(4)和(6)相稳定区边界的纵向高度差表示为$ \left({W}_{\rm{max}}-{W}_{\rm{max}}^{'}\right) $ ，它与加速梯度以及加速腔的βs有关，分别取βs等于0.6和0.12，电场梯度从3到25 MV/m，间隔为1 MV/m，得到的变化趋势如图2所示。
图 2 (在线彩图)相稳定区边界高度差随加速梯度的变化关系
可以看出，βs越小，加速梯度越大，相稳定区边界的纵向高度差越大。这是因为βs一定，加速梯度越大，粒子通过加速单元的速度变化量就越大，而同样的加速梯度下，βs越大，速度变化量相对于βs反而越小，速度变化量越大方程(4)和(6)描述的相运动轨迹的高度差就越大。所以在不满足：(1)实际粒子速度与同步粒子速度相差非常小；(2)加速梯度足够小的情况下，方程(6)对粒子纵向运动的描述就会产生偏差。在实际加速腔应用中，粒子相位滑动比较小的距离内，方程(4)求解的粒子能量增益比方程(6)求解的值更大。
-
粒子在加速腔中的速度改变量主要受三方面的影响：(1)加速梯度，加速梯度越大，粒子通过一个加速单元的速度改变量越大；(2)粒子能量，注入粒子能量越接近腔体设计的同步粒子能量，其在每个间隙的加速效率越高；(3)单元数N，N越大，粒子在加速腔中总的速度改变量就越大。在一个加速结构中，我们最关心的就是通过这个加速结构的束流是否能够得到最大的能量增益，速度变化量的大小对总能量增益的计算必定会产生影响，下面对粒子能量增益进行研究。
-
假定单腔内粒子速度没有变化，根据式(3)的描述，渡越时间因子与梯度无关，束流在该加速腔中获得的总增量增益与同步相位之间应满足式(1)所示的标准余弦关系。而考虑粒子速度的变化，当单元数比较多时，加速梯度不同，渡越时间因子随粒子注入能量的变化也不同。
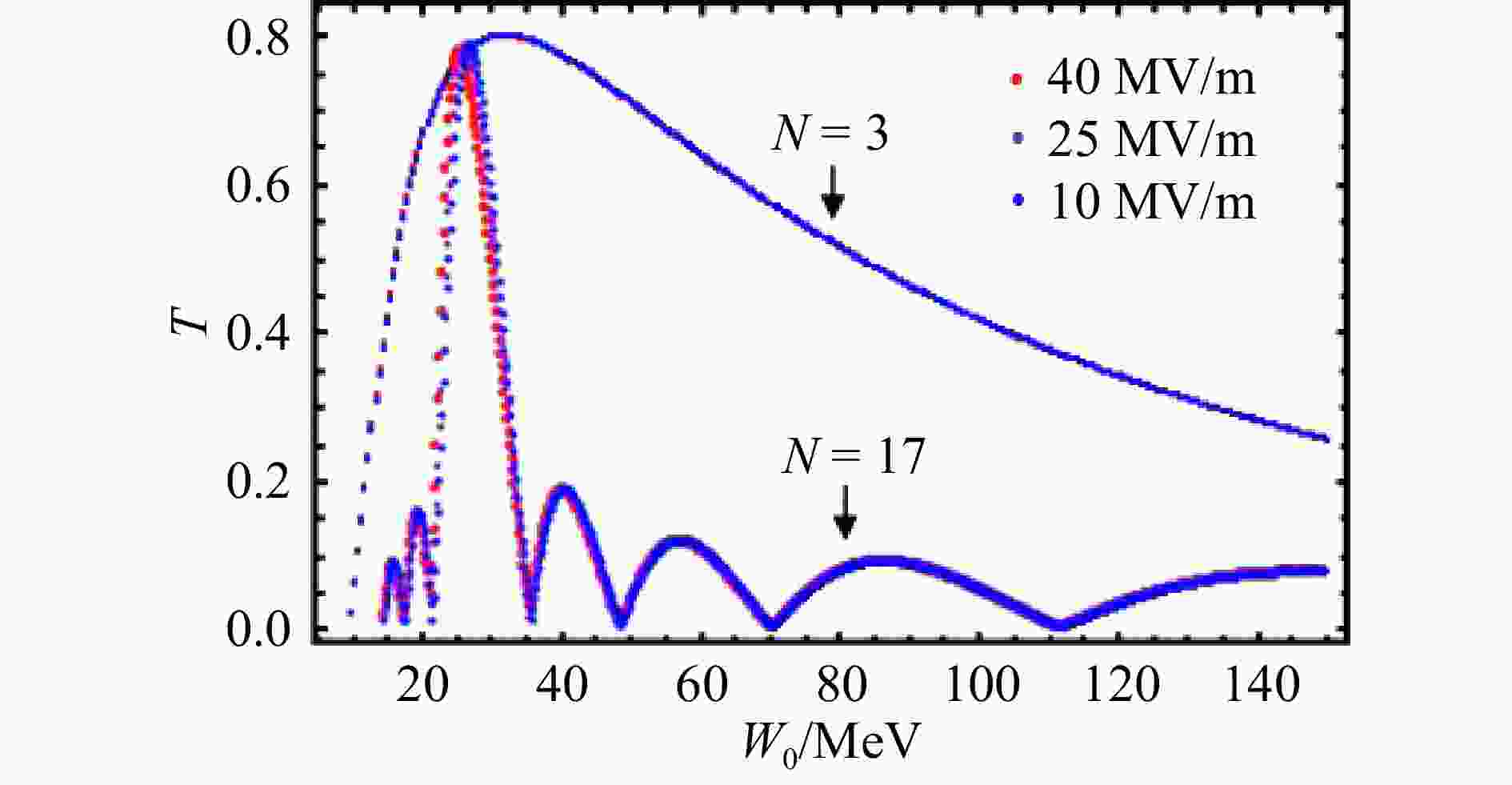
实际加速腔常用在渡越时间因子T大于0.5的范围内，在这个范围内粒子的相运动轨迹通常位于稳定区以内，通过选择合适的注入相位，就可以使粒子得到最大的能量增益。所以我们主要研究T大于0.5粒子的能量增益变化情况。先对不同单元数的T求解，分别取单元数等于17和3，βs等于0.238，同步相位等于–90º。严格的束流运动方程由方程(4)给出，计算工具是Mathematica。分别取加速梯度等于40，25和10 MV/m，其T随粒子注入能量的变化曲线如图3所示。
图 3 (在线彩图)T与入口粒子能量的关系曲线
观察N=17的曲线，随着加速梯度
$ {E}_{0} $ 的增加，最优β和T的最大值均逐渐减小，因为粒子运动过程是先加速后减速的。前半程粒子速度小于同步粒子速度，粒子加速；后半程粒子速度大于同步粒子速度，粒子减速。加速梯度越大，粒子速度变化量越大，粒子速度与同步粒子速度的差值就越大，所以在加速梯度增大时，最优β反而减小。相比于N=17，N=3时，即使加速梯度不同，T随粒子能量变化的曲线并没有差别，最优β也相同，并且相比于17个单元，3个单元时T大于0.5对应的入口粒子能量的范围也更大。随着单元数N的减少，同一T对应的入口粒子能量区间就越大。以加速梯度为35 MV/m例，研究T大于0.5区间内的粒子的相运动轨迹，由T随粒子能量变化曲线可以得到T对应的粒子入口能量，选择合适的注入相位使粒子的总能量增益最大。N=17时，不同入口能量的粒子其相运动轨迹如图4所示。可以看出T=0.78，粒子入口能量等于26.16 MeV的粒子经过17个单元总能量增益最大；而T越小，对应粒子的总能量增益就越小，在相图上，其相运动轨迹越靠外，逐渐偏离相稳定区，T等于0.6和0.5粒子的相运动轨迹已经在相图的非稳定区。还可以看到，同一T对应的两个粒子能量，一个大于同步粒子能量，一个小于同步粒子能量，其相运动轨迹并不关于
$ \delta W=0 $ 的轴线完全对称，这是因为T随粒子能量变化曲线在粒子能量小于最优能量的前半段，变化率大于粒子能量大于最优能量的后半段，所以同一T对应的两个粒子能量与同步粒子能量的差值也不相等，其相运动轨迹关于$ \delta W\!=\!0 $ 轴线也不对称。
图 4 (在线彩图)
$ {E}_{0}=35\;{\rm{ MV}}/{\rm{m}} $ 不同能量粒子的相运动轨迹图5为T=0.7对应的两个入口能量的粒子在一个周期内的能量增益的变化曲线，同步粒子能量为27.76 MeV。可以看到其能量增益变化曲线也不相同。用余弦函数分别对结果进行拟合，如图中虚线所示。可以看到以下特点：(1)关于能量增益为0的轴线不对称：粉色曲线入口粒子能量小于同步粒子能量，相对于标准余弦曲线，能量增益曲线整体上移，加速部分能量变化量的最大值大于减速部分能量变化量的最大值；棕色曲线入口粒子能量大于同步粒子能量，相对于标准余弦曲线，能量增益曲线整体下移，加速部分能量变化量的最大值小于减速部分能量变化量的最大值。(2)关于相位为0的轴线不对称：能量增益的最大值不在同步相位等于零处取得，相对于标准余弦曲线，两条曲线能量增益最大值对应的相位在坐标轴上有右移的趋势。(3)棕色曲线代表的粒子入口能量与同步粒子能量的差值更小，其能量增益与同步相位的关系曲线与标准余弦曲线的偏离更小。
图 5 (在线彩图)
$ {E}_{0}=35\;{\rm{MV}}/{\rm{m}} $ 、$ T=0.7 $ ，$ {W}_{0}<{W}_{\rm{s}} $ 和$ {W}_{0}>{W}_{\rm{s}} $ 的粒子能量增益与同步相位的关系曲线这种不对称性也表现在同一能量的粒子其加速和减速的相运动轨迹上，如图4中黑色点和粉色点轨迹所示。由于初始相位的不同，在相图左半部分粒子做减速运动，右半部分粒子做加速运动。可以看出：图中粉色点代表粒子入口粒子能量小于同步粒子能量，其加速段运动轨迹更靠近相图的稳定区，加速部分能量变化量(右部)大于减速部分能量变化量(左部)；相反，黑色点代表粒子入口粒子能量大于同步粒子能量，减速段运动轨迹更靠近相图的稳定区，减速部分能量变化量(左部)大于加速部分能量变化量(右部)。
结合相运动轨迹，对比不同T对应能量粒子的能量增益变化曲线的差异，可以发现：在加速梯度一定的情况下，T越小，其相运动轨迹更靠近非稳定区，粒子总能量增益越小；而对于同一T的不同能量的粒子，粒子能量与同步粒子能量的差值越小，能量增益变化曲线与标准余弦曲线的偏差越小。
-
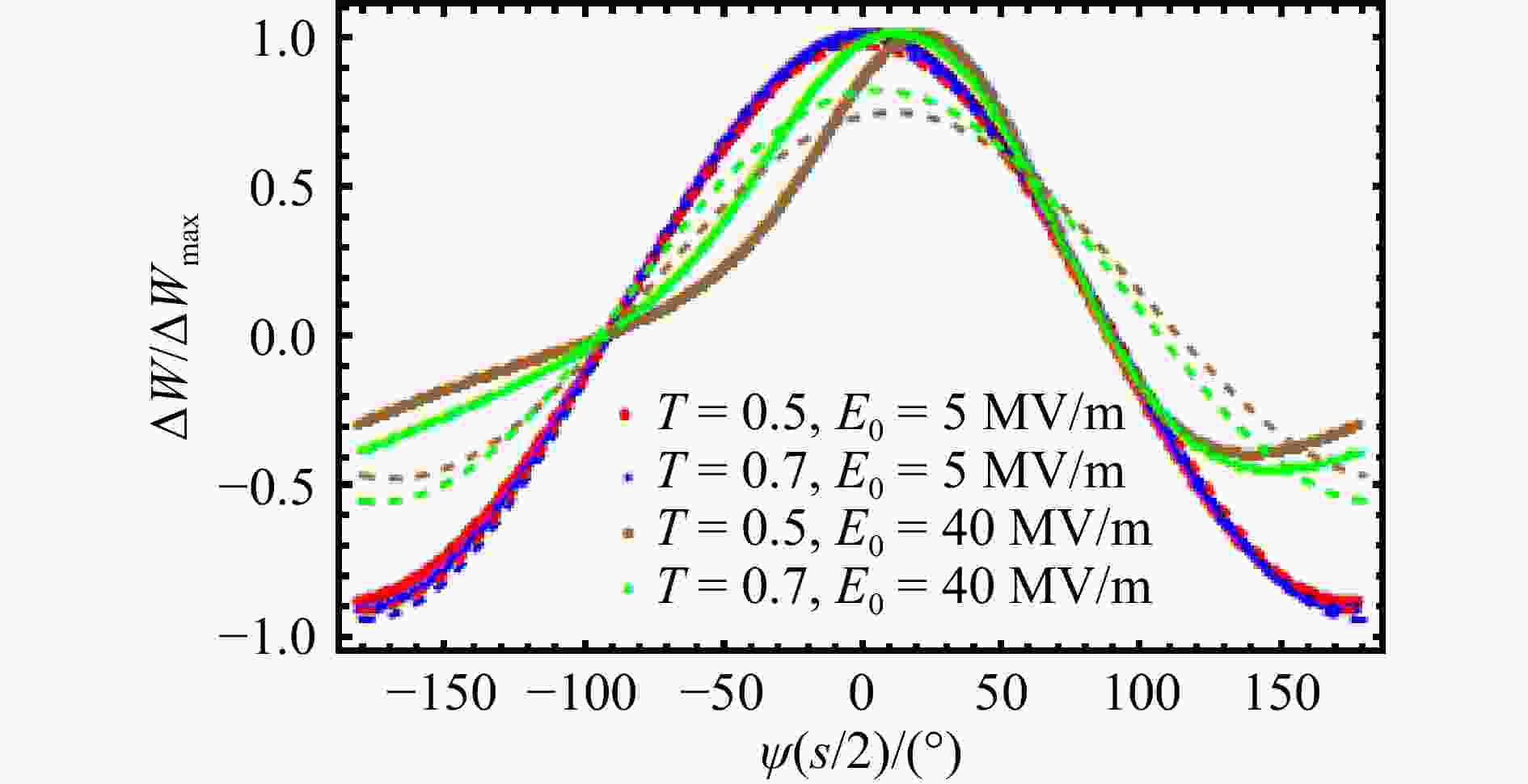
对17个单元的加速腔，取加速梯度40和5 MV/m。计算粒子能量增益变化曲线，并用余弦函数对能量增益的计算结果进行拟合，用同样颜色的曲线表示拟合函数，如图6。可以看出，加速梯度越高，粒子能量增益变化曲线偏离标准余弦曲线越多。这是因为加速梯度越大，粒子通过单腔的速度变化量就越大，相对于粒子的能量增益与同步相位之间就不再符合严格的标准余弦关系。结合4.1节讨论的结果，同一加速梯度，T越小，粒子入口能量与同步粒子差值越大，粒子能量增益变化曲线偏离标准余弦曲线也越大。
图 6 (在线彩图)不同加速梯度下粒子能量增益变化曲线对比
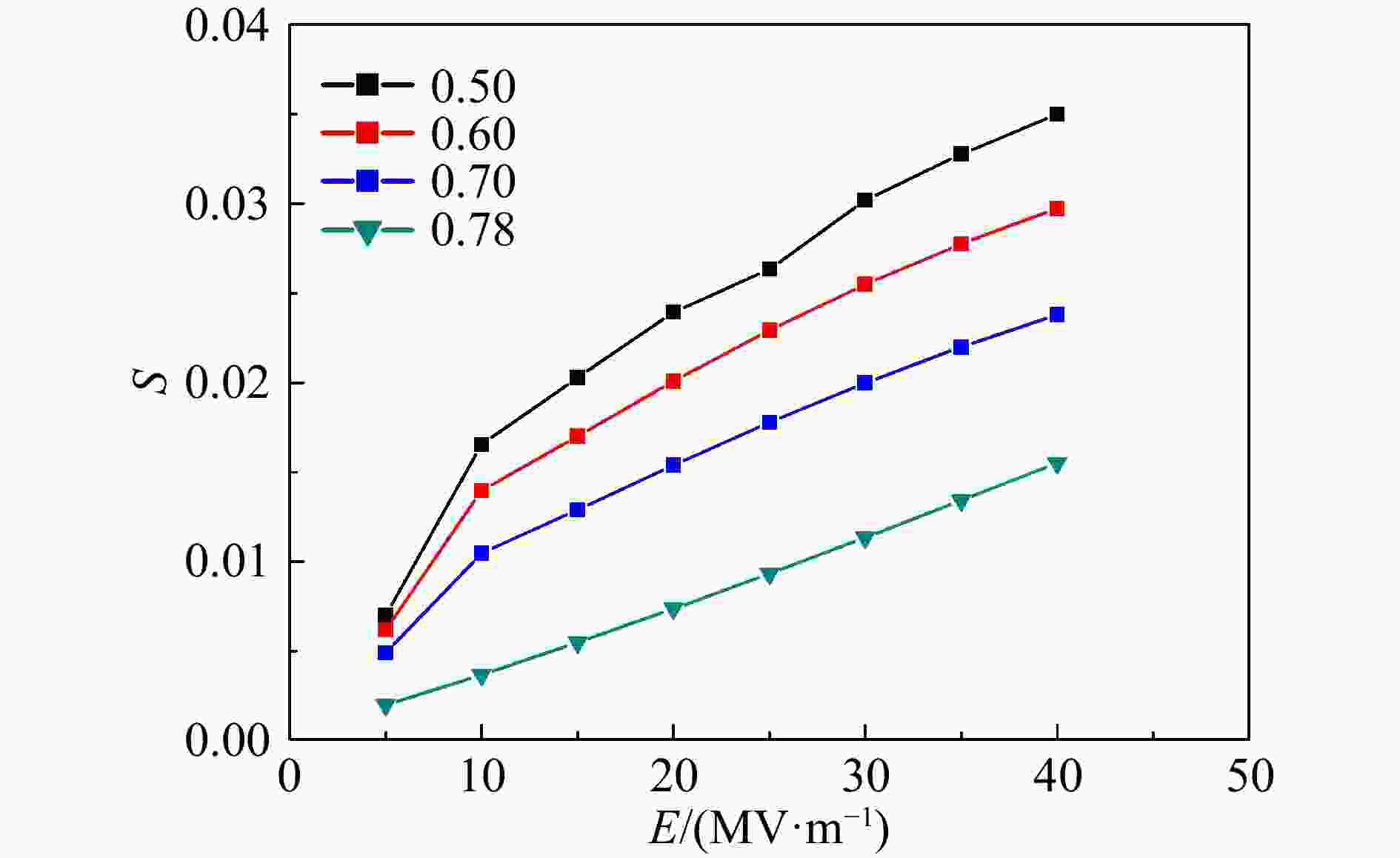
为了对图6中能量增益变化曲线相对于标准余弦曲线的偏离进行定量分析，我们定义参数S来衡量粒子能量增益变化曲线与余弦函数重合程度，S的表达式为
$$ \begin{split} {S}^{2}=&\frac{1}{n}\left[{\left({y'}_{\!1}-\frac{{y}_{1}}{{y}_{\rm{max}}}\right)}^{2}+{\left({y'}_{\!2}-\frac{{y}_{2}}{{y}_{\rm{max}}}\right)}^{2}+\right.\\&\left.{\left({y'}_{\!3}-\frac{{y}_{3}}{{y}_{\rm{max}}}\right)}^{2}+\dots \right], \end{split}$$ yi代表粒子能量变化量，
$ {y}_{\rm{max}} $ 代表能量变化量绝对值的最大值，$ {y}_{i}^{'} $ 为拟合的余弦函数的函数值大小。在拟合之前，对能量增益的大小进行归一化处理，所以拟合函数始终是一个周期上的余弦函数。$ \sqrt{S} $ 表示能量增益变化曲线与拟合曲线之间的面积差，该值越大，表明能量增益变化曲线偏离余弦曲线越多。图7不同颜色折线分别代表对于不同T的粒子的能量增益，其参数S随加速梯度的变化。可以看出：同一能量的粒子,加速梯度越大，参数S的值越大，同一加速梯度，T越小，粒子能量与同步粒子能量的差值越大，参数S越大。结合不同加速梯度不同能量粒子的能量增益越变化曲线以及拟合曲线的函数图像，以及参数S的值，可以得到一个范围：当$ \sqrt{S}/4 $ 大于0.018时，能量增益变化曲线与余弦曲线偏离较大，能量增益与同步相位不满足公式(1)的余弦关系；当$ \sqrt{S}/4 $ 小于0.018时，能量增益变化曲线与标准余弦曲线基本重合，可以认为整个运动过程，能量增益仍然满足式(1)。
图 7 (在线彩图)不同T，S随加速梯度变化的关系图
-
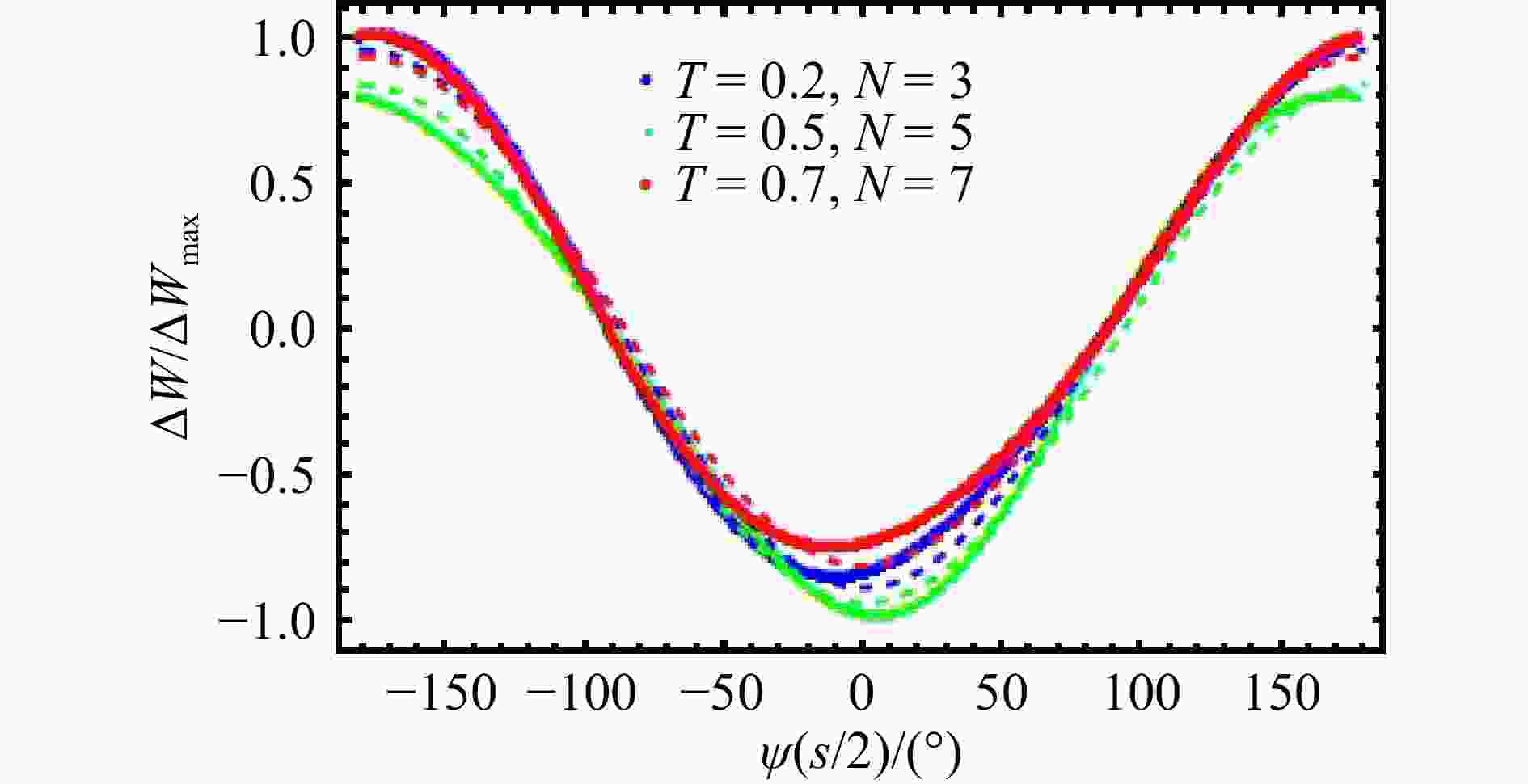
由图3可知，单元数较少的加速腔具有更大的能量接受范围。例如N=3的加速腔，由于单腔中加速单元个数比较少，T更接近式(3)推导的结果。不同加速梯度下，T的变化曲线是几乎没有改变的。且对于3个单元的加速腔，由于其T大于0.5对应的粒子入口能量范围较大，所以，粒子入口能量与同步粒子能量的差值也就比较大。我们分别取N=3，5, 7，加速梯度等于40 MV/m,，计算不同T下粒子能量增益变化曲线。采用余弦函数对计算结果拟合，并用同样颜色的虚线表示拟合的函数曲线，如图8所示。
图 8 (在线彩图)不同单元数N和T的粒子能量增益变化曲线
由图8可知，对于3个单元的加速腔，在T小于0.2时，能量增益曲线相对于余弦曲线开始有较大偏离。对于5个单元和7个单元的加速腔，在T分别小于0.5时和0.7时，能量增益曲线相对于余弦曲线才开始有较大偏离。这种偏离只发生在图3 T变化曲线的低能段，高能段并不适用。因此单元数越少，粒子的能量增益满足余弦关系所对应的T就越小，粒子入口能量的范围也越大。
-
对于等单元长度多间隙这种加速结构，同步粒子的相位始终是
$ -90° $ ，但在粒子实际运动过程中，粒子注入速度并不一定等于同步粒子速度，具体速度的差值与选择的T有关，所以实际粒子到达整个加速结构间隙中心的相位会与同步相位产生一定的偏差。假设在加速单元中粒子速度始终不变，粒子入口相位、出口相位以及加速间隙相位之前满足方程(2)的关系。但实际粒子在运动过程中，速度是时刻改变的，速度变化量的大小又和加速梯度、粒子能量、加速单元个数等参数有关。通过求解严格的束流运动方程(4)，可以得到粒子在其间隙中心相位与出口和入口处平均相位之间的关系如图9(a)和9(b)所示。9(a)和9(b)分别对应17个单元的加速腔和3个单元的加速腔，粒子入口能量为最优β对应的能量。
图 9 (在线彩图)不同加速梯度下间隙中心相位与出口和入口处平均相位的关系
图9中虚线代表
$\phi \left( {{s / 2}} \right) = {\phi _{{\rm{in}}}} + {\phi _{{\rm{out}}}}$ 的直线，可以看出，当N=17时，加速梯度越大，加速间隙相位与平均相位之间的线性关系越差，但是在间隙中心相位等于90°时，由于粒子最终没有得到加速，所以间隙中心相位始终等于入口和出口相位的平均值；N=3时，由于粒子速度变化不明显，在不同的加速梯度下，间隙中心相位始终等于入口和出口的平均相位，满足方程(2)的关系。 -
本文通过对粒子在等单元长度多间隙加速结构中运动的分析，讨论了粒子相运动以及能量增益和相位变化规律，得到了以下结论：(1)与薄透镜近似下的束流纵向运动方程(6)相比，严格的束流运动方程(4)对粒子运动的描述更精确，且在粒子能量与同步能量相差较大和加速梯度较高时，这种差异更明显；(2)粒子能量与同步粒子能量的差值越大，加速梯度越大，加速过程中粒子的速度改变量就越大，能量增益变化曲线偏离标准余弦曲线越多；(3)粒子速度变化比较明显时，能量增益变化曲线相对于标准余弦曲线的偏离有以下趋势：入口粒子能量小于同步粒子能量，能量增益曲线整体上移，加速部分能量变化量的最大值大于减速部分能量变化量的最大值；入口粒子能量大于同步粒子能量，能量增益曲线整体下移，加速部分能量变化量的最大值小于减速部分能量变化量的最大值。能量增益的最大值不在相位等于零处取得，相对于零点有右移的趋势；(4)假设在加速单元中粒子速度始终不变，同步相位等于粒子入口相位和出口相位的平均值，实际粒子运动过程中，只有在单元数较少的情况下，如N=3时，这种关系才近似满足。
-
摘要: 等单元长度多间隙加速结构是一种非同步加速结构，当粒子在加速结构中的速度变化很明显时，粒子在每个间隙的相位是不相同的，薄透镜近似下的束流纵向运动方程没有考虑粒子在加速结构中的速度变化，这在单腔的能量增益相对于粒子能量很小的情况下是合理的，但是当粒子在加速结构中的速度有明显变化时，这种处理方式是不够的。本文从带电粒子在电磁场中的运动方程出发，通过目前普遍采用的理论建立了束流在这种加速结构中的纵向运动方程，通过数值方法得到了粒子在这种结构的相运动，计算了不同初始能量的粒子在不同的电场梯度及单元数的加速腔中运动的能量变化情况。结果显示：粒子相运动与不考虑粒子速度变化的薄透镜近似下的相运动轨迹有明显差异，当粒子速度变化超过一定值后，薄透镜近似下束流纵向运动方程在计算束流能量增益时与同步相位之间满足的余弦关系不再成立，并给出了能量增益变化曲线相对余弦曲线的偏离情况与电场梯度、间隙数、初始能量等参数的关系。
-
关键词:
- 等单元长度多间隙加速结构 /
- 纵向运动方程 /
- 相运动 /
- 能量增益特性 /
- 相位变化
Abstract: The equidistant multi-gap acceleration structure is an asynchronous acceleration structure, when the velocity of the particle in the accelerated structure changes significantly, the phase of the particles at each gap is different. Current theories based on thin lens approximation do not take into account the variation in the velocity of the particles in the accelerated structure. This is reasonable in cases where the energy gain in a single cavity is small relative to the particle energy or where the acceleration gradient is small. This treatment is no longer sufficient when there is a significant change in the velocity of the particle in the structure. In this paper, the longitudinal motion dynamics of the beam in this equidistant multi-gap acceleration structure are modeled. By numerical simulations the phase space trajectories are obtained. The phase space trajectories are used to analyze the particles motion in the structure. The energy variations of particles with different initial energies are calculated when the electrical field gradients and gap numbers are different. Results show that compared with the properties of the beam motion predicted by the thin lens approximation theory, phase space trajectories are different, and its effects on energy gain as functions of acceleration gradient, the input energy, the cell numbers and so on are studied. -
图 5 (在线彩图)
$ {E}_{0}=35\;{\rm{MV}}/{\rm{m}} $ 、$ T=0.7 $ ，$ {W}_{0}<{W}_{\rm{s}} $ 和$ {W}_{0}>{W}_{\rm{s}} $ 的粒子能量增益与同步相位的关系曲线 -
[1] 郁庆长. 高能物理与核物理, 2001(05): 429. doi: 10.3321/j.issn:0254-3052.2001.05.011 YU Qingchang. High Energh Physics and Nuclear Physics, 2001(05): 429. (in Chinese) doi: 10.3321/j.issn:0254-3052.2001.05.011 [2] MINAEV S, RATZINGER U, PODLECH H, et al. Physical Review Special Topics-Accelerators and Beams, 2009, 12(12): 120101. doi: 10.1103/physrevstab.12.120101 [3] BAHNG J, JANG S, PARK S H, et al. Journal of the Korean Physical Society, 2019, 75(3): 209. doi: 10.3938/jkps.75.209 [4] JANG S, KIM E S. Nuclear Science and Techniques, 2019, 30(6): 95. doi: 10.1007/s41365-019-0616-0 [5] LI Zhuihui. Chinese Physics C, 2015, 39(9): 097001. doi: 10.1088/1674-1137/39/9/097001 [6] 欧阳华甫, 郁庆长. 高能物理与核物理, 2001(12): 1225. doi: 10.3321/j.issn:0254-3052.2001.12.015 OUYANG Huafu, YU Qingchang. High Energh Physics and Nuclear Physics, 2001(12): 1225. (in Chinese) doi: 10.3321/j.issn:0254-3052.2001.12.015 [7] 周立农, 张沐天, 罗紫华, 等. 高能物理与核物理, 1998, 22(11): 1042. ZHOU Linong, ZHANG Mutian, LUO Zihua, et al. High Energh Physics and Nuclear Physics, 1998, 22(11): 1042. (in Chinese) [8] WANGLER T P. RF Linear Accelerators[M]. Germany: John Wiley & Sons, 2008: 175. [9] OSTROUMOV P N. New Journal of Physics, 2006, 8(11): 281. doi: 10.1088/1367-2630/8/11/281 -
点击查看大图
图(9)
计量
- 文章访问数: 561
- HTML全文浏览量: 115
- PDF下载量: 32
- 被引次数: 0
甘公网安备 62010202000723号