-
人们已经熟知,对称性即物理系统在(某种)变换(或者说,操作)下的不变性(invariance)。由于变换可以是连续变换(例如连续地进行无穷多步无穷小角度的转动)也可以是分离变换(例如一步进行有限角度的转动),因此对称性既可以是连续的也可以是分立的。描述对称性的性质、规律等的学说称为群论,于是群论可以分为连续群和离散群(包括点群(或者说空间群)和置换群)。类似于前述的相应于转动任意角度都保持不变的状态称为高对称(性)态,仅在一些特殊转动角度下才保持不变的状态称为低对称态。由高对称态到低对称态变化的现象称为对称性破缺,由低对称性态到高对称性态变化的现象称为对称性恢复。如果描述系统动力学性质的拉格朗日量(拉氏量)在变换下保持不变、但系统的真空态(即基态)发生变化,则称这样的对称性破缺为自发破缺(spontaneous symmetry breaking),其中拉氏量的表述形式保持不变、但其中的相互作用强度变化引起真空态变化的破缺称为动力学破缺。如果系统的拉氏量在变换下发生变化,则称相应的对称性破缺为明显破缺(explicit symmetry breaking)。
我们还知道,一个不均匀物质系统中、可以由力学手段分离的组分完全形同、物理和化学性质完全相同的均匀状态称为该物质的相,例如,冰、水、水蒸气分别是物质
$ {\rm{H}}_{2} {\rm{O}} $ 的固相、液相、气相。并且,在确定条件下,物质由一相转变为另一相的现象称为相变。与前述对称性的概念比较知,每一个物相都对应具有一个(甚至多个)对称性的物质状态,相变自然可以由对称性的破缺或恢复来描述。另一方面,强相互作用系统包括原子核和由原子核组成的物质系统、强子及由各种强子形成的强子物质系统、由形成强子的夸克和胶子组成的夸克胶子物质。并且,现在认识到的宇宙物质的演化过程是:由最早出现的零质量的夸克、胶子和轻子到有有限裸质量(严格来讲是流质量,从而区分出三代六味)的夸克、胶子和轻子,到强子(具有色自由度的夸克和胶子被禁闭,从而强子化)和轻子,到原子核(强子核合成为原子核)和轻子,再到原子核与轻子中的电子复合成原子,然后形成星系、再到我们现在的宇宙。顾名思义,轻子即静质量较小的物质粒子,例如处于真空中的电子的静质量仅是质子的静质量的约1/1836,由此知,现代宇宙的组分单元中的主要质量携带者是原子核,或者说是强子。而强子是由夸克和胶子形成的束缚态,于是在宇宙演化的各不同阶段携带质量的主要成分都是夸克和胶子,进而宇宙强相互作用物质的演化过程可以归结为夸克胶子物质的相变过程。由于描述夸克、胶子及其间相互作用的动力学理论是量子色动力学(简称为QCD),因此上述相变常简称为QCD相变。并且,QCD相变就是强相互作用系统的对称性破缺(或恢复)。上述简述表明,强相互作用系统的对称性及其破缺是揭示宇宙演化各阶段中质量的主要携带者的性质及其演化过程的性质和规律的载体,从而是现代物理学研究的核心内容。本文仅对强相互作用物质在早期宇宙物质演化过程中的对称性及其破缺予以简要介绍,并简要介绍原子核的对称性及其破缺的一些内容。
-
为方便具体讨论强相互作用系统的对称性及其破缺,我们先讨论典型李代数(李群)的费米子实现和玻色子实现,以及这些系统的子代数(子群)结构,并说明微观粒子系统的最大对称性及其可能的主要破缺方式[1-2]。
-
我们知道,对
$ n $ 维矢量X$ = \{x_{1} , x_{2} , \cdots , x_{n} \} $ ,如果变换$ X \longrightarrow X^{\prime} \!=\! U X $ 保证$$ { \langle X^{\prime} \big\vert X^{\prime} \rangle = \langle {UX} \big\vert {UX} \rangle = \langle {X} \big\vert {U^{\dagger} U} X \rangle = \langle {X} \big\vert {X} \rangle \, , } $$ 则称所有这样的幺正矩阵
$ U_{n\times n} $ 的集合构成的群为$ n $ 维幺正群($ {\rm{U}}(n) $ 群),即保持$ \sum \limits_{i = 1}^n {x_{i}^{\ast} } x_{i} $ 不变的变换矩阵$ U $ 的集合形成的群为$ {\rm{U}}(n) $ 群。其中保持变换矩阵的行列式$ { \det U \!=\! 1 } $ 的$ {\rm{U}}(n) $ 群称为$ {\rm{SU}}(n) $ 群。并且,所有保持复二次型$ { \sum \limits_{i = 1}^{n} {x_{i} ^{2}}} $ 不变的变换矩阵$ O_{n\times n} $ 的集合形成的群称为正交群。其中保持变换矩阵的行列式$ { \det O_{n\times n} \!=\! 1 } $ 的$ {\rm{O}}(n) $ 群称为$ {\rm{{SO}}}(n) $ 群。再者,对$ 2n $ 维矢量$ X \!=\! \{ x_{1}, x_{2} , \cdots, x_{n} , x_{n+1} , x_{n+2} , \cdots, x_{2n} \} $ 和$ Y\!= \!\{ y_{1} , y_{2} , \cdots , y_{n} , y_{n+1} , y_{n+2} , \cdots , y_{2n} \} $ ,在变换$ X \longrightarrow X^{\prime} \!=\! M X $ 和$ Y \longrightarrow Y^{\prime} \!=\! M Y $ 下,如果$$ \sum\limits_{i = 1}^{n} \left( {x_{i} y_{n+i} } - y_{i} x_{n+i} \right) = {\text{常数}} \, , $$ 则称变换矩阵
$ M_{2n \times 2n} $ 的集合形成的群为斜交群,也称为辛群(symplectic group),记为$ {{\rm{SP}}}(2n) $ .对于连续多步变换,人们常(至少试图)采用一步变换等价地表述连续多步变换达到的效果,例如,三维空间中的一点I经一步欧拉角为
$ (\alpha_{1},\alpha_{2},\alpha_{3}) $ 的转动后紧接一步欧拉角为$ (\beta_{1},\beta_{2},\beta_{3}) $ 的转动变换到F,人们可以把上述由I到F的两步变换表述为欧拉角为$ (\gamma_{1},\gamma_{2},\gamma_{3}) $ 的一步转动所致,这种等效表述中欧拉角(常一般地称之为群参数)之间的函数关系$ \gamma = \phi(\alpha , \beta) $ 称为变换之间的合成函数。合成函数连续可微的连续群称为李群。前述的幺正群、正交群和斜交群都是李群。系统的研究表明,李群的变换性质由无穷小生成元表征,无穷小生成元则由合成函数的微商等决定。并且一个李群的无穷小生成元的全体构成相应于该李群的李代数。于是,抽象地讲,李群对应于
$ n $ 维空间中的微分流形,而李代数对应上述流形的$ n $ 维切空间—一个满足所有初等几何原理的线性空间。上述介绍表明,作为一个线性空间的李代数,既是一组矢量,也是相应于反映原始的变换意义的一组算符。从而,李代数既可以由矢量形式实现,也可以由矩阵形式实现。系统研究表明,记第
$ m $ 行第$ m' $ 列的矩阵元为$ 1 $ 、其它矩阵元都为$ 0 $ 的$ N \times N $ 矩阵为$ E'_{mm} $ ,显然这样的矩阵之间有对易关系$$ [E'_{m m}, \; E'_{n n}] = E'_{m n} \delta_{m'n} - E'_{n m} \delta'_{mn} \text{。} $$ (1) 这些对易关系式显然与
$ {\rm{su}}(N) $ 李代数(亦称为$ A_{N-1} $ 李代数)的对易关系(李群理论中常称之为李乘积)完全相同。这表明,这样的矩阵的集合构成su($ N $ )李代数。物理上,为保证厄密性,常考虑其线性组合。根据李代数与李群的关系,这些矩阵$ E_{m m'} $ (及其合适的线性组合)即为SU$ (N) $ 群的无穷小生成元。引入反对称矩阵
$ \varXi_{ij} \!=\! E_{i j} - E_{j i} $ ,其间的李乘积规则为$$ [ \varXi_{ij} \, \; \varXi_{kl}] = \delta_{il} \varXi_{jk} + \delta_{jk} \varXi_{il} - \delta_{ik} \varXi_{jl} - \delta_{jl} \varXi_{ik} \, , $$ (2) 这表明,这样的
$ \varXi_{ij} $ 的集合构成so($ N $ )李代数。根据李代数与李群的关系,$ \varXi_{ij} $ 为SO$ (N) $ 群的无穷小生成元。显然,SO$ (N) $ 群为SU$ (N) $ 群的一个子群,因为集合$ \{\varXi_{ij} \} $ 为$ \{ E_{m m'} \} $ 的一个子集。引入对称度规张量
$ G_{ij} \!=\! G_{ji} $ ,记任一$ N $ 维矢量的基矢为$ e_{i} $ ,其对偶基为$ \bar{\,e}_{i} \!=\! Ge_{i} $ ,定义$$ {\cal{S}}_{ij} = e_{i}\bar{\,e}_{j} + e_{j} \bar{\,e}_{i} \, , \qquad {\cal{H}}_{ij} = \bar{\,e}_{i} e_{j} = - \bar{\,e}_{j} e_{i} \, , $$ 则有
$$ [ {\cal{S}}_{ij} \, \; {\cal{S}}_{kl}] = {\cal{H}}_{jk} {\cal{S}}_{il} + {\cal{H}}_{jl} {\cal{S}}_{ik} + {\cal{H}}_{ik} {\cal{S}}_{jl} + {\cal{H}}_{il} {\cal{S}}_{jk} \text{ 。} $$ (3) 这表明,这样的
$ {\cal{S}}_{ij} $ 的集合构成sp($ 2N $ )李代数,并且$ {\cal{S}}_{ij} $ 为相应的SP$ (2N) $ 群的无穷小生成元。显然,SP$ (2N) $ 群为SU$ (2N) $ 群的一个子群,因为集合$ \{{\cal{S}}_{ij} \} $ 为$ \{ E_{m m'} \} $ 的一个子集。 -
现在我们认识的微观粒子可以分为费米子和玻色子两类。费米子为自旋量子数
$ s $ 为半奇数、统计规律满足费米–狄拉克分布律的微观粒子,玻色子为自旋量子数$ s $ 为整数、统计规律满足玻色–爱因斯坦分布律的微观粒子。由于在空间中运动的微观粒子还有轨道角动量$ \vec{\,l} $ ,因此微观粒子的状态常用$ \vert n j m\rangle $ 标记(因为考虑自旋–轨道耦合作用情况下,轨道角动量和自旋都不再是守恒量,但总角动量仍为守恒量),其中$ n $ 为由粒子所受的动力学作用决定的主量子数,$ j $ 、$ m $ 分别为总角动量量子数、总角动量在$ z $ 方向上的投影量子数(具体取值为$ m\! =\! -j , -j + 1 , \cdots, j-1 , j $ )。三维空间的转动在数学上表述为以角动量的三个分量对应的角动量算符为无穷小生成元的SO(3)群表征的变换,转动不变即具有SO(3)对称性。数学研究表明,SO(3)群(准确到同构意义上)唯一决定一个so(3)李代数,so(3)李代数的元素即SO(3)群的无穷小生成元$ \{l_{1},l_{2},l_{3}\} $ . 我们知道,前述的总角动量量子数$ j $ 为对应于轨道角动量$ \vec{\,l} $ 与自旋$ \vec{s} $ 耦合而成的总角动量$ \vec{j} $ 的量子数,其取值由轨道角动量量子数$ l $ 和自旋量子数$ s $ 决定,并可具体表述为$$ \begin{split} j =& |l - s|,\;|l - s| + 1,\; \cdots ,l + s - 1,\;l + s,\\ m =& {m_l} + {m_s}, \end{split} $$ (数学上,上一式称为直积群按
$ \rm{SO(3)}\otimes \rm{SO(3)} \supset \rm{SO(3)} $ 约化(破缺)中的群表示的约化分支律,下一式称为约化的权守恒条件)。由于$ l $ 为整数,由上式则知,对于玻色子,$ j $ 为整数;对于费米子,$ j $ 为半奇数。鉴于此,对于玻色子,人们常用$ \vert l m \rangle $ 标记其状态;对于费米子,人们常用$ \vert j m \rangle $ 标记其状态。进而,玻色子的产生、湮灭算符常分别标记为$ b^{\dagger}_{lm} $ 、$ b_{lm} $ ,费米子的产生、湮灭算符常分别标记为$ a^{\dagger}_{jm} $ 、$ b_{jm} $ 。玻色子的产生、湮灭算符之间有对易关系$$\begin{split} &{[{b_{lm}},\;{b_{l'm'}}] = [b_{lm}^\dagger ,\;b_{l'm'}^\dagger ] = 0}\\ &{[{b_{lm}},\;b_{l'm'}^\dagger ] = {\delta _{ll'}}{\delta _{mm'}}{\text{。}}} \end{split}$$ 费米子的产生、湮灭算符之间有反对易关系
$$ \begin{split} &\{ a_{jm} , \; a_{j'm'}\} = \{a^{\dagger}_{jm} , \; a^{\dagger}_{j'm'} \} = 0 \\& \{a_{jm} , \; a_{j'm'}^{\dagger}\} = \delta_{ll'} \delta_{mm'} \text{。} \end{split} $$ 对总角动量都为
$ j $ 、$ z $ 方向投影为$ m $ 的费密子,将其产生、湮灭算符简写为$ a^{\dagger}_{m}\; ( = a^{\dagger}_{j \; m}) $ ,$ a_{m} \; ( = a_{j \; m}) $ ,再记产生算符与湮灭算符的组合(乘积)为$ a^{\dagger}_{m} a_{m^{\prime}} $ ,其中$ m, \, m^{\prime} \!=\! -j, -j+1,\cdots, j-1, j $ ,$ m \neq m^{\prime} $ ,直接计算得$$ \big[ a^{\dagger}_{p} a_{p^{\prime}} , \; a^{\dagger}_{q} a_{q^{\prime}} \big] = \delta_{p^{\prime} q} a^{\dagger}_{p} a_{q^{\prime}} - \delta_{p q^{\prime}} a_{q}^{\dagger} a_{p^{\prime}} \text{。} $$ 很显然,该对易关系与式(1)所示的
$ {\rm{su}}(N) \; (N \!= 2j + 1 \!=\! {\text{偶数}}) $ 李代数的李乘积规则完全相同。因为上述组合的数目为$ 2 C_{2 j +1}^{2}\! = 2 \frac{(2 j +1) !}{((2j + 1)-2)! 2 !} \!=\! 2j (2j + 1) $ ,与su($ 2n $ ) (其中$ 2 n \!=\! 2 j +1\!=\! {\text{偶数}} $ )李代数的非零根的数目相同,所以su($ 2j+1 $ )李代数(亦即$ A_{2j} $ 李代数,$ 2j \!=\! {\text{奇数} } $ )可以由(全同)费米子来实现,其元素可以由(全同)费米子的产生算符与湮灭算符的组合表述为$ a^{\dagger}_{m}a_{m^{\prime}} $ 。相应地,SU($ 2j +1 $ )群可以由(全同)费米子来实现,其无穷小生成元可以由(全同)费米子的产生算符与湮灭算符的组合表述为$ a^{\dagger}_{m}a_{m^{\prime}} $ 。将全同玻色子系统中角动量为
$ l $ (非负整数)、其在$ z $ 方向上投影为$ m $ (取$ 2l+1 $ 个数值:$ \{ -l $ 、$ -l+1 $ 、$ \cdots $ 、$ l-1 $ 、$ l \} $ ,即自由度空间为$ 2l+1 $ 维)的玻色子的产生、湮灭算符分别简记为$ b^{\dagger}_{m}\;( = b^{\dagger}_{l\; m}) $ 、$ b_{m}\;( = b_{l \; m}) $ ,再记产生算符与湮灭算符之间的组合(乘积)为$ b^{\dagger}_{m} b_{m^{\prime}} $ ,其中$ m, \, m^{\prime} \!=\! -l, -l+1,\cdots, l-1, l $ ,$ m \neq m^{\prime} $ ,直接计算得$$ \big[ b^{\dagger}_{p} b_{p^{\prime}} , \; b^{\dagger}_{q} b_{q^{\prime}} \big] = \delta_{p^{\prime} q} b^{\dagger}_{p} b_{q^{\prime}} - \delta_{p q^{\prime}} b_{q}^{\dagger} b_{p^{\prime}} \text{。} $$ 很显然,该对易关系也与式(1)所示的su(
$ N $ )李代数的李乘积规则完全相同。因为上述组合的数目为$ 2 C_{21+1}^{2} \!=\! 2 \frac{(2 l +1) !}{((2l + 1)-2)! 2 !} \!=\! 2l (2l + 1) $ ,与su($ N $ ) (其中$ N \!=\! 2 l +1 \!=\! {\text{奇数} }$ )李代数的非零根的数目相同,所以su($ N $ )李代数($ A_{N-1}^{} $ 李代数),$ N \!=\! 21 +1 \!=\! {\text{奇数} } $ ,可以由(全同)玻色子来实现,其元素可以由(全同)玻色子的产生算符与湮灭算符的组合表述为$ b^{\dagger}_{m} b_{m^{\prime}} $ 。相应的,SU($ N $ )($ N \!=\! 2 l +1 \!=\!{\text{奇数} } $ )群可以由(全同)玻色子来实现,其无穷小生成元可以由(全同)玻色子的产生算符与湮灭算符的组合表述为$ b^{\dagger}_{m} b_{m^{\prime}} $ 。上述讨论表明,全同玻色子系统和全同费米子系统都具有幺正对称性。由一般线性群到特殊线性群、再到正交群等的关系可知,幺正对称性为全同粒子系统的最大对称性,其维数
$ n $ 即其中单粒子的角动量的自由度数,亦即$ n_{ {\text{费米子}}} \!=\! 2 j+1 \!=\! {\text{偶数}} $ ,$ n_{\text{玻色子}} \!=\! 2 j+1 \!=\! {\text{奇数} } $ 。由于不同角动量的玻色子/费米子的产生、湮灭算符总是对易的,因此上述的全同玻色子系统的对称性和全同费米子系统的对称性都可以推广到多种角动量的玻色子/费米子形成的非全同多粒子系统,例如,SU(8)对称性可以是对应总角动量
$ j \!=\! 7/2 $ 的全同费米子系统的对称性,也可以是对应总角动量分别为$ j \!=\! 1/2 $ 、$ j \!=\! 5/2 $ 的非全同费米子系统的对称性,还可以是对应角动量$ l \!=\! 0 $ 的s玻色子与角动量$ l = 3 $ 的f玻色子形成的非全同玻色子系统的对称性。 -
与
$ A_{N}^{} $ 李代数(su($ N+1 $ )李代数)$ N \!=\! 2 l \!=\! {\text{偶数}} $ ,的全同玻色子实现相同,记角动量为$ l $ 、其$ z $ -分量为$ m $ 的全同玻色子的产生算符、湮灭算符分别为$ b_{m}^{\dagger}\;( = b^{\dagger}_{l\; m}) $ 、$ b_{m} \; ( = b_{l \; m}) $ ,并记$ b^{\dagger}_{m} b_{m^{\prime}} - b^{\dagger}_{m^{\prime}} b_{m} \!=\! \varXi _{m m^{\prime}} $ ,其中$ m, \, m^{\prime} \!=\! -l, -l+1,\cdots, l-1, l $ ,$ m \neq m^{\prime} $ ,直接计算得$$ \big[ \varXi_{p p^{\prime}} , \; \varXi_{q q^{\prime}} \big] = \delta_{p q^{\prime} } \varXi_{p^{\prime} q} + \delta_{p^{\prime} q} \varXi_{p q^{\prime}} - \delta_{p q} \varXi_{p^{\prime} q^{\prime}} - \delta_{p^{\prime} q^{\prime}} \varXi_{p q} \text{。} $$ 这表明,
$ \varXi_{m m^{\prime}} $ 的李乘积规则与式(2)所示的so($ 2 l +1 $ )李代数的李乘积规则完全相同。所以李代数so($ 2l+1 $ )($ B_{l} $ 李代数)可以由角动量为$ l $ 的全同玻色子来实现,其元素可以由(全同)玻色子的产生算符与湮灭算符的组合表述为$$ \varXi _{m m^{\prime}} = b^{\dagger}_{m} b_{m^{\prime}} - b^{\dagger}_{m^{\prime}} b_{m} \text{。} $$ 相应地,SO(
$ 2l +1 $ )群可以由(全同)玻色子来实现,其无穷小生成元可以由(全同)玻色子的产生算符与湮灭算符的组合表述为$$ \varXi _{m m^{\prime}} = b^{\dagger}_{m} b_{m^{\prime}} - b^{\dagger}_{m^{\prime}} b_{m} \text{。} $$ 这表明,单玻色子角动量为
$ l $ 的全同玻色子系统具有正规子代数$ {\rm{SO}}(2l+1) $ ,其中$ 2l+1 \!=\! {\text{奇数} } $ 。显然,对于由多种非全同玻色子形成的多粒子体系,其最大对称性$ {\rm{U}}(\sum_{i}(2l_{i}+1)) $ 有正规子代数$ {\rm{O}}(\sum_{i}(2l_{i}+1)) $ 。并且,其维数$ n \!=\! \sum_{i}(2l_{i}+1) $ 可以是奇数也可以是偶数,例如,由角动量$ l = 0 $ 的s玻色子和角动量$ l = 2 $ 的d玻色子系统具有最大对称性$ {\rm{U}}(6) $ ,并有正规子代数$ {\rm{SO}}(6) $ 。由此知,玻色子系统的$ {\rm{U}}(\sum_{i}(2l_{i}+1)) $ 对称性可能破缺到$ {\rm{O}}(\sum_{i}(2l_{i}+1)) $ 对称性,甚至更低的对称性(例如表征转动不变的SO(3)对称性)。 -
与
$ A_{N}^{} $ 李代数(su($ N+1 $ )李代数),$ N \!=\! 2 j \!=\! {\text{奇数} } $ ,的全同费米子实现相同,记总角动量为$ j $ 、其$ z $ -分量为$ m $ 的全同费米子的产生算符、湮灭算符分别为$ a_{m}^{\dagger} $ $( =\! a^{\dagger}_{j \; m}) $ 、$ a_{m}\;( =\! a_{j \; m}) $ ,并进一步记$ a^{\dagger}_{m} a_{m^{\prime}}\! +\! a^{\dagger}_{m^{\prime}} a_{m} \!= \varXi _{m m^{\prime}} $ ,其中$ m, \, m^{\prime} \!=\! -j, -j+1,\cdots, j-1, j $ ,$ m \neq m^{\prime} $ ,直接计算得$$ \big[ \varXi_{p p^{\prime}} , \, \varXi_{q q^{\prime}} \big] = {\cal{H}}_{p^{\prime} q } \varXi_{p q^{\prime}} + {\cal{H}}_{p^{\prime} q^{\prime}} \varXi_{p q} + {\cal{H}}_{p q} \varXi_{p^{\prime} q^{\prime}} + {\cal{H}}_{p q^{\prime}} \varXi_{p^{\prime} q} \text{。} $$ 这表明,
$ \varXi_{m m^{\prime}} $ 的李乘积规则与式(3)所示的sp($ 2 j \!+\!1 $ )李代数的李乘积规则完全相同。所以sp($ 2j+1 $ )李代数($ C_{(2j+1)/2} $ 李代数,$ j = $ 半奇数)可以由总角动量为$ j $ 的全同费米子来实现,其元素可以由全同费米子的产生算符与湮灭算符的组合表述为$$ \varXi _{m m^{\prime}} = a^{\dagger}_{m} a_{m^{\prime}} + a^{\dagger}_{m^{\prime}} a_{m} \text{。} $$ 相应地,SP(
$ 2j +1 $ )($ j\! =\! $ 半奇数)群可以由全同费米子来实现,其无穷小生成元可以由全同费米子的产生算符与湮灭算符的组合表述为$$ \varXi _{m m^{\prime}} = a^{\dagger}_{m} a_{m^{\prime}} + a^{\dagger}_{m^{\prime}} a_{m} \text{。} $$ 这表明,单费米子总角动量为
$ j $ 的全同费米子系统具有正规子代数$ {\rm{sp}}(2j+1) $ ,其中$ 2j+1 \!=\! {\text{偶数}} $ . 显然,对于由多种非全同费米子形成的多粒子体系,其最大对称性$ {\rm{U}}\big[\sum_{i}(2j_{i}+1)\big] $ 有正规子代数$ {\rm{sp}}\big[\sum_{i}(2j_{i}+1)\big] $ 。并且,其维数$ n \!=\! \sum_{i}(2j_{i}+1) $ 只能是偶数,例如,由角动量$ j \!=\! 1/2,\,3/2,\,5/2 $ 的三类费米子形成的系统具有最大对称性$ {\rm{U}}(12) $ ,并有正规子代数$ {\rm{sp}}(12) $ 。由此知,费米子系统的$ {\rm{U}}\big[\sum_{i}(2j_{i}+1)\big] $ 对称性可能破缺到$ {\rm{SP}}\big[\sum_{i}(2j_{i}+ 1)\big] $ 对称性,甚至更低的对称性(例如表征转动不变的SO(3)对称性)。 -
按照现在的宇宙学说,我们的宇宙起源于一次大爆炸。在大爆炸之后的极短时间内,引力可能是量子化的,宇宙处于四种基本相互作用超大统一的状态。演化约10–44 s(1019 GeV),引力与其它三种相互作用分离开来,但强相互作用、弱相互作用和电磁相互作用仍处于大统一状态。再至约10–35 s(1015 GeV),弱相互作用与电磁相互作用仍处于统一的状态,但强相互作用分离开来,从而出现夸克、反夸克及电子和中微子等轻子。在从此至约10–10 s(102 GeV)的时间内,参与强相互作用的夸克及反夸克各自没有差别,具有高度的对称性(常称之为具有味对称性,实际尚未出现不同味道)。到约10–10 s,电磁作用与弱相互作用分离,即发生电弱对称性破缺,夸克分为三代六味。所谓六味即夸克分为具有六种不同流质量(近似来讲,即裸质量)的夸克(反夸克),它们分别称为上夸克、下夸克、奇异夸克、粲夸克、底夸克、顶夸克,常简记为u、d、s、c、b、t夸克,这些夸克还有被称为红、绿、蓝的三种颜色(具体讨论见3.2.2节)。到约10–5 s (10–1 GeV),色自由度禁闭,夸克(反夸克)及胶子强子化为强子。再到102 s,强子开始合成为原子核。再经复合阶段和星系形成阶段,形成我们现在的宇宙。按照现在对于物质结构的认识,宏观的物质由分子组成,分子由原子组成,原子由原子核和电子组成,原子核由强子组成,强子由夸克(和胶子)组成,夸克又分为味对称性破缺和具有味对称性两个阶段。由此知,正如引言中所述,我们现在的宇宙中携带质量的主要成分是由处于不同状态的夸克胶子物质演化而来,或者说,强相互作用物质的演化即夸克胶子物质的演化。由于描述强相互作用的基本理论是QCD,因此前述的强相互作用物质的演化过程常被称为QCD相变过程。由于一个物质相对应于一种确定的对称性,相变过程即对称性破缺或恢复过程。这里仅从强相互作用系统的对称性及其破缺角度简要介绍早期宇宙物质中强互作用物质的演化,尤其是可见物质质量的起源。
-
如前所述,早期宇宙中强相互作用物质的演化过程可以概括为:由零质量(味对称)的夸克到非零质量(味对称性破缺)的夸克,再到囚禁于强子中的夸克(少体的夸克集团),再到束缚在一起的多个夸克集团中的夸克。从引言中已经提到的质量问题考虑,原初的夸克是零质量的具有味对称性的夸克,经电弱破缺作用后夸克的味对称性破缺,从而夸克获得流质量,对于组成核子等强子的轻味夸克—u夸克和d夸克,其流质量平均仅约
$ 3.4 $ MeV,由三个这样的夸克形成的核子(质子和中子)的质量仅约$ 10 $ MeV。但我们已经熟知,核子的质量为约$ 939 $ MeV。由此知,由与电弱破缺相应的希格斯机制产生的核子的质量仅占核子实际质量的约1%。99%的核子质量的来源自然成为关乎可见物质质量起源(或者说费米子质量起源)的物理学基本问题,甚至可以说自然科学中的重大基本问题之一。相应地,具有色自由的夸克和胶子由所处空间范围不受限制转变到囚禁于半径不到$ 1 $ fm的很小的空间范围内,并且色自由度不再可见,亦即出现色禁闭。显然,可见质量起源问题和色禁闭机制问题是直接揭示可见物质及其质量起源的基本问题。也基于此,在20年前的世纪之交,人们将这两个问题合并作为“世纪大奖”的七个基本问题之一[3],并被《科学》杂志转引为其125个重要基本科学问题之一[4]。在关于强相互作用的基本理论——QCD下,其基本自由度是夸克和胶子,由上一节的讨论知,对于夸克的三维颜色自由度,其规范对称群为
$ {\rm{SU}}_{\mathrm{c}}(3) $ ,其中$ \mathrm{c} $ 即颜色的简称。拉氏量为$$ {L_{{\rm{QCD}}}} = \sum\limits_{f = 1}^{{N_f}} {\bar q_f^{}} (x)({\rm{i}}\not\!\!D - m_f^0)q_f^{}(x) - \frac{1}{4}G_{\mu \nu }^a(x)G_a^{\mu \nu }(x){\mkern 1mu} ,$$ 其中
$ q_{f}^{}(x) $ 为夸克场,$ N_{f} $ 为夸克味道数,$ m_{f}^{0} $ 为$ f $ 味道夸克的流质量。$ D_{\mu}^{} = \partial_{\mu} - {\rm i}g\frac{\lambda^{a}}{2}A^{a}_{\mu} $ 为协变微分,$ g $ 为耦合常数,$ \lambda^{a} $ 为$ {\rm{SU}}_{\mathrm{c}}(3) $ 的生成元(即常说的Gell-Mann矩阵)。$ G^{a}_{\mu\nu}(x) $ 为胶子场的场强张量,定义为$$ G^{a}_{\mu\nu}(x) = \partial_{\mu} A^{a}_{\nu}(x) - \partial_{\nu} A^{a}_{\mu}(x) + g f^{abc} A^{b}_{\mu}(x) A^{c}_{\nu}(x) \, , $$ 其中
$ A^{a}_{\mu}(x) $ 表示胶子场,$ f^{abc} $ 为$ {\rm{SU}}_{\mathrm{c}}(3) $ 群的结构常数。由上述两式可以看到,胶子之间具有自相互作用(这是QCD与QED的最重要区别)。为描述四维时空的性质,人们推广描述量子数为$ 1/2 $ 的自旋的泡利矩阵$ \sigma_{k}(k \!=\! 1,2,3) $ (数学上,它们即SU(2)群的生成元)、定义狄拉克矩阵($ \gamma $ 矩阵):$$ \gamma_{k}^{} = \Bigg{(} \begin{array}{*{20}{c}} 0 & -{\rm i}\sigma_{k}^{} \\ {\rm i} \sigma_{k}^{} & 0 \\ \end{array} \Bigg{)} \, , \quad \gamma_{4}^{} = \Bigg{(} \begin{array}{*{20}{c}} I_{2 \times 2}^{} & 0 \\ 0 & -I_{2 \times 2}^{} \\ \end{array} \Bigg{)} \text{。} $$ 显然有
$ \gamma_{\mu}^{\dagger} \!=\! \gamma_{\mu}^{} $ ,$ \{\gamma_{\mu}^{} , \gamma_{\nu}^{} \} \!=\! 2 \delta_{\mu \nu}^{} $ ,$ (\mu, \nu \!=\! 1,2,3,4) $ 。再定义,$$ \gamma_{5}^{} = \gamma_{1}^{} \gamma_{2}^{} \gamma_{3}^{} \gamma_{4}^{} = \Bigg{(} \begin{array}{*{20}{c}} 0 & -I_{2 \times 2}^{} \\ -I_{2\times 2}^{} & 0 \\ \end{array} \Bigg{)} , $$ 显然有
$ \gamma_{5}^{\dagger} \!=\! \gamma_{5}^{} $ ,并且对$ \mu \!=\! 1,2,3,4 $ ,$ \{\gamma_{5}^{} , \gamma_{\mu}^{} \} \!=\! 0 $ 。人们常称$ \gamma_{5}^{} $ 为螺旋度算符。引入算符
$$ {\cal P}^{\rm L} = \frac{1}{2}(1+ \gamma_{5}^{})\, , \qquad {\cal P}^{\rm R} = \frac{1}{2}(1- \gamma_{5}^{})\, , $$ (4) 根据其直观图像,人们分别称
$ {\cal P}^{\rm L} $ 、$ {\cal P}^{\rm R} $ 为左、右手转动投影算符。由之对夸克场作用,则将夸克分为左手和右手转动两类,即有$$ {\cal P}^{\rm{L},\rm{R}}q = \frac{1}{2}(1\pm \gamma_5)q = q^{\rm{L},\rm{R}} \text{。} $$ (5) 相应地,
$$ \overline{q^{\rm{L},\rm{R}}} = (\gamma_{4}^{} q^{\rm{L},\rm{R}})^{\dagger} = \overline{q} \frac{1}{2}(1\mp \gamma_{5}^{}) \text{。} $$ 于是有
$$ \bar{q}_{f}^{}(x) \not\!\! {D} q_{f}^{}(x) = \bar{q}^{\rm L}_{f}(x) \not \!\!{D} q^{\rm L}_{f}(x) + \bar{q}^{\rm R}_{f} (x) \not \!\!{D} q^{\rm R}_{f}(x) \text{。} $$ (6) 这表明,左手夸克与右手夸克不会通过胶子直接发生相互作用。
在手征转动变换
$ {\rm e}^{-{\rm i} \gamma_{5}^{} \Theta} $ 下,$$ q^{\rm L}_{f}\rightarrow {{\rm{e}}}^{-{\rm i} \Theta_{\rm L}}q^{\rm L}_{f}\, , \qquad q^{\rm R}_{f} \rightarrow {{\rm{e}}}^{-{\rm i} \Theta_{\rm R}}q^{\rm R}_{f} \, , $$ (7) 从而式(6)的形式保持不变,即具有手征转动不变性。对于纯规范场部分,由于其不含夸克,在手征变换下自然保持不变。那么,零质量的费米子系统具有手征(转动)对称性。
但是,由手征转动变换算符知,费米子的质量项
$$ {m_{f}^{0}} \bar{q}_{f}^{} (x) q_{f}^{} (x) = m_{f}^{0} \big{[} \bar{q}^{\rm R}_{f}(x) q^{\rm L}_{f}(x) + \bar{q}^{\rm L}_{f}(x) q^{\rm R}_{f}(x) \big{]} \, , $$ (8) 会破坏手征对称性。
总之,在
$ m_{f}^{0}\!=\! 0 $ 的情况下,QCD的拉氏量具有手征对称性;当$ m_{f}^{0} \neq 0 $ 时,手征对称性发生破缺。这也说明,手征对称性破缺使零质量的费米子转变为有质量的费米子。更进一步,手征对称性破缺是费米子获得质量的源泉。然而,如本小节开头所言,仅由具有较小固有质量(流质量)的三个夸克根本不可能形成实验观测到的核子的质量,因为相应于电弱破缺的希格斯机制引起的夸克的流质量确实很小。由此知,可见物质质量的起源应该不仅仅是通常所说的电弱破缺引起的味对称性破缺,而应该还有其它因素。对手征对称性破缺的深入研究表明,其破缺方式有两种,一种称为手征对称性明显破缺(Explicit Chiral Symmetry Breaking,常简记为ECSB),另一种是手征对称性自发破缺(Spontaneous Chiral Symmetry Breaking,常简记为SCSB)。手征对称性明显破缺(ECSB)即相应于上述拉氏量的固有质量的破缺。上述固有质量(实际为流质量,或重整化标度不变的质量)起源于电弱层次上的真空破缺,从而有人认为传统意义上的电弱层次上的真空自发破缺,相应于狭义的Higgs机制,不可能产生实验上观测到的可见物质的质量。手征对称性自发破缺指系统的拉格朗日量的形式保持不变、但系统的真空发生破缺。考察系统的拉氏量可知,拉氏量的形式保持不变情况下,其中的相应于耦合常数的相互作用强度可以发生变化。事实上,QCD的耦合常数确实不是不变的,而是动量依赖的,因此人们称之为跑动耦合常数,从而有微扰QCD与非微扰QCD之分(大动量情况下,相互作用很弱,即有渐近自由[5],从而可以采用微扰方法求解QCD,即有微扰QCD。然而,在小动量情况下,相互作用强度很强,跑动耦合常数接近1、甚至大于1,无法采用微扰方法进行求解,从而必须直接在非微扰情况下进行求解。由此知,相应于强子结构、QCD相变等的问题都是非微扰QCD的典型问题。这些正是非微扰QCD的困难和重要之所在)。这种由动力学相互作用(可能是上述的仅相互作用强度变化,也可能相互作用的形式就发生变化)导致的手征对称性破缺称为手征对称性动力学破缺(Dynamical Chiral Symmetry Breaking,常简记为DCSB)。如果DCSB仅仅由作用强度变化引起,而相互作用的形式保持不变,则它实际是(广义的)SCSB。
为具体表征QCD的真空结构及其破缺,人们引入手征夸克凝聚
$ \langle \bar{q} q \rangle $ 等概念,并以之作为DCSB的序参量。相应于表征手征对称性及其破缺的Goldstone定理,人们采用$ \pi $ -介子的质量和弱衰变常数等作为表征DCSB的观测量,更直观地,人们采用夸克的动力学质量在零动量极限的值(简称之为组分夸克质量)或欧几里得质量(由在壳条件决定的质量)表征DCSB。利用QCD的Dyson-Schwinger(DS)方程方法[6](目前建立的几乎唯一的既具有手征对称性破缺的性质又具有禁闭性质的连续场论方法[7])计算得到的表征手征对称性破缺的一些特征量(夸克质量、夸克凝聚、$ \pi $ 介子质量等)随相互作用强度变化的行为如图1所示。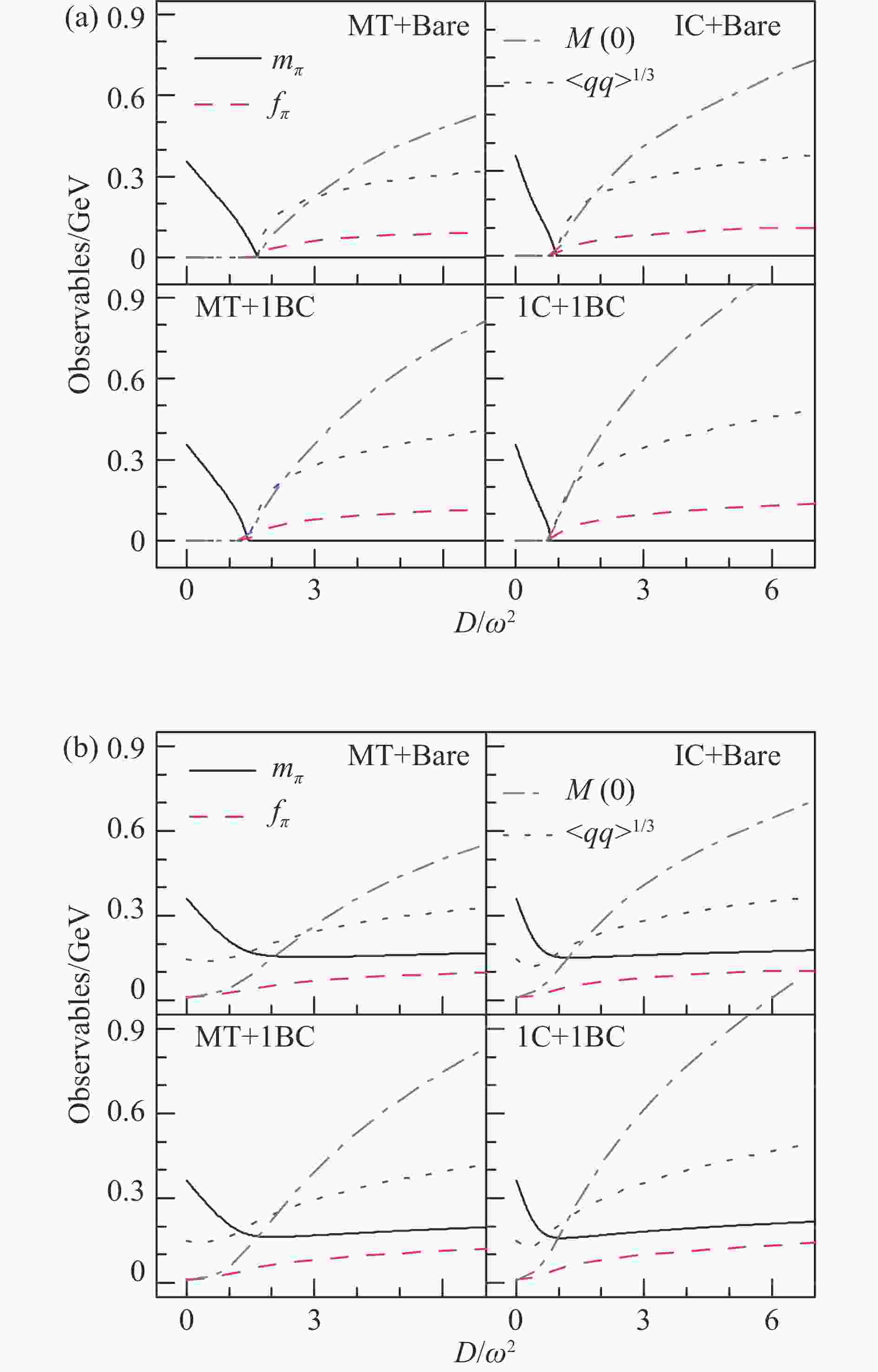
图 1 (在线彩图)组分夸克质量、夸克凝聚、
$\pi$ 介子质量和衰变常数随夸克-胶子相互作用的有效强度变化的行为(取自文献[8]),其中(a)为对应手征极限($m_{f}^{0} \!=\! 0$ )情况的结果,(b)为对应超越手征极限 ($m_{f}^{0}\! =\! 5$ MeV)情况的结果由图1可知,在手征极限下,如果相互作用强度不够大,组分夸克质量、手征夸克凝聚和
$ \pi $ 介子衰变常数都保持手征对称情况下的零值;在相互作用强度大于一个临界值的情况下,组分夸克质量、手征夸克凝聚和$ \pi $ 介子衰变常数才具有相应于手征对称性破缺的非零值,$ \pi $ 介子质量变为相应于(Goldstone定理决定的)手征对称性破缺的零值,并且这些非零值的绝对值随相互作用强度增大而增大,而$ \pi $ 介子的质量保持零值不变。这些结果表明,相互作用是手征对称性破缺的另一个源泉,也就是一定存在DCSB。所以,DCSB是夸克组分质量及可见物质质量的最主要来源的物理机制。并且,在超越手征极限情况下,也就是具有硬破缺的情况下,DCSB仍然是可见物质的质量的最主要来源。比较具有硬破缺与没有硬破缺情况可知,质量产生的过程和机制基本相同,只是具有硬破缺情况下,在临界作用强度附近各特征量的绝对值渐变增大,而在无硬破缺情况下,其演化行为的变化率有突变。更精细的研究表明,无硬破缺情况下的质量产生过程(即DCSB)是二级相变,有硬破缺情况下的质量产生过程是连续过渡[9-10]。
具体到现实的包含
$ {\rm u} $ 、$ {\rm d} $ 两味夸克的系统,手征极限下的手征对称性可以改写为$$ {\rm{SU}}_{ \rm{L}}(2) \otimes {\rm{SU}}_{ \rm{R}}(2) = {\rm{SU}}_{ \rm{V}}(2) \otimes {\rm{SU}}_{ \rm{A}}(2) \text{。} $$ 这表明,由这样的夸克(反夸克)组成的每一个(零质量)强子都有一个自旋和重子数等都分别相同但宇称相反的(零质量)强子与之对应。但实验测得的强子谱中并没有这样的宇称伙伴态(例如,
$ J^{P} \!=\! 0^{-} $ 的基态赝标量介子$ \pi $ 的质量为约138 MeV,而$ J^{P} \!=\! 0^{+} $ 的标量介子$ \sigma $ 的质量约为(400~550) MeV;$ J^{P} \!=\! 1^{-} $ 的基态矢量介子$ \rho $ 的质量为约775 MeV,而$ J^{P} \!=\! 1^{+} $ 的轴矢量介子$ a_{1} $ 的质量约为1 230 MeV)。由此可知,上述对称性一定发生了破缺。由于重子数守恒(或者说,同位旋转动对称性仍然保持),则手征对称性破缺可以表述为$$ {\rm{SU}}_{ \rm{L}}(2) \otimes {\rm{SU}}_{ \rm{R}}(2) \supset {\rm{SU}}_{ \rm{V}}(2) \otimes {\rm U}_{ \rm{A}}(1) \, , $$ 从而手征对称变换使得每一个强子变换为一个宇称相反的强子和一个零质量的Goldstone玻色子。在超越手征极限情况下,上述零质量的Goldstone玻色子变为赝Goldstone玻色子。并且可以得到能够描述强子性质等的以介子为自由度的拉氏量(即有手征展开理论)。
对于
$ {\rm u} $ 、$ {\rm d} $ 、$ {\rm s} $ 三味夸克系统,在手征极限下,系统具有手征对称性$ {\rm{SU}}_{ \rm{L}}(3) \otimes {\rm{SU}}_{ \rm{R}}(3) $ ,并有破缺方式$$ {\rm{SU}}_{ \rm{L}}(3) \otimes {\rm{SU}}_{ \rm{R}}(3) \supset {\rm{SU}}_{ \rm{V}}(3) \otimes {\rm{U}}_{ \rm{A}}(1)\text{。} $$ 在超越手征极限情况下,当然应该考虑流质量引起的明显破缺的贡献,由之也可以得到能够描述强子性质等的以介子为自由度的拉格朗日量,并相当好地描述强子等的性质,例如,赝标量的赝Goldstone玻色子–
$ \pi $ 等介子的质量、轻衰变常数与夸克的流质量($ m_{\rm u}^{0} $ 、$ m_{\rm d}^{0} $ 、$ m_{\rm s}^{0} $ )及由DCSB引起的手征夸克凝聚($ \langle \bar{q} q \rangle $ )之间有关系(常被称为Gell-Mann–Oakes–Renner关系)[11]:$$ \begin{align} m_{\pi}^{2} f_{\pi}^{2} = & - \big{(} m_{\rm u}^{0} + m_{\rm d}^{0} \big{)} \big{\langle} \bar{q} q \big{\rangle}_{0} \, , \\ m_{K^{+}}^{2} f_{\pi}^{2} = & - \big{(} m_{\rm u}^{0} + m_{\rm s}^{0} \big{)} \big{\langle} \bar{q} q \big{\rangle}_{0} \, , \\ m_{K^{0}}^{2} f_{\pi}^{2} = & -\big{(} m_{\rm d}^{0} + m_{\rm s}^{0} \big{)} \big{\langle} \bar{q} q \big{\rangle}_{0}\, , \\ m_{\eta^{0}}^{2} f_{\pi}^{2} = & - \frac{1}{3}\big{(} m_{\rm u}^{0} + m_{\rm d}^{0} + 4 m_{\rm s}^{0} \big{)} \big{\langle} \bar{q} q \big{\rangle}_{0} \, , \\ m_{\pi \eta}^{2} f_{\pi}^{2} = & - \frac{1}{\sqrt{3}} \big{(} m_{\rm u}^{0} - m_{\rm d}^{0} \big{)} \big{\langle} \bar{q} q \big{\rangle}_{0} \, , \end{align} $$ 其中
$ m_{\pi \eta}^{} $ 为$ \pi^{0} $ 与$ \eta^{0} $ 的混合态的质量。具体计算表明,自发破缺赋予宇称相反的强子伙伴态的质量差异不会太大,然而实验上测得的质量差异却很大,例如,矢量介子
$ \rho $ 的质量为约775 MeV,轴矢量介子$ a_{1}^{} $ 的质量为约1 230,450 MeV的质量差异一定不仅源自狭义的SCSB,而且DCSB发挥了更重要的作用,精细的计算[12]表明,只有在同时考虑DCSB对夸克传播子和对夸克–胶子相互作用顶角的贡献的情况下,这一质量劈裂才能得以较好描述。关于考虑了DCSB效应的夸克–胶子相互作用顶角的表述,目前建立的有Chang–Liu–Roberts-Qin模型[13]。由基于DCSB理论在描述强子质量谱和强子结构等方面的成功(例如文献[6, 12, 14-16]等)知道,DCSB确实是可见物质质量的最主要源泉。总之,手征对称性及DCSB是强相互作用的基本特征(性质),是利用QCD研究可见物质质量起源和强子质量谱及强子结构的最重要的因素。目前,手征对称性及其破缺的概念和研究方法还已被应用于宇宙学、凝聚态物理等学科的研究中,例如:电弱对称性破缺、(反)铁磁相变、超流现象、光的偏振、等等。限于篇幅和本文的范畴,这里不展开介绍。
-
前已述及,在涉及原子核、强子、轻子以及夸克、胶子的现象和过程中,起主要作用的有电磁作用、强作用和弱作用。强相互作用物质的演化自然涉及强作用、弱作用和电磁作用这三种基本相互作用。
-
我们知道,电磁场的性质和规律既可以由电场强度
$ {{E}} $ 、磁感应强度$ {{B}} $ 及麦克斯韦方程组描述,也可以由电势$ \varphi $ 和磁矢势$ {{A}} $ 描述,其间的关系为$$ {{E}} = - \nabla \varphi - \frac{\partial {{A}}}{\partial t} \, , \quad {{B}} = \nabla \times {{A}} \text{。} $$ 并且麦克斯韦方程组可以改写为
$$ \begin{split} \nabla^{2} {{A}} - \frac{1}{c^{2}} \frac{\partial ^{2}{{A}}}{\partial t^{2}} & = - \mu_{0}^{} {{J}} \, , \\ \nabla^{2} \varphi - \frac{1}{c^{2}} \frac{\partial ^{2}\varphi}{\partial t^{2}} & = - \frac{\rho}{\varepsilon_{0}^{}} \text{。} \end{split} $$ (9) 考虑对矢量势
$ {{A}} $ 和标量势$ \varphi $ 各做变换,$$ {{A}} \longrightarrow {{A}}^{\prime} = {{A}} + \nabla{\Theta} \, , \quad \varphi \longrightarrow \varphi^{\prime} = \varphi - \frac{\partial \Theta}{\partial t} \, , $$ (10) 其中
$ \Theta $ 为任意的关于时空坐标的函数,直接计算可知,无论对该变换中的函数$ \Theta $ 取什么形式,变换之后的电场强度和磁感应强度都与变换之前的相同。这表明,给定一个函数
$ \Theta $ ,即对式(10)所示的变换给定一个条件,就确定一组电磁势$ \{ {{A}}, \varphi \} $ ,进而可以确定电场强度$ {{E}} $ 和磁感应强度$ {{B}} $ 。这样的每一个确定电磁势的条件,称为一种规范(gauge),式(10)所示的变换则称为规范变换(gauge transformation),可直接观测的电场强度和磁感应强度不依赖于所取规范的基本性质称为规范不变性(gauge invariance),或规范对称性(gauge symmetry)。经典电磁理论是第一个规范场论(gauge field theory)。根据上述规范不变性,对电磁场问题实际求解时常采用库仑规范
$$ \nabla \cdot {{A}} = 0 , $$ (相应地,应有
$ \nabla^{2} \Theta = 0 $ ),或洛仑兹规范$$ \nabla \cdot {{A}} + \frac{1}{c^{2}} \frac{\partial \varphi}{\partial t} = 0 , $$ (其中
$ c^{2} \!=\! \frac{1}{\varepsilon_{0}^{} \mu_{0}^{}} $ ),以降低实际计算的复杂度。我们还知道,记一维时间和三维空间中的矢量为四维空间矢量
$$ x_{\mu}^{} = ({{X}} , \; {\rm i}ct) \, , $$ 空间的度规为
$ g_{\mu \nu}^{} \!=\! \delta_{\mu \nu} $ ,对之可作变换$x_{\mu}^{\prime} \!=\! U_{\mu \nu}^{} x_{\nu}^{}$ $ (\mu , \nu \!=\! 1,2,3,4)$ 。在古典的时空观中,时间与三维空间各自独立,互不影响,变换时各自按伽利略变换而变换。然而,在考虑高速运动情况下,时间和空间不是相互独立的,并且物理规律具有协变性。时空变换的协变性由洛仑兹协变性表述为
$$ {x_{1}^{\prime}}^{2} + {x_{2}^{\prime}}^{2} + {x_{3}^{\prime}}^{2} - c^{2} {t^{\prime}}^{2} = {x_{1}^{}}^{2} + {x_{2}^{}}^{2} +{x_{3}^{}}^{2} - c^{2} {t}^{2} = {\text{常量}} \, , $$ 也就是要求变换为幺正保模变换。对速度为
$ v $ 的沿$ x $ -轴(即1轴)方向的惯性运动,洛仑兹变换矩阵为$$ U = \left( \begin{array}{cccc} \gamma & 0 & 0 & {\rm i} \beta \gamma \\ 0 & 1 & 0 &0 \\ 0 & 0 & 1 & 0 \\ - {\rm i} \beta \gamma & 0 & 0 & \gamma \\ \end{array} \right) \, , $$ 其中
$ \beta \!=\! \dfrac{v}{c} $ ,$ \gamma \!=\! \frac{1}{\sqrt{1 - \beta^{2}}} $ ,$ c $ 为真空中的光速。类似地,动量和能量可以构成四动量
$$ p_{\mu}^{} = ({{P}} \, , \; {\rm i}\frac{E}{c}) \, , $$ 能量和动量守恒表述为
$ \quad p_{\mu}^{} p_{\mu}^{} \!=\! {{P}}^{2} - \frac{E^{2}}{c^{2}} \!=\! {\text{常量}} \, , $ 即$$ m^{2} c^{4} = {{P}}^{2} c^{2} + m_{0}^{2} c^{4} \, , \quad m = \gamma m_{0}^{} \text{。} $$ 电磁场中的电流密度和电荷密度则可以构成四维电流密度矢量
$$ J_{\mu}^{} = ({{J}} , \; {\rm i}c \rho) \, , $$ 电荷守恒定律
$ \nabla \cdot {{J}} + \frac{\partial \rho}{\partial t} \!=\! 0 $ 则表述为$$ \partial _{\mu} J_{\mu} = \frac{\partial J_{\mu}^{}}{\partial x_{\mu}^{}} = 0 \text{。} $$ 记矢量势
$ {{A}} $ 和标量势$ \varphi $ 构成电磁场四矢势为$$ A_{\mu}^{} = \Big{(} {{A}} \, , \; {\rm i} \frac{\varphi}{c} \Big{)} \, , $$ 式(9)所述的确定电磁场的矢量势和标量势的方程可以(合并)表述为
$$ {\partial _{\mu}^{}}^{2} A_{\nu} = - \mu_{0}^{} J_{\nu}^{} \, , $$ 其中
$ {\partial _{\mu}^{}}^{2} \!=\! \frac{\partial}{\partial x_{\mu}^{}} \frac{\partial}{\partial x_{\mu}^{}} \!=\! \nabla^{2} - \frac{1}{c^{2}} \frac{\partial ^{2}}{\partial t^{2}} \text{。} $ 更进一步,定义反对称四维张量
$$ F_{\mu \nu}^{} = \partial_{\mu}^{} A_{\nu}^{} - \partial_{\nu}^{} A_{\mu}^{} = \frac{\partial A_{\nu}^{}}{\partial x_{\mu}^{}} - \frac{\partial A_{\mu}^{}}{\partial x_{\nu}^{}} \, , $$ (11) 则麦克斯韦方程组中关于电荷的高斯定理和推广的安培环路定理可以合并表述为
$$ \partial_{\nu}^{} F_{\mu \nu}^{} = \mu_{0}^{} J_{\mu}^{} \, , $$ (12) 另两个方程(磁场的高斯定理和法拉第电磁感应定律)可以合并表述为
$$ \partial_{\lambda}^{} F_{\mu \nu}^{} + \partial_{\mu}^{} F_{\nu \lambda}^{} + \partial_{\nu}^{} F_{\lambda \mu}^{} = 0 \text{。} $$ (13) 电磁作用中的电荷守恒则表述为
$$ \partial _{\mu}^{} J_{\mu}^{} = 0 \, , $$ 其中的电流密度由系统中的费米子场
$ \{ \psi_{i}^{} \} $ 及标记其相应的电荷算符的本征值的参数$ \{ q_{i}^{} \} $ 表述为$$ J_{\mu}^{} = \sum \limits_{i} q_{i}^{} \bar{\psi}_{i}^{} \gamma_{\mu}^{} \psi_{i}^{} \, , $$ 其中
$ \gamma_{\mu}^{} $ 为费米子与电磁场(规范场)的相互作用顶角的表述形式。该守恒律对应U(1) 规范不变性。根据群的指数实现形式,该U(1)变换群可表述为
$$ U = {\rm e}^{{\rm i}q \Theta}, $$ 于是,费米子场的变换为
$$ \psi_{i}^{} \longrightarrow \psi_{i}^{\prime} = {\rm e}^{{\rm i}q_{i}^{} \Theta(x) } \psi_{i}^{}(x) \text{。} $$ 并且,由四维空间坐标的定义和电磁场四矢量的定义知,式(10)所示的电磁场的矢量势和标量势的规范变换,即规范场的规范变换,可以由四维形式表述为
$$ A_{\mu}^{}(x) \longrightarrow A_{\mu}^{\prime}(x) = A_{\mu}^{}(x) + \partial _{\mu} \Theta \text{。} $$ (14) 显然,在此规范变换下,式(11)所示的电磁场张量保持不变,从而电磁作用系统的规范场部分
$ F_{\mu \nu}^{} F^{\mu \nu} $ 具有规范不变性。再考察费米子场部分
$$ {\cal{L}}_{F}^{} = \sum \limits_{k} \bar{\psi}_{k}^{} \big{(} {\rm i} \gamma^{\mu} \partial_{\mu}^{} - m \big{)} \psi_{k}^{} \, , $$ 由于
$$ \partial_{\mu}^{} \psi_{k}^{\prime} = {\rm e}^{{\rm i} q_{k}^{} \Theta} \big{(} \partial_{\mu}^{} + {\rm i} q_{k}^{} \partial_{\mu}^{} \Theta \big{)} \psi_{k}^{} \, , $$ 即多出
$ \big{(} {\rm i} q_{k}^{} \partial_{\mu}^{} \Theta \big{)} \psi_{k}^{} $ 项,为保证规范不变,考虑前述的规范场的变换形式,如果将微分$ \partial_{\mu}^{} $ 修改为$ \partial_{\mu}^{} - {\rm i} q A_{\mu}(x) $ ,则前述的多出项恰好可以与规范场的变换中的$ \partial_{\mu}^{} \Theta $ 项抵消。这样的修改之后的微分算符$ \partial_{\mu}^{} - {\rm i} q A_{\mu}(x) $ 称为协变微分算符,常记为$ D_{\mu}^{} $ . 因此电磁场中规范不变的费米子场部分的拉氏量为$$ {\cal{L}}_{F}^{} = \sum \limits_{k} \bar{\psi}_{k}^{} \big{(} {\rm i} \gamma^{\mu} D_{\mu}^{} - m \big{)} \psi_{k}^{} \, , $$ 其中
$ D_{\mu}^{} = \partial_{\mu}^{} - {\rm i} q A_{\mu}(x) $ 为协变微分算符。总之,电磁作用系统具有U(1)规范对称性,其拉氏量为
$$ {\cal{L}}_{EM}^{} = \sum \limits_{k} \bar{\psi}_{k}^{} \big{(} {\rm i} \gamma^{\mu} D_{\mu}^{} - m \big{)} \psi_{k}^{} - \frac{1}{4} F^{\mu \nu} F_{\mu \nu}^{} \, , $$ (15) 运动方程为
$$ \big{(} {\rm i} \gamma^{\mu} \partial_{\mu}^{} - m \big{)} \psi = q \gamma^{\mu}A_{\mu}^{} \psi \, ,$$ (16) $$ \partial_{\mu}^{} F^{\mu \nu}=q \bar{\psi} \gamma^{\nu} \psi \text{。} $$ (17) 至此,我们简要介绍了关于电磁场及其中运动的粒子的基本理论,给出了系统的拉氏密度和运动方程,对之求解即可确定系统的性质。尤其说明了系统具有U(1)规范对称性,因此,可以选择合适的规范(条件),以简化对实际问题进行求解的复杂度和难度。
上述讨论表明,规范场论是基于对称性变换可以全局实施也可以局部实施的思想的一类物理理论,规范对称性是物理系统遵循的基本原理,这就是说,在某种变换下,物理系统的拉格朗日量的表述形式及物理可观测量(的值)保持不变。较具体地,如果在每一时空点同时实施变换时系统的拉氏量都保持不变,则系统具有全局对称性,例如上一小节讨论的手征对称性。如果在时空的特定区域实施一些对称变换而不影响到另外一个区域,则系统具有局部对称性(local symmetry),规范场论即是反映局部对称性的物理理论。另一方面,对称性即不变性、简并性,因此规范对称性反映了系统表述的一个冗余性,正是这种冗余性使得我们在实际应用时可以通过考虑规范条件(选用规范),简化计算。
再者,前述的关于电磁场的讨论仅是在经典层面上的讨论,尚未量子化。第一个量子化的规范理论即是关于电磁场的量子理论-量子电动力学(Quantum Electrodynamics,QED),它涉及量子化方案、规范固定、重整化、正规化等等一系列专门的理论方法和技术,这里不予介绍。建议读者参阅量子规范场论的专著或教科书。下面的讨论也局限在对称性及其破缺层面,不涉及量子化。
-
截止到20世纪60年代前期对强子谱的研究表明,在夸克模型框架下,如果夸克仅具有(固有)质量、自旋、宇称、电荷、超荷、同位旋、重子数、奇异数等内禀自由度,则无法解释实验观测到的
$ \Delta^{++}(\frac{3}{2}) $ 的存在性(自旋量子数$ \frac{3}{2} $ 说明其中的3个夸克都处于$ \big{\vert}\frac{1}{2} \, \frac{1}{2} \big{\rangle} $ 状态,带2个单位正电荷说明其中的3个夸克都带电荷$ \frac{2}{3} e $ ,即该粒子是由3个处于相同状态的u夸克组合而成。这显然与泡利不相容原理矛盾)。那么,夸克(反夸克)除具有前述的自旋等内禀自由度外,还有一个重要的自由度,人们称之为颜色。由于实验上观测到的强子都不带颜色自由度,也就是无色的,因此人们认为颜色自由度相应于通常的三原色,因此人们常用红(red, r)、绿(green, g)、兰(blue, b)对之进行标记。前述关于强子结构的讨论说明夸克一定具有新的自由度(例如命名为色自由度),但关于色自由度为3维、具有SU(3)对称性、且夸克处于其基础表示
$ [1]_{3} $ 等基本概念的建立,正负电子碰撞产物和介子衰变产物等的实验研究具有决定性作用。按照夸克模型,正负电子碰撞可以湮灭成光子,进而衰变成多种强子,产生强子的总截面与产生$ \mu^{+} \mu^{-} $ 的截面的比值为$$ R = \frac{\sigma( {\rm{e}}^{+} {\rm{e}}^{-} \rightarrow { \rm{hadrons}})}{\sigma( {\rm{e}}^{+} {\rm{e}}^{-} \rightarrow {\rm{\mu }}^{+} {\rm{\mu }}^{-} )} = \frac{e^{2} \sum _{q} {Q_{q}^{}}^{2} }{e^{2}} = \sum \limits_{q} {Q_{q}^{}}^{2} \, , $$ 其中
$ Q_{q}^{} $ 为夸克$ q $ 携带的电荷数。截止最近的考虑到u、d、s、c和b夸克组成的强子的实验结果为$ \frac{11}{3} $ ,这与上述求和中关于每一味夸克都有系数3的情况下的结果完全相同,而不考虑系数3情况下的理论结果与实验结果相差3倍。这显然与夸克具有色自由度、且处于色SU(3)对称群的基础表示(3维表示)的物理图像一致。由关于李群和李代数的基本理论、尤其是关于李代数的实现方式的讨论可知,具有3个维度的空间的变换矩阵对应的行列式确定(为1)的最大对称群为SU(3)群,况且su(3)李代数可以由全同粒子实现,因此色空间具有SU(3)对称性。在进一步的QCD的框架下,传递夸克间相互作用的规范场为胶子场。根据群的指数实现形式,该SU(3)变换群可以表述为
$$ U = {\rm e}^{{\rm i} \Theta^{a} \lambda^{a} } \, , $$ 其中
$ \lambda^{a} $ 为SU(3)群的生成元(即Gell-Mann矩阵)$$ \lambda_{1} = \left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right) \, , \quad \lambda_{2} = \left( \begin{array}{ccc} 0 & -{\rm i} & 0 \\ {\rm i} & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right) \, , $$ $$ \lambda_{3} = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \\ \end{array} \right) \, , \quad \lambda_{4} = \left( \begin{array}{ccc} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ \end{array} \right) \, , $$ $$ \lambda_{5} = \left( \begin{array}{ccc} 0 & 0 & -{\rm i} \\ 0 & 0 & 0 \\ {\rm i} & 0 & 0 \\ \end{array} \right) \, , \quad \lambda_{6} = \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{array} \right) \, , $$ $$ \lambda_{7} = \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & -{\rm i} \\ 0 & {\rm i} & 0 \\ \end{array} \right) \, , \quad \lambda_{8} = \frac{1}{\sqrt{3}} \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -2 \\ \end{array} \right) \text{。} $$ 相应地,费米子场的变换为
$$ \psi (x) \longrightarrow \psi^{\prime}(x) = {\rm e}^{{\rm i}\Theta^{a}(x) \lambda^{a} } \psi(x) \text{。} $$ 对拉氏量中的费米子场部分
$$ {\cal{L}}_{F}^{} = \sum \limits_{k} \bar{\psi}_{k}^{} \big{(} {\rm i} \gamma^{\mu} \partial_{\mu}^{} - m \big{)} \psi_{k}^{} \, , $$ 仿照关于U(1)规范下(电磁场中)的讨论,将微分算符
$ \partial_{\mu}^{} \; (\mu \!=\! 1,2,3,4) $ 扩展为协变微分算符$$ D_{\mu}^{} = \partial_{\mu}^{} - {\rm i} g A_{\mu}^{a}(x) \lambda^{a} \, , $$ (18) 其中
$ g $ 为(待定)常量,$ A_{\mu}^{a}(x) $ 为规范场(胶子场)四矢量,则SU(3)对称的规范场(胶子场)中与费米子相关的拉氏量可以表述为$$ {\cal{L}}_{F}^{} = \sum \limits_{k} \bar{\psi}_{k}^{} \big{(} {\rm i} \gamma^{\mu} D_{\mu}^{} - m \big{)} \psi_{k}^{} \text{。} $$ 进一步具体计算可知,保持
$ {\rm{SU}}_{C}(3) $ 规范不变的胶子场场强张量由规范场(胶子场)在色空间中的分量表述为$$ G_{\mu \nu}^{a} = \partial_{\mu}^{} A_{\nu}^{a} - \partial_{\nu}^{} A_{\mu}^{a} + g f^{abc} A_{\mu}^{b} A_{\nu}^{c} \text{。} $$ (19) 其中的
$ f^{abc} $ 为SU(3)群的结构常数。总之,强相互作用具有色SU(3)(非阿贝尔)规范对称性,夸克场对应于SU(3)群的基础表示(3维表示),规范场(胶子场)对应于SU(3)群的伴随表示(8维表示),系统的拉氏量(的经典形式)为
$$ {\cal{L}}_{ \rm{QCD}}^{} = \sum \limits_{k} \bar{\psi}_{k}^{} \big{(} {\rm i} \gamma^{\mu} D_{\mu}^{} - m \big{)} \psi_{k}^{} - \frac{1}{4} G^{\mu \nu} G_{\mu \nu}^{} \, , $$ (20) 其中的协变微分的表述形式和规范场场强张量的表述形式分别如式(18)、(19)所示。
至此,我们简要介绍了关于强相互作用的规范场(胶子场)及其中运动的费米子的基本理论,给出了系统的拉氏密度,说明了系统具有SU(3)规范对称性,因此,我们可以选择合适的规范(规范条件),以简化对实际问题进行求解的复杂度和难度。由于表述形式非常复杂,我们没有具体讨论运动方程。实际应用时应考虑其量子化、规范固定、重整化和正规化等。对于SU(3)规范场的量子化,它远比U(1)规范下的复杂,虽然已经发展了Faddeev-Popov等量子化方案[17],但其中仍存在Gribov拷贝(规范条件存在多个解)的问题[17-18]。对于这些问题的研究仍然是当今非阿贝尔规范场理论研究中的重要课题。并且,在关于强相互作用的研究中,很多重要问题都是非微扰的,例如色禁闭的机制、强子内部的夸克和胶子结构等等,虽然已经发展建立了可以实际应用的DS方程方法,但相关研究仍然是当今强相互作用理论研究中的最重要课题。
-
(1) 电弱统一作用的规范对称性
我们知道,电磁作用中电场部分是有源无旋场、磁场部分为无源有旋场,电荷是守恒量,于是系统具有U(1)规范对称性(3.2.1节中已予介绍和讨论)。弱作用的发现可以追溯到原子核的
$ \beta $ 衰变,其元过程是中子转变为质子、放出电子和(反电子型)中微子,即$$ n \longrightarrow p + e^{-} + \bar{\nu}_{e}^{} \text{。} $$ 后来又发现了
$ \Lambda $ 超子转变为质子、并放出电子和(反电子型)中微子的过程$$ \Lambda \longrightarrow p + e^{-} + \bar{\nu}_{e}^{} \text{。} $$ 由于
$ \beta $ 衰变过程涉及的粒子的质量差异很小,因此弱作用过程涉及的质子和中子通常表述为同位旋的二重态。早期建立的描述$ \beta $ 衰变的理论是矢量流-轴矢流理论,其有效拉氏量为$$ {\cal{L}}_{ \rm{eff}}^{} = - 2 \sqrt{2} G J_{\mu}^{\dagger} (x) J^{\mu}(x) \, , $$ 其中
$ G $ 为费米的$ \beta $ 衰变常数,在自然单位之下$ G \!=\! 1.165 \times 10^{-5} \, \rm{GeV}^{-2} $ ,带电流$ J_{\mu}^{} $ 可以表述为矢量流与轴矢流叠加的形式。在夸克为基本自由度的层面上,$ J_{\mu}^{} $ 常一般地表述为$$ J_{\mu}^{} = \sum \limits_{f} \overline{\Psi}^{f} \gamma^{\mu} T_{-} \Psi^{f} \, , $$ (21) 其中
$ T_{-} $ 为同位旋的降算符(与中子转变为质子过程中同位旋第3分量变化的表述习惯一致),并可由矩阵形式表述为$$ T_{\pm} = T_{1}^{} \pm {\rm i} T_{2}^{} = \frac{1}{2} \big{(} \sigma_{1}^{} \pm {\rm i} \sigma_{2}^{} \big{)} \, , $$ 其中
$ \sigma_{k}^{} $ 为泡利矩阵,$ T_{+} $ 为同位旋的升算符。考察放出电子的
$ \beta $ 衰变及强子的夸克结构可知,该过程可以在夸克层面上表述为$$\begin{aligned} d \longrightarrow u + e^{-} + \overline{\nu}_{e}^{} \text{,} \\ s \longrightarrow u + e^{-} + \overline{\nu}_{e}^{} \text{。} \end{aligned} $$ 这表明,强子中的所谓的
${d}$ 夸克很可能实际上是通常意义上的${ d}$ 夸克与具有相同电荷的${s}$ 夸克的混合态,并记之为$$ d^{\prime} = d \cos{\Theta_{c}^{}} + s \sin{\Theta_{\rm C}^{}} \, , $$ 其中
$\Theta_{\rm C}^{}$ 称为Cabibbo角。于是,弱作用中涉及的费米子场可以统一标记为$$ \Psi_{L}^{f} = \frac{1}{2} \big{(} 1 + \gamma_{5}^{} \big{)} \Big{\{} \Big{(} \begin{array}{*{20}{c}} \nu_{e}^{} \\ e^{-} \\ \end{array} \Big{)}\, , \Big{(} \begin{array}{*{20}{c}} \nu_{\mu}^{} \\ \mu^{-} \\ \end{array} \Big{)}\, , \Big{(} \begin{array}{*{20}{c}} u \\ d^{\prime} \\ \end{array} \Big{)} \Big{\}} \text{。} $$ 类似于强作用中的质子、中子为同位旋二重态,这里的同位旋为弱同位旋,相应的粒子都为弱同位旋二重态,例如,
$ T_{\nu_{e}^{},3} \!=\! T_{\nu_{\mu}^{},3} \!=\! \frac{1}{2} $ ,$ T_{e^{-},3} \!=\! T_{\mu^{-},3} \!=\! -\frac{1}{2} $ 。于是,人们认为这些费米子具有(整体的)SU(2)对称性。相应地,由SU(2)的生成元的对易关系$ \;\big{[} T_{+} \, , \; T_{-} \big{]} \!=\! 2 T_{3}^{} \!=\! 2 \sigma_{3}^{} $ 知,应该存在与前述的带电流强度相当的(电)中性流(相应于$ T_{3} $ )。然而,实验发现奇异数不守恒的中性流转变(例如,$ \rm{K}_{L}^{0} \rightarrow \mu^{+} \mu^{-} $ ,或$ \rm{K}^{0} \leftrightarrow \bar{ \rm{K}}^{0} $ )振幅相比于通常的弱作用过程被压低了多个数量级。为解决这一问题,Glashow与合作者引入粲夸克(c夸克),并将s夸克也视为s与d的混合态$ s^{\prime}\! =\! - d \sin{\Theta_{\rm C}^{}} + s \cos{\Theta_{\rm C}} $ ,并有第4组费米子二重态$$ \Big{(} \begin{array}{*{20}{c}} c \\ s^{\prime} \\ \end{array} \Big{)}\text{。} $$ 按照截止现在的认识,上述左手费米子二重态还包括第三代夸克和第三代轻子,即
$$ \Big{(} \begin{array}{*{20}{c}} \nu_{\tau}^{} \\ \tau \\ \end{array} \Big{)} \, , \qquad \Big{(} \begin{array}{*{20}{c}} t \\ b \\ \end{array} \Big{)}\text{。} $$ 与弱作用(左手粒子)流相对应的(弱)荷算符为
$$ \hat{T}^{\rm L}_{i} = \int J^{i}_{4} {\rm d}^{3}x \, , $$ 被积函数中的下标4代表流的时空第4分量,上标
$ i $ 代表流中同位旋的第$ i $ 分量。这些荷算符满足对易关系$$ \big{[} \hat{T}_{i}^{\rm L} \, , \; \hat{T}_{j}^{\rm L} \big{]} = {\rm i} \varepsilon_{ijk}^{} \hat{T}_{k}^{\rm L} \, , $$ 其中
$ \varepsilon_{ijk}^{} $ 为原同位旋SU(2)群的结构常数。由此知,这些算符构成一个su(2)代数,由之可生成SU(2)群。上述讨论表明,弱作用具有SU(2)对称性,尤其是原始的标准的
$ \beta $ 衰变过程即在该对称性下由同位旋降算符($ T_{-} $ )作用而实现的过程,而同位旋的三分量对应中性流。根据前述的规范理论的基本概念,为将弱作用与电磁作用纳入到同一个理论框架之下,应该从其电荷守恒出发考虑。
为清楚表示弱作用过程中涉及的粒子的电荷、弱同位旋及超荷之间的关系,定义弱超荷算符
$$ \hat{Y} = \hat{Q} - \hat{T}_{3}^{\rm L} \text{。} $$ 这样,前述的左手轻子(中微子、电子等)都对应该弱超荷算符的本征态(弱超荷都为
$ -\frac{1}{2} $ )。显然,$$ \big{[} T^{\rm L}_{i} \, , \; \hat{Y} \big{]} = 0 \text{。} $$ 总之,弱作用中的弱荷和包含电荷的弱超荷构成
$ {\rm{SU}}_{ \rm{L}}^{}(2) \otimes U_{ {\rm{Y}}}^{}(1) $ 对称性的四个生成元,与它们相应,在电弱统一理论中有四个规范玻色场。记这四个玻色场分别为$ W^{a}\; \; (a = 1,2,3) $ 、$ B $ ,则它们与$ {\rm{SU}}_{ \rm{L}}^{}(2) \otimes U_{ {\rm{Y}}}^{}(1) $ 的流间的耦合作用为$$ g J_{\mu}^{a} W^{a}_{\mu} + g^{\prime} J^{Y}_{\mu} B_{\mu}^{} \, , $$ 其中
$ g $ 、$ g^{\prime} $ 为相互独立的参数。与通常的SU(2)群的生成元之间的关系一样,由上述的
$ W^{1,2}_{\mu} $ 可得到荷电的规范玻色子$$ W_{\mu}^{\pm} = \frac{1}{\sqrt{2}} \big{(} W_{\mu}^{1} \pm i W_{\mu}^{2} \big{)} \text{。} $$ 根据弱超荷为电荷与同位旋第三分量的线性叠加,电磁作用的规范场(光子场)
$ A_{\mu}^{} $ 相应的$ W^{3} $ 与$ B $ 的线性组合则得到$ Z $ 玻色子,并有温伯格角$ \Theta_{W}^{} $ 表征其间的耦合($ \tan{\Theta_{W}^{}} \!=\! \frac{g^{\prime}}{g} $ )。如果这里所有的矢量玻色子都与光子一样,是零质量的,则显然无法描述实验测得的弱作用强度远小于电磁作用强度的事实,因此这里的规范玻色子
$ W^{\pm} $ 和$ Z $ 不仅应该是非零质量的,而且是相当重的。1982年CERN的关于宇称不守恒的中性流过程的实验得到$ \sin^{2}{\Theta_{W}^{} } \!\approx 0.23 $ ,进而得到$ M_{W}^{} \! \approx \! 80\, \rm{GeV} $ ,$ M_{Z}^{} \!\approx \!92\, \rm{GeV} $ 。 这些规范玻色子的质量与理论预言结果符合得相当好,从而确立了电弱统一理论。并且,使$ W^{\pm} $ 和$ Z $ 获得质量的机制是使非阿贝尔规范不变性自发破缺的Higgs机制[19-21]。(2) 标准模型的规范对称性及进一步发展
包含已经实现了量子化的强作用、弱作用和电磁作用的物理理论称为(粒子)物理学的标准模型(Standard Model)理论。根据标准模型中的强作用部分具有
$ {\rm{SU}}_{ \rm{C}}^{}(3) $ 规范对称性和电弱作用部分具有$ {\rm{SU}}_{ \rm{L}}^{}(2) \otimes {\rm U}_{ {\rm{Y}}}^{}(1) $ 对称性,标准模型具有规范对称性$$ {\rm{SU}}_{ \rm{C}}^{}(3) \otimes {\rm{SU}}_{ \rm{L}}^{}(2) \otimes {\rm U}_{ {\rm{Y}}}^{}(1) \text{。} $$ 但标准模型存在参数多、无法解释三代夸克和三代轻子中分别具有相同的量子数、无法给出质子和电子具有数值相同符号相反的电荷的机制、无法给出存在三个独立的规范作用参数且其数值差异可能巨大的机制等问题。为解决这些问题,物理学家已在建立真正实现强作用、弱作用和电磁作用统一描述的探索方面付出了巨大努力,并取得了一些实质性的进展。人们称实现了强作用、弱作用和电磁作用统一描述的理论为大统一模型。
大统一模型的一个原则是,其规范对称群必须包含
$$ {\rm{SU}}_{ \rm{C}}^{}(3) \otimes {\rm{SU}}_{ \rm{L}}^{}(2) \otimes {\rm U}_{ {\rm{Y}}}^{}(1), $$ 为其子群。目前建立的大统一模型有SU(5)模型、SO(10)模型等等。这些模型已经在很大程度解决了前述的问题,但仍存在诸如质子寿命与实验相差两个数量级(实验测得质子寿命的下限为
$ \tau_{ \rm{p}}^{} \approx 10^{32} $ a,但SU(5)模型给出约$ 10^{30} $ a的结果)等问题。因此,人们仍在致力解决这些问题。解决这些问题的方案一个方面是对现有的理论进行修正和补充,另一方面发展建立了超对称(Supersymmetry)模型、人工色(Techincolor)模型、复合希格斯(Composite Higgs)模型等。由于这些方案比较专门,这里不予具体介绍。近年致力于统一四种基本相互作用的超大统一理论的研究也很活跃,并且我国学者已取得可喜进展(如文献[22]等)。但其量子化仍是需要解决的问题。
-
我们知道,原子核由强子组成①,并且,轻原子核是典型的量子少体束缚态,重原子核是典型的量子多体束缚态。由于核子和超子是费米子,而介子为玻色子,那么通常的不考虑介子组分的原子核为多费米子系统。如果考虑核子等费米子之间的配对效应,这些核子对可以近似为玻色子,于是偶偶原子核和奇奇原子核也可以近似为玻色子系统。并且奇质量数原子核(常简记为奇A核)可近似为既包含费米子又包含玻色子的多粒子系统(重核和中重核)或少体系统(轻核)。由本文第2节的讨论可知,多粒子系统具有幺正对称性,并且幺正对称性可以破缺到正交对称性(玻色子系统)或斜交对称性(费米子系统),因此作为量子束缚态的原子核具有对称性,并且其对称性可能破缺。考虑篇幅限制,本节对原子核的对称性也仅作简要介绍。
-
回顾上述讨论知,多玻色子系统具有最大对称性
$ {\rm{U}}(\sum_{i}(2l_{i}+1)) $ ,其中的维数$ N \!=\! \sum_{i}(2l_{i}+1) $ 为其组分粒子的内禀空间的自由度的维数,并且有子代数链$$ {\rm{su}}(\sum\limits_{i}(2l_{i}+1))\supset {\rm{so}}(\sum\limits_{i}(2l_{i}+1)) \text{。} $$ 多费米子系统具有最大对称性
$ {\rm{U}}(\sum_{i}(2j_{i}^{}+1)) $ ,其中的维数$ N \!=\! \sum_{i}(2j_{i}^{}+1) $ 亦为其组分粒子的内禀空间的自由度的维数,并且有子代数链$$ {\rm{su}}(\sum\limits_{i}(2j_{i}^{}+1))\supset {\rm{sp}}(\sum\limits_{i}(2j_{i}^{}+1)) \text{。} $$ 这表明,玻色子系统的对称性可以由最大的幺正对称性破缺到维数相同的正交对称性。当然也可以破缺到维数较低的幺正对称性,例如,前述的由角动量
$ l \!=\! 0 $ 的s玻色子和角动量$ l \!=\! 2 $ 的d玻色子系统的最大对称性$ {\rm{U}}(6) $ 可以破缺到$ {\rm{SO}}(6) $ (同构于SU(4))也可以破缺到SU(5),还可以破缺到SU(3)。并且,费米子系统的对称性可以由最大的幺正对称性破缺到维数相同的斜交对称性(亦即辛对称性)。当然也可以破缺到维数较低的幺正对称性,例如,前述的由总角动量$ j \!=\! 1/2 , \, 3/2, \, 5/2 $ 的费米子形成的系统的最大对称性$ {\rm{U}}(12) $ 可以破缺到$ {\rm{SP}}(12) $ ,还可以破缺到U(10),甚至U(6)。由于多粒子系统通常都具有转动不变性,亦即SO(3)对称性,并且原子核的主要成分是费米子(核子和超子),因此,原子核具有幺正对称性
$ {\rm{SU}}(\sum_{i}(2j_{i}^{}+1)) $ ,并有下述群链标记的动力学破缺$$ {\rm{SU}}(\sum\limits_{i}(2j_{i}^{}+1))\supset {\rm{SP}}(\sum\limits_{i}(2j_{i}^{}+1)) \supset \cdots \supset {\rm{SO}}(3)\text{。} $$ 如果再考虑同位旋对称性,则有
$$ {\rm{SU}}(\sum\limits_{i}(4j_{i}^{}+2))\supset {\rm{SP}}(\sum\limits_{i}(4j_{i}^{}+2)) \supset \cdots \supset {\rm{SO}}(3)\text{。} $$ 考虑将核子对近似为玻色子,从而原子核可以近似为玻色子情况下,原子核具有幺正对称性
$ {\rm{SU}}(\sum_{i}(2l_{i}+1)) $ ,并有下述群链标记的动力学破缺$$ {\rm{SU}}(\sum\limits_{i}(2l_{i}+1))\supset {\rm{SO}}(\sum\limits_{i}(2l_{i}+1)) \supset \cdots \supset {\rm{SO}}(3)\text{。} $$ -
由于不同(总)角动量的粒子的产生算符、湮灭算符都相互对易,因此需要认真处理的重要部分为全同粒子部分。前已说明,原子核具有SO(3)不变性,即有确定的总角动量
$ J $ ,从而由单粒子角动量为$ j $ 的全同费密子形成的原子核的波函数可以写为$$ |n \; \nu \; \alpha \; J \; M \rangle, $$ 其中
$ n $ 为单粒子轨道$ j $ 上的粒子数,$ \nu $ 为单粒子角动量为$ j $ 的粒子系统的辛弱数(即不配成角动量为$ 0 $ 的对的粒子数)。显然总角动量$ J $ 的可能取值及其出现的次数是描述这样的原子核状态的关键物理量。按照前述的原子核的对称性及其破缺的方式,原子核的辛弱数
$ \nu $ 可以由U$ (2j+1) $ 的不可约表示(常简记为$ {\rm{IRREP}} $ )$ [1^n] $ 按群链U$ (2j+1) \supset {\rm{SP}}(2j+1) $ 约化(即$ [1^n] \!=\! \oplus_{\nu} (1^{\nu}) $ )的规则确定,并可简单表述为$$ \nu = \Bigg{\{} \begin{array}{ll} n, n-2,\cdots, 0 \, , \qquad n = {\text{偶数}}; \\ n,n-2,\cdots,1\, , \qquad n = {\text{奇数}}\text{。} \end{array} $$ (22) $ J $ 为单粒子轨道$ j $ 上的粒子数为$ n $ 、辛弱数为$ \nu $ 的态的角动量,即SP$ (2j+1) $ 群的表示$ (1^{\nu}) $ 按群链SP$ (2j+1) \supset {\rm{SO}}(3) $ 约化时得到的SO(3)群的IRREP. 因为SP$ (N) \supset {\rm{SO}}(3) $ 的约化为非简单可约,即可能有多个态对应于同一个$ J $ 和同一个$ \nu $ ,所以需要引入附加量子数$ \alpha $ 来区分$ n $ 、$ \nu $ 、$ J $ 都分别相同的态。一个简单的确定附加量子数$ \alpha $ 的方案是先确定SP$ (N) \supset {\rm{SO}}(3) $ 约化的重复度$ \eta $ ($ \eta \!=\! 0 $ 表明不存在总角动量为$ J $ 的态,$ \eta \neq 0 $ 表明存在$ \eta $ 个总角动量为$ J $ 的态),那么取$ \alpha \in [1, \, \eta] $ 即可确定附加量子数。关于
$ {\rm{SP}}(N) \supset {\rm{SO}}(3) $ 约化的重复度,乍看起来,是一个简单的问题。但事实上,虽经长期研究(例如文献[23-29]等),到现在尚无直观表述的一般公式,但人们发展建立了通过划分进行递推(标准的由最高权态递推确定所有权集合)的方案,并已有相应的计算机程序[23-24]。实用中常见的$ { j \!=\! 7/2 } $ 、$ { j \!=\! 9/2 } $ 、$ { j \!=\! 11/2 } $ 、$ { j \!=\! 13/2 } $ 、$ { j \!=\! 15/2 } $ 系统的具体数值可参见文献[2]。关于全同玻色子系统的具有确定辛弱数
$ \nu $ 的总角动量为$ L $ 的重复度,确定方案与全同费密子系统的相同[23-24],只是因为$ 2 l + 1 = {\text{奇数} } $ ,SP$ (2j+1) $ 群应换为SO$ (2l + 1) $ 。并且,对$ d $ 玻色子系统已有解析计算公式[30]。$ d $ 玻色子、$ f $ 玻色子、$ g $ 玻色子、$ h $ 玻色子和$ i $ 玻色子等系统的一些具体数值可参见文献[2]. -
我们知道,对于多体系统,确定相互作用的哈密顿量(计算相互作用矩阵元)及计算跃迁矩阵元的关键问题是计算全同粒子系统的矩阵元,即计算产生算符
$ a_{jm}^{\dagger} $ 和湮灭算符$ a_{jm}^{} $ 的矩阵元$$ \langle {j}^{n} \, \tau \, \alpha \, J \big{|} a^{\dagger}_{j} \big{|} {j}^{n-1} \, \tau^{\prime} \, \alpha^{\prime} \, J^{\prime} \rangle \, , \quad \langle {j}^{n} \, \tau \, \alpha \, J \big{|} \tilde{a}_{j} \big{|} {j}^{n+1} \, \tau^{\prime} \, \alpha^{\prime} \, J^{\prime} \rangle \, , $$ 其中
$ \tilde{a}_{jm}^{} \!=\! (1)^{j-m} a_{j\, -m}^{} $ 为与产生算符相应的不可约张量,$ j \!=\! l\! =\! {\text{整数}} $ 对应玻色子系统,$ j \!=\! {\text{半奇数}} $ 对应费米子系统。这两类矩阵元分别为由粒子数为$ n-1 $ 、辛弱数为$ \tau^{\prime} $ 、总角动量为$ J^{\prime} $ 的全(反)对称态添加一个粒子形成粒子数为$ n $ 、辛弱数为$ \tau $ 、总角动量为$ J $ 的全(反)对称态的矩阵元,或者由粒子数为$ n+1 $ 、辛弱数为$ \tau^{\prime} $ 、总角动量为$ J^{\prime} $ 的全(反)对称态减少一个粒子形成粒子数为$ n $ 、辛弱数为$ \tau $ 、总角动量为$ J $ 的全(反)对称态的矩阵元。由于在考虑角动量
$ j $ 与$ J^{\prime} $ 耦合形成的角动量为$ J $ 的态中既有全(反)对称的成分,又有非全(反)对称的成分,但$ \vert j^{n} \, \tau \, \alpha \, J \, M \rangle $ 为全(反)对称态,因此通常称角动量层次上的耦合态$ \vert [(j^{n-1} \, \tau^{\prime} \, \alpha ^{\prime} \, J^{\prime} \, M^{\prime})(jm)]\, JM \rangle $ 为母态,物理态(全(反)对称态)$ \vert j^{n} \, \tau \, \alpha \, J \, M \rangle $ 为母态中包含的全(反)对称部分,即有$$ \begin{split}\big{\vert} j^{n} \, \tau \, \alpha \, J \, M \rangle =& \sum\limits_{\alpha ' \, J'} \langle (n-1) \, \tau ' \, \alpha ' \, J' j J \big\vert \big\} n \; \tau \; \alpha \; J \rangle \times \\ &\big{\vert} \big[(j^{n-1} \, \tau^{\prime} \, \alpha ^{\prime} \, J^{\prime} \, M^{\prime})(jm)\big]\, JM \rangle \, , \\[-13pt] \end{split} $$ (23) 或者说
$$ \begin{split}& \langle n \; \tau \; \alpha \; J \; M \big| a^{\dagger}_{jm} \big| n - 1 \; \tau^{\prime} \; \alpha^{\prime} \; J^{\prime} \; M^{\prime} \rangle \\ =& \langle J^{\prime} \, M^{\prime} \, j \, m \big| J \; M \rangle \langle (n - 1) \; \tau^{\prime} \; \alpha^{\prime} \; J^{\prime} \; j \; J \big| \big\} n \, \tau \, \alpha \, J \rangle \times \\ & \langle n \| a^\dagger \| (n - 1) \rangle_{U(N)} \, ,\\[-13pt] \end{split} $$ (24) 其中
$ \langle J^{\prime} \, M^{\prime} \, j \, m | J \; M \rangle $ 为角动量耦合的CG(Clebsch-Gordancoefficients)系数;$ \langle (n - 1) \; \tau^{\prime} \; \alpha^{\prime} \; J^{\prime} \; j \; J \vert \} n \, \tau \, \alpha \, J \rangle $ 称为母分系数(coefficient of fractional parentage,简称为CFP),即母态中包含的全(反)对称的成分的概率幅;$ \langle n \| a^\dagger \| (n-1) \rangle_{{\rm U}(N)} $ 为产生算符的$ {\rm{U}}(N) $ 对称层次上的约化矩阵元,即仅考虑粒子数变化的约化矩阵元。由此还可以知道,对于确定全同粒子系统的波函数,母分系数是其核心,尽管这一问题在多粒子壳模型开始发展时就被提出[31-32],直到20世纪90年代中前期,人们才给出了计算具有确定辛弱数的系统的母分系数的理论方法和计算程序[24, 33-34]。通过直接计算
$ a^{\dagger}_{jm} $ 、$ \tilde{a}_{jm} $ 与标记系统状态的群链$ {\rm{U}}(N) \supset {\rm{SP}}(N) \supset {\rm{SO}}(3) $ (其中$ N \!=\! 2j+1 $ )中的各个群的生成元间的对易关系可知,产生算符$ a^{\dagger}_{jm} $ 及与湮灭算符相联系的算符$ \tilde{a}_{jm}^{} $ 是U$ (N) $ 群的1秩不可约张量、SP$ (N) $ 群的1秩不可约张量、SO$ (3) $ 群的$ j $ 秩不可约张量,并且$ a^{\dagger}_{jm} $ 和$ -\tilde{a}_{jm} $ 还构成准自旋群$ {\rm{SU}}(2)_q $ 的$ 1/2 $ 秩不可约张量,分别对应于$ \{1/2,-1/2\} $ 、$ \{1/2,1/2\} $ 分量。那么,上述矩阵元应该在U$ (N) $ 、SP$ (N) $ 和SO$ (3) $ 等层次上都满足相应的不可约张量的耦合关系(或者说$ {\rm{IRREP}} $ 的乘积的约化规律),根据产生算符是U$ (N) $ 的1秩不可约张量的性质,利用U$ (N) $ 的Wigner-Eckart定理和Racah因子分解引理,得$$ \begin{split}& \langle n \; \tau \; \alpha \; J \; M | a^{\dagger}_{jm} | n-1 \; \tau ' \; \alpha ' \; J ' \; M ' \rangle \\ =& \bigg{\langle} \begin{array}{*{20}{c}} [1] & [1^{n-1}] \\ (1) & (1^{\tau '}) \end{array} \bigg{|} \begin{array}{*{20}{c}} [1^n] \\ (1^{\tau}) \end{array} \bigg{\rangle} \bigg{\langle} \begin{array}{*{20}{c}} (1) & (1^{\tau '}) \\ j & \alpha ' \; J ' \end{array} \Bigg{|} \begin{array}{*{20}{c}} (1^{\tau}) \\ \alpha \; J \end{array} \bigg{\rangle}\times \\& \langle J ' \, M ' \; j \, m | J \, M \rangle \langle n \| a^\dagger \| n-1 \rangle_{{\rm U}(N)} \, , \end{split} $$ (25) 其中
$ \Big{\langle} \begin{array}{*{20}{c}} [1] & [1^{n-1}] \\ (1) & (1^{\tau '}) \end{array} \Big{|} \begin{array}{*{20}{c}} [1^n] \\ (1^{\tau}) \end{array} \Big{\rangle} $ ,$ \Big{\langle} \begin{array}{*{20}{c}} (1) & (1^{\tau '}) \\ j & \alpha ' \; J ' \end{array} \Big{|} \begin{array}{*{20}{c}} (1^\tau) \\ \alpha \; J \end{array} \Big{\rangle} $ 分别为$ {\rm{U}}(N) \supset {\rm{SP}}(N) $ ,$ {\rm{SP}}(N) \supset {\rm{SO}}(3) $ 的约化系数(常称之为同位标量因子,简记为ISF)。$ \langle J^{\prime} \, M^{\prime} \; j \, m | J \, M \rangle $ 为$ {\rm{SO}}(3) $ 的CG系数。那么,求出$ {\rm{U}}(N) \supset {\rm{SP}}(N) $ 和$ {\rm{SP}}(N) \supset {\rm{SO}}(3) $ 的ISF便可求得CFP。由于系统增加一个粒子后,这个粒子可以与原系统中的没有配对的一个粒子配成对,也可能不配对,因此有
$ \tau\! =\! \tau^{\prime} -1 $ 和$ \tau \!=\! \tau^{\prime} + 1 $ 两种情况,亦即有$ \tau^{\prime} \!=\! \tau -1 $ 和$ \tau^{\prime} \!=\! \tau + 1 $ 两种情况。那么,对于$ {\rm{SP}}(N) \supset {\rm{SO}}(3) $ 的ISF,我们既需要考虑$ \Big{\langle} \begin{array}{*{20}{c}} (1) & (1^{\tau-1}) \\ j & \alpha ' \; J^{\prime} \end{array} \Big{|} \begin{array}{*{20}{c}} (1^\tau) \\ \alpha \; J \end{array} \Big{\rangle} $ ,还需要考虑$ \Big{\langle} \begin{array}{*{20}{c}} (1) & (1^{\tau + 1 }) \\ j & \alpha ' \; J^{\prime} \end{array} \Big{|} \begin{array}{*{20}{c}} (1^\tau) \\ \alpha \; J \end{array} \Big{\rangle} $ 。同理,关于矩阵元$ \langle {j}^{n} \, \tau \, \alpha \, J \big{|} \tilde{a}_{j} \big{|} {j}^{n+1} \, \tau^{\prime} \, \alpha^{\prime} \, J^{\prime} \rangle $ 的计算,也可以转化为计算相应的CFP,也涉及上述两种$ {\rm{SP}}(N) \supset {\rm{SO}}(3) $ 的ISF。由产生和湮灭算符的关系以及它们均为SP
$ (N) $ 群的$ (1) $ 秩不可约张量,经过细致的计算分析可以证明,$ {\rm{SU}}(N) \supset {\rm{SP}}(N) $ 的ISF为$$ \begin{split} &\left\langle {\left. {\begin{array}{*{20}{c}} {[1]}&{[{1^{n - 1}}]}\\ {(1)}&{({1^{\tau - 1}})} \end{array}} \right|\begin{array}{*{20}{c}} {[{1^n}]}\\ {({1^\tau })} \end{array}} \right\rangle = \sqrt {\frac{{\tau (N - n - \tau + 2)}}{{n(N - 2\tau + 2)}}} ,\\ &\left\langle {\left. {\begin{array}{*{20}{c}} {[1]}&{[{1^{n - 1}}]}\\ {(1)}&{({1^{\tau + 1}})} \end{array}} \right|\begin{array}{*{20}{c}} {[{1^n}]}\\ {({1^\tau })} \end{array}} \right\rangle = - \sqrt {\frac{{(n - \tau )(N - \tau + 2)}}{{n(N - 2\tau + 2)}}} {\text{。}} \end{split}$$ 并且,
$ {\rm{SP}}(N) \supset {\rm{SO}}(3) $ 的上述两类ISF间存在倒易律:$$ \begin{split}& \bigg{\langle} \begin{array}{*{20}{c}} (1) & (1^{\tau+1}) \\ j & \alpha ' \; J^{\prime} \end{array} \bigg{|} \begin{array}{*{20}{c}} (1^\tau) \\ \alpha \; J \end{array} \bigg{\rangle} \\ =& (-)^{j+J^{\prime}-J}{ \sqrt{\frac{(2J^{\prime} + 1)(\tau+1) (N+2-2\tau)}{(2J+1)(N-2\tau)(N+2-\tau)}} } \times \\& \bigg{\langle} \begin{array}{*{20}{c}} (1) & (1^\tau) \\ j & \alpha \; J \end{array} \bigg{|} \begin{array}{*{20}{c}} (1^{(\tau+1)}) \\ \alpha^{\prime} \; J^{\prime} \end{array} \bigg{\rangle} \, , \end{split} $$ (26) 于是,我们只需要确定
$ {\rm{SP}}(N) \supset {\rm{SO}}(3) $ 的ISF$ \Big{\langle} \begin{array}{*{20}{c}} (1) & (1^{\tau -1}) \\ j & \alpha ' \; J ' \end{array} \bigg{|} \begin{array}{*{20}{c}} (1^{\tau}) \\ \alpha \; J \end{array} \Big{\rangle} $ 。关于
$ {\rm{SP}}(N) \supset {\rm{SO}}(3) $ 的ISF,目前尚无解析公式,只能通过递推计算确定。递推公式为$$ \bigg{\langle} \begin{array}{*{20}{c}} (1) & (1^{\tau - 1}) \\ j & \alpha _{1}^{} \; J_{1} \end{array} \bigg{|} \begin{array}{*{20}{c}} (1^{\tau}) \\ (\alpha_{1}^{\prime} \, J_{1}^{\prime}) \; J \end{array} \bigg{\rangle} = \frac{P(\tau \; [\alpha_{1}^{\prime} \; J_{1}^{\prime}] \; \alpha_{1}^{} \; J_{1} \; J)} {\sqrt{ \tau \, P(\tau \; [\alpha_{1}^{\prime} \; J_{1}^{\prime}] \; \alpha_{1}^{\prime} \; J_{1}^{\prime} \; J)}} \, , $$ (27) 其中
$$ \begin{split}& P(\tau \; [\alpha_{1}^{\prime} \; J_{1}^{\prime}] \; \alpha_{1}^{} \; J_{1}^{} \; J) = \delta_{\alpha_{1}^{\prime} \; \alpha_{1}^{}}\delta_{J_{1}^{\prime} \; J_{1}^{}} +\\&(-1)^{J_{1} + J_{1}^{\prime}}( \tau - 1)\sqrt{(2J_{1}^{} + 1)(2J_{1}^{} +1)} \times \\& \sum \limits_{\alpha_{2}^{} \; J_{2}} \bigg[ \bigg{\{} \begin{array}{ccc} j & J_{2} & J_{1}^{\prime} \\ j & J & J_{1}^{} \end{array} \bigg{\}} + { \frac{2\delta_{J \; J_{2}}(-)^{\tau}} {(2J+1)(N-2\tau+4)} } \bigg] \times \\& \bigg{\langle} \begin{array}{*{20}{c}} (1) & (1^{\tau - 2}) \\ j & \alpha _{2}^{} \, J_{2} \end{array} \bigg{|} \begin{array}{*{20}{c}} (1^{(\tau- 1)}) \\ \alpha_{1}^{} \, J_{1} \end{array} \bigg{\rangle} \bigg{\langle} \begin{array}{*{20}{c}} (1) & (1^{\tau - 2}) \\ j & \alpha _{2}^{} \, J_{2} \end{array} \bigg{|} \begin{array}{*{20}{c}} (1^{(\tau- 1)}) \\ \alpha_{1}^{\prime} \, J_{1} ' \end{array} \bigg{\rangle} \, , \qquad \end{split} $$ 其初值为
$ \Big{\langle} \begin{array}{*{20}{c}} (1) & (1) \\ j & j \end{array} \Big{|} \begin{array}{*{20}{c}} (1^{2}) \\ J \end{array} \Big{\rangle} \!=\! 1 $ (其中$ J \!=\! 0,\, 2,\, \cdots, 2j-1)$ 。对于玻色子系统(对核子对等作玻色子近似,原子核可近似为玻色子系统),单体矩阵元的计算与上述费米子系统的几乎完全相同,只是由于玻色子系统的总波函数是全对称的,前述的
$ {\rm{U}}(N) \supset {\rm{SP}}(N) $ 的ISF和$ {\rm{SP}}(N) \supset {\rm{SO}}(3) $ 的ISF应分别换为$ {\rm{U}}(N) \supset {\rm{SO}}(N) $ 的ISF和$ {\rm{SO}}(N) \supset {\rm{SO}}(3) $ 的ISF[35-36],并且初值为$ \Big{\langle} \begin{array}{*{20}{c}} (1) & (1) \\ l & l \end{array} \Big{|} \begin{array}{*{20}{c}} (2) \\ L \end{array} \Big{\rangle} = 1 \; \; ({\text{其中}}\, L = 0,\, 2,\, \cdots, 2l) \text{。} $ 具体的计算不再重述。利用这些递推关系和倒易律可以得到所有的
$ {\rm{SP}}(N)\supset {\rm{SO}}(3) $ 的ISF和$ {\rm{SO}}(N) \supset {\rm{SO}}(3) $ 的ISF,再考虑$ {\rm{U}}(N) \supset {\rm{SP}}(N) $ 、$ {\rm{U}}(N) \supset {\rm{SO}}(N) $ 的ISF以及$ {\rm{SO}}(3) \otimes {\rm{SO}}(3) \supset {\rm{SO}}(3) $ 的CG系数,即可得到具有确定辛弱数的母分系数,进而可以得到所需的矩阵元。利用这一方法编制的计算全同费密子系统、全同玻色子系统以及包含同位旋(F旋)的费密子(玻色子)系统的计算机程序[24, 37]可以处理任意有物理意义的系统的单体矩阵元(母分系数)的计算问题,并且计算效率极高。 -
人们知道,原子核由强子组成,强子由夸克和胶子组成。实验发现,很多宏观物质系统在较低温度等条件下,有超导或超流等集体运动现象;原子核与分子一样,不仅具有能量近似为常量的近振动光谱和能量随角动量近似成线性关系的近转动光谱,还有明显大于单粒子激发或退激发引起的电四极矩和E2、E1跃迁几率;并且相对论性核-核碰撞形成的胶子夸克物质具有接近理想流体的特征和性质。这些现象表明,这些多粒子系统具有全体粒子都共同参与的集体运动,并且集体运动有振动、转动等多种模式。实验还发现,在一些条件下,这些集体运动模式会发生变化,即发生集体运动模式相变(常简称为形状相变)。相关研究当然是现代物理学的重要研究内容。我们还知道,相变即对称性的破缺或恢复,是对称性理论的重要研究范畴。因此,本节简要介绍多粒子系统的集体运动状态的代数研究方法。
-
前已述及,多粒子系统的集体运动即多粒子系统的所有组分粒子共同参与的整体运动,并且这种集体运动具有不同的模式。相应地,多粒子系统呈现不同的形状。多粒子系统的形状是多粒子系统内组分物质密度分布发生剧烈变化之处的包络面所呈的形状。显然这一形状由系统内组分粒子的集体运动和单粒子运动两种模式共同决定,因此一直是多粒子系统性质研究中的重要课题。稍具体地,讨论单粒子运动时常用的平均势场即为与多粒子系统中物质分布的形状密切相关的变形场。组分物质呈不同形状分布的系统的振动、转动等集体运动模式也各不相同,这就是说,集体运动模式与多粒子系统的所有组分粒子的空间分布形状决定,而多粒子系统的组分粒子的空间分布形状又随集体运动模式的不同而变化,二者互为表里,相辅相成。
为简单地表述多粒子系统的组分物质分布的形状,人们常将多粒子系统假设为由多个粒子因集体关联而整体运动形成的液滴,液滴的形状由随标记方向的角度变化而变化的径向函数
$ R(\theta, \varphi) $ 表征,并通过按球谐函数展开来实现。例如,人们常采用三个欧拉角$ (\theta _{1}^{} ,\theta _{2}^{} ,\theta _{3}^{} ) $ 和内禀变量$ \beta $ 、$ \gamma $ 等来表征其形状和空间取向,其中三个欧拉角定义随体坐标的方向,内禀变量定义多体系统的形状相对于球形的形变,即有$$ R(\theta , \phi ) = R_{0}^{} \Big{[} 1 + \sum \limits_{k\, m} \alpha_{k m}^{*} Y_{ k m}(\theta , \varphi) \Big{]} \, , $$ (28) 其中
$ \theta $ 、$ \varphi $ 等为实验室坐标系中表示方向的坐标。实验室坐标系与随体坐标系之间的关系可以由展开系数张量$ \alpha_{k\mu} $ 之间的关系表述为$$ \alpha _{l m} = \sum\limits_{k m'} {a_{l m'} D^{k}_{m m' } (\Omega )} \, , \quad \Omega = (\theta _{1}^{} ,\theta _{2}^{} ,\theta _{3}^{} ) \, , $$ (29) 其中
$ D $ 函数是Wigner转动矩阵。与电磁场的多极展开类似,人们常称$ 2^{k} $ 为多粒子系统的形变极次。对于常见的较简单的轴对称的四极形变,系数$ a_{2\nu}^{}\!=\! a_{\nu}^{} $ 可以由Bohr-Wheeler参数化方案表述为$$ a_{0}^{} = \beta \cos \gamma\, , \quad a_{\pm 2} = \frac{1}{\sqrt 2 }\beta \sin \gamma \, , \quad a_{\pm 1} = 0\text{。} $$ (30) 对于更高极次形变的参数化表述仍是目前研究的课题。
对于原子核,已经观测到或者已经预言的形状多种多样,将径向分布按球谐函数
$ Y_{km}(\theta,\varphi) $ 展开后,相应于$ k = 2 $ 的四极形变可以呈长椭球形、扁椭球形、三轴不对称形等形状;八极形变则呈空间反演不对称的梨形、香蕉形、镐头形等形状;十六极形变则呈纺锤形等。实验上已经观测到的最高极形变是十六极形变。实验观测和理论研究还表明,一个同位素链或一个同中子素链中的原子核具有分别对应于不同集体运动模式的E2跃迁几率和双核子分离能等性质,即原子核的同位旋(具有SU(2)对称性)变化可以引起原子核的集体运动模式变化,即出现集体运动模式相变(形状相变),并可能出现不同形状共存的现象。集体运动模式相变普遍存在于各个质量区,并且超重核区也存在结构丰富的形变和形状共存[38]。而激发态核的集体运动模式(形变)则更富含物理内容,如超形变带、回弯现象、同核异能态(isomeric states)等都与形变直接相关。并且,角动量、温度等因素变化都会驱动集体运动模式相变。总之,原子核具有多种集体运动模式(或状态),并且有多种模式共存和各种奇异的状态,其间的演化(相变)是基础物理研究的重要内容。
-
早在1926年,薛定谔在探索量子谐振子的经典解释时,就找到一种现在称为“相干态”的解。1963年,Glauber正式提出相干态的概念,并在对量子光学中电磁场的关联函数的研究中,说明相干态为湮灭算符的本征态。同时,Klauder开始为任意李群寻找相应的相干态,经过十年努力,他们发现相干态与群的陪集有一一对应关系,并发展了一套构造相干态的方法。由于物理系统基本都有一定的群结构,因此自然可以将相干态与具有确定动力学对称性的物理系统相联系,从而可以利用代数方法研究多粒子系统的集体运动状态。
(1) 相干态的概念
我们知道,一维坐标空间(记为
$ x $ )平移群的生成元$ {\mathbb{X}}_{x}^{}\! =\! \frac{\rm d}{{\rm d}x} $ ,它显然可以由量子力学中的动量算符$ \hat{p} $ 表述为$ {\mathbb{X}}_{x} \!=\! \frac{\rm d}{{\rm d}x} \!=\! \frac{{\rm i}}{\hbar} \hat{p} $ . 那么,由群操作的指数实现可知,经坐标空间平移$ d $ 后,一维谐振子的基态$ \big{\vert} \psi_{0}^{}(x) \rangle $ 改变为$$ \big{\vert} \psi_{0}^{} (x - d) \rangle = {\rm e}^{-\frac{{\rm i}}{\hbar} \hat{p} d} \big{\vert} \psi_{0}^{}(x) \rangle \text{。} $$ 在占有数表象中,动量算符
$ \hat{p} $ 可以表述为玻色子的产生算符与湮灭算符的线性叠加,即有$$ \hat{p} = {\rm i} \sqrt{\frac{m \hbar \omega}{2} } \big{(} b^{\dagger} - b \big{)} \text{。} $$ 于是,上述坐标空间平移之后的态还可以表述为
$$ \big{\vert} \psi_{0}^{} (x - d) \big{\rangle} = {\rm e}^{\sqrt{\frac{m \omega}{2\hbar} } d ( b^{\dagger} - b )} \big{\vert} \psi_{0}^{}(x) \big{\rangle} \text{。} $$ 同理,对动量空间作平移之后的态也可以表述为类似的形式,差别仅在于上述的产生算符与湮灭算符的反相位叠加换为同相位叠加(因为
$ \hat{x}\!=\! \sqrt{\frac{\hbar}{2 m \omega} } \big{(} b^{\dagger} + b \big{)} $ )。推而广之,在相空间中有位移之后的态都可以由位移之前的态表述为
$$ \big{\vert} S \big{\rangle} = {\rm e}^{(S^{*} b^{\dagger} - S b)} \big{\vert} 0 \big{\rangle} \text{。} $$ (31) 该状态即被称为相干态,
$ S $ 称为相空间参数,其物理意义是在相空间中有位移之后的谐振子基态波函数。考虑算符的函数
$$ {\rm e}^{(S^{*}b^{\dagger} - Sb)} = {\rm e}^{S^{*}b^{\dagger}} {\rm e}^{-Sb} {\rm e}^{-\frac{1}{2}S^{*} S} \, , \quad {\text{和}} \quad b\big{\vert} 0 \rangle = \big{\vert} 0 \rangle \, , $$ 知
$$ \big{\vert} S \big{\rangle} = {\rm e}^{-\frac{1}{2}S^{*} S} {\rm e}^{S^{*}b^{\dagger}} \big{\vert} 0 \big{\rangle} = {\rm e}^{-\frac{1}{2}S^{*} S} \sum \limits_{n}\frac{{S^{*}}^{n}}{\sqrt{n!}} \big{\vert} n \big{\rangle} \, , $$ 其中
$ \vert n \rangle $ 为粒子数算符$ \hat{n} = b^{\dagger} b $ 的本征态。这表明,相干态为各种粒子数本征态的线性叠加,或者说,相干态是粒子数不守恒的态。但其平均值为$$ \left\langle {S|\hat n|S} \right\rangle = {{\rm e}^{ - {S^*}S}}\sum\limits_n {\frac{{{{({S^*}S)}^n}}}{{(n - 1)!}}} = |S{|^2}, $$ 即粒子数算符在相干态上的期望值为相空间参数的模的平方。据此,人们通常取具有确定粒子数的态作为相干态的近似表述,并称之为投影相干态、或内禀相干态。
(2) Heisenberg–Weyl群与相干态的构建
因为产生算符
$ \hat{b}^{\dagger} $ 、湮灭算符$ \hat{b} $ 和单位算符$ \hat{I} $ 构成Heisenberg–Weyl (HW)代数$ \{ \hat{b}^{\dagger}, \hat{b}, \hat{I} \} $ ,其代数关系为$$ \big{[} \hat{b} , \; \hat{b}^{\dagger} \big{]} = \hat{I} \, , \quad \big{[} \hat{b} , \; \hat{I} \big{]} = \big{[} \hat{b}^{\dagger} , \; \hat{I} \big{]} = 0 \text{。} $$ HW代数中的一般元素可以表述为
$$ \theta \hat{I} + {\rm i} \big{(} S \hat{b} - S^{*} \hat{b}^{\dagger} \big{)} \, , $$ 其中
$ \theta $ 为实数,$ S $ 为复数。由此HW代数中的一般元素可以构建一组新的元素
$$ T(\theta , S) = {\rm e}^{ {\rm i} \theta \hat{I} + ( S^{*} \hat{b}^{\dagger} - S \hat{b} ) } \text{。} $$ 直接计算可知,
$$ T ( \theta , S) T(\theta^{\prime} , S^{\prime}) = T ( \theta + \theta^{\prime} + {\rm Re}(S^{*} S) , S+S^{\prime})\text{。} $$ 这表明,由HW代数可以构成三参数李群,Heisenberg–Weyl(HW)群。
显然,
$ T(\theta, S) $ 可以唯一分解为$$ T(\theta, S) = T(0,S) T(\theta, 0)\, , $$ 这表明,集合
$ \{ T(\theta, 0) \} $ 构成HW群的子群,而集合$ \{ T(0,S) \} $ 构成HW群的(相应于上述子群的)陪集。上述算符
$ T $ 也可视为HW群的不可约表示空间$ {\cal V} $ 上的算符,空间$ {\cal V} $ 的基矢可以表述为$$ \Big{\{} \big{\vert} n \big{\rangle} = \frac{1}{\sqrt{n!}} (\hat{b}^{\dagger})^{n} \big{\vert} 0 \big{\rangle} \; \; \big{\vert} \; \; n = 0, 1 , 2, \cdots \Big{\}} \text{。} $$ 对HW的子群(记之为
$ {\cal M} $ )中的元素$ T(\theta, 0) \in {\cal G} $ ,将之作用到参考态,我们有$$ T(\theta , 0) \big{\vert} 0 \big{\rangle} = {\rm e}^{{\rm i} \theta} \big{\vert} 0 \big{\rangle} \text{。} $$ 将元素
$ T(\theta, S) \in \rm{HW} $ 作用到基态,我们有$$ T(\theta , S) \big{\vert} 0 \big{\rangle} = {\rm e}^{{\rm i} \theta} T(0, S) \big{\vert} 0 \big{\rangle} \text{。} $$ 与相干态的定义比较知,对
$ T(0,S) \in \rm{HW}/{\cal M} $ ,$$ T(0 , S) \big{\vert} 0 \big{\rangle} = {\rm e}^{(S^{*} \hat{b}^{\dagger} - S \hat{b})} \big{\vert} 0 \big{\rangle} = \big{\vert} S \big{\rangle} \text{。} $$ 这表明,相干态是定义在
$ \rm{HW} $ 的子群$ {\cal M} $ 的陪集空间$ \rm{HW}/{\cal M} $ 上的态。(3)广义相干态及其构建
显然,将前述的HW群推广到一般的李群
$ {\cal{G}} $ ,人们可以广义地建立相干态。一般地,对于李代数为
$ {\mathfrak{g}} $ 的群$ {\cal{G}} $ ,可以按照一定的程序找到与其相联系的几何空间,例如对于转动群SO(3),可以将几何参数$ \theta $ 、$ \varphi $ 与其表示相联系,从而可以用球谐函数来描述SO(3)群的几何结构。如果这种程序不唯一,则通常选取有明显物理意义的一种。这种程序首先将李代数分成两部分
$ {\mathfrak{g}} \!=\! {\mathfrak{h}} \oplus {\mathfrak{p}} \, , $ 其中$ {\mathfrak{h}} $ 是$ {\mathfrak{g}} $ 的不变子代数,在对易关系下封闭,而$ {\mathfrak{p}} $ 则不一定封闭。几何空间的参数与$ {\mathfrak{p}} $ 中的元素一一对应,其数目即几何空间的维数。$ {\mathfrak{g}} $ 的表示提供一组基态$ \big{\vert} \Lambda \big{\rangle} $ ,其中有一个称为极值态(extremal state)的态$ \big{\vert} \Lambda _ { \rm{ext}} \big{\rangle} $ ,它定义为李代数中有最多数目的元素可以湮灭它的态。这样,几何空间的参数$ \eta _{i}^{} $ 可以按照前述的相干态的定义而定义,其中$ p_{i}^{} $ 是$ {\mathfrak{p}} $ 中的元素,即有$$ \big{\vert} \eta_{i}^{} \big{\rangle} = \exp \left [\sum\limits{i} \eta _{i}^{} p_{i}^{} \right] \big{|} \Lambda _{\rm ext} \rangle \text{。} $$ 由于代数
$ {\mathfrak{g}} $ 可能有几个不同的不变子代数$ {\mathfrak{h}} $ ,因此可以存在几个不同的几何空间。在实际应用中,常定义几何空间为与满足物理条件的最大不变子代数相联系的空间。由第二节的讨论知,多粒子系统的状态可以由典型李群标记的动力学对称性描述,因此多粒子系统的集体运动状态可以利用代数方法进行研究。研究的具体步骤是,将内禀相干态中的$ n $ 粒子态写为各种组分粒子的产生算符的叠加形式(其中的叠加系数为表征集体运动状态的几何参数函数),将哈密顿量写为相应粒子表象的形式,然后计算哈密顿量在内禀相干态下的期望值,根据最小作用原理确定稳定的集体运动状态。关于对原子核的集体运动的具体描述见4.4.3节的讨论。 -
(1) 基本理论框架
人们知道,原子核是包含多个核子、甚至超子的量子束缚系统。核子–核子之间、多核子之间、超子–超子之间及核子–超子之间的相互作用都很复杂,因此很难直接从第一性原理出发研究这样的量子多体系统的性质。于是,对于简单的由核子组成的原子核,人们提出平均场近似的思想(当时还没有发现包含超子的超核),认为每个核子都在其它核子共同形成的平均场中运动,除平均场之外,核子-核子之间的剩余相互作用可以作微扰处理。这样,原子核的哈密顿量可以表示为
$$ \hat{H} = \sum\limits_{i = 1}^{A}\Big[ \hat{T}_{i} + V(i)\Big] + \sum\limits_{i<j}V'(ij) \, , $$ (32) 其中
$ \hat{T}_{i} \!=\! \frac{\hat{{{p_{i}}}}}{2m} $ 为第$ i $ 个核子的动能,$ V(i) $ 为第$ i $ 个核子所受的平均场(也称为单粒子位势),$ V'(ij) $ 是第$ i $ 个核子和第$ j $ 个核子之间的剩余相互作用势。原子核的状态由求解这一平均场近似所得的状态来描述。总之,壳模型的核心思想就是平均场近似。(2) 平均场的形式
因为每个组分粒子感受的平均场由所有其它组分粒子共同提供,所以人们认为该平均场近似地正比于原子核的密度分布,于是,该平均场可以表示为
$$ V(r) = \frac{-V_{0}}{1 + \exp(\frac{r-R_{0}}{a})} \, , $$ (33) 其中
$ V_{0} $ 为作用强度,取值大约在$ 50 $ MeV,或者稍大一些;$ R_{0} $ 为原子核的平均半径,可以近似表示为R0=$r_{0} \, A^{1/3} $ ,$ A $ 为原子核的质量数,$ r_{0} \!=\! (1.12 \sim 1.25) $ fm;$ a $ 为原子核的表面厚度,其数值大约为0.65 fm。该平均场位势通常称为Woods-Saxon势。很显然,Woods-Saxon势的形式很复杂,难以由之进行计算(尤其在过去计算机资源不够发达的时代)。考察Woods-Saxon势随径向坐标
$ r $ 的变化行为知,Woods-Saxon势表述的平均有心力场的径向变化行为介于方势阱势和谐振子势之间,因此人们通常采用谐振子势近似模拟核子所受的平均场,也可以由(无限深)球方势阱近似模拟核子所受的平均场。考察Woods-Saxon势的形式知,这一平均场仅考虑了其它核子的分布提供的平均相互作用,既没有包含质子与中子之间的差异,也没有包含质子与质子之间的库仑排斥作用。于是,人们提出考虑上述两种因素、从而对核子所处平均场进行修正的方案:考虑前一因素的修正称为(不)对称能修正,仍是目前研究的一个热点,因为其在饱和核物质密度之上的行为不清楚;考虑后一因素的修正即通常的库仑能修正。再者,由于原子核内的组分粒子除了由平均场决定的空间运动自由度之外,还有自旋自由度,从经典物理的角度考虑,自旋磁矩会受到相对运动在其所在处产生的磁场的作用,由于磁场的磁感应强度正比于相对运动的轨道角动量
$ {{\,l}} $ ,而自旋磁矩正比于自旋$ {{s}} $ ,于是轨道角动量与自旋之间有形如$ {{l}}\cdot {{s}} $ 的自旋-轨道耦合作用。再考察Woods-Saxon势随径向的变化率(梯度)知,该梯度在核内部区域基本为$ 0 $ ,在核表面具有很大的正的数值,于是自旋-轨道耦合作用可表述②为$$ V_{sl} = - \xi(r) \hat{{{s}}} \cdot \hat{{{l}}} = - \frac{1}{2 m^{2} c^{2}} \frac{1}{r} \frac{{\rm d} V(r)}{{\rm d} r} \; \hat{{{s}}} \cdot \hat{{{l}}} \text{。} $$ 该修正最早由Mayer夫人和Jensen分别提出(他们因此获得1963年的诺贝尔物理学奖)。从对称性的角度看,即考虑对称性破缺
$ {\rm{SO}}_{l}(3) \otimes {\rm{SU}}_{s}(2) \supset {\rm{SO}}_{j}(3) $ 的贡献。(3) 单粒子能级和壳结构
所谓单粒子能级,即假设原子核的状态仅由在所有其它核子形成的平均场中运动的一个核子的状态描述的情况下的能级。
在求解平均场近似的单粒子能谱的基础上,考虑上述自旋-轨道耦合引起的能级分裂效应(与原子中的表现不同,在原子核中,总角动量量子数
$ j \!=\! l+\frac{1}{2} $ 的态的能级向下分裂),人们得到可以描述原子核的幻数2, 8, 20, 28, 50, 82等的单粒子能谱(任何一本核结构理论书中都有,这里不再引述),这说明,原子核的单粒子能谱具有壳层结构。因此,相应的模型常被称为单粒子壳模型。近年的研究表明,极端丰中子原子核和极端丰质子原子核的单粒子能谱(壳结构)偏离通常的单粒子能谱,即出现新的壳结构(例如,通常情况下的子壳成为主壳),这种现象称为壳融化。有关滴线核的壳结构的研究是当代核物理的重要研究内容。 -
如前所述,壳模型的基本思想是把每个核子的运动都看作是在其它核子形成的平均场中的运动,并且通常将该平均场近似为有心力场,例如Woods-Saxon势的形式。显然,对于满壳外有多个核子的情况,求解式(32)所示的哈密顿量的本征方程很困难,即采用坐标表象很难实现具体计算。因此人们采用占有数表象处理这一复杂问题。
占有数表象中,包含核子(费密子)的单体和两体相互作用并且保持粒子数守恒的哈密顿量可以写为
$$ H = E_0+ \sum\limits_{\alpha\beta } {\varepsilon _{\alpha \beta } } a_\alpha ^{\dagger} a_\beta + \sum\limits_{\alpha \beta \gamma \delta } {\frac{1}{2}} u_{\alpha \beta \gamma \delta } a_\alpha ^{\dagger} a_\beta ^{\dagger} a_\gamma a_\delta \, , $$ (34) 其中
$ a^{\dagger}_{\alpha} $ 、$ a_{\beta} $ 分别为角动量为$ j_{\alpha} $ 、$ j_{\beta} $ 的核子的产生、消灭算符,服从费密子的反对易规则。为保证宇称守恒,这些核子所处单粒子“轨道”的轨道角动量须满足$ l_{\alpha} + l_{\beta} +l_{\gamma} + l_{\delta} = $ 偶数。显然,作为多费米子的束缚态的原子核具有$ U\big[\sum_{i}(2j_{i}^{}+1)\big] $ 对称性,其中的求和包括对所有可能的单粒子轨道求和。如果考虑同位旋对称性,则有$ U\big[\sum_{i}(4j_{i}^{}+2)\big] $ 对称性。通常,人们也将之表示为多极展开的形式,即有
$$ H = E_0+ \sum\limits_{\alpha} {\varepsilon _{\alpha } } \hat{n}_{\alpha} + \sum\limits_{K} {\Lambda_{K}} ( a_{\alpha} ^{\dagger} \tilde{a}_{\gamma})^{K} \cdot ( a_{\beta}^{\dagger} \tilde{a}_{\delta} )^{K} \, , $$ (35) 其中
$ \hat{n}_{\alpha} = \sum \limits_{m_{\alpha}}a^{\dagger}_{l_{\alpha}m_{\alpha}} a_{l_{\alpha}m_{\alpha}} $ 为单粒子轨道$ j_{\alpha} $ 上的核子数算符,$ \Lambda_{K} $ 为$ K $ 极相互作用强度,$ \tilde {a}_{\alpha} = ( - 1)^{j_{\alpha} + m_{\alpha}} a_{l_{\alpha}(-m_{\alpha})} $ 为与$ a^{\dagger}_{l_{\alpha}m_{\alpha}} $ 共轭的$ j_{\alpha} $ 秩不可约张量,$ [ {A B} ]^{K} $ 表示$ A $ 和$ B $ 两个不可约张量耦合而成的$ K $ 秩不可约张量。即有$$ [ {A^{\lambda}\, B^{{\lambda }'}} ]_{M}^{K} = \sum\limits_{m{m}'} {\left\langle {\lambda m{\lambda }'} \right.{m}'\left| {KM} \right\rangle A_{\lambda m} B_{{\lambda }'{m}'} } \text{。} $$ (36) 其中求和中的系数
$ \left\langle {\lambda m{\lambda }'} \right.{m}'\left| {KM} \right\rangle $ 为CG系数。$ (A^\lambda \cdot B^\lambda ) $ 表示两个不可约张量$ A $ 与$ B $ 的标量积。总核子数为
$ N $ 、总角动量为$ J $ 的核态的波函数可以一般地表述为$$ \big| {N, J} \big\rangle = \sum\limits_{ \begin{array}{*{20}{c}} n_{\mu} \tau_{\mu} \\ \alpha_{\mu} J_{\mu} \kappa \end{array}} {C_{n_{\mu} \tau_{\mu} \alpha_{\mu} J_{\mu} \kappa } } \big{|} {\prod\limits_{ \begin{array}{*{20}{c}} n_{\mu} \tau_{\mu} \\ \alpha_{\mu} J_{\mu} \kappa \end{array}} \big{|} n_{\mu} \tau_{\mu} \alpha_{\mu} J_{\mu} \big{\rangle} ; \kappa ; J } \big{\rangle} \, , $$ (37) $ C_{n_{\mu} \tau_{\mu} \alpha_{\mu} J_{\mu} \kappa} $ 为需要通过求解确定的系数,$ \big{|} \prod\limits_{n_{\mu} \tau_{\mu} \alpha_{\mu} J_{\mu} \kappa } \big{|} n_{\mu} \tau_{\mu} \alpha_{\mu} J_{\mu} \big{\rangle} ; \kappa ; J \big{\rangle} $ 为波函数的基,其中$ n_{\mu} $ 为单核子轨道$ j_{\mu} $ 上的核子数,$ \tau_{\mu} $ 为单核子总角动量为$ j_{\mu} $ 的核子的辛弱数(即不配成角动量为$ 0 $ 的对的粒子数),它可以由$ {\rm{U}}(N) $ 的$ {\rm{IRREP}} $ $ [1^n] $ 按群链$ {\rm{U}}(N) \supset {\rm{SP}}(N) $ 约化[即$ [1^{n_{\mu}}] = \oplus_{\tau_{\mu}} (1^{{\tau}_{\mu}}) $ ]的规则确定。记$ n = \min (n_{\mu}, N-n_{\mu}) $ ,其约化分支律如式(22)所示。$ \alpha_{\mu} $ 为区分$ n_{\mu} $ 、$ \tau_{\mu} $ 、$ J_{\mu} $ 都相同的态的附加量子数,$ \kappa $ 为区分各相同的$ n_{\mu} $ 、$ \tau_{\mu} $ 、$ \alpha_{\mu} $ 、$ J_{\mu} $ 耦合成的相同的$ J $ 的附加量子数。为具体求解并确定由多个(价)费米子形成的原子核的状态和性质(波函数、能谱、电磁极矩和电磁跃迁强度等),我们需要先选定描述系统状态的基矢,计算并确定哈密顿量在相应基矢空间中的哈密顿量矩阵,进而对角化前述的哈密顿量矩阵、确定相应状态的能量和相应的波函数(即确定前述的
$ C_{n_{\mu} \tau_{\mu} \alpha_{\mu} J_{\mu} \kappa} $ );然后通过计算电磁多极矩算符的矩阵元,进而确定系统的电磁性质。具体地,我们首先确定上述基矢,然后计算出所有的矩阵元,再求解线性方程组。为确定基矢,我们需要采用4.1.2小节所述的方法确定全同的角动量为$ j_{\mu} $ 的核子耦合形成的总角动量$ J_{\mu} $ 和相应的重复度$ \eta_{\mu} $ ,从而,取$ \alpha_{\mu} \in [1, \, \eta_{\mu}] $ 即可确定附加量子数。为确定矩阵元,我们先通过插入完备集将问题转化为计算单体算符的矩阵元$ \langle {j_{\mu}}^{n_{\mu}} \, \tau_{\mu} \, \alpha_{\mu} \, L_{\mu} \big{|} a^{\dagger}_{\mu} \big{|} {j_{\mu}}^{n_{\mu}-1} \, \tau_{\mu}^{\prime} \, \alpha_{\mu}^{\prime} \, L_{\mu}^{\prime} \rangle $ 和$ \langle {j_{\mu}}^{n_{\mu}} \, \tau_{\mu} \, \alpha_{\mu} \, L_{\mu} \big{|} \tilde{a}_{\mu} \big{|} {j_{\mu}}^{n_{\mu}+1} \, \tau_{\mu}^{\prime} \, \alpha_{\mu}^{\prime} \, L_{\mu}^{\prime} \rangle $ 等。利用4.1.3小节所述的方法,我们可以很好地解决这一问题。进而求解能量本征方程,确定原子核的能量本征值和本征函数。再进而,利用所得波函数,再利用4.1.3小节所述的方法计算单体矩阵元,即可确定确定原子核的电磁性质(磁矩、电多极矩(电偶极矩、电四极矩、电八极矩等)、电磁跃迁强度(几率)等)。 -
(1) 物理思想
人们知道,多数原子核由核子(包括质子和中子)组成,相当一部分原子核还包含超子,核子和超子都是费米子,因此原子核是一个包含多个费米子的量子束缚系统。但直接在费米子层次上对原子核的性质进行研究遇到模型空间太大等问题。值得庆幸的是,集体运动等现象表明,原子核内的组分粒子具有配对的现象。于是人们引入BCS(Bardeen-Cooper-Schrieffer)方法、无规位相近似(RPA)方法等进行研究,并发展建立了相互作用玻色子近似方法(IBA,下节对之予以介绍),并在具体的研究中取得巨大成功。虽然可以通过玻色映射方法在IBA与壳模型建立起联系,但其微观基础仍需探究。于是人们直接从构建费米子对出发研究原子核的结构等性质,从而实现建立既有小的模型空间、又有清楚确定的微观基础的模型理论的目标。这样的具体描述费米子对系统的动力学对称性等性质的理论模型,按其发展过程,分别称为Ginocchio模型[39]、费米子动力学对称模型[40]、
$ SD $ 对壳模型[41]等。(2) 代数结构与动力学对称性
基于原子核集体运动源于对关联的基本观点(实际上,定量的关系不久前才建立[42])和IBA对很多原子核的结构和性质描述的成功(考虑到其微观基础不很清楚,人们常称之为IBM),人们得知,由核子配成的角动量为0的
$ S $ 对和角动量为2的$ D $ 对对原子核的性质具有决定性的作用(当然,对高自旋、大形变等原子核态,还需要$ G $ 对等高角动量对。为统一描述偶宇称态和奇宇称态,还需要$ F $ 对和$ P $ 对。下面仅以由$ S $ 对和$ D $ 对构成的系统为例进行具体讨论)。考虑对两个全同的费米子构成$ S $ 对和$ D $ 对进行描述的方便,且避免描述单核子态$ \big{\vert} j m \big{\rangle} $ 时核子的轨道角动量$ l $ 不完全确定的问题,人们将单核子总角动量$ j $ 视为由$ k $ 部分与$ i $ 部分简单叠加而成,即有单核子态的$ k $ –$ i $ 基表述$$ a_{jm_{j}}^{\dagger} = \sum \limits_{m \mu} \langle k\, m \; i\, \mu \big{\vert} j \, m_{j} \rangle b_{kmi\mu}^{\dagger} \, , $$ 其中
$ k $ 称为赝轨道(角动量)量子数,$ i $ 称为赝自旋量子数,$ a_{jm_{j}}^{\dagger} $ 、$ b_{kmi\mu}^{\dagger} $ 分别为通常的壳模型中的单核子态产生算符、$ k $ –$ i $ 基下的单核子态产生算符。于是,核子对有由$ k $ 活跃形成的对$$ S_{k}^{\dagger} = \sqrt{\frac{\Omega_{ki}^{}}{2}} \big{(} b_{ki}^{\dagger} b_{ki}^{\dagger} \big{)}^{00}_{00} \, , \quad D_{k}^{\dagger} = \sqrt{\frac{\Omega_{ki}^{}}{2}} \big{(} b_{ki}^{\dagger} b_{ki}^{\dagger} \big{)}^{20}_{m0} \, , $$ 和由
$ i $ 活跃形成的对$$ S_{i}^{\dagger} = \sqrt{\frac{\Omega_{ki}^{}}{2}} \big{(} b_{ki}^{\dagger} b_{ki}^{\dagger} \big{)}^{00}_{00} \, , \quad D_{i}^{\dagger} = \sqrt{\frac{\Omega_{ki}^{}}{2}} \big{(} b_{ki}^{\dagger} b_{ki}^{\dagger} \big{)}^{02}_{0m} \text{。} $$ 其中
$ \Omega_{ki}^{} \!=\! \frac{1}{2}(2 k + 1)(2i +1) $ 。为保证这样的
$ S $ 对和D对具有费米子对的基本性质(全反对称),$ k $ 和$ i $ 的取值只能是$ \quad k \!=\! 1 \, , \quad i \!=\! \frac{3}{2} \text{。} $ 核子之间除有配对现象和对作用(
$ S^{\dagger} S $ 、$ D^{\dagger} \cdot D $ 、等,其中$ S $ 、D为相应对湮灭算符)外,还有多极作用(如(35)式示)。核子的多极(矩)算符也有$ k $ 活跃和$ i $ 活跃两种构成方式,它们是$$ P_{k,q}^{ R} = \sqrt{\frac{\Omega_{ki}^{}}{2}} \big{(} b_{1i}^{\dagger} \tilde{b}_{1i}^{} \big{)}^{R0}_{q0} \, , \quad (R = 0 , 1, 2) \, , $$ $$ \;\; P_{i,q}^{ R} = \sqrt{\frac{\Omega_{ki}^{}}{2}} \big{(} b_{k\frac{3}{2}}^{\dagger} \tilde{b}_{k \frac{3}{2}}^{} \big{)}^{0R}_{0q} \, , \quad (R = 0, 1, 2, 3) \text{。} $$ $ k $ 活跃情况下,$ S $ 对和D对产生、湮灭算符各$ 6 $ 个,多极(矩)算符共$ 9 $ 个,总共$ 21 $ 个算符。具体计算这些算符的对易关系可知,它们构成sp(6)李代数。由此可知,这样的系统具有SP(6)对称性。$ i $ 活跃情况下,$ S $ 对和D对产生、湮灭算符也各$ 6 $ 个,多极(矩)算符共$ 16 $ 个,总共$ 28 $ 个算符。具体计算这些算符的对易关系知,它们构成so(8)李代数。由此知,这样的系统具有SO(8)对称性。显然,还可能有
$ i $ 和$ k $ 都活跃的情况。这种情况下,系统的最大对称群为SO(24)。更一般地,如前所述,最大对简并度为$ \Omega \!=\! \frac{2 j +1}{2} $ 的系统的最大费米子动力学对称性群为$ {\rm{SU}}(4\Omega) $ 。中重核的每一壳层除具有正常的单核子态外,还有入侵态(由自旋-轨道耦合作用导致高
$ l $ 的能级降低很多所致,例如pf壳中的$ g_{9/2}^{} $ 态即为入侵态),常称之为非正常态。为考虑入侵态与正常态的区别,记之只能耦合成角动量为$ 0 $ 的对,其对产生算符为$$ {{\cal{S}}}^{\dagger} = \sqrt{\frac{\Omega_{0}^{}}{2}} \big{(} b_{k i}^{\dagger} b_{k i}^{\dagger} \big{)}^{00}_{00} = \sqrt{\frac{\Omega_{0}^{}}{2}} \big{(} a_{j_{0}^{}}^{\dagger} a_{j_{0}^{}}^{\dagger} \big{)}^{00}_{00}\, , $$ 单极作用算符为
$$ {\cal P}^{0} = \sqrt{\frac{\Omega_{0}^{}}{2}} \big{(} a_{j_{0}^{}}^{\dagger} \tilde{a}_{j_{0}^{}}^{} \big{)}^{0}_{0} = \frac{1}{2} n_{0} \, , $$ 其中
$ \Omega_{0}^{} \!=\! j_{0}^{} + \frac{1}{2} $ 。具体计算对易关系知,
$ \{ {\cal{S}}^{\dagger} \, , {\cal{S}}\, , {\cal P}^{0} \} $ 构成一su(2)李代数。由此知,一个壳层内的非正常态具有$ {\cal SU}(2) $ 对称性。对正常态,当然也有SU(2)对称性。为统一描述角动量为0的对,还引入广义的对产生算符
$ {S^{T}}^{\dagger} $ 和广义单极算符(亦即核子对数算符)$ {P^{0T}} $ $$ {S^{T}}^{\dagger} = S^{\dagger} + {{\cal{S}}}^{\dagger} = \sum \limits_{j} \sqrt{\frac{\Omega_{j}^{}}{2}} \big{(} a_{j}^{\dagger} a_{j}^{\dagger} \big{)}^{0}_{0} \, , $$ $$ {P^{0T}} = P^{0} + {{\cal P}}^{0} = \sum \limits_{j} \sqrt{\frac{\Omega_{j}^{}}{2}} \big{(} a_{j}^{\dagger} \tilde{a}_{j}^{} \big{)}^{0}_{0} \, , $$ 其中求和包括正常单核子态和非正常单核子态。显然,
$ \{ {S^{T}}^{\dagger} \, , S^{T}\, , {P}^{0T} \} $ 也构成一SU(2)李代数,记系统的相应于此的对称性群为$ {\cal SU}^{T}(2) $ 。总之,一个壳层内的态具有
$ \mathrm{SP}(6) \otimes {\cal SU}(2) $ 对称性,或$ {\rm{SO}}(8) \otimes {\cal SU}(2) $ 对称性。这样的直接在费米子层次上考虑配对效应及相互作用的模型称为费米子动力学对称模型(简记为FDSM)[40]。仅考虑正常态而不考虑非正常态(入侵态)的$ k $ –$ i $ 基模型实际在FDSM建立之前由Ginocchio[39]提出,因此常称之为Ginocchio模型(或SO(8)模型、SP(6)模型)。具体分析对易关系知,上述SO(8)群有SO(7)、SO(6)、SO(5)
$ \otimes $ SU(2)等子群,SP(6)群有SU(3)、SU(2)$ \otimes $ SO(3)等子群,因此SO(8)模型有4条动力学对称性群链、SP(6)有3动力学对称性群链。关于这些动力学对称性群链的具体表述、其中各群的生成元、二阶Casimir算子、IRREP及二阶casimir算子的本征值等,限于篇幅,这里不具体列出,有兴趣的读者请参阅原始文献,或文献[2]中的综述。为具体研究原子核的质量、能谱等性质,人们常取某一对称性极限的态为基矢,于是,人们常具体讨论各种动力学对称性极限下的状态。由于非正常态部分比较简单(最大对称群为SU(2)),其与正常态部分的耦合(仅在SU(2)或U(1)层次)也比较简单,因此我们对正常态部分的群链及群表示约化的分支律简要介绍如下。
1) SO(7)动力学对称性
描述SO(8)的破缺到正则子群SO(7)的动力学对称性群链及其中各群的
$ {\rm{IRREP}} $ 的标记为$$ \begin{aligned}& {\rm{SO}}(8) \supset {\rm{SO}}(7) \supset {\rm{SO}}(5) \otimes {\rm{U}}(1) \supset {\rm{SO}}(5) \supset {\rm{SO}}(3) \, , \\& \;\;N_{1}^{} \quad\quad\;\;\; \omega_{1}^{} \quad\quad\;\;\; \tau \quad\quad\;\;\; n_{1}^{}\quad\quad\;\; \tau \quad\;\;\;\;\;\quad L \;\; \end{aligned} $$ 谱生成规则(群表示约化分支律)为:相应于SO(8)的
$ {\rm{IRREP}} $ $ N_{1}^{} \; (\leqslant \frac{\Omega}{2}) $ ,SO(7)的$ {\rm{IRREP}} $ 为$ (\theta_{1}^{} , \, \theta_{2}^{} , \, \theta_{3}^{} ) = ( \omega_{1}^{}, 0, 0 ) = (\omega_{1}^{} ) $ ,其中$$ \omega_{1}^{} = N_{1}^{} - \frac{\omega}{2} = \big{\{} N_{1}^{} , \; N_{1}^{} -1 , \; N_{1}^{} -2 , \; \cdots , \; 1, \; 0 \big{\}} \, ; $$ 其中
$ \frac{\omega}{2} $ 为由正常态费米子配成的$ S $ 对的数目。相应于SO(7)的$ {\rm{IRREP}} $ $ \omega_{1}^{} $ ,SO(5)$ \otimes $ U(1)的$ {\rm{IRREP}} $ 为$$ \begin{split} (\tau , \, \xi ) \otimes [n_{1}^{} ] =& (\tau , 0 ) \otimes [ n_{1}^{} ] = \sum \limits_{l = \omega_{1}^{}}^{N_{1}^{}} \sum \limits_{R = 0}^{\big{[} \frac{l - \omega_{1}^{}}{2} \big{]}} \\&\big{(} l - \omega_{1}^{} - 2 R, \, 0 \big{)} \otimes \big{[} \pm \big{(} N_{1}^{} - \omega_{1}^{} \big{)} \big{]} \, ; \end{split} $$ 相应于SO(5)的
$ {\rm{IRREP}} $ $ \tau $ ,SO(3)的$ {\rm{IRREP}} $ $ L $ 为$$ \begin{split} L =& \tau - 3 n_{\Delta}^{} , \; \tau - 3 n_{\Delta}^{} + 1 , \; \tau - 3 n_{\Delta}^{} + 2 , \cdots , \\& 2(\tau - 3 n_{\Delta}^{}) - 2 , \; 2 (\tau - 3 n_{\Delta}^{} ) \, , \end{split} $$ 其中
$ n_{\Delta}^{} \!=\! 0, \, 1, \, 2, \cdots , \big{[} \frac{\tau}{3} \big{]} $ (物理上,对应于三个费米子形成的总赝自旋为0的集团的数目)。2) SO(6)动力学对称性
描述SO(8)的破缺到正则子群SO(6)的动力学对称性群链及其中各群的
$ {\rm{IRREP}} $ 的标记为$$ \begin{array}{ccccccccc} {\rm{SO}}(8) & \supset & {\rm{SO}}(6) & \otimes & {\rm{U}}(1) & \supset & {\rm{SO}}(5) & \supset & {\rm{SO}}(3) \, , \\ N_{1}^{} & {} & \sigma ^{} & {} & n_{1}^{} & {} & \tau & {} & L \;\; \\ \end{array} $$ 谱生成规则为:相应于SO(8)的
$ {\rm{IRREP}} $ $ N_{1}^{} \; (\leqslant \frac{\Omega}{2}) $ ,SO(6)的$ {\rm{IRREP}} $ 为$ (\sigma_{1}^{} , \, \sigma_{2}^{} , \, \sigma_{3}^{} ) \!=\! ( \sigma, 0, 0 ) \!=\! (\sigma ) $ ,其中$$ \sigma = N_{1}^{} \, , \; N_{1}^{} -2 \, , \; N_{1}^{} - 4 \, , \; \cdots \, , \; 0\, {\text{或}}\, 1 \, ; $$ 相应于SO(6)的
$ {\rm{IRREP}} $ $ \sigma $ ,SO(5)的$ {\rm{IRREP}} $ $ \tau $ 为$$ \tau = \big{\{} \sigma , \; \sigma -1 , \; \sigma -2 , \; \cdots , 1, \; 0 \big{\}} \, ; $$ SO(5)的
$ {\rm{IRREP}} $ $ \tau $ 到SO(3)的$ {\rm{IRREP}} $ $ L $ 的约化规则与前述的相同(下同,不再重述)。3) SO(5)动力学对称性
描述SO(8)的破缺到
$ {\rm{SO}}(5) \otimes {\rm{SU}}(2) $ 的动力学对称性群链及其中各群的$ {\rm{IRREP}} $ 的标记为$$ \begin{array}{ccccccccc} {\rm{SO}}(8) & \supset & {\rm{SO}}(5) & \otimes & {\rm{SU}}(2) & \supset & {\rm{SO}}(5) & \supset & {\rm{SO}}(3) \, , \\ N_{1}^{} & {} & \tau & {} & \nu_{1}^{} & {} & \tau & {} & L \;\; \end{array} $$ 谱生成规则为:相应于SO(8)的
$ {\rm{IRREP}} $ $ N_{1}^{} \; (\leqslant \frac{\Omega}{2}) $ ,记$ \kappa \!=\! N_{1}^{} , \, N_{1}^{} - 1 , \, N_{1}^{} - 2 , \, \cdots , 1 , \; 0 $ ,则SO(5)的$ {\rm{IRREP}} $ $ \tau $ 、SU(2)的$ {\rm{IRREP}} $ $ \nu_{1}^{} $ 分别为$$ \tau = \kappa, \; \kappa -2 , \; \kappa -4 , \; \cdots , 0 \; {\text{或}}\; 1 \, , $$ $$ \nu_{1}^{} = 2 \kappa\text{。} $$ 4) SU(3)动力学对称性
描述SP(6)的破缺到
$ {\rm{SU}}(3) $ 的动力学对称性群链及其中各群的$ {\rm{IRREP}} $ 标记为$$ \begin{array}{ccccccccc} \mathrm{SP}(6) & \supset & {\rm{SU}}(3) & \supset & {\rm{SO}}(3) \, , \\ N_{1}^{} & {} & (\lambda , \; \mu ) & {} & L \;\; \\ \end{array} $$ 谱生成规则为:对SP(6)的
$ {\rm{IRREP}} $ $ N_{1}^{} $ (正常态费米子配成的$ S $ 对和D对数),相应的SU(3)的$ {\rm{IRREP}} $ $ (\lambda , \, \mu) $ 为$$ (\lambda \, , \; \mu ) = (2 N_{1}^{} - 6 p - 4q \, , \; 2 q ) \, , $$ 其中
$ p,\, q $ 为保证$ \lambda\geqslant 0, \; \mu \geqslant 0 $ 的所有非负整数。相应于SU(3)的$ {\rm{IRREP}} $ $ (\lambda , \; \mu) $ ,SO(3)的$ {\rm{IRREP}} $ $ L $ 为$$ L = \bigg{\{} \begin{array}{ll} \lambda + \mu , \; \lambda + \mu - 2 , \; \cdots , 0\; {\text{或}}\; 1, & \; {\text{如果}}K = 0 ; \\ \lambda + \mu , \; \lambda + \mu - 1 , \; \cdots , K + 1, \; K , & \; {\text{如果}}K \neq 0 ; \\ \end{array} $$ 其中
$ K \!=\! \min(\lambda , \mu), \, \min(\lambda , \mu) - 2 , \, \cdots , 0 $ 或$ 1 $ 。5) SU(2)动力学对称性
描述SP(6)的破缺到
$ {\rm{SU}}(2) \otimes {\rm{SO}}(3) $ 的动力学对称性群链及其中各群的$ {\rm{IRREP}} $ 标记为$$ \begin{array}{ccccccc} \mathrm{SP}(6) & \supset & {\rm{SU}}(2) & \otimes & {\rm{SO}}(3) & \supset & {\rm{SO}}(3) \, , \\ N_{1}^{} & {} & \nu _{1}^{} & {} & L & {} & J \;\; \\ \end{array} $$ 谱生成规则为:相应于SP(6)的不可约表示
$ N_{1}^{} $ ,记$ \kappa \!=\! N_{1}^{} , \, N_{1}^{} - 1 , \, N_{1}^{} - 2 , \, \cdots , 1 , \; 0 $ ,则SU(2)的$ {\rm{IRREP}} $ $ \nu_{1}^{} $ 、SO(3)的$ {\rm{IRREP}} $ $ L $ 分别为$$ \nu_{1}^{} = 2 \kappa \, , $$ $$ L = \lambda \, , \; \lambda + 1 \, , \; \lambda + 2 \, , ; \cdots , \; 2\lambda - 2 \, , \; 2\lambda \, , $$ 其中
$$\lambda = \tau \, , \; \tau - 3 \, , \; \tau - 6 \, , \cdots \, , \tau - 3 \big{[} \frac{\tau}{3} \big{]} ; $$ $$\tau = \kappa, \; \kappa -2 , \; \kappa -4 , \; \cdots , 0 \; {\text{或}}\; 1\, \text{。} $$ 从形式上看,相应于实验观测的守恒的角动量的SO(3)的不可约表示为
$ \nu_{1}^{} \otimes L $ 对应的各种$ J $ ,事实上,从前述不同种类的费米子对的数目及角动量的关系知,$ J = L $ 。具体讨论系统的能谱时,一般采用的方案是,把某一动力学对称性下的系统的哈密顿量表述为动力学对称性群链中各群的Casimir算子的线性叠加的形式(考虑单体和两体相互作用情况下,对Casimir算子仅需考虑到二阶),将根据前述的谱生成规则确定的各群的
$ {\rm{IRREP}} $ (标记系统状态的量子数)代入Casimir算子的本征值的表达式,即可确定系统的能谱。由前述的谱生成规则知,FDSM的SO(7)、SO(5)和SU(2)动力学对称性的能谱对应于振动谱,SU(3)动力学对称性的能谱对应于转动谱。将系统的跃迁算符表述为系统的对称性群的生成元的线性叠加,利用群表示的直积约化规则,即可得到相应的跃迁矩阵元,进而即可得到可与实验测量结果比较的跃迁几率。对于实际的原子核,由于其中组分粒子间的相互作用的复杂性,严格具有上述某一动力学对称性极限的极少,从而通常都是处于两种或多种动力学对称性混合(或者说,两种或多种动力学对称性间的过渡)的状态。与通常的求解量子力学的本征值问题一样,人们常取具有某一动力学对称性(例如,SO(7))的波函数作为基。系统的哈密顿量常记为
$$ \begin{split} \hat{H} =& \varepsilon_{0}^{} \hat{n}_{0}^{} + \varepsilon_{1}^{} \hat{n}_{1}^{} + \sum \limits_{\phi, \phi^{\prime}} G_{0}^{\phi \phi^{\prime}} S_{\phi}^{\dagger} \cdot S_{\phi^{\prime}} +\\& \sum \limits_{\phi, \phi^{\prime}} G_{2}^{\phi \phi^{\prime}} D_{\phi}^{\dagger} \cdot D_{\phi^{\prime}}+ \sum \limits_{r, \phi, \phi^{\prime}} B_{r}^{\phi \phi^{\prime}} P_{\phi}^{r} \cdot P_{\phi}^{r} \text{。} \end{split} $$ 按照4.1.3节所述的方法计算出各单体算符的矩阵元,进而即可确定相互作用的哈密顿量,并求得其本征值和本征波函数。实际求解需要极大的数值计算工作量。
FDSM不仅已在描述原子核的性质方面获得成功,还已被推广到描述超导态及其相变(文献[43]等),并有可能描述量子霍尔效应(例如,文献[44]等)。限于篇幅,这里不予具体介绍。关于超导方面的应用,可参阅原始文献,也可参阅文献[2]中的综述。
-
前已提及,原子核具有多种不同模式的集体运动,相应地,原子核呈现不同的形状。对短程剩余相互作用的分析表明,同一子壳中的一对核子有很强的倾向组成
$ L \!=\! 0 $ 、2的核子对。对玻色展开方法的深入研究表明,偶偶核低能集体运动态的性质主要由这些满壳层外价核子所组成的核子对、并且粒子数守恒的相互作用决定。于是,对于中重及重偶偶核的低激发偶宇称态,Iachello等[45]采用$ s $ 和$ d $ 玻色子来模拟这些费米子对,唯象地引入它们之间的相互作用,建立了壳模型的相互作用玻色子近似理论。但事实上,这些近似为玻色子的核子对的结构并不完全清楚,因此多数学者称之为相互作用玻色子模型(简称IBM)。由于玻色子数守恒,IBM具有确定的对称性(据此,人们称之为一种代数模型),于是人们可以从群结构角度出发构造Hamiltonian和相应的波函数,研究其动力学对称性破缺。并且,利用相干态理论研究原子核的集体运动模式和形状相变。本节简要介绍IBM的物理思想、理论框架、最简单的相互作用玻色子模型(IBM1)、IBM在原子核集体运动模式及形状相变研究中的应用。 -
(1) 基本思想与物理假定
相互作用玻色子模型的基本思想很简单,它假设偶偶原子核包含一个不活泼的核心(双满壳)和偶数个价核子;这些价核子两两配成对,这些核子对可以看作是玻色子,这些玻色子之间有相互作用;玻色子的数目等于满壳外价核子数的一半或价空穴数的一半(分别对应于价核子不超过、超过半满壳的原子核)。
(2) 理论框架与分类
1) 理论框架结构
$ \langle i \rangle $ 哈密顿量记角动量分别为
$ l_{\alpha} $ 、$ l_{\beta} $ 的玻色子的产生、湮灭算符分别为$ b^{\dagger}_{\alpha} $ 、$ b_{\beta} $ ,则包含玻色子的单体和两体相互作用并且保持粒子数守恒的哈密顿量可以表述为$$ H = E_0+ \sum\limits_{\alpha\beta } {\varepsilon _{\alpha \beta } } b_\alpha ^{\dagger} b_\beta + \sum\limits_{\alpha \beta \gamma \delta } {\frac{1}{2}} u_{\alpha \beta \gamma \delta } b_\alpha ^{\dagger} b_\beta ^{\dagger} b_\gamma b_\delta \text{。} $$ (38) 为保证宇称守恒要求
$ l_{\alpha} + l_{\beta} +l_{\gamma} + l_{\delta} \!=\! $ 偶数。通常,人们也将之表示为多极展开的形式,即有$$ H = E_0+ \sum\limits_{\alpha\beta } {\varepsilon _{\alpha \beta } } b_\alpha ^{\dagger} b_\beta + \sum\limits_{K} {\Lambda_{K}} ( b_{\alpha} ^{\dagger} \tilde{b}_{\gamma})^{K} \cdot ( b_{\beta}^{\dagger} \tilde{b}_{\delta} )^{K} \, , $$ (39) 其中
$ \Lambda_{K} $ 为$ K $ 极相互作用强度,$ \tilde {b}_{\alpha} \!=\! ( -1)^{l_{\alpha} + m_{\alpha}} b_{ l_{\alpha}(-m_{\alpha})} $ 为与$ b^{\dagger}_{l_{\alpha}m_{\alpha}} $ 共轭的$ l_{\alpha} $ 秩不可约张量,$ [ {A B} ]^{K} $ 表示$ A $ 和$ B $ 两个不可约张量耦合而成的$ K $ 秩不可约张量(耦合规则如式(36)所示),$ (A^\lambda \cdot B^\lambda ) $ 表示两个同秩不可约张量$ A $ 与$ B $ 的标量积。$ \langle ii \rangle $ 波函数总玻色子数为
$ N $ 、总角动量为$ L $ 的状态的波函数可以一般地表示为$$ \left| {N, L} \right\rangle = \sum\limits_{n_\mu \tau_{\mu} \alpha_{\mu} } {A_{n_{\mu} \tau_{\mu} \alpha_{\mu} } } \Big{|} \prod\limits_{n_{\mu} \tau_{\mu} \alpha_{\mu}} \big[\big{|} n_s ; n_{\mu} \tau_{\mu} \alpha_{\mu} L_{\mu} \big{\rangle} \big] \, \kappa ; L \Big{\rangle} \, , $$ 其中
$ n_s \!=\! N - \sum\limits_\mu {n_\mu} $ 为系统中的$ s $ 玻色子数,$ n_{\mu} $ 为角动量为$ l_{\mu} $ 的玻色子数,$ \tau_{\mu} $ 为角动量为$ l_{\mu} $ 的玻色子的辛弱数(即不配成角动量为$ 0 $ 的对的粒子数),$ \alpha_{\mu} $ 为区分$ n_{\mu} $ 、$ \tau_{\mu} $ 、$ L_{\mu} $ 都分别相同的态的附加量子数,其数值取$ 1 $ 到由$ \tau_{\mu} $ 约化到$ L_{\mu} $ ($ {\rm{SO}}(2 l_{\mu}+1) $ 到$ {\rm{SO}}(3) $ 的约化)的重复度$ \eta_{\mu} $ 之间的各种值($ \eta_{\mu} $ 的值由4.1.2节所述的方法确定。$ \eta_{\mu} \!=\! 0 $ 说明相应的态不存在)。系数$ A_{n_{\mu} \tau_{\mu} \alpha_{\mu}} $ 通过对角化哈密顿量确定。$ \langle iii \rangle $ 跃迁算符为了研究原子核的电磁性质及能级间的电磁跃迁,还要研究玻色子与电磁场的相互作用。局限于单体相互作用的跃迁算符可以用玻色子的产生、湮灭算符耦合成的不可约张量表述为
$$ T_{\mu} ^{K} = t_0^0 \delta _{K0} + \sum\limits_{l{l}'} {t_{l{l}'}^{K} } [ {b_l^{\dagger} \tilde {b}_{l'} } ]_{\mu} ^{K} \text{。} $$ (40) 对这一表述中的秩数
$ K $ 具体化,即有E0、M1、E2、M3、E4等跃迁的算符,由之即可计算原子核的相应极次的电磁(约化)跃迁几率和多极矩(例如,电四极矩、磁矩、电偶极矩等)等电磁性质。并可利用多极展开形式简单地表述,例如:$$ \begin{split} \hat{T}_0^{\rm E0} =& {\gamma }'_0 + \sum\limits{\alpha} {\beta }'_0 \hat{n}_{\alpha} \, , \\ \hat{T}_\mu ^{\rm M1} =& {\beta }'_1 \hat{L}_\mu \, , \\ \hat{T}_\mu ^{\rm E2} =& \alpha _2 \hat{Q}_\mu \, , \\ \hat{T}_\mu ^{\rm M3} =& \beta _3 \hat{U}_\mu \, , \\ \hat{T}_\mu ^{\rm E4} =& \beta _4 \hat{V}_\mu \,, \end{split}$$ (41) 其中
$ \hat{L} $ 为角动量算符,$ \hat{Q}_{\mu} \!=\! \hat{Q}^{2}_{\mu} $ 为电四极算符,$ \hat{U}_{\mu} \!=\! \hat{U}^{3}_{\mu} $ 为磁八极算符,$ \hat{Q}_{\mu} \!=\! \hat{V}^{4}_{\mu} $ 为电十六极算符。2) 分类
根据模型中考虑的玻色子的组分,人们将IBM分为IBM1、IBM2、IBM3、IBM4、sdgIBM、spdfIBM、spdfgIBM、IBFM、IBFFM等。
$ \langle i \rangle $ IBM1IBM1即最简单的玻色子组分仅为
$ s $ 和$ d $ 、并且不区分质子玻色子和中子玻色子的相互作用玻色子模型。由于$ s $ 玻色子仅有一个自由度、$ d $ 玻色子有五个自由度,由幺正群的玻色子实现理论知,该系统的最大对称群为U(6),该对称群有三种破缺方式,相应的最大子群分别为U(5)、SU(4)(即SO(6))、SU(3)。$ \langle ii \rangle $ IBM2IBM2为区分质子玻色子和中子玻色子、并且它们的组分都为
$ s $ 玻色子和$ d $ 玻色子的相互作用玻色子模型。分别以$ \pi $ 、$ \nu $ 标记质子玻色子、中子玻色子,则整个原子核的对称性为$ {\rm{U}}_{\pi}(6) \otimes U_{\nu}(6) $ 。考虑$ {\rm{U}}_{\pi}(6) $ 、$ {\rm{U}}_{\nu}(6) $ 的子群结构、并认为这些质子玻色子子群和中子玻色子子群可以在相同的水平上耦合,则知,IBM2下的原子核具有$ {\rm{U}}_{\pi + \nu}(5) $ 、$ {\rm{SO}}_{\pi +\nu}(6) $ 、$ {\rm{SU}}_{\pi + \nu}(3) $ 、$ {\rm{SU}}_{\pi +\nu}^{\ast}(3) $ 四种动力学对称性。显然,IBM2的态空间比IBM1的态空间大了很多,由之可以描述同位旋混合对称态(在IBM2中,人们还常以$ F $ 旋二重态分别标记质子玻色子、中子玻色子)和三轴形变态、剪刀态等奇异核态。限于篇幅,这里不予具体讨论,有兴趣深入了解的读者可以参阅龙桂鲁的博士论文(清华大学,1987年)[46]。$ \langle iii \rangle $ IBM3和IBM4前述的IBM1和IBM2都仅适用于描述重核和中重核的低激发态的性质。对于轻核,价质子和价中子处于相同的大(主)壳,那么,为了利用相互作用玻色子模型研究轻核的低激发态的性质,在考虑质子玻色子和中子玻色子(对应核子对的同位旋的第三分量分别为
$ -1 $ 、$ +1 $ )的同时,还需要考虑质子中子玻色子(相应核子对的同位旋的第三分量为$ 0 $ )。由于核子为费密子,在考虑玻色子是核子对的近似的本质下,我们需要考虑泡利原理的限制,于是玻色子可以分为自旋$ s\!=\! 0 $ 、同位旋$ \tau\! =\! 1 $ 与自旋$ s \!=\! 1 $ 、同位旋$ \tau \!=\! 0 $ 的两类。仅考虑自旋$ s \!= \!0 $ 、同位旋$ \tau \!=\! 1 $ 的玻色子的IBM称为IBM3,既考虑自旋$ s \!=\! 0 $ 、同位旋$ \tau \!=\! 1 $ 的玻色子又考虑自旋$ s \!=\! 1 $ 、同位旋$ \tau \!=\! 0 $ 的玻色子的IBM称为IBM4。由前述讨论知,IBM4中的玻色子的自旋-同位旋空间为6维,即有
$ {\rm{U}}_{ST}(6) $ 对称性。在简单的仅考虑角动量分别为$ 0 $ 、$ 2 $ 的$ s $ 、$ d $ 玻色子的情况下,原子核的最大对称性则为$ {\rm{U}}(36) \supset {\rm{U}}_{sd}(6) \otimes {\rm{U}}_{ST}(6) $ 。由于$ {\rm{U}}_{sd}(6) $ 具有$ {\rm{U}}(5) $ 、$ {\rm{SO}}(6) $ 、$ {\rm{SU}}(3) $ 三种动力学对称性,而$ {\rm{U}}_{ST}(6) $ 具有$ {\rm{SU}}_{ST}(3) $ 和$ {\rm{SO}}_{S}(3)\otimes {\rm{SO}}_{T}(3) $ 两种动力学对称性,在相同对称性层次上耦合而成的原子核的对称性则有$ {\rm{SU}}(3) $ 和$ {\rm{SO}}(3) $ 两种。由于质子中子玻色子可以由偶数个价核子中的核子形成,也可以由奇数个价核子中的核子形成,因此IBM4既适用于轻偶偶核,也适用于轻奇奇核。有关具体讨论请参见文献[47],这里不再细述。$ \langle iv \rangle $ sdgIBM为描述稀土区大形变原子核的性质和十六极形变核的性质,人们提出不仅需要
$ s $ 玻色子和$ d $ 玻色子,还需要考虑角动量为4的$ g $ 玻色子,从而提出了sdg相互作用玻色子模型。sdgIBM具有U(15)对称性,并具有SU(6)、SU(5)、SU(3)三种动力学对称性群链,较系统的讨论请见文献[48]。将通常由最大子群的全对称表示的态空间描述原子核低激发态性质的研究方案推广到考虑非全对称表示,利用sdgIBM的SU(5)对称性较好地描述了超形变核态的转动带的性质[49]。$ \langle v \rangle $ spdfIBM与spdfgIBM为统一描述原子核的四极形变和具有空间反演不对称性的八极形变态,人们引入
$ f $ 玻色子和$ p $ 玻色子,建立了spdf相互作用玻色子模型。spdfIBM的最大对称群为U(16),它具有142条具有物理意义的群链(不仅具有U(15)、O(16)、SU(5)、O(6)、SU(3)动力学对称性,还具有O(10)和O(4)等动力学对称性),较详细的讨论请参见刘玉鑫的博士论文(清华大学,1992年)[50]。将偶宇称部分扩展到还包含$ g $ 玻色子,即有spdfgIBM.$ \langle vi \rangle $ IBFM与IBFFM为利用IBM的思想和方法研究奇-A核低激发态的性质,人们提出了相互作用玻色子-费密子模型(简称IBFM),其基本思想是将偶偶部分近似为玻色子系统,单个的(或拆对的)核子(费米子)与玻色子部分之间有相互作用。IBFM中,原子核的最大对称群是
$ {\rm{U}}^{B}(m) \otimes {\rm{U}}^{F}(n) $ ,其中$ m \!=\! \sum\limits_{l_{i}}(2l_{i}+1) $ ($ l_{i} $ 为所考虑的玻色子的各个组分的单粒子角动量),$ n \!=\! \sum\limits_{j_{i}}(2j_{i}^{}+1) $ ($ j_{i}^{} $ 为所考虑的单核子可能占据的核子的各单粒子组态的角动量)。这些玻色子的对称群与费密子的对称群可以耦合成超对称群,从而原子核具有动力学超对称性。对玻色子部分考虑最简单的U(6)对称性,对费密子考虑不同的单粒子轨道,提出了U(6/4)($ j \!=\! \frac{3}{2} $ )、U(6/6)($ j \!=\! \frac{3}{2} $ 、$ \frac{1}{2} $ )、U(6/12)($ j \!=\! \frac{1}{2} $ 、$ \frac{3}{2} $ 、$ \frac{5}{2} $ )、U(6/20)($ j \!=\! \frac{1}{2} $ 、$ \frac{3}{2} $ 、$ \frac{5}{2} $ 、$ \frac{7}{2} $ )等动力学超对称性,并且实验上找到了一些具有动力学超对称性的原子核。有兴趣深入探讨的读者可参见文献[51-52]等。将IBFM的思想进一步扩展,人们还提出了IBFFM,较好地描述了一些奇奇核的低激发态性质。
-
上小节的概述表明,IBM1是不区分质子玻色子和中子玻色子、且组分仅包括
$ s $ 和$ d $ 玻色子的相互作用玻色子模型,因此,IBM1是最简单的IBM。由于其简单,人们对IBM1的认识最深入最清楚。相应地,应用也最广泛。因此,本小节对之给予较具体的讨论。(1) 理论框架
1) 哈密顿量
由式(38)或式(39)所示的IBM的哈密顿量的一般形式可知,仅包含
$ s $ 和$ d $ 玻色子的IBM1的哈密顿量可以表述为$$ \begin{split} H = & h'_0 + \varepsilon '_d (d^{\dagger} \cdot \tilde d) + \\ & \frac{1} {2}\sum\limits_{K = 0,2,4} {\sqrt {2K + 1} C'_{K} \left[ {\left[ {d^{\dagger} d^{\dagger} } \right]^{K} \left[ {\tilde d\tilde d} \right]^{K} } \right]^0 }+ \\ & v_0 \left\{ {\left[ {d^{\dagger} d^{\dagger} } \right]^0 \left[ {ss} \right]^0 + h.c.} \right\} + \\ & v_2 \left\{ {\left[ {\left[ {d^{\dagger} d^{\dagger} } \right]^{2} \big{[} \tilde{d} s \big{]}^{2} } \right]^{0} + h.c.} \right\} \text{。} \end{split} $$ (42) 该式表明,除去
$ {h}'_{0} $ 外,该模型只有六个可调节的参量,因此最一般情况下的IBM1是一个六参数的模型。在实际应用中也常采用多极展开形式:$$\begin{split} H =&{ {{E'}_0} + \varepsilon {n_d} + {c_1}(\hat L \cdot \hat L) + {c_2}\left[ {\hat Q(\chi ) \cdot \hat Q(\chi )} \right] + }\\ &{{c_3}(\hat U \cdot \hat U) + {c_4}(\hat V \cdot \hat V),} \end{split}$$ (43) 其中
$$ \begin{align} \hat{n}_{d} & = (d^{\dagger} \cdot \tilde d) \, , \\ \hat{L}_{q} & = \sqrt {10} [ {d^{\dagger} \tilde d} ]^1_q \, , \\ \hat{Q}_{\mu} (\chi) & = [ {d^{\dagger} \tilde s + s^{\dagger} \tilde d} ]^2_\mu + \chi [ {d^{\dagger} \tilde d}]^2_\mu \, , \\ \hat{U}_{\mu} & = [ {d^{\dagger} \tilde d} ]^3_\mu \, , \\ \hat{V}_{\mu} & = [ {d^{\dagger} \tilde d} ]^4_\mu \text{。} \end{align} $$ 2) 跃迁算符
将上一小节中关于电磁跃迁算符讨论的结果应用到仅有
$ s $ 玻色子和$ d $ 玻色子的情况知,IBM1中的E0、M1、E2、M3、E4跃迁算符可以简单地表示为$$ \begin{split} \hat{T}_0^{\rm E0} =& {\gamma }'_0 + {\beta }'_0 \hat{n}_d \, , \\ \hat{T}_\mu ^{\rm M1} =& g \hat{L}_{\mu} \, , \\ \hat{T}_\mu ^{\rm E2} =& e_{2} \hat{Q}_\mu (\chi) \, , \\ \hat{T}_\mu ^{\rm M3} =& g_{3} \hat{U}_\mu \, , \\ \hat{T}_\mu ^{\rm E4} =& e_{4} \hat{V}_\mu \, , \end{split} $$ (44) 其中
$ g_{i}^{} $ 常被称为转动g因子,$ e_{i} $ 等常被称为相应极次的有效电荷。3) 波函数
将上一小节中关于波函数讨论的结果应用到仅有
$ s $ 玻色子和$ d $ 玻色子的情况可知,IBM1下,总玻色子数为$ N $ 、角动量为$ L $ 的原子核的波函数可以表示为$$ \left| {N, L } \right\rangle = \sum\limits_{n_{d} \tau \alpha } {A_{n_{d} \tau \alpha} \left| {n_s , (n_{d} \tau \alpha) } L \right\rangle }\, , $$ (45) 其中
$ n_{d} $ 为$ d $ 玻色子数,$ n_{s} + n_{d} \!=\! N $ ,$ \tau $ 为$ d $ 玻色子的辛弱数,$ \alpha $ 为区分$ n_{d} $ 、$ \tau $ 、$ L $ 分别相同的态的附加量子数,其数值取$ 1 $ 到由$ \tau $ 约化到$ L $ ($ {\rm{SO}}(5)\supset {\rm{SO}}(3) $ 的约化)的重复度之间的各种值。系数$ A_{n_{d}\tau \alpha} $ 通过对角化哈密顿量确定。(2) 代数结构与动力学对称性极限
在IBM1中,原子核是由
$ s $ 玻色子和$ d $ 玻色子形成的束缚系统,由典型李群的玻色子实现理论可知道,该系统具有确定的对称性,并具有一些动力学对称性极限。1) 对称性群及其Casimir算子
$ s $ 玻色子和$ d $ 玻色子的产生算符及其共轭算符分别为$ 0 $ 秩、$ 2 $ 秩不可约张量,由之构成36个不可约张量:$$ \begin{array}{ll} G_{0}^{0} (s,s) = [ {s^{\dagger} s} ]_0^0 , \quad G_{0}^{0} (d,d) = [ {d^{\dagger} \tilde {d}} ]_0^0 ,& \quad ({\text{各}}\ 1 {\text{个}})\\ G_{\mu} ^{1} (d,d) = [ {d^{\dagger} \tilde {d}} ]_\mu ^1 ,& \quad (3{\text{个}}) \\ G_{\mu} ^{2} (d,d) = [ {d^{\dagger} \tilde {d}} ]_\mu ^2 ,& \quad (5{\text{个}}) \\ G_{\mu} ^{2} (d,s) = [ {d^{\dagger} s} ]_\mu ^2 , \quad G_{\mu} ^{2} (s,d) = [ {s^{\dagger} \tilde {d}} ]_\mu ^2 , & \quad ({\text{各}}\ 5{\text{个}}) \\ G_{\mu} ^{3} (d,d) = [ {d^{\dagger} \tilde {d}} ]_\mu ^3 ,& \quad (7{\text{个}}) \\ G_{\mu} ^{4} (d,d) = [ {d^{\dagger} \tilde {d}} ]_\mu ^4 ,& \quad (9{\text{个}}) \end{array} $$ 计算其间的对易关系知,这36个张量算符(
$ G_{q}^{k} (l,{l}') \!=\! [ {b_l^{\dagger} \tilde {b}_{l'} } ]_{q}^{k} , \; ( {l,{l}' \!=\! 0,2} ) $ )构成U(6)群的生成元。考察U(6)群的上述36个生成元知,该U(6)群有子群U(5)、SO(6)(SU(4))、SU(3)、SO(5)、SO(3),这些子群的无穷小生成元如表1所列。
表 1 IBM1的对称性群链中各子群的生成元
群 生成元 U(5) $[d^{\dagger}\tilde{d}]^{k}_{q} , \qquad k = 0,1,2,3,4$ SU(3) $ \hat{L}_{q}=\sqrt{10}[d^{\dagger} \tilde{d} ]^{1}_{q} \; , \quad \hat{Q}_{\mu}=[d^{\dagger} s + s^{\dagger}\tilde{d}]^{2}_{\mu} - \frac{\sqrt{7}}{2}[d^{\dagger}\tilde{d}]^{2}_{\mu} $ SO(6) $ [d^{\dagger}\tilde{d}]^{1}_{q} , \qquad [d^{\dagger}\tilde{d}]^{3}_{\nu}\, , \qquad [d^{\dagger} s + s^{\dagger}\tilde{d}]^{2}_{\mu} $ SO(5) $[d^{\dagger}\tilde{d}]^{1}_{q} \, , \qquad [d^{\dagger}\tilde{d}]^{3}_{\nu}$ SO(3) $L_{q}=\sqrt{10}[d^{\dagger} \tilde{d} ]^{1}_{q} $ 存在子群SO(3)表明,原子核具有空间转动不变的子空间。再考察各子群的特征知,上述U(6)破缺到表示空间具有转动不变性的群链(以SO(3)结尾)的最大对称群分别为U(5)、SO(6)、SU(3),由此知,IBM1具有三种动力学对称性,相应的对称性群链为:
$$ \begin{array}{l} {\rm{U}}(6) \supset {\rm{U}}(5) \supset {\rm{SO}}(5) \supset {\rm{SO}}(3) \, , \qquad \qquad \qquad ({\rm{I}}) \\ {\rm{U}}(6) \supset {\rm{SU}}(3) \supset {\rm{SO}}(3) \, , \qquad \qquad \qquad \qquad \quad ({\rm{I}}{\rm{I}}) \\ {\rm{U}}(6) \supset {\rm{SO}}(6) \supset {\rm{SO}}(5) \supset {\rm{SO}}(3) \, , \qquad \qquad \quad ({\rm{I}}{\rm{I}}{\rm{I}}) \end{array} $$ 这些动力学对称性群链中各子群的Casimir算子的算符表达形式及本征值如表2所列。
表 2 对称性群链中各子群的Casimir算子及其本征值
阶数 表达形式 本征值 $C_{1{\rm U}(5)}$ $\sqrt{5} [d^{\dagger}\tilde{d}]^{0}_{0}$ $n_d$ $C_{2{\rm U}(5)}$ $\sum \limits_{k=0}^{4} [d^{\dagger} \tilde{d}]^{k} \cdot [d^{\dagger}\tilde{d})]^{k}$ $n_d (n_d + 4)$ $C_{2{\rm SU}(3)}$ $2 \hat{Q} \cdot \hat{Q} + \frac{3}{4} \hat{L} \cdot \hat{L}$ $\begin{array}{l} \lambda ^2 +\mu ^2 + \lambda \mu\\+3(\lambda + \mu) \end{array}$ $C_{2{\rm O}(6)}$ $\begin{array}{l} [d^{\dagger} s + s^{\dagger}\tilde{d}]^{2}_{\mu} \cdot [d^{\dagger} s + s^{\dagger}\tilde{d}]^{2}_{\mu}\\+ 2\sum \limits_{k=1,3} [d^{\dagger}\tilde{d}]^{k}_{q} \cdot [d^{\dagger}\tilde{d}]^{k}_{q} \end{array}$ $\sigma (\sigma + 4)$ $C_{2{\rm O}(5)}$ $2 \sum \limits_{k=1,3} [d^{\dagger}\tilde{d}]^{k}_{q} \cdot [d^{\dagger}\tilde{d}]^{k}_{q} $ $\tau ( \tau + 3)$ $C_{2{\rm O}(3)}$ $\hat{L} \cdot \hat{L} $ $L(L+1)$ 前已说明,IBM1是一个最多6参量的模型,其哈密顿量最多只有6个独立的项。上述对称性表明,描述IBM1的动力学对称性群链中也只有6个线性独立的Casimir算子
$ C_{1 {\rm{U}}(5)} $ 、$ C_{2 {\rm{U}}(5)} $ 、$ C_{2 {\rm{SO}}(6)} $ 、$ C_{2 {\rm{SU}}(3)} $ 、$ C_{2 {\rm{SO}}(5)} $ 、$ C_{2 {\rm{SO}}(3)} $ ,因此IBM1的哈密顿量还可以由上述Casimir算子表述为$$ \begin{split} H =& {h}''_0 + A_{1}\, C_{1{\rm{U}}(5)} + A_{2}\, C_{2 {\rm{U}}(5)} + A_{3}\, C_{2{\rm{SU}}(3)} + \\& A_{4}\, C_{2{\rm{SO}}(6)} + B \, C_{2{\rm{SO}}(5)} + C\, C_{2{\rm{SO}}(3)} \text{。} \end{split} $$ (46) 注意,这里没有出现U(6)群的Casimir算子,这是因为对于具有确定总玻色子数的状态,U(6)群的Casimir算子的本征值为常量,其贡献已包含在常量
$ {h}''_{0} $ 中。上述讨论表明,IBM1的哈密顿量有正规排列、多极展开和Casimir算子三种表述形式,利用玻色子的产生算符、湮灭算符之间的对易关系和上述各子群的Casimir算子的定义,不难得到这三种表述形式之间的转换关系,这里不再具体列出。
2) 动力学对称性极限
上面给出了IBM1的三个动力学对称性群链,于是可以利用其中某一个群链中各群的不可约表示对应的量子数来标记IBM1中原子核的状态,并对之进行分类。并且,如果哈密顿量只包含某一群链中的群的Casimir算子,则按这一群链表示的态矢就是这一哈密顿量的本征态矢,本征能量就是这些Casimir算子的本征值的线性组合,计算将大大简化。由式(46)知,只需要保持某一动力学对称性群链中各子群的Casimir算子的项中的系数不为
$ 0 $ 就可以实现上述极限情况。下面分别对IBM1的三种动力学对称性极限予以讨论。$ \langle i \rangle $ U(5)极限具有U(5)对称性的哈密顿量为
$$ H = {h}''_0 + A_{1}\, C_{1{\rm{U}}(5)} + A_{2}\, C_{2 {\rm{U}}(5)} + B \, C_{2{\rm{SO}}(5)} + C\, C_{2{\rm{SO}}(3)} , $$ 波函数可以表示为
$ \psi_{ {\rm{U}}(5)}^{} \!=\! \big{|} {N,n_d ,\tau , \alpha, L, M} \big{\rangle} $ ,其中$ N $ 、$ n_{d} $ 、$ \tau $ 、$ L $ 、$ M $ 分别为标记U(6)、U(5)、SO(5)、SO(3)、SO(2)群的IRREP的量子数,其物理意义分别是系统的总玻色子数、$ d $ 玻色子数、不配成角动量为$ 0 $ 的对的$ d $ 玻色子的数、角动量量子数、角动量在$ z $ 方向上的投影量子数,$ \alpha $ 为区分$ N $ 、$ n_{d} $ 、$ \tau $ 、$ L $ 等都分别相同的态的附加量子数,记3个$ d $ 玻色子组合成$ L\!=\! 0 $ 的集团的数目为$ n_{\Delta}^{} $ ,则可取$ \alpha\! =\! n_{\Delta}^{} $ 。由群表示的约化规则可知,U(5)对称性下的谱生成规则(各量子数的取值规则)如下:对一个确定的总玻色子数
$ N $ ,$$ n_{d} = N,\, N - 1, \cdots ,1,\, 0\, ; $$ 对一个确定的
$ d $ 玻色子数$ n_{d} $ ,$$ \tau = n_{d} , \; n_{d} - 2, \cdots ,1 \; {\text{或}}\;0\;(n_d = {\text{奇数}}\; {\text{或}}\;{\text{偶数}}) \, ; $$ 对一个确定的
$ \tau $ (与费米子下的相同),$$ \begin{split} L =& \tau - 3 n_{\Delta}^{} , \, \tau - 3 n_{\Delta}^{} + 1, \, \cdots , \, 2\left( {\tau - 3 n_{\Delta}^{} } \right) - \\&2,\, 2\big{(} {\tau - 3 n_{\Delta}^{} } \big{)} \text{。} \end{split} $$ 该态的能量可以由标记它的量子数表述为
$$ \begin{split} & E \left[ {N,n_{d} ,\tau , n_{\Delta}^{} ,L,M} \right] = E_{0} + A_{1} n_{d}^{} +\\ &\quad A_{2} n_{d}^{} (n_{d}^{} + 4) + B \, \tau ( \tau + 3) + C \, L(L + 1) \text{。} \end{split} $$ (47) 以
$ N \!=\! 3 $ 为例的U(5)对称核的典型能谱及其与$ {^{110} \rm{Cd}} $ 原子核的实验测量能谱的比较如图2所示。
图 2 U(5)动力学对称性的典型能谱(其中上侧标记的量子数为
$(\tau , n_{\Delta}^{})$ ,自下而上各组态分别对应nd=0, 1, 2, 3)及与110Cd的低激发态能谱的实验观测结果的比较(取自文献[53])由图2知,U(5)对称的核态具有非简谐振动的特征,这是因为,按照动力学对称性的概念,哈密顿量中
$ C_{1{\rm{U}}(5)} $ 起主要作用,其它项都是微扰,如果将其它项完全忽略,则为典型的简谐振动。如前所述,在IBM中,E2跃迁算符是保持总玻色子数不变的2秩不可约张量算符,并可一般地表述为
$$ \hat{T}(\rm E2)_{q}^{} = e_{2}^{} \hat{Q}^{2}_{q}(\chi) = e_{2}^{} \{(s^\dagger\tilde{d}+d^\dagger\tilde{s})_{q}^{2} + \chi (d^{\dagger}\tilde{d})_{q}^{2} \}\, , $$ (48) 其中
$ e_{2} $ 、$ \chi $ 是参数,$ e_{2} $ 为有效电荷,$ \chi $ 决定$ \hat{T} $ (E2)$ _{q} $ 中两项的相对重要性,称为$ \hat{T} $ (E2)$ _q $ 的形式参数(或结构参数)。E2跃迁的约化跃迁几率为$$ B({\rm E2}, \, L_i \rightarrow L_f) = \frac{| \langle L_f \| \hat{T}({\rm E2}) \| L_i \rangle |^{2} }{2L_i+1} \text{。} $$ 在U(5)对称性极限下,常取
$ \chi \!=\! 0 $ ,于是有:$$ \hat{T}({\rm E2})_q = e_2(s^\dagger\tilde{d}+d^\dagger\tilde{s})_q^{2}\text{。} $$ 对U(5)对称性核态,计算
$ \hat{T}({\rm E2})_{q} $ 的约化矩阵元则得其E2跃迁的选择定则是$$ \Delta n_d = \pm1\, , \qquad \Delta\tau = \pm 1 \, . $$ 并可得到U(5)极限下各带内及带间的E2跃迁的约化跃迁几率的具体表达式,例如,对
$ \tau \!=\! n_{d} $ 、$ n_{\Delta} \!=\! 0 $ 、带头角动量为0的带(Y$ _{0} $ 带,即基带)内的E2跃迁:$$ L_i = 2n_d+2,L_f = 2n_d;\; \; B({\rm E2}) = e_2^2(n-n_d)(n_d+1)\, ; $$ 对
$ \tau \!=\! n_{d} $ 、$ n_{\Delta} \!=\! 0 $ 、带头角动量为2的带(常称为Y$ _2 $ 带)的带内E2跃迁:$$ L_i = 2n_d,L_f = 2n_d-2;\; \; B({\rm E2}) = {e_2^2(n-n_d)(4n_d+3)\over(4n_d-1)}\text{。} $$ 对
$ {\rm{Y}}_{2}^{} $ 带到$ {\rm{Y}}_{0}^{} $ 带的带间E2跃迁:$$ L_i = 2n_d,L_f = 2n_d;\; \; B({\rm E2}) = {e_2^2(n-n_d)(4n_d+2)\over(4n_d-1)}\text{。} $$ $ \langle ii \rangle $ SU(3)极限具有SU(3)对称性的哈密顿量为
$$ H = E_{0} + A_{3}\, C_{2{\rm{SU}}(3)} + C\, C_{2{\rm{SO}}(3)} \text{。} $$ 相应的态矢为
$$ \; \psi_{ {\rm{SU}}(3)}^{} = \big{|} {[N],(\lambda ,\mu ),K,L,M} \big{\rangle} \, , \;\; $$ 其中
$ (\lambda ,\mu ) $ 、$ L $ 分别为SU(3)群、$ {\rm{SO}}(3) $ 群的IRREP,$ K $ 为由SU(3)到SO(3)约化的附加量子数。根据群表示的约化规则,各量子数取值如下:对一个确定的
$ N $ (总玻色子数),$$ (\lambda\, , \mu) = (2N - 6 p - 4q, 2q )\, ; $$ 其中
$ p\geqslant 0 $ ,$ q\geqslant 0 $ ,且$ \lambda = 2N - 6 p - 4 q \geqslant 0\text{。} $ 对一个确定的表示
$ (\lambda \, , \mu) $ ,$$ K = 0,\,1,\, 2, \, \cdots \, , \, \min \{\lambda ,\mu \} \, ; $$ 并且
$$ L = \left\{ {\begin{array}{l} \lambda + \mu ,\, \lambda + \mu -2 ,\, \lambda + \mu -4 , 0, \; {\text{或}}\, 1, \\ \qquad \qquad\qquad \qquad\qquad \qquad\qquad \qquad \,K = 0 \, ; \\ \lambda + \mu ,\, \lambda + \mu -1 ,\,\lambda + \mu -2 ,\, \cdots, K+1 ,\, K\, , \\ \qquad \qquad\qquad \qquad\qquad \qquad \qquad\qquad ~K \ne 0 \text{。} \end{array}} \right.\, $$ 该具有SU(3)对称性的核态的能量为
$$ \begin{aligned}& E\big[ {[N],(\lambda ,\mu ),K,L,M} \big] = E_{0}^{} + \\&\quad \frac{1}{2}A_{3} \left[ \lambda ^2 + \mu^2 + \lambda \mu + 3(\lambda + \mu ) \right] + C \, L(L + 1) \text{。} \end{aligned} $$ 以总玻色子数
$ N \!=\! 12 $ 为例的具有SU(3)对称性的原子核的典型能谱(的一部分)及其与156Gd的低激发态能谱的实验测量结果的比较如图3所示。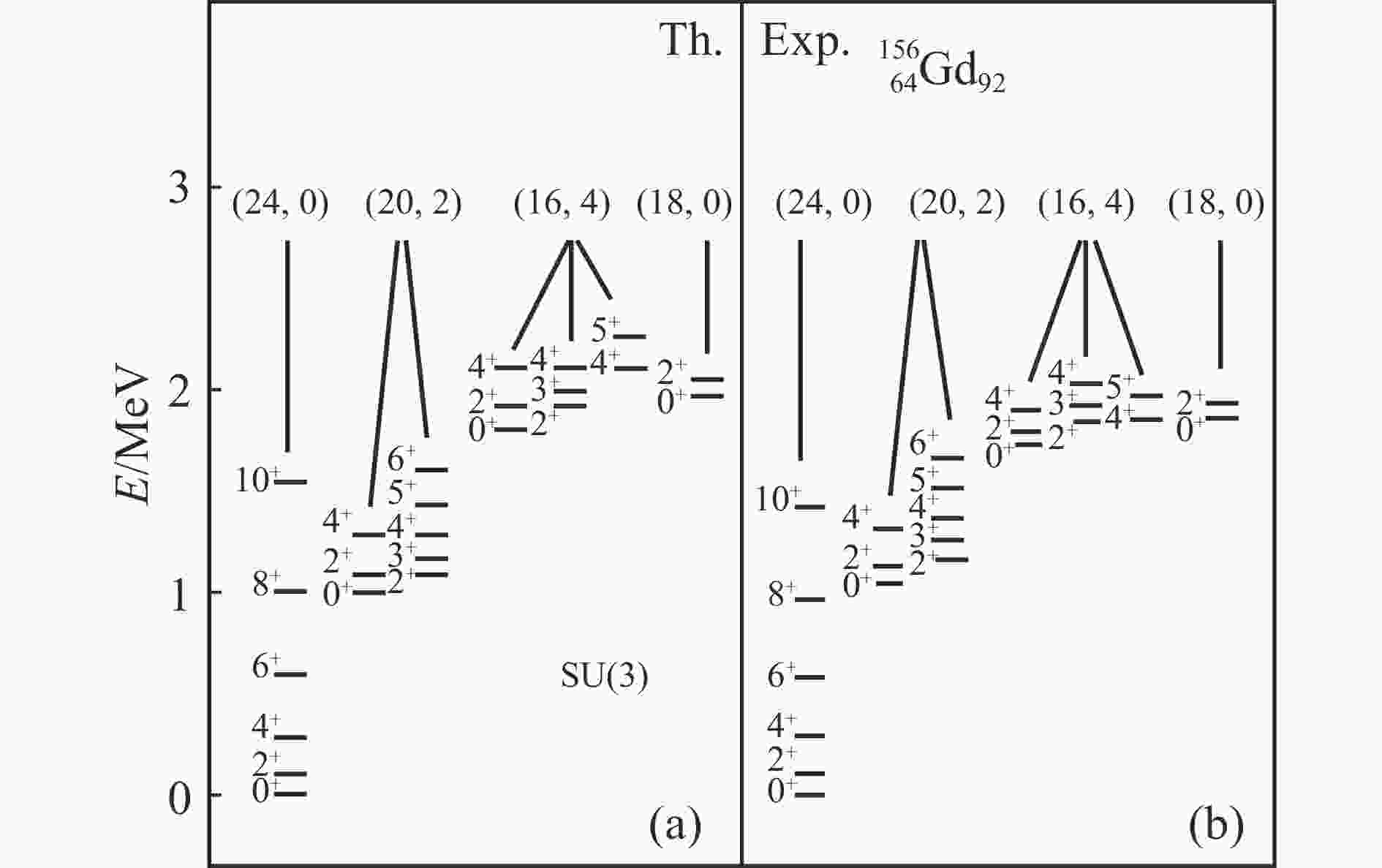
图 3 以N=12为例的SU(3)动力学对称性的典型能谱的一部分(a)及其与156Gd的低激发态能谱(b)的实验观测结果的比较(取自文献[53])
由图3知,对于属于SU(3)的一个IRREP
$ (\lambda , \mu) $ 的一系列态,其能量随角动量$ L $ 的变化都具有$ L(L+1) $ 的行为,即带内跃迁产生的$ \gamma $ 光子的能量随角动量线性变化。这表明,SU(3)动力学对称性极限对应定轴转动核态。在SU(3)动力学对称性极限下,E2跃迁算符为
$$ \hat{T}(\rm E2)_q = e_2 \hat{Q}_q = e_2 \bigg{\{} (d^{\dagger} s + s^{\dagger}\tilde{d})_q^{2} - \frac{\sqrt{7}}{2}(d^{\dagger}\tilde{d})_q^{2} \bigg{\}} \text{。} $$ 由于该
$ \hat{T}(E2) $ 正比于SU(3)群的无穷小生成元$ Q_q^{2} $ ,则直接有E2跃迁的选择定则$$ \Delta \lambda = 0 \, , \qquad \Delta \mu = 0 \text{。} $$ (49) 由此知,
$ \beta $ 带与基态带之间的跃迁和$ \gamma $ 带与基态带之间的跃迁都是禁戒的。计算得,基态带内的E2跃迁的约化跃迁几率为
$$ \begin{aligned} B({\rm E2}\, , \, (L+2)_{g} \rightarrow L_{g}) =& e_{2}^{2} \frac{3 (L+1) (L+2)}{4 (2L + 3) (2L + 5 )}\times \\ & (2 N -L) (2N + L + 3) \, , \end{aligned} $$ 基态带内角动量为
$ L $ 的态的电四极矩为$$ Q(L) = -e_{2} \sqrt{\frac{2 \pi}{5}} \frac{L}{2L + 3} (4N + 3 )\text{。} $$ 其它带内各态间的E2跃迁的约化跃迁几率及各态的电四极矩也有类似的形式,这里不予细述。
$ \langle iii \rangle $ O(6)极限具有SO(6)动力学对称性的哈密顿量为
$$ H = E_{0} + A_{4}\, C_{2{\rm{SO}}(6)} + B \, C_{2{\rm{SO}}(5)} + C\, C_{2{\rm{SO}}(3)} \text{。} $$ 相应的核态的态矢可以写为
$$ \psi_{ {\rm{SO}}(6)}^{} = \big{|} {N,\sigma , \tau , n_\Delta ,L,M} \big{\rangle} \, , $$ 其中
$ \sigma $ 、$ \tau $ 、$ L $ 分别为$ {\rm{SO}}(6) $ 、SO(5)、$ {\rm{SO}}(3) $ 的IRREP,其物理意义分别是未配对的玻色子数(广义辛弱数)、除去$ s $ 玻色子后的未配对的$ d $ 玻色子数、原子核的角动量。谱生成规则由群表示的约化规则表述中下。对一个确定的总玻色子数
$ N $ ,$$ \sigma = N,\, N - 2, \cdots ,1\;{\text{或}} \; 0 \qquad (N = {\text{奇数或偶数}}) \, ; $$ 对一个确定的
$ \sigma $ ,$$ \tau = \sigma ,\sigma - 1, \cdots ,0 \, ; $$ 对确定的
$ \tau $ ,$ L $ 等的取值与前述的相同,不再重述。由量子数
$ \sigma $ 、$ \tau $ 、$ n_{\Delta}^{} $ 和$ L $ 标记的具有SO(6)对称性的核态的能量为$$ \begin{array}{l} E[N,\sigma , \tau , n_\Delta ,L,M] = E_{0} + A_{4} \sigma (\sigma + 4) + B\, \tau ( \tau + 3) \\ \qquad\qquad\qquad\qquad\qquad + C\, L(L + 1) \text{。} \end{array} $$ 以总玻色子数等于6为例的具有SO(6)对称性的原子核的典型能谱的一部分及与196Pt原子核的低激发态能谱的实验观测结果的比较如图4所示。
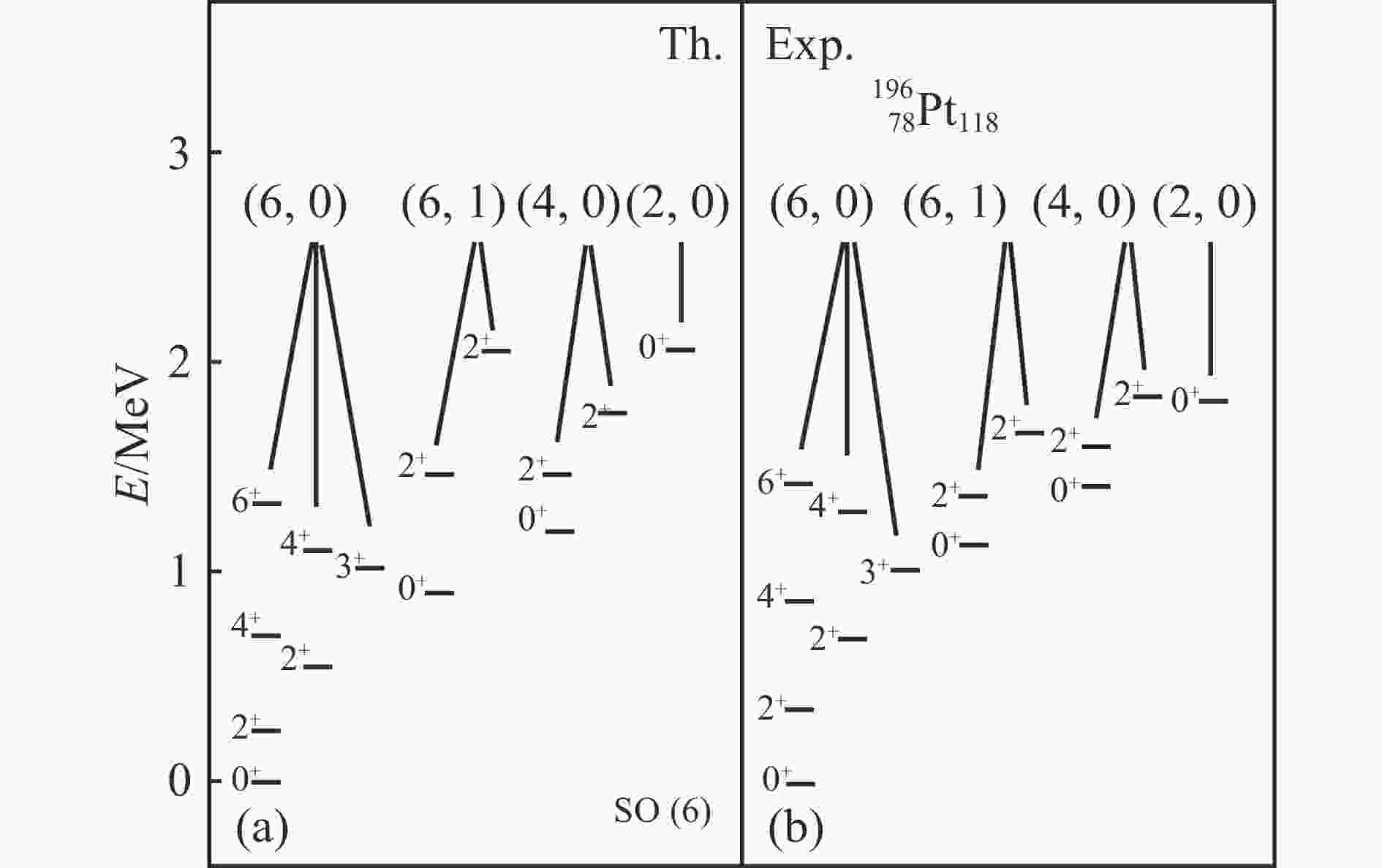
图 4 以N=6为例的SO(6)对称核态的典型能谱的一部分(a,其中上侧标记的量子数为
$(\sigma , n_{\Delta}^{})$ ,自下而上各态分别对应τ=0, 1, 2, 3)及其与196Pt的低激发态能谱的实验观测结果(b)的比较(取自文献[53])考察图4可知,横向整体看,具有SO(6)对称性的核态的能谱与U(5)对称的核态的能谱具有类似之处,但一些多重态的顺序有差别;上下来看,具有SO(6)对称性的核态的每一条能带具有近似的转动特征。此后将说明,SO(6)对称的核态为不定轴转动态。
SO(6)动力学对称性极限下,E2跃迁算符为
$$ \hat{T}(E2)_q = e_2 \big{(} d^\dagger\tilde{s}+s^\dagger\tilde{d} \big{)}_{q}^{2} \text{。} $$ 由于
$ \hat{T}(\rm E2)_q $ 为SO(6)群的无穷小生成元,则其跃迁的选择定则为$$ \Delta \sigma = 0 \, , \qquad \Delta \tau = \pm 1 \text{。} $$ 据此容易得到SO(6)对称性极限下的E2跃迁的约化跃迁几率,例如
$$ \begin{split}& B({\rm E2}\, , \, \sigma\, \sigma\, (\tau + 1)\; 0 \; (2 \tau + 2) \rightarrow \sigma \, \sigma \, \tau \, 0 \, 2\tau ) \\ =& e_{2}^{2} \frac{(\sigma-\tau)(\sigma+\tau+4)(\tau+1)} {2\tau + 5 } \, , \end{split} $$ $$ \begin{split}& B({\rm E2}\, , \, \sigma \, \sigma \, (\tau + 1 ) \; 0 \; 2\tau \rightarrow \sigma \, \sigma \, \tau \; 0 \; 2\tau ) \\ =& e_{2}^{2} \frac{(\sigma-\tau)(\sigma+\tau+4)(4\tau+2)}{(2\tau+5)(4\tau-1)} \text{。} \end{split} $$ 总之,理论上,具有动力学对称性的核态及其能谱和跃迁几率都很容易确定,且各有特点。实验上,人们已经找到很多近似具有前述的动力学对称性的原子核。
关于奇-A核和奇-奇核的超对称模型也取得成功,并找到了196Au等代表性原子核[54]。
-
(1)IBM1中原子核集体运动的相干态理论框架
回顾前述IBM1的群结构知,U(6)群的最大不变子群是U(5)
$ \oplus $ U(1),其代数包括:$$ \begin{split} {\mathfrak{g}}: &[d^{\dagger} \tilde{d}]_\mu ^{k} \;(k = 0,1,2,3,4), \; [d^{\dagger} \tilde{s}]_\mu ^{2}, \; [s^{\dagger} \tilde{d}]_\mu ^{2}, \; [s^{\dagger} \tilde{s}]_0 ^{0}; \\ {\mathfrak{h}}: &[d^{\dagger} \tilde{d}]_\mu ^{k} \; (k = 0,1,2,3,4), \; [s^{\dagger} \tilde{s}]_0 ^{0};\\ {\mathfrak{p}}: &[d^{\dagger} \tilde{s}]_\mu ^{2}, \; [s^{\dagger} \tilde{d}]_\mu ^{2}\text{。} \end{split} $$ (50) 显然,
$ {\mathfrak{h}} $ 为$ {\mathfrak{g}} $ 的最大不变子代数,$ {\mathfrak{p}} $ 为$ {\mathfrak{h}} $ 的陪集。由于$ {\mathfrak{p}} $ 中含有10个元素,且其中5个是另5个的厄密共轭,由4.2.2小节的讨论知,与该5维空间对应,我们可以定义与IBM1对应的5维几何空间(集体运动空间)。由于极值态(可以被所有的$ d_{\mu}^{} $ 湮灭)为$$ \big{\vert} \Lambda_{\rm ext} \big{\rangle} : \frac{1}{N_{s}} s^{\dagger\,N} \big{\vert} 0 \big{\rangle} \equiv \big{\vert} s^{N} \big{\rangle} \, , $$ 则相应的相干态为
$$ \big{\vert} N, \eta_{\mu}^{} \big{\rangle} = \exp \left[ \sum {\mu} \eta _ \mu [d^{\dagger} \tilde{s}]^2_\mu+\sum {\mu} \eta^*_\mu [s^{\dagger} \tilde{d}]^2_\mu \right ] \big{\vert} s^{N} \big{\rangle} \text{。} $$ 并有常用的内禀相干态(亦称“投影”相干态):
$$ \big{\vert} {N;\alpha _{\mu}^{} } \big{\rangle} = \bigg{(} {s^{\dagger} + \sum\limits_\mu {\alpha _\mu d_\mu ^{\dagger} } } \bigg{)}^N \big{\vert} 0 \big{\rangle} \, , $$ 其中
$ \alpha _{\mu}^{} $ 是相干态中表征集体运动性质的集体(或称几何)参数。进一步采用4.2.2小节所述的参数化方案,与随体坐标系相应的内禀相干态可以在$ N $ 个$ s $ 和$ d $ 玻色子的空间中表示为$$ \begin{split} \big{\vert} {N;\beta ,\gamma } \big{\rangle} =& \big{(} {s^{\dagger} + \beta_{2} \cos{\gamma_{2}} d_{0}^{\dagger}} +\\& {\frac{1}{\sqrt{2}} \beta_{2} \sin{\gamma_{2}} ( d_{2}^{\dagger} + d_{-2}^{\dagger} ) } \big{)}^{N} \big{\vert} 0 \big{\rangle}\text{。} \end{split} $$ (51) 在该内禀态下计算原子核的电四极矩和E2跃迁几率,并将所得结果与Bohr-Mottelson集体模型中的结果比较,由利用不同方法对同一个物理量计算的结果应该相等(即规范对称性)可知,对于大多数稀土区原子核,集体模型中的形变参数
$ \{\beta , \gamma \} $ 与这里的“形变”参数$ \{ \beta_{2}, \gamma_{2}\} $ 之间有关系[53]$$ \beta \approx 0.15\beta_{2}^{} \, , \qquad \gamma = \gamma_{2} \text{。} $$ 这表明,在IBM1的内禀相干态中引入的参数
$ \beta_{2}^{} $ 、$ \gamma_{2} $ 可以像集体模型中的形变参数$ \beta $ 、$ \gamma\, $ 一样描述原子核表面的形状,因此,我们也称之为原子核的形变参数,并在此后(略去下标)简记之为$ \beta $ 、$ \gamma $ 。采用这一内禀态计算哈密顿量的期望值,即可得到原子核的基态的能量泛函(曲面)
$$ E(N;\beta ,\gamma ) = \frac{{\left\langle {N;\beta ,\gamma |H} \right.\left| {N;\beta ,\gamma } \right\rangle }}{{\left\langle {N;\beta ,\gamma \left| {N;\beta ,\gamma } \right.} \right\rangle }},$$ (52) 进而,根据最小作用原理,由能量泛函曲面取极小值
$$ \begin{split}& \frac{\partial E}{\partial \beta } = 0 \, , \qquad \;\; \; \frac{\partial E}{\partial \gamma } = 0\, ; \\ & \frac{\partial^{2} E}{\partial \beta^{2} } > 0 \, , \qquad \frac{\partial^{2} E}{\partial \gamma^{2} } > 0\, , \qquad \frac{\partial^{2} E}{\partial \beta \partial \gamma } > 0 \, , \end{split} $$ 即可得到以形变参数
$ \{ \beta , \gamma \} $ 标记的稳定原子核的形状。由于上述内禀相干态的角动量恒为0,因此它仅对应原子核的基态,这样只能得到原子核基态的形状。为研究低激发态的集体运动性质,我们需要采用角动量投影方法得到非零角动量激发态。我们知道,角动量投影算符可以表示为
$$ P_{MK}^{\rm L} = \frac{{2L + 1}} {{8\pi ^2 }}\int {D^{*L} _{MK} } (\Omega)R(\Omega ){\rm d}\Omega \, , $$ 其中
$ R(\Omega ) $ 为转动算符,$ D_{MK}^L(\Omega ) $ 为转动矩阵,$ \Omega $ 为欧拉转动角$ (\alpha ',\beta ',\gamma') $ 。将该角动量投影算符作用到前述内禀相干态上即得具有确定角动量的相干态[55-56]$$ \big{\vert} {N;\alpha _\mu ; L} \big{\rangle} = P^{\rm L}_{MK} \bigg{(} {s^{\dagger} + \sum\limits_\mu {\alpha _\mu d_\mu ^{\dagger} } } \bigg{)}^{N} \big{\vert} 0 \big{\rangle} \text{。} $$ 对于基态带中的各态,上式中
$ K \!=\! M \!=\! 0 $ 。经过角动量投影后,原子核的基带中各角动量态(可以认为是相同角动量中能量最低的态,亦即Yrast态)的能量泛函可以表示为
$$ E(L,\beta,\gamma) = \left\langle \hat{H} \right\rangle _{G,L} = \frac{{\left\langle {N;\beta ,\gamma } \right|HP_{00}^L \left| {N;\beta ,\gamma } \right\rangle }} {{\left\langle {N;\beta ,\gamma} \right|P_{00}^L \left| {N;\beta ,\gamma } \right\rangle }}\text{。} $$ 再利用能量极小的稳定性条件,即可确定各Yrast态的形变参数、得到它们的集体运动性质。
(2)IBM1中原子核的集体运动模式及形状相变
利用上述理论框架在IBM1下直接计算,即得相应的原子核的集体运动模式。下面给出计算结果,并对原子核形状相变予以简要讨论。
1) U(5)对称性极限:
IBM1的U(5)对称性下的哈密顿量可改写为
$$ H = E_0+ \varepsilon_{d}^{} n_{d}^{} + \sum \limits_{K = 0,2,4} \frac{1}{2} (2K+1)^{1/2} c_{K} \big[[d^{\dagger} d^{\dagger}]^{K}[\tilde{d} \tilde{d}]^{K}\big]^{0} , $$ 不考虑角动量投影情况下的(基态的)能量泛函为
$$ \begin{split} E(N;\beta ,\gamma ) =& \frac{{\left\langle {N;\beta ,\gamma } \right|H\left| {N;\beta ,\gamma } \right\rangle }}{{\left\langle {N;\beta ,\gamma \left| {N;\beta ,\gamma } \right.} \right\rangle }} = {E_0} + {\varepsilon _d}N\frac{{{\beta ^2}}}{{1 + {\beta ^2}}} +\\& {f_1}N(N - 1)\frac{{{\beta ^4}}}{{{{\left( {1 + {\beta ^2}} \right)}^2}}}, \end{split} $$ 其中
$ f_{1}^{} \!=\! \frac{c_0}{10} + \frac{c_2}{7} + \frac{9c_4}{35} $ 。显然该函数与$ \gamma $ 无关,而在$ \beta \!=\! 0 $ 处有一个极小值,因此它对应的形状为球形。相应的集体运动模式为四极振动。对考虑角动量投影情况下的能量泛函很难给出解析表达式。相应于总玻色子数
$ N = 15 $ 的数值结果如图5所示。由图5易知,非零的低角动量态与基态一样,位能面极小出现在$ \beta \!=\! 0 $ ,且与$ \gamma $ 无关,即原子核整体呈现球形,具有四极振动的集体运动模式。而高角动量态(例如$ L \!=\! 10 $ )位能面极小出现在$ \beta \approx \pm 0.5 $ 、$ \gamma \approx 0, \pm \frac{\pi}{3} $ ,即原子核呈椭球形形变、或铁饼形形变,具有定轴转动的集体运动模式。由此知,IBM1可以很好地描述原子核角动量驱动形状相变[57].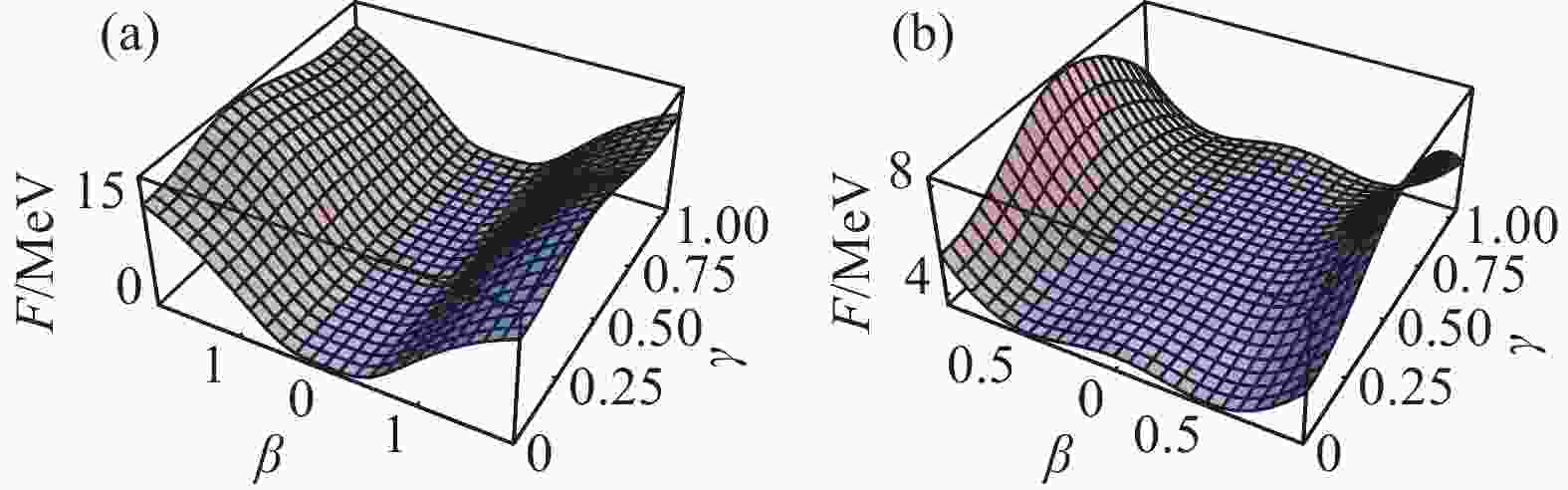
图 5 (在线彩图)总玻色子数等于15的具有U(5)对称性的原子核的角动量L=2(a)和角动量L=10(b)的态的位能曲面(对应哈密顿量中参数取
$A_{1}\!=\! 1.0$ MeV,$A_2 \!=\! 0.15$ MeV,$B \!=\! -0.4$ MeV,$C \!=\! 0.006$ MeV,$A_{3} \!= \! A_{4} \!=\! 0$ ,取自文献[58])2) SU(3)对称性极限
IBM1的SU(3)对称性下的哈密顿量可改写为
$$ H = E_0 -\kappa 2 (\hat{Q}(-\sqrt{7}/2) \cdot \hat{Q}(-\sqrt{7}/2) ) + \kappa^{\prime} (\hat{L} \cdot \hat{L}) \, , $$ 不考虑角动量投影的(基态的)能量泛函为
$$ \begin{split} E(N;\beta ,\gamma ) =& E_{0} + {\kappa^{\prime}} \frac{6N\beta^2}{1 + \beta ^2} - \kappa_{2} \bigg{[} \frac{N}{1 + \beta^2} \bigg{(} {5 + \frac{11}{4} \beta^{2}} \bigg{)}+ \\ & \frac{N(N - 1)}{( {1 + \beta ^2} )^2} \bigg{(} {\frac{\beta ^4}{2} + 2\sqrt 2 \beta ^{3} \cos{3\gamma} + 4\beta ^{2}}\bigg{)} \bigg{]}\, , \end{split} $$ 该能量函数在
$ \gamma \!=\! 0 $ 、$ \beta \ne 0 $ 有极小值,在$ N \to \infty $ 时,极小值位于$ \beta \!=\! \sqrt 2 $ . 这表明,原子核呈长椭球形。并且,对应于$ \overline { {\rm{SU}}(3)} $ ($ \hat{Q} $ 算符中的结构参数$ \chi \!=\! \frac{\sqrt{7}}{2} $ ),原子核呈扁椭球形。因其物质分布呈椭球形状,并且描述其形状的$ \gamma $ 角为定值,所以该对称性对应的集体运动模式为定轴转动。具体地,$ \chi \!=\! -\frac{\sqrt{7}}{2} $ 情况下为绕垂直于物质分布的对称轴的轴的定轴转动,$ \chi \!=\! \frac{\sqrt{7}}{2} $ 情况下为绕物质分布的对称轴的定轴转动。与U(5)对称情况相同,考虑角动量投影情况下的位能面泛函也难以给出解析表达式。相应于总玻色子数
$ N \!=\! 15 $ 的数值结果如图6所示。由图6易知,具有SU(3)对称性的低角动量态呈长椭球形变,但有呈扁椭球形状的亚稳态,具有定轴转动的集体运动模式。随角动量升高,原子核逐渐演化为仅呈长椭球形变形状。
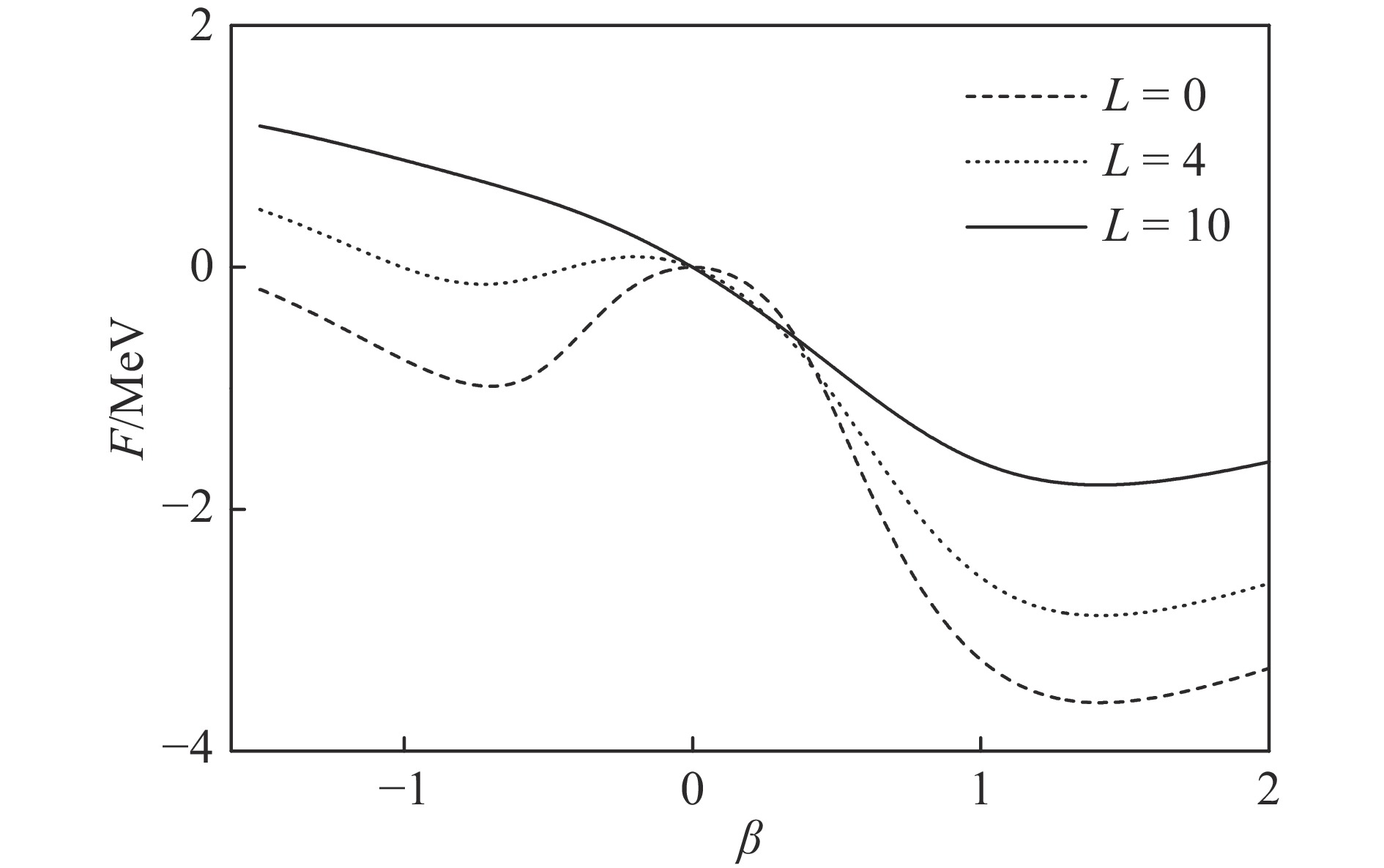
图 6 N=15的具有SU(3)对称性的原子核的角动量L=0, 4, 10的态的位能曲面(对应参数
$A_3 \!=\! 1$ 。取自文献[58])3) SO(6)对称性极限
IBM1的SO(6)对称性下的哈密顿量可以改写为
$$ H = E_{0} + A P^{\dagger} \cdot P + \frac{B}{12} C_{2 {\rm{SO}}(5)} + \frac{C}{2} C_{2 {\rm{SO}}(3)} \, , $$ 其中
$ P \!=\! \frac{1}{2}(\tilde{d} \cdot \tilde{d})-\frac{1}{2}(s \cdot s)\; $ 为广义对湮灭算符。不考虑角动量投影情况下的(即基态的)位能面泛函为$$ \begin{split} E(N;\beta ,\gamma ) =&{E_0} + \big(2B + 6C\big)\frac{{N{\beta ^2}}}{{1 + {\beta ^2}}} + \\ &\frac{A}{4}N\big(N - 1\big){\bigg(\frac{{1 - {\beta ^2}}}{{1 + {\beta ^2}}}\bigg)^2}{\text{。}} \end{split}$$ 显然,该能量泛函曲面与
$ \gamma $ 无关,在$ \beta \ne 0 $ 处有一个极小值。在$ N \to \infty $ 时,极小值位于$ \beta \!=\! 1 $ 。这表明,SO(6)对称性下的物质分布呈$ \gamma $ 不稳定的椭球形,集体运动模式为不定轴转动,相当于量子陀螺除有自转之外还有进动和章动。考虑角动量投影情况下的位能面泛函的数值计算结果的一个实例如图7所示。由图7易知,具有SO(6)对称性的低角动量态与角动量为0的基态一样,具有不定轴转动的集体运动模式。随着角动量升高,位能面逐渐在
$ \beta \!\approx\! \pm 1 $ 、$ \gamma \!\approx\! \frac{\pi}{6} $ 出现极小值,在角动量达到较高值(例如图中的$ L \!=\! 14 $ )时,两个极小值很明显,且它们中间有明显的相当高的位垒;这表明,原子核呈明显的三轴形变的形状。然而,在角动量很高(例如图中的接近最大角动量20的$ L \!=\! 18 $ )情况下,位能面在$ \beta \!=\! 0 $ 处出现不依赖于$ \gamma $ 的深谷、并在$ \gamma \approx \frac{\pi}{6} $ 处出现不依赖于$ \beta $ 的深谷,这表明,原子核不再有稳定的形状,亦即出现振动与三轴形变的形状共存态。上述结果表明,SO(6)对称的基态和低激发态具有不定轴转动的集体运动模式,并且随角动量升高出现由不定轴转动到三轴形变态的相变,并可能出现振动与三轴形变共存的状态。
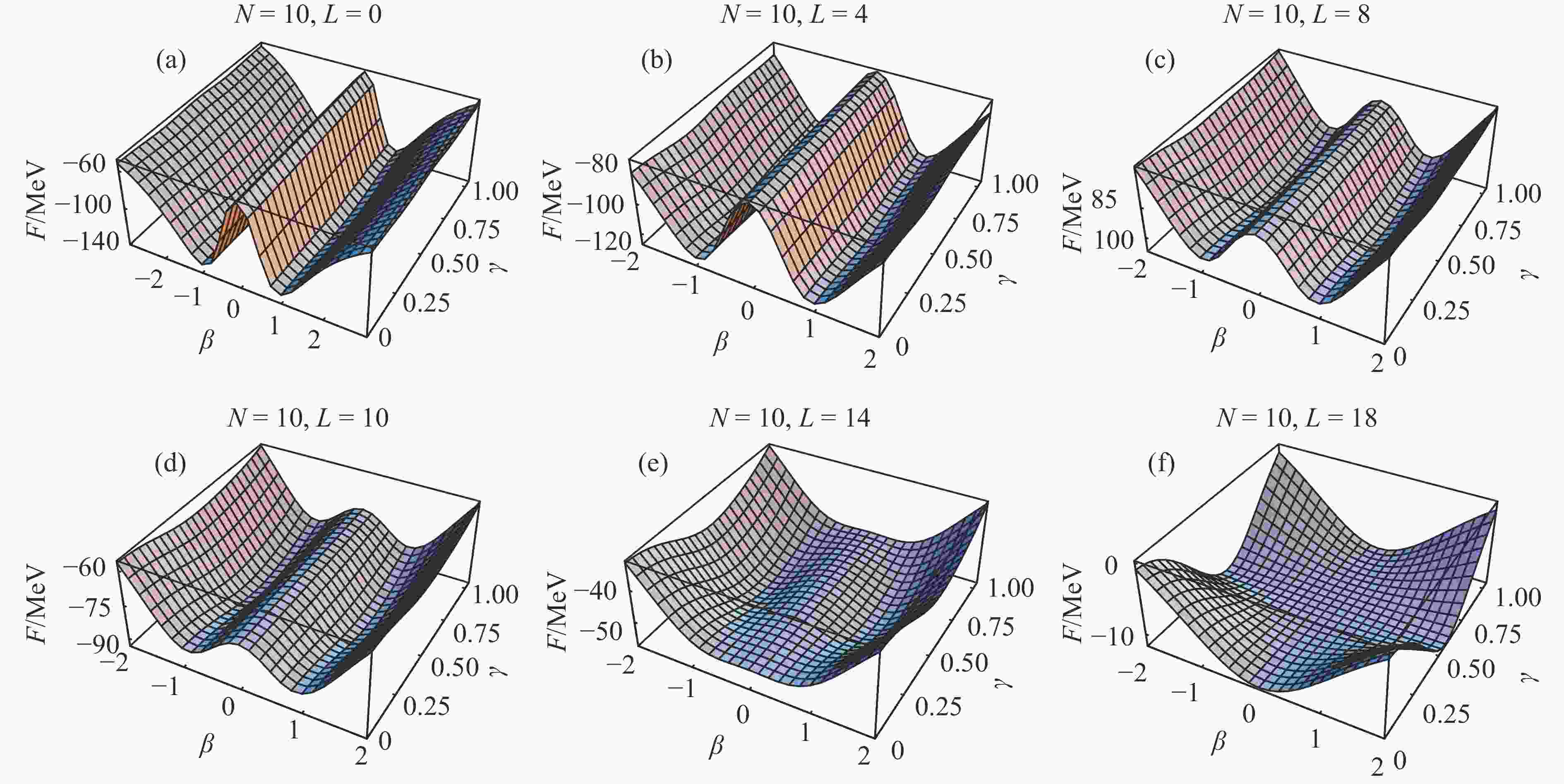
图 7 (在线彩图)
$N \!=\! 10$ 的具有SO(6)对称性的原子核的位能曲面随角动量变化的行为(对应哈密顿量中参数$A_{4} \!=\! -1$ MeV、$A_{1} = A_{2} = A_{3} = B = C = 0$ 。取自文献[58])(3) 原子核集体运动模式的相变(形状相变)
前已述及,原子核的集体运动模式的演化称为原子核的集体运动模式相变。由于原子核的集体运动模式变化都相应有组成原子核的物质的包络面的演化,因此常称之为原子核的形状相变。又由于原子核的形状和确定的集体运动模式都相应于一定的动力学对称性,因此原子核的集体运动模式相变(形状相变)是原子核的动力学对称性的破缺或恢复的自然体现。例如,对IBM1下的核态,由于
$ {\rm{U}}(5) \supset {\rm{SU}}(4) \supset {\rm{SU}}(3) $ ,而SU(4)同构于SO(6),并且U(5)、SO(6)、SU(3)对称性分别对应于四极振动、不定轴转动、定轴转动(包括三轴转动)的集体运动模式,那么前述的角动量驱动由振动到定轴转动的形状相变即由U(5)对称性到SU(3)对称性的破缺的表现。具体地,人们常采用下述哈密顿展开具体研究,
$$ \hat{H} = \varepsilon \Big{(} \eta \hat{n}_d - \frac{{1 - \eta }} {N} {\hat{Q}(\chi ) \cdot \hat{Q}(\chi )} \Big{)} \, , \\ $$ (53) 其中
$ \varepsilon $ 为一标度因子,$ \hat{n}_{d} $ 为U(5)的一阶Casimir算子,$ \hat{Q}(\chi) $ 为式(48)所示的四极算符,并且$ \eta \in \left[ 0,\, 1 \right] $ 、$ \chi \in \left[ - \sqrt 7/2,\, \sqrt 7 /2 \right] $ 为控制参量。对称性分析表明,该哈密顿量即$$ \begin{split} \hat{H} =& \bigg{[} {\eta - \frac{{2(1 - \eta )\chi }} {{7N}} \bigg{(} {\chi + \frac{{\sqrt{7} }} {2}} \bigg{)}} \bigg{]} C_{1 {\rm{U}}(5)}^{} + \\& \frac{{2(\eta - 1)\chi }} {{7N}} \bigg{(} {\chi + \frac{{\sqrt{7} }}{2}} \bigg{)} C_{2 {\rm{U}}(5)}^{}- \\& \frac{{(\eta - 1)\chi }} {{\sqrt{7} N}} C_{2 {\rm{SU}}(3)}^{} + \frac{{2(\eta - 1)(\chi + \frac{{\sqrt{7} }} {2})}} {{\sqrt{7} N}}C_{2 {\rm{SO}}(6)}^{}- \\& \frac{{2(\eta - 1)\big{(} \chi + \frac{{\sqrt{7} }} {2} \big{)} \big{(} \chi + \sqrt{7} \big{)}}} {{7N}}C_{2 {\rm{SO}}(5)}^{} -\\& \frac{{(1 - \eta )\chi (\chi + 2\sqrt{7} )}} {{14N}}C_{2 {\rm{SO}}(3)}^{} \text{。} \end{split} $$ (54) 由此易知,如果取
$ \chi \!=\! 0, \; \eta \in [1,\, 0] $ ,则上述哈密顿量描述U(5)对称与SO(6)对称之间过渡区的原子核的性质;如果取$ \chi \!=\! -\frac{\sqrt{7}}{2},\; \eta \in [1,\,0] $ ,则上述哈密顿量描述U(5)对称与SU(3)对称之间过渡区的原子核的性质;如果$ \eta \!=\! 0, \; \chi \in [0,\, -\frac{\sqrt{7}}{2}] $ ,则上述哈密顿量描述SO(6)对称与SU(3)对称之间过渡区的原子核的性质。取哈密顿量如式(53)(有控制参数$ \eta $ 、$ \chi $ )、波函数为式(51)所示的内禀相干态,即可计算得到原子核的能量泛函$ E(N;\beta,\gamma) $ 和每核子平均能量$ \varepsilon \!=\! E(N;\beta ,\gamma ) / N $ ,进而得到能量泛函曲面的极小值点和相应的每核子能量值$ \varepsilon _{\min }^{} $ ,然后考察$ \varepsilon _{\min}^{} $ 与哈密顿量中各项耦合系数的函数关系及其导数关系,可以证明,由U(5)对称破缺到SO(6)对称(四极振动到不定轴转动)的相变为二级相变,由U(5)对称破缺到SU(3)对称(四极振动到定轴转动)的相变为一级相变。这些对应关系常由Castan三角形表征,推广的Casten三角形如图8所示。前述讨论已表明,IBM1可以很好地描述转动驱动的原子核的形状相变,有关相图分别如图9,10所示。
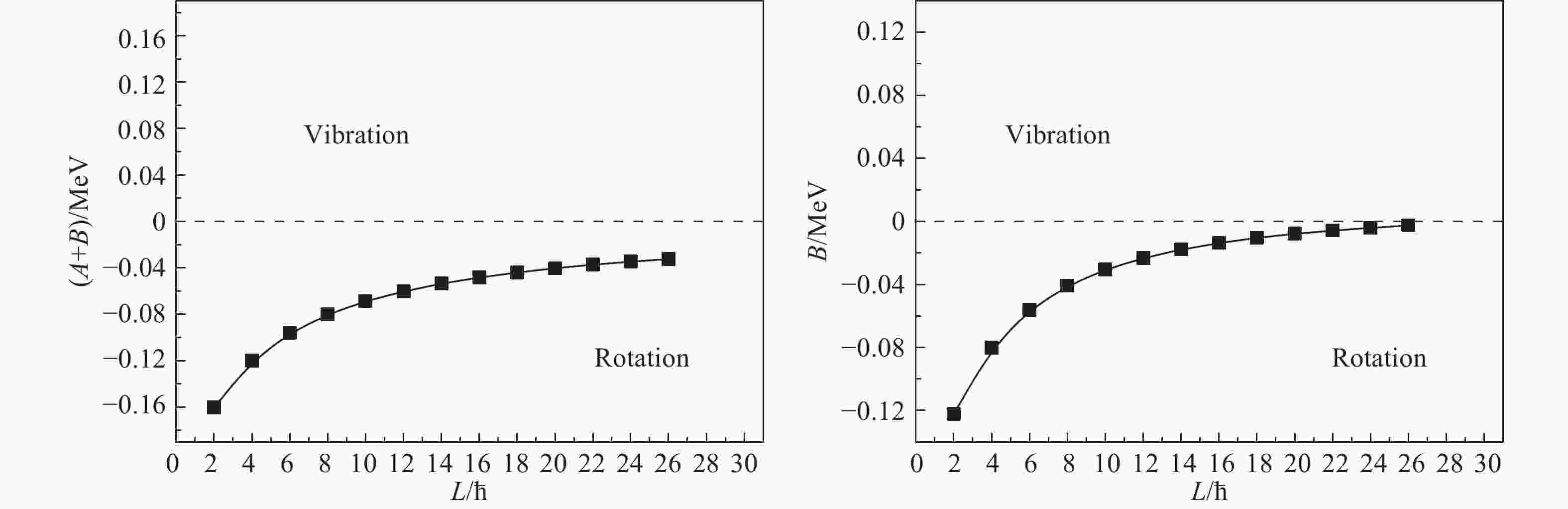
图 9 总玻色子数N=15的具有U(5)对称性的核态的相图的计算结果(取自文献[58])
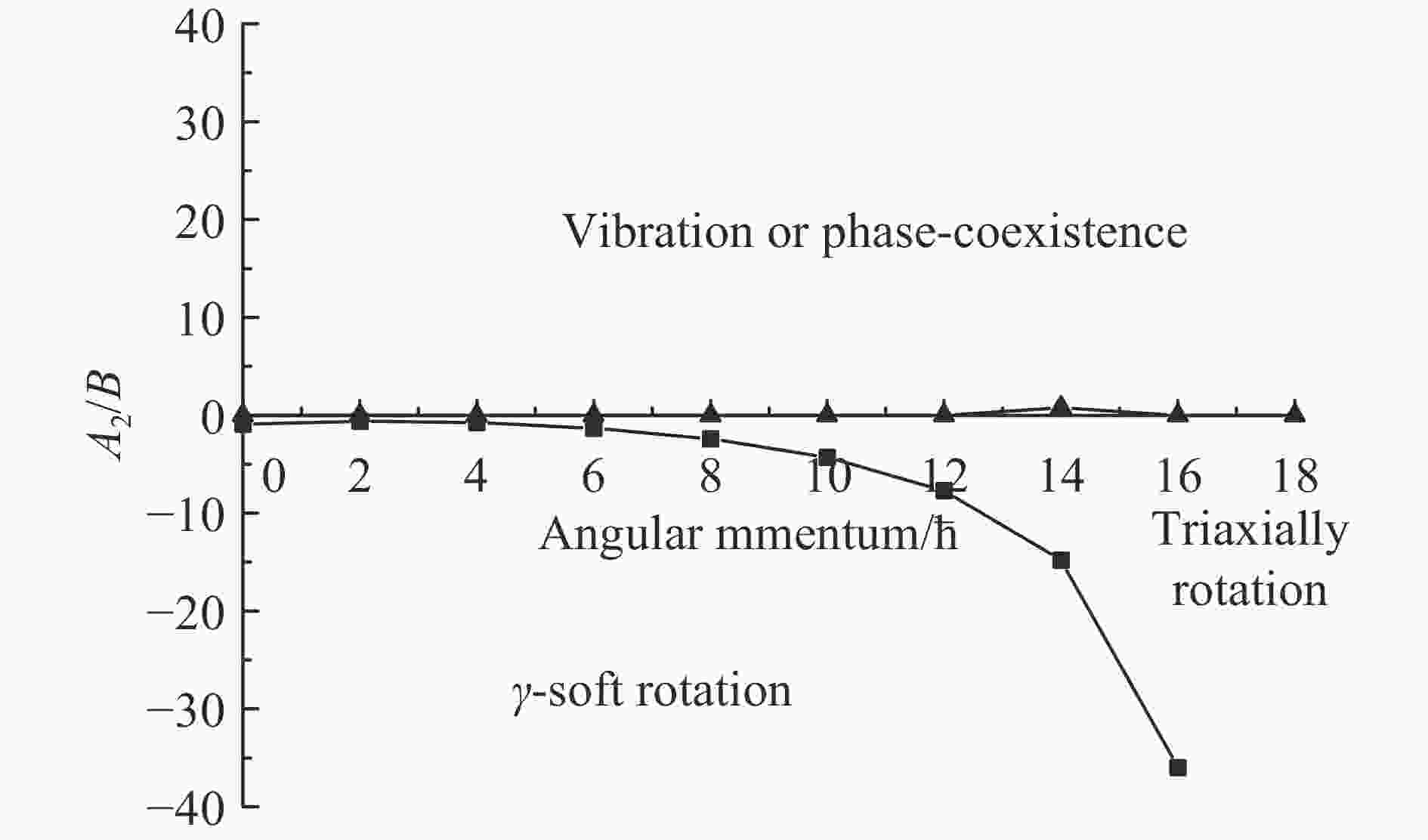
图 10 总玻色子数N=10的具有SO(6)对称性的原子核的相图的计算结果(取自文献[58])
对于其物理机制,限于篇幅,这里不再讨论,有兴趣的读者可参阅文献[58-59]等。
引起原子核形状相变的因素很多,除了前述的转动(角动量)。还有同位旋(一个同位素链(或同中子素链)中原子核基态具有不同的集体运动模式)、激发能、温度等等。精细的研究表明,上述参数
$ \eta $ 与原子核中的核子配对形成的玻色子数成线性关系[60-61],因此,利用上述哈密顿量可以很好地研究同位旋驱动的原子核形状相变。在区分质子玻色子和中子玻色子的IBM2下,关于原子核集体运动模式及形状相变的研究也已广泛展开,它自然地包含三轴形变核态[62],并且Casten三角形扩展到Iachello四面体[63]。
除了IBM之外,集体模型、Hartree-Fock-Bogoliubov(HFB)理论、有限温度推转HFB理论、配对壳模型、推转IBM、以及Landau理论等方法都被用来研究原子核的形状相变,还提出了双中子分离能、E2跃迁能量与跃迁初态角动量的比值、E2跃迁几率比等实验观测量来表征原子核形状相变,并区分相变的级次。内容极其丰富,限于篇幅,这里不再具体介绍,有兴趣的读者请参阅综述文献[64]。
(4)原子核形状相变的临界点状态的对称性描述
我们知道,二级相变和一级相变都有确定的临界状态。通过分析一般的二级相变的临界点的特征和一级相变的临界点的特征,Iachello教授提出了描述由振动到不定轴转动相变的临界点附近状态性质的E(5)对称性模型—玻尔哈密顿量中仅有关于
$ \beta $ 的无限深势阱的模型[65],和描述由振动到定轴转动相变临界点性质的X(5)对称性模型—玻尔哈密顿量中有关于$ \gamma $ 呈谐振子势和关于$ \beta $ 呈无限深势阱的模型[66],并给出其能谱和E2跃迁等的跃迁几率,还找到一些代表性原子核(例如文献[67-69]等等)。尽管E(5)模型和X(5)模型在实际应用中取得很大成功,但它们都仅是求解上述势阱下的玻尔哈密顿量的结果,没有代数结构,也就是没有动力学对称性。
事实上,系统的哈密顿量具有平移和转动不变性,即具有五维欧几里得对称性。推广占有数表象中玻色子算符与坐标及动量间的关系知,
$ d $ -玻色子的产生、湮灭算符可以由五维空间的坐标和动量表述为$$ \tilde{d}_{\mu} = \frac{1}{\sqrt{2}}\left[q_{\mu}^{} + {\rm i}\tilde{p}_{\mu}^{} \right], \quad d^{\dagger}_{\mu} = \frac{1}{\sqrt{2}}\left[q_{\mu}^{} - {\rm i} \tilde{p}_{\mu}\right]\text{。} $$ 于是,五维欧几里得群(Eu(5))的生成元可以表述为
$$ T_{\mu}^{(2)} = {\rm i}\tilde{p}_{\mu}^{} = \frac{1}{\sqrt{2}}[\tilde{d}_{\mu}^{} - d_{\mu}^{\dagger} ], $$ $$ T_{\mu}^{(\lambda)} = {\rm i}\sqrt{2}(q \tilde{p})_{\mu}^{\lambda} = \sqrt{2}(d^{\dagger} \tilde{d})_{\mu}^{\lambda}, \qquad \lambda = 1,3\text{。} $$ Casimir算子则为
$$ C_{2, { {\rm{Eu}}(5)}} = \tilde{p}^2 = \hat{n}_{d}^{} + \frac{5}{2} - \frac{1}{2} \bigg{(} \hat{P}^{\dagger}_{d} + \hat{P}_{d}^{} \bigg{)} \, , $$ 其中
$ \hat{n}_{d}^{} \!=\! \sum_{\mu} d^{\dagger} _{\mu} d_{\mu}^{} $ ,$ \hat{P}_{d}^{} \!=\! \sum_{\mu} (-1)^{\mu} d_{\mu}^{} d_{-\mu}^{} $ 。那么,Eu(5)动力学对称性的哈密顿量为$$ \hat{H}_{ {\rm{Eu}}(5)} = \alpha \bigg{[} \hat{n}_{d}^{} + \frac{5}{2} - \frac{1}{2} \bigg{(} \hat{P}^{\dagger}_{d} + \hat{P}_{d} \bigg{)} \bigg{]} \, , $$ (55) 其中
$ \alpha $ 为一标度因子。该哈密顿量可以在具有U(5)对称性($ {{\rm{U}}(5)}\supset {{{\rm{O}}}(5)} \supset {{{\rm{O}}}(3)} $ )的基$ \{| n_{d}^{} \, \tau \; n_{\Delta}^{} \; L \rangle\} $ 下对角化。前述讨论表明,过渡区核态的哈密顿量可以表述为
$$ \hat{H}(\eta,\; \chi) = \varepsilon \left[ (1-\eta)\hat{n}_{d}^{} - \frac{\eta}{aN}\hat{Q}^{\chi} \cdot \hat{Q}^{\chi} \right] \, , $$ 其中
$ \hat{Q}^{\chi} \!=\! (d^{\dagger} s + s^{\dagger} \tilde{d})^{(2)} + \chi (d^{\dagger} \tilde{d})^{(2)} $ ,$ \eta $ 和$ \chi $ 是控制参数,$ \varepsilon $ 是标度因子,$ a $ 是可调参数(亦即标度因子)。在内禀相干态方法下的具体计算表明,对于U(5)–O(6)对称性之间的相变和U(5)–SU(3)对称性之间的相变,在大$ N $ 极限下(相应于经典集体运动),它们的临界状态都可以由参数$ \chi $ 决定的临界参数$$ \eta_{c}^{} = \frac{7a}{7a+28+2\chi^{2} } \, , $$ 来表述(仅相差标度因子
$ a $ )。具体地,$ \chi \!=\! 0 $ 对应E(5)模型,$ \chi \!=\! - \frac{\sqrt{7}}{2}\;(\approx -1.32) $ 对应X(5)模型。这表明,上述哈密顿量可以统一描述E(5)和X(5)临界点对称性。更具体的理论分析和数值检验见文献[70]。我们称之为F(5)临界点对称性模型。另一方面,对于哈密顿量为
$ \hat{H} \!=\! -\bigtriangledown^2/(2M)+k\beta^{2n} $ (其中$ k\propto M^{t} $ )的系统的研究[71]表明,其能谱有标度因子$ M^{(t-n)/(n+1)} $ 。显然,$ M^{(t-n)/(n+1)}\mid_{n\rightarrow\infty} =\! M^{-1} $ 。对于原子核,其质量当然近似正比于其组分粒子数目,于是该标度行为可以近似表述为$ N^{-1} $ 标度律。F(5)临界点对称性模型下,$ \chi \!=\! 0 $ (E(5)模型)和$ \chi \!=\! -1.32 $ (X(5)模型)两种特殊情况下的能谱和E2跃迁几率随系统中玻色子数目变化的行为如图11所示。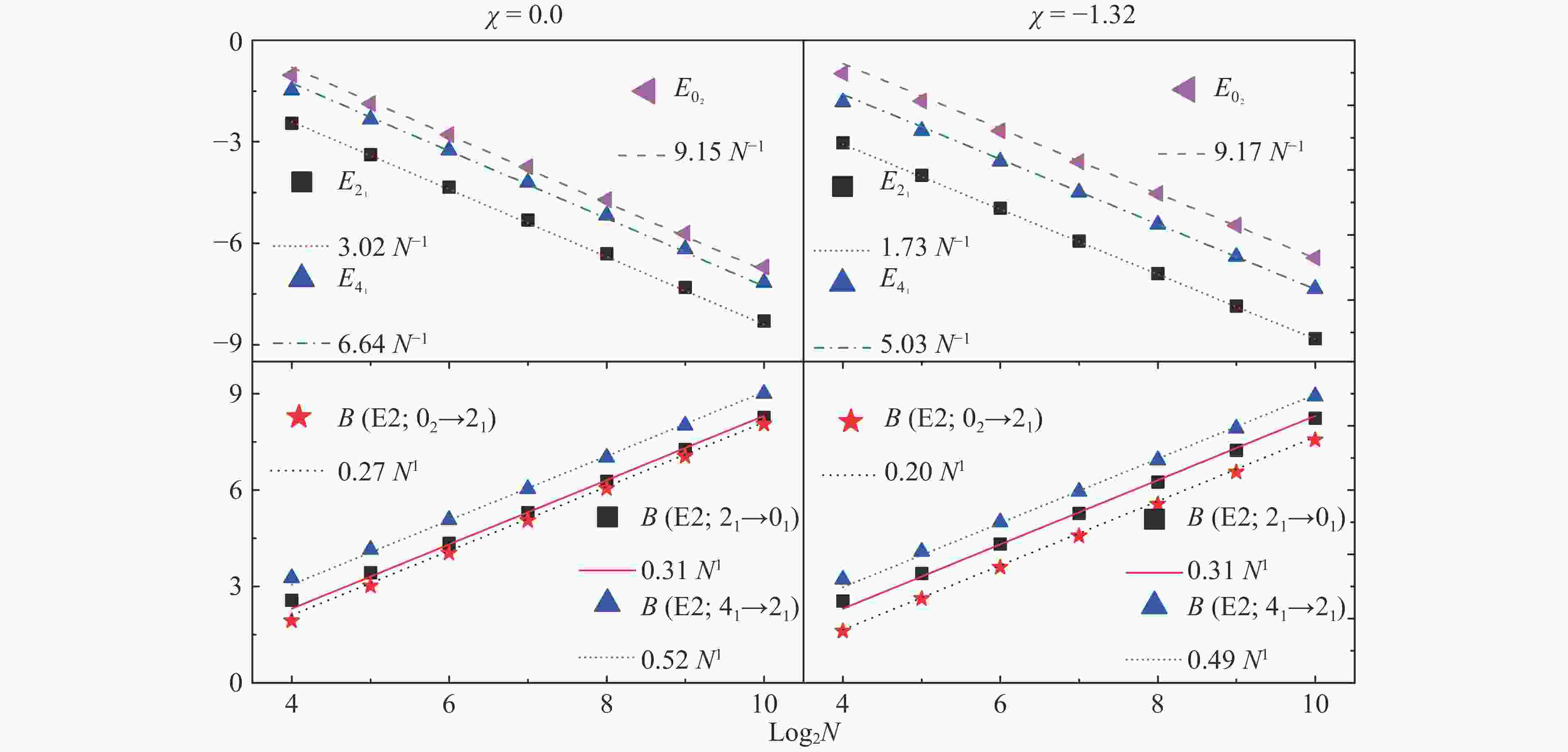
图 11 (在线彩图)F(5)临界点对称性模型的两种特殊情况下对一些典型能谱和E2跃迁几率随系统粒子数
$N$ 变化的行为的计算结果(取自文献[70])显然,F(5)临界点对称性模型可以很好地描述临界点状态的能谱的
$ N^{-1} $ 标度行为,并说明临界点状态的E2跃迁几率具有$ N^{1} $ 的标度行为。上述标度行为表明,对于有限粒子数系统,F(5)临界点对称性模型也可以描述其相变临界点状态的性质。总之,对于原子核形状相变临界点状态的描述,不仅已经对U(5)–O(6)对称性之间的相变和U(5)–SU(3)对称性之间的相变等分别建立了E(5)模型、X(5)模型等,还建立了统一描述这些临界点状态性质的具有清楚的动力学对称性结构的F(5)模型。
-
就可见物质及其质量而言,我们现在的宇宙的主要成分是强相互作用物质,因为电子质量仅仅是核子质量的1/1 836。而对称性是物理学基本原理的表征、是决定现象的本质。但对称性意味着简并性,因此物质世界的丰富多彩源自于对称性的破缺。于是,强相互作用系统的对称性及其破缺自然是物理学领域,乃至整个自然科学领域中重要的问题之一。相关研究既取得重大进展又仍是目前活跃的前沿研究领域[72]。
本文对强相互作用系统的对称性及其破缺进行了简要介绍。主要包括三个方面,其一是对称性及其破缺的基本概念与基本的数学上所说的对称性的微观粒子实现;其二是早期宇宙强相互作用物质演化过程的对称性及其破缺,尤其是可见物质质量的产生以及强相互作用等基本相互作用的对称性及其破缺;其三是原子核的对称性及其破缺,尤其是作为强相互作用多体系统的束缚态研究中的基本理论方法、(多粒子)壳模型及玻色子近似模型、集体运动的描述及集体运动模式演化(形状相变)的研究方法及进展简况。
限于篇幅,本文所介绍的主要是基础性的具有普适意义的内容,没有具体涉及基础性很强但比较专门的内容,例如:关于由夸克胶子到强子的色禁闭(即强子化)问题、原子核及核物质的液气相变问题、内禀节点分析方法及在轻核结构研究中的应用问题、多粒子系统性质计算程序正确性的对称性群链检验方法、原子核的集团结构问题、超重原子核形状相结构及其相变问题、很高自旋态下集体运动的恢复问题、温度等因素对原子核的相结构及相变影响的问题等等。
在结束这一综述之际,我们为这种挂一漏万的内容选取方式深表歉意。同时,考虑其普适性,该文省略了绝大部分的推导,也牺牲了一些数学上和量子(规范)场论层面上的严谨性,这里也深表歉意,并希望私信交流补充。
Symmetries and Their Breaking of Strong Interaction System
-
摘要: 本文简要介绍对称性及其破缺的概念和基本的数学上所说的幺正对称性等的微观粒子实现,从而为利用抽象的数学描述物理问题奠定基础。本文还简要介绍早期宇宙强相互作用物质演化过程的对称性及其破缺,尤其是可见物质质量的产生(比如DCSB)以及强相互作用等基本相互作用的规范对称性和破缺,为有意向探讨早期宇宙强相互作用物质演化的青年学者和研究生提供必要的知识储备,并打开一扇窗口。同时,还简要讨论原子核的对称性及其破缺,尤其是作为强相互作用多体系统的束缚态研究中的基本理论方法、(多粒子)壳模型及相互作用玻色子近似模型(IBM)、集体运动的描述及集体运动模式演化(形状相变)的研究方法及进展简况,提供一些在基本理论方法与前沿研究课题之间建立桥梁的实例。Abstract: This article reviews concisely the symmetries and their breaking of strong interaction system. To establish the bridge between the abstract symmetry concept and principle in mathematics and the application in physics to reveal the underlying principle of strong interaction, we describe not only the abstract concept but also the realization of the unitary and other symmetries with the microscopic particles. We then describe the evolution of the strong interaction matter in the early universe in view of the symmetries and their breaking, especially on the dynamical generation of the observable mass(i.e., DCSB) and those of the strong and other interactions (gauge symmetry and breaking). We make also a survey of the symmetries and their breaking of nucleus, with concentration on the general methods of studying the many-body system in the symmetry point of view, the multi-particle shell model and the interacting boson approximation (IBM), the modes of nuclear collective motion and their evolution (i.e., nuclear shape phase transition). The survey intends to link the fundamental approaches with the practical investigations in the related frontiers of research properly and promptly.
-
图 1 (在线彩图)组分夸克质量、夸克凝聚、
$\pi$ 介子质量和衰变常数随夸克-胶子相互作用的有效强度变化的行为(取自文献[8]),其中(a)为对应手征极限($m_{f}^{0} \!=\! 0$ )情况的结果,(b)为对应超越手征极限 ($m_{f}^{0}\! =\! 5$ MeV)情况的结果图 2 U(5)动力学对称性的典型能谱(其中上侧标记的量子数为
$(\tau , n_{\Delta}^{})$ ,自下而上各组态分别对应nd=0, 1, 2, 3)及与110Cd的低激发态能谱的实验观测结果的比较(取自文献[53])图 3 以N=12为例的SU(3)动力学对称性的典型能谱的一部分(a)及其与156Gd的低激发态能谱(b)的实验观测结果的比较(取自文献[53])
图 4 以N=6为例的SO(6)对称核态的典型能谱的一部分(a,其中上侧标记的量子数为
$(\sigma , n_{\Delta}^{})$ ,自下而上各态分别对应τ=0, 1, 2, 3)及其与196Pt的低激发态能谱的实验观测结果(b)的比较(取自文献[53])图 5 (在线彩图)总玻色子数等于15的具有U(5)对称性的原子核的角动量L=2(a)和角动量L=10(b)的态的位能曲面(对应哈密顿量中参数取
$A_{1}\!=\! 1.0$ MeV,$A_2 \!=\! 0.15$ MeV,$B \!=\! -0.4$ MeV,$C \!=\! 0.006$ MeV,$A_{3} \!= \! A_{4} \!=\! 0$ ,取自文献[58])图 6 N=15的具有SU(3)对称性的原子核的角动量L=0, 4, 10的态的位能曲面(对应参数
$A_3 \!=\! 1$ 。取自文献[58])图 7 (在线彩图)
$N \!=\! 10$ 的具有SO(6)对称性的原子核的位能曲面随角动量变化的行为(对应哈密顿量中参数$A_{4} \!=\! -1$ MeV、$A_{1} = A_{2} = A_{3} = B = C = 0$ 。取自文献[58])图 9 总玻色子数N=15的具有U(5)对称性的核态的相图的计算结果(取自文献[58])
图 10 总玻色子数N=10的具有SO(6)对称性的原子核的相图的计算结果(取自文献[58])
图 11 (在线彩图)F(5)临界点对称性模型的两种特殊情况下对一些典型能谱和E2跃迁几率随系统粒子数
$N$ 变化的行为的计算结果(取自文献[70])表 1 IBM1的对称性群链中各子群的生成元
群 生成元 U(5) $[d^{\dagger}\tilde{d}]^{k}_{q} , \qquad k = 0,1,2,3,4$ SU(3) $ \hat{L}_{q}=\sqrt{10}[d^{\dagger} \tilde{d} ]^{1}_{q} \; , \quad \hat{Q}_{\mu}=[d^{\dagger} s + s^{\dagger}\tilde{d}]^{2}_{\mu} - \frac{\sqrt{7}}{2}[d^{\dagger}\tilde{d}]^{2}_{\mu} $ SO(6) $ [d^{\dagger}\tilde{d}]^{1}_{q} , \qquad [d^{\dagger}\tilde{d}]^{3}_{\nu}\, , \qquad [d^{\dagger} s + s^{\dagger}\tilde{d}]^{2}_{\mu} $ SO(5) $[d^{\dagger}\tilde{d}]^{1}_{q} \, , \qquad [d^{\dagger}\tilde{d}]^{3}_{\nu}$ SO(3) $L_{q}=\sqrt{10}[d^{\dagger} \tilde{d} ]^{1}_{q} $ 表 2 对称性群链中各子群的Casimir算子及其本征值
阶数 表达形式 本征值 $C_{1{\rm U}(5)}$ $\sqrt{5} [d^{\dagger}\tilde{d}]^{0}_{0}$ $n_d$ $C_{2{\rm U}(5)}$ $\sum \limits_{k=0}^{4} [d^{\dagger} \tilde{d}]^{k} \cdot [d^{\dagger}\tilde{d})]^{k}$ $n_d (n_d + 4)$ $C_{2{\rm SU}(3)}$ $2 \hat{Q} \cdot \hat{Q} + \frac{3}{4} \hat{L} \cdot \hat{L}$ $\begin{array}{l} \lambda ^2 +\mu ^2 + \lambda \mu\\+3(\lambda + \mu) \end{array}$ $C_{2{\rm O}(6)}$ $\begin{array}{l} [d^{\dagger} s + s^{\dagger}\tilde{d}]^{2}_{\mu} \cdot [d^{\dagger} s + s^{\dagger}\tilde{d}]^{2}_{\mu}\\+ 2\sum \limits_{k=1,3} [d^{\dagger}\tilde{d}]^{k}_{q} \cdot [d^{\dagger}\tilde{d}]^{k}_{q} \end{array}$ $\sigma (\sigma + 4)$ $C_{2{\rm O}(5)}$ $2 \sum \limits_{k=1,3} [d^{\dagger}\tilde{d}]^{k}_{q} \cdot [d^{\dagger}\tilde{d}]^{k}_{q} $ $\tau ( \tau + 3)$ $C_{2{\rm O}(3)}$ $\hat{L} \cdot \hat{L} $ $L(L+1)$ -
[1] 孙洪洲, 韩其智. 李代数李超代数及在物理中的应用[M]. 北京: 北京大学出版社, 1999. SUN H Z, HAN Q Z. Lie Algebras, Lie Superalgebras and Applications in Physics[M]. Beijing: Peking University Press. 1999. (in Chinese) [2] 刘玉鑫. 李群和李代数及其应用[M]. 北京: 北京大学出版社, 2020 (正编印). LIU Y X. Lie Group, Lie Algebra and Their Applications[M]. Beijing: Peking University Press, 2020. (in Chinese) [3] ATIYAH M. The Millennium Prize Problems[M]. New York: Springer, 2000. [4] KENNEDY D, NORMAN C. Science, 2005, 309(5731): 75. doi: 10.1126/science.309.5731.75 [5] GROSS D J, WILCZEK F. Phys Rev Lett, 1973, 30: 1343; POLITZER H D. Phys Rev Lett, 1973, 30: 1346. [6] ROBERTS C D, WILLIAMS A G. Prog Part Nucl Phys, 1994, 33: 477; ROBERTS C D, SCHMIDT S M. Prog Part Nucl Phys, 2000, 45: S1; ALKOFER R, VON SMEKAL L. Phys Rept, 2001, 353: 281; MARIS P ROBERTS C D. Int J Mod Phys, E, 2003, 12(3): 297; BASHIR A, CHANG L, CLOET I C, et al. Commun Theor Phys, 2012, 58(1): 79. [7] MCLERRAN L, PISARSKI R D. Nucl Phys, A, 2007, 796(1): 83. [8] WANG K L, QIN S X, LIU Y X, et al. Phys Rev D, 2012, 86(11): 114001. doi: 10.1103/PhysRevD.86.114001 [9] QIN S X, CHANG L, CHEN H, et al. Phys Rev Lett, 2011, 106: 172301. doi: 10.1103/PhysRevLett.106.172301 [10] GAO F, LIU Y X. Phys Rev D, 2016, 94: 076009. doi: 10.1103/PhysRevD.94.076009 [11] GELL-MANN M, OAKES R J, RENNER B. Phys Rev, 1968, 175(5): 2195; GLASHOW S L, WEINBERG S Phys Rev Lett, 1968, 20(5): 224. [12] CHANG L, ROBERTS C D. Phys Rev C, 2012, 85: 052201(R). [13] CHANG L, LIU Y X, ROBERTS C D. Phys Rev Lett, 2011, 106: 072001; QIN S X, CHANG L, LIU Y X, et al. Phys Lett B, 2013, 722: 384; TANG C, GAO F, LIU Y X. Phys Rev D, 2019, 100: 056001. [14] CLOET I C, ROBERTS C D. Prog Part Nucl Phys, 2014, 77(1): 1; EICHMANN G, SANCHIS-ALEPUZ H, WILLIAMS R. Prog Part Nucl Phys, 2016, 91(1): 1. [15] CHANG L, CLOET I C, COBOS-MARTINEZ J J, et al. Phys Rev Lett, 2013, 110(13): 132001; CHANG L, CLOET I C, ROBERTS C D, et al. Phys Rev Lett, 2013, 111(14): 141802; BINOSI D, CHANG L, PAPAVASSILIOU J, et al. Phys Lett B, 2015, 742(2): 183. [16] QIN S X, ROBERTS C D, SCHMIDT S M. Few-body Syst, 2018, 97(11): 114017; WANG Q W, QIN S X, ROBERTS C D, et al. Phys Rev D, 2018, 98(5): 054019; QIN S X, ROBERTS C D, SCHMIDT S M. Few-body Syst, 2019, 60(2): 26. [17] GRIBOV V N. Nucl Phys, B, 1978, 139(1-1): 1. [18] VANDERSICKEL N, ZWANZIGER D. Phys Rep, 2012, 520(4): 175. doi: 10.1016/j.physrep.2012.07.003 [19] ’THOOFT G. Nucl Phys B, 1971, 33: 173. [20] WEINBERG S. Phys Rev Lett, 1967, 19(21): 1264. doi: 10.1103/PhysRevLett.19.1264 [21] SALAM A. Weak and Electromagnetic Interactions[C]// SVARTHOLM N. Proc of the 8th Nobel Symposium on Elementary Particle Theory, Relativistic Groups and Analyticity, Sweden, Stockholm: Almquvist and Wiksell, 1968: 367. [22] WU Y L. Phys Rev D, 2016, 93: 024012; Eur Phys J C, 2018, 78: 28. [23] WANG J J, SUN H Z. High Energy Phys, Nucl Phys(Chinese version), 1990, 14: 842; High Energy Phys, Nucl Phys(English version), 1993, 17(4): 395. [24] LIU Y X, SUN H Z, ZHAO E G. Comput Phys Commnn, 1992, 70: 154; LIU Y X, HAN Q Z, WANGJ J, Comput Phys Commun, 1995, 85: 89; WANG J J, HAN Q Z, LIU Y X. Comput Phys Commun, 1995, 85(1): 99. [25] GINOCCHIO J N, HAXTON W C. The Fractional Quantum Hall Effect and the Rotation Group[C]//GRUBER B.Symmetries in Science VI. New York: Springer, 1993: 263. [26] ZAMICK L, ESCUDEROS A. Phys Rev C, 2005, 71: 054308. Phys Rev C, 2005, 72: 044317. [27] ZHAO Y M, ARIMA A. Phys Rev C, 2003, 68: 044310; Phys Rev C, 2004, 70: 034306; Phys Rev C, 2005, 71: 047304; Phys Rev C, 2005, 72: 054307; Phys Rev C, 2005, 72: 064333; ZHANG L, ZHAO Y M, JIA L Y, et al. Phys Rev C, 2008, 77: 014301; JIANG H, PAN F, ZHAO Y M, et al. Phys Rev C, 2013, 87: 034313; BAO M, ZHAO Y M, ARIMA A. Phys Rev C, 2016, 93: 014307. [28] TALMI I. Phys Rev C, 2005, 72: 037302. doi: 10.1103/PhysRevC.72.037302 [29] QI C. Phys Rev C, 2010, 81: 034318; QI C, WANG X B, XU Z X, et al. Phys Rev C 2010, 82: 014304. [30] 孙洪洲. 高能物理与核物理, 1980, 4: 478. SUN H Z. High Energy Physics and Nuclear Physics, 1980, 4: 478. (in Chinese) [31] SHALIT A D, TALMI I. Nuclear Shell Theory[M]. New York: Academic Press, 1963. [32] LAWSON R D. Theory of The Nuclear Shell Model[M]. Oxford: Oxford University Press, 1980. [33] SUN H Z, HAN Q Z, ZHANG M, et al. Commun Theor Phys, 1989, 11(4): 441; Commun Theor Phys, 1989, 11(4): 449. [34] SUN H Z, HAN Q Z, WANG J J. Commun Theor Phys, 1993, 19(4): 467; Commun Theor Phys, 1993, 20(3): 329. [35] SUN H Z, ZHANG M, HAN Q Z, et al. J Phys A, 1989, 22(22): 4769; J Phys A, 1990, 23(11): 1959. [36] SUN H Z, HAN Q Z, CHIANG H C, et al. Commun Theor Phys, 1995, 28(1): 19. [37] HAN Q Z, HSIEH S T, CHIANG H C, et al. Comput Phys Commun, 1995, 85: 463. doi: 10.1016/0010-4655(94)00136-P [38] CWIOK S, HEENEN P H, NAZAREWICZ W. Nature, 2005, 433(7027): 705. doi: 10.1038/nature03336 [39] GINOCCHIO J N. Phys Lett B, 1978, 79(3): 173; Ann Phys (N.Y.), 1980, 126(1): 234. [40] WU C L, FENG D X, CHEN X G, et al. Phys Lett B, 1986, 168(4): 313; Phys Rev C, 1987, 36(3): 1157. [41] CHEN J Q. Nucl Phys A, 1997, 626(3): 686; CHEN J Q, LUO Y A. Nucl Phys A, 1998, 639(3-4): 615; LUO Y A, CHEN J Q, DRAAYER J P. Nucl Phys A, 2000, 669(1-2): 101; ZHAO Y M, YOSHINAGA N, YAMAJI S, et al. Phys Rev C, 2000, 62(1): 014304; ZHAO Y M, YAMAJI S, YOSHINAGA N, et al. Phys Rev C, 2000, 62(1): 014315. [42] HOU Z F, ZHANG Y, LIU Y X. Phys Lett B, 2010, 688(4-5): 298. doi: 10.1016/j.physletb.2010.04.015 [43] GUIDRY M, WU L A, SUN Y, WU C L. Phys Rev B, 2001, 63(13): 134516; WU L A, GUIDRY M, SUN Y, et al. Phys Rev B, 2003, 67(1): 014515; SUN Y, GUIDRY M, WU C L. Phys Rev B, 2006, 73(13): 134519; Phys Rev B, 2007, 75(13): 134511. Phys Rev B, 2008, 78(17): 174524; GUIDRY M, SUN Y, WU C L. New J Phys, 2009, 11(12): 123023. [44] WU L A, MURPHY M, GUIDRY M. Phys Rev B, 2017, 95: 115. [45] IACHELLO F, ARIMA A. Phys Lett B, 1974, 53(4): 309; ARIMA A, IACHELLO F. Phys Rev Lett, 1975, 35(16): 1069. [46] 龙鲁桂. 质子-中子相互作用玻色子模型及其各种极限[D]. 北京: 清华大学, 1987. LONG L G. Proton-Neutron Interacting Boson Model and Its Dynamical Symmetries[D]. Beijing: Tsinghua University, 1987. (in Chinese) [47] HAN Q Z, SUN H Z, LI G H. Phys Rev C, 1987, 35(2): 786. doi: 10.1103/PhysRevC.35.786 [48] SUN H Z, MOSHINSKY M, FRANK A, et al. Kinam, 1983, 5: 135. [49] LIU Y X, SUN H Z, ZHAO E G. Commun Theor Phys, 1997, 27(1): 71; LIU Y X, GAO D F. Phys Rev C, 2001, 63(4): 044317. [50] 刘玉鑫. spdf相互作用玻色子模型及其应用[D]. 北京: 清华大学, 1992. LIU Y X. spdf Interacting Boson Model and Its Applica-tions[D]. Beijing: Tsinghua University, 1992. (in Chinese) [51] IACHELLO F, SCHOLTEN O. Phys Rev Lett, 1979, 43(10): 679; IACHELLO F. Phys Rev Lett, 1980, 44(12): 772. [52] SUN H Z, HAN Q Z. Physica Energiae Fortis et Physica Nuclearis, 1982, 6(4): 401; SUN H Z, FRANK A, VAN ISACKER P. Phys Lett B, 1983, 124(5): 275; SUN H Z, FRANK A, VAN ISACKER P. Phys Rev C, 1983, 27(5): 2430; SUN H Z, VALLIERES M, FENG D H, et al. Phys Rev C, 1984, 29(1): 352(R); LING Y S, ZHANG M, XU J M, et al. Phys Lett B, 1984, 148(1-3): 13; VAN ISACKER P, FRANK A, SUN H Z. Ann Phys (N.Y.), 1984, 157(1): 183; SUN H Z, FENG D H, VALLIIERES M, et al. Phys Rev C, 1985, 31(5): 1899. [53] IACHELLO F, ARIMA A. The Interacting Boson Model[M]. Cambridge (UK): Cambridge University Press, 1987 [54] METZ A, JOLIE J, GRAW G, et al. Phys Rev Lett, 1999, 83(8): 1542. doi: 10.1103/PhysRevLett.83.1542 [55] KUYUCAK S, MORRISON I. Phys Rev Lett, 1987, 58(4): 315; Phys Rev C, 36(2): 774. [56] 穆良柱. 转动驱动的原子核形状相变的相互作用玻色字模型研究[D]. 北京大学, 2005 MU L Z. Study of Rotation-Driven Nuclear Shape Phase Transitions within the Interacting Boson Model[D]. Peking University, 2005. (in Chinese) [57] REGAN P H, BEAUSANG C W, ZAMFIR N V, et al. Phys Rev Lett, 2003, 90(15): 152502. doi: 10.1103/PhysRevLett.90.152502 [58] ZHAO Y, LIU Y, MU L Z, et al. Int J Mod Phys, E, 2006, 15(8): 1711. doi: 10.1142/S0218301306005502 [59] LIU Y X, MU L Z, WEI H Q. Phys Lett B, 2006, 633(1): 49. doi: 10.1016/j.physletb.2005.11.018 [60] ZAMFIR N V, VONBRENTANO P, CASTEN R F, et al. Phys Rev C, 2002, 66(2): 021304(R). doi: 10.1103/PhysRevC.66.021304 [61] ZHANG Y, HOU Z F, LIU Y X. Phys Rev C, 2007, 76(1): 011305(R). doi: 10.1103/PhysRevC.76.011305 [62] CAPRIO M A, IACHELLO F. Phys Rev LETT, 2004, 93(24): 242502. doi: 10.1103/PhysRevLett.93.242502 [63] IACHELLO F. Phys Rev LETT, 2003, 91(13): 132502. doi: 10.1103/PhysRevLett.91.132502 [64] CEJNAR P, JOLIE J, CASTEN R F. Rev Mod Phys, 2010, 82(3): 2155. doi: 10.1103/RevModPhys.82.2155 [65] IACHELLO F. Phys Rev Lett, 2000, 85(17): 3580. doi: 10.1103/PhysRevLett.85.3580 [66] IACHELLO F. Phys Rev Lett, 2001, 87(5): 052502. doi: 10.1103/PhysRevLett.87.052502 [67] CASTEN R F, ZAMFIR N V. Phys Rev Lett, 2000, 85(17): 3584. doi: 10.1103/PhysRevLett.85.3584 [68] CASTEN R F, ZAMFIR N V. Phys Rev Lett, 2001, 87(5): 052503. doi: 10.1103/PhysRevLett.87.052503 [69] ZHANG D L, LIU Y X. Phys Rev C, 2002, 65(5): 057301. doi: 10.1103/PhysRevC.65.057301 [70] ZHANG Y, LIU Y X, PAN F, et al. Phys Lett B, 2014, 732(1): 55. [71] ROWE D J, TURNER P S, ROSENSTEEL G. Phys Rev Lett, 2004, 93(23): 232502. doi: 10.1103/PhysRevLett.93.232502 [72] Committee on the Assessment of and Outlook for Nuclear Physics. Nuclear Physics: Exploring the Heart of Matter[M]. Washington DC: The National Academies Press, 2012 . -








 下载:
下载:





































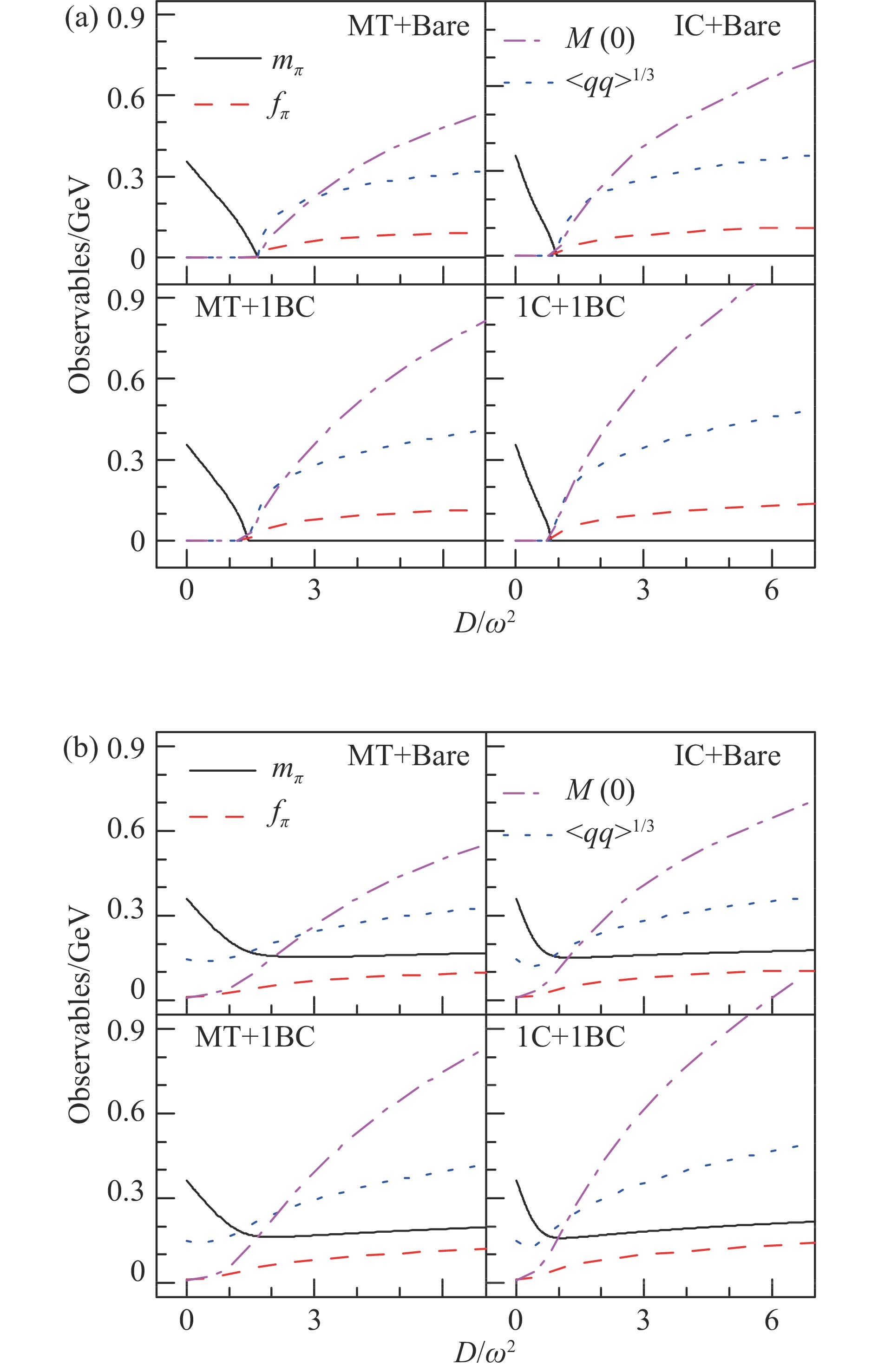




























































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号