-
众所周知,强相互作用将夸克和胶子束缚在一起形成强子——比如质子和中子等。当前,描述强相互作用的基本理论是量子色动力学(QCD),它是基于色
$ SU(3) $ 对称性的非Abelian规范场论。QCD的非Abelian特性造成很多奇异的现象,比如低能标下的色禁闭和高能标下的渐进自由。色禁闭是指强相互作用在低能标下,例如真空中,总是将承载色荷的粒子——夸克和胶子囚禁在色单态的强子中;这使得孤立的夸克和胶子是不能够被观测到的。然而,随着能标的提高,例如增加一团强子物质的温度或重子数密度,QCD会发生解除禁闭的强子-夸克相变,从而形成退禁闭的夸克胶子物质。假如能标足够高,强相互作用耦合常数会变得很小,而且会随着能标的继续增加而越来越小,这一性质即QCD的渐进自由[1-2]。渐进自由特性使得在极高能标下我们可以对QCD施行微扰论计算。实际上,实现退禁闭的强子-夸克相变的条件是极为苛刻的,因为QCD的禁闭能标
$ \Lambda_{\rm{QCD}}\sim 200 $ MeV 是很高的,这转换成温度大概为$ T_c\sim \Lambda_{\rm{QCD}}\sim 10^{12} $ K。这样的高温在宇宙大爆炸之后大约$ 10^{-6} $ s的时候出现过,在地面上,只有高能重离子碰撞才能够达到。目前运行中的高能重离子碰撞机包括美国纽约布鲁克海文国家实验室的相对论重离子对撞机(RHIC)和欧洲核子中心的大型强子对撞机(LHC),前者从2000年开始运行,当前其运行的Au+Au碰撞的最高能量可以达到$ \sqrt{s} $ =200 GeV;后者从2010年开始运行,当前其运行的Pb+Pb碰撞的最高能量可以达到$ \sqrt{s} $ =5.02 TeV。在这些对撞机中,两个原子核被加速到接近于光速运动,然后碰撞,大量的动能聚集在非常小的空间中形成极高的能量密度从而使得退禁闭所需要的条件得以满足。这样产生的退禁闭的夸克胶子物质通常称为夸克胶子等离子体(QGP),它的内部依然存在剧烈的相互作用从而使得它可以在极短的时间内达到局域热平衡。RHIC和LHC 实验产生了大量的数据来支持QGP 的存在,同时也揭示了QGP的一系列非比寻常的性质。比如,QGP是一团“最理想的流体”,即它的切粘滞系数与熵密度之比是我们目前所知的 所有流体中最小的;QGP 可以与高能喷注(即具有很大的横动量的粒子或粒子束)剧烈相互作用从而使得穿行于QGP 中的高能喷注很快失去能量,这一现象称为喷注淬火;由于QGP是一团色等离子体,它会屏蔽处于其中的色荷(类似于电磁等离子体中电荷受到的Debye屏蔽),因此QGP中的重夸克偶素,比如$ J/\Psi $ ,很容易由于这种色屏蔽作用而解离,这样在末态观察到的$ J/\Psi $ 数目就会减少,这一现象称为$ J/\Psi $ 压低;详见文献[3]的介绍。除了上面这些有趣的现象和效应外,近年来人们又认识到高能重离子碰撞中产生的QGP实际上是处于极强磁场和涡旋场中的,并且磁场和涡旋场会在QGP中引起奇妙的宏观量子效应。这些效应反过来又增加了我们探测和理解QCD和QGP的手段[4-7]。这成为近年来高能核物理一个重要的研究方向。接下来我们首先从重离子碰撞中磁场和涡旋场的产生谈起。我们将采用自然单位制
$ c\! =\! \hbar \!=\! k_B \!\!=\! 1 $ 。 -
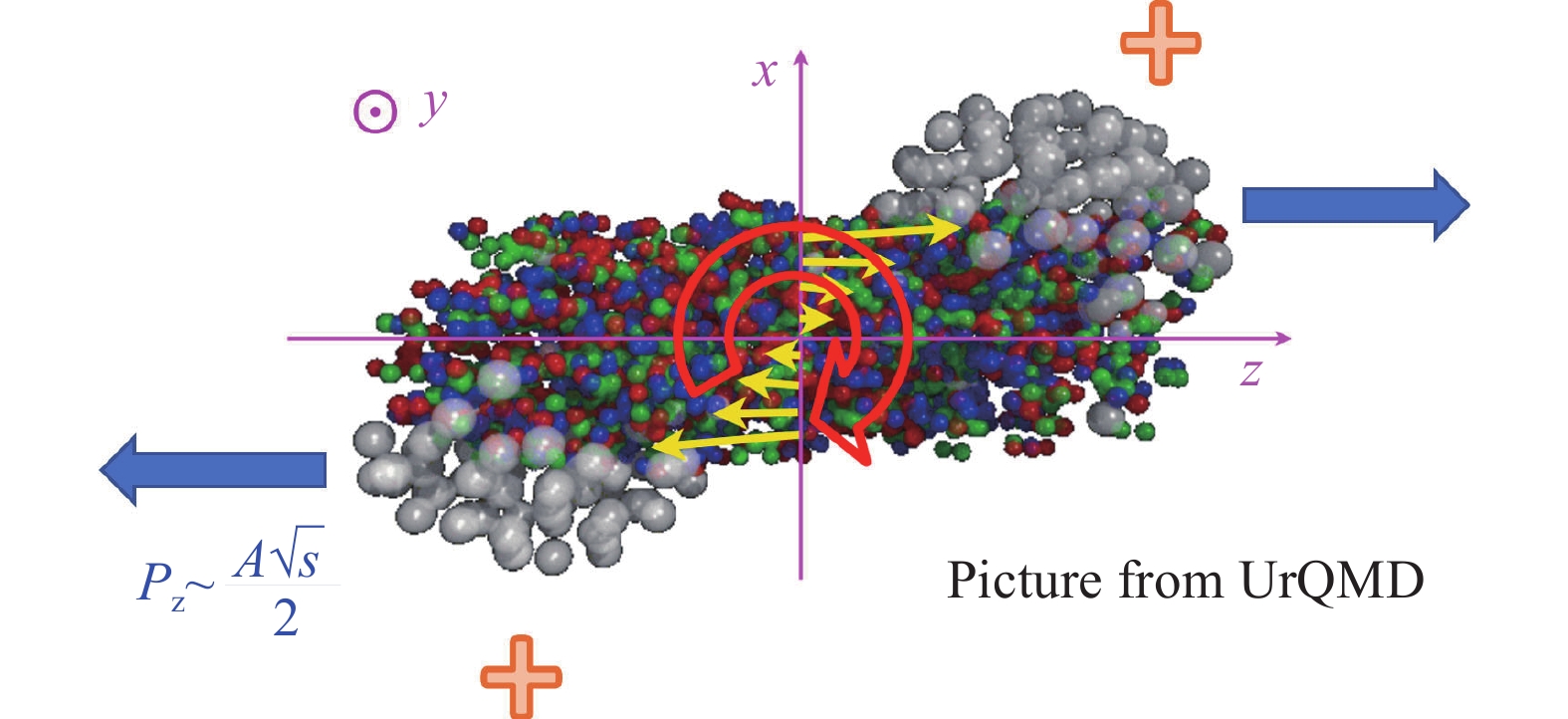
我们考虑两个原子核发生非对心碰撞的情况,其碰撞几何如图1所示,其中
$ z $ 方向为束流方向(与弹 核(projectile)运动方向相同),$ x $ 方向为碰撞参数方向(从靶核(target)指向弹核),$ y $ 方向沿着$ \hat{ z}\times\hat{ x} $ ,$ x - z $ 平面构成作用平面(reaction plane)。由于原子核携带正电,当它在高速运动时就形成一股强瞬时电流,因而产生环绕其运动方向的瞬时磁场。在两个原子核碰撞的瞬间,由于几何对称性,容易看出碰撞中心处的磁场相叠加并沿着$ -y $ 方向。我们可以简单估计一下该磁场的强度。考虑RHIC实验中Au+Au在$ \sqrt{s} \!=\! 200 $ GeV,碰撞参数$ b \!=\! 10 $ fm情况下的碰撞,假设电荷集中于原子核的中心,那么我们利用Biot-Savart公式得到磁场的$ y $ 分量为$$ eB_y\approx -2Z_{\rm{Au}} \gamma\frac{e^2}{4 \pi}\frac{v_z}{(b/2)^2}\approx -10 m_ \pi^2\approx -10^{19}\;{\rm G},$$ (1) 其中
$ e $ 为基本电荷(电子电荷的绝对值),$ m_ \pi\!\approx \!140 $ MeV为$ \pi $ 介子质量,$v_z \!=\! \sqrt{1-(2m_N/\sqrt{s})^2}\approx 0.999\,95$ ($ m_N $ 为核子质量)为原子核相对于实验室参考系的运动速度,$ \gamma \!=\! 1/\sqrt{1-v_z^2}\approx 100 $ 为Lorentz收缩因子,$ Z_{\rm{Au}} \!=\! 79 $ 为Au原子核中的质子数。这是非常强的磁场,它远大于电子和轻夸克(u, d夸克)的质量平方,因而有能力引发重要的量子效应。实际上这也是我们目前所知的当前宇宙中最强的磁场,比普通中子星甚至磁星(magnetar)的表面磁场还要强很多,后者约为
$ 10^{14}\sim 10^{15} $ Gauss。我们上面只是粗糙的估计,更准确的计算可以通过比如HIJING[8-9]、AMPT[10]等输运模型来给出所有碰撞前和碰撞后的带电粒子的动量和位置,然后采用Lienard-Wiechert 势[5]来计算。同时我们也可以估计量子修正对计算结果的影响(实际上很小)[5],考虑质子电荷分布的影响[11-12],考虑逐事例涨落造成的磁场大小和方向的涨落[11,13-14] 等。近年来这方面的研究相当活跃,这里无法列举所有文献,详见综述文章[5-6]。我们在图2中所示为采用HIJING 计算出的RHIC Au+Au碰撞和LHC Pb+Pb 碰撞中磁场和电场随碰撞参数的变化;另外,比较$ 200 $ GeV和$ 2.76 $ TeV时的电磁场可以看出电磁场的强度大致正比于碰撞能量$ \sqrt{s} $ [14]。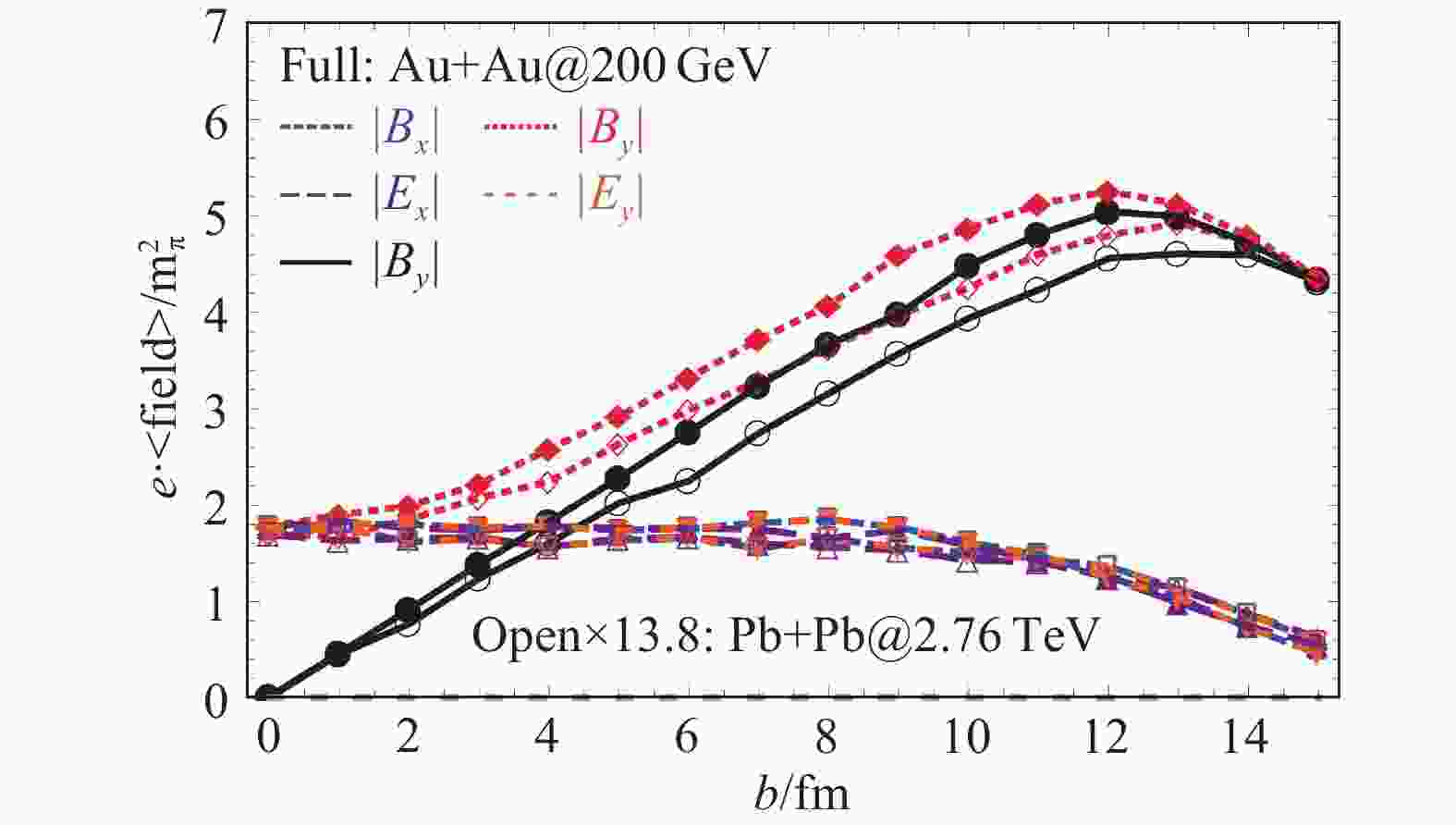
图 2 (在线彩图)重离子碰撞中产生的电磁场随碰撞参数的变化[14]
再次考虑非对心碰撞,设碰撞能量为
$ \sqrt{s} $ ,碰撞参数为$ b $ ,那么系统就具有总角动量$$ J_y\approx -\frac{Ab\sqrt{s}}{2}, $$ (2) 其中
$ A $ 为每个原子核的总核子数。对于RHIC实验中Au+Au在$ \sqrt{s} $ =200 GeV,$ b $ =10 fm 的碰撞中,我们得到$ |J_y|\approx 10^6\hbar $ 。相较于碰撞过程产生的强子的总自旋来说(譬如产生约1 000个强子,每个强子自旋$ \sim\hbar $ ,那么总自旋约$ 10^3\hbar $ ),这是非常巨大的角动量。在碰撞后,这一总角动量的一部分会沉积在碰撞区域被产生的夸克胶子物质携带。由于夸克胶子物质的流体特性,这部分角动量不会使得夸克胶子物质如同刚体那样整体转动起来,而是在其中诱导出强烈的流体涡旋。流体涡旋的强度由涡度(vorticity)给出,用$ {{\omega}} $ 表示,在非相对论流体力学中,它定义为$$ {{\omega}} = \frac{1}{2}{{\nabla}}\times{{v}}, $$ (3) 其中
$ {{v}} $ 为流体的速度。涡度的物理含义为流体微元的定域角速度。在相对论流体力学中,对应于不同的物理目标,我们可以定义不同的涡度。几种常见的涡度为运动涡度、温度涡度、热涡度等。运动涡度为上面非相对论涡度的自然推广,$$ \omega^ \mu = \frac{1}{2} \epsilon^{ \mu \nu \rho \sigma}u_ \nu \partial_ \rho u_ \sigma, $$ (4) 其中:
$ u^ \mu \!=\! \gamma(1,{{v}}) $ 为流体4-速度,$ \gamma = 1/\sqrt{1-{{{v}}}^2} $ 为Lorentz收缩因子。通常为了方便也经常使用张量表示$ \omega_{ \mu \nu}\! =\! (1/2)( \partial_ \nu u_ \mu\!- \!\partial_ \mu u_ \nu) $ ,因而$ \omega^ \mu \!=\! -(1/2) \epsilon^{ \mu \nu \rho \sigma}u_ \nu \omega_{ \rho \sigma} $ 。温度涡度定义为$$ \omega_{\rm T}^{ \mu} = \frac{1}{2} \epsilon^{ \mu \nu \rho \sigma} u_ \nu \partial_ \rho (Tu_ \sigma), $$ (5) 其中
$ T $ 为温度。它的特殊性在于对于理想中性流体而言,$ T \omega_{\rm T}^ \mu $ 是守恒的,即$ \partial_ \mu(T \omega_{\rm T}^{ \mu}) = 0 $ 。热涡度定义为(以张量形式)$$ \varpi_{ \mu \nu} = \frac{1}{2}\big[ \partial_ \nu( \beta u_ \mu)- \partial_ \mu( \beta u_ \nu)\big], $$ (6) 其中
$ \beta \!=\! 1/T $ 。热涡度的重要性在于它刻画了处于整体热平衡下的转动流体的特征,并在这种情况下它决定了 与流体达到热平衡的粒子的自旋极化密度[15],我们后面会重点讨论粒子的自旋极化问题。图3给出的是采用HIJING模型计算出的非相对论和相对论涡度随着碰撞参数的变化[16];它们先随$ b $ 增加,因为沉积的角动量在增加,后减小,因为两个原子核的碰撞区域最后会变小。图3 是先对每个碰撞事例的涡度在碰撞区域做了空间平均再对$ 10^5 $ 个碰撞事例平均之后的结果。我们看到涡度可以达到$ \sim 10 $ MeV(或等价地$ \sim10^{21} $ s–1)的量级,这是我们迄今为止所知道的最大的流体涡度,因而我们也称QGP 为“the most vortical fluid”。图4显示的是采用AMPT 模型计算出的热涡度随时间的变化,可以看到随着碰撞能量增加热涡度反而减小[17];这是一种纯粹的相对论相应,我们后面会分析其原因。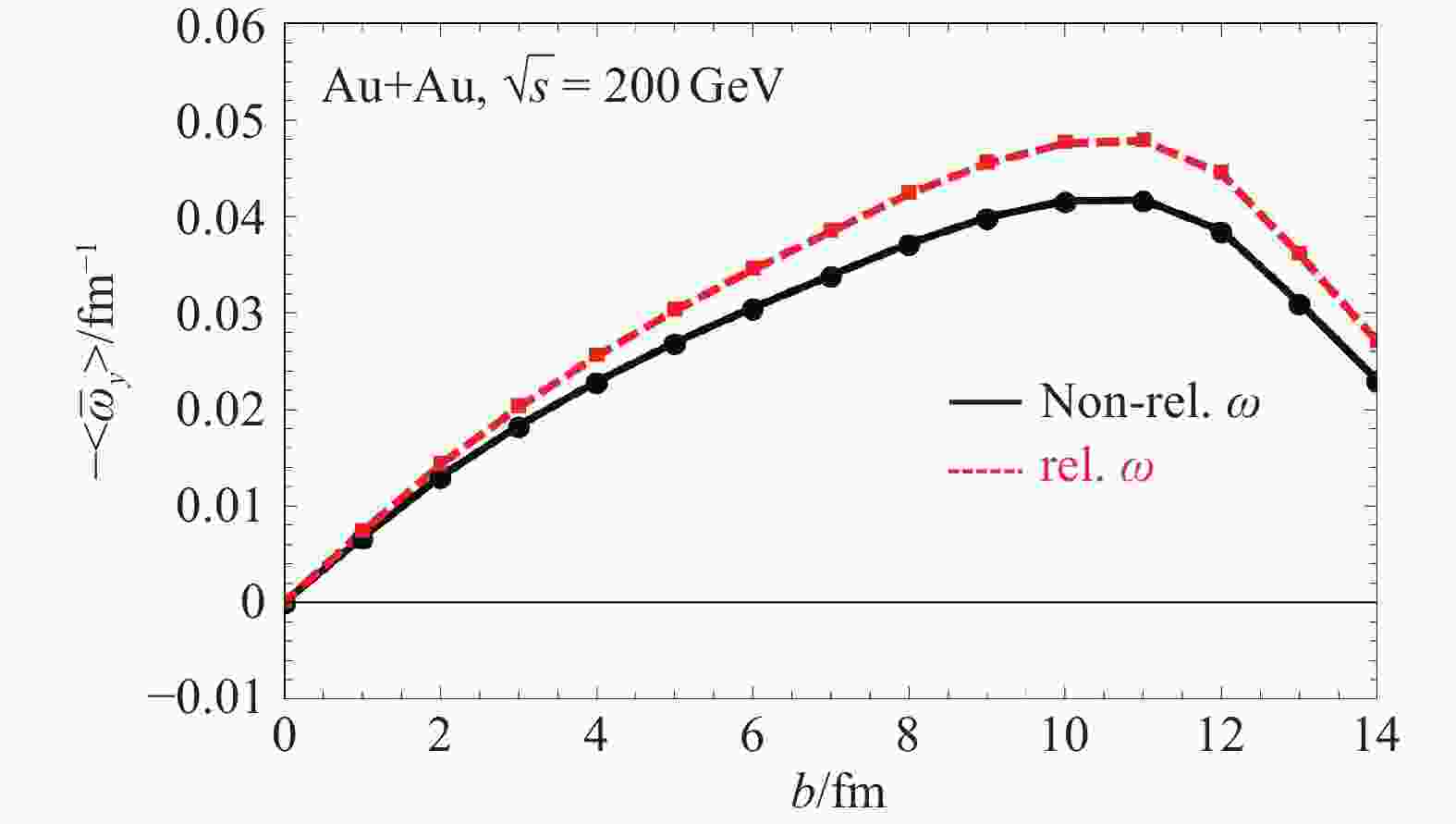
图 3 (在线彩图)重离子碰撞中产生的非相对论涡度和相对论运动涡度随碰撞参数的变化[16]
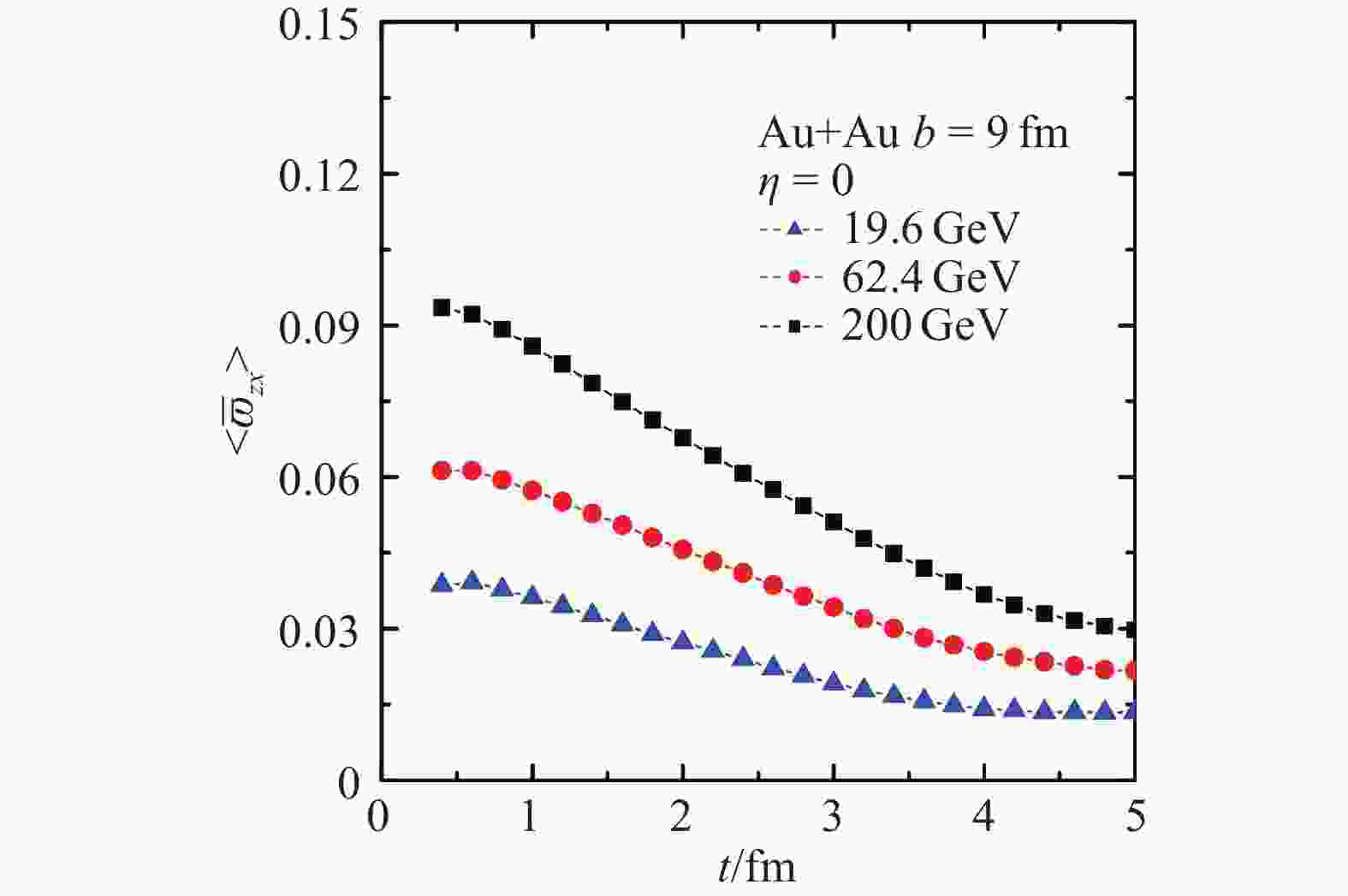
图 4 (在线彩图)重离子碰撞中产生的热涡度随时间的变化[17]
-
既然高能重离子碰撞可以产生极强的磁场和流体涡旋,那么它们对QGP有什么影响呢?是否可以提供给我们探测QGP性质的新的手段呢?在本节我们将讨论与电磁场和流体涡旋密切相关的手征反常输运现象的成因和性质。下一节我们讨论它们在重离子碰撞实验中的意义和目前的实验进展。
要理解手征反常输运现象,我们需要先回顾一下手征反常的物理内涵。我们考虑均匀磁场中带电量为
$ e> 0$ 的无质量Dirac粒子;设磁场方向为$ z $ 。直接求解Dirac方程可以给出Landau能级$ {\cal{E}}_n $ 满足$$ {\cal{E}}_n^2 = p_z^2+2neB, $$ (7) 其中
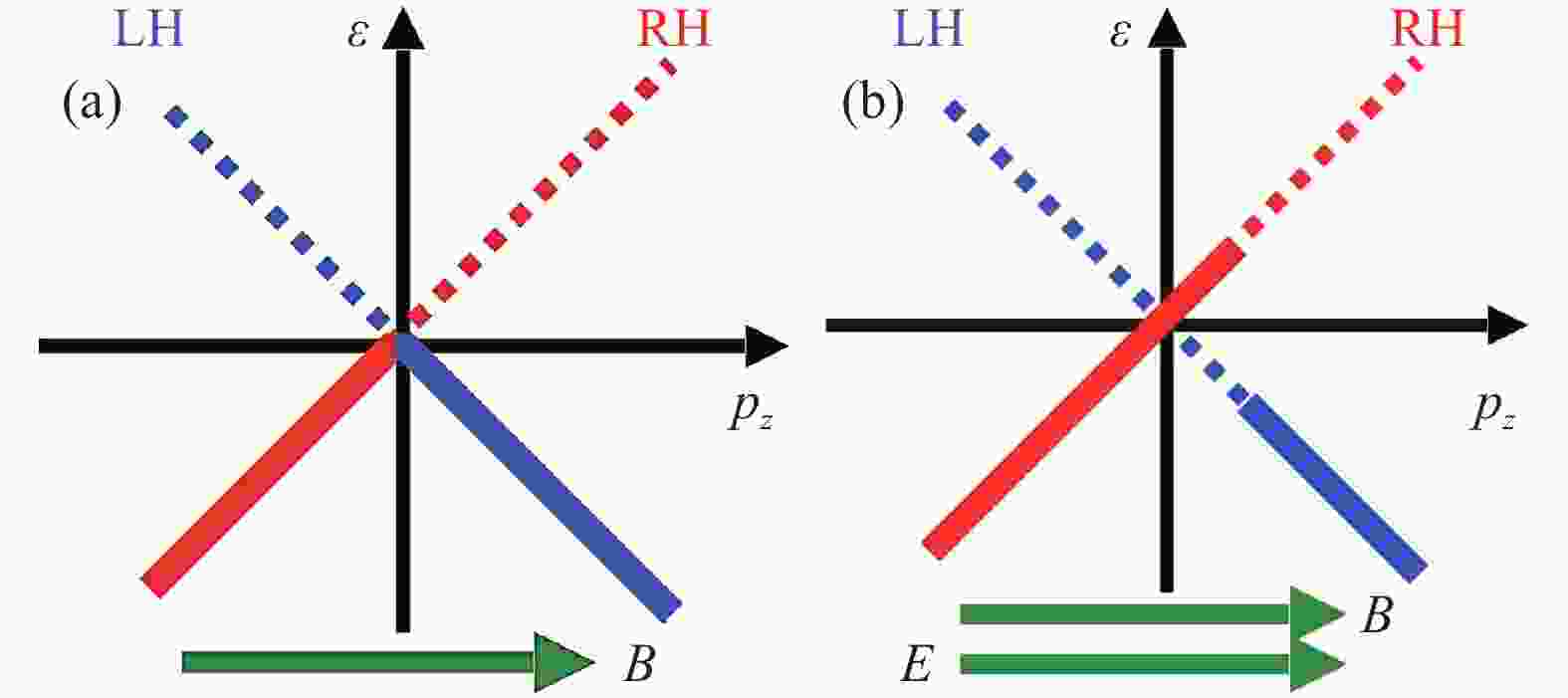
$ n \!=\! 0,1,2,\cdots $ 标记不同Landau能级,$ p_z $ 为沿着磁场方向的粒子动量,$ B $ 为磁场大小。对应$ n $ =0的是最低Landau能级(LLL),其色散关系见图5(a)(其中实线表示被粒子占据的态而虚线表示允许占据但尚未被粒子占据的态),它很特殊。首先,它是无能隙的;其次,处于LLL上的费米子自旋是完全极化的,即都沿着磁场方向;再者,LLL的动力学是1+1维的,因为横向运动被禁锢。这时,我们可以定义LLL上的费米子的手征如下:若$ p_z $ 平行于自旋方向则为右手,反之则为左手。在这种情况下,右手和左手费米子数目$ N_{\rm{R}} $ 和$ N_{\rm{L}} $ 都是守恒的,即$ \partial_ \mu J^ \mu_{\rm{R/L}}\! =\! 0 $ ,其中$ J^ \mu_{\rm{R/L}} \!=\! (1/2) {\bar \psi} \gamma^ \mu (1\pm \gamma_5) \psi $ ;或等价地,矢量流与轴矢流是守恒的,即$ \partial_ \mu J^ \mu_{V/A} = 0 $ ,其中$ J^ \mu_{V/A} \!=\! J^ \mu_{\rm{R}}\pm J^ \mu_{\rm{L}} $ 。假如沿着磁场方向施加电场E,如图5(b);那么在$ p_z $ =0附近电场就会使得向下运动的粒子逐步转为向上运动,即将一部分左手粒子变为右手粒子。这时,总粒子数$ N_{ V} \!=\! N_{\rm{R}}+N_{\rm{L}} $ 还是守恒的,但$ N_A\! =\! N_{\rm{R}}-N_{\rm{L}} $ 不再守恒。假设右手和左手费米子的费米面分别为$ p_{\rm{F}}^{\rm{R/L}} $ ,那么我们有$ N_{\rm{R/L}}\! =\! V[p_{\rm{F}}^{\rm{R/L}}/(2 \pi)] [eB/(2 \pi)] $ ,其中$ eB/(2 \pi) $ 为横向态密度,$ V $ 为系统体积。因此,$ {\rm{d}}N_{\rm{R/L}}/{\rm{d}}t \!=\! V[\dot{p}_{\rm{F}}^{\rm{R/L}}/(2 \pi)] [eB/(2 \pi)] = \pm V[eE/(2 \pi)][eB/(2 \pi)] $ ,或等价地,$ {\rm{d}}N_{V}/{\rm{d}}t \!=\! 0 $ ,$ {\rm{d}}N_A/{\rm{d}}t \!=\! Ve^2EB/(2 \pi^2) $ 。后者写为微分形式即是我们熟知的手征反常,$$ \partial_ \mu J^ \mu_A = \frac{e^2}{2 \pi^2}{{E}}\cdot{{B}}. $$ (8) 尽管我们只考虑了LLL的贡献,但得到的手征反常实际上是精确的,因为其他Landau能级对于自旋上下是对称的,故而不贡献。
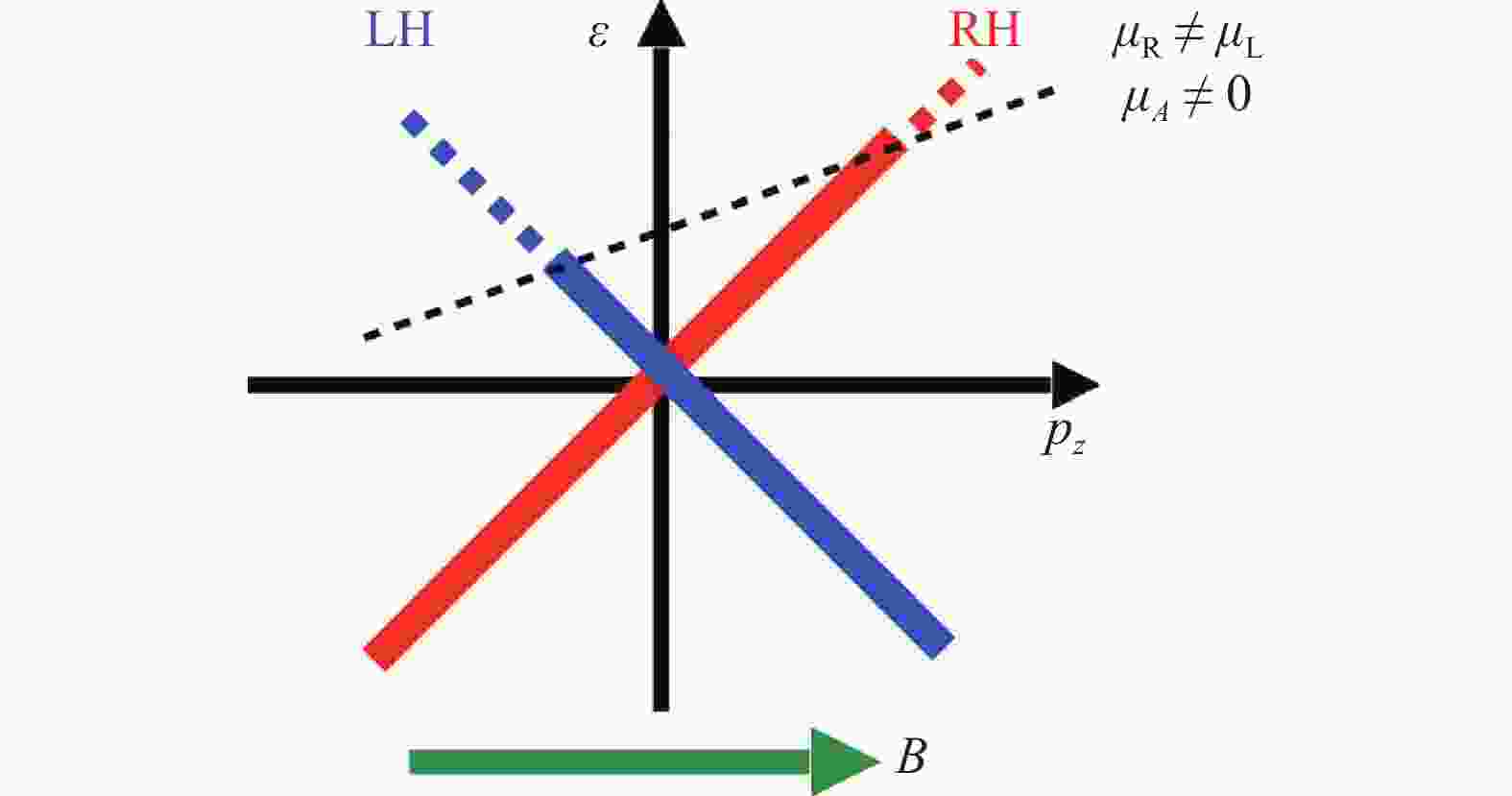
现在我们去掉电场,但考虑右手和左手粒子费米面不相同的情况,如图6所示。由LLL 粒子产生的右手和左手流由相应的数密度乘以粒子的速度(因为粒子无质量,其速度为1)给出,
$$ J_{\rm{R/L}} = \pm n^{}_{\rm{R/L}} = \pm\frac{p_{\rm{F}}^{\rm{R/L}}}{2 \pi}\frac{eB}{2 \pi}, $$ (9) 其中负号是因为左手粒子沿磁场反方向运动。因此我们得到
$$ J_{V} = \frac{p_{\rm{F}}^{\rm{R}}-p_{\rm{F}}^{\rm{L}}}{2 \pi}\frac{eB}{2 \pi} = \frac{ \mu_A}{2 \pi^2}eB, $$ (10) $$ J_{A} = \frac{p_{\rm{F}}^{\rm{R}}+p_{\rm{F}}^{\rm{L}}}{2 \pi}\frac{eB}{2 \pi} = \frac{ \mu_{ V}}{2 \pi^2}eB, $$ (11) 其中
$ \mu_{V/A} \!=\! (p_{\rm{F}}^{\rm{R}}\pm p_{\rm{F}}^{\rm{L}})/2 $ 为矢量化学势和轴化学势。这两个公式分别表达了手征磁效应[18-19]和 手征分离效应[20-21],它们是根源于手征反常的宏观量子效应,不受费米子间相互作用的修改,具有普适性。手征磁效应说明在手征费米系统中(即$ \mu_A\!\neq\! 0 $ 的系统)外磁场可以诱导出沿磁场方向的矢量流(比如电流,重子数流等)。另外,由于磁场和矢量流具有相同的时间反演宇称,手征磁效应是不破坏时间反演不变性的,因而它的发生不会伴随耗散,可看作一种特殊的“超导”现象。由于它的这些新奇的性质,除了在高能核物理领域外,手征磁效应也在凝聚态物理、天体物理、冷原子物理中被广泛研究,特别是在凝聚态物理中,与手征磁效应密切相关的Weyl和Dirac半金属中的负磁阻等现象已被实验证实,可见文献[22]。从式(10)和(11)可以看出,在外磁场中矢量荷与轴荷的演化将会耦合在一起造成波动模式的出现,如同电场和磁场的耦合演化造成电磁波一样。带入流守恒方程
$ \partial_ \mu J^ \mu_{V/A} $ =0,并考虑小的密度涨落,很容易得到两个波动方程$ \partial_t \delta n_{\rm{R/L}}\!\pm\! v_{\rm{CMW}} \partial_z \delta n_{\rm{R/L}} $ =0,其中$ v^{}_{\rm{CMW}} \!=\! eB/ $ $ (4 \pi^2 \chi) $ ($ \chi \!=\! \partial n_{\rm{R}}/ \partial \mu_{\rm{R}}\approx \partial n_{\rm{L}}/ \partial \mu_{\rm{L}} $ )。它们描述了两个密度波,分别沿着和逆着磁场方向传播,波速为$ v^{}_{\rm{CMW}} $ ;它们被称为手征磁波[23]。在经典力学里,Larmor定理告诉我们,一个在磁场中运动的带电粒子等价于一个在以
$ \omega \!=\! eB/(2m) $ 为转动速度的非惯性系中运动的粒子。这启示我们,转动或涡旋也会引起类似于磁场中出现的手征磁效应和手征分离效应的现象。基于这种类比,我们考虑一个在转动参考系中的无质量费米子,它受到Coriolis力的作用,$ {{F}} \!=\! 2|{{p}}|\dot{ x}\times{{\omega}} $ ;这里,我们假设转动速度很小,因而忽略了离心力——它是正比于$ \omega^2 $ 的。由于Coriolis力非常像Lorentz力,我们可以考虑转动“Landau能级”问题。(但应注意,严格地说,由于离心力的存在,转动系中的量子力学问题不是束缚态问题,不会产生真正的Landau能级。)同样地,考虑LLL,左右手粒子的数密度为$ n_{\rm{R/L}} \!=\! (2 \pi)^{-2}\int_0^\infty {\rm{d}}p_z 2p_z \omega \theta(p_{\rm{F}}^{\rm{R/L}}-p_z) \!=\! (p_{\rm{F}}^{\rm{R/L}})^2/ (2 \pi)^2 $ 。我们得到$$ J_{V} = n^{}_{\rm{R}}-n^{}_{\rm{L}} = \frac{ \mu_{ V} \mu_A}{ \pi^2} \omega, $$ (12) $$ J_{A} = n^{}_{\rm{R}}+n^{}_{\rm{L}} = \frac{ \mu^2_{ V}+ \mu_A^2}{2 \pi^2} \omega\text{。} $$ (13) 它们与式(10)和(11)相对应,称为矢量和轴矢手征涡效应[24]。需要指出的是,更严格的推导显示在
$ J_A $ 中应包含一项$ T^2 \omega/6 $ [25]。另外要注意,这些结果只在$ O( \omega) $ 阶上成立。类似于手征磁波的出现,从式(12)和(13)我们也预计会有手征涡波的出现[26]。这时,考虑密度涨落,连续性方程给出
$ \partial_t \delta n_{\rm{R/L}}\pm v_{\rm{CVW}} \partial_z \delta n_{\rm{R/L}} \!=\! 0 $ ,其中$ v_{\rm{CVW}} \!=\! \mu_{V0} \omega/(2 \pi^2 \chi) $ 。这是手征涡波的波动方程,同样也有两支,分别沿着和逆着转动或涡旋方向传播。这里与手征磁波不同的是必须存在背景矢量密度(由$ \mu_{V0} $ 刻画)才会出现手征涡波。我们在图2看到,重离子碰撞中实际上有很强的涨落电场产生。其实在Cu+Au这种非对称碰撞中也有电场产生,其强度可以和磁场比拟[27-28]。那么自然的问题是,是否有由电场引起的反常输运现象呢?答案是肯定的:在同时具有
$ \mu_{ V} $ 和$ \mu_A $ 的情况下,电场会引起轴流,这一现象称为手征电分离效应[29]。微扰QCD计算表明,在高温QGP中的手征 电分离效应由下式给出[30]$$ {{J}}_{A}\approx 14.516\,3 {{\rm{Tr}}}(Q_eQ_A)\frac{ \mu_{ V} \mu_A}{T^2}\frac{T}{g^4\ln(1/g)}e{{E}}, $$ (14) 其中
$ g $ 为QCD耦合常数,$ Q_e $ 和$ Q_A $ 为味道空间中的电荷和轴矩阵。当然,电场也可以引起普通的电流,即欧姆电流。与手征磁效应很不同,手征电分离效应和欧姆电流的产生是伴随着熵的产生的,是有耗散的。同样地,手征电分离效应和普通的欧姆电流也会耦合在一起,形成两支密度波,可以叫做手征电波,其传播速度正比于电场[29]。综上所述,手征费米系统在外电磁场和涡旋场中的输运性质由普通欧姆定律、手征电分离效应、手征磁效应、手征分离效应、手征涡效应描述。同时,有与之伴随的特定波动模式出现,即手征电波、手征磁波、手征涡波。接下来我们考虑它们在重离子碰撞中的意义和实验信号。
-
手征反常输运本身毫无疑问是非常有趣的物理现象,这也是为什么它们吸引包括核物理、粒子物理、凝聚态物理、天体物理、冷原子物理、量子光学等物理学诸多分支的大量学者研究的原因。但对于重离子碰撞物理,它们更具有特别的意义,即它们提供给我们现在已知的仅有的探测高温下QCD是否发生宇称和电荷共轭-宇称破坏(P与CP破坏)的手段。我们知道QCD 理论本身并不排斥出现P与CP破坏,但强相互作用在真空中在很高的实验精度上是P和CP对称的,这即是著名的强CP疑难。但同时理论研究显示,在高温环境中会出现由热效应激发的Sphaleron可以造成QCD中规范场的具有不同拓扑缠绕数的简并基态的经典跃迁[31-32]。而一旦这种跃迁发生,就可能造成QGP中出现宏观的宇称破缺,这时胶子可以通过QCD 层次的手征反常把右手夸克转化为左手夸克或者相反,从而使得左右手夸克的数目有差别,即出现有限
$ \mu_A $ 。这时候,电磁场或流体涡旋就会诱发出手征磁效应、手征涡效应、手征电分离效应等;因此探测手征反常输运对QCD物理来说是具有极为重要的物理意义的。(1) 手征磁效应的探测 由于重离子碰撞中产生的
$ \mu_A $ 具有很强的空间涨落和逐事例涨落,手征磁效应引起的电荷分离平均来讲是零。我们能够观测的是电荷分离的涨落,这可以通过测量下列两粒子关联函数来实现[33],$$ \gamma_{ \alpha \beta} = \langle\cos(\phi_ \alpha+\phi_ \beta-2\Psi_{\rm{RP}}) \rangle, $$ (15) 其中
$ \alpha, \beta \!=\! \pm $ 表示电荷,$ \phi_ \alpha, \phi_ \beta $ 表示粒子的方位角,$ \Psi_{\rm{RP}} $ 表示作用平面的方位角,$ \langle\cdots \rangle $ 表示粒子对平均和事例平均。很容易看出来,若发生相对于作用平面的电荷分离,将使得异号关联$ \gamma_{+-} $ 和$ \gamma_{-+} $ (统一记为$ \gamma_{\rm{OS}} $ )大于零而同号关联$ \gamma_{++} $ 和$ \gamma_{–} $ (统一记为$ \gamma_{\rm{SS}} $ )小于零。实验中,需要引入第三个粒子来确定$ \Psi_{\rm{RP}} $ ,因此实际上是观测三粒子关联函数。RHIC的STAR实验组在2009年发表了第一个测量结果(Au+Au碰撞,$ \sqrt{s}\! =\! 200 $ GeV),如图7所示,定性上和手征磁效应的预言吻合[34]。之后,ALICE 实验组也发布了在LHC能量下的测量结果,也定性满足手征磁效应的预期[35-36],同时STAR实验组也发布了不同碰撞能量下的结果[37],显示在大约20 GeV以上关于$ \gamma $ 关联函数的测量结果并不敏感依赖于碰撞能量,这也与手征磁效应的预期一致。然而,人们很快意识到$ \gamma $ 关联函数中含有很强的非手征磁效应的背景效应的贡献,主要是和横动量守恒以及定域电荷守恒有关的贡献[38-41]。横动量守恒要求若有一个末态强子具有横动量$ {{p}}^{}_{\rm T} $ ,则必然有另一个或一束强子具有横动量$ -{{p}}^{}_{\rm T} $ ;这给$ \gamma_{ \alpha \beta} $ (无论$ \alpha, \beta $ 的符号)一个内蕴的背对背关联,它正比于$ \langle\cos(2\phi+ \pi-2\Psi_{\rm{RP}}) \rangle/N \!=\! -v_2/N $ ,其中$ v_2 $ 为椭圆流系数,$ N $ 为带电粒子多重数。定域电荷守恒是由于我们知道QGP本身是近乎电中性的,因而正、负电荷差不多定域地成对产生(无论来源于共振态衰变、cluster 衰变等等),统计上来说这样产生的正、负电荷会趋向从相近的方位角发射出来,从而给$ \gamma_{\rm{OS}} $ 一个正比于$ \langle\cos(2\phi-2\Psi_{\rm{RP}}) \rangle/N \!=\! v_2/N $ 的贡献。定性上来说,这些背景效应也可以给出与图7类似的结果。对于横动量守恒的贡献,由于它不依赖于电荷,因此不会贡献给$ \Delta \gamma \!=\! \gamma_{\rm{OS}}- \gamma_{\rm{SS}} $ ,所以可用$ \Delta \gamma $ 作为观测量来去除。因此,现在实验上一个主要挑战是如何去除掉来源于定域电荷守恒的贡献。值得指出的是LHC的CMS实验组[42-43]在2017年发表了5.02 TeV碰撞能量下小系统(p+Pb碰撞系统)中
$ \gamma $ 关联函数的测量结果,结果如图7(b)所示。图中可见$ \gamma $ 关联函数在p+Pb和Pb+Pb中的结果基本重合。但是在p+Pb碰撞中磁场方向与物质几何不会有强烈关联,因而$ \gamma $ 关联函数中应几乎不含有手征磁效应的贡献。这说明在5.02 TeV下的大系统(Pb+Pb碰撞系统)中的偏心度较大的碰撞事例中也应该几乎没有手征磁效应的贡献。STAR实验组在2019年也发表类似的结果(对于d+Pb碰撞系统)[44]。这些结果预示着,至少对于偏心度较大的碰撞中,末态观测到的$ \gamma $ 关联函数主要由与椭圆流有关的背景效应贡献。为了能够去除与椭圆流有关的背景贡献,在2018年,RHIC运行了同量素(isobar)碰撞实验。该实验中含有两组碰撞系统,一组为
$ ^{96}_{40}{\rm{Zr}}+^{96}_{40}{\rm{Zr}} $ ,另一组为$ ^{96}_{44}{\rm{Ru}}+^{96}_{44}{\rm{Ru}} $ 。这两组碰撞系统中的原子核具有相同的质量数,但电荷数相差$ 10\% $ 。因此,在相同的碰撞几何和碰撞能量下,可以预计它们产生大致相同的$ v_2 $ 但是产生的磁场相差约$ 10\% $ 。若$ \Delta \gamma $ 中不含有手征磁效应的贡献,它在这两个碰撞系统中的结果应该接近;反之,若$ \Delta \gamma $ 中含有手征磁效应的贡献,我们应该看到它在这两个碰撞系统中的差异。但差异的大小决定于手征磁效应在$ \Delta \gamma $ 中的贡献比例。令$ \epsilon_2 $ 表示火球的椭圆偏心度,令$ R_{ \epsilon_2}\! =\! 2( \epsilon_2^{{\rm{Ru}}+{\rm{Ru}}}- \epsilon_2^{{\rm{Zr}}+{\rm{Zr}}})/( \epsilon_2^{{\rm{Ru}}+{\rm{Ru}}}+ \epsilon_2^{{\rm{Zr}}+{\rm{Zr}}}) $ 表示两个碰撞系统中碰撞偏心度的相对差异(注意,一般来说,$ \epsilon_2 $ 正比于$ v_2 $ );类似地,可以引入$ R_{B^2} $ 来 表示磁场在出平面方向(out-of-plane方向)投影的平方值(理论研究表明,手征磁效应的贡献正比于该量[11-12])的相对大小,引入$ R_{S} $ 来表示观测到的关联函数$ S $ 的相对差异,其中$ S\!=\! N_{\rm{part}} \Delta \gamma $ 为修正的$ \gamma $ 关联函数(乘以$ N_{\rm{part}}\propto N $ 是为了抵消多重数的稀释效应)。因为$ R_{ \epsilon_2} $ ,$ R_{B^2} $ 和$ R_S $ 都必然很小,我们有$ R_{S} \!=\! (1-{\rm{bg}})R_{B^2}+{\rm{bg}} R_{ \epsilon_2} $ 。由于$ R_{ \epsilon_2} $ 和$ R_{B^2} $ 都是理论上可以计算的,我们就可以用此式预言$ R_{S} $ 随不同的背景比例$ {\rm{bg}} $ 的变化;图8给出背景比例为$ {\rm{bg}} \!=\! 2/3 $ ,事例数为400万时的相对差异[45]。可以看出,这时可以在$ 5 \sigma $ 的显著性水平上判断是否有手征磁效应的发生。在2018年的同量素碰撞实验中产生了大约63亿个碰撞事例,这时即便背景比例达到约$ 88\% $ ,也可以在大约$ 5 \sigma $ 的显著性水平上判断是否有手征磁效应发生。而如果背景比例达到$ 93\% $ ,我们依然可以在大 约$ 3 \sigma $ 的显著性水平上判断是否有手征磁效应发生。目前,STAR实验组正在对这些数据进行分析,其结果有望在近期公布。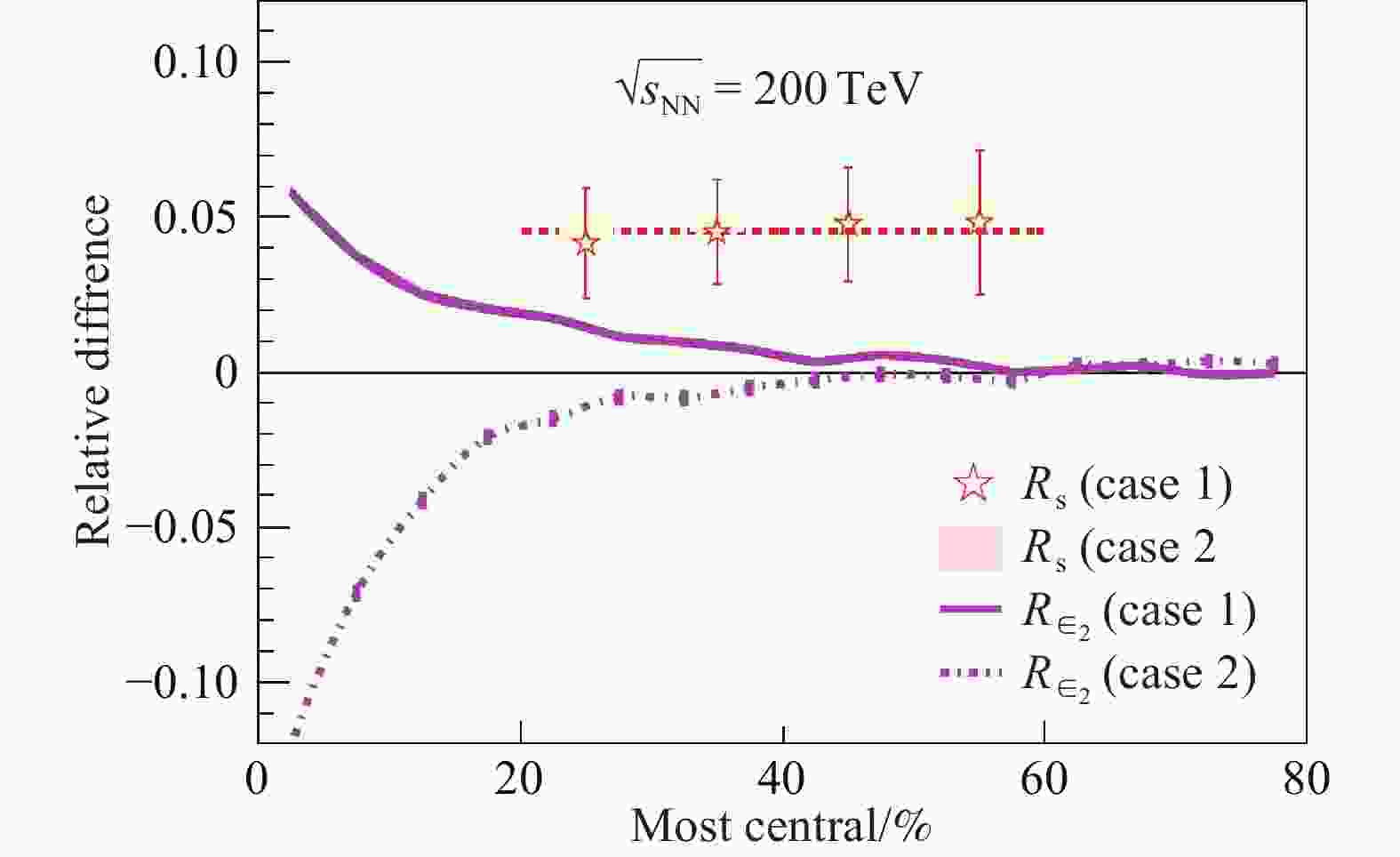
图 8 (在线彩图)理论上计算给出的同量素碰撞中碰撞偏心度
$ \epsilon_2$ 和修正的$\gamma$ 关联,$S \!=\! N_{\rm{part}} \Delta \gamma$ ,在背景比例为${\rm{bg}} \!=\! 2/3$ ,事例数为400万时的相对差异[45](2) 其他手征反常输运现象的探测 手征磁波可以同时传递电荷和轴荷,仔细分析可发现它可以在QGP中引起电荷的四极矩结构,即使得正电荷趋向于分布在QGP火球的上下端而负电荷趋向于分布在火球的中部。这样,当火球膨胀冷却后负电荷强子(比如
$ \pi^- $ )就倾向于沿着作用平面飞出,而正电荷强子(比如$ \pi^+ $ )倾向于从出平面方向飞出,于是造成$ \pi^- $ 的$ v_2 $ 比$ \pi^+ $ 的$ v_2 $ 大,且二者之差正比于净电荷不对称度$ A_{\rm{ch}} \!=\! (N_+-N_-)/ (N_++N_-) $ (因为手征分离效应正比于$ \mu_{ V} $ )[46]。在 2015年和2016年,RHIC的STAR实验组和LHC的ALICE实验组分别发表了相关的实验结果,并且发现确实如手征磁波预言的那样,$ v_2( \pi^-)-v_2( \pi^+)\propto A_{\rm{ch}} $ [47-48]。当然,实验观测到的结果是受到其他物理效应的影响的,比如电场效应、强子平均场效应、测量过程的快度截断等;在无法将这些效应去除掉之前,我们不能断言发现了手征磁波。去除这些额外的物理效应是当前实验上重要的研究课题。由于重离子碰撞中的涡旋场大致也是垂直于作用平面的,因此可以预计矢量手征涡效应会引起相对于作用平面的重子数的分离。因而可以仿照手征磁效应的观测量来构造类似的观测量,比如,
$ \eta_{ \alpha \beta} \!=\! \langle\cos(\phi_ \alpha+ \phi_ \beta- 2\Psi_{\rm{RP}}) \rangle $ ,其中$ \alpha, \beta \!=\! \pm $ 表示重子或反重子,$ \phi_ \alpha, \phi_ \beta $ 表示重子或反重子的方位角。STAR 实验组发布的数据显示,与手征涡效应定性吻合的重子数分离信号确实在$ \Lambda, \bar{ \Lambda} $ 超子和质子、反质子的关联中反映出来,其对碰撞中心度的依赖性也呈现出类似图7 所示的特征[49]。但是,如同对于手征磁效应和手征磁波的探测一样,$ \eta_{ \alpha \beta} $ 也受到其他物理效应的影响(比如横动量守恒和定域重子数守恒等),未来也需要设计新的观测量或实验手段来去除它们。对于手征涡波来说,它可以引起QGP火球中重子数四极矩结构,即重子数趋向于集中到火球的上下端而反重子趋向于集中到火球中间,在火球膨胀冷却后就造成反重子(比如$ \bar \Lambda $ )的$ v_2 $ 比重子(比如$ \Lambda $ )的$ v_2 $ 大一些,且二者只差正比于净重子 不对称度$ A_\pm^{ \Lambda} \!=\! (N_ \Lambda-N_{\bar \Lambda})/(N_ \Lambda+N_{\bar \Lambda}) $ ,见图9[26]。由于每个碰撞事例产生的$ \Lambda $ 和$ \bar \Lambda $ 数量很少,它们的$ v_2 $ 差异具有很大统计误差,当前RHIC正在运行的 束流能量扫描二期工程将会提供大量的数据,届时期望有足够的统计量来进行分析。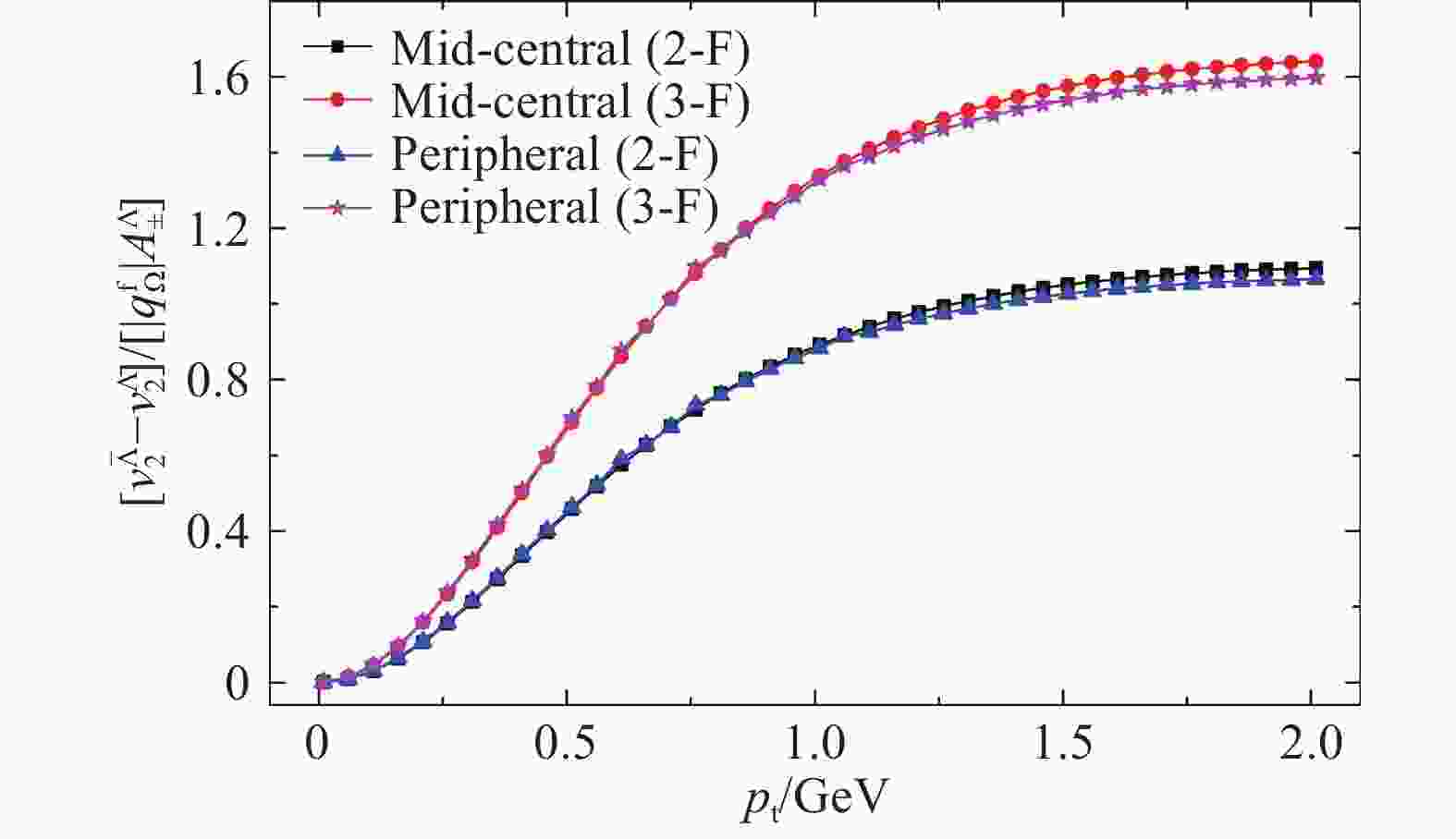
图 9 (在线彩图)由手征涡波造成的
$\bar \Lambda$ 和$\Lambda$ 椭圆流差异[26]手征电分离效应的观测需要电场,所以Cu+Au碰撞是理想的系统。在非对心Cu+Au碰撞中,电场大致是从Au核指向Cu核的,同时磁场大致是垂直于作用平面的[28]。这样,手征电分离效应会使得轴荷沿着碰撞参数方向发生分离,比如说Cu一侧聚集更多右手夸克而Au一侧聚集更多左手夸克,那么在手征磁效应作用下就会出现如图10所示的四极 矩结构,其中我们也考虑了欧姆电流引起的电荷沿碰撞参数方向的分离。这种四极矩结构造成正电荷和负电荷的事例平面(event plane)不一致,即
$ \Delta\Psi \!=\! \langle|\Psi_2^+-\Psi_2^-| \rangle $ 不为零且随着碰撞中心度增加,其中$ \Psi^\pm_2 $ 表示分别利用正电荷和负电荷强子重构出的二阶事例平面[50]。除此之外,也可以利用关联函数$ \zeta_{ \alpha \beta} \!=\! \langle\cos[2(\phi_ \alpha+\phi_ \beta-2\Psi_{\rm{RP}})] \rangle $ 来探测[50]。但是,由于手征电分离效应正比于$ \mu_{ V} \mu_A/T^2 $ ,比手征磁效应要微弱,所以需要更多的统计量来进行探测。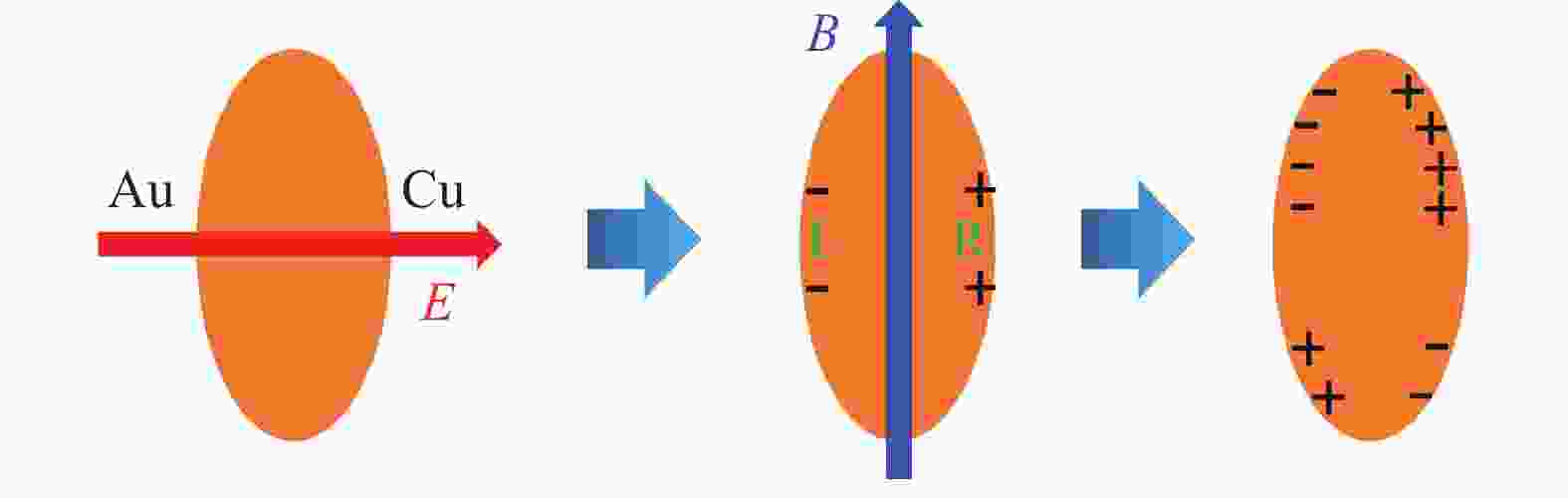
图 10 (在线彩图)由手征电分离效应与手征磁效应在Cu+Au碰撞中造成的特定电荷分布[29]
-
流体涡旋的一个重要效应是极化流体中粒子的自旋。其微观机制是自旋轨道耦合:粒子随流体微元转动的轨道角动量会极化它的自旋[51]。假设系统达到了整体热平衡,我们可以用统计力学的方法来考虑这一问题,这时系统的密度算符为
$ \hat{ \rho} \!=\! Z^{-1}\exp \left[- \beta( \hat{H}- \hat{{ S}}\cdot \omega) \right] $ ,那么自旋极化为$ { P} \!=\! {{\rm{Tr}}}[\hat{S}\hat{ \rho}]/s $ ($ \hat{{ S}} $ 为自旋算符,$ s $ 为自旋量子数)。对于自旋1/2的粒子,有$ \hat{{ S}} \!=\! { \sigma}/2 $ ,所以$ { P} \!=\! {{\omega}}/(2T)+o( \omega/T) $ 。这种简单的估计可以更加严格化,对于费米子,可以求出自旋四矢量的平均值为[15,52]$$ S^ \mu(x,p) = -\frac{s(s+1)}{6m}(1-n_{\rm{F}}) \epsilon^{ \mu \nu \rho \sigma}p_ \nu\varpi_{ \rho \sigma}(x)+O(\varpi^2), $$ (16) 其中
$ n_{\rm{F}}(p_0) $ ($ p_0 \!=\! \sqrt{{{p}}^2+m^2} $ )为Fermi-Dirac分布函数,$ \varpi_{ \rho \sigma}(x) $ 即我们在第2节中介绍的热涡度。对于$ \Lambda $ 和$ \bar \Lambda $ 超子来说,$ s $ =1/2,且它们质量很大,可近似$ 1-n_{\rm{F}}\approx 1 $ 。在粒子的静止系中,$ S^{* \mu} \!=\! (0,{{ S}}^*) $ ,其中$ {{ S}}^* $ 可有Lorentz变化得到$$ { S}^{*} = { S}-\frac{{{p}}\cdot{ S}}{p_0(p_0+m)}{{p}}{\text{。}} $$ (17) 那么,就得到在粒子静止系中的自旋极化矢量为
$$ { P}^* = \frac{{ S}^*}{s}{\text{。}} $$ (18) 将图4中给出的理论计算得到的在中心快度区的热涡度分量
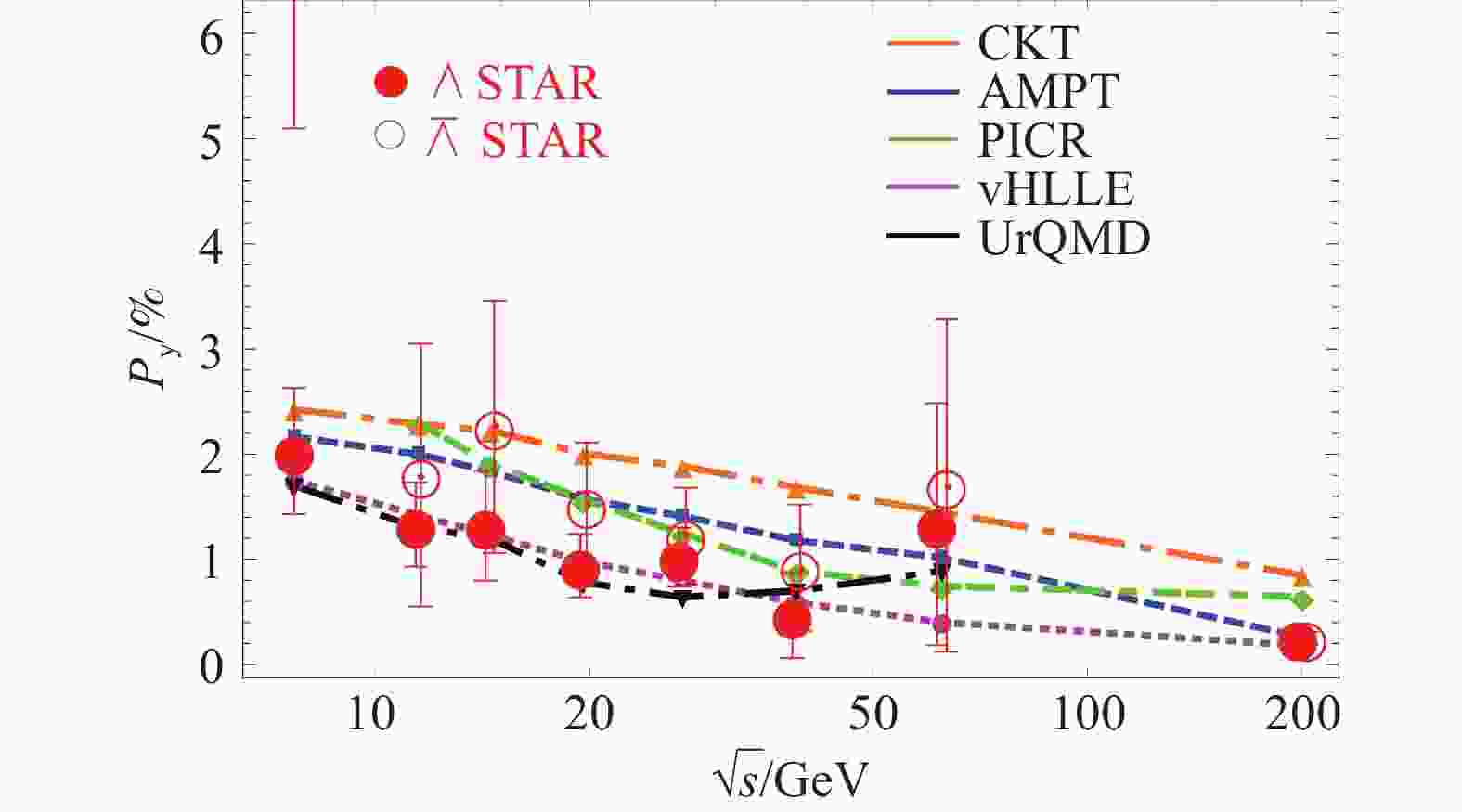
$ \varpi_{zx} $ 带入上面公式(16)~(18)中,我们就能得到自旋极化的$ y $ 分量$ P_y $ ,即沿着整体角动量方向的自旋极化,也叫整体自旋极化。我们将最近人们采用不同的数值方法得到的整体自旋极化的结果显示在图11中。其中的理论计算包括手征输运理论(CKT)[53]、AMPT模型[17]、两种不同的流体力学模型(vHLLE和PICR)[54-55]、UrQMD模型[56]。该图中同时显示了STAR实验组对$ \Lambda $ 和$ \bar \Lambda $ 自旋极化的实验数据点[57-58],可以看到理论计算和实验结果吻合的很好。图11显示出两个重要的特征。第一,整体自旋极化是随着碰撞能量的增加而减小的。这看起来和直觉不符,因为随着能量的增加,系统总角动量也相应增加。但图4显示涡度本身确实是随着碰撞能量增加而减小的。这实际上是一种相对论效应:随着碰撞能量的增加,产生的热密物质在中心快度区具有越来越好的沿着束流方向的boost不变性,从而使得涡度越来越小[16,59]。但应注意,在碰撞能量非常低的时候,整个系统是完全非相对论性的,这时涡度应该随着碰撞能量增加而增加。第二,尽管误差范围很大,实验显示$ \bar \Lambda $ 的整体自旋极化大于$ \Lambda $ 。这也许反映了磁场的效应,因为磁场可以通过Zeeman效应(与粒子磁矩的耦合)极化自旋,而$ \bar \Lambda $ 的磁矩大于零,$ \Lambda $ 的磁矩小于零,所以磁场会增加$ \bar \Lambda $ 的自旋极化而压低$ \Lambda $ 的自旋极化。从图11我们看到,对于整体自旋极化,理论计算可以很好地解释实验数据。但是,STAR 实验组最近发布了微分自旋极化的结果(differential spin polarization),即在不同运动学区域,比如给定方位角或横动量内的自旋极化[58,60]。这时候理论计算结果和实验数据产生了极大的分歧。具体地,基于流体力学模型和输运模型的计算显示,在中心快度区
$ P_y(\phi) $ ($ \phi $ 为方位角)随着$ \phi $ 从$ 0 $ 到$ \pi/2 $ 是逐渐增加的,但是实验结果却恰好相反,如图12所示[17]。类似的,对于在非对心碰撞中产生的自旋极化的$ z $ 分量$ P_z(\phi) $ ,理论研究显示$ P_z(\phi) $ 随着$ \phi $ 从0到$ 2 \pi $ 是在第一、三象限为负,二、四象限为正,与图13左图所示的理论计算的热涡度相同[17,61-62],但实验结果也恰好相反[60],见图13右图所示STAR在2019年的实验结果。用公式表达即是,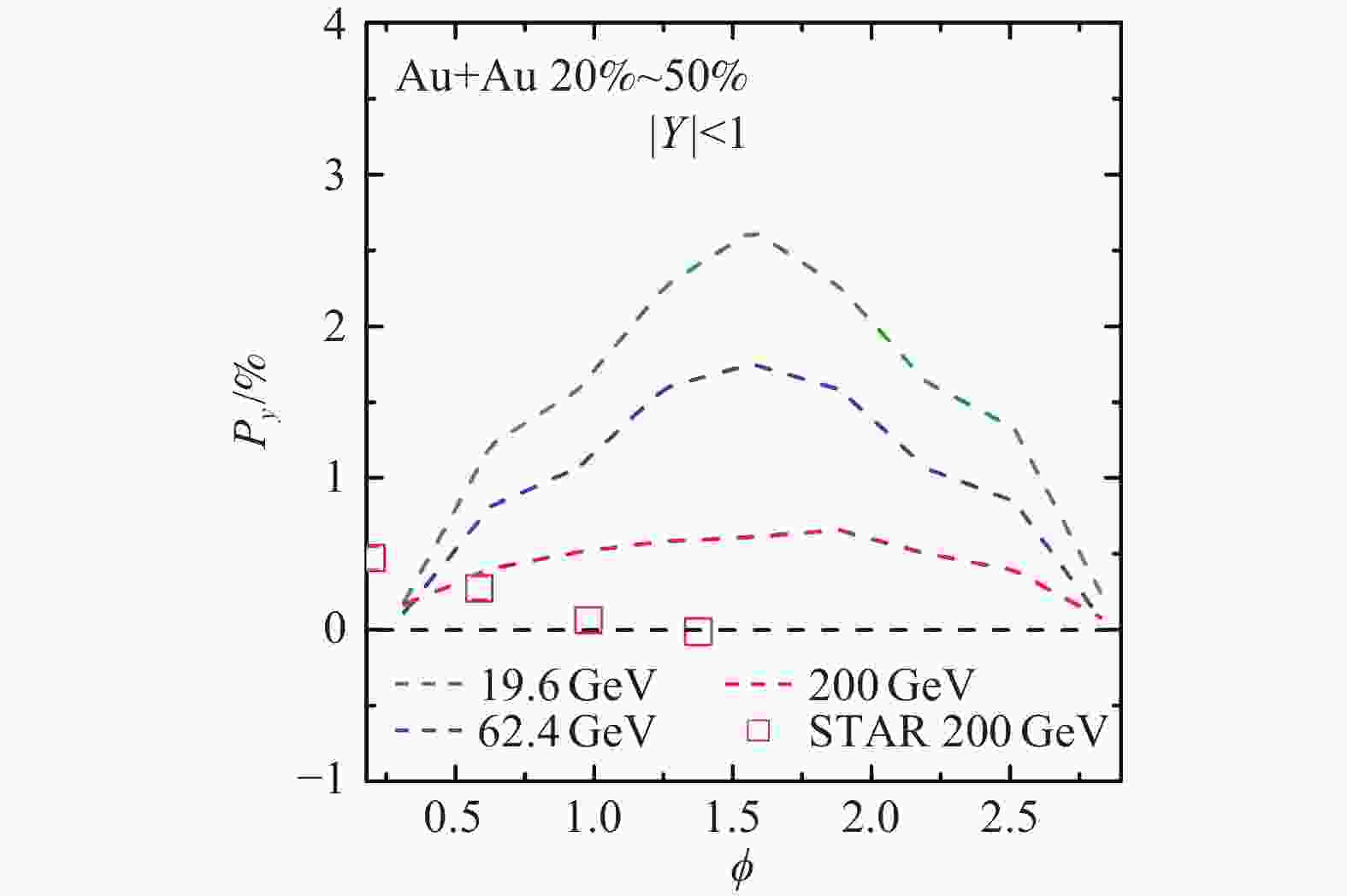
图 12 (在线彩图)中心快度区,自旋极化
$P_y$ 随着方位角$\phi$ 的变化[17]$$ \begin{split} \frac{{\rm{d}}P_{y,z}}{{\rm{d}}\phi} =& P_{y,z}+2 f_{2y,z}\sin\big[2(\phi-\Psi_{\rm{RP}})\big]+\\&2 g_{2y,z}\cos\big[2(\phi-\Psi_{\rm{RP}})\big]+\cdots, \end{split} $$ (19) 其中二阶调和系数
$ f_{2y,z} $ 和$ g_{2y,z} $ 在理论和实验上显示了符号差异,即$ f_{2z}^{\rm{ther}}<0, g_{2y}^{\rm{ther}}<0 $ ,而$ f_{2z}^{\exp}>0, g_{2y}^{\exp}>0 $ 。这构成了当前一个重大的疑难,称为自旋极化的“符号疑难”,它预示着我们采用平衡态的流体涡度来理解实验上自旋极化的观测结果可能是不恰当的。需要特别说明的是为什么纵向热涡度会产生如图13所示的空间分布。虽然我们前面介绍了非对心重离子碰撞中的整体角动量是产生流体涡旋的原因,但这并不是唯一的原因。实际上,流体涡旋可以由不同的机制导致。一个重要的机制是碰撞后系统的非均匀的膨胀。试想一个非对心碰撞,产生的热密夸克胶子物质在初期大致呈现纺锤型,且它受到热压力的膨胀将主要是沿着作用平面方向的,这也是为什么实验上看到正的椭圆流的原因。这时,容易看出来,由于这种不均匀的膨胀会诱导出“四个旋涡”结构,分别占据
$ x - y $ 平面的四个象限。当然,除了这种流体速度的不均匀性外,温度的分布也是不均匀的,二者结合的总的效果给出如图13所示的特殊的涡旋结构。 -
为了解决上一节中提到的自旋极化的“符号疑难”,人们已经做了很大尝试[63-68]。但从理论角度来讲,一个根本问题是无法回避的,即在计算自旋极化时的平衡态假设是否合适,即自旋自由度是否完全与热涡度绑定(见式(16))。我们知道,碰撞后的热密系统并不是处于整体热平衡状态,因而自旋极化原则上不应由热涡度完全确定。这时,若我们考虑流体力学框架(流体力学在描述重离子碰撞的整体演化(bulk evolution)是十分成功的),就需要将自旋极化密度(或等效地,自旋化学势)作为和温度
$ T $ 与流体速度$ u^ \mu $ 一样的动力学变量来处理,这样得到的理论称为自旋流体力学[69-70]。在所谓的一阶自旋流体力学中,流体的能量动量张量、自旋张量在Landau-Lifshitz框架下写为
$$ \begin{split}& T^{ \mu \nu} = eu^ \mu u^ \nu-P \Delta^{ \mu \nu}+ \sigma_ \eta^{ \mu \nu}+ \sigma_ \zeta^{ \mu \nu}+2q^{[ \mu}u^{ \nu]}+ \phi^{ \mu \nu},\\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Sigma^{ \mu, \alpha \beta} = u^ \mu S^{ \alpha \beta},\\[-13pt] \end{split} $$ (20) 其中
$ e $ 为能量密度,$ P $ 为压强,$ \sigma^{ \mu \nu}_ \eta, \sigma^{ \mu \nu}_ \zeta $ 为粘性张量,$ q^{ \mu} $ 和$ \phi^{ \mu \nu}\! =\! \phi^{[ \mu \nu]} $ 为和自旋自由度相关的量,它们表示扭动自旋张量时间分量与空间分量的力矩的强弱,它们的本构关系可以表达为$$ \sigma_ \eta^{ \mu \nu} = 2 \eta \partial_\perp^{ \langle \mu}u^{ \nu \rangle}, $$ (21) $$ \sigma_ \zeta^{ \mu \nu} = \zeta \theta \Delta^{ \mu \nu}, $$ (22) $$ q^ \mu = \lambda(D u^ \mu+ \beta \partial_\perp^ \mu T-4 \Omega^{ \mu \nu}u_ \nu), $$ (23) $$ \phi^{ \mu \nu} = 2 \gamma( \partial_\perp^{[ \mu}u^{ \nu]}+2 \Omega^{ \mu \nu}_\perp), $$ (24) 上式中
$ X^{[ \alpha \beta]} \!=\! (X^{ \alpha \beta}-X^{ \beta \alpha})/2 $ 表示对指标全反对称化,$ X^{ \langle \alpha \beta \rangle} \!=\! (X^{ \alpha \beta}+X^{ \beta \alpha})/2- {X^ \mu}_ \mu \Delta^{ \alpha \beta}/3 $ 表示对称无迹化,$ \theta \!=\! \partial_ \mu u^ \mu $ 为流体膨胀率,$ \Delta_{ \mu \nu}\! =\! g_{ \mu \nu}-u_ \mu u_ \nu $ 为投影张量,$ D \!=\! u\cdot \partial $ 为随动时间导数,$ \partial^ \mu_\perp \!=\! \Delta^{ \mu \nu} \partial_ \nu $ 为空间导数,$ \Omega^{ \mu \nu} $ 为自旋化学势,$ \Omega^{ \mu \nu}_\perp \!=\! \Delta_{ \mu \rho} \Delta_{ \nu \sigma} \Omega^{ \rho \sigma} $ 。这里,$ \eta, \zeta, \lambda, \gamma $ 为输运系数,它们必须为半正定的,它们的物理意义为切粘滞系数、体粘滞系数、boost热导率和转动粘滞系数[70]。基本的流体力学运动方程为$$ \partial_ \mu T^{ \mu \nu} = 0, $$ (25) $$ \partial_ \mu \Sigma^{ \mu, \alpha \beta} = 4q^{[ \beta}u^{ \alpha]}+2 \phi^{ \beta \alpha}{\text{。}} $$ (26) 为了使上述方程组封闭,我们还需要知道状态方程,它联系着
$ e,P,S^{ \alpha \beta} $ 。在实际数值计算中,一阶相对论流体力学在大动量处有非物理模式破坏相对论因果律并且有数值不稳定性的问题,其原因是上述本构关系中流体的“响应”(本构关系的左边)与“力”(本构关系的右边)无迟豫地成正比关系。为了克服这些问题,我们可以引入相应的迟豫时间,从而形成最简单的Israel-Stewart本构关系,
$$ \tau_ \eta (D \sigma_ \eta^{ \mu \nu})_\perp+ \sigma_ \eta^{ \mu \nu} = 2 \eta \partial_\perp^{ \langle \mu}u^{ \nu \rangle}, $$ (27) $$ \tau_ \zeta (D \sigma_ \zeta^{ \mu \nu})_\perp+ \sigma_ \zeta^{ \mu \nu} = \zeta \theta \Delta^{ \mu \nu}, $$ (28) $$ \tau_ \lambda (Dq^ \mu)_\perp+q^ \mu = \lambda(D u^ \mu+ \beta \partial_\perp^ \mu T-4 \Omega^{ \mu \nu}u_ \nu), $$ (29) $$ \tau_ \gamma (D \phi^{ \mu \nu})_\perp+ \phi^{ \mu \nu} = 2 \gamma( \partial_\perp^{[ \mu}u^{ \nu]}+2 \Omega^{ \mu \nu}_\perp), $$ (30) 其中
$ (\cdots)_\perp $ 表示取垂直于$ u^ \mu $ 的分量。这时候$ \sigma_ \eta^{ \mu \nu}, \sigma_ \zeta^{ \mu \nu}, q^ \mu, \phi^{ \mu \nu} $ 本身也变为动力学变量,需要引入相应的初始条件。这样,我们就得到了一组可用于数值计算的流体力学方程组,将来我们将使用这一方程组研究自旋极化在重离子碰撞中的产生和演化,期望可以对自旋极化的“符号疑难”给出解答。为了更好地理解自旋流体力学,我们考察它所允许的集体模式。我们考虑一个静止的流体中的涨落,
$$ e = e_0+ \delta e,\;\;\; P = P_0+ \delta P,\;\;\; S^{ \mu \nu} = 0 + \delta S^{ \mu \nu},\; $$ (31) $$ \sigma_ \eta^{ \mu \nu} = 0 + \delta \sigma_ \eta^{ \mu \nu}, \;\; \sigma_ \zeta^{ \mu \nu} = 0 + \delta \sigma_ \zeta^{ \mu \nu},\;\; v^i = 0+ \delta v^i\text{。} $$ (32) 保留涨落的一阶项,流体力学方程为
$$ \partial_t \delta e+(e_0+P_0) \partial_i \delta v^i+ \partial_i \delta q^i = 0, $$ (33) $$ (e_0+P_0) \partial_t \delta v^i + \partial_i \delta P+ \partial_j \delta \sigma_\eta^{ji}+ \partial_j \delta \sigma_ \zeta^{ji}\\ - \partial_t \delta q^i+ \partial_j \delta\phi^{ji} = 0, $$ (34) $$ \partial_t \delta S^{0i}-2 \delta q^i = 0, $$ (35) $$ \partial_t \delta S^{ij}+2 \delta phi^{ij} = 0\text{。} $$ (36) 相应地,Israel-Stewart本构方程也要保留到涨落的一阶项。这样,我们得到一组关于涨落的线性方程,在频率-动量空间中,这组线性方程变为代数方程。要求其行列式为零可以解出集体模式的色散关系:
$$ \omega = -{\rm{i}} \tau_\eta^{-1},\;\; -{\rm{i}} \tau_ \zeta^{-1},\;\; -{\rm{i}} \tau_ \lambda^{-1},\;\; -{\rm{i}} \tau_ \gamma^{-1}, $$ (37) $$ \omega = -{\rm{i}} \tau_s^{-1},\;\; -{\rm{i}} \tau_b^{-1}, $$ (38) $$ \omega = -{\rm{i}} \tau_s^{-1}-{\rm{i}} \frac{ \gamma}{e_0+P_0} {{{k}}}^2,\;\;-{\rm{i}} \tau_b^{-1}-{\rm{i}} \frac{4c_s^2 \lambda} {e_0+P_0} {{{k}}}^2, $$ (39) $$ \omega = -{\rm{i}} \frac{ \eta}{e_0+P_0} {{{k}}}^2, $$ (40) $$ \omega = \pm c_s | {{{k}}}|-{\rm{i}} \frac{ \zeta+4 \eta/3}{2(e_0+P_0)} {{{k}}}^2\text{。} $$ (41) 其中
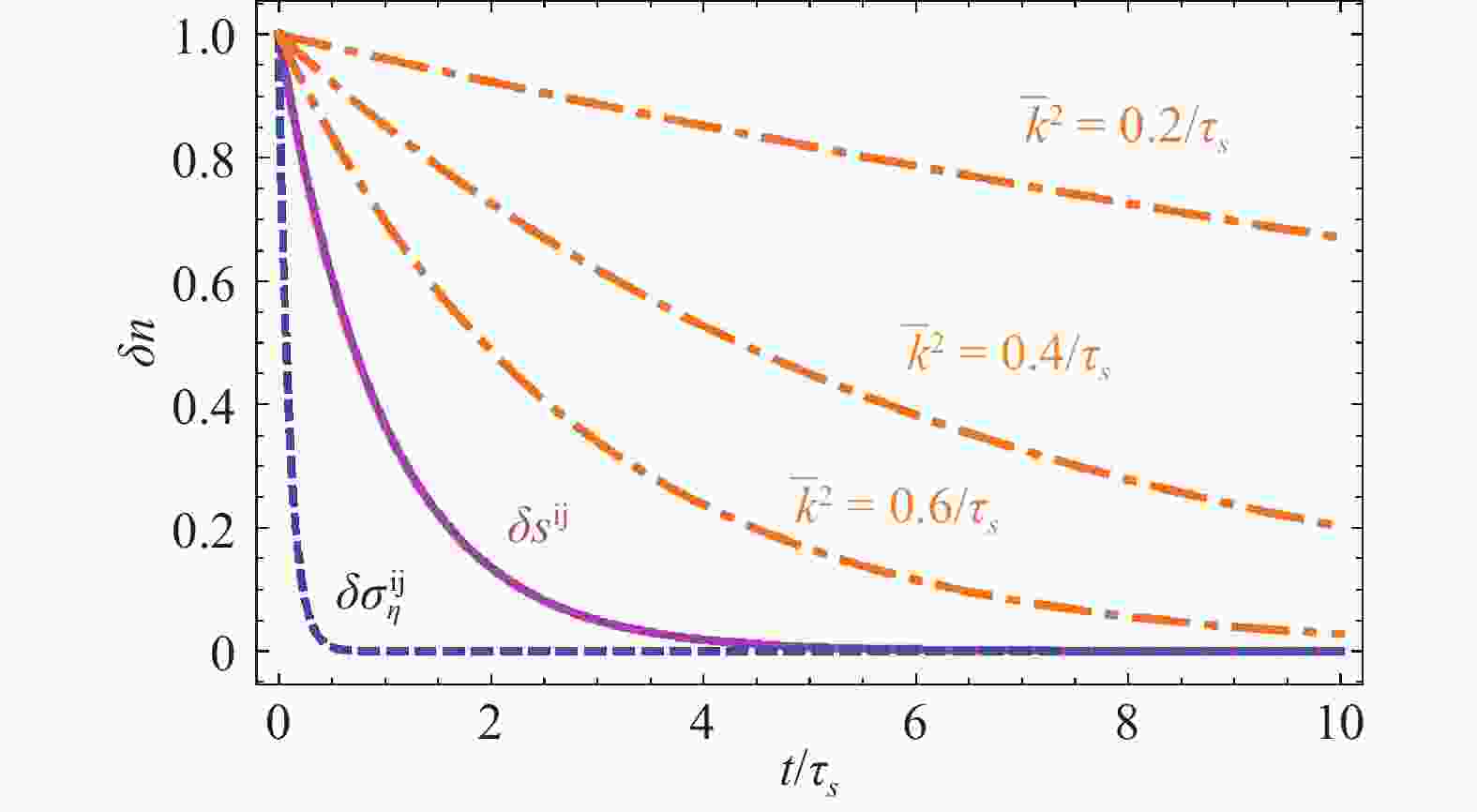
$ \tau_s \!=\! ( \partial S^{ij}/ \partial \omega^{ij})/(8 \gamma) $ ,$ \tau_b \!=\! ( \partial S^{0i}/ \partial \omega^{0i})/(8 \lambda) $ ,$ c_s^2 \!=\! \partial P/ \partial e $ (声速的平方);我们假定了$ \tau_{\eta, \zeta, \lambda, \gamma}\ll \tau_{s,b} $ 并且只保留了动量的低阶项。这些模式中,式(37)表示相应的Israel-Stewart场向Navier-Stokes场(由式(21)~(24)给出)的定域迟豫;式(38)表示自旋密度涨落向平衡态的定域迟豫;式(39)也表示自旋密度涨落向平衡态的迟豫,但该模式与模式(38)不同的是伴随着自旋密度的扩散;式(40)表示剪切模式的粘性耗散;式(41)表示传播模式(即声波)同时伴随着粘性耗散。这样,我们看到从线性分析中可以得到很多关于自旋流体力学的集体模式的性质,而且清楚地看到自旋密度 不构成传播模式,而总是伴随着耗散的,这与自旋本身不是守恒量有关。我们在图14中给出了几种典型模式的时间演化。可以看到,Israel-Stewart场很快就弛豫到了相应的Navier-Stokes场,同时,自旋涨落也在有限时间弛豫为零,这说明这两种场都不是严格意义上的流体力学模式。与之不同的是剪切模式,可以看到,随着动量的减小,剪切模式的弛豫越来越缓慢,这是因为它是真正的流体力学模式的缘故。 -
本文中,我们介绍了重离子碰撞中产生的夸克胶子物质在强磁场和涡旋场中的特殊性质,着重回顾了由电磁场和流体涡旋引起的与手征反常密切相关的输运现象,并且讨论了由流体涡旋引起的强子的自旋极化问题。这些问题是当前高能核物理中引起广泛兴趣的课题。手征反常输运现象提供给我们非常难得的可以在重离子碰撞实验中探测QCD的规范场非平庸拓扑结构以及强相互作用在高温环境中可能的P与CP破坏问题的手段。强子的自旋极化问题提供给我们新的探测夸克胶子物质特性的探针,这如同固体物理学在过去40年中从电子学时代步入 自旋电子学(spintronics)时代一样,强子自旋极化的探测使得夸克胶子等离子体的研究也从过去的电子学 时代逐步进入了亚原子自旋电子学时代,因而具有重要的意义。同时我们也看到,这些课题构成一个新的交叉研究领域,与粒子物理、天体物理、凝聚态物理、冷原子物理等研究方向紧密关联,许多问题具有共同的物理背景,这里面还有很多的课题等待我们深入探索。
作为展望,以下两个问题将是我们将来主要的研究方向。(1) 定量地计算手征磁效应等反常输运现象在重离子碰撞中的信号,同时定量计算背景效应的贡献,进而和实验数据比对。这主要有两个难点需要克服,一个是如何从理论上计算初始状态的手征荷密度的分布,另一个是如何得到在夸克胶子等离子体中磁场的时间演化。目前,这两个问题都有很多研究在进行,有希望在不远的将来巨大重要进展。(2) 通过自旋流体力学和自旋输运理论研究超子定域自旋极化的符号疑难。这里在理论上的难点主要是要完善自旋流体力学的理论框架,计算其中的输运系数,推导自旋输运理论中的碰撞项并 推导从自旋输运理论出发推导自旋流体力学。从数值计算的角度,需要我们推广过去被广泛使用的相对论流体力学程序到自旋流体力学,同时推广过去的输运模型(比如AMPT等)到自旋输运模型。这方面的研究刚刚开始,但已经吸引很多学者投入其中,是有望在近期有进展的。同时需要指出的是,将来在这些研究中取得的理论与方法也可以跨领域应用到凝聚态物理、天体物理、冷原子物理等相关课题的研究中。
Quark Gluon Matter in Strong Magnetic and Vortical Fields
-
摘要: 相对论重离子碰撞可以产生高温的夸克胶子物质,同时也产生极强的电磁场和流体涡旋。在强电磁场和涡旋场中的夸克胶子物质呈现出新奇的宏观量子现象,比如手征磁效应、手征涡效应、手征分离效应、手征电分离效应、自旋极化现象等。它们一方面给我们提供了可以探测高温下量子色动力学的非平庸规范场拓扑结构、强相互作用的宇称破坏、夸克胶子物质中的自旋动力学等的实验手段,另一方面也与物理学其他分支,比如粒子物理、凝聚态物理、天体物理、冷原子物理等发生紧密联系,形成新的交叉研究领域。本文旨在对这些宏观量子现象的产生机制以及它们在相对论重离子碰撞中的探测等做一回顾和展望。特别地,我们揭示出重离子碰撞的磁场强度可以达到
$10^{18}\sim 10^{20}$ G,流体涡旋可以达到$10^{22}$ s–1;这是我们已知当前宇宙中最强的磁场和流体涡旋。我们定量地对同量素碰撞实验做了分析,发现即便背景比例达到93%以上,当前的同量素碰撞实验仍然可在大约$3\sigma$ 的显著性水平上判断是否有手征磁效应的发生。我们系统地给出了满足因果律的自旋流体力学方程,并推导了其中的集体激发模式,这将有助于理解超子自旋极化中出现的符号问题。Abstract: Relativistic heavy-ion collisions generate high-temperature quark gluon plasma with extremely strong electromagnetic and fluid vortical fields. The quark gluon plasma exhibits intriguing macroscopic quantum phenomena in the presence of strong electromagnetic and vortical fields, e.g., the chiral magnetic effect, chiral vortical effects, chiral separation effect, chiral electric separation effect, and spin polarization. These phenomena provide us a unique experimental means to study the nontrivial topological sector of the quantum chromodynamics, e.g., possible parity violation of strong interaction at high temperature, and subatomic spintronics of quark gluon plasma. They are also closely related to other subfields of physics, such as particle physics, condensed matter physics, astrophysics, and cold atomic physics, and thus form a new interdisciplinary research area. The goal of the present article is to give an introduction to these phenomena and to review the current status of their experimental search in heavy-ion collisions. In particular, we find that the magnetic fields generated in heavy-ion collisions can reach$10^{18}\sim 10^{20}$ G and the fluid vorticity can reach$10^{22}$ s–1; these are the known strongest magnetic fields and vorticity in the current universe. We quantitatively analyze the isobar collisions and find that, even if the background level is of 93%, the current isobar collisions can still test the occurrence of the chiral magnetic effect at$3\sigma$ significance level. We give the causal set of equations of spin hydrodynamics and give the collective modes in it; the spin hydrodynamics is useful to resolve the sign problem appearing in the comparison between theoretical calculations and experimental measurements of the spin polarization of hyperons. -
图 2 (在线彩图)重离子碰撞中产生的电磁场随碰撞参数的变化[14]
图 3 (在线彩图)重离子碰撞中产生的非相对论涡度和相对论运动涡度随碰撞参数的变化[16]
图 4 (在线彩图)重离子碰撞中产生的热涡度随时间的变化[17]
图 8 (在线彩图)理论上计算给出的同量素碰撞中碰撞偏心度
$ \epsilon_2$ 和修正的$\gamma$ 关联,$S \!=\! N_{\rm{part}} \Delta \gamma$ ,在背景比例为${\rm{bg}} \!=\! 2/3$ ,事例数为400万时的相对差异[45]图 9 (在线彩图)由手征涡波造成的
$\bar \Lambda$ 和$\Lambda$ 椭圆流差异[26]图 10 (在线彩图)由手征电分离效应与手征磁效应在Cu+Au碰撞中造成的特定电荷分布[29]
图 12 (在线彩图)中心快度区,自旋极化
$P_y$ 随着方位角$\phi$ 的变化[17] -
[1] GROSS D J, WILCZEK F. Phys Rev Lett, 1973, 30: 1343. doi: 10.1103/PhysRevLett.30.1343 [2] POLITZER H D. Phys Rev Lett, 1973, 30: 1346. doi: 10.1103/PhysRevLett.30.1346 [3] 黄旭光, 庄鹏飞. 物理, 2017, 46(5): 273. doi: 10.7693/wl20170501 HUANG X G, ZHANG P F. Physics, 2017, 46(5): 273. (in Chinese) doi: 10.7693/wl20170501 [4] HARZEEV K D E, LIAO J, VOLOSHIN S A, et al. Prog Part Nucl Phys, 2016, 88: 1. doi: 10.1016/j.ppnp.2016.01.001 [5] HUANG X G. Rept Prog Phys, 2016, 79(7): 076302. doi: 10.1088/0034-4885/79/7/076302 [6] HATTORI K, HUANG X G. Nucl Sci Tech, 2017, 28(2): 26. doi: 10.1007/s41365-016-0178-3 [7] ZHAO J, WANG F. Prog Part Nucl Phys, 2019, 107: 200. doi: 10.1016/j.ppnp.2019.05.001 [8] WANG X N, GYULASSY M. Phys Rev D, 1991, 44: 3501. doi: 10.1103/PhysRevD.44.3501 [9] DENG W T, WANG X N, XU R. Phys Rev C, 2011, 83: 014915. doi: 10.1103/PhysRevC.83.014915 [10] LIN Z W, KO C M, LI B A, et al. Phys Rev C, 2005, 72: 064901. doi: 10.1103/PhysRevC.72.064901 [11] BLOCZYNSKI J, HUANG X G, ZHANG X, et al. Phys Lett B, 2013, 718: 1529. doi: 10.1016/j.physletb.2012.12.030 [12] BLOCZYNSKI J, HUANG X G, ZHANG X, et al. Nucl Phys A, 2015, 939: 85. doi: 10.1016/j.nuclphysa.2015.03.012 [13] BZDAK A, SKOKOV V. Phys Lett B, 2012, 710: 171. doi: 10.1016/j.physletb.2012.02.065 [14] DENG W T, HUANG X G. Phys Rev C, 2012, 85: 044907. doi: 10.1103/PhysRevC.85.044907 [15] BECATTINI F, CHANDRA V, ZANNA L D, et al. Annals Phys, 2013, 338: 32. doi: 10.1016/j.aop.2013.07.004 [16] DENG W T, HUANG X G. Phys Rev C, 2016, 93(6): 064907. doi: 10.1103/PhysRevC.93.064907 [17] WEI D X, DENG W T, HUANG X G. Phys Rev C, 2019, 99: 1. doi: 10.1103/PhysRevC.99.014905 [18] KHARZEEV D E, MCLERRAN L D, WARRINGA H J. Nucl Phys A, 2008, 803: 227. doi: 10.1016/j.nuclphysa.2008.02.298 [19] FUKUSHIMA K, D KHARZEEV E, WARRINGA H J. Phys Rev D, 2008, 78: 074033. doi: 10.1103/PhysRevD.78.074033 [20] SON D, ZHITNITSKY A R. Phys Rev D, 2004, 70: 074018. doi: 10.1103/PhysRevD.70.074018 [21] METLITSKI M A, ZHITNITSKY A R. Phys Rev D, 2005, 72: 045011. doi: 10.1103/PhysRevD.72.045011 [22] LI Q, KHARZEEV D E, ZHANG C, et al. Nature Physics, 2016, 12: 550. doi: 10.1038/nphys3648 [23] KHARZEEV D E, YEE H U. Phys Rev D, 2011, 83: 085007. doi: 10.1103/PhysRevD.83.085007 [24] SON D T, SUROWKA P. Phys Rev Lett, 2009, 103: 191601. doi: 10.1103/PhysRevLett.103.191601 [25] LANDSTEINER K, MEGIAS E, PENA-BENITEZ F. Phys Rev Lett, 2011, 107: 021601. doi: 10.1103/PhysRevLett.107.021601 [26] JIANG Y, HUANG X G, LIAO J. Phys Rev D, 2015, 92(7): 071501. doi: 10.1103/PhysRevD.92.071501 [27] HIRONO Y, M HONGO, HIRANO T. Phys Rev C, 2014, 90(2): 021903. doi: 10.1103/PhysRevC.90.021903 [28] DENG W T, HUANG X G. Phys Lett B, 2015, 742: 296. doi: 10.1016/j.physletb.2015.01.050 [29] HUANG X G, LIAO J. Phys Rev Lett, 2013, 110(23): 232302. doi: 10.1103/PhysRevLett.110.232302 [30] JIANG Y, HUANG X G, LIAO J. Phys Rev D, 2015, 91(4): 045001. doi: 10.1103/PhysRevD.91.045001 [31] MCLERRAN L D, MOTTOLA E, SHAPOSHNIKOV M E. Phys Rev D, 1991, 43: 2027. doi: 10.1103/PhysRevD.43.2027 [32] ARNOLD P B, SON D, YAFFE L G. Phys Rev D, 1997, 55: 6264. doi: 10.1103/PhysRevD.55.6264 [33] VOLOSHIN S A. Phys Rev C, 2004, 70: 057901. doi: 10.1103/PhysRevC.70.057901 [34] ABELEV B I, AGGARWAL M M, AHAMMED Z, et al. Phys Rev Lett, 2009, 103: 251601. doi: 10.1103/PhysRevLett.103.251601 [35] ABELEV B, ADAM J, ADAMOVÁ D, et al. Phys Rev Lett, 2013, 110(1): 012301. doi: 10.1103/PhysRevLett.110.012301 [36] AZIZ S. arXiv: 2005.06177[hep-ex]. [37] ADAMCZYK L, ADKINS J K, AGAKISHIEV G, et al. Phys Rev Lett, 2014, 113: 052302. doi: 10.1103/PhysRevLett.113.052302 [38] WANG F. Phys Rev C, 2010, 81: 064902. doi: 10.1103/PhysRevC.81.064902 [39] PRATT S, SCHLICHTING S, GAVIN S. Phys Rev C, 2011, 84: 024909. doi: 10.1103/PhysRevC.84.024909 [40] SCHLICHTING S, PRATT S. Phys Rev C, 2011, 83: 014913. doi: 10.1103/PhysRevC.83.014913 [41] BZDAK A, KOCH V, LIAO J. Phys Rev C, 2011, 83: 014905. doi: 10.1103/PhysRevC.83.014905 [42] KHACHATRYAN V, SIRUNYAN A M, TUMASYAN A, et al. Phys Rev Lett, 2017, 118(12): 122301. doi: 10.1103/PhysRevLett.118.122301 [43] SIRUNYAN A M, TUMASYAN A, ADAM W, et al. Phys Rev C, 2018, 97(4): 044912. doi: 10.1103/PhysRevC.97.044912 [44] ADAM J, ADAMCZYK L, ADAMS J R, et al. Phys Lett B, 2019, 798: 134975. doi: 10.1016/j.physletb.2019.134975 [45] DENG W T, HUANG X G, MA G L, et al. Phys Rev C, 2016, 94: 041901. doi: 10.1103/PhysRevC.94.041901 [46] BURNIER Y, KHARZEEV D E, LIAO J, et al. Phys Rev Lett, 2011, 107: 052303. doi: 10.1103/PhysRevLett.107.052303 [47] ADAMCZYK L, ADKINS J K, AGAKISHIEV G, et al. Phys Rev Lett, 2015, 114(25): 252302. doi: 10.1103/PhysRevLett.114.252302 [48] ADAM J, ADAMOVÁ D, AGGARWA M M, et al. Phys Rev C, 2016, 93(4): 044903. doi: 10.1103/PhysRevC.93.044903 [49] ZHAO F. Nucl Phys A, 2014, 931: 746. doi: 10.1016/j.nuclphysa.2014.08.108 [50] MA G L, HUANG X G. Phys Rev C, 2015, 91(5): 054901. doi: 10.1103/PhysRevC.91.054901 [51] LIANG Z T, WANG X N. Phys Rev Lett, 2005, 94: 102301. doi: 10.1103/PhysRevLett.94.102301 [52] FANG R H, PANG L G, WANG Q, et al. Phys Rev C, 2016, 94(2): 024904. doi: 10.1103/PhysRevC.94.024904 [53] Y SUN, KO C M. Phys Rev C, 2017, 96(2): 024906. doi: 10.1103/PhysRevC.96.024906 [54] XIE Y, WANG D, CSERNAI L P. Phys Rev C, 2017, 95(3): 031901. doi: 10.1103/PhysRevC.95.031901 [55] KARPENKO I, BECATTINI F. Eur Phys J C, 2017, 77(4): 213. doi: 10.1140/epjc/s10052-017-4765-1 [56] VITIUK O, BRAVINA L V, ZABRODIN E E. Phys Lett B, 2020, 803: 135298. doi: 10.1016/j.physletb.2020.135298 [57] ADAMCZYK L, ADKINS J K, AGAKISHIEV G, et al. Nature, 2017, 548: 62. doi: 10.1038/nature23004 [58] ADAM J, ADAMCZYK L, ADAMS J R, et al. Phys Rev C, 2018, 98: 014910. doi: 10.1103/PhysRevC.98.014910 [59] JIANG Y, LIN Z W, LIAO J. Phys Rev C, 2016, 94(4): 044910. doi: 10.1103/PhysRevC.94.044910 [60] ADAM J, ADAMCZYK L, ADAMS J R, et al. Phys Rev Lett, 2019, 123(13): 132301. doi: 10.1103/PhysRevLett.123.132301 [61] BECATTINI F, KARPENKO I. Phys Rev Lett, 2018, 120(1): 012302. doi: 10.1103/PhysRevLett.120.012302 [62] XIA X L, LI H, TANG Z B, et al. Phys Rev C, 2018, 98: 024905. doi: 10.1103/PhysRevC.98.024905 [63] SUN Y, KO C M. Phys Rev C, 2019, 99(1): 011903. doi: 10.1103/PhysRevC.99.011903 [64] CSERNAI L, KAPUSTA J, WELLE T. Phys Rev C, 2019, 99(2): 021901. doi: 10.1103/PhysRevC.99.021901 [65] FLORKOWSKI W, KUMAR A, RYBLEWSKI R, et al. Phys Rev C, 2019, 100(5): 054907. doi: 10.1103/PhysRevC.100.054907 [66] BECATTINI F, CAO G, SPERANZA E. Eur Phys J C, 2019, 79(9): 741. doi: 10.1140/epjc/s10052-019-7213-6 [67] XIA X L, LI H, HUANG X G, et al. Phys Rev C, 2019, 100(1): 014913. doi: 10.1103/PhysRevC.100.014913 [68] WU H Z, PANG L G, HUANG X G, et al. Phys Rev Research, 2019, 1: 033058. doi: 10.1103/PhysRevResearch.1.033058 [69] FLORKOWSKI W, FRIMAN B, JAISWAL A, et al. Phys Rev C, 2018, 97(4): 041901. doi: 10.1103/PhysRevC.97.041901 [70] HATTORI K, HONGO M, HUANG X G, et al. Phys Lett B, 2019, 795: 100. doi: 10.1016/j.physletb.2019.05.040 -











 下载:
下载:























































































































































































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号