-
核天体物理是核物理与天体物理的交叉学科,利用核物理的方法研究天体物理中恒星演化、元素起源、能量来源等重要问题[1-4]。组成人体和自然界的化学元素是如何起源的?我们赖以生存的太阳能来自哪里?太阳还能燃烧多久,它寿终正寝时会变成什么样子?各种复杂奇妙的天文现象,从像太阳这样的稳态恒星到像新星、X射线爆发、超新星这样的爆炸现象,从引发引力波的中子星合并到黑洞的形成,背后的机理是什么?这些都是核天体物理关注的焦点问题。事实上,发生在不同天体能区的核过程,是天体物理系统的能量产生和演化的原因,决定了太阳及各种恒星的命运,也决定了化学元素的起源和合成过程。在遥远而消失已久的恒星的炽热内部,核反应产生的元素经过数十亿年的时间,经常被释放到星际区域,聚集成气体云,产生新一代恒星,从而导致一个仍在进行的周期性演化。
元素的合成通过各种核反应进行[2,4],如
$({\rm{p}},\,{\rm{\alpha}})$ ,(p,n),$({\rm{\alpha}},\,{\rm{n}})$ ,$({\rm{\alpha}},\,{\rm{p}})$ ,(n,p),$({\rm{n}},\,{\rm{\alpha}})$ ,辐射俘获反应,如$({\rm{p}},\,{\rm{\gamma}}),\;({\rm{n}},\,{\rm{\gamma}}),\;({\rm{\alpha}},\,{\rm{\gamma}})$ 和光离解反应等。天体环境中的核反应是依靠粒子的热运动引发的,主要发生在Gammow能区($E_{\rm{G}}$ ),其能量是由在一定温度下粒子速度的麦克斯韦-玻尔兹曼分布与相互作用粒子之间的库仑位垒穿透概率的卷积决定的。$E_{\rm{G}}$ 通常处于很低的能量区间,比如在太阳中的核反应Gammow峰的能量在$5\thicksim25$ keV范围。因此,许多天体物理模型都需要低能区核反应速率的数据。最理想的方案当然是在实验室中直接测量有关的反应速率。然而,由于库仑斥力的存在,且通常库仑位垒远高于天体反应能量($E_{\rm{C}}\gg E_{\rm{G}}$ ),带电粒子之间的核反应只能通过位垒穿透效应发生,截面随能量降低而急剧减小。这给天体能区核反应截面直接测量带来巨大的困难,当Gammow能区存在较强的共振时,直接测量有可能得到所需的统计计数,而一般情况下,除了部分库仑位垒较低的轻粒子核反应,直接测量都异常困难,有些几乎是不可能的。通常,为了得到天体能区的反应截面,需要将在较高能量上可以直接测量的反应截面向低能方向进行外推。核天体物理中,为克服核反应截面随能量下降呈近似指数式衰减而淹没掉变化细节,引入了随能量变化相对平缓的S因子以便清晰显示低能区的变化趋势,并在R矩阵等理论的帮助下进行外推。S(E)因子与反应截面
$\sigma(E)$ 的关系定义为[2]$$S(E)=\sigma(E)E\exp(2\pi\eta),$$ 其中:E是质心系能量;
$\eta=Z_1Z_2e^2/(4\pi\epsilon_0\hbar v)$ 是索末菲参数,与两碰撞核的电荷数($Z_1$ ,$Z_2$ )及反应入射道的相对速度(v)有关,其中$\epsilon_0$ 为真空介电常数,$\hbar$ 为约化普朗克常数,e为基本电荷。由于反应截面中的库仑位垒穿透因子的主要影响被S(E)表达式中的指数因子所抵消,S(E)因子随能量的变化比截面$\sigma(E)$ 随能量的变化缓慢得多。尽管如此,外推过程仍会引入较大的不确定性,尤其是未知能区可能存在对截面有很大贡献的低能共振或阈下共振时,难以确定其具体位置和强度。为了直接测量更低能区的反应截面,人们建造了深地实验室(LUNA[5]、JUNA[6]等)以屏蔽宇宙射线降低噪声影响,并建造强流加速器和高效率探测装置。随着研究的深入,部分轻核反应的测量接近或达到
$E_{\rm{G}}$ 范围。然而,新的研究发现,在极低能区,实验室中的直接测量还受到电子屏蔽效应的影响[7-9]。核外电子云或处于等离子体状态的电子会对发生核反应的核产生屏蔽效应,由于电子屏蔽,降低了有效核电荷数,造成有效库仑位垒降低,从而使得截面增强,偏离“裸核”反应截面,并且电子屏蔽效应的影响随着能量的降低而迅速增强。这种效应一般用电子屏蔽势${{\rm{U}}_{\rm{e}}}$ 来表征:$$f_{\rm{lab}}(E)=\dfrac{\sigma_{\rm{s}}(E)}{\sigma_{\rm{b}}(E)}=\dfrac{S_{\rm{s}}(E)}{S_{\rm{b}}(E)}\sim\exp{\left(\pi\eta\dfrac{U_{\rm{e}}^{\rm{lab}}}{E}\right)}$$ 其中:E为质心系能量;s、b分别表示“屏蔽”和“裸核”两种条件。
$U_{\rm{e}}^{\rm{lab}}$ 表示实验室条件下测量的电子屏蔽势,以与天体环境的等离子状态下相区别($U_{\rm{e}}^{\rm{plasma}}$ )。实验发现,电子屏蔽势一般在十几到几百eV的量级,并且所有的实验测量值都比理论模型预言的最大值还高[10],目前为止,这一现象还没有令人满意的理论模型加以解释。通常,在$E<100\;U_{\rm{e}}$ 的能区电子屏蔽效应的影响已非常明显,不能被忽略。由于低能核反应在天体环境(等离子体状态)与实验室环境(离子+原子)条件的差别,实验室条件下与核天体情形下的电子屏蔽因子是不同的。因此,一般的,从实验室中测量的低能反应截面计算天体等离子体环境中的热核反应数据必须经过两步修正:
$$\sigma_{\rm{lab}}\rightarrow\sigma_{\rm{bare}}\rightarrow\sigma_{\rm{plasma}}{\text{。}}$$ 因此,即便直接测量接近或达到Gammow能区,为消除电子屏蔽效应造成对裸核反应截面的偏离,还是需要从电子屏蔽效应可以忽略的高能区数据(
$E>1\,000\;U_{\rm{e}}$ )进行外推。所以,寻求另外的方法直接得到核反应的 “裸核”截面对于天体核反应截面测量和电子屏蔽效应的深入研究具有重要意义[11]。由于以上原因,为了克服低能核反应直接测量过程中遭遇到的库仑位垒截面抑制和电子屏蔽效应截面偏离的困难,避免外推引入的不确定性,人们开始探索间接测量方法。目前,在核反应理论的框架下发展出几种通过其他相关反应来间接获得天体物理感兴趣的核反应截面的方法[12]。其中主要有特洛伊木马方法(TrojanHorseMethod,THM)、库仑解离方法(CD)和渐进归一化系数方法(ANC)。电磁解离方法是将靶核的库仑场当作
${\rm{\gamma}}$ 源,通过逆反应来研究辐射俘获过程;渐进归一化系数方法则通过转移反应提取原子核基态的渐进归一化系数来计算辐射俘获反应的矩阵元;特洛伊木马方法主要用于在入射道与出射道都不涉及γ量子的非弹性反应过程,特别适合低能区带电粒子裸核反应截面测量。本文将在介绍特洛伊木马方法基本原理的基础上,重点讨论最近发表的有关核天体物理应用中一些最重要的实验结果及未来展望。
-
特洛伊木马方法[13-15],作为实验核天体物理中一种有效的间接测量方法,它能够利用准自由反应机制(Quasi-free,QF),通过适当的三体反应在库仑位垒以上能量的截面测量,提取天体物理相关的两体反应在天体能区的裸核反应截面和S(E)因子随能量变化的依赖关系。
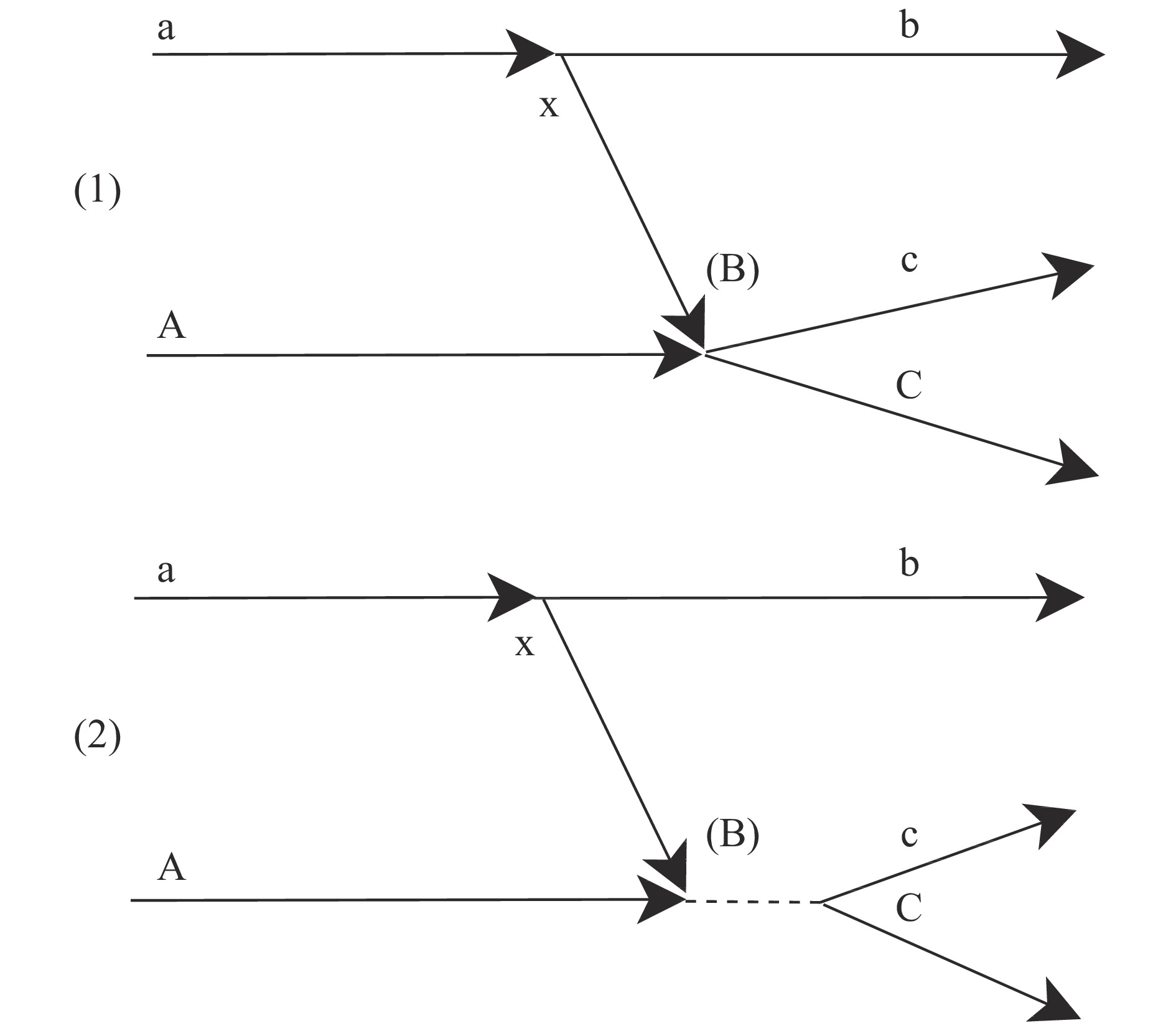
特洛伊木马方法基本原理如图1所示,对于一个天体物理感兴趣的带电粒子两体反应A+x
$\rightarrow$ C+c,选取一个和它密切相关的三体反应A+a$\rightarrow$ C+c+b来测量,其中,核a可看作是由结合得比较松散的两部分组成:a=(x$\oplus$ b)。选择适当的运动学条件,使得在核反应前后核b的能量和动量变化非常小,核反应就可以看作是在核A与x之间发生的,b核只是A+x反应的旁观者。这样的核反应过程就是通常所谓的准自由反应。其中:x称为该准自由反应的参与者(Participator);b称为该反应的旁观者(Spectator);而“运载”核x的母核a,称为“木马核”。若适当选取入射粒子能量,使得A+a入射道的相对能量
$E_{\rm{Aa}}$ 高于库仑位垒$E_{\rm{C}}$ ,三体反应可以垒上顺利进行,截面大,易测量。同时,x借助于木马核a的运载,到达核A的核力相互作用区域内与A发生反应,即A+x反应借助于准自由过程伴随A+a核反应而发生。因为$E_{\rm{Aa}}$ 要部分用于克服x在木马核a内的束缚能(即x与b之间的结合能)$\varepsilon_{\rm{a}}$ ;同时考虑到x核在a中有费米运动的动量分布,当x与A的运动方向相同时,它们之间的相对运动可以大部分甚至全部被抵消。因此,即使$E_{\rm{Aa}}$ 较大,A+x体系的相对能量$E_{\rm{Ax}}$ 也可以很小,直至等于零。而且,对一个束流能量点$E_{\rm{Aa}}$ 的测量,可以得到$E_{\rm{Ax}}$ 在一个能量区间(由费米动量分布范围决定)的数据。于是,借助于木马核的准自由反应,可以从较高能量(高于库仑位垒)的三体反应实验测量数据得到极低能区(天体能区)的两体反应截面随能量的变化信息,而不再受库仑位垒穿透效应对截面抑制的根本困难,“特洛伊木马”方法也由此得名。另一方面,由于三体反应的入射道能量在库仑位垒之上,电子屏蔽效应的影响完全可以忽略不计,提取到的数据可以看作是两体反应“裸核”反应截面。特洛伊木马理论推导的主要目标就是要利用核反应理论找出三体反应和两体反应之间的联系。特洛伊木马方法理论基本框架最早是由Baur等[13]在1986年提出的,基于直接核反应的准自由反应机制,采用平面波冲击近似(PWIA),将三体反应截面分解为与两体反应核作用相关的三部分:运动学因子
$K_{\rm{F}}$ 、木马核内动量分布$|W|^2$ 、能量半离壳(Half-Off-Energy-Shell,HOES)的核相互作用两体反应截面−它和实际两体反应截面(能量在壳,On-Energy-Shell,OES)之间相差一个库仑穿透作用需要进一步考虑进去。$$ \frac{{\rm{d}}^3\sigma}{{\rm{d}}E_{\rm{Cc}}{\rm{d}}\Omega_{\rm{Bb}}{\rm{d}}\Omega_{\rm{Cc}}}=K_{\rm{F}}|W|^2\Big(\frac{{\rm{d}}\sigma}{{\rm{d}}\Omega}\Big)^{\rm{HOES}}_{{\rm{Ax}}\rightarrow{\rm{Cc}}}$$ (1) 2000年,Typel等[14]用平面波玻恩近似(PWBA)进行推导,并与PWIA结果进行比较,PWBA也可以将三体反应截面分解为三部分,两体反应截面部分的形式上有所差别。2003年,Typel等[15]合作对THM理论进行了系统的研究,对精确的三体反应的T矩阵元进行扭曲波玻恩近似(DWBA)[15]处理,然后利用表面近似将三体反应截面与两体反应的S矩阵元联系起来,在此基础上,进一步采用局域动量近似等简化处理,最终将三体反应截面分解为三部分,形式上与PWIA结果相似,但两体反应截面中自然出现了库仑穿透因子项
$P_l$ 。$$ \frac{{\rm{d}}^3\sigma}{{\rm{d}}E_{\rm{Cc}}{\rm{d}}\Omega_{Bb}{\rm{d}}\Omega_{\rm{Cc}}}=K_{\rm{F}}|W|^2\sum\limits_lP_l\Big(\frac{{\rm{d}}\sigma^{}_l}{{\rm{d}}\Omega}\Big)^{\rm{OES}}_{{\rm{Ax}}\rightarrow{\rm{Cc}}}$$ (2) 2007年,Mukhamedzhanov等[16]在少体近似和格林函数理论处理基础上,考虑了能量离壳效应和初末态相互作用,提出可以用R-矩阵近似来处理共振过程。2018年,Bertulani等[17]合作,用包含非弹破裂(InclusiveNon-ElasticBreakup,INEB)模型对特洛伊木马方法的理论基础进行探讨,证明了在三体理论的DWBA限定条件下,具有两步特性的NIBA截面的直接部分,在结构上与一步过程THM截面相似。
特洛伊木马方法的运动学条件约束及能量关系:通常选用s-波占主导地位的基态核作为木马,其费米动量振幅在零点具有最大值,根据三体反应准自由条件及能量守恒可以得到两体反应与三体反应的能量关系[15]
$$ E_{\rm{Ax}}^{\rm{qf}}=E_{\rm{Aa}}\left(1-\frac{\mu_{\rm{Aa}}}{\mu_{\rm{Bb}}}\frac{\mu_{\rm{bx}}^{2}}{m_{\rm{x}}^2}\right)-\varepsilon_{\rm{a}}$$ (3) 其中,
$\varepsilon_{\rm{a}}=(m_{\rm{x}}+m_{\rm{b}}-m_{\rm{a}})c^2$ 为木马核的束缚能。实际上,$E_{\rm{Ax}}$ 是以$E_{\rm{Ax}}^{\rm{qf}}$ 为中心的能量区间:$E_{\rm{Ax}}=(E_{\rm{Ax}}^{\rm{qf}}- E_{\rm{cut}}$ ,$E_{\rm{Ax}}^{\rm{qf}}+E_{\rm{cut}})$ ,其中,$E_{\rm{cut}}$ 是以费米运动动量宽度所决定的能量截断。因此对应一个束流能量点,可以得到准自由能量点附近一段能量区间的两体反应数据。利用能量关系(3),可以选择对应天体能区两体反应相匹配的准自由三体反应的入射道最佳束流能量。利用截面关系(2),可以从准自由三体反应事件中提取天体能区感兴趣的两体反应截面并进一步得到S(E)因子。于是,借助于木马核的准自由反应,我们可以从较高能区(高于库仑位垒)的三体反应实验数据得到极低能区(天体能区)的天体物理相关两体反应的裸核反应截面等信息。该方法克服了因库仑位截面垒抑制造成的直接测量的困难,也避免了电子屏蔽效应的困扰,而且不需要外推,没有了外推过程的不确定性。
-
根据特洛伊木马方法理论的基本关系式−能量关系(3)和截面关系
$(1)\thicksim(2)$ ,可以将该方法应用于低能区的天体核反应截面实验测量[18]。首先,需要选择一个合适的木马核,木马核应该具有明显的成团结构a=(x
$\oplus$ b),结构较松散,即结合能$\varepsilon_{\rm{a}}$ 较小,容易发生准自由破裂,而且基态波函数比较清楚,通常以s-波($l=0$ )为主导。我们知道,天体环境中最丰富的元素是H和He,因此p、
${\rm{\alpha}}$ 引发的核反应是天体环境中最常见的核过程。实验中最常用的木马核是氘核,它可以提供质子,研究$({\rm{p}},\,{\rm{\alpha}})$ 、(p,n)等常见天体核反应;还可以提供中子,研究中子引发的核反应,它的独特优点在于中子能量可以自由控制。另一个常用的木马核是$^6{\rm{Li}}$ ,它可以提供${\rm{\alpha}}$ 粒子,研究$({\rm{\alpha}},\,{\rm{p}})$ 、$({\rm{\alpha}},\,{\rm{n}})$ 等常见天体核反应,也可以提供$d$ 粒子,研究轻核聚变反应。常用的木马核及其基本性质见表1。另外,值得一提的是几个有潜力的木马核候选者,见表2。它们可以为短寿命放射性核素(如t、$^5{\rm{He}}$ 、$^8{\rm{Be}}$ )引发的核反应提供研究的可能性。表 1 常用木马核及其基本性质
木马核 结构 束缚能$ \epsilon_{\rm{a}}$/MeV 角动量$l$ $^2{\rm{H}}$ $^2{\rm{H}}=({\rm{p}} \oplus {\rm{n}})$ 2.225 0 $^3{\rm{He}}$ $^3{\rm{He}}=({\rm{d}} \oplus {\rm{p}})$ 5.493 0 $ ^6{\rm{Li}}$ $ ^6{\rm{Li}}=({\rm{\alpha}} \oplus {\rm{d}})$ 1.474 0 $ ^{14}{\rm{N}}$ $ ^{14}{\rm{N}}=(^{12}{\rm{C}} \oplus {\rm{d}})$ 10.272 0 $^{16}{\rm{O}}$ $^{16}{\rm{O}}=(^{12}{\rm{C}} \oplus {\rm{\alpha}}) $ 7.162 0 $^{20}{\rm{Ne}}$ $^{20}{\rm{Ne}}=(^{16}{\rm{O}} \oplus {\rm{\alpha}})$ 4.730 0 表 2 有潜力的木马核及其基本性质
木马核 结构 束缚能$ \epsilon_{\rm{a}}$/MeV 角动量$l$ $^7{\rm{Li}}$ $^7{\rm{Li}}=({\rm{\alpha}} \oplus {\rm{t}})$ 2.467 1 $ ^9{\rm{Be}}$ $ ^9{\rm{Be}}=(^8{\rm{Be}} \oplus {\rm{n}})$ 1.665 1 $ ^9{\rm{Be}}$ $ ^9{\rm{Be}}=(^5{\rm{He}}\oplus {\rm{\alpha}} )$ 2.464 0 其次,根据能量关系式(3)确定入射道能量
$E_{\rm{Aa}}$ ,使其高于库仑位垒,同时$E_{\rm{Ax}}$ 在天体物理感兴趣的能区。木马核a可以做入射粒子也可以做靶核,根据实验测量是否方便来确定。然后,根据准自由条件确定探测器布局。实验要对三体反应出射粒子中的两个进行运动学完全测量。例如,测量C和c粒子的探测器位置并不是随意的,而是受准自由运动学条件约束,这样的一对角度称为“准自由角度对”−在这个位置准自由过程截面最大。“准自由角度对”依赖于两体反应的散射角。
需要特别指出的是:得到三体反应数据后,在提取两体反应信息之前,需要先对特洛伊木马方法的适用性进行检验。首先,看三体反应中是否存在明显的准自由过程,以及准自由过程能否从其它的过程中分离出来。为此可以考察出射粒子“准自由角度对”的关联效应,以及旁观者的动量分布。数据处理中要对“子核”在木马核中的动量分布宽度加以限制,使其满足准自由条件的要求。在确认准自由过程存在并可分离之后,用特洛伊木马方法提取两体反应信息,将其与直接数据相比较(在电子屏蔽效应不明显的较高能区),从而检验方法的有效性。激发函数,角分布都可以用来作有效性检验。
特洛伊木马方法应用于实验核天体反应间接测量,始于1990年代,是由意大利国家核物理实验室(INFN-LNS)核天体物理组发展起来的[12,18]。从轻核聚变反应、天体核物理的锂问题、轻核素Li、Be、B的相关核反应,到AGB星中C、N、O、F相关的核反应过程、s-过程的中子源反应、中等质量恒星的碳燃烧过程,一直到中子核反应测量和放射性束流核反应,进行了一系列的间接测量,不仅检验了特洛伊木马方法的有效性、可靠性,也获得了一批突破性的研究成果[18]。
在国内,我们从2003年去INFN-LNS做访问学者开始,参与特洛伊木马方法的实验应用研究[19-20]。回国后,继续开展这方面的工作,主要进行了
$^9{\rm{Be}}$ 相关核反应的间接测量[21-24],在此过程中建立起了整套数据分析与模拟平台[25],提出一种新的准自由事件挑选方法[21-22]。另外,在这些数据中寻找到$^9{\rm{Be}}=(^8{\rm{Be}}\oplus{\rm{n}})$ 的初步证据,为研究$^8{\rm{Be}}$ 引发的核反应研究(如$3{\rm{\alpha}}$ -过程)提供了一个可能的新途径[23]。此外,我们还利用木马核$^6{\rm{Li}}=({\rm{\alpha}}\oplus{\rm{d}})$ 完成了${\rm{d}}({\rm{d}},{\rm{p}}){\rm{t}}$ 低能区截面测量[26-27],得到了比意大利INFN-LNS同一实验结果精度更高、数据点更多、能区更低的实验数据,指出特洛伊木马方法中束流能量大小的适当选择对测量截面精度的影响,并进一步确定了低能轻核聚变过程中木马选择无关性检验。特洛伊木马方法应用于天体核反应间接测量基本情况见表3[18]所列。下面,我们仅就近期几个比较重要的THM应用进行介绍和讨论。
表 3 利用特洛伊木马方法实验进行天体核反应间接测量基本情况列表
两体反应 三体反应 木马核 $ E_0 /{\rm{MeV}}$ $ {E}_{\rm{Ax}}^{\rm{qf}}/{\rm{MeV}} $ $^1{\rm{H}}({\rm{p}},\,{\rm{p}})^1{\rm{H}}$ $^2{\rm{H}}({\rm{p}},\,{\rm{pp}}){\rm{n}}$ $^2{\rm{H}}=({\rm{p}}\oplus {\rm{n}})$ 5 0.5 $^2{\rm{H}}({\rm{d}},\,{\rm{p}})^3{\rm{H}}$ $^2{\rm{H}}(^6{\rm{Li}},\,{\rm{pt}}){\rm{\alpha}}$ $ ^6{\rm{Li}}=({\rm{d}}\oplus {\rm{\alpha}})$ 9.5, 11, 14 0.089, 0.342, 0.866 $^2{\rm{H}}({\rm{d}},\,{\rm{p}})^3{\rm{H}}$ $^2{\rm{H}}(^3{\rm{He}},\,{\rm{pt}})^1{\rm{H}}$ $^3{\rm{He}}=({\rm{d}}\oplus {\rm{p}})$ 17 0.178 $^2{\rm{H}}({\rm{d}},\,{\rm{n}})^3{\rm{He}}$ $^2{\rm{H}}(^3{\rm{He}},\,{\rm{n}}^3{\rm{He}})^1{\rm{H}}$ $^3{\rm{He}}=({\rm{d}}\oplus {\rm{p}})$ 17 0.178 $^2{\rm{H}}(^3{\rm{He}},\,{\rm{p}})^4{\rm{He}}$ $ ^6{\rm{Li}}(^3{\rm{He}},\,{\rm{p}}{\rm{\alpha}})4{\rm{He}}$ $ ^6{\rm{Li}}=({\rm{d}}\oplus {\rm{\alpha}})$ 5, 6 0.53-0.93 $ ^6{\rm{Li}}({\rm{d}},\,{\rm{\alpha}})^4{\rm{He}}$ $ ^6{\rm{Li}}(^6{\rm{Li}},\,{\rm{\alpha}} {\rm{\alpha}})^4{\rm{He}}$ $ ^6{\rm{Li}}=({\rm{d}}\oplus {\rm{\alpha}})$ 5.0 0.0 $ ^6{\rm{Li}}({\rm{d}},\,{\rm{\alpha}})^4{\rm{He}}$ $ ^6{\rm{Li}}(^3{\rm{He}},\,{\rm{\alpha}} {\rm{\alpha}})^1{\rm{H}}$ $^3{\rm{He}}=({\rm{d}}\oplus {\rm{p}})$ 17.5 3.25 $ ^6{\rm{Li}}({\rm{p}},\,{\rm{\alpha}})^3{\rm{He}}$ $^2{\rm{H}}(^6{\rm{Li}},\,{\rm{\alpha}} ^3{\rm{He}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ $14 \thicksim36.6$ $0.00 \thicksim 3.03 $ $^7{\rm{Li}}({\rm{p}},\,{\rm{\alpha}})^4{\rm{He}}$ $^7{\rm{Li}}({\rm{d}},\,{\rm{\alpha}} {\rm{\alpha}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ $ 19\thicksim22,\,28\thicksim48$ $0.16\thicksim0.54,\,1.3\thicksim3.8$ $^7{\rm{Li}}({\rm{p}},\,{\rm{\alpha}})^4{\rm{He}}$ $^7{\rm{Li}}(^3{\rm{He}},\,{\rm{\alpha}} {\rm{\alpha}})^2{\rm{H}}$ $^3{\rm{He}}=({\rm{d}}\oplus {\rm{p}})$ 33 4.15 $ ^6{\rm{Li}}({\rm{n}},\,{\rm{t}})^4{\rm{He}}$ $^2{\rm{H}}(^6{\rm{Li}},\,{\rm{t}}{\rm{\alpha}})^1{\rm{H}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 14 0.0 $^7{\rm{Be}}({\rm{n}},\,{\rm{\alpha}})^4{\rm{He}}$ $^2{\rm{H}}(^7{\rm{Be}},\,{\rm{\alpha}} {\rm{\alpha}})^1{\rm{H}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 20.4 0.33 $ ^9{\rm{Be}}({\rm{p}},\,{\rm{\alpha}})^6{\rm{Li}}$ $^2{\rm{H}}(^9{\rm{Be}},\,{\rm{\alpha}} ^6{\rm{Li}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 22.25 0.012 $ ^9{\rm{Be}}({\rm{p}},\,{\rm{d}})^8{\rm{Be}}$ $^2{\rm{H}}(^9{\rm{Be}},\,{\rm{d}} ^8{\rm{Be}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 22.25 0.012 $^{10}{\rm{B}}({\rm{p}},\,{\rm{\alpha}})^7{\rm{Be}}$ $^{10}{\rm{B}}(^2{\rm{H}},\,{\rm{\alpha}} ^7{\rm{Be}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 27, 28 0.24, 0.34 $^{11}{\rm{B}}({\rm{p}},\,{\rm{\alpha}})^8{\rm{Be}}$ $^{11}{\rm{B}}(^2{\rm{H}},\,{\rm{\alpha}} ^8{\rm{Be}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 27 0.04 $^{12}{\rm{C}}({\rm{\alpha}},\,{\rm{\alpha}})^{12}{\rm{C}}$ $ ^6{\rm{Li}}(^{12}{\rm{C}},\,{\rm{\alpha}} ^{12}{\rm{C}})^2{\rm{H}}$ $ ^6{\rm{Li}}=({\rm{d}}\oplus {\rm{\alpha}})$ 18 3.03 $^{12}{\rm{C}}(^{12}{\rm{C}},\,{\rm{p}})^{23}{\rm{Na}} $ $^{12}{\rm{C}}(^{16}{\rm{O}},\,{\rm{p}}^{23}{\rm{Na}}){\rm{\alpha}}$ $^{16}{\rm{O}}=(^{12}{\rm{C}}\oplus {\rm{\alpha}})$ 25 2.22 $^{12}{\rm{C}}(^{12}{\rm{C}},\,{\rm{\alpha}})^{20}{\rm{Ne}} $ $^{12}{\rm{C}}(^{16}{\rm{O}},\,{\rm{\alpha}}^{20}{\rm{Ne}}){\rm{\alpha}}$ $^{16}{\rm{O}}=(^{12}{\rm{C}}\oplus {\rm{\alpha}})$ 25 2.22 $^{12}{\rm{C}}(^{12}{\rm{C}},\,{\rm{\alpha}})^{20}{\rm{Ne}} $ $^{12}{\rm{C}}(^{14}{\rm{N}},\,{\rm{\alpha}}^{20}{\rm{Ne}})^2{\rm{H}}$ $ ^{14}{\rm{N}}=(^{12}{\rm{C}}\oplus {\rm{d}})$ 30 2.5 $^{12}{\rm{C}}(^{12}{\rm{C}},\,{\rm{p}})^{23}{\rm{Na}} $ $^{12}{\rm{C}}(^{14}{\rm{N}},\,{\rm{p}}^{23}{\rm{Na}})^2{\rm{H}}$ $ ^{14}{\rm{N}}=(^{12}{\rm{C}}\oplus {\rm{d}})$ 30 2.5 $^{13}{\rm{C}}({\rm{\alpha}},\,{\rm{n}})^{16}{\rm{O}}$ $ ^6{\rm{Li}}(^{13}{\rm{C}},\,{\rm{n}} ^{16}{\rm{O}})^2{\rm{H}}$ $ ^6{\rm{Li}}=({\rm{d}}\oplus {\rm{\alpha}})$ 7.82 2.50 $ ^{15}{\rm{N}}({\rm{p}},\,{\rm{\alpha}})^{12}{\rm{C}}$ $^2{\rm{H}}(^{15}{\rm{N}},\,{\rm{\alpha}} ^{12}{\rm{C}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 60 1.55 $^{17}{\rm{O}}({\rm{p}},\,{\rm{\alpha}})^{14}{\rm{N}}$ $^2{\rm{H}}(^{17}{\rm{O}},\,{\rm{\alpha}} ^{14}{\rm{N}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 45 0.29 $^{17}{\rm{O}}({\rm{n}},\,{\rm{\alpha}})^{14}{\rm{C}}$ $^2{\rm{H}}(^{17}{\rm{O}},\,{\rm{\alpha}} ^{14}{\rm{C}})^{1}{\rm{H}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 41, 43.5 0.072, 0.212 $^{18}{\rm{O}}({\rm{p}},\,{\rm{\alpha}})^{15}{\rm{N}}$ $^2{\rm{H}}(^{18}{\rm{O}},\,{\rm{\alpha}} ^{15}{\rm{N}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 54 0.64 $ ^{18}{\rm{F}}({\rm{p}},\,{\rm{\alpha}})^{15}{\rm{O}}$ $^2{\rm{H}}(^{18}{\rm{F}},\,{\rm{\alpha}} ^{15}{\rm{O}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 52 0.53 $^{{\rm{19}}}{\rm{F}}({\rm{p}},\,{\rm{\alpha}})^{16}{\rm{O}}$ $^2{\rm{H}}(^{19}{\rm{F}},\,{\rm{\alpha}} ^{16}{\rm{O}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 50 0.29 $^{{\rm{19}}}{\rm{F}}({\rm{\alpha}},\,{\rm{p}})^{22}{\rm{Ne}}$ $^{{\rm{19}}}{\rm{F}}(^6{\rm{Li}},\,{\rm{p}} ^{22}{\rm{Ne}})^2{\rm{H}}$ $ ^6{\rm{Li}}=({\rm{d}}\oplus {\rm{\alpha}})$ 6.0 1.82 -
$^{{\rm{13}}}{\rm{C}}{({\rm{\alpha}},{\rm{n}})^{16}}{\rm{O}}$ 核反应被认为是低质量恒星(3-4倍太阳质量)渐近巨分支阶段(AGB)低温慢中子俘获核合成(s-过程)产生重核素(核素质量范围从$A=90$ 到204中的大多数核素)的主要中子源。在$10^8$ K的温度下,它活跃在渐近巨支星的氦燃烧壳层内,对应于$^{{\rm{13}}}{\rm{C}}{({\rm{\alpha}},{\mkern1mu}{\rm{n}})^{16}}{\rm{O}}$ 反应的有效能量区间在$140\thicksim230$ keV之间。在这一能区,天体物理S(E)因子被$-3$ keV的阈下共振(对应于$^{{\rm{17}}}{\rm{O}}$ 的6.356 MeV能级)所支配,从而导致S(E)因子急剧增加。尽管它在天体物理中起着至关重要的作用,但在s-过程能量窗口内没有直接测量数据。近年来,人们进行了一些直接和间接的测量,以确定天体物理感兴趣能区(约$190\pm40$ keV)的截面。然而,外推(例如通过R-矩阵)和间接测量方法(例如ANC)给出不一致的结果,其贡献的大小仍有争议。在天体物理能区这种差异有3倍或更多,这导致了高度不确定的反应速率,并影响了低质量恒星中的中子释放。因此,特洛伊木马方法被应用到$^{{\rm{13}}}{\rm{C}}{{{\rm{(}}^{\rm{6}}}{\rm{Li,dn)}}^{{\rm{16}}}}{\rm{O}}$ 准自由反应中,以获得这种贡献的实验估计[28-30]。在这项工作中,结合了ANC和THM两种间接测量方法,以明确地确定$^{{\rm{13}}}{\rm{C(\alpha,n}}{{\rm{)}}^{{\rm{16}}}}{\rm{O}}$ 天体物理S因子的绝对值,使得实验精确度大大提高,参见图2。此工作首次通过特洛伊木马方法和n-分宽度推导出了6.356 MeV能级的ANC,虽然测量了该能级的更大ANC,但实验S(E)-因子与文献中$140\thicksim230$ keV能区的最新推断一致。由于ANC与THM两种方法相结合的创新应用,使得在$^{{\rm{13}}}{\rm{C(\alpha,n}}{{\rm{)}}^{{\rm{16}}}}{\rm{O}}$ 研究中获得了前所未有的精度。
图 2 (在线彩图) 利用特洛伊木马方法间接测量
$ ^{{\rm{13}}}{\rm{C}}{({\rm{\alpha }},{\mkern 1mu} {\rm{n}})^{16}}{\rm{O}}$ 核反应S(E)因子[29] -
在恒星环境中观测到的
$^{{\rm{19}}}{\rm{F}}$ 丰度系统性地超过了核合成理论模型预测的丰度,氟元素的核合成是核天体物理学中最吸引人的待解决问题之一。它触发了新一轮的测量研究热潮,这可能会改变目前公认的氟产生的范式,并确立氟作为一个研究AGB星内层的精确探针。$^{{\rm{19}}}{\rm{F(p,\alpha}}{{\rm{)}}^{{\rm{16}}}}{\rm{O}}$ 反应是AGB星富质子外层的一个重要氟破坏通道,它可能在缺氢的后AGB星核合成中起作用。到目前为止,由于库仑势垒的阻碍效应,直接测量没有到达天体物理感兴趣的能区($E_{\rm{c.m.}}\lesssim300$ keV)。因此,可以利用特洛伊木马方法,通过对$^{\rm{2}}{\rm{H}}{{\rm{(}}^{{\rm{19}}}}{\rm{F,}}{{\rm{\alpha}}^{{\rm{16}}}}{\rm{O)n}}$ 和$^{{\rm{19}}}{\rm{F}}{{\rm{(}}^{\rm{3}}}{\rm{He,}}{\mkern1mu}{{\rm{\alpha}}^{{\rm{16}}}}{\rm{O)d}}$ 反应的准自由事件来提取天体能区的$^{{\rm{19}}}{\rm{F(p,}}{\mkern1mu}{\rm{\alpha}}{{\rm{)}}^{{\rm{16}}}}{\rm{O}}$ 核反应数据[31-32]。${\rm{\alpha}}_0$ 反应道的THM测量表明存在以前没有观察到的共振结构,如图3所示,这导致在天体物理温度下的反应速率增加到1.7倍,对恒星核合成具有潜在的影响。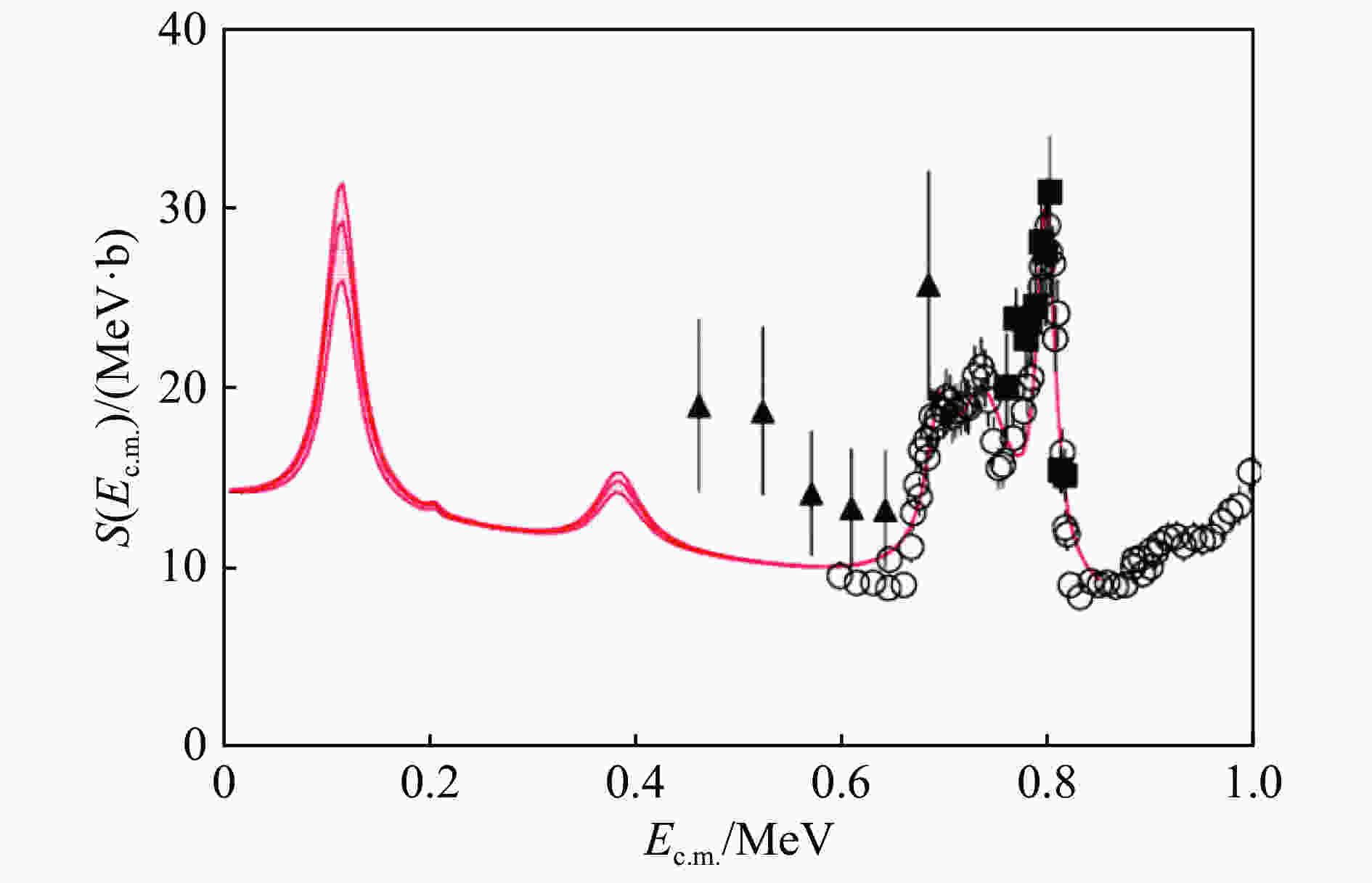
图 3 (在线彩图) 利用特洛伊木马方法间接测量
$ ^{{\rm{19}}}{\rm{F}}({\rm{p}},{\rm{\alpha}}){}^{16}{\rm{O}}$ 核反应S(E)因子[32]另一个影响
$^{{\rm{19}}}{\rm{F}}$ 破坏过程的重要反应是富氦环境中的$^{{\rm{19}}}{\rm{F}}({\rm{\alpha}},{\rm{p}}){}^{22}{\rm{Ne}}$ 核反应,感兴趣的天体反应能区在在$0.2\thicksim0.8$ MeV之间(远低于库仑势垒,3.8 MeV)。通过直接测量研究该反应时的最低能量约为0.66 MeV,仅覆盖Gamow窗口的上边缘,因此反应率的评估基于外推。为了研究较低的能量,采用特洛伊木马方法,利用6 MeV的$^6{\rm{Li}}$ 束流引发的准自由反应$^{{\rm{19}}}{\rm{F}}(^6{\rm{Li}},\,{\rm{p}}^{22}{\rm{Ne}})^2{\rm{H}}$ 的测量,提取$^{{\rm{19}}}{\rm{F}}({\rm{\alpha}},\,{\rm{p}})({\rm{\alpha}},\,{\rm{p}}){}^{22}{\rm{Ne}}$ 反应在1 MeV以下能区(完全覆盖了感兴趣的天体物理区域,并重叠了已有的直接数据进行归一化处理)的反应截面,在Gamow窗口中首次检测到了几个共振[33]。计算显示,在天体物理温度下,反应速率与文献相比增加了4倍,这可能会导致潜在的重要天体物理影响。 -
碳燃烧核反应决定中等以上质量(超过8个太阳质量)恒星晚期演化阶段的命运走向和吸积中子星形成Ia型超新星的引爆临界点[2-4,34]。一般认为,典型的恒星碳燃烧过程的温度条件为0.8 GK[34],对应的质心能量及其宽度约为
$E_{\rm{G}}=(1.5\pm0.3)$ MeV。在更广泛的核天体研究过程中(从刚刚能触发碳燃烧的最小质量恒星到足以产生爆炸的超新星),碳燃烧的温度范围从$0.6\thicksim1.2$ GK,对应能量区域大约从1到3 MeV。碳燃烧反应主要涉及两个过程:$^{12}{\rm{C}}(^{12}{\rm{C}},\,{\rm{\alpha}}){}^{20}$ Ne($Q=4.62$ MeV)和$^{12}{\rm{C}}(^{12}{\rm{C}},{\rm{p}}){}^{23}$ Na($Q=2.24$ MeV),这两个反应道的分支比很接近[34]。直接测量主要有两种方法:测量出射的轻带电粒子
${\rm{\alpha}}$ 或质子;也可以测量剩余核激发态($^{20}{\rm{Ne}}^*$ 、$^{23}{\rm{Na}}^*$ )退激产生的特征伽马射线(此方法不能测量${\rm{\alpha}}_0$ 与$p_0$ 反应道)。从1960年代至今[35-38],人们已经通过直接测量得到了很宽能量范围的截面数据,并发现$^{12}{\rm{C}}+^{12}{\rm{C}}$ 反应存在较强的准分子共振现象。目前最低能量已经测到2.1 MeV,到达天体能区的上边缘,并发现此处有一个较强的共振,如果此共振被进一步证实,对$T=0.8$ GK附近的恒星,将使得现有的${\rm{\alpha}}$ 衰变反应道非共振反应率增加到5倍[37]。然而,由于
$^{12}{\rm{C}}+^{12}{\rm{C}}$ 的库仑位垒高度约7.8 MeV,比核天体感兴趣的伽莫夫能量高得多,当直接测量向低能方向进一步推进时,截面因库仑位垒抑制效应急剧下降到nb以下,如此低的截面使得直接测量变得非常困难。由于直接测量数据的缺乏,能量低于2.1 MeV的关键天体数据主要依靠从高能量区向低能量区外推。然而,不同的理论模型对低能区变化趋势给出迥然不同的预测,因为没有实验数据,对这些模型的正确性难以判断。其中,Cooper等[39]预言了共振峰在碳燃烧中存在的可能性,如果能够用实验数据来证明该共振结构的存在,会显著地影响如今大部分模型所采用的碳燃烧反应率数值。由于模型无法准确预测可能存在的准分子共振的能量位置和强度,使得理论外推更加的不准确,从而给天体模型的计算结果带来巨大的不确定度。如何精确地确定天体能区的碳燃烧反应截面,是许多核物理学者和天文学者努力要解决的关键问题。虽然低能区的直接测量数据最具有说服力,但到目前为止,THM是唯一能深入2 MeV以下能区进行测量的工具。文献[40]报道了用特洛伊木马方法测量
$^{12}{\rm{C}}(^{12}{\rm{C}},{\rm{\alpha}}_{0,1}) {}^{20}{\rm{Ne}}$ 和$^{12}{\rm{C}}(^{12}{\rm{C}},{\rm{p}}_{0,1}){}^{23}{\rm{Na}}$ 在$0.8\thicksim2.7$ MeV能区的反应数据(下标0和1分别代表$^{20}{\rm{Ne}}$ 和$^{23}{\rm{Na}}$ 的基态和第一激发态),该工作采用$^{14}{\rm{N}}=(^{12}{\rm{C}}\oplus{\rm{d}})$ 作为木马核提供$^{12}{\rm{C}}$ 和氘。实验结果显示,提取的截面在天体能区有几个强的共振(图4),验证了Cooper等[39]理论预言,这些共振会导致在相关温度下反应率大幅度增加。特别是,在$5\times10^8\;{\rm{K}}$ 左右,反应率被提高到比平滑外推参考值大25倍以上。这一发现可能意味着降低了大质量恒星中碳燃烧点火所需的温度和密度,降低了吸积中子星的超爆点火深度,以使观测结果与理论模型相一致。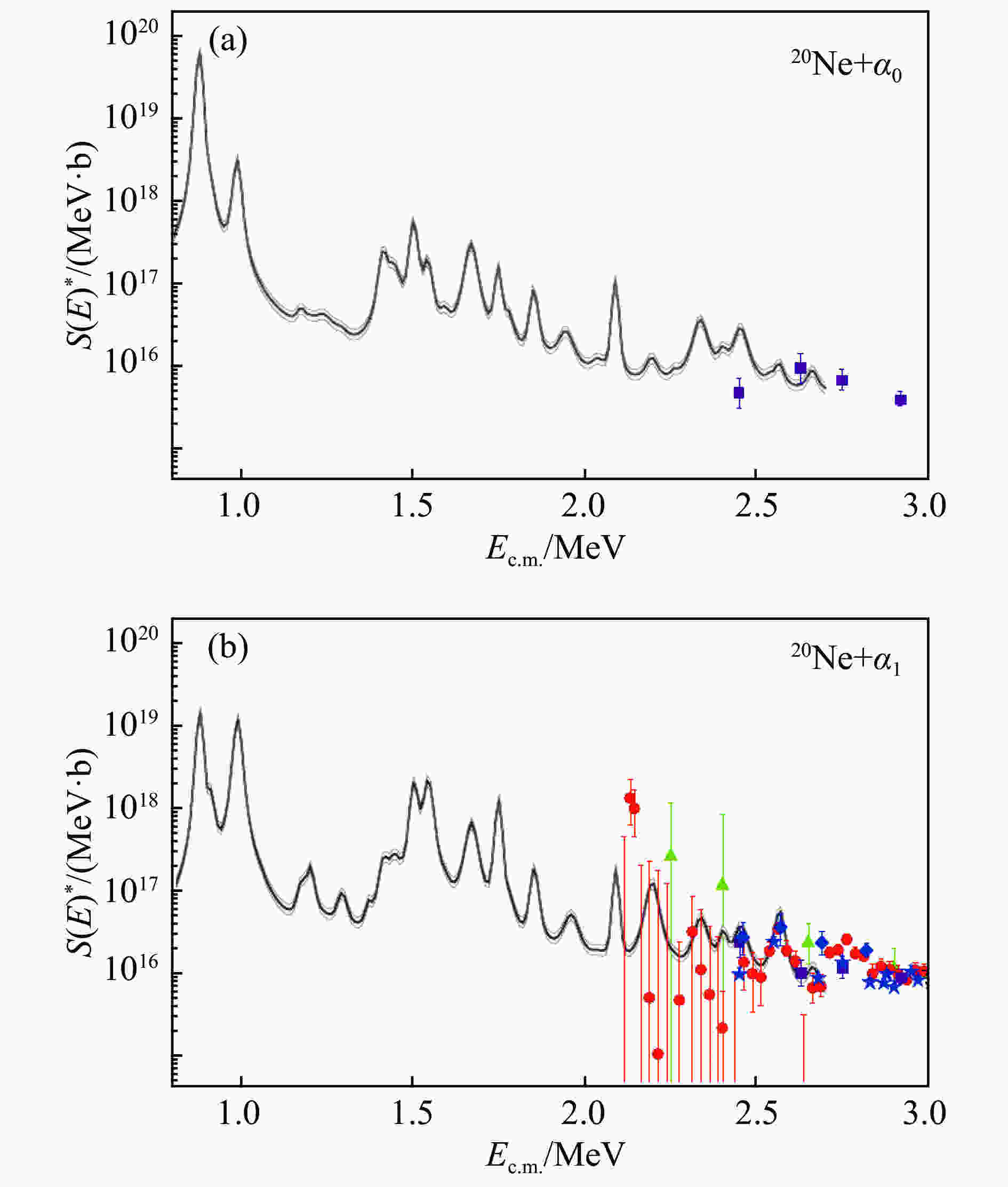
图 4 (在线彩图) 利用特洛伊木马方法间接测量
$ ^{12}{\rm{C}}(^{12}{\rm{C}},{\rm{\alpha}}_{0,1}){}^{20}{\rm{Ne}}$ 核反应$ S^*(E)$ 因子,发现天体能区有多个强共振[40]然而,该研究结果也引起了诸多的质疑和争议[41-44],比如低能区S*(E)因子的走势是否合理,PWIA是否需要加入库仑与核力修正,事件选择中可能包含了部分非准自由的干扰事件。Zhang等[41]认为可以通过低能区
$^{12}{\rm{C}}+^{13}{\rm{C}}$ 核反应截面测量为$^{12}{\rm{C}}+^{12}{\rm{C}}$ 核反应截面在低能区的上限给出一个限定,这在已经测量的很宽的一段能区都是成立的,因此可以期望外推到伽莫夫低能区,结果显示,THM数据[40]在低能区存在远高于上限的走势,因此对其可靠性提出质疑。当然,如果存在很强的共振是否可以突破其上限,需要天体能区的实验测量做判断。Mukhamedzhanov等[42-43]对特洛伊木马方法的PWIA近似处理在$^{12}{\rm{C}}+^{12}{\rm{C}}$ 核反应中是否会产生较大偏差也提出不同看法,认为需要从理论上发展引入末态相互作用(库仑及核力)的模型对该结果给出修正,修正后的低能$S^*(E)$ 上升趋势被压低下来,基本控制在CC-M3Y+Rep理论提出的上限以下(图5),但Tumino[44]认为,修正后的$S^*(E)$ 整体基线向高能端翘起是不正确的,也是与直接测量数据相背离的,并指出Mukhamedzhanov提出的修正理论所预言的旁观者粒子主要分布在后角度,这与准自由事件要求的旁观者主要集中在小角度前冲完全相违背。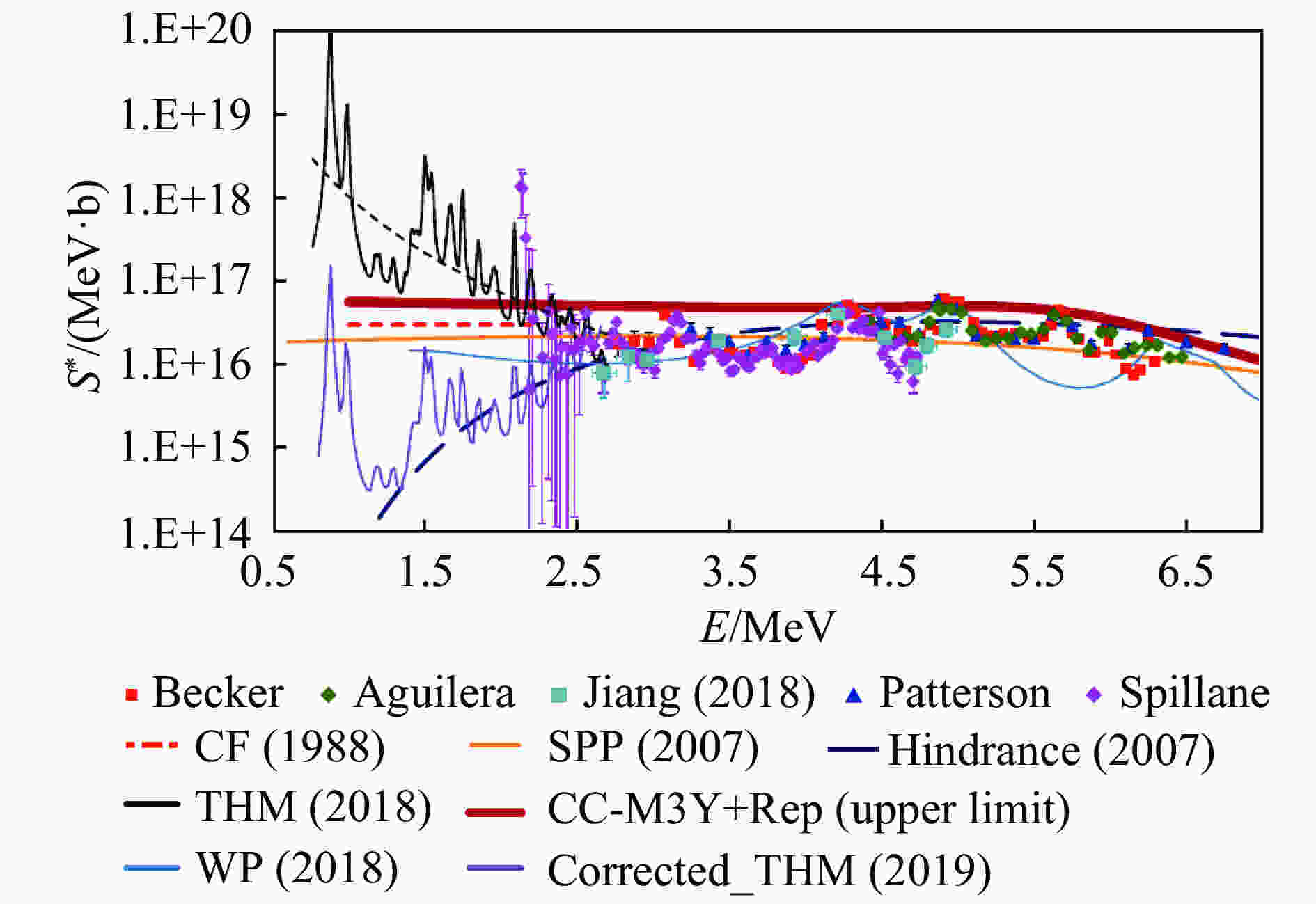
图 5 (在线彩图)
$ ^{12}{\rm{C}}+^{12}{\rm{C}}$ 核反应$ S^*(E)$ 因子不同实验测量结果及理论模型预测的比较,THM数据按A.M.M.修正前(深黑色线)后(浅灰色线)的趋势差别显著[43]以上种种争议和质疑,都需要实验上做进一步的测量和检验,无论是采用直接测量方法,还是间接测量方法。最近,Tang等[38]提出一种利用厚靶实验技术测量
$^{12}{\rm{C}}+^{12}{\rm{C}}$ 核反应截面的方法,但限于低能库仑位垒抑制效应对截面的影响,目前给出的能量区间在$3.4\thicksim4.0$ MeV,离天体物理感兴趣的能区还有一定距离,进一步的直接测量工作也在中国锦屏地下实验室核天体物理(JUNA)实验平台积极筹备。另外,值得注意的是,文献[40]实验所用木马核$^{14}{\rm{N}}=(^{12}{\rm{C}}\oplus{\rm{d}})$ 是一个较强的束缚核(其结合能$e_{\rm{a}}=10.27$ MeV),是否适合作为木马核产生准自由反应也是一个值得讨论、需要检验的问题,如果准自由事件远少于级联过程,而事件挑选中混入较多的级联事件等干扰过程被误认为是准自由事件,会使得结果产生较大偏离,这也可能是造成强共振趋势过高的一个原因。因此,最好能重新设计实验,利用一个不同的木马核进行交叉检验,验证方法及数据的可靠性。最近,我们正在积极准备开展新的实验,拟选用结合能相对较小($e_{\rm{a}}=7.16$ MeV)的$^{16}{\rm{O}}=(^{12}{\rm{C}}\oplus{\rm{\alpha}})$ 作为木马核(它不仅束缚能低,而且成团结构明显,更适合作为木马核产生准自由反应),对特洛伊木马方法有效性及数据可靠性进行交叉检验,澄清分歧,并对THM理论近似处理引起的偏差进行调查。同时,Mukhamedzhano新发展的修正理论也需要用实验检验其可靠性和有效性,这方面的工作也在积极筹备中。 -
中子诱发的核反应在核天体物理中起着重要作用,如原初大爆炸核合成、非均匀大爆炸核合成、通过s-过程(慢中子俘获)的重元素生成、超新星爆发核合成过程等。为了克服实验中中子束的产生问题,选取
${\rm{d=}}({\rm{p}}\oplus{\rm{n}})$ 作为木马核,应用特洛伊木马方法研究中子诱发的核反应是一个可行的途径。氘核作为最常用的木马核,它具有显而易见的成团结构
${\rm{d=}}({\rm{p}}\oplus{\rm{n}})$ ,而且束缚能很低,只有2.225 MeV,基态以s-波主导,具有清晰明确的基态波函数(Hulthen函数),其在动量空间的傅里叶变换为$$\varphi({{p}}_s)=\frac{1}{\pi}\sqrt{\dfrac{ab(a+b)}{(a-b)^2}}\left(\dfrac{1}{a^2+p^2_s}-\dfrac{1}{b^2+p^2_s}\right),$$ 其中,
$a=0.2317$ fm–1,$b=1.202$ fm–1。氘核作为木马核,不仅能提供质子,研究
$({\rm{p}},\,{\rm{\alpha}})$ ,(p,n),(p,d)等常见的天体核反应。还能提供虚拟中子源,用以研究中子引发的核反应。其独特优点是中子能量可以经由氘核加速实现连续可调,从而得到任意能量的单能中子。实验上,已经用特洛伊木马方法对中子核反应进行了研究,如:$^{17}{\rm{O}}({\rm n},\,{\rm{\alpha}})^{14}{\rm{C}}$ [45],$^7{\rm{Be}}({\rm n},\,{\rm{\alpha}})^4{\rm{He}}$ [46],充分显示了该方法在中子核反应研究中的可靠性和应用前景。随着世界上越来越多的放射性束装置的建成,与放射性核素相关的核反应研究逐渐展开。最近,意大利利用放射性离子束(RIB)通过特洛伊木马方法测量了与超新星核合成关键信息相关的影响放射性同位素
$^{18}{\rm{F}}$ 丰度的破坏反应$^{18}{\rm{F}}({\rm{p}},\,{\rm{\alpha}}){}^{15}{\rm{O}}$ ,这是该方法首次用于放射性核的核反应研究[47]。核合成过程,尤其是s-过程和r-过程的研究中,涉及到大量的不稳定放射性核素与中子的核反应过程。由于短寿命的放射性核与中子都无法直接作为靶材料,因此,利用放射性离子束轰击氘化聚乙烯靶,通过特洛伊木马方法间接测量放射性核素与中子发生的核反应具有特殊意义。
另外,对于轻元素的核合成研究,由于自然界中缺乏稳定的质量数
$A=5$ 和8的核素,对这些核素参与的核反应过程的研究非常困难。特别是$^8{\rm{Be}}$ (半衰期为$6\times 10^{-17}$ s)与$^5{\rm{He}}$ (半衰期为$5\times10^{-22}$ s),既不可能做束流引出,更不可能作为实验靶。而引入木马核$^9{\rm{Be}}=(^8{\rm{Be}}\oplus{\rm{n}})$ 或$^9{\rm{Be}}=(^5{\rm{He}}\oplus{\rm{\alpha}})$ ,则为$A=5$ 和8的核素参与的核反应研究打开了一扇窗。在Wen等[23]的工作中,初步显示了$^9{\rm{Be}}=(^8{\rm{Be}}\oplus{\rm{n}})$ 成团结构存在的可能性,由于数据统计误差较大,需要进一步实验进行确认,这将为$^8{\rm{Be}}$ 发生的核反应研究提供一个可能的途径,比如与$3{\rm{\alpha}}$ 过程形成$^{12}{\rm{C}}$ (HollyState)相关$^8{\rm{Be}}+{\rm{\alpha}}\rightarrow^{12}{\rm{C}}$ 核反应研究。$^9{\rm{Be}}=(^5{\rm{He}}\oplus{\rm{\alpha}})$ 成团结构也被实验工作所证实[48-50],为开展$^5{\rm{He}}$ 相关的核反应提供了可能。 -
特洛伊木马方法是实验核天体物理中一种非常有效的间接测量方法,它利用准自由反应机制,通过适当的三体反应在库仑位垒以上能区的截面测量,提取直接两体反应难以达到的天体能区的反应截面。
该方法可以克服低能核反应直接测量中库仑位垒隧穿效应造成截面抑制和极低能区电子屏蔽效应引起截面增强的双重困难,间接提取天体物理感兴趣能区的带电粒子核反应“裸核”反应截面与天体S(E)因子随能量变化的依赖关系,与直接测量数据归一后,还可为电子屏蔽效应的深入研究提供有效信息。由于该方法无需外推,从而可避免外推过程引入的不确定性,适于研究极低能区的共振与阈下共振。
得益于特洛伊木马方法的独特优势,该方法在带电粒子核反应天体能区实验间接测量中被广泛应用。该方法还可用于研究中子核反应和不稳定核诱发的反应。特别是在r-过程和多信使天文学框架下重元素的核合成中,涉及众多放射性原子核与中子发生的核反应,由于两者都无法直接作为靶材料,特洛伊木马方法在此类核反应研究中具有特殊重要的意义。此外,以
$^9{\rm{Be}}$ 为木马核,将为$A=5$ 、8的极短寿命核素相关的核反应研究提供一种可能的途径。当然,作为一种间接测量方法,特洛伊木马方法也有一些局限性:首先,它依赖于核反应理论,理论上为简化计算往往需要引入一些近似处理,这些近似对于结果的最终影响需要做进一步研究,进而不断改善理论模型。其次,该方法需要对三体反应做运动学完全测量,对探测器的能量和角度分辨率要求较高,这一直是实验的一个难点。还有,应用特洛伊木马方法之前,都需要对特定核反应中准自由反应机制是否存在及能否与其它级联过程等干扰反应区分开做检验,否则可能得到偏离甚至错误的结果。
Recent Progress of the Trojan Horse Method and Its Application
-
摘要: 特洛伊木马方法是实验核天体物理中一种重要的间接测量方法,特别适合极低能区带电粒子裸核反应截面测量。在介绍特洛伊木马方法基本原理的基础上,重点讨论该方法近期在核天体物理应用中的一些重要实验结果,以及对未来研究的展望。主要介绍:AGB星s-过程关键中子源反应
$ ^{{\rm{13}}}{\rm{C(\alpha ,n}}{{\rm{)}}^{{\rm{16}}}}{\rm{O}}$ 的间接测量,AGB星氟丰度超常现象相关核反应间接测量,以及最近热点–中等以上质量恒星碳燃烧核反应间接测量结果及相关争议。Abstract: The Trojan Horse Method(THM) is an important indirect method in experimental nuclear astrophysics. The S(E) factor of a two-body reaction in Gammow energy range related to astrophysics can be extracted from an appropriate three-body reaction measurement above the Coulomb barrier, under the quasi-free reaction condition. The method can overcome the difficulties caused by the Coulomb barrier suppression and the electron screening effect in direct measurement. While no extrapolation is needed, the method can also avoid the uncertainty in the extrapolation process. THM has a wide application in the experimental nuclear astrophysical study, low-energy fusion data measurement, neutron-induced reaction, electron screening effect and other important research fields. After a short introduction of the THM, this paper will focus on some of the most important experimental results in nuclear astrophysics measured by THM recently and the prospect of its future applications. The following key reactions will mainly be discussed: the indirect measurement of the key neutron source reaction$ ^{{\rm{13}}}{\rm{C(\alpha ,n}}{{\rm{)}}^{{\rm{16}}}}{\rm{O}}$ in the s-process of AGB stars, the indirect measurement of the nuclear reaction related to the fluorine abundance anomaly in AGB stars, as well as the recent hot spot, the indirect measurement results of the carbon burning reaction in medium or massive stars.-
Key words:
- Trojan-horse method /
- astrophysical energies /
- bare nucleus /
- S(E) factor /
- electron screening
-
图 2 (在线彩图) 利用特洛伊木马方法间接测量
$ ^{{\rm{13}}}{\rm{C}}{({\rm{\alpha }},{\mkern 1mu} {\rm{n}})^{16}}{\rm{O}}$ 核反应S(E)因子[29]图 3 (在线彩图) 利用特洛伊木马方法间接测量
$ ^{{\rm{19}}}{\rm{F}}({\rm{p}},{\rm{\alpha}}){}^{16}{\rm{O}}$ 核反应S(E)因子[32]图 4 (在线彩图) 利用特洛伊木马方法间接测量
$ ^{12}{\rm{C}}(^{12}{\rm{C}},{\rm{\alpha}}_{0,1}){}^{20}{\rm{Ne}}$ 核反应$ S^*(E)$ 因子,发现天体能区有多个强共振[40]图 5 (在线彩图)
$ ^{12}{\rm{C}}+^{12}{\rm{C}}$ 核反应$ S^*(E)$ 因子不同实验测量结果及理论模型预测的比较,THM数据按A.M.M.修正前(深黑色线)后(浅灰色线)的趋势差别显著[43]表 1 常用木马核及其基本性质
木马核 结构 束缚能 $ \epsilon_{\rm{a}}$ /MeV角动量 $l$ $^2{\rm{H}}$ $^2{\rm{H}}=({\rm{p}} \oplus {\rm{n}})$ 2.225 0 $^3{\rm{He}}$ $^3{\rm{He}}=({\rm{d}} \oplus {\rm{p}})$ 5.493 0 $ ^6{\rm{Li}}$ $ ^6{\rm{Li}}=({\rm{\alpha}} \oplus {\rm{d}})$ 1.474 0 $ ^{14}{\rm{N}}$ $ ^{14}{\rm{N}}=(^{12}{\rm{C}} \oplus {\rm{d}})$ 10.272 0 $^{16}{\rm{O}}$ $^{16}{\rm{O}}=(^{12}{\rm{C}} \oplus {\rm{\alpha}}) $ 7.162 0 $^{20}{\rm{Ne}}$ $^{20}{\rm{Ne}}=(^{16}{\rm{O}} \oplus {\rm{\alpha}})$ 4.730 0 表 2 有潜力的木马核及其基本性质
木马核 结构 束缚能 $ \epsilon_{\rm{a}}$ /MeV角动量 $l$ $^7{\rm{Li}}$ $^7{\rm{Li}}=({\rm{\alpha}} \oplus {\rm{t}})$ 2.467 1 $ ^9{\rm{Be}}$ $ ^9{\rm{Be}}=(^8{\rm{Be}} \oplus {\rm{n}})$ 1.665 1 $ ^9{\rm{Be}}$ $ ^9{\rm{Be}}=(^5{\rm{He}}\oplus {\rm{\alpha}} )$ 2.464 0 表 3 利用特洛伊木马方法实验进行天体核反应间接测量基本情况列表
两体反应 三体反应 木马核 $ E_0 /{\rm{MeV}}$ $ {E}_{\rm{Ax}}^{\rm{qf}}/{\rm{MeV}} $ $^1{\rm{H}}({\rm{p}},\,{\rm{p}})^1{\rm{H}}$ $^2{\rm{H}}({\rm{p}},\,{\rm{pp}}){\rm{n}}$ $^2{\rm{H}}=({\rm{p}}\oplus {\rm{n}})$ 5 0.5 $^2{\rm{H}}({\rm{d}},\,{\rm{p}})^3{\rm{H}}$ $^2{\rm{H}}(^6{\rm{Li}},\,{\rm{pt}}){\rm{\alpha}}$ $ ^6{\rm{Li}}=({\rm{d}}\oplus {\rm{\alpha}})$ 9.5, 11, 14 0.089, 0.342, 0.866 $^2{\rm{H}}({\rm{d}},\,{\rm{p}})^3{\rm{H}}$ $^2{\rm{H}}(^3{\rm{He}},\,{\rm{pt}})^1{\rm{H}}$ $^3{\rm{He}}=({\rm{d}}\oplus {\rm{p}})$ 17 0.178 $^2{\rm{H}}({\rm{d}},\,{\rm{n}})^3{\rm{He}}$ $^2{\rm{H}}(^3{\rm{He}},\,{\rm{n}}^3{\rm{He}})^1{\rm{H}}$ $^3{\rm{He}}=({\rm{d}}\oplus {\rm{p}})$ 17 0.178 $^2{\rm{H}}(^3{\rm{He}},\,{\rm{p}})^4{\rm{He}}$ $ ^6{\rm{Li}}(^3{\rm{He}},\,{\rm{p}}{\rm{\alpha}})4{\rm{He}}$ $ ^6{\rm{Li}}=({\rm{d}}\oplus {\rm{\alpha}})$ 5, 6 0.53-0.93 $ ^6{\rm{Li}}({\rm{d}},\,{\rm{\alpha}})^4{\rm{He}}$ $ ^6{\rm{Li}}(^6{\rm{Li}},\,{\rm{\alpha}} {\rm{\alpha}})^4{\rm{He}}$ $ ^6{\rm{Li}}=({\rm{d}}\oplus {\rm{\alpha}})$ 5.0 0.0 $ ^6{\rm{Li}}({\rm{d}},\,{\rm{\alpha}})^4{\rm{He}}$ $ ^6{\rm{Li}}(^3{\rm{He}},\,{\rm{\alpha}} {\rm{\alpha}})^1{\rm{H}}$ $^3{\rm{He}}=({\rm{d}}\oplus {\rm{p}})$ 17.5 3.25 $ ^6{\rm{Li}}({\rm{p}},\,{\rm{\alpha}})^3{\rm{He}}$ $^2{\rm{H}}(^6{\rm{Li}},\,{\rm{\alpha}} ^3{\rm{He}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ $14 \thicksim36.6$ $0.00 \thicksim 3.03 $ $^7{\rm{Li}}({\rm{p}},\,{\rm{\alpha}})^4{\rm{He}}$ $^7{\rm{Li}}({\rm{d}},\,{\rm{\alpha}} {\rm{\alpha}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ $ 19\thicksim22,\,28\thicksim48$ $0.16\thicksim0.54,\,1.3\thicksim3.8$ $^7{\rm{Li}}({\rm{p}},\,{\rm{\alpha}})^4{\rm{He}}$ $^7{\rm{Li}}(^3{\rm{He}},\,{\rm{\alpha}} {\rm{\alpha}})^2{\rm{H}}$ $^3{\rm{He}}=({\rm{d}}\oplus {\rm{p}})$ 33 4.15 $ ^6{\rm{Li}}({\rm{n}},\,{\rm{t}})^4{\rm{He}}$ $^2{\rm{H}}(^6{\rm{Li}},\,{\rm{t}}{\rm{\alpha}})^1{\rm{H}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 14 0.0 $^7{\rm{Be}}({\rm{n}},\,{\rm{\alpha}})^4{\rm{He}}$ $^2{\rm{H}}(^7{\rm{Be}},\,{\rm{\alpha}} {\rm{\alpha}})^1{\rm{H}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 20.4 0.33 $ ^9{\rm{Be}}({\rm{p}},\,{\rm{\alpha}})^6{\rm{Li}}$ $^2{\rm{H}}(^9{\rm{Be}},\,{\rm{\alpha}} ^6{\rm{Li}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 22.25 0.012 $ ^9{\rm{Be}}({\rm{p}},\,{\rm{d}})^8{\rm{Be}}$ $^2{\rm{H}}(^9{\rm{Be}},\,{\rm{d}} ^8{\rm{Be}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 22.25 0.012 $^{10}{\rm{B}}({\rm{p}},\,{\rm{\alpha}})^7{\rm{Be}}$ $^{10}{\rm{B}}(^2{\rm{H}},\,{\rm{\alpha}} ^7{\rm{Be}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 27, 28 0.24, 0.34 $^{11}{\rm{B}}({\rm{p}},\,{\rm{\alpha}})^8{\rm{Be}}$ $^{11}{\rm{B}}(^2{\rm{H}},\,{\rm{\alpha}} ^8{\rm{Be}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 27 0.04 $^{12}{\rm{C}}({\rm{\alpha}},\,{\rm{\alpha}})^{12}{\rm{C}}$ $ ^6{\rm{Li}}(^{12}{\rm{C}},\,{\rm{\alpha}} ^{12}{\rm{C}})^2{\rm{H}}$ $ ^6{\rm{Li}}=({\rm{d}}\oplus {\rm{\alpha}})$ 18 3.03 $^{12}{\rm{C}}(^{12}{\rm{C}},\,{\rm{p}})^{23}{\rm{Na}} $ $^{12}{\rm{C}}(^{16}{\rm{O}},\,{\rm{p}}^{23}{\rm{Na}}){\rm{\alpha}}$ $^{16}{\rm{O}}=(^{12}{\rm{C}}\oplus {\rm{\alpha}})$ 25 2.22 $^{12}{\rm{C}}(^{12}{\rm{C}},\,{\rm{\alpha}})^{20}{\rm{Ne}} $ $^{12}{\rm{C}}(^{16}{\rm{O}},\,{\rm{\alpha}}^{20}{\rm{Ne}}){\rm{\alpha}}$ $^{16}{\rm{O}}=(^{12}{\rm{C}}\oplus {\rm{\alpha}})$ 25 2.22 $^{12}{\rm{C}}(^{12}{\rm{C}},\,{\rm{\alpha}})^{20}{\rm{Ne}} $ $^{12}{\rm{C}}(^{14}{\rm{N}},\,{\rm{\alpha}}^{20}{\rm{Ne}})^2{\rm{H}}$ $ ^{14}{\rm{N}}=(^{12}{\rm{C}}\oplus {\rm{d}})$ 30 2.5 $^{12}{\rm{C}}(^{12}{\rm{C}},\,{\rm{p}})^{23}{\rm{Na}} $ $^{12}{\rm{C}}(^{14}{\rm{N}},\,{\rm{p}}^{23}{\rm{Na}})^2{\rm{H}}$ $ ^{14}{\rm{N}}=(^{12}{\rm{C}}\oplus {\rm{d}})$ 30 2.5 $^{13}{\rm{C}}({\rm{\alpha}},\,{\rm{n}})^{16}{\rm{O}}$ $ ^6{\rm{Li}}(^{13}{\rm{C}},\,{\rm{n}} ^{16}{\rm{O}})^2{\rm{H}}$ $ ^6{\rm{Li}}=({\rm{d}}\oplus {\rm{\alpha}})$ 7.82 2.50 $ ^{15}{\rm{N}}({\rm{p}},\,{\rm{\alpha}})^{12}{\rm{C}}$ $^2{\rm{H}}(^{15}{\rm{N}},\,{\rm{\alpha}} ^{12}{\rm{C}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 60 1.55 $^{17}{\rm{O}}({\rm{p}},\,{\rm{\alpha}})^{14}{\rm{N}}$ $^2{\rm{H}}(^{17}{\rm{O}},\,{\rm{\alpha}} ^{14}{\rm{N}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 45 0.29 $^{17}{\rm{O}}({\rm{n}},\,{\rm{\alpha}})^{14}{\rm{C}}$ $^2{\rm{H}}(^{17}{\rm{O}},\,{\rm{\alpha}} ^{14}{\rm{C}})^{1}{\rm{H}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 41, 43.5 0.072, 0.212 $^{18}{\rm{O}}({\rm{p}},\,{\rm{\alpha}})^{15}{\rm{N}}$ $^2{\rm{H}}(^{18}{\rm{O}},\,{\rm{\alpha}} ^{15}{\rm{N}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 54 0.64 $ ^{18}{\rm{F}}({\rm{p}},\,{\rm{\alpha}})^{15}{\rm{O}}$ $^2{\rm{H}}(^{18}{\rm{F}},\,{\rm{\alpha}} ^{15}{\rm{O}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 52 0.53 $^{{\rm{19}}}{\rm{F}}({\rm{p}},\,{\rm{\alpha}})^{16}{\rm{O}}$ $^2{\rm{H}}(^{19}{\rm{F}},\,{\rm{\alpha}} ^{16}{\rm{O}}){\rm{n}}$ ${\rm{d = }}({\rm{p}} \oplus {\rm{n}})$ 50 0.29 $^{{\rm{19}}}{\rm{F}}({\rm{\alpha}},\,{\rm{p}})^{22}{\rm{Ne}}$ $^{{\rm{19}}}{\rm{F}}(^6{\rm{Li}},\,{\rm{p}} ^{22}{\rm{Ne}})^2{\rm{H}}$ $ ^6{\rm{Li}}=({\rm{d}}\oplus {\rm{\alpha}})$ 6.0 1.82 -
[1] BURBIDGE E M, BURBIDGE G R, FOWLER W A, et al. Rev of Mode Phys, 1957, 29(4): 547. doi: 10.1103/RevModPhys.29.547 [2] WALLERSTEIN G, IBEN I, PARKER P, et al. Rev of Mode Phys, 1997, 69(4): 995. doi: 10.1103/RevModPhys.69.995 [3] ROLFS C E, RODNEY W S, RODNEY W S. Cauldrons in the Cosmos: Nuclear Astrophysics[M]. Chicago: University of Chicago Press, 1988. [4] BERTULANI C A, KAJINO T. Progress in Particle and Nuclear Physics, 2016, 89: 56. doi: 10.1016/j.ppnp.2016.04.001 [5] BROGGINI C, BEMMERER D, CACIOLLI A, et al. Progress in Particle and Nuclear Physics, 2018, 98: 55. doi: 10.1016/j.ppnp.2017.09.002 [6] LIU W P, LI Z H, HE J J, et al. EPJ Web of Conferences. EDP Sciences, 2016, 109: 09001. doi: 10.1051/epjconf/201610909001 [7] ASSENBAUM H J, LANGANKE K, ROLFS C. Zeitschrift Für Physik A Atomic Nuclei, 1987, 327(4): 461. doi: 10.1007/BF01289572 [8] ALIOTTA M, RAIOLA F, GYURKY G, et al. Nucl Phys A, 2001, 690(4): 790. doi: 10.1016/S0375-9474(01)00366-9 [9] RAIOLA F, GANG L, BONOMO C, et al. The European Physical Journal A-Hadrons and Nuclei, 2004, 19(2): 283. doi: 10.1140/epja/i2003-10125-0 [10] BRACCI L, FIORENTINI G, MELEZHIK V S, et al. Nucl Phys A, 1990, 513(2): 316. doi: 10.1016/0375-9474(90)90101-Q [11] PIZZONE R G, SPITALERI C, CHERUBINI S, et al. Nucl Phys A, 2010, 834(1-4): 673c. doi: 10.1016/j.nuclphysa.2010.01.121 [12] TRIBBLE R E, BERTULANI C A, LA COGNATA M, et al. Reports on Progress in Physics, 2014, 77(10): 106901. doi: 10.1088/0034-4885/77/10/106901 [13] BAUR G. Phys Lett B, 1986, 178(2-3): 135. doi: 10.1016/0370-2693(86)91483-8 [14] TYPEL S, WOLTER H H. Few-Body Systems, 2000, 29(1-3): 75. doi: 10.1007/s006010070010 [15] TYPEL S, BAUR G. Annals of Physics, 2003, 305(2): 228. doi: 10.1016/S0003-4916(03)00060-5 [16] MUKHAMEDZHANOV A M, BLOKHINTSEV L D, IRGAZIEV B F, et al. Journal of Physics G: Nuclear and Particle Physics, 2007, 35(1): 014016. doi: 10.1088/0954-3899/35/1/014016 [17] BERTULANI C A, HUSSEIN M S, TYPEL S. Phys Lett B, 2018, 776: 217. doi: 10.1016/j.physletb.2017.11.050 [18] SPITALERI C, LA COGNATA M, LAMIA L, et al. The European Physical Journal A, 2019, 55(9): 161. doi: 10.1140/epja/i2019-12833-0 [19] 李成波, PIZZONE R G, SPITALERI C, 等. 原子核物理评论, 2005, 22(3): 248. doi: 10.11804/NuclPhysRev.22.03.248 LI C B, PIZZONE R G, SPITALERI C, et al. Nuclear Physics Review, 2005, 22(3): 248. (in Chinese) doi: 10.11804/NuclPhysRev.22.03.248 [20] ROMANO S, LAMIA L, SPITALERI C, et al. The European Physical Journal A-Hadrons and Nuclei, 2006, 27(1): 221. doi: 10.1140/epja/i2006-08-034-5 [21] WEN Q G, LI C B, ZHOU S H, et al. Phys Rev C, 2008, 78(3): 035805. doi: 10.1103/PhysRevC.78.035805 [22] WEN Q G, LI C B, ZHOU S H, et al. Journal of Physics G: Nuclear and Particle Physics, 2011, 38(8): 085103. doi: 10.1088/0954-3899/38/8/085103 [23] WEN Q G, LI C B, ZHOU S H, et al. Phys Rev C, 2016, 93(3): 035803. doi: 10.1103/PhysRevC.93.035803 [24] 傅元勇, 李成波, 文群刚, 等. 原子核物理评论, 2014, 31(4): 444. doi: 10.11804/NuclPhysRev.31.04.444 FU Y Y, LI C B, WEN Q G, et al. Nuclear Physics Review, 2014, 31(4): 444. (in Chinese) doi: 10.11804/NuclPhysRev.31.04.444 [25] LI C B, WEN Q G, ZHOU S H, et al. Chin Phys C, 2015, 39(5): 11. doi: 10.1088/1674-1137/39/5/054001 [26] LI C, WEN Q, FU Y, et al. Phys Rev C, 2015, 92(2): 025805. doi: 10.1103/PhysRevC.92.025805 [27] LI C, WEN Q, TUMINO A, et al. Phys Rev C, 2017, 95(3): 035804. doi: 10.1103/PhysRevC.95.035804 [28] LA COGNATA M, SPITALERI C, TRIPPELLA O, et al. Phys Rev Lett, 2012, 109(23): 232701. doi: 10.1103/PhysRevLett.109.232701 [29] LA COGNATA M, SPITALERI C, TRIPPELLA O, et al. The Astrophysical Journal, 2013, 777(2): 143. doi: 10.1088/0004-637X/777/2/143 [30] TRIPPELLA O, LA COGNATA M. The Astrophysical Journal, 2017, 837(1): 41. doi: 10.3847/1538-4357/aa5eb5 [31] LOMBARDO I, DELL’AQUILA D, DI LEVA A, et al. Phys Lett B, 2015, 748: 178. doi: 10.1016/j.physletb.2015.06.073 [32] LA COGNATA M, PALMERINI S, SPITALERI C, et al. The Astrophysical Journal, 2015, 805(2): 128. doi: 10.1088/0004-637X/805/2/128 [33] PIZZONE R G, D'AGATA G, LA COGNATA M, et al. The Astrophysical Journal, 2017, 836(1): 57. doi: 10.3847/1538-4357/836/1/57 [34] WOOSLEY S E, HEGER A, WEAVER T A. Rev of Mode Phys, 2002, 74(4): 1015. doi: 10.1103/RevModPhys.74.1015 [35] BROMLEY D A, KUEHNER J A, ALMQVIST E. Phys Rev Lett, 1960, 4(7): 365. doi: 10.1103/PhysRevLett.4.365 [36] ALMQVIST E, BROMLEY D A, KUEHNER J A. Phys Rev Lett, 1960, 4(10): 515. doi: 10.1103/PhysRevLett.4.515 [37] SPILLANE T, RAIOLA F, ROLFS C, et al. , Phys Rev Lett, 2007, 98(12): 122501. doi: 10.1103/PhysRevLett.98.122501 [38] TANG X, MA S, FANG X, et al. Nuclear Science and Techniques, 2019, 30(8): 126. doi: 10.1007/s41365-019-0652-9 [39] COOPER R L, STEINER A W, BROWN E F. The Astrophysical Journal, 2009, 702: 660. doi: 10.1088/0004-637X/702/1/660 [40] TUMINO A, SPITALERI C, LA COGNATA M, et al. Nature, 2018, 557(7707): 687. doi: 10.1038/s41586-018-0149-4 [41] ZHANG N T, WANG X Y, TUDOR D, et al. Phys Lett B, 2020, 801: 135170. doi: 10.1016/j.physletb.2019.135170 [42] MUKHAMEDZHANOV A M, PANG D Y, KADYROV A S. Phys Rev C, 2019, 99(6): 064618. doi: 10.1103/PhysRevC.99.064618 [43] BECK C, MUKHAMEDZHANOV A M, TANG X. European Physical Journal A, 2020, 56(3): 87. doi: 10.1140/epja/s10050-020-00075-2 [44] TUMINO A, SPITALERI C, COGNATA M L, et al. ArXiv Preprint, 2018, ArXiv: 1807.06148. [45] GUARDO G L, SPITALERI C, LAMIA L, et al. Phys Rev C, 2017, 95(2): 025807. doi: 10.1103/PhysRevC.95.025807 [46] LAMIA L, MAZZOCCO M, PIZZONE R G, et al. The Astrophysical Journal, 2019, 879(1): 23. doi: 10.3847/1538-4357/ab2234 [47] PIZZONE R G, ROEDER B T, MCCLESKEY M, et al. The European Physical Journal A, 2016, 52(2): 24. doi: 10.1140/epja/i2016-16024-3 [48] ROOS P G, PUGH H G, JAIN M, et al. Phys Rev, 1968, 176(4): 1246. doi: 10.1103/PhysRev.176.1246 [49] FALLICA P G, LATTUADA M, RIGGI F, et al. Phys Rev C, 1981, 24(4): 1394. doi: 10.1103/PhysRevC.24.1394 [50] SPITALERI C, LATTUADA1 M, CVETINOVIC1 A, et al. Eur Phys J A, 2020, 56: 18. doi: 10.1140/epja/s10050-020-00026-x -







 下载:
下载:























































































































































































































































































 甘公网安备 62010202000723号
甘公网安备 62010202000723号