-
In the theory of nuclear structure, it is of great value to study magic nuclei and their nearby isotopes. Jiang
$ et\; al. $ [1] used different effective interactions to study isotopes near$ ^{16} {\rm{O}}$ , which reduced the theoretical error of shell model calculation to some extent. Similarly, Qin$ et\; al $ .[2] in their studies of$ ^{132} {\rm{Sn}}$ and its nearby hole nuclei have found that different truncation in the large shell model calculation has a certain influence on the energy level structure and electric quadrupole transition in the nuclear region. Sn isotopes with proton magicity provide a unique opportunity to study the microscopic basis of various phenomenological nuclear models. Mass number of Sn isotopes lies in between 100~132 with the neutron number being occupying the magic subshells between 50 and 82. Thus it allows to investigate that: (i) how the closure of proton shell at$ Z=50 $ is maintained with additional valence neutrons, (ii) how the collective characteristics develop and the importance of many body effects. Using the Holt et al. defined effective interaction and the shell model based single particle energy, the basic spectral properties for heavy nuclei of$ ^{120-130} {\rm{Sn}}$ isotopes are well described, and quite good results are obtained for nuclei far away from$ ^{132} {\rm{Sn}}$ [3]. Thus, making it very important to study the Sn isotope chain and the energy spectrum of$ ^{116} {\rm{Sn}}$ for understanding astrophysical events such as celestial collapse, supernova or neutron star formation[4].In the past, a large number of experimental and theoretical studies have been carried out to explore the structure, energy level density and some thermodynamic properties of Sn isotopes[5-8]. The energy level density can be used to describe the average amount of the nucleus and to calculate the reaction cross section and characteristics. Further, It is very essential for understanding the nuclear synthesis of stars[9-10], and can be used as an input parameter for neutron and proton capture reactions[11], contributing in studying the nuclear reaction rate in astrophysics. The energy level density, mass and nuclear density distribution of neutron-rich
$ ^{124-145} {\rm{Sn}}$ nuclei are very helpful in studying the direct neutron capture closely related to the astronuclear physics[12]. The structure of the energy level density is related to shell gap, the Cooper pair of nuclei, or the change of nuclear shape. In the low energy region of 5 MeV between$ ^{116} {\rm{Sn}}$ and$ ^{132} {\rm{Sn}}$ , the increase of neutron number is very sensitive to the change of shell structure. The study of this energy region can provide information about the shell evolution in open-shell nuclei[13] with increasing excitation energy and by interpolation of energy level density involving phenomenological theory[14-15]. Energy level density is not only the function of excitation energy, but also the starting point of extracting entropy, temperature and heat capacity.Without considering the cross-shell excitation, this paper uses the modern realistic interaction and shell model truncation to study the lowest 10 000 states of
$ ^{108-124} {\rm{Sn}}$ in the subspace of unpair nucleon with generalized-seniority quantum number 8, which can give the inner shell structure, as well as the angular momentum and parity related properties. Since$ ^{116} {\rm{Sn}}$ has the same number of holes in the isotope of Sn as the number of particles, so the situation is more complicated and is analyzed emphatically. -
The light Sn isotopes between the closed shells with
$N=50$ and 82 is the longest chain that can be calculated by the shell model[16]. With the increase in size and number of valence nucleons and the broken Cooper pairs, the space size of the exact shell model will also increase. For heavy nucleus, the dimension will increase even more, which will bring certain difficulties to the calculation. The introduction of seniority truncation can effectively reduce the matrix dimension[17-18]. By using the fast algorithm of generalized seniority and modern realistic interaction, the real CD-Bonn nucleon-nucleon potential[19] has been calculated, and the perturbed G matrix method is used to normalize the interaction, considering the core polarization effect[20]. The lowest 10 000 states (5 000 of each parity) of$ ^{108-124} {\rm{Sn}}$ in the subspace of unpaired nucleons are calculated when the generalized seniority truncates the quantum number 8.For the model space, the orbits with proton number 50 and neutron number between 50~82 are selected, and the isospin symmetry condition is considered in the effective Hamiltonian[16]. Set subspace
$ \left| S,\; M \right \rangle $ , where$S~(S = S_{{{\pi }}}+S_{{\nu}}$ ,${\rm{\pi }}$ ,${\rm { \nu}}$ represent protons and neutrons, respectively) is the total generalized alteration,$M (M = M_{{\rm{\pi }}} + M_{\nu}$ ) is the total magnetic projection. The Hamiltonian H contains three parts:$H = H_{{\rm{\pi }}} + H_{\nu} + H_{{\rm{\pi }}\nu}(H_{{\rm{\pi }}\nu}$ is proton neutron interaction). For this article, there are no valence protons, so the proton part is not considered, only valence neutrons are discussed. Partition calculation is used in the calculation, which is more effective and faster than the accurate shell model. The truncation of Generalized seniority is consistent with the idea of condensation of coherent pairs with the same pair of structures and has a smaller size[21]. The Hamiltonian is taken from Ref. [16]. Common practice in the calculation of the full configuration-interacting shell model is to express the effective Hamiltonian with the energy of a single particle and the numerical value of the two-body matrix elements, see the following formula:$$ \begin{split} H =& \sum\limits_{\alpha} \epsilon _{\alpha}\hat{N}_{\alpha}+\\ &\frac{1}{4} \sum\limits_{\alpha \beta \delta \gamma JT} \left \langle j_{\alpha} j_{\beta} \right| V \left| j_{\gamma} j_{\delta} \right \rangle _{JT} A^+_{JT;j_{\alpha}j_{\beta}} A_{JT;j_{\delta}j_{\gamma}}\,,\end{split} $$ (1) where
$ \alpha = \{ nljt \} $ represents the single particle orbitals,$ \epsilon _{\alpha} $ represents the corresponding single particle energy;$ \hat{N} _{\alpha} $ is the particle number operator;$ \left \langle j_{\alpha} j_{\beta} \right| V \left| j_{\gamma} j_{\delta} \right \rangle $ is a two-body matrix element coupled to a good spin J and isospin T;$ ( A_{JT} ) A^{+}_{JT} $ is Fermion's annihilation (creation) operator.For the calculation of energy level density, different models have been established before. Back at least in 1936, Bethe proposed the Fermi gas model (FGM), which is only applicable to high-energy areas[22]. The first model tested, the back-shifted Fermi-gas model (BSFGM) contains three parameters
$ a $ ,$ \sigma $ and E1. U and J represent excitation energy and spin, respectively[see Eq. (2)][23-27]. Then developed the standard Bethe formula independent of a specific model to the more generalized Bethe formula. The generalized formula for double-closed shell$ ^{208}{\rm Pb} $ is better than the standard one[28]. Later, the constant-temperature model (CTM) was proposed[29-30]. There are two parameters$ E_0 $ and$ T $ , which can very well represent the experimental data of Sn below the the neutron separation energy. Considering pairing correlation, shell effect, and collectiveness, generalized superfluid model has appeared, and the energy density is shown. However, this model ignores the rotating collective effect[31]. The Oslo cyclotron group extracted the nuclear level density by measuring$ \gamma $ -ray spectra below low spin[32-35].$$ \rho(U,J) = \frac{\exp\big\{2\sqrt{[a(U-E_1)]}\big\}f(J)}{24\sqrt{2}\sigma a^{\frac{1}{4}}(U-E_1)^{\frac{5}{4}}}\,. $$ (2) The thermodynamic quantity can be extracted by the energy level density, and the microcanonical entropy can be derived. The microcanonical entropy
$ S(E) $ is a measure of the number of ways to arrange quantum systems under a given excitation energy. The microcanonical entropy can be calculated according to Eq. (3)[36], where$ \varOmega (E) $ represents the multiplicity [see Eq. (4)],$ \rho _0 $ is determined by the ordered system in which the ground state entropy of even-even nuclei is zero. For$ ^{116} {\rm{Sn}}$ ,$ \rho_0 = 0.135 $ MeV–1[14] ,$$ \ S(E) = k_{\rm{B}}\ln\varOmega(E)\,, $$ (3) $$ \varOmega(E) = \frac{\rho(E)}{\rho_0}. $$ (4) -
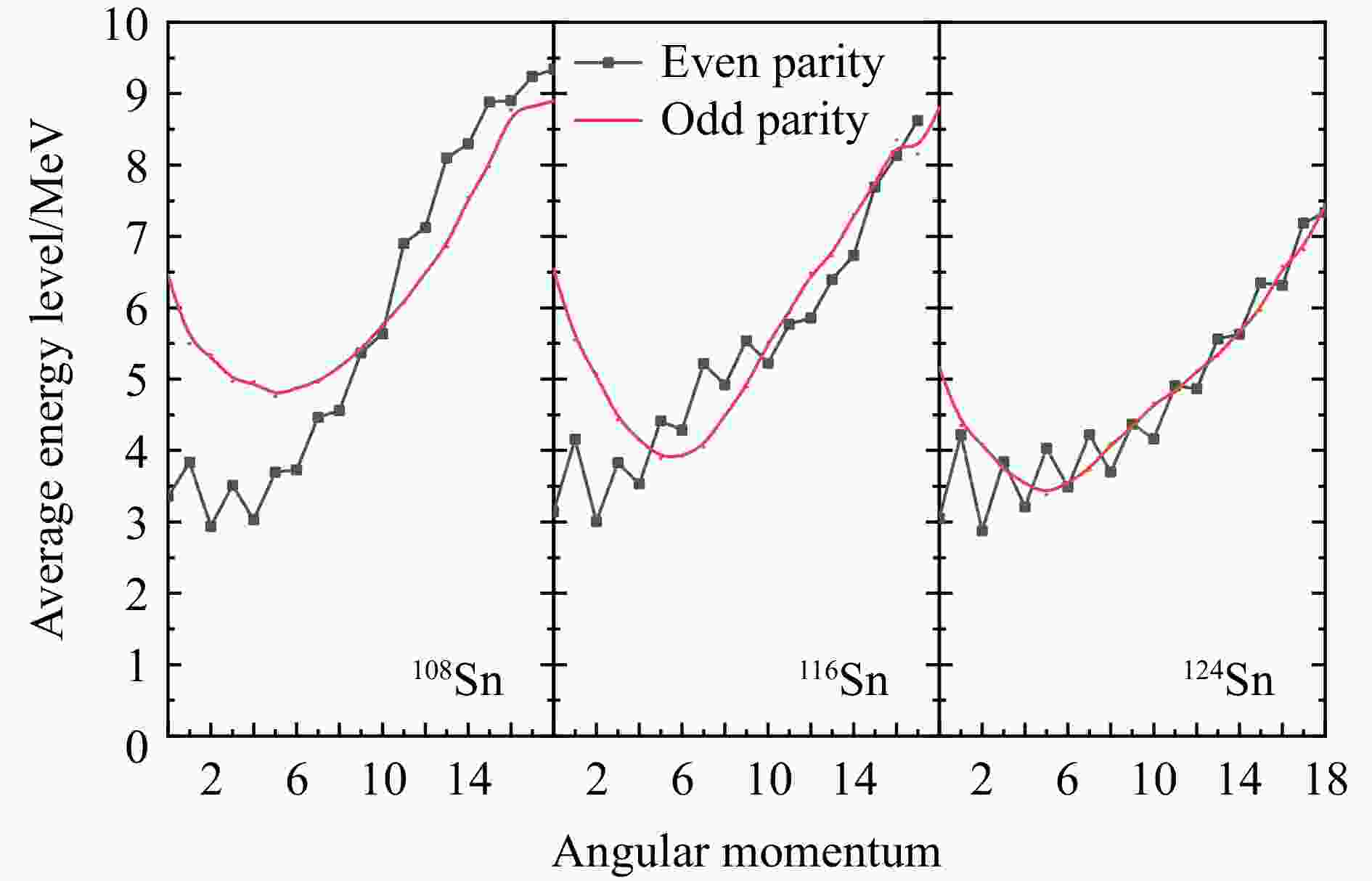
In this paper, the energy level density has been calculated according to shell model. The lowest 10000 energy levels are obtained in the neutron number 50~82 subshell. Red line in Fig. 1 represents the calculated energy level density using the BSFG model for the data taken from the Refs. [14, 26-27], and the histogram in blue color represents the calculation performed in the present work. A good agreement of energy level density in between the results can be seen from the plotted data as a function of excitation energy. It can be seen from Fig. 1 that the energy level density of
$ ^{116} {\rm{Sn}}$ shows an obvious ladder structure. The microscopic calculation based on the seniority number shows that the ladder structure in the energy level density function can be explained by continuously destroying the nucleon Cooper pair. The position of the ladder structure in the excitation energy-level density curve depends on the exact position of the Fermi energy in the single-particle energy level framework. The smoothness of the ladder structure depends on the intensity of the seniority number nonconservative interaction, such as the quadrupole-quadrupole interaction relative to the pairing interaction and the average single particle energy level spacing. At low energy, the energy level density is very small, and there is an obvious fluctuation of energy level density ratio when$ E <7 $ MeV. The 7.0~7.5 MeV level density ratio increases all the time. The energy level density ratio increases slowly at higher energy. According to the thermodynamic calculation of the actual shell model single-particle spectrum, this conclusion is also reached. The behavior of the total energy level density near the closed shell can no longer use this formula. From the calculated energy level density diagram, it increases in logarithmic coordinates.Fig. 2 discusses the variation of the angular momentum ratio with the mass number in the case of high, medium and low angular momentum. The high angular momentum (blue line)
$ L > 10 $ , the middle angular momentum (red line)$ L $ =6~10 increases with the increase of the mass number, and the low angular momentum (black line)$ L $ =0~5 decreases with the increase of the mass number. With the increase of the number of masses and particles, more particles will make a transition to the excited state orbitals, and the total angular momentum after angular momentum coupling increases, so the middle and high angular momentum increases with the mass number. Thus, utilizing the above mentioned phenomena, the behavior of angular momentum ratio with increasing excitation energy has been studied in case of the most complex$ ^{116} {\rm{Sn}}$ isotope. Fig. 3 selects$ ^{116} {\rm{Sn}}$ to divide the calculated 10 000 states into low angular momentum (black line), middle angular momentum (red line) and high angular momentum (blue line). The divided three-segment angular momentum has a peak at 8 MeV. The peak value at low angular momentum almost coincides with that at middle angular momentum, and the peak at high angular momentum is also similar. Under the influence of Pauli exclusion principle, low angular momentum is more likely to occur at low energy. At high energy, neutrons can appear in 16 different orbitals and are no longer affected by the Pauli exclusion principle, so the probabilities of middle, high and low angular momentum are approximately equal.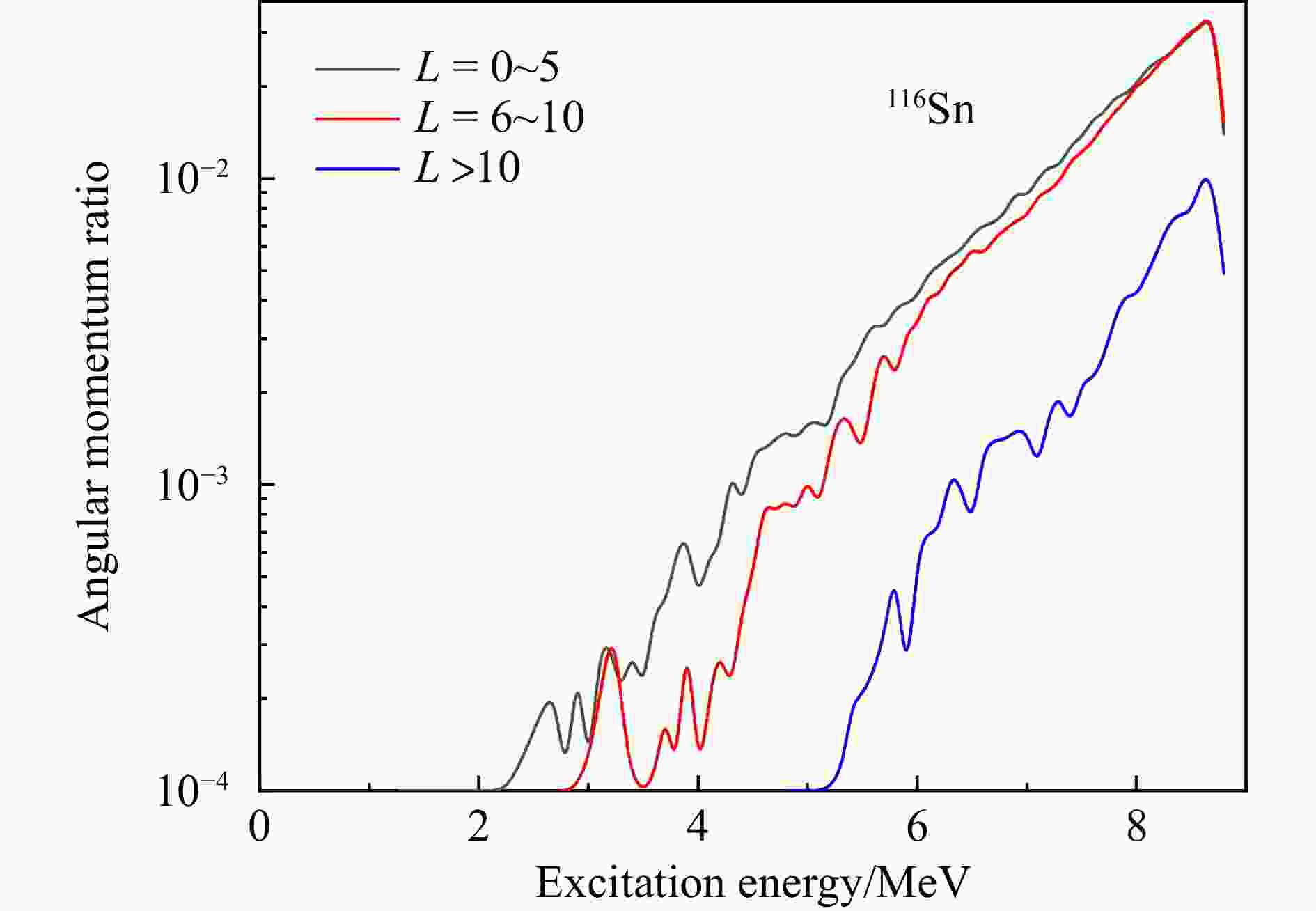
Figure 3. (color online) The distribution of angular momentum ratio under different excitation energies.
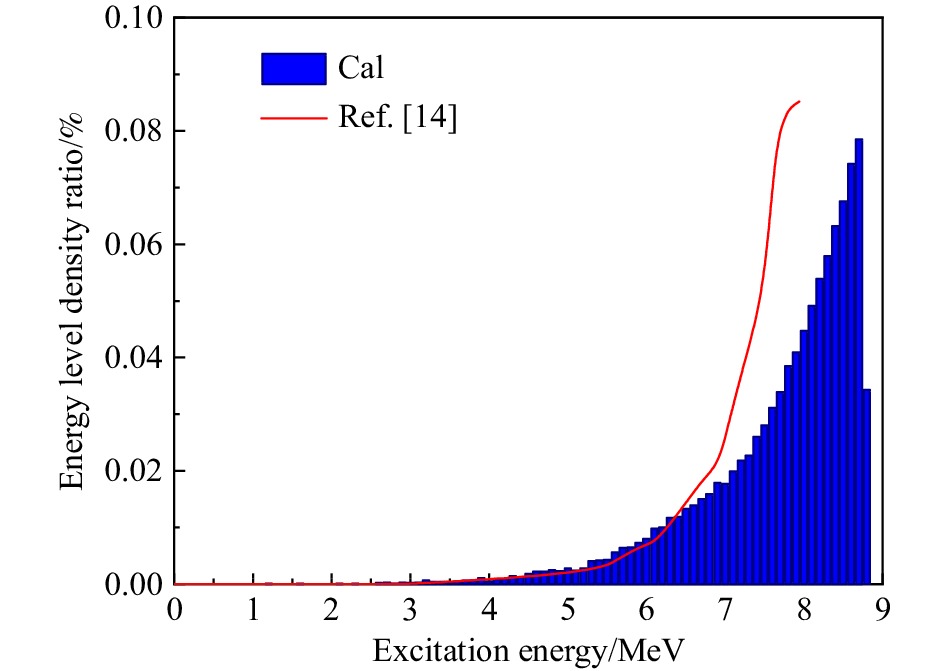
The three isotopes
$ ^{108} {\rm{Sn}}$ ,$ ^{116} {\rm{Sn}}$ , and$ ^{124} {\rm{Sn}}$ of Sn are selected from light to heavy. The average values of the lowest energy levels are drawn according to angular momentum and parity, as shown in Fig. 4. Even parity and odd parity show different situations. The odd parity decreases first and then increases with the change of angular momentum, and the average of the lowest energy level decreases to the lowest between 5 and 6 angular momentum. When the parity is even, there is an obvious odd-even effect of angular momentum. The average value of the lowest energy level is high for odd angular momentum, and low for even angular momentum. Even parity and even angular momentum reduce system energy. Different parity brings different effects and energies. According to Pauli exclusion principle, odd parity can offset the energy brought by angular momentum, while even parity cannot. Even parity has high symmetry, and the odd angular momentum destroys the symmetry, so the energy is higher than the even angular momentum, so it has odd-even effect of angular momentum. As the angular momentum and mass number increase, the gap between the parity's odd-even effect decreases. When the number of valence particles is small and the number of states is small, the odd-even effect difference will be large according to the Pauli exclusion principle. When the number of valence particles is large, the Pauli exclusion effect is partially offset, so the odd-even effect difference becomes smaller. Similarly, for one of the isotopes, the parity difference becomes smaller as the angular momentum increases, due to the partial Pauli exclusion effect being offset.The entropy can be calculated according to the energy level density. In this paper, the microcanonical entropy is calculated according to Eq. (5), and the entropy divided by parity is shown in Fig. 5. The red line is an even parity, the black line is an odd parity, and the blue line is the case where parity is not distinguished. There is a peak around 8.7 MeV, and then it shows a downward trend. The entropy of even and odd parity is in between 6.0~8.7 MeV and is close to coincide, indicating that parity distribution is symmetric. The odd parity fluctuates at low energies. Without distinguishing parity, entropy is also affected by the fluctuation of odd parity in the low-energy range, and there is a certain fluctuation. The higher the energy, the greater the entropy, indicating the greater the degree of confusion. The
$Z=50$ of Sn is a closed shell, which prevents the proton pair from breaking, so it is possible that the neutron pair breaking causes the fluctuation of entropy. -
In this paper, the shell model and truncation algorithm are used to calculate the lowest 10 000 states of Sn isotopes, and the relevant properties of Sn are studied based on the calculated results. The number of holes and the number of particles in the Sn isotope of
$ ^{116} {\rm{Sn}}$ is 8. The energy level density of$ ^{116} {\rm{Sn}}$ is calculated, and it is found that the curve with excitation energy shows a stepped structure, which is related to the break of the Cooper pair. The distribution of angular momentum ratio under different excitation energies is different. At low energy, under the influence of Pauli exclusion principle, the probability of occurrence of low angular momentum is large; at high energy, the probability of occurrence of medium, high and low angular momentum is approximately equal. The average value of the lowest energy level of$ ^{108} {\rm{Sn}}$ ,$ ^{116} {\rm{Sn}}$ and$ ^{124} {\rm{Sn}}$ under the change of angular momentum has great difference in the parity of odd and even. The odd-even effect of angular momentum appears in the even parity case, which can be explained by the Pauli exclusion principle. The microcanonical entropy is derived from the energy level density. Entropy fluctuates with odd parity at low energy, which is related to the broken neutron pairs.Acknowledgements Thanks to Prof. JIA Liyuan of University of Shanghai for Science and Technology for participating in the discussion and providing program support.
-
摘要: 能级密度在研究核物理的动力学、热力学性质中具有重要的物理意义。本文利用壳模型和截断算法计算了Sn同位素的最低10 000个状态。
$^{116}{\rm{Sn}}$ 在Sn同位素中空穴数和粒子数都为8,能级最为复杂,根据$^{116}{\rm{Sn}}$ 能级密度研究了能级密度与角动量的关系和体系的微正则熵。研究发现在偶宇称时的最低平均能级出现明显的角动量奇偶效应,用泡利不相容原理得到合理解释。进一步,又研究了Sn同位素的此性质,得到相同的结论。$^{116}{\rm{Sn}}$ 的微规范熵在低能量段受奇宇称的波动,这与中子对的断裂有关。Abstract: Energy level density plays an important role in the study of kinetic and thermodynamic properties of nuclear physics. In this paper, shell model and the truncation algorithm are used to calculate the lowest 10 000 states of Sn isotopes. The number of holes and the number of particles in the$^{116}{\rm{Sn}}$ isotope of Sn is 8, and the energy level is the most complex. According to the$^{116}{\rm{Sn}}$ energy level density, the relationship between energy level density and angular momentum and the microcanonical entropy of the system are studied. It is found that the lowest average energy level under even parity has an obvious odd-even effect of angular momentum, which can be reasonably explained by Pauli exclusion principle. Furthermore, the properties of different Sn isotopes are studied and a similiar conclusion is obtained. The microcanonical entropy of$^{116}{\rm{Sn}}$ is fluctuated by odd parity in the low energy band, which is related to the fracture of neutron pairs.-
Key words:
- 116Sn /
- level densities /
- Pauli exclusion principle
-
-
[1] JIANG Junji, JIN Rui, WANG Hankui. Nuclear Physics Review, 2020, 37(3): 563. (in Chinese) doi: 10.11804/NuclPhysRev.37.2019CNPC54 [2] QIN Wei, WANG Hankui, SUN Yang, et al. Nuclear Physics Review, 2017, 34(3): 488. (in Chinese) doi: 10.11804/NuclPhysRev.34.03.488 [3] HOLT A, ENGELAND T, HJORTH-JENSEN M, et al. Nucl Phys A, 1998, 634: 41. doi: 10.1016/S0375-9474(98)00146-8 [4] BASSAUER S, VON NEUMANN-COSEL P, REINHARD P G, et al. Phys Lett B, 2020, 810: 135804. doi: 10.1016/j.physletb.2020.135804 [5] GRAWE H, LEWITOWICZ M. Nucl Phys A, 2001, 693: 116. doi: 10.1016/S0375-9474(01)01138-1 [6] BANU A, GERL J, FAHLANDER C,et al. Phys Rev C, 2005, 72: 061305. doi: 10.1103/PhysRevC.72.061305 [7] ORCE J N, CHOUDRY S N, CRIDER B, et al. Phys Rev C, 2007, 76: 021302. doi: 10.1103/PhysRevC.76.021302 [8] GUAZZONI P, ZETTA L, COVELLO A, et al. Phys Rev C, 2012, 85: 054609. doi: 10.1103/PhysRevC.85.054609 [9] MELBY E, BERGHOLT L, GUTTORMSEN M, et al. Phys Rev Lett, 1999, 83: 3150. doi: 10.1103/PhysRevLett.83.3150 [10] GORIELY S. Nucl Phys A, 1996, 605: 28. doi: 10.1016/0375-9474(96)00162-5 [11] AL-QURAISHI S I, GRIMES S M, MASSEY T N, et al. Phys Rev C, 2001, 63: 065803. doi: 10.1103/PhysRevC.63.065803 [12] RAUSCHER T, BIEBER R, OBERHUMMER H, et al. Phys Rev C, 1998, 57: 2031. doi: 10.1103/PhysRevC.57.2031 [13] YÜKSEL E, COLÒ G, KHAN E, et al. Phys Rev C, 2018, 97(6): 064308. doi: 10.1103/PhysRevC.97.064308 [14] AGVAANLUVSAN U, LARSEN A, GUTTORMSEN M, et al. Phys Rev C, 2009, 79: 014320. doi: 10.1103/PhysRevC.79.014320 [15] TOFT H K, LARSEN A C, AGVAANLUVSAN U, et al. Phys Rev C, 2010, 81: 064311. doi: 10.1103/PhysRevC.81.064311 [16] QI C, XU Z X. Phys Rev C, 2012, 86: 044323. doi: 10.1103/PhysRevC.86.044323 [17] JIA L. J Phys G, 2015, 42(11): 115105. doi: 10.1088/0954-3899/42/11/115105 [18] ALHASSID Y, LIU S, NAKADA H. Phys Rev Lett, 1999, 83: 4265. doi: 10.1103/PhysRevLett.83.4265 [19] MACHLEIDT R. Phys Rev C, 2001, 63: 024001. doi: 10.1103/PhysRevC.63.024001 [20] HJORTH-JENSEN M, KUO T, OSNES E. Phys Rept, 1995, 261: 125. doi: 10.1016/0370-1573(95)00012-6 [21] TALMI I. Nuclear Physics A, 1994, 570(1): 319. [22] BETHE H A. Phys Rev, 1936, 50: 332. doi: 10.1103/PhysRev.50.332 [23] GADIOLI E, ZETTA L. Phys Rev, 1968, 167: 1016. doi: 10.1103/PhysRev.167.1016 [24] HUIZENGA J R, VONACH H K, KATSANOS A A, et al. Phys Rev, 1969, 182: 1149. doi: 10.1103/PhysRev.182.1149 [25] VONACH H, HILLE M. Nucl Phys A, 1969, 127: 289. doi: 10.1016/0375-9474(69)90572-7 [26] EGIDY T V, BUCURESCU D. Phys Rev C, 2005, 72: 044311. doi: 10.1103/PhysRevC.72.044311 [27] GILBERT A, CAMERON A G W. Canadian Journal of Physics, 1965, 43(8): 1446. doi: 10.1139/p65-139 [28] PAAR V, PEZER R. Phys Rev C, 1997, 55: 1637. doi: 10.1103/PhysRevC.55.R1637 [29] ERICSON T. Nuclear Physics, 1959, 11: 481. [30] GILBERT A, CHEN F S, CAMERON A G W. Canadian Journal of Physics, 1965, 43(7): 1248. doi: 10.1139/p65-120 [31] IGNATYUK A V, WEIL J L, RAMAN S, et al. Phys Rev C, 1993, 47: 1504. doi: 10.1103/PhysRevC.47.1504 [32] TVETER T, BERGHOLT L, GUTTORMSEN M, et al. Phys Rev Lett, 1996, 77: 2404. doi: 10.1103/PhysRevLett.77.2404 [33] SCHILLER A, BJERVE A, GUTTORMSEN M, et al. Phys Rev C, 2001, 63: 021306. doi: 10.1103/PhysRevC.63.021306 [34] SCHILLER A, BERGHOLT L, GUTTORMSEN M, et al. Nucl Instr and Meth A, 2000, 447: 495. doi: 10.1016/S0168-9002(99)01187-0 [35] GUTTORMSEN M, HJORTH-JENSEN M, MELBY E, et al. Phys Rev C, 2001, 63: 044301. doi: 10.1103/PhysRevC.63.044301 [36] GUTTORMSEN M, BJERVE A, HJORTH-JENSEN M, et al. Phys Rev C, 2000, 62: 024306. doi: 10.1103/PhysRevC.62.024306 -
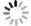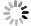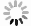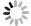






 下载:
下载:




























































 甘公网安备 62010202000723号
甘公网安备 62010202000723号