远离$ \beta $稳定线的奇特核性质研究是近几十年来国际核物理研究的一个前沿领域^[1-3]。近滴线核具有奇特的衰变模式，拓广和深化了核物理研究的内容。在由稳定线向滴线靠近的过程中，这些具有极端中质比的近滴线核素，由于在衰变时母核与衰变子核在束缚能上的差别变大，会有很多在稳定线附近并不允许的衰变道打开，衰变模式逐渐由$ \beta $衰变倾向于$ \beta $缓发粒子衰变。实验已证实$ \beta $缓发中子发射^[4]、$ \beta $缓发单质子发射^[5-10]、$ \beta $缓发多质子发射^[11-13]、$ \beta $缓发$ \gamma $-质子发射^[14]等衰变模式存在。$ \beta $缓发粒子衰变是一个两步过程：首先，母核发生慢$ \beta $衰变布居子核的激发态，然后快发射一个或者多个粒子。通过探测这些出射粒子，可以全面地描述一个核态的衰变特征^[2]。因此，$ \beta $衰变谱学研究成为了获取滴线附近核结构信息的强有力的工具，感兴趣奇特核的能级能量、宽度、自旋、同位旋、能级密度等谱学信息可以从实验数据中提取出来。

原子核是一个包含质子和中子这两种类型费米子的独特量子多体系统，质子与中子除电荷不同的特征外，基于强相互作用的电荷无关性假设，可以被认作为同一粒子。Heisenberg于1932年提出同位旋的概念来描述这种中子和质子间的变换不变性，所有的核子具有相同的同位旋$ t \!=\! 1/2 $，但质子和中子分别具有不同的同位旋第三分量$ t_z \!=\! -1/2 $和$ t_z \!=\! 1/2 $。原子核的同位旋则可以通过质子和中子同位旋的“合成”得到。中子数和质子数交换后形成的核素互为镜像核。因核力近似具有电荷无关性，同位旋对称性这一概念能够很好地描述稳定线附近的镜像核间的各种现象。但当核素向滴线靠近的过程中，由于受质子间库仑相互作用及电荷相关核力的影响变强，会出现同位旋对称性破缺的情况。研究同位旋对称性和同位旋对称性的破缺，对进一步深入理解核力和核结构具有重要的意义。目前在$ sd $壳的镜像原子核间，已经发现不少同位旋对称性破缺现象^[15-20]。因此，将高精确度的$ \beta $衰变测量推广到更多核素上去，可以更好地理解同位旋对称性破缺现象，从而在微观模型中更清楚地认识同位旋对称性破缺的机制^[21-24]。

²⁸S的同位旋第三分量$ T_{Z} \!=\! -2 $，是质子滴线内相当轻的硫的同位素。有关²⁸S的$ \beta $衰变实验的报告仅有一篇，该实验由Pougheon等^[25]在GANIL通过³⁶Ar初级束轰击天然镍靶产生²⁸S，然后使用6块硅探测器组成的探测阵列进行探测。其实验未使用测量$ \gamma $射线的探测器进行$ \beta $-$ \gamma $和$ {\rm p} $-$ \gamma $符合测量，没有获得关于²⁸S的准确$ \beta $延迟衰变质子发射衰变道的信息以及$ \beta $延迟衰变$ \gamma $发射的相关信息。为了获取²⁸S $ \beta $延迟衰变中的$ \gamma $跃迁信息和得到$ \beta $衰变子核²⁸P激发态的布居情况，探究在镜像核$ \rm ^{28}S \rightarrow{^{28}P} $和$ \rm ^{28}Mg \rightarrow {^{28}Al} $的衰变中可能出现的同位旋对称性破缺，需要对实验技术做出进一步地改进，开展新的²⁸S的$ \beta $延迟$ \gamma $衰变实验研究。

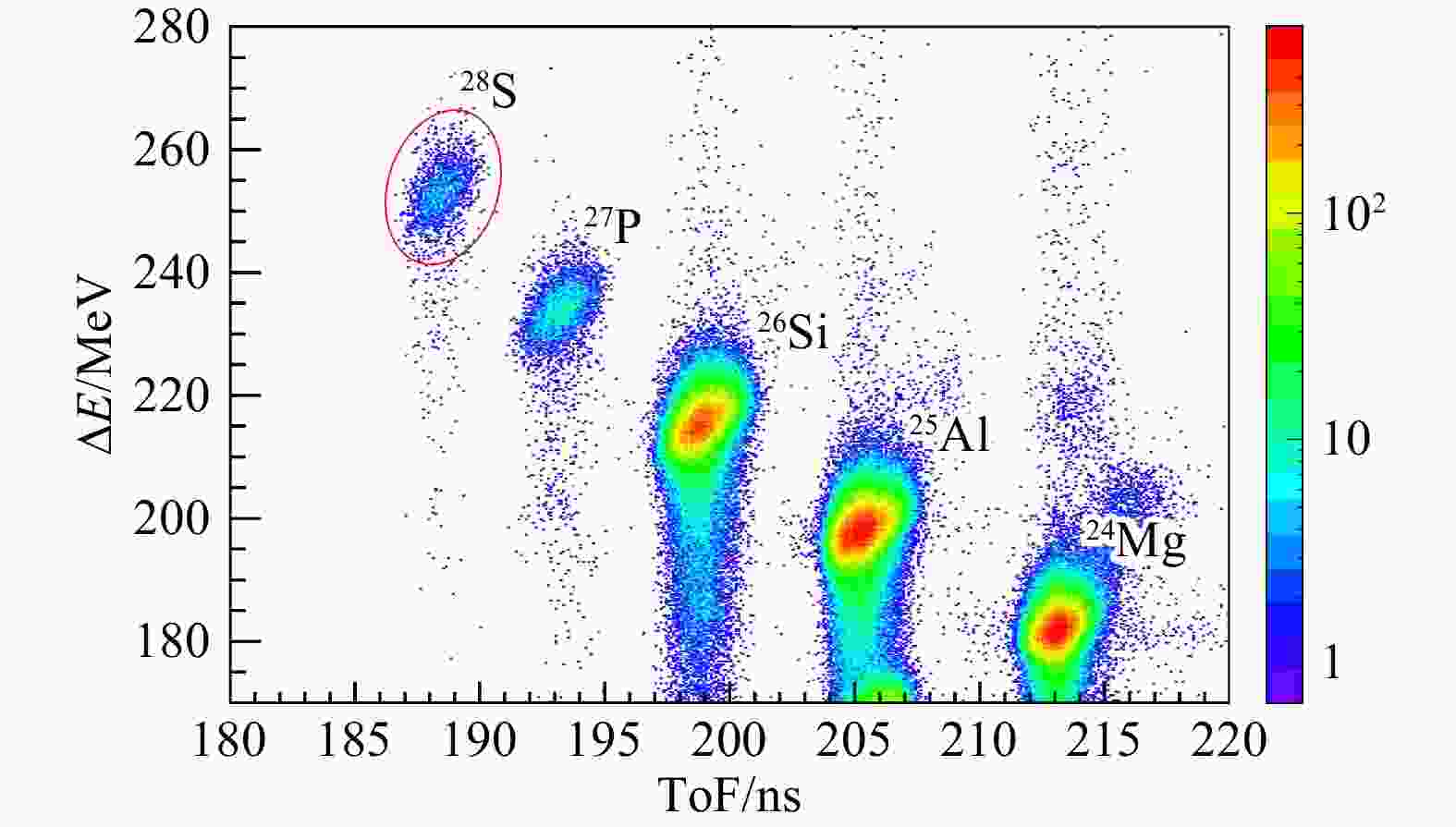
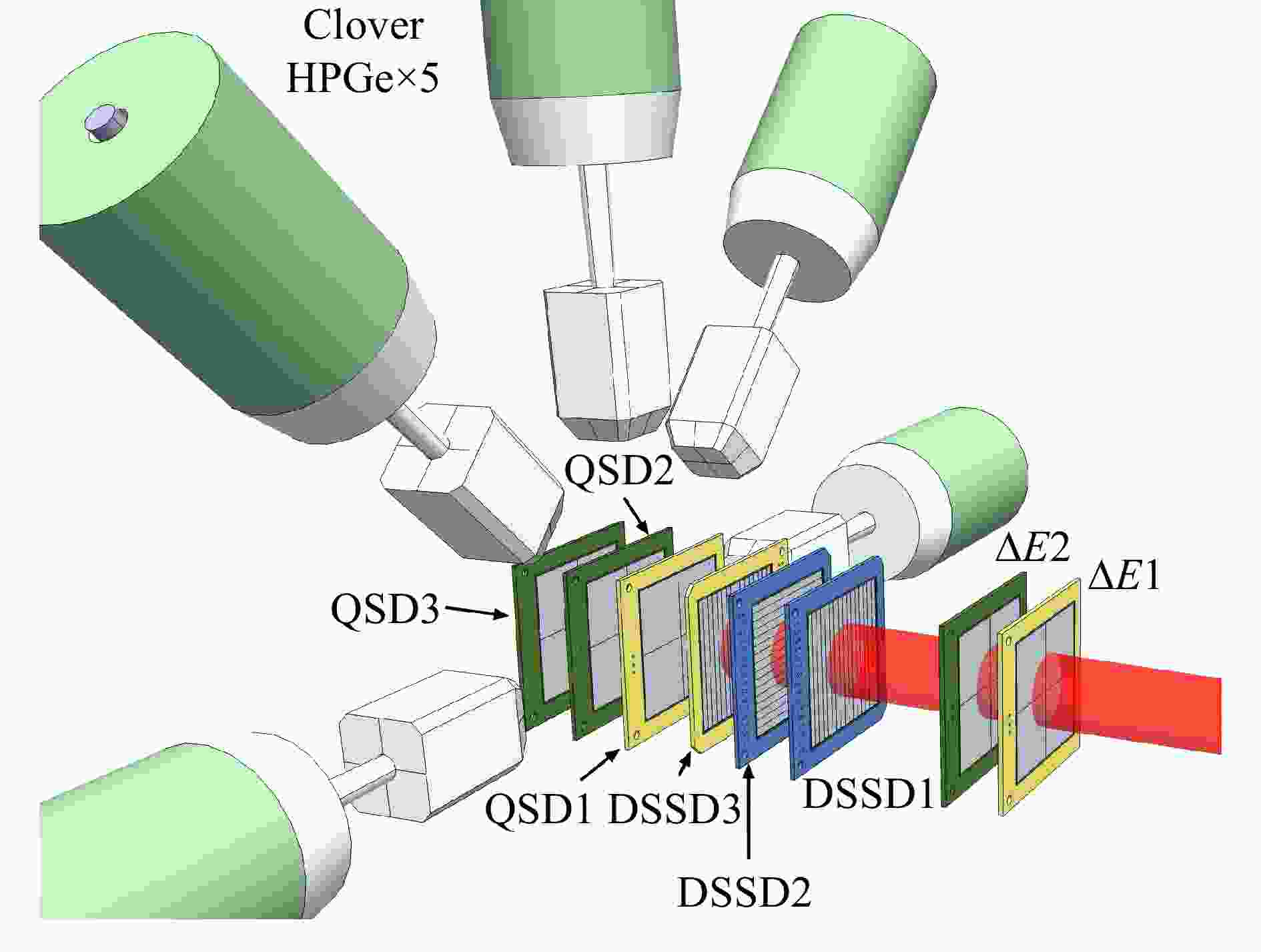
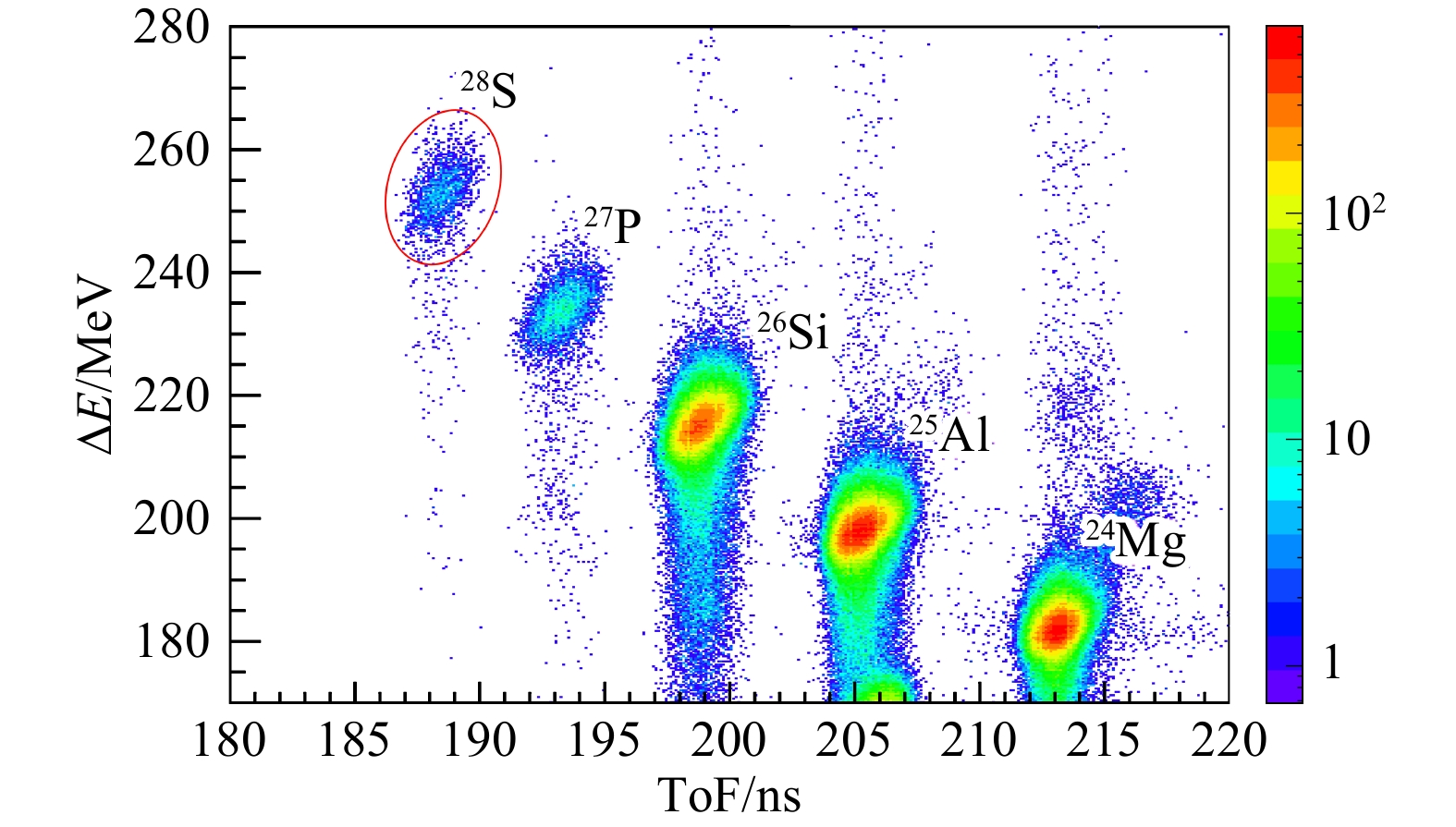
本次实验于2017年11月在兰州重离子加速器国家实验室(HIRFL)^[26]上完成，使用分离扇回旋加速器提供的流强约为100 enA、能量为80.6 MeV/u的$ \rm ^{32}S $初级束，通过轰击1 581 µm厚的⁹Be靶发生弹核碎裂反应来产生感兴趣的核素。反应后产生的碎片进入兰州放射性束流线(RIBLL-1)^[27]，使用磁钢度-能损-磁钢度($B_\rho$-ΔE-$ B_\rho $)的方式进行消色差选择和分离。实验所使用的探测技术在之前的文章中已有详细介绍^[28-29]。次级束在穿过两块位于束流线上的塑料闪烁体T1、T2和硅探测阵列中的两块大面积四分硅探测器ΔE 1、ΔE 2后，可以获得飞行时间ToF(Time-of-Flight)和能损ΔE的信息，将其组合后得到ΔE-ToF二维鉴别图谱。参考LISE++程序^[30]模拟的结果，对获得的ΔE-ToF图谱进行刻度，可以将目标核素²⁸S从图1中清晰准确地分辨出来。实验使用两块大面积四分硅探测器来测量次级束中离子的能损信息，通过对两块硅探测器获得的时间和能量信号进行多重符合，减少了在实验中探测器由于损伤等原因对获取的数据造成的影响，使目标核素²⁸S更加清晰可靠地与束流中其他污染核素区分开来。在最终得到的次级束中，²⁸S的平均纯度为0.11%，平均强度为1.2 pps(particles per second)。

图  1  (在线彩图)²⁸S次级束ΔE-ToF二维鉴别图谱

实验中所使用的探测阵列主要由双面硅条探测器DSSD(double-sided silicon strip detector)^[31]、大面积四分硅探测器QSD(quadrant silicon detector)^[32]和Clover型高纯锗探测器(Clover-type high-purity germanium detector)组成，图2是探测阵列的示意图。次级束中的目标核²⁸S，在穿过两块用于探测能损的大面积四分硅探测器(ΔE 1、ΔE 2)后，按照一定比例注入到厚度分别为142 μm的DSSD1、40 μm的DSSD2和304 μm的DSSD3中发生衰变并被探测。在硅探测阵列前方安置了3组共9块不同厚度的铝降能片，由步进电机驱动控制其厚度，来达到将目标核的能量下降到合适程度的目的。每块DSSD在正反两面各划分为16条，一面沿$ X $轴排列一面沿$ Y $轴排列，这使得组成的每一组$ X $-$ Y $像素格都可以被看做一个探测单元。所以，即使在此次实验中连续束模式的高注入率下，每个单元格内的注入事件率仍可以保持较低的水平，从而能够准确地获取到注入重离子和产生的带电粒子的位置信息和时间信息。再通过关联每一个注入事件和衰变事件的信号，能够将实验中位置和时间不合理的干扰信号筛除。顺着束流前进的方向，在DSSD3后设置了一块厚度为1 546 μm的大面积四分硅探测器QSD1。由于QSD1拥有足够的厚度，衰变产生的$ \beta $粒子在其中的能损足够大，能够被有效地探测。QSD1也兼具了探测穿过DSSD3的重离子和从DSSD3后表面逃逸的$ \beta $缓发粒子的功能。在由弹核碎裂反应产生的次级束中，存在着诸如¹H、²H、³H、⁴He等轻离子，其在探测范围约百兆电子伏特的ΔE探测器中能量损失太小而无法分辨。因此，在束流最下游设置了两块厚度约为300 μm的大面积四分硅探测器QSD2和QSD3，来对这些束流中的轻离子进行反符合测量，以减少它们带来的干扰。在硅探测器阵列的周围，环绕布置了5个Clover型的高纯锗探测器，用以探测原子核激发态退激产生的$ \gamma $射线。

图  2  (在线彩图)探测阵列示意图

整个探测阵列在连续束模式下工作，总计有效时间约17 h。使用³²S初级束轰击⁹Be靶发生弹核碎裂反应，然后通过RIBLL-1消色差分离选择次级束。在经过220 μm厚的铝降能片后，目标核²⁸S恰好阻止在三块双面硅条探测器中(DSSD1、DSSD2、DSSD3)。其中共48 108个目标核²⁸S，占注入重离子总数的83.4%，被阻停在DSSD3的前表面附近。由于DSSD2厚度仅有40 μm，对$ \beta $粒子的探测效率极低，并不适合用其与$ \gamma $射线进行符合，故数据分析主要以DSSD3上获取的信号为主。注入DSSD的²⁸S从基态发生$ \beta $衰变布居²⁸P的激发态，然后发射质子或发射$ \gamma $射线退激，退激过程中产生的$ \gamma $射线将被放置在硅探测阵列周围的高纯锗探测器同时测量。

选用⁶⁰Co、¹³⁷Cs、¹³³Ba和¹⁵²Eu四个标准放射源对高纯锗探测器进行能量刻度。同时，选取次级束流中有较高统计量且有可靠文献数据的²⁵Si、²⁶P和²²Al三个核作为内放射源，选用了它们在$ \beta $延迟$ \gamma $衰变中绝对强度较高的9个$ \gamma $跃迁，对$ \beta $延迟$ \gamma $射线的绝对探测效率进行了刻度^[29]。具体选用了四个来自²⁵Si的$ \beta $延迟$ \gamma $跃迁，其能量和相应的绝对强度为452 keV [18.4(42)%]、493 keV [15.3(34)%]、945 keV [10.4(23)%]和1 612 keV [15.2(32)%]^[33]，两个来自²⁶P的988 keV [5.7(3)%]和1 796 keV [58(3)%]的$ \beta $延迟$ \gamma $跃迁^[19]，以及三个来自²²Al的1 248.5(20) keV [38.2(69)%]、1 985.6(13) keV [31.1(54)%]、2 062.3(15) keV [34.1(58)%]的$ \beta $延迟$ \gamma $跃迁^[34]。

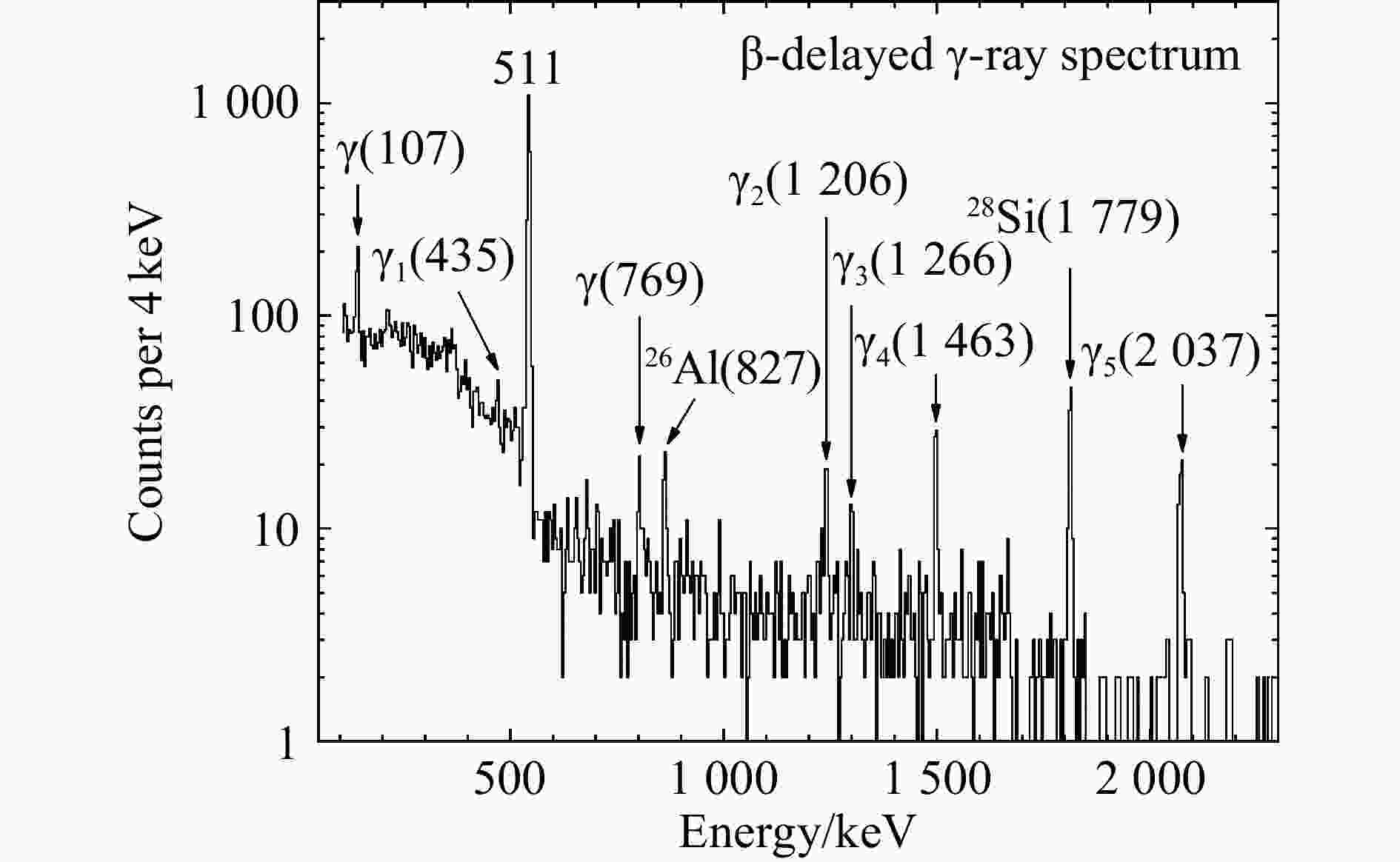
将高纯锗探测器探测到的$ \gamma $射线与DSSD3内²⁸S衰变发射的$ \beta $粒子进行符合，最终得到的$ \beta $延迟$ \gamma $射线谱如图3所示，这是首次获得的²⁸S的$ \beta $延迟$ \gamma $射线谱。图中共有10个$ \gamma $峰可以被清晰地分辨，每个峰的中心能量值标注在上方，单位为keV。其中，三个没有以$ \gamma $符号标记的峰分别是已知的能量为511 keV的正负电子湮灭峰以及两个污染$ \gamma $峰。从图1中可以看见，在通过RIBLL-1分离后的次级束中，同时存在着²⁷P、²⁶Si、²⁵Al、²⁴Mg等核素。其中统计量高过目标核²⁸S百倍的²⁶Si，在发生$ \beta $衰变布居²⁶Al的1 057.7 keV激发能级后，退激产生了能量为827 keV的$ \gamma $射线^[35]，该$ \gamma $跃迁表现为一个污染峰出现在谱中。而另一个具有很高统计的中心能量为1 779 keV的污染$ \gamma $峰，对应²⁸Si 1 779 keV的第一激发态退激到基态的$ \gamma $跃迁，它由目标核²⁸S衰变到子核²⁸P后，再次发生$ \beta $衰变到²⁸Si后产生^[36]。

图  3  ²⁸S $ \beta $延迟$ \gamma $射线谱

图3中以$ \gamma $符号标注的中心能量值分别为107, 435, 769, 1 206, 1 266, 1 463, 2 037 keV的$ \gamma $峰对应7条$ \gamma $射线，由衰变子核²⁸P的激发态退激产生。由于统计数量较少，且每个Clover型高纯锗探测器的绝对探测效率极低，并没有进行$ \gamma $-$ \gamma $的符合分析。但是发生$ \beta $延迟$ \gamma $衰变的质子束缚态，通常是能量相对较低的激发态，且Clover型高纯锗探测器具有极高的分辨率，每条$ \gamma $射线的跃迁过程可以参考已知的²⁸P的能级纲图得到^[36]。确定各个$ \gamma $射线的发射能级后，再对比理论计算结果，得到能量为107(2) keV和769(2) keV的$ \gamma $射线由级联发射产生。107 keV的$ \gamma $射线由²⁸P的107(2) keV第一激发态退激到基态产生，769 keV的$ \gamma $射线由²⁸P的876(3) keV第二激发态退激到107(2) keV的第一激发态产生。$ \gamma_{1-5} $是五条$ \beta $延迟$ \gamma $射线，均由²⁸S发生$ \beta $延迟衰变布居²⁸P的激发态后退激产生。

各个$ \gamma $跃迁的绝对强度$ I_{\gamma} $可以用下式算出：

式中$ N_{\gamma} $为对应$ \beta $延迟$ \gamma $射线的统计数量。$ N_{\rm impl} $是注入DSSD3的重离子总数。$ \varepsilon_{\beta\gamma} $则是$ \beta $延迟$ \gamma $射线的绝对探测效率，该绝对探测效率等同于双面硅条探测器对$ \beta $粒子的探测效率乘以高纯锗探测器对$ \gamma $射线的绝对探测效率。在整个分析过程中，能量和绝对强度的误差均是按照标准不确定度传递公式，考虑了由分析程序在拟合中给出的统计误差以及整个实验过程中所包含的系统误差，最终给出了对应的结果。所有$ \beta $延迟$ \gamma $射线的能量($ E_{\gamma} $)、绝对强度($ I_{\gamma} $)和$ \gamma $跃迁的初末态能级，以及对应的误差范围均列在表1中。

提取实验测量得到的$ \gamma $射线的能量、绝对强度和初末态能级等信息，可以获得²⁸P衰变布居能级的能量和$ \beta $衰变分支比，其数据结果见表2。²⁸S衰变布居到²⁸P的2 144(3) keV激发能级的$ \beta $衰变分支比为26.1 (45)%，由该能级退激产生的能量为1 266 和2 037 keV的两个$ \gamma $跃迁的绝对强度相加给出。该激发能级的能量值，可以选择2 037 和107 keV $ \gamma $跃迁的组合或是1 266 , 769和107 keV $ \gamma $跃迁的组合给出，在考虑相对强度的大小和级联发射关系后，选择第一个组合以相加的方式计算得到2 144(3) keV的结果。²⁸S衰变布居到²⁸P的1 570(3) keV激发能级的$ \beta $衰变分支比为20.5 (31)%，由1 463 keV的$ \gamma $跃迁给出。该激发能级的能量值则是通过1 463 和107 keV的$ \gamma $跃迁计算所得。能量为435 和1 206 keV的两条$ \gamma $射线由²⁸S衰变布居到²⁸P的1 313(3) keV激发能级退激产生，故考虑这两条$ \gamma $射线的绝对强度，得到该激发能级的分支比为17.6 (16)%，激发能级的能量值则是由1 206 和107 keV的$ \gamma $跃迁计算给出。选择1 206 而非435 keV的$ \gamma $跃迁进行计算，同样是考虑了其较简单的退激过程，并且都同样参考了²⁸P的107 keV第一激发态的能量值。分析结果给出的所有激发能级的能量和分支比的误差范围，均按照标准不确定度传递公式传递得到。对比此结果中的²⁸P各能级的能量值与表2中Nuclear Data Sheets(NDS)^[36]给出的结果，其数值在误差范围内是一致的。

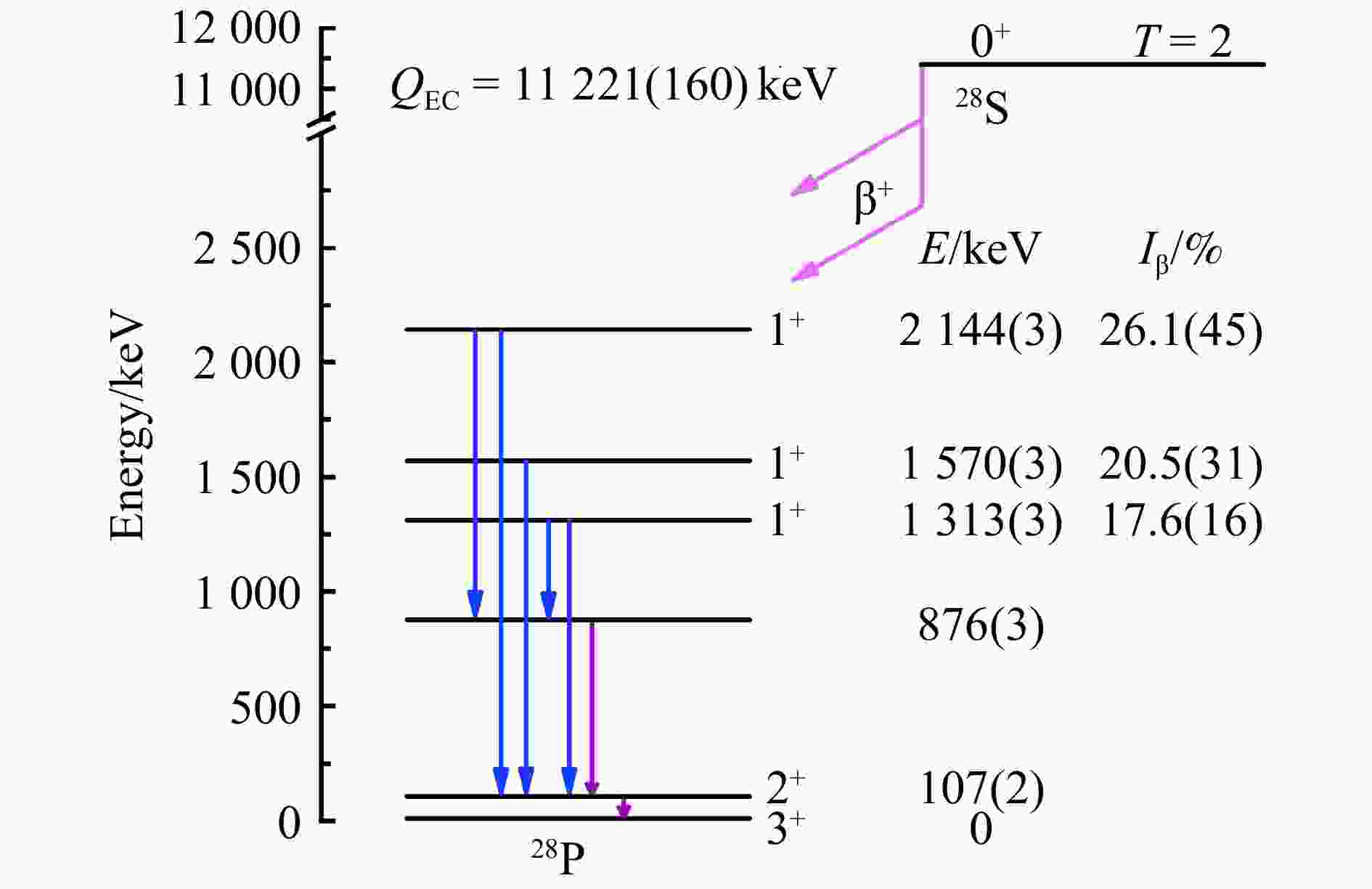
依据壳模型计算结果，位于$ 0^+ $基态的²⁸S发生$ \beta $延迟$ \gamma $衰变后，将主要布居到²⁸P的$ 1^+ $激发态上。通过所获得的数据结果，最终推得²⁸S发生$ \beta $延迟$ \gamma $衰变并布居到²⁸P低激发态的部分衰变纲图如图4所示。图中，5条$ \beta $延迟$ \gamma $射线用蓝色箭头线表示，2条级联发射的$ \gamma $射线则用紫色箭头线表示，$ Q_{\mathrm{EC}} \!=\! 11\,221(160) $ keV的结果参考AME2016^[37]给出。

图  4  (在线彩图)²⁸S部分衰变纲图

依托兰州重离子加速器国家实验室的兰州放射性束流线，完成了近质子滴线核²⁸S的$ \beta $延迟$ \gamma $衰变研究。本次实验使用由QSD及DSSD组成的硅探测阵列和Clover型高纯锗探测器，在连续束的高注入条件下，准确地对每个注入和衰变事件之间建立了关联。首次研究了²⁸S的$ \beta $延迟$ \gamma $衰变，获得并指认了5个来自²⁸S $ \beta $延迟衰变布居能级的$ \gamma $跃迁，并给出了这些来自质子束缚态的$ \gamma $跃迁的绝对强度。进一步得到了²⁸S $ \beta $衰变布居至²⁸P的激发态能级的信息，获得了3个²⁸S $ \beta $衰变到²⁸P激发态的分支比，其能量和对应分支比分别为1 313(3) keV [17.6(16)%]、1 570(3) keV [20.5(31)%]和2 144(3) keV [26.1(45)%]。最后，根据实验获得的数据结果给出了²⁸S的部分$ \beta $衰变纲图。此次实验的结果与之前的研究工作符合很好并得到了全新的内容，在未来可以进一步和理论计算结果相结合，探索²⁸S与其镜像核²⁸Mg之间的同位旋对称性破缺现象，构建更加完整的²⁸S的衰变纲图。